A Novel Tropical Cyclone Size Estimation Model Based on a Convolutional Neural Network Using Geostationary Satellite Imagery
Abstract
1. Introduction
2. Data and Model Design
2.1. Data
2.2. Convolutional Neural Network (CNN)
2.3. Model Optimization
2.4. Gradient-Weighted Class Activation Mapping
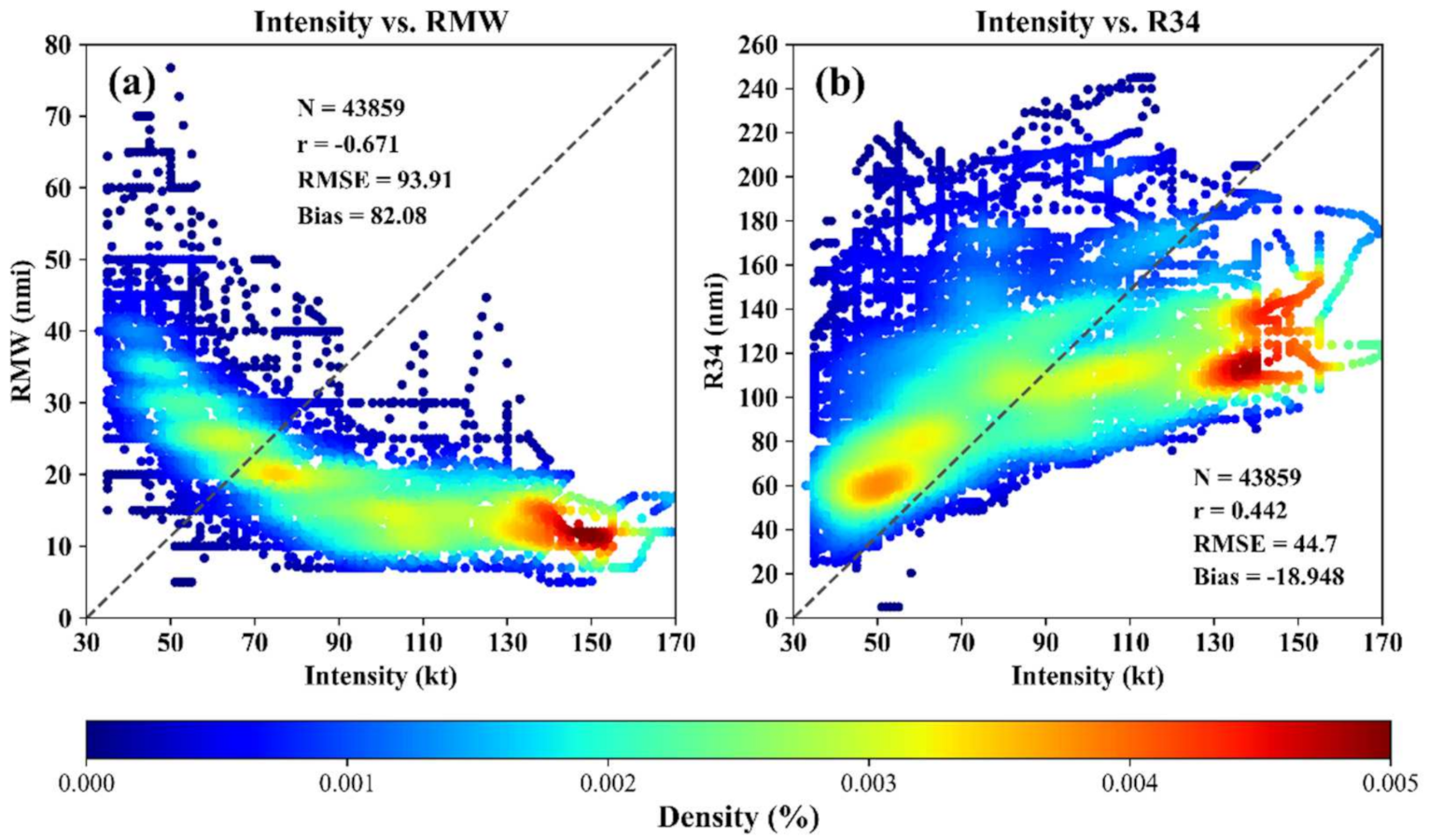
3. Results and Discussion
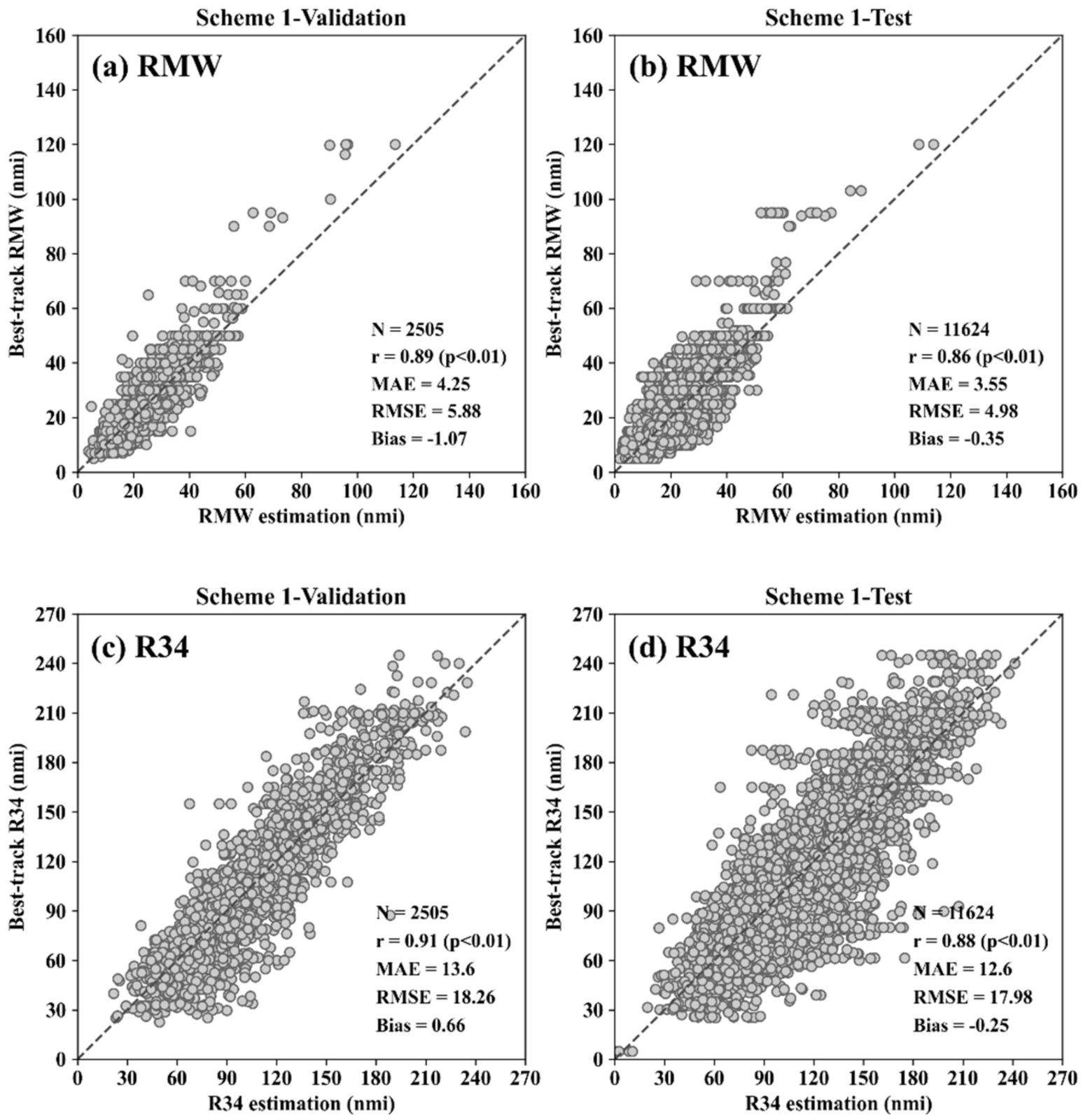
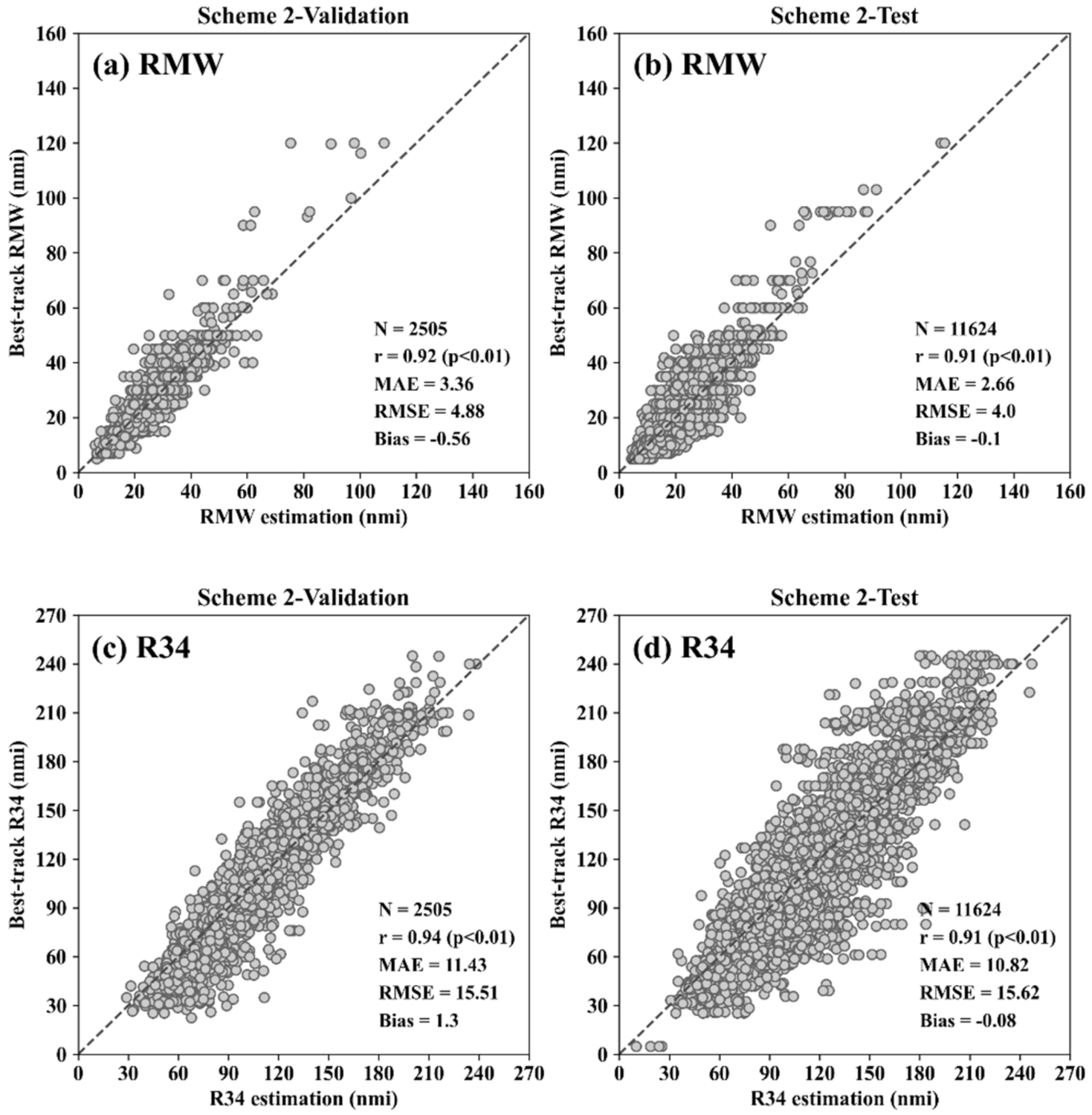
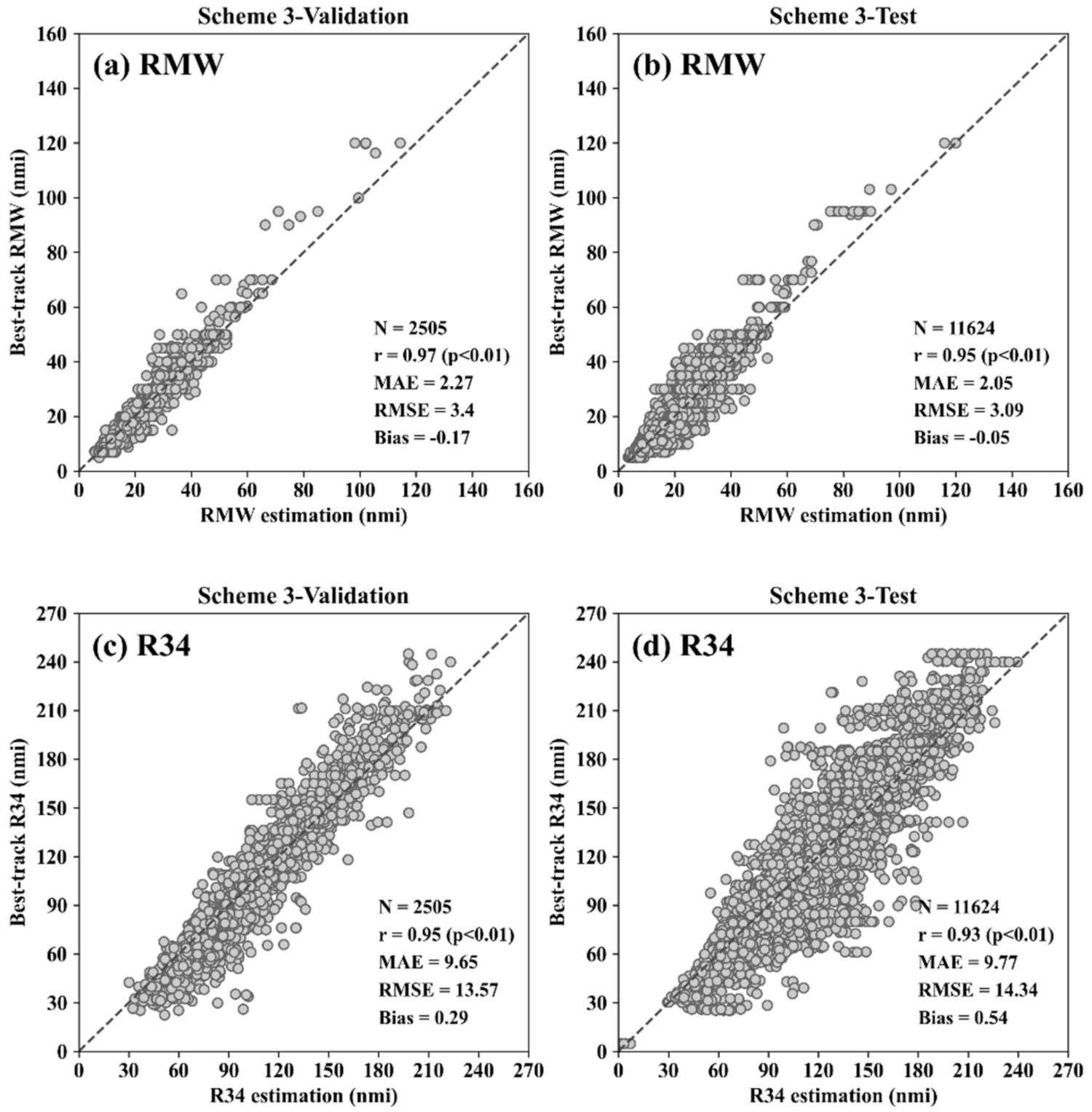
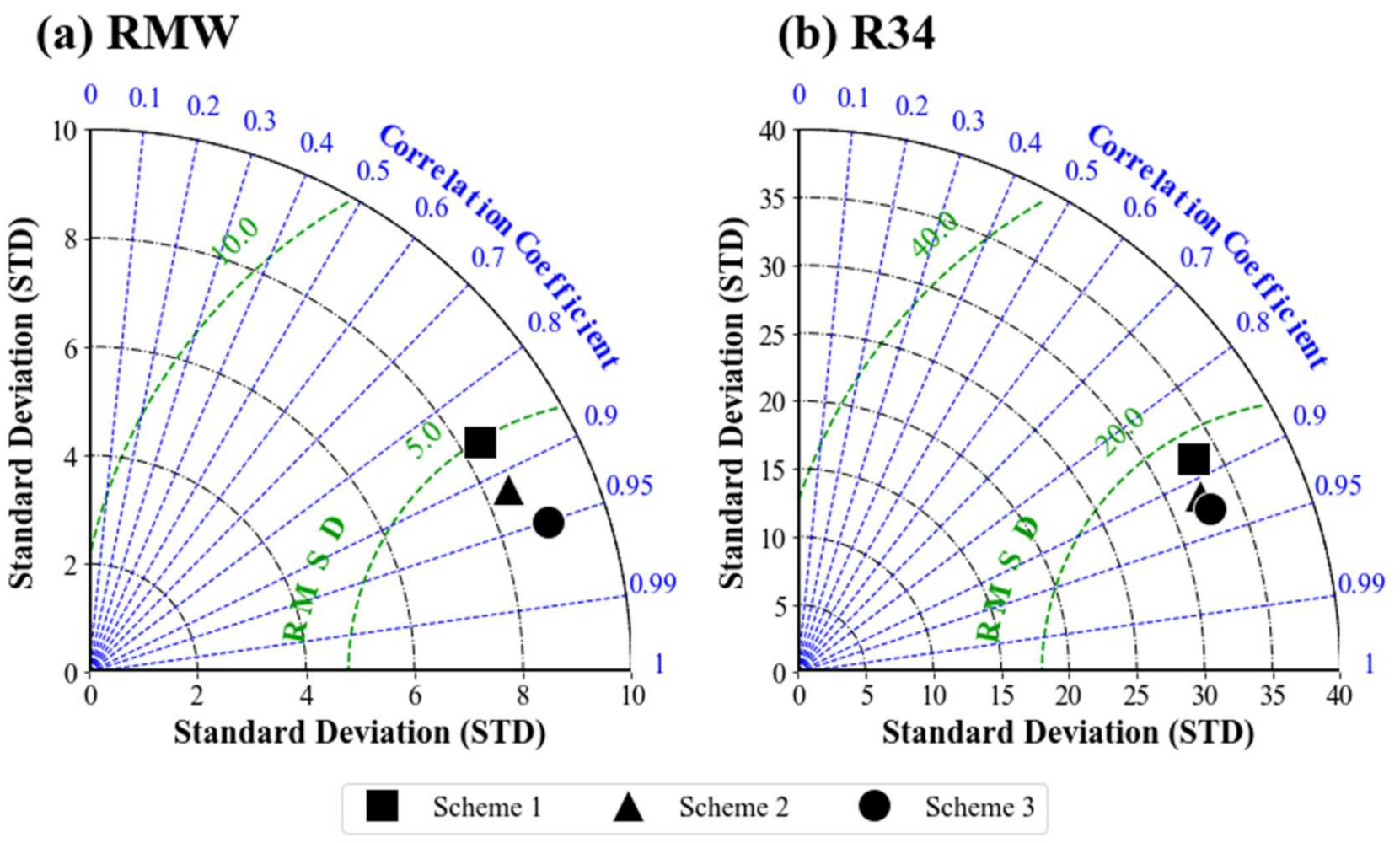
3.1. Performance of the Three CNN Schemes
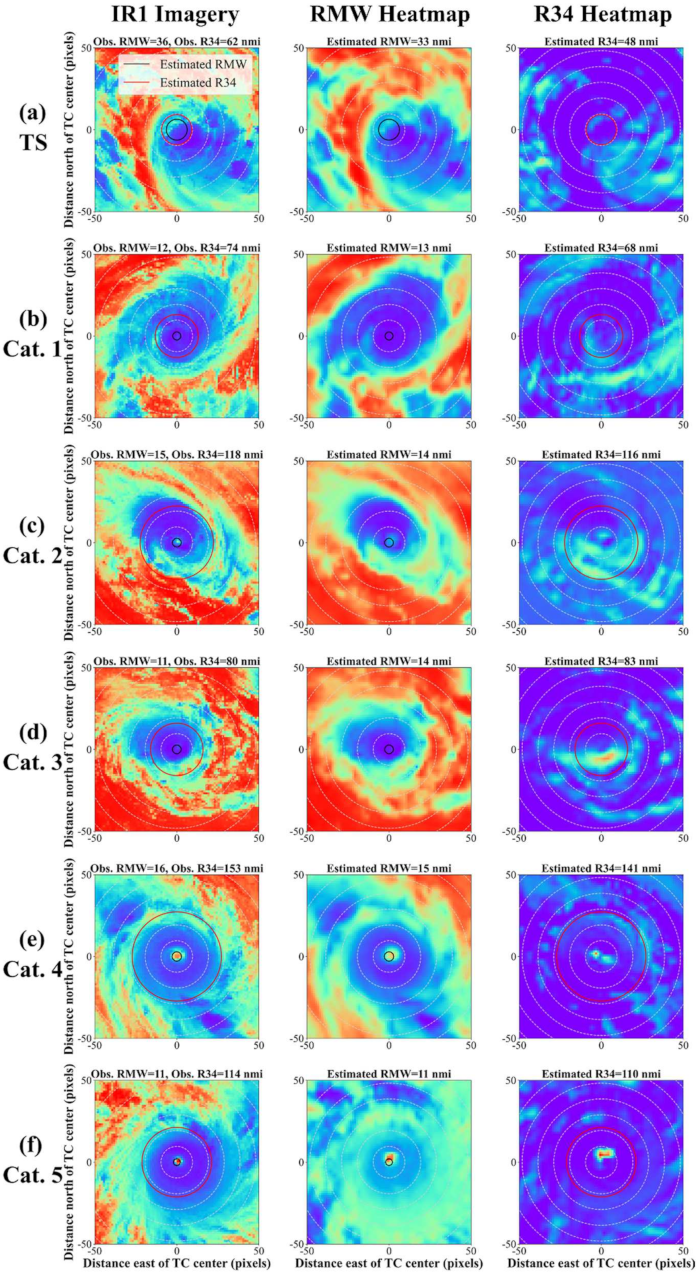
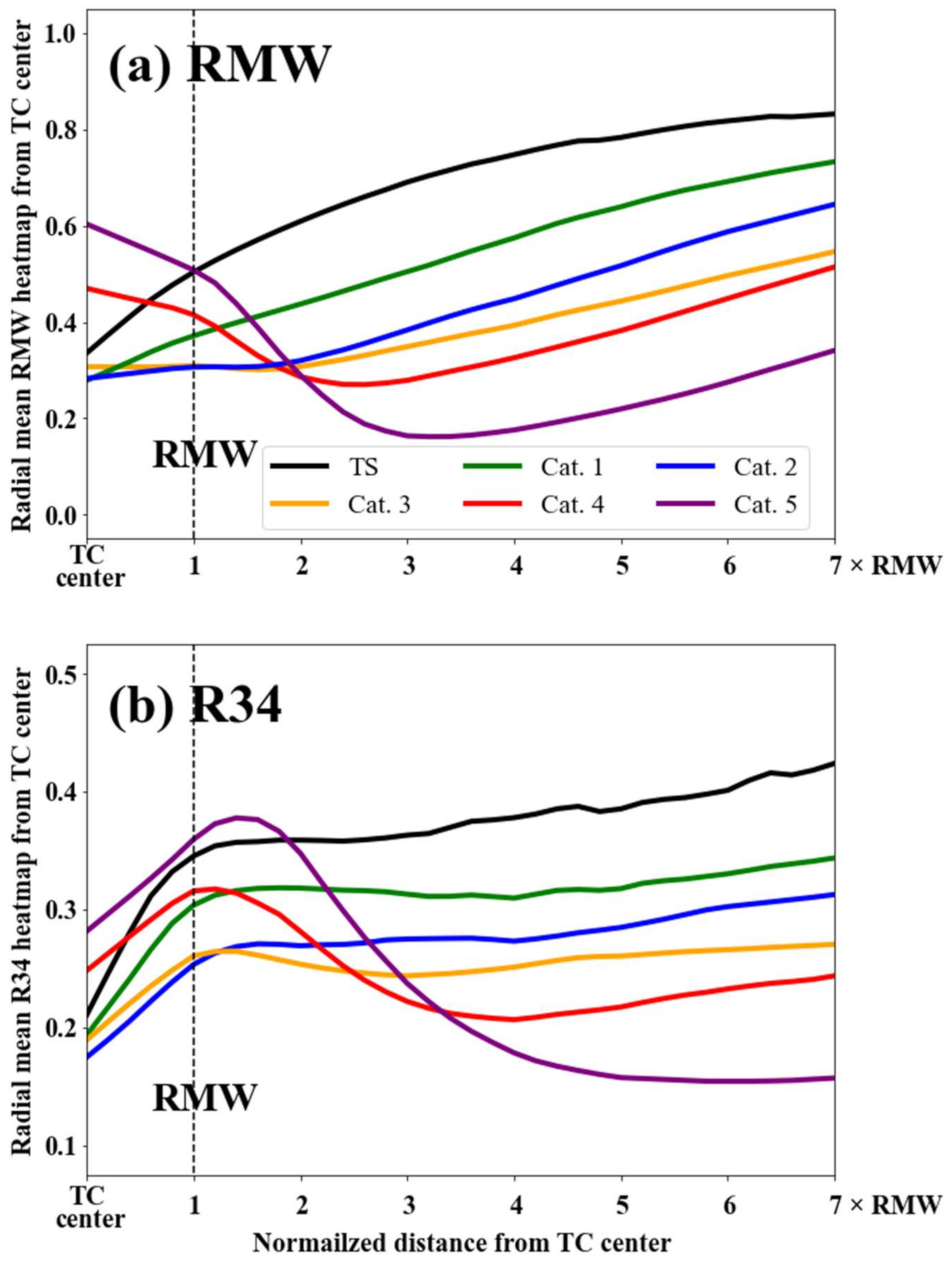
3.2. Class Activation Mapping
3.3. Sensitivity Test of Dropout and Pooling Layers
4. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chavas, D.R.; Lin, N.; Emanuel, K. A model for the complete radial structure of the tropical cyclone wind field. Part I: Comparison with observed structure. J. Atmos. Sci. 2015, 72, 3647–3662. [Google Scholar] [CrossRef]
- Kimball, S.K.; Mulekar, M.S. A 15-year climatology of North Atlantic tropical cyclones. Part I: Size parameters. J. Clim. 2004, 17, 3555–3575. [Google Scholar] [CrossRef]
- Moyer, A.C.; Evans, J.L.; Powell, M. Comparison of observed gale radius statistics. Meteorol. Atmos. Phys. 2007, 97, 41–55. [Google Scholar] [CrossRef]
- Merrill, R.T. A comparison of large and small tropical cyclones. Mon. Weather Rev. 1984, 112, 1408–1418. [Google Scholar] [CrossRef]
- Weatherford, C.L.; Gray, W.M. Typhoon structure as revealed by aircraft reconnaissance. Part I: Data analysis and climatology. Mon. Weather Rev. 1988, 116, 1032–1043. [Google Scholar] [CrossRef]
- Maclay, K.S.; DeMaria, M.; Vonder Haar, T.H. Tropical cyclone inner-core kinetic energy evolution. Mon. Weather Rev. 2008, 136, 4882–4898. [Google Scholar] [CrossRef]
- Knaff, J.A.; Sampson, C.R.; DeMaria, M.; Marchok, T.P.; Gross, J.M.; McAdie, C.J. Statistical tropical cyclone wind radii prediction using climatology and persistence. Weather Forecast. 2007, 22, 781–791. [Google Scholar] [CrossRef]
- Knaff, J.A.; Sampson, C.R. After a decade are Atlantic tropical cyclone gale force wind radii forecasts now skillful? Weather Forecast. 2015, 30, 702–709. [Google Scholar] [CrossRef]
- Chan, K.T.; Chan, J.C. Impacts of initial vortex size and planetary vorticity on tropical cyclone size. Q. J. R. Meteorol. Soc. 2014, 140, 2235–2248. [Google Scholar] [CrossRef]
- Chan, K.T.; Chan, J.C. Global climatology of tropical cyclone size as inferred from QuikSCAT data. Int. J. Clim. 2015, 35, 4843–4848. [Google Scholar] [CrossRef]
- Wu, L.; Tian, W.; Liu, Q.; Cao, J.; Knaff, J.A. Implications of the observed relationship between tropical cyclone size and intensity over the western North Pacific. J. Clim. 2015, 28, 9501–9506. [Google Scholar] [CrossRef]
- Brennan, M.J.; Hennon, C.C.; Knabb, R.D. The operational use of QuikSCAT ocean surface vector winds at the National Hurricane Center. Weather Forecast. 2009, 24, 621–645. [Google Scholar] [CrossRef]
- Demuth, J.L.; DeMaria, M.; Knaff, J.A.; Vonder Haar, T.H. Evaluation of Advanced Microwave Sounding Unit tropical-cyclone intensity and size estimation algorithms. J. Appl. Meteorol. 2004, 43, 282–296. [Google Scholar] [CrossRef]
- Demuth, J.L.; DeMaria, M.; Knaff, J.A. Improvement of Advanced Microwave Sounding Unit tropical cyclone intensity and size estimation algorithms. J. Appl. Meteorol. Climatol. 2006, 45, 1573–1581. [Google Scholar] [CrossRef]
- Hsu, S.A.; Babin, A. Estimating the radius of maximum wind via satellite during Hurricane Lili (2002) over the Gulf of Mexico. Natl. Weather Assoc. Electron. J. 2005, 6, 1–6. [Google Scholar]
- Mueller, K.J.; DeMaria, M.; Knaff, J.; Kossin, J.P.; Vonder Haar, T.H. Objective estimation of tropical cyclone wind structure from infrared satellite data. Weather Forecast. 2006, 21, 990–1005. [Google Scholar] [CrossRef]
- Kwon, M. Estimation and statistical characteristics of the radius of maximum wind of tropical cyclones using COMS IR imagery. Atmosphere 2012, 22, 473–481. (In Korean) [Google Scholar] [CrossRef]
- Lee, Y.K.; Kwon, M. An Estimation of the of Tropical Cyclone Size Using COMS Infrared Imagery. Atmosphere 2015, 25, 569–573. (In Korean) [Google Scholar] [CrossRef]
- Knaff, J.A.; Longmore, S.P.; DeMaria, R.T.; Molenar, D.A. Improved tropical-cyclone flight-level wind estimates using routine infrared satellite reconnaissance. J. Appl. Meteorol. Climatol. 2015, 54, 463–478. [Google Scholar] [CrossRef]
- Knaff, J.A.; Slocum, C.J.; Musgrave, K.D.; Sampson, C.R.; Strahl, B.R. Using routinely available information to estimate tropical cyclone wind structure. Mon. Weather Rev. 2016, 144, 1233–1247. [Google Scholar] [CrossRef]
- Olander, T.L.; Velden, C.S. ADT-Advanced Dvorak Technique User’s Guide; University of Wisconsin-Madison: Madison, WI, USA, 2015. [Google Scholar]
- Knaff, J.A.; Harper, B.A. KN1: Tropical cyclone surface wind structure and wind-pressure relationships. In Proceedings of the WMO Seventh International Workshop on Tropical Cyclones, La Reunion, France, 15–20 November 2010; p. 35. [Google Scholar]
- Kossin, J.P.; Knaff, J.A.; Berger, H.I.; Herndon, D.C.; Cram, T.A.; Velden, C.S.; Murnane, R.J.; Hawkins, J.D. Estimating hurricane wind structure in the absence of aircraft reconnaissance. Weather Forecast. 2007, 22, 89–101. [Google Scholar] [CrossRef]
- Bentamy, A.; Croize-Fillon, D.; Perigaud, C. Characterization of ASCAT measurements based on buoy and QuikSCAT wind vector observations. Ocean Sci. 2008, 4, 265–274. [Google Scholar] [CrossRef]
- Knaff, J.A.; DeMaria, M.; Molenar, D.A.; Sampson, C.R.; Seybold, M.G. An automated, objective, multiple-satellite-platform tropical cyclone surface wind analysis. J. Appl. Meteorol. Clim. 2011, 50, 2149–2166. [Google Scholar] [CrossRef]
- Hong, S.; Shin, I. Wind speed retrieval based on sea surface roughness measurements from spaceborne microwave radiometers. J. Appl. Meteorol. Clim. 2013, 52, 507–516. [Google Scholar] [CrossRef]
- Muroi, C. Brief History and recent activities of RSMC Tokyo-Typhoon Centre. Trop. Cyclone Res. Rev. 2018, 7, 57–64. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. In Proceedings of the ICLR 2015, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Pradhan, R.; Aygun, R.S.; Maskey, M.; Ramachandran, R.; Cecil, D.J. Tropical cyclone intensity estimation using a deep convolutional neural network. IEEE Trans. Image Process. 2018, 27, 692–702. [Google Scholar] [CrossRef] [PubMed]
- Combinido, J.S.; Mendoza, J.R.; Aborot, J. A Convolutional Neural Network Approach for Estimating Tropical Cyclone Intensity Using Satellite-based Infrared Images. In Proceedings of the 2018 24th ICPR, Beijing, China, 20–24 August 2018. [Google Scholar]
- Wimmers, A.; Velden, C.; Cossuth, J.H. Using deep learning to estimate tropical cyclone intensity from satellite passive microwave imagery. Mon. Weather Rev. 2019, 147, 2261–2282. [Google Scholar] [CrossRef]
- Lee, J.; Im, J.; Cha, D.H.; Park, H.; Sim, S. Tropical cyclone intensity estimation using multi-dimensional convolutional neural networks from geostationary satellite data. Remote Sens. 2019, 12, 108. [Google Scholar] [CrossRef]
- Chen, B.F.; Chen, B.; Lin, H.T.; Elsberry, R.L. Estimating tropical cyclone intensity by satellite imagery utilizing convolutional neural networks. Weather Forecast. 2019, 34, 447–465. [Google Scholar]
- Tian, W.; Huang, W.; Yi, L.; Wu, L.; Wang, C. A CNN-Based Hybrid Model for Tropical Cyclone Intensity Estimation in Meteorological Industry. IEEE Access 2020, 8, 59158–59168. [Google Scholar] [CrossRef]
- Wang, X.; Wang, W.; Yan, B. Tropical Cyclone Intensity Change Prediction Based on Surrounding Environmental Conditions with Deep Learning. Water 2020, 12, 2685. [Google Scholar] [CrossRef]
- Wang, C.; Xu, Q.; Li, X.; Cheng, Y. CNN-Based Tropical Cyclone Track Forecasting from Satellite Infrared Images. In IGARSS 2020—2020 IEEE International Geoscience and Remote Sensing Symposium; IEEE: Piscataway, NJ, USA, 2020; pp. 5811–5814. [Google Scholar]
- Ou, M.L.; Won, J.-K. Introduction to the COMS Program and its application to meteorological services of Korea. In Proceedings of the 2005 EUMETSAT Meteorological Satellite Conference, Dubrovnik, Croatia, 19–23 September 2005; pp. 19–23. [Google Scholar]
- Schmetz, J.; Tjemkes, S.A.; Gube, M.; Van de Berg, L. Monitoring deep convection and convective overshooting with METEOSAT. Adv. Space Res. 1997, 19, 433–441. [Google Scholar] [CrossRef]
- Velden, C.S.; Hayden, C.M.; Nieman, S.J.W.; Paul Menzel, W.; Wanzong, S.; Goerss, J.S. Upper-tropospheric winds derived from geostationary satellite water vapor observations. Bull. Am. Meteorol. Soc. 1997, 78, 173–195. [Google Scholar] [CrossRef][Green Version]
- Ralph, F.M.; Neiman, P.J.; Wick, G.A. Satellite and CALJET aircraft observations of atmospheric rivers over the eastern North Pacific Ocean during the winter of 1997/98. Mon. Weather Rev. 2004, 132, 1721–1745. [Google Scholar] [CrossRef]
- Durry, G.; Amarouche, N.; Zéninari, V.; Parvitte, B.; Lebarbu, T.; Ovarlez, J. In situ sensing of the middle atmosphere with balloonborne near-infrared laser diodes. Spectrochim. Acta Part A 2004, 60, 3371–3379. [Google Scholar] [CrossRef]
- Kruk, M.C.; Knapp, K.R.; Levinson, D.H.; Diamond, H.J.; Kossin, J.P. An Overview of the International Best Track Archive for Climate Stewardship (IBTrACS). In Proceedings of the 21st Conference on Climate Variability and Change, Phoenix, AZ, USA, 11–15 January 2010. 7B.1. [Google Scholar]
- Knapp, K.R.; Kruk, M.C.; Levinson, D.H.; Diamond, H.J.; Neumann, C.J. The International Best Track Archive for Climate Stewardship (IBTrACS). Bull. Am. Meteorol. Soc. 2010, 91, 363–376. [Google Scholar] [CrossRef]
- Glorot, X.; Bengio, Y. Understanding the difficulty of training deep feedforward neural networks. In Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics, Sardinia, Italy, 13–15 May 2010; pp. 249–256. [Google Scholar]
- Tensorflow. Available online: https://www.tensorflow.org/api_docs/python/tf/keras/initializers/GlorotUniform/ (accessed on 15 December 2021).
- Arnekvist, I.; Carvalho, J.F.; Kragic, D.; Stork, J.A. The effect of target normalization and momentum on dying relu. arXiv 2020, arXiv:2005.06195. [Google Scholar]
- Abdulnabi, A.H.; Wang, G.; Lu, J.; Jia, K. Multi-task CNN model for attribute prediction. IEEE Trans. Multimed. 2015, 17, 1949–1959. [Google Scholar] [CrossRef]
- Caruana, R. Multitask learning. Mach. Learn. 1997, 28, 41–75. [Google Scholar] [CrossRef]
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M.; et al. Tensorflow: A system for large-scale machine learning. In Proceedings of the 12th {USENIX} Symposium on Operating Systems Design and Implementation (OSDI’16), Savannah, GA, USA, 2–4 November 2016; pp. 265–283. [Google Scholar]
- Li, L.; Jamieson, K.; DeSalvo, G.; Rostamizadeh, A.; Talwalkar, A. Hyperband: A novel bandit-based approach to hyperparameter optimization. J. Mach. Learn. Res. 2017, 18, 6765–6816. [Google Scholar]
- LeCun, Y.; Boser, B.; Denker, J.S.; Henderson, D.; Howard, R.E.; Hubbard, W.; Jackel, L.D. Handwritten digit recognition with a back-propagation network. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 1989; pp. 396–404. [Google Scholar]
- Keras Tuner. Available online: https://keras-team.github.io/keras-tuner/ (accessed on 30 October 2021).
- Nair, V.; Hinton, G.E. Rectified linear units improve restricted boltzmann machines. In Proceedings of the 27th International Conference on Machine Learning (ICML), Haifa, Israel, 21–24 June 2010. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2015, arXiv:1412.6980. [Google Scholar]
- Cauchy, A. Méthode générale pour la résolution des systemes d’équations simultanées. Comp. Rend. Sci. 1847, 25, 536–538. [Google Scholar]
- Polyak, B.T. Some methods of speeding up the convergence of iteration methods. USSR Comput. Math. Math. Phys. 1964, 4, 1–17. [Google Scholar] [CrossRef]
- Nemirovski, A.; Juditsky, A.; Lan, G.; Shapiro, A. Robust stochastic approximation approach to stochastic programming. SIAM J. Optim. 2009, 19, 1574–1609. [Google Scholar] [CrossRef]
- Duchi, J.; Hazan, E.; Singer, Y. Adaptive subgradient methods for online learning and stochastic optimization. J. Mach. Learn. Res. 2011, 12, 2121–2159. [Google Scholar]
- Zeiler, M.D. Adadelta: An adaptive learning rate method. arXiv 2012, arXiv:1212.5701. [Google Scholar]
- Hinton, G.E. A practical guide to training restricted Boltzmann machines. In Neural Networks: Tricks of the Trade; Springer: Berlin/Heidelberg, Germany, 2012; pp. 599–619. [Google Scholar]
- Sutskever, I.; Martens, J.; Dahl, G.; Hinton, G. On the importance of initialization and momentum in deep learning. In Proceedings of the 30th International Conference on Machine Learning, Atlanta, GA, USA, 16–21 June 2013; pp. 1139–1147. [Google Scholar]
- Dozat, T. Incorporating Nesterov Momentum into Adam. In Proceedings of the 4th International Conference on Learning Prepresentations (ICLR), San Juan, Puerto Rico, 2–4 May 2016. [Google Scholar]
- Raskutti, G.; Wainwright, M.J.; Yu, B. Early stopping and non-parametric regression: An optimal data-dependent stopping rule. J. Mach. Learn. Res. 2014, 15, 335–366. [Google Scholar]
- Chi, J.; Li, X.; Wang, H.; Gao, D.; Gerstoft, P. Sound source ranging using a feed-forward neural network trained with fitting-based early stopping. J. Acoust. Soc. Am. 2019, 146, EL258–EL264. [Google Scholar] [CrossRef]
- Selvaraju, R.R.; Cogswell, M.; Das, A.; Vedantam, R.; Parikh, D.; Batra, D. Grad-cam: Visual explanations from deep networks via gradient-based localization. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 618–626. [Google Scholar]
- Zhou, B.; Khosla, A.; Lapedriza, A.; Oliva, A.; Torralba, A. Learning deep features for discriminative localization. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 2921–2929. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Adv. Neural Inf. Process. Syst. 2012, 25, 1097–1105. [Google Scholar] [CrossRef]
- Zhang, P.; Ke, Y.; Zhang, Z.; Wang, M.; Li, P.; Zhang, S. Urban land use and land cover classification using novel deep learning models based on high spatial resolution satellite imagery. Sensors 2018, 18, 3717. [Google Scholar] [CrossRef] [PubMed]
- Reasor, P.D.; Montgomery, M.T.; Grasso, L.D. A new look at the problem of tropical cyclones in vertical shear flow: Vortex resiliency. J. Atmos. Sci. 2004, 61, 3–22. [Google Scholar] [CrossRef]
- Sampson, C.R.; Wittmann, P.A.; Tolman, H.L. Consistent tropical cyclone wind and wave forecasts for the US Navy. Weather Forecast. 2010, 25, 1293–1306. [Google Scholar] [CrossRef]
- Lazarus, S.M.; Wilson, S.T.; Splitt, M.E.; Zarillo, G.A. Evaluation of a wind-wave system for ensemble tropical cyclone wave forecasting. Part I: Winds. Weather Forecast. 2013, 28, 297–315. [Google Scholar] [CrossRef][Green Version]
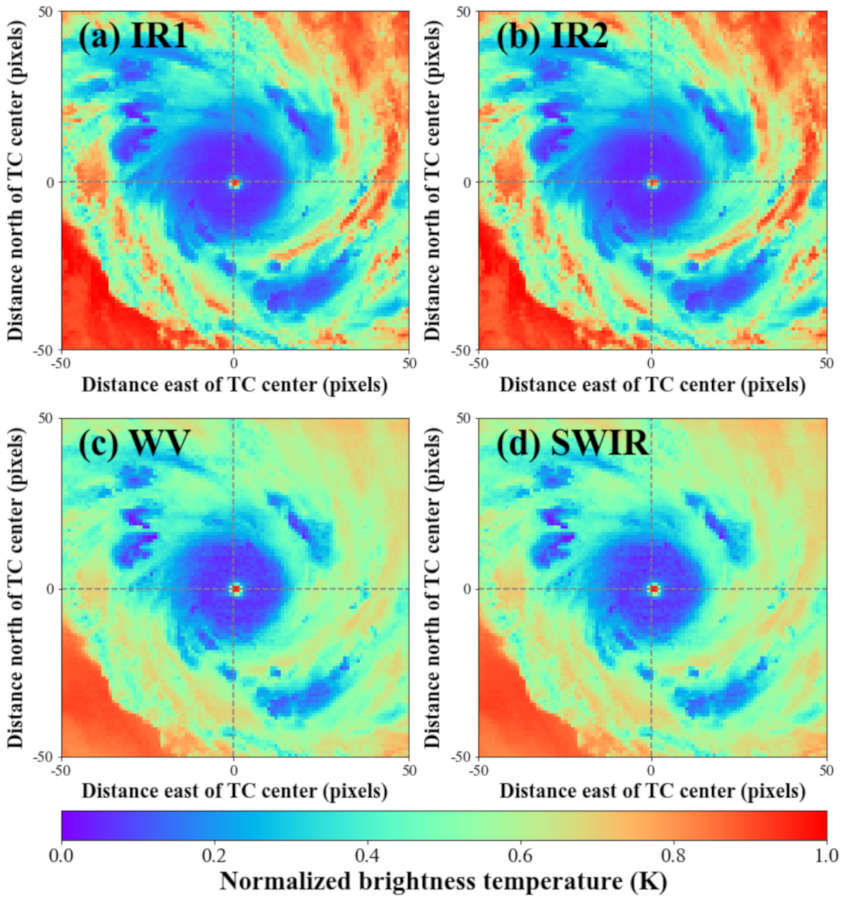
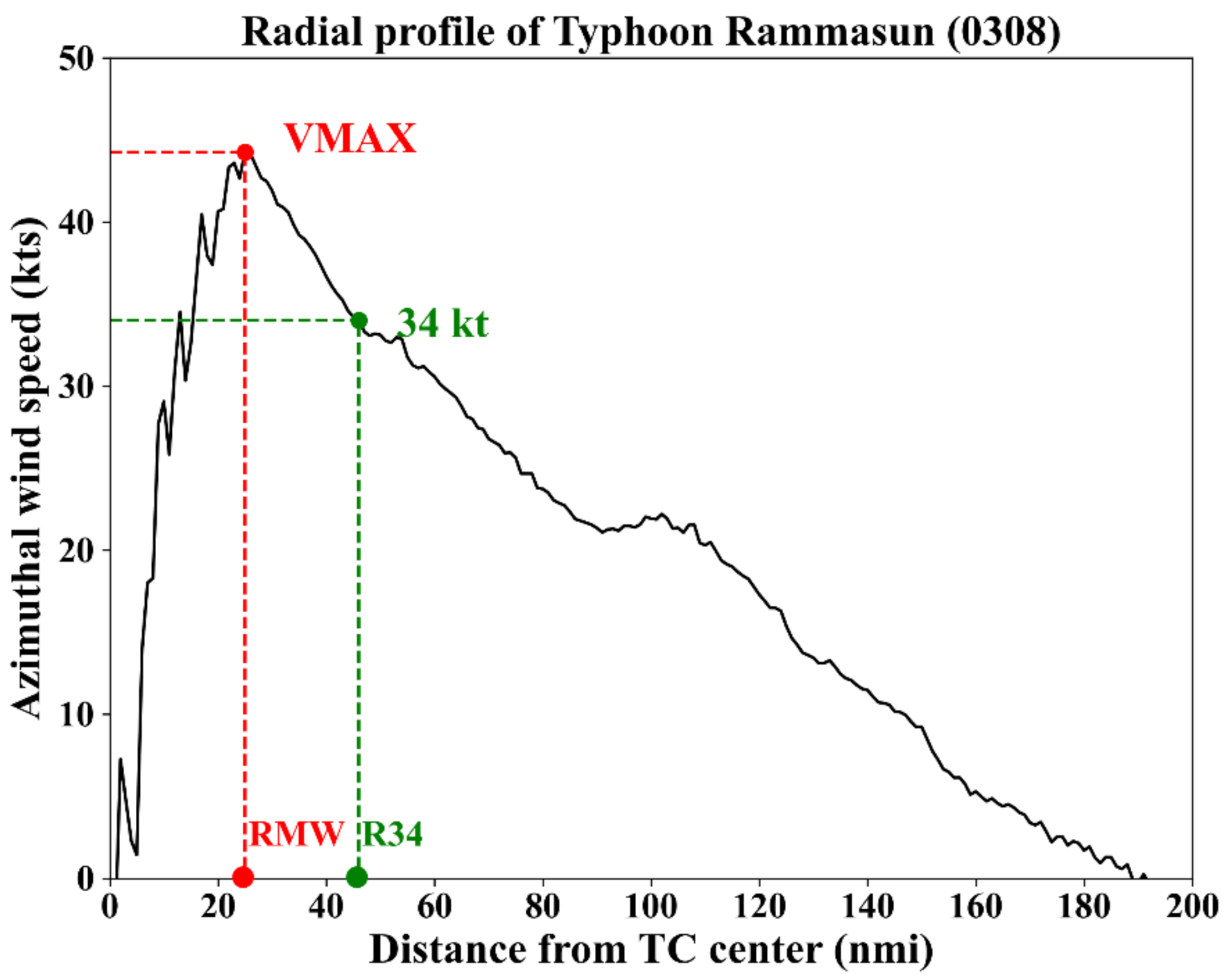
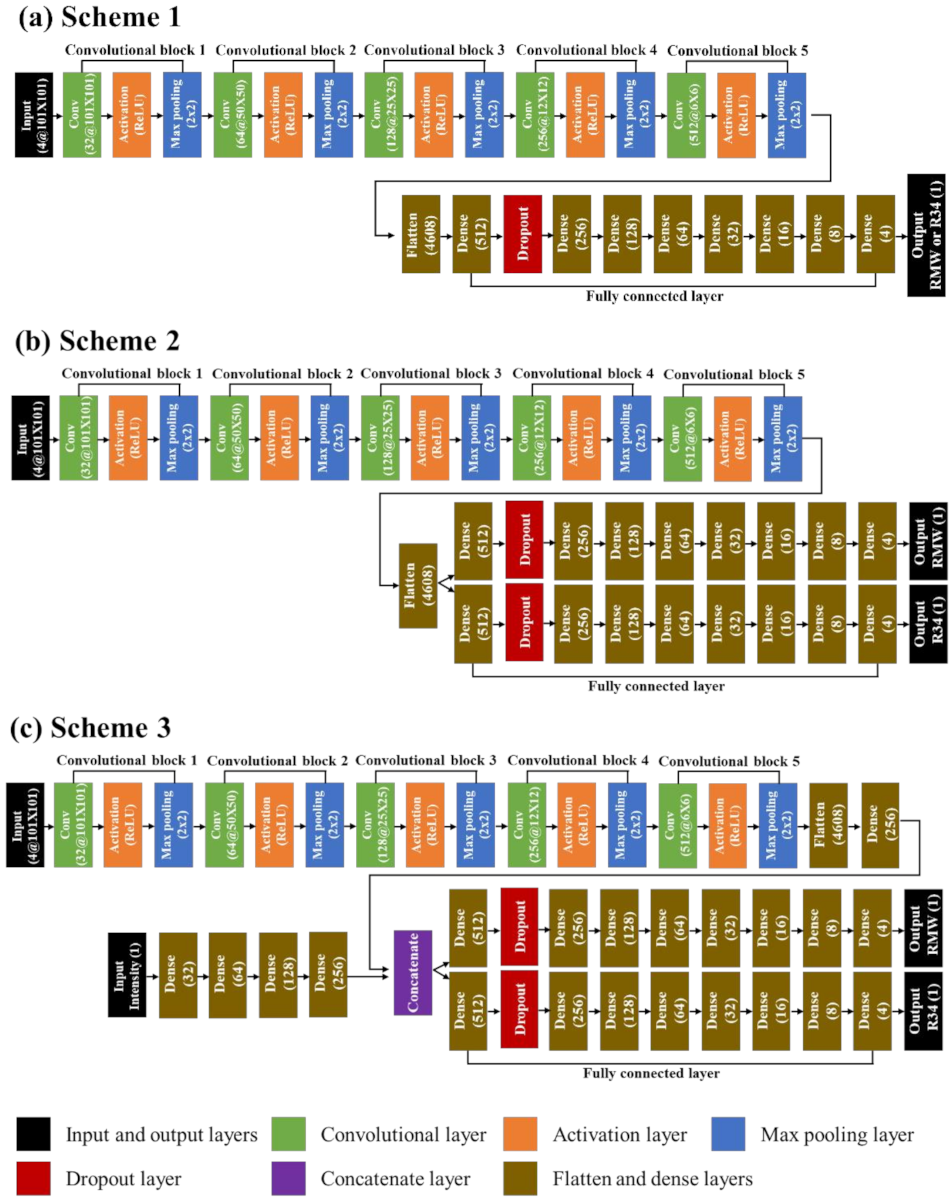
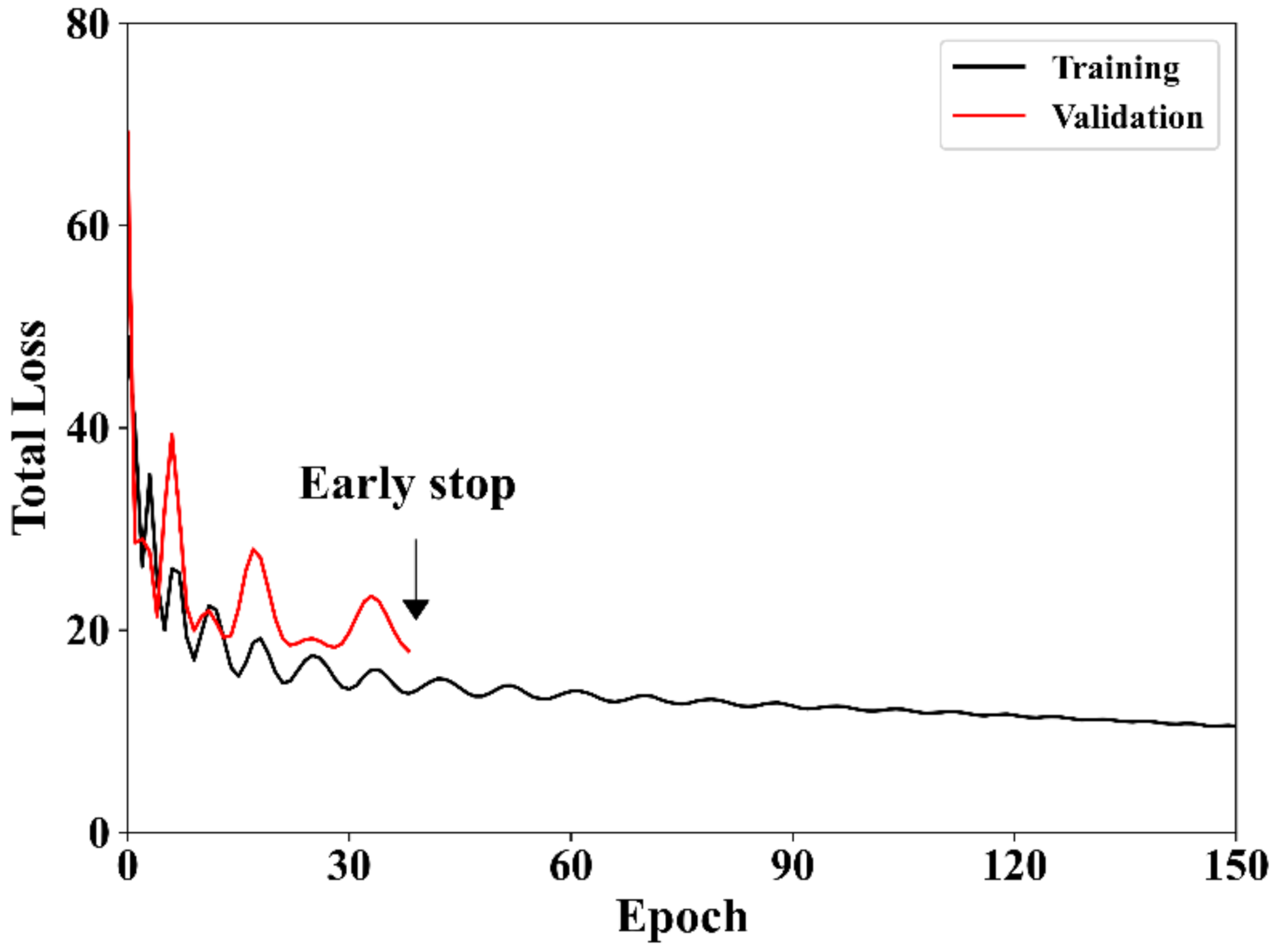
| Data Set | Sample Size |
|---|---|
| Training | 29,730 |
| Validation | 2505 |
| Testing | 11,624 |
| Total | 43,859 |
| Model | Layer | Size of the Selected Filter (Range) | Size of the Selected Dropout Rate (Range) | Size of the Selected Learning Rate (Range) |
|---|---|---|---|---|
| Scheme 1 (RMW) | Conv 1 | 7 (3, 5, 7, 9) | – | – |
| Conv 2 | 9 (3, 5, 7, 9) | – | – | |
| Conv 3 | 7 (3, 5, 7, 9) | – | – | |
| Conv 4 | 9 (3, 5, 7, 9) | – | – | |
| Conv 5 | 7 (3, 5, 7, 9) | – | – | |
| Dropout | – | 0.25 (0.25, 0.50, 0.75) | – | |
| Adam optimizer | – | – | 10−6 (10−3, 10−4, 10−5, 10−6) | |
| Scheme 1 (R34) | Conv 1 | 3 (3, 5, 7, 9) | – | – |
| Conv 2 | 9 (3, 5, 7, 9) | – | – | |
| Conv 3 | 3 (3, 5, 7, 9) | – | – | |
| Conv 4 | 9 (3, 5, 7, 9) | – | – | |
| Conv 5 | 9 (3, 5, 7, 9) | – | – | |
| Dropout | – | 0.25 (0.25, 0.50, 0.75) | – | |
| Adam optimizer | – | – | 10−3 (10−3, 10−4, 10−5, 10−6) | |
| Scheme 2 | Conv 1 | 5 (3, 5, 7, 9) | – | – |
| Conv 2 | 3 (3, 5, 7, 9) | – | – | |
| Conv 3 | 5 (3, 5, 7, 9) | – | – | |
| Conv 4 | 9 (3, 5, 7, 9) | – | – | |
| Conv 5 | 3 (3, 5, 7, 9) | – | – | |
| Dropout (RMW) | – | 0.75 (0.25, 0.50, 0.75) | – | |
| Dropout (R34) | – | 0.5 (0.25, 0.50, 0.75) | – | |
| Adam optimizer | – | – | 10−4 (10−3, 10−4, 10−5, 10−6) | |
| Scheme 3 | Conv 1 | 5 (3, 5, 7, 9) | – | – |
| Conv 2 | 9 (3, 5, 7, 9) | – | – | |
| Conv 3 | 5 (3, 5, 7, 9) | – | – | |
| Conv 4 | 7 (3, 5, 7, 9) | – | – | |
| Conv 5 | 9 (3, 5, 7, 9) | – | – | |
| Dropout (RMW) | – | 0.5 (0.25, 0.50, 0.75) | – | |
| Dropout (R34) | – | 0.75 (0.25, 0.50, 0.75) | – | |
| Adam optimizer | – | – | 10−5 (10−3, 10−4, 10−5, 10−6) |
| TC Size | Method | Region | Period Covered | Correlation | MAE (nmi) |
|---|---|---|---|---|---|
| RMW | Kossin et al. [23] | AO | 1995–2004 | 0.58 | 13.11 |
| Scheme 3 (this study) | WNP | 2011–2016 | 0.95 | 2.05 | |
| R34 | Demuth et al. [14] | AO, ENP | 1999–2004 | 0.89 | 16.90 |
| Knaff et al. [20] | AO, ENP | 2011–2013 | – | 37.00 | |
| Scheme 3 (this study) | WNP | 2011–2016 | 0.93 | 9.77 |
| Model | RWW | R34 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Corr. | RMSE (nmi) | MAE (nmi) | Bias (nmi) | Corr. | RMSE (nmi) | MAE (nmi) | Bias (nmi) | ||
| With dropout layers | Scheme 1 | 0.89 * (0.86 *) | 5.88 (4.98) | 4.25 (3.55) | −1.07 (−0.35) | 0.91 * (0.88 *) | 18.26 (17.98) | 13.60 (12.60) | 0.66 (−0.25) |
| Scheme 2 | 0.92 * (0.91 *) | 4.88 (4.00) | 3.36 (2.66) | −0.56 (−0.10) | 0.94 * (0.91 *) | 15.51 (15.62) | 11.43 (10.82) | 1.30 (−0.08) | |
| Scheme 3 | 0.97 * (0.95 *) | 3.40 (3.09) | 2.27 (2.05) | −0.17 (−0.05) | 0.95 * (0.93 *) | 13.57 (14.34) | 9.65 (9.77) | 0.29 (0.54) | |
| Without dropout layers | Scheme 1 | 0.93 * (0.92 *) | 4.83 (4.04) | 3.29 (2.66) | −1.06 (−0.41) | 0.93 * (0.90 *) | 15.77 (16.75) | 11.46 (11.54) | 1.42 (0.12) |
| Scheme 2 | 0.94 * (0.92 *) | 4.45 (3.80) | 2.97 (2.48) | −0.92 (−0.31) | 0.94 * (0.91 *) | 15.72 (16.23) | 11.42 (11.19) | 0.88 (−0.45) | |
| Scheme 3 | 0.95 * (0.93 *) | 4.16 (3.64) | 2.90 (2.50) | −0.13 (−0.12) | 0.94 * (0.92 *) | 15.11 (15.26) | 11.11 (10.82) | −0.12 (−0.18) | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baek, Y.-H.; Moon, I.-J.; Im, J.; Lee, J. A Novel Tropical Cyclone Size Estimation Model Based on a Convolutional Neural Network Using Geostationary Satellite Imagery. Remote Sens. 2022, 14, 426. https://doi.org/10.3390/rs14020426
Baek Y-H, Moon I-J, Im J, Lee J. A Novel Tropical Cyclone Size Estimation Model Based on a Convolutional Neural Network Using Geostationary Satellite Imagery. Remote Sensing. 2022; 14(2):426. https://doi.org/10.3390/rs14020426
Chicago/Turabian StyleBaek, You-Hyun, Il-Ju Moon, Jungho Im, and Juhyun Lee. 2022. "A Novel Tropical Cyclone Size Estimation Model Based on a Convolutional Neural Network Using Geostationary Satellite Imagery" Remote Sensing 14, no. 2: 426. https://doi.org/10.3390/rs14020426
APA StyleBaek, Y.-H., Moon, I.-J., Im, J., & Lee, J. (2022). A Novel Tropical Cyclone Size Estimation Model Based on a Convolutional Neural Network Using Geostationary Satellite Imagery. Remote Sensing, 14(2), 426. https://doi.org/10.3390/rs14020426








