Hybrid Compact Polarimetric SAR Calibration Considering the Amplitude and Phase Coefficients Inconsistency
Abstract
:1. Introduction
2. Model and Motivation
3. Polarimetric Calibration Schemes
3.1. Calibration Scheme Ignoring Crosstalk (ICT)
| Algorithm 1: ICT calibration scheme |
| Input: Measured scattering vectors ; |
| Output: Distortion parameters , , and ; |
 |
3.2. Calibration Scheme Considering Crosstalk (CCT)
| Algorithm 2: CCT calibration scheme |
| Input: Measured scattering vectors ; |
| Output: Distortion parameters , , and ; |
 |
4. Results
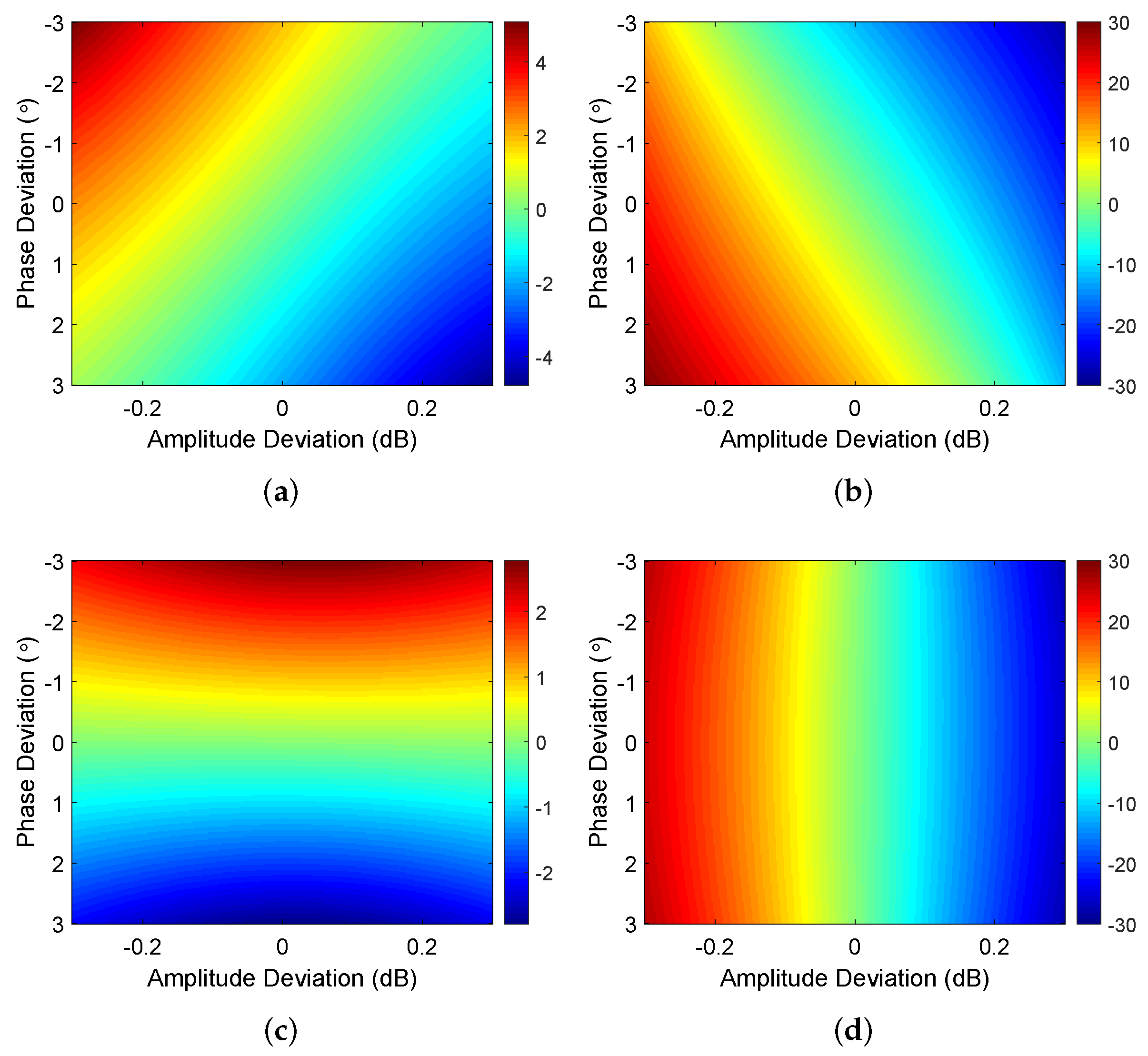
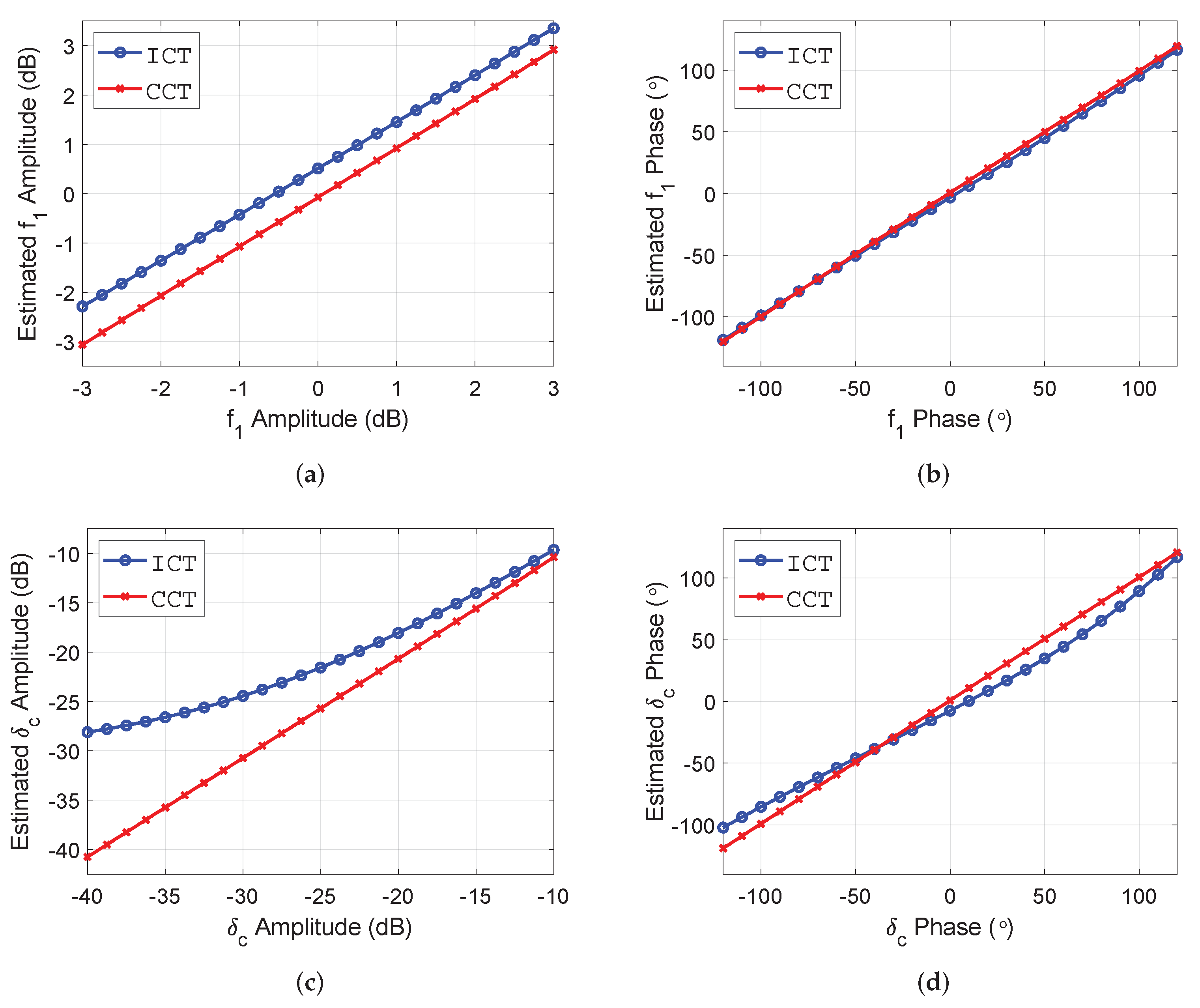
4.1. The Effect of Crosstalk on Calibration Schemes
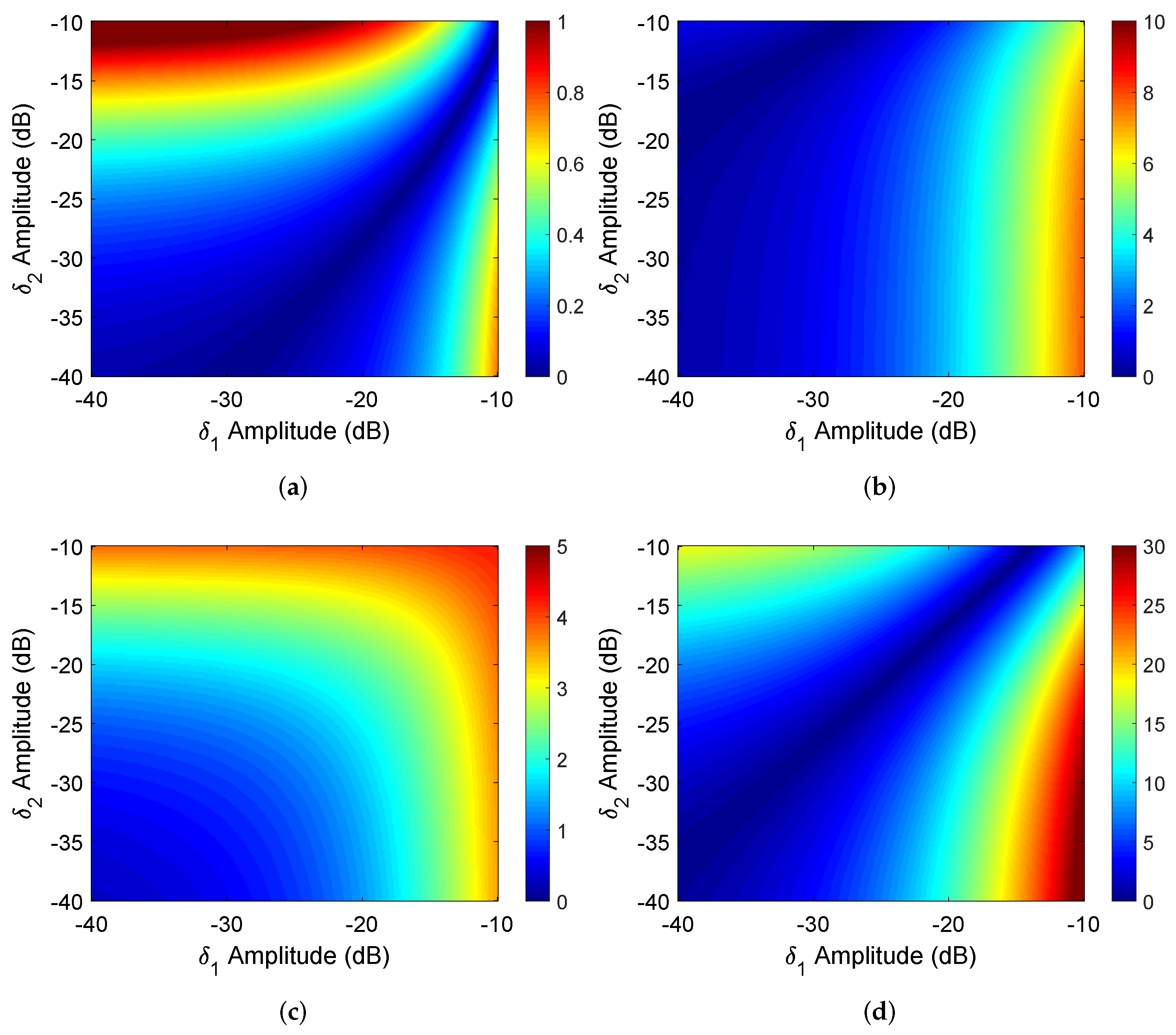
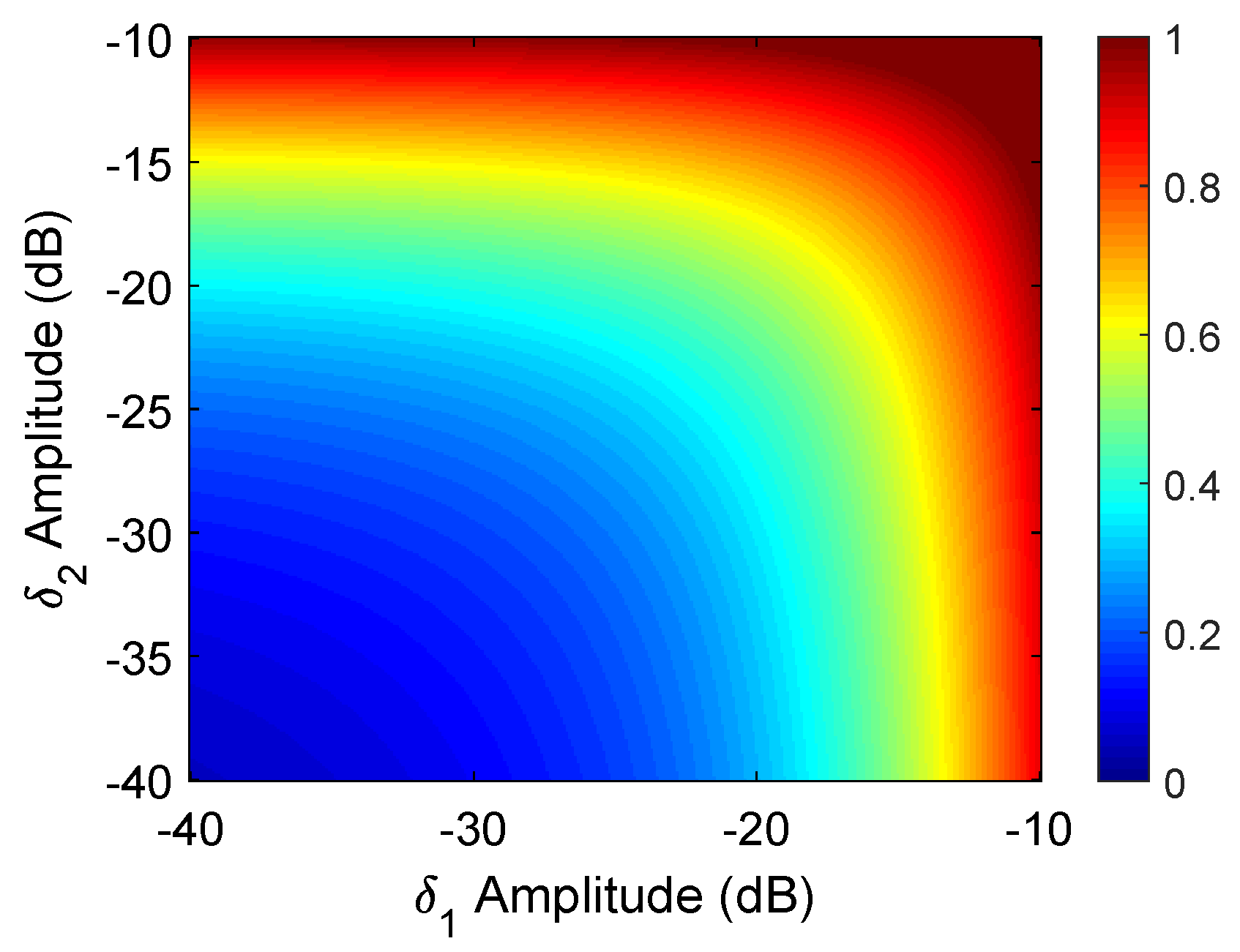
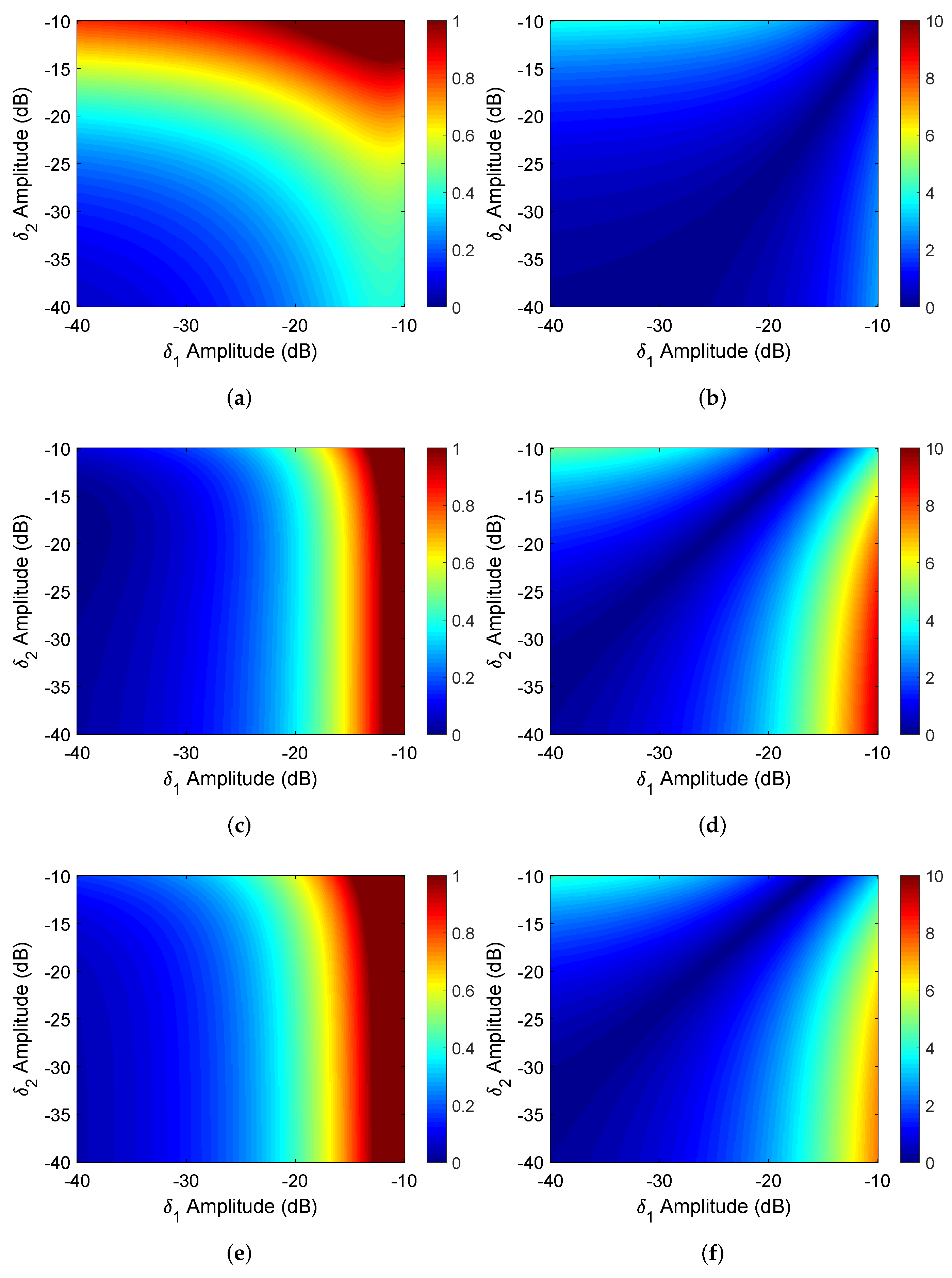
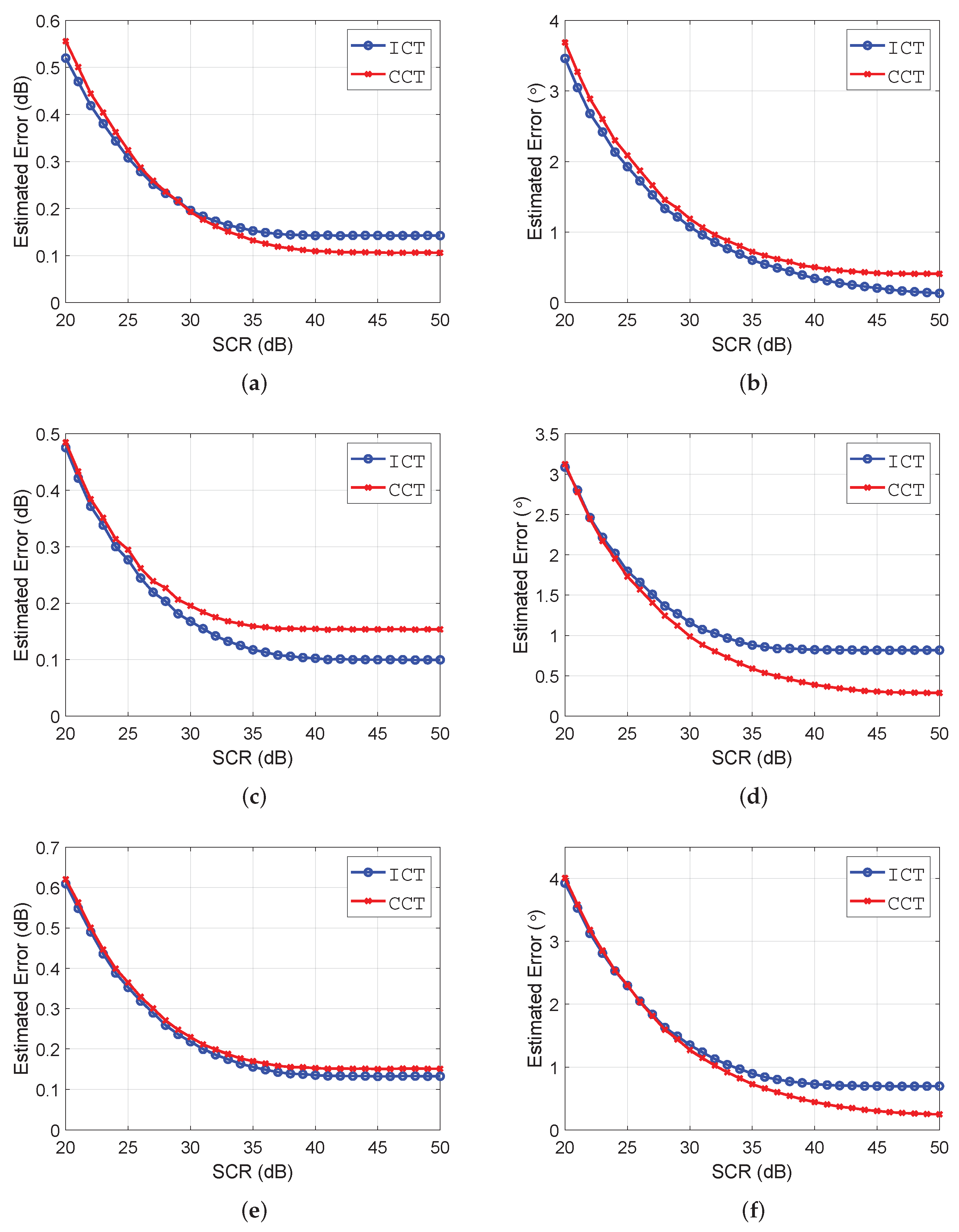
4.2. Estimation Accuracy of Distortion Parameters
4.3. Effects of Clutter on Calibration Accuracy
4.4. Results of AIRCAS L-Band Airborne SAR Data
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Calculate the Axial Ratio (AR) from Transmission Crosstalk δc
References
- Raney, R.K. Hybrid-polarity SAR architecture. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3397–3404. [Google Scholar] [CrossRef] [Green Version]
- White, L.; Millard, K.; Banks, S.; Richardson, M.; Pasher, J.; Duffe, J. Moving to the RADARSAT Constellation Mission: Comparing Synthesized Compact Polarimetry and Dual Polarimetry Data with Fully Polarimetric RADARSAT-2 Data for Image Classification of Peatlands. Remote Sens. 2017, 9, 573. [Google Scholar] [CrossRef] [Green Version]
- Yin, J.; Yang, J. Framework for Reconstruction of Pseudo Quad Polarimetric Imagery from General Compact Polarimetry. Remote Sens. 2021, 13, 530. [Google Scholar] [CrossRef]
- Hou, W.; Zhao, F.; Liu, X.; Wang, R. General Two-Stage Model-Based Three-Component Hybrid Compact Polarimetric SAR Decomposition Method. IEEE J. Sel. Topics Appl. Earth Observ. Remote Sens. 2021, 14, 4647–4660. [Google Scholar] [CrossRef]
- Hou, W.; Zhao, F.; Liu, X.; Zhang, H.; Wang, R. A Unified Framework for Comparing the Classification Performance between Quad-, Compact-, and Dual-Polarimetric SARs. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–14. [Google Scholar] [CrossRef]
- Dabboor, M.; Geldsetzer, T. Towards sea ice classification using simulated RADARSAT Constellation Mission compact polarimetric SAR imagery. Remote Sens. Environ. 2014, 140, 189–195. [Google Scholar] [CrossRef]
- Ponnurangam, G.G.; Jagdhuber, T.; Hajnsek, I.; Rao, Y. Soil moisture estimation using hybrid polarimetric SAR data of RISAT-1. IEEE Trans. Geosci. Remote Sens. 2015, 54, 2033–2049. [Google Scholar] [CrossRef]
- Olthof, I.; Rainville, T. Evaluating Simulated RADARSAT Constellation Mission (RCM) Compact Polarimetry for Open-Water and Flooded-Vegetation Wetland Mapping. Remote Sens. 2020, 12, 1476. [Google Scholar] [CrossRef]
- Raney, R.K. Hybrid dual-polarization synthetic aperture radar. Remote Sens. 2019, 11, 1521. [Google Scholar] [CrossRef] [Green Version]
- Spudis, P.; Nozette, S.; Bussey, B.; Raney, K.; Winters, H.; Lichtenberg, C.L.; Marinelli, W.; Crusan, J.C.; Gates, M.M. Mini-SAR: An imaging radar experiment for the Chandrayaan-1 mission to the Moon. Curr. Sci. 2009, 96, 533–539. [Google Scholar]
- Vondrak, R.; Keller, J.; Chin, G.; Garvin, J. Lunar Reconnaissance Orbiter (LRO): Observations for lunar exploration and science. Space Sci. Rev. 2010, 150, 7–22. [Google Scholar] [CrossRef]
- Misra, T.; Rana, S.; Desai, N.; Dave, D.; Rajeevjyoti Arora, R.K.; Rao, C.; Bakori, B.; Neelakantan, R.; Vachchani, J. Synthetic aperture radar payload on-board RISAT-1: Configuration, technology and performance. Curr. Sci. 2013, 104, 446–461. [Google Scholar]
- Kankaku, Y.; Suzuki, S.; Osawa, Y. ALOS-2 mission and development status. In Proceedings of the 2013 IEEE International Geoscience and Remote Sensing Symposium—IGARSS, Melbourne, Australia, 21–26 July 2013; pp. 2396–2399. [Google Scholar]
- Thompson, A.A. Overview of the RADARSAT Constellation Mission. Can. J. Remote Sens. 2015, 41, 401–407. [Google Scholar] [CrossRef]
- Brisco, B.; Mahdianpari, M.; Mohammadimanesh, F. Hybrid Compact Polarimetric SAR for Environmental Monitoring with the RADARSAT Constellation Mission. Remote Sens. 2020, 12, 3283. [Google Scholar] [CrossRef]
- Jung, Y.T.; Park, S.E. Comparative Analysis of Polarimetric SAR Calibration Methods. Remote Sens. 2018, 10, 2060. [Google Scholar] [CrossRef] [Green Version]
- Freeman, A.; Dubois-Fernandez, P.; Truong-Loi, M.L. Compact Polarimetry at longer wavelengths-calibration. In Proceedings of the 7th European Conference on Synthetic Aperture Radar, Friedrichshafen, Germany, 2–5 June; pp. 1–4.
- Truong-Loï, M.L.; Dubois-Fernandez, P.; Pottier, E.; Freeman, A.; Souyris, J.C. Potentials of a compact polarimetric SAR system. In Proceedings of the 2010 IEEE International Geoscience and Remote Sensing Symposium—IGARSS, Honolulu, HI, USA, 25–30 July 2010; pp. 742–745. [Google Scholar]
- Babu, A.; Kumar, S.; Agrawal, S. Polarimetric calibration of RISAT-1 compact-pol data. IEEE J. Sel. Topics Appl. Earth Observ. Remote Sens. 2019, 12, 3731–3736. [Google Scholar] [CrossRef]
- Kumar, S.; Babu, A.; Agrawal, S.; Asopa, U.; Shukla, S.; Maiti, A. Polarimetric calibration of spaceborne and airborne multifrequency SAR data for scattering-based characterization of manmade and natural features. Adv. Space Res. 2021. [Google Scholar] [CrossRef]
- Chen, J.; Quegan, S. Calibration of spaceborne CTLR compact polarimetric low-frequency SAR using mixed radar calibrators. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2712–2723. [Google Scholar] [CrossRef]
- Sabry, R. A tool for analysis and calibration of compact polarimetry SAR mode anomaly. IEEE Geosci. Remote Sens. Lett. 2018, 15, 424–428. [Google Scholar] [CrossRef]
- Touzi, R.; Shimada, M.; Motohka, T.; Nedelcu, S. Assessment of PALSAR-2 Compact Non-Circularity Using Amazonian Rainforests. IEEE Trans. Geosci. Remote Sens. 2020, 58, 7472–7482. [Google Scholar] [CrossRef]
- Tan, H.; Hong, J. Calibration of compact polarimetric SAR images using distributed targets and one corner reflector. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4433–4444. [Google Scholar] [CrossRef]
- Freeman, A.; Alves, M.; Chapman, B.; Cruz, J.; Kim, Y.; Shaffer, S.; Sun, J.; Turner, E.; Sarabandi, K. SIR-C data quality and calibration results. IEEE Trans. Geosci. Remote Sens. 1995, 33, 848–857. [Google Scholar] [CrossRef]
- Ulander, L.M.H.; Hawkins, R.K.; Livingstone, C.E.; Lukowski, T.I. Absolute radiometric calibration of the CCRS SAR. IEEE Trans. Geosci. Remote Sens. 1991, 29, 922–933. [Google Scholar] [CrossRef]
- Bhiravarasu, S.S.; Chakraborty, T.; Putrevu, D.; Pandey, D.K.; Kumar, R. Chandrayaan-2 Dual-Frequency SAR (DFSAR): Performance Characterization and Initial Results. Planet. Sci. J. 2021, 2, 134. [Google Scholar] [CrossRef]
- Sharma, S.; Dadhich, G.; Rambhia, M.; Mathur, A.K.; Prajapati, R.; Patel, P.; Shukla, A. Radiometric calibration stability assessment for the RISAT-1 SAR sensor using a deployed point target array at the Desalpar site, Rann of Kutch, India. Int. J. Remote Sens. 2017, 38, 7242–7259. [Google Scholar] [CrossRef]
- Zhao, L.; Li, Y.; Zhang, Q.; Liu, J.; Yuan, X.; Chen, Q. Design and Verification of Image Quallity Indexes of GF-3 Satellite. Spacecr. Eng. 2017, 6, 18–23. [Google Scholar] [CrossRef]
- Whitt, M.; Ulaby, F.; Polatin, P.; Liepa, V. A general polarimetric radar calibration technique. IEEE Trans. Antennas Propag. 1991, 39, 62–67. [Google Scholar] [CrossRef]
- Roweis, S. Levenberg-Marquardt Optimization. Notes; University of Toronto: Toronto, ON, Canada, 1996. [Google Scholar]
- Ranganathan, A. The levenberg-marquardt algorithm. Tutor. LM Algorithm 2004, 11, 101–110. [Google Scholar]
- Yang, J.; Peng, Y.N.; Lin, S.M. Similarity between two scattering matrices. Electron. Lett. 2001, 37, 193–194. [Google Scholar] [CrossRef]
- Tan, H. Study on Methods of Calibration and Correction of Compact Polarimetric SAR. Ph.D. Thesis, University Chinese Academy of Sciences, Beijing, China, June 2016. [Google Scholar]
- Wright, P.A.; Quegan, S.; Wheadon, N.S.; Hall, C.D. Faraday rotation effects on L-band spaceborne SAR data. IEEE Trans. Geosci. Remote Sens. 2003, 41, 2735–2744. [Google Scholar] [CrossRef]
- Lee, J.S.; Pottier, E. Polarimetric Radar Imaging: From Basics to Applications; CRC Press: New York, NY, USA, 2017. [Google Scholar]
- Knittel, G. The polarization sphere as a graphical aid in determining the polarization of an antenna by amplitude measurements only. IEEE Trans. Antennas Propag. 1967, 15, 217–221. [Google Scholar] [CrossRef]
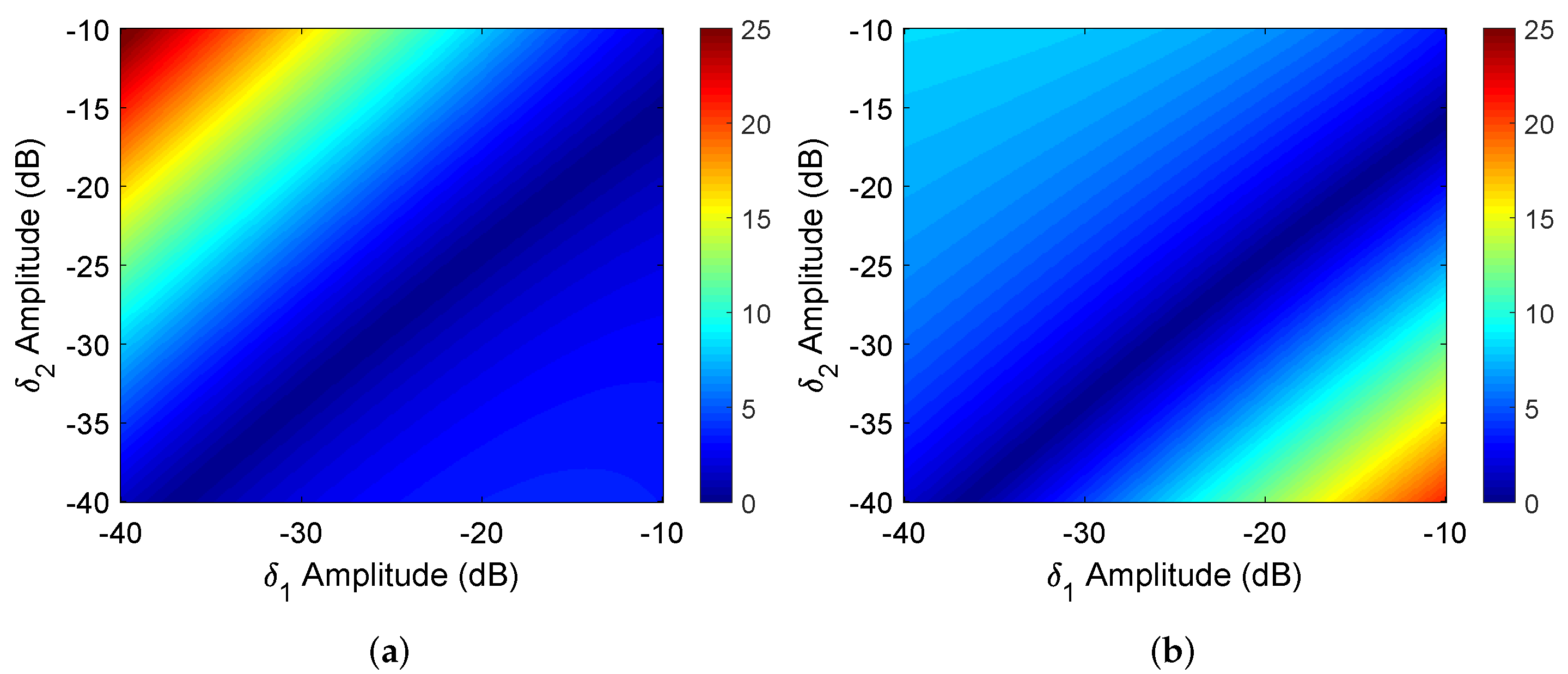
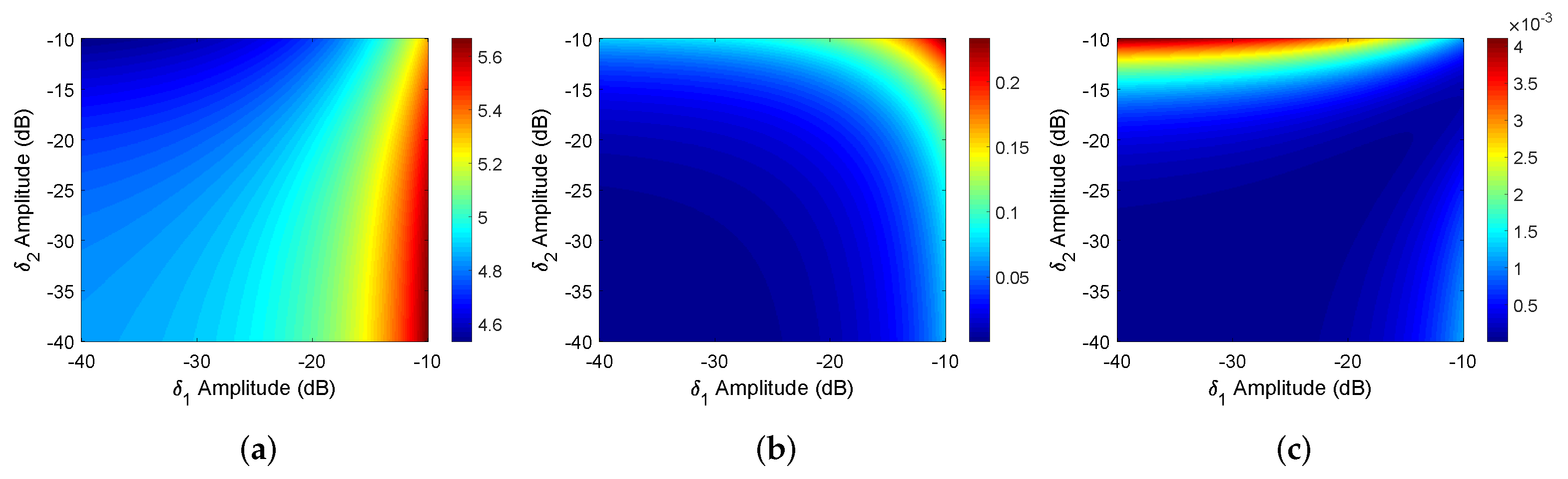
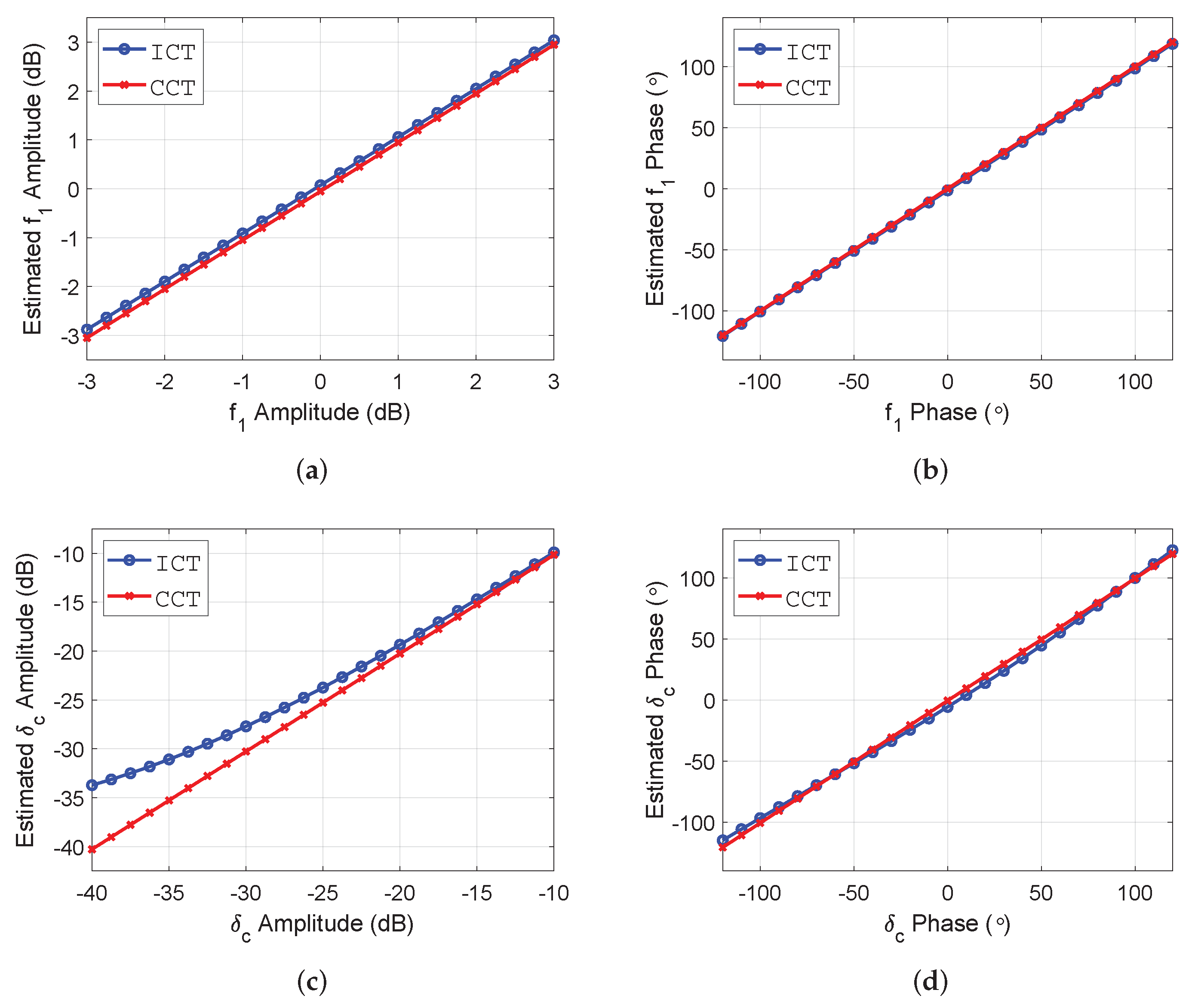
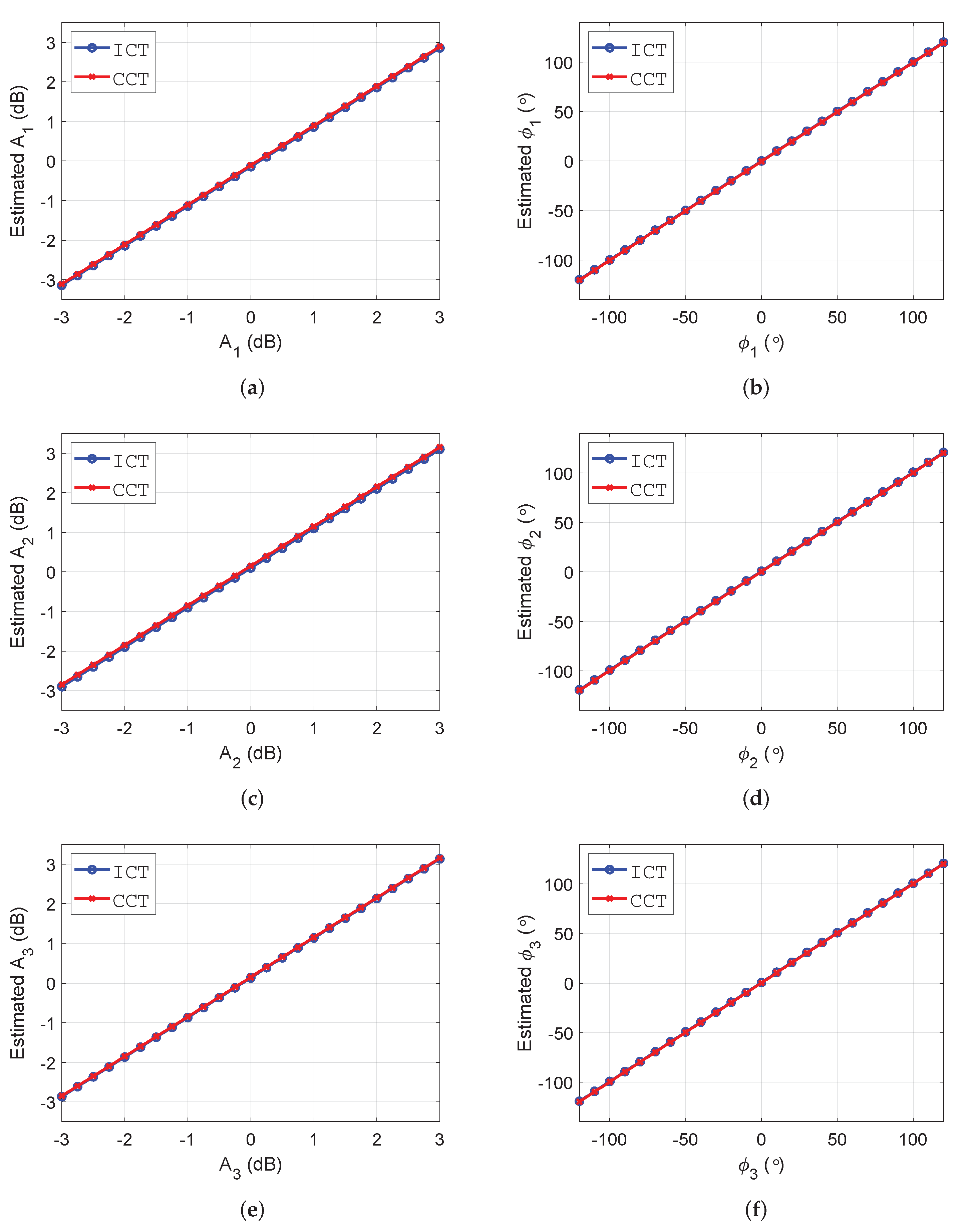



| Distortion | Receiving Crosstalk Level (dB) | ||||||
|---|---|---|---|---|---|---|---|
| Parameters | −40 | −35 | −30 | −25 | −20 | −15 | −10 |
| (dB) | 0.10 | 0.18 | 0.31 | 0.54 | 1.01 | 2.11 | 5.04 |
| 0.67 | 1.20 | 2.11 | 3.72 | 6.62 | 11.92 | 21.34 | |
| (dB) | 0.49 | 0.85 | 1.42 | 2.73 | 5.80 | 14.77 | 36.30 |
| 3.38 | 6.02 | 10.76 | 19.50 | 36.71 | 75.57 | 219.78 | |
| (dB) | 0.07 | 0.13 | 0.22 | 0.40 | 0.72 | 1.35 | 4.23 |
| (dB) | 0.09 | 0.17 | 0.30 | 0.54 | 0.96 | 1.75 | 3.32 |
| (dB) | 0.09 | 0.15 | 0.27 | 0.49 | 0.89 | 1.63 | 3.10 |
| 0.46 | 0.82 | 1.44 | 2.55 | 4.63 | 8.69 | 17.27 | |
| 0.58 | 1.03 | 1.84 | 3.26 | 5.77 | 10.20 | 18.01 | |
| 0.51 | 0.91 | 1.61 | 2.84 | 4.99 | 8.74 | 15.59 | |
| AR (dB) | 0.10 | 0.18 | 0.31 | 0.54 | 0.90 | 1.43 | 2.15 |
| Distortion | Receiving Crosstalk Level (dB) | ||||||
|---|---|---|---|---|---|---|---|
| Parameters | −40 | −35 | −30 | −25 | −20 | −15 | −10 |
| (dB) | 0.03 | 0.05 | 0.09 | 0.17 | 0.32 | 0.66 | 1.51 |
| 0.18 | 0.32 | 0.56 | 1.02 | 1.95 | 3.87 | 8.78 | |
| (dB) | 0.14 | 0.26 | 0.46 | 0.81 | 1.45 | 2.59 | 4.69 |
| 0.89 | 1.58 | 2.80 | 4.99 | 8.86 | 15.73 | 27.75 | |
| (dB) | 0.06 | 0.11 | 0.20 | 0.37 | 0.67 | 1.25 | 2.44 |
| (dB) | 0.08 | 0.15 | 0.27 | 0.49 | 0.89 | 1.65 | 3.18 |
| (dB) | 0.08 | 0.15 | 0.26 | 0.48 | 0.87 | 1.60 | 3.07 |
| 0.40 | 0.72 | 1.28 | 2.29 | 4.12 | 7.55 | 14.20 | |
| 0.51 | 0.90 | 1.61 | 2.86 | 5.12 | 9.21 | 16.88 | |
| 0.49 | 0.87 | 1.55 | 2.76 | 4.93 | 8.88 | 16.25 | |
| AR (dB) | 0.03 | 0.05 | 0.09 | 0.17 | 0.32 | 0.61 | 1.24 |
| Distortion | ICT | CCT | ||
|---|---|---|---|---|
| Parameters | T2D | T2D | T2D | T2D |
| (dB) | −0.40 | −0.44 | −0.43 | −0.54 |
| −7.13 | −6.74 | 0.17 | 0.19 | |
| (dB) | −21.92 | −22.27 | −18.69 | −18.70 |
| 164.87 | 162.11 | 136.53 | 136.50 | |
| (dB) | 19.73 | 19.20 | 19.70 | 19.22 |
| (dB) | 18.68 | 18.70 | 18.53 | 18.59 |
| (dB) | 17.61 | 17.63 | 17.71 | 17.78 |
| 101.63 | 185.76 | 97.49 | 181.84 | |
| 141.47 | 141.27 | 137.66 | 137.63 | |
| −90.01 | −90.19 | −94.57 | −94.47 | |
| AR (dB) | 1.40 | 1.34 | 2.03 | 2.03 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hou, W.; Zhao, F.; Liu, X.; Liu, D.; Han, Y.; Gao, Y.; Wang, R. Hybrid Compact Polarimetric SAR Calibration Considering the Amplitude and Phase Coefficients Inconsistency. Remote Sens. 2022, 14, 416. https://doi.org/10.3390/rs14020416
Hou W, Zhao F, Liu X, Liu D, Han Y, Gao Y, Wang R. Hybrid Compact Polarimetric SAR Calibration Considering the Amplitude and Phase Coefficients Inconsistency. Remote Sensing. 2022; 14(2):416. https://doi.org/10.3390/rs14020416
Chicago/Turabian StyleHou, Wentao, Fengjun Zhao, Xiuqing Liu, Dacheng Liu, Yonghui Han, Yao Gao, and Robert Wang. 2022. "Hybrid Compact Polarimetric SAR Calibration Considering the Amplitude and Phase Coefficients Inconsistency" Remote Sensing 14, no. 2: 416. https://doi.org/10.3390/rs14020416
APA StyleHou, W., Zhao, F., Liu, X., Liu, D., Han, Y., Gao, Y., & Wang, R. (2022). Hybrid Compact Polarimetric SAR Calibration Considering the Amplitude and Phase Coefficients Inconsistency. Remote Sensing, 14(2), 416. https://doi.org/10.3390/rs14020416







