Capability of GPM IMERG Products for Extreme Precipitation Analysis over the Indonesian Maritime Continent
Abstract
1. Introduction
2. Materials and Methods
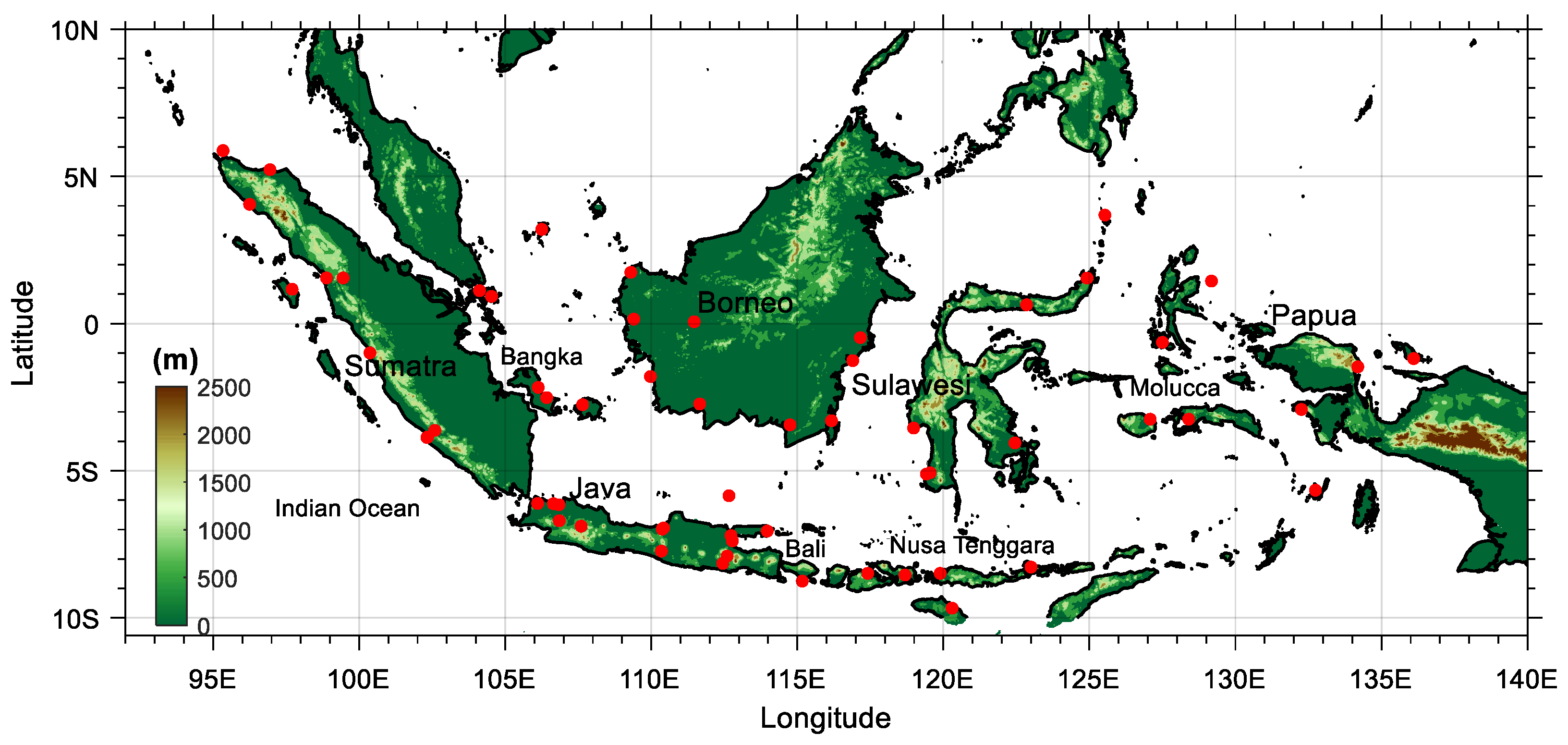
2.1. Study Area and Rain Gauge Data
2.2. GPM IMERG Precipitation Products
2.3. Validation Metrics Assessment
3. Results and Discussion
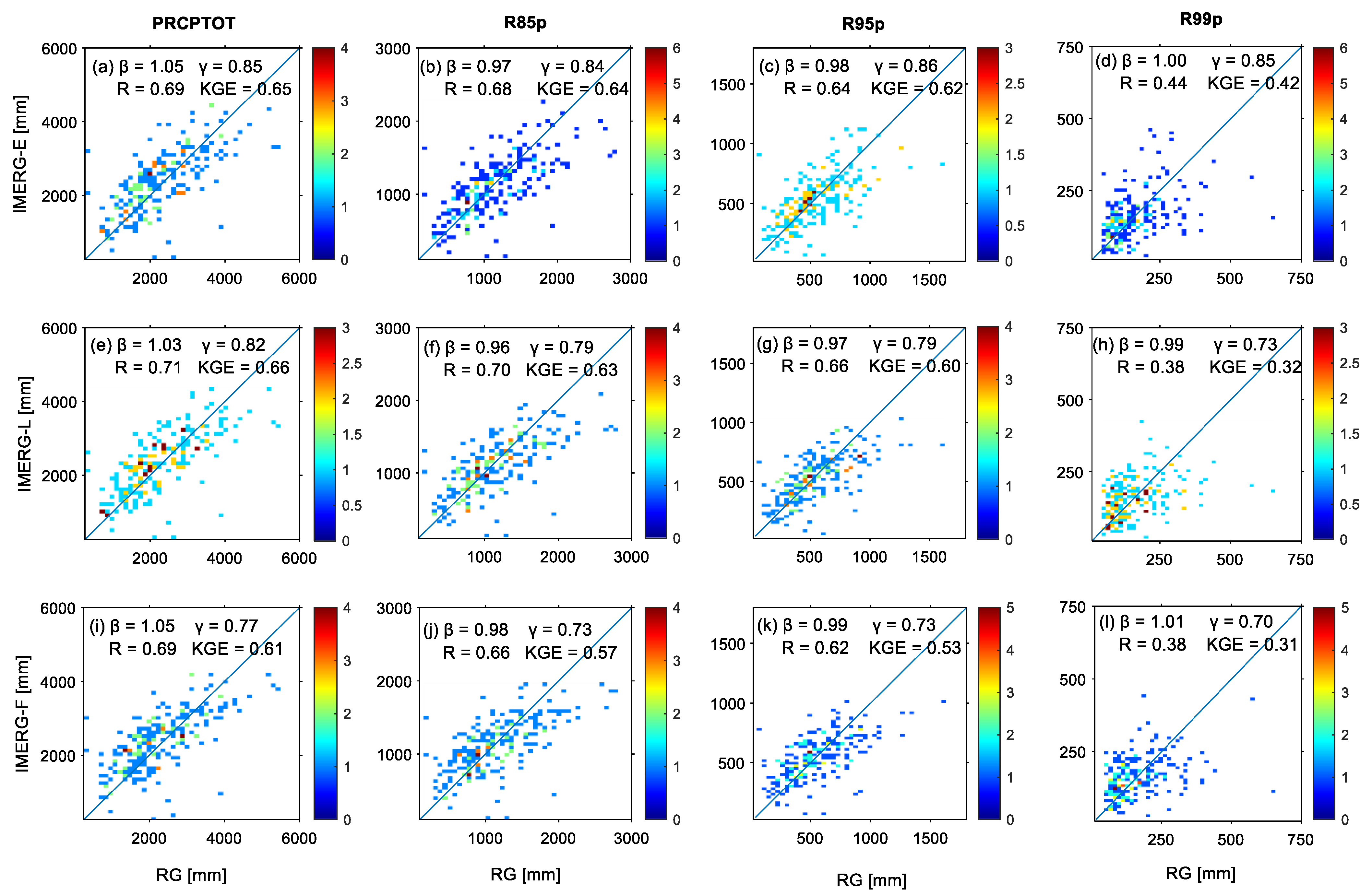
3.1. Precipitation-Amount-Based Indices’ Assessment
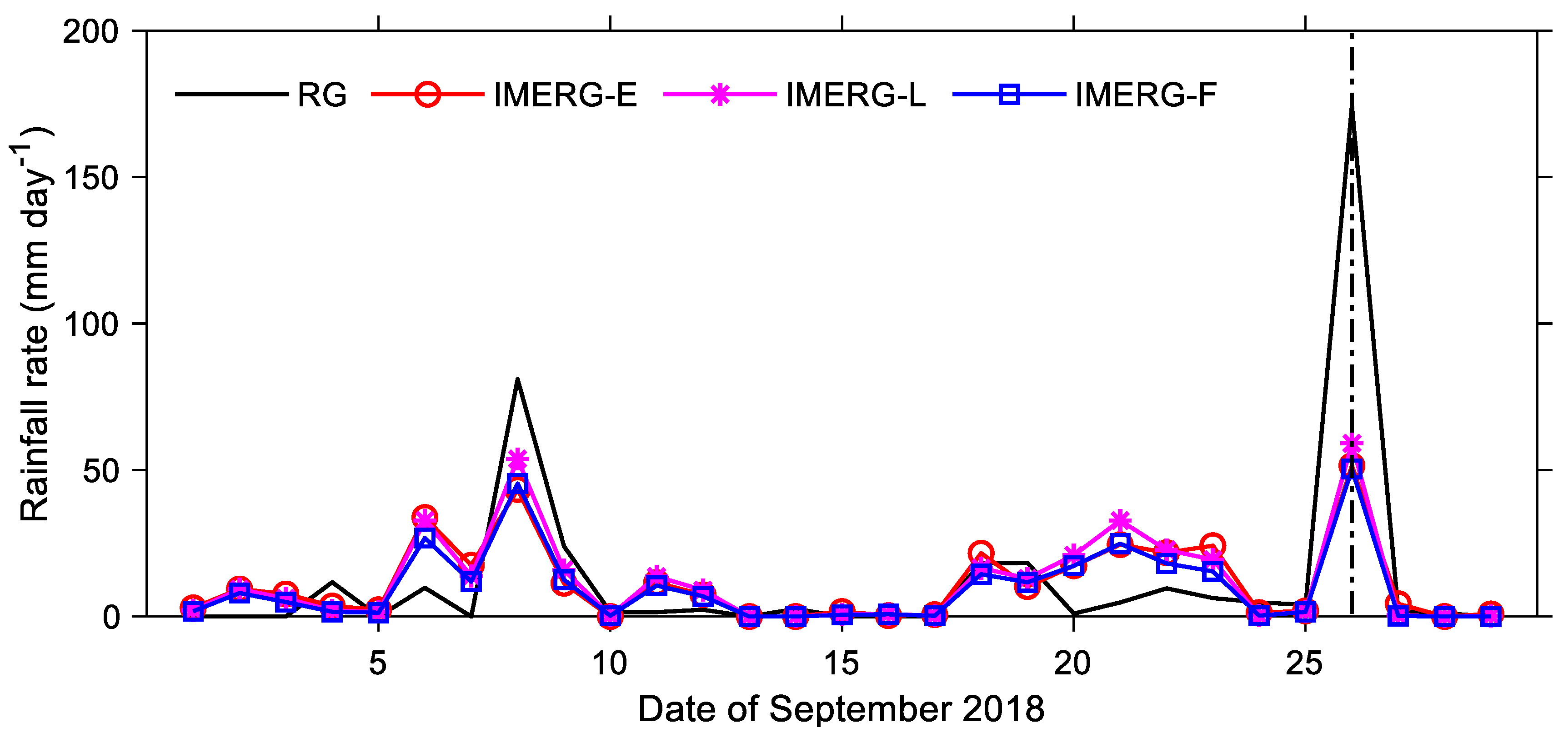
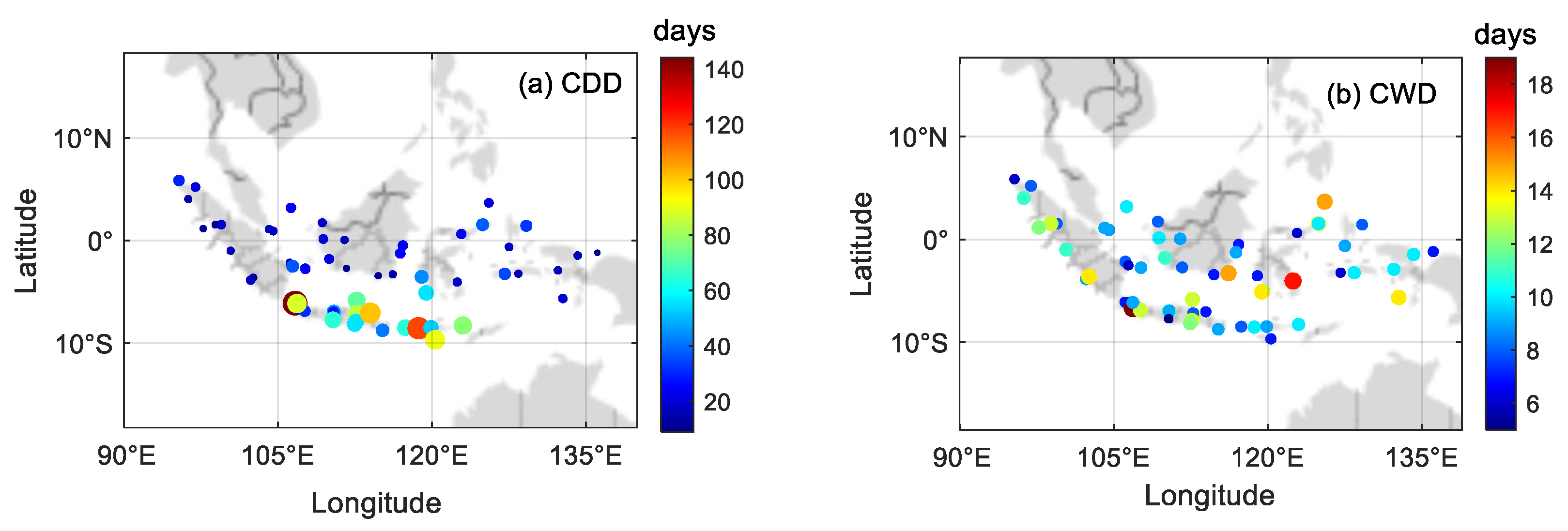
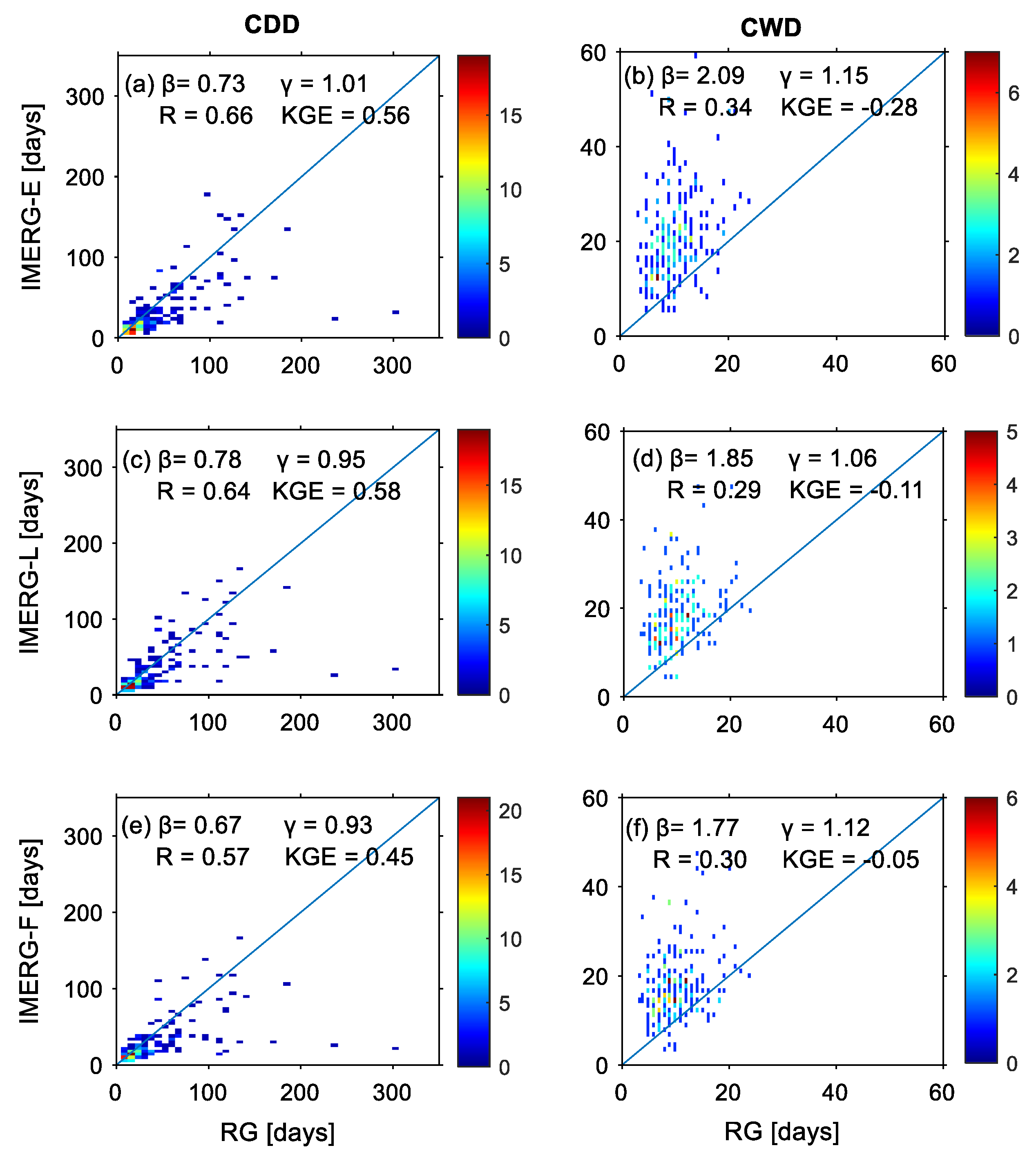
3.2. Precipitation-Duration-Based Indices’ Assessment
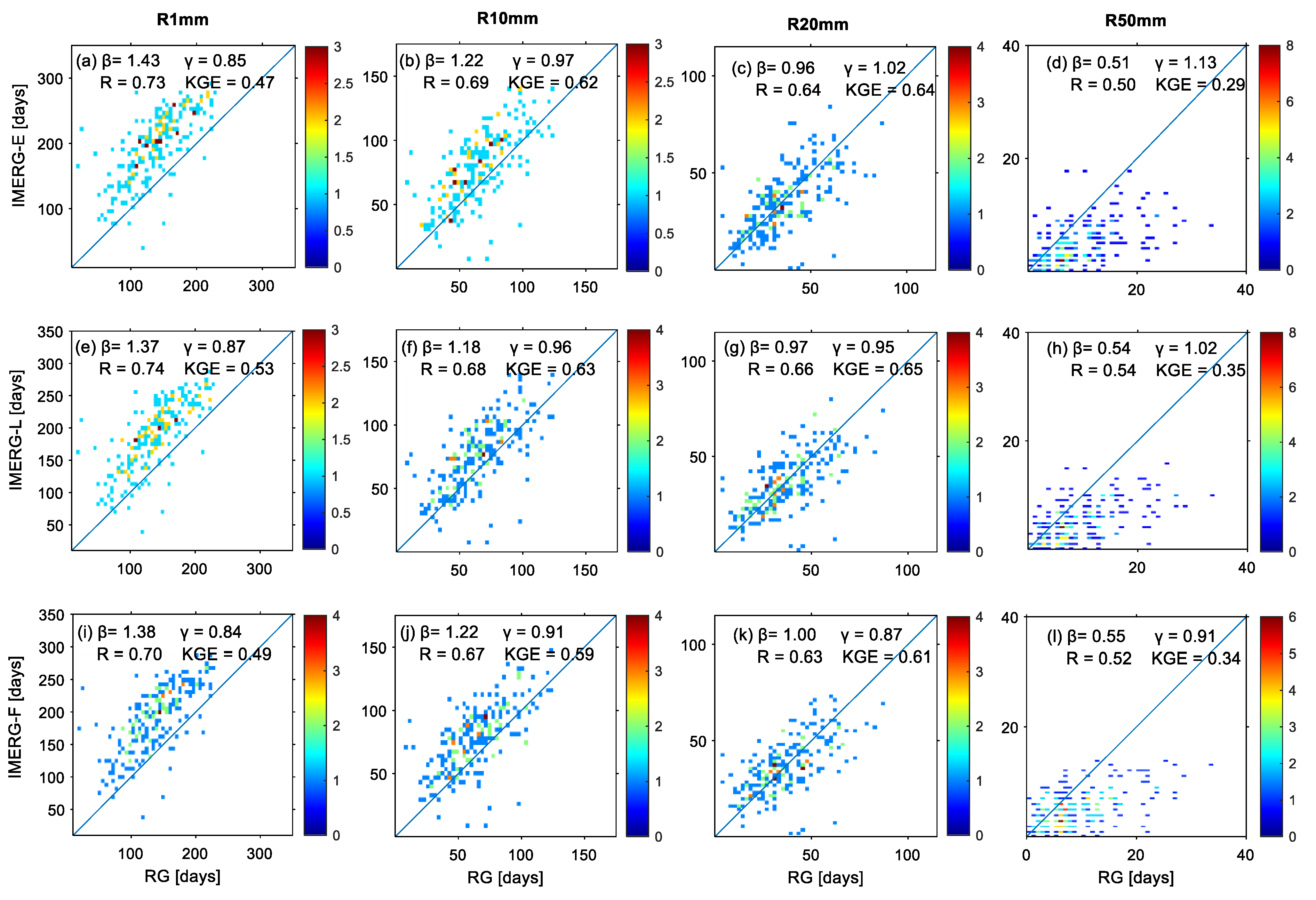
3.3. Precipitation-Frequency-Based Indices’ Assessment
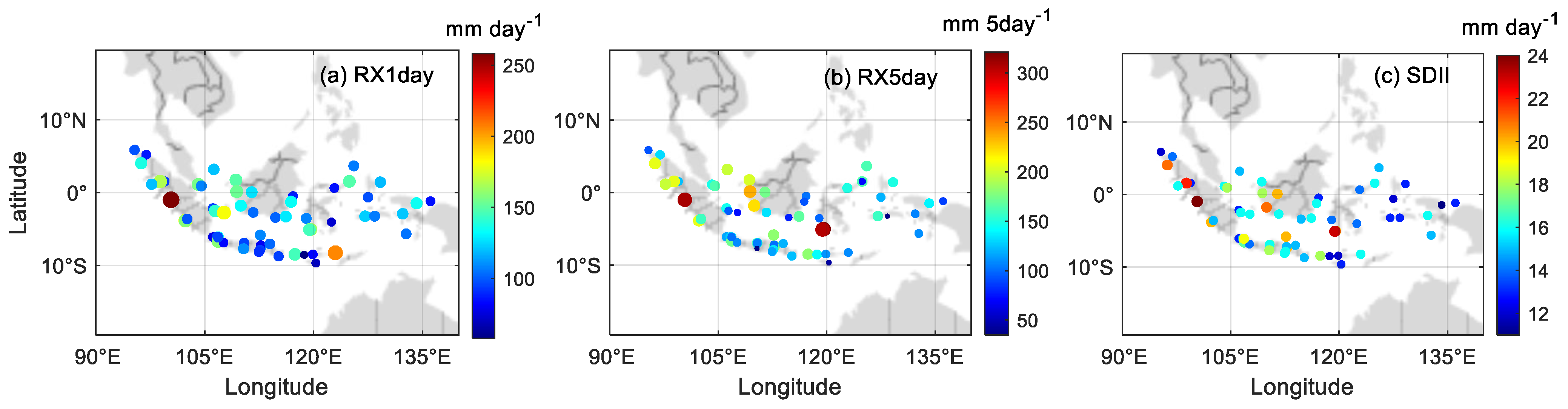
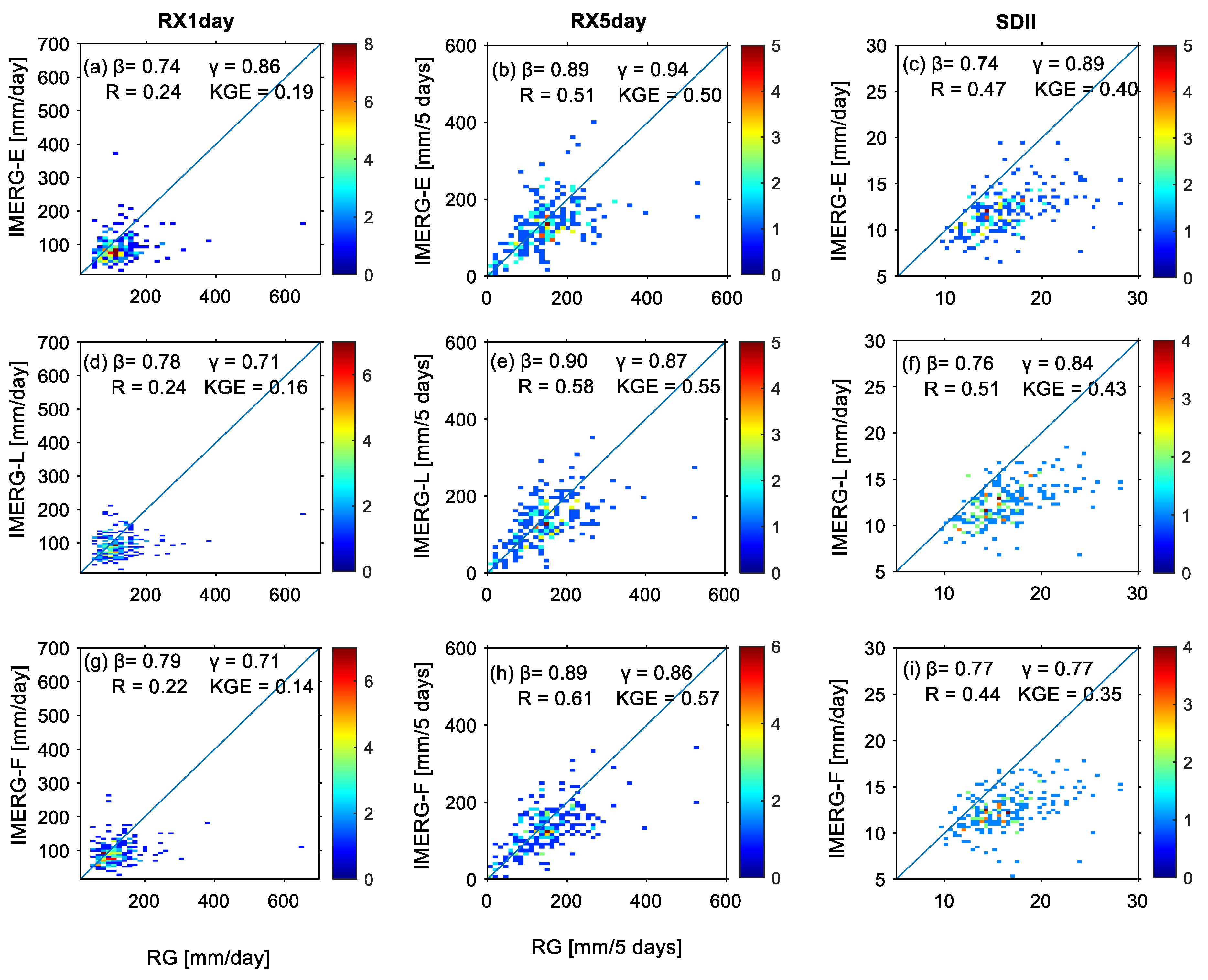
3.4. Precipitation-Intensity-Based Indices’ Assessment
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dentener, F.J.; Easterling, D.R.; Cooper, O. Chapter 2: Observations: Atmosphere and Surface. In IPCC Climate Change 2013: The Physical Science Basis; IPCC: Geneva, Switzerland, 2013. [Google Scholar]
- Pfahl, S.; O’Gorman, P.A.; Fischer, S.P.E.M. Understanding the regional pattern of projected future changes in extreme precipitation. Nat. Clim. Chang. 2017, 7, 423–427. [Google Scholar] [CrossRef]
- Gao, L.; Huang, J.; Chen, X.; Chen, Y.; Liu, M. Contributions of natural climate changes and human activities to the trend of extreme precipitation. Atmos. Res. 2018, 205, 60–69. [Google Scholar] [CrossRef]
- Eekhout, J.P.C.; Hunink, J.E.; Terink, W.; de Vente, J. Why increased extreme precipitation under climate change negatively affects water security. Hydrol. Earth Syst. Sci. 2018, 22, 5935–5946. [Google Scholar] [CrossRef]
- Myhre, G.; Alterskjær, K.; Stjern, C.W.; Hodnebrog, Ø.; Marelle, L.; Samset, B.H.; Sillmann, J.; Schaller, N.; Fischer, E.; Schulz, M.; et al. Frequency of extreme precipitation increases extensively with event rareness under global warming. Sci. Rep. 2019, 9, 1–10. [Google Scholar] [CrossRef]
- Ossandón, Á.; Rajagopalan, , B.; Kleiber, W. Spatial-temporal multivariate semi-Bayesian hierarchical framework for extreme precipitation frequency analysis. J. Hydrol. 2021, 600, 126499. [Google Scholar] [CrossRef]
- Tabari, H. Climate change impact on flood and extreme precipitation increases with water availability. Sci. Rep. 2020, 10, 1–10. [Google Scholar] [CrossRef]
- Kirschbaum, D.B.; Adler, R.F.; Adler, D.S.; Peters-Lidard, C.; Huffman, G. Global Distribution of Extreme Precipitation and High-Impact Landslides in 2010 Relative to Previous Years. J. Hydrometeorol. 2012, 13, 1536–1551. [Google Scholar] [CrossRef]
- Ávila, A.; Justino, F.; Wilson, A.; Bromwich, D.; Amorim, M. Recent precipitation trends, flash floods and landslides in southern Brazil. Environ. Res. Lett. 2016, 11, 114029. [Google Scholar] [CrossRef]
- Spinoni, J.; Barbosa, P.; Bucchignani, E.; Cassano, J.; Cavazos, T.; Christensen, J.H.; Christensen, O.B.; Coppola, E.; Evans, J.; Geyer, B.; et al. Future Global Meteorological Drought Hot Spots: A Study Based on CORDEX Data. J. Clim. 2020, 33, 3635–3661. [Google Scholar] [CrossRef]
- Ulfah, S.; Marzuki, M.; Susilo, A. Analysis Vulnerability Disaster of Landslide in Lantan Village Using Geoelectric Data and Sentinel Image. J. Penelit. Pendidik. IPA 2021, 7, 794–801. [Google Scholar] [CrossRef]
- Trezzini, F.; Giannella, G.; Guida, T. Landslide and Flood: Economic and Social Impacts in Italy. In Landslide Science and Practice: Social and Economic Impact and Policies; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Salvati, P.; Petrucci, O.; Rossi, M.; Bianchi, C.; Pasqua, A.A.; Guzzetti, F. Gender, age and circumstances analysis of flood and landslide fatalities in Italy. Sci. Total Environ. 2018, 610–611, 867–879. [Google Scholar] [CrossRef]
- Winter, M.G.; Peeling, D.; Palmer, D.; Peeling, J. Economic impacts of landslides and floods on a road network. AUC Geogr. 2019, 54, 207–220. [Google Scholar] [CrossRef]
- Simpson, J.; Keenan, T.D.; Ferrier, B.; Simpson, R.H.; Holland, G.J. Cumulus mergers in the maritime continent region. Theor. Appl. Clim. 1993, 51, 73–99. [Google Scholar] [CrossRef]
- Wu, P.; Arbain, A.A.; Mori, S.; Hamada, J.-I.; Hattori, M.; Syamsudin, F.; Yamanaka, M.D. The Effects of an Active Phase of the Madden-Julian Oscillation on the Extreme Precipitation Event over Western Java Island in January 2013. Sci. Online Lett. Atmos. 2013, 9, 79–83. [Google Scholar] [CrossRef]
- Supari; Tangang, F.; Juneng, L.; Aldrian, E. Observed changes in extreme temperature and precipitation over Indonesia. Int. J. Clim. 2017, 37, 1979–1997. [Google Scholar] [CrossRef]
- Baranowski, D.B.; Flatau, M.K.; Flatau, P.J.; Karnawati, D.; Barabasz, K.; Labuz, M.; Latos, B.; Schmidt, J.M.; Paski, J.A.I. Marzuki Social-media and newspaper reports reveal large-scale meteorological drivers of floods on Sumatra. Nat. Commun. 2020, 11, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Marzuki, H.H.; Shimomai, T.; Randeu, W.L. Cumulative Distributions of Rainfall Rate Over Sumatra. Prog. Electromagn. Res. M 2016, 49, 1–8. [Google Scholar] [CrossRef][Green Version]
- Marzuki, H.H.; Kozu, T.; Shimomai, T.; Shibagaki, Y.; Takahashi, Y. Precipitation microstructure in different Madden–Julian Oscillation phases over Sumatra. Atmos. Res. 2016, 168, 121–138. [Google Scholar] [CrossRef]
- Takama, T.; Aldrian, E.; Kusumaningtyas, S.D.A.; Sulistya, W. Identified vulnerability contexts for a paddy production assessment with climate change in Bali, Indonesia. Clim. Dev. 2016, 9, 110–123. [Google Scholar] [CrossRef]
- Muis, I.; Ismail; Erlangga, H. Engkus Post disaster social vulnerability: Policy analysis and implementation in communities in Indonesia. J. Crit. Rev. 2019, 6, 59–66. [Google Scholar] [CrossRef]
- Handayani, W.; Chigbu, U.E.; Rudiarto, I.; Putri, I.H.S. Urbanization and Increasing Flood Risk in the Northern Coast of Central Java—Indonesia: An Assessment towards Better Land Use Policy and Flood Management. Land 2020, 9, 343. [Google Scholar] [CrossRef]
- BNPB. Available online: https://dibi.bnpb.go.id/ (accessed on 17 November 2021).
- Tangang, F.; Supari, S.; Chung, J.X.; Cruz, F.; Salimun, E.; Ngai, S.T.; Juneng, L.; Santisirisomboon, J.; Santisirisomboon, J.; Ngo-Duc, T.; et al. Future changes in annual precipitation extremes over Southeast Asia under global warming of 2 °C. APN Sci. Bull. 2018, 8, 436. [Google Scholar] [CrossRef]
- Supari; Tangang, F.; Juneng, L.; Cruz, F.; Chung, J.X.; Ngai, S.T.; Salimun, E.; Mohd, M.S.F.; Santisirisomboon, J.; Singhruck, P.; et al. Multi-model projections of precipitation extremes in Southeast Asia based on CORDEX-Southeast Asia simulations. Environ. Res. 2020, 184, 109350. [Google Scholar] [CrossRef]
- Villarini, G.; Mandapaka, P.V.; Krajewski, W.F.; Moore, R.J. Rainfall and sampling uncertainties: A rain gauge perspective. J. Geophys. Res. Atmos. 2008, 113, 9214. [Google Scholar] [CrossRef]
- Boni, G.; Parodi, A.; Rudari, R. Extreme rainfall events: Learning from raingauge time series. J. Hydrol. 2006, 327, 304–314. [Google Scholar] [CrossRef]
- Nandargi, S.; Dhar, O.N. Extreme rainfall events over the Himalayas between 1871 and 2007. Hydrol. Sci. J. 2011, 56, 930–945. [Google Scholar] [CrossRef]
- Supari; Tangang, F.; Salimun, E.; Aldrian, E.; Sopaheluwakan, A.; Juneng, L. ENSO modulation of seasonal rainfall and extremes in Indonesia. Clim. Dyn. 2018, 51, 2559–2580. [Google Scholar] [CrossRef]
- Lengfeld, K.; Kirstetter, P.-E.; Fowler, H.J.; Yu, J.; Becker, A.; Flamig, Z.; Gourley, J.J. Use of radar data for characterizing extreme precipitation at fine scales and short durations. Environ. Res. Lett. 2020, 15, 085003. [Google Scholar] [CrossRef]
- Kidd, C.; Becker, A.; Huffman, G.; Muller, C.L.; Joe, P.; Skofronick-Jackson, G.; Kirschbaum, D. So, How Much of the Earth’s Surface Is Covered by Rain Gauges? Bull. Am. Meteorol. Soc. 2017, 98, 69–78. [Google Scholar] [CrossRef]
- Meischner, P. Weather Radar: Principles and Advanced Applications; Springer: Berlin/Heidelberg, Germany, 2005; ISBN 3540003282. [Google Scholar]
- Indonesian Agency for Meteorological. Climatological and Geophysics-Weather Radar. Available online: https://www.bmkg.go.id/cuaca/citra-radar.bmkg?lang=EN (accessed on 18 November 2021).
- Paski, J.A.I.; Alfahmi, F.; Permana, D.S.; Makmur, E.E.S. Reconstruction of Extreme Rainfall Event on September 19-20, 2017, Using a Weather Radar in Bengkulu of Sumatra Island. Sci. World J. 2020, 2020, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Lewandowski, P.A.; Eichinger, W.E.; Kruger, A.; Krajewski, W.F. Lidar-Based Estimation of Small-Scale Rainfall: Empirical Evidence. J. Atmos. Ocean. Technol. 2009, 26, 656–664. [Google Scholar] [CrossRef]
- Shipley, S.T.; Eloranta, E.W.; Weinman, J.A. Measurement of Rainfall Rates by Lidar. J. Appl. Meteorol. 1974, 13, 800–807. [Google Scholar] [CrossRef]
- Mandapaka, P.V.; Lewandowski, P.; Eichinger, W.E.; Krajewski, W.F. Multiscaling analysis of high resolution space-time lidar-rainfall. Nonlinear Process. Geophys. 2009, 16, 579–586. [Google Scholar] [CrossRef]
- Mega, T.; Yamamoto, M.K.; Abo, M.; Shibata, Y.; Hashiguchi, H.; Nishi, N.; Shimomai, T.; Shibagaki, Y.; Yamamoto, M.; Yamanaka, M.D.; et al. First simultaneous measurement of vertical air velocity, particle fall velocity, and hydrometeor sphericity in stratiform precipitation: Results from 47 MHz wind-profiling radar and 532 nm polarization lidar observations. Radio Sci. 2012, 47, 4823. [Google Scholar] [CrossRef]
- Kurniadi, A.; Weller, E.; Min, S.; Seong, M. Independent ENSO and IOD impacts on rainfall extremes over Indonesia. Int. J. Clim. 2021, 41, 3640–3656. [Google Scholar] [CrossRef]
- Lubis, S.W.; Respati, M.R. Impacts of convectively coupled equatorial waves on rainfall extremes in Java, Indonesia. Int. J. Clim. 2021, 41, 2418–2440. [Google Scholar] [CrossRef]
- Muhammad, F.R.; Lubis, S.W.; Setiawan, S. Impacts of the Madden–Julian oscillation on precipitation extremes in Indonesia. Int. J. Clim. 2021, 41, 1970–1984. [Google Scholar] [CrossRef]
- Xiao, S.; Xia, J.; Zou, L. Evaluation of Multi-Satellite Precipitation Products and Their Ability in Capturing the Characteristics of Extreme Climate Events over the Yangtze River Basin, China. Water 2020, 12, 1179. [Google Scholar] [CrossRef]
- Kitoh, A.; Endo, H. Changes in precipitation extremes projected by a 20-km mesh global atmospheric model. Weather. Clim. Extremes 2016, 11, 41–52. [Google Scholar] [CrossRef]
- Jiang, S.; Liu, S.; Ren, L.; Yong, B.; Zhang, L.; Wang, M.; Lu, Y.; He, Y. Hydrologic Evaluation of Six High Resolution Satellite Precipitation Products in Capturing Extreme Precipitation and Streamflow over a Medium-Sized Basin in China. Water 2017, 10, 25. [Google Scholar] [CrossRef]
- Liu, C.-Y.; Aryastana, P.; Liu, G.-R.; Huang, W.-R. Assessment of satellite precipitation product estimates over Bali Island. Atmos. Res. 2020, 244, 105032. [Google Scholar] [CrossRef]
- Pinto, I.; Lennard, C.; Tadross, M.; Hewitson, B.; Dosio, A.; Nikulin, G.; Panitz, H.-J.; Shongwe, M.E. Evaluation and projections of extreme precipitation over southern Africa from two CORDEX models. Clim. Change 2015, 135, 655–668. [Google Scholar] [CrossRef]
- Jiang, L.; Bauer-Gottwein, P. How do GPM IMERG precipitation estimates perform as hydrological model forcing? Evaluation for 300 catchments across Mainland China. J. Hydrol. 2019, 572, 486–500. [Google Scholar] [CrossRef]
- Endo, H.; Kitoh, A.; Mizuta, R.; Ishii, M. Future Changes in Precipitation Extremes in East Asia and Their Uncertainty Based on Large Ensemble Simulations with a High-Resolution AGCM. Sci. Onilne Lett. Atmos. 2017, 13, 7–12. [Google Scholar] [CrossRef]
- Tan, M.L.; Duan, Z. Assessment of GPM and TRMM Precipitation Products over Singapore. Remote Sens. 2017, 9, 720. [Google Scholar] [CrossRef]
- Tan, M.L.; Santo, H. Comparison of GPM IMERG, TMPA 3B42 and PERSIANN-CDR satellite precipitation products over Malaysia. Atmos. Res. 2018, 202, 63–76. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Braithwaite, D.; Hsu, K.; Joyce, R.; Kidd, C.; Nelkin, E.J.; Xie, P. NASA Global Precipitation Measurement (GPM) Integrated Multi-Satellite Retrievals for GPM (IMERG); Algorithm Theor. Basis Doc. Version 4.5; NASA: Washington, DC, USA, 2015. [Google Scholar]
- Fang, J.; Yang, W.; Luan, Y.; Du, J.; Lin, A.; Zhao, L. Evaluation of the TRMM 3B42 and GPM IMERG products for extreme precipitation analysis over China. Atmos. Res. 2019, 223, 24–38. [Google Scholar] [CrossRef]
- Zhou, C.; Gao, W.; Hu, J.; Du, L.; Du, L. Capability of IMERG V6 Early, Late, and Final Precipitation Products for Monitoring Extreme Precipitation Events. Remote Sens. 2021, 13, 689. [Google Scholar] [CrossRef]
- Yang, M.; Liu, G.; Chen, T.; Chen, Y.; Xia, C. Evaluation of GPM IMERG precipitation products with the point rain gauge records over Sichuan, China. Atmos. Res. 2020, 246, 105101. [Google Scholar] [CrossRef]
- Li, P.; Xu, Z.; Ye, C.; Ren, M.; Chen, H.; Wang, J.; Song, S. Assessment on IMERG V06 Precipitation Products Using Rain Gauge Data in Jinan City, Shandong Province, China. Remote Sens. 2021, 13, 1241. [Google Scholar] [CrossRef]
- Mayor, Y.G.; Tereshchenko, I.; Fonseca-Hernández, M.; Pantoja, D.A.; Montes, J.M. Evaluation of Error in IMERG Precipitation Estimates under Different Topographic Conditions and Temporal Scales over Mexico. Remote Sens. 2017, 9, 503. [Google Scholar] [CrossRef]
- Da Silva, N.A.; Webber, B.G.M.; Matthews, A.J.; Feist, M.M.; Stein, T.H.M.; Holloway, C.E.; Abdullah, M.F.A.B. Validation of GPM IMERG Extreme Precipitation in the Maritime Continent by Station and Radar Data. Earth Space Sci. 2021, 8, 1738. [Google Scholar] [CrossRef]
- Sharifi, E.; Steinacker, R.; Saghafian, B. Multi time-scale evaluation of high-resolution satellite-based precipitation products over northeast of Austria. Atmos. Res. 2018, 206, 46–63. [Google Scholar] [CrossRef]
- Ravidho, R.; Marzuki, M.; Helmi, Y.; Ayu, P.N.; Hiroyuki, H.; Toyoshi, S.; Vonnisa, M.; Ulfah, S.; Suryanto, W.; Sholihun, S. Ground validation of GPM IMERG-F precipitation products with the point rain gauge records on the extreme rainfall over a mountainous area of Sumatra Island. J. Penelit. Pendidik. IPA, 2022; 8, in press. [Google Scholar]
- Yusnaini, H.; Ramadhan, R.; Marzuki, M.; Ningsih, A.P.; Hashiguchi, H.; Shimomai, T.; Vonnisa, M.; Harmadi, H.; Suryanto, W.; Sholihun, S. Statistical Comparison of IMERG Precipitation Products with Optical Rain Gauge Observations over Kototabang, Indonesia. J. ILMU Fis. Univ. Andalas 2022, 14, 10–20. [Google Scholar]
- As-Syakur, A.R.; Osawa, T.; Miura, F.; Nuarsa, I.W.; Ekayanti, N.W.; Dharma, I.G.B.S.; Adnyana, I.W.S.; Arthana, I.W.; Tanaka, T. Maritime Continent rainfall variability during the TRMM era: The role of monsoon, topography and El Niño Modoki. Dyn. Atmos. Oceans 2016, 75, 58–77. [Google Scholar] [CrossRef]
- Kurniawan, A. Evaluasi Pengukuran Curah Hujan Antara Hasil Pengukuran Permukaan (AWS, HELLMAN, OBS) dan Hasil Estimasi (Citra Satelit =GSMaP) Di Stasiun Klimatologi Mlati Tahun. J. Geogr. Edukasi Lingkung. 2020, 4, 1–7. [Google Scholar] [CrossRef]
- GEBCO Gridded Bathymetry Data. Available online: https://www.gebco.net/data_and_products/gridded_bathymetry_data/ (accessed on 18 November 2021).
- Bappenas. RAN API Review: Scientific Base Study of Atmospheric Climate Projections; Bappenas: Jakarta, Indonesia, 2018. [Google Scholar]
- Mori, S.; Jun-Ichi, H.; Tauhid, Y.I.; Yamanaka, M.D.; Okamoto, N.; Murata, F.; Sakurai, N.; Hashiguchi, H.; Sribimawati, T. Diurnal Land–Sea Rainfall Peak Migration over Sumatera Island, Indonesian Maritime Continent, Observed by TRMM Satellite and Intensive Rawinsonde Soundings. Mon. Weather Rev. 2004, 132, 2021–2039. [Google Scholar] [CrossRef]
- Hou, A.Y.; Kakar, R.K.; Neeck, S.; Azarbarzin, A.A.; Kummerow, C.D.; Kojima, M.; Oki, R.; Nakamura, K.; Iguchi, T. The global precipitation measurement mission. Bull. Am. Meteorol. Soc. 2014, 95, 701–722. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Braithwaite, D.; Hsu, K.; Joyce, R.; Kidd, C.; Nelkin, E.J.; Sorooshian, S.; Tan, J.; Xie, P. NASA Global Precipitation Measurement (GPM) Integrated Multi-Satellite Retrievals for GPM (IMERG); Algorithm Theoretical Basis Document (ATBD) Version; NASA: Washington, DC, USA, 2019. [Google Scholar]
- Schneider, U.; Becker, A.; Finger, P.; Meyer-Christoffer, A.; Ziese, M.; Rudolf, B. GPCC’s new land surface precipitation climatology based on quality-controlled in situ data and its role in quantifying the global water cycle. Arch. Meteorol. Geophys. Bioclimatol. Ser. B 2014, 115, 15–40. [Google Scholar] [CrossRef]
- Tan, J.; Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J. IMERG V06: Changes to the Morphing Algorithm. J. Atmos. Ocean. Technol. 2019, 36, 2471–2482. [Google Scholar] [CrossRef]
- Huang, W.-R.; Chang, Y.-H.; Liu, P.-Y. Assessment of IMERG precipitation over Taiwan at multiple timescales. Atmos. Res. 2018, 214, 239–249. [Google Scholar] [CrossRef]
- Tan, M.L.; Samat, N.; Chan, N.W.; Roy, R. Hydro-Meteorological Assessment of Three GPM Satellite Precipitation Products in the Kelantan River Basin, Malaysia. Remote Sens. 2018, 10, 1011. [Google Scholar] [CrossRef]
- Hamza, A.; Anjum, M.; Cheema, M.M.; Chen, X.; Afzal, A.; Azam, M.; Shafi, M.K.; Gulakhmadov, A. Assessment of IMERG-V06, TRMM-3B42V7, SM2RAIN-ASCAT, and PERSIANN-CDR Precipitation Products over the Hindu Kush Mountains of Pakistan, South Asia. Remote Sens. 2020, 12, 3871. [Google Scholar] [CrossRef]
- Indonesian National Board for Disaster Management. Badan Nasional Penanggulangan Bencana. B. Indonesian Disaster Information Data. Available online: https://dibi.bnpb.go.id/xdibi/index (accessed on 18 November 2021).
- Marzuki, M.; Yusnaini, H.; Ramadhan, R.; Tangang, F.; Bin Amirudin, A.A.; Hashiguchi, H.; Shimomai, T.; Vonnisa, M. Characteristics of Precipitation Diurnal Cycle over a Mountainous Area of Sumatra Island including MJO and Seasonal Signatures Based on the 15-Year Optical Rain Gauge Data, WRF Model and IMERG. Atmosphere 2021, 13, 63. [Google Scholar] [CrossRef]
- ETCCDI. Climate Change Indices. Available online: http://etccdi.pacificclimate.org/list_27_indices.shtml (accessed on 18 November 2021).
- Yin, H.; Sun, Y. Characteristics of extreme temperature and precipitation in China in 2017 based on ETCCDI indices. Adv. Clim. Change Res. 2018, 9, 218–226. [Google Scholar] [CrossRef]
- Alexander, L.V.; Zhang, X.; Peterson, T.C.; Caesar, J.; Gleason, B.; Klein Tank, A.M.G.; Haylock, M.; Collins, D.; Trewin, B.; Rahimzadeh, F.; et al. Global observed changes in daily climate extremes of temperature and precipitation. J. Geophys. Res. Atmos. 2006, 111, D5. [Google Scholar] [CrossRef]
- Hong, Y.; Hsu, K.-L.; Moradkhani, H.; Sorooshian, S. Uncertainty quantification of satellite precipitation estimation and Monte Carlo assessment of the error propagation into hydrologic response. Water Resour. Res. 2006, 42, 42. [Google Scholar] [CrossRef]
- Sun, S.; Wang, J.; Shi, W.; Chai, R.; Wang, G. Capacity of the PERSIANN-CDR Product in Detecting Extreme Precipitation over Huai River Basin, China. Remote Sens. 2021, 13, 1747. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Tang, G.; Clark, M.P.; Papalexiou, S.M.; Ma, Z.; Hong, Y. Have satellite precipitation products improved over last two decades? A comprehensive comparison of GPM IMERG with nine satellite and reanalysis datasets. Remote Sens. Environ. 2020, 240, 111697. [Google Scholar] [CrossRef]
- Hosseini-Moghari, S.-M.; Tang, Q. Validation of GPM IMERG V05 and V06 Precipitation Products over Iran. J. Hydrometeorol. 2020, 21, 1011–1037. [Google Scholar] [CrossRef]
- As-Syakur, A.R.; Tanaka, T.; Osawa, T.; Mahendra, M.S. Indonesian rainfall variability observation using TRMM multi-satellite data. Int. J. Remote Sens. 2013, 34, 7723–7738. [Google Scholar] [CrossRef]
- Love, B.S.; Matthews, A.J.; Lister, G.M.S. The diurnal cycle of precipitation over the Maritime Continent in a high-resolution atmospheric model. Q. J. R. Meteorol. Soc. 2011, 137, 934–947. [Google Scholar] [CrossRef]
- Wu, J.; Zhou, B.T.; Xu, Y. Response of precipitation and its extremes over China to warming: CMIP5 simulation and projection. Acta Geophys. Sin. 2015, 58, 461–473. [Google Scholar] [CrossRef]
- Adfy, D.M.; Marzuki, M. Analisis Kerawanan Bencana Longsor dari Karakteristik Hujan, Pergerakan Tanah dan Kemiringan Lereng di Kabupaten Agam. J. Fis. Unand 2021, 10, 8–14. [Google Scholar]
- Li, Z.; Tang, G.; Hong, Z.; Chen, M.; Gao, S.; Kirstetter, P.; Gourley, J.J.; Wen, Y.; Yami, T.; Nabih, S.; et al. Two-decades of GPM IMERG early and final run products intercomparison: Similarity and difference in climatology, rates, and extremes. J. Hydrol. 2021, 594, 125975. [Google Scholar] [CrossRef]
- Yang, Z.; Hsu, K.; Sorooshian, S.; Xu, X.; Braithwaite, D.; Verbist, K.M.J. Bias adjustment of satellite-based precipitation estimation using gauge observations: A case study in Chile. J. Geophys. Res. Atmos. 2016, 121, 3790–3806. [Google Scholar] [CrossRef]
- Aldrian, E.; Susanto, R.D. Identification of three dominant rainfall regions within Indonesia and their relationship to sea surface temperature. Int. J. Clim. 2003, 23, 1435–1452. [Google Scholar] [CrossRef]
- Marzuki, M.; Suryanti, K.; Yusnaini, H.; Tangang, F.; Muharsyah, R.; Vonnisa, M.; Devianto, D. Diurnal variation of precipitation from the perspectives of precipitation amount, intensity and duration over Sumatra from rain gauge observations. Int. J. Clim. 2021, 41, 4386–4397. [Google Scholar] [CrossRef]
- Nepal, B.; Shrestha, D.; Sharma, S.; Shrestha, M.S.; Aryal, D.; Shrestha, N. Assessment of GPM-Era Satellite Products’ (IMERG and GSMaP) Ability to Detect Precipitation Extremes over Mountainous Country Nepal. Atmosphere 2021, 12, 254. [Google Scholar] [CrossRef]
- Ning, S.; Song, F.; Udmale, P.; Jin, J.; Thapa, B.R.; Ishidaira, H. Error Analysis and Evaluation of the Latest GSMap and IMERG Precipitation Products over Eastern China. Adv. Meteorol. 2017, 2017, 1–16. [Google Scholar] [CrossRef]
- Chen, C.; Chen, Q.; Duan, Z.; Zhang, J.; Mo, K.; Li, Z.; Tang, G. Multiscale Comparative Evaluation of the GPM IMERG v5 and TRMM 3B42 v7 Precipitation Products from 2015 to 2017 over a Climate Transition Area of China. Remote Sens. 2018, 10, 944. [Google Scholar] [CrossRef]
- Yong, B.; Ren, L.-L.; Hong, Y.; Wang, J.-H.; Yong, B.; Jiang, S.H.; Chen, X.; Wang, W. Hydrologic evaluation of Multisatellite Precipitation Analysis standard precipitation products in basins beyond its inclined latitude band: A case study in Laohahe basin, China. Water Resour. Res. 2010, 46, 759–768. [Google Scholar] [CrossRef]
- Tang, G.; Ma, Y.; Long, D.; Zhong, L.; Hong, Y. Evaluation of GPM Day-1 IMERG and TMPA Version-7 legacy products over Mainland China at multiple spatiotemporal scales. J. Hydrol. 2016, 533, 152–167. [Google Scholar] [CrossRef]
- Tian, F.; Hou, S.; Yang, L.; Hu, H.; Hou, A. How Does the Evaluation of the GPM IMERG Rainfall Product Depend on Gauge Density and Rainfall Intensity? J. Hydrometeorol. 2018, 19, 339–349. [Google Scholar] [CrossRef]
- Mahmoud, M.; Mohammed, S.; Hamouda, M.; Mohamed, M. Impact of Topography and Rainfall Intensity on the Accuracy of IMERG Precipitation Estimates in an Arid Region. Remote Sens. 2020, 13, 13. [Google Scholar] [CrossRef]
- Henning, D. Cloud dynamics: E.M. Agee and T. Asai (Editors). Proceedings of a Symposium held at the Third General Assembly of IAMAP, Hamburg, West Germany, 17–28 August D. Reidel Publishing Co., Dordrecht, in co-edition with Terra Scientific Publishing Company, Tokyo, 1982, VII + 423 pp., Dfl.115.00, US$49.50, hardcover. Dyn. Atmos. Oceans 1987, 11, 90–92. [Google Scholar] [CrossRef]
- Manz, B.; Páez-Bimos, S.; Horna, N.; Buytaert, W.; Ochoa-Tocachi, B.; Lavado-Casimiro, W.; Willems, B. Comparative Ground Validation of IMERG and TMPA at Variable Spatiotemporal Scales in the Tropical Andes. J. Hydrometeorol. 2017, 18, 2469–2489. [Google Scholar] [CrossRef]
- Yuan, F.; Zhang, L.; Soe, K.M.W.; Ren, L.; Zhao, C.; Zhu, Y.; Jiang, S.; Liu, Y. Applications of TRMM- and GPM-Era Multiple-Satellite Precipitation Products for Flood Simulations at Sub-Daily Scales in a Sparsely Gauged Watershed in Myanmar. Remote Sens. 2019, 11, 140. [Google Scholar] [CrossRef]
- Freitas, E.D.S.; Coelho, V.; Xuan, Y.; Melo, D.D.C.; Gadelha, A.N.; Santos, E.A.; Galvão, C.D.O.; Filho, G.M.R.; Barbosa, L.R.; Huffman, G.J.; et al. The performance of the IMERG satellite-based product in identifying sub-daily rainfall events and their properties. J. Hydrol. 2020, 589, 125128. [Google Scholar] [CrossRef]
- Li, Z.; Chen, M.; Gao, S.; Hong, Z.; Tang, G.; Wen, Y.; Gourley, J.J.; Hong, Y. Cross-Examination of Similarity, Difference and Deficiency of Gauge, Radar and Satellite Precipitation Measuring Uncertainties for Extreme Events Using Conventional Metrics and Multiplicative Triple Collocation. Remote Sens. 2020, 12, 1258. [Google Scholar] [CrossRef]


| Category | Name | Definition | Unit |
|---|---|---|---|
| Precipitation-amount-based indices | PRCPTOT | Annual total precipitation in wet days (RR ≥ 1 mm) | mm |
| R85p | Annual total precipitation when RR ≥ 85th percentile of wet days | mm | |
| R95p | Annual total precipitation when RR ≥ 95th percentile of wet days | mm | |
| R99p | Annual total precipitation when RR ≥ 99th percentile of wet days | mm | |
| Precipitation-duration-based indices | CDD | Maximum number of consecutive days with precipitation ≤1 mm | days |
| CWD | Maximum number of consecutive days with precipitation ≥1 mm | days | |
| Precipitation-frequency-based indices | R1mm | Annual count of days when precipitation ≥1 mm | days |
| R10mm | Annual count of days when precipitation ≥10 mm | days | |
| R20mm | Annual count of days when precipitation ≥20 mm | days | |
| R50mm | Annual count of days when precipitation ≥50 mm | days | |
| Precipitation-intensity-based indices | RX1day | Annual maximum 1-day precipitation | mm day−1 |
| RX5day | Annual maximum consecutive 5-days precipitation amount | mm 5 day−1 | |
| SDII | Annual total precipitation divided by the number of wet days in the year | mm day−1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ramadhan, R.; Marzuki, M.; Yusnaini, H.; Muharsyah, R.; Suryanto, W.; Sholihun, S.; Vonnisa, M.; Battaglia, A.; Hashiguchi, H. Capability of GPM IMERG Products for Extreme Precipitation Analysis over the Indonesian Maritime Continent. Remote Sens. 2022, 14, 412. https://doi.org/10.3390/rs14020412
Ramadhan R, Marzuki M, Yusnaini H, Muharsyah R, Suryanto W, Sholihun S, Vonnisa M, Battaglia A, Hashiguchi H. Capability of GPM IMERG Products for Extreme Precipitation Analysis over the Indonesian Maritime Continent. Remote Sensing. 2022; 14(2):412. https://doi.org/10.3390/rs14020412
Chicago/Turabian StyleRamadhan, Ravidho, Marzuki Marzuki, Helmi Yusnaini, Robi Muharsyah, Wiwit Suryanto, Sholihun Sholihun, Mutya Vonnisa, Alessandro Battaglia, and Hiroyuki Hashiguchi. 2022. "Capability of GPM IMERG Products for Extreme Precipitation Analysis over the Indonesian Maritime Continent" Remote Sensing 14, no. 2: 412. https://doi.org/10.3390/rs14020412
APA StyleRamadhan, R., Marzuki, M., Yusnaini, H., Muharsyah, R., Suryanto, W., Sholihun, S., Vonnisa, M., Battaglia, A., & Hashiguchi, H. (2022). Capability of GPM IMERG Products for Extreme Precipitation Analysis over the Indonesian Maritime Continent. Remote Sensing, 14(2), 412. https://doi.org/10.3390/rs14020412






