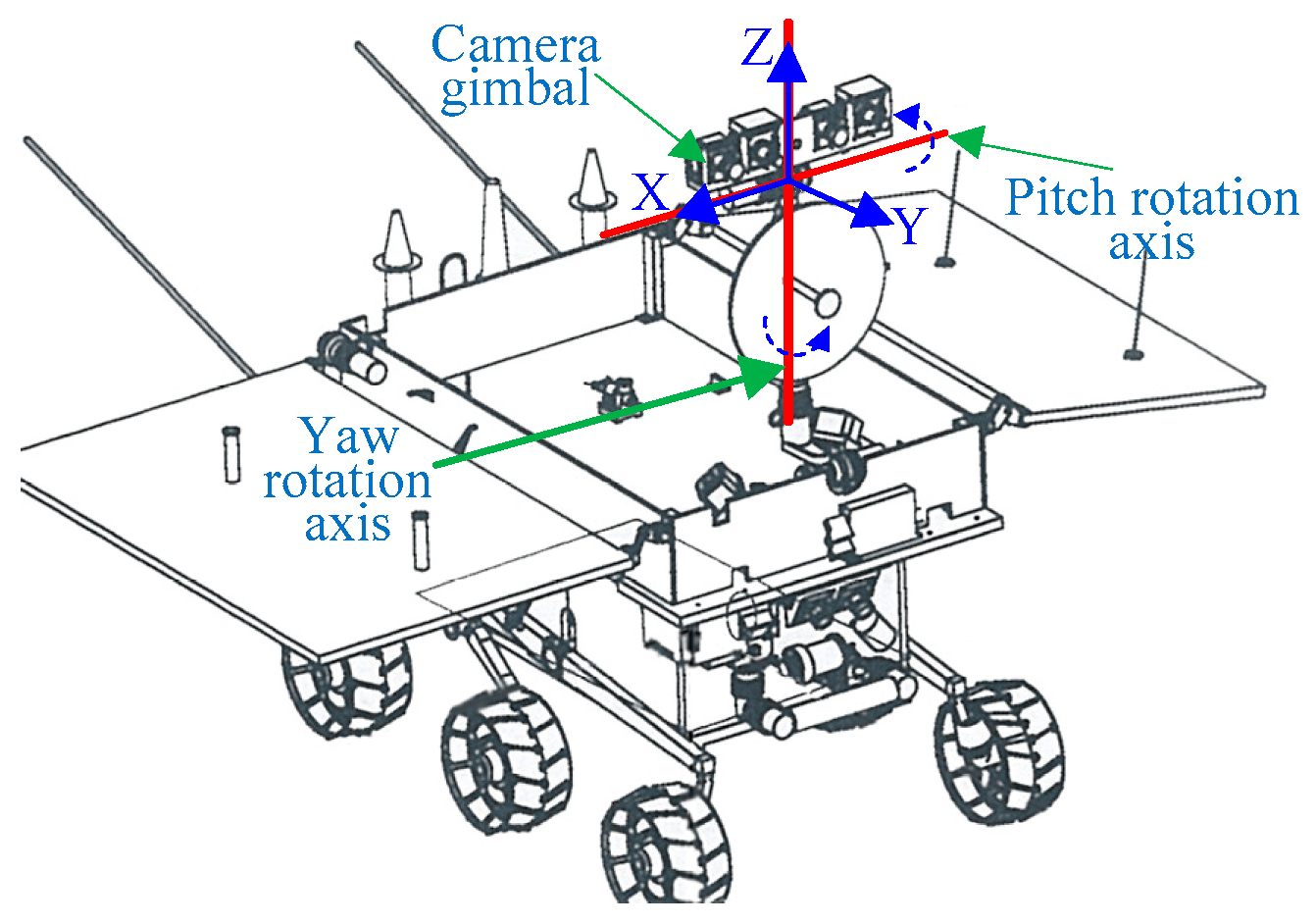
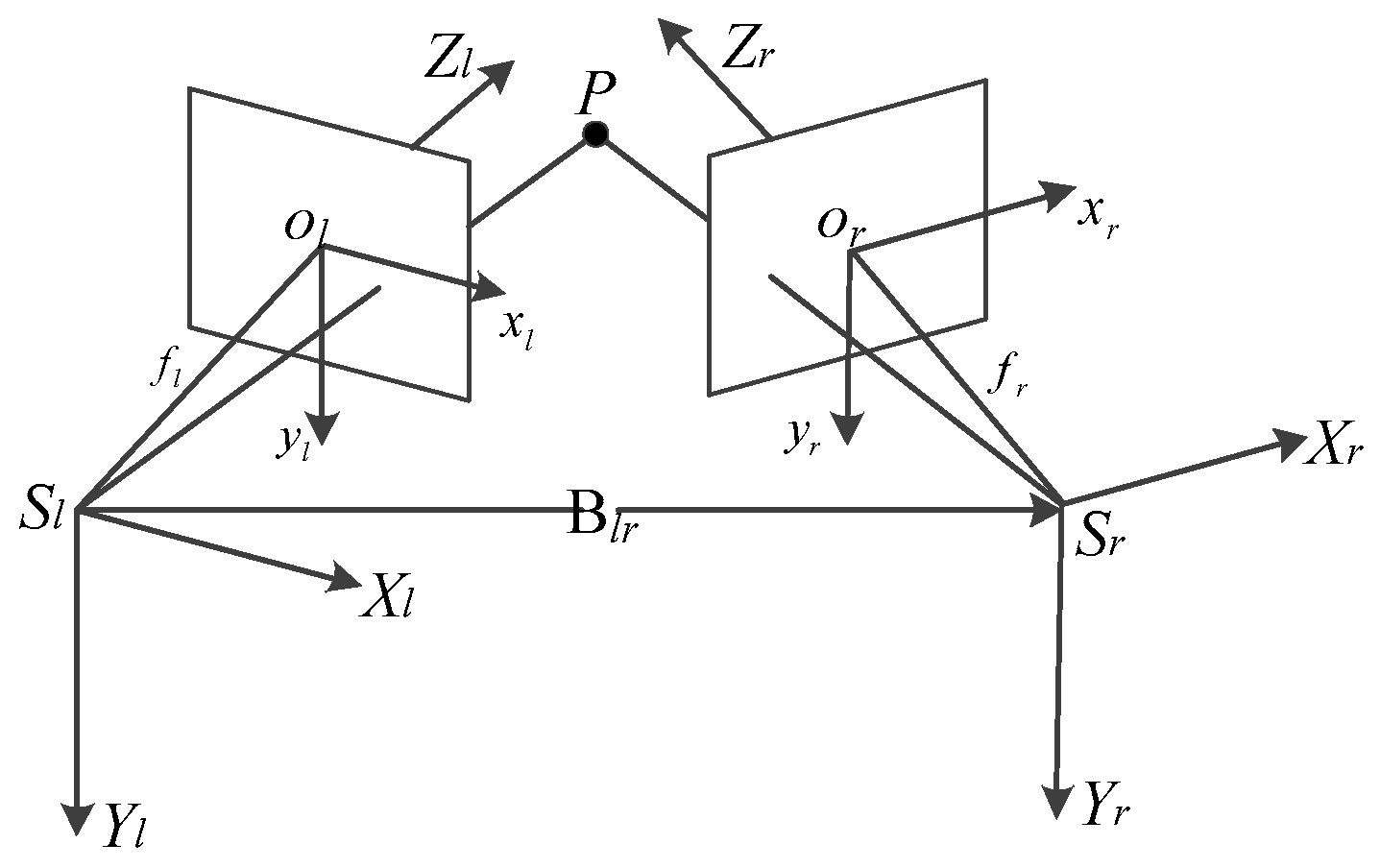
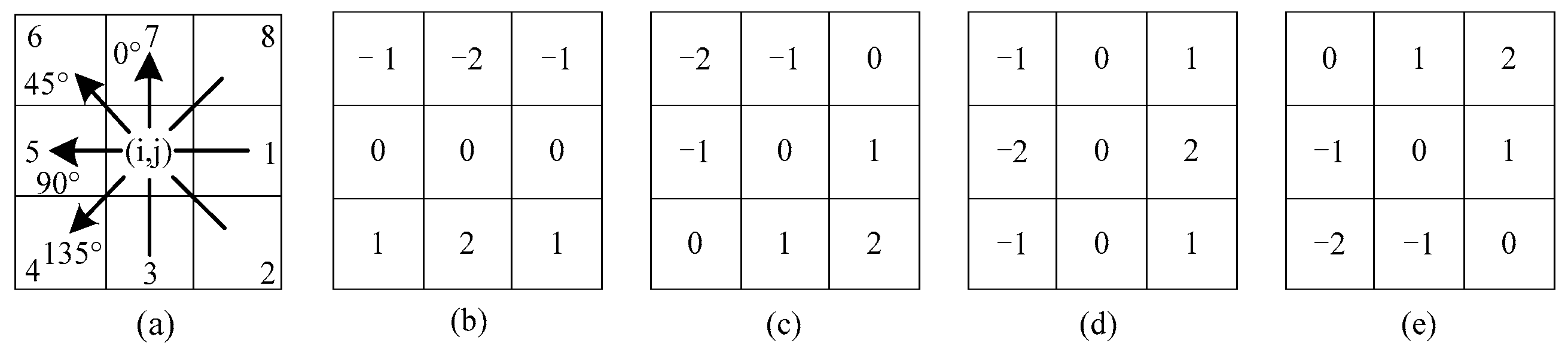
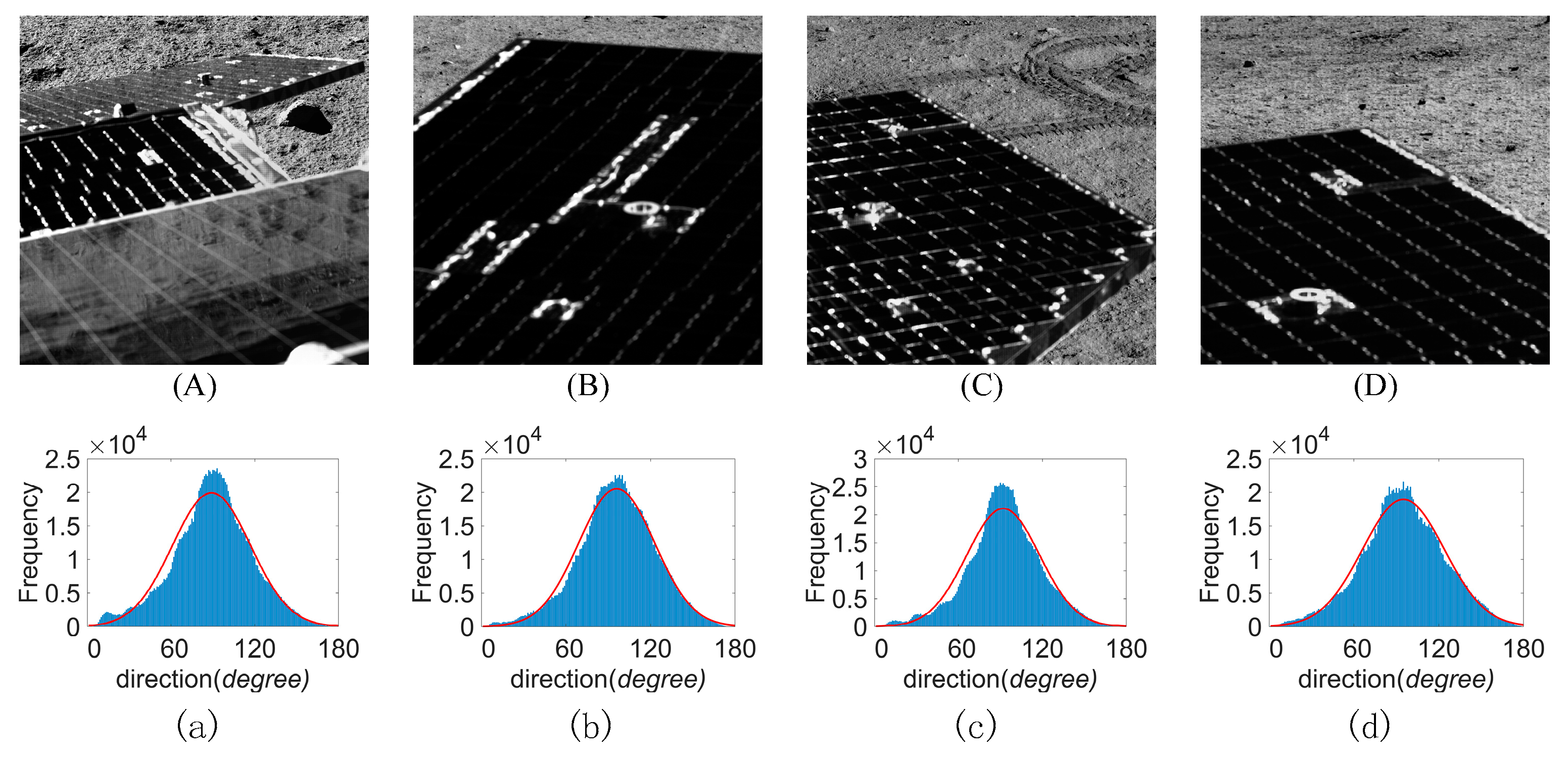
1. Introduction
With the continuous development of aerospace technologies, many countries have carried out extensive exploration of extraterrestrial bodies, such as to the moon and Mars [
1,
2,
3]. To successfully conduct these tasks, such as planetary rover navigation, high-precision mapping of the detection area, the determination of interior orientation (IO) elements, exterior orientation (EO) elements, and distortion parameters of the cameras are of great significance [
4,
5]. Because of the influences of environmental factors, such as temperature and pressure, and engine vibration during landing, the camera parameters can be inevitable changed. In 2004, China officially launched the lunar exploration project and named it the “Chang’e Project”. Chang’e-3 is a lunar probe launched in the second phase of China’s lunar exploration project. It consists of a lander and a patrol (“Yutu” lunar rover). The “Yutu” rover patrolled the lunar surface at a speed of 200 m per hour and a rhythm of about 7 m per “step”, and carried out various scientific exploration tasks, including lunar surface morphology and geological structure, lunar surface material composition, available resources, earth plasma layer, etc. The planetary rover is equipped with a pair of stereo navigation cameras for navigation and positioning [
3]. Taking Chang’e-3 as an example, the landing process can be divided into the main deceleration stage (15 km), the approaching stage (2 km), the hovering stage (100 m), the obstacle avoidance stage (100 m–30 m), the slow-falling stage (30 m–3 m), and the free-falling stage (<3 m). The vibrations during near-orbit braking, hovering, landing, and particularly free falling can change various parameters of the camera to varying degrees. Therefore, the in-orbit stereo camera self-calibration of planetary rovers is an important study object.
In laboratory conditions, the stereo camera can be calibrated through various high-precision control points, calibration plates, etc. However, when it is in orbit, it is challenging to obtain enough control points or use high-precision calibration plates. Therefore, various information in-orbit must be used as constraints to calibrate the stereo camera. Taking China’s Chang’e-3 as an example, after the planetary rover exits the lander, the camera takes images of the lander for calibration, since the positions and dimensions of multiple components on the lander are rigorously designed and measured in the laboratory. In addition, the solar panel parallel features of the planetary rover can also be used as constraints for the in-orbit self-calibration of stereo cameras. Existing camera calibration methods are designed under laboratory conditions, and the in-orbit self-calibration of stereo cameras remains challenging to complete based on the aforementioned various constraints.
Many studies have been carried out regarding camera calibration. In the early stage, the calibration of traditional monocular cameras is mainly based on the direct linear transformation (DLT) method proposed by Karara and Abdal-Aziz, in which the DLT is performed on pixel coordinates of target points and their spatial coordinates to solve the transformation parameters. Since lens distortion is not considered in the DLT, the calibration accuracy is not ideal [
6]. Tsai et al. proposed the radial alignment constraint (RAC) algorithm in 1986 based on DLT. Specifically, after introducing the radial distortion factor and combining it with the linear transformation of the perspective matrix, the calibration parameters can be calculated. The accuracy of the RAC method is improved to a certain extent. However, since it only considers the first-order radial distortion parameters, the efficiency of this method is still limited [
7]. Based on the RAC algorithm, Weng et al. improved the distortion model and further improved the applicability of the radial consistency constraint algorithms [
8].
To overcome the limitation that the special environment does not meet the calibration requirement and to improve calibration adaptability, Faugeras and Luong proposed the camera self-calibration technology. Specifically, self-calibration is achieved by taking at least two images with a certain degree of overlap and establishing the epipolar transformation relationship to solve the Kruppa equation. However, this method has low accuracy and poor stability, and the Kruppa equation has the singular value problem [
9,
10]. To solve this problem, Zeller et al. took the sum of the distances from the pixels to the corresponding epipolar line as a constraint and used the Levenberg-Marquardt (LM) algorithm to optimize the equation to obtain the IO elements of the camera. However, the method has the problem of over-parameterization [
11]. Jiang et al. and Merras et al. used the epipolar constraint, the LM algorithm, and the genetic algorithm to obtain the optimal solutions for the camera’s IO and EO elements [
12,
13]. In addition, according to the homography from the calibration plane to the image plane, Zhang et al. solved the IO and the EO separately, which achieved high calibration accuracy. Moreover, because the method has the advantages of easy implementation, high precision, and good robustness, it has been widely adopted by scholars all over the world, which substantially promotes the development of three-dimensional (3D) computer vision from the laboratory to the real world [
14].
Regarding the calibration of binocular cameras, Tan et al. first reconstructed the homography transformation relationship between a stereo image pair based on the homologous points extracted from the stereo image pair and then obtained the calibration parameters based on this transformation. This method has the advantages of strong adaptability, flexibility, and high speed but has poor stability and low accuracy [
15]. Shi et al. used no less than six non-coplanar 3D lines to perform DLT, carried out linear estimation of the projection matrix, and jointly used a nonlinear optimization algorithm and distortion parameters to perform a combined adjustment. This method is a novel calibration method [
16]. Moreover, Caprile et al. proposed the classic vanishing point theory in 1990, that is, two or more parallel lines can converge at one point after infinite extension, and the convergence point is called the vanishing point [
17]. Wei et al. introduced the vanishing point theory into camera calibration. Multiperspective images of the target are first taken, and then the convergence point after perspective projection, i.e., the vanishing point, is obtained using the spatial parallel lines in the three orthogonal directions of a cube. Camera self-calibration is realized based on the relationship between the parallel lines and the geometric parameters to be calibrated. Since three parallel lines in orthogonal directions are needed in this method, the scope of application is limited [
18]. In addition, Fan et al. proposed a self-calibration method based on the circular point pattern [
19]. Zhao et al. used several tangent circles passing the endpoints of the diameter as the calibration target. Since the tangent lines of the circles at the two ends are parallel, the vanishing point is determined, and camera calibration is then carried out based on the image plane coordinates of the circle points [
20]. Based on this work, Peng et al. proposed a plane transformation-based calibration method. By fitting the pixel coordinates of the actual circle center, Zhang’s method is used for camera calibration and achieves a high calibration accuracy [
21]. To date, most studies have focused on the establishment of bundle adjustment models for camera calibration. Brown et al. first applied bundle adjustment to camera calibration by constructing a mathematical model combining the perspective projection model and distortion model, which enabled the use of nonmetric cameras for photogrammetry [
22]. Huang et al. Proposed the fusion beam method and high-precision global navigation satellite system (GNSS) to self-calibration. However, GNSS cannot be used in deep space exploration [
23]. Deng et al. used the LM algorithm to optimize the calibration results based on the relative position between the binocular stereo cameras. Moreover, Zheng et al. and Xie et al. further optimized the model based on indicators such as the unit weight root-mean-square error (RMSE) to improve the calibration accuracy and obtain good calibration parameters [
24,
25]. Subsequently, Liu et al. applied the bundle adjustment method to the positioning of planetary rovers, and it has a certain application value [
26].
The first studies on the stereo camera calibration of planetary rovers were from Bell and Mahboub et al. Specifically, based on the high-precision calibration points on the Curiosity Rover and the central attitude horizontal-vertical (CAHV) model [
27], the in-orbit stereo camera calibration of the Curiosity Rover was achieved [
28,
29]. Gennery et al. introduced the radial distortion parameter to the CAHV model and proposed the CAHVOR model (C is the vector from the origin of the ground coordinate system to the photography center, A is the unit vector perpendicular to the image plane, H and V are the horizontal vector and the vertical vector respectively, and the three are orthogonal to each other. O is the unit vector of the optical axis. When the image plane is not perpendicular to the optical axis, O is used to describe the direction of the optical axis, when the two are perpendicular, A and O coincide. R is the radial distortion parameter in the ground coordinate system.) [
30], which has been applied in the camera calibration of the Opportunity and Courage Rovers.. The teleoperation system of planetary rovers in China’s deep space exploration missions mostly uses photogrammetric mathematical models, and the conversion relationship between the mathematical models and the CAHVOR models is very complex. In addition, China’s planetary rovers are not equipped with high-precision calibration points. Therefore, the above methods cannot be directly applied for the in-orbit camera calibration of China’s planetary rovers. According to the geometric characteristics of the planetary rover itself and the carried objects, Workman et al. took the fixed geometric relationships among the planetary rover, the sun, and the horizon as constraints for camera self-calibration, but the improvement in calibration accuracy was limited [
31]. Wang et al. used the rotation angle between the stereo cameras as the constraint for camera calibration [
32], yet the in-orbit test has not been conducted.
In summary, although the above methods have achieved promising results, the in-orbit stereo camera calibration in the deep space exploration missions needs to be implemented in accordance with the actual conditions of each country. Because of limited available features on the planetary surface and possible high light intensity, a target-based calibration scheme is difficult to implement, and thus, self-calibration technology needs to be developed. This study proposed a self-calibration bundle adjustment method with multiple feature constraints for in-orbit camera calibration. We summarize our contributions as follows:
(1) A combined self-calibration bundle adjustment method with multiple feature constraints is constructed, which makes full use of the limited conditions in orbit, can complete the calibration under the condition of a small amount of observation data, and effectively improves the calibration accuracy in-orbit.
(2) An adaptive intensity weighted line extraction method is proposed, which ensures the completeness of line detection in different directions and effectively improves the extraction effect.
(3) The redundant observations with different constraints are analyzed, and the relationship between the redundant observations and the standard deviation of the model adjustment result is obtained, which provides a reference for the optimization of other bundle adjustment models.
(4) The proposed method can provide a reference for in-orbit camera calibration of planetary rovers in the deep space exploration missions of all countries.
The remaining sections of this paper are as follows:
Section 2 describes the overall process and each part of the proposed method.
Section 3 presents a series of experiments on different experimental conditions, and the results are compared.
Section 4 provides the conclusions.
3. Materials and Methods
To test the accuracy of the proposed feature-based self-calibration model, various types of experiments were carried out in a general laboratory, the simulated experimental field built by the China Academy of Space Technology (CAST), and under in-orbit conditions using the Chang’e-3 rover. In the general laboratory test, the calibration results of high-precision calibration plates were used as the initial values. In the lunar test site experiment, high-precision checkpoints were used to verify the calibration accuracy. For the in-orbit test, the dimensions of the national flag, solar panels, and other components were used.
3.1. Experiments in General Laboratory
The Zhang calibration method was used to perform an accurate calibration. A high-precision (0.1 mm) standard calibration plate with 15 × 11 grids and an edge length of 50 mm and a simulated planetary rover (
Figure 10) equipped with stereo navigation cameras were used. In this study, 13 image pairs were obtained at a fixed focal length. Then, the stereo camera was calibrated using MATLAB calibration toolbox [
43]. The calibration process is mainly composed of three steps, i.e., corner detection, calibration of IO and EO elements and distortion parameters, and optimal solution calculation via reprojection.
We analyzed the calibration results by re-projection error. The statistical results can be concluded that the average error of reprojection obtained by using 13 pairs of images is 0.3 pixels. The reprojection error of Camera 1 was slightly larger than that of Camera 2, indicating that the quality of Camera 1 was lower than that of Camera 2. Moreover, the reprojection errors of the 13th image pair were above 0.4 pixels. To obtain accurate calibration results, the 13th image pair was discarded. After that, the reprojection error of the left and right cameras was reduced to 0.2 pixels. The IO elements and distortion parameters obtained during calibration are shown in
Table 1.
After the calibration, the camera parameters could be used as the initial values of the proposed combined adjustment method. The method mainly includes four steps: (1) extraction of the coordinates of the virtual control points and the matching points, (2) determination of the initial EO elements, (3) self-calibration bundle adjustment with multiple constraints, and (4) accuracy assessment.
Specifically, the image point coordinate extraction software was used to extract the coordinates of the virtual control points with sub-pixel precision. Then the proposed method in
Section 2.3 was used to extract the straight line of the solar panel area. There were 10 pairs of virtual control points in the lander images and 13 pairs in the solar panel images. The virtual control points are shown in
Figure 11. Since it is impossible to simulate the actual lighting environment of solar panels, the comparison experiment of line extraction is implemented in
Section 3.3.
Before adjustment, the initial value of EO must be obtained. In this study, the DLT algorithm was used to calculate the initial values of the EO elements. The error equations of the left and right images were constructed separately.
Based on the above initial data, the proposed self-calibration bundle adjustment model with multiple constraints was used to carry out parameters calibration, and the LM algorithm was used for adjustment. Since the first image pair did not contain line features, only distance and coplanar constraint conditions were used. The model converged after 10 iterations, and the unit weight RMSE was 2.0 mm. The average reprojection error of the images was 2.7 pixels by the left and right camera. The second image pair contained line features, so collinear constraint was included in the calibration. The adjustment was then carried out based on the two pairs of images, and RMSE was reduced to 1.0 mm. The average reprojection error of the images was 1.1 pixels by the left camera and 0.9 pixels by the right camera. The average reprojection error indicated that the accuracy of the result was higher when the collinear constraint was included (using two pairs of images). Thus, the use of collinear constraints can effectively improve the accuracy of the calibration parameters.
The errors of calibration results when using one pair and two pairs of stereo images are shown in
Table 2.
Table 2 shows the RMSE of each parameter after the adjustment of the two pairs of images, and it was substantially lower than that of the first image pair. Among the key parameters, the relative accuracy of the camera focal length
f increased by 43.6% on average, the coordinates of the principal points
and
increased by 44.6% and 49.7%, respectively, and
,
,
, and
increased by 38.4%, 34.1%, 56.6%, and 50.1%, respectively. Thus, the addition of a collinear constraint significantly improved the calibration results. In addition, since there were more constraints for calibration using two pairs of images, this approach is beneficial to the calibration of the parameters.
To verify the accuracy of the calibration results, the proposed method was compared with the classic self-calibration bundle adjustment method, CAHVOR, and Vanishing Points. The results of these methods were compared with the coordinates obtained by the total station measurement system.
Table 3 shows the errors at 20 checkpoints obtained by different methods.
Table 3 shows that the proposed method had a higher accuracy than the other three methods, with an average error of less than 1 mm. Compared with the other three methods, the accuracy of our method is improved by 25.0%, 40.0%, and 43.8% respectively. The error of the bundle adjustment method was slightly larger than that of the proposed method and the errors of CAHVOR and vanishing points were much larger.
The above results show that the proposed method can effectively realize camera calibration using multiple pairs of images. The constraints increased the robustness of the calibration results and the accuracy of the parameters. Thus, it can perform the calculation and inspection of the IO elements and lens distortion in the stereo camera under the in-orbit condition.
3.2. Experiments in Simulated Lunar Environment
To simulate the various working conditions of the planetary rover in a real deep space environment, the CAST has established a large indoor test field with parallel light arrays, volcanic ash-simulated lunar soil, rocks, craters, and various types of planetary vehicle prototypes.
Figure 12 shows the indoor test field and the prototype rover.
The prototype rover took eight pairs of images at different photographic stations of the indoor test field. Sixty-four checkpoints were arranged in the field of view of the stereo navigation cameras to verify the calibration accuracy. The coordinates of the checkpoints were measured with a high-precision total station measurement system (Leica TS50,
Figure 13a), and the angle measurement accuracy was 0.5 s.
Figure 13b shows the moving trajectory of the planetary rover and the photographic stations.
Figure 14 shows the 64 checkpoints for stereo cameras.
The stereo navigation cameras of the Chang’e-3 prototype were used to collect 27 pairs of stereo images for calibration. Then, the proposed model was used (without the collinear constraint since the prototype was not equipped with solar panels) to verify the IO elements and the radial and tangential distortion parameters. The calibrated parameters of the stereo navigation cameras are shown in
Table 4.
According to the calibration results, it can be concluded that the differences in the calibration parameters of the proposed method and the calibration plate were between 2.8 pixels and 6.2 pixels. Specifically, the differences in the focal length f of the left and right cameras were 6.2 pixels and 4.6 pixels, respectively, the differences in the coordinates of principal points and were 2.8 pixels, 5.0 pixels, 3.1 pixels, and 4.3 pixels, respectively, and the results of , , , and were close.
Since the calibration method based on the calibration plate and the proposed method are different types of models, it is difficult to directly compare the accuracy from the differences. Therefore, checkpoints were used to verify the accuracy of the results. The space intersection appropriate for multi-images was used to calculate the coordinates of 64 checkpoints in the object coordinate system. Taking the coordinates of the checkpoints measured by the total station measurement system as the true values, the calibration results of the four methods were compared, and the results are shown in
Table 5.
From the statistical results of checkpoint errors, it can be concluded that the proposed method with multiple constraints was significantly more accurate than the self-calibration bundle adjustment model, which was more accurate than the other two methods. Compared with the other three methods, the average accuracy increased by 31.58%, 49.72%, and 45.50%, the maximum error decreased by 26.46%, 59.11%, and 43.41%, and the RMS decreased by 36.44%, 45.09%, and 43.86%. Overall, the proposed method was 42.27%, 42.99%, and 42.35% better than the other methods. The test results indicated that the constraints improved the robustness and accuracy of the adjustment model, and the proposed multiple constraints were effective.
Four pairs of checkpoints in
Figure 15 were used for verification. The distance was calculated based on their coordinates obtained by the adjustment. The accuracy of the distance is shown in
Table 6.
According to the statistical results of the distance error, it can be concluded that the distance deviation between checkpoints was between 0.9 mm and 1.8 mm, with an average deviation of 1.4 mm. Thus, the camera parameters and checkpoint coordinates calculated by the proposed method have high accuracy, demonstrating the reliability of the proposed method.
3.3. In-Orbit Calibration and Analysis
After the planetary rover separated from the lander, it adjusted its moving direction and took sequential images at five photographic stations, i.e., photographic stations X, A, B, C and D (
Figure 16). Ten pairs of stereo images from the top of the lander, photographic stations C and D are used to verify the effectiveness of the proposed method under in-orbit conditions.
The in-orbit calibration process of the navigation cameras can be divided into four steps: (1) extraction of the image point coordinates of the virtual control points and the matching connection points, (2) calculation of the initial EO elements, (3) self-calibration bundle adjustment with multiple constraints, and (4) accuracy assessment. Since no checkpoints with known coordinates were on the lunar surface, the accuracy of the camera parameters was evaluated based on the dimensions of the devices on the rover and the positioning results of the planetary rover.
(1) Manual extraction of the coordinates of the virtual control points. The sub-pixel coordinate extraction of the connecting points is carried out with the software specially designed for the Chang’e-3 mission. A total of 9 pairs of connection points were extracted from the images taken at station D and were taken as the control points. Another 8 pairs of feature points were extracted as distance constraints from the images of the solar panel taken at station C.
Figure 17 shows the distribution of virtual control points on the solar panel of the lander and planetary rover whose coordinates are measured on the ground.
(2) Automatic matching of the connection points. The parameters to be solved included the position and orientation of the camera and the virtual control points were not uniformly distributed in the image; therefore, to improve the accuracy of the model solution, the stereo images were matched to build a set of connection points.
Figure 18 shows the matching results of two pairs of stereo images.
(3) Extraction of line features on the solar panel. The adaptive line extraction method proposed in
Section 2.3 was used to extract the line features in the images of the solar panel.
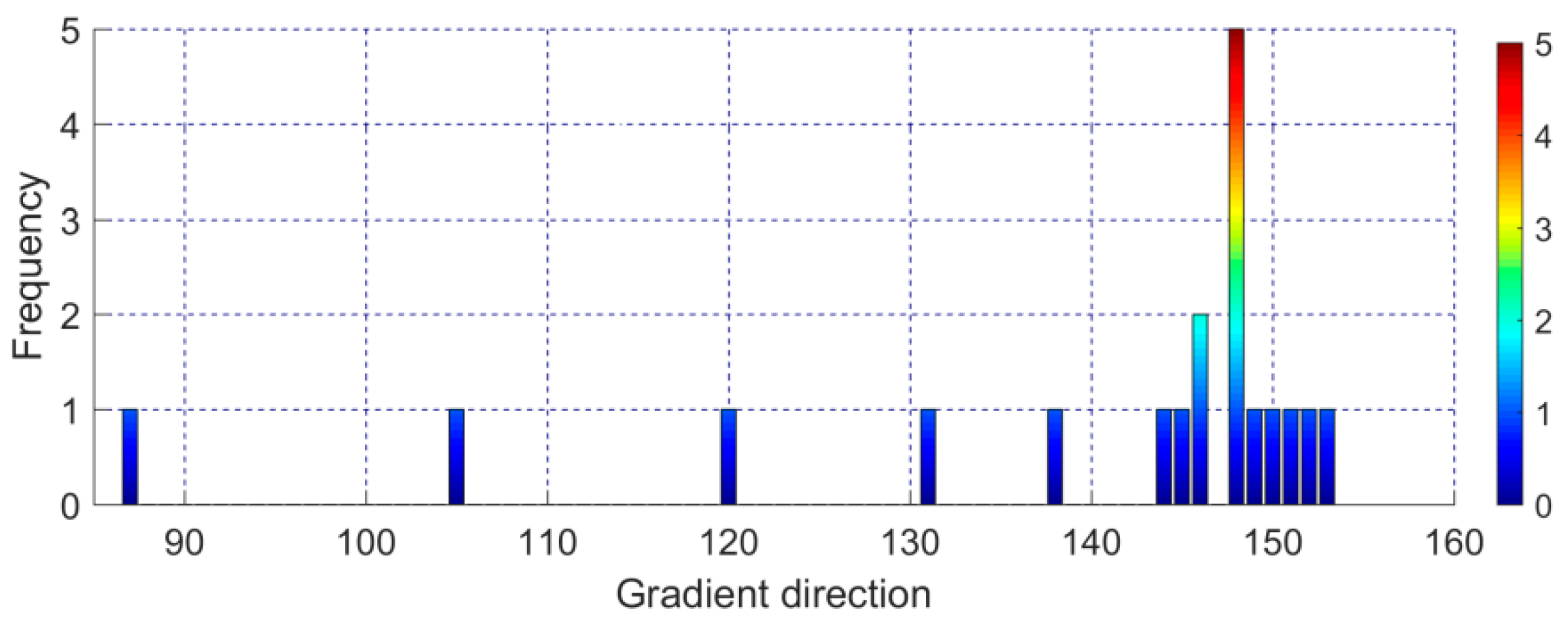
Figure 19 shows the result of line extraction using the proposed method and the classic LSD (line segment detector) method.
The results show that the proposed method extracted more lines. Especially, the lines with smaller gradients were also extracted. The main reason was that the threshold of the proposed method was adaptively determined according to the gradient direction of the line, which effectively overcame the problem that the global unified threshold cannot be used for extraction because of the large brightness difference in the solar panel area in the stereo image due to the color and illumination.
According to the extracted coordinates of the image point, the coordinates of the connection point, and the initial camera parameters obtained before launching, the initial EO elements were solved by the DLT algorithm. Then, the self-calibration bundle adjustment method with multiple constraints was used for 3 image pairs of the top of the lander and 7 image pairs from each of photographic stations C and D. The IO elements and distortion parameters and the corresponding RMSEs obtained by the combined adjustment are shown in
Table 7.
Table 7 shows that the proposed method obtained the camera’s IO elements and distortion parameters with high accuracy. The average RMSE of focal length
f and coordinates of the principal points
and
was only 0.1 pixel, 0.2 pixels, and 0.2 pixels, respectively. Thus, the proposed method was feasible under in-orbit conditions and can provide technical references for in-orbit calibration of planetary rovers in deep space exploration missions.
Furthermore, the influence of different constraints on the calibration was analyzed. Combining the above observations and different constraints, 7 different models were established. Since the same points are used for collinear and coplanar constraints, both are used as constraints at the same time. Finally, the median errors of various models are obtained after adjustment, and the details are shown in
Table 8.
From the above experimental results, it can be concluded that BA can be solved without constraints, but the standard deviation is larger than other models with additional constraints, indicating that the proposed constraints are beneficial to the adjustment.
Compared with the BA, the standard deviation of the various models with different constraints is reduced by 8%, 61%, 63%, 62%, 75%, and 76%, respectively, indicating that the accuracy of the proposed method is significantly improved. Since there are more redundant observations than other models, CCC and RC have a greater effect on the improvement of calibration accuracy. we found the sums of squared residuals of BA with different additional constraints are pretty close. The larger the redundancy number, the smaller the estimation precision of calibration parameters. So the redundancy number of BA with different additional constraints is larger than that of BA. Thus, the calibration parameters estimation precision of BA with different additional constraints is better, and the adoption of various models proposed in this paper as geometric constraints is more rational.
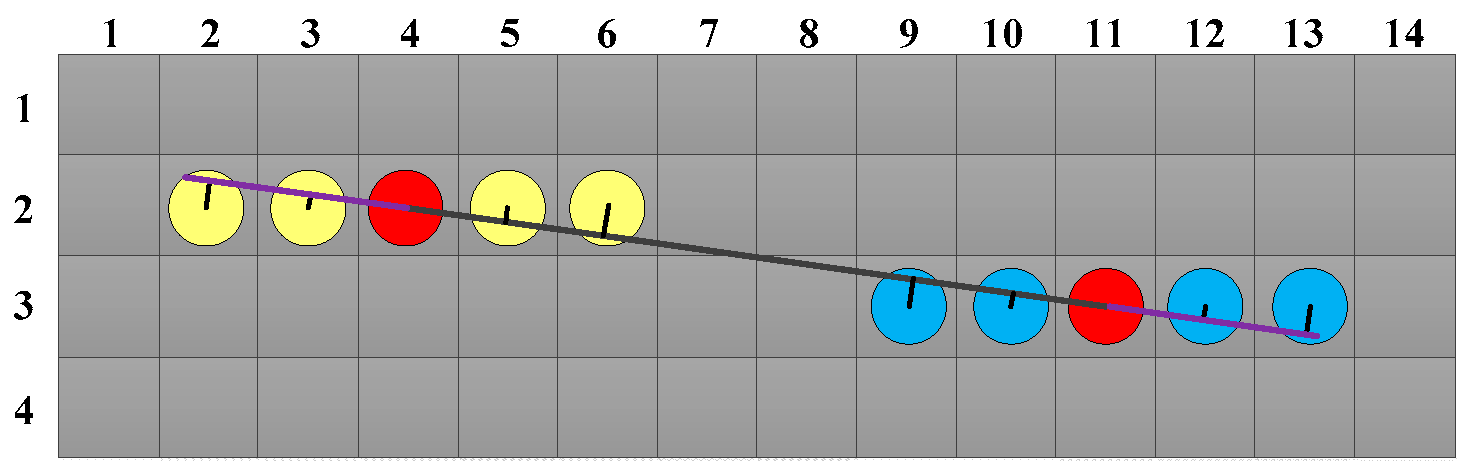
In addition, the accuracy of the parameters was indirectly verified using the size of the national flag.
Figure 20 shows the manually extracted corner points of the national flag, and
Table 9 shows the design size and calculated size of the national flag and the differences.
According to
Table 9, the calculation errors were not more than 2 mm, indicating that using the IO elements and distortion parameters calculated by the proposed method to solve the space coordinates of other points can achieve good accuracy.
Based on the line extraction results of the solar panel from images taken by stereo cameras at different photographic stations and angles, the coordinates of the intersection points between lines, and the calculated parameters, the lengths of multiple OSRs were calculated and compared with the true value.
Figure 21 shows the endpoints of the OSRs after line extraction. The length and width of the OSR obtained by the 3D coordinates calculated by the binocular vision measurement method were compared with the design values, as shown in
Table 10.
Table 10 shows that the calculated OSR dimensions from images of different angles and distances were accurate. The average length of calculated by the parameters obtained by the proposed method was 31.2 mm, and the average width was 39.8 mm, with an average deviation from the designed value of 0.4 mm and 1.0 mm, respectively. Thus, the camera parameters obtained by the proposed method have good accuracy. In particular, the lens distortion parameters have good reliability and accuracy.
In summary, the classic bundle adjustment model has good accuracy. However, in the absence of constraints, the point position may still deviate in the light direction during the adjustment process. With the addition of distance constraints and coplanar constraints, the spatial geometric structure of the observations is more stable and reliable, thereby reducing the point deviation during the solution, and ultimately improving the accuracy of camera parameter calibration. In addition, the relative pose constraints of the left and right navigation cameras can also realize the spatial geometric constraints of the EO, making the model during the adjustment more stable and the solution more accurate.
4. Conclusions
Accurate IO elements of the stereo camera are crucial for the in-orbit navigation and positioning of planetary rovers. High-precision in-orbit parameter calibration can provide a reference for path planning of the planetary rover and play a key role in ensuring the safety of the planetary rover and improving the efficiency of scientific missions. In deep space exploration missions, the variables that can be used for in-orbit camera calibration are very limited. Therefore, an in-orbit stereo camera self-calibration method of planetary rovers with multiple constraints was proposed. Based on the bundle method of the binocular stereo camera, four types of constraints were included to construct the self-calibration bundle adjustment model with multiple constraints, i.e., the constraint of the distance between feature points on the lander and the planetary rover, the collinear constraint of the connection points on the solar panel, the coplanar constraint of feature points on the solar panel and national flag, and the relative position and orientation constraint of the left and right cameras. Given the problem of unsatisfactory distribution of line gradient features in the solar panel images, an adaptive line extraction method based on brightness weighting was proposed to ensure the accuracy of line extraction in different directions. Through various types of experiments, the following conclusions were obtained:
(1) In the simulations in a general laboratory, two pairs of stereo images were used in the adjustment. The results showed that using the extracted linear features as additional constraints can effectively improve the accuracy of the obtained camera parameters, and the reprojection error was reduced to 1.0 pixels. Overall, the accuracy of various parameters was improved by 34.1–56.6%.
(2) In the experiments at the simulated experimental field built by CAST, 64 checkpoints were used to test the calibration accuracy. The results showed that the average error of the proposed method was only 2.1 mm, which was 31.58%, 49.72%, and 45.50% better than the classic self-calibration bundle adjustment method, CAHVOR, and Vanishing Points, respectively. Four pairs of checkpoints were selected for distance verification, and the average distance error was only 1.4 mm.
(3) In the in-orbit calibration test of the Chang’e-3 planetary rover, the average RMSE of the focal length and the principal point coordinates was only 0.2 pixels for the left camera and right camera. The maximum error in flag dimensions was 2.0 mm and the minimum error was 0.2 mm. The maximum error in the length of the OSR of the solar panel was 1.5 mm, and the minimum error was 0.1 mm.
Based on the above results, the proposed method can obtain high-precision IO elements and lens distortion parameters of the stereo cameras under in-orbit conditions, which provide a reference for in-orbit camera calibration of planetary rovers in the deep space exploration missions of all countries.