Estimation of 1-km Resolution All-Sky Instantaneous Erythemal UV-B with MODIS Data Based on a Deep Learning Method
Abstract
:1. Introduction
- We used MODIS data, whose spectral bands contain cloud and aerosol information, as the original input for retrieving UV-B. Compared with traditional satellite-based methods, MODIS data have higher resolution and do not contain UV bands.
- We compared machine learning methods to retrieve erythemal UV-B from the MODIS top-of-atmosphere (TOA) input.
- We established a deep learning framework that can develop high-level features from inputs for erythemal UV-B retrieval, which avoids hand-crafting features that may fail to generalize new data. We introduced the residual structure to the proposed neural network, where the coarse representation of raw inputs for erythemal UV-B retrieval is refined in a cascading manner.
- We established datasets at SURFRAD and UVMRP sites and performed model training and testing at different sites.
2. Related Work
2.1. Satellite-Based Erythemal UV-B Retrieval
2.2. Deep Learning and Machine Learning in Remote Sensing Estimation of Surface Solar Radiation
3. Data
3.1. Ground Measurements
3.2. Satellite Data
3.2.1. OMI Ozone Data
3.2.2. MODIS Level 1 Data
3.2.3. MODIS Surface Reflectance
4. Methodology
4.1. Benchmark Models
4.1.1. Random Forest Regressor
4.1.2. Support Vector Machine (SVM)
4.1.3. Fully Connected Neural Network (FCNN)
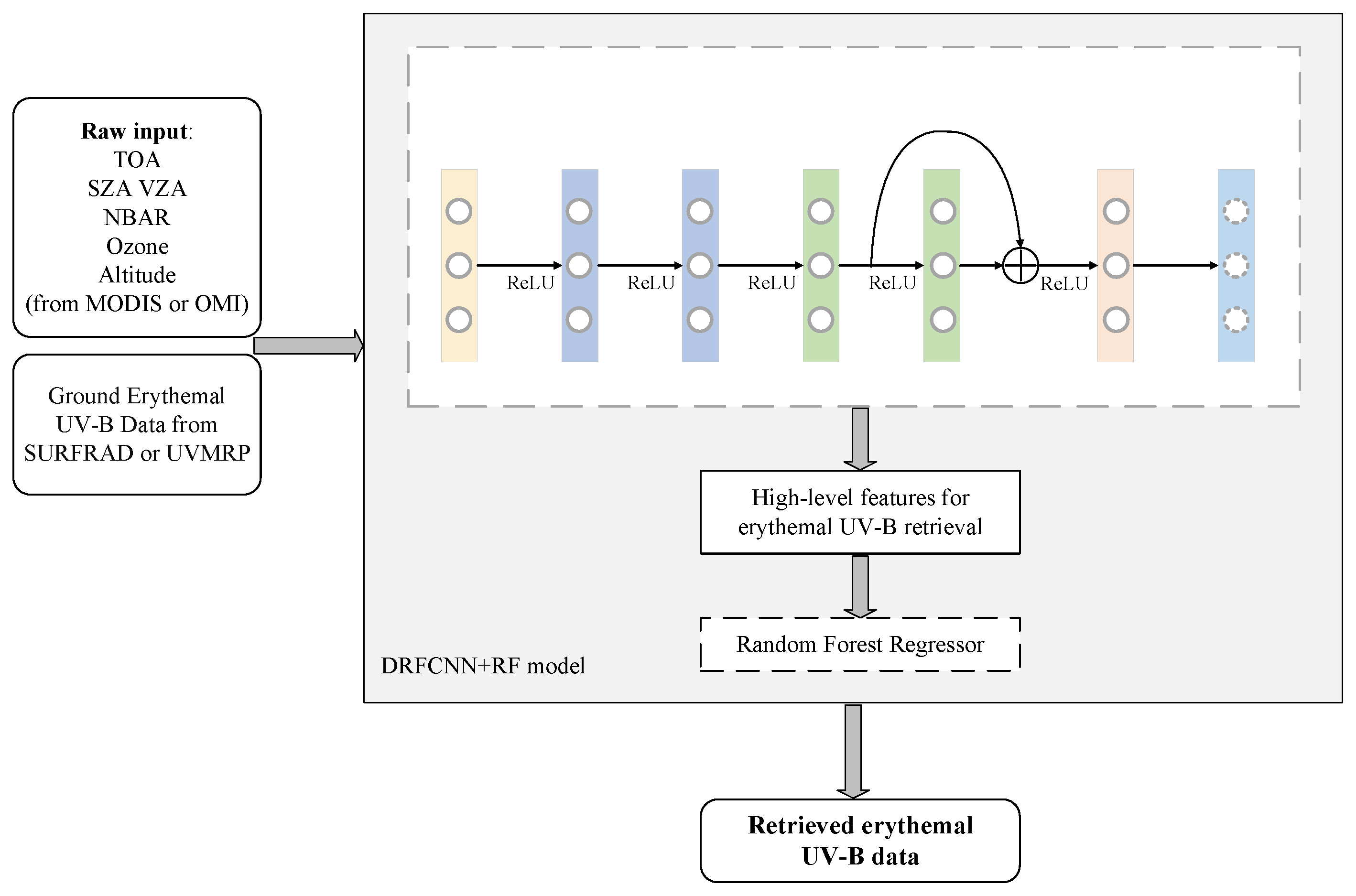
4.2. The Proposed Model: Deep Residual Fully Connected Network (DRFCN)-Random Forest Regressor (RF)
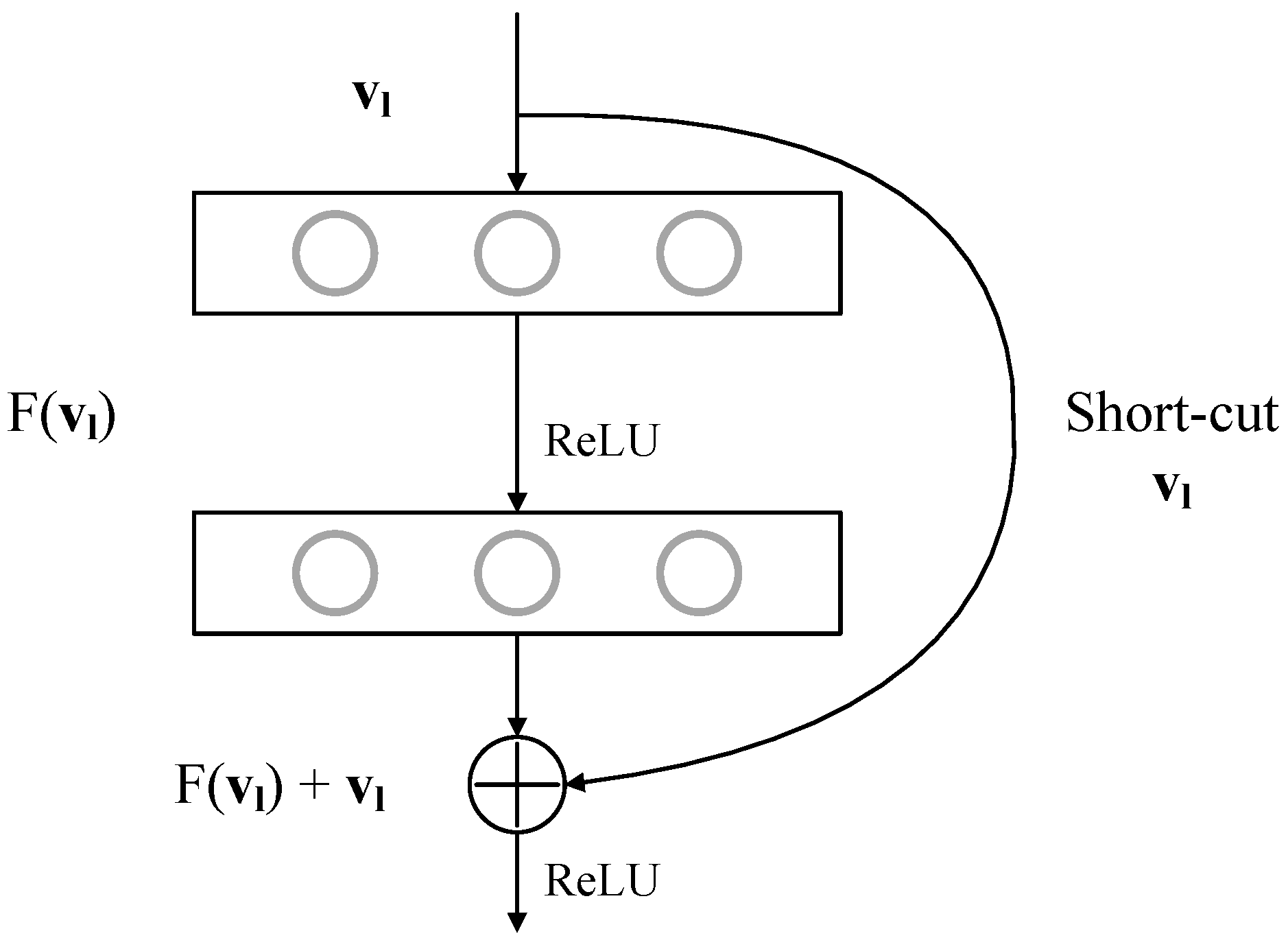
- Deep feature extraction: The first part is a deep residual fully connected network (DRFCN), which converts MODIS TOA and other parameters in a data-driven manner into a representation that is more meaningful to the surface erythemal UV-B retrieval. The proposed DRFCN, while implementing progressive data distillation through these layers, uses the residual links to fuse the data refined from the shallow network. In addition, the residual connections construct short-cuts for gradient propagation, which leads to more stable training dynamics than simple feedforward networks. Finally, we obtain the best data representation for erythemal UV-B retrieval, which we call the deep feature.
- Random forest regressor: After the deep features are extracted from the pre-trained residual network, they are used to fit an external RFR, a robust decision tree-based ensemble model to obtain the final predicted erythemal UV-B value. Although each depth feature of the RF input in the proposed method cannot point out the specific physical meaning, they are another manifestation of these parameters with specific physical significance.
Deep Residual Fully Connected Network (DRFCN)
4.3. Benchmark Model Combination for Comparison
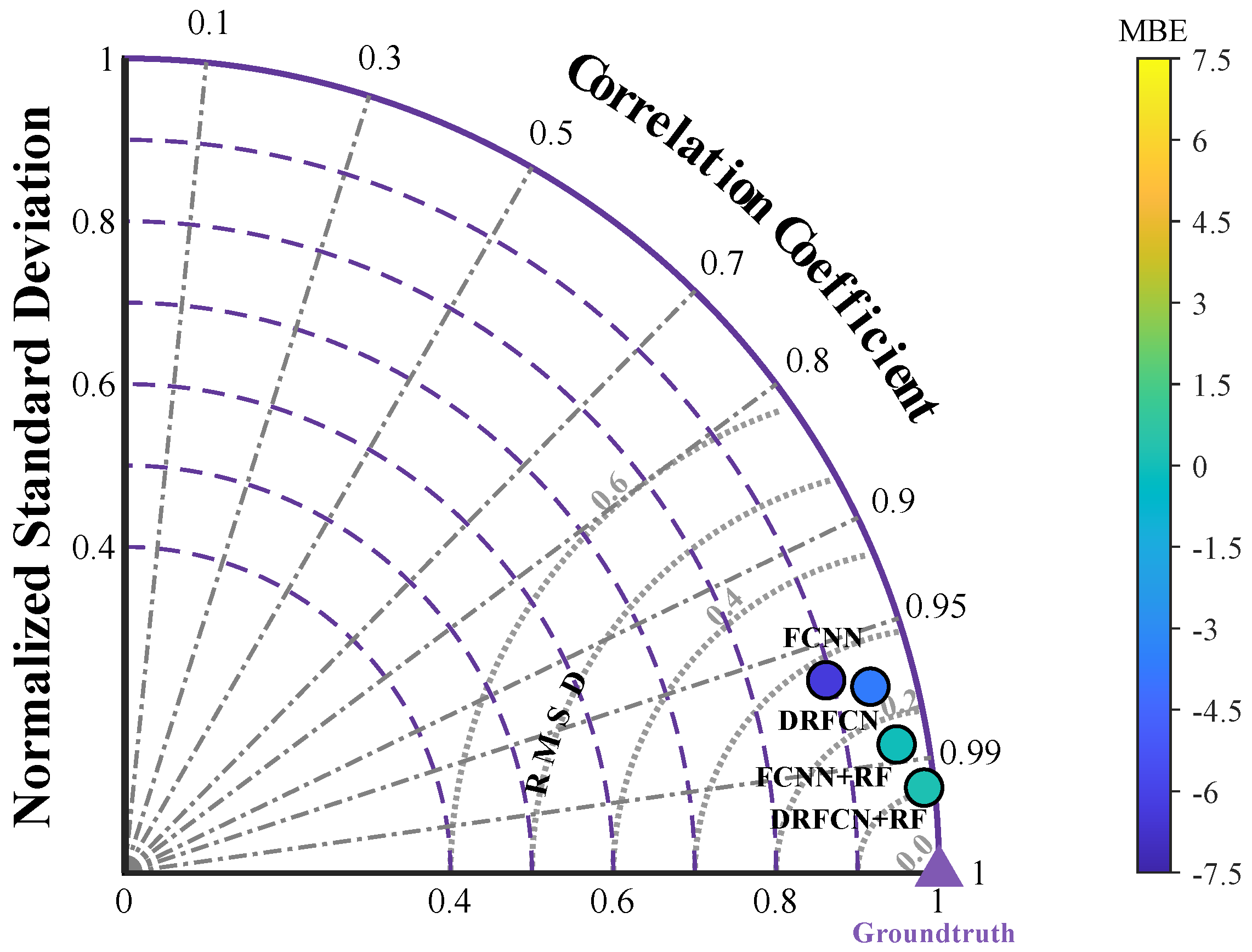
4.3.1. Ablation Study: FCNN, DRFCN, FCNN+RF, and DRFCN+RF
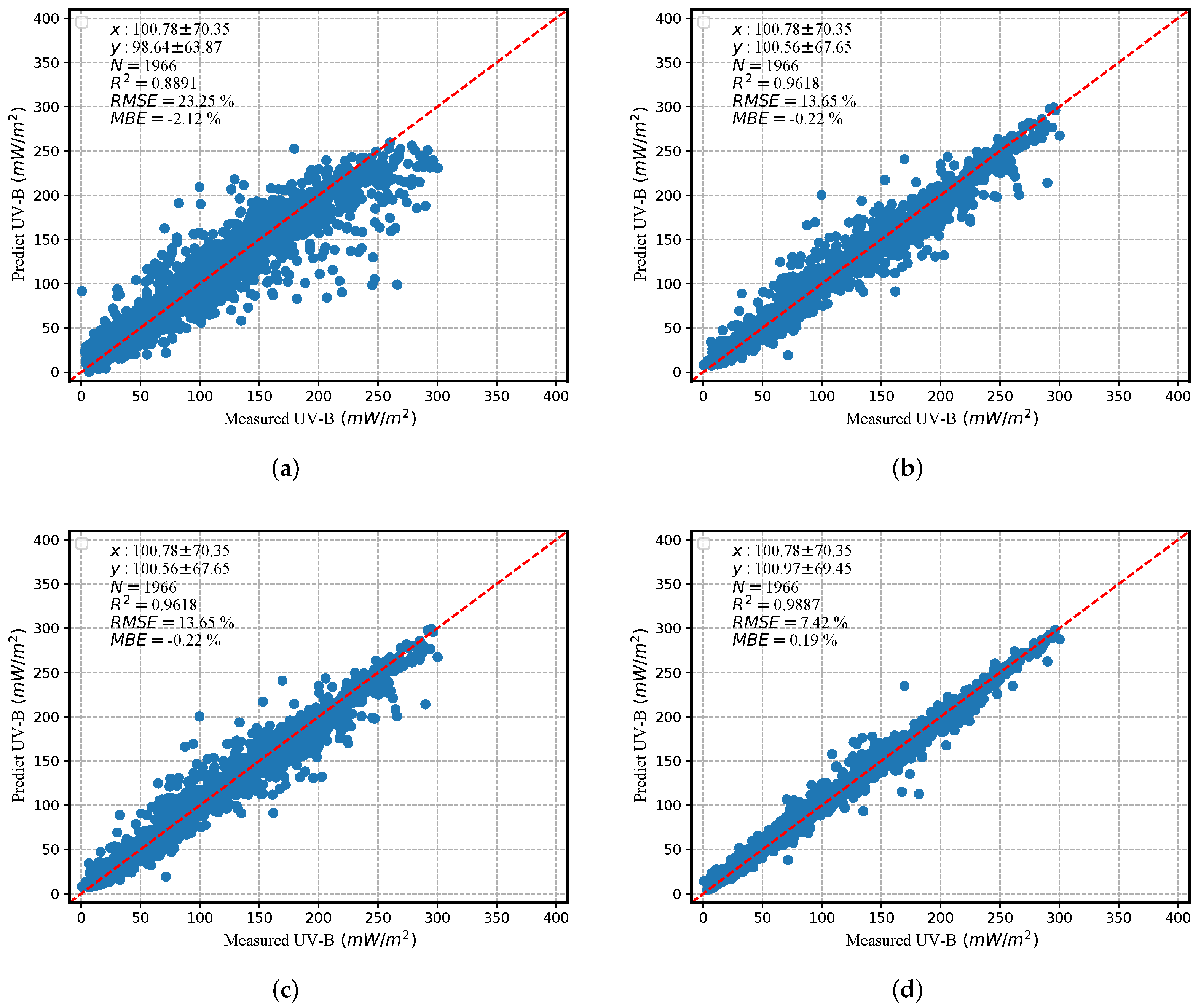
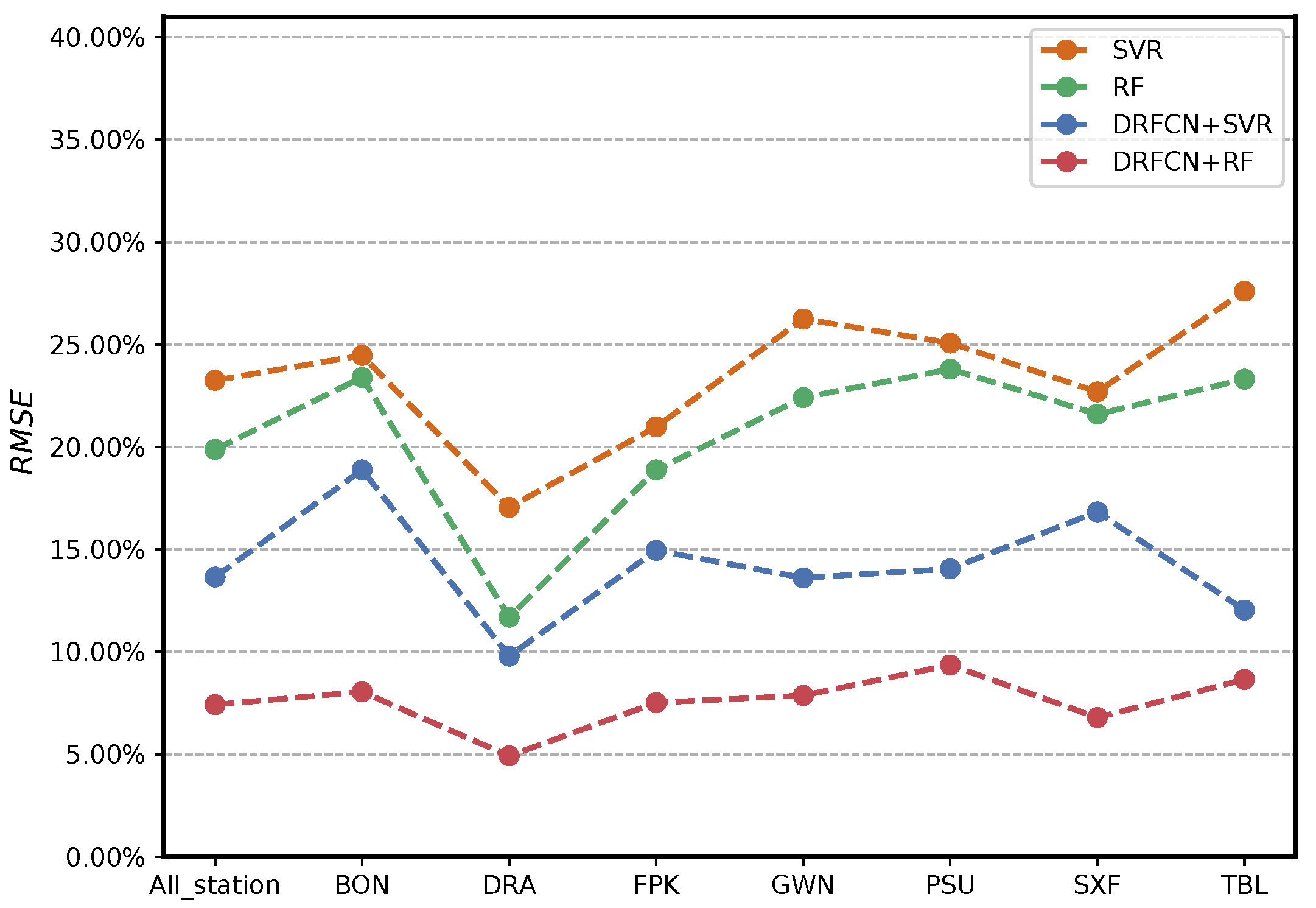
4.3.2. Method Intercomparison: SVR, RF, DRFCN+SVR, and DRFCN+RF
4.4. Dataset
4.5. Evaluation Strategy
4.6. Evaluation Metrics
5. Comparison Results
5.1. Evaluation on SURFRAD Test Set
5.1.1. Parameter Sensitivity Analysis
5.1.2. Ablation of DRFCN+RF Model
5.1.3. Method Inter-Comparison
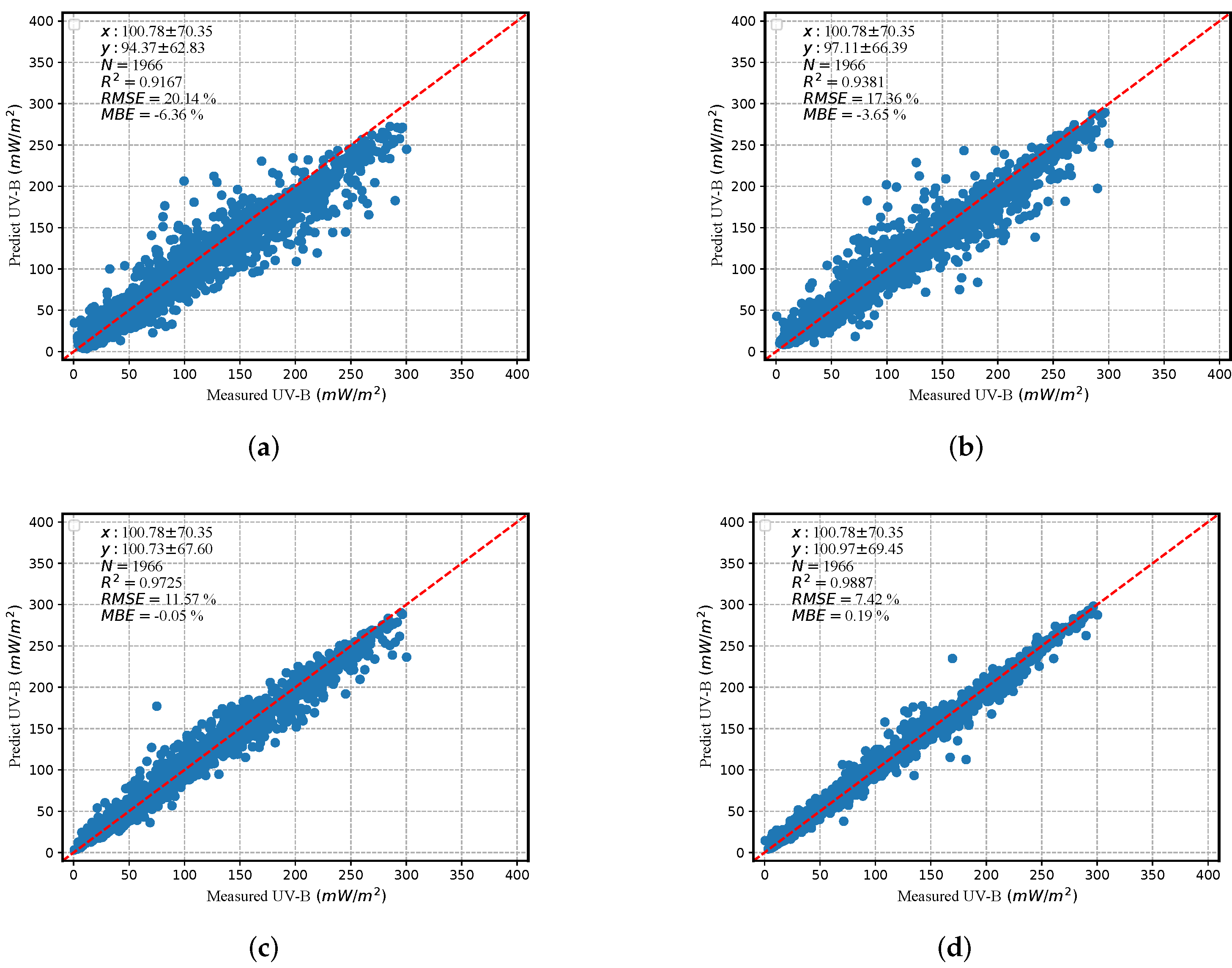
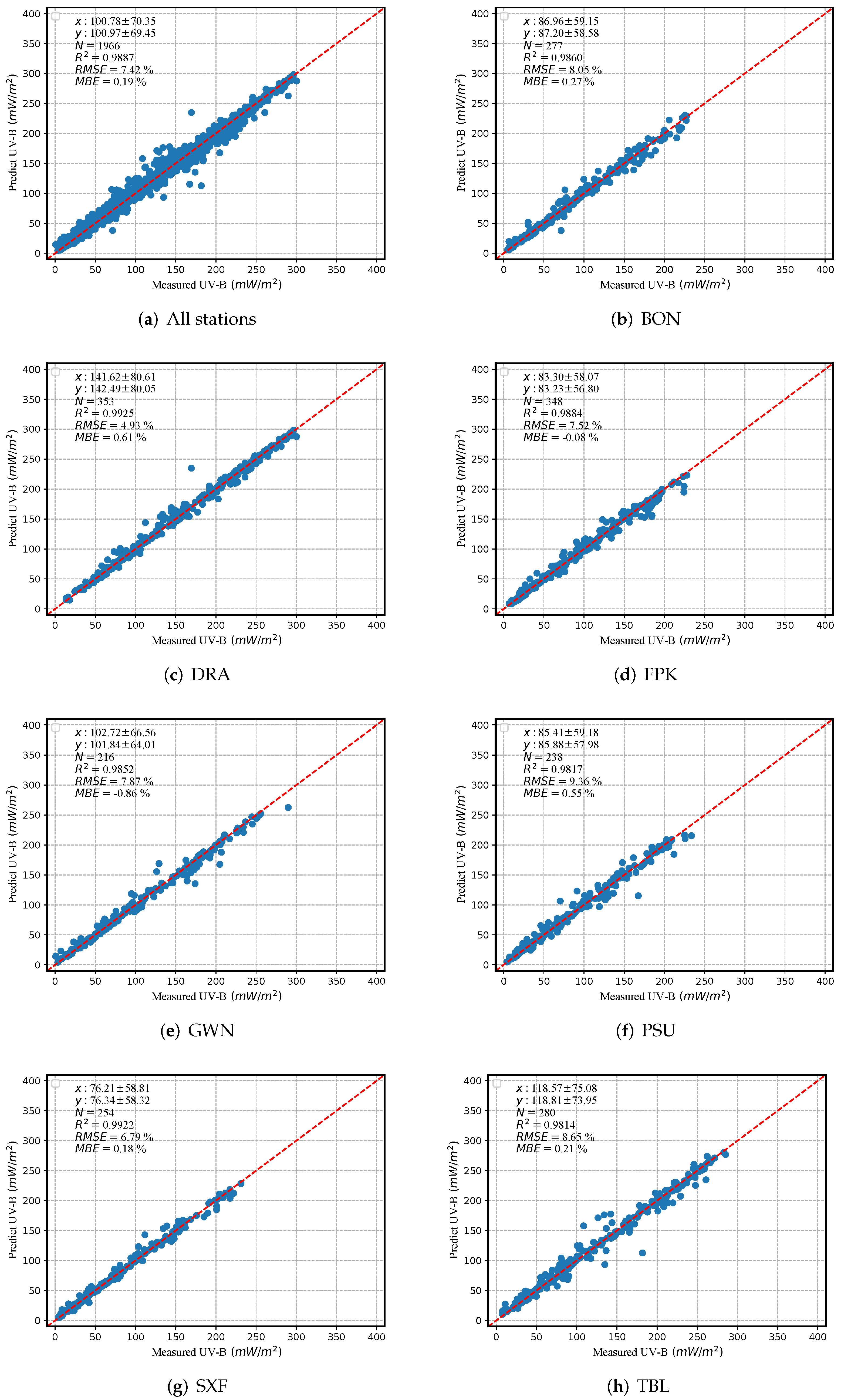
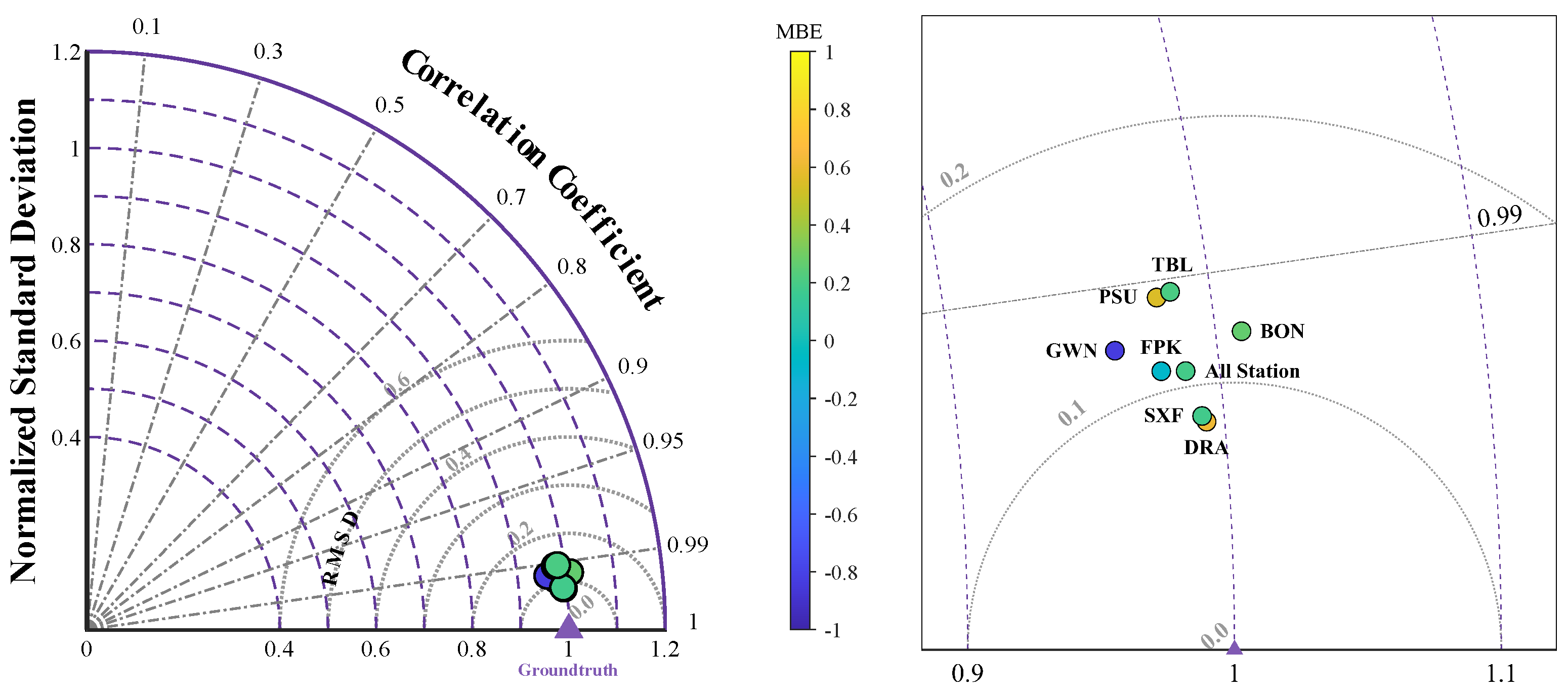
5.1.4. Evaluation of DRFCN+RF Model
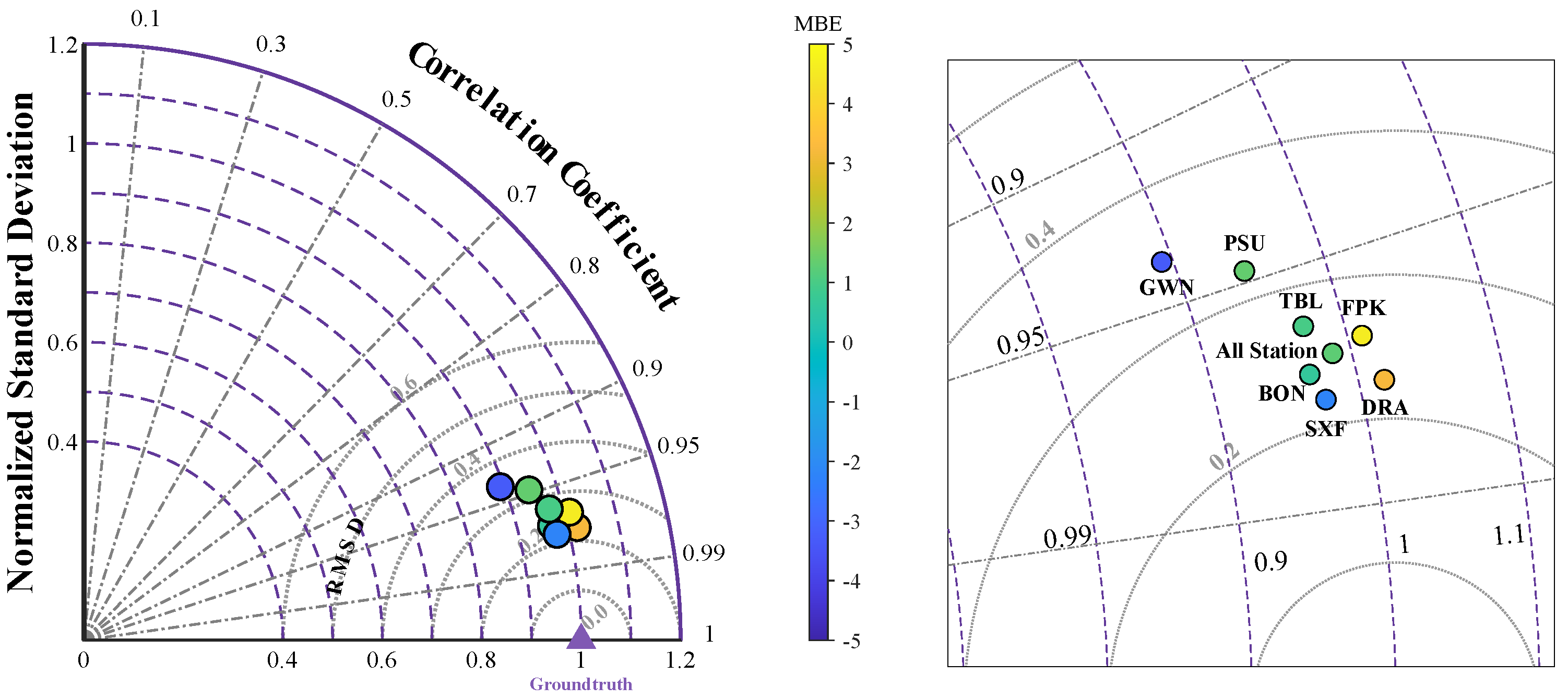
5.2. Model Evaluation with SURFRAD-2017 Dataset
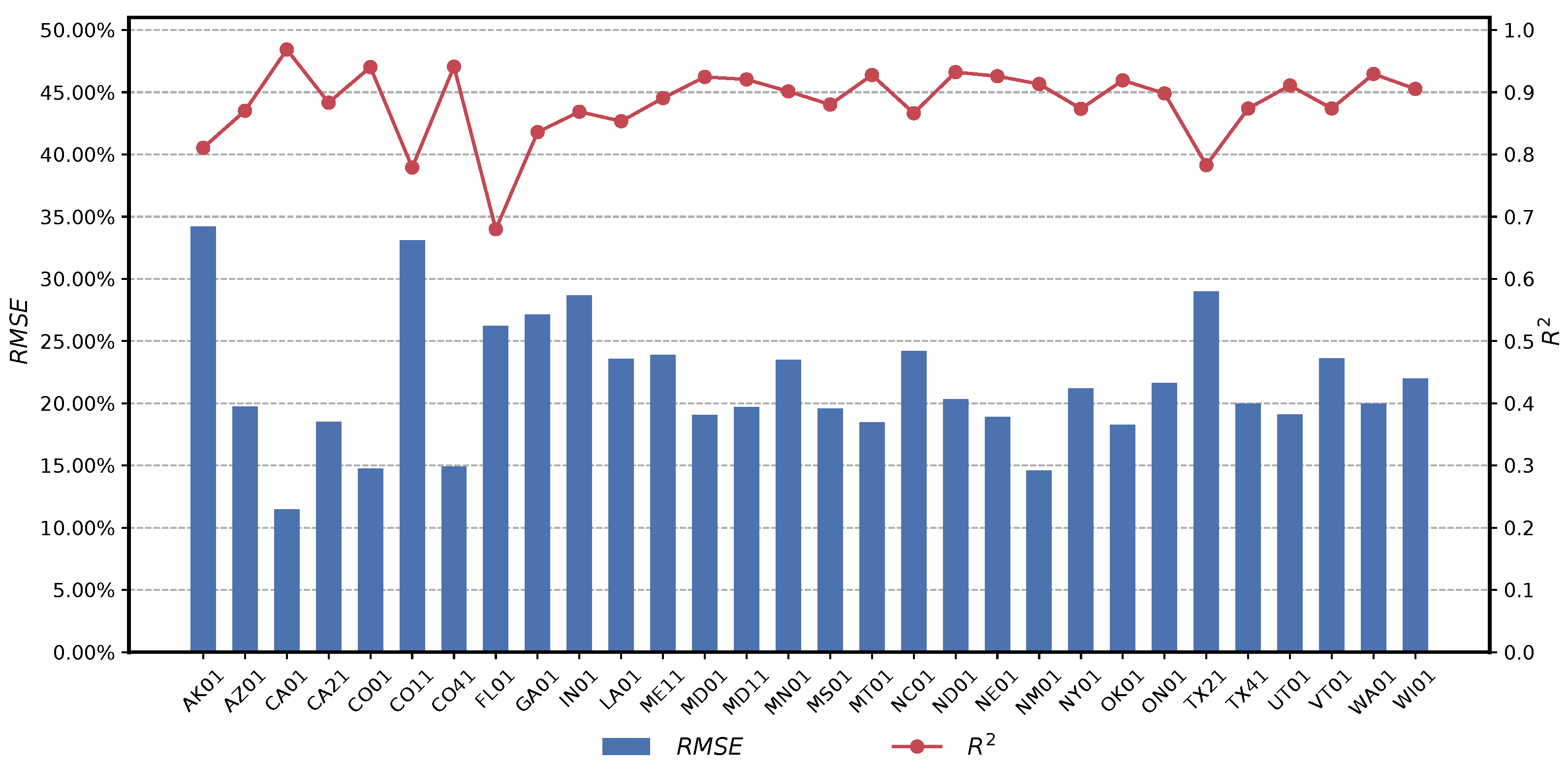
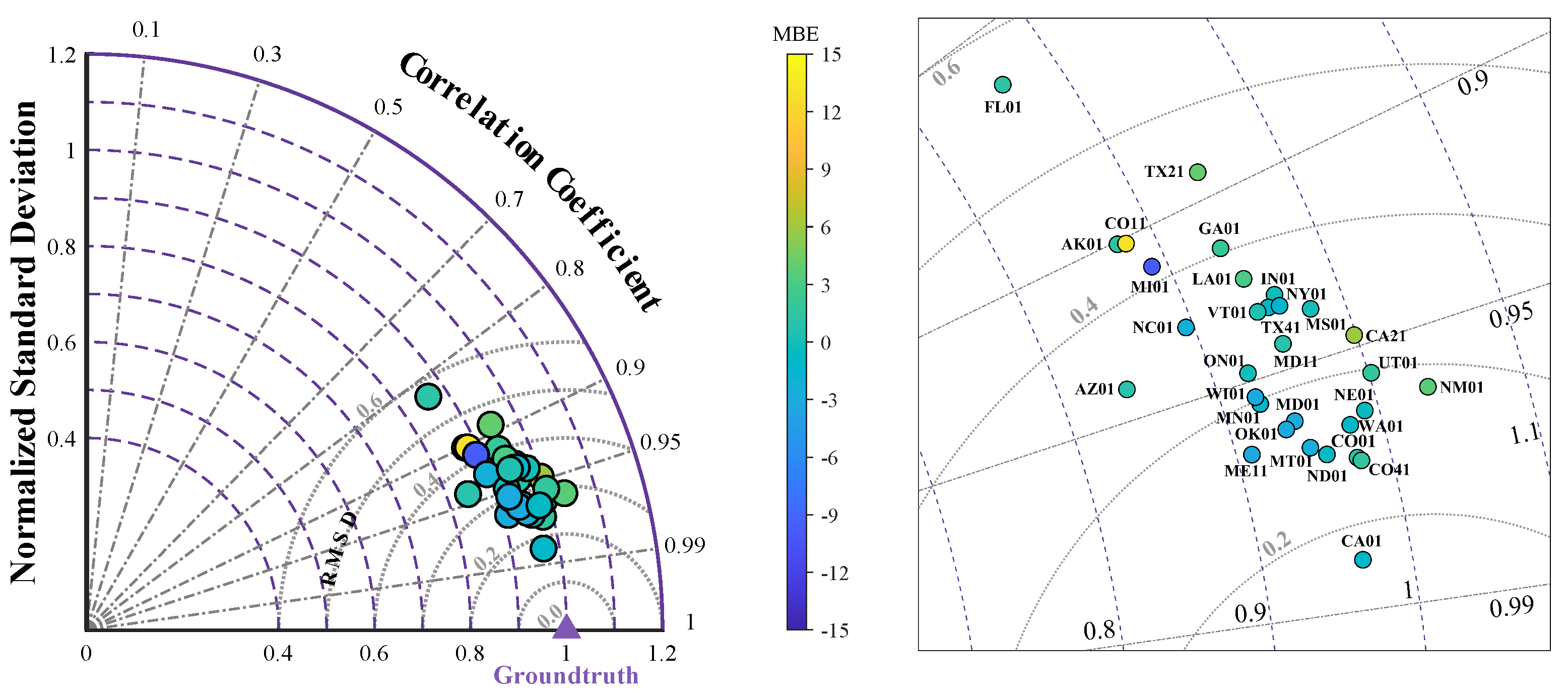
5.3. Model Validation against UVMRP Dataset
5.4. Discussions
5.4.1. UV-B Retrieval Ability of Different Algorithms
5.4.2. Generalization Ability of DRFCN+RF
5.4.3. Broader Impact of DRFCN+RF
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MODIS | Moderate resolution imaging spectroradiometer |
| UV | Ultraviolet |
| UV-B | Ultraviolet-B |
| TOA | Top-of-atmosphere |
| SZA | Solar zenith angle |
| VZA | View zenith angle |
| SAA | Solar azimuth angles |
| VAA | View azimuth angle |
| NBAR | Nadir bidirectional reflectance distribution function-adjusted reflectance |
| COD | Cloud optical depth |
| AOD | Aerosol optical depth |
| SURFRAD | Surface radiation budget network |
| UVMRP | UV-B monitoring and research program |
| NDACC | International network for the detection of atmospheric composition change |
| NOAA | National oceanic and atmospheric administration |
| USDA | United states department of agriculture |
| TOMS/EP | Total ozone mapping spectrometer onboard the earth probe satellite |
| OMI | Ozone monitoring instrument |
| GOME-2 | Global ozone monitoring experiment-2 |
| TEMIS | Tropospheric emission monitoring internet service |
| RT | Radiative transfer |
| LUT | Look-up-table |
| AVHRR/3 | Third advanced very high-resolution radiometer |
| CERN | Chinese ecosystem research network |
| ML | Machine learning |
| SVM | Support vector machine |
| SVR | Support vector regression |
| RF | Random forest |
| RFR | Random forest regressor |
| ANN | Artificial neural networks |
| GA-ANN | Genetic algorithm-ANN |
| DL | Deep learning |
| DNN | Deep neural networks |
| FCNN | Fully connected neural network |
| DRFCN | Deep residual fully connected network |
| Mean bias error | |
| Normalized mean bias error | |
| Root mean square error | |
| Normalized root-mean-square error | |
| Coefficient of determination | |
| R | Coefficient of correlation |
| Normalized standard deviation | |
| Normalized centered root-mean-square difference |
References
- Gray, L.J.; Beer, J.; Geller, M.; Haigh, J.D.; Lockwood, M.; Matthes, K.; Cubasch, U.; Fleitmann, D.; Harrison, G.; Hood, L.; et al. Solar influences on climate. Rev. Geophys. 2010, 48. [Google Scholar] [CrossRef]
- Singh, S.; Lodhi, N.K.; Mishra, A.K.; Jose, S.; Kumar, S.N.; Kotnala, R. Assessment of satellite-retrieved surface UVA and UVB radiation by comparison with ground-measurements and trends over Mega-city Delhi. Atmos. Environ. 2018, 188, 60–70. [Google Scholar] [CrossRef]
- Utrillas, M.; Marín, M.; Esteve, A.; Salazar, G.; Suárez, H.; Gandía, S.; Martínez-Lozano, J. Relationship between erythemal UV and broadband solar irradiation at high altitude in Northwestern Argentina. Energy 2018, 162, 136–147. [Google Scholar] [CrossRef]
- Holick, M.F. Biological effects of sunlight, ultraviolet radiation, visible light, infrared radiation and vitamin D for health. Anticancer Res. 2016, 36, 1345–1356. [Google Scholar]
- Serrano, M.A.; Cañada, J.; Moreno, J.C.; Gurrea, G. Solar ultraviolet doses and vitamin D in a northern mid-latitude. Sci. Total Environ. 2017, 574, 744–750. [Google Scholar] [CrossRef]
- Young, C. Solar ultraviolet radiation and skin cancer. Occup. Med. 2009, 59, 82–88. [Google Scholar] [CrossRef] [Green Version]
- Xiang, Y.; Laurent, B.; Hsu, C.H.; Nachtergaele, S.; Lu, Z.; Sheng, W.; Xu, C.; Chen, H.; Ouyang, J.; Wang, S.; et al. RNA m 6 A methylation regulates the ultraviolet-induced DNA damage response. Nature 2017, 543, 573–576. [Google Scholar] [CrossRef]
- Young, A.R.; Claveau, J.; Rossi, A.B. Ultraviolet radiation and the skin: Photobiology and sunscreen photoprotection. J. Am. Acad. Dermatol. 2017, 76, S100–S109. [Google Scholar] [CrossRef] [Green Version]
- Bernard, J.J.; Gallo, R.L.; Krutmann, J. Photoimmunology: How ultraviolet radiation affects the immune system. Nat. Rev. Immunol. 2019, 19, 688–701. [Google Scholar] [CrossRef] [PubMed]
- McKinlay, A.; Diffey, B. A reference spectrum for ultraviolet induced erythema in human skin. CIE J. 1987, 6, 17–22. [Google Scholar]
- Iqbal, M. An Introduction to Solar Radiation; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Sola, Y.; Lorente, J.; Campmany, E.; De Cabo, X.; Bech, J.; Redaño, A.; Martínez-Lozano, J.; Utrillas, M.; Alados-Arboledas, L.; Olmo, F.; et al. Altitude effect in UV radiation during the Evaluation of the Effects of Elevation and Aerosols on the Ultraviolet Radiation 2002 (VELETA-2002) field campaign. J. Geophys. Res. Atmos. 2008, 113. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Gong, W.; Luo, M.; Wang, W.; Hu, B.; Zhang, M. Comparison of different UV models for cloud effect study. Energy 2015, 80, 695–705. [Google Scholar] [CrossRef]
- Fountoulakis, I.; Bais, A.F.; Fragkos, K.; Meleti, C.; Tourpali, K.; Zempila, M.M. Short-and long-term variability of spectral solar UV irradiance at Thessaloniki, Greece: Effects of changes in aerosols, total ozone and clouds. Atmos. Chem. Phys. 2016, 16, 2493–2505. [Google Scholar] [CrossRef] [Green Version]
- Zempila, M.M.; Fountoulakis, I.; Taylor, M.; Kazadzis, S.; Arola, A.; Koukouli, M.E.; Bais, A.; Meleti, C.; Balis, D. Validation of OMI erythemal doses with multi-sensor ground-based measurements in Thessaloniki, Greece. Atmos. Environ. 2018, 183, 106–121. [Google Scholar] [CrossRef] [Green Version]
- Calbó, J.; Pages, D.; González, J.A. Empirical studies of cloud effects on UV radiation: A review. Rev. Geophys. 2005, 43. [Google Scholar] [CrossRef] [Green Version]
- Kim, J.; Cho, H.K.; Mok, J.; Yoo, H.D.; Cho, N. Effects of ozone and aerosol on surface UV radiation variability. J. Photochem. Photobiol. B Biol. 2013, 119, 46–51. [Google Scholar] [CrossRef]
- Renaud, A.; Staehelin, J.; Fröhlich, C.; Philipona, R.; Heimo, A. Influence of snow and clouds on erythemal UV radiation: Analysis of Swiss measurements and comparison with models. J. Geophys. Res. Atmos. 2000, 105, 4961–4969. [Google Scholar] [CrossRef]
- Augustine, J.A.; Hodges, G.B.; Cornwall, C.R.; Michalsky, J.J.; Medina, C.I. An update on SURFRAD—The GCOS surface radiation budget network for the continental United States. J. Atmos. Ocean. Technol. 2005, 22, 1460–1472. [Google Scholar] [CrossRef]
- Driemel, A.; Augustine, J.; Behrens, K.; Colle, S.; Cox, C.; Cuevas-Agulló, E.; Denn, F.M.; Duprat, T.; Fukuda, M.; Grobe, H.; et al. Baseline Surface Radiation Network (BSRN): Structure and data description (1992–2017). Earth Syst. Sci. Data 2018, 10, 1491–1501. [Google Scholar] [CrossRef] [Green Version]
- Liang, S.; Zheng, T.; Liu, R.; Fang, H.; Tsay, S.C.; Running, S. Estimation of incident photosynthetically active radiation from Moderate Resolution Imaging Spectrometer data. J. Geophys. Res. Atmos. 2006, 111. [Google Scholar] [CrossRef] [Green Version]
- Wang, D.; Liang, S.; Zhang, Y.; Gao, X.; Brown, M.G.; Jia, A. A New Set of MODIS Land Products (MCD18): Downward Shortwave Radiation and Photosynthetically Active Radiation. Remote Sens. 2020, 12, 168. [Google Scholar] [CrossRef] [Green Version]
- Tanskanen, A.; Lindfors, A.; Määttä, A.; Krotkov, N.; Herman, J.; Kaurola, J.; Koskela, T.; Lakkala, K.; Fioletov, V.; Bernhard, G.; et al. Validation of daily erythemal doses from Ozone Monitoring Instrument with ground-based UV measurement data. J. Geophys. Res. Atmos. 2007, 112. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.; Wang, J.; García, L.C.; Liu, Y.; Krotkov, N.A. OMI surface UV irradiance in the continental United States: Quality assessment trend analysis and sampling issues. Atmos. Chem. Phys. Discuss. 2018, 1–40. [Google Scholar] [CrossRef]
- Zempila, M.M.; van Geffen, J.H.; Taylor, M.; Fountoulakis, I.; Koukouli, M.E.; Van Weele, M.; Van Der A, R.J.; Bais, A.; Meleti, C.; Balis, D. TEMIS UV product validation using NILU-UV ground-based measurements in Thessaloniki, Greece. Atmos. Chem. Phys. 2017, 17, 7157–7174. [Google Scholar] [CrossRef] [Green Version]
- Bernhard, G.; Arola, A.; Dahlback, A.; Fioletov, V.; Heikkilä, A.; Johnsen, B.; Koskela, T.; Lakkala, K.; Svendby, T.M.; Tamminen, J. Comparison of OMI UV observations with ground based measurements at high northern latitudes. Atmos. Chem. Phys. 2015, 15, 7391–7412. [Google Scholar] [CrossRef] [Green Version]
- Kujanpää, J.; Kalakoski, N. Operational surface UV radiation product from GOME-2 and AVHRR/3 data. Atmos. Meas. Tech. Discuss. 2015, 8, 4399–4414. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Liang, S.; Wild, M.; Jiang, B. Analysis of surface incident shortwave radiation from four satellite products. Remote Sens. Environ. 2015, 165, 186–202. [Google Scholar] [CrossRef]
- Liu, H.; Hu, B.; Zhang, L.; Wang, Y.; Tian, P. Spatiotemporal characteristics of ultraviolet radiation in recent 54 years from measurements and reconstructions over the Tibetan Plateau. J. Geophys. Res. Atmos. 2016, 121, 7673–7690. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; Hu, B.; Zhang, L.; Zhao, X.; Shang, K.; Wang, Y.; Wang, J. Ultraviolet radiation over China: Spatial distribution and trends. Renew. Sustain. Energy Rev. 2017, 76, 1371–1383. [Google Scholar] [CrossRef]
- Voyant, C.; Notton, G.; Kalogirou, S.; Nivet, M.L.; Paoli, C.; Motte, F.; Fouilloy, A. Machine learning methods for solar radiation forecasting: A review. Renew. Energy 2017, 105, 569–582. [Google Scholar] [CrossRef]
- Zhang, Y.; He, T.; Liang, S.; Wang, D.; Yu, Y. Estimation of all-sky instantaneous surface incident shortwave radiation from Moderate Resolution Imaging Spectroradiometer data using optimization method. Remote Sens. Environ. Interdiscip. J. 2018, 209, 468–479. [Google Scholar] [CrossRef]
- Dave, J. Meaning of Successive Iteration of the Auxiliary Equation in the Theory of Radiative Transfer. Astrophys. J. 1964, 140, 1292. [Google Scholar] [CrossRef]
- Tanskanen, A.; Krotkov, N.A.; Herman, J.R.; Arola, A. Surface ultraviolet irradiance from OMI. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1267–1271. [Google Scholar] [CrossRef]
- Lindfors, A.; Kaurola, J.; Arola, A.; Koskela, T.; Lakkala, K.; Josefsson, W.; Olseth, J.A.; Johnsen, B. A method for reconstruction of past UV radiation based on radiative transfer modeling: Applied to four stations in northern Europe. J. Geophys. Res. Atmos. 2007, 112. [Google Scholar] [CrossRef]
- Antón, M.; Cachorro, V.; Vilaplana, J.; Toledano, C.; Krotkov, N.; Arola, A.; Serrano, A.; de La Morena, B. Comparison of UV irradiances from Aura/Ozone Monitoring Instrument (OMI) with Brewer measurements at El Arenosillo (Spain)–Part 1: Analysis of parameter influence. Atmos. Chem. Phys. Discuss. 2010, 10, 5979–5989. [Google Scholar] [CrossRef] [Green Version]
- Antón, M.; Cachorro, V.; Vilaplana, J.; Krotkov, N.; Serrano, A.; Toledano, C.; de La Morena, B.; Herman, J. Total ozone mapping spectrometer retrievals of noon erythemal-CIE ultraviolet irradiance compared with Brewer ground-based measurements at El Arenosillo (southwestern Spain). J. Geophys. Res. Atmos. 2007, 112. [Google Scholar] [CrossRef] [Green Version]
- Huang, G.; Li, Z.; Li, X.; Liang, S.; Yang, K.; Wang, D.; Zhang, Y. Estimating surface solar irradiance from satellites: Past, present, and future perspectives. Remote Sens. Environ. 2019, 233, 111371. [Google Scholar] [CrossRef]
- Linares-Rodriguez, A.; Ruiz-Arias, J.A.; Pozo-Vazquez, D.; Tovar-Pescador, J. An artificial neural network ensemble model for estimating global solar radiation from Meteosat satellite images. Energy 2013, 61, 636–645. [Google Scholar] [CrossRef]
- Chen, J.; He, T.; Jiang, B.; Liang, S. Estimation of all-sky all-wave daily net radiation at high latitudes from MODIS data. Remote Sens. Environ. 2020, 245, 111842. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, L.; Du, B. Deep learning for remote sensing data: A technical tutorial on the state of the art. IEEE Geosci. Remote Sens. Mag. 2016, 4, 22–40. [Google Scholar] [CrossRef]
- Yuan, Q.; Shen, H.; Li, T.; Li, Z.; Li, S.; Jiang, Y.; Xu, H.; Tan, W.; Yang, Q.; Wang, J.; et al. Deep learning in environmental remote sensing: Achievements and challenges. Remote Sens. Environ. 2020, 241, 111716. [Google Scholar] [CrossRef]
- Yeom, J.M.; Park, S.; Chae, T.; Kim, J.Y.; Lee, C.S. Spatial assessment of solar radiation by machine learning and deep neural network models using data provided by the COMS MI geostationary satellite: A case study in South Korea. Sensors 2019, 19, 2082. [Google Scholar] [CrossRef] [Green Version]
- De Mazière, M.; Thompson, A.M.; Kurylo, M.J.; Wild, J.D.; Bernhard, G.; Blumenstock, T.; Braathen, G.O.; Hannigan, J.W.; Lambert, J.C.; Leblanc, T.; et al. The Network for the Detection of Atmospheric Composition Change (NDACC): History, Status and Perspectives. Atmos. Chem. Phys. 2018, 18, 4935–4964. [Google Scholar] [CrossRef] [Green Version]
- Augustine, J.A.; DeLuisi, J.J.; Long, C.N. SURFRAD–A national surface radiation budget network for atmospheric research. Bull. Am. Meteorol. Soc. 2000, 81, 2341–2358. [Google Scholar] [CrossRef] [Green Version]
- Levelt, P.F.; van den Oord, G.H.; Dobber, M.R.; Malkki, A.; Visser, H.; de Vries, J.; Stammes, P.; Lundell, J.O.; Saari, H. The ozone monitoring instrument. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1093–1101. [Google Scholar] [CrossRef]
- Levelt, P.F.; Hilsenrath, E.; Leppelmeier, G.W.; van den Oord, G.H.; Bhartia, P.K.; Tamminen, J.; de Haan, J.F.; Veefkind, J.P. Science objectives of the ozone monitoring instrument. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1199–1208. [Google Scholar] [CrossRef]
- Levelt, P.F.; Joiner, J.; Tamminen, J.; Veefkind, J.P.; Bhartia, P.K.; Stein Zweers, D.C.; Duncan, B.N.; Streets, D.G.; Eskes, H.; McLinden, C.; et al. The Ozone Monitoring Instrument: Overview of 14 Years in Space. Atmos. Chem. Phys. 2018, 18, 5699–5745. [Google Scholar] [CrossRef] [Green Version]
- Bhartia, P. OMI/Aura TOMS-like Ozone, Aerosol Index, Cloud Radiance Fraction L3 1 Day 1 Degree × 1 Degree V3; NASA Goddard Space Flight Center, Goddard Earth Sciences Data and Information Services Center (GES DISC): Greenbelt, MD, USA, 2012.
- Bhartia, P.K.; Wellemeyer, C.G.; Taylor, S.L.; Nath, N.; Gopolan, A. Solar Backscatter Ultraviolet (SBUV) version 8 profile algorithm. In Proceedings of the Quadrennial Ozone Symposium, Kos, Greece, 1–8 June 2004; pp. 295–296. [Google Scholar]
- Bhartia, P.K. Total ozone from backscattered ultraviolet measurements. In Observing Systems for Atmospheric Composition; Springer: Berlin/Heidelberg, Germany, 2007; pp. 48–63. [Google Scholar]
- Barnes, W.L.; Pagano, T.S.; Salomonson, V.V. Prelaunch characteristics of the moderate resolution imaging spectroradiometer (MODIS) on EOS-AM1. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1088–1100. [Google Scholar] [CrossRef] [Green Version]
- Ahmad, S.; Salomonson, V.; Barnes, W.; Xiong, X.; Leptoukh, G.; Serafino, G. P1.6 Modis Radiances and Reflectances for Earth System Science Studies and Environmental Applications. 2002, pp. 188–192. Available online: https://www.researchgate.net/profile/William-Barnes-12/publication/242079549_P16_MODIS_RADIANCES_AND_REFLECTANCES_FOR_EARTH_SYSTEM_SCIENCE_STUDIES_AND_ENVIRONMENTAL_APPLICATIONS/links/541361cf0cf2bb7347db227a/P16-MODIS-RADIANCES-AND-REFLECTANCES-FOR-EARTH-SYSTEM-SCIENCE-STUDIES-AND-ENVIRONMENTAL-APPLICATIONS.pdf (accessed on 31 November 2021).
- Antonanzas, J.; Osorio, N.; Escobar, R.; Urraca, R.; Martinez-de Pison, F.J.; Antonanzas-Torres, F. Review of photovoltaic power forecasting. Sol. Energy 2016, 136, 78–111. [Google Scholar] [CrossRef]
- Chollet, F. Deep Learning with Python; Apress: Bangalore, India, 2018. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; Springer: Cham, Switzerland, 2015; pp. 234–241. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Taylor, K.E. Summarizing multiple aspects of model performance in a single diagram. J. Geophys. Res. Atmos. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]
- Taylor, K.E. Taylor Diagram Primer. 2005. Available online: http://wwwpcmdi.llnl.gov/about/staff/Taylor/CV/Taylor_diagram_primer.pdf (accessed on 31 November 2021).
- Zhang, H.; Wang, J.; Castro García, L.; Zeng, J.; Dennhardt, C.; Liu, Y.; Krotkov, N.A. Surface erythemal UV irradiance in the continental United States derived from ground-based and OMI observations: Quality assessment, trend analysis and sampling issues. Atmos. Chem. Phys. 2019, 19, 2165–2181. [Google Scholar] [CrossRef] [Green Version]
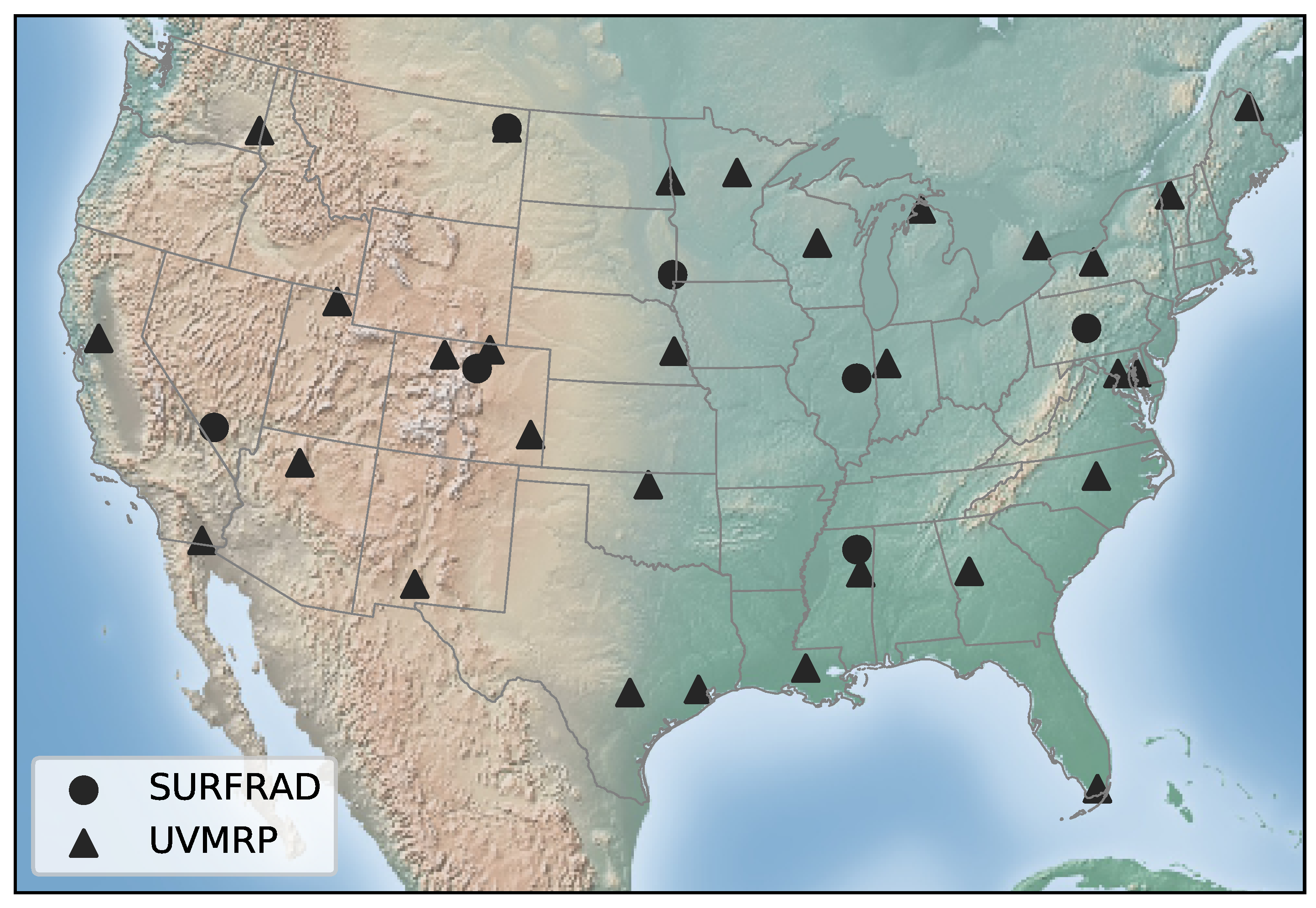
| Observation Network | Station ID | Location | Latitude (°N) | Longitude (°W) | Elevation (m) |
|---|---|---|---|---|---|
| SURFRAD | BON | Bondville, Illinois | 40.05 | 88.37 | 213 |
| DRA | Desert Rock, Nevada | 36.62 | 116.02 | 1007 | |
| FPK | Fort Peck, Montana | 48.31 | 105.10 | 634 | |
| GWN | Goodwin Creek, Mississippi | 34.25 | 89.87 | 98 | |
| PSU | Penn. State Univ., Pennsylvania | 40.72 | 77.93 | 376 | |
| SXF | Sioux Falls, South Dakota | 43.73 | 96.62 | 473 | |
| TBL | Table Mountain, Boulder, Colorado | 40.12 | 105.24 | 1689 | |
| UVMRP | AK01 | Fairbanks, Alaska | 65.12 | 147.43 | 509 |
| AZ01 | Flagstaff, Arizona | 36.06 | 112.18 | 2073 | |
| CA01 | Davis, California | 38.53 | 121.78 | 18 | |
| CA21 | Holtville, California | 32.81 | 115.45 | −18 | |
| CO01 | Nunn, Colorado | 40.81 | 104.76 | 1641 | |
| CO11 | Steamboat Springs, Colorado | 40.46 | 106.74 | 3220 | |
| CO41 | Lamar, Colorado | 38.07 | 102.62 | 1131 | |
| FL01 | Homestead, Florida | 25.39 | 80.68 | 0 | |
| GA01 | Griffin, Georgia | 33.18 | 84.41 | 267 | |
| IN01 | West Lafayette, Indiana | 40.47 | 86.99 | 216 | |
| LA01 | Baton Rouge, Louisiana | 30.36 | 91.17 | 6 | |
| ME11 | Presque Isle, Maine | 40.70 | 68.04 | 155 | |
| MD01 | Queenstown, Maryland | 38.92 | 76.15 | 5 | |
| MD11 | Beltsville, Maryland | 39.01 | 76.95 | 64 | |
| MI01 | Pellston, Michigan | 45.56 | 84.68 | 230 | |
| MN01 | Grand Rapids, Minnesota | 47.18 | 93.53 | 424 | |
| MS01 | Starkville, Mississippi | 33.47 | 88.78 | 88 | |
| MT01 | Poplar, Montana | 48.31 | 105.10 | 634 | |
| NC01 | Raleigh, North Carolina | 35.73 | 78.68 | 120 | |
| ND01 | Fargo, North Dakota | 46.90 | 96.81 | 275 | |
| NE01 | Mead, Nebraska | 41.15 | 96.49 | 355 | |
| NM01 | Las Cruces, New Mexico | 32.62 | 106.74 | 1317 | |
| NY01 | Geneva, New York | 42.88 | 77.03 | 219 | |
| OK01 | Billings, Oklahoma | 36.60 | 97.49 | 317 | |
| ON01 | Toronto, Ontario | 43.78 | 79.47 | 210 | |
| TX21 | Seguin, Texas | 29.57 | 97.98 | 172 | |
| TX41 | Houston, Texas | 29.72 | 95.34 | 76 | |
| UT01 | Logan, Utah | 41.67 | 111.89 | 1369 | |
| VT01 | Burlington, Vermont | 44.53 | 72.87 | 390 | |
| WA01 | Pullman, Washington | 46.76 | 117.19 | 805 | |
| WI01 | Dancy, Wisconsin | 44.71 | 89.77 | 381 |
| Model Input | (mW/m) | (%) | (mW/m) | (%) | |
|---|---|---|---|---|---|
| TOA | 0.8733 | −7.62 | −7.56% | 25.03 | 24.84% |
| TOA + SZA + VZA | 0.9217 | −4.01 | −3.98% | 19.68 | 19.53% |
| TOA + SZA + VZA + altitude | 0.9401 | −2.79 | −2.77% | 17.21 | 17.08% |
| TOA + SZA + VZA + altitude + VAA + SAA | 0.9266 | −4.00 | −3.97% | 19.06 | 18.91% |
| TOA + SZA + VZA + altitude + latitude | 0.9330 | −3.18 | −3.16% | 18.21 | 18.07% |
| TOA + SZA + VZA + altitude + ozone | 0.9649 | −1.03 | −1.02% | 13.1 | 13.08% |
| TOA + SZA + VZA + altitude + ozone + surface reflectance | 0.9887 | 0.19 | 0.19% | 7.48 | 7.42% |
| All stations | |||||
|---|---|---|---|---|---|
| Model | (mW/m) | R | |||
| FCNN | 0.9167 | 20.14% | 0.9644 | 0.8931 | 0.27 |
| DRFCN | 0.9381 | 17.36% | 0.9703 | 0.9437 | 0.24 |
| FCNN+RF | 0.9725 | 11.57% | 0.9865 | 0.9609 | 0.17 |
| DRFCN+RF | 0.9887 | 7.42% | 0.9944 | 0.9872 | 0.11 |
| BON | |||||
| Model | (mW/m) | R | |||
| FCNN | 0.9034 | 21.14% | 0.9519 | 0.9512 | 0.31 |
| DRFCN | 0.9196 | 19.29% | 0.9597 | 0.9726 | 0.28 |
| FCNN+RF | 0.9691 | 11.96% | 0.9844 | 0.9896 | 0.18 |
| DRFCN+RF | 0.9859 | 8.05% | 0.9930 | 0.9903 | 0.12 |
| DRA | |||||
| FCNN | 0.9441 | 13.45% | 0.9818 | 0.9108 | 0.20 |
| DRFCN | 0.9686 | 10.90% | 0.9852 | 0.9642 | 0.17 |
| FCNN+RF | 0.9790 | 8.25% | 0.9901 | 0.9579 | 0.14 |
| DRFCN+RF | 0.9925 | 4.92% | 0.9963 | 0.9932 | 0.09 |
| FPK | |||||
| Model | (mW/m) | R | |||
| FCNN | 0.9312 | 18.29% | 0.9697 | 0.8951 | 0.26 |
| DRFCN | 0.9498 | 15.63% | 0.9775 | 0.9278 | 0.22 |
| FCNN+RF | 0.9585 | 14.21% | 0.9800 | 0.9646 | 0.20 |
| DRFCN+RF | 0.9884 | 7.52% | 0.9943 | 0.9780 | 0.11 |
| GWN | |||||
| Model | (mW/m) | R | |||
| FCNN | 0.8769 | 22.73% | 0.9563 | 0.8260 | 0.32 |
| DRFCN | 0.8990 | 20.59% | 0.9601 | 0.8544 | 0.30 |
| FCNN+RF | 0.9612 | 12.76% | 0.9850 | 0.9152 | 0.19 |
| DRFCN+RF | 0.9852 | 7.87% | 0.9931 | 0.9617 | 0.12 |
| PSU | |||||
| Model | (mW/m) | R | |||
| FCNN | 0.8804 | 23.97% | 0.9422 | 0.8987 | 0.34 |
| DRFCN | 0.8946 | 22.49% | 0.9470 | 0.9184 | 0.32 |
| FCNN+RF | 0.9661 | 12.75% | 0.9831 | 0.9727 | 0.18 |
| DRFCN+RF | 0.9817 | 9.36% | 0.9909 | 0.9797 | 0.13 |
| SXF | |||||
| Model | (mW/m) | R | |||
| FCNN | 0.9170 | 22.23% | 0.9655 | 0.8999 | 0.27 |
| DRFCN | 0.9417 | 18.62% | 0.9727 | 0.9426 | 0.23 |
| FCNN+RF | 0.9653 | 14.37% | 0.9828 | 0.9632 | 0.19 |
| DRFCN+RF | 0.9922 | 6.79% | 0.9961 | 0.9917 | 0.09 |
| TBL | |||||
| Model | (mW/m) | R | |||
| FCNN | 0.8623 | 23.50% | 0.9400 | 0.8517 | 0.35 |
| DRFCN | 0.9002 | 20.00% | 0.9511 | 0.9433 | 0.30 |
| FCNN+RF | 0.9716 | 10.66% | 0.9863 | 0.9531 | 0.17 |
| DRFCN+RF | 0.9814 | 8.65% | 0.9906 | 0.9849 | 0.14 |
| All stations | |||||
|---|---|---|---|---|---|
| Model | (mW/m) | R | |||
| SVR | 0.8890 | 23.25% | 0.9441 | 0.9078 | 0.33 |
| RF | 0.9188 | 19.88% | 0.9586 | 0.9534 | 0.28 |
| DRFCN+SVR | 0.9618 | 13.65% | 0.9809 | 0.9615 | 0.19 |
| DRFCN+RF | 0.9887 | 7.42% | 0.9944 | 0.9872 | 0.11 |
| BON | |||||
| Model | (mW/m) | R | |||
| SVR | 0.8706 | 24.47% | 0.9363 | 0.9539 | 0.36 |
| RF | 0.8818 | 23.39% | 0.9394 | 0.9556 | 0.34 |
| DRFCN+SVR | 0.9229 | 18.88% | 0.9610 | 0.9852 | 0.28 |
| DRFCN+RF | 0.9859 | 8.05% | 0.9930 | 0.9903 | 0.12 |
| DRA | |||||
| Model | (mW/m) | R | |||
| SVR | 0.9102 | 17.05% | 0.9597 | 0.8895 | 0.29 |
| RF | 0.9578 | 11.69% | 0.9787 | 0.9759 | 0.21 |
| DRFCN+SVR | 0.9704 | 9.79% | 0.9856 | 0.9578 | 0.17 |
| DRFCN+RF | 0.9925 | 4.92% | 0.9963 | 0.9932 | 0.09 |
| FPK | |||||
| Model | (mW/m) | R | |||
| SVR | 0.9094 | 20.98% | 0.9541 | 0.9717 | 0.30 |
| RF | 0.9267 | 18.88% | 0.9627 | 0.9504 | 0.27 |
| DRFCN+SVR | 0.9540 | 14.95% | 0.9771 | 0.9637 | 0.21 |
| DRFCN+RF | 0.9884 | 7.52% | 0.9943 | 0.9780 | 0.11 |
| GWN | |||||
| Model | (mW/m) | R | |||
| SVR | 0.8359 | 26.25% | 0.9254 | 0.8071 | 0.40 |
| RF | 0.8803 | 22.41% | 0.9389 | 0.9134 | 0.35 |
| DRFCN+SVR | 0.9558 | 13.61% | 0.9825 | 0.9169 | 0.20 |
| DRFCN+RF | 0.9852 | 7.87% | 0.9931 | 0.9617 | 0.12 |
| PSU | |||||
| Model | (mW/m) | R | |||
| SVR | 0.8691 | 25.07% | 0.9339 | 0.9678 | 0.36 |
| RF | 0.8821 | 23.80% | 0.9405 | 0.9164 | 0.34 |
| DRFCN+SVR | 0.9588 | 14.05% | 0.9797 | 0.9682 | 0.20 |
| DRFCN+RF | 0.9817 | 9.36% | 0.9909 | 0.9797 | 0.13 |
| SXF | |||||
| Model | (mW/m) | R | |||
| SVR | 0.9135 | 22.69% | 0.9558 | 0.9473 | 0.29 |
| RF | 0.9255 | 21.06% | 0.9626 | 0.9935 | 0.27 |
| DRFCN+SVR | 0.9524 | 16.83% | 0.9764 | 0.9648 | 0.22 |
| DRFCN+RF | 0.9922 | 6.79% | 0.9961 | 0.9917 | 0.09 |
| TBL | |||||
| Model | nRMSE (mW/m) | R | |||
| SVR | 0.8101 | 27.60% | 0.9093 | 0.8604 | 0.42 |
| RF | 0.8645 | 23.31% | 0.9315 | 0.9420 | 0.36 |
| DRFCN+SVR | 0.9638 | 12.04% | 0.9827 | 0.9424 | 0.19 |
| DRFCN+RF | 0.9814 | 8.65% | 0.9906 | 0.9849 | 0.14 |
| Stations | (mW/m) | (%) | (mW/m) | (%) | R | |||
|---|---|---|---|---|---|---|---|---|
| BON | 0.9859 | 0.24 | 0.27% | 7.00 | 8.05% | 0.9930 | 0.9903 | 0.12 |
| DRA | 0.9925 | 0.87 | 0.61% | 6.97 | 4.92% | 0.9963 | 0.9932 | 0.09 |
| FPK | 0.9884 | −0.07 | −0.08% | 6.27 | 7.52% | 0.9943 | 0.9781 | 0.11 |
| GWN | 0.9852 | −0.88 | −0.83% | 8.09 | 7.87% | 0.9932 | 0.9617 | 0.12 |
| PSU | 0.9817 | 0.47 | 0.55% | 8.00 | 9.36% | 0.9909 | 0.9797 | 0.13 |
| SXF | 0.9922 | 0.13 | 0.18% | 5.18 | 6.79% | 0.9961 | 0.9917 | 0.09 |
| TBL | 0.9814 | 0.25 | 0.21% | 10.25 | 8.65% | 0.9907 | 0.9850 | 0.14 |
| All station | 0.9887 | 0.19 | 0.19% | 7.48 | 7.42% | 0.9944 | 0.9872 | 0.11 |
| Stations | (mW/m) | (%) | (mW/m) | (%) | R | |||
|---|---|---|---|---|---|---|---|---|
| BON | 0.9430 | 0.56 | 0.64% | 14.86 | 16.91% | 0.9712 | 0.9680 | 0.23 |
| DRA | 0.9451 | 4.53 | 3.24% | 18.14 | 12.95% | 0.9748 | 1.0176 | 0.22 |
| FPK | 0.9296 | 3.68 | 4.60% | 16.75 | 20.95% | 0.9669 | 1.0099 | 0.25 |
| GWN | 0.8966 | −3.39 | −3.32% | 20.25 | 19.85% | 0.9382 | 0.8924 | 0.31 |
| PSU | 0.8971 | 1.21 | 1.33% | 19.03 | 20.83% | 0.9473 | 0.9445 | 0.32 |
| SXF | 0.9515 | −1.61 | −2.19% | 13.96 | 18.91% | 0.9758 | 0.9750 | 0.21 |
| TBL | 0.9258 | 1.09 | 1.01% | 19.29 | 17.94% | 0.9624 | 0.9722 | 0.27 |
| All station | 0.9367 | 1.24 | 1.27% | 17.45 | 17.88% | 0.9686 | 0.9870 | 0.25 |
| Site Code | R | |||||
|---|---|---|---|---|---|---|
| AK01 | 0.8107 | 34.19% | 1.19% | 0.9009 | 0.8751 | 0.43 |
| AZ01 | 0.8703 | 19.72% | 0.99% | 0.9420 | 0.8436 | 0.34 |
| CA01 | 0.9687 | 11.47% | −1.01% | 0.9845 | 0.9670 | 0.18 |
| CA21 | 0.8832 | 18.52% | 5.90% | 0.9475 | 0.9986 | 0.32 |
| CO01 | 0.9405 | 14.77% | 1.08% | 0.9700 | 0.9777 | 0.24 |
| CO11 | 0.7790 | 33.08% | 12.96% | 0.9019 | 0.8804 | 0.43 |
| CO41 | 0.9412 | 14.92% | −1.64% | 0.9706 | 0.9798 | 0.24 |
| FL01 | 0.6798 | 26.22% | 1.19% | 0.8258 | 0.8620 | 0.56 |
| GA01 | 0.8359 | 27.12% | 2.09% | 0.9153 | 0.9364 | 0.40 |
| IN01 | 0.8687 | 28.67% | −0.22% | 0.9324 | 0.9578 | 0.36 |
| LA01 | 0.8534 | 23.56% | 2.94% | 0.9256 | 0.9426 | 0.38 |
| MD11 | 0.9255 | 18.93% | −3.02% | 0.9647 | 0.9101 | 0.27 |
| MD01 | 0.9206 | 19.70% | −2.62% | 0.9607 | 0.9437 | 0.28 |
| ME11 | 0.8906 | 23.87% | 1.02% | 0.9442 | 0.9518 | 0.33 |
| MN01 | 0.9114 | 23.48% | −1.27% | 0.9553 | 0.9249 | 0.30 |
| MS01 | 0.8802 | 19.58% | -0.00% | 0.9387 | 0.9770 | 0.35 |
| MT01 | 0.9369 | 17.26% | −0.72% | 0.9682 | 0.9585 | 0.25 |
| NC01 | 0.8663 | 24.19% | −2.14% | 0.9320 | 0.8949 | 0.36 |
| ND01 | 0.9323 | 20.31% | −2.59% | 0.9663 | 0.9490 | 0.26 |
| NE01 | 0.9259 | 18.91% | −0.57% | 0.9624 | 0.9905 | 0.27 |
| NM01 | 0.9132 | 14.60% | 3.71% | 0.9614 | 1.0353 | 0.28 |
| NY01 | 0.8734 | 21.19% | −1.28% | 0.9348 | 0.9509 | 0.36 |
| OK01 | 0.9192 | 18.27% | −2.95% | 0.9618 | 0.9367 | 0.27 |
| ON01 | 0.8981 | 21.64% | −0.05% | 0.9480 | 0.9234 | 0.32 |
| TX21 | 0.7828 | 28.98% | 4.06% | 0.8915 | 0.9443 | 0.46 |
| TX41 | 0.8738 | 19.99% | −1.42% | 0.9354 | 0.9583 | 0.35 |
| UT01 | 0.9109 | 19.10% | 1.73% | 0.9559 | 1.0017 | 0.30 |
| VT01 | 0.8739 | 23.61% | 0.51% | 0.9349 | 0.9432 | 0.35 |
| WA01 | 0.9294 | 19.97% | −0.85% | 0.9642 | 0.9786 | 0.27 |
| WI01 | 0.9053 | 21.98% | −2.98% | 0.9536 | 0.9232 | 0.30 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, R.; He, T. Estimation of 1-km Resolution All-Sky Instantaneous Erythemal UV-B with MODIS Data Based on a Deep Learning Method. Remote Sens. 2022, 14, 384. https://doi.org/10.3390/rs14020384
Zhao R, He T. Estimation of 1-km Resolution All-Sky Instantaneous Erythemal UV-B with MODIS Data Based on a Deep Learning Method. Remote Sensing. 2022; 14(2):384. https://doi.org/10.3390/rs14020384
Chicago/Turabian StyleZhao, Ruixue, and Tao He. 2022. "Estimation of 1-km Resolution All-Sky Instantaneous Erythemal UV-B with MODIS Data Based on a Deep Learning Method" Remote Sensing 14, no. 2: 384. https://doi.org/10.3390/rs14020384
APA StyleZhao, R., & He, T. (2022). Estimation of 1-km Resolution All-Sky Instantaneous Erythemal UV-B with MODIS Data Based on a Deep Learning Method. Remote Sensing, 14(2), 384. https://doi.org/10.3390/rs14020384







