Abstract
The use of machine learning algorithms to classify complex landscapes has been revolutionized by the introduction of deep learning techniques, particularly in remote sensing. Convolutional neural networks (CNNs) have shown great success in the classification of complex high-dimensional remote sensing imagery, specifically in wetland classification. On the other hand, the state-of-the-art natural language processing (NLP) algorithms are transformers. Although the transformers have been studied for a few remote sensing applications, the integration of deep CNNs and transformers has not been studied, particularly in wetland mapping. As such, in this study, we explore the potential and possible limitations to be overcome regarding the use of a multi-model deep learning network with the integration of a modified version of the well-known deep CNN network of VGG-16, a 3D CNN network, and Swin transformer for complex coastal wetland classification. Moreover, we discuss the potential and limitation of the proposed multi-model technique over several solo models, including a random forest (RF), support vector machine (SVM), VGG-16, 3D CNN, and Swin transformer in the pilot site of Saint John city located in New Brunswick, Canada. In terms of F-1 score, the multi-model network obtained values of 0.87, 0.88, 0.89, 0.91, 0.93, 0.93, and 0.93 for the recognition of shrub wetland, fen, bog, aquatic bed, coastal marsh, forested wetland, and freshwater marsh, respectively. The results suggest that the multi-model network is superior to other solo classifiers from 3.36% to 33.35% in terms of average accuracy. Results achieved in this study suggest the high potential for integrating and using CNN networks with the cutting-edge transformers for the classification of complex landscapes in remote sensing.
1. Introduction
Wetlands are basically regions flooded or saturated by water for at least a portion of the year, though this definition differs widely depending on the field of interest [1,2,3]. Wetlands are vital for biodiversity, ecological security, and humans as they perform a variety of functions and provide various ecosystem services [4,5,6]. Wetland services include climate regulation, water filtration, flood and drought mitigation, shoreline erosion preservation, soil protection, and wildlife habitat, among others [7,8,9,10]. Wetlands have deteriorated and degraded considerably around the world in recent decades as a result of increased human activity and climatic changes [11,12,13]. Wetland degradation has resulted in significant ecological repercussions such as biodiversity loss, habitat fragmentation, floods, and droughts [14,15,16]. Around two-thirds of the world’s wetlands have been lost or drastically altered since the turn of the last century [17,18]. Land-use change due to the settlement of Europeans, development, agriculture, and associated bi-products such as re-direction of run-off and pollution were all historical drivers of wetland loss in Canada [19]. On the other hand, climate change has recently emerged as a serious environmental challenge that has the potential to aggravate ongoing wetland loss and change [20,21]. Studies show how climate change has the potential to increase the number of fires and affect the ability of wetlands and neighboring habitats to recover from natural disasters [22,23]. On the other hand, even though wetlands make up only 6% of worldwide land cover, wetland species account for 24% of the world’s invasive plants [24]. Invasive species pose a severe threat to coastal wetlands because they can develop in dense, monolithic stands, out-competing native species and affecting the structure of wetlands [24]. A coastal wetland is an environment with a depth range between the lower subtidal zone, where sunlight can penetrate and sustain photosynthesis by benthic plant communities, and the landward border, where the sea’s hydrologic influence is ceded to groundwater and atmospheric processes [25,26]. These wetlands, which connect land and sea, are characterized by complicated hydrological processes that are susceptible to degradation [27,28,29]. For enhancing our understanding of ecosystem conditions and management strategies, such as biodiversity protection, habitat assessment, and quantification of biogeochemical cycles and spatial patterns, precise and up-to-date information on the spatial variability of wetlands is of great importance [30,31].
Wetland mapping on a large scale has long been difficult due to the high cost of gathering data and wetland ecosystems’ extremely dynamic and remote nature [32,33]. Long-term monitoring of wetlands across Canada necessitates substantial field labor as well as long-term human commitment and financial investment [34]. As such, data acquisition using remote sensing methods opens unimagined possibilities for large-scale wetland mapping [35]. Although remote sensing, like any tool, has limitations in wetland mapping and monitoring, it has several features that make it well-suited for these tasks. For example, remote sensing is both cost and time-effective because it eliminates the need for site visits while also covering huge geographic areas [36]. Furthermore, remote sensing-generated wetland maps can be updated on a frequent basis based on the temporal frequency of the photos used for classification [37]. Another attribute of remote sensing that makes it ideal for wetland mapping applications is its capacity to collect data from any point on the planet, including inaccessible locations where wetlands are common. The spectral responses of wetlands in various areas of the electromagnetic spectrum are utilized to understand their characteristics. Given their sensitivity to various properties of wetland vegetation, previous research reported improvement in wetland mapping by integrating multi-source remote sensing data acquired from optical and synthetic aperture radar (SAR) sensors [7,9]. For example, in Canada [6,26] and South Africa [9], despite the excellent results achieved from single source optical data, a synergic methodology based on merging Sentinel-1 SAR data and Sentinel-2 optical data proved to be more efficient for mapping of wetlands.
Another important criterion for accurate wetland classification using remote sensing tools is the selection of an appropriate classification algorithm based on in-house supplies, such as the presence of training data and computational power, as well as the complexity and dimensionality of the satellite imagery to be classified. For example, algorithms such as maximum likelihood cannot categorize multi-dimensional remote sensing data adequately. Algorithms such as decision tree (DT) [38], random forest (RF) [39], and support vector machines (SVM) [40] had better performance for the classification of high-dimensional data. Despite the success of these supervised classifiers for image classification in remote sensing, deep learning methods have received great attention for remote sensing image classification [41,42,43,44,45,46,47]. In remote sensing applications, deep learning approaches, notably the convolutional neural network (CNN), have currently outperformed classification algorithms such as RF [48,49,50,51]. Instead of learning from empirical feature design, deep learning algorithms learn from representation. Internal feature representations are learned automatically; hence these methods are regarded as highly efficient approaches for image classification tasks. The reason for this superiority is that, compared with shallow models such as RF, deep learning algorithms usually find more generalized patterns in data [52,53]. Moreover, deep learning approaches’ higher performance is also due to their ability to include feature extraction in the optimization process [54]. CNN, a deep learning model inspired by biological processes, is commonly used for remote sensing image classification that has achieved high accuracy in high-dimensional and complicated situations [55,56,57,58]. CNNs have historically dominated computer vision modeling, specifically image classification. After the introduction of AlexNet [59] and its groundbreaking performance on the ImageNet image classification task, CNN architectures have grown to become more powerful through increased size [60], more extended connections [61], and more advanced convolutions [62]. However, in natural language processing (NLP), transformers are now the most widely used architecture [63]. The transformer is renowned for its use of attention to model long-range patterns in data. It was designed for sequence modeling and transduction activities. Its enormous success in the language domain has prompted researchers to investigate its application in computer vision. It has lately shown success on a number of tasks, including a few remote sensing image classifications [64,65,66,67].
Despite the promising results achieved from the transformers in a few remote sensing studies, this cutting-edge method’s capability integrated with deep CNNs has not been investigated in wetland mapping. As such, this research aims to assess and illustrate the transformer’s efficacy integrated with the capabilities of deep CNNs in the classification of complex coastal wetlands. In particular, we develop a multi-model that uses three networks of a well-known two-dimensional deep CNN of VGG-16 that uses the extracted features of optical Sentinel-2 image, a three-dimensional CNN that utilizes normalized backscattering coefficients of SAR Sentinel-1 imagery, and a Swin transformer that employs a digital elevation model (DEM) generated from LiDAR point clouds. To the best of our knowledge, the integration of transformers and CNNs has not been used and evaluated in the remote sensing image classification, specifically for complex wetland classification.
2. Methods
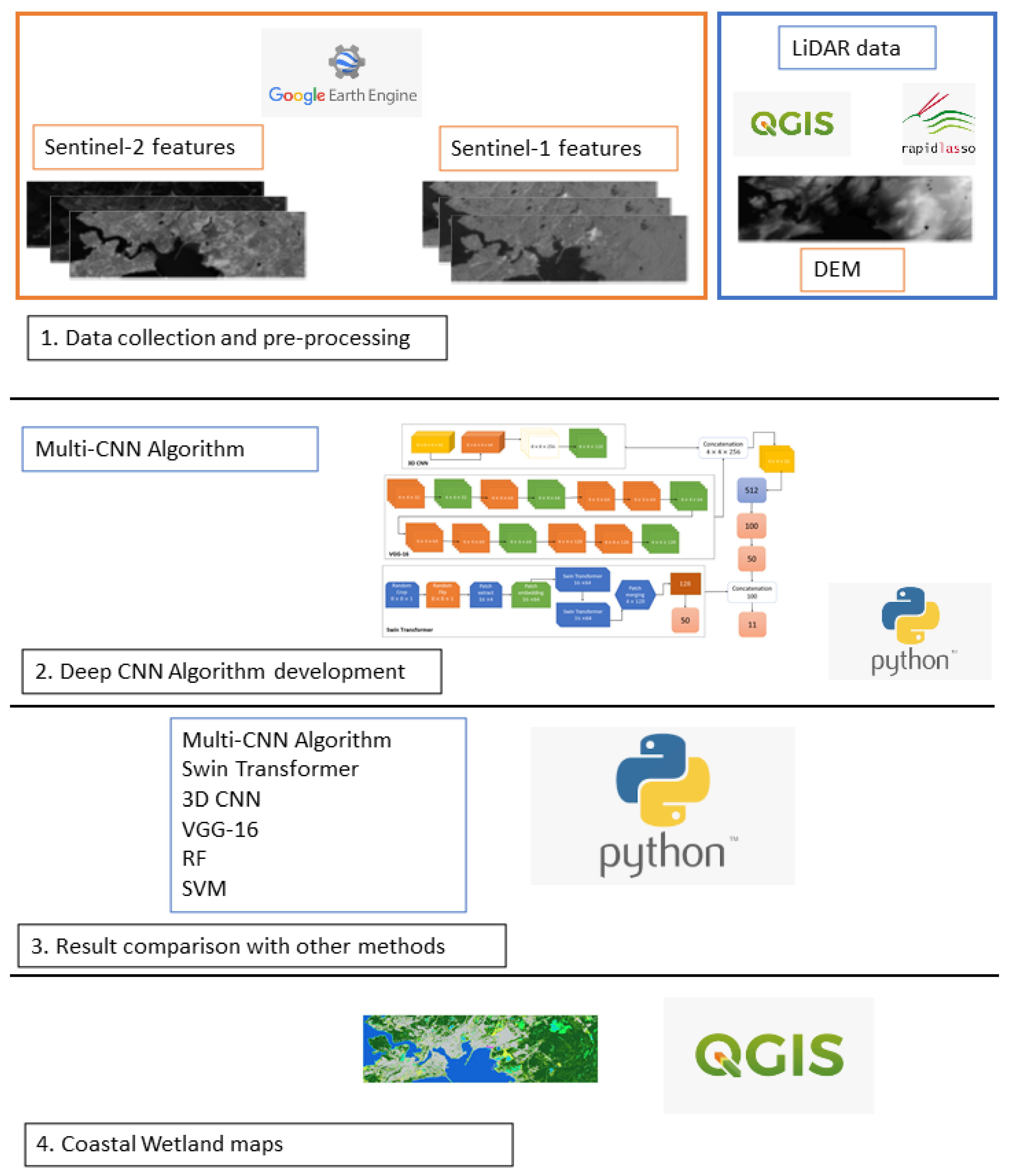
Figure 1 presents the flowchart of the proposed method. As seen, Sentinel-1 and Sentinel-2 features were collected from the Google Earth Engine (GEE) platform, while DEM was generated from LiDAR data with the use of QGIS software and the LAS tool. Then, the Python programming language was employed to develop the proposed multi-model DCNN classifier. Results of the proposed classifier were then compared with Swin transformer, 3D CNN, VGG-16, RF, and SVM classifiers. Finally, coastal wetland classified maps were produced in QGIS software.
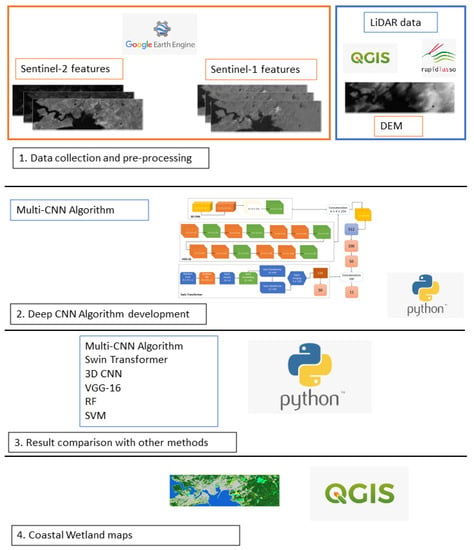
Figure 1.
The flowchart of developed classifiers in this study.
2.1. The Proposed Multi-Model Deep Learning Classifier
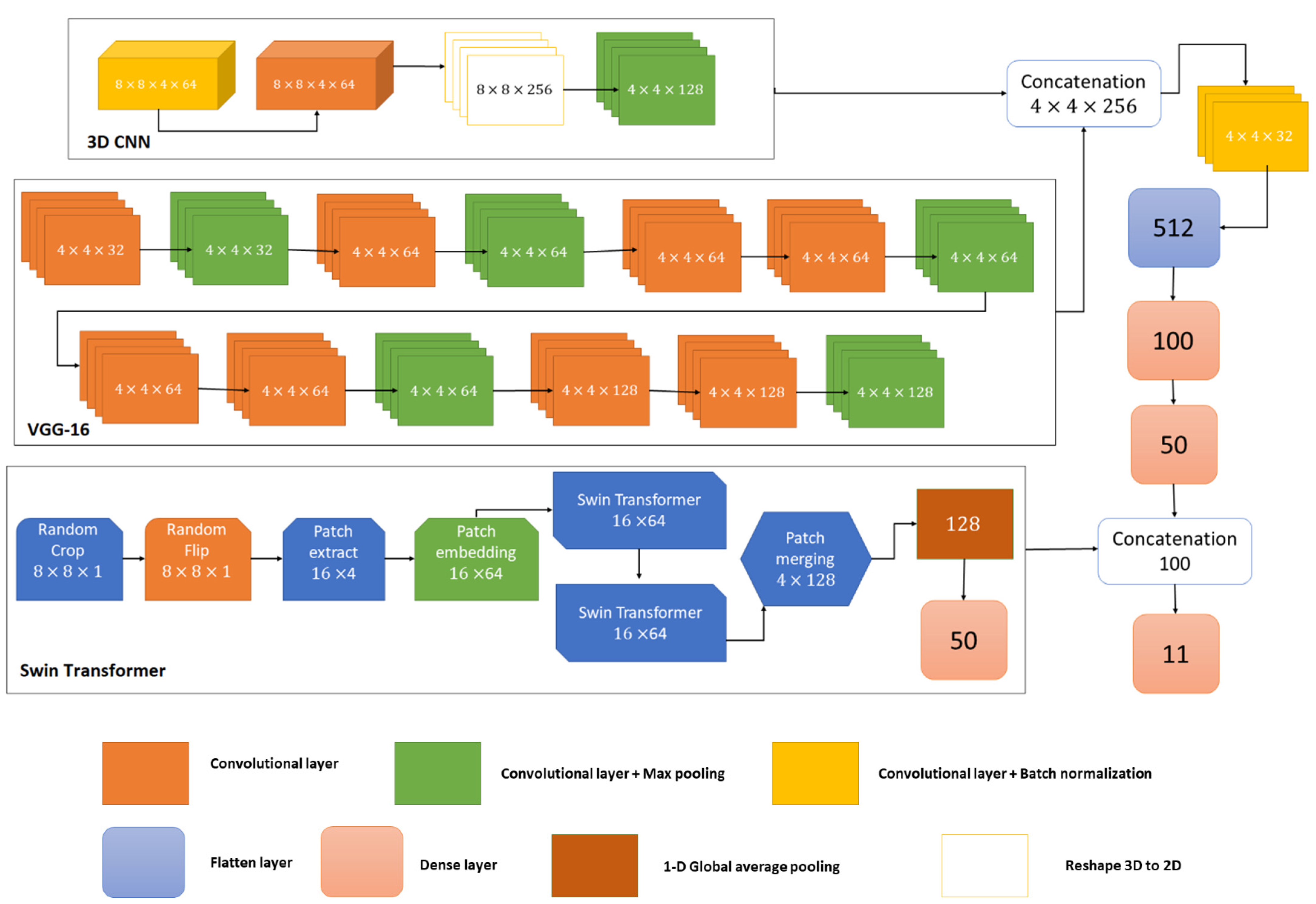
The architecture of the proposed multi-model deep learning algorithm for the classification of coastal wetlands is presented in Figure 2. To efficiently use and integrate capabilities and power of CNN networks with the state-of-the-art transformers, the proposed multi-model deep learning network has three branches: a modified version of VGG-16 CNN, a 3D CNN, and the Swin transformer. We experimentally used image patches of for Sentinel-2 features with 12 bands in the VGG-16 network, image patches of for Sentinel-1 features with four bands in the 3D CNN network, and image patches of for the DEM generated from the LiDAR data with one band in the Swin transformer network. The reason behind using smaller image patch sizes is that using larger image patches would significantly affect the linear objects of urban areas (i.e., they will lose their linear geometry). Moreover, urban regions would be over-classified by the utilization of large image patches.
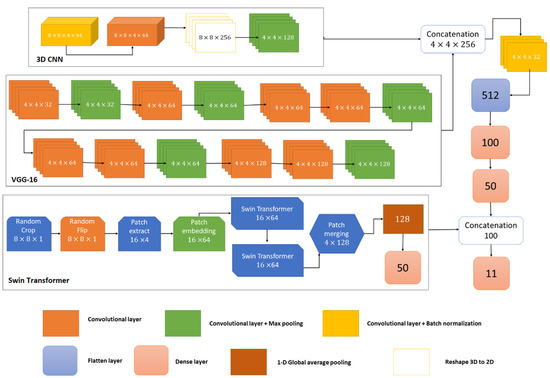
Figure 2.
The architecture of the proposed multi-model deep learning algorithm.
The 3D CNN network has three convolutional layers (i.e., two 3-D convolutional layers and one 2-D convolutional layer). As seen in Figure 2, in the 3D CNN, experimentally, we used image patches of four backscattering coefficients of , , , and . The first two 3D convolutional layers have 64 filters (). Then, we reshaped the 3D convolutional layer into 2D. The last layer is a 2D convolutional layer with 128 filters, followed by a max-pooling layer that reduces the image patches into . On the other hand, we experimentally used image patches of 12 spectral bands and indices of Sentinel-2 image in the VGG-16 network. There are 13 convolutional layers in the well-known CNN network of VGG-16, as presented in Figure 2. It is worth highlighting that to decrease the computation cost of the VGG-16 deep CNN network, we reduced the number of filters compared with the original VGG-16 architecture. In addition, as we are using image patches of for the input of the VGG-16 network, we are using max-pooling layers with kernel sizes of . Then, the feature output of the 3D CNN and VGG-16 networks was concatenated to form image patches of with 256 filters. Afterward, we used a flatten layer of size 512, followed by two dense layers with sizes of 100 and 50.
We used the DEM data with a patch size of in the Swin transformer network. It is worth highlighting that the first two layers of the Swin transformer model (i.e., random crop and random flip) are data augmentation techniques. Afterward, in the patch extract layer, from input images, image patches of were extracted and transformed into linear features of size , resulting in an output feature of . Then, in the patch embedding layer, as we used an embedding dimension of 64, the output feature was size . In the embedding layer, image patches are converted (i.e., translated) into vector data to be used in transformers. Afterward, the output vectors are passed into the Swin transformers. Then, the output features of the Swin transformer are merged by a patch merging layer resulting in an output feature of , followed by a 1-D global average pooling with a size of 128. The final layer of the Swin transformer is a dense layer of size 50 that is concatenated by the concatenation of the results of the other two networks of 3D CNN and VGG-16 into a feature size of 100. The final layer of the multi-model deep learning algorithm is a dense layer with a size of 11 using a softmax activation function. The Swin transformer is discussed in more detail in the next section.
2.2. Study Area and Data Collection
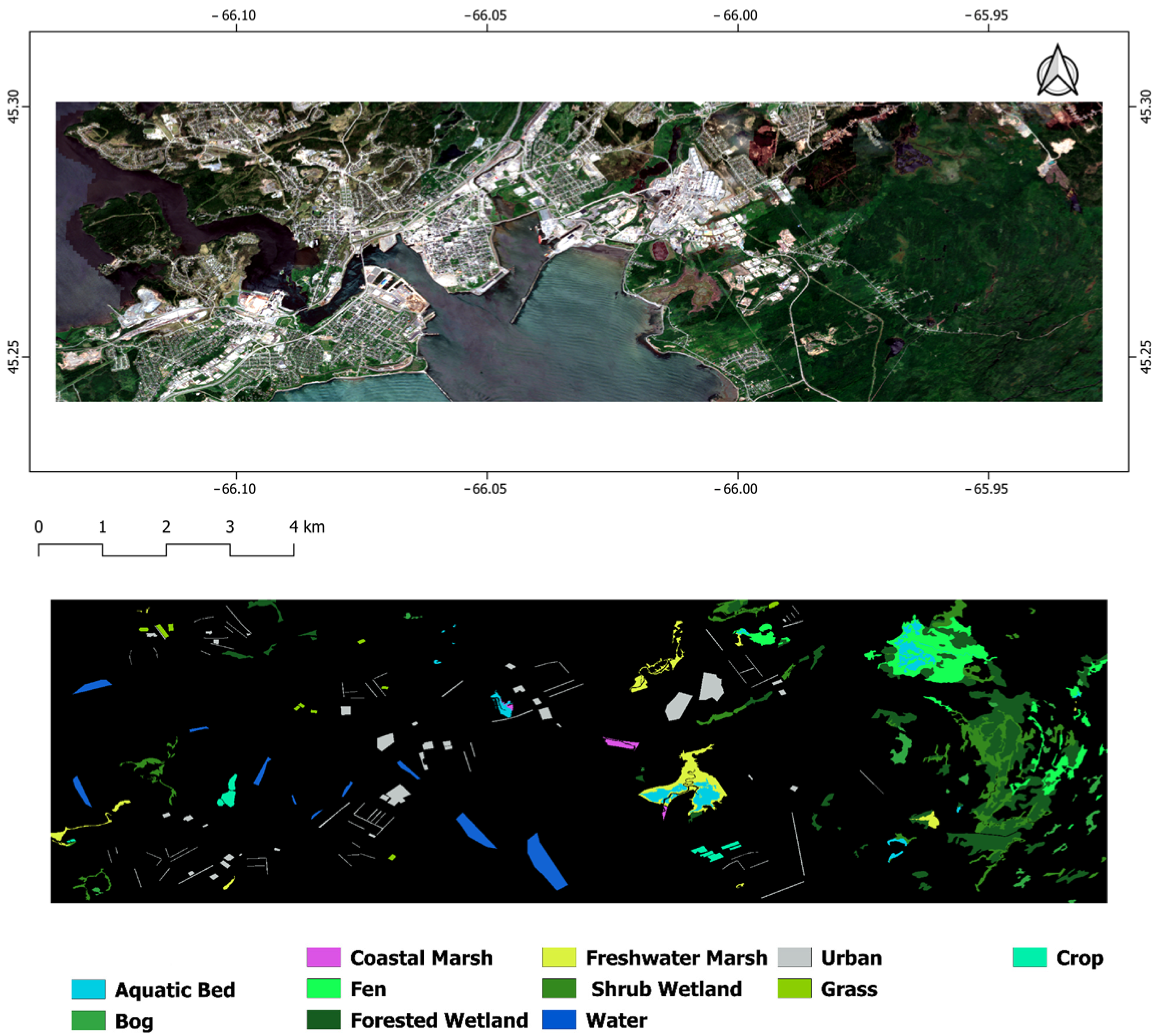
The study area is located in Saint John city in the southcentral part of New Brunswick province, Canada (see Figure 3). Saint John city, which is on the Bay of Fundy, has an area of approximately 326 km2 with a population of around 71,000. The city is divided by the south-flowing river, while the Kennebecasis River, which enters the Saint John River near Grand Bay, runs through the east side. At the confluence of the two rivers and the Bay of Fundy, Saint John harbor is a deep-water harbor with no ice all year. The city has a humid continental climate.

Figure 3.
Sentinel-2 true color of the study area of Saint John city located in New Brunswick, Canada, and spatial distribution of ground truth data in the pilot site.
We used Sentinel-1, Sentinel-2, and LiDAR data to classify seven wetland classes, including aquatic bed, bog, coastal marsh, fen, forested wetlands, freshwater marsh, and shrub wetland. The wetland ground truth data was acquired from the 2021 wetland inventory of New Brunswick (http://www.snb.ca/geonb1/e/DC/catalogue-E.asp, accessed on 6 December 2021) (see Figure 3). Wetland inventory is collected and yearly updated by the Canadian Department of Environment and Local Government (ELG). Wetland maps are provided by the Department of Environment and Local Government in notifying primary users of wetlands and potential regulatory obligations for land development. To avoid over-classification of wetlands in the pilot site, we manually extracted four additional non-wetland classes of water, urban, grass, and crop through visual interpretation of very high-resolution imagery of Google Earth. The number of training and test data is presented in Table 1. It is worth highlighting that we used a stratified random sampling technique to divide our ground truth data into 50% as training and 50% as test samples.

Table 1.
The number of training and test pixels for the wetland and non-wetland classes in the pilot site of Saint John, New Brunswick, Canada.
The Sentinel-1 and Sentinel-2 image features, including normalized backscattering coefficients, spectral bands, and indices (see Table 2), were created in Google Earth Engine code editor (https://code.earthengine.google.com/, accessed on 6 December 2021). In this study, for extracting features of Sentinel-1 and Sentinel-2 data, the median image values between 1st June to 1st September 2020 were created utilizing the GEE code editor. It is worth highlighting that GEE provides Sentinel-2 level-2A data that is pre-processed by sen2cor software [68]. Although bands of Sentinel-2 image have different spatial resolutions (10 m, 20 m, and 60 m), all bands are resampled into 10 m spatial resolutions in the GEE code editor. On the other hand, the GEE platform provides Sentinel-1 ground range detected (GRD) data, including , , , and that is log scaled at 10 m spatial resolution. The provided Sentinel-1 data are pre-processed by Sentinel-1 toolbox, including thermal noise removal, radiometric calibration, and terrain correction. To improve the classification accuracy of wetlands in the pilot site of Saint John, we created a DEM from LiDAR data using Las Tools (https://rapidlasso.com/lastools/, accessed on 6 December 2021) in QGIS software. It should be noted that the DEM was resampled into 10 m to be stacked with the Sentinel-1 and Sentinel-2 image features. It is worth highlighting that the LiDAR data had a point density of 6 points per 1 m2.

Table 2.
The normalized backscattering coefficients, spectral bands, and indices used in this study ( = normalized difference vegetation index, = normalized difference build-up index).
2.3. Experimental Setting
In this study, we used the Adam optimizer to train our proposed multi-model deep learning network as well as the other deep learning models, including the modified version of the VGG-16 network, 3D CNN, and Swin transformer with a learning rate of 0.0002. We set the maximum training iteration to 100 epochs with a batch size of 32. In the Swin transformer, we used patch size, dropout rate, number of attention heads, embedding dimension, number of multi-layer perceptron, and shift size of , 0.03, 8, 64, 256, and 1, respectively. It is worth highlighting that for the implementation of classifiers, we used a graphical processing unit (GPU) of NVIDIA GeForce RTX 2070, an Intel processor (i.e., i7-10750H central processing unit (CPU) of 2.60 GHz), and a 16 GB random access memory (RAM) operating on 64-bit Windows 11 in our experiments. All deep learning algorithms were developed in the Python TensorFlow library, while the RF and SVM classifiers were implemented using sklearn Python library.
2.4. Evaluation Metrics
To assess the quantitative performance of the developed models, coastal wetland classification results were evaluated in terms of average accuracy, recall, overall accuracy, precision, and kappa index statistical metrics (Equations (1)–(6)):
where is the marginal total of row I, the total number of observations is shown by N, and is observation in row i and column i.
2.5. Comparison with Other Classifiers
For the evaluation of the efficiency of the proposed multi-model deep learning algorithm, the coastal wetland classification results were compared with several algorithms, including:
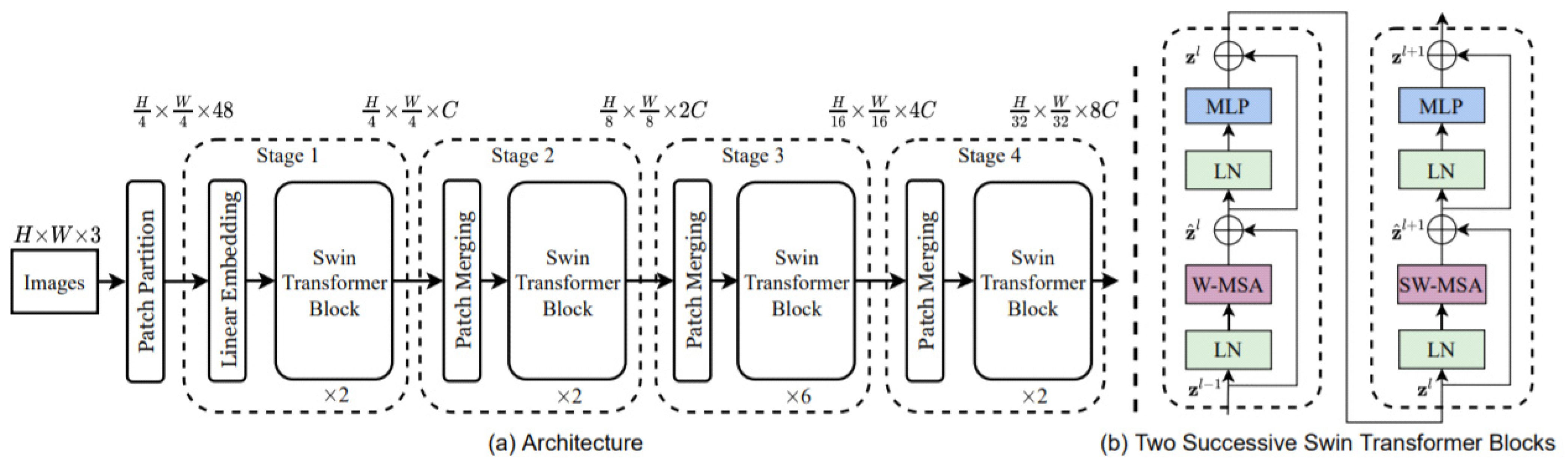
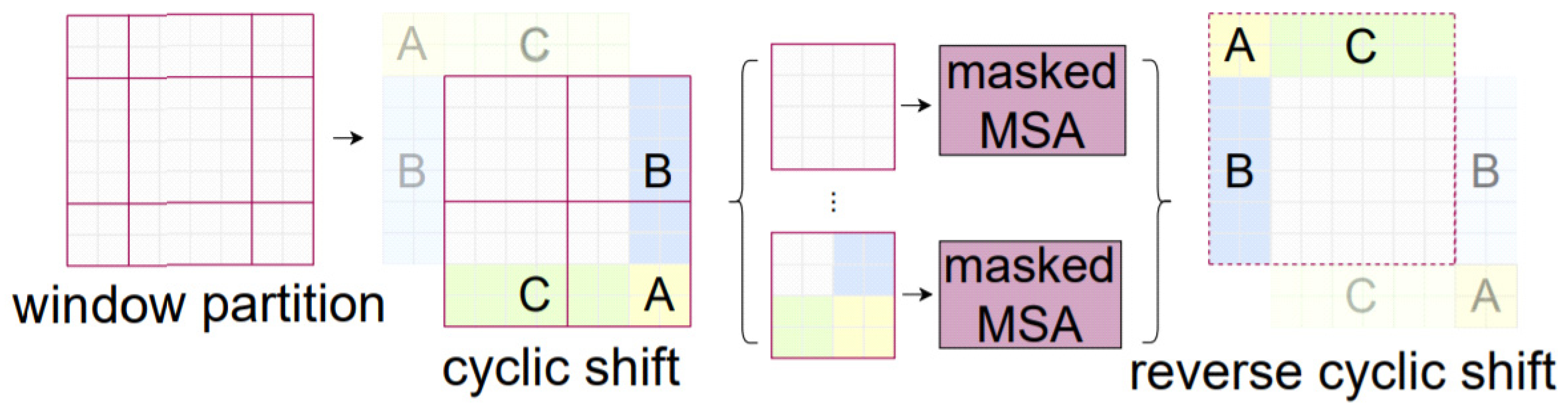
Swin Transformer—Differences between the two domains of language and vision, including substantial variations in the scale of visual entities and the high resolution of pixels in pictures compared with words in texts, pose challenges in adapting transformer models from language to vision. As such, the Swin transformer introduced a hierarchical transformer whose representation is computed with shifted windows to address these issues [69] (see Figure 4). The shifted windowing technique improves efficiency by limiting self-attention computation to non-overlapping local windows while allowing for cross-window connectivity. This hierarchical architecture can predict at multiple scales and has a linear computing complexity as image size increases. Swin transformer’s characteristics make it suitable for a wide range of vision tasks, such as image classification.
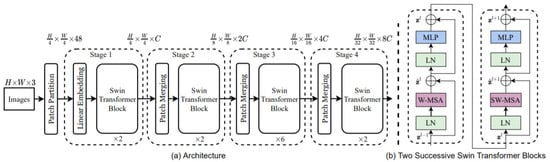
Figure 4.
(a) The architecture of a Swin transformer; (b) two successive Swin transformer blocks. SW-MSA and W-MSA are multi-head self-attention modules with shifted windowing and regular settings, respectively [69].
The shifted window partitioning strategy is successful in image classification, object detection, and semantic segmentation as it introduces links between neighboring non-overlapping windows in the previous layer (see Figure 5).
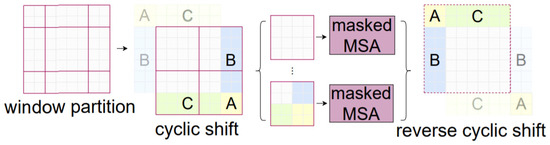
Figure 5.
Illustration of high efficiency of batch computation for self-attention in shifted window partitioning [69].
Swin transformer blocks are computed consecutively using the shifting window partitioning method as (see Equations (7)–(10)):
where and present the outputs of (S)W-MSA and MLP module of block , respectively. SW-MSA and W-MSA are multi-head self-attention modules with shifted windowing and regular settings, respectively (for more information, refer to Liu et al. [69]).
Random Forest—In remote sensing image classification, RF [70] is an extensively used ensemble learning method that has shown great success in high-dimensional and complex issues [7,71,72,73]. Moreover, RF is also an effective feature selection technique as it reveals the importance of each band of earth observation images. As such, RF is regarded as one of the most used methods for accurate image classification. It is worth highlighting that the use of highly-important features does not guarantee that this is the best combination of features for a specific issue. For example, high-dimensional data typically has a high number of correlated variables, which negatively impacts the feature selection process [74]. Within complex heterogeneous landscapes with low inter-class discrimination and high intra-class variability, supervised classification of remote sensing data using machine learning techniques such as RF has the power to tackle drawbacks of using a single index or simple linear regression models [75,76].
Support Vector Machine—The SVM [40] is non-parametric, unlike conventional statistic-based parametric classification techniques. The distribution of the data set has no influence on SVM. This is one of the benefits of SVMs over other statistical methods such as maximum likelihood, which require data distribution to be known in advance. SVMs, in particular, use the training data to generate an optimal hyperplane (a line in the simplest scenario) for dividing the dataset into a discrete number of predetermined classes [77]. It is worth mentioning that the SVM’s accuracy is mostly determined by the variants and parameters used. It should be noted that while SVM is among the most utilized non-parametric machine learning algorithms, its performance decreases with a large amount of training data [78].
Convolutional Neural Network—Deep learning algorithms based on CNNs have become a prominent remote sensing image classification topic in the last decade [55,56,58,79]. The input nodes for the classifier in CNN classification include a single-pixel and local sets of adjacent pixels. The CNN learning process includes determining appropriate convolutional operations and weights for different kernels or moving windows, which enables the network to model useful spatial contextual information at various spatial scales [80,81]. Different filters and convolutional layers extract spatial, spectral, edge, and textural information, enabling a high degree of data generalization in CNNs. Because CNNs enable local connection and weight sharing principle, CNN has shown great robustness and effectiveness in spatial feature extraction of remote sensing images compared with other deep learning techniques such as RF. The convolution, pooling, and fully connected layers comprise a CNN architecture. The convolution layer contains two key elements: kernels (i.e., filters) and biases. The filters are designed to extract certain information from the image of interest. By decreasing the resolution of the feature map, the pooling layer provides translation invariance. Finally, the fully connected layer uses the extracted information from all the previous layer’s feature maps to create a classification map [82]. Based on the weights (W) and biases (B) of the previous layers, in each layer (l) of a CNN, low-, intermediate-, and high-level features are extracted that are updated in the next iteration (Equations (11) and (12)):
where , , and denote the total number of training samples, the learning rate, and a regularization parameter. Moreover, m, t, and C are momentum, updating step, and cost function. According to the dataset of interest, to obtain an optimal result, regularizing parameter (), the learning rate (), and momentum () are fine-tuned.
VGG-16 [83]—The University of Oxford’s Visual Geometry Group created this 16-layer network with approximately 138 million parameters that were trained and evaluated on the ImageNet dataset. The original VGG-16 model architecture is consists of kernel-sized filters that enable the network to learn more complex features by increasing the network’s depth [84]. It is worth highlighting that to reduce the complexity of the original VGG-16 model and reduce the computation cost, we experimentally replaced some of the kernel-sized filters with kernels while reducing the number of filters.
3. Results
3.1. Comparison Results on the Saint John Pilot Site
Comparison results of the complex coastal wetland classification using the developed models are shown in Table 3. It is worth highlighting that we used image patches of in the solo 3D CNN, Swin transformer, and VGG-16 networks. The proposed multi-model deep learning network achieved the best results compared with other classifiers, including the Swin transformer, VGG-16, 3D CNN, RF, and SVM classifiers in terms of average accuracy, overall accuracy, and kappa index with values of 92.68%, 92.30%, and 90.65%, respectively. In terms of F-1 score, the multi-model network obtained values of 0.87, 0.88, 0.89, 0.91, 0.93, 0.93, and 0.93 for the recognition of shrub wetland, fen, bog, aquatic bed, coastal marsh, forested wetland, and freshwater marsh, respectively. The multi-model network outperformed the solo 3D CNN, Swin transformer, and VGG-16 in terms of average accuracy by 8.92%, 13.93%, and 17.31%, respectively. Based on the results, in terms of average accuracy, the Swin transformer (78.75%) network achieved slightly better results compared with the well-known deep CNN network of VGG-16 (75.37%). On the other hand, the RF classifier had the best performance over the solo 3D CNN, Swin transformer, VGG-16, and SVM in terms of average accuracy by 5.56%, 10.57%, 13.95%, and 29.99%, respectively. The results revealed the higher capability of the RF classifier over the SVM algorithm in dealing with a noisy, complex, and high-dimensional remote sensing environment. It is worth highlighting that the performance of the SVM classifier highly depends on the predefined parameters and kernels. As such, in this study, we examined different kernel types, including linear, radial basis function (RBF), polynomial, and sigmoid. The SVM with a polynomial kernel achieved the best results, as shown in Table 3.

Table 3.
Results of the proposed multi-model compared with other classifiers in terms of average accuracy, precision, F1-score, and recall (AB = aquatic bed, BO = bog, CM = coastal marsh, FE = fen, FM = freshwater marsh, FW = forested wetland, SB = shrub wetland, W = water, U = urban, G = grass, C = crop, AA = average accuracy, OA = overall accuracy, and K = kappa).
Overall, better results obtained by the multi-model algorithm over other solo classifiers showed the superiority of using a model consisting of several different networks over a single deep learning network. Each network of the multi-model algorithm extracted different useful information from multi-data sources (i.e., Sentinel-1, Sentinel-2, and DEM), resulting in significantly improved coastal wetland classification over a single network deep learning model (see Table 3).
3.2. Confusion Matrices
The highest confusion between wetlands was obtained by the SVM classifier. The SVM algorithm had issues with the correct classification of coastal marsh, bog, and shrub wetlands (refer to Table S1 of Supplementary Materials). As discussed in the previous sections, the inherited complexity of the Saint John environment, speckle noise of Sentinel-1 data, and the number of training data can be attributed as the reasons behind the underperformance of the SVM classifier over the other implemented methods. On the other hand, the proposed multi-model deep learning algorithm achieved the least confusion between the wetlands.
3.3. Classification Maps
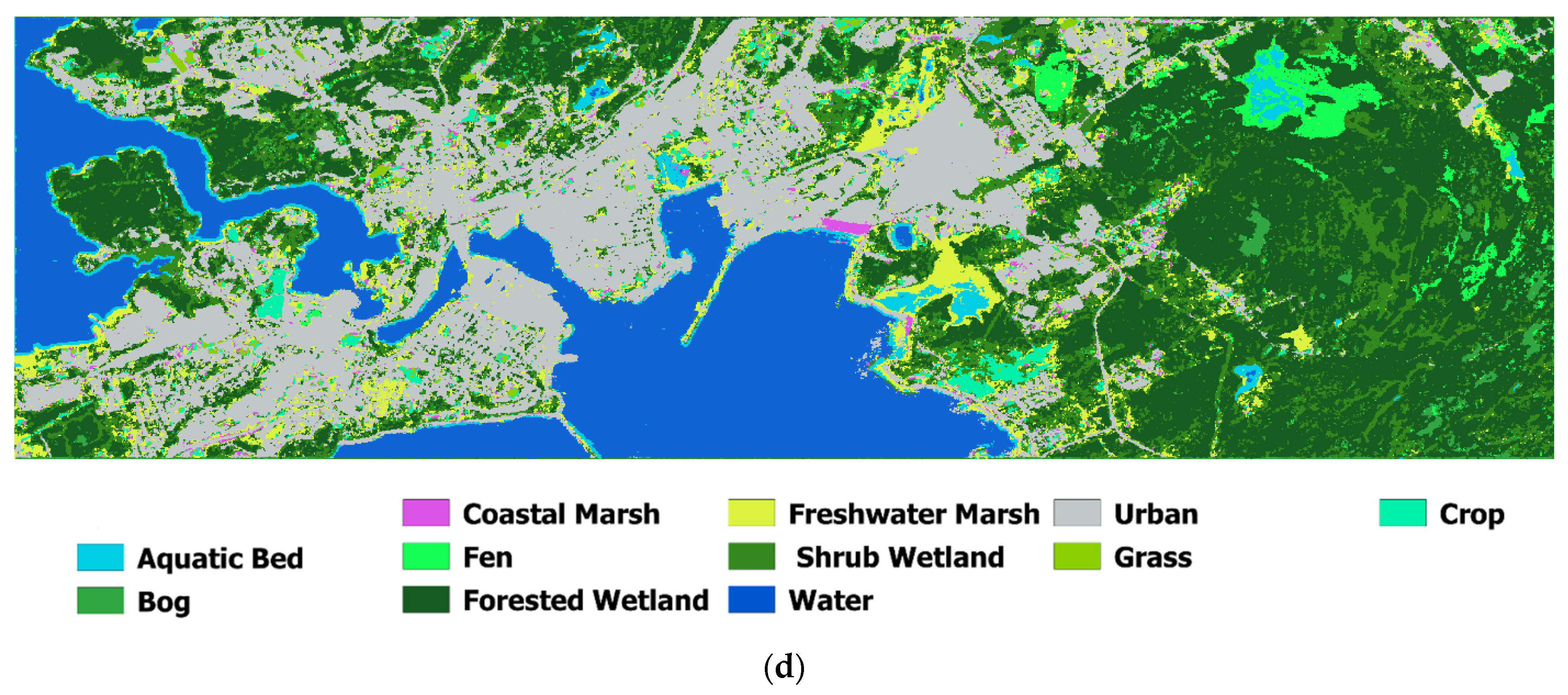
Figure 6 presents the coastal wetlands classification maps using the proposed multi-model deep learning algorithm, 3D CNN, VGG-16, Swin transformer, RF, and SVM classifiers. The proposed deep learning classifier obtained the best visual result compared with other machine learning methods. For instance, the SVM classifier showed under-classification for the recognition of coastal wetland class while other methods, including 3D CNN, Swin transformer, VGG-16, and RF had over-classification of the coastal wetlands. Moreover, for the identification of the aquatic bed wetlands, 3D CNN, VGG-16, and RF classifiers showed over-classification, as shown in Figure 6. It should be noted that systematic stripes in Figure 6f,g that are wetlands classified by the RF and SVM algorithms are due to the resampling technique of nearest neighbor that was used for mosaicking several patches of high-resolution LiDAR DEM data. It is possible to remove such noises by using image smoothing techniques such as a three by three mean filter, but we did not utilize them to investigate the effects of such noises on the performance of patch-based (i.e., CNNs) and pixel-based (i.e., traditional algorithms) classifiers. From Figure 6, it is clear that patch-based classifiers that consider both spatial and spectral information are not affected by such noises compared with pixel-based techniques that only consider spectral information.

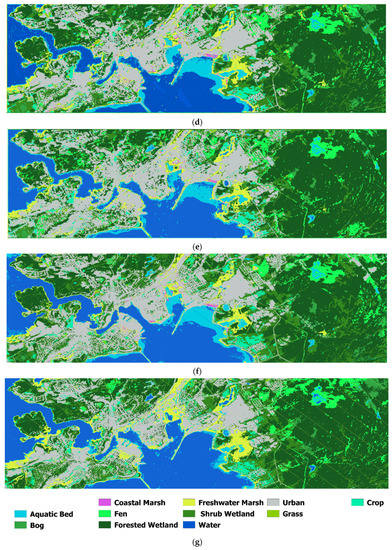
Figure 6.
(a) The Sentinel-2 true color of the pilot site of Saint John city, (b) coastal wetland classification maps using the proposed multi-model deep learning algorithm, (c) Swin Transformer, (d) 3D CNN, (e) VGG-16, (f) random forest, and (g) support vector machine.
3.4. Ablation Study
To better understand the contribution of each network of the proposed multi-model algorithm, including the VGG-16 that uses the extracted features of Sentinel-2 data, 3D CNN that employs the backscattering coefficients of Sentinel-1 image, and the Swin transformer the utilizes the generated DEM from LiDAR data, we performed an ablation study. As seen in Table 4, the VGG-16 using the Sentinel-2 features reached an average accuracy and overall accuracy of 73.93% and 79.75%, respectively. By adding the 3D CNN network and using Sentinel-1 features, the average accuracy, and overall accuracy significantly improved by 17.21% and 9.62%. In addition, by adding the Swin transformer network and the DEM data, the best visual and quantitative results were achieved. The inclusion of the Swin transformer improved the average and overall accuracies by 1.54% and 2.93%, respectively. Moreover, the inclusion of DEM by Swin transformer significantly improved the visual result of the proposed deep learning classifier. For instance, over-classification of coastal wetland and under-classification of water classes were visually improved in the multi-model algorithm, as seen in Figure 7.

Table 4.
Results of the proposed multi-model compared with other classifiers in terms of average accuracy, precision, F1-score, and recall (AB = aquatic bed, BO = bog, CM = coastal marsh, FE = fen, FM = freshwater marsh, FW = forested wetland, SB = shrub wetland, W = water, U = urban, G = grass, C = crop, AA = average accuracy, OA = overall accuracy, and K = kappa).
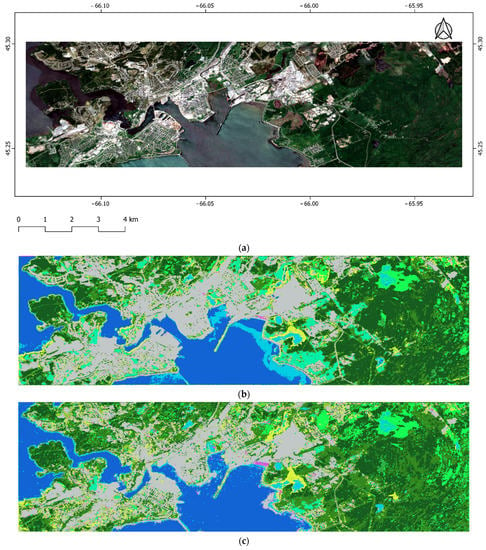
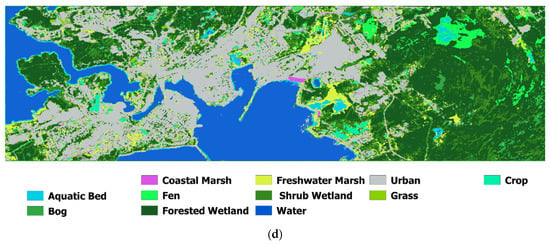
Figure 7.
Coastal wetland classification using: (a) Sentinel-2 true color of the study area, (b) the VGG-16 network (Sentinel-2 features), (c) VGG-16 and second 3D CNN networks (Sentinel-1 and Sentinel-2 features, respectively), and (d) the multi-model network.
The inclusion of each network considerably decreased the confusion between wetland and non-wetland classes. For instance, high confusion between bog, coastal marsh, and shrub wetlands resulting from the VGG-16 network was significantly decreased by adding the 3D CNN network and Sentinel-1 features (refer to Table S2 of Supplementary Materials).
3.5. Effect of Different Data Sources on Wetland Classification Accuracy
To better understand how different data sources, including backscattering features from Sentinel-1, spectral features of Sentinel-2, and DEM generated from LiDAR data contribute to the coastal wetland classification, we conducted several experiments with the use of an RF classifier as seen in Table 5. Although the inclusion of SAR data did not considerably improve the average accuracy of wetland classification, the F-1 scores of wetlands of shrub, aquatic bed, freshwater marsh, and coastal marsh improved by 1%, 2%, 3%, and 5%, respectively. On the other hand, the use of DEM data improved the average accuracy, overall accuracy, and kappa by 5.48%, 3.82%, and 4.69%, respectively. F-1 scores of forested wetland, aquatic bed, fen, shrub, freshwater marsh, coastal marsh, and bog improved by 2%, 3%, 6%, 6%, 8%, 8%, and 13%, respectively, with the inclusion of DEM data.

Table 5.
Results of the RF classifier with different data sources in terms of average accuracy, precision, F1-score, and recall (AB = aquatic bed, BO = bog, CM = coastal marsh, FE = fen, FM = freshwater marsh, FW = forested wetland, SB = shrub wetland, W = water, U = urban, G = grass, C = crop, AA = average accuracy, OA = overall accuracy, K = kappa, S1 = Sentinel-1, S2 = Sentinel-2, DEM = DEM from LiDAR data).
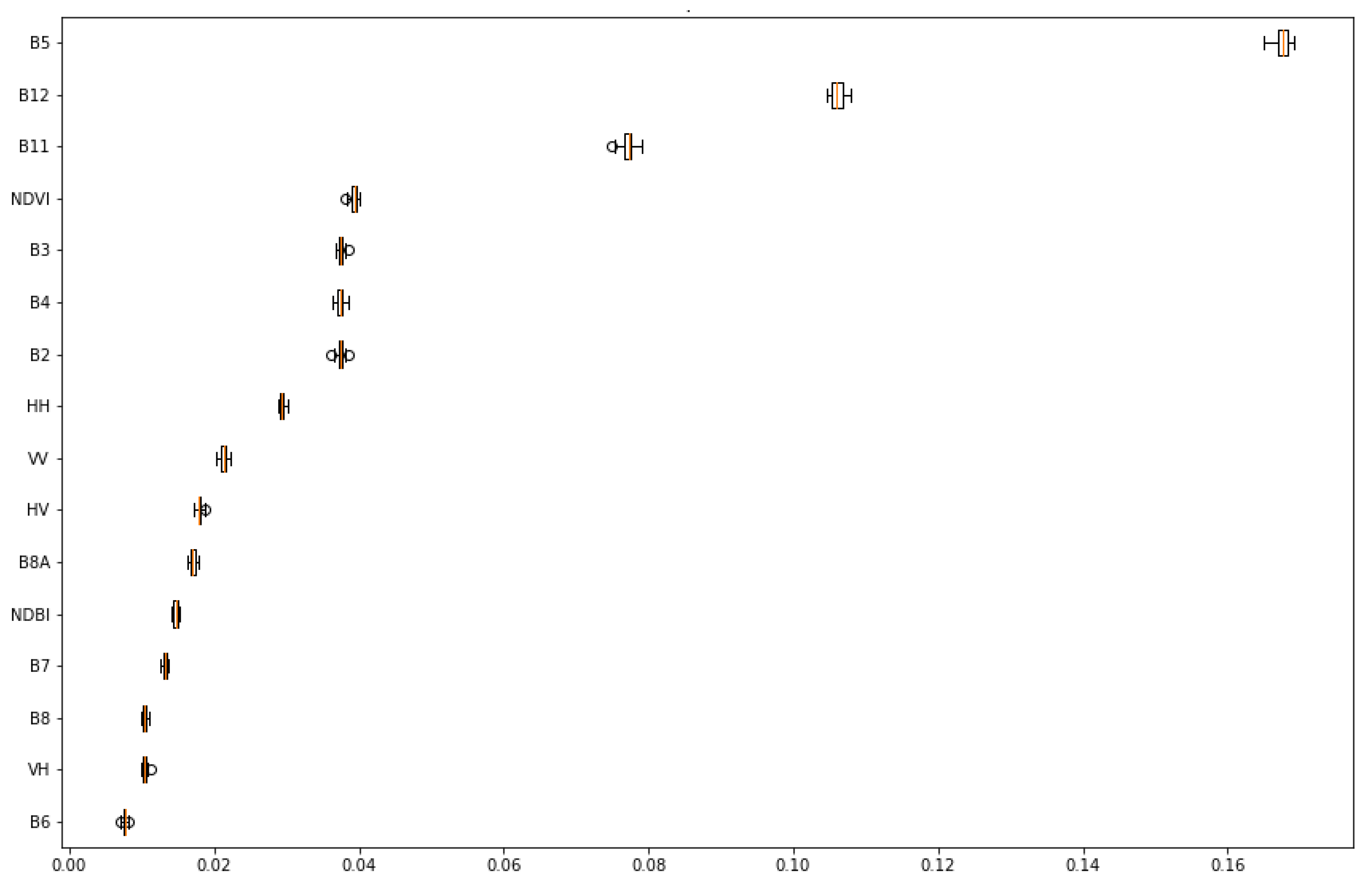
Moreover, the variable importance was measured to better understand the significance and contribution of different extracted Sentinel-1 and Sentinel-2 features. We ran the RF classifier [52] 30 times for the spectral analysis, as shown in Figure 8. As expected, Sentinel-2 bands and indices were more effective for classifying coastal wetlands than the Sentinel-1 backscattering features. Based on the Gini index for the prediction of the test data, the most influential variable for coastal wetland classification was the first vegetation red edge band (i.e., B5). In the RF classifier for attribute selection measure, typically, the Gini index [85] is used. In contrast, the least effective variable was the second vegetation red edge band (i.e., B6). Moreover, the most effective feature of Sentinel-1 was the band. The reason is that is sensitive to double bounce scattering for flooded vegetation, a suitable Sentinel-1 feature for recognizing coastal wetlands. In addition, compared with , the is less affected by the water roughness that is useful for the identification of non-water bodies from water regions.
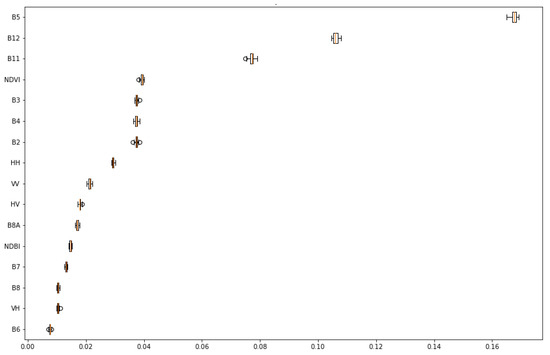
Figure 8.
The variable importance of extracted features of Sentinel-1 and Sentinel-2 on the final coastal wetland classification by the RF classifier based on the Gini importance index.
3.6. Effect of Different Spatial Resolutions on Wetland Classification Accuracy
Effects of spatial resolution on coastal classification accuracy were investigated by the comparison of classification results of the proposed multi-model for 10 m and 30 m spatial resolution data sources, as seen in Table 6. Based on the results, higher 10 m spatial resolution data sources outperformed the lower 10 m spatial resolution data sources by 7.71%, 7.68%, and 9.26%, respectively, by the proposed multi-model classifier in terms of average accuracy, overall accuracy, and kappa index. The reason can be explained by greater details and more information extracted from high-resolution images, specifically while dealing with a complex landscape such as wetlands with a high level of inter-class similarity.

Table 6.
Results of the proposed multi-model for different spatial resolutions in terms of average accuracy, precision, F1-score, and recall (AB = aquatic bed, BO = bog, CM = coastal marsh, FE = fen, FM = freshwater marsh, FW = forested wetland, SB = shrub wetland, W = water, U = urban, G = grass, C = crop, AA = average accuracy, OA = overall accuracy, K = kappa, 10 = 10 m spatial resolution, and 30 = 30 m spatial resolution).
3.7. Computation Cost
In analyzing the computation cost in terms of time, the RF classifier with 2 min training time showed the best performance over the other implemented classifiers, including the SVM, VGG-16, 3D CNN, Swin transformer, and the proposed multi-model network with training times of 20, 40, 50, 60, and 90 min, respectively.
4. Discussion
Various research teams have conducted substantial research to improve wetland mapping in Canada by utilizing various data sources and approaches [35,36,48,86]. For example, Jamali et al. [87] used Sentinel-1 and Sentinel-2 data to classify five wetlands in Newfoundland, Canada: bog, fen, marsh, swamp, and shallow water, with a high average accuracy of 92.30% using very deep CNN networks and a generative adversarial network (GAN). According to their research, creating synthetic samples of Sentinel-1 and Sentinel-2 data considerably improved the classification accuracy of wetland mapping. Moreover, the synergic use of several satellite data has shown its superiority over a single satellite sensor by various research [7,8,87]. Results achieved in this study confirm the superiority of using different satellite data over solo Earth image data to improve the classification of a complex landscape of coastal wetlands. For instance, the F-1 scores of forested wetland, aquatic bed, fen, shrub, freshwater marsh, coastal marsh, and bog improved by 2%, 3%, 6%, 6%, 8%, 8%, and 13%, respectively with the utilization of DEM data in this research. Moreover, due to the higher distinguishable backscattering coefficients of Sentinel-1 features in wetlands and the high capability of the developed 3D CNN network in the extraction of useful information from training image patches, the accuracy of the proposed network was considerably improved.
On the other hand, most wetland mapping approaches in New Brunswick, as described by LaRocque et al. [88], depend on manual interpretation of high-resolution data. In the Saint John city study area, there is little literature on the usage of cutting-edge deep learning technologies. Although LaRocque et al. [88] reported that using Landsat 8 OLI, ALOS-1 PALSAR, Sentinel-1, and LiDAR-derived topographic metrics, the RF classifier achieved an overall accuracy of 97.67% in New Brunswick. Because our classifiers, the number of training data, and satellite data are different, we cannot precisely compare their results to this study’s acquired results. Based on the results, the proposed multi-model classifier with average accuracy, overall accuracy, and kappa index of 92.68%, 92.30%, and 90.65%, respectively, is highly capable of precise coastal wetland classification. As, in this study, the DEM was generated from LiDAR data, it would be difficult to create such precise height data for a large-scale wetland mapping. This is the main limitation of our study; however, several studies have shown the possibility of creating accurate and high-resolution DEM from Sentinel-1 data using the SAR interferometry technique [89,90].
As discussed in the previous sections, transformers have achieved great success in solving NLP issues. Although they have shown high potential for a few computers vision issues, a challenging issue in remote sensing complex landscape classification over the usual computer vision image classification is a much higher resolution of remote sensing satellite images. Considering that vision transformers have a complexity of with the increase in the pixel resolution, we selected the Swin transformer as it has a much lower linear complexity of with the increase in the resolution of image pixels. In other words, the Swin transformer is much more computationally efficient than other vision transformers. The other benefit of transformer networks is their higher generalization capability over CNN networks. An additional advantage of transformers over CNNs is that the relationship between different features of an image is also considered (i.e., positional encoding or attention mechanism). However, transformers require much more training data than that of the CNN models to reach their full image classification capability, which is a challenge in the remote sensing field. As positional relation between a pixel and its neighboring features is important in a DEM layer, we used a Swin transformer that considers the positional relationship to extract useful information. This led to increases of 1.54% and 2.93% in average and overall accuracies of the proposed multi-model algorithm. Our results show that integrating CNNs with transformers opens a new window for advancing new technologies and methods for complex scene classification in remote sensing.
5. Conclusions
Innovative methodologies and technology for wetland mapping and monitoring are critical because of the significant benefits that wetland functions provide to humans and wildlife. Wetlands are among the most difficult ecosystems to classify because of their dynamic and complicated structure, which lacks clear-cut boundaries and vegetation forms that are similar. As such, for the preservation and monitoring of coastal wetlands in the pilot site of Saint John city situated in New Brunswick, Canada, we explored the potential of the integration of the state-of-the-art transformers (i.e., Swin transformer) with a modified version of VGG-16 CNN network and a 3D CNN model. We used different data sources for each network, including spectral bands and indices of Sentinel-2 in the VGG-16 network, backscattering coefficients of Sentinel-1 in the 3D CNN, and a DEM generated from LiDAR data in the Swin transformer network and compared the achieved results with several solo CNN models as well as two shallow conventional classifiers of RF and SVM. The results suggest that the multi-model network in terms of average accuracy significantly improved the classification of coastal wetlands over other solo algorithms, including the RF, SVM, Swin transformer, VGG-16, and 3D CNN from 3.36% to 33.35%. Moreover, the utilization of multi-source data significantly increased the classification accuracy of Saint John city’s complex landscape. For instance, the inclusion of extracted features of Sentinel-1 and DEM increased the F-1 scores of the VGG-16 CNN network for the classification of shrub wetland, aquatic bed, fen, freshwater marsh, and bog by 1%, 3%, 3%, 8%, and 11%, respectively.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/rs14020359/s1, Table S1: Confusion matrices of the implemented models including the proposed multi-model deep learning model, Swin Transformer, 3D CNN, VGG-16, Random Forest, and Support Vector Machine; Table S2: Confusion matrices of the Multi-model, VGG-16, and VGG-16 + 3D CNN.
Author Contributions
Conceptualization, A.J. and M.M.; methodology, A.J. and M.M.; formal analysis, A.J.; writing—original draft preparation, A.J. and M.M.; writing—review and editing, A.J. and M.M.; supervision, M.M.; funding acquisition, M.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Python Codes are available through GitHub from (https://github.com/aj1365/MultiModelCNN, accessed on 6 December 2021).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Mahdianpari, M.; Jafarzadeh, H.; Granger, J.E.; Mohammadimanesh, F.; Brisco, B.; Salehi, B.; Homayouni, S.; Weng, Q. A Large-Scale Change Monitoring of Wetlands Using Time Series Landsat Imagery on Google Earth Engine: A Case Study in Newfoundland. GIScience Remote Sens. 2020, 57, 1102–1124. [Google Scholar] [CrossRef]
- Tiner, R.W. Wetland Indicators: A Guide to Wetland Formation, Identification, Delineation, Classification, and Mapping, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Kaplan, G.; Avdan, U. Monthly Analysis of Wetlands Dynamics Using Remote Sensing Data. ISPRS Int. J. Geo-Inf. 2018, 7, 411. [Google Scholar] [CrossRef] [Green Version]
- Mao, D.; Wang, Z.; Du, B.; Li, L.; Tian, Y.; Jia, M.; Zeng, Y.; Song, K.; Jiang, M.; Wang, Y. National Wetland Mapping in China: A New Product Resulting from Object-Based and Hierarchical Classification of Landsat 8 OLI Images. ISPRS J. Photogramm. Remote Sens. 2020, 164, 11–25. [Google Scholar] [CrossRef]
- Davidson, N.C. The Ramsar Convention on Wetlands. In The Wetland Book I: Structure and Function, Management and Methods; Springer Publishers: Dordrecht, The Netherlands, 2016. [Google Scholar]
- Fariba Mohammadimanesh; Bahram Salehi; Masoud Mahdianpari; Brian Brisco; Eric Gill Full and Simulated Compact Polarimetry SAR Responses to Canadian Wetlands: Separability Analysis and Classification. Remote Sens. 2019, 11, 516. [CrossRef] [Green Version]
- Jamali, A.; Mahdianpari, M.; Brisco, B.; Granger, J.; Mohammadimanesh, F.; Salehi, B. Deep Forest Classifier for Wetland Mapping Using the Combination of Sentinel-1 and Sentinel-2 Data. GIScience Remote Sens. 2021, 58, 1072–1089. [Google Scholar] [CrossRef]
- Mahdianpari, M.; Salehi, B.; Mohammadimanesh, F.; Homayouni, S.; Gill, E. The First Wetland Inventory Map of Newfoundland at a Spatial Resolution of 10 m Using Sentinel-1 and Sentinel-2 Data on the Google Earth Engine Cloud Computing Platform. Remote Sens. 2019, 11, 43. [Google Scholar] [CrossRef] [Green Version]
- Amani, M.; Salehi, B.; Mahdavi, S.; Brisco, B. Spectral Analysis of Wetlands Using Multi-Source Optical Satellite Imagery. ISPRS J. Photogramm. Remote Sens. 2018, 144, 119–136. [Google Scholar] [CrossRef]
- Slagter, B.; Tsendbazar, N.E.; Vollrath, A.; Reiche, J. Mapping Wetland Characteristics Using Temporally Dense Sentinel-1 and Sentinel-2 Data: A Case Study in the St. Lucia Wetlands, South Africa. Int. J. Appl. Earth Obs. Geoinf. 2020, 86, 102009. [Google Scholar] [CrossRef]
- Asselen, S.V.; Verburg, P.H.; Vermaat, J.E.; Janse, J.H. Drivers of Wetland Conversion: A Global Meta-Analysis. PLoS ONE 2013, 8, e81292. [Google Scholar] [CrossRef] [Green Version]
- Mohammadimanesh, F.; Salehi, B.; Mahdianpari, M.; Brisco, B.; Motagh, M. Wetland Water Level Monitoring Using Interferometric Synthetic Aperture Radar (InSAR): A Review. Can. J. Remote Sens. 2018, 44, 247–262. [Google Scholar] [CrossRef]
- Mahdianpari, M.; Salehi, B.; Mohammadimanesh, F.; Brisco, B. An Assessment of Simulated Compact Polarimetric SAR Data for Wetland Classification Using Random Forest Algorithm. Can. J. Remote Sens. 2017, 43, 468–484. [Google Scholar] [CrossRef]
- Mao, D.; Wang, Z.; Wu, J.; Wu, B.; Zeng, Y.; Song, K.; Yi, K.; Luo, L. China’s Wetlands Loss to Urban Expansion. Land Degrad. Dev. 2018, 29, 2644–2657. [Google Scholar] [CrossRef]
- Kirwan, M.L.; Megonigal, J.P. Tidal Wetland Stability in the Face of Human Impacts and Sea-Level Rise. Nature 2013, 504, 53–60. [Google Scholar] [CrossRef] [PubMed]
- Mahdianpari, M.; Granger, J.E.; Mohammadimanesh, F.; Salehi, B.; Brisco, B.; Homayouni, S.; Gill, E.; Huberty, B.; Lang, M. Meta-Analysis of Wetland Classification Using Remote Sensing: A Systematic Review of a 40-Year Trend in North America. Remote Sens. 2020, 12, 1882. [Google Scholar] [CrossRef]
- Connor, R. The United Nations World Water Development Report 2015: Water for a Sustainable World; UNESCO publishing: Paris, France, 2015. [Google Scholar]
- Mahdianpari, M. Advanced Machine Learning Algorithms for Canadian Wetland Mapping Using Polarimetric Synthetic Aperture Radar (PolSAR) and Optical Imagery. Ph.D. Thesis, Memorial University of Newfoundland, St. John’s, NL, Canada, 2019. [Google Scholar]
- Byun, E.; Finkelstein, S.A.; Cowling, S.A.; Badiou, P. Potential Carbon Loss Associated with Post-Settlement Wetland Conversion in Southern Ontario, Canada. Carbon Balance Manag. 2018, 13, 6. [Google Scholar] [CrossRef] [PubMed]
- Breeuwer, A.; Robroek, B.J.M.; Limpens, J.; Heijmans, M.M.P.D.; Schouten, M.G.C.; Berendse, F. Decreased Summer Water Table Depth Affects Peatland Vegetation. Basic Appl. Ecol. 2009, 10, 330–339. [Google Scholar] [CrossRef]
- Edvardsson, J.; Šimanauskienė, R.; Taminskas, J.; Baužienė, I.; Stoffel, M. Increased Tree Establishment in Lithuanian Peat Bogs—Insights from Field and Remotely Sensed Approaches. Sci. Total Environ. 2015, 505, 113–120. [Google Scholar] [CrossRef] [PubMed]
- Boucher, D.; Gauthier, S.; Thiffault, N.; Marchand, W.; Girardin, M.; Urli, M. How Climate Change Might Affect Tree Regeneration Following Fire at Northern Latitudes: A Review. New For. 2020, 51, 543–571. [Google Scholar] [CrossRef] [Green Version]
- Stralberg, D.; Wang, X.; Parisien, M.-A.; Robinne, F.-N.; Sólymos, P.; Mahon, C.L.; Nielsen, S.E.; Bayne, E.M. Wildfire-Mediated Vegetation Change in Boreal Forests of Alberta, Canada. Ecosphere 2018, 9, e02156. [Google Scholar] [CrossRef]
- Zedler, J.B.; Kercher, S. Causes and Consequences of Invasive Plants in Wetlands: Opportunities, Opportunists, and Outcomes. Crit. Rev. Plant Sci. 2004, 23, 431–452. [Google Scholar] [CrossRef]
- Perillo, G.; Wolanski, E.; Cahoon, D.R.; Hopkinson, C.S. Coastal Wetlands: And Integrated Ecosystem Approach; Elsevier: Oxford, UK, 2018. [Google Scholar]
- Hosseiny, B.; Mahdianpari, M.; Brisco, B.; Mohammadimanesh, F.; Salehi, B. WetNet: A Spatial-Temporal Ensemble Deep Learning Model for Wetland Classification Using Sentinel-1 and Sentinel-2. IEEE Trans. Geosci. Remote Sens. 2021, 1–14. [Google Scholar]
- Dawson, T.P.; Jackson, S.T.; House, J.I.; Prentice, I.C.; Mace, G.M. Beyond Predictions: Biodiversity Conservation in a Changing Climate. Science 2011, 332, 53–58. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Howes, N.C.; FitzGerald, D.M.; Hughes, Z.J.; Georgiou, I.Y.; Kulp, M.A.; Miner, M.D.; Smith, J.M.; Barras, J.A. Hurricane-Induced Failure of Low Salinity Wetlands. Proc. Natl. Acad. Sci. USA 2010, 107, 14014. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mitsch, W.J.; Gosselink, J.G. The Value of Wetlands: Importance of Scale and Landscape Setting. Ecol. Econ. 2000, 35, 25–33. [Google Scholar] [CrossRef]
- Zhu, P.; Gong, P. Suitability Mapping of Global Wetland Areas and Validation with Remotely Sensed Data. Sci. China Earth Sci. 2014, 57, 2283–2292. [Google Scholar] [CrossRef]
- Zhu, Q.; Peng, C.; Chen, H.; Fang, X.; Liu, J.; Jiang, H.; Yang, Y.; Yang, G. Estimating Global Natural Wetland Methane Emissions Using Process Modelling: Spatio-Temporal Patterns and Contributions to Atmospheric Methane Fluctuations. Glob. Ecol. Biogeogr. 2015, 24, 959–972. [Google Scholar] [CrossRef]
- Mahdianpari, M.; Brisco, B.; Granger, J.; Mohammadimanesh, F.; Salehi, B.; Homayouni, S.; Bourgeau-Chavez, L. The Third Generation of Pan-Canadian Wetland Map at 10 m Resolution Using Multisource Earth Observation Data on Cloud Computing Platform. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 8789–8803. [Google Scholar]
- Mahdianpari, M.; Jafarzadeh, H.; Granger, J.E.; Mohammadimanesh, F.; Brisco, B.; Salehi, B.; Homayouni, S.; Weng, Q. Monitoring of 30 Years Wetland Changes in Newfoundland, Canada. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021; pp. 88–91. [Google Scholar]
- Granger, J.E.; Mahdianpari, M.; Puestow, T.; Warren, S.; Mohammadimanesh, F.; Salehi, B.; Brisco, B. Object-Based Random Forest Wetland Mapping in Conne River, Newfoundland, Canada. J. Appl. Remote Sens. 2021, 15, 038506. [Google Scholar] [CrossRef]
- Mahdianpari, M.; Salehi, B.; Mohammadimanesh, F.; Brisco, B.; Homayouni, S.; Gill, E.; DeLancey, E.R.; Bourgeau-Chavez, L. Big Data for a Big Country: The First Generation of Canadian Wetland Inventory Map at a Spatial Resolution of 10-m Using Sentinel-1 and Sentinel-2 Data on the Google Earth Engine Cloud Computing Platform. Can. J. Remote Sens. 2020, 46, 15–33. [Google Scholar] [CrossRef]
- Amani, M.; Brisco, B.; Mahdavi, S.; Ghorbanian, A.; Moghimi, A.; DeLancey, E.R.; Merchant, M.; Jahncke, R.; Fedorchuk, L.; Mui, A.; et al. Evaluation of the Landsat-Based Canadian Wetland Inventory Map Using Multiple Sources: Challenges of Large-Scale Wetland Classification Using Remote Sensing. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 32–52. [Google Scholar] [CrossRef]
- Mohammadimanesh, F.; Salehi, B.; Mahdianpari, M.; Homayouni, S. Unsupervised Wishart Classfication of Wetlands in Newfoundland, Canada Using Polsar Data Based on Fisher Linear Discriminant Analysis. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 41, 305. [Google Scholar] [CrossRef] [Green Version]
- Bennett, K.P. Global Tree Optimization: A Non-Greedy Decision Tree Algorithm. Comput. Sci. Stat. 1994, 26, 156–160. [Google Scholar]
- Belgiu, M.; Drăguţ, L. Random Forest in Remote Sensing: A Review of Applications and Future Directions. ISPRS J. Photogramm. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-Vector Networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Hamida, A.B.; Benoit, A.; Lambert, P.; Amar, C.B. 3-D Deep Learning Approach for Remote Sensing Image Classification. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4420–4434. [Google Scholar] [CrossRef] [Green Version]
- Algan, G.; Ulusoy, I. Image Classification with Deep Learning in the Presence of Noisy Labels: A Survey. Knowl.-Based Syst. 2021, 215, 106771. [Google Scholar] [CrossRef]
- Hong, D.; Gao, L.; Yokoya, N.; Yao, J.; Chanussot, J.; Du, Q.; Zhang, B. More Diverse Means Better: Multimodal Deep Learning Meets Remote-Sensing Imagery Classification. IEEE Trans. Geosci. Remote Sens. 2021, 59, 4340–4354. [Google Scholar] [CrossRef]
- DeLancey, E.R.; Simms, J.F.; Mahdianpari, M.; Brisco, B.; Mahoney, C.; Kariyeva, J. Comparing Deep Learning and Shallow Learning for Large-Scale Wetland Classification in Alberta, Canada. Remote Sens. 2020, 12, 2. [Google Scholar] [CrossRef] [Green Version]
- Mahdianpari, M.; Salehi, B.; Rezaee, M.; Mohammadimanesh, F.; Zhang, Y. Very Deep Convolutional Neural Networks for Complex Land Cover Mapping Using Multispectral Remote Sensing Imagery. Remote Sens. 2018, 10, 1119. [Google Scholar] [CrossRef] [Green Version]
- Rezaee, M.; Mahdianpari, M.; Zhang, Y.; Salehi, B. Deep Convolutional Neural Network for Complex Wetland Classification Using Optical Remote Sensing Imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 3030–3039. [Google Scholar] [CrossRef]
- Ghanbari, H.; Mahdianpari, M.; Homayouni, S.; Mohammadimanesh, F. A Meta-Analysis of Convolutional Neural Networks for Remote Sensing Applications. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 3602–3613. [Google Scholar] [CrossRef]
- Jamali, A.; Mahdianpari, M.; Brisco, B.; Granger, J.; Mohammadimanesh, F.; Salehi, B. Wetland Mapping Using Multi-Spectral Satellite Imagery and Deep Convolutional Neural Networks: A Case Study in Newfoundland and Labrador, Canada. Can. J. Remote Sens. 2021, 47, 243–260. [Google Scholar] [CrossRef]
- Taghizadeh-Mehrjardi, R.; Mahdianpari, M.; Mohammadimanesh, F.; Behrens, T.; Toomanian, N.; Scholten, T.; Schmidt, K. Multi-Task Convolutional Neural Networks Outperformed Random Forest for Mapping Soil Particle Size Fractions in Central Iran. Geoderma 2020, 376, 114552. [Google Scholar] [CrossRef]
- Mahdianpari, M.; Salehi, B.; Mohammadimanesh, F.; Motagh, M. Random Forest Wetland Classification Using ALOS-2 L-Band, RADARSAT-2 C-Band, and TerraSAR-X Imagery. ISPRS J. Photogramm. Remote Sens. 2017, 130, 13–31. [Google Scholar] [CrossRef]
- Mahdianpari, M.; Salehi, B.; Mohammadimanesh, F.; Brisco, B.; Mahdavi, S.; Amani, M.; Granger, J.E. Fisher Linear Discriminant Analysis of Coherency Matrix for Wetland Classification Using PolSAR Imagery. Remote Sens. Environ. 2018, 206, 300–317. [Google Scholar] [CrossRef]
- Jamali, A.; Mahdianpari, M.; Brisco, B.; Granger, J.; Mohammadimanesh, F.; Salehi, B. Comparing Solo Versus Ensemble Convolutional Neural Networks for Wetland Classification Using Multi-Spectral Satellite Imagery. Remote Sens. 2021, 13, 2046. [Google Scholar] [CrossRef]
- Mohammadimanesh, F.; Salehi, B.; Mahdianpari, M.; Gill, E.; Molinier, M. A New Fully Convolutional Neural Network for Semantic Segmentation of Polarimetric SAR Imagery in Complex Land Cover Ecosystem. ISPRS J. Photogramm. Remote Sens. 2019, 151, 223–236. [Google Scholar] [CrossRef]
- Jeppesen, J.H.; Jacobsen, R.H.; Inceoglu, F.; Toftegaard, T.S. A Cloud Detection Algorithm for Satellite Imagery Based on Deep Learning. Remote Sens. Environ. 2019, 229, 247–259. [Google Scholar] [CrossRef]
- Alhichri, H.; Alswayed, A.S.; Bazi, Y.; Ammour, N.; Alajlan, N.A. Classification of Remote Sensing Images Using EfficientNet-B3 CNN Model With Attention. IEEE Access 2021, 9, 14078–14094. [Google Scholar] [CrossRef]
- Kattenborn, T.; Leitloff, J.; Schiefer, F.; Hinz, S. Review on Convolutional Neural Networks (CNN) in Vegetation Remote Sensing. ISPRS J. Photogramm. Remote Sens. 2021, 173, 24–49. [Google Scholar] [CrossRef]
- Khan, M.A.; Akram, T.; Zhang, Y.-D.; Sharif, M. Attributes Based Skin Lesion Detection and Recognition: A Mask RCNN and Transfer Learning-Based Deep Learning Framework. Pattern Recognit. Lett. 2021, 143, 58–66. [Google Scholar] [CrossRef]
- Zhang, C.; Pan, X.; Li, H.; Gardiner, A.; Sargent, I.; Hare, J.; Atkinson, P.M. A Hybrid MLP-CNN Classifier for Very Fine Resolution Remotely Sensed Image Classification. ISPRS J. Photogramm. Remote Sens. 2018, 140, 133–144. [Google Scholar] [CrossRef] [Green Version]
- Cao, J.; Cui, H.; Zhang, Q.; Zhang, Z. Ancient Mural Classification Method Based on Improved AlexNet Network. Stud. Conserv. 2020, 65, 411–423. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.J.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR) 2016, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Huang, G.; Liu, Z.; Van Der Maaten, L.; Weinberger, K.Q. Densely Connected Convolutional Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition 2017, Honolulu, HI, USA, 21–26 July 2017; pp. 4700–4708. [Google Scholar]
- Xie, S.; Girshick, R.; Dollár, P.; Tu, Z.; He, K. Aggregated ’Residual Transformations for Deep Neural Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition 2017, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention Is All You Need. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 5998–6008. [Google Scholar]
- Bazi, Y.; Bashmal, L.; Rahhal, M.M.A.; Dayil, R.A.; Ajlan, N.A. Vision Transformers for Remote Sensing Image Classification. Remote Sens. 2021, 13, 516. [Google Scholar] [CrossRef]
- He, J.; Zhao, L.; Yang, H.; Zhang, M.; Li, W. HSI-BERT: Hyperspectral Image Classification Using the Bidirectional Encoder Representation From Transformers. IEEE Trans. Geosci. Remote Sens. 2020, 58, 165–178. [Google Scholar] [CrossRef]
- Hong, D.; Han, Z.; Yao, J.; Gao, L.; Zhang, B.; Plaza, A.; Chanussot, J. SpectralFormer: Rethinking Hyperspectral Image Classification with Transformers. IEEE Trans. Geosci. Remote Sens. 2021, 1. [Google Scholar] [CrossRef]
- Mohammadimanesh, F.; Salehi, B.; Mahdianpari, M.; Brisco, B.; Motagh, M. Multi-Temporal, Multi-Frequency, and Multi-Polarization Coherence and SAR Backscatter Analysis of Wetlands. ISPRS J. Photogramm. Remote Sens. 2018, 142, 78–93. [Google Scholar] [CrossRef]
- Louis, J.; Debaecker, V.; Pflug, B.; Main-Knorn, M.; Bieniarz, J.; Mueller-Wilm, U.; Cadau, E.; Gascon, F. Sentinel-2 Sen2Cor: L2A Processor for Users. In Living Planet Symposium 2016, SP-740, Proceedings of the ESA Living Planet Symposium 2016, Prague, Czech Republic, 9–13 May 2016; Spacebooks Online: Bavaria, Germany, 2016; pp. 1–8. ISBN 978-92-9221-305-3. ISSN 1609-042X. [Google Scholar]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin Transformer: Hierarchical Vision Transformer Using Shifted Windows. arXiv 2021, arXiv:2103.14030. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 54, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Azeez, N.; Yahya, W.; Al-Taie, I.; Basbrain, A.; Clark, A. Regional Agricultural Land Classification Based on Random Forest (RF), Decision Tree, and SVMs Techniques; Springer: Berlin/Heidelberg, Germany, 2020; pp. 73–81. [Google Scholar]
- Collins, L.; McCarthy, G.; Mellor, A.; Newell, G.; Smith, L. Training Data Requirements for Fire Severity Mapping Using Landsat Imagery and Random Forest. Remote Sens. Environ. 2020, 245, 111839. [Google Scholar] [CrossRef]
- Rodriguez-Galiano, V.F.; Ghimire, B.; Rogan, J.; Chica-Olmo, M.; Rigol-Sanchez, J.P. An Assessment of the Effectiveness of a Random Forest Classifier for Land-Cover Classification. ISPRS J. Photogramm. Remote Sens. 2012, 67, 93–104. [Google Scholar] [CrossRef]
- Aldrich, C. Process Variable Importance Analysis by Use of Random Forests in a Shapley Regression Framework. Minerals 2020, 10, 420. [Google Scholar] [CrossRef]
- Collins, L.; Griffioen, P.; Newell, G.; Mellor, A. The Utility of Random Forests for Wildfire Severity Mapping. Remote Sens. Environ. 2018, 216, 374–384. [Google Scholar] [CrossRef]
- Gibson, R.; Danaher, T.; Hehir, W.; Collins, L. A Remote Sensing Approach to Mapping Fire Severity in South-Eastern Australia Using Sentinel 2 and Random Forest. Remote Sens. Environ. 2020, 240, 111702. [Google Scholar] [CrossRef]
- Sheykhmousa, M.; Mahdianpari, M.; Ghanbari, H.; Mohammadimanesh, F.; Ghamisi, P.; Homayouni, S. Support Vector Machine Versus Random Forest for Remote Sensing Image Classification: A Meta-Analysis and Systematic Review. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 6308–6325. [Google Scholar] [CrossRef]
- Razaque, A.; Ben Haj Frej, M.; Almi’ani, M.; Alotaibi, M.; Alotaibi, B. Improved Support Vector Machine Enabled Radial Basis Function and Linear Variants for Remote Sensing Image Classification. Sensors 2021, 21, 4431. [Google Scholar] [CrossRef] [PubMed]
- Liang, J.; Deng, Y.; Zeng, D. A Deep Neural Network Combined CNN and GCN for Remote Sensing Scene Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 4325–4338. [Google Scholar] [CrossRef]
- Sit, M.; Demiray, B.Z.; Xiang, Z.; Ewing, G.J.; Sermet, Y.; Demir, I. A Comprehensive Review of Deep Learning Applications in Hydrology and Water Resources. Water Sci. Technol. 2020, 82, 2635–2670. [Google Scholar] [CrossRef] [PubMed]
- Ma, L.; Liu, Y.; Zhang, X.; Ye, Y.; Yin, G.; Johnson, B.A. Deep Learning in Remote Sensing Applications: A Meta-Analysis and Review. ISPRS J. Photogramm. Remote Sens. 2019, 152, 166–177. [Google Scholar] [CrossRef]
- Bera, S.; Shrivastava, V.K. Analysis of Various Optimizers on Deep Convolutional Neural Network Model in the Application of Hyperspectral Remote Sensing Image Classification. Int. J. Remote Sens. 2020, 41, 2664–2683. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. In Proceedings of the International Conference on Learning Representations, Banff, Canada, 14–16 April 2014. [Google Scholar]
- Srivastava, S.; Kumar, P.; Chaudhry, V.; Singh, A. Detection of Ovarian Cyst in Ultrasound Images Using Fine-Tuned VGG-16 Deep Learning Network. SN Comput. Sci. 2020, 1, 81. [Google Scholar] [CrossRef] [Green Version]
- Quinlan, J.R. C4.5: Programs for Machine Learning; Morgan Kaufmann: San Mateo, CA, USA, 1993. [Google Scholar]
- Amani, M.; Mahdavi, S.; Berard, O. Supervised Wetland Classification Using High Spatial Resolution Optical, SAR, and LiDAR Imagery. J. Appl. Remote Sens. 2020, 14, 024502. [Google Scholar] [CrossRef]
- Jamali, A.; Mahdianpari, M.; Mohammadimanesh, F.; Brisco, B.; Salehi, B. A Synergic Use of Sentinel-1 and Sentinel-2 Imagery for Complex Wetland Classification Using Generative Adversarial Network (GAN) Scheme. Water 2021, 13, 3601. [Google Scholar] [CrossRef]
- LaRocque, A.; Phiri, C.; Leblon, B.; Pirotti, F.; Connor, K.; Hanson, A. Wetland Mapping with Landsat 8 OLI, Sentinel-1, ALOS-1 PALSAR, and LiDAR Data in Southern New Brunswick, Canada. Remote Sens. 2020, 12, 2095. [Google Scholar] [CrossRef]
- Mohammadi, A.; Karimzadeh, S.; Jalal, S.J.; Kamran, K.V.; Shahabi, H.; Homayouni, S.; Al-Ansari, N. A Multi-Sensor Comparative Analysis on the Suitability of Generated DEM from Sentinel-1 SAR Interferometry Using Statistical and Hydrological Models. Sensors 2020, 20, 7214. [Google Scholar] [CrossRef] [PubMed]
- Devaraj, S.; Yarrakula, K. Evaluation of Sentinel 1–Derived and Open-Access Digital Elevation Model Products in Mountainous Areas of Western Ghats, India. Arab. J. Geosci. 2020, 13, 1103. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).