Earth Observation via Compressive Sensing: The Effect of Satellite Motion
Abstract
:1. Introduction
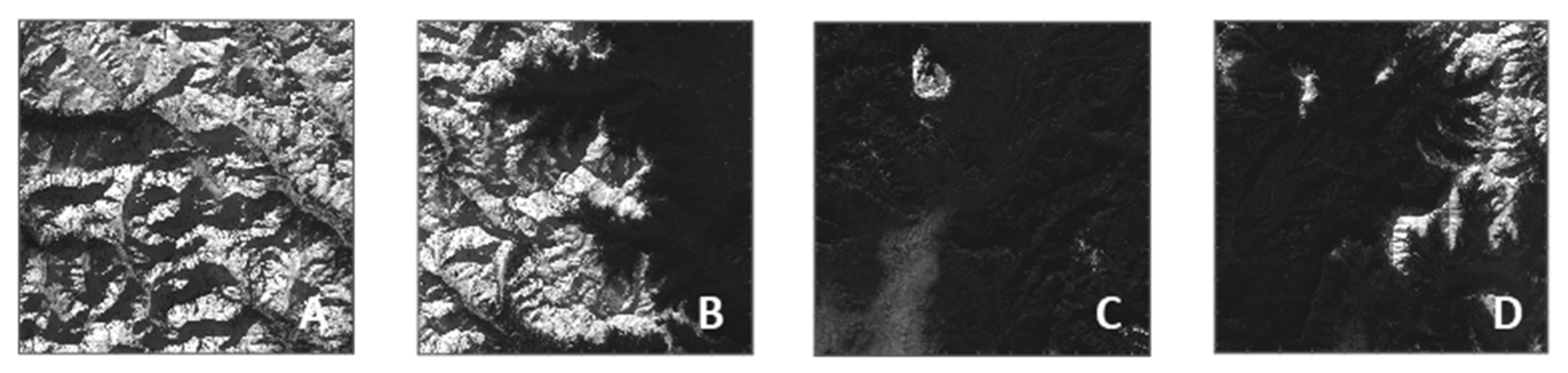
2. Materials and Methods
3. Results
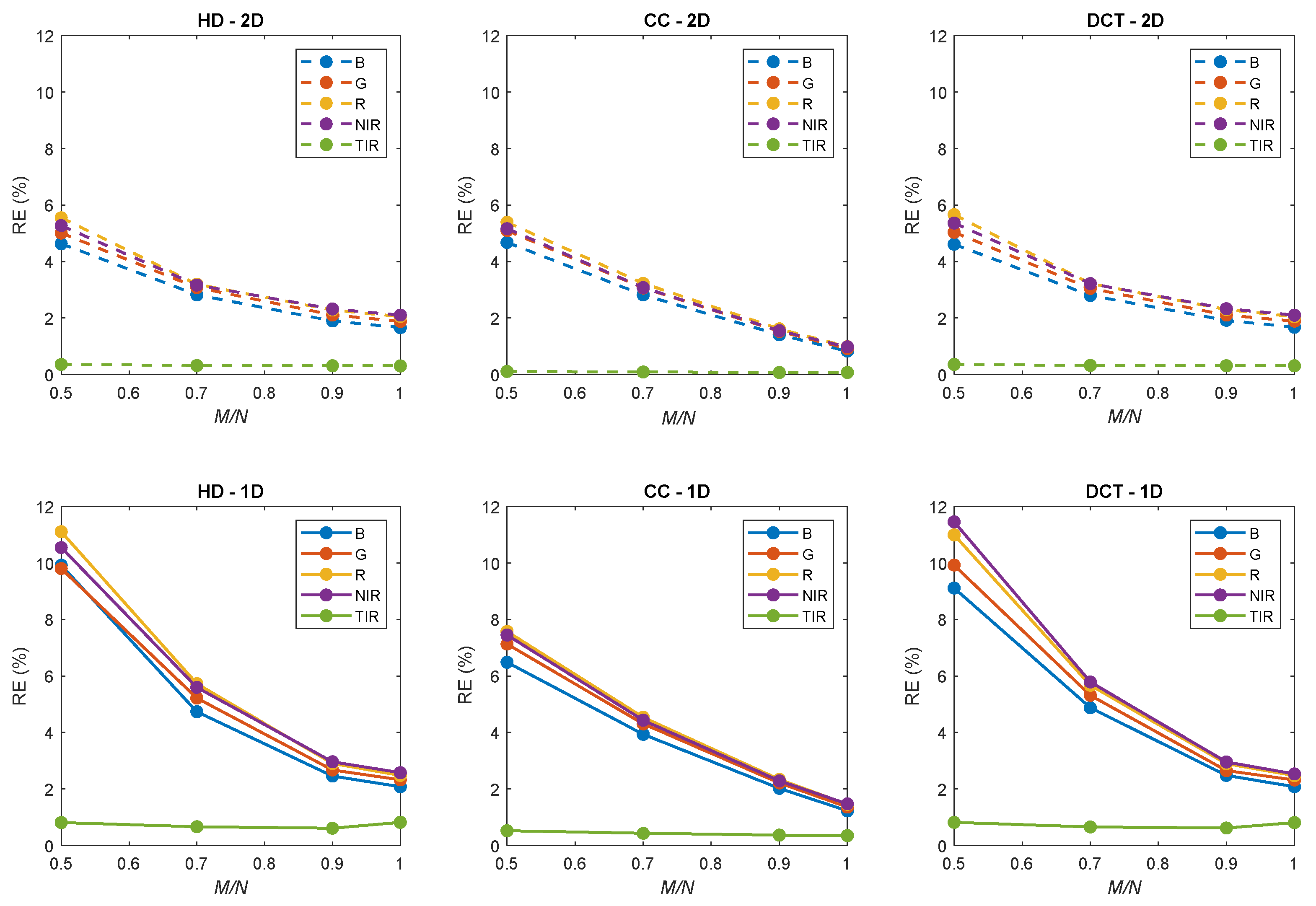
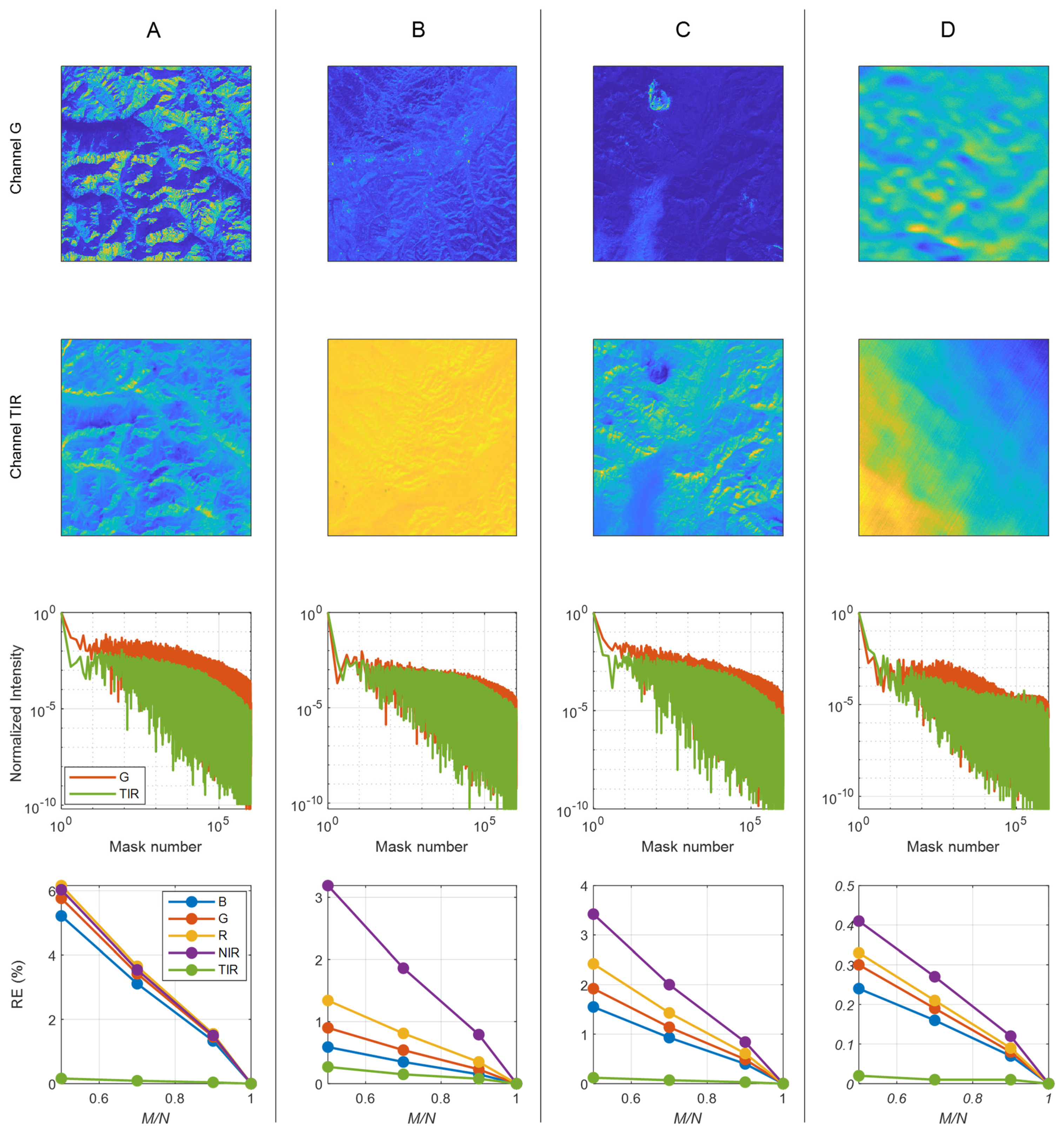
3.1. Reconstruction Performances of Static Images
3.2. Reconstruction Performances of Dynamic Images
4. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Elmasry, G.; Kamruzzaman, M.; Sun, D.W.; Allen, P. Principles and Applications of Hyperspectral Imaging in Quality Eval-uation of Agro-Food Products: A Review. Crit. Rev. Food Sci. Nutr. 2012, 52, 999–1023. [Google Scholar] [CrossRef] [PubMed]
- Adão, T.; Hruška, J.; Pádua, L.; Bessa, J.; Peres, E.; Morais, R.; Sousa, J.J. Hyperspectral imaging: A review on UAV-based sensors, data processing and applications for agriculture and forestry. Remote Sens. 2017, 9, 1110. [Google Scholar] [CrossRef] [Green Version]
- Jia, T.; Chen, D.; Wang, J.; Xu, D. Single-Pixel Color Imaging Method with a Compressive Sensing Measurement Matrix. Appl. Sci. 2018, 8, 1293. [Google Scholar] [CrossRef] [Green Version]
- Boldrini, B.; Kessler, W.; Rebner, K.; Kessler, R.W. Hyperspectral Imaging: A Review of Best Practice, Performance and Pitfalls for in-line and on-line Applications. J. Near Infrared Spectrosc. 2012, 20, 483–508. [Google Scholar] [CrossRef]
- Lu, G.; Fei, B. Medical hyperspectral imaging: A review. J. Biomed. Opt. 2014, 19, 010901. [Google Scholar] [CrossRef]
- Dong, X.; Jakobi, M.; Wang, S.; Köhler, M.H.; Zhang, X.; Koch, A.W. A review of hyperspectral imaging for nanoscale materials research. Appl. Spectrosc. Rev. 2018, 54, 285–305. [Google Scholar] [CrossRef]
- Manolakis, D.; Lockwood, R.; Cooley, T. Hyperspectral Imaging Remote Sensing: Physics, Sensors, and Algorithms; Cambridge University Press: Cambridge, UK, 2016; pp. 1–709. ISBN 9781107083660. [Google Scholar]
- Sandau, R. Status and trends of small satellite missions for Earth observation. Acta Astronaut. 2010, 66, 1–12. [Google Scholar] [CrossRef]
- Staenz, K.; Mueller, A.; Heiden, U. Overview of terrestrial imaging spectroscopy missions. In Proceedings of the 2013 IEEE International Geoscience and Remote Sensing Symposium—IGARSS, Melbourne, Australia, 21–26 July 2013; pp. 3502–3505. [Google Scholar]
- Belward, A.S.; Skøien, J.O. Who launched what, when and why; trends in global land-cover observation capacity from civilian earth observation satellites. ISPRS J. Photogramm. Remote Sens. 2015, 103, 115–128. [Google Scholar] [CrossRef]
- National Research Council. National Research Council Earth Science and Applications from Space: National Imperatives for the Next Decade and Beyond; The National Academies Press: Washington, DC, USA, 2007; pp. 1–428. [Google Scholar]
- Paganini, M.; Petiteville, I.; Ward, S.; Dyke, G.; Steventon, M.; Harry, J.; Kerblat, F. Satellite Earth Observations in Support of the Sustainable Development Goals: The CEOS Earth Observation Handbook; Special 2018 Edition; The Committee on Earth Observation Satellites and the European Space Agency: Paris, France, 2018. [Google Scholar]
- Chuvieco, E. Earth Observation of Global Change; Springer: New York, NY, USA, 2008; ISBN 9781402063572. [Google Scholar]
- Cogliati, S.; Sarti, F.; Chiarantini, L.; Cosi, M.; Lorusso, R.; Lopinto, E.; Miglietta, F.; Genesio, L.; Guanter, L.; Damm, A.; et al. The PRISMA imaging spectroscopy mission: Overview and first performance analysis. Remote Sens. Environ. 2021, 262, 112499. [Google Scholar] [CrossRef]
- Candès, E.; Romberg, J. L1 Magic: Recovery of Sparse Signals via Convex Programming; California Institute of Technology: Pasadena, CA, USA, 2005; Available online: http://brainimaging.waisman.wisc.edu/~chung/BIA/download/matlab.v1/l1magic-1.1/l1magic_notes.pdf (accessed on 28 December 2021).
- Candès, E.J.; Romberg, J.K.; Tao, T. Stable signal recovery from incomplete and inaccurate measurements. Commun. Pure Appl. Math. 2006, 59, 1207–1223. [Google Scholar] [CrossRef] [Green Version]
- Candes, E.J.; Wakin, M. An Introduction to Compressive Sampling. IEEE Signal Process. Mag. 2008, 25, 21–30. [Google Scholar] [CrossRef]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Duarte, M.; Sarvotham, S.; Baron, D.; Wakin, M.; Baraniuk, R. Distributed Compressed Sensing of Jointly Sparse Signals. In Proceedings of the Conference Record of the Thirty-Ninth Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 30 October–2 November 2005; pp. 1537–1541. [Google Scholar] [CrossRef] [Green Version]
- Haupt, J.; Nowak, R. Signal Reconstruction from Noisy Random Projections. IEEE Trans. Inf. Theory 2006, 52, 4036–4048. [Google Scholar] [CrossRef]
- Baraniuk, R.G. Compressive Sensing. IEEE Signal Process. Mag. 2007, 24, 118–124. [Google Scholar] [CrossRef]
- Duarte, M.F.; Davenport, M.A.; Takbar, D.; Laska, J.N.; Sun, T.; Kelly, K.F.; Baraniuk, R.G. Single-pixel imaging via compres-sive sampling: Building simpler, smaller, and less-expensive digital cameras. IEEE Signal Process. Mag. 2008, 25, 83–91. [Google Scholar] [CrossRef] [Green Version]
- Takhar, D.; Laska, J.N.; Wakin, M.; Duarte, M.; Baron, D.; Sarvotham, S.; Kelly, K.; Baraniuk, R.G. A new compressive imaging camera architecture using optical-domain compression. In Proceedings of the Computational Imaging IV, San Jose, CA, USA, 15 January 2006; Volume 6065, p. 606509. [Google Scholar]
- Gibson, G.M.; Johnson, S.D.; Padgett, M.J. Single-pixel imaging 12 years on: A review. Opt. Express 2020, 28, 28190. [Google Scholar] [CrossRef] [PubMed]
- Sun, T.; Kelly, K. Compressive Sensing Hyperspectral Imager. In Proceedings of the Frontiers in Optics 2009/Laser Science XXV/Fall 2009 OSA Optics & Photonics Technical Digest, San Jose, CA, USA, 11–15 October 2009; p. CTuA5. [Google Scholar]
- Chen, H.; Asif, S.; Sankaranarayanan, A.; Veeraraghavan, A. FPA-CS: Focal plane array-based compressive imaging in short-wave infrared. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 2358–2366. [Google Scholar]
- Mahalanobis, A.; Shilling, R.; Murphy, R.; Muise, R. Recent results of infrared compressive sensing. Appl. Opt. 2014, 53, 8060–8070. [Google Scholar] [CrossRef]
- Gehm, M.; John, R.; Brady, D.J.; Willett, R.M.; Schulz, T.J. Single-shot compressive spectral imaging with a dual-disperser architecture. Opt. Express 2007, 15, 14013–14027. [Google Scholar] [CrossRef]
- Wagadarikar, A.; John, R.; Willett, R.; Brady, D. Single disperser design for coded aperture snapshot spectral imaging. Appl. Opt. 2008, 47, B44–B51. [Google Scholar] [CrossRef] [Green Version]
- Arce, G.R.; Brady, D.J.; Carin, L.; Arguello, H.; Kittle, D.S. Compressive Coded Aperture Spectral Imaging: An Introduction. IEEE Signal Process. Mag. 2014, 31, 105–115. [Google Scholar] [CrossRef]
- Wu, Y.; Mirza, O.; Arce, G.R.; Prather, D.W. Development of a digital-micromirror-device-based multishot snapshot spectral imaging system. Opt. Lett. 2011, 36, 2692–2694. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- August, Y.; Vachman, C.; Rivenson, Y.; Stern, A. Compressive hyperspectral imaging by random separable projections in both the spatial and the spectral domains. Appl. Opt. 2013, 52, D46–D54. [Google Scholar] [CrossRef]
- Baraniuk, R.G.; Goldstein, T.; Sankaranarayanan, A.; Studer, C.; Veeraraghavan, A.; Wakin, M. Compressive Video Sensing: Algorithms, architectures, and applications. IEEE Signal Process. Mag. 2017, 34, 52–66. [Google Scholar] [CrossRef]
- Edgar, M.P.; Gibson, G.; Bowman, R.; Sun, B.; Radwell, N.; Mitchell, K.J.; Welsh, S.; Padgett, M. Simultaneous real-time visible and infrared video with single-pixel detectors. Sci. Rep. 2015, 5, 10669. [Google Scholar] [CrossRef] [PubMed]
- Fowler, J.E. Compressive pushbroom and whiskbroom sensing for hyperspectral remote-sensing imaging. In Proceedings of the 2014 IEEE International Conference on Image Processing (ICIP), Paris, France, 27–30 October 2014; pp. 684–688. [Google Scholar]
- Pariani, G.; Zanutta, A.; Basso, S.; Bianco, A.; Striano, V.; Sanguinetti, S.; Colombo, R.; Genoni, M.; Benetti, M.; Freddi, R.; et al. Compressive sampling for multispectral imaging in the vis-NIR-TIR: Optical design of space telescopes. In Proceedings of the Space Telescopes and Instrumentation 2018: Optical, Infrared, and Millimeter Wave, Austin, TX, USA, 10–15 June 2018; Volume 10698, p. 106985O. [Google Scholar]
- Guzzi, D.; Coluccia, G.; Labate, D.; Lastri, C.; Magli, E.; Nardino, V.; Palombi, L.; Pippi, I.; Coltuc, D.; Marchi, A.Z.; et al. Optical compressive sensing technologies for space applications: Instrumental concepts and performance analysis. In Proceedings of the International Conference on Space Optics—ICSO 2018, Chania, Greece, 12 July 2019; Volume 11180, p. 111806B. [Google Scholar]
- Noblet, Y.; Bennett, S.; Griffin, P.F.; Murray, P.; Marshall, S.; Roga, W.; Jeffers, J.; Oi, D. Compact multispectral pushframe camera for nanosatellites. Appl. Opt. 2020, 59, 8511. [Google Scholar] [CrossRef]
- Arnob, M.P.; Nguyen, H.; Han, Z.; Shih, W.-C. Compressed sensing hyperspectral imaging in the 09–25 μm shortwave infrared wavelength range using a digital micromirror device and InGaAs linear array detector. Appl. Opt. 2018, 57, 5019–5024. [Google Scholar] [CrossRef]
- Willett, R.; Duarte, M.F.; Davenport, M.A.; Baraniuk, R.G. Sparsity and Structure in Hyperspectral Imaging: Sensing, Reconstruction, and Target Detection. IEEE Signal Process. Mag. 2013, 31, 116–126. [Google Scholar] [CrossRef] [Green Version]
- Colombo, R.; Garzonio, R.; Di Mauro, B.; Dumont, M.; Tuzet, F.; Cogliati, S.; Pozzi, G.; Maltese, A.; Cremonese, E. Introducing Thermal Inertia for Monitoring Snowmelt Processes with Remote Sensing. Geophys. Res. Lett. 2019, 46, 4308–4319. [Google Scholar] [CrossRef]
- Li, C. An Efficient Algorithm for Total Variation Regularization with Applications to the Single Pixel Camera and Compressive Sensing. Master’s Thesis, Rice University, Houston, TX, USA, September 2009. [Google Scholar]
- Candes, E.J.; Romberg, J.; Tao, T. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information. IEEE Trans. Inf. Theory 2006, 52, 489–509. [Google Scholar] [CrossRef] [Green Version]
- Bai, H.; Wang, A.; Zhang, M. Compressive Sensing for DCT Image. In Proceedings of the 2010 International Conference on Computational Aspects of Social Networks, Taiyuan, China, 26–28 September 2010; pp. 378–381. [Google Scholar]
- Zhou, G.; Du, Y. A MEMS-driven Hadamard transform spectrometer. In Proceedings of the MOEMS and Miniaturized Systems XVII, San Francisco, CA, USA, 30–31 January 2018; Volume 10545, p. 105450X. [Google Scholar]
- Yu, W.-K. Super Sub-Nyquist Single-Pixel Imaging by Means of Cake-Cutting Hadamard Basis Sort. Sensors 2019, 19, 4122. [Google Scholar] [CrossRef] [Green Version]
- Sun, M.-J.; Meng, L.-T.; Edgar, M.P.; Padgett, M.J.; Radwell, N. A Russian Dolls ordering of the Hadamard basis for compressive single-pixel imaging. Sci. Rep. 2017, 7, 3464. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Irons, J.R.; Dwyer, J.L. An overview of the Landsat Data Continuity Mission. In Proceedings of the SPIE Defense, Security, and Sensing, Orlando, FL, USA, 29 April 2010; Volume 7695, p. 769508. [Google Scholar]
- Knight, E.J.; Kvaran, G. Landsat-8 Operational Land Imager Design, Characterization and Performance. Remote Sens. 2014, 6, 10286–10305. [Google Scholar] [CrossRef] [Green Version]
- Gan, L. Block Compressed Sensing of Natural Images. In Proceedings of the 2007 15th International Conference on Digital Signal Processing, Cardiff, UK, 1–4 July 2007; pp. 403–406. [Google Scholar]
- Ke, J.; Lam, E.Y. Object reconstruction in block-based compressive imaging. Opt. Express 2012, 20, 22102–22117. [Google Scholar] [CrossRef] [PubMed]
- Bennett, S.; Noblet, Y.; Griffin, P.F.; Murray, P.; Marshall, S.; Jeffers, J.; Oi, D. Compressive Sampling Using a Pushframe Camera. IEEE Trans. Comput. Imaging 2021, 7, 1069–1079. [Google Scholar] [CrossRef]




| Channel | Wavelength (µm) | Resolution (m) |
|---|---|---|
| 2 | 0.450–0.515 | 30 |
| 3 | 0.525–0.600 | 30 |
| 4 | 0.630–0.680 | 30 |
| 5 | 0.845–0.885 | 30 |
| 10 | 10.600–11.200 | 100 |
| Simulation Parameters | |
|---|---|
| Channel | R, G, B, NIR, TIR |
| Basis set | DCT; HD; CC |
| Reconstruction method | TVAL (1D–2D); direct (1D–2D) |
| 0.1; 0.3; 0.5; 0.7; 0.9; 1 | |
| 0%; 5% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oggioni, L.; Sanchez del Rio Kandel, D.; Pariani, G. Earth Observation via Compressive Sensing: The Effect of Satellite Motion. Remote Sens. 2022, 14, 333. https://doi.org/10.3390/rs14020333
Oggioni L, Sanchez del Rio Kandel D, Pariani G. Earth Observation via Compressive Sensing: The Effect of Satellite Motion. Remote Sensing. 2022; 14(2):333. https://doi.org/10.3390/rs14020333
Chicago/Turabian StyleOggioni, Luca, David Sanchez del Rio Kandel, and Giorgio Pariani. 2022. "Earth Observation via Compressive Sensing: The Effect of Satellite Motion" Remote Sensing 14, no. 2: 333. https://doi.org/10.3390/rs14020333
APA StyleOggioni, L., Sanchez del Rio Kandel, D., & Pariani, G. (2022). Earth Observation via Compressive Sensing: The Effect of Satellite Motion. Remote Sensing, 14(2), 333. https://doi.org/10.3390/rs14020333







