Combining Spectral and Texture Features of UAS-Based Multispectral Images for Maize Leaf Area Index Estimation
Abstract
:1. Introduction
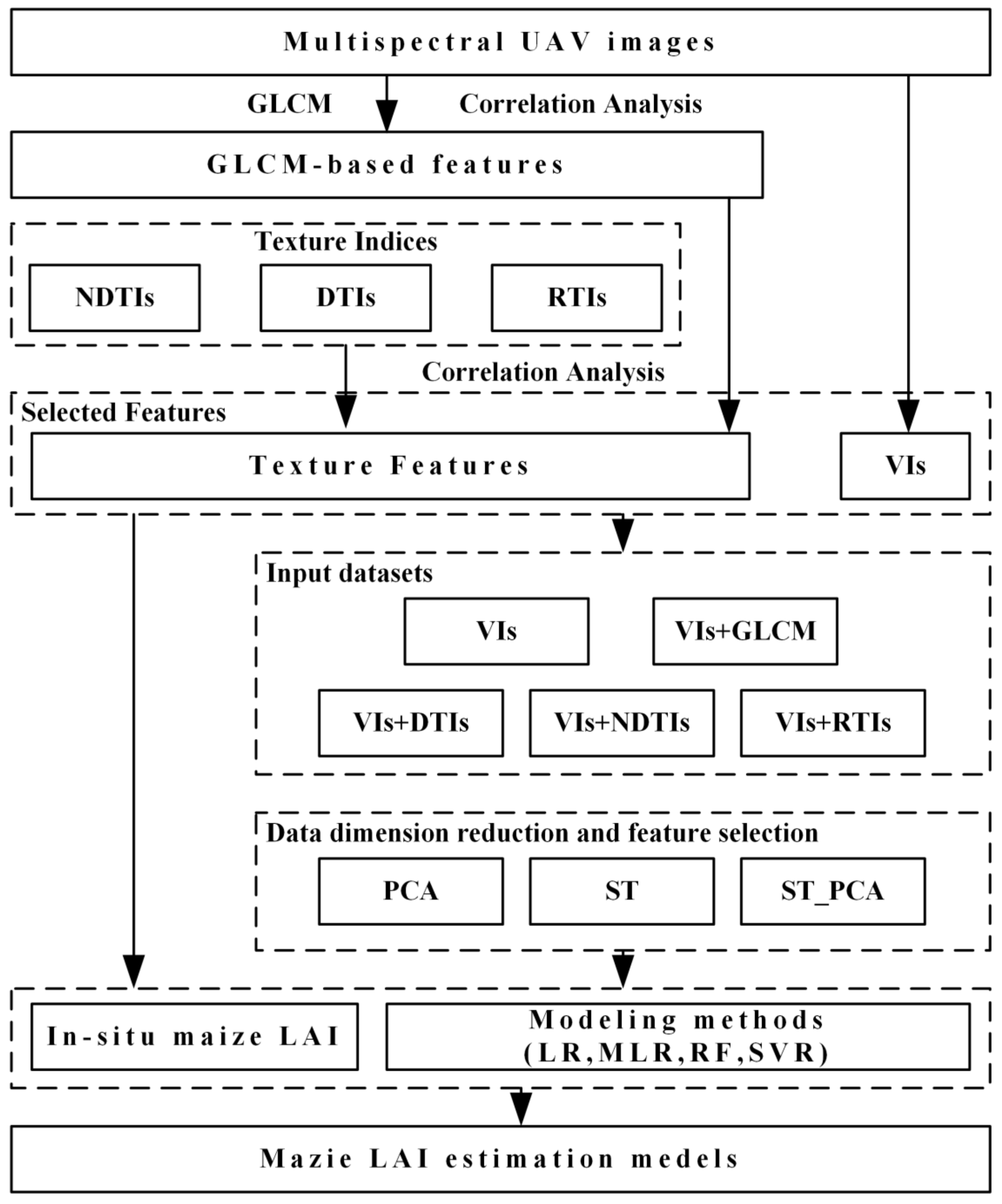
2. Materials and Methods
2.1. Experimental Site
2.2. UAS-Based Image Acquisition and LAI Measurements
2.3. Vegetation Index (VI) Calculation
2.4. Texture Analysis
2.5. Principal Component Analysis (PCA) and Stepwise Selection (ST)
2.6. Modeling Methods
2.7. Statistical Methods
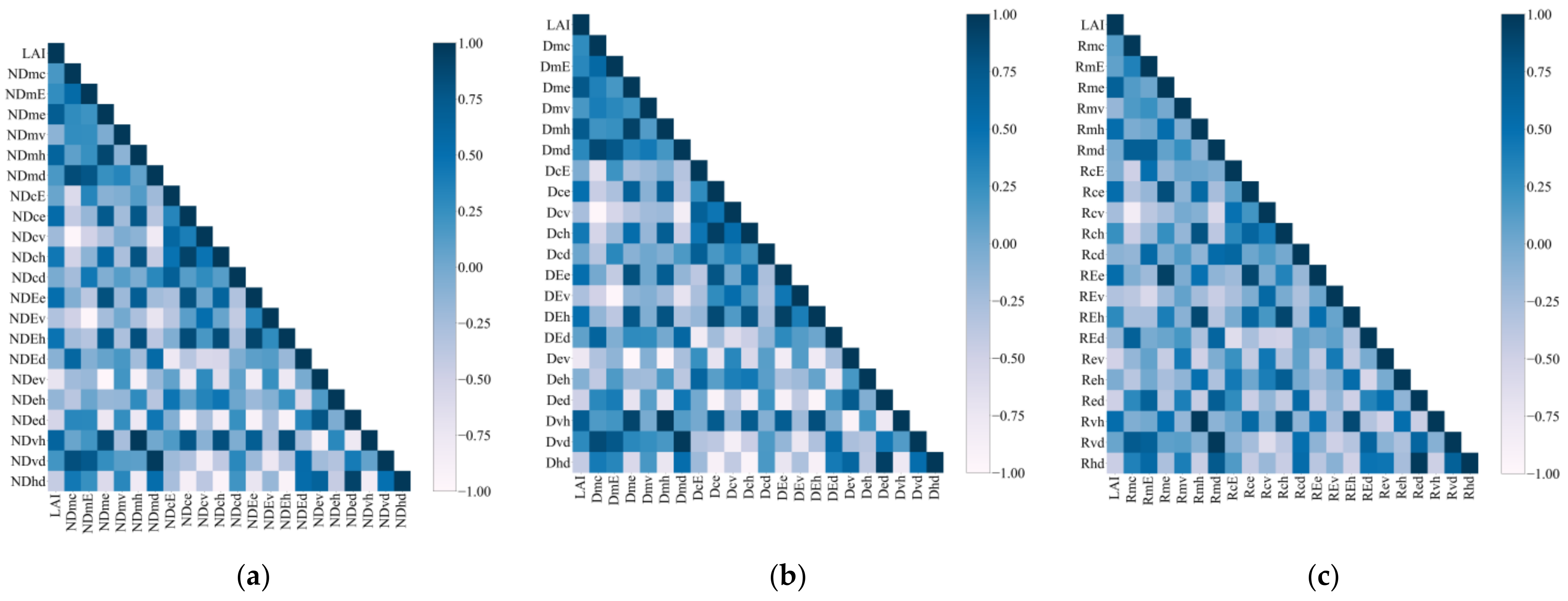
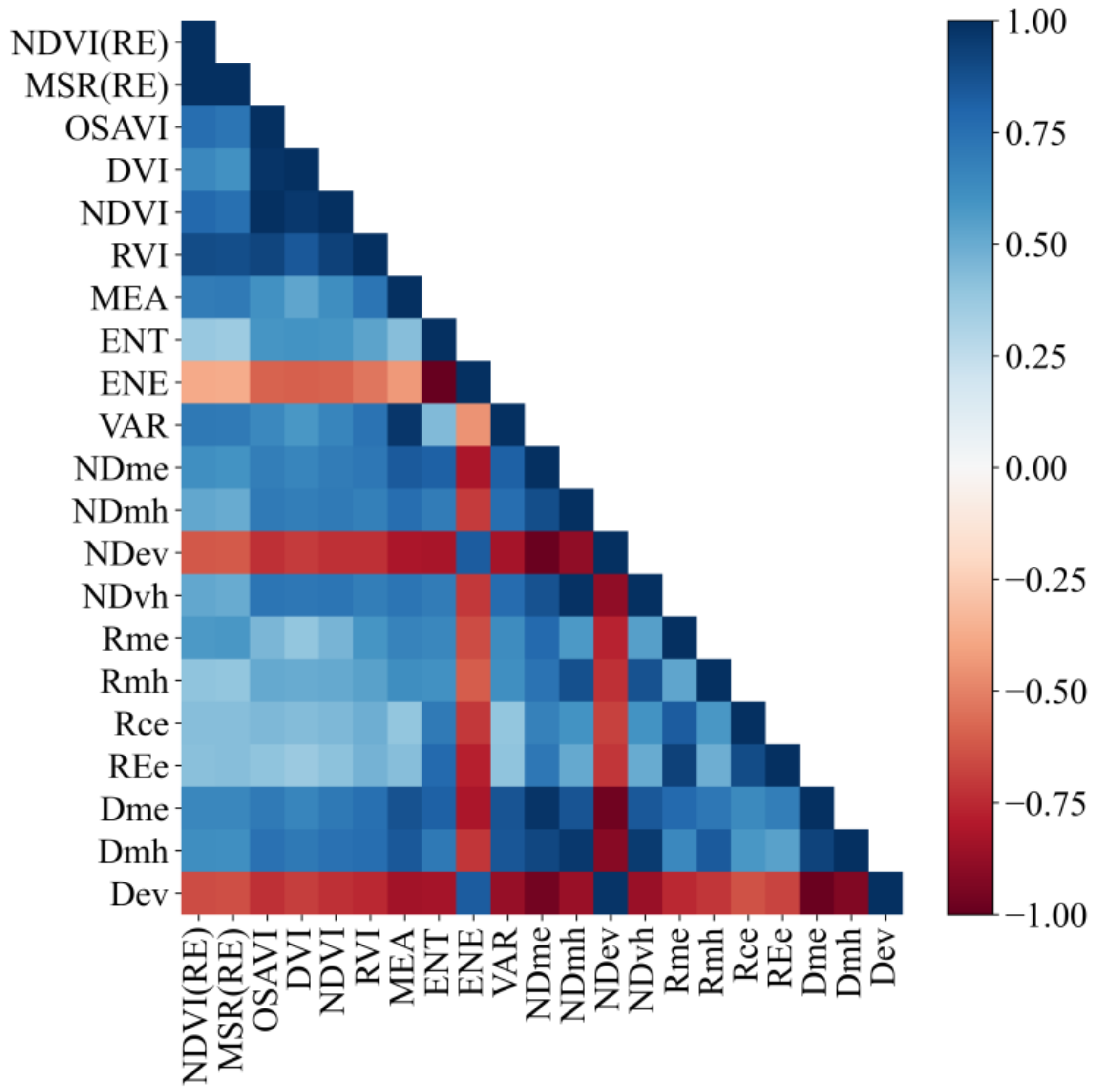
2.7.1. Correlation Analysis
2.7.2. Validation of the Regression Models
3. Results
3.1. Correlation Analysis of Features and In Situ LAI Data
3.2. Analysis of the Results of Maize LAI Estimation Model Based on Single Features
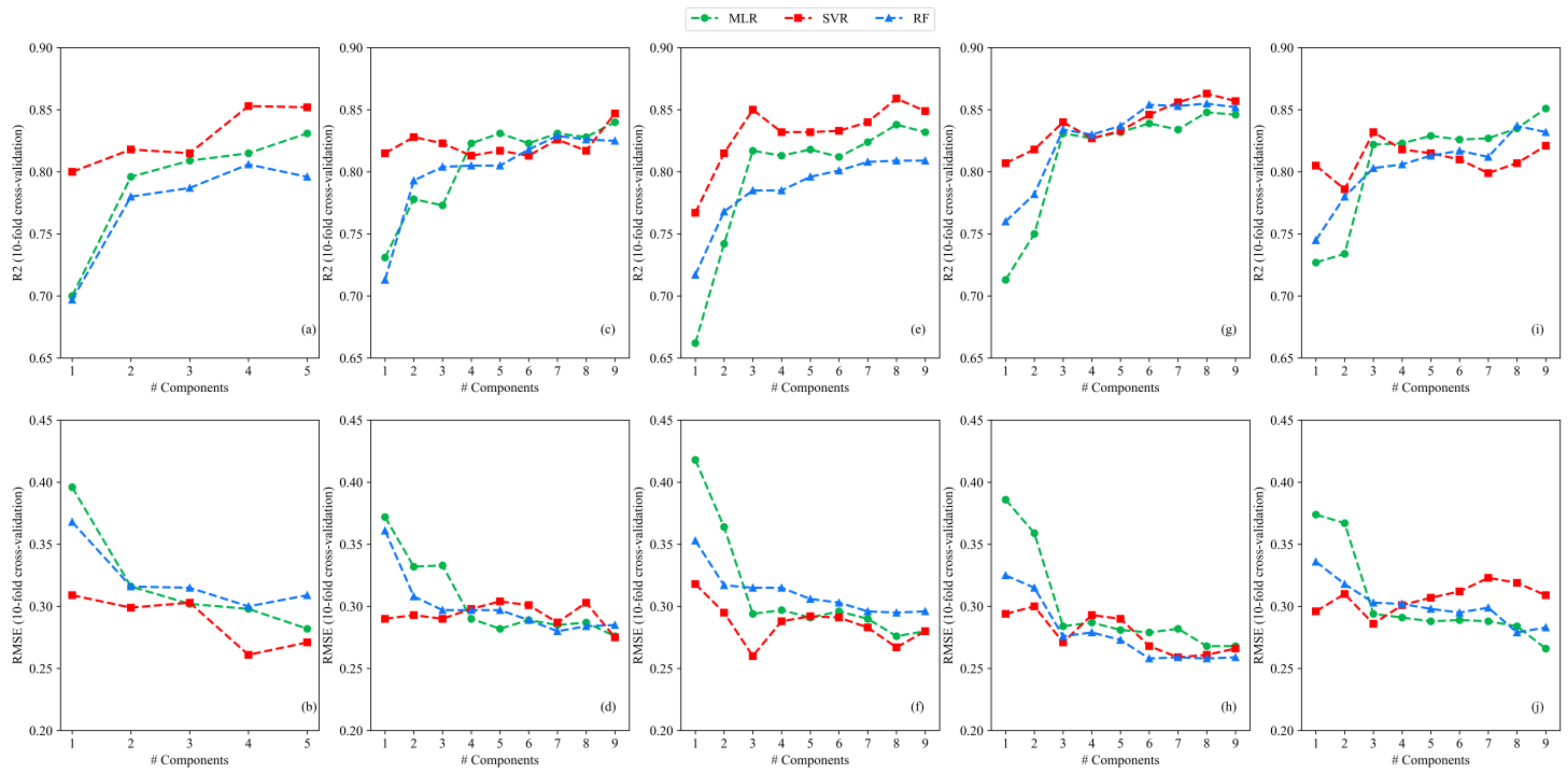
3.3. Analysis of the Results of LAI Estimation Model Based on Multiple Regression
4. Discussion
4.1. The Effect of Spectral Features and Texture Features for Maize LAI Estimation
4.2. Comparison of Different Multivariate Regression Methods
4.3. Effects of Different Kinds of Texture Features on Maize LAI Estimation Models
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Watson, D.J. Comparative Physiological Studies on the Growth of Field Crops: II. The Effect of Varying Nutrient Supply on Net Assimilation Rate and Leaf Area. Ann. Bot. 1947, 11, 375–407. [Google Scholar] [CrossRef]
- Li, X.; Zhang, Y.; Luo, J.; Jin, X.; Xu, Y.; Yang, W. Quantification winter wheat LAI with HJ-1CCD image features over multiple growing seasons. Int. J. Appl. Earth Obs. Geoinf. 2016, 44, 104–112. [Google Scholar] [CrossRef]
- Padalia, H.; Sinha, S.K.; Bhave, V.; Trivedi, N.K.; Senthil Kumar, A. Estimating canopy LAI and chlorophyll of tropical forest plantation (North India) using Sentinel-2 data. Adv. Space Res. 2020, 65, 458–469. [Google Scholar] [CrossRef]
- Zhao, J.; Li, J.; Liu, Q.; Fan, W.; Zhong, B.; Wu, S.; Yang, L.; Zeng, Y.; Xu, B.; Yin, G. Leaf Area Index Retrieval Combining HJ1/CCD and Landsat8/OLI Data in the Heihe River Basin, China. Remote Sens. 2015, 7, 6862–6885. [Google Scholar] [CrossRef] [Green Version]
- Yu, D.; Zha, Y.; Shi, L.; Ye, H.; Zhang, Y. Improving sugarcane growth simulations by integrating multi-source observations into a crop model. Eur. J. Agron. 2022, 132, 126410. [Google Scholar] [CrossRef]
- Dong, T.; Liu, J.; Shang, J.; Qian, B.; Ma, B.; Kovacs, J.M.; Walters, D.; Jiao, X.; Geng, X.; Shi, Y. Assessment of red-edge vegetation indices for crop leaf area index estimation. Remote Sens. Environ. 2019, 222, 133–143. [Google Scholar] [CrossRef]
- Kaplan, G.; Rozenstein, O. Spaceborne Estimation of Leaf Area Index in Cotton, Tomato, and Wheat Using Sentinel-2. Land 2021, 10, 505. [Google Scholar] [CrossRef]
- Hu, Q.; Yang, J.; Xu, B.; Huang, J.; Memon, D.-M.S.; Yin, G.; Zeng, Y.; Zhao, J.; Ke, L. Evaluation of Global Decametric-Resolution LAI, FAPAR and FVC Estimates Derived from Sentinel-2 Imagery. Remote Sens. 2020, 12, 912. [Google Scholar] [CrossRef] [Green Version]
- Darvishzadeh, R.; Skidmore, A.; Schlerf, M.; Atzberger, C.; Corsi, F.; Cho, M. LAI and chlorophyll estimation for a heterogeneous grassland using hyperspectral measurements. ISPRS J. Photogramm. Remote Sens. 2008, 63, 409–426. [Google Scholar] [CrossRef]
- Yamaguchi, T.; Tanaka, Y.; Imachi, Y.; Yamashita, M.; Katsura, K. Feasibility of Combining Deep Learning and RGB Images Obtained by Unmanned Aerial Vehicle for Leaf Area Index Estimation in Rice. Remote Sens. 2020, 13, 84. [Google Scholar] [CrossRef]
- Zheng, G.; Moskal, L.M. Retrieving Leaf Area Index (LAI) Using Remote Sensing: Theories, Methods and Sensors. Sensors 2009, 9, 2719–2745. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Mao, X. Comparison of Canopy Closure Estimation of Plantations Using Parametric, Semi-Parametric, and Non-Parametric Models Based on GF-1 Remote Sensing Images. Forests 2020, 11, 597. [Google Scholar] [CrossRef]
- Cohrs, C.W.; Cook, R.L.; Gray, J.M.; Albaugh, T.J. Sentinel-2 Leaf Area Index Estimation for Pine Plantations in the Southeastern United States. Remote Sens. 2020, 12, 1406. [Google Scholar] [CrossRef]
- Huang, D.; Yang, W.Z.; Tan, B.; Rautiainen, M.; Zhang, P.; Hu, J.N.; Shabanov, N.V.; Linder, S.; Knyazikhin, Y.; Myneni, R.B. The importance of measurement errors for deriving accurate reference leaf area index maps for validation of moderate-resolution satellite LAI products. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1866–1871. [Google Scholar] [CrossRef]
- Middinti, S.; Thumaty, K.C.; Gopalakrishnan, R.; Jha, C.S.; Thatiparthi, B.R. Estimating the leaf area index in Indian tropical forests using Landsat-8 OLI data. Int. J. Remote Sens. 2017, 38, 6769–6789. [Google Scholar] [CrossRef]
- Mao, H.; Meng, J.; Ji, F.; Zhang, Q.; Fang, H. Comparison of Machine Learning Regression Algorithms for Cotton Leaf Area Index Retrieval Using Sentinel-2 Spectral Bands. Appl. Sci. 2019, 9, 1459. [Google Scholar] [CrossRef] [Green Version]
- Maimaitijiang, M.; Sagan, V.; Sidike, P.; Hartling, S.; Esposito, F.; Fritschi, F.B. Soybean yield prediction from UAV using multimodal data fusion and deep learning. Remote Sens. Environ. 2020, 237, 111599. [Google Scholar] [CrossRef]
- Tian, J.; Wang, L.; Li, X.; Gong, H.; Shi, C.; Zhong, R.; Liu, X. Comparison of UAV and WorldView-2 imagery for mapping leaf area index of mangrove forest. Int. J. Appl. Earth Obs. Geoinf. 2017, 61, 22–31. [Google Scholar] [CrossRef]
- Gong, Y.; Yang, K.; Lin, Z.; Fang, S.; Wu, X.; Zhu, R.; Peng, Y. Remote estimation of leaf area index (LAI) with unmanned aerial vehicle (UAV) imaging for different rice cultivars throughout the entire growing season. Plant Methods 2021, 17, 88. [Google Scholar] [CrossRef] [PubMed]
- Lan, Y.; Huang, Z.; Deng, X.; Zhu, Z.; Huang, H.; Zheng, Z.; Lian, B.; Zeng, G.; Tong, Z. Comparison of machine learning methods for citrus greening detection on UAV multispectral images. Comput. Electron. Agric. 2020, 171, 105234. [Google Scholar] [CrossRef]
- Duan, B.; Liu, Y.; Gong, Y.; Peng, Y.; Wu, X.; Zhu, R.; Fang, S. Remote estimation of rice LAI based on Fourier spectrum texture from UAV image. Plant Methods 2019, 15, 124. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Y.-M.; Jiang, M.-J. Comparison of inversion method of maize leaf area index based on UAV hyperspectral remote sensing. Multimed. Tools Appl. 2019, 79, 16385–16401. [Google Scholar] [CrossRef]
- Tunca, E.; Koksal, E.S.; Cetin, S.; Ekiz, N.M.; Balde, H. Yield and leaf area index estimations for sunflower plants using unmanned aerial vehicle images. Environ. Monit. Assess. 2018, 190, 682. [Google Scholar] [CrossRef] [PubMed]
- Luo, P.; Liao, J.; Shen, G. Combining Spectral and Texture Features for Estimating Leaf Area Index and Biomass of Maize Using Sentinel-1/2, and Landsat-8 Data. IEEE Access 2020, 8, 53614–53626. [Google Scholar] [CrossRef]
- Ghasemi, N.; Sahebi, M.R.; Mohammadzadeh, A. Biomass Estimation of a Temperate Deciduous Forest Using Wavelet Analysis. IEEE Trans. Geosci. Remote Sens. 2013, 51, 765–776. [Google Scholar] [CrossRef]
- Zhou, J.; Yan Guo, R.; Sun, M.; Di, T.T.; Wang, S.; Zhai, J.; Zhao, Z. The Effects of GLCM parameters on LAI estimation using texture values from Quickbird Satellite Imagery. Sci. Rep. 2017, 7, 7366. [Google Scholar] [CrossRef]
- Zhang, J.; Qiu, X.; Wu, Y.; Zhu, Y.; Cao, Q.; Liu, X.; Cao, W. Combining texture, color, and vegetation indices from fixed-wing UAS imagery to estimate wheat growth parameters using multivariate regression methods. Comput. Electron. Agric. 2021, 185, 106138. [Google Scholar] [CrossRef]
- Guo, Y.H.; Fu, Y.S.; Hao, F.H.; Zhang, X.; Wu, W.X.; Jin, X.L.; Bryant, C.R.; Senthilnath, J. Integrated phenology and climate in rice yields prediction using machine learning methods. Ecol. Indic. 2021, 120, 106935. [Google Scholar] [CrossRef]
- Chang, C.C.; Lin, C.J. LIBSVM: A Library for Support Vector Machines. ACM Trans. Intell. Syst. Technol. 2011, 2, 1–27. [Google Scholar] [CrossRef]
- Joachims, T. Making large-scale support vector machine learning practical. In Advances in Kernel Methods: Support Vector Learning; MIT Press: Cambridge, MA, USA, 1999; pp. 169–184. [Google Scholar]
- Zhai, L.; Li, S.; Zou, B.; Sang, H.; Fang, X.; Xu, S. An improved geographically weighted regression model for PM2.5 concentration estimation in large areas. Atmos. Environ. 2018, 181, 145–154. [Google Scholar] [CrossRef]
- Li, S.; Yuan, F.; Ata-Ui-Karim, S.T.; Zheng, H.; Cheng, T.; Liu, X.; Tian, Y.; Zhu, Y.; Cao, W.; Cao, Q. Combining Color Indices and Textures of UAV-Based Digital Imagery for Rice LAI Estimation. Remote Sens. 2019, 11, 1763. [Google Scholar] [CrossRef] [Green Version]
- Karpouzli, E.; Malthus, T.J.; Place, C.J. Hyperspectral discrimination of coral reef benthic communities in the western Caribbean. Coral Reefs 2004, 23, 141–151. [Google Scholar] [CrossRef]
- Afrasiabian, Y.; Noory, H.; Mokhtari, A.; Nikoo, M.R.; Pourshakouri, F.; Haghighatmehr, P. Effects of spatial, temporal, and spectral resolutions on the estimation of wheat and barley leaf area index using multi- and hyper-spectral data (case study: Karaj, Iran). Precis. Agric. 2020, 22, 660–688. [Google Scholar] [CrossRef]
- Shao, G.; Han, W.; Zhang, H.; Liu, S.; Wang, Y.; Zhang, L.; Cui, X. Mapping maize crop coefficient Kc using random forest algorithm based on leaf area index and UAV-based multispectral vegetation indices. Agric. Water Manag. 2021, 252. [Google Scholar] [CrossRef]
- He, Y.; Bo, Y.; Chai, L.; Liu, X.; Li, A. Linking in situ LAI and fine resolution remote sensing data to map reference LAI over cropland and grassland using geostatistical regression method. Int. J. Appl. Earth Obs. Geoinf. 2016, 50, 26–38. [Google Scholar] [CrossRef] [Green Version]
- Richetti, J.; Boote, K.J.; Hoogenboom, G.; Judge, J.; Johann, J.A.; Uribe-Opazo, M.A. Remotely sensed vegetation index and LAI for parameter determination of the CSM-CROPGRO-Soybean model when in situ data are not available. Int. J. Appl. Earth Obs. Geoinf. 2019, 79, 110–115. [Google Scholar] [CrossRef]
- Zhang, M.; Su, W.; Fu, Y.; Zhu, D.; Xue, J.-H.; Huang, J.; Wang, W.; Wu, J.; Yao, C. Super-resolution enhancement of Sentinel-2 image for retrieving LAI and chlorophyll content of summer corn. Eur. J. Agron. 2019, 111, 125938. [Google Scholar] [CrossRef]
- Becker, F.; Choudhury, B.J. Relative sensitivity of normalized difference vegetation Index (NDVI) and microwave polarization difference Index (MPDI) for vegetation and desertification monitoring. Remote Sens. Environ. 1988, 24, 297–311. [Google Scholar] [CrossRef]
- Gitelson, A.; Merzlyak, M.N. Spectral Reflectance Changes Associated with Autumn Senescence of Aesculus hippocastanum L. and Acer platanoides L. Leaves. Spectral Features and Relation to Chlorophyll Estimation. J. Plant Physiol. 1994, 143, 286–292. [Google Scholar] [CrossRef]
- Wu, C.; Niu, Z.; Tang, Q.; Huang, W.J.A.; Meteorology, F. Estimating chlorophyll content from hyperspectral vegetation indices: Modeling and validation. Agric. For. Meteorol. 2008, 148, 1230–1241. [Google Scholar] [CrossRef]
- Rondeaux, G.; Steven, M.; Baret, F. Optimization of soil-adjusted vegetation indices. Remote Sens. Environ. 1996, 55, 95–107. [Google Scholar] [CrossRef]
- Peñuelas, J.; Isla, R.; Filella, I.; Araus, J.L. Visible and near-infrared reflectance assessment of salinity effects on barley. Crop Sci. 1997, 37, 198–202. [Google Scholar] [CrossRef]
- Jordan, C.F. Derivation of Leaf-Area Index from Quality of Light on the Forest Floor. Ecology 1969, 50, 663–666. [Google Scholar] [CrossRef]
- Haralick, R.M.; Shanmugam, K.; Dinstein, I. Textural Features for Image Classification. IEEE Trans. Syst. Man Cybern. 1973, SMC-3, 610–621. [Google Scholar] [CrossRef] [Green Version]
- Zheng, H.; Cheng, T.; Zhou, M.; Li, D.; Yao, X.; Tian, Y.; Cao, W.; Zhu, Y. Improved estimation of rice aboveground biomass combining textural and spectral analysis of UAV imagery. Precis. Agric. 2018, 20, 611–629. [Google Scholar] [CrossRef]
- Ul-Saufie, A.Z.; Yahaya, A.S.; Ramli, N.A.; Rosaida, N.; Hamid, H.A. Future daily PM10 concentrations prediction by combining regression models and feedforward backpropagation models with principle component analysis (PCA). Atmos. Environ. 2013, 77, 621–630. [Google Scholar] [CrossRef]
- Derksen, S.; Keselman, J. Backward, Forward and Stepwise Automated Subset Selection Algorithms: Frequency of Obtaining Authentic and Noise Variables. Br. J. Math. Stat. Psychol. 1992, 45, 265–282. [Google Scholar] [CrossRef]
- Li, Z.-W.; Xin, X.-P.; Tang, H.; Yang, F.; Chen, B.-R.; Zhang, B.-H. Estimating grassland LAI using the Random Forests approach and Landsat imagery in the meadow steppe of Hulunber, China. J. Integr. Agric. 2017, 16, 286–297. [Google Scholar] [CrossRef]
- Yuan, H.; Yang, G.; Li, C.; Wang, Y.; Liu, J.; Yu, H.; Feng, H.; Xu, B.; Zhao, X.; Yang, X. Retrieving Soybean Leaf Area Index from Unmanned Aerial Vehicle Hyperspectral Remote Sensing: Analysis of RF, ANN, and SVM Regression Models. Remote Sens. 2017, 9, 309. [Google Scholar] [CrossRef] [Green Version]
- Qu, Y.; Gao, Z.; Shang, J.; Liu, J.; Casa, R. Simultaneous measurements of corn leaf area index and mean tilt angle from multi-directional sunlit and shaded fractions using downward-looking photography. Comput. Electron. Agric. 2021, 180, 105881. [Google Scholar] [CrossRef]
- Wang, L.A.; Zhou, X.; Zhu, X.; Dong, Z.; Guo, W. Estimation of biomass in wheat using random forest regression algorithm and remote sensing data. Crop J. 2016, 4, 212–219. [Google Scholar] [CrossRef] [Green Version]
- Camps-Valls, G.; Bruzzone, L.; Rojo-Rojo, J.L.; Melgani, F. Robust Support Vector Regression for Biophysical Variable Estimation from Remotely Sensed Images. IEEE Geosci. Remote Sens. Lett. 2006, 3, 339–343. [Google Scholar] [CrossRef]
- Pearson, K. LIII. On lines and planes of closest fit to systems of points in space. Lond. Edinb. Dublin Philos. Mag. J. Sci. 2010, 2, 559–572. [Google Scholar] [CrossRef] [Green Version]
- Mananze, S.; Pôças, I.; Cunha, M. Retrieval of Maize Leaf Area Index Using Hyperspectral and Multispectral Data. Remote Sens. 2018, 10, 1942. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Cheng, T.; Guo, W.; Xu, X.; Qiao, H.; Xie, Y.; Ma, X. Leaf area index estimation model for UAV image hyperspectral data based on wavelength variable selection and machine learning methods. Plant Methods 2021, 17, 49. [Google Scholar] [CrossRef] [PubMed]
- Zheng, H.; Cheng, T.; Li, D.; Yao, X.; Tian, Y.; Cao, W.; Zhu, Y. Combining Unmanned Aerial Vehicle (UAV)-Based Multispectral Imagery and Ground-Based Hyperspectral Data for Plant Nitrogen Concentration Estimation in Rice. Front. Plant. Sci. 2018, 9, 936. [Google Scholar] [CrossRef] [PubMed]
| Experiment | Date | Samples | Number of Aerial Photos | Growth Stage |
|---|---|---|---|---|
| Experiment 1 | 03 August 2020 | 35 | 414 | Jointing |
| Experiment 2 | 28 August 2020 | 14 | 270 | Booting |
| Experiment 3 | 08 September 2020 | 37 | 336 | Tasseling |
| Experiment 4 | 18 September 2020 | 17 | 558 | Pustulation |
| Device | Specification | |
|---|---|---|
| P4 Multispectral | Resolution | 1600 × 1300 pixels |
| Weight | 1487 g | |
| Wavelength range | Blue: 450 ± 16 nm Green: 560 ± 16 nm Red: 650 ± 16 nm Red-edge (RE): 730 ± 16 nm Near-infrared (NIR): 840 ± 26 nm | |
| Calibration whiteboard | Reflectivity | 90% |
| Vegetation Index | Formula | Reference |
|---|---|---|
| Difference Vegetation Index (DVI) | [39] | |
| Normalized Difference Red-Edge vegetation index (NDVIRE) | [40] | |
| Modified Red-Edge Simple Ratio Index (MSRRE) | [41] | |
| Optimization of Soil-Adjusted Vegetation Index (OSAVI) | [42] | |
| Normalized Difference Vegetation Index (NDVI) | [43] | |
| Ratio Vegetation Index (RVI) | [44] |
| VI | DVI | NDVIRE | RVI | MSRRE | OSAVI | NDVI |
|---|---|---|---|---|---|---|
| r | 0.659 | 0.906 | 0.899 | 0.908 | 0.769 | 0.789 |
| Texture | ENE (e) | CON (c) | ENT (E) | VAR (v) | MEA (m) | HOM (h) | DIS (d) |
|---|---|---|---|---|---|---|---|
| Band | RE | RE | G | R | NIR | G | R |
| Step | 4 | 4 | 4 | 4 | 2 | 2 | 2 |
| Angle | |||||||
| r | −0.518 | 0.56 | 0.514 | 0.749 | 0.754 | −0.445 | 0.378 |
| Method | R2 | RMSE | R2 | RMSE | R2 | RMSE | R2 | RMSE | R2 | RMSE | R2 | RMSE |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| NDVIRE | MSRRE | OSAVI | DVI | NDVI | RVI | |||||||
| LR | 0.750 | 0.347 | 0.752 | 0.343 | 0.509 | 0.518 | 0.335 | 0.602 | 0.547 | 0.498 | 0.743 | 0.355 |
| SVR | 0.748 | 0.348 | 0.743 | 0.352 | 0.699 | 0.373 | 0.288 | 0.629 | 0.759 | 0.336 | 0.773 | 0.326 |
| RF | 0.690 | 0.372 | 0.689 | 0.373 | 0.583 | 0.428 | −0.242 | 0.769 | 0.749 | 0.341 | 0.753 | 0.338 |
| MEA | ENT | ENE | VAR | NDme | NDmh | |||||||
| LR | 0.402 | 0.539 | 0.074 | 0.699 | 0.080 | 0.697 | 0.404 | 0.541 | 0.334 | 0.579 | 0.259 | 0.63 |
| SVR | 0.456 | 0.521 | 0.109 | 0.684 | 0.116 | 0.682 | 0.413 | 0.547 | 0.381 | 0.559 | 0.273 | 0.638 |
| RF | 0.136 | 0.644 | −0.075 | 0.718 | −0.128 | 0.731 | 0.118 | 0.641 | 0.105 | 0.668 | −0.151 | 0.765 |
| NDev | NDvh | Dme | Dmh | Dev | Dvh | |||||||
| LR | 0.352 | 0.572 | 0.262 | 0.630 | 0.427 | 0.534 | 0.419 | 0.549 | 0.413 | 0.543 | 0.393 | 0.564 |
| SVR | 0.372 | 0.565 | 0.261 | 0.642 | 0.445 | 0.518 | 0.416 | 0.562 | 0.453 | 0.522 | 0.398 | 0.573 |
| RF | −0.073 | 0.724 | −0.175 | 0.781 | 0.314 | 0.564 | 0.125 | 0.667 | 0.213 | 0.611 | 0.002 | 0.713 |
| Rme | Rmh | Rce | REe | |||||||||
| LR | 0.259 | 0.631 | 0.086 | 0.699 | 0.095 | 0.693 | 0.096 | 0.694 | ||||
| SVR | 0.371 | 0.574 | 0.259 | 0.645 | 0.149 | 0.685 | 0.083 | 0.700 | ||||
| RF | 0.109 | 0.668 | −0.148 | 0.765 | −0.151 | 0.757 | −0.118 | 0.732 | ||||
| Method | VIs | VIs + GLCM | VIs + NDTIs | VIs + DTIs | VIs + RTIs | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| R2 | RMSE | R2 | RMSE | R2 | RMSE | R2 | RMSE | R2 | RMSE | |
| MLR | 0.832 | 0.280 | 0.840 | 0.275 | 0.831 | 0.279 | 0.846 | 0.268 | 0.848 | 0.267 |
| SVR | 0.834 | 0.282 | 0.836 | 0.282 | 0.844 | 0.272 | 0.848 | 0.270 | 0.818 | 0.306 |
| RF | 0.802 | 0.303 | 0.826 | 0.283 | 0.815 | 0.288 | 0.813 | 0.289 | 0.816 | 0.288 |
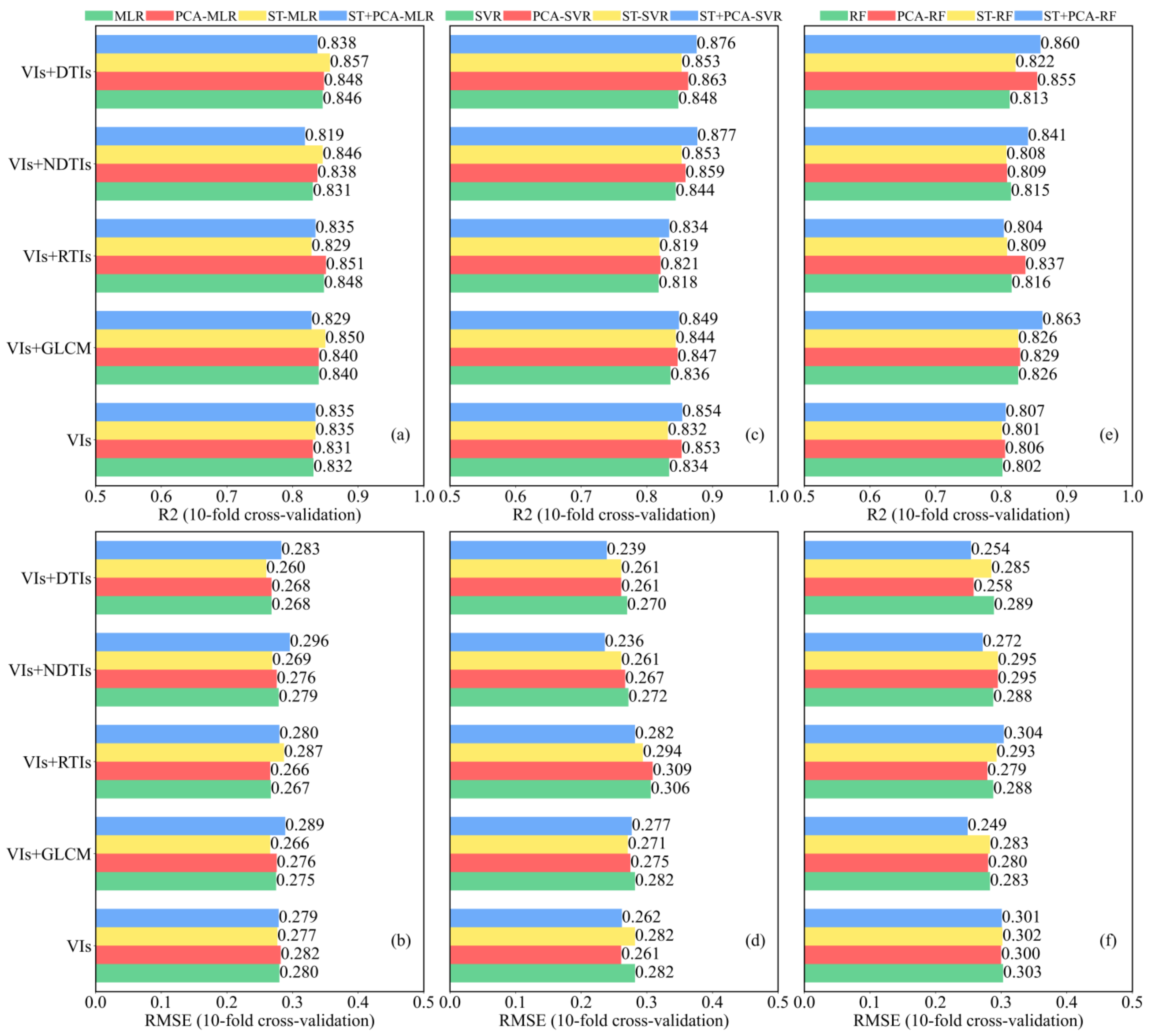
| Input Set | Selected Features | Methods | R2 | RMSE |
|---|---|---|---|---|
| VIs | MSRRE, NDVIRE, NDVI, DVI, OSAVI | MLR SVR RF | 0.835 0.832 0.801 | 0.277 0.282 0.302 |
| VIs+ GLCM | MSRRE, ENE, DVI, OSAVI, NDVIRE, MEA | MLR SVR RF | 0.850 0.844 0.826 | 0.266 0.271 0.283 |
| VIs+ NDTIs | MSRRE, NDme, NDVIRE, NDVI, DVI | MLR SVR RF | 0.846 0.853 0.808 | 0.269 0.261 0.295 |
| VIs+ DTIs | MSRRE, Dmh, NDVIRE, NDVI, DVI | MLR SVR RF | 0.857 0.853 0.822 | 0.260 0.261 0.285 |
| VIs+ RTIs | MSRRE, RVI, Rme, Rmh | MLR SVR RF | 0.829 0.819 0.809 | 0.287 0.294 0.293 |
| Data Size | VIs | VIs + DTIs | VIs + NDTIs | |||
|---|---|---|---|---|---|---|
| R2 | RMSE | R2 | RMSE | R2 | RMSE | |
| 40 | 0.335 | 0.264 | 0.347 | 0.268 | 0.331 | 0.266 |
| 50 | 0.506 | 0.269 | 0.573 | 0.282 | 0.548 | 0.279 |
| 60 | 0.590 | 0.277 | 0.647 | 0.274 | 0.638 | 0.272 |
| 70 | 0.718 | 0.288 | 0.748 | 0.269 | 0.741 | 0.267 |
| 80 | 0.755 | 0.286 | 0.778 | 0.258 | 0.778 | 0.258 |
| 90 | 0.793 | 0.270 | 0.817 | 0.256 | 0.816 | 0.251 |
| 100 | 0.816 | 0.232 | 0.837 | 0.247 | 0.839 | 0.247 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Zhang, K.; Sun, Y.; Zhao, Y.; Zhuang, H.; Ban, W.; Chen, Y.; Fu, E.; Chen, S.; Liu, J.; et al. Combining Spectral and Texture Features of UAS-Based Multispectral Images for Maize Leaf Area Index Estimation. Remote Sens. 2022, 14, 331. https://doi.org/10.3390/rs14020331
Zhang X, Zhang K, Sun Y, Zhao Y, Zhuang H, Ban W, Chen Y, Fu E, Chen S, Liu J, et al. Combining Spectral and Texture Features of UAS-Based Multispectral Images for Maize Leaf Area Index Estimation. Remote Sensing. 2022; 14(2):331. https://doi.org/10.3390/rs14020331
Chicago/Turabian StyleZhang, Xuewei, Kefei Zhang, Yaqin Sun, Yindi Zhao, Huifu Zhuang, Wei Ban, Yu Chen, Erjiang Fu, Shuo Chen, Jinxiang Liu, and et al. 2022. "Combining Spectral and Texture Features of UAS-Based Multispectral Images for Maize Leaf Area Index Estimation" Remote Sensing 14, no. 2: 331. https://doi.org/10.3390/rs14020331
APA StyleZhang, X., Zhang, K., Sun, Y., Zhao, Y., Zhuang, H., Ban, W., Chen, Y., Fu, E., Chen, S., Liu, J., & Hao, Y. (2022). Combining Spectral and Texture Features of UAS-Based Multispectral Images for Maize Leaf Area Index Estimation. Remote Sensing, 14(2), 331. https://doi.org/10.3390/rs14020331







