Climate Normalized Spatial Patterns of Evapotranspiration Enhance the Calibration of a Hydrological Model
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Site
2.2. Hydrological Model
2.3. Observational Data
2.4. Model Evaluation
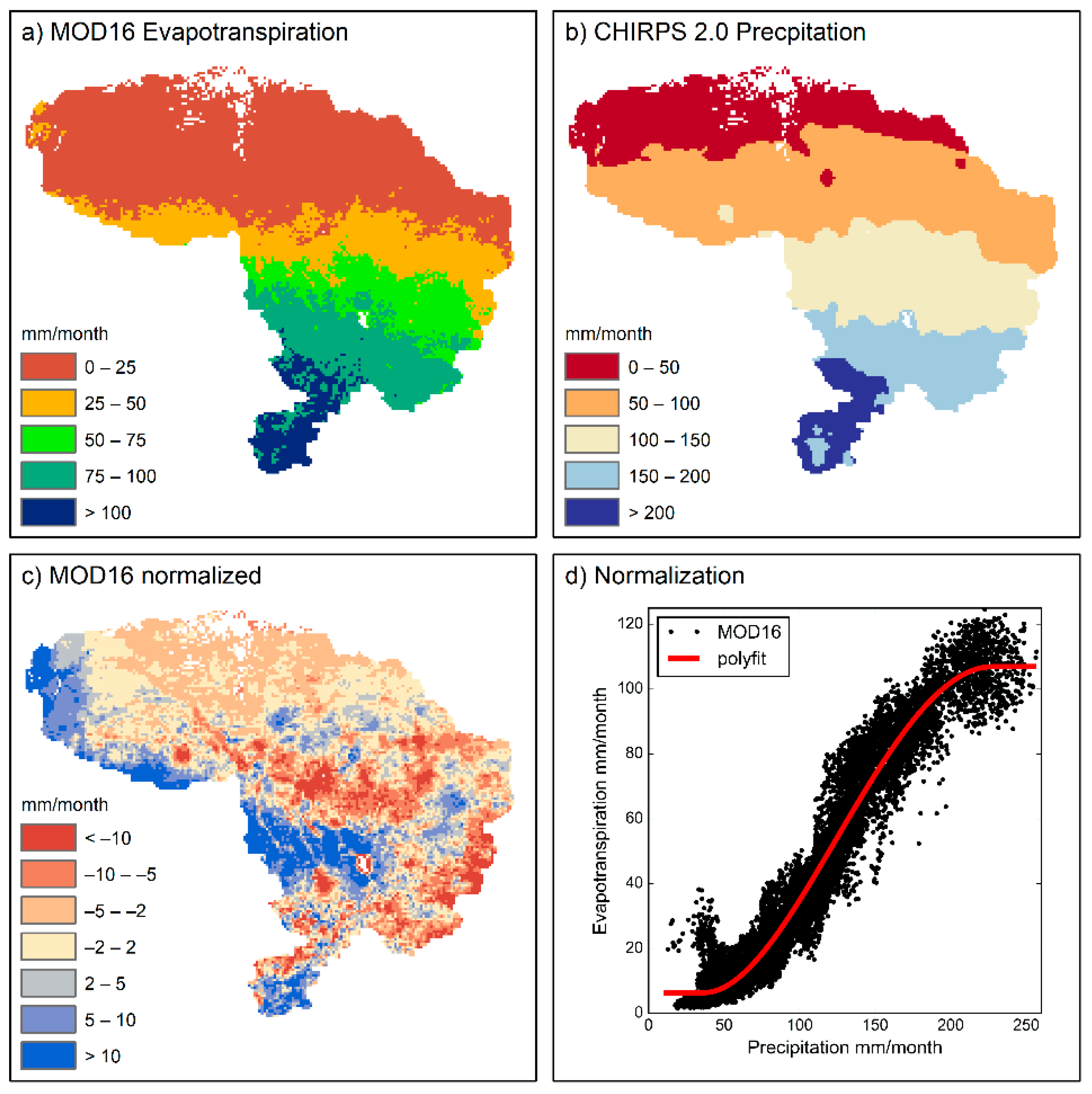
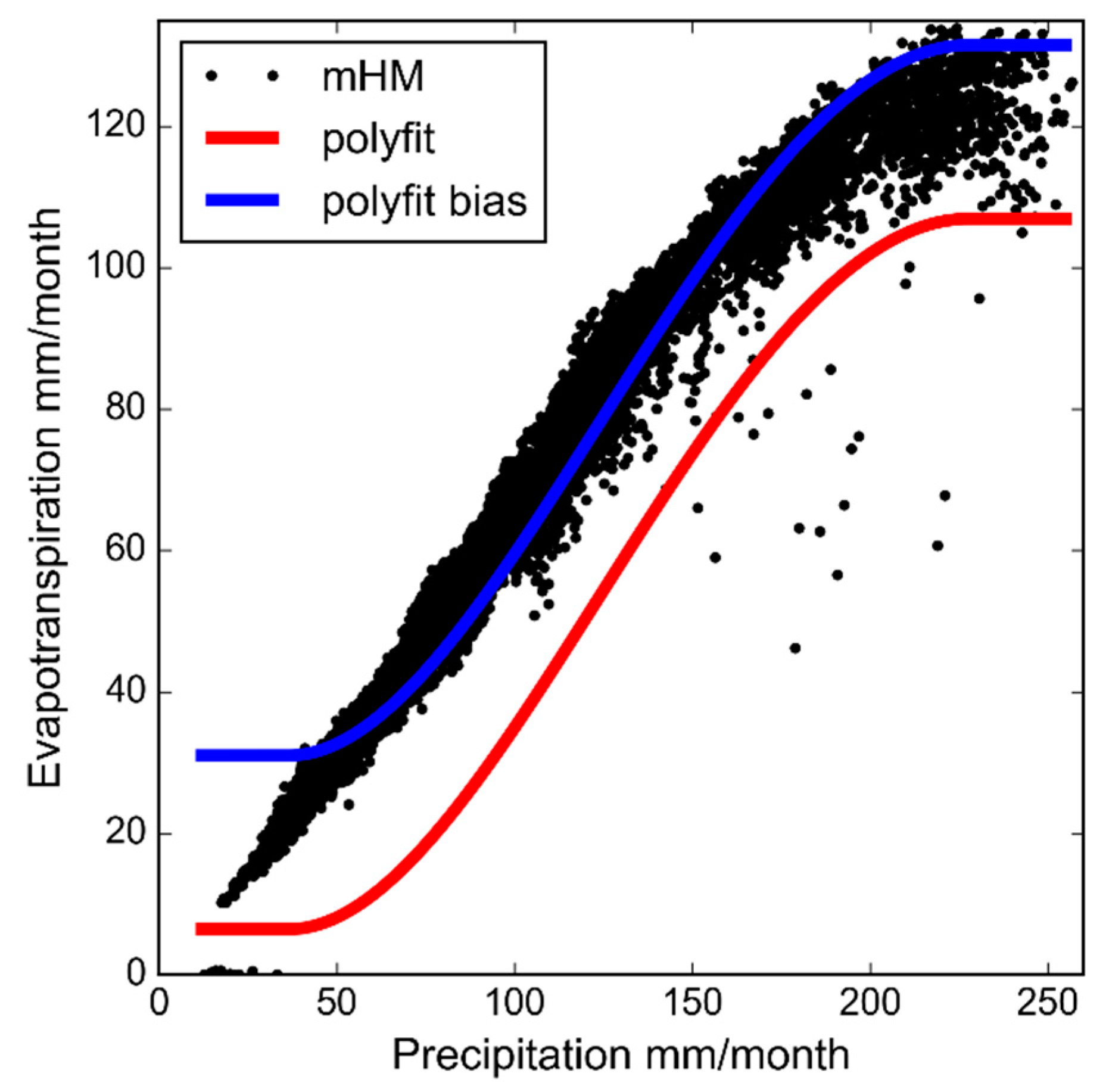
2.5. Climate Normalization
2.6. Calibration Experiments
3. Results
3.1. Sensitivity Analysis
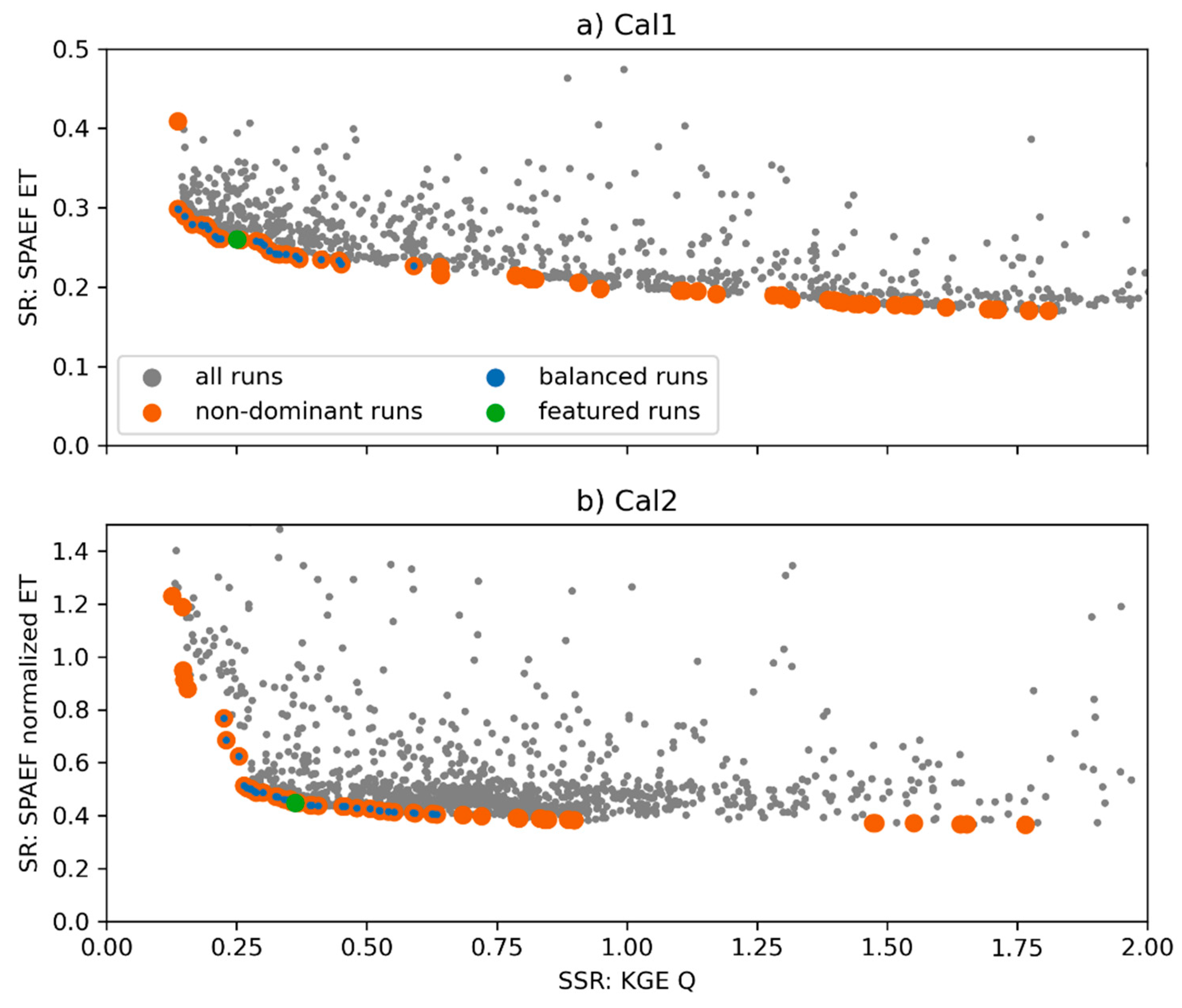
3.2. Pareto Front
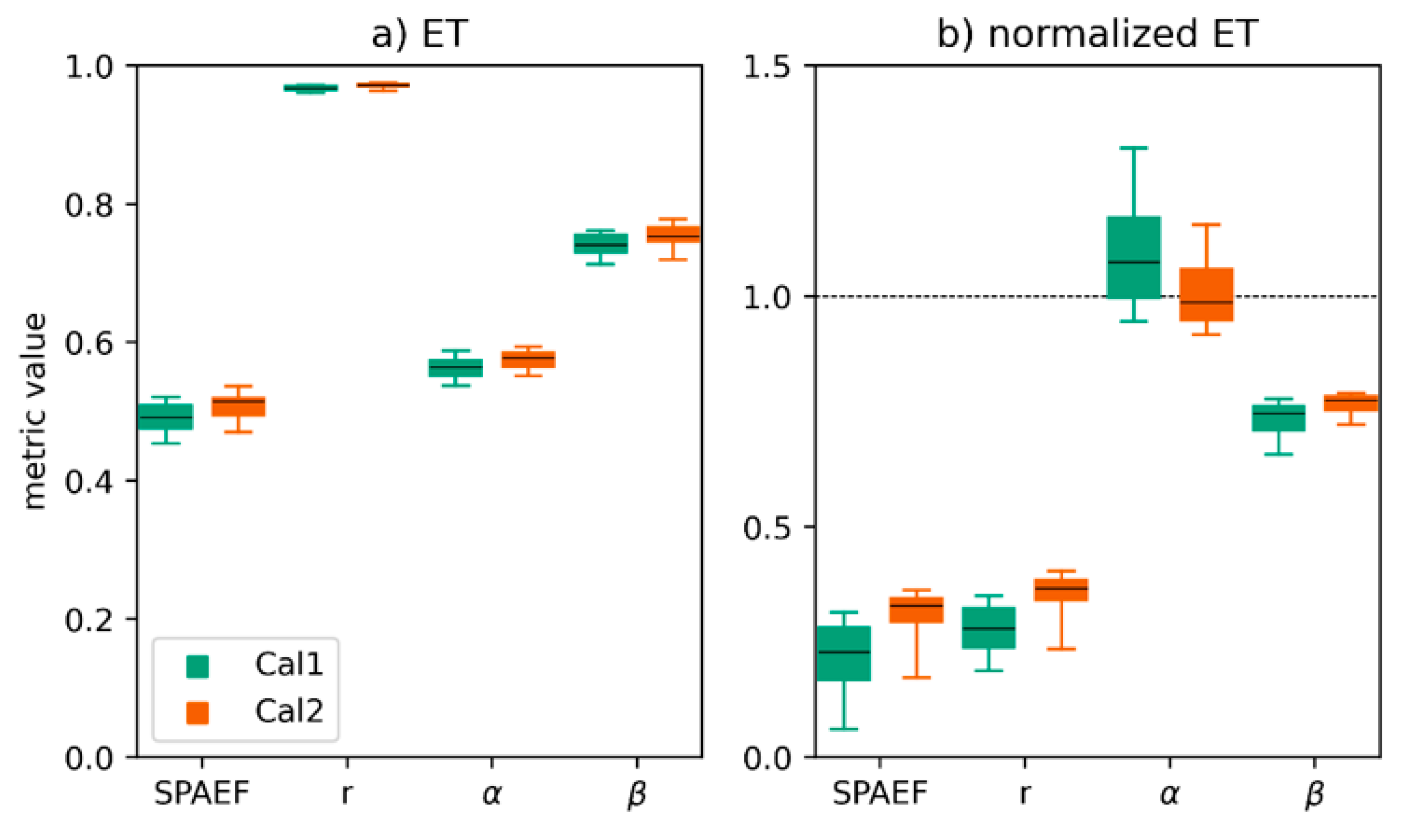
3.3. Evapotranspiration Evaluation
3.4. Discharge Evaluation
4. Discussion
4.1. Normalization Method
4.2. Calibration Strategy
4.3. Limitations
5. Conclusions
- (1)
- The multi-objective calibration of the Senegal River basin resulted in a well-defined Pareto front that highlighted tradeoffs between the temporal Q performance at four stations and the spatial pattern performance for long-term average rainy-season ET.
- (2)
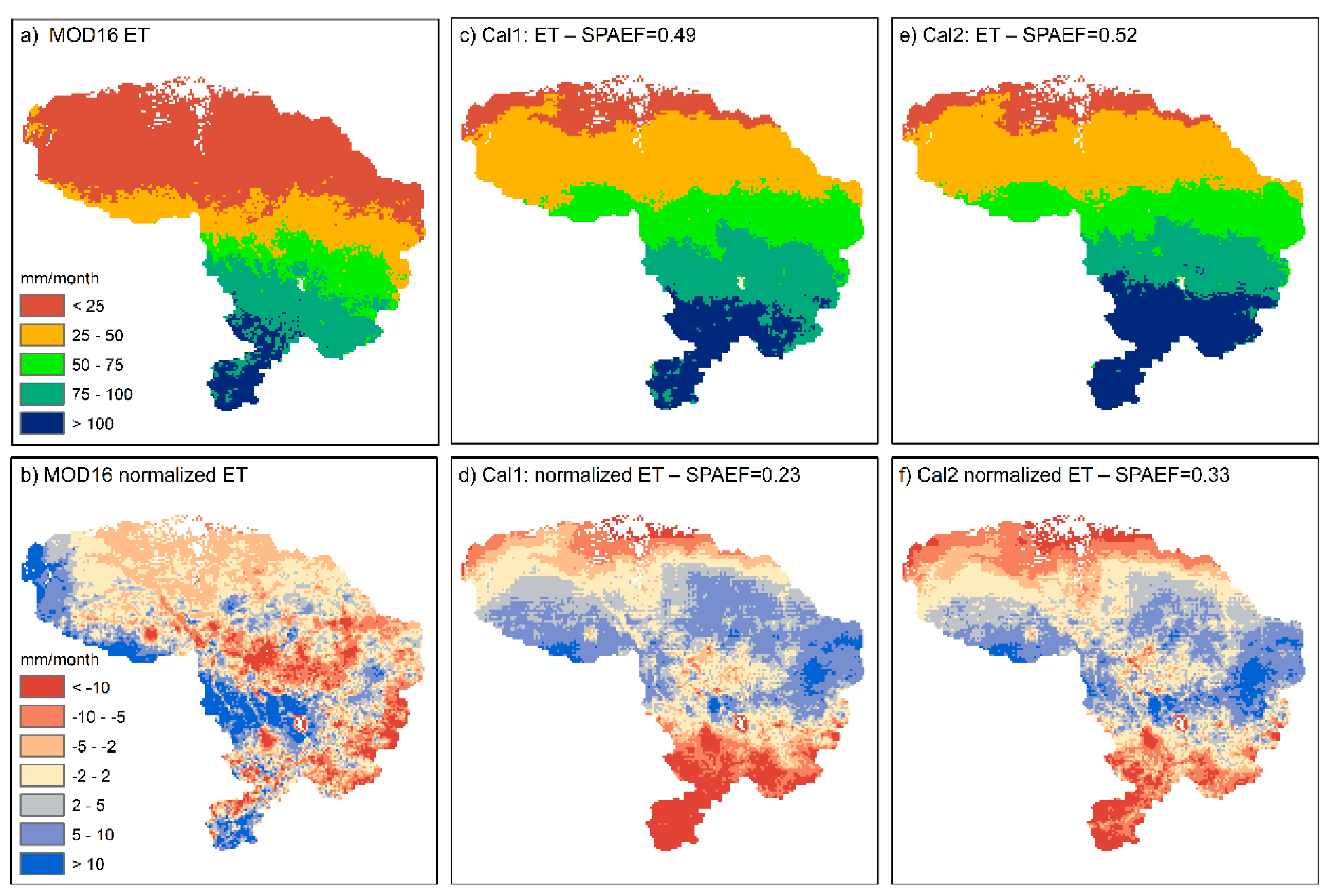
- Climate normalizing of ET was successfully implemented using a polynomial trend model linking the distinct north-south gradient in precipitation to the spatial pattern of ET. The normalized spatial pattern conveys more complexity, i.e., hydrological processes related to soil and vegetation variability, than the original spatial pattern.
- (3)
- The sensitivity of model parameters varied between the original ET pattern and the normalized ET pattern which supported the conclusion that the normalized pattern contained alternative information related to different processes.
- (4)
- Calibrating against climate normalized patterns did not compromise the performance of the original patterns and a very comparable performance was obtained between the two calibration experiments for the original ET pattern. However, the spatial pattern performance for the normalized pattern increased from SPAEF = 0.23 in Cal1 to SPAEF = 0.33 in Cal2.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Demirel, M.C.; Mai, J.; Mendiguren, G.; Koch, J.; Samaniego, L.; Stisen, S. Combining satellite data and appropriate objective functions for improved spatial pattern performance of a distributed hydrologic model. Hydrol. Earth Syst. Sci. 2018, 22, 1299–1315. [Google Scholar] [CrossRef]
- Mendiguren, G.; Koch, J.; Stisen, S. Spatial pattern evaluation of a calibrated national hydrological model—A remote-sensing-based diagnostic approach. Hydrol. Earth Syst. Sci. 2017, 21, 5987–6005. [Google Scholar] [CrossRef]
- Soltani, M.; Bjerre, E.; Koch, J.; Stisen, S. Integrating remote sensing data in optimization of a national water resources model to improve the spatial pattern performance of evapotranspiration. J. Hydrol. 2021, 603, 127026. [Google Scholar] [CrossRef]
- Hunink, J.E.; Eekhout, J.P.C.; de Vente, J.; Contreras, S.; Droogers, P.; Baille, A. Hydrological Modelling using Satellite-based Crop Coefficients: A Comparison of Methods at the Basin Scale. Remote Sens. 2017, 9, 174. [Google Scholar] [CrossRef]
- Samaniego, L.; Kumar, R.; Thober, S.; Rakovec, O.; Zink, M.; Wanders, N.; Eisner, S.; Müller Schmied, H.; Sutanudjaja, E.; Warrach-Sagi, K.; et al. Toward seamless hydrologic predictions across spatial scales. Hydrol. Earth Syst. Sci. 2017, 21, 4323–4346. [Google Scholar] [CrossRef]
- Mizukami, N.; Clark, M.P.; Newman, A.J.; Wood, A.W.; Gutmann, E.D.; Nijssen, B.; Rakovec, O.; Samaniego, L. Towards seamless large-domain parameter estimation for hydrologic models. Water Resour. Res. 2017, 53, 8020–8040. [Google Scholar] [CrossRef]
- Conradt, T.; Wechsung, F.; Bronstert, A. Three perceptions of the evapotranspiration landscape: Comparing spatial patterns from a distributed hydrological model, remotely sensed surface temperatures, and sub-basin water balances. Hydrol. Earth Syst. Sci. 2013, 17, 2947–2966. [Google Scholar] [CrossRef]
- Koch, J.; Jensen, K.H.; Stisen, S. Toward a true spatial model evaluation in distributed hydrological modeling: Kappa statistics, Fuzzy theory, and EOF-analysis benchmarked by the human perception and evaluated against a modeling case study. Water Resour. Res. 2015, 51, 1225–1246. [Google Scholar] [CrossRef]
- Stisen, S.; Koch, J.; Sonnenborg, T.O.; Refsgaard, J.C.; Bircher, S.; Ringgaard, R.; Jensen, K.H. Moving beyond run-off calibration —Multivariable optimization of a surface-subsurface-atmosphere model. Hydrol. Process. 2018, 32, 2654–2668. [Google Scholar] [CrossRef]
- Koch, J.; Demirel, M.C.; Stisen, S. The SPAtial EFficiency metric (SPAEF): Multiple-component evaluation of spatial patterns for optimization of hydrological models. Geosci. Model Dev. 2018, 11, 1873–1886. [Google Scholar] [CrossRef]
- Zink, M.; Mai, J.; Cuntz, M.; Samaniego, L. Conditioning a Hydrologic Model Using Patterns of Remotely Sensed Land Surface Temperature. Water Resour. Res. 2018, 54, 2976–2998. [Google Scholar] [CrossRef]
- Dembélé, M.; Hrachowitz, M.; Savenije, H.H.G.; Mariéthoz, G.; Schaefli, B. Improving the Predictive Skill of a Distributed Hydrological Model by Calibration on Spatial Patterns With Multiple Satellite Data Sets. Water Resour. Res. 2020, 56, e2019WR026085. [Google Scholar] [CrossRef]
- Koch, J.; Siemann, A.; Stisen, S.; Sheffield, J. Spatial validation of large scale land surface models against monthly land surface temperature patterns using innovative performance metrics. J. Geophys. Res. Atmos. 2016, 121, 5430–5452. [Google Scholar] [CrossRef]
- Ko, A.; Mascaro, G.; Vivoni, E.R. Strategies to Improve and Evaluate Physics-Based Hyperresolution Hydrologic Simulations at Regional Basin Scales. Water Resour. Res. 2019, 55, 1129–1152. [Google Scholar] [CrossRef]
- Stisen, S.; Soltani, M.; Mendiguren, G.; Langkilde, H.; Garcia, M.; Koch, J. Spatial patterns in actual evapotranspiration climatologies for europe. Remote Sens. 2021, 13, 2410. [Google Scholar] [CrossRef]
- Rakovec, O.; Mizukami, N.; Kumar, R.; Newman, A.J.; Thober, S.; Wood, A.W.; Clark, M.P.; Samaniego, L. Diagnostic Evaluation of Large-Domain Hydrologic Models Calibrated Across the Contiguous United States. J. Geophys. Res. Atmos. 2019, 124, 13991–14007. [Google Scholar] [CrossRef]
- Koster, R.D.; Mahanama, S.P.P. Land surface controls on hydroclimatic means and variability. J. Hydrometeorol. 2012, 13, 1604–1620. [Google Scholar] [CrossRef]
- Guzinski, R.; Nieto, H.; Stisen, S.; Fensholt, R. Inter-comparison of energy balance and hydrological models for land surface energy flux estimation over a whole river catchment. Hydrol. Earth Syst. Sci. 2015, 19, 2017–2036. [Google Scholar] [CrossRef]
- Budyko, M.I. Climate and Life; Academic Press Inc.: New York, NY, USA, 1974; 508p. [Google Scholar]
- Greve, P.; Burek, P.; Wada, Y. Using the Budyko Framework for Calibrating a Global Hydrological Model. Water Resour. Res. 2020, 56, e2019WR026280. [Google Scholar] [CrossRef]
- Kushwaha, A.P.; Tiwari, A.D.; Dangar, S.; Shah, H.; Mahto, S.S.; Mishra, V. Multimodel assessment of water budget in Indian sub-continental river basins. J. Hydrol. 2021, 603, 126977. [Google Scholar] [CrossRef]
- Gharari, S.; Shafiei, M.; Hrachowitz, M.; Kumar, R.; Fenicia, F.; Gupta, H.V.; Savenije, H.H.G. A constraint-based search algorithm for parameter identification of environmental models. Hydrol. Earth Syst. Sci. 2014, 18, 4861–4870. [Google Scholar] [CrossRef][Green Version]
- Samaniego, L.; Kumar, R.; Attinger, S. Multiscale parameter regionalization of a grid-based hydrologic model at the mesoscale. Water Resour. Res. 2010, 46, W05523. [Google Scholar] [CrossRef]
- Kumar, R.; Samaniego, L.; Attinger, S. Implications of distributed hydrologic model parameterization on water fluxes at multiple scales and locations. Water Resour. Res. 2013, 49, 360–379. [Google Scholar] [CrossRef]
- Stisen, S.; Jensen, K.H.; Sandholt, I.; Grimes, D.I.F. A remote sensing driven distributed hydrological model of the Senegal River basin. J. Hydrol. 2008, 354, 131–148. [Google Scholar] [CrossRef]
- Bodian, A.; Diop, L.; Panthou, G.; Dacosta, H.; Deme, A.; Dezetter, A.; Ndiaye, P.M.; Diouf, I.; Visch, T. Recent trend in hydroclimatic conditions in the Senegal River basin. Water 2020, 12, 436. [Google Scholar] [CrossRef]
- Samaniego, L.; Brenner, J.; Craven, J.; Cuntz, M.; Dalmasso, G.; Demirel, C.M.; Jing, M.; Kaluza, M.; Kumar, R.; Langenberg, B.; et al. Mesoscale Hydrologic Model-mHM. v5.11.1. 2021. Available online: https://www.ufz.de/index.php?en=40114 (accessed on 6 January 2022).
- Thober, S.; Cuntz, M.; Kelbling, M.; Kumar, R.; Mai, J.; Samaniego, L. The multiscale routing model mRM v1.0: Simple river routing at resolutions from 1 to 50 km. Geosci. Model Dev. 2019, 12, 2501–2521. [Google Scholar] [CrossRef]
- Kumar, R.; Livneh, B.; Samaniego, L. Toward computationally efficient large-scale hydrologic predictions with a multiscale regionalization scheme. Water Resour. Res. 2013, 49, 5700–5714. [Google Scholar] [CrossRef]
- Poméon, T.; Diekkrüger, B.; Kumar, R. Computationally efficient multivariate calibration and validation of a grid-based hydrologic model in sparsely gauged West African river basins. Water 2018, 10, 1418. [Google Scholar] [CrossRef]
- Dembélé, M.; Ceperley, N.; Zwart, S.J.; Salvadore, E.; Mariethoz, G.; Schaefli, B. Potential of satellite and reanalysis evaporation datasets for hydrological modelling under various model calibration strategies. Adv. Water Resour. 2020, 143, 103667. [Google Scholar] [CrossRef]
- Dembele, M.; Schaefli, B.; Van De Giesen, N. Suitability of 17 gridded rainfall and temperature datasets for large-scale hydrological modelling in West Africa. Hydrol. Earth Syst. Sci. 2020, 24, 5379–5406. [Google Scholar] [CrossRef]
- Hengl, T.; Heuvelink, G.B.M.; Kempen, B.; Leenaars, J.G.B.; Walsh, M.G.; Shepherd, K.D.; Sila, A.; MacMillan, R.A.; De Jesus, J.M.; Tamene, L.; et al. Mapping soil properties of Africa at 250 m resolution: Random forests significantly improve current predictions. PLoS ONE 2015, 10, e0125814. [Google Scholar] [CrossRef]
- Friedl, M.; Gray, J.; Sulla-Menashe, D. MCD12Q2 MODIS/Terra+Aqua Land Cover Dynamics Yearly L3 Global 500m SIN Grid V006. Available online: https://lpdaac.usgs.gov/products/mcd12q2v006/ (accessed on 6 August 2021).
- Myneni, R.B.; Knyazikhin, Y.; Park, T. MCD15A2H MODIS/Terra+Aqua Leaf Area Index/FPAR 8-Day L4 Global 500m SIN Grid V006. Available online: https://doi.org/10.5067/MODIS/MCD15A2H.006 (accessed on 6 August 2021).
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 147, 4186–4227. [Google Scholar] [CrossRef]
- Hargreaves, G.H.; Samani, Z.A. Reference Crop Evapotranspiration from Temperature. Appl. Eng. Agric. 1985, 1, 96–99. [Google Scholar] [CrossRef]
- Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Husak, G.; Rowland, J.; Harrison, L.; Hoell, A.; et al. The climate hazards infrared precipitation with stations—A new environmental record for monitoring extremes. Sci. Data 2015, 2, 150066. [Google Scholar] [CrossRef] [PubMed]
- Funk, C.C.; Peterson, P.J.; Landsfeld, M.F.; Pedreros, D.H.; Verdin, J.P.; Rowland, J.D.; Romero, B.E.; Husak, G.J.; Michaelsen, J.C.; Verdin, A.P. A Quasi-Global Precipitation Time Series for Drought Monitoring; Data Series 832; US Geological Survey: Reston, VA, USA, 2014; pp. 1–12.
- Running, S.; Mu, Q.; Zhao, M. MOD16A2 MODIS/Terra Net Evapotranspiration 8-Day L4 Global 500m SIN Grid V006. Available online: https://doi.org/10.5067/MODIS/MOD16A2.006 (accessed on 10 November 2021).
- Hulsman, P.; Savenije, H.H.G.; Hrachowitz, M. Learning from satellite observations: Increased understanding of catchment processes through stepwise model improvement. Hydrol. Earth Syst. Sci. 2021, 25, 957–982. [Google Scholar] [CrossRef]
- Weerasinghe, I.; Bastiaanssen, W.; Mul, M.; Jia, L.; Van Griensven, A. Can we trust remote sensing evapotranspiration products over Africa. Hydrol. Earth Syst. Sci. 2020, 24, 1565–1586. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Knoben, W.J.M.; Freer, J.E.; Woods, R.A. Technical note: Inherent benchmark or not? Comparing Nash-Sutcliffe and Kling-Gupta efficiency scores. Hydrol. Earth Syst. Sci. 2019, 23, 4323–4331. [Google Scholar] [CrossRef]
- Matott, L.S. OSTRICH: An Optimization Software Tool, Documentation and User’s Guide, version 17; University at Buffalo Center for Computational Research: Buffalo, NY, USA, 2017; p. 79. [Google Scholar]
- Tolson, B.; Sharma, V.; Swayne, D.A. Parallel Implementations of the Dynamically Dimensioned Search (DDS) Algorithm. In Proceedings of the 7th International Symposium on Environmental Software Systems, Prague, Czech Republic, 22–25 May 2007. [Google Scholar]
- Demirel, M.C.; Koch, J.; Mendiguren, G.; Stisen, S. Spatial pattern oriented multicriteria sensitivity analysis of a distributed hydrologic model. Water 2018, 10, 1188. [Google Scholar] [CrossRef]
- Beck, H.E.; Vergopolan, N.; Pan, M.; Levizzani, V.; Van Dijk, A.I.J.M.; Weedon, G.P.; Brocca, L.; Pappenberger, F.; Huffman, G.J.; Wood, E.F. Global-scale evaluation of 22 precipitation datasets using gauge observations and hydrological modeling. Hydrol. Earth Syst. Sci. 2017, 21, 6201–6217. [Google Scholar] [CrossRef]
- Dion, P.; Martel, J.L.; Arsenault, R. Hydrological ensemble forecasting using a multi-model framework. J. Hydrol. 2021, 600, 126537. [Google Scholar] [CrossRef]
- Koch, J.; Cornelissen, T.; Fang, Z.; Bogena, H.; Diekkrüger, B.; Kollet, S.; Stisen, S. Inter-comparison of three distributed hydrological models with respect to seasonal variability of soil moisture patterns at a small forested catchment. J. Hydrol. 2016, 533, 234–249. [Google Scholar] [CrossRef]
- Bhuiyan, M.A.E.; Nikolopoulos, E.I.; Anagnostou, E.N.; Polcher, J.; Albergel, C.; Dutra, E.; Fink, G.; Martínez-De La Torre, A.; Munier, S. Assessment of precipitation error propagation in multi-model global water resource reanalysis. Hydrol. Earth Syst. Sci. 2019, 23, 1973–1994. [Google Scholar] [CrossRef]





| Parameter Name | Description | Cal1 | Cal2 |
|---|---|---|---|
| canintfact | canopy interception factor | 0.110 | 0.120 |
| ptflowconst | ptf saturated water content: constant | 0.876 | 0.700 |
| ptflowclay | ptf saturated water content: coefficient clay content | 0.002 | 0.001 |
| ptflowdb | ptf saturated water content: coefficient bulk density | 0.255 | 0.159 |
| ptfhigconst | ptf saturated water content: constant | 0.749 | 0.795 |
| ptfhigdb | ptf saturated water content: coefficient bulk density | 0.100 | 0.100 |
| ptfksconst | ptf hydraulic conductivity: constant | 0.574 | 0.600 |
| ptfkssand | ptf hydraulic conductivity: coefficient sand content | 0.012 | 0.013 |
| ptfksclay | ptf hydraulic conductivity: coefficient clay content | 0.015 | 0.015 |
| rotfrcoffor | root fraction coefficient forest | 0.990 | 0.990 |
| rotfrcofsa | root fraction coefficient sand | 0.001 | 0.001 |
| rotfrcofcl | root fraction coefficient clay | 0.995 | 0.993 |
| fcmin | field capacity scaling: minimum | 0.108 | 0.044 |
| fcdelta | field capacity scaling: range | 0.300 | 0.496 |
| jarvis | jarvis soil moisture threshold | 0.996 | 0.994 |
| infshapef | infiltration shape factor | 1.610 | 1.410 |
| pet_af | PET scaling: minimum forest | 0.504 | 0.500 |
| pet_ap | PET scaling: minimum permeable | 0.552 | 0.516 |
| pet_b | PET scaling: range | 2.190 | 2.880 |
| pet_c | PET scaling: shape | 0.154 | 0.145 |
| Q | ET | Normalized ET | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| KGE | SPAEF | r | α | β | SPAEF | r | α | β | ||
| Cal1 n = 28 | median | 0.73 | 0.49 | 0.97 | 0.56 | 0.74 | 0.23 | 0.28 | 1.07 | 0.75 |
| std | 0.05 | 0.02 | 0.00 | 0.01 | 0.01 | 0.08 | 0.05 | 0.12 | 0.04 | |
| Cal2 n = 42 | median | 0.70 | 0.52 | 0.97 | 0.58 | 0.75 | 0.33 | 0.37 | 0.99 | 0.78 |
| std | 0.05 | 0.02 | 0.00 | 0.01 | 0.01 | 0.05 | 0.04 | 0.07 | 0.02 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koch, J.; Demirel, M.C.; Stisen, S. Climate Normalized Spatial Patterns of Evapotranspiration Enhance the Calibration of a Hydrological Model. Remote Sens. 2022, 14, 315. https://doi.org/10.3390/rs14020315
Koch J, Demirel MC, Stisen S. Climate Normalized Spatial Patterns of Evapotranspiration Enhance the Calibration of a Hydrological Model. Remote Sensing. 2022; 14(2):315. https://doi.org/10.3390/rs14020315
Chicago/Turabian StyleKoch, Julian, Mehmet Cüneyd Demirel, and Simon Stisen. 2022. "Climate Normalized Spatial Patterns of Evapotranspiration Enhance the Calibration of a Hydrological Model" Remote Sensing 14, no. 2: 315. https://doi.org/10.3390/rs14020315
APA StyleKoch, J., Demirel, M. C., & Stisen, S. (2022). Climate Normalized Spatial Patterns of Evapotranspiration Enhance the Calibration of a Hydrological Model. Remote Sensing, 14(2), 315. https://doi.org/10.3390/rs14020315








