Super-Resolution Range and Velocity Estimations for SFA-OFDM Radar
Abstract
:1. Introduction
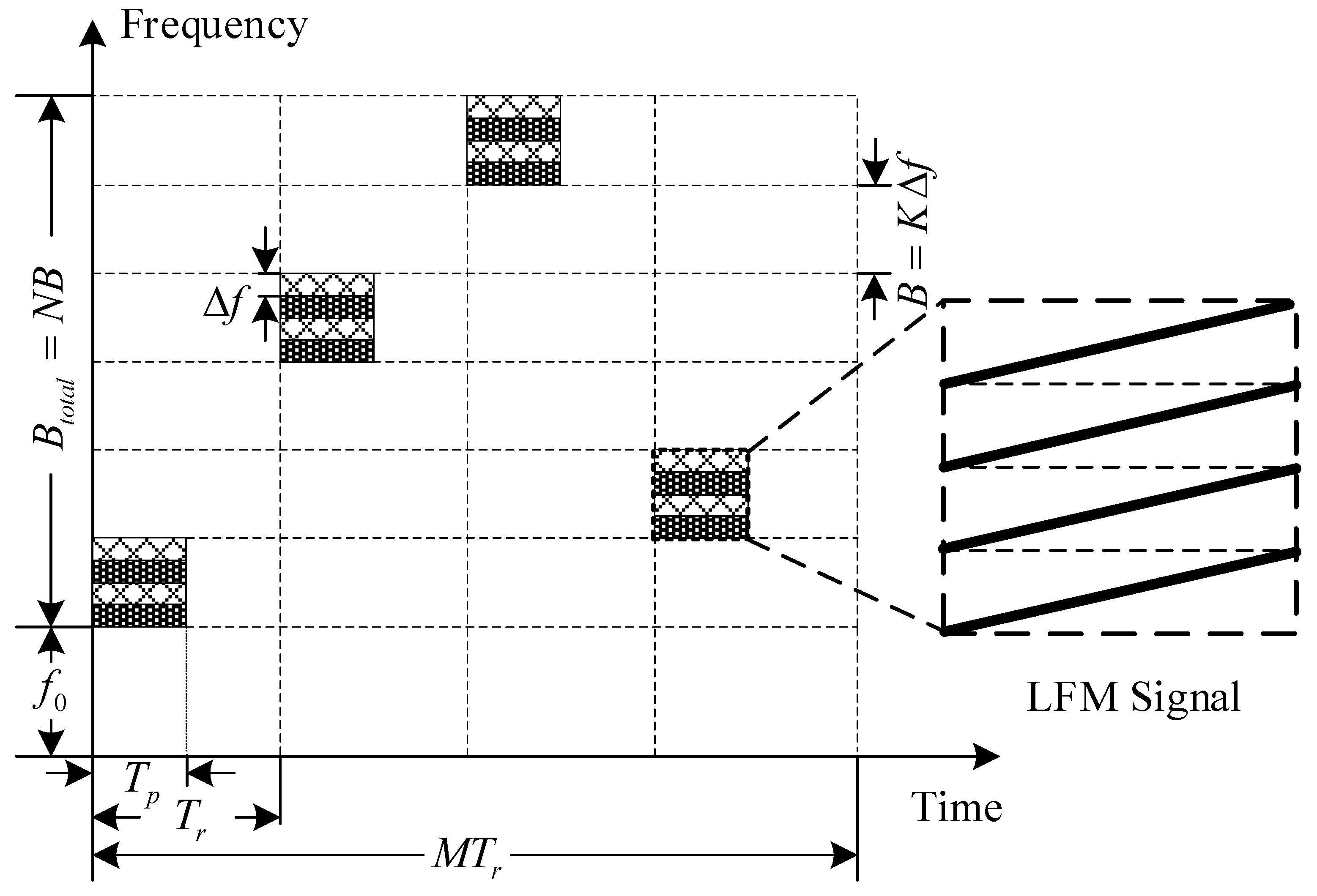
2. SFA-OFDM Radar Signal Model
3. Signal Processing
3.1. Subcarrier Synthesis Processing
3.2. Super-Resolution Range and Velocity Estimations
3.3. Resolving Range Ambiguity
4. Performance Evaluation
4.1. Range and Velocity Resolution
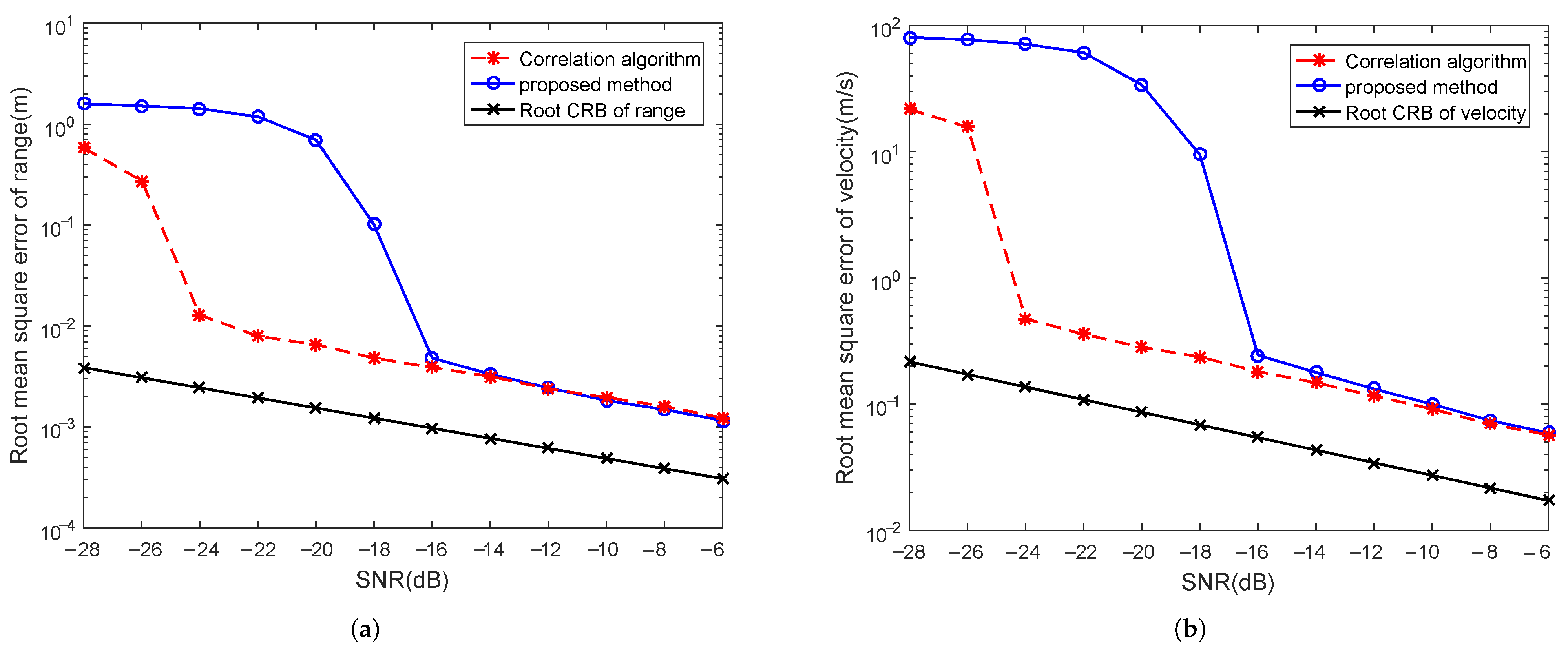
4.2. CRLBs on Range and Velocity Estimations
5. Simulations
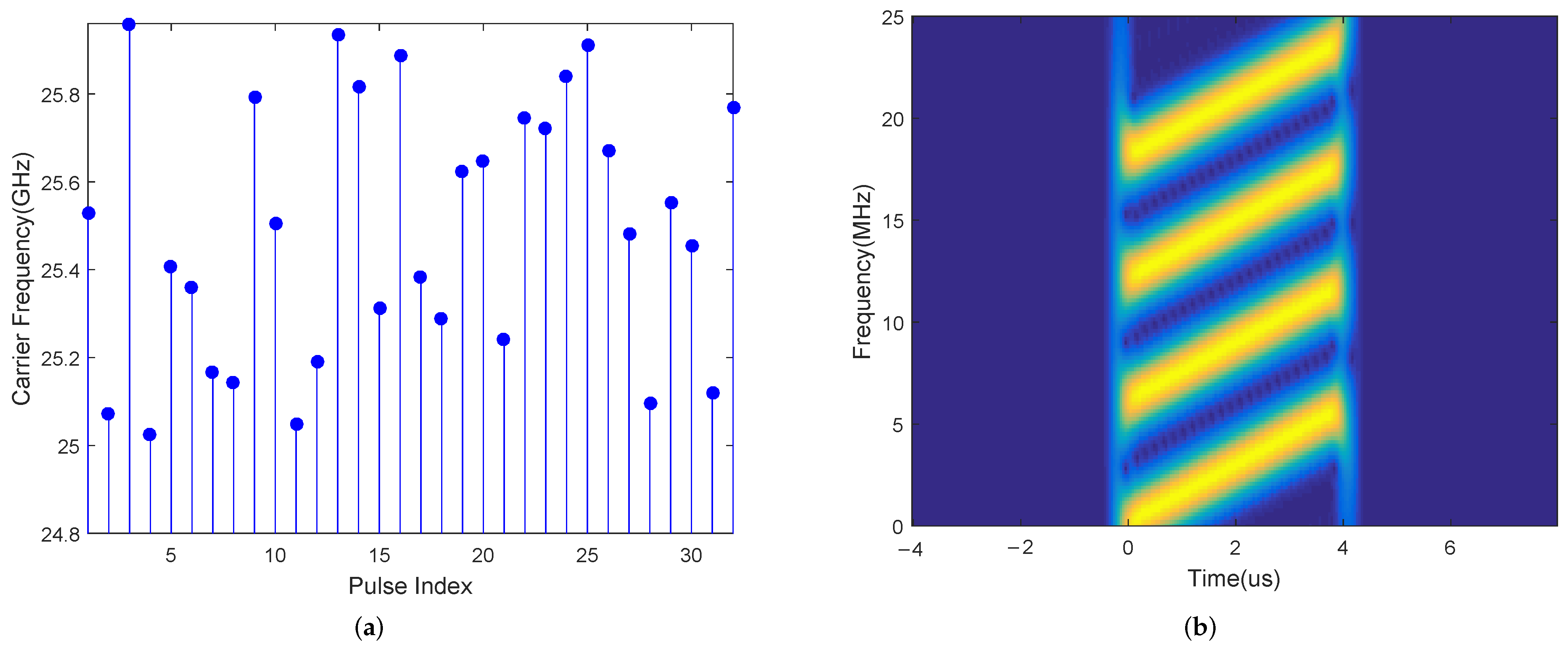
5.1. Signal Processing
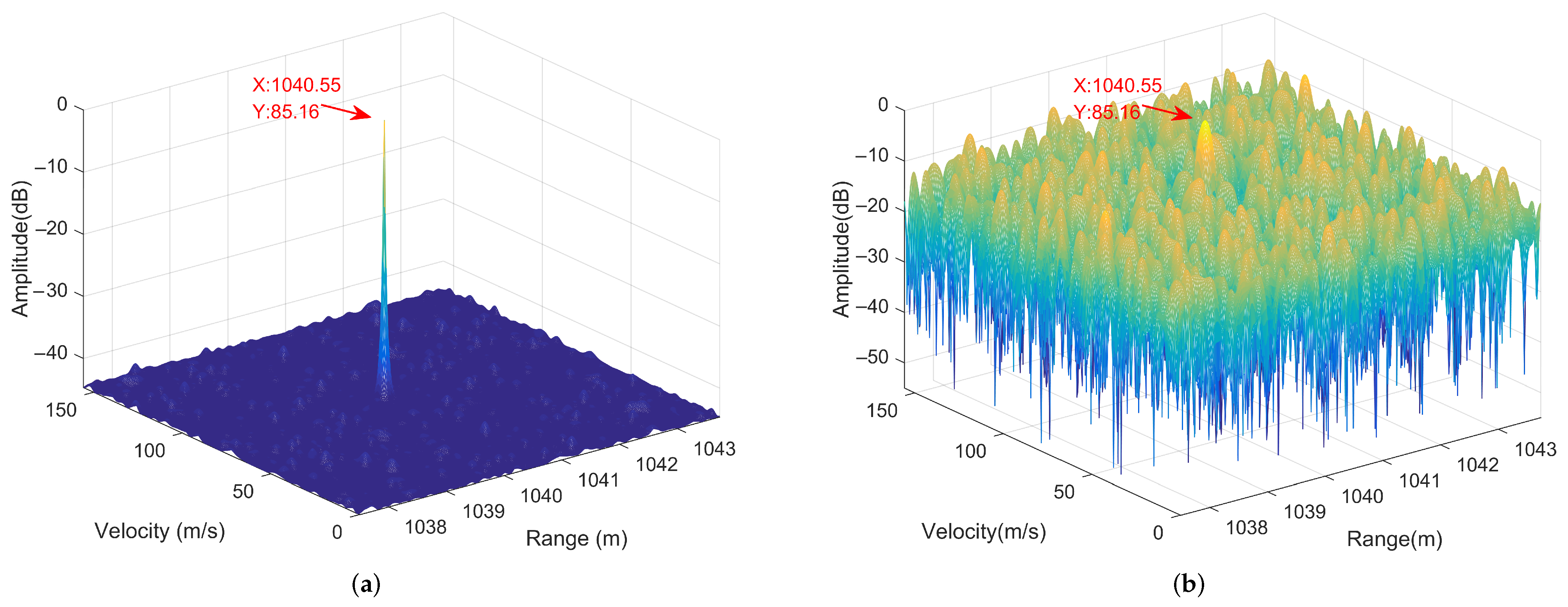
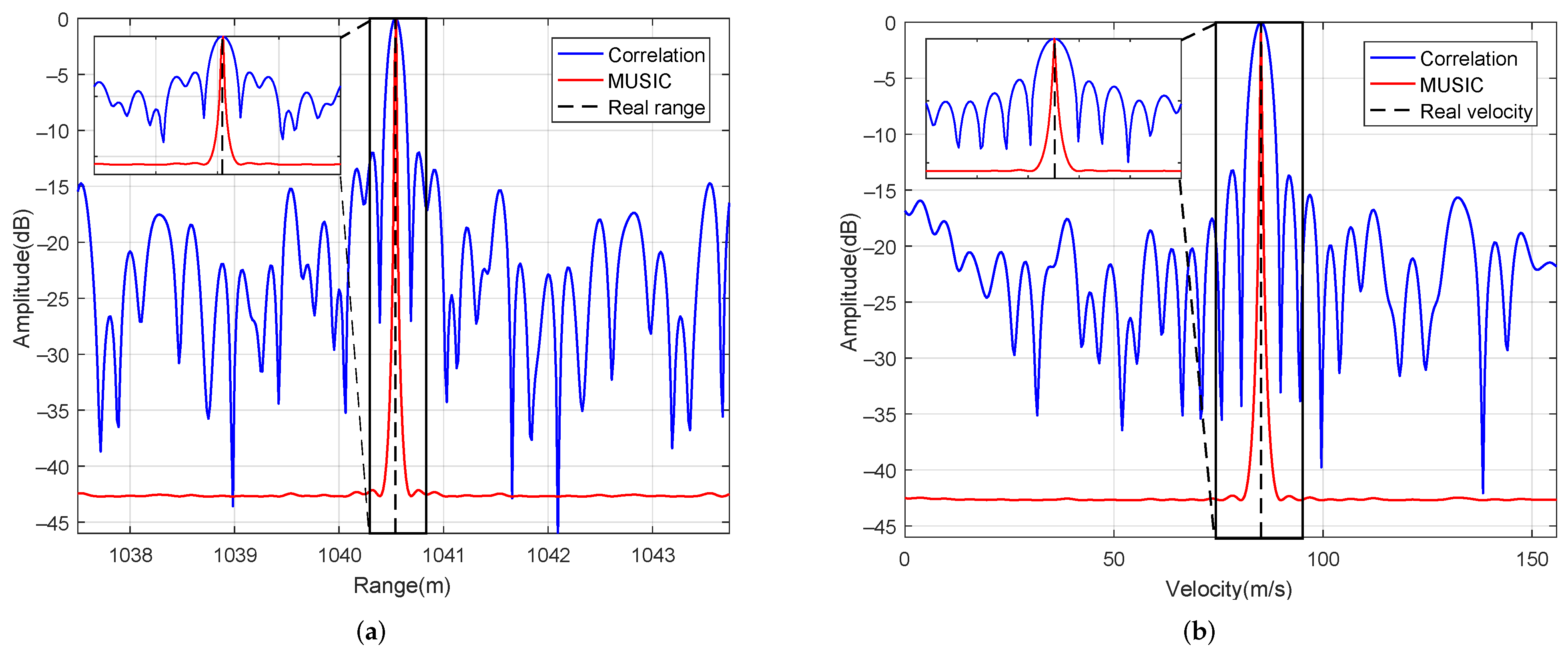
5.2. Estimation Performance
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hwang, T.; Yang, C.; Wu, G.; Li, S.; Li, G.Y. OFDM and Its Wireless Applications: A Survey. IEEE Trans. Veh. Technol. 2009, 58, 1673–1694. [Google Scholar] [CrossRef]
- Siriwongpairat, W.; Su, W.; Olfat, M.; Liu, K.R. Multiband-OFDM MIMO coding framework for UWB communication systems. IEEE Trans. Signal Process. 2006, 54, 214–224. [Google Scholar] [CrossRef]
- Wang, M.M.; Xiao, L.; Brown, T.; Dong, M. Optimal symbol timing for OFDM wireless communications. IEEE Trans. Wirel. Commun. 2009, 8, 5328–5337. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, B.; Lei, P. Ambiguity function analysis for OFDM radar signals. In Proceedings of the 2016 CIE International Conference on Radar (RADAR), Guangzhou, China, 10–13 October 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Demeechai, T.; Chang, T.G.; Siwamogsatham, S. Performance of a Frequency-Domain OFDM-Timing Estimator. IEEE Commun. Lett. 2012, 16, 1680–1683. [Google Scholar] [CrossRef]
- Zhang, T.; Xia, X.G. OFDM Synthetic Aperture Radar Imaging With Sufficient Cyclic Prefix. IEEE Trans. Geosci. Remote Sens. 2015, 53, 394–404. [Google Scholar] [CrossRef] [Green Version]
- Slimane, Z.; Abdelmalek, A.; Feham, M. OFDM Based UWB Synthetic Aperture Through-wall Imaging Radar. In Proceedings of the 2008 Third International Conference on Broadband Communications, Information Technology Biomedical Applications, Pretoria, South Africa, 23–26 November 2008; pp. 293–300. [Google Scholar] [CrossRef]
- Sen, S.; Tang, G.; Nehorai, A. Multiobjective Optimization of OFDM Radar Waveform for Target Detection. IEEE Trans. Signal Process. 2011, 59, 639–652. [Google Scholar] [CrossRef]
- Chabriel, G.; Barrère, J. Adaptive Target Detection Techniques for OFDM-Based Passive Radar Exploiting Spatial Diversity. IEEE Trans. Signal Process. 2017, 65, 5873–5884. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Liao, G.; Chen, Y.; Xu, J.; Yin, Y. Super-Resolution Range and Velocity Estimations With OFDM Integrated Radar and Communications Waveform. IEEE Trans. Veh. Technol. 2020, 69, 11659–11672. [Google Scholar] [CrossRef]
- Chiriyath, A.R.; Ragi, S.; Mittelmann, H.D.; Bliss, D.W. Novel Radar Waveform Optimization for a Cooperative Radar-Communications System. IEEE Trans. Aerosp. Electron. Syst. 2019, 55, 1160–1173. [Google Scholar] [CrossRef]
- Cao, N.; Chen, Y.; Gu, X.; Feng, W. Joint Radar-Communication Waveform Designs Using Signals From Multiplexed Users. IEEE Trans. Commun. 2020, 68, 5216–5227. [Google Scholar] [CrossRef]
- Huo, K.; Deng, B.; Liu, Y.; Jiang, W.; Mao, J. The principle of synthesizing HRRP based on a new OFDM phase-coded stepped-frequency radar signal. In Proceedings of the IEEE 10th International Conference on Signal Processing Proceedings, Beijing, China, 24–28 October 2010; pp. 1994–1998. [Google Scholar] [CrossRef]
- Schweizer, B.; Knill, C.; Schindler, D.; Waldschmidt, C. Stepped-Carrier OFDM-Radar Processing Scheme to Retrieve High-Resolution Range-Velocity Profile at Low Sampling Rate. IEEE Trans. Microw. Theory Tech. 2018, 66, 1610–1618. [Google Scholar] [CrossRef] [Green Version]
- Nuss, B.; Mayer, J.; Marahrens, S.; Zwick, T. Frequency Comb OFDM Radar System With High Range Resolution and Low Sampling Rate. IEEE Trans. Microw. Theory Tech. 2020, 68, 3861–3871. [Google Scholar] [CrossRef]
- Nuss, B.; de Oliveira, L.G.; Zwick, T. Frequency Comb MIMO OFDM Radar With Nonequidistant Subcarrier Interleaving. IEEE Microw. Wirel. Components Lett. 2020, 30, 1209–1212. [Google Scholar] [CrossRef]
- Quan, Y.; Wu, Y.; Li, Y.; Sun, G.; Xing, M. Range–Doppler reconstruction for frequency agile and PRF-jittering radar. IET Radar Sonar Navig. 2018, 12, 348–352. [Google Scholar] [CrossRef]
- Huang, P.; Dong, S.; Liu, X.; Jiang, X.; Liao, G.; Xu, H.; Sun, S. A Coherent Integration Method for Moving Target Detection Using Frequency Agile Radar. IEEE Geosci. Remote Sens. Lett. 2019, 16, 206–210. [Google Scholar] [CrossRef]
- Huang, T.; Liu, Y.; Xu, X.; Eldar, Y.C.; Wang, X. Analysis of Frequency Agile Radar via Compressed Sensing. IEEE Trans. Signal Process. 2018, 66, 6228–6240. [Google Scholar] [CrossRef] [Green Version]
- Lellouch, G.; Pribic, R.; van Genderen, P. OFDM waveforms for frequency agility and opportunities for Doppler processing in radar. In Proceedings of the 2008 IEEE Radar Conference, Rome, Italy, 26–30 May 2008; pp. 1–6. [Google Scholar] [CrossRef]
- Lellouch, G.; Pribic, R.; van Genderen, P. Frequency agile stepped OFDM waveform for HRR. In Proceedings of the 2009 International Waveform Diversity and Design Conference, Kissimmee, FL, USA, 8–13 February 2009; pp. 90–93. [Google Scholar] [CrossRef]
- Long, X.; Li, K.; Tian, J.; Wang, J.; Wu, S. Ambiguity Function Analysis of Random Frequency and PRI Agile Signals. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 382–396. [Google Scholar] [CrossRef]
- Knill, C.; Schweizer, B.; Sparrer, S.; Roos, F.; Fischer, R.F.H.; Waldschmidt, C. High Range and Doppler Resolution by Application of Compressed Sensing Using Low Baseband Bandwidth OFDM Radar. IEEE Trans. Microw. Theory Tech. 2018, 66, 3535–3546. [Google Scholar] [CrossRef] [Green Version]
- Knill, C.; Schweizer, B.; Stephany, S.; Werbunat, D.; Waldschmidt, C. FMCW-Interference of Frequency Agile OFDM Radars. In Proceedings of the 2020 17th European Radar Conference (EuRAD), Utrecht, The Netherlands, 10–15 January 2021; pp. 160–163. [Google Scholar] [CrossRef]
- Knill, C.; Schweizer, B.; Waldschmidt, C. Interference-Robust Processing of OFDM Radar Signals Using Compressed Sensing. IEEE Sens. Lett. 2020, 4, 1–4. [Google Scholar] [CrossRef]
- Rida, I.; Al-Maadeed, S.; Mahmood, A.; Bouridane, A.; Bakshi, S. Palmprint Identification Using an Ensemble of Sparse Representations. IEEE Access 2018, 6, 3241–3248. [Google Scholar] [CrossRef]
- Schmidt, R. Multiple emitter location and signal parameter estimation. IEEE Trans. Antennas Propag. 1986, 34, 276–280. [Google Scholar] [CrossRef] [Green Version]
- Cheng, F.; He, Z.; Liu, H.; Li, J. The parameter setting problem of signal OFDM-LFM for MIMO radar. In Proceedings of the 2008 International Conference on Communications, Circuits and Systems, Xiamen, China, 25–27 May 2008; pp. 876–880. [Google Scholar] [CrossRef]
- Lord, R.; Inggs, M. High range resolution radar using narrowband linear chirps offset in frequency. In Proceedings of the 1997 South African Symposium on Communications and Signal Processing, COMSIG ’97, Grahamstown, South Africa, 9–10 September 1997; pp. 9–12. [Google Scholar] [CrossRef]
- Li, Y.; Huang, T.; Xu, X.; Liu, Y.; Wang, L.; Eldar, Y.C. Phase Transitions in Frequency Agile Radar Using Compressed Sensing. IEEE Trans. Signal Process. 2021, 69, 4801–4818. [Google Scholar] [CrossRef]
- Zoltowski, M. Synthesis of sum and difference patterns possessing common nulls for monopulse bearing estimation with line arrays. IEEE Trans. Antennas Propag. 1992, 40, 25–37. [Google Scholar] [CrossRef]
- Friedlander, B. A sensitivity analysis of the MUSIC algorithm. IEEE Trans. Acoust. Speech Signal Process. 1990, 38, 1740–1751. [Google Scholar] [CrossRef]
- Kay, S.M. Fundamentals of Statistical Signal Processing: Estimation and Detection Theory; PRT Prentice Hall: Englewood Cliffs, NJ, USA, 1993. [Google Scholar]
- Trees, H.L.V. Optimum Array Processing: Part IV of Detection, Estimation, and Modulation Theory; Wiley: Hoboken, NJ, USA, 2004. [Google Scholar]


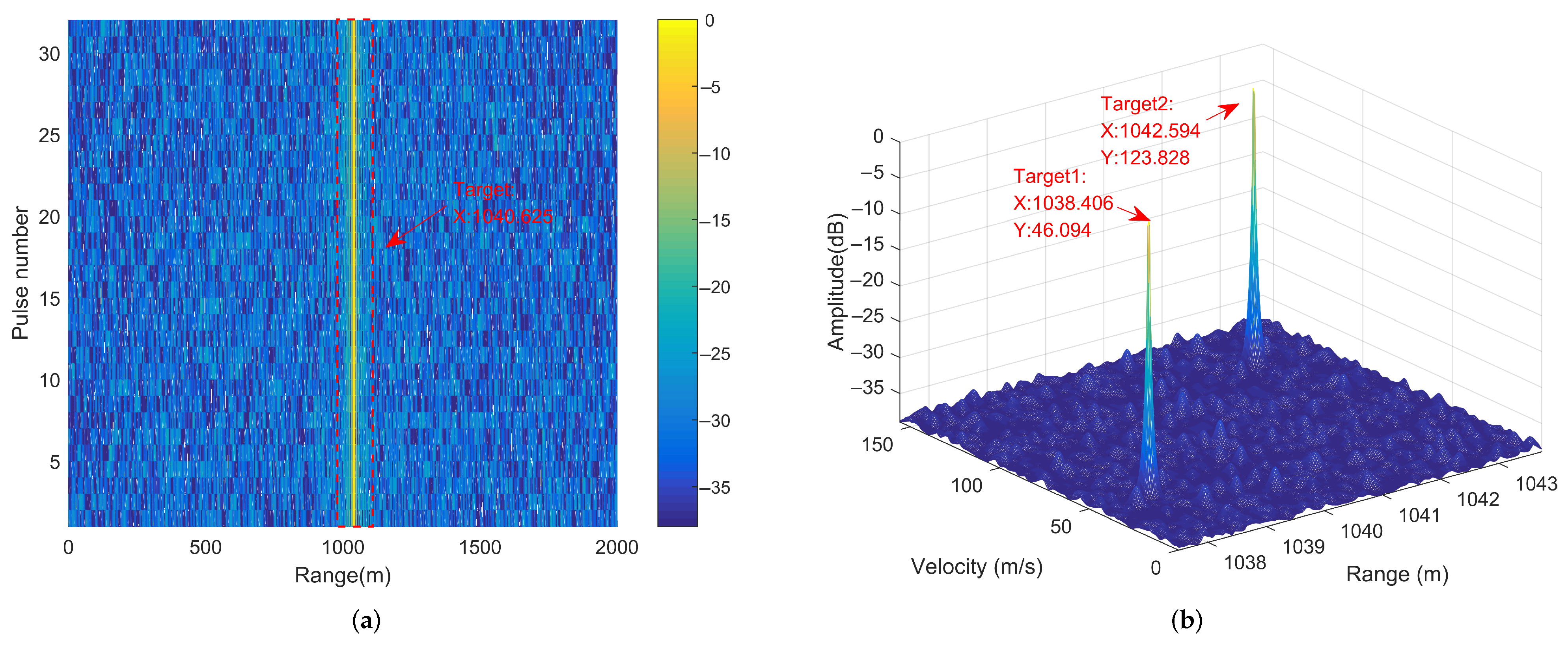
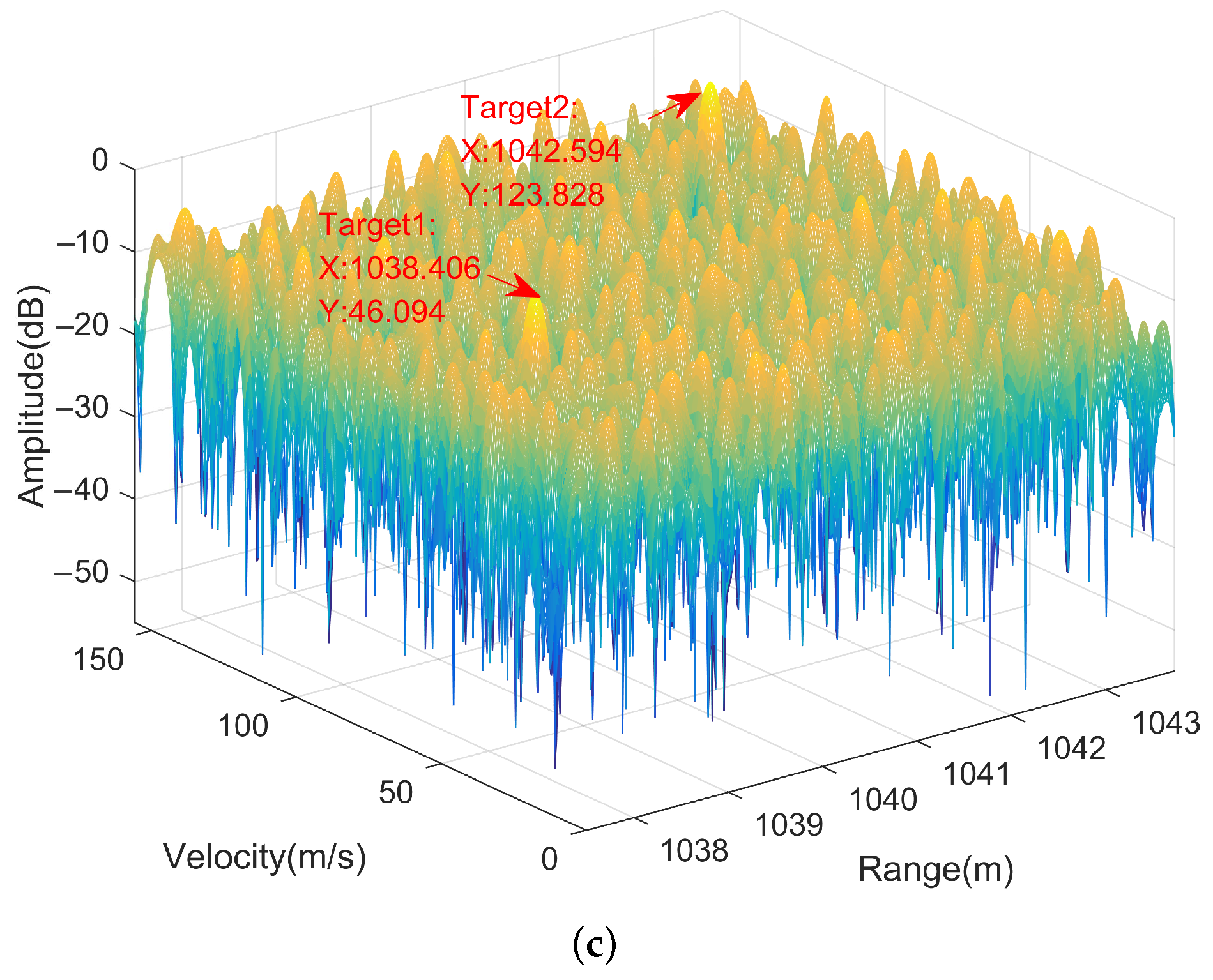
| Parameter (Unit) | Symbol | Value |
|---|---|---|
| Number of subcarriers | K | 4 |
| Number of pulses | M | 32 |
| Total number of available frequencies | N | 40 |
| Pulse width (us) | 4 | |
| Pulse repetition interval (us) | 40 | |
| Subcarrier bandwidth (MHz) | 6 | |
| Frequency hopping interval (MHz) | B | 24 |
| Chirp rate (MHz/us) | 1.5 | |
| Lowest carrier frequency (GHz) | 24 | |
| Sample rate (MHz) | 24 |
| Target | Range (Unit) | Velocity (Unit) |
|---|---|---|
| Target1 | 1038.4 m | 46 m/s |
| Target2 | 1042.6 m | 124 m/s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Quan, Y.; Wu, Y.; Xing, M. Super-Resolution Range and Velocity Estimations for SFA-OFDM Radar. Remote Sens. 2022, 14, 278. https://doi.org/10.3390/rs14020278
Liu Z, Quan Y, Wu Y, Xing M. Super-Resolution Range and Velocity Estimations for SFA-OFDM Radar. Remote Sensing. 2022; 14(2):278. https://doi.org/10.3390/rs14020278
Chicago/Turabian StyleLiu, Zhixing, Yinghui Quan, Yaojun Wu, and Mengdao Xing. 2022. "Super-Resolution Range and Velocity Estimations for SFA-OFDM Radar" Remote Sensing 14, no. 2: 278. https://doi.org/10.3390/rs14020278
APA StyleLiu, Z., Quan, Y., Wu, Y., & Xing, M. (2022). Super-Resolution Range and Velocity Estimations for SFA-OFDM Radar. Remote Sensing, 14(2), 278. https://doi.org/10.3390/rs14020278







