Backscattering Analysis Utilizing Relaxed Hierarchical Equivalent Source Algorithm (RHESA) for Scatterers in Vegetation Medium
Abstract
1. Introduction
1.1. Analytical Method
1.2. RHESA
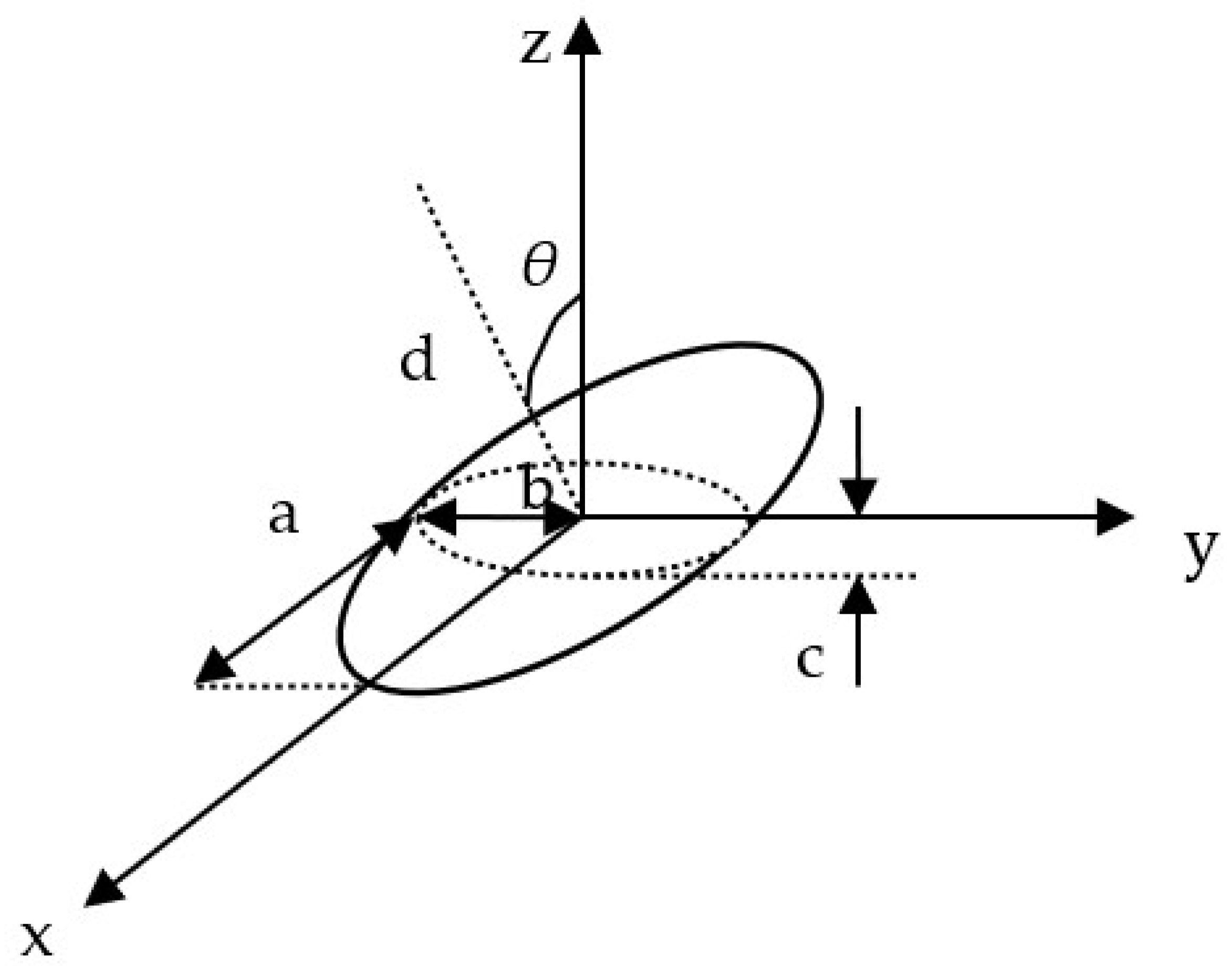
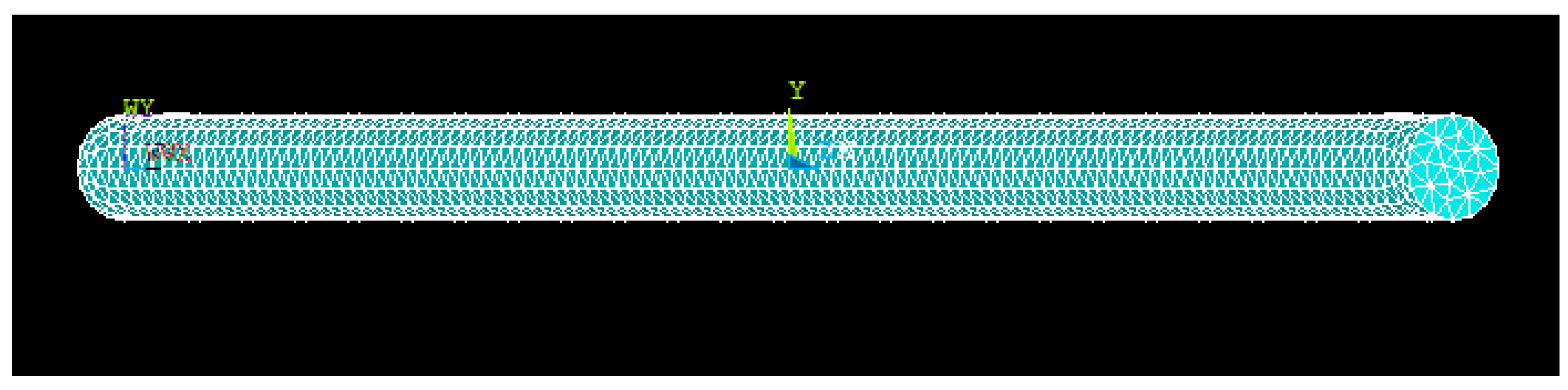
2. Methodology
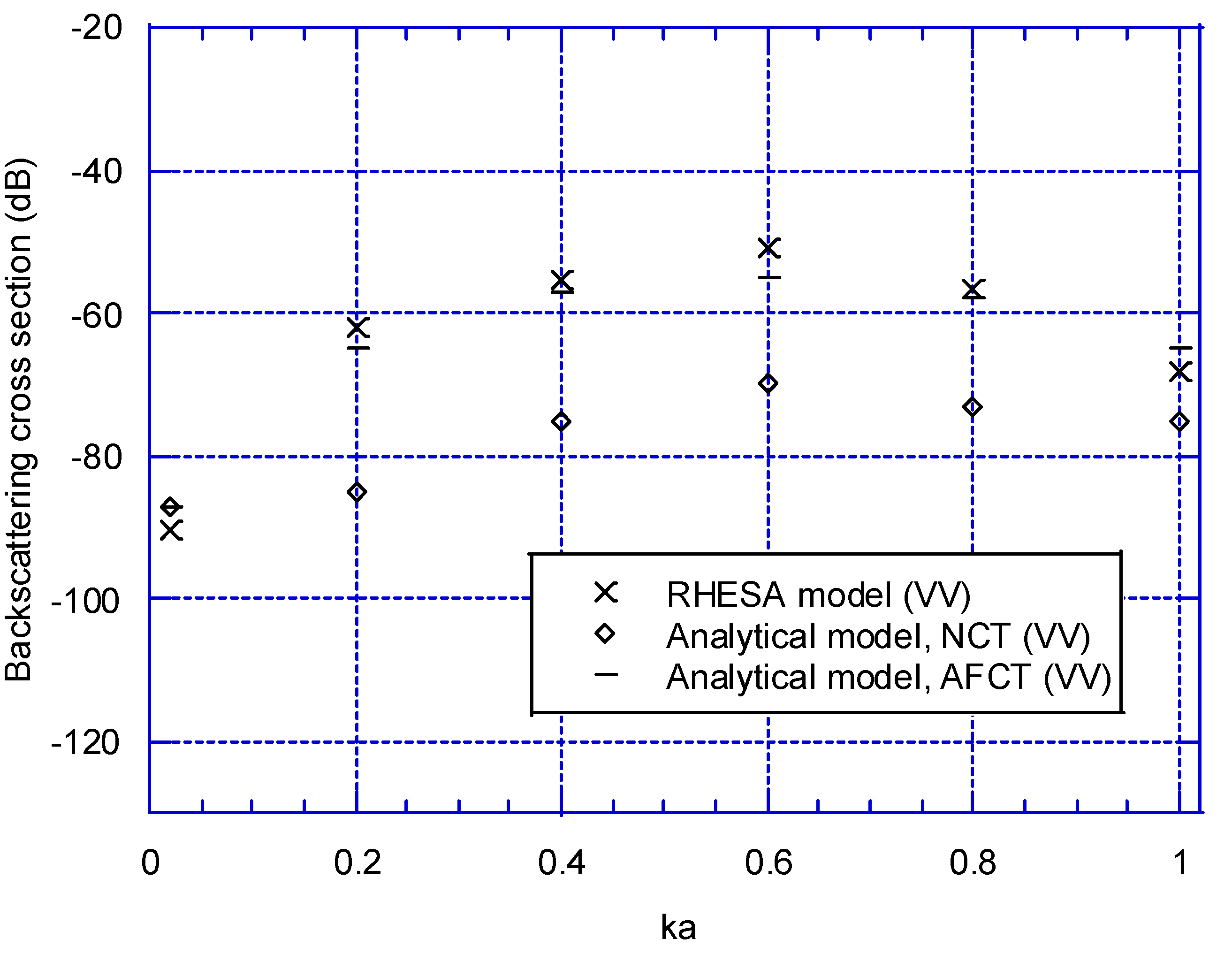
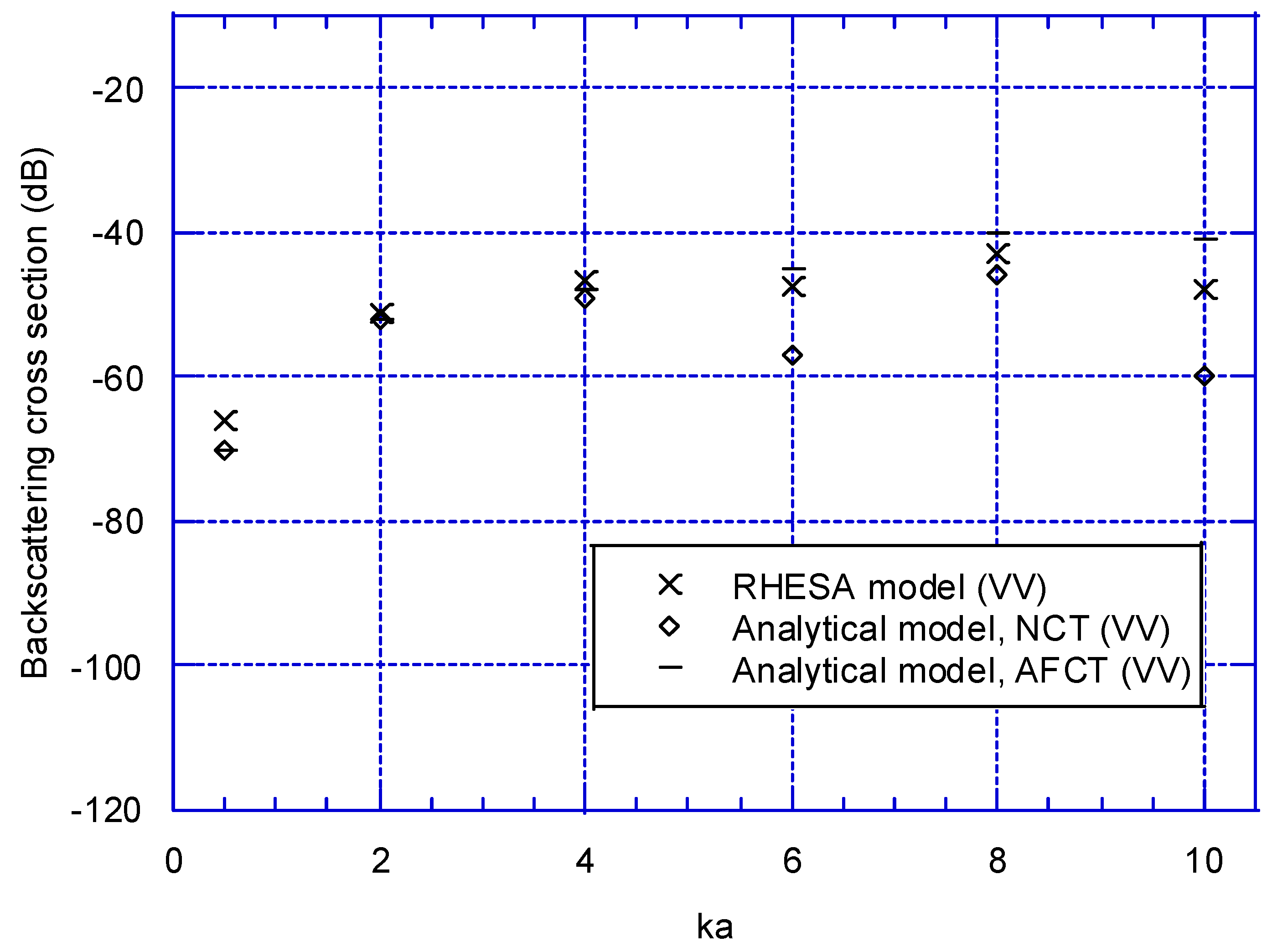
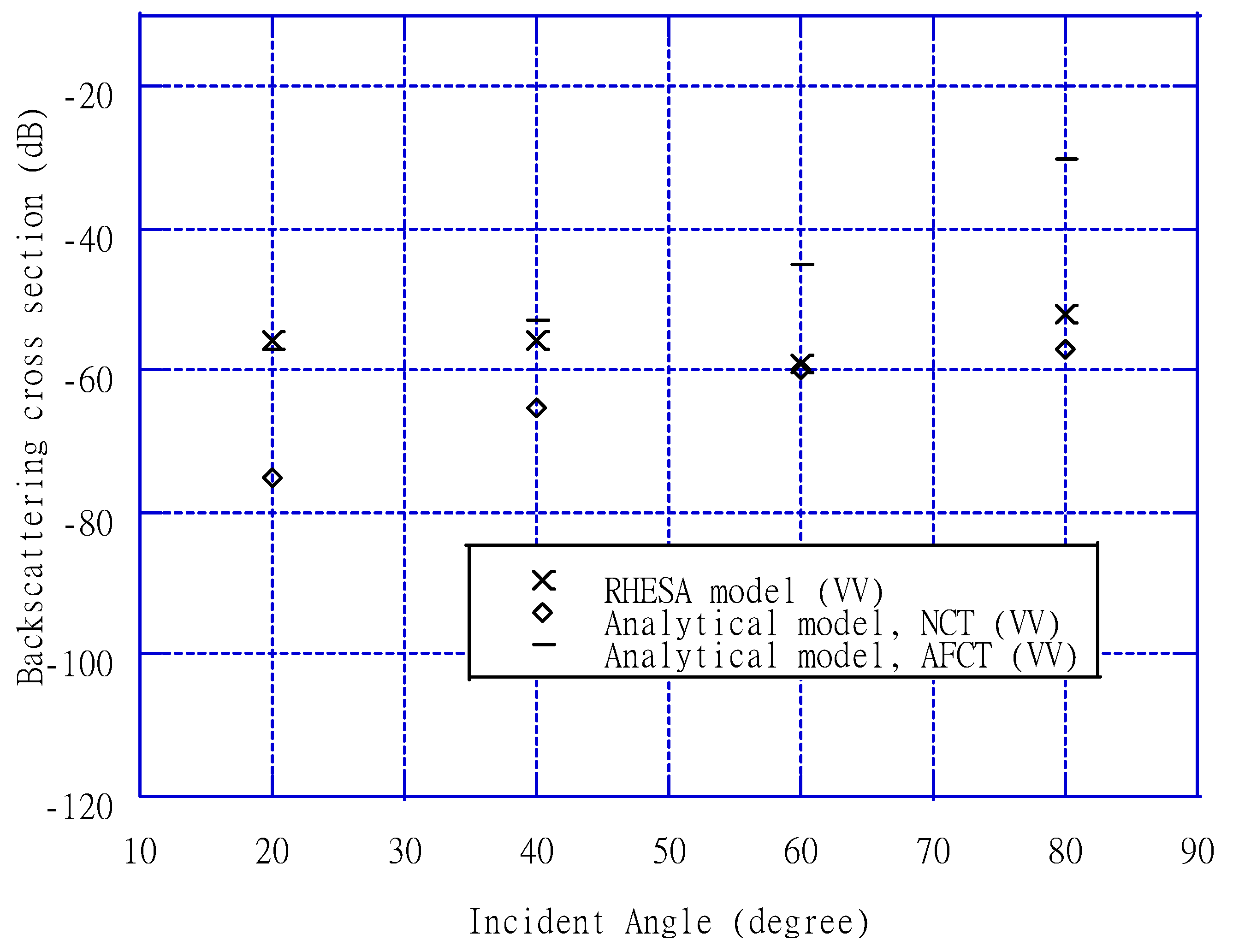
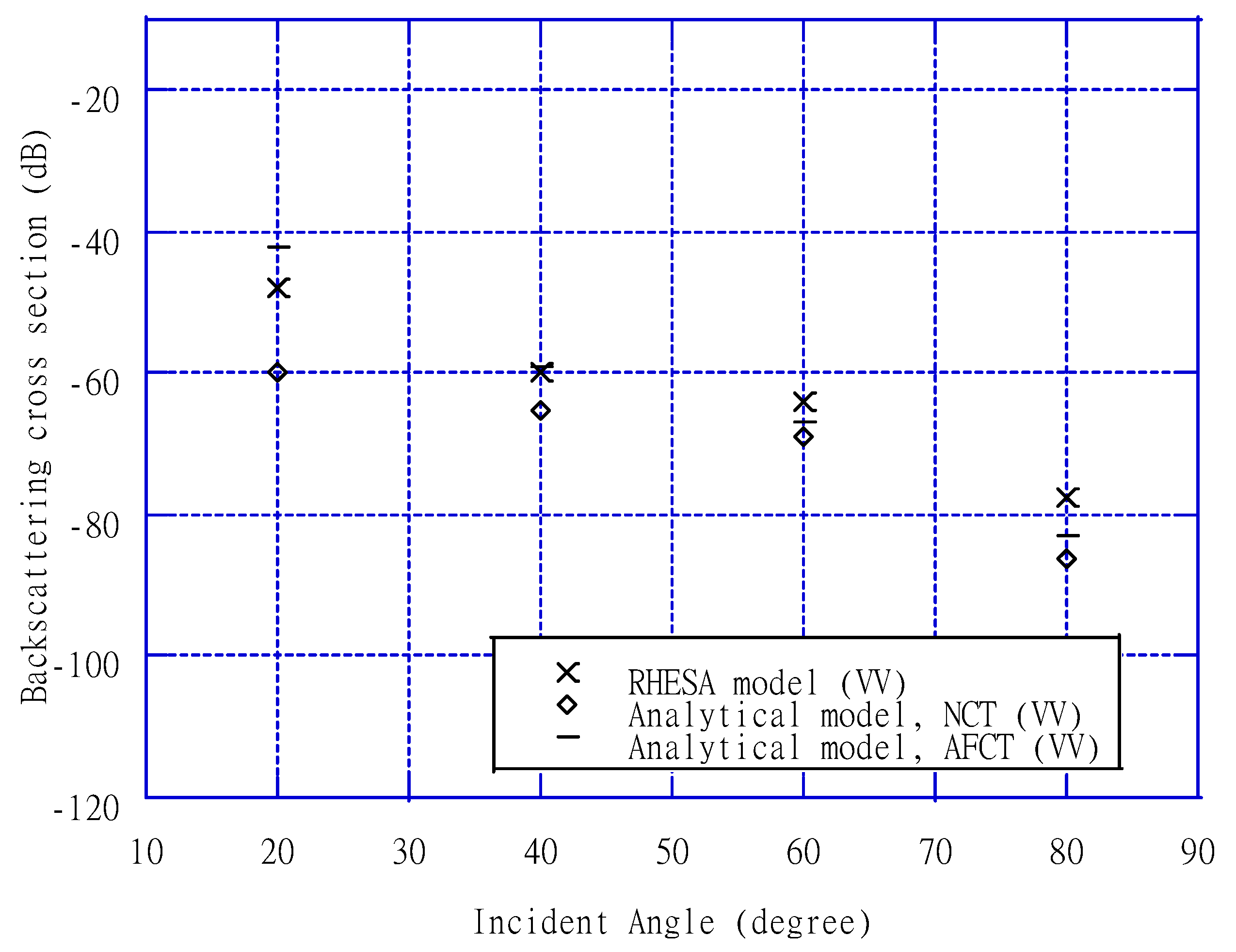
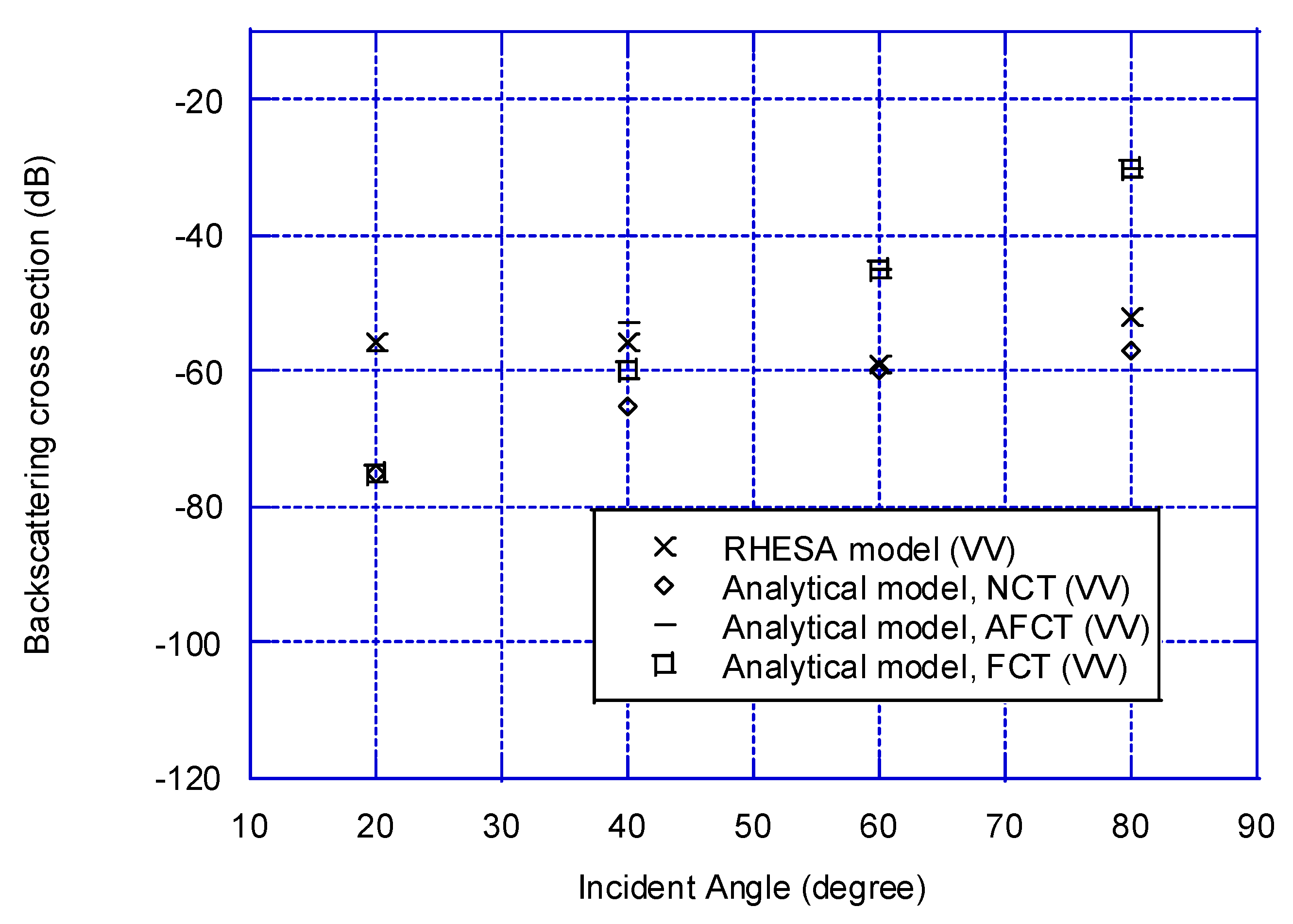
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ishimaru, A. Wave Propagation and Scattering in Random Media; Academic Press: New York, NY, USA, 1978; Volume 2. [Google Scholar]
- Ewe, H.T.; Chuah, H.T.; Fung, A.K. A backscatter model for a dense discrete medium: Analysis and numerical results. Remote Sens. Environ. 1998, 65, 195–203. [Google Scholar] [CrossRef]
- Ewe, H.T.; Chuah, H.T. A study of Fresnel scattered field for non-spherical discrete scatterers. Prog. Electromagn. Res. 2000, 25, 189–222. [Google Scholar] [CrossRef]
- Ao, C.O. Electromagnetic Wave Scattering by Discrete Random Media with Remote Sensing Applications. Ph.D. Thesis, University of California, Berkeley, CA, USA, 2001. [Google Scholar]
- Ewe, H.T. A Microwave Scattering Model for an Electrically Dense Discrete Random Medium. Ph.D. Thesis, Multimedia University, Cyberjaya, Malaysia, 1999. Unpublished doctoral dissertation. [Google Scholar]
- Wu, T.D.; Chen, K.S.; Shi, J.; Lee, H.W.; Fung, A.K. A study of an AIEM model for bistatic scattering from randomly rough surfaces. IEEE Trans. Geosci. Remote Sens. 2008, 46, 2584–2598. [Google Scholar]
- Syahali, S.; Ewe, H.T. Backscattering Analysis for Snow Remote Sensing Model with Higher Order of Surface-Volume Scattering. Prog. Electromagn. Res. M 2016, 48, 25–36. [Google Scholar] [CrossRef][Green Version]
- Syahali, S.; Ewe, H.T. Remote Sensing Backscattering Model for sea ice: Theoretical modelling and Analysis. Adv. Polar Sci. 2013, 24, 248–257. [Google Scholar]
- Eom, H.J.; Fung, A.K. A scatter model for vegetation up to Ku-band. Remote Sens. Environ. 1984, 15, 185–200. [Google Scholar] [CrossRef]
- Koay, J.Y.; Ewe, H.T.; Chuah, H.T. A Study of Fresnel Scattered Fields for Ellipsoidal and Elliptic-Disk-Shaped Scatterers. IEEE Trans. Geosci. Remote Sens. 2008, 46, 1091–1103. [Google Scholar] [CrossRef]
- Koay, J.Y.; Lee, Y.J.; Ewe HTAnd Chuah, H.T. Electromagnetic Wave Scattering in Dense Media: Applications in the Remote Sensing of Sea Ice and Vegetation. In Electromagnetic Scattering: A Remote Sensing Perspective; WSPC: Singapore, 2017; pp. 303–339. [Google Scholar]
- Toh, C.M.; Ewe, H.T.; Tey, S.H.; Tay, Y.H. A Study on Oil Palm Remote Sensing at L-Band with Dense Medium Microwave Backscattering Model. IEEE Trans. Geosci. Remote Sens. 2019, 57, 8037–8047. [Google Scholar] [CrossRef]
- Li, M.; Chew, W.C. Wave-Field Interaction with Complex Structures. IEEE Trans. Antennas Propag. 2007, 55, 130–138. [Google Scholar] [CrossRef]
- Velamparambil, S.; Chew, W.C.; Song, J. 10 Million Unknowns: Is It That Big? IEEE Antennas Progation Mag. 2003, 45, 43–58. [Google Scholar] [CrossRef]
- Sumithra, P.; Thiripurasundari, D. Review on Computational Electromagnetics. Adv. Electromagn. 2017, 6, 42. [Google Scholar] [CrossRef]
- Lum, C.F.; Fu, X.; Ewe, H.T.; Jiang, L.J. A study of scattering from snow embedded with non-spherical shapes of scatterers with Relaxed Hierarchical Equivalent Source Algorithm (RHESA). Prog. Electromagn. Res. M 2017, 61, 51–60. [Google Scholar] [CrossRef][Green Version]
- Lum, C.F.; Ewe, H.T.; Xin, F.; Jiang, L.J.; Chuah, H.T. An analysis of scattering from snow with relaxed hierachical equivalent source algorithm. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1434–1437. [Google Scholar]
- Lum, C.F.; Fu, X.; Ewe, H.T.; Jiang, L.J. A Study of Scattering from a Layer of Random Discrete Medium with Hierarchical Equivalent Source Algorithm (HESA). In Proceedings of the Progress in Electromagnetic Research Symposium (PIERS), Shanghai, China, 8–11 August 2016. [Google Scholar]
- Kumaresan, H.A.; Ewe, H.T.; Vetharatnam, G.; Jiang, L.-J. Model Computation with Second-Order Radiative Transfer Equation for Snow Medium Using Coupled Finite Element Method and Method of Moment and Relaxed Hierarchical Equivalent Source Algorithm. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021; pp. 1417–1420. [Google Scholar]
- Fu, X.; Jiang, L.J.; Ewe, H.T. A novel relaxed hierarchical equivalent source algorithm (RHESA) for electromagnetic scattering analysis of dielectric objects. J. Electromagn. Waves Appl. 2016, 30, 1631–1642. [Google Scholar] [CrossRef]
- Chandrasekhar, S. Radiative Transfer; Dover: New York, NY, USA, 1960. [Google Scholar]
- Karam, M.A.; Fung, A.K. Leaf-shape effects in electromagnetic wave scattering from vegetation. IEEE Trans. Geosci. Remote Sens. 1989, 27, 687–697. [Google Scholar] [CrossRef]
- Fung, A.K. Microwave Scattering and Emission Models and Their Applications; Artech House: Norwood, MA, USA, 1994. [Google Scholar]
- Stratton, J.A. Electromagnetic Theory; McGraw-Hill: New York, NY, USA, 1941. [Google Scholar]
- Van de Hulst, H.C. Light Scattering by Small Particles; John Wiley and Sons: New York, NY, USA, 1957. [Google Scholar]
- Chuah, H.T.; Tjuatja, S.; Fung, A.K.; Bredow, J.W. A phase matrix for a dense discrete random medium: Evaluation of volume scattering coefficient. IEEE Trans. Geosci. Remote Sens. 1996, 34, 1137–1143. [Google Scholar] [CrossRef]
- Gibson, W.C. The Method of Moments in Electromagnetics; Taylor & Francis Group, LLC: Oxfordshire, UK, 2008. [Google Scholar]
- Jin, J.; Chew, W.C. Computational Electromagnetics: The Method of Moments; The Electrical Engineering Handbook; Elsevier Inc.: Amsterdam, The Netherlands, 2005. [Google Scholar]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Syahali, S.; Ewe, H.-T.; Vetharatnam, G.; Jiang, L.-J. Backscattering Analysis Utilizing Relaxed Hierarchical Equivalent Source Algorithm (RHESA) for Scatterers in Vegetation Medium. Remote Sens. 2022, 14, 5051. https://doi.org/10.3390/rs14195051
Syahali S, Ewe H-T, Vetharatnam G, Jiang L-J. Backscattering Analysis Utilizing Relaxed Hierarchical Equivalent Source Algorithm (RHESA) for Scatterers in Vegetation Medium. Remote Sensing. 2022; 14(19):5051. https://doi.org/10.3390/rs14195051
Chicago/Turabian StyleSyahali, Syabeela, Hong-Tat Ewe, Gobi Vetharatnam, and Li-Jun Jiang. 2022. "Backscattering Analysis Utilizing Relaxed Hierarchical Equivalent Source Algorithm (RHESA) for Scatterers in Vegetation Medium" Remote Sensing 14, no. 19: 5051. https://doi.org/10.3390/rs14195051
APA StyleSyahali, S., Ewe, H.-T., Vetharatnam, G., & Jiang, L.-J. (2022). Backscattering Analysis Utilizing Relaxed Hierarchical Equivalent Source Algorithm (RHESA) for Scatterers in Vegetation Medium. Remote Sensing, 14(19), 5051. https://doi.org/10.3390/rs14195051










