Understanding Intensity–Duration–Frequency (IDF) Curves Using IMERG Sub-Hourly Precipitation against Dense Gauge Networks
Abstract
1. Introduction
- How different are the IMERG AMS and the gauge-based AMS?
- How does areal averaging before the AMS (AB-AMS) and after the AMS (AA-AMS) affect the precipitation AMS?
- Which CDF fits the IMERG AMS better?
- What is the performance of IMERG IDF curves at grid and local scales?
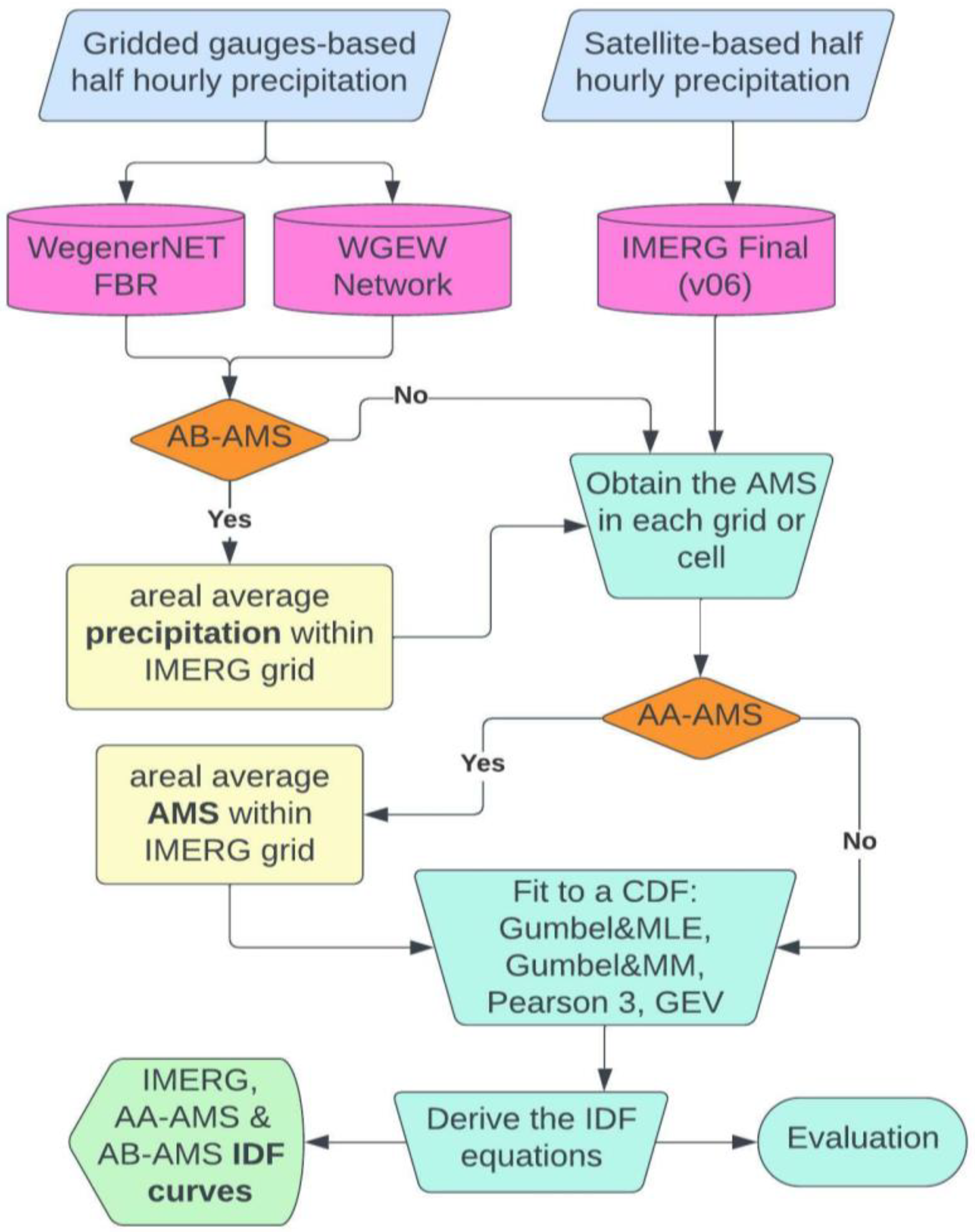
2. Materials and Methods
2.1. Data
2.1.1. Integrated Multi-SatellitE Retrievals for GPM (IMERG)
2.1.2. WegenerNet Feldbach Region (FBR) Network
2.1.3. Walnut Gulch Experimental Watershed (WGEW) Network
2.2. Matching the IMERG Grid to Gauge Cells
2.3. Obtain the Annual Maximum Series (AMS)
2.4. Compute the Intensity
2.5. Frequency Analysis: Fitting a PDF to the AMS
2.6. Regression Model: Derive the IDF Equation
2.7. Metrics for Evaluation
2.7.1. Grid-Scale Performance
2.7.2. Local-Scale Performance
3. Results and Discussion
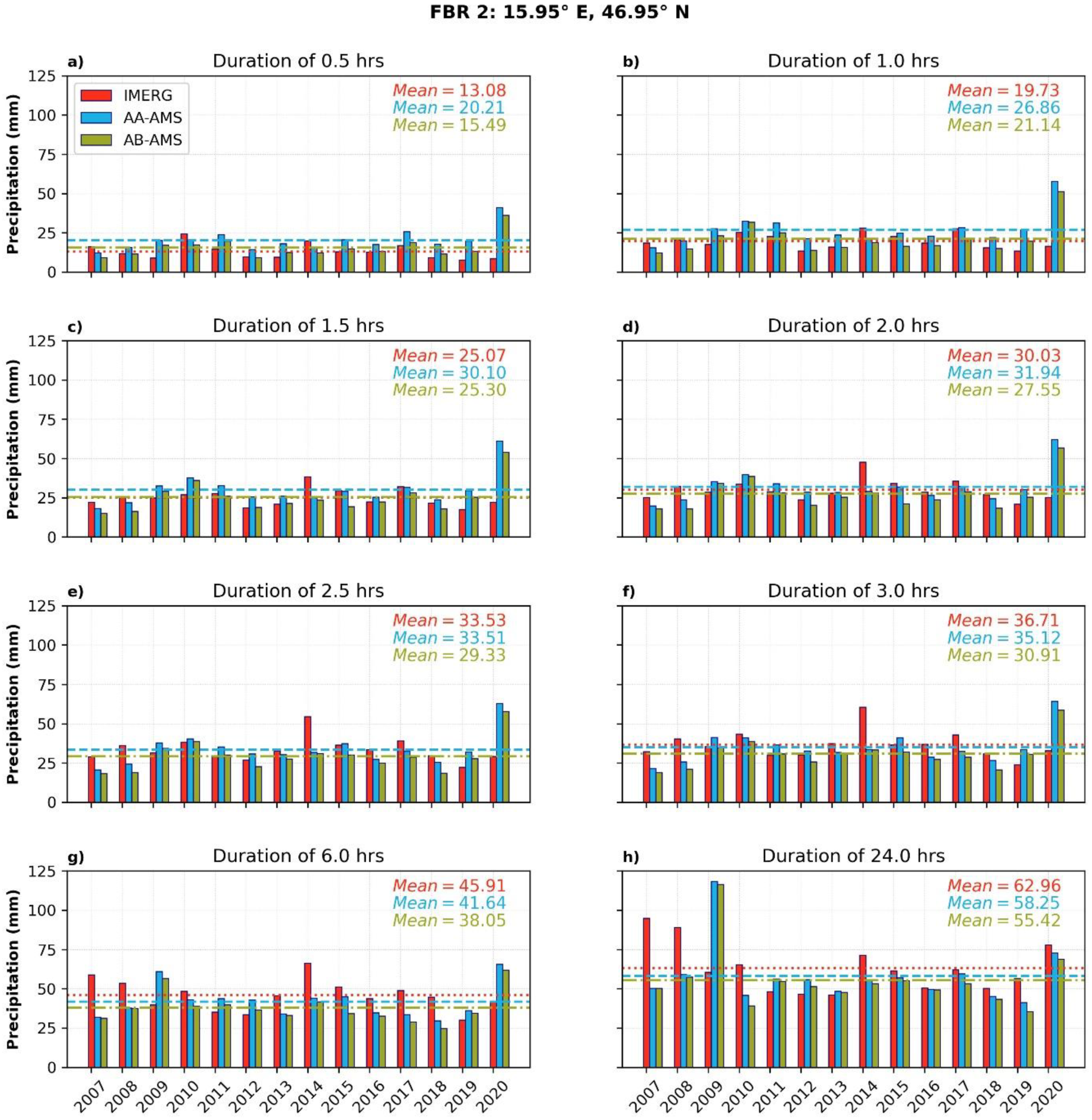
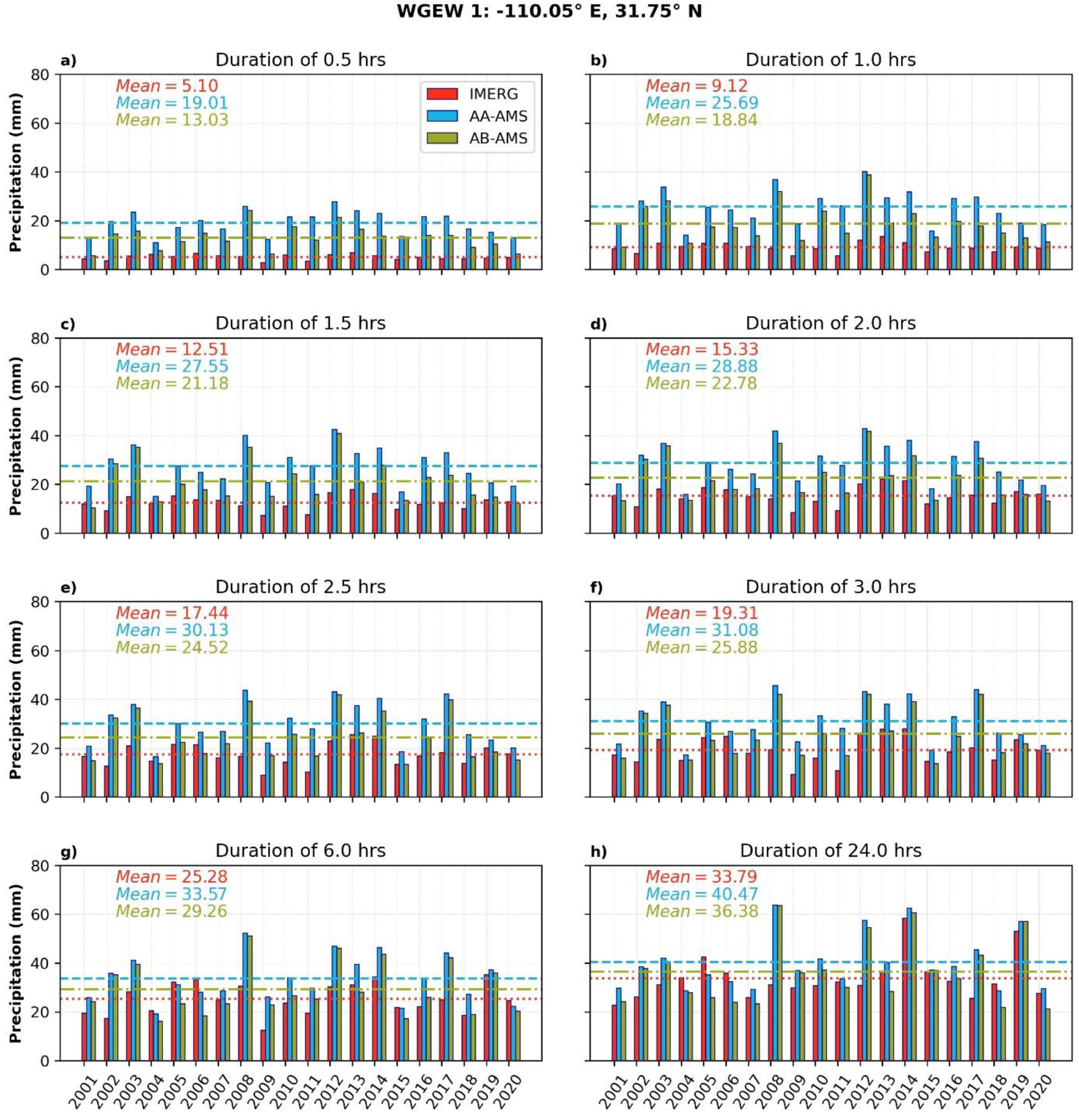
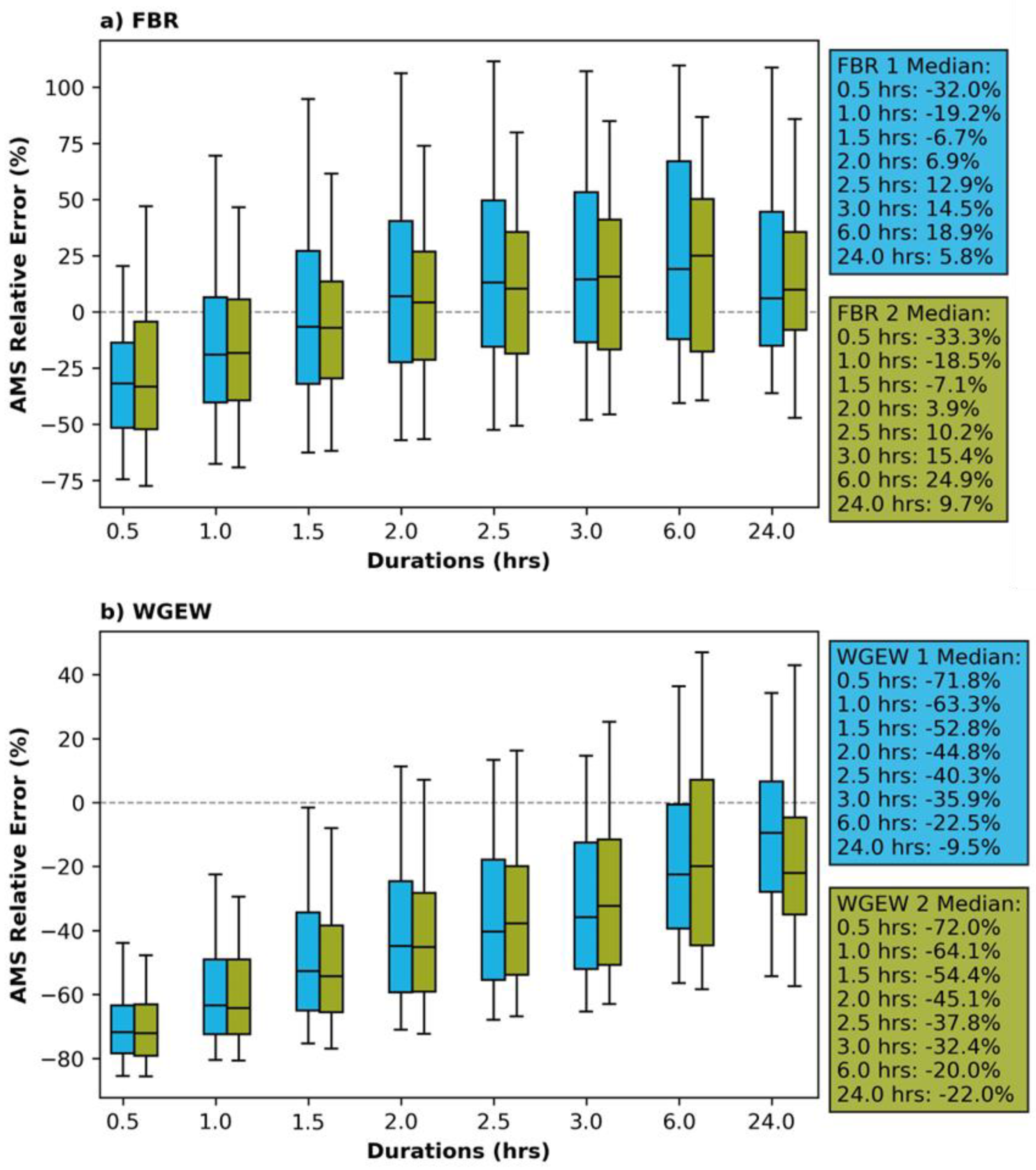
3.1. Statistical Comparison between the IMERG AMS and the Gauge-Based AMS
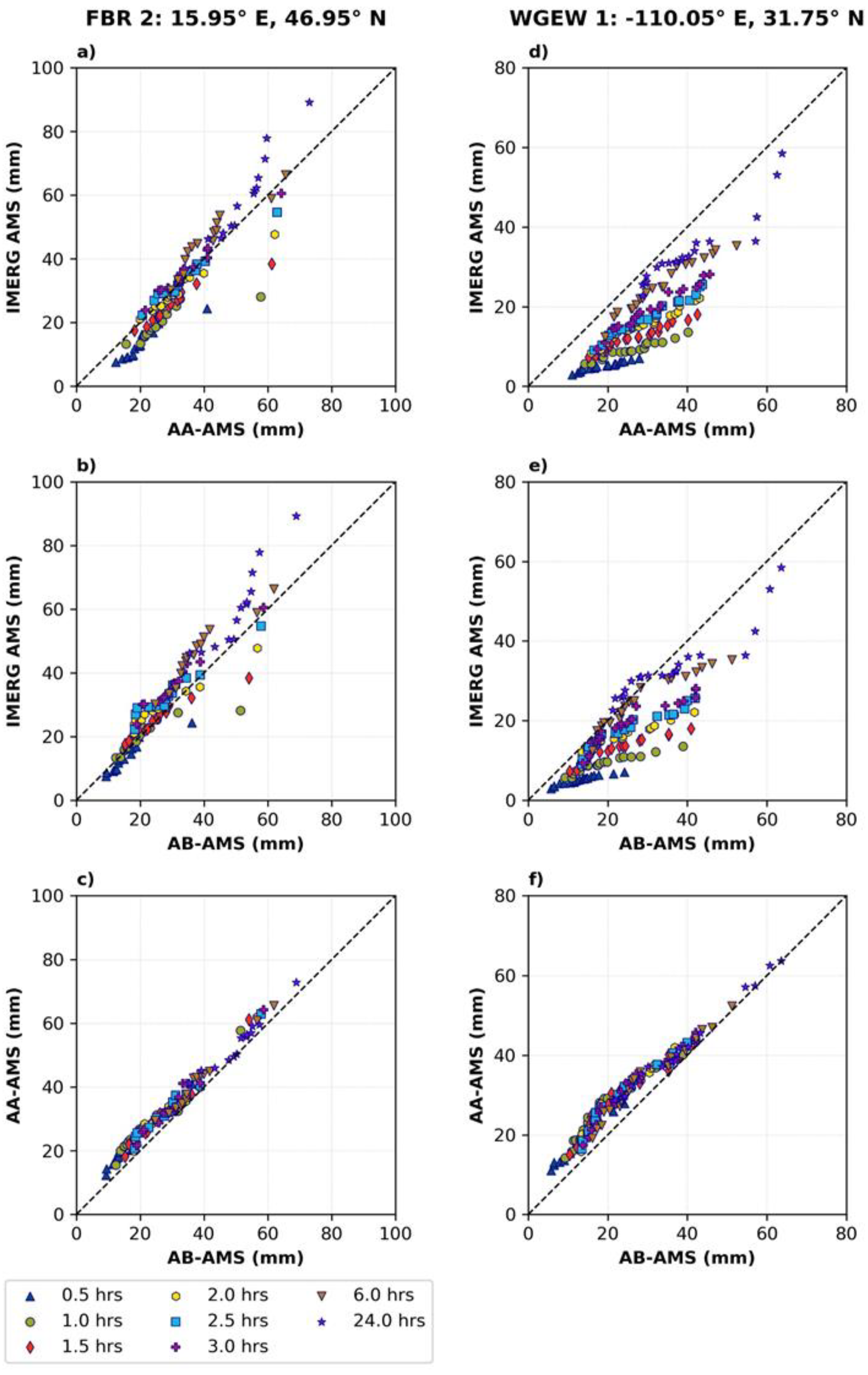
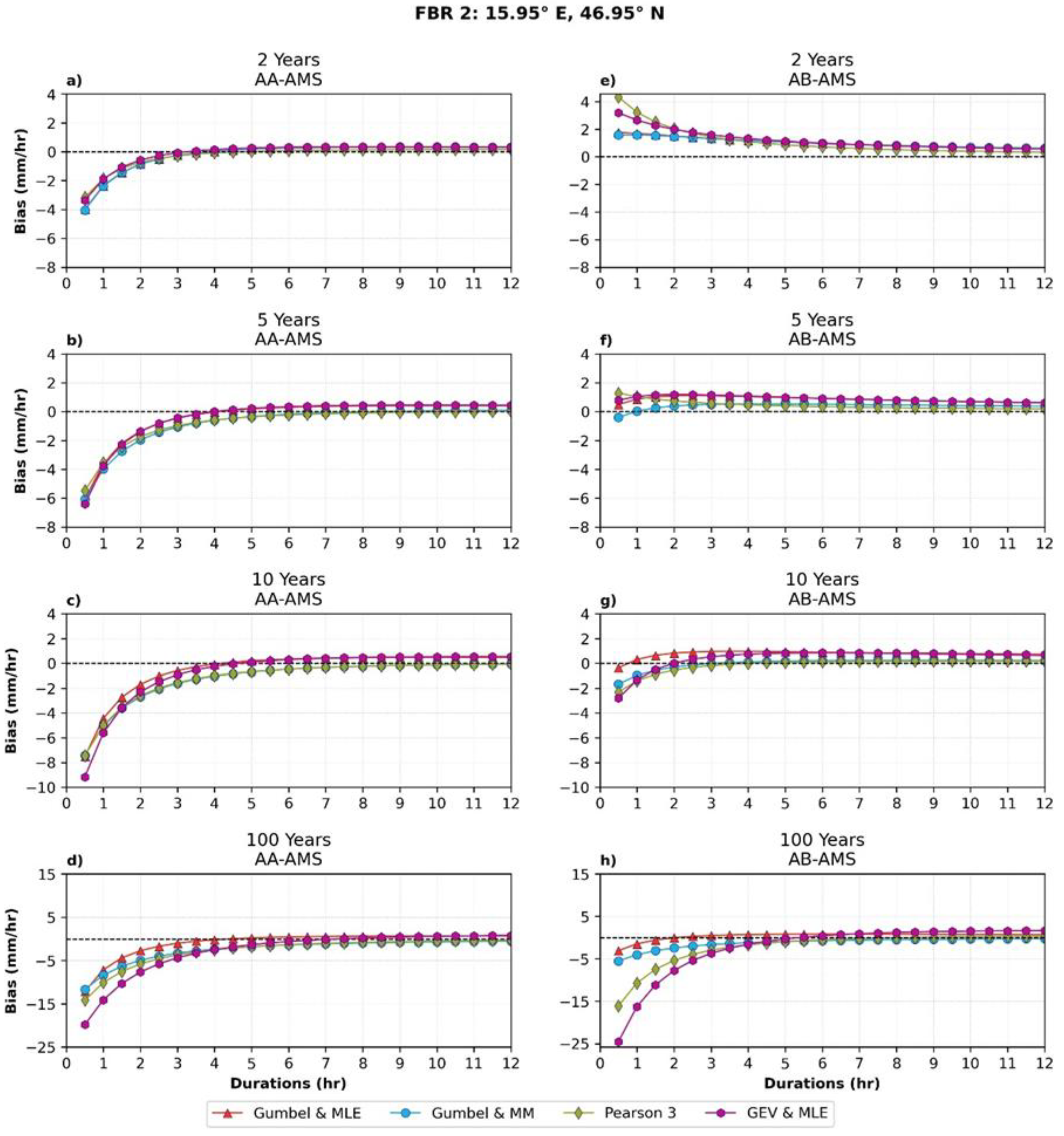
3.2. AA-AMS versus AB-AMS
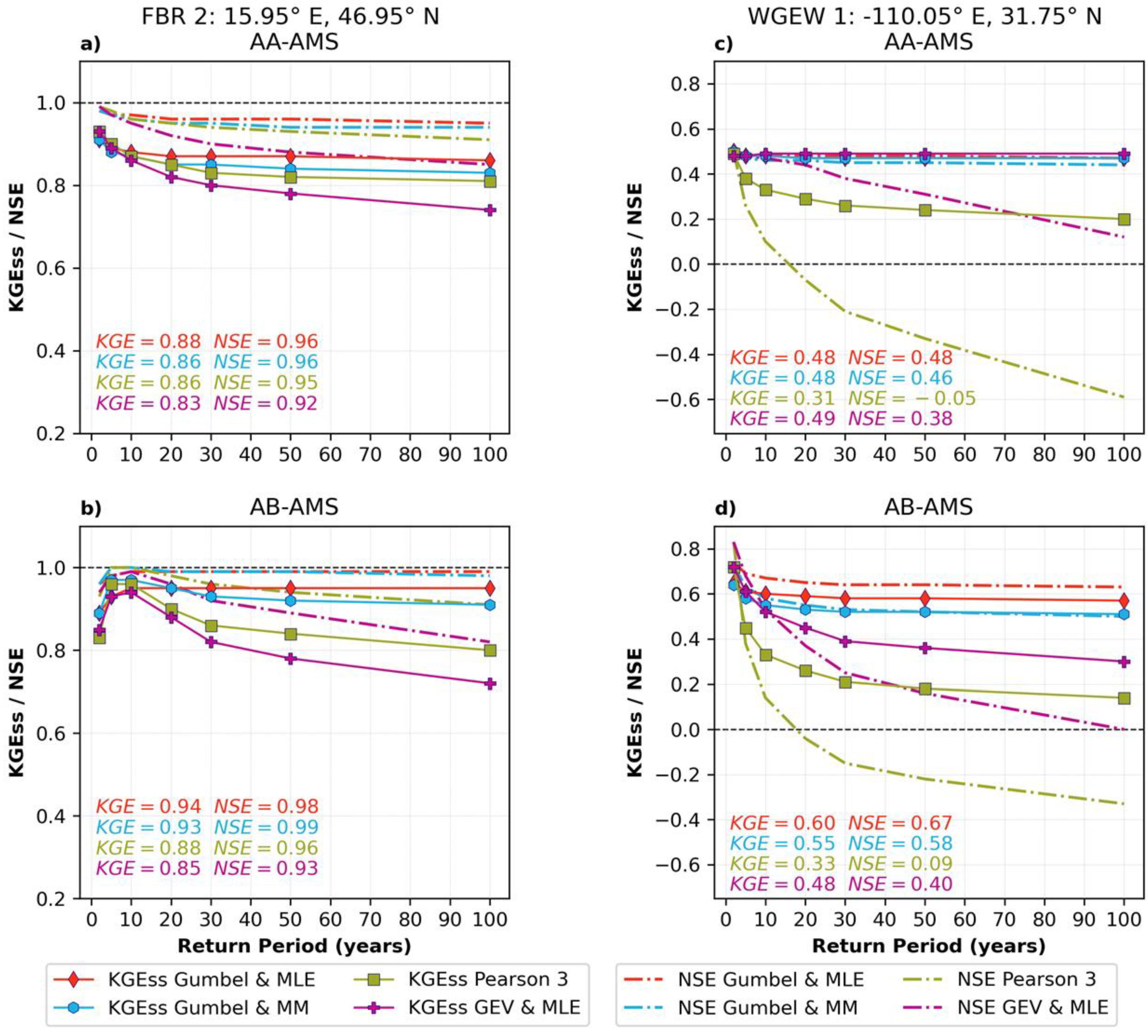
3.3. CDF Goodness of Fit
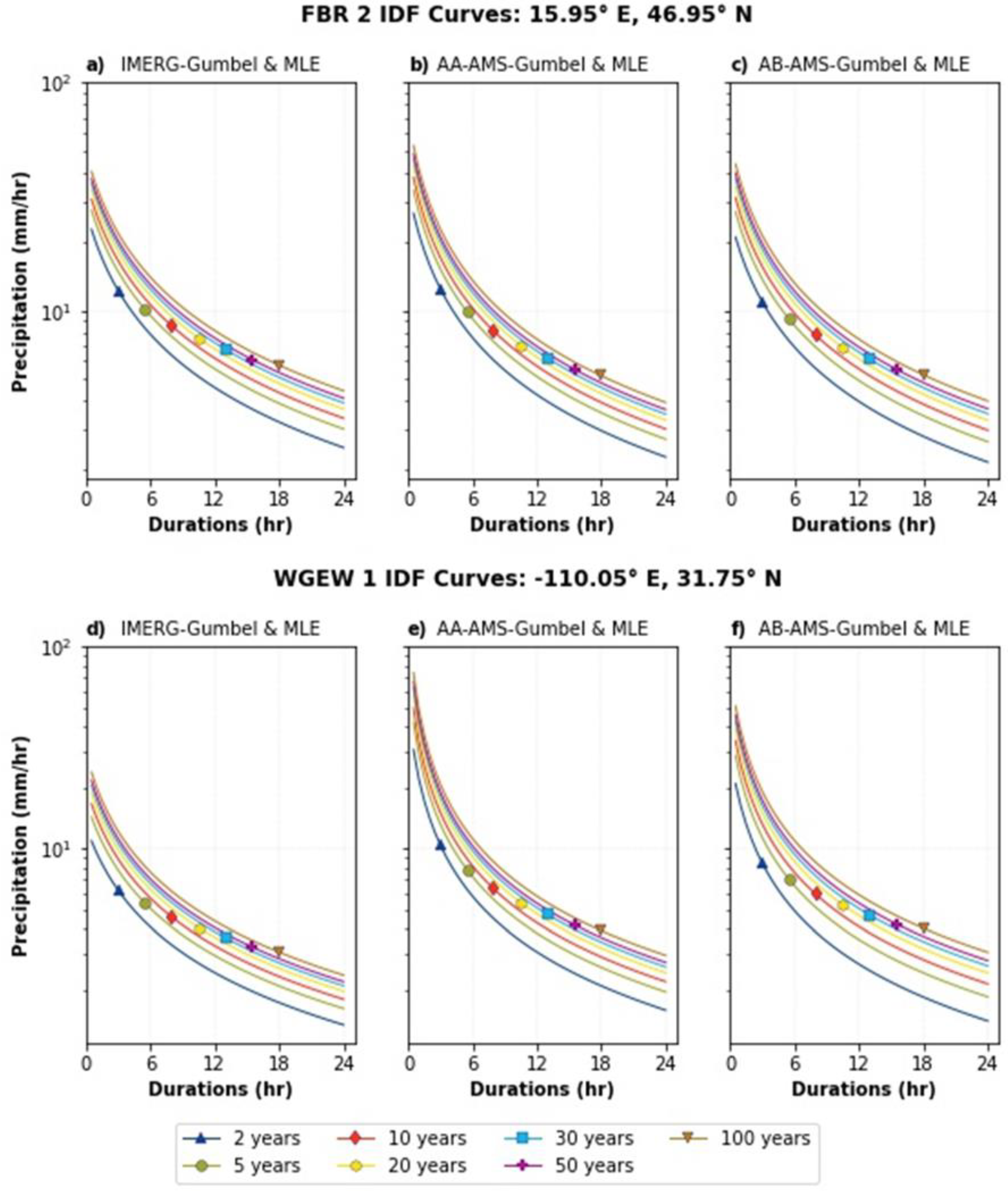
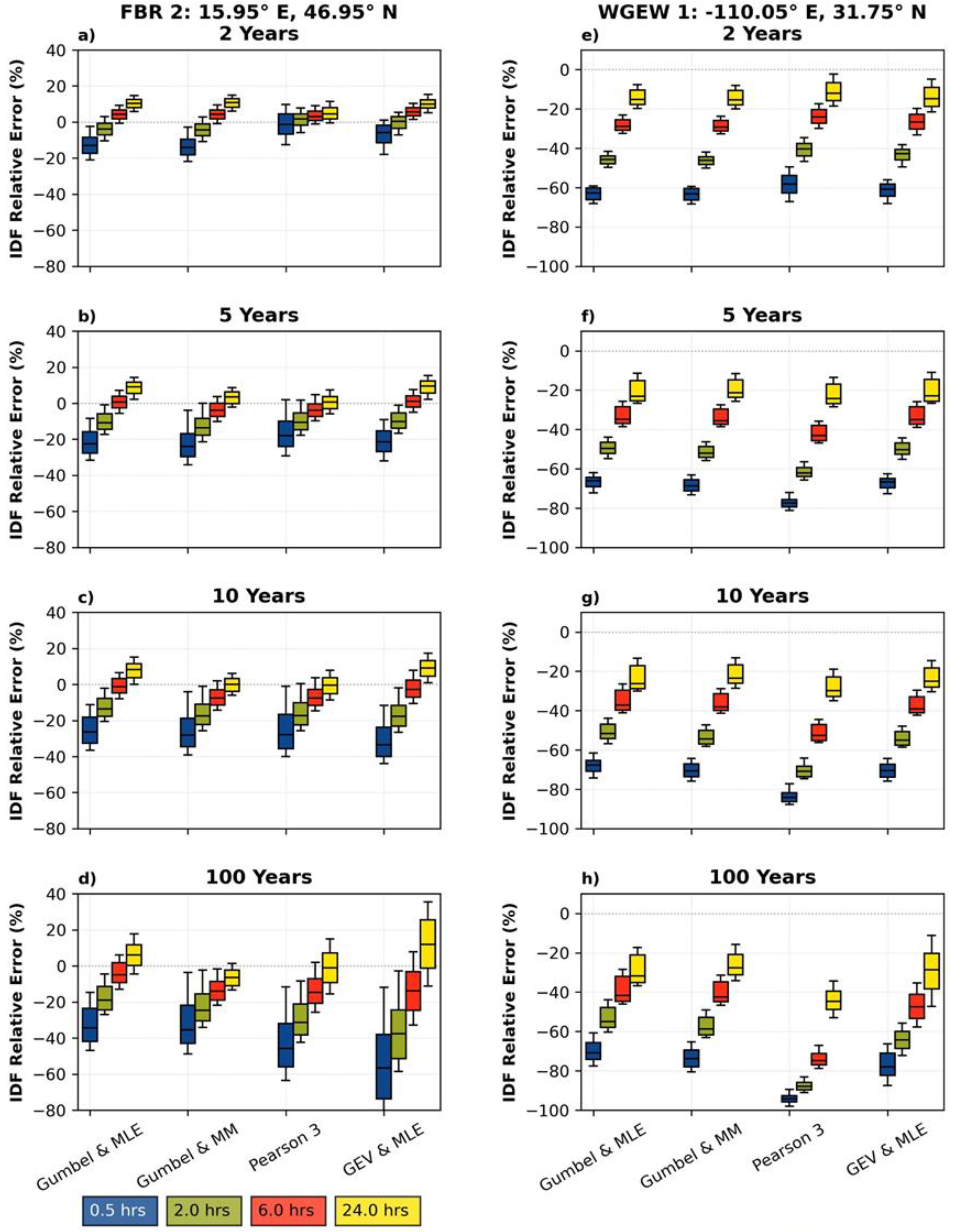
3.4. Grid-Scale: Performance of the IMERG IDF Equations
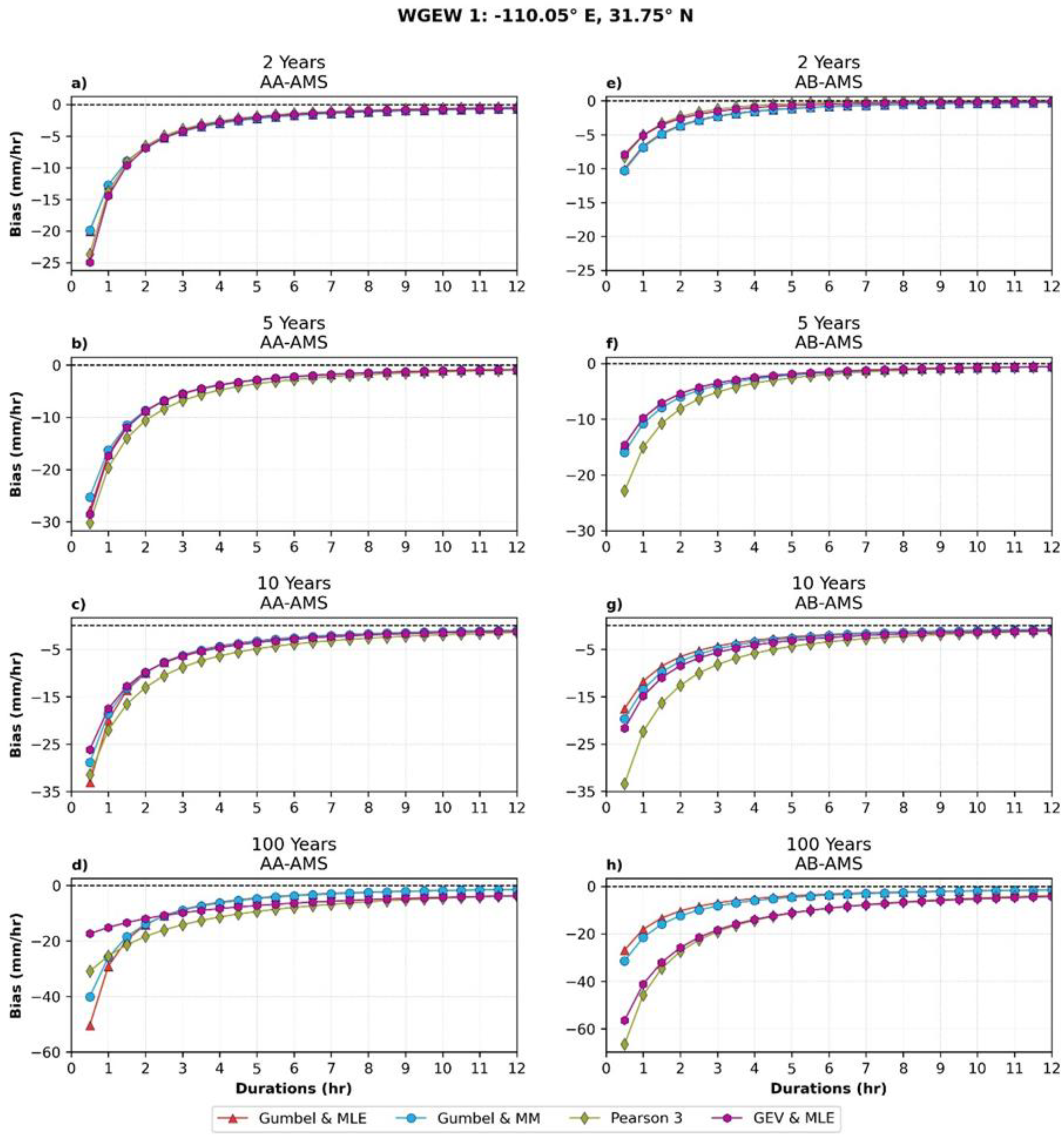
3.5. Assessment of IMERG AMSs and IDF Equations at Local Scale
3.6. IDF Relationships under Climate Change
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Statistical Comparison between the IMERG AMS and the Gauge-Based AMS
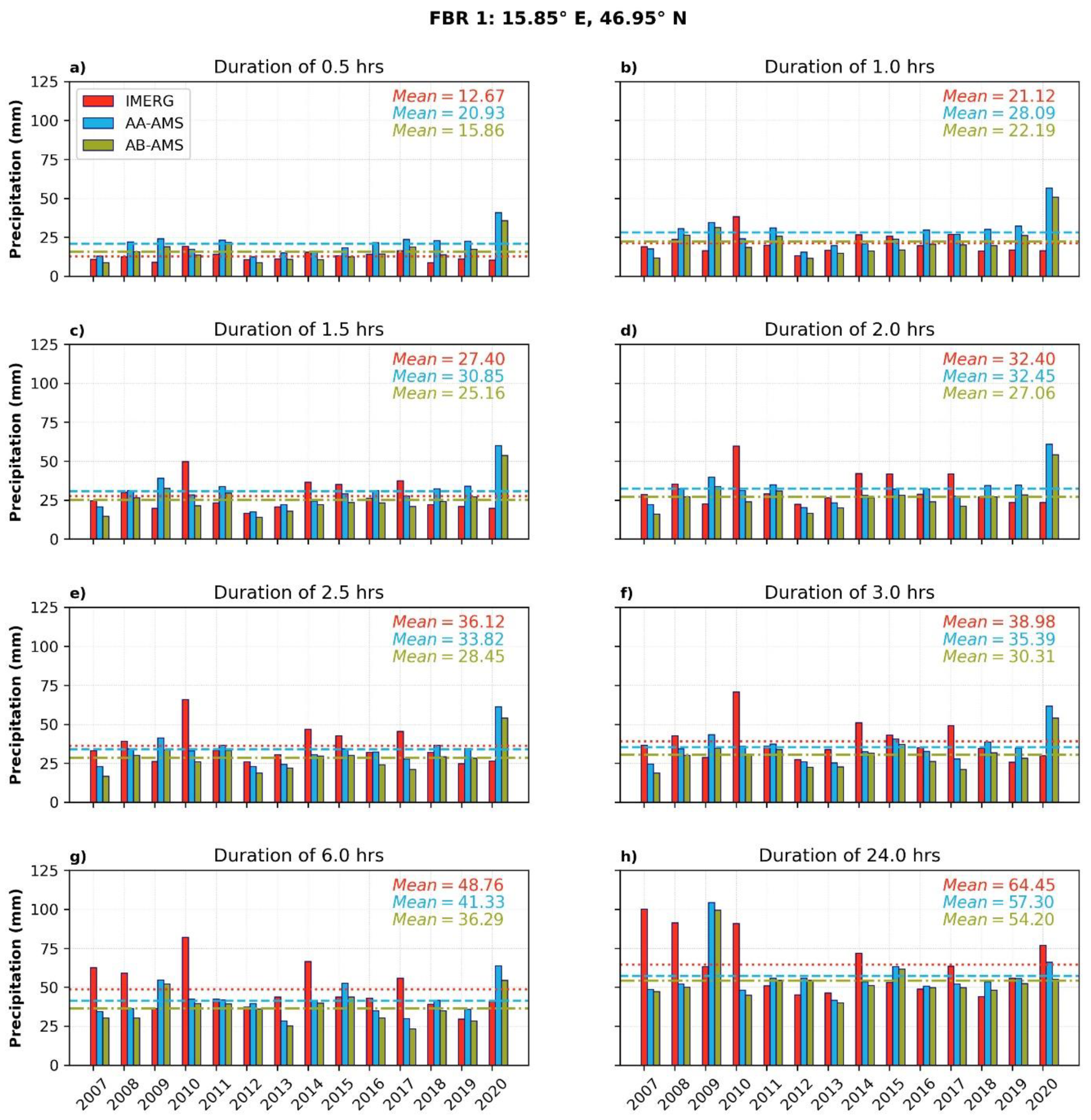
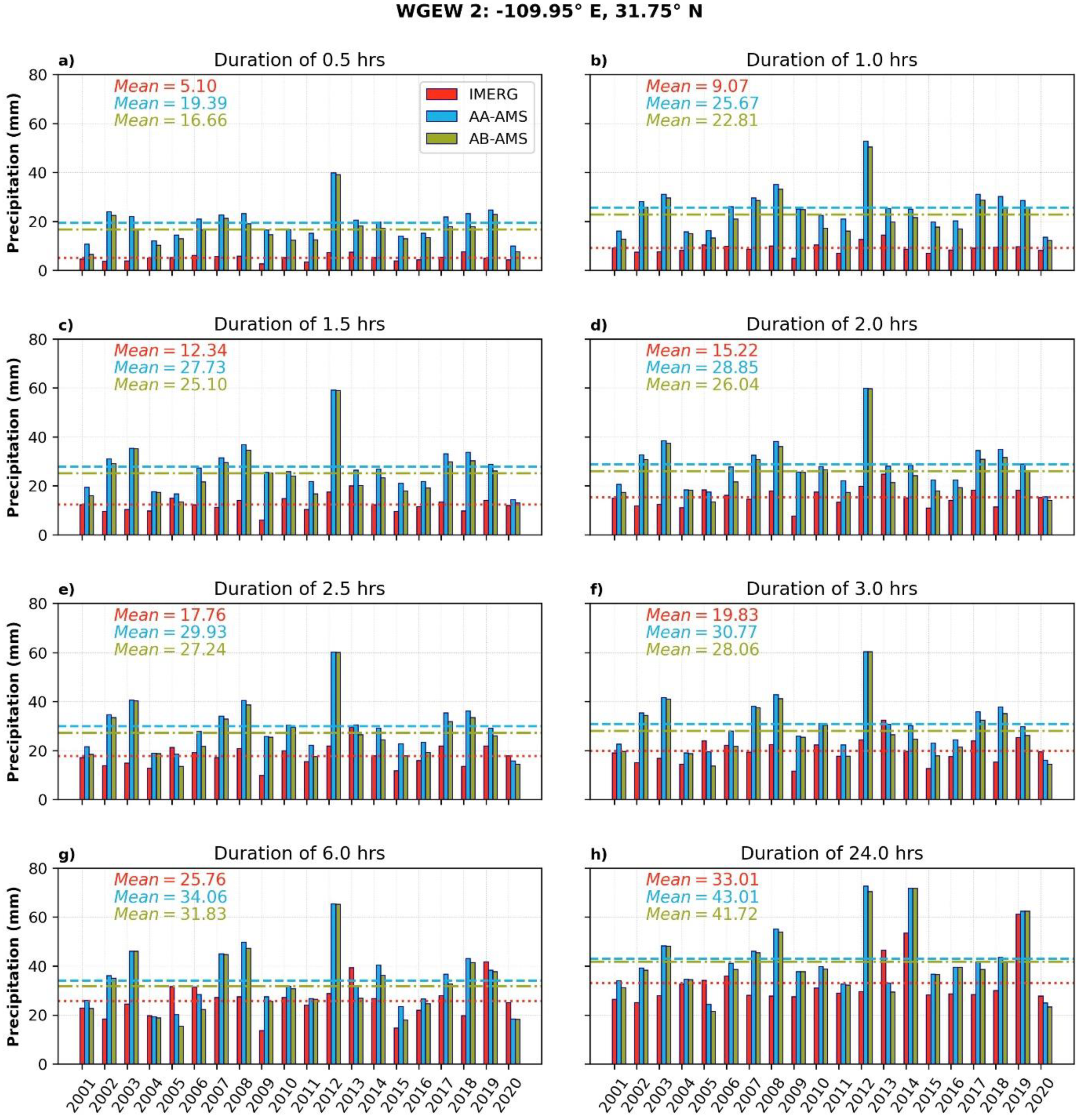
Appendix A.2. AA-AMS versus AB-AMS
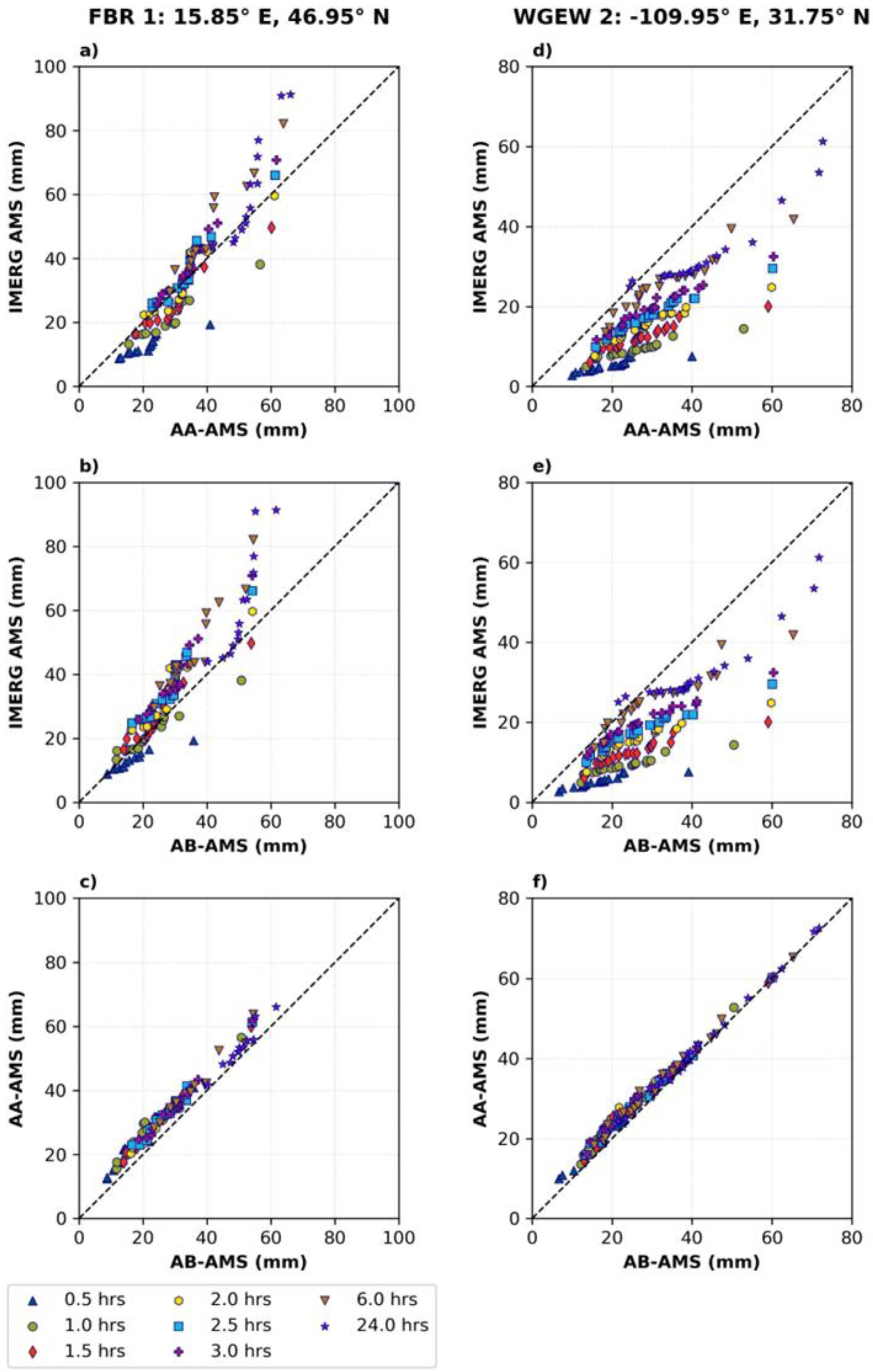
Appendix A.3. Grid-Scale: Performance of the IMERG IDF Equations
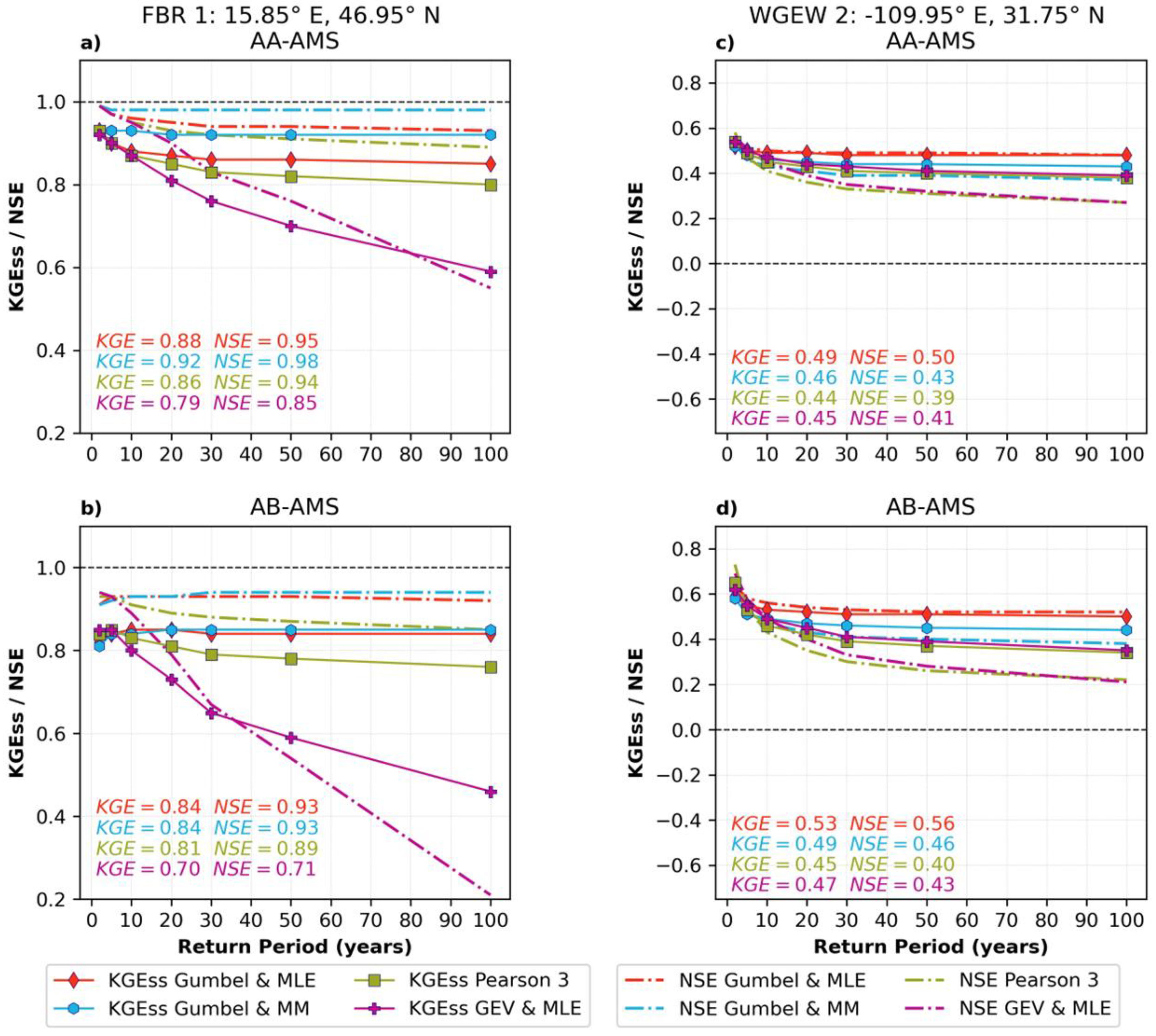
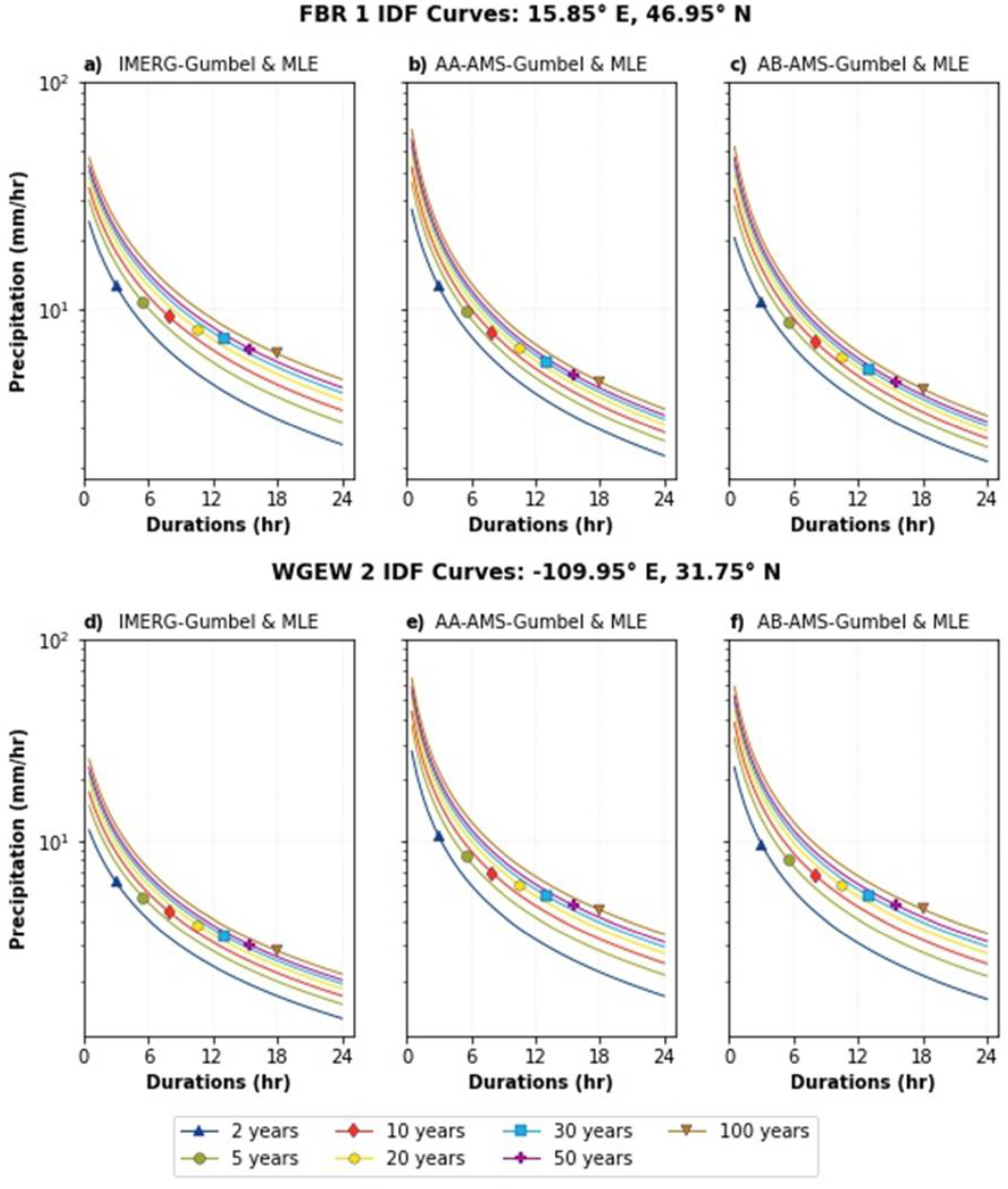
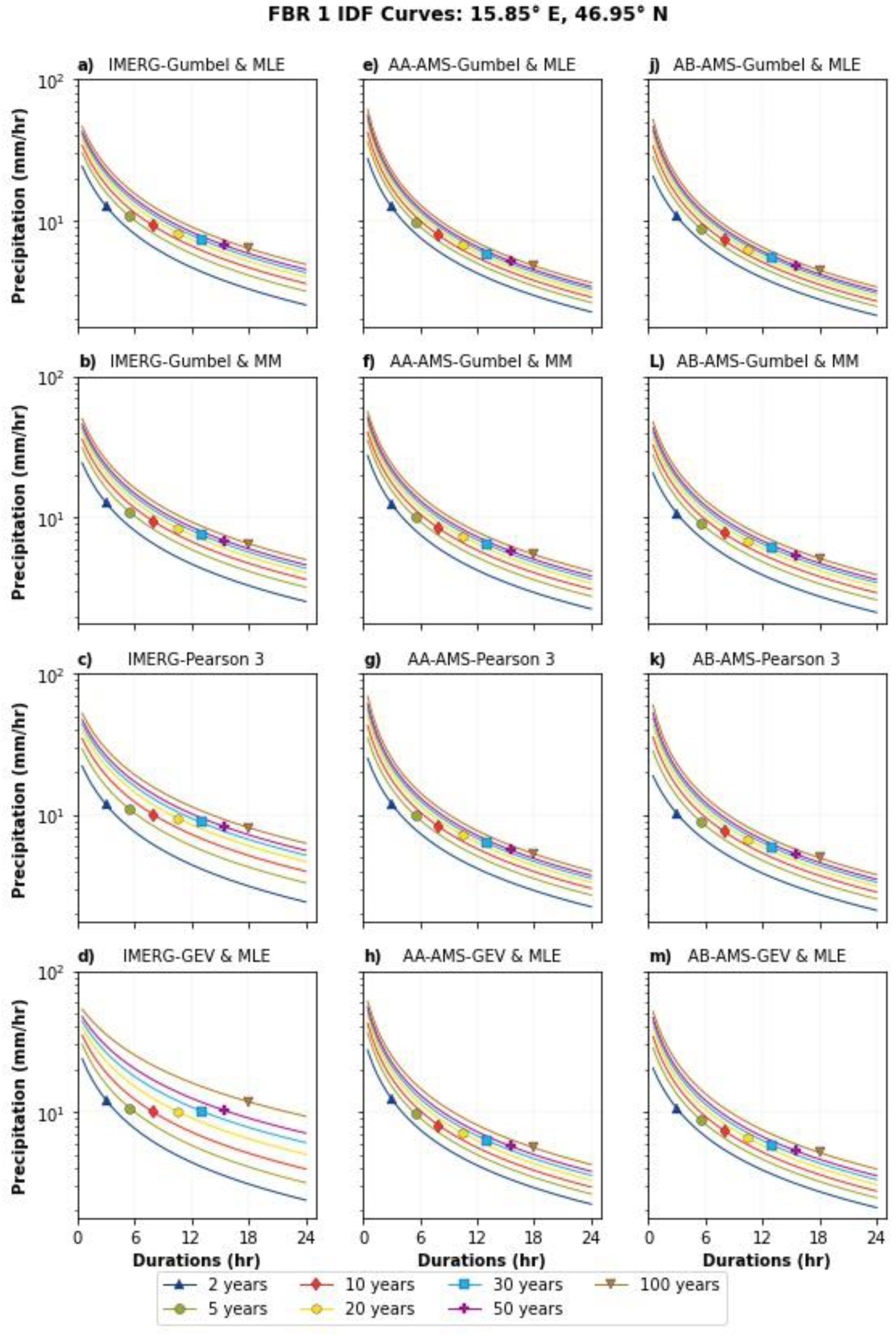
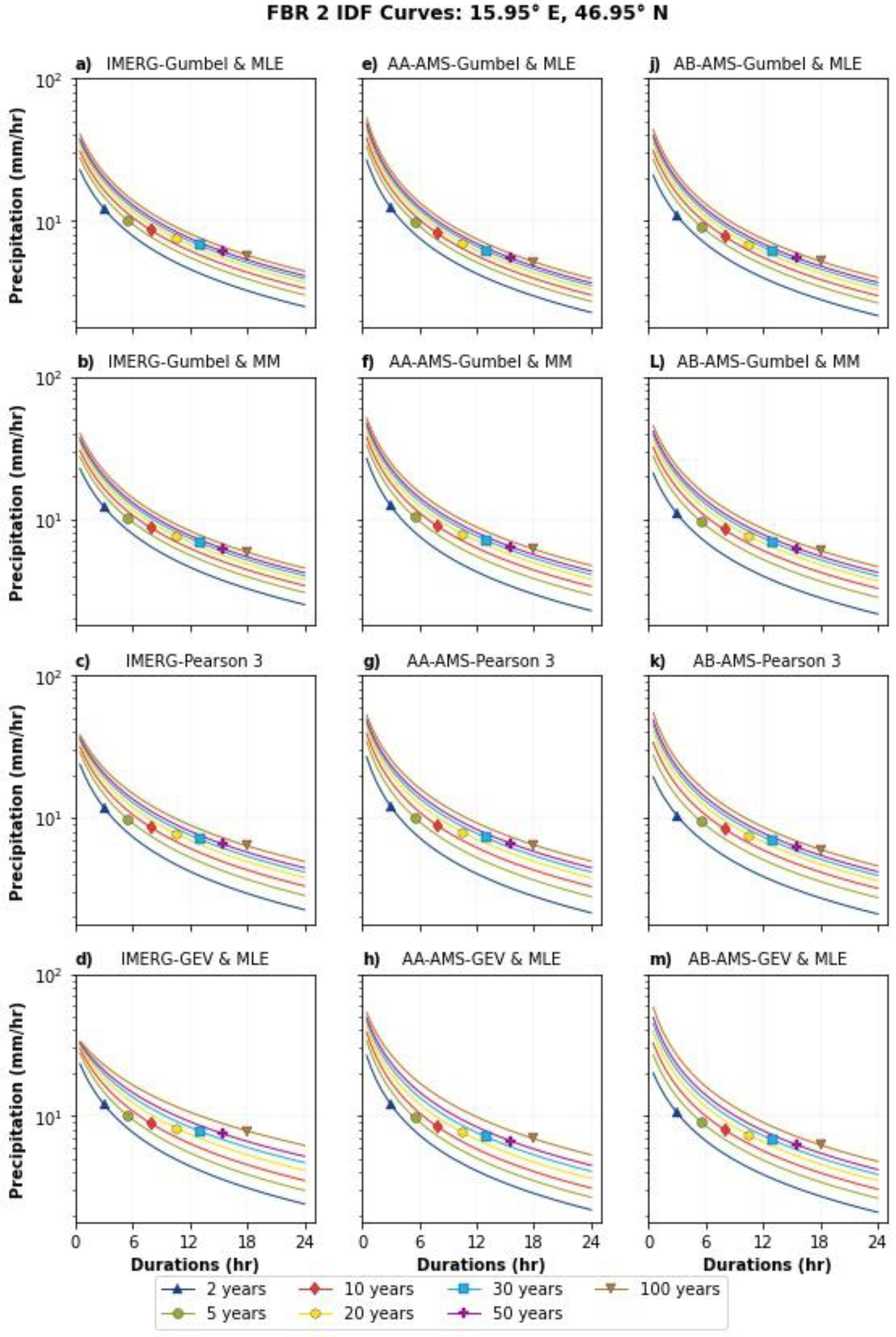
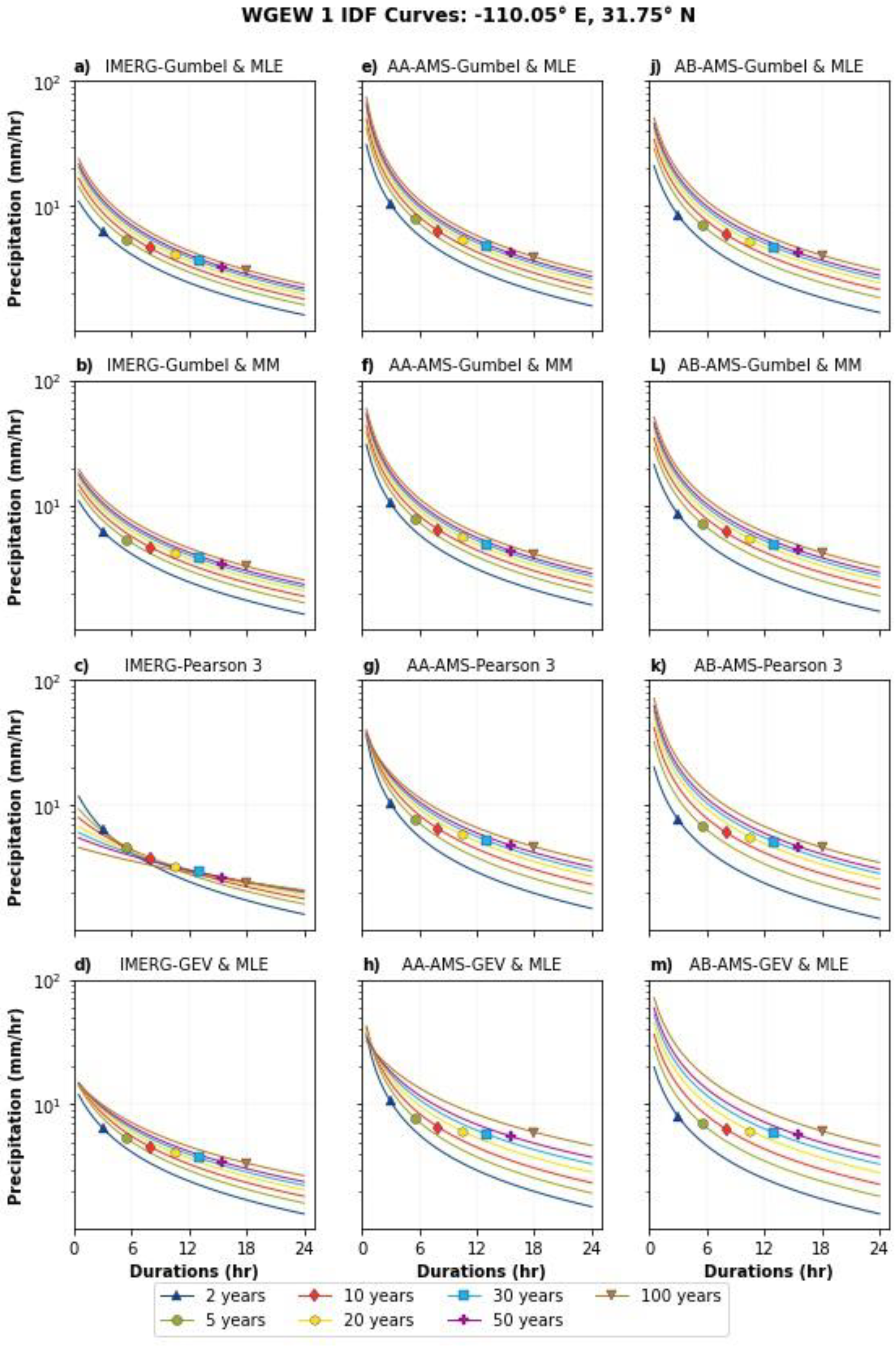
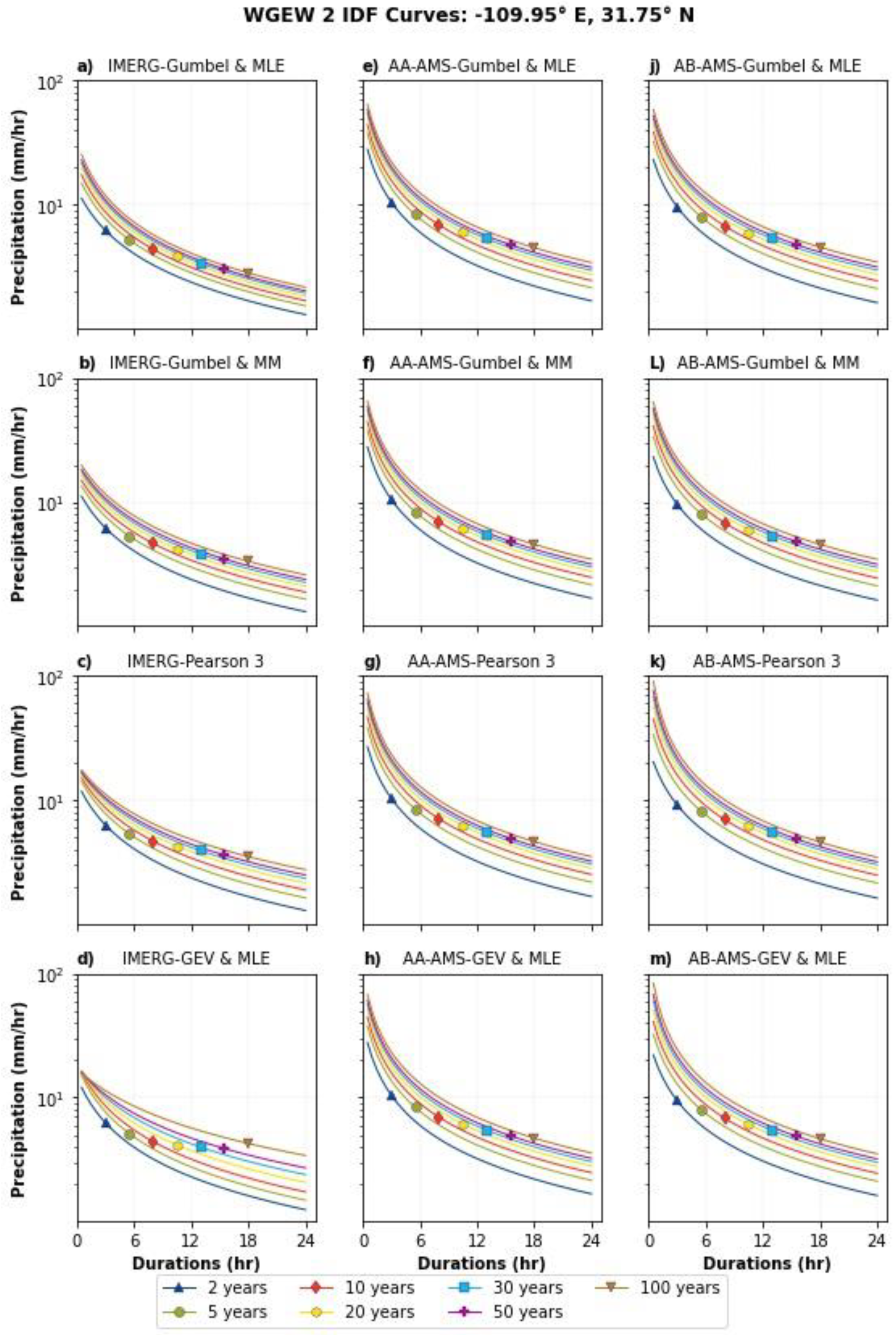

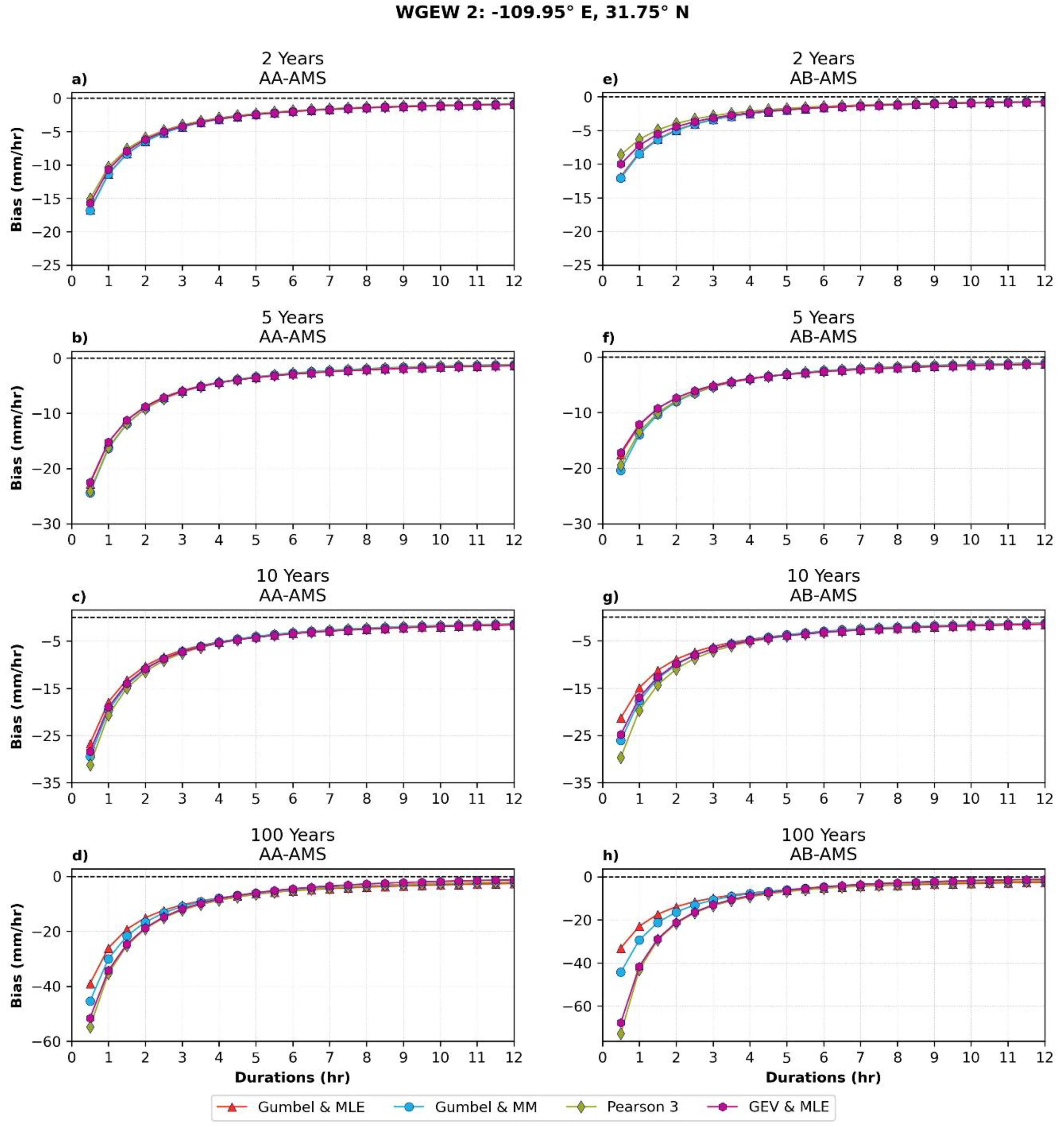
Appendix A.4. Assessment of IMERG AMSs and IDF Equations at Local Scale
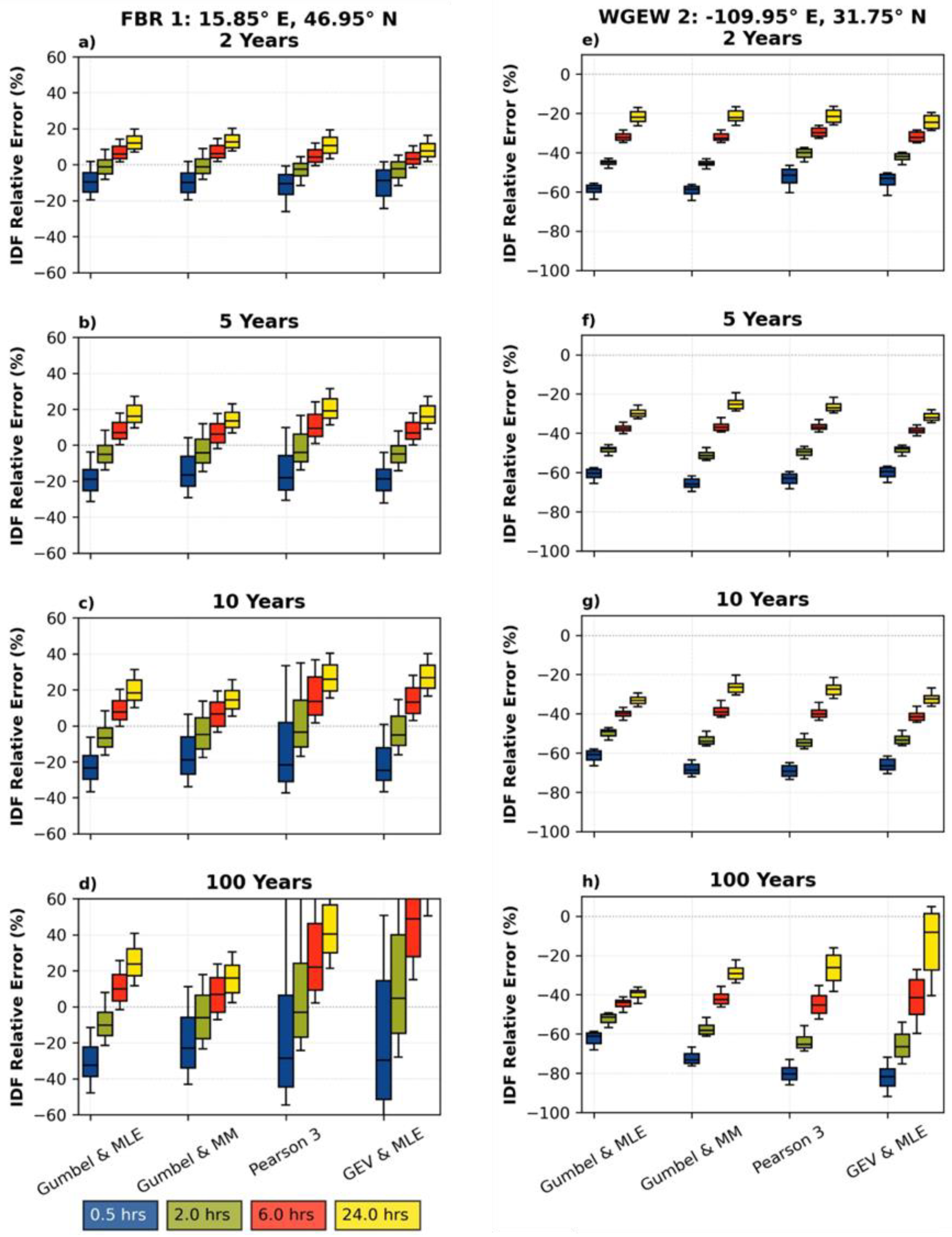
References
- Langsdorf, S.; Löschke, S.; Möller, V.; Okem, A. Climate Change 2022 Impacts, Adaptation and Vulnerability Working Group II Contribution to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; IPC: Geneva, Switzerland, 2022; ISBN 9789291691593. [Google Scholar]
- Bedient, P.B.; Huber, W.C. Hydrology and Floodplain Analysis; Addison-Wesley: Boston, MA, USA, 1989; ISBN 9780201517118. [Google Scholar]
- Sun, Y.; Wendi, D.; Kim, D.E.; Liong, S.Y. Deriving Intensity–Duration–Frequency (IDF) Curves Using Downscaled in Situ Rainfall Assimilated with Remote Sensing Data. Geosci. Lett. 2019, 6, 17. [Google Scholar] [CrossRef]
- Kidd, C.; Becker, A.; Huffman, G.J.; Muller, C.L.; Joe, P.; Skofronick-Jackson, G.; Kirschbaum, D.B. So, How Much of the Earth’s Surface Is Covered by Rain Gauges? Bull. Am. Meteorol. Soc. 2017, 98, 69–78. [Google Scholar] [CrossRef] [PubMed]
- Noor, M.; Ismail, T.; Shahid, S.; Asaduzzaman, M.; Dewan, A. Evaluating Intensity-Duration-Frequency (IDF) Curves of Satellite-Based Precipitation Datasets in Peninsular Malaysia. Atmos. Res. 2021, 248, 105203. [Google Scholar] [CrossRef]
- Endreny, T.A.; Imbeah, N. Generating Robust Rainfall Intensity–Duration–Frequency Estimates with Short-Record Satellite Data. J. Hydrol. 2009, 371, 182–191. [Google Scholar] [CrossRef]
- Ombadi, M.; Nguyen, P.; Sorooshian, S.; Hsu, K. lin Developing Intensity-Duration-Frequency (IDF) Curves from Satellite-Based Precipitation: Methodology and Evaluation. Water Resour. Res. 2018, 54, 7752–7766. [Google Scholar] [CrossRef]
- Marra, F.; Morin, E.; Peleg, N.; Mei, Y.; Anagnostou, E.N. Intensity-Duration-Frequency Curves from Remote Sensing Rainfall Estimates: Comparing Satellite and Weather Radar over the Eastern Mediterranean. Hydrol. Earth Syst. Sci. 2017, 21, 2389–2404. [Google Scholar] [CrossRef]
- Kyaw, A.K.; Shahid, S.; Wang, X. Remote Sensing for Development of Rainfall Intensity–Duration–Frequency Curves at Ungauged Locations of Yangon, Myanmar. Water 2022, 14, 1699. [Google Scholar] [CrossRef]
- Fuchsberger, J.; Kirchengast, G.; Kabas, T. WegenerNet High-Resolution Weather and Climate Data from 2007 to 2020. Earth Syst. Sci. Data 2021, 13, 1307–1334. [Google Scholar] [CrossRef]
- Huffman, G.J.; Stocker, E.F.; Bolvin, D.T.; Nelkin, E.J.; Tan, J. GPM IMERG Final Precipitation L3 Half Hourly 0.1 Degree × 0.1 Degree V06. Available online: https://disc.gsfc.nasa.gov/datasets/GPM_3IMERGHH_06/summary (accessed on 6 October 2022).
- Huffman, G.J. Coauthors NASA Global Precipitation Measurement (GPM). Integrated Multi-SatellitE Retrievals for GPM (IMERG); Version 6; Algorithm Theoretical Basis Doc.; NASA: Washington, DC, USA, 2019; 38p.
- Kirchengast, G.; Kabas, T.; Leuprecht, A.; Bichler, C.; Truhetz, H. Wegener Net a Pioneering High-Resolution Network for Monitoring Weather and Climate. Bull. Am. Meteorol. Soc. 2014, 95, 227–242. [Google Scholar] [CrossRef]
- Kabas, T. WegenerNet Klimastationsnetz Region Feldbach: Experimenteller Aufbau Und Hochauflösende Daten Für Die Klima- Und Umweltforschung; Wegener Center für Klima und Globalen Wandel: Graz, Austria, 2012; ISBN 9783950311242. [Google Scholar]
- Tan, J.; Petersen, W.A.; Kirstetter, P.E.; Tian, Y. Performance of IMERG as a Function of Spatiotemporal Scale. J. Hydrometeorol. 2017, 18, 307–319. [Google Scholar] [CrossRef]
- Goodrich, D.C.; Keefer, T.O.; Unkrich, C.L.; Nichols, M.H.; Osborn, H.B.; Stone, J.J.; Smith, J.R. Long-Term Precipitation Database, Walnut Gulch Experimental Watershed, Arizona, United States. Water Resour. Res. 2008, 44, W05S04. [Google Scholar] [CrossRef]
- Garcia, M.; Peters-Lidard, C.D.; Goodrich, D.C.; Garcia, M.; Peters-Lidard, C.D.; Goodrich, D.C. Spatial Interpolation of Precipitation in a Dense Gauge Network for Monsoon Storm Events in the Southwestern United States. Water Resour. Res. 2008, 44, W05S13. [Google Scholar] [CrossRef]
- World Meteorological Organization. WMO-No. 168: Guide to Hydrological Practices, 6th ed.; WHO: Geneva, Switzerland, 2009. [Google Scholar]
- Stedinger, J.R.; Vogel, R.M.; Foufoula-Georgiou, E. Frequency Analysis of Extreme Events. In Handbook of Hydrology; Maidment, D.R., Ed.; McGraw-Hill: New York, NY, USA, 1997; pp. 18.1–18.66. [Google Scholar]
- Benjamin, J.R.; Cornell, C.A. Probability, Statistics, and Decision for Civil Engineers; Dover Publications: New York, NY, USA, 2014; ISBN 9780486780726. [Google Scholar]
- Haan, C.T. Statistical Methods in Hydrology, 2nd ed.; Iowa State Press: Ames, IA, USA, 2002; ISBN 0813815037. [Google Scholar]
- Koutsoyiannis, D.; Kozonis, D.; Manetas, A. A Mathematical Framework for Studying Rainfall Intensity-Duration-Frequency Relationships. J. Hydrol. 1998, 206, 118–135. [Google Scholar] [CrossRef]
- Lau, A.; Perez, A.J. Generation of Intensity, Duration, Frequency Relationships in Watersheds of the Republic of Panama. Ph.D. Thesis, Universidad Tecnologica de Panama, Panama City, Panama, 2015. [Google Scholar]
- Vuong, H.; Minh, T.; Lavane, K.; Lanh, L.T.; van Thinh, L.; Phuoc Cong, N.; van Ty, T.; Downes, N.K.; Kumar, P. Developing Intensity-Duration-Frequency (IDF) Curves Based on Rainfall Cumulative Distribution Frequency (CDF) for Can Tho City, Vietnam. Earth 2022, 3, 866–880. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River Flow Forecasting through Conceptual Models Part I—A Discussion of Principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the Mean Squared Error and NSE Performance Criteria: Implications for Improving Hydrological Modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Knoben, W.J.M.; Freer, J.E.; Woods, R.A. Technical Note: Inherent Benchmark or Not? Comparing Nash-Sutcliffe and Kling-Gupta Efficiency Scores. Hydrol. Earth Syst. Sci. 2019, 23, 4323–4331. [Google Scholar] [CrossRef]
- Nashwan, M.S.; Shahid, S.; Wang, X. Assessment of Satellite-Based Precipitation Measurement Products over the Hot Desert Climate of Egypt. Remote. Sens. 2019, 11, 555. [Google Scholar] [CrossRef]
- Chen, H.; Yong, B.; Kirstetter, P.E.; Wang, L.; Hong, Y. Global Component Analysis of Errors in Three Satellite-Only Global Precipitation Estimates. Hydrol. Earth Syst. Sci. 2021, 25, 3087–3104. [Google Scholar] [CrossRef]
- Tan, J.; Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Rajagopal, M. SHARPEN: A Scheme to Restore the Distribution of Averaged Precipitation Fields. J. Hydrometeorol. 2021, 22, 2105–2116. [Google Scholar] [CrossRef]
- Cui, W.; Dong, X.; Xi, B.; Feng, Z.H.E.; Fan, J. Can the GPM IMERG Final Product Accurately Represent MCSs’ Precipitation Characteristics over the Central and Eastern United States? J. Hydrometeorol. 2020, 21, 39–57. [Google Scholar] [CrossRef]
- Tan, J.; Petersen, W.A.; Kirchengast, G.; Goodrich, D.C.; Wolff, D.B. Evaluation of Global Precipitation Measurement Rainfall Estimates against Three Dense Gauge Networks. J. Hydrometeorol. 2018, 19, 517–532. [Google Scholar] [CrossRef]
- Martel, J.-L.; François, B.P.; Lucas-Picher, P.; Troin, M.; Arsenault, R. Climate Change and Rainfall Intensity–Duration–Frequency Curves: Overview of Science and Guidelines for Adaptation. J. Hydrol. Eng. 2021, 26, 03121001. [Google Scholar] [CrossRef]
- Kourtis, I.M.; Tsihrintzis, V.A. Update of Intensity-Duration-Frequency (IDF) Curves under Climate Change: A Review. Water Supply 2022, 22, 4951–4974. [Google Scholar] [CrossRef]

| Gridded Rainfall | Spatial Resolution | Temporal Resolution | Period | Reference |
|---|---|---|---|---|
| IMERG Final | 0.1° × 0.1° | Half-hour | Corresponding to the ground networks period | Huffman et al. [12] |
| FBR Network | 200 × 200 m | Half-hour | 2007 to 2020 | Kirchengast et al. [13] |
| WGEW Network | 100 × 100 m | Half-hour | 2001 to 2020 | Garcia et al. and Goodrich et al. [16,17] |
| Method | PDF or CDF [19] |
|---|---|
| Gumbel | |
| Pearson 3 | |
| GEV |
| Statistic | Formula | Range | Optimal Value |
|---|---|---|---|
| Mean bias ratio | 0 to 1 | 1 | |
| Pearson correlation | −1 to 1 | 1 | |
| Bias | −∞ to +∞ | 0 | |
| Nash–Sutcliffe efficiency coefficient | 0 to 1 | 1 | |
| Kling–Gupta efficiency | −∞ to 1 | 1 | |
| Kling–Gupta efficiency skill score | −∞ to 1 | 1 | |
| Percent of relative error | −∞ to +∞ | 0 |
| Region | Statistic | IMERG against | 0.5 h | 1 h | 1.5 h | 2 h | 2.5 h | 3 h | 6 h | 24 h |
|---|---|---|---|---|---|---|---|---|---|---|
| FBR | Ratio | AA-AMS | 0.63 | 0.74 | 0.86 | 0.97 | 1.03 | 1.07 | 1.14 | 1.10 |
| AB-AMS | 0.82 | 0.94 | 1.04 | 1.14 | 1.21 | 1.24 | 1.28 | 1.16 | ||
| Bias | AA-AMS | −7.69 | −7.05 | −4.24 | −0.98 | 1.16 | 2.59 | 5.85 | 5.93 | |
| AB-AMS | −2.80 | −1.24 | 1.00 | 3.91 | 5.94 | 7.23 | 10.16 | 8.90 | ||
| Pcorr | AA-AMS | −0.18 | −0.11 | −0.11 | −0.13 | −0.12 | −0.08 | −0.19 | 0.02 | |
| AB-AMS | −0.09 | −0.06 | −0.10 | −0.10 | −0.05 | 0.01 | −0.13 | 0.01 | ||
| WGEW | Ratio | AA-AMS | 0.27 | 0.35 | 0.45 | 0.53 | 0.59 | 0.63 | 0.75 | 0.80 |
| AB-AMS | 0.35 | 0.44 | 0.54 | 0.63 | 0.68 | 0.73 | 0.84 | 0.86 | ||
| Bias | AA-AMS | −14.10 | −16.58 | −15.22 | −13.60 | −12.43 | −11.35 | −8.30 | −8.34 | |
| AB-AMS | −9.74 | −11.73 | −10.72 | −9.13 | −8.28 | −7.40 | −5.02 | −5.65 | ||
| Pcorr | AA-AMS | 0.45 | 0.39 | 0.35 | 0.35 | 0.38 | 0.39 | 0.38 | 0.48 | |
| AB-AMS | 0.45 | 0.32 | 0.29 | 0.28 | 0.32 | 0.33 | 0.31 | 0.45 |
| Region | CDF | IMERG | AA-AMS | AB-AMS | |||
|---|---|---|---|---|---|---|---|
| D | p Value | D | p Value | D | p Value | ||
| FBR | GEV | 0.14 | 0.89 | 0.16 | 0.81 | 0.14 | 0.88 |
| Gumbel and MLE | 0.16 | 0.79 | 0.16 | 0.80 | 0.15 | 0.85 | |
| Gumbel and MM | 0.16 | 0.80 | 0.18 | 0.70 | 0.16 | 0.79 | |
| Pearson 3 | 0.18 | 0.69 | 0.19 | 0.66 | 0.19 | 0.65 | |
| WGEW | GEV | 0.12 | 0.88 | 0.12 | 0.88 | 0.12 | 0.87 |
| Gumbel and MLE | 0.14 | 0.80 | 0.12 | 0.87 | 0.13 | 0.81 | |
| Gumbel and MM | 0.14 | 0.74 | 0.13 | 0.83 | 0.13 | 0.81 | |
| Pearson 3 | 0.33 | 0.65 | 0.18 | 0.81 | 0.13 | 0.80 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lau, A.; Behrangi, A. Understanding Intensity–Duration–Frequency (IDF) Curves Using IMERG Sub-Hourly Precipitation against Dense Gauge Networks. Remote Sens. 2022, 14, 5032. https://doi.org/10.3390/rs14195032
Lau A, Behrangi A. Understanding Intensity–Duration–Frequency (IDF) Curves Using IMERG Sub-Hourly Precipitation against Dense Gauge Networks. Remote Sensing. 2022; 14(19):5032. https://doi.org/10.3390/rs14195032
Chicago/Turabian StyleLau, Alcely, and Ali Behrangi. 2022. "Understanding Intensity–Duration–Frequency (IDF) Curves Using IMERG Sub-Hourly Precipitation against Dense Gauge Networks" Remote Sensing 14, no. 19: 5032. https://doi.org/10.3390/rs14195032
APA StyleLau, A., & Behrangi, A. (2022). Understanding Intensity–Duration–Frequency (IDF) Curves Using IMERG Sub-Hourly Precipitation against Dense Gauge Networks. Remote Sensing, 14(19), 5032. https://doi.org/10.3390/rs14195032






