Next Article in Journal
Spatial Representativeness of Eddy Covariance Measurements in a Coniferous Plantation Mixed with Cropland in Southeastern China
Next Article in Special Issue
Shallow Sea Topography Detection from Multi-Source SAR Satellites: A Case Study of Dazhou Island in China
Previous Article in Journal
Integrating a UAV-Derived DEM in Object-Based Image Analysis Increases Habitat Classification Accuracy on Coral Reefs
Previous Article in Special Issue
Improving the Reconstruction of Vertical Temperature Profiles on Account of Oceanic Front Impacts
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 14
Issue 19
10.3390/rs14195021
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Reconstruction of Monthly Surface Nutrient Concentrations in the Yellow and Bohai Seas from 2003–2019 Using Machine Learning

by
Hao Liu
1,
Lei Lin
1,2,*,
Yujue Wang
2,
Libin Du
1,
Shengli Wang
1,
Peng Zhou
2,
Yang Yu
3,
Xiang Gong
4 and
Xiushan Lu
1
1
College of Ocean Science and Engineering, Shandong University of Science and Technology, Qingdao 266590, China
2
State Key Laboratory of Estuarine and Coastal Research, East China Normal University, Shanghai 200241, China
3
Key Laboratory of Ocean Circulation and Waves, Institute of Oceanology, and Center for Ocean Mega-Science, Chinese Academy of Sciences, Qingdao 266071, China
4
School of Mathematics and Physics, Qingdao University of Science and Technology, Qingdao 266061, China
*
Author to whom correspondence should be addressed.
Remote Sens. 2022, 14(19), 5021; https://doi.org/10.3390/rs14195021
Submission received: 25 August 2022 / Revised: 6 October 2022 / Accepted: 7 October 2022 / Published: 9 October 2022
(This article belongs to the Special Issue Applications of Remote Sensing in Oceanography: Prospects and Challenges)
Browse Figures
Versions Notes

Abstract

:
Monitoring the spatiotemporal variability of nutrient concentrations in shelf seas is important for understanding marine primary productivity and ecological problems. However, long time-series and high spatial-resolution nutrient concentration data are difficult to obtain using only on ship-based measurements. In this study, we developed a machine-learning approach to reconstruct monthly sea-surface dissolved inorganic nitrogen (DIN), dissolved inorganic phosphorus (DIP), and dissolved silicate (DSi) concentrations in the Yellow and Bohai seas from 2003–2019. A large amount of in situ measured data were first used to train the machine-learning model and derive a reliable model with input of environmental data (including sea-surface temperature, salinity, chlorophyll-a, and Kd490) and output of DIN, DIP, and DSi concentrations. Then, longitudinal (2003–2019) monthly satellite remote-sensing environmental data were input into the model to reconstruct the surface nutrient concentrations. The results showed that the nutrient concentrations in nearshore (water depth < 40 m) and offshore (water depth > 40 m) waters had opposite seasonal variabilities; the highest (lowest) in summer in nearshore (offshore) waters and the lowest (highest) in winter in nearshore (offshore) waters. However, the DIN:DIP and DIN:DSi in most regions were consistently higher in spring and summer than in autumn and winter, and generally exceeded the Redfield ratio. From 2003–2019, DIN showed an increasing trend in nearshore waters (average 0.14 μmol/L/y), while DSi showed a slight increasing trend in the Changjiang River Estuary (0.06 μmol/L/y) but a decreasing trend in the Yellow River Estuary (–0.03 μmol/L/y), and DIP exhibited no significant trend. Furthermore, surface nutrient concentrations were sensitive to changes in sea-surface temperature and salinity, with distinct responses between nearshore and offshore waters. We believe that our novel machine learning method can be applied to other shelf seas based on sufficient observational data to reconstruct a long time-series and high spatial resolution sea-surface nutrient concentrations.

Graphical Abstract

1. Introduction

Nutrients in the ocean are essential for marine phytoplankton growth and thus play an important role in marine primary production [1]. Dissolved inorganic nitrogen (DIN), dissolved inorganic phosphorus (DIP), and dissolved silicate (DSi) are three of the most important nutrients, among others, for marine phytoplankton. Their concentrations and ratios can significantly affect the primary productivity level in the ocean and the state of marine ecosystems [2,3,4]. For instance, excessively high nutrient concentrations or an imbalanced nutrient ratio in coastal oceans can lead to seawater eutrophication, causing disorders in the structure of phytoplankton populations and, in serious cases, large-scale algal blooms, which have serious impacts on marine fisheries and the marine environment [5]. Therefore, monitoring DIN, DIP, and DSi concentrations and their spatiotemporal variation is important for understanding the level and variability of marine primary productivity and addressing environmental problems such as marine eutrophication and algal blooms.
However, it is not easy to obtain data on marine DIN, DIP, and DSi concentrations. Commonly, concentrations of these nutrients can be acquired by collecting in situ seawater samples from marine survey cruises and measuring them in the laboratory [6,7,8]. This method is accurate and can provide first-hand information on ocean nutrient concentrations. However, owing to the relatively high financial costs of survey cruises and the limited number of observation stations, it is difficult to obtain high spatial resolution and continuous long time-series nutrient concentration data by in situ observations, which may result in uncertainty in analyses of the spatiotemporal variability of nutrient concentrations.
Owing to the limitations of in situ observations, numerical simulation of low trophic-level ecological processes and nutrient transport and transformation processes using marine ecosystem dynamic models has become an important means to compute the spatiotemporal distribution of nutrients in the ocean (e.g., Dutkiewicz et al. [9]; Luo et al. [10]). This approach is based on an understanding of physical and biogeochemical processes in the ocean, and the results are highly interpretable. However, biological processes in the ocean are very complex and remain unclear [11]. Thus, the current marine ecosystem dynamic model may not correctly model or parametrize biological processes [12,13]. This uncertainty may introduce a large bias in the results of the modeled nutrient concentrations, which may reduce confidence in the prediction results of the numerical model [14]. In addition, the establishment and setup of marine ecosystem dynamic models is complicated and difficult as they usually require the coupling of a hydrodynamic model and a biological model, and the setting of tens of parameters (e.g., Geary et al. [15]; Piroddi et al. [16]). Furthermore, running the numerical model usually involves a high computational cost, especially for high-resolution modeling. These issues hinder the application of the marine ecosystem dynamic modeling approach. With the rapid increase in oceanic data, the machine-learning approach, which has the advantages of low computational cost and easy learning, has attracted increasing attention and has been widely used in the simulation and prediction of marine hydrology and ecology, such as seawater temperature [17], sea ice [18,19], chlorophyll-a concentrations [20], seawater carbon dioxide [21], marine phytoplankton abundances [22] and microbiome [23]. Machine-learning methods use a large amount of data to obtain a strongly nonlinear and complex relationship model between the input and output variables. Machine-learning methods focus more on the accuracy of prediction than on inherent processes [24]; thus, they are appropriate for situations that focus on prediction results rather than the inherent mechanism.
Satellite remote sensing is an alternative and important means of monitoring marine environments (e.g., sea-surface temperature, sea surface chlorophyll-a concentration, and seawater turbidity) with the characteristics of large spatial coverage and long time series. However, because there is no direct physical relationship between nutrient concentration and water color, satellite remote sensing cannot directly monitor marine nutrient concentrations [25]. Water nutrient concentrations can be monitored indirectly using the relationship between nutrient concentration and satellite-derived information to retrieve marine nutrient data. For example, Du et al. [26] used satellite remote sensing estimation of the total phosphorus concentration in the Taihu Lake based on a semi-analytical model of the absorption coefficient. Wang et al. [25] and Huang et al. [27] used machine learning and satellite remote-sensing reflectance to retrieve DIN and DIP concentrations in the Changjiang River Estuary region and Shenzhen Bay, respectively. These studies focused on relatively small spatial-scale regions (i.e., lakes, estuaries, or bays). However, to the best of our knowledge, the applicability of nutrient data retrieval by satellite remote sensing in continental shelf sea areas on a relatively large spatial scale has not previously been examined. Moreover, the machine-learning model based on satellite absorption coefficient or remote-sensing reflectance data cannot evaluate the relationship between the marine environmental factors (e.g., temperature, salinity, and phytoplankton) and nutrient concentration. In this study, we propose a novel method to reconstruct large spatial scales and long time-series sea surface nutrient concentrations in typical shelf seas, that is, the Yellow and Bohai seas (YBS) with a total area of ~460,000 km2 (Figure 1a), by using a machine-learning method along with in situ measured and satellite-derived marine environmental data. In contrast to previous studies, we first established a machine-learning model of marine environmental factors (input) and DIN, DIP, and DSi concentrations (output), which were trained using an in situ measured dataset. Then, by inputting the long time-series satellite-derived environmental data into the model, we reconstructed the monthly sea-surface nutrient concentrations in the YBS from 2003–2019. Finally, sensitivity experiments of the model were conducted to evaluate the effects of different environmental factors on nutrients. The method that can be applied to other shelf seas to reconstruct a long time-series and high spatial resolution sea-surface nutrient concentrations based on sufficient observational data.
The remainder of this paper is organized as follows. In Section 2, the design of the sea surface nutrient reconstruction method with the machine-learning model, dataset source, and machine-learning algorithms are described. In Section 3, we compare the results of the three machine-learning algorithms and analyze the spatial distribution and temporal variation characteristics of DIN, DIP, and DSi from the best-performance model and the effects of different environmental factors. The advantages and limitations of the machine-learning approach and dynamics of nutrient variability in the YBS are discussed in Section 4. Finally, a brief conclusion is presented in Section 5.

2. Data and Methods

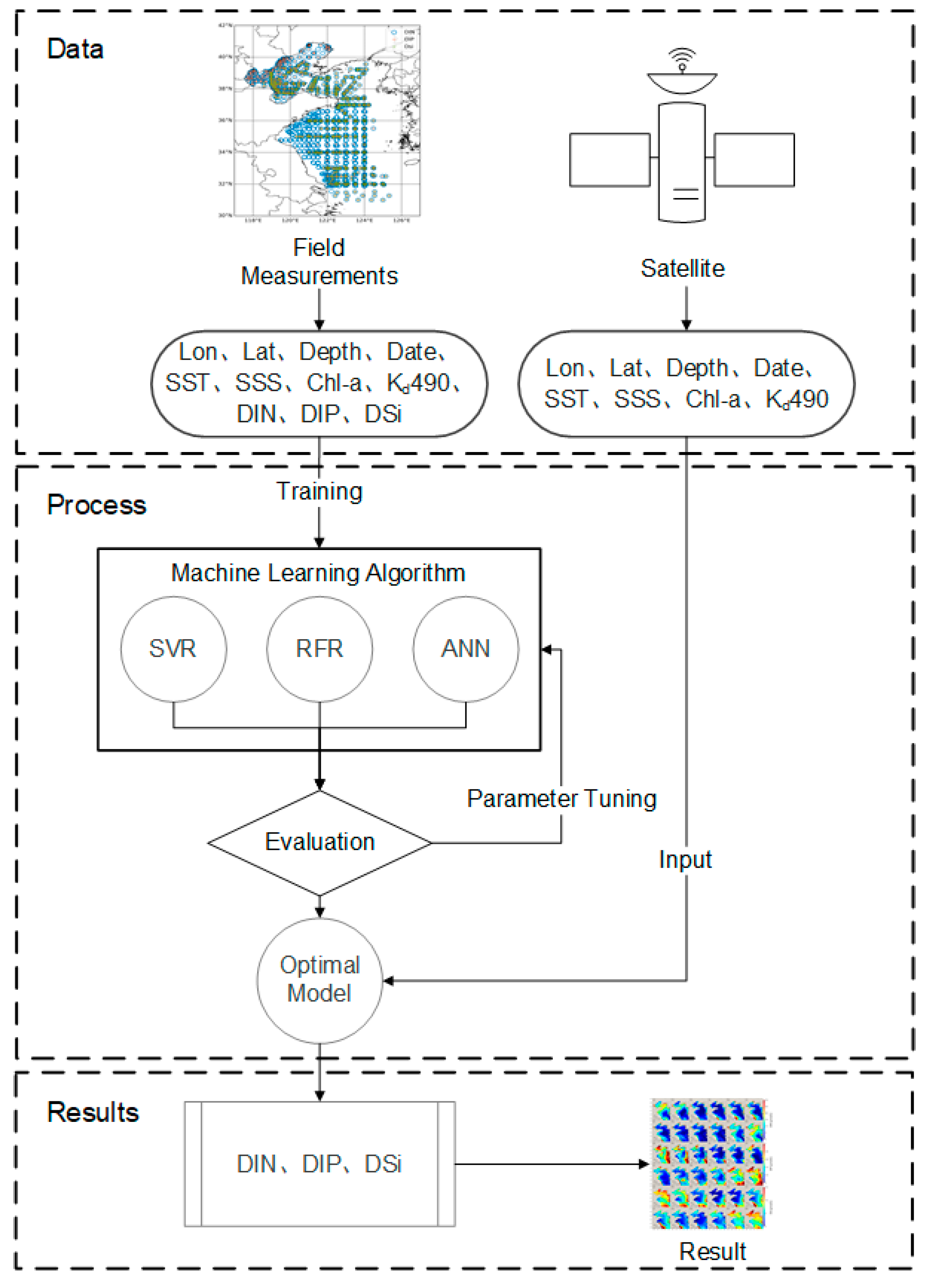
2.1. Design of the Machine-Learning Model for Sea Surface Nutrient Concentrations

As shown in Figure 2, in situ measured data were used to train the machine-learning model, then the best trained model was selected, and finally large spatial-scale and long time-series satellite data were input into the model to derive the reconstructed results of nutrient concentrations.
In the machine-learning models, the sea-surface nutrient concentrations (DIN, DIP, and DSi) were set as the output variables. The variability in nutrient concentrations in shelf seas is related to time and space, and is influenced by the hydrological environment (e.g., temperature and river runoff) and biogeochemical elements (e.g., phytoplankton activity and suspended particulate matter). Thus, the model input variables included eight predictors: longitude (Lon) and latitude (Lat), time (t) (using a cosine and sine transformation of the date of the year to create a seasonal cycle, based on ideas put forward by Sammartino et al. [28]), water depth at the sampling site (depth), sea-surface temperature (SST), sea-surface salinity (SSS), chlorophyll-a concentration (Chl-a), and suspended matter concentration (represented using the water diffuse attenuation coefficient Kd490); Lon, Lat, and t can represent the spatial and temporal variability of the nutrients; SST, SSS, and depth can influence the water mixing and thus represent the effects of the hydrological environment, while Chl-a represents biological effects and the suspended matter concentration represents the effect of the suspended particulate matter. However, the suspended matter concentration (SMC) was not directly measured during the cruises; thus, we replaced it with the Kd490 satellite products, given the strong positive correlation between SMC and Kd490 [29]. In addition, river discharge and precipitation can also influence the nutrients, while their influence could be reflected by SSS as the river discharge and precipitation indirectly influence SSS. Thus, river discharge and precipitation were not considered as input variables in the model. The observed SST, SSS, and Chl-a were directly measured during the cruises. All input and output variables were standardized before use to remove the impact of oversized data.
Three machine-learning algorithms [i.e., the support vector regression (SVR), random forest regression (RFR), and artificial neural network (ANN)] were used to train the nutrient models. The prediction accuracy and results of the three algorithms were then compared, and the model with the optimal performance was selected. Finally, the monthly mean data (SST, SSS, Chl-a, and Kd490) for 2003–2019 from the satellite for the predictors were input into the machine-learning model to derive the spatiotemporal variation in the surface nutrient concentrations in the YBS.

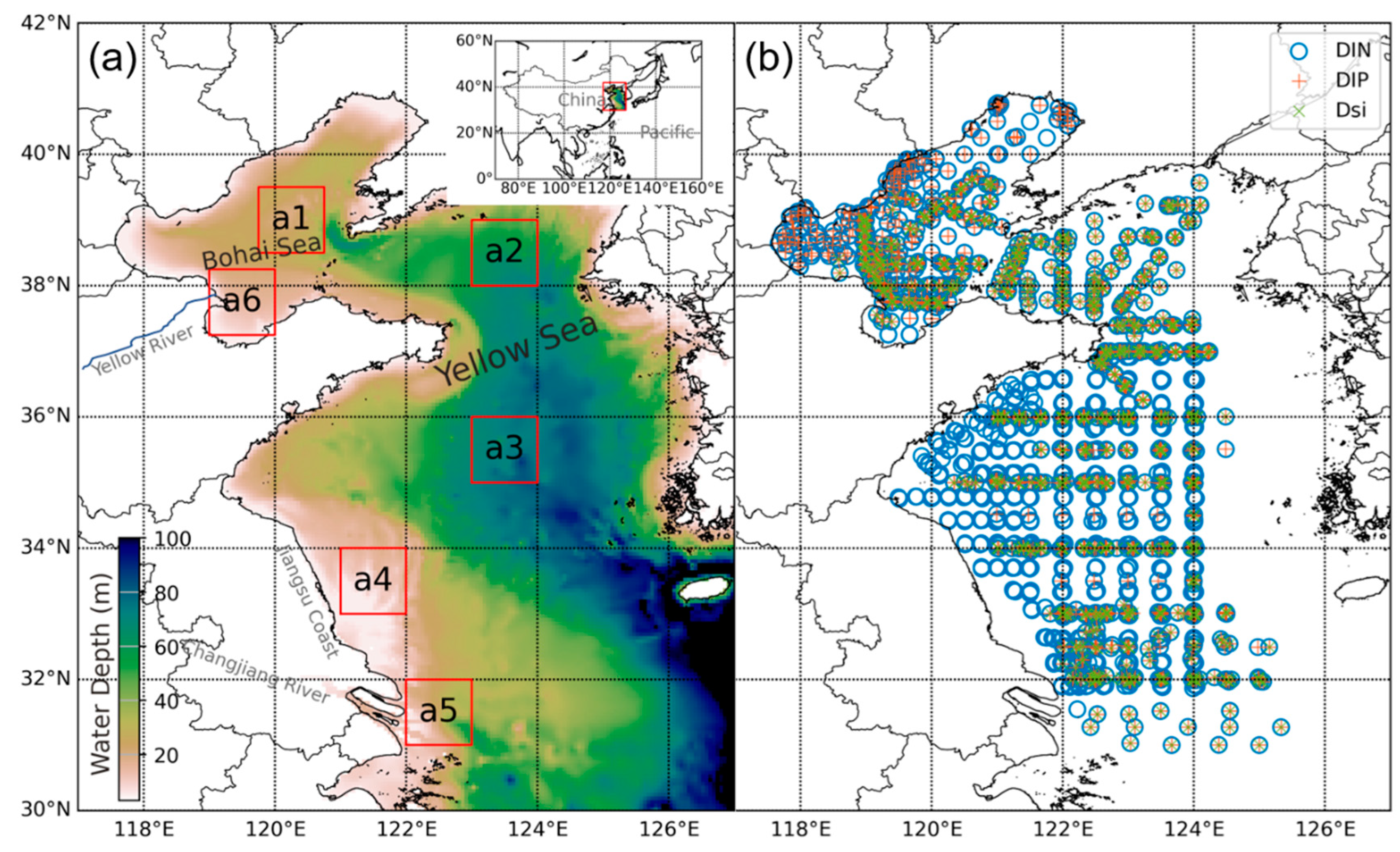
2.2. Data Sources

2.2.1. In Situ Measured Data

In this study, in situ measured environmental and nutrient data from the YBS were used to train the nutrient machine-learning model. Most data were collected from 10 cruises in the YBS from 2010–2019 (Table 1). A total of 1081 surface water samples were collected during these cruises. SST, SSS, DIN, DIP, DSi, and Chl-a in the surface layer (3-m water depth) were measured at ~100 sites in each cruise (Figure 1b). SST and SSS were measured in situ using a conductivity–temperature–depth instrument (CTD, SeaBird 911 plus). The DIN, DIP, and DSi of the samples were analyzed in the laboratory using flow injection analysis (AA3, Bran + Luebbe, Germany). DIN is the total concentration of NO3−, NO2−, and NH4+. Chl-a was extracted with 15 mL of 90% acetone in the dark for 24 h in a refrigerator and concentrations were detected using a Chl-a fluorescence method. More details on the sample measurement processes in these cruises are presented in Wang et al. [30] and Lin et al. [31]. In addition to the data of the 10 cruises, other in situ measured data in the YBS were derived from published literature and the 2016 field survey by the Ecological Environment Department of Shandong Providence (more details are presented in Table 1). Finally, 2372 samples of DIN, 1852 samples of DIP, and 1271 samples of DSi were collected, which constituted the dataset for establishing the machine-learning model.

2.2.2. Satellite Data

Satellite-derived sea-surface environmental data were input into the trained machine-learning model to obtain the reconstructed sea-surface nutrient concentrations. The monthly mean SST and Kd490 data in the YBS from 2003–2019 were obtained from moderate-resolution imaging spectroradiometer (MODIS) satellite products of the National Aeronautics and Space Administration (NASA) (downloaded from https://coastwatch.pfeg.noaa.gov/erddap/index.html (accessed on 3 August 2021)). Monthly mean Chl-a data from 2003–2019 were acquired from Wang et al. [30], they established a novel statistical algorithm for satellite-derived Chl-a, using the generalized additive model (GAM) algorithm to alleviate the effect of suspended sediments and colored dissolved organic matter on Chl-a concentrations and improve the data accuracy. The detailed GAM algorithm and Chl-a validation for the Yellow Sea were published by Wang et al. [30], and we used it as one of the biogeochemical elements variables for model input. All these data had a spatial resolution of ~4 km. Satellite data products for global SSS, such as Soil Moisture Active Passive (SMAP, https://podaac.jpl.nasa.gov/dataset/OISSS_L4_multimission_7day_v1 (accessed on 3 August 2021)), can be used as the input data. However, these SSS satellite products do not cover the Bohai Sea region. Therefore, we used SSS data from a hydrodynamic model of the eastern shelf seas of China, which has been established and validated [43]. However, when the coverage area of the satellite SSS data increases in the future, it can replace the modeled SSS data.

2.3. Machine-Learning Algorithms

Three popular machine-learning algorithms, SVR, RFR, and ANN, were used to establish the nutrient machine-learning models.
The support vector machine (SVM) is a binary classification model in which the main idea is to solve nonlinear problems in low-dimensional spaces by mapping samples from low-dimensional feature spaces to high-dimensional feature spaces using nonlinear functions, which are effective in solving small-sample, nonlinear, and high-dimensional pattern recognition problems [44,45,46]. SVR is a branch of the SVM; here, we used a grid search method with 5-fold cross-validation to find the parameters C and Gamma to minimize the mean square error to complete the model. Our final model had a C of 100 and a Gamma of 0.1 for DIN; a C of 1 and a Gamma of 0.1 for DIP; and a C of 10 and a Gamma of 1 for DSi.
RFR is an integrated learning algorithm based on multiple regression decision trees [24]. The results are taken from the average regression prediction for each decision tree. RFR has good randomness [47]; not only are the training samples of each tree randomly sampled by bootstrap method resampling, but the set of segmentation attributes of each node in the tree is also determined by random selection, which ensures the variability of each regression tree and improves the predictive capability of the model, ensures good tolerance to noise and outliers, and avoids overfitting to a certain extent. We used an RFR algorithm with 500 trees to build the model.
An ANN is an information-processing model built by simulating biological neural networks [48]. It uses the network structure to calculate the relationship between the input and output by simulating the activation and transmission process of human neurons, and, finally, builds a model that minimizes the error between the output result and the real result. An ANN consists of a large number of interconnected neurons forming a series of input, hidden, and output layers, which are connected by weight lines such that information flows from the input layer to the output layer. An activation function was used to make it suitable for nonlinear situations when calculations were performed between the upper and lower layers. In this study, after trialing and comparing various settings, the DIN, DIP, and DSi models were finally established by using one layer input, two hidden layers, and one layer output with 32 neurons in each hidden layer, and using the Adam optimization algorithm with a dropout ratio of 10% and a learning rate and the ReduceLROnPlateau decay method. The difference is that the second layer of DIN uses the rectified linear unit (ReLU) activation function, the third layer uses the exponential linear unit (ELU) activation function, the learning rate is set to 0.0005, and the weight decay is set to 0.0001; the activation functions used in DIP are all ReLUs, the learning rate is set to 0.00045, the weight decay is set to 0.00001; the activation functions used in DSi are all ELUs, the learning rate is set to 0.0005, and the weight decay is set to 0.00001.

2.4. Evaluation of Machine-Learning Models

We trained the machine-learning models for the three nutrients using different algorithms. All observed sample datasets were randomly divided into training, validation, and test sets at a ratio of 8:1:1. The models were repeatedly trained and validated using training and validation sets. The test set was compared with the prediction results of the model to evaluate the accuracy of the machine-learning models based on three indicators: root mean square error (RMSE), correlation coefficient (R), and skill score (SS).
RMSE represents the standard deviation of the difference between the observed and predicted models, which was calculated as follows:
RMSE = ∑ i = 1 N ( O b s i − M o d i ) 2 N ,
where N is the total number of samples used in the test; and Obsi and Modi are the observed and model values of the nutrient concentration for the ith sample, respectively.
R represents the correlation coefficient between the model and observed results, and was calculated as follows:
R = ∑ i = 1 N [ ( M o d i − M o d ¯ ) ∗ ( O b s i − O b s ¯ ) ] ∑ i = 1 N ( M o d i − M o d ¯ ) 2 ∗ ∑ i = 1 N ( O b s i − O b s ¯ ) 2 ,
where the overbar represents the mean value.
SS is widely used to evaluate model performance; it quantifies the magnitude of the model bias relative to the observation variance and was calculated as follows:
SS = 1 − ∑ i = 1 N ( M o d i − O b s i ) 2 ∑ i = 1 N ( O b s i − O b s ¯ ) 2 ,
The model performance level is categorized by SS as follows: >0.65 excellent; 0.65–0.5 very good; 0.5–0.2 good; and <0.2 poor [49].

2.5. Analysis of Effects of Environmental Factors

To understand the effects of different environmental factors on nutrient concentrations, a series of sensitivity experiments were conducted as described by Chen et al. [14]. In the experiments, we varied each of the environmental predictors (including SST, SSS, Chl-a, and Kd490) while holding the other predictors constant. Then, we used the ANN model which had the best performance (see Section 3.1) to calculate the response of the nutrient concentration to each environmental predictor. In the experiment, the input SSS (and SST) varied by −2, −1.5, −1, −0.5, +0.5, +1, +1.5, and +2 PSU (°C) relative to the values in the original experiment (i.e., the control run), respectively, while inputting the Chl-a and Kd490 varied by −10%, −7.5%, −5%, −2.5%, +2.5%, +5%, +7.5%, +10% relative to the values in the original experiment, respectively, owing to their much larger variance. The modeled nutrient concentrations in the YBS region from 2003–2019 for each experiment were output and their temporal averages were calculated and compared with the original model results to quantify the effects of environmental variability on nutrient concentrations.

3. Results

We first compared and evaluated the performance of a nutrient model using different machine-learning algorithms. We then analyzed the results of the model that exhibited the best performance and examined the variability of the sea-surface nutrient concentration in the YBS from 2003–2019. Finally, the sensitivity experiment results were used to analyze the effects of environmental factors.

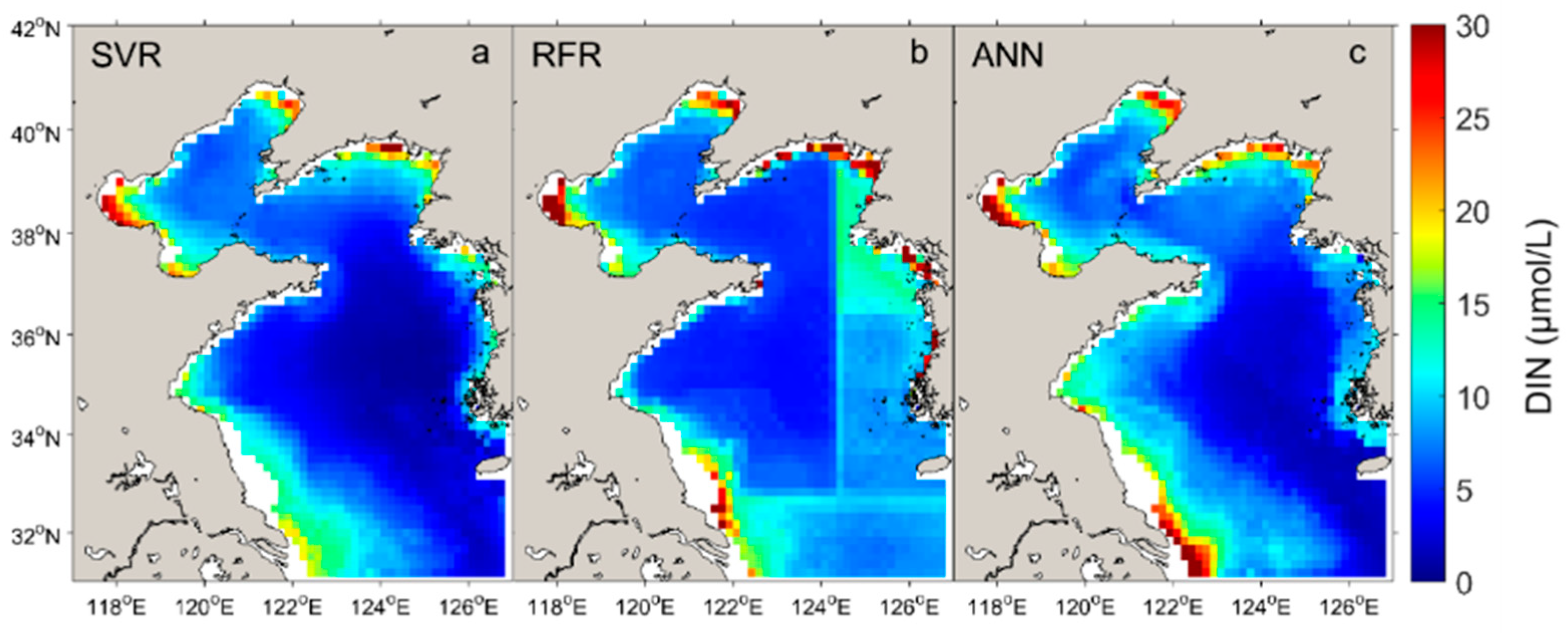
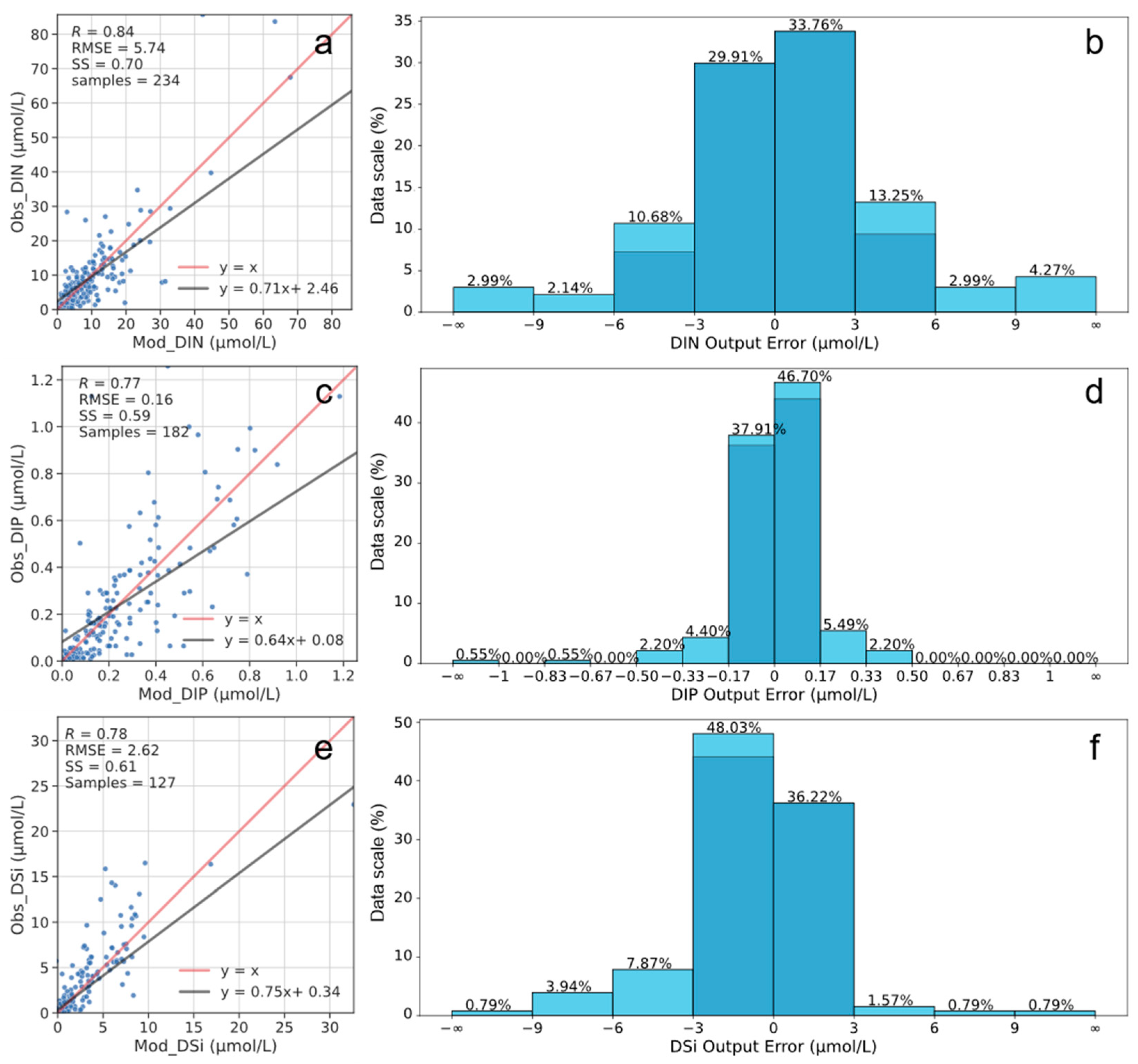
3.1. Evaluation of Machine-Learning Models

The test results of the nutrient models with different machine-learning algorithms are shown in Table 2. Generally, the performances of the three models were satisfactory, with all R values >0.7 and all SS values >0.5. The DIN model results obtained the highest R value (>0.8) for all three machine-learning algorithms, which was probably due to the larger amount of training data for DIN. In terms of the three evaluation indicators, the RFR algorithm obtained the highest accuracy among the three machine-learning algorithms, followed by ANN (Table 2). However, the spatial distribution of the nutrient concentrations of the RFR model showed a sudden change in the spatial distribution of the modeled nutrient concentrations (e.g., Figure 3), suggesting some degree of overfitting of the RFR model. Thus, in the following text, we mainly focus on the results of ANN, rather than RFR, as ANN showed good performance in both the evaluation indicators and spatial distribution. A good performance of the ANN was also suggested by previous oceanographic studies [28,47,50].
The detailed test results for the ANN models for the three nutrient concentrations are shown in Figure 4. The R values for DIN, DIP, and DSi were 0.84, 0.77, and 078, respectively, suggesting a good correlation between the model and observed results. The RMSE values of the DIN, DIP, and DSi were 5.74, 0.16, and 2.62 μmol/L, respectively. The histogram of the model bias distribution showed that >63% of the DIN bias was within the range of ±3 μmol/L, >80% of the DIP bias was within the range of ±0.17 μmol/L, and >80% of the DSi bias was within the range of ±3 μmol/L. The SS values for the ANN models of DIN, DIP, and DSi were 0.70, 0.59, and 0.61, respectively, suggesting good model performances. Thus, the trained ANN models were reliable for reconstructing nutrient concentrations in the YBS.

3.2. Surface Nutrient Concentrations of the YBS from 2003–2019

The monthly mean surface DIN, DIP, and DSi concentrations in the YBS from 2003–2019 were derived from the ANN models by inputting the monthly mean SST, SSS, Chl-a, and Kd490 from 2003–2019. The spatiotemporal variability of DIN, DIP, and DSi concentrations and their ratios were analyzed. To explore the regional difference in the seasonal variation, we selected six representative subregions [Figure 1a; the subregions of the Bohai Sea (BS), North Yellow Sea (NYS), South Yellow Sea (SYS), Subei Coastal water (SCW), Changjiang River Estuary (CRE), and Yellow River Estuary (YRE)]. The spatial mean nutrient concentrations in each subregion were calculated, and the seasonal and interannual variations were analyzed.

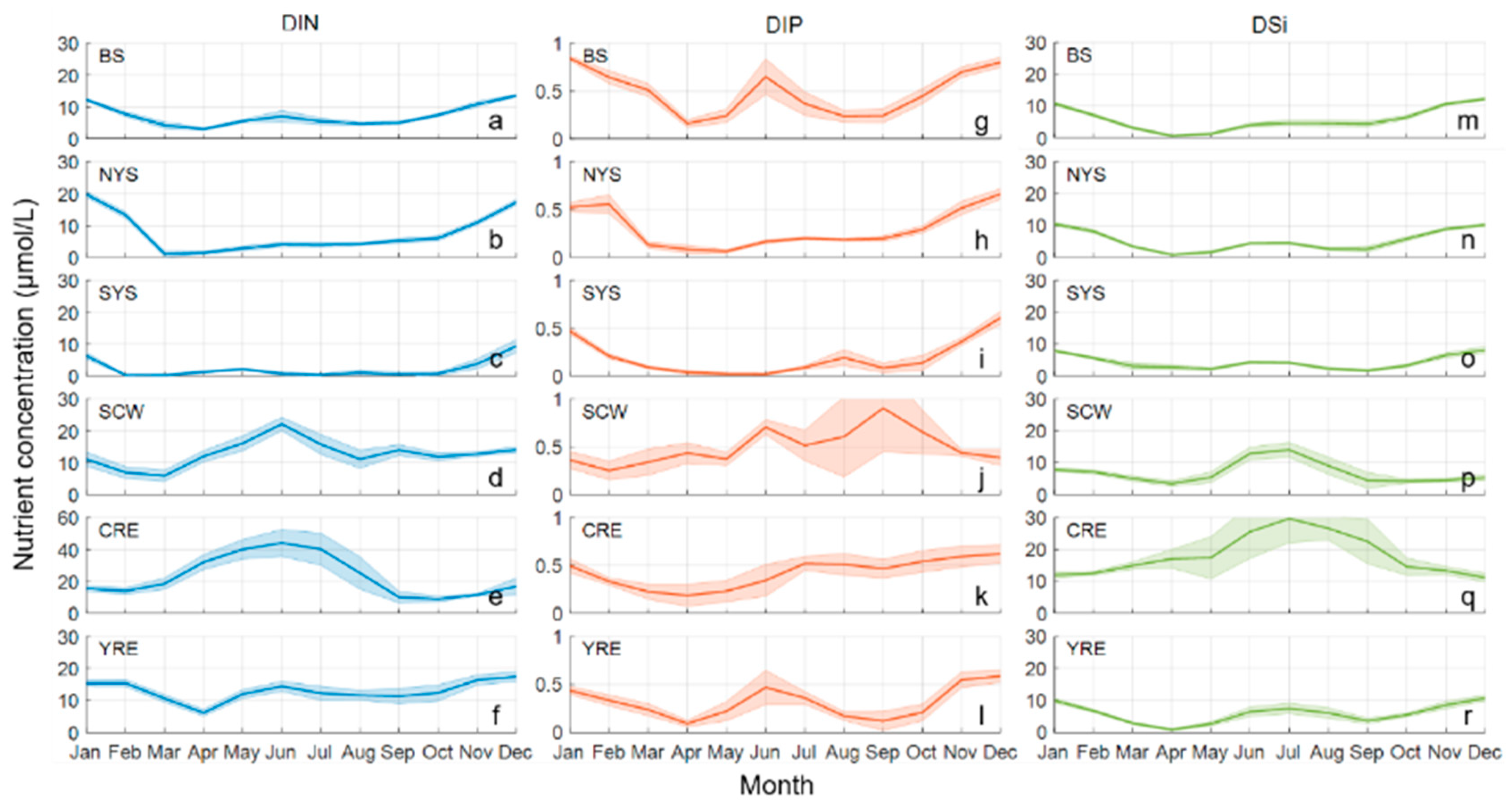
3.2.1. Regional and Seasonal Variations

As shown in Figure 5, all three nutrients showed relatively high concentrations in nearshore waters (water depth ≤ 40 m) and relatively low concentrations in deep offshore waters (water depth > 40 m). The average DIN, DIP, and DSi concentration were 11.09, 0.41, and 6.74 μmol/L in the nearshore waters, and 4.24, 0.37, and 5.59 μmol/L in offshore waters, respectively. The DIN and DSi concentrations were highest in the CRE region with annual average concentrations of 23.0 μmol/L and 18.1 μmol/L, respectively, and lowest in the SYS region with annual average concentrations of 2.4 μmol/L and 4.1 μmol/L, respectively. The highest and lowest DIP concentrations occurred in the SCW region (annual average concentration of 0.50 μmol/L) and the SYS region (annual average concentration of 0.19 μmol/L), respectively.
The nutrient concentrations in the different regions showed different seasonal variabilities (Figure 6). Nutrient concentrations were relatively high in winter (January and December) in offshore waters (i.e., SYS and NYS) and high in summer in coastal waters (i.e., SCW, CRE, and YRE). Generally, DIN, DIP, and DSi in the same region showed similar seasonal variability. However, in the BS, DIP showed a high concentration in June (0.6 μmol/L), whereas the DIN and DSi concentrations remained low in summer.

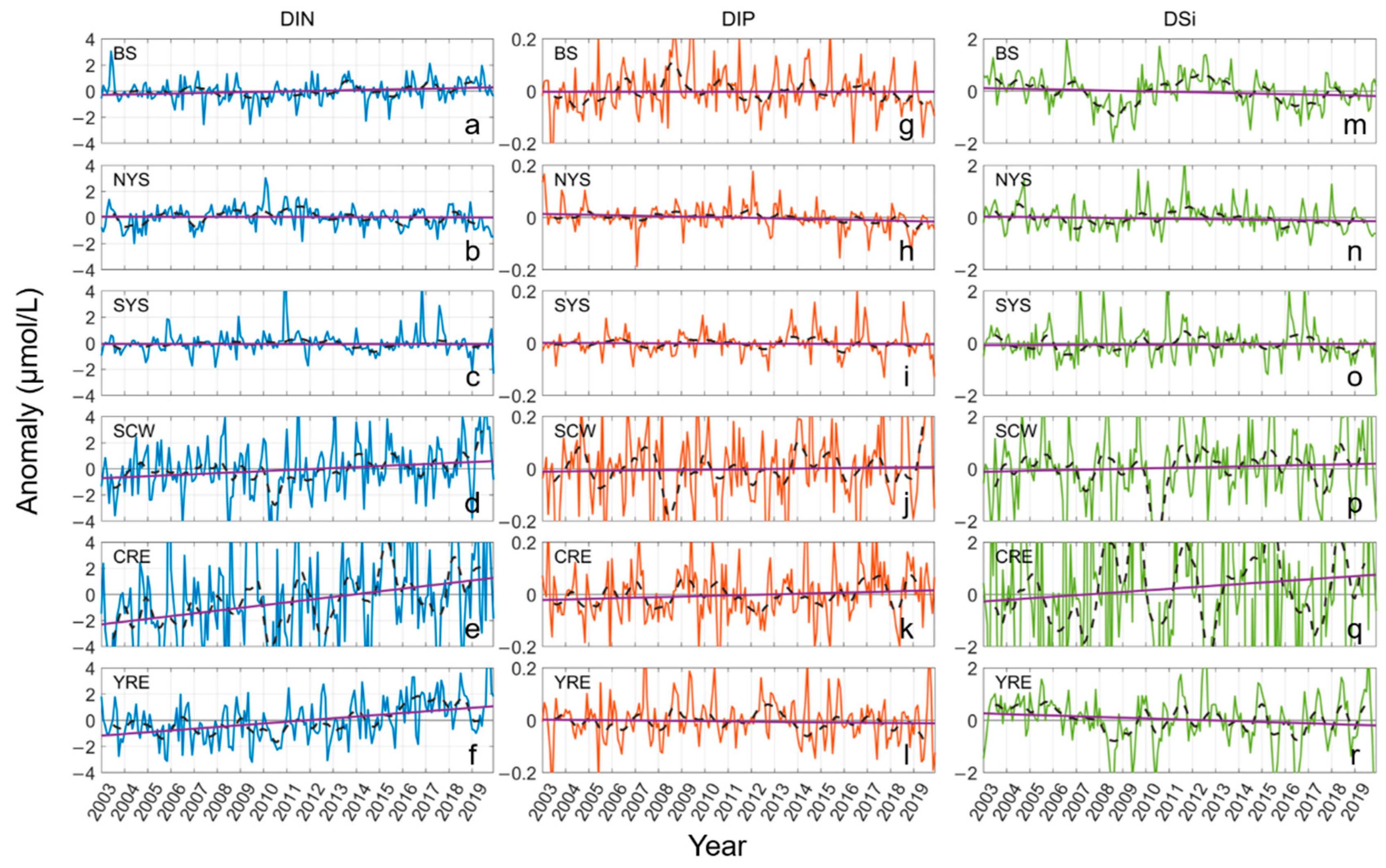
3.2.2. Interannual Trends

To analyze the interannual trend of nutrient concentrations from 2003–2019, we calculated the monthly anomalies of DIN, DIP, and DSi concentrations by subtracting the corresponding climatological monthly mean concentration from the monthly values, and conducted a linear regression on the anomalies. As shown in Figure 7, there were no significant interannual trends in the three nutrient concentrations in the BS, NYS, and SYS, which are relatively deep. The DIN concentration in nearshore waters showed an increasing trend (0.08, 0.21, and 0.13 μmol/L/y for SCW, CRE, and YRE, respectively) and the largest increasing trend occurred in the estuarine regions. The DSi concentration showed increasing trends in the CRE (0.06 μmol/L/y) and SCW (0.02 μmol/L/y), and a decreasing trend in the YRE (−0.03 μmol/L/y). However, the DIP concentration showed no significant interannual trends in either nearshore or offshore waters. The fluctuation of the monthly anomalies of DIN, DIP, and DSi concentrations suggested that the interannual variability of the nutrient concentrations in nearshore waters was much greater than that in offshore waters.

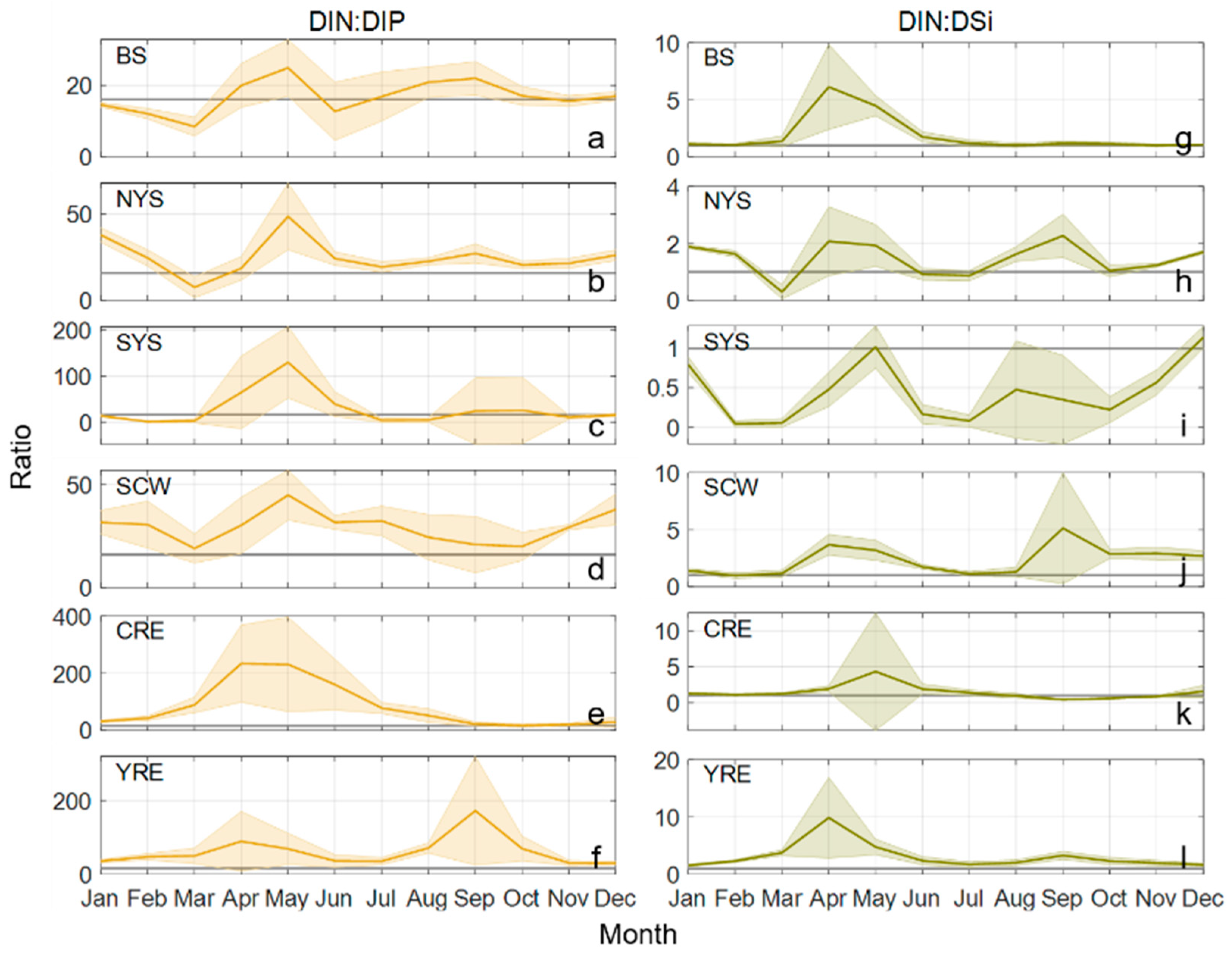
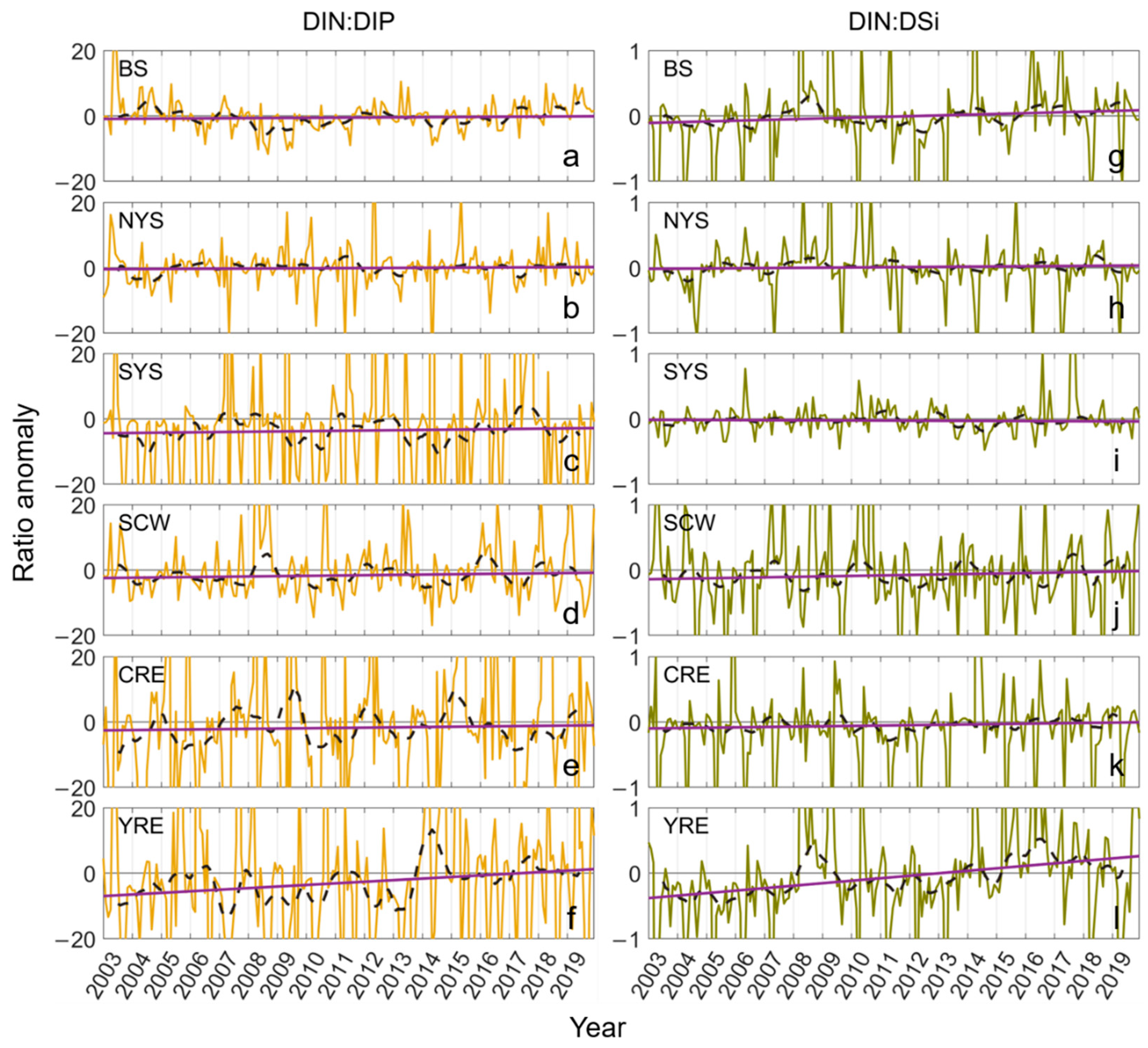
3.2.3. Nutrient Ratios

DIN, DIP, and DSi ratios are important for phytoplankton growth and communities [36]. Here, the DIN:DIP and DIN:DSi ratios in the six subregions were calculated to understand the variability in the nutrient ratios in the YBS. The classical Redfield ratio (i.e., N:P:Si = 16:1:16) was used as the threshold for nutrient limitation and was compared with the calculated nutrient ratios. Generally, the DIN:DIP and DIN:DSi ratios in most seasons were >16:1 and >1:1, respectively (Figure 8), indicating excess nitrogen in the YBS. These ratios were higher in nearshore waters than in offshore waters. The DIN:DIP ratios in the SCW, CRE, and YRE were ≥17 and up to 100 in spring, indicating strong DIP limitation in nearshore waters. In offshore waters, the DIN:DIP ratios were generally >16:1 in most months, except for January–March and June in the BS, March in the NYS, and January–March and July–August in the SYS, when the ratios were slightly less than 16:1. Except for SYS, the DIN:DSi in all five subregions was >1:1 in all years, and peaks occurred in spring.
There were no significant interannual trends in nutrient ratios from 2003–2019 in the six subregions except for the YRE (Figure 9), suggesting that the nutrient ratios were relatively stable in most areas of the YBS over these 17 years. In the YRE region, both DIN:DIP and DIN:DSi showed increasing trends over the study period, which were related to rapid increases in DIN and decreases in DSi (Figure 7). In addition, the fluctuation in the nutrient ratios suggested that the nutrient variability was more intense in nearshore waters than in offshore waters, corresponding to the great variability of the nutrient concentrations in nearshore waters (Figure 7).

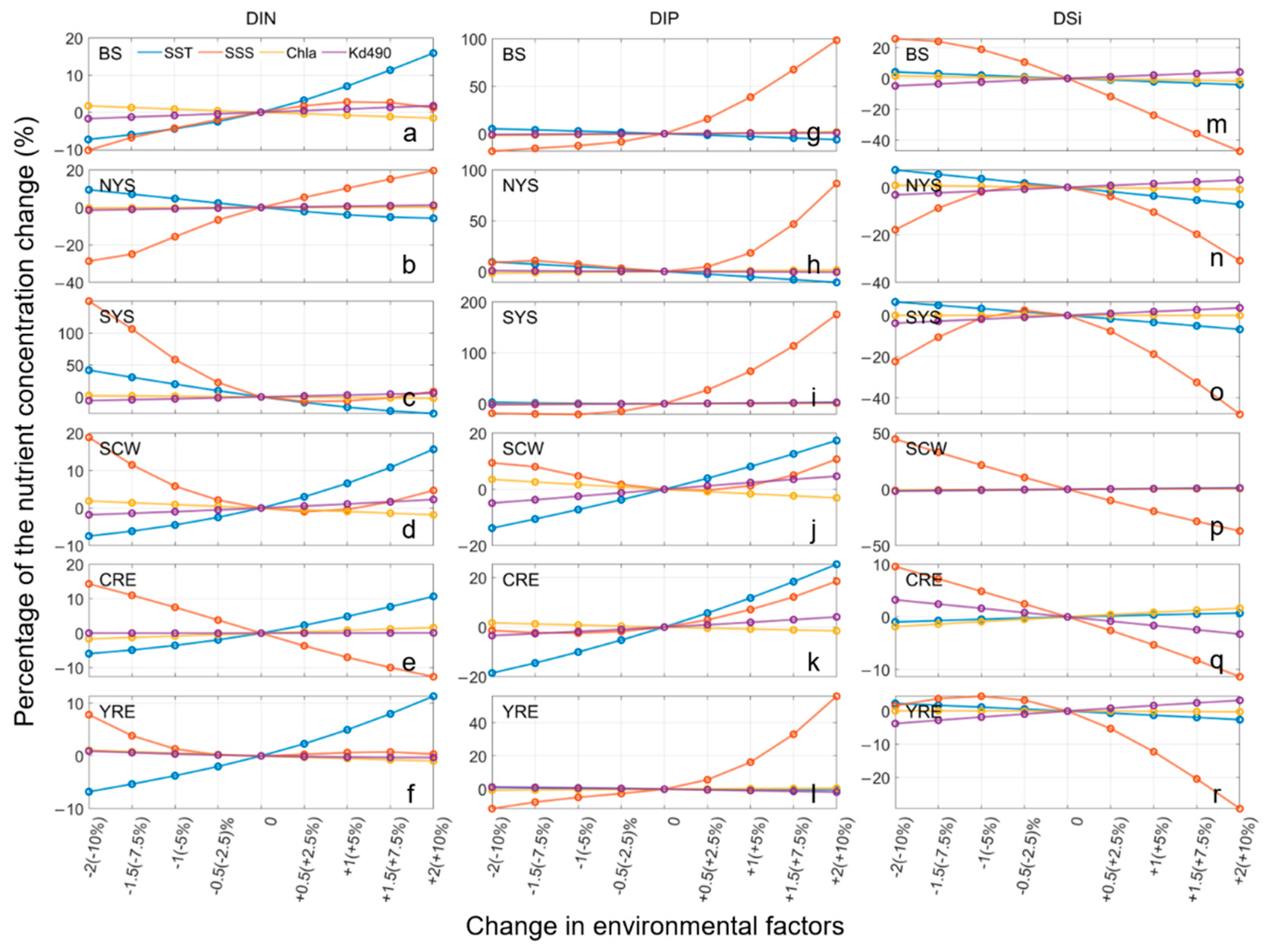
3.3. Effects of Environmental Factors

The effects of each environmental factor (SST, SSS, Chl-a, and Kd490) were further explored using a series of sensitivity experiments in which the annual mean nutrient concentration responses to the change in each factor were calculated (Figure 10). The experimental results showed that the effects of SST and SSS on the three nutrient concentrations were more significant than those of Chl-a and Kd490 in all regions. With increasing SST, the DIN concentration increased in nearshore waters (average increases of 5.8%/°C, 5.6%/°C, 4.2%/°C, and 4.4%/°C in BS, SCW, CRE, and YRE, respectively) but decreased in offshore waters (average decreases of −4.2%/°C and −17.7%/°C in NYS and SYS, respectively). The effects of SST on DIP and DSi were weaker than that on DIN; with increasing SST, DIP concentrations increased in the southwestern coastal area of the Yellow Sea (average increases of 7.7%/°C and 10.9%/°C in SCW and CRE, respectively) and decreased in all other regions (average decreases of −2.9%/°C, −5.1%/°C, 0.4%/°C, and −0.07%/°C in BS and NYS, YRE, and SYS, respectively). As for DIP, the DSi concentrations increased with increasing SST in the southwest part of the Yellow Sea (average increases of 0.6%/°C and 0.4%/°C in SCW and CRE, respectively) and decreased in all other regions (average decreases of −2.1%/°C, −3.6%/°C, −3.3%/°C, and −1.2%/°C in BS, NYS, SYS, and CRE, respectively).
Generally, with an increase in SSS, the DIN concentration decreased with average values of −33.2%/PSU, −3.2%/PSU, −7.1%/PSU, and −0.8%/PSU in SYS, SCW, CRE, and YRE, respectively, and the DSi concentration decreased in all regions (average decreases of −20.4%/PSU, −4.0%/PSU, −8.1%/PSU, −20.5%/PSU, −5.1%/PSU, and −8.2%/PSU in BS, NYS, SYS, SCW, CRE, and YRE, respectively); DIP increased in all regions except SCW, where there was an average decrease of −1.1%/PSU. However, DIN increased with increasing SSS in BS and NYS. The effects of SSS changes on DIP in offshore waters (i.e., BS, NYS, and SYS; average increase of 26.9%/PSU) were stronger than those in nearshore waters (average increase of 6.1%/PSU).

4. Discussion

4.1. Advantages and Limitations of the Machine-Learning Approach

This study proposed and examined a machine-learning method to reconstruct a large spatial scale and long time-series of marine nutrient concentrations in shelf seas. Using machine-learning modeling, the relationships between accessible marine environmental parameters (SST, SSS, Chl-a, and Kd490) and marine nutrient concentrations, sea-surface nutrient concentrations and their variability in the YBS were reconstructed by combining satellite-derived surface environmental data. Compared with the conventional ecological dynamics numerical simulation, the machine-learning method focuses more on the accuracy of the prediction results rather than the inherent processes of the system [51], which can greatly reduce the complexity and difficulty of modeling and the computational cost while ensuring prediction accuracy [52]. With the persistent and rapid increase in marine observation data, machine learning is becoming an additional popular and important method to simulate and predict the marine environment [53].
However, the marine environment is complex and diverse and the processes and rates of biogeochemical cycling exhibit significant regional differences [54]. In situ measured data used for training machine-learning models usually have a strong spatial limitation. Thus, machine-learning models established using data from a specific region may not be applicable to other marine areas [51]. The machine-learning model in this study was established based on in situ measurements of longitude, latitude and other data from YBS, thus, the applicability of this model in other marine areas remains to be tested.
There remains room for improvement in the accuracy of the machine-learning model in this study. The quantity of the dataset used to train the model is an important factor that affects the accuracy of machine-learning models. The amount of data is limited by resources, and there is room for improvement in the degree of data continuity and the data distribution range. Additional measured data may further improve the accuracy of the model [52]. Due to the inherent fluidity of the ocean, nutrient concentrations in shelf seas are affected by physical processes such as ocean currents and turbulent mixing [55]. Although the inputted marine environmental parameters in our model construction are also influenced by ocean dynamic processes and can reflect these physical processes to some extent, it is unclear whether the machine-learning model can accurately consider the influence of these physical processes on the predicted nutrient concentrations. In addition, satellite-derived SST, Chl-a, and Kd490 were used to drive the model to reconstruct monthly nutrient concentrations. Although these satellite products have been validated and used in YBS studies [56,57], suggesting that their quality is acceptable, they usually have some biases from the in situ measured values, which could also affect the accuracy of nutrient concentrations calculated by the model to a certain extent. The comparison of the reconstructive nutrient concentration with the observation data showed that compared with the original model trained by in situ measured data, the RMSE of DIN, DIP and DSi increased to ~30–40%, and the R and SS decreased ~0.1–0.2 (Table 3), suggesting the satellite remote sensing data increased the nutrient biases to some extent. On one hand, the biases of satellite data input in the model can directly induce the increase in the bias of the reconstructive nutrients. On the other hand, the reconstructive nutrients were monthly averaged and had a despondency in time with the in situ instantaneously measured data. In the future, the model accuracy will gradually improve with increases in the observation dataset and quality of satellite products.
Machine-learning algorithms are diverse and are continuously updated, and other machine-learning algorithms can be further tested to improve the prediction accuracy of the model. In addition, owing to data limitations, only the nutrient concentrations at the sea surface were reconstructed in this study. In the future, with the acquisition of more profiling data, the spatial three-dimensional nutrient concentrations can be reconstructed.

4.2. Dynamics of Spatiotemporal Variability of Nutrients in the YBS

To understand the reconstructed results and examine their rationality in combination with previous studies, we discussed the dynamics of the variability in sea-surface nutrients in the YBS from four aspects: regional and seasonal variations, interannual trends, nutrient ratio, and the effects of environmental factors.

4.2.1. Regional and Seasonal Variations

Our results (Figure 5 and Figure 6) showed that the DIN, DIP, and DSi concentrations were high in nearshore waters (CJE, YRE, and JCW) and low in offshore waters (NYS, SYS, and BS), which is consistent with previous field investigations and understandings of nutrients in the YBS [58]. Meanwhile, nutrient concentrations in nearshore and offshore waters showed different seasonal variations; the concentrations in offshore waters were higher in winter and lower in other seasons, whereas those in nearshore waters (especially in estuary areas) were usually highest in summer.
River runoff inputs large amounts of terrigenous nutrients to nearshore waters, along with strong mixing and tides, resulting in high nutrient concentrations in estuaries and nearshore waters [42,58,59]. The YBS region is influenced by the East Asian monsoon climate, with the rainy season being May–August [60]. In the rainy season, the large amount of terrigenous nutrients brought by the runoff causes the nutrient concentrations in the nearshore waters to peak in spring and summer. In contrast, the offshore waters of the YBS (i.e., SYS and NYS) are far from the estuary and are less influenced by terrigenous nutrients [61]. In addition, frequent strong stratification in offshore waters limits the nutrient supply from the bottom layer to the euphotic layer, which, combined with the assimilation of phytoplankton, results in relatively low nutrient concentrations in these offshore waters [58,62,63,64]. In winter, intense sea surface cooling and winds can enhance vertical mixing [62], which brings rich bottom nutrients to the upper layer and significantly increases sea-surface nutrient concentrations [65]. Moreover, there is a strong light limitation for phytoplankton in the YBS in winter [31], resulting in the relatively weak phytoplankton absorption of nutrients, thus resulting in higher surface nutrient concentrations in the offshore water in the YBS in winter than in other seasons.
The concentration of DIP is higher in the winter and spring in the south of Jeju Island, which has a large difference with DIN and DSi. In winter and spring, the sea area around Jeju Island is influenced by the Yellow Sea Warm Current, which originates from the Kuroshio. The Kuroshio Subsurface Water is of high DIP [66], which could be the source of the high DIP content near Jeju Island in winter and spring.

4.2.2. Interannual Trends

The results of this study showed a significant increasing trend in DIN in nearshore waters during 2003–2019. DSi had decreasing and increasing trends in the YRE and CRE, respectively, and DIN and DSi showed no significant changes in offshore waters. DIP showed no significant changes throughout the YBS area. River inputs are important external sources of nutrients for nearshore waters [67,68]. With increases in agricultural fertilization, sewage discharge, and aggravated soil erosion, the amount of DIN entering the ocean continues to increase [61,69], resulting in an increasing trend in DIN concentrations from 2003–2019 in most nearshore waters of the YBS, and a particularly evident increasing trend in estuarine areas. Decreases in DSi in the YRE region and BS were probably due to the influence of the construction of dams and reservoirs and irrigation, which resulted in the reduction of the Yellow River sediment flux to the Bohai Sea [70], as river water input is one of the most important contributors to DSi in the Bohai Sea [71]. The interannual fluctuation of DSi in the CRE region was large. However, it showed an overall increasing trend from 2003–2019, which has also been found in several previous studies [72,73,74]. The increase in DSi in CRE may have been related to enhanced silicate weathering and scouring of riverbed sediments in the middle and lower reaches of the Changjiang River following the completion of the Three Gorges Dam [72,73,74]. The YBS is generally a phosphorus-limited sea [75], and its absorption and utilization by phytoplankton maintains low DIP concentrations. Due to the excess DIN and DSi, changes in DIN and DSi may not significantly affect changes in DIP. Nutrients in offshore waters are dominated by local biogeochemical cycling and sediment release [61,76], therefore the interannual variations in nutrients in the surface layer in offshore waters were not significant.

4.2.3. Nutrient Ratios

The DIN:DIP ratios in most areas of the YBS were much higher than the Redfield ratio in the spring and summer, indicating a strong DIP-limitation for plankton growth, whereas DIP limitation was weak to some extent in autumn and winter, similar to the results of [42]. With enhanced phytoplankton biological activity in spring and summer, DIP consumption by phytoplankton in the upper layer and the low DIP stock in water were the main reasons for the high DIN:DIP ratio [42]. Terrigenous nutrients, such as the Changjiang and Yellow rivers, are characterized by high nitrogen concentrations [71,77]. The high nitrogen input from rivers resulted in higher DIN:DIP and DIN:DSi ratios in nearshore waters than in offshore waters in the YBS [71,75,78,79,80]. Similar to DIN:DIP, the DIN:DSi ratios in most areas of the YBS were larger in spring and summer than in autumn and winter. Although in most cases the DIN:DSi ratios were slightly larger than the Redfield ratio, the DSi concentrations were >5 μmol/L, which is sufficiently high for phytoplankton growth [81]. Thus, compared to DIP, DSi was not a major limiting factor for phytoplankton growth [75]. Nutrient ratios did not change significantly from 2003–2019; however, DIN:DIP and DIN:DSi in the YRE, CRE, and JCW showed increasing trends, which may have been related to increases in terrigenous DIN fluxes [69,82].

4.2.4. Effects of Environmental Factors

The sensitivity experimental results of the model showed that YBS sea-surface nutrient concentrations exhibited a strong response to changes in SST and SSS, which is similar to the conclusions of previous studies in other seas [83,84,85]. Shelf sea nutrient concentrations are strongly influenced by the physical environment of the ocean, while salinity and temperature are important factors reflecting the marine physical environment, such as the mixing of different water masses and the stratification intensity. Sensitivity experiments suggested that the DIN and DSI increased with an increase in SSS, whereas, the DIP decreased (Figure 10). YBS waters are mainly composed of fresh water introduced by river runoff (terrigenous source) and high-salinity seawater (oceanic source), and the salinity changes reflect the changes in the mixing ratios of terrigenous and oceanic-source waters. The nutrient concentrations and structures of terrigenous and oceanic-source waters differ considerably, whereby terrigenous-source waters tend to have higher DIN and DSi concentrations and a high DIN:DIP ratio, whereas oceanic-source waters tend to have relatively high DIP concentration [86]. The increase in SSS observed in this study indicated a lower proportion of terrigenous-source waters and a higher proportion of oceanic-source waters, which can explain the decreases in DIN and DSi and the increase in DIP with the increase in SSS. In addition, DIP could be released from terrigenous particulate phosphorus with an increase in salinity [87,88], which may have been an additional cause of the positive correlation between DIP and SSS. The experimental results also showed that with increasing SST, DIN increased significantly in the nearshore waters, whereas all three nutrients in the deep offshore waters decreased slightly (Figure 10). The increasing SST could represent a longer spring and summer season, and, thus, increased nutrient inputs from terrigenous sources, resulting in a positive relationship between surface DIN and SST in nearshore waters [42]. In contrast, the sea-surface nutrient concentration in offshore waters is significantly influenced by stratification [65]. The increasing SST indicated intensified stratification that could inhibit vertical mixing and upward nutrient transport, which may explain the decrease in nutrient concentrations with the increase in SST in offshore waters. Compared with SST and SSS, Chl-a and Kd490 had relatively weak effects on nutrient concentrations (Figure 10), which may have been because the strong DIP limitation maintained a relatively low phytoplankton biomass, and the nutrient uptake by phytoplankton was much less than the DIN and DSi stocks in water.

5. Conclusions

This study established a machine-learning model of sea-surface nutrients based on in situ measured data, and reconstructed the monthly sea-surface DIN, DIP, and DSi concentrations in the YBS from 2003–2019 using satellite remote-sensing data and a machine-learning model. The ANN machine-learning algorithm showed the best nutrient prediction performance. Based on the ANN reconstructed results, the following conclusions can be drawn: (1) The nutrient concentrations were relatively high in nearshore waters and low in offshore waters, and opposite seasonal variability was observed in nearshore and offshore waters. (2) From 2003–2019, DIN in the nearshore waters showed an increasing trend; DSi showed decreasing and increasing trends in the YRE and CRE, respectively, and DIP showed no significant trend. (3) DIN:DIP and DIN:DSi ratios exceeded the Redfield ratio in spring and summer, were slightly lower than the Redfield ratio in autumn and winter, and both showed increasing trends in some nearshore water areas from 2003–2019. (4) Generally, DIN and DSi decreased and DIP increased with an increase in SSS. With an increase in SST, the nutrient concentration increased in nearshore waters and decreased in offshore waters. This study proposed a machine-learning method to reconstruct a long time-series and high spatial resolution sea-surface nutrient concentrations in the YBS. This method is easy to implement and can be applied to other shelf seas if sufficient observational data is available.

Author Contributions

H.L.: Methodology, Software, Writing-Original draft preparation. L.L.: Conceptualization, Methodology, Funding acquisition, Writing-Reviewing and Editing. Y.W.: Formal analysis, Investigation. L.D.: Formal analysis. S.W.: Software. P.Z.: Data curation. Y.Y.: Formal analysis. X.G.: Formal analysis. X.L.: Supervision. All authors have read and agreed to the published version of the manuscript.

Funding

This study was supported by the National Natural Science Foundation of China (Grant No. 42030402, 41876127, and 41706011), and the Open Research Fund of State Key Laboratory of Estuarine and Coastal Research (Grant number SKLEC-KF202105). Xiang Gong was supported by CAS Key Laboratory of Coastal Environmental Processes and Ecological Remediation, YICCAS (Grant number 2020KFJJ04). The data acquisition and sample collection were supported by the National Natural Science Foundation of China (NSFC) Open Research Cruise (Cruise No. NORC2010-02, NORC2011-01, NORC2012-01, NORC2013-01, NORC2014-01, NORC2015-01, NORC2016-01, NORC2017-01, NORC2018-01, and NORC2019-01), funded by the Shiptime Sharing Project of NSFC.

Data Availability Statement

These satellite data used in this study can be downloaded from the U.S. National Aeronautics and Space Administration (NASA) website (http://oceancolor.gsfc.nasa.gov, accessed on 3 August 2021).

Acknowledgments

We would like to thank NASA for providing access to the satellite data.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Redfield, A.C.; Ketchum, B.H.; Richards, F.A. The Influence of Organisms on the Composition of Sea-Water. Sea Ideas Obs. Prog. Study Seas 1963, 2, 26–77. [Google Scholar]
  2. Howarth, R.W. Nutrient Limitation of Net Primary Production in Marine Ecosystems. Annu. Rev. Ecol. Syst. 1988, 19, 89–110. [Google Scholar] [CrossRef]
  3. Kristiansen, S.; Hoell, E.E. The Importance of Silicon for Marine Production. Hydrobiologia 2002, 484, 21–31. [Google Scholar] [CrossRef]
  4. Tyrrell, T. The Relative Influences of Nitrogen and Phosphorus on Oceanic Primary Production. Nature 1999, 400, 525–531. [Google Scholar] [CrossRef]
  5. Jessen, C.; Bednarz, V.N.; Rix, L.; Teichberg, M.; Wild, C. Marine Eutrophication. In Environmental Indicators; Armon, R.H., Hänninen, O., Eds.; Springer: Dordrecht, The Netherlands, 2015; pp. 177–203. ISBN 978-94-017-9499-2. [Google Scholar]
  6. Chen, B.; Liu, H. Relationships between Phytoplankton Growth and Cell Size in Surface Oceans: Interactive Effects of Temperature, Nutrients, and Grazing. Limnol. Oceanogr. 2010, 55, 965–972. [Google Scholar] [CrossRef] [Green Version]
  7. George, J.A.; Lonsdale, D.J.; Merlo, L.R.; Gobler, C.J. The Interactive Roles of Temperature, Nutrients, and Zooplankton Grazing in Controlling the Winter–Spring Phytoplankton Bloom in a Temperate, Coastal Ecosystem, Long Island Sound. Limnol. Oceanogr. 2015, 60, 110–126. [Google Scholar] [CrossRef]
  8. Kubo, A.; Hashihama, F.; Kanda, J.; Horimoto-Miyazaki, N.; Ishimaru, T. Long-Term Variability of Nutrient and Dissolved Organic Matter Concentrations in Tokyo Bay between 1989 and 2015. Limnol. Oceanogr. 2019, 64, S209–S222. [Google Scholar] [CrossRef]
  9. Dutkiewicz, S.; Follows, M.J.; Bragg, J.G. Modeling the Coupling of Ocean Ecology and Biogeochemistry. Glob. Biogeochem. Cycles 2009, 23. [Google Scholar] [CrossRef] [Green Version]
  10. Luo, F.; Gou, H.; Li, R.; Wang, H.; Chen, Z.; Lin, W.; Li, K. Numerical Simulation on Marine Environmental Capacity in the Open Sea Area of Northern Jiangsu Province Using a Three-Dimensional Water Quality Model Based on FVCOM. Reg. Stud. Mar. Sci. 2021, 45, 101856. [Google Scholar] [CrossRef]
  11. Mitra, A.; Flynn, K.J. Promotion of Harmful Algal Blooms by Zooplankton Predatory Activity. Biol. Lett. 2006, 2, 194–197. [Google Scholar] [CrossRef] [PubMed]
  12. Dutkiewicz, S.; Cermeno, P.; Jahn, O.; Follows, M.J.; Hickman, A.E.; Taniguchi, D.A.A.; Ward, B.A. Dimensions of Marine Phytoplankton Diversity. Biogeosciences 2020, 17, 609–634. [Google Scholar] [CrossRef]
  13. Franks, P.J.S. Planktonic Ecosystem Models: Perplexing Parameterizations and a Failure to Fail. J. Plankton Res. 2009, 31, 1299–1306. [Google Scholar] [CrossRef] [Green Version]
  14. Chen, B.; Liu, H.; Xiao, W.; Wang, L.; Huang, B. A Machine-Learning Approach to Modeling Picophytoplankton Abundances in the South China Sea. Prog. Oceanogr. 2020, 189, 102456. [Google Scholar] [CrossRef]
  15. Geary, W.L.; Bode, M.; Doherty, T.S.; Fulton, E.A.; Nimmo, D.G.; Tulloch, A.I.T.; Tulloch, V.J.D.; Ritchie, E.G. A Guide to Ecosystem Models and Their Environmental Applications. Nat. Ecol. Evol. 2020, 4, 1459–1471. [Google Scholar] [CrossRef] [PubMed]
  16. Piroddi, C.; Coll, M.; Liquete, C.; Macias, D.; Greer, K.; Buszowski, J.; Steenbeek, J.; Danovaro, R.; Christensen, V. Historical Changes of the Mediterranean Sea Ecosystem: Modelling the Role and Impact of Primary Productivity and Fisheries Changes over Time. Sci. Rep. 2017, 7, 44491. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  17. Zheng, G.; Li, X.; Zhang, R.-H.; Liu, B. Purely Satellite Data–Driven Deep Learning Forecast of Complicated Tropical Instability Waves. Sci. Adv. 2020, 6, eaba1482. [Google Scholar] [CrossRef] [PubMed]
  18. Andersson, T.R.; Hosking, J.S.; Pérez-Ortiz, M.; Paige, B.; Elliott, A.; Russell, C.; Law, S.; Jones, D.C.; Wilkinson, J.; Phillips, T.; et al. Seasonal Arctic Sea Ice Forecasting with Probabilistic Deep Learning. Nat. Commun. 2021, 12, 5124. [Google Scholar] [CrossRef] [PubMed]
  19. Cannata, A.; Cannavò, F.; Moschella, S.; Gresta, S.; Spina, L. Exploring the Link between Microseism and Sea Ice in Antarctica by Using Machine Learning. Sci. Rep. 2019, 9, 13050. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  20. Pahlevan, N.; Smith, B.; Schalles, J.; Binding, C.; Cao, Z.; Ma, R.; Alikas, K.; Kangro, K.; Gurlin, D.; Hà, N.; et al. Seamless Retrievals of Chlorophyll-a from Sentinel-2 (MSI) and Sentinel-3 (OLCI) in Inland and Coastal Waters: A Machine-Learning Approach. Remote Sens. Environ. 2020, 240, 111604. [Google Scholar] [CrossRef]
  21. Chen, S.; Hu, C.; Barnes, B.B.; Wanninkhof, R.; Cai, W.-J.; Barbero, L.; Pierrot, D. A Machine Learning Approach to Estimate Surface Ocean PCO2 from Satellite Measurements. Remote Sens. Environ. 2019, 228, 203–226. [Google Scholar] [CrossRef]
  22. Cheng, Y.; Bhoot, V.N.; Kumbier, K.; Sison-Mangus, M.P.; Brown, J.B.; Kudela, R.; Newcomer, M.E. A Novel Random Forest Approach to Revealing Interactions and Controls on Chlorophyll Concentration and Bacterial Communities during Coastal Phytoplankton Blooms. Sci. Rep. 2021, 11, 19944. [Google Scholar] [CrossRef] [PubMed]
  23. Coutinho, F.H.; Thompson, C.C.; Cabral, A.S.; Paranhos, R.; Dutilh, B.E.; Thompson, F.L. Modelling the Influence of Environmental Parameters over Marine Planktonic Microbial Communities Using Artificial Neural Networks. Sci. Total Environ. 2019, 677, 205–214. [Google Scholar] [CrossRef] [PubMed]
  24. Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
  25. Wang, D.; Cui, Q.; Gong, F.; Wang, L.; He, X.; Bai, Y. Satellite Retrieval of Surface Water Nutrients in the Coastal Regions of the East China Sea. Remote Sens. 2018, 10, 1896. [Google Scholar] [CrossRef] [Green Version]
  26. Du, C.; Li, Y.; Lyu, H.; Liu, N.; Zheng, Z.; Li, Y. Remote Estimation of Total Phosphorus Concentration in the Taihu Lake Using a Semi-Analytical Model. Int. J. Remote Sens. 2020, 41, 7993–8013. [Google Scholar] [CrossRef]
  27. Huang, J.; Wang, D.; Gong, F.; Bai, Y.; He, X. Changes in Nutrient Concentrations in Shenzhen Bay Detected Using Landsat Imagery between 1988 and 2020. Remote Sens. 2021, 13, 3469. [Google Scholar] [CrossRef]
  28. Sammartino, M.; Marullo, S.; Santoleri, R.; Scardi, M. Modelling the Vertical Distribution of Phytoplankton Biomass in the Mediterranean Sea from Satellite Data: A Neural Network Approach. Remote Sens. 2018, 10, 1666. [Google Scholar] [CrossRef] [Green Version]
  29. Lei, S.; Xu, J.; Li, Y.; Lyu, H.; Liu, G.; Zheng, Z.; Xu, Y.; Du, C.; Zeng, S.; Wang, H.; et al. Temporal and Spatial Distribution of Kd(490) and Its Response to Precipitation and Wind in Lake Hongze Based on MODIS Data. Ecol. Indic. 2020, 108, 105684. [Google Scholar] [CrossRef]
  30. Wang, Y.; Liu, D.; Tang, D. Application of a Generalized Additive Model (GAM) for Estimating Chlorophyll-a Concentration from MODIS Data in the Bohai and Yellow Seas, China. Int. J. Remote Sens. 2017, 38, 639–661. [Google Scholar] [CrossRef]
  31. Lin, L.; Wang, Y.; Liu, D. Vertical Average Irradiance Shapes the Spatial Pattern of Winter Chlorophyll-a in the Yellow Sea. Estuar. Coast. Shelf Sci. 2019, 224, 11–19. [Google Scholar] [CrossRef]
  32. Sui, Q.; Bin, X.; Hanbing, X.; Yi, C.; Bijuan, C.; Zhengguo, C.; Dongsheng, D. Study on Temporal and Spatial Variation of Nutrients and Evaluation on Eutrophication in the Seawater of the Bohai Sea in Winter and Spring of 2014. Prog. Fish. Sci. 2016, 37, 10–15. [Google Scholar]
  33. Mi, T.Z.; Yao, Q.; Meng, J.; Zhang, X.L.; Liu, S.M. Distributions of Nutrients in the Southern Yellow Sea and East China Sea in Spring and Summer 2011. Chin. J. Oceanol. Limnol. 2012, 43, 678–688. [Google Scholar]
  34. Cui, Y.; Wang, B.; Chen, Q.; Huang, G.; Niu, Z. Distribution of Dissolved Silicate and Changes of Si: N and Si: P Ratio in Yangtze River Estuary before and after Impoundment of Three Gorges Reservoir. Acta Sci. Circumstantiae 2013, 33, 1974–1979. [Google Scholar] [CrossRef]
  35. Dong, S.; Liu, S.; Ren, J.; Li, J.; Zhang, J. Preliminary Estimates of Cross Shelf Transport Flux of Nutrients in the East China Sea in Spring. Mar. Environ. Sci. 2016, 35, 385–391. [Google Scholar] [CrossRef]
  36. Ye, R.; Liu, Y.; Cui, Y.; Wang, Z.; Ye, X. Temporal and Spatial Distributions of Nutrient Structure and Limitation on Phytoplankton in The East China Sea. Oceanol. Et Limnol. Sin. 2015, 46, 311–320. [Google Scholar] [CrossRef]
  37. Li, Z.; Song, S.; Li, C. Distribution of Chlorophyll a and Its Correlation with the Formation of Hypoxia in the Changjiang River Estuary and Its Adjacent Waters. Mar. Sci. 2016, 40, 1–10. [Google Scholar] [CrossRef]
  38. Li, Z.; Song, S.; Li, C.; Yu, Z. Preliminary Discussion on the Phytoplankton Assemblages and Its Response to the Environmental Changes in the Changjiang (Yangtze)River Estuary and Its Adjacent Waters during the Dry Season and the Wet Season. Acta Oceanol. Sin. 2017, 39, 124–144. [Google Scholar] [CrossRef]
  39. Chen, T.; Song, S.; Liu, Y.; Li, C. The 2015-2016 Annual Variation of Dinoflagellate Community and Amoebophrya Infections in The Changjiang (Yangtze) River Estuary and Adjacent Waters. Oceanol. Et Limnol. Sin. 2019, 50, 139–148. [Google Scholar] [CrossRef]
  40. Lv, M.; Luan, Q.; Peng, L.; Cui, Y.; Wang, J. Assemblages of Phytoplankton in the Yellow Sea in Response to the Physical Processes During the Summer of 2014. Adv. Mar. Sci. 2016, 35, 70–84. [Google Scholar] [CrossRef]
  41. Wei, Q.-S.; Yu, Z.-G.; Wang, B.-D.; Fu, M.-Z.; Xia, C.-S.; Liu, L.; Ge, R.-F.; Wang, H.-W.; Zhan, R. Coupling of the Spatial–Temporal Distributions of Nutrients and Physical Conditions in the Southern Yellow Sea. J. Mar. Syst. 2016, 156, 30–45. [Google Scholar] [CrossRef]
  42. Guo, C.; Zhang, G.; Sun, J.; Leng, X.; Xu, W.; Wu, C.; Li, X.; Pujari, L. Seasonal Responses of Nutrient to Hydrology and Biology in the Southern Yellow Sea. Cont. Shelf Res. 2020, 206, 104207. [Google Scholar] [CrossRef]
  43. Yu, Y.; Gao, H.; Shi, J.; Guo, X.; Liu, G. Diurnal Forcing Induces Variations in Seasonal Temperature and Its Rectification Mechanism in the Eastern Shelf Seas of China. J. Geophys. Res. Oceans 2017, 122, 9870–9888. [Google Scholar] [CrossRef] [Green Version]
  44. Cortes, C.; Vapnik, V. Support-Vector Networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
  45. Noble, W.S. What Is a Support Vector Machine? Nat. Biotechnol. 2006, 24, 1565–1567. [Google Scholar] [CrossRef] [PubMed]
  46. Vapnik, V.N. The Nature of Statistical Learning Theory, 2nd ed.; Springer: New York, NY, USA, 2000; ISBN 978-0-387-98780-4. [Google Scholar]
  47. Aparna, S.G.; D’Souza, S.; Arjun, N.B. Prediction of Daily Sea Surface Temperature Using Artificial Neural Networks. Int. J. Remote Sens. 2018, 39, 4214–4231. [Google Scholar] [CrossRef]
  48. McCulloch, W.S.; Pitts, W. A Logical Calculus of the Ideas Immanent in Nervous Activity. Bull. Math. Biophys. 1943, 5, 115–133. [Google Scholar] [CrossRef]
  49. Allen, J.I.; Somerfield, P.J.; Gilbert, F.J. Quantifying Uncertainty in High-Resolution Coupled Hydrodynamic-Ecosystem Models. J. Mar. Syst. 2007, 64, 3–14. [Google Scholar] [CrossRef]
  50. Landschützer, P.; Gruber, N.; Bakker, D.C.E.; Schuster, U.; Nakaoka, S.; Payne, M.R.; Sasse, T.P.; Zeng, J. A Neural Network-Based Estimate of the Seasonal to Inter-Annual Variability of the Atlantic Ocean Carbon Sink. Biogeosciences 2013, 10, 7793–7815. [Google Scholar] [CrossRef] [Green Version]
  51. Elith, J.; Leathwick, J.R. Species Distribution Models: Ecological Explanation and Prediction Across Space and Time. Annu. Rev. Ecol. Evol. Syst. 2009, 40, 677–697. [Google Scholar] [CrossRef]
  52. Lou, R.; Lv, Z.; Dang, S.; Su, T.; Li, X. Application of Machine Learning in Ocean Data. Multimed. Syst. 2021. [Google Scholar] [CrossRef]
  53. Li, X.; Liu, B.; Zheng, G.; Ren, Y.; Zhang, S.; Liu, Y.; Gao, L.; Liu, Y.; Zhang, B.; Wang, F. Deep-Learning-Based Information Mining from Ocean Remote-Sensing Imagery. Natl. Sci. Rev. 2020, 7, 1584–1605. [Google Scholar] [CrossRef] [PubMed]
  54. Levin, S.A. The Problem of Pattern and Scale in Ecology: The Robert H. MacArthur Award Lecture. Ecology 1992, 73, 1943–1967. [Google Scholar] [CrossRef]
  55. Paparella, F.; Vichi, M. Stirring, Mixing, Growing: Microscale Processes Change Larger Scale Phytoplankton Dynamics. Front. Mar. Sci. 2020, 7, 654. [Google Scholar] [CrossRef]
  56. Lin, L.; Liu, D.; Luo, C.; Xie, L. Double Fronts in the Yellow Sea in Summertime Identified Using Sea Surface Temperature Data of Multi-Scale Ultra-High Resolution Analysis. Cont. Shelf Res. 2019, 175, 76–86. [Google Scholar] [CrossRef]
  57. Wang, Y.; Tian, X.; Gao, Z. Evolution of Satellite Derived Chlorophyll-a Trends in the Bohai and Yellow Seas during 2002–2018: Comparison between Linear and Nonlinear Trends. Estuar. Coast. Shelf Sci. 2021, 259, 107449. [Google Scholar] [CrossRef]
  58. Shi, X.; Qi, M.; Tang, H.; Han, X. Spatial and Temporal Nutrient Variations in the Yellow Sea and Their Effects on Ulva Prolifera Blooms. Estuar. Coast. Shelf Sci. 2015, 163, 36–43. [Google Scholar] [CrossRef]
  59. Milliman, J.D.; Farnsworth, K.L. River Discharge to the Coastal Ocean: A Global Synthesis; Cambridge University Press: Cambridge, UK, 2011; ISBN 978-1-107-61218-1. [Google Scholar]
  60. Hwang, J.H.; Van, S.P.; Choi, B.-J.; Chang, Y.S.; Kim, Y.H. The Physical Processes in the Yellow Sea. Ocean. Coast. Manag. 2014, 102, 449–457. [Google Scholar] [CrossRef]
  61. Wang, Y.; Liu, Y.; Guo, H.; Zhang, H.; Li, D.; Yao, Z.; Wang, X.; Jia, C. Long-Term Nutrient Variation Trends and Their Potential Impact on Phytoplankton in the Southern Yellow Sea, China. Acta Oceanol. Sin. 2022, 41, 54–67. [Google Scholar] [CrossRef]
  62. Huang, T.-H.; Chen, C.-T.A.; Lee, J.; Wu, C.-R.; Wang, Y.-L.; Bai, Y.; He, X.; Wang, S.-L.; Kandasamy, S.; Lou, J.-Y.; et al. East China Sea Increasingly Gains Limiting Nutrient P from South China Sea. Sci. Rep. 2019, 9, 5648. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  63. Kim, D.; Shim, J.; Yoo, S. Seasonal Variations in Nutrients and Chlorophyll-a Concentrations in the Northern East China Sea. Ocean Sci. J. 2006, 41, 125–137. [Google Scholar] [CrossRef]
  64. Obenour, D.R.; Michalak, A.M.; Zhou, Y.; Scavia, D. Quantifying the Impacts of Stratification and Nutrient Loading on Hypoxia in the Northern Gulf of Mexico. Environ. Sci. Technol. 2012, 46, 5489–5496. [Google Scholar] [CrossRef] [PubMed]
  65. Doney, S.C. Plankton in a Warmer World. Nature 2006, 444, 695–696. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  66. Zhou, P.; Song, X.; Yuan, Y.; Wang, W.; Chi, L.; Cao, X.; Yu, Z. Intrusion of the Kuroshio Subsurface Water in the Southern East China Sea and Its Variation in 2014 and 2015 Traced by Dissolved Inorganic Iodine Species. Prog. Oceanogr. 2018, 165, 287–298. [Google Scholar] [CrossRef]
  67. Dittmar, T.; Kattner, G. The Biogeochemistry of the River and Shelf Ecosystem of the Arctic Ocean: A Review. Mar. Chem. 2003, 83, 103–120. [Google Scholar] [CrossRef]
  68. Qu, H.J.; Kroeze, C. Past and Future Trends in Nutrients Export by Rivers to the Coastal Waters of China. Sci. Total Environ. 2010, 408, 2075–2086. [Google Scholar] [CrossRef] [PubMed]
  69. Wang, B.; Xin, M.; Wei, Q.; Xie, L. A Historical Overview of Coastal Eutrophication in the China Seas. Mar. Pollut. Bull. 2018, 136, 394–400. [Google Scholar] [CrossRef] [PubMed]
  70. Wang, H.; Yang, Z.; Saito, Y.; Liu, J.P.; Sun, X.; Wang, Y. Stepwise Decreases of the Huanghe (Yellow River) Sediment Load (1950–2005): Impacts of Climate Change and Human Activities. Glob. Planet. Chang. 2007, 57, 331–354. [Google Scholar] [CrossRef]
  71. Wang, J.; Yu, Z.; Wei, Q.; Yao, Q. Long-Term Nutrient Variations in the Bohai Sea Over the Past 40 Years. J. Geophys. Res. Ocean. 2019, 124, 703–722. [Google Scholar] [CrossRef] [Green Version]
  72. Ran, X.; Yu, Z.; Chen, H.; Zhang, X.; Guo, H. Silicon and Sediment Transport of the Changjiang River (Yangtze River): Could the Three Gorges Reservoir Be a Filter? Environ. Earth Sci. 2013, 70, 1881–1893. [Google Scholar] [CrossRef]
  73. Ran, X.; Wu, W.; Song, Z.; Wang, H.; Chen, H.; Yao, Q.; Xin, M.; Liu, P.; Yu, Z. Decadal Change in Dissolved Silicate Concentration and Flux in the Changjiang (Yangtze) River. Sci. Total Environ. 2022, 839, 156266. [Google Scholar] [CrossRef] [PubMed]
  74. Wang, X.; Yang, S.; Ran, X.; Liu, X.-M.; Bataille, C.P.; Su, N. Response of the Changjiang (Yangtze River) Water Chemistry to the Impoundment of Three Gorges Dam during 2010–2011. Chem. Geol. 2018, 487, 1–11. [Google Scholar] [CrossRef]
  75. Wang, B.; Wang, X.; Zhan, R. Nutrient Conditions in the Yellow Sea and the East China Sea. Estuar. Coast. Shelf Sci. 2003, 58, 127–136. [Google Scholar] [CrossRef]
  76. Liu, S.M.; Altabet, M.A.; Zhao, L.; Larkum, J.; Song, G.D.; Zhang, G.L.; Jin, H.; Han, L.J. Tracing Nitrogen Biogeochemistry During the Beginning of a Spring Phytoplankton Bloom in the Yellow Sea Using Coupled Nitrate Nitrogen and Oxygen Isotope Ratios. J. Geophys. Res. Biogeosci. 2017, 122, 2490–2508. [Google Scholar] [CrossRef]
  77. Tong, Y.; Zhao, Y.; Zhen, G.; Chi, J.; Liu, X.; Lu, Y.; Wang, X.; Yao, R.; Chen, J.; Zhang, W. Nutrient Loads Flowing into Coastal Waters from the Main Rivers of China (2006–2012). Sci. Rep. 2015, 5, 16678. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  78. Harrison, P.J.; Hu, M.H.; Yang, Y.P.; Lu, X. Phosphate Limitation in Estuarine and Coastal Waters of China. J. Exp. Mar. Biol. Ecol. 1990, 140, 79–87. [Google Scholar] [CrossRef]
  79. Zhang, J.; Yu, Z.G.; Raabe, T.; Liu, S.M.; Starke, A.; Zou, L.; Gao, H.W.; Brockmann, U. Dynamics of Inorganic Nutrient Species in the Bohai Seawaters. J. Mar. Syst. 2004, 44, 189–212. [Google Scholar] [CrossRef]
  80. Zhou, M.; Shen, Z.; Yu, R. Responses of a Coastal Phytoplankton Community to Increased Nutrient Input from the Changjiang (Yangtze) River. Cont. Shelf Res. 2008, 28, 1483–1489. [Google Scholar] [CrossRef]
  81. Justić, D.; Rabalais, N.N.; Turner, R.E.; Dortch, Q. Changes in Nutrient Structure of River-Dominated Coastal Waters: Stoichiometric Nutrient Balance and Its Consequences. Estuar. Coast. Shelf Sci. 1995, 40, 339–356. [Google Scholar] [CrossRef]
  82. Xin, M.; Wang, B.; Xie, L.; Sun, X.; Wei, Q.; Liang, S.; Chen, K. Long-Term Changes in Nutrient Regimes and Their Ecological Effects in the Bohai Sea, China. Mar. Pollut. Bull. 2019, 146, 562–573. [Google Scholar] [CrossRef]
  83. Burford, M.A.; Webster, I.T.; Revill, A.T.; Kenyon, R.A.; Whittle, M.; Curwen, G. Controls on Phytoplankton Productivity in a Wet–Dry Tropical Estuary. Estuar. Coast. Shelf Sci. 2012, 113, 141–151. [Google Scholar] [CrossRef] [Green Version]
  84. Paetsch, J.; Gouretski, V.; Hinrichs, I.; Koul, V. Distinct Mechanisms Underlying Interannual to Decadal Variability of Observed Salinity and Nutrient Concentration in the Northern North Sea. J. Geophys. Res.-Oceans 2020, 125, e2019JC015825. [Google Scholar] [CrossRef] [Green Version]
  85. Zainol, Z.; Akhir, M.F.; Abdullah, S. Hydrodynamics, Nutrient Concentrations, and Phytoplankton Biomass in a Shallow and Restricted Coastal Lagoon under Different Tidal and Monsoonal Environmental Drivers. Reg. Stud. Mar. Sci. 2020, 38, 101376. [Google Scholar] [CrossRef]
  86. Fang, T.-H. Phosphorus Speciation and Budget of the East China Sea. Cont. Shelf Res. 2004, 24, 1285–1299. [Google Scholar] [CrossRef]
  87. Carritt, D.E.; Goodgal, S. Sorption Reactions and Some Ecological Implications. Deep. Sea Res. 1954, 1, 224–243. [Google Scholar] [CrossRef]
  88. Meng, J.; Yu, Z.; Yao, Q.; Bianchi, T.S.; Paytan, A.; Zhao, B.; Pan, H.; Yao, P. Distribution, Mixing Behavior, and Transformation of Dissolved Inorganic Phosphorus and Suspended Particulate Phosphorus along a Salinity Gradient in the Changjiang Estuary. Mar. Chem. 2015, 168, 124–134. [Google Scholar] [CrossRef]
Remotesensing 14 05021 g001 550
Figure 1. (a) Topography and the model domain of the Yellow and Bohai Seas (YBS). Six representative subregions (red boxes a1–a6) were selected and analyzed in this study. Boxes a1–a6 show the locations of the regions of the Bohai Sea (BS), the North Yellow Sea waters (NYS), South Yellow Sea waters (SYS), Subei Coastal Waters (SCW), Changjiang River Estuary water (CRE), and Yellow River Estuary water (YRE), respectively. (b) Sampling sites for measured dissolved inorganic nitrogen (DIN), inorganic phosphorus (DIP), and (DSi) data used in the model training.
Figure 1. (a) Topography and the model domain of the Yellow and Bohai Seas (YBS). Six representative subregions (red boxes a1–a6) were selected and analyzed in this study. Boxes a1–a6 show the locations of the regions of the Bohai Sea (BS), the North Yellow Sea waters (NYS), South Yellow Sea waters (SYS), Subei Coastal Waters (SCW), Changjiang River Estuary water (CRE), and Yellow River Estuary water (YRE), respectively. (b) Sampling sites for measured dissolved inorganic nitrogen (DIN), inorganic phosphorus (DIP), and (DSi) data used in the model training.
Remotesensing 14 05021 g001
Remotesensing 14 05021 g002 550
Figure 2. Process of modeling nutrient concentrations based on the in situ measured and satellite data and the machine-learning approaches. Lon, longitude; Lat, latitude; SST, sea surface temperature; SSS, sea surface salinity; Chl-a, chlorophyll-a; DIN, dissolved inorganic nitrogen; DIP, dissolved inorganic phosphorus; DSi, dissolved silicate; SVR, support vector regression; RFR, random forest regression; ANN, artificial neural network.
Figure 2. Process of modeling nutrient concentrations based on the in situ measured and satellite data and the machine-learning approaches. Lon, longitude; Lat, latitude; SST, sea surface temperature; SSS, sea surface salinity; Chl-a, chlorophyll-a; DIN, dissolved inorganic nitrogen; DIP, dissolved inorganic phosphorus; DSi, dissolved silicate; SVR, support vector regression; RFR, random forest regression; ANN, artificial neural network.
Remotesensing 14 05021 g002
Remotesensing 14 05021 g003 550
Figure 3. Spatial distributions of the modeled dissolved inorganic nitrogen concentrations in 2015 with different machine-learning algorithms. SVR, support vector regression; RFR, random forest regression; ANN, artificial neural network. (a) SVR, (b) RFR, (c) ANN.
Figure 3. Spatial distributions of the modeled dissolved inorganic nitrogen concentrations in 2015 with different machine-learning algorithms. SVR, support vector regression; RFR, random forest regression; ANN, artificial neural network. (a) SVR, (b) RFR, (c) ANN.
Remotesensing 14 05021 g003
Remotesensing 14 05021 g004 550
Figure 4. Evaluation of the artificial neural network models for: (a,b) dissolved inorganic nitrogen (DIN) concentrations, (c,d) dissolved inorganic phosphorus (DIP) concentrations, and (e,f) dissolved silicate (DSi) concentrations. (a,c,e) show the correlations between the model and observed results; (b,d,f) show the error distributions of the model output. R, correlation coefficient; RMSE, root mean square error; SS, skill score.
Figure 4. Evaluation of the artificial neural network models for: (a,b) dissolved inorganic nitrogen (DIN) concentrations, (c,d) dissolved inorganic phosphorus (DIP) concentrations, and (e,f) dissolved silicate (DSi) concentrations. (a,c,e) show the correlations between the model and observed results; (b,d,f) show the error distributions of the model output. R, correlation coefficient; RMSE, root mean square error; SS, skill score.
Remotesensing 14 05021 g004
Remotesensing 14 05021 g005 550
Figure 5. Spatial distributions of climatological monthly mean concentrations of dissolved inorganic nitrogen (DIN), dissolved inorganic phosphorus (DIP), and dissolved silicate (DSi) from 2003–2019.
Figure 5. Spatial distributions of climatological monthly mean concentrations of dissolved inorganic nitrogen (DIN), dissolved inorganic phosphorus (DIP), and dissolved silicate (DSi) from 2003–2019.
Remotesensing 14 05021 g005
Remotesensing 14 05021 g006 550
Figure 6. Climatological monthly mean concentrations of: (a–f) dissolved inorganic nitrogen (DIN), (g–l) dissolved inorganic phosphorus (DIP), and (m–r) dissolved silicate (DSi) for the six subregions from 2003–2019. Shading denotes the standard deviations. BS, Bohai Sea; NYS, North Yellow Sea waters; SYS, South Yellow Sea waters; SCW, Subei Coastal Waters; CRE, Changjiang River Estuary water; YRE, Yellow River Estuary water.
Figure 6. Climatological monthly mean concentrations of: (a–f) dissolved inorganic nitrogen (DIN), (g–l) dissolved inorganic phosphorus (DIP), and (m–r) dissolved silicate (DSi) for the six subregions from 2003–2019. Shading denotes the standard deviations. BS, Bohai Sea; NYS, North Yellow Sea waters; SYS, South Yellow Sea waters; SCW, Subei Coastal Waters; CRE, Changjiang River Estuary water; YRE, Yellow River Estuary water.
Remotesensing 14 05021 g006
Remotesensing 14 05021 g007 550
Figure 7. Monthly mean anomalies of: (a–f) dissolved inorganic nitrogen (DIN), (g–l) dissolved inorganic phosphorus (DIP), and (m–r) dissolved silicate (DSi) concentrations in six subregions from 2003–2019. Black dashed lines are 12-month moving averages. Blues lines are trend lines from linear regressions on the moving-average results. BS, Bohai Sea; NYS, North Yellow Sea waters; SYS, South Yellow Sea waters; SCW, Subei Coastal Waters; CRE, Changjiang River Estuary water; YRE, Yellow River Estuary water.
Figure 7. Monthly mean anomalies of: (a–f) dissolved inorganic nitrogen (DIN), (g–l) dissolved inorganic phosphorus (DIP), and (m–r) dissolved silicate (DSi) concentrations in six subregions from 2003–2019. Black dashed lines are 12-month moving averages. Blues lines are trend lines from linear regressions on the moving-average results. BS, Bohai Sea; NYS, North Yellow Sea waters; SYS, South Yellow Sea waters; SCW, Subei Coastal Waters; CRE, Changjiang River Estuary water; YRE, Yellow River Estuary water.
Remotesensing 14 05021 g007
Remotesensing 14 05021 g008 550
Figure 8. Climatological monthly mean values of the: (a–f) dissolved inorganic nitrogen: dissolved inorganic phosphorus ratio (DIN:DIP); and (g–l) dissolved inorganic nitrogen: dissolved silicate ratio (DIN:DSi) for the six subregions. Gray lines in (a–f) and (g–l) indicate the ratios of 16:1 and 1:1, respectively. BS, Bohai Sea; NYS, North Yellow Sea waters; SYS, South Yellow Sea waters; SCW, Subei Coastal Waters; CRE, Changjiang River Estuary water; YRE, Yellow River Estuary water.
Figure 8. Climatological monthly mean values of the: (a–f) dissolved inorganic nitrogen: dissolved inorganic phosphorus ratio (DIN:DIP); and (g–l) dissolved inorganic nitrogen: dissolved silicate ratio (DIN:DSi) for the six subregions. Gray lines in (a–f) and (g–l) indicate the ratios of 16:1 and 1:1, respectively. BS, Bohai Sea; NYS, North Yellow Sea waters; SYS, South Yellow Sea waters; SCW, Subei Coastal Waters; CRE, Changjiang River Estuary water; YRE, Yellow River Estuary water.
Remotesensing 14 05021 g008
Remotesensing 14 05021 g009 550
Figure 9. Monthly mean anomalies of: (a–f) the dissolved inorganic nitrogen: dissolved inorganic phosphorus ratio (DIN:DIP); and (g–l) the dissolved inorganic nitrogen: dissolved silicate ratio (DIN:DSi) in the six subregions from 2003–2019. Black dashed lines are 12-month moving averages. Blues lines are trend lines from linear regressions on moving-average results. BS, Bohai Sea; NYS, North Yellow Sea waters; SYS, South Yellow Sea waters; SCW, Subei Coastal Waters; CRE, Changjiang River Estuary water; YRE, Yellow River Estuary water.
Figure 9. Monthly mean anomalies of: (a–f) the dissolved inorganic nitrogen: dissolved inorganic phosphorus ratio (DIN:DIP); and (g–l) the dissolved inorganic nitrogen: dissolved silicate ratio (DIN:DSi) in the six subregions from 2003–2019. Black dashed lines are 12-month moving averages. Blues lines are trend lines from linear regressions on moving-average results. BS, Bohai Sea; NYS, North Yellow Sea waters; SYS, South Yellow Sea waters; SCW, Subei Coastal Waters; CRE, Changjiang River Estuary water; YRE, Yellow River Estuary water.
Remotesensing 14 05021 g009
Remotesensing 14 05021 g010 550
Figure 10. Relative changes in: (a–f) dissolved inorganic nitrogen (DIN), (g–l) dissolved inorganic phosphorus (DIP), and (m–r) dissolved silicate (DSi) concentrations for six sub-regions with changes in four environmental factors, i.e., sea surface temperature (SST), salinity (SSS), chlorophyll-a (Chl-a), and the water diffuse attenuation coefficient (Kd490). The values of the horizontal axis tick label denote the change relative to that in the control run. Note that the horizontal axis tick label values changed from −2 to +2 for SST (°C) and SSS (PSU), and from −10% to +10% for Chl-a and Kd490. BS, Bohai Sea; NYS, North Yellow Sea waters; SYS, South Yellow Sea waters; SCW, Subei Coastal Waters; CRE, Changjiang River Estuary water; YRE, Yellow River Estuary water.
Figure 10. Relative changes in: (a–f) dissolved inorganic nitrogen (DIN), (g–l) dissolved inorganic phosphorus (DIP), and (m–r) dissolved silicate (DSi) concentrations for six sub-regions with changes in four environmental factors, i.e., sea surface temperature (SST), salinity (SSS), chlorophyll-a (Chl-a), and the water diffuse attenuation coefficient (Kd490). The values of the horizontal axis tick label denote the change relative to that in the control run. Note that the horizontal axis tick label values changed from −2 to +2 for SST (°C) and SSS (PSU), and from −10% to +10% for Chl-a and Kd490. BS, Bohai Sea; NYS, North Yellow Sea waters; SYS, South Yellow Sea waters; SCW, Subei Coastal Waters; CRE, Changjiang River Estuary water; YRE, Yellow River Estuary water.
Remotesensing 14 05021 g010
Table
Table 1. Summary of in situ measured measurements in the Yellow and Bohai seas (YBS). DIN, dissolved inorganic nitrogen; DIP, inorganic phosphorus; DSi, dissolved silicate.
Table 1. Summary of in situ measured measurements in the Yellow and Bohai seas (YBS). DIN, dissolved inorganic nitrogen; DIP, inorganic phosphorus; DSi, dissolved silicate.
Data SourceSampling TimeNumber of Samples
DINDIPDSi
Cruise 1 in this study29 April–4 May 2010918991
Cruise 2 in this study2–20 May 2012116115116
Cruise 3 in this study2–19 November 2012105105105
Cruise 4 in this study28 April–18 May 2014106123122
Cruise 5 in this study8–23 November 2014123123123
Cruise 6 in this study14–30 January 2016777777
Cruise 7 in this study17 August–5 September 2015109107106
Cruise 8 in this study28 March–16 April 2018111113113
Cruise 9 in this study24 July–8 September 2018117117117
Cruise 10 in this study8 April–6 May 2019858585
Field Survey by EDSPMarch–October 2016425425\
Sui et al. [32]February & May 2014100100\
Mi et al. [33]6–25 April & 12–29 August 2011747474
Cui et al. [34]May 2011\\1
Dong et al. [35]10 May–5 June 2011666
Ye et al. [36]February & May & August & November 2013161216
Li et al. [37,38]4–20 March & 17–28 August 2013444
Chen et al. [39]2 February 2015–1 January 2016213622
Lv et al. [40]5–23 August 20144848\
Wei et al. [41](21 January, 15 April, 21 October), 2007 & 24 July 2006545\\
Guo et al. [42](4 May, 12 November), 2014 & 4 September 2015 & 22 January 2016939393
Total 237218521271
Table
Table 2. Correlation coefficient (R), root mean square error (RMSE), and skill score (SS) values for the test of the nutrient models with different machine-learning algorithms. DIN, dissolved inorganic nitrogen; DIP, inorganic phosphorus; DSi, dissolved silicate; SVR, support vector regression; RFR, random forest regression; ANN, artificial neural network.
Table 2. Correlation coefficient (R), root mean square error (RMSE), and skill score (SS) values for the test of the nutrient models with different machine-learning algorithms. DIN, dissolved inorganic nitrogen; DIP, inorganic phosphorus; DSi, dissolved silicate; SVR, support vector regression; RFR, random forest regression; ANN, artificial neural network.
Nutrient modelIndicatorSVRRFRANN
DINR0.810.840.84
RMSE (μmol/L)6.134.985.74
SS0.660.700.70
DIPR0.710.840.77
RMSE (μmol/L)0.180.130.16
SS0.510.710.59
DSiR0.730.870.78
RMSE (μmol/L)2.872.052.62
SS0.540.760.61
Table
Table 3. Correlation coefficient (R), root mean square error (RMSE), and skill score (SS) values for the reconstructive nutrient concentrations.
Table 3. Correlation coefficient (R), root mean square error (RMSE), and skill score (SS) values for the reconstructive nutrient concentrations.
IndicatorDINDIPDSi
R0.740.580.61
RMSE (μmol/L)6.770.213.69
SS0.540.340.37
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Liu, H.; Lin, L.; Wang, Y.; Du, L.; Wang, S.; Zhou, P.; Yu, Y.; Gong, X.; Lu, X. Reconstruction of Monthly Surface Nutrient Concentrations in the Yellow and Bohai Seas from 2003–2019 Using Machine Learning. Remote Sens. 2022, 14, 5021. https://doi.org/10.3390/rs14195021

AMA Style

Liu H, Lin L, Wang Y, Du L, Wang S, Zhou P, Yu Y, Gong X, Lu X. Reconstruction of Monthly Surface Nutrient Concentrations in the Yellow and Bohai Seas from 2003–2019 Using Machine Learning. Remote Sensing. 2022; 14(19):5021. https://doi.org/10.3390/rs14195021

Chicago/Turabian Style

Liu, Hao, Lei Lin, Yujue Wang, Libin Du, Shengli Wang, Peng Zhou, Yang Yu, Xiang Gong, and Xiushan Lu. 2022. "Reconstruction of Monthly Surface Nutrient Concentrations in the Yellow and Bohai Seas from 2003–2019 Using Machine Learning" Remote Sensing 14, no. 19: 5021. https://doi.org/10.3390/rs14195021

APA Style

Liu, H., Lin, L., Wang, Y., Du, L., Wang, S., Zhou, P., Yu, Y., Gong, X., & Lu, X. (2022). Reconstruction of Monthly Surface Nutrient Concentrations in the Yellow and Bohai Seas from 2003–2019 Using Machine Learning. Remote Sensing, 14(19), 5021. https://doi.org/10.3390/rs14195021

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop