AC-WGAN-GP: Generating Labeled Samples for Improving Hyperspectral Image Classification with Small-Samples

Abstract

The lack of labeled samples severely restricts the classification performance of deep learning on hyperspectral image classification. To solve this problem, Generative Adversarial Networks (GAN) are usually used for data augmentation. However, GAN have several problems with this task, such as the poor quality of the generated samples and an unstable training process. Thereby, knowing how to construct a GAN to generate high-quality hyperspectral training samples is meaningful for the small-sample classification task of hyperspectral data. In this paper, an Auxiliary Classifier based Wasserstein GAN with Gradient Penalty (AC-WGAN-GP) was proposed. The framework includes AC-WGAN-GP, an online generation mechanism, and a sample selection algorithm. The proposed method has the following distinctive advantages. First, the input of the generator is guided by prior knowledge and a separate classifier is introduced to the architecture of AC-WGAN-GP to produce reliable labels. Second, an online generation mechanism ensures the diversity of generated samples. Third, generated samples that are similar to real data are selected. Experiments on three public hyperspectral datasets show that the generated samples follow the same distribution as the real samples and have enough diversity, which effectively expands the training set. Compared to other competitive methods, the proposed framework achieved better classification accuracy with a small number of labeled samples.

1. Introduction

Hyperspectral imaging sensors can capture more spectral data than just visible light. The data takes the form of continuous spectral features and can be used for the accurate identification of a variety of surface materials on planet earth [1]. With the development of hyperspectral sensors, the spatial and spectral resolution of the collected hyperspectral images (HSI) are increasing higher and higher [2]. Therefore, hyperspectral remote sensing finds important applications in many fields [3,4], including mining [5], astronomy [6], agriculture [7], environmental science [8,9], wasteland fire tracking, and biological threat detection [10]. HSI classification technology is an important content of hyperspectral remote sensing of earth observation technology. Its specific task is the classification of the objects represented by each pixel in HSI.

Early HSI classification mostly used traditional machine learning and statistical methods, such as K Nearest Neighbor (KNN) [11], support vector machine (SVM) [12], distance classifier [13], and naive Bayes classifier [14]. These methods rely on manually designed features. However, the characteristics of hyperspectral images such as high dimensionality and much spatial information make it difficult for a single traditional classification model to achieve good results. Some methods of dimension reduction are used, such as principal component analysis (PCA) [15], linear discriminant analysis [16], and band selection methods [17]. A space-spectral fusion method based on conditional random fields is proposed in [18]. In another method, the original spectral features and extracted spatial features through the Gabor filter bank form a space-spectral fusion feature [19]. The above methods use original hyperspectral samples for training. Those conventional models require a lot of prior knowledge and expert experience. Although manual features based on prior knowledge show good performance for some datasets, they are not related to the data and task themselves. So, their generalization ability is limited [20].

Recently, classifiers based on deep learning are widely used in HSI classification. Deep learning can extract deep features automatically, which is more convenient and effective. For example, the stack autoencoder network (SAE) [21] and the convolutional neural network (CNN) [22] are used to extract spectral and spatial features. 1D-CNN only focuses on hyperspectral vectors, but good classification accuracy has been obtained [23]. 3D-CNN performs convolution operations on three-dimensional HSI patch samples, considering both the spatial and spectral dimensions [24]. Pu et al. proposed a spatial and spectral convolutional neural network to extract spatial-spectral features [25]. Ding et al. combined spectral information and spatial coordinates to generate probability maps to fuse spectral and spatial information [26]. Very recently, transformer shows great potential in the field of computer vision [27]. L. Sun, G. Zhao, Y. Zheng, and Z. Wu used CNN to obtain HSI feature maps, then the serialized feature map is fed into the transformer module [28]. The deep features are extracted adaptively according to different training sets. Thus, classifiers based on deep features are generally better than conventional ones [20]. However, they always require a great number of labeled samples to optimize the parameters, labelling samples are expensive in the field of hyperspectral image processing. Thus, most hyperspectral classification is performed with small sample sizes.

Hyperspectral image classification with small sample sizes involves semi-supervised learning, self-supervised learning, and sample augmentation methods. Both semi-supervised learning and self-supervised learning try to mine information from abundant unlabelled samples. DAE-GCN [29] propose a deep autoencoder model to extract relevant features from the HSI and constructs a spectral-spatial graph to train a semi-supervised graph convolutional network. L. Zhao, W. Luo, Q. Liao, S. Chen, and J [30] introduced a module to generate HSI sample pairs and used the available samples for training a self-supervised learning model based on a Siamese network. Then labeled samples are used to fine-tune the model. Li T. et al. [31] proposed a dual-branch residual neural network. A self-supervised learning pre-training method with the idea of recovering intermediate unlabelled pixel information through artificially divided image cube samples is designed. Then pre-trained weights and a few labeled samples are used for the training classifier. However, the semi-supervised and self-supervised learning methods are based on existing enough unlabeled samples. In fact, for some hyperspectral classifiers, unlabeled samples are also insufficient. So, in order to increase the number of samples, many data augmentation methods are proposed. Early sample augmentation methods [32] generate new samples by rotating, adding noise, and linearly combining existing original samples, assuming that these newly generated samples and original samples share the same label. Wang C. et al. established a data mixture model to augment the labeled training set quadratically [33]. The paradigm of conventional data augmentation methods is relatively fixed. And it cannot guarantee that the generated samples conform to the correct distribution and provide useful information.

Nowadays, many scholars use generative adversarial networks to learn the implicit distribution function of the base samples, and then produce new samples with the same distribution by random sampling. Traditional GAN networks [34] only generate samples of the same class, but cannot generate samples of multiple classes, resulting in that the generated samples cannot improve the classification accuracy effectively. To generate labeled samples, Odena et al. proposed the Auxiliary Classifier GAN (AC-GAN) [35]. As an approach to solving the multi-classification problem, its discriminator is used to output corresponding label probabilities, and each generated sample has a corresponding class label. In practice, both the truthfulness of the data and the likelihood of correct classification are taken into account by the objective function of the discriminator. The classification branch is added to alleviate the HSI classification problem using limited training samples. Based on these ideas, Y. Zhan et al. designed a GAN network with a one-dimensional spectral structure [36], trained a one-dimensional GAN network with unlabeled samples, and then converted the trained discriminator into a classification network. Chen et al. designed a 1D and 3D GAN network for HSI classification, combining the generated samples with the real training samples into a new class [37], which was fine-tuned in the discriminator to improve the final classification performance. Multiscale conditional adversarial networks [38] use multiple scales and stages to achieve a coarse-to-fine fashion. This method can achieve high-quality data augmentation with a small number of training samples. J. Feng et al. combined a self-supervised classifier and GAN [39]. The pretext cluster task was designed by leveraging abundant unlabeled samples, then transferring the learned cluster representation from the cluster task. HyperViTGAN [40] is proposed to deal with the class imbalance problem of HSI data. It also involves an external semi-supervised classifier to share the task of the discriminator in GAN. In response to gradient disappearance and mode collapse, Liang et al. proposed an average minimization loss constrained by unlabeled data for HSI [41]. Gulrajani et al. introduced WGAN-GP into the network to make training smoother and more efficient [42]. We find that when GAN is used to generate hyperspectral data, inputs are often noise or noise-label, lacking guidance and constraint from prior knowledge. It leads to unstable and low-quality generated results on multi-category tasks. Besides, although the generator may fit the distribution of real data well, the network that has been trained with fixed parameters cannot generate data that satisfies the diversity under the same distribution. Additionally, some of the generated samples may be far from the real samples and not all the generated samples are helpful to the hyperspectral image classification.

In this article, we propose a new generative network named AC-WGAN-GP based on AC-GAN and WGAN-GP. The proposed framework utilizes guidance from prior knowledge and improves label reliability by a separate classifier. The online generation mechanism improves the diversity of generated sample sets. A selection algorithm based on KNN is presented to choose more reliable samples for training. The proposed framework can offer high-quality labeled samples with diversity and veracity to expand the training set. The contributions of this work can be summarized as follows.

• We construct a new generative network named AC-WGAN-GP to generate labeled samples of different classes. We also design the new input of the generator including PCA features and category information are used to guide the process of generating ad noise to maintain the diversity of samples. Considering the task of generating multi-category labeled samples, we add a separate classifier to strengthen the difference between samples of different categories.
• The online generation mechanism is studied profoundly. Instead of generating samples after the network has converged, the online generation mechanism makes AC-WGAN-GP periodically keep the generated samples during the training process, thereby significantly improving the diversity of the generated sample set.
• A lightweight sample selection method is designed to efficiently select samples that are similar to real ones from the generated sample set. The function of the proposed algorithm also includes smoothing the label to reduce the error of using cross-entropy loss. Finally, the augmented training set is constructed by the generated samples and original real samples.

We organize the rest of this article as follows. Section 2 is used to review a series of GAN. The detailed introduction of the proposed method is presented in Section 3. Section 4 evaluates the proposed method and comparison with competing methods in this paper, Finally, Section 5 concludes the paper.

2. Related Work

In this section, we have a review of GAN, WGAN, and WGAN-GP and analyze their advantages and disadvantages.

2.1. GAN

The core idea of GAN originates from the celebrated Nash equilibrium of game theory. In GAN, the two players are set as one generator and one discriminator. While the generator strives to learn the distribution of real data, the discriminator aims to correctly determine whether the input data comes from real data or from the generated fake data. Each of these two players seeks to win the competitive game by constantly optimizing itself and improving its generation or discrimination ability. This is a learning optimization process and the goal is to attain Nash equilibrium between the two competing players.

For generator $G$, the random noise variable $z$ (characterized by the distribution $p\left(z\right)$) serves as input. The sample generated by $G$ conforming as far as possible to the distribution $p\left(x\right)$ of real data is characterized by $G\left(z\right)$. Meanwhile, the input sample to the discriminator $D$ is labeled 1 if it is a real sample $x$, and it is labeled 0 if it is generated by $G\left(z\right)$. We reiterate that $D$ aims to achieve the discrimination of the data sources, while $G$ seeks to ensure consistency between the performance $D\left(G\left(z\right)\right)$ of the sample $G\left(z\right)$ on $D$ and the performance $D\left(x\right)$ of the real data $x$ on $D$. The generator and discriminator are competing with each other and the iterative optimization process leads to a continuous improvement of the performance for each of them. Finally, the game approaches a state that the discrimination ability cannot be further improved. At this state the generator $G$ might be safely assumed that it attains its goal of learning the distribution of the real data. From the above process, the task undertaken by the GAN is to address a minimax problem. The objective function of the GAN can be described as the minmax formulation:

$$\underset{G}{\min }\underset{D}{\max }V({\theta }_D,{\theta }_G)=E_{x\sim p(x)}[\log D(x)]+E_{z\sim p(z)}[\log (1-D(G(z)))]$$

(1)

where $E$ is the mathematical expectation, $x\sim p\left(x\right)$ is the random variables that fit the probability distribution of real samples, $z\sim p\left(z\right)$ is the random variables that fit the probability distribution of generated samples, ${\theta }_D,{\theta }_G$ are two parts of loss function from generator and discriminator. The GAN is trained via an alternating optimization method. We start training by fixing the generator $G$ and optimizing the discriminator $D$. Then, we alternate by fixing the discriminator $D$ and optimizing the generator $G$. The global optimal solution is reached when and only when $p\left(g\right)=p\left(x\right)$. The parameters of $D$ are generally updated k times while those of $G$ are updated only once when training.

2.2. WGAN and WGAN-GP

However, the problems undermining the utility of the traditional GAN include training difficulties, incapability of the optimization function of the generator, and the lack of diversity of the generated samples. Moreover, the GAN suffers the shortcoming of gradient disappearance when training is based on gradient descent. The Jensen–Shannao divergence measures the overlap between two distributions. The shortcoming arises when the common part between the real and generated sample distributions is diminished, and the Jensen–Shannon divergence of the objective function used by conventional GAN becomes a constant, thereby producing a discontinuity of the optimization objective. With an eye on handling the deficiency of a disappearing training gradient, Arjovsky et al. were the first to introduce the Wasserstein GAN (WGAN) [43] model, together with the associated concept of the Wasserstein distance proposed by Rubner, Y., Tomasi, C. and Guibas, L.J. [44] A mathematical transformation is used to convert the Wasserstein distance into a solvable form, and this distance can be approximated through adding a parameter’s numerically limited in discriminator network. Subject to the approximate optimal discriminator obtained, optimizing the generator to decrease the Wasserstein distance can effectively shorten the distance between the generated distribution $p\left(g\right)$ and the distribution $p\left(x\right)$ of real data. Mathematically, the objective function of WGAN is given by:

$$\underset{G}{\min }\underset{D}{\max }{E}_{x\sim p(x)}[D(x)]+E_{\tilde{x}\sim p(g)}[D(\tilde{x})]$$

(2)

where $\tilde{x}$ is a random variable that fit the distribution of generated samples. Here $D$ is the set of 1-Lipschitz functions, which needs to satisfy Lipchitz continuity so as to use the Wasserstein distance. Lipschitz continuity is a restriction on continuous functions, which requires that the derivative of the functions must be less than a constant $K$.

To satisfy this condition, I. Gulrajani [42] et al. limits the weight of $D$ to a range, thereby introducing WGAN-GP as an improved version of WGAN. A new Lipchitz continuous restriction technique named gradient punishment is proposed to handle both problems of gradient disappearance and gradient explosion. Instead of directly constraining the value of the gradient, the authors added a regularization term. Detailed formulas and explanations are shown in the next section.

3. The Proposed Method

Figure 1 shows the overall framework for the HSI classification with a small sample size based on the AC-WGAN-GP, which is composed of four parts: the preprocessing based on Gaussian smoothing, the AC-WGAN-GP network, online sample generation, and sample selection algorithm based on KNN.

3.1. Smoothing-Based Preprocessing

The spectral vectors of neighboring pixels are assumed to be related because they are likely to be part of an image of a semantically homogeneous component.

This paper uses gaussian filter to exploit the neighboring information because gaussian filter has rotation invariance. Gaussian kernel has fixed parameters. Therefore, each pixel will perform a weighted calculation with the neighboring pixels through the Gaussian kernel. Gaussian filter weighted the sum of the pixels according to the spatial distance between the neighboring pixels and the central pixels to obtain smoothed HSI patches. As the data complexity increases, the structure of networks used for learning also needs to be designed to be more complex. The smoothed HSI patches contain some spatial information while discarding harmful information. We think that the generator and discriminator can be designed with a simpler structure because of the smoothed input patches. The Gaussian smoothing process can be considered a spatial feature extraction.

After the normalization of the original hyperspectral image, a patch is taken as the input of gaussian filtering for each pixel $x_{mn}$, which can be expressed as $x_{mn}\in R^{M\times N\times H}$ (where M is the width, N is the height, and H is the number of bands), and the smoothed image is:

$$x_{mn}^{smooth}=\frac{{\displaystyle {\sum }_i{\displaystyle {\sum }_j{x}_{ij}\exp (-\parallel (i,j)-(m,n){\parallel }^2/2{\sigma }^2)}}}{{\displaystyle {\sum }_i{\displaystyle {\sum }_j\exp (-\parallel (i,j)-(m,n){\parallel }^2/2{\sigma }^2)}}}$$

(3)

where $x_{ij}$ is the pixel in $x\in R^{M\times N\times H}$, $\left(i,j\right)$ is the spatial coordinate of the pixel, $\left(m,n\right)$ is the spatial coordinate of the central pixel $x_{mn}$. In practice, we restrict the sums to a distance of $3\sigma$ from $\left(i,j\right)$, since pixels far from that have a negligible contribution. $3\sigma$ is the window size and $\sigma$ is adjusted when experimenting and selected from collection [1, 1.67, 2.33, 3, 3.67, 4.33, 5].

3.2. AC-WGAN-GP

In the proposed method, the AC-WGAN-GP is constructed based on part of the theories of AC-GAN and WGAN-GP. We design an input of the generator so that the generator can be guided from the manual feature and different labels. So, the difficulty of generating high quality samples in different categories decreases. We also design a new structure by adding an auxiliary classifier to form a separate classifier $C$. Accordingly, the new optimization function is also designed. Thereby, the output fake labels and the generated samples are in parallel. Finally, fake labels and fake samples can be generated simultaneously from a limited number of real training samples thus expanding the training set. The architecture of AC-WGAN-GP is shown in Figure 2.

A network used to generate multi-category samples in different distribution is difficult. Besides adding label information to the input of generator, we believe that the manual features also can be used as prior information. So, the input of generator $G$ introduces the principal components of real sample pixel $X_{real}$ as additional constraints to guide $G$. The vector of noise extends a number of dimensions to accommodate the principal components extracted from $X_{real}$ and one-hot labels. With the above input, the generator can be guided to generate high-quality samples in a targeted manner. Furtherly, we employ the Principal component analysis (PCA) to reduce the dimensionality of the HSIs. Indian pines dataset has 200 spectral bands, Salinas dataset has 224 spectral bands, and KSC dataset has 176 spectral bands. We select the first 30 principal components (PC), expressed as $X_{PC}$. So, the input of generator $G$ includes three parts: Gaussian noise variable $z$; one-hot coded class information $c$; and 30-dimensional PC $x_{PC}$ of single pixel. On the basis of traditional Gaussian noise, prior knowledge of various labels and samples are added. The generated sample can be expressed as $X_{fake}=G\left(z,c,x_{pc}\right)$.

In our AC-WGAN-GP, an independent classifier $C$ is used to output fake one-hot labels independently. Refs. [39,40] show the methods of combining an independent classifier with GAN. The task of the generator in AC-WGAN-GP is generating samples of different categories, which is difficult to control. So, we have to add the category-correct constraints to the objective function. To reinforce the function of generating samples from different categories, we separate a classifier $C$ that uses part of the loss function of the generator. Besides, it is difficult for the discriminator to discriminate between the real and fake samples while outputting the category of the generated samples. The function of $C$ includes two points. Firstly, $C$ is responsible for generating the labels of fake samples efficiently. Secondly, when optimizing AC-WGAN-GP, the loss function of $C$ could ensure the generated samples belong to the corresponding input category information, thereby increasing the gap between samples of different categories. A classifier based on CNN is suitable. The input of the classifier $C$ is the same as the input of the discriminator. The classifier is trained by real samples and their labels and then predicts the labels of fake samples. The cross-entropy loss of $C$ is formally unified with the loss functions of the generator and discriminator. Therefore, we consider AC-WGAN-GP as a whole network during training.

The input of discriminator $D$ is composed of the real single pixel $X_{real}$, the generated fake sample $X_{fake}$ labeled as c, and the output of $D$ is a probability distribution $P(S|X)$. The function of the discriminator is to judge the real or fake samples. The purpose of designing $D$ and $C$ is that each part of the AC-WGAN-GP is assigned a specific task.

In the above framework, referring to Deep Convolution Generative Adversarial Network (DCGAN) [45], $G$ adopts the form of a fractionally-stride convolutional neural network, while $D$ and $C$ adopt the form of a standard CNN. The Batch norm layer is used in generator $G$ and discriminator $D$ to normalize features, which improves the training speed and makes the training more stable. The Leak-ReLU activation function, not the ReLU one, is used in the discriminator to prevent gradient sparsity, and no activation function is used at the last layer of the discriminator. The ReLU activation function is employed in the generator, while the tanh activation function is utilized solely in the output layer. Classifier $C$ consists of a convolutional layer and a full-connection one, and finally connects a Softmax activation function to output the probability of classification. In the training process, according to the idea of fixing one part to train another part, $G$, $D$ and $C$ fix the parameters of two networks, optimize the remaining network parameters, and iterate alternately in this way to complete the whole training process. The specific network parameter design is shown in Section 4. The input to the generator is our designed vector, a noise-label-principal component vector. We can select the output of the generator to the parts we need, such as fake labels or fake pixel vectors.

After designing the architecture of the AC-WGAN-GP, we propose a suitable optimization function. The multi-classification problem can be realized by the Auxiliary Classifier GAN (AC-GAN), which was introduced by Odena et al. [35]. We treat its loss function as a prototype. The objective function contains the likelihood of data source $L_S$ and the likelihood of category $L_C$. Updating the parameters of $D$ is achieved by maximizing $L_S+L_C$, while updating the parameters of G is attained by maximizing $L_C-L_S$.

$$L_s=E[\log P(S=real|X_{real})]+E[\log P(S=fake|X_{fake})]$$

(4)

$$L_c=E[\log P(C=c|X_{real})]+E[\log P(C=c|X_{fake})]$$

(5)

The structure of $L_s$, $L_c$ is similar and both use cross entropy loss. The two parts of $L_s$ are responsible for judging the real samples and fake samples respectively. $S$ represents the judgement result of the discriminator. Discrimination can also be viewed as a binary classification problem. And the two parts of $L_c$ classify real and fake samples. $C$ defines as labels the classifier output, and $c$ represents the ground truth labels.

Based on above equations, the discriminator optimizes $L_D$ in the training process is obtained. We define $\widehat{x}$ as sampling uniformly along straight lines between pairs of points sampled from the data distribution $p\left(x\right)$ and the generator distribution $p\left(g\right)$ in sample space. $\widehat{x}\sim p\left(\widehat{x}\right)$ represents the random variable that fits the distribution of $p\left(\widehat{x}\right)$. $\tilde{x}$ is the random variable that fits the distribution of fake samples $G\left(z,c,x_{pc}\right)$. $\nabla$ is the gradient. The first and second part is responsible for judging whether the sample is real or fake. The third part is the gradient penalty. $L_D$ is showed in the following formula:

$$L_D=E_{\tilde{x}\sim p(g)}[D(\tilde{x})]-E_{x\sim p(x)}[D(x)]+\lambda E_{\widehat{x}\sim p(\widehat{x})}[{(\parallel {\nabla }_{\widehat{x}}D(\widehat{x}){\parallel }_2-1)}^2]$$

(6)

As a regular choice and part of the objective function of the generator, the class cross entropy loss is the objective functions of the classifier. As shown in the following formula:

$$L_c=-E_{x\sim p(x)}[\log P(C=c|X_{real})]$$

(7)

where $C$ is defined as the labels of the network forward output, and $c$ is the ground truth labels of training samples.

The objective function of the generator consists of two parts. One part comes from discriminator $D$, which ensures that the discriminator does not recognize the sample produced by the generator. The other part comes from classifier $C$, which ensures that the samples generated by the generator belong to the corresponding class $c$ to the greatest extent. The second part reinforces the connection between category information and generated samples. Therefore, the sum of these two parts constitutes the objective function for the generator G is defined as:

$$L_G=-E_{\tilde{x}\sim p(g)}[D(\tilde{x})]-E[\log p(C=c|X_{fake})]$$

(8)

3.3. Online Sample Generation

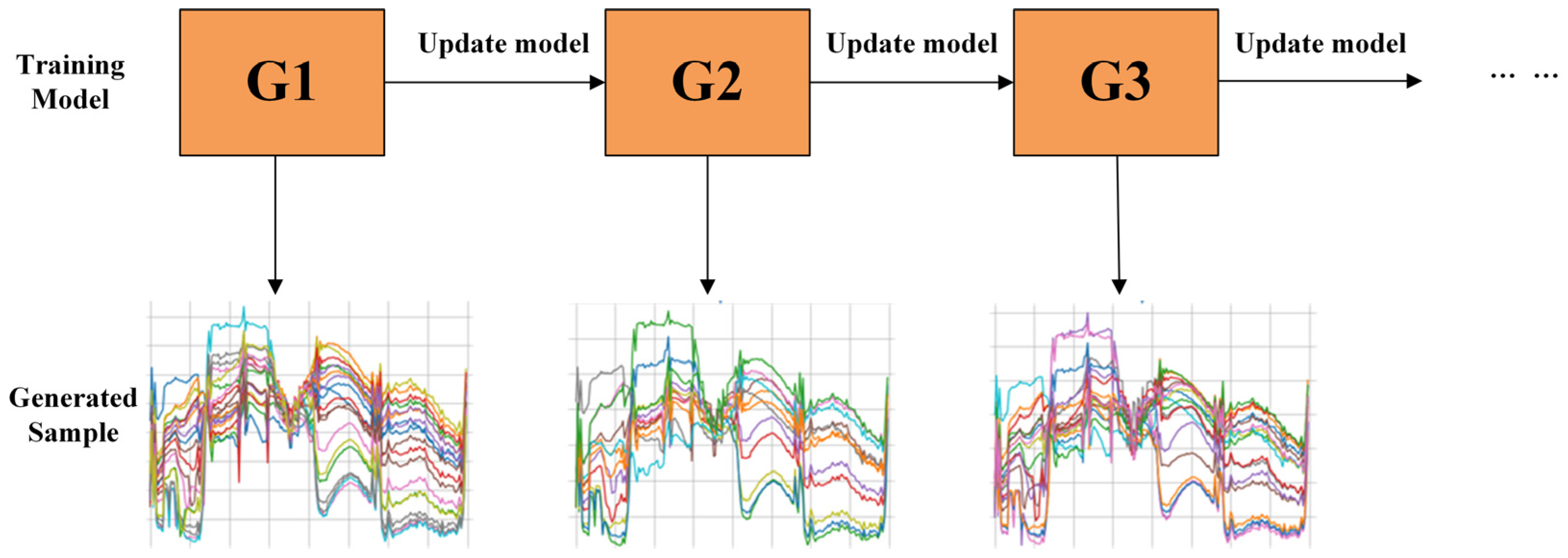
Generally, after GAN is trained, the parameters of each network are fixed, then the required input data generator is sent to the generator to generate false samples. Although the trained network can fit the distribution of training samples of different classes and input gaussian noise Z is also random, the parameters and other inputs of GAN are fixed, so the diversity of fake data generated by AC-WGAN-GP is poor. Therefore, we find it is appropriate to design a GAN-friendly mechanism named online sample generation.

Firstly, AC-WGAN-GP is trained by the above training methods described in Section 3.2, and then we observe the loss value of the network. After the network reaches a certain section of convergence, the online generation strategy starts. Although the network is not well-trained, and the loss curve is still trending downward, we can start to gather some of the faked samples and labels at one certain epoch. Then AC-WGAN-GP will continue to train to optimize network parameters. After a certain number of training epochs, AC-WGAN-GP will generate samples online again. Finally, the samples generated online in each time are collected. In order to ensure the diversity of samples and the balance between different classes, we can keep the abundant online generated samples which might include all categories of hyperspectral samples if the computer memory allows. In this way, we can also alleviate the pressure to tune the variables of the online generation mechanism. As shown in Figure 3, online sample generation can take advantage of plenty of models to generate samples with higher diversity. And the abundant generated fake samples and labels will be filtrated in the next part.

3.4. Sample Selection Algorithm Based on KNN

The online sample generation guarantees the diversity of generated samples, but due to GAN’s unique properties, it is not guaranteed that all generated samples have good quality and be similar to real samples. Therefore, for the samples $\left(X_{fake},C_{fake}\right)$ generated by GAN, an extra selection method is needed to select samples that are close to real samples thus can promote classification accuracy. The algorithm includes two steps: samples selection and label smoothing.

To ensure the total number of parameters and operation time of the entire framework are appropriate, a brief and effective method is demanded. Firstly, the total set of original real data is divided into a training set $\left(X_{train},C_{train}\right)$ and a temporary set $X_t$. We use the clustering algorithm to divide the temporary set into N clusters. And then the central samples of each cluster and a part of the temporary set samples around central samples $X_t^{\prime }$ ($X_t^{\prime }\in X_t$) are randomly taken to form a mini set. The clustering algorithm we employ are K-MEANS clustering algorithm, DBSCAN clustering algorithm, EM algorithm, and Mean shift clustering algorithm. For each algorithm, we repeat the above operations, and finally take the union of the mini sets to form $X_u^{″}$. In the generated sample set, KNN is used to select the closest sample to each test sample $x_u^{″}$ ($x_u^{″}\in X_u^{″}$). Finally, the selected generated samples constitute the ultimate generated sample set. The generated fake samples selected by this algorithm can be representative and similar with the real samples.

The samples in $\left(X_{fake}^{\prime },C_{fake}^{\prime }\right)$ originate from the overall generated distribution. Each sample is characterized by its own label, but, nevertheless, it might mix information from other classes. In deep learning, when calculating cross-entropy with one-hot coded labels, only the loss of the correct class (the class with the label coded as 1) is considered, but the loss of the wrong class (the class with the label coded as 0) is not considered. It may lead to overfitting, gradient explosion or gradient disappearance [46]. In order to distinguish the labels of generated samples and labels of real samples and reduce the negative impact of labelling errors when training, we use label smoothing regularization (LSR) [47] to consider the distribution of wrong classes. We conduct the LSR processing on the labels of fake samples set. $C_{fake}^{\prime }$ represents the generated one-hot label, $\epsilon \in \left[0,1\right]$, K represents the number of classes. The smoothing process is shown as:

$$C_{fake}^{″}=C_{fake}^{\prime }(1-\epsilon )+\frac{\epsilon }{K}$$

(9)

After the above operations, smooth labels improve the generalization ability of the network.

After implementing the algorithm, we obtain the final fake hyperspectral samples and their corresponding labels to augment limited training datasets. At the same time, the quality and diversity of the generated samples are also guaranteed to a certain extent. Algorithm 1 summarizes selection of generated samples and label smoothing.

Algorithm 1. Samples selection and label smoothing
Input: Generated sample set G, dataset D, the number of categories N, clustering algorithm list L (K-MEANS, DBSCAN, EM and Mean shift), the hyperparameter represents the volume of random set M, the hyperparameter for KNN k Output: selected samples and smoothing labels $\left(X_{fake}^{\prime },C_{fake}^{″}\right)$
Step1:	Randomly divided D into training set A and temporary set B
Step2:	Union the clustering set:           For $i=0,\cdots ,3$, do
	$set{B}_i=L[i](B)$
	$Set central C={\mathsf{\Theta }}_i\in B_i,len({\mathsf{\Theta }}_i)=N$
	$Set random R={\mathsf{\Phi }}_i\in B_i,len({\mathsf{\Phi }}_i)=M$
Step3:	$\mathrm{Union}\mathrm{the}\mathrm{set}:B^{\prime }={\mathsf{\Theta }}_1{{\displaystyle \cup }}^{}{\mathsf{\Theta }}_2{{\displaystyle \cup }}^{}{\mathsf{\Theta }}_3{{\displaystyle \cup }}^{}{\mathsf{\Theta }}_4{{\displaystyle \cup }}^{}{\mathsf{\Phi }}_1{{\displaystyle \cup }}^{}{\mathsf{\Phi }}_2{{\displaystyle \cup }}^{}{\mathsf{\Phi }}_3{{\displaystyle \cup }}^{}{\mathsf{\Phi }}_4, len\left(B^{\prime }\right)=n$,
Step4:	$\mathrm{On}\mathrm{the}G=\{\left(x_1,c_1\right),\cdots ,\left(x_q,c_q\right)\},$                $G^{\prime }=KNN\left(B^{\prime }, G, k\right)$           For$c^{\prime } in G^{\prime }$, do                 $c^{\prime }=LSR\left(c^{\prime }\right)$
Step5:	$\mathrm{Output}{G}^{\prime }=\{\left(x_1,{c_1}^{\prime }\right),\cdots ,\left(x_p,{c_p}^{\prime }\right)\},$

4. Experiments and Result Analysis

In this experiment, firstly we introduce basic information such as datasets, training samples, and evaluation metrics. Then detailed experimental settings are given. The third section analyzes the quality of pixels generated using proposed method. In next section, we study the effect of real and generated pixel ratios on the classification results and perform the ablation experiments of the final sample selection module. Finally, we compare AC-GAN-GP and CNN classifier with classifiers based on traditional methods, convolution and GAN, demonstrating the effectiveness of our proposed method on task of hyperspectral classification with small samples. We implemented AC-WGAN-GP with the tensorflow framework on a PC server with two NVIDIA GTX1080TI GPU and 22 GB memory. The average time for training AC-WGAN-GP, generating and classifying is 210 min and 15 s.

4.1. Hyperspectral Datasets

In this experiment, three popular datasets of hyperspectral images are used as experimental data named the Indian Pines dataset, the Salinas dataset, and the Kennedy Space Centre (KSC) dataset.

Indian Pines: The dataset of the Indian Pines comprises a hyperspectral image of agricultural and forest areas in India, which is collected by remote sensing equipment utilizing an airborne visible/infrared imaging spectrometer (AVIRIS). Note that the image in the dataset comprises $145\times 145$ pixels, and its spatial resolution is 20 m/pixel. The Indian Pines dataset consists of 220 spectral bands, 20 of which severely water-absorbing bands are removed, and we conduct experiments on the remaining 200 spectral bands. For this dataset, we consider 16 classes to be of interest, excluding background pixels. Figure 4a shows the three-band false color image and the ground reference map of the Indian Pines image.

Salinas: Salinas data was also taken by the aforementioned AVIRIS imaging spectrometer, and it is an image of the Salinas valley, a prominent valley notable for being a highly productive region in California, the United States of America (USA) The image is with a spatial resolution of 3.7 m, and it originally had 224 bands, out of which we used only 204 bands for classification. We exclude 20 bands that could not be reflected by water, namely the 108th–112th, 154th–167th bands and the 224th band. The image is characterized by a size of $512\times 217$ pixels, which are divided into 16 classes. Figure 4b shows the three-band false color image and ground reference map of the Salinas image.

KSC: The NASA’s AVIRIS equipment collected data over the Kennedy Space Centre (KSC) in the south-eastern state of Florida, United States of America almost a quarter of a century ago. This spectroradiometer equipment obtained 224 bands each characterized by a width of 10 nm and having a median wavelength ranging from 400 nm to 2500 nm. The image consists of $512\times 217$ pixels and possesses a spatial resolution of 18 m/pixel. Only 176 bands are used for further analysis after all water absorbing bands and low SNR bands are eliminated. For classification purposes, we define 13 classes, which represent a variety of land cover types in the pertinent environment for the given site. Figure 4c shows the three-band false color image and the ground reference map of the KSC image.

For each of these three datasets, we divide the initial dataset into two subsets named a training set and a testing one. The training set is composed of 200 samples, and is extracted by random sampling. In other words, the proportion of training samples on the three datasets are 2.0%, 1.0%, 3.8%, which satisfies the requirement of few-shot experiments. The remaining samples are taken as the testing set.

Table 1. Land cover types and total number of samples in the Indian Pines dataset.

No.	Color	Name	Number	No.	Color	Name	Number
1		Alfalfa	46	9		Oats	20
2		Corn-notill	1428	10		Soybean-notill	972
3		Corn-mintill	830	11		Soybean-mintill	2455
4		Corn	237	12		Soybean-clean	593
5		Grass-pasture	483	13		Wheat	205
6		Grass-trees	730	14		Woods	1265
7		Grass-pasture-mowed	28	15		Buildings-Grass-Trees	386
8		Hay-windrowed	478	16		Stone- Steel-Towers	93
Total Numbers				10,249

,

Table 2. Land cover types and total number of samples in the Salinas dataset.

No.	Color	Name	Number	No.	Color	Name	Number
1		Brocoli_green_weeds_1	2009	9		Soil_vinyard_develop	6203
2		Brocoli_green_weeds_2	3726	10		Corn_senesced_green_weeds	3278
3		Fallow	1976	11		Lettuce_romaine_4wk	1068
4		Fallow_rough_pow	1394	12		Lettuce_romaine_5wk	1927
5		Fallow_smooth	2678	13		Lettuce_romaine_6wk	916
6		Stubble	3959	14		Lettuce_romaine_7wk	1070
7		Celery	3579	15		Vinyard_untrained	7268
8		Grapes_untrained	11,271	16		Vinyard_vertical_trellis	1807
Total Numbers				54,129

and

Table 3. Land cover types and total number of samples in the KSC dataset.

No.	Color	Name	Number	No.	Color	Name	Number
1		Scrub	761	8		Graminoid marsh	431
2		Willow swamp	243	9		Spartina marsh	520
3		CP hammock	256	10		Cattail marsh	404
4		Slash pine	252	11		Salt marsh	419
5		Oak/Broadleaf	161	12		Mud flats	503
6		Hardwood	229	13		Water	927
7		Swamp	105
Total Numbers				5211

show the legend of each category.

Table 4. Land cover classes, number of training samples and total samples in Indian Pines.

Classes Name	Train Numbers	All Numbers
Alfalfa	3	46
Corn-notill	29	1428
Corn-min	17	830
Corn	5	237
Grass-pasture	10	483
Grass-trees	15	730
Grass-pasture mowed	3	28
Hay-windrowed	10	478
Oats	3	20
Soybean-notill	19	972
Soybean-mintill	49	2455
Soybean-clean	12	593
Wheat	4	205
Woods	25	1265
Buildings-Grass-Trees	8	386
Stone-Steel-Towers	3	93
Total	215	10,249

,

Table 5. Land cover classes, number of training samples and total samples in Salinas.

Classes Name	Train Numbers	All Numbers
Brocoli_green_weeds_1	20	2009
Brocoli_green_weeds_2	37	3726
Fallow	20	1976
Fallow_rough_plow	14	1394
Fallow_smooth	27	2678
Stubble	40	3959
Celery	36	3579
Grapes_untrained	113	11,271
Soil_vinyard_develop	62	6203
Corn_senesced_green_weeds	33	3278
Lettuce_romaine_4wk	11	1068
Lettuce_romaine_4wk	19	1927
Lettuce_romaine_4wk	9	916
Lettuce_romaine_4wk	11	1070
Vinyard_untrained	73	7268
Vinyard_vertical_trellis	18	1807
Total	543	54,129

and

Table 6. Land cover classes, number of training samples, and total samples in KSC.

Classes Name	Train Numbers	All Numbers
Scrub	29	761
Willow swamp	9	243
CP hammock	10	256
Slash pine	10	252
Oak/Broadleaf	6	161
Hardwood	11	229
Swamp	4	105
Graminoid marsh	16	431
Spartina marsh	20	520
Cattail marsh	15	404
Salt marsh	16	419
Mud flats	19	503
Water	35	927
Total	200	5211

present the number of training samples selected from each dataset and the total number of samples.

4.2. Experimental Setting

The training/testing sample used in the experiment is a single pixel. Each pixel can be used as feature to train the AC-WGAN-GP and the CNN classifiers, as it corresponds to a unique label. The number of classes in the dataset is represented by n. All HSIs data are normalized between −1 and 1 at the beginning of the experiment. We utilize randomly-selected training and testing sets to repeat the experiment 10 times, and subsequently report the average obtained accuracy. For quantitative evaluation of the experimental results, we utilize the popular metrics of the overall accuracy (OA), the average accuracy (AA) and the kappa correlation coefficient ($\kappa$). The definitions of all OA, AA, and Kappa are shown as follows:

(1) OA: OA assesses the proportion of correctly identified samples to all the samples.

$$OA=\frac{{{\displaystyle \sum }}_{i=1}^{\bar{C}}{h}_{ii}}{N}$$

(10)

where N is the total number of labeled samples, $h_{ii}$ represents the number of class i samples divided into class i, and $\bar{C}$ is the total number of categories.

(2) AA: AA represents the mean of the percentage of the correctly identified samples.

$$AA=\frac{1}{\bar{C}}{{\displaystyle \sum }}_{i=1}^{\bar{C}}\frac{h_{ii}}{N_i}$$

(11)

where $\bar{C}$ is the total number of categories, $h_{ii}$ represents the number of samples of category i divided into category i, and $N_i$ represents the number of samples of category i.

(3) Kappa: Kappa coefficient denotes the interrater reliability for categorical variables.

$$Kappa=\frac{N{{\displaystyle \sum }}_i^{\bar{C}}{h}_{ii}-{{\displaystyle \sum }}_i^{\bar{C}}\left(h_{i+}{h}_{+i}\right)}{N^2-{{\displaystyle \sum }}_i^{\bar{C}}\left(h_{i+}{h}_{+i}\right)}$$

(12)

where $h_{i+}$ and $h_{+i}$, respectively, represent the total number of samples of category i true category and the number of samples predicted to be category i.

The size of the window in Gaussian smoothing kernel is 11 and the sigma for the Gaussian smoothing kernel is 0.1. The network structure and parameters for generators, discriminators, and classifiers in AC-WGAN-GP are described in detail in

Table 7. The architecture of the AC-WGAN-GP.

Net	Number	Input Size	Layer	Bn	Stride	Padding	Activation Function	Output Size
G	1	100+30+classnumber	Fn (1/16H×512) Reshape	Yes	-	-	ReLU	1/16H×1×512
	2	1/16H×1×512	Deconv1d (3×1×512×256)	Yes	2×1	SAME	ReLU	1/8H×1×256
	3	1/8H×1×256	Deconv1d (3×1×256×128)	Yes	2×1	SAME	ReLU	1/4H×1×128
	4	1/4H×1×128	Deconv1d (3×1×128×64)	Yes	2×1	SAME	ReLU	1/2H×1×64
	5	1/2H×1×64	Deconv1d (3×1×64×1)	No	2×1	SAME	Tanh	1/16H×1×1
D	1	H×1×1	Conv1d (3×1×1×64)	No	2×1	SAME	LeakyReLU	1/2H×1×64
	2	1/2H×1×64	Conv1d (3×1×64×128)	Yes	2×1	SAME	LeakyReLU	1/4H×1×128
	3	1/4H×1×128	Conv1d (3×1×128×256)	Yes	2×1	SAME	LeakyReLU	1/8H×1×256
	4	1/8H×1×256	Conv1d (3×1×256×512)	Yes	2×1	SAME	LeakyReLU	1/16H×1×512
	5	1/16H×1×512	Flatten Fn(32H×1)	No	-	-	-	1
C	2	H×1×1	Conv (15×1×1×64) Flatten	No	15×1	SAME	Tanh	1/15H×1×64
	3	1/15H×1×64	Fn (64/15H×C’)	No	-	-	Softmax	C’

. In the table Deconv represents the fractionally-strided convolutional neural network layer, conv represents the convolutional neural network layer, Fn represents the full connection layer, BN represents the Batchnorm layer, stride represents the step size of convolution, and Padding represents the way of filling. The input of generator $G$ is a vector composed of noise, one-hot label and 30-dimensional principal components. The sample generated by $G$ is a single pixel with the size of $H\times 1\times 1$. The input of $D$ is $\left(X_{fake},C_{fake}\right)$ and $\left(X_{real},C_{real}\right)$, and the output is a scalar, which represents whether the input sample is a real sample or a false sample. $C$ has the same input as $D$, and the output is the probability that pixels belong to each category. The size of the mini-batch is set to 64 for training AC-WGAN-GP and CNN, the learning rate ranges from 0.1 to 0.0001, and the value of the label smoothing parameter is 0.1.

4.3. Analysis of Generated Samples

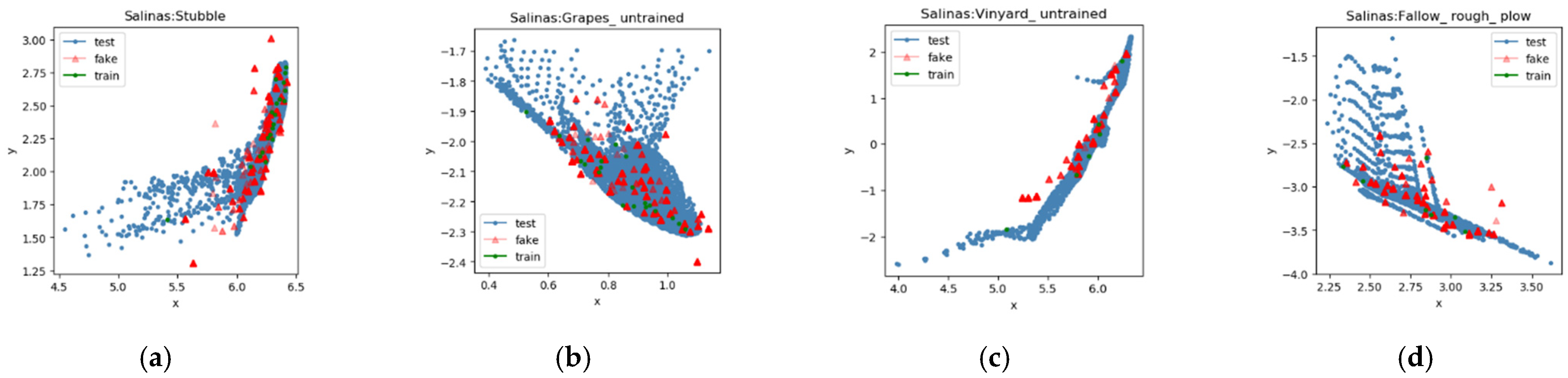
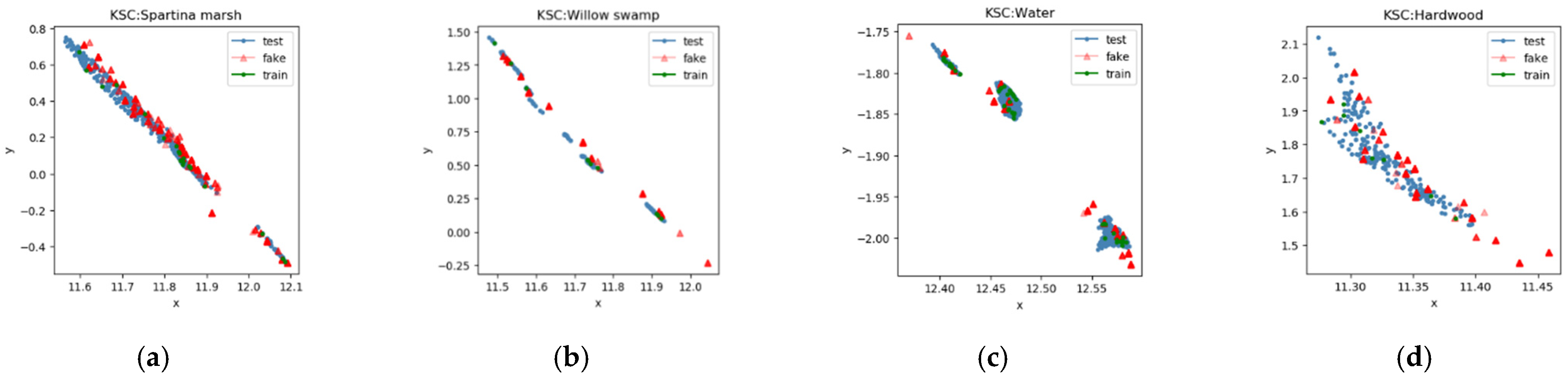
Before using the generated samples for classification, we have to check the distribution of the generated samples. We check whether the distributions of generated samples and real samples are consistent. Because the distribution of each class is different, each class has its own distribution. When generating samples, our method generates labeled samples, so the generated samples belonging to the same category should possess the same distribution as that of the real samples. In order to verify whether the generated samples and real samples of the same class have the same distribution, we extract the principal components of the generated samples and real samples through PCA first, and then select the two first principal components. As shown in Figure 5, Figure 6 and Figure 7, the red triangle represents the generated sample, the blue point represents the real test sample, and the green point represents the real training sample. The figure shows that, for most categories, the AC-WGAN-GP network can generate samples that have a similar distribution to original samples in the feature space. However, for the classes with too few real training samples, the generated sample distribution and the real sample distribution show some differences. Such as Grass-pasture-mowed class in the Indian Pines dataset, the number and distribution of real samples and fake samples are different. In addition, it can be seen from the figure that AC-WGAN-GP tends to imitate simple distributions better, but sometimes complex distributions cannot be well fitted. There are two reasons for this difference. One is that too few training samples are sent to AC-WGAN-GP network, the convergence is not complete; the other is that the randomly selected training samples are not evenly distributed in the class, which cannot represent the overall distribution of this class. For these two reasons, GAN does not perform well in generating a small number of class samples. This is also a common problem of GAN. Intuitively, the sample distribution generated by AC-WGAN-GP is correct.

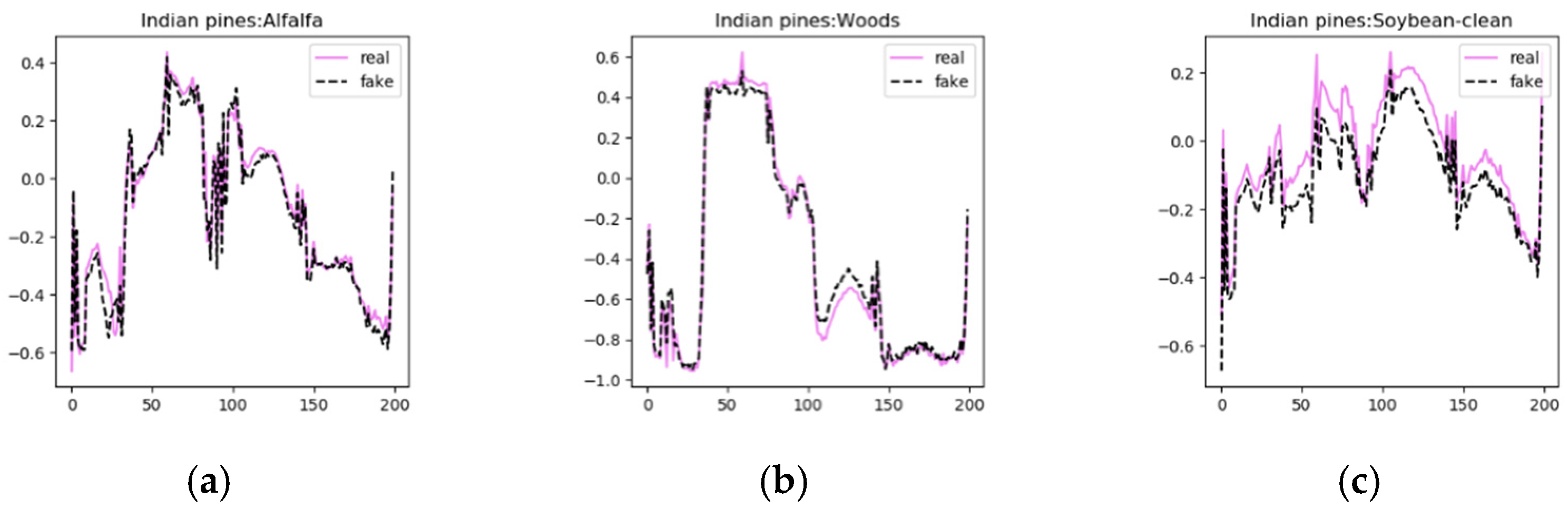
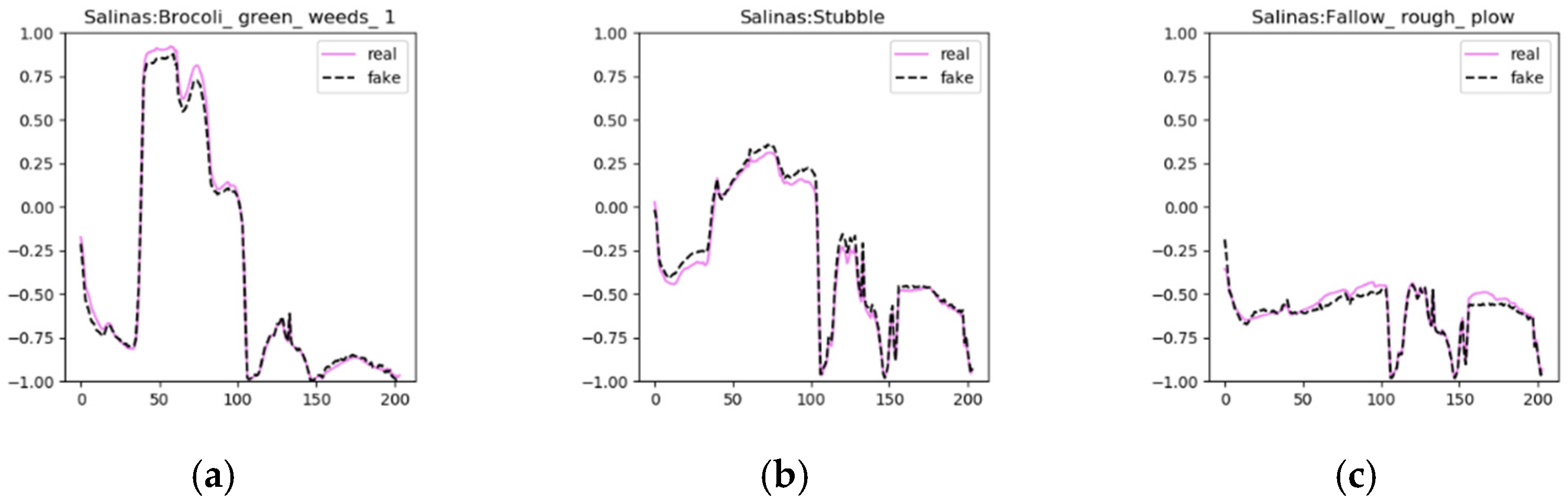
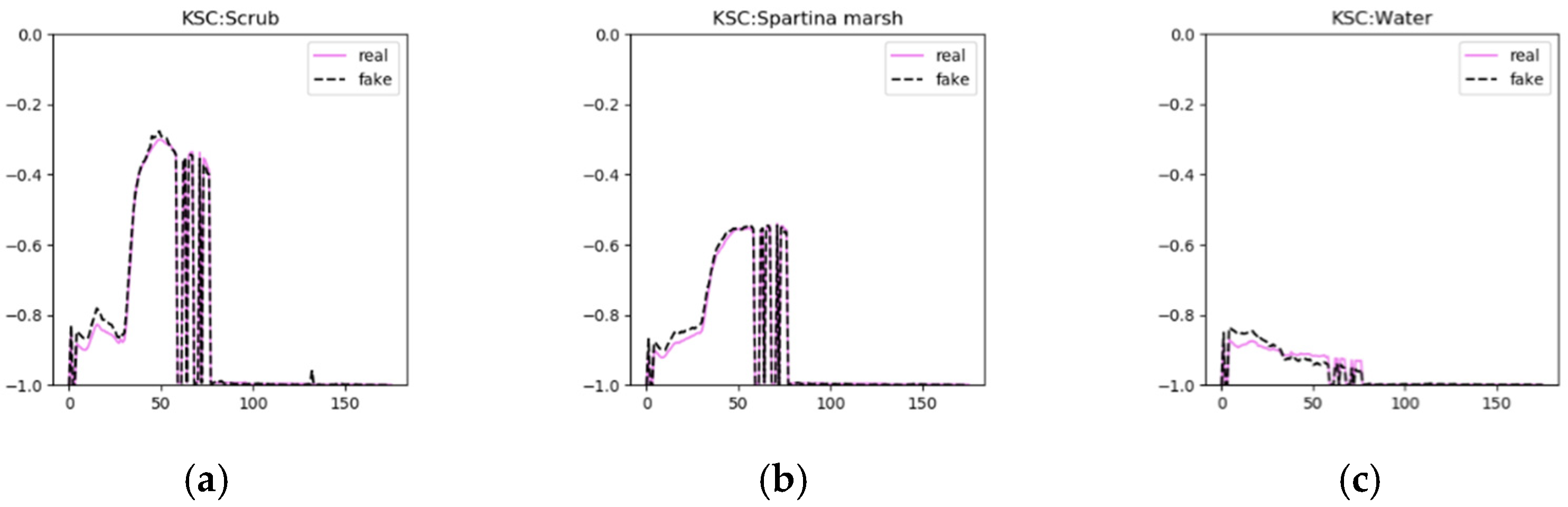
In the visualization experiment, three classes of generated fake samples and real samples were selected from the three data sets for visual display, as shown in Figure 8, Figure 9 and Figure 10. The solid red line represents the real sample and the dotted black line represents the generated sample. The figure indicates that the generated sample is very similar to the real sample of the corresponding class, but not completely consistent, meet the demands that generated samples need to be consistent with the real sample distribution and have a certain diversity. The generator can learn the different characteristics of each class and generate different samples according to the class. We obtain a model that fits multiple class distributions and fills in the lack of diversity in the sample space using limited samples by utilizing AC-WGAN-GP.

In addition to analyzing the distribution difference according to the visual results obtained by the category, the experiments in this subsection also give numerical results on whether the real samples and the generated samples are consistent in the global distribution. A 1-Nearest Neighbor classifier (1-NN classifier) is used for evaluating whether the two distributions are consistent. Given two sets of samples, the real samples are labeled as positive samples and denoted as $S_r$, and the generated samples are labeled as negative samples and denoted as $S_f$. Train 1 nearest neighbor classifier by $S_r$ and $S_f$, and then use them as test samples to obtain new labels, calculate the classification accuracy of the 1-NN classifier, and express it as the Transfer(T) accuracy. When the number of samples is very large, if two distributions are consistent and not completely replicated, the T accuracy of the 1-NN classifier should be 50%. Because when the generated samples are only the results of simple replication of real samples, the T accuracy rate is 0%. When the two distributions do not match at all, the T accuracy rate is 100%.

Table 8. 1-NN accuracy (%) and average spectral distance of generated and real samples.

Dataset	Indian Pines	Salinas	KSC
$\left|S_r\right|=\left|S_f\right|$	10,249	10,852	5211
1-NN accuracy (Real) (%)	58.22	65.03	74.24
1-NN accuracy (Fake) (%)	56.00	62.80	65.16
1-NN accuracy (Average) (%)	57.11	63.91	69.70
Average Spectral Distance	0.5028	0.3421	0.1135

calculates the T accuracy of the three HSIs datasets, and the table also shows the average spectral distance between the generated samples and the real samples. We select the number of samples shown in the first row of the table for calculation. The average T accuracies of the three datasets are 57.11%, 69.70% and 63.91%, respectively, which are relatively close to the ideal generative distribution effect. When the average T accuracy rate is closer to 50% and the average spectral distance is smaller, the effect of adding the generated samples to the real training samples for data enhancement is more obvious.

4.4. Generated Sample and Real Sample Mixed Ratio Analysis

The ratio of the real samples and generated samples in training sets may affect the result of classification. So, we conduct an experiment to investigate the effect of injecting different proportions of fake samples on classification accuracy. We selected several representative and common mixing proportions 1:0, 4:1, 2:1, 1:1, 1:2, 1:4.

Table 9. Effect of different mixing proportions in training sets.

Real:Fake	1:0	4:1	2:1	1:1	1:2	1:4
Dataset	Indian Pines
OA (%)	91.28	91.88	92.44	92.51	91.87	92.43
AA (%)	92.15	88.87	88.90	90.59	89.15	90.33
Kappa×100	90.88	90.74	91.39	91.46	90.74	91.39
Dataset	Salinas
OA (%)	96.06	96.83	96.97	96.86	96.78	96.73
AA (%)	97.43	98.26	98.47	97.93	98.29	97.79
Kappa×100	95.61	96.48	96.63	96.50	96.41	96.37
Dataset	KSC
OA (%)	97.56	98.71	98.84	98.92	98.86	98.91
AA (%)	95.43	97.38	97.66	97.46	97.69	97.43
Kappa×100	97.29	98.57	98.72	98.80	98.74	98.74

lists the experimental results, which indicate that both the Indian pines dataset and the KSC dataset achieve the best classification accuracy when the ratio between the real samples and the fake samples is 1:1, and the Salinas dataset achieves the best precision at 2:1. The accuracy of the three datasets with fake samples is improved compared with that without fake samples.

This experiment indirectly proves that the distribution of samples generated by AC-WGAN-GP is correct and makes up for the lack of diversity of small training samples in the sample space. The method has a positive impact on the classification results. Among them, Indian Pines and KSC classification accuracy are the best when the ratio of real and false samples is 1:1, and classification accuracy on Salinas is the best when the ratio of real and false samples is 2:1. It may indicate that the sample quality generated by the model on datasets Indian Pines and KSC is slightly better. From Table 9,

Table 10. Effect of fake sample selection method.

Method	KNN Selection			Random Selection
	Indian Pines	Salinas	KSC	Indian Pines	Salinas	KSC
OA (%)	92.51	96.97	98.92	92.31	96.57	98.44
AA (%)	90.59	98.47	97.46	89.53	98.04	97.02
Kappa×100	91.46	96.63	98.80	91.25	96.19	98.26

,

Table 11. The Classification Accuracy of various methods for Indian Pines. Bold values indicate the best result for a row.

Indian Pines
Method	3D-RBF- SVM	EMP-SVM	1D-CNN	1D-S-SVM	3D-Aug-GAN	1D-S-CNN	3D-CNN	AC-WGAN-GP
OA (%)	58.01	69.34	67.18	88.31	91.10	91.28	86.47	92.51
AA (%)	50.56	52.63	55.18	81.07	83.76	92.15	70.41	90.59
Kappa×100	52.07	64.51	62.37	86.69	89.95	90.08	84.12	91.46
1	77.35	15.94	8.70	39.13	31.24	84.78	14.70	71.74
2	18.52	39.16	57.14	94.04	82.05	94.01	86.34	94.26
3	54.66	70.75	28.67	71.81	77.19	79.40	89.49	80.12
4	32.30	54.74	25.74	97.05	91.31	96.20	42.00	93.67
5	9.73	68.37	76.60	82.19	88.51	84.68	85.91	85.71
6	85.53	96.21	91.37	97.67	93.51	98.36	92.75	98.90
7	10.27	100.00	7.14	75.00	41.76	100.00	12.00	100.00
8	78.50	85.00	98.33	94.14	98.32	99.37	100.00	100.00
9	12.32	15.78	5.00	45.00	21.96	100.00	10.00	90.00
10	62.28	75.92	64.30	85.18	75.17	85.08	78.72	90.12
11	66.86	81.23	72.50	88.31	91.37	90.26	95.52	92.83
12	28.25	31.85	56.66	86.34	86.45	90.73	89.47	92.75
13	99.18	98.23	93.67	79.02	52.20	98.05	80.00	99.02
14	85.98	90.85	90.51	97.07	94.64	99.76	84.55	99.92
15	13.82	94.28	26.94	75.91	95.26	76.42	69.54	79.79
16	87.78	95.24	79.57	89.25	89.38	96.77	89.34	80.64

,

Table 12. The Classification Accuracy of various methods for Salinas. Bold values indicate the best result for a row.

Salinas
Method	3D-RBF- SVM	EMP-SVM	1D-CNN	1D-S-SVM	3D-Aug-GAN	1D-S-CNN	3D-CNN	AC-WGAN-GP
OA (%)	83.09	85.90	85.28	95.76	93.67	96.06	88.15	96.86
AA ($)	85.46	82.53	89.29	96.96	90.89	97.43	77.76	97.93
Kappa×100	81.07	84.02	83.61	95.28	92.55	95.61	86.05	96.50
1	94.15	77.97	98.36	97.01	99.14	97.31	60.17	99.90
2	98.57	99.75	98.55	98.36	94.23	100.00	95.04	100.00
3	90.56	50.40	85.43	90.64	76.74	98.79	84.69	100.00
4	98.93	98.72	96.27	98.21	100.00	96.77	97.63	97.20
5	95.23	97.44	81.63	96.23	90.14	99.14	99.95	98.69
6	99.25	99.94	99.85	99.97	99.70	100.00	99.96	99.19
7	98.82	99.88	99.53	100.00	99.90	98.88	87.50	99.89
8	78.50	98.50	77.27	91.94	90.57	92.83	89.65	91.15
9	94.11	99.33	98.69	99.55	100.00	100.00	99.38	100.00
10	85.65	93.99	81.66	90.54	99.03	87.58	98.20	95.91
11	90.63	82.30	78.46	98.69	97.69	98.22	92.20	99.53
12	99.48	100.00	93.41	99.90	99.56	100.00	34.54	99.84
13	20.08	99.12	97.71	99.78	79.60	99.89	19.20	90.83
14	66.29	97.64	91.68	99.16	78.88	99.63	90.38	99.91
15	59.14	13.80	55.74	92.06	71.33	90.36	91.59	95.03
16	66.96	93.79	94.52	99.34	90.12	99.50	18.49	99.83

and

Table 13. The Classification Accuracy of various methods for KSC. Bold values indicate the best result for a row.

KSC
Method	3D-RBF- SVM	EMP-SVM	1D-CNN	1D-S-SVM	3D-Aug-GAN	1D-S-CNN	3D-CNN	AC-WGAN-GP
OA (%)	76.13	90.59	88.04	96.54	98.12	97.56	95.63	98.92
AA ($)	64.60	85.83	81.35	94.46	94.76	95.43	89.65	97.46
Kappa×100	73.52	89.41	86.67	96.15	98.05	97.29	94.95	98.80
1	88.68	87.82	96.32	100.00	98.71	100.00	91.71	100.00
2	69.77	80.14	88.07	100.00	81.28	100.00	89.73	100.00
3	70.73	87.64	85.16	77.73	98.57	76.95	92.16	97.66
4	57.32	86.64	51.19	88.89	87.63	89.68	86.94	100.00
5	42.85	77.02	49.69	73.91	98.89	73.91	94.79	69.56
6	32.24	89.66	54.59	99.56	100.00	100.00	90.92	100.00
7	10.00	83.37	73.33	100.00	98.20	100.00	91.57	100.00
8	42.23	91.78	85.85	89.09	75.05	100.00	96.22	99.77
9	84.00	97.12	94.23	100.00	99.32	100.00	99.53	100.00
10	81.88	97.06	99.00	100.00	100.00	100.00	99.81	100.00
11	96.75	99.64	91.89	98.81	100.00	100.00	99.79	100.00
12	86.32	99.24	89.07	100.00	97.71	100.00	97.69	100.00
13	100.00	100.00	99.14	100.00	100.00	100.00	100.00	100.00

, the bold number in the tables represents the best result in the comparison.

4.5. Effectiveness Analysis of Sample Selection Algorithm

We make a comparison of the classification accuracy of KNN selecting fake samples and randomly selected fake samples to verify the function of our selection algorithm. Table 10 presents the experimental results and indicates that the accuracy of the KNN sample selection method on the three datasets is higher than that of random sample selection method. The OA, AA and KAPPA index using KNN selection on Indian Pines dataset are respectively higher than the random selection method 0.2%, 1.06%, 0.21%. On Salinas and KSC datasets, the number is 0.4%, 0.43%, 0.44% and 0.48%, 0.44%, 0.64%. It shows that the KNN sample selection method is effective and necessary. The selection algorithm we proposed selects the generated samples that are similar to the real samples and has a positive effect on classification.

4.6. Classification Result

As a most important way of assessing the performance, we compare it with several other competing algorithms including SVM, CNN, and GAN on small-size training sets (See Section 4.2 for specific quantities). Recognizing the well-known advantages of support vector machines (SVM), this paper introduces some HSIs classifiers based on SVM for comparison, namely 3D-RBF-SVM and EMP-SVM [12]. 3D-RBF-SVM input is an image block, the SVM classifiers are using the radial basis function kernel. As a typical deep learning model, 1D-CNN [23] and 3D-CNN [24] also have good classification performance, and are used to compare. Furthermore, 3D-Aug-GAN [37] also uses a GAN network to augment the training set and improves classification accuracy, which is used for comparison with our AC-WGAN-GP. Meanwhile, 1D-S-SVM and 1D-S-CNN are also used for comparison. Where S stands for gaussian smoothing, 1D means that the input is a single pixel, and the structure of CNN is the same as that of classifier C. These improved classifiers will verify the effect of smoothing operation and whether AC-WGAN-GP augments the training set thus improving the accuracy of classification. All of the above methods use the same training samples in a small size. Besides, we add a HSI classifiers also using samples with small size named AML [48] for comparison.

The qualitative evaluation of various methods is shown in Table 11, Table 12 and Table 13.

Table 14. Compare the AML and AC-WGAN-GP with different sizes of training sets on Indian Pines.

Dataset	Indian Pines		Salinas
Training set proportion	5%	10%	1%	5%
methods	AML
OA (%)	77.04	82.95	91.63	94.54
AA (%)	77.72	83.29	94.58	97.15
Kappa×100	74.46	81.89	93.15	95.52
Dataset	AC-WGAN-GP
OA (%)	92.44	93.58	96.86	97.04
AA (%)	92.76	94.23	97.93	97.88
Kappa×100	91.61	93.01	96.50	96.95

shows the comparison of the recent classifier AML and AC-WGAN-GP. The visual classification results are shown in Figure 11, Figure 12 and Figure 13. Based on the above experimental results, some observations and discussions can be focused on.

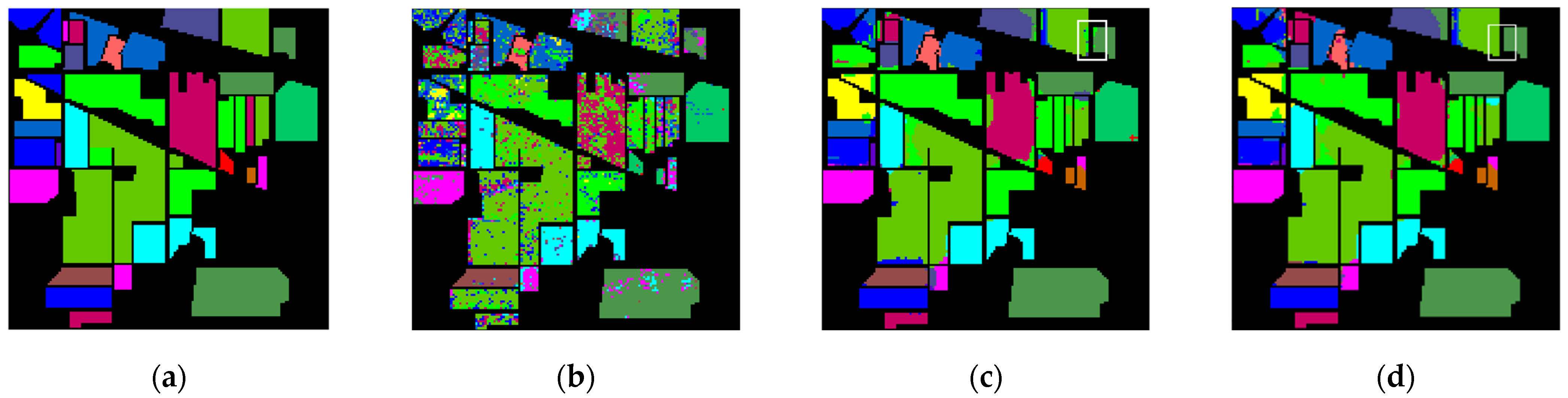
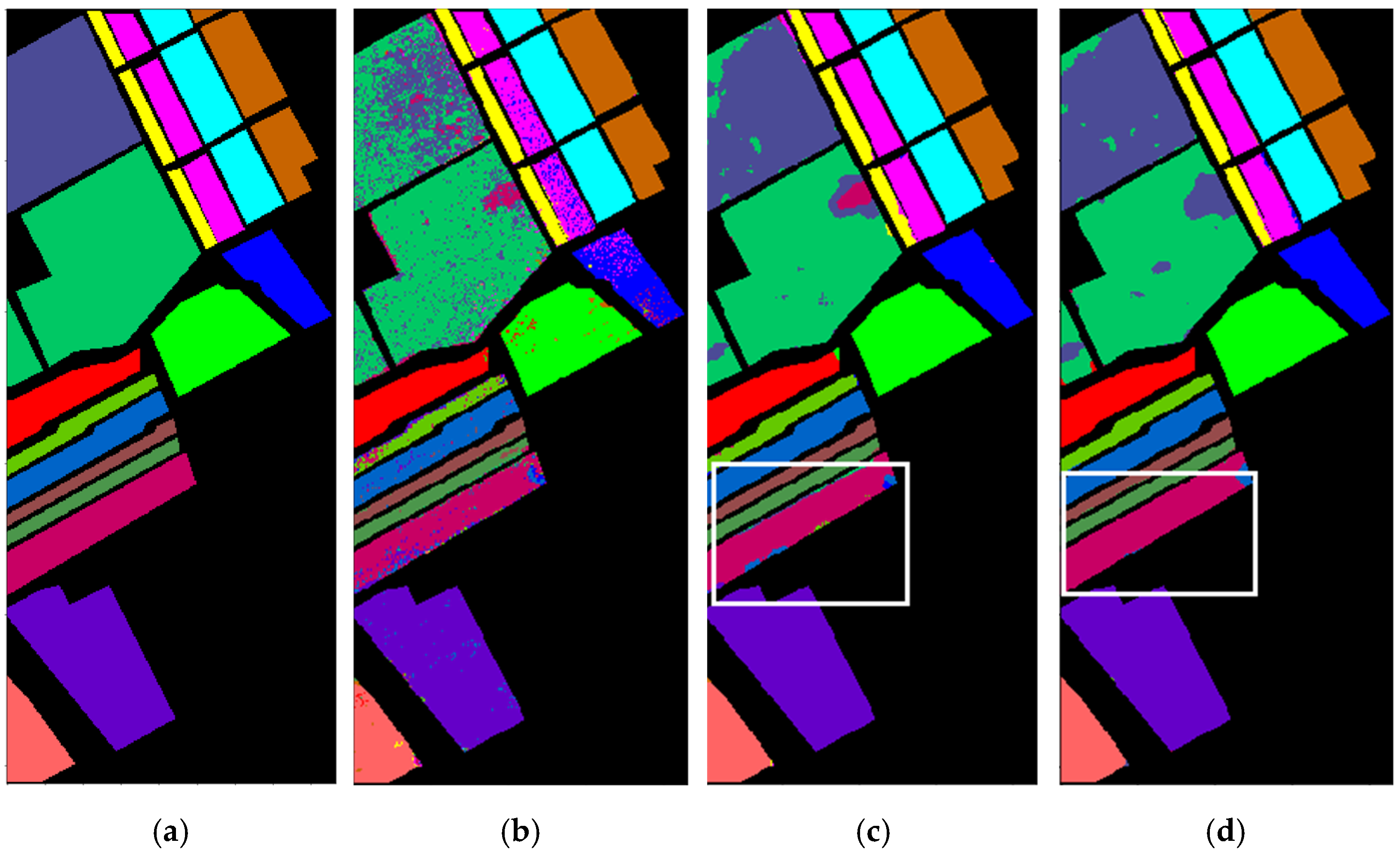
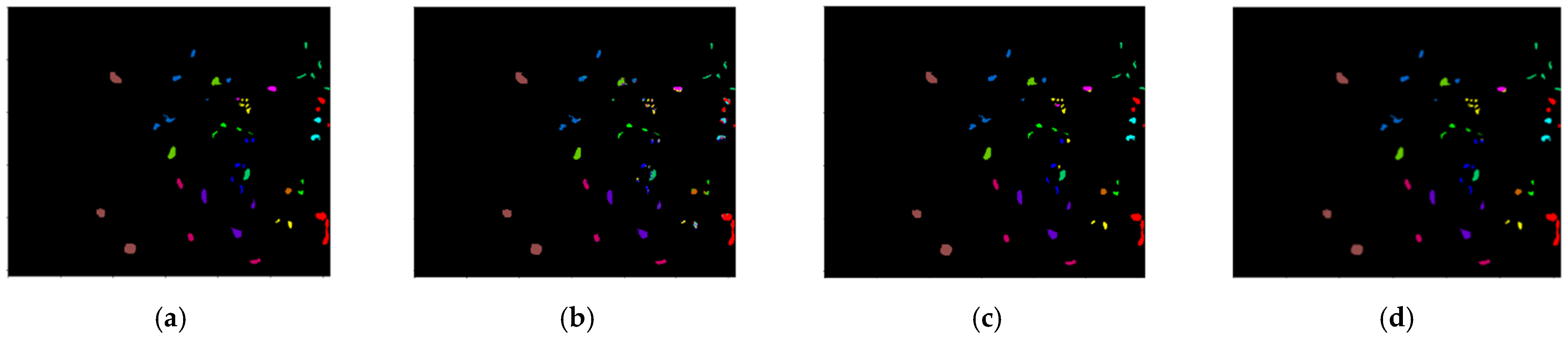
First of all, it can be seen from the visual classification map in Figure 11, Figure 12 and Figure 13. Gaussian smoothing of the data with the 1D-CNN classifier, and our proposed AC-WGAN-GP model. It can be seen that the third and fourth column results are significantly better than the second column. And significant differences between the third and fourth sets of prediction plots are marked by white boxes. In Indian Pines, the classification result of the 1D-S-CNN algorithm demonstrates that compared with the method only using CNN, the noise inside the class is small, but the class boundary produces more error points, which shows that the use of Gaussian smoothing can effectively smooth the spectral samples inside the class, but it is easier to confuse the spatial features at the boundary, and obtain the wrong class boundary. But after using AC-WGAN-GP to augment data, the class boundary in the white box is significantly improved. In Salinas, algorithms confuse some of the categories 8 and 15 samples in this data set, making more misclassification points. The reason for this problem is that the spectral characteristics of the two types are relatively similar, and the classification difficulty comes higher. It is difficult for many algorithms to completely distinguish these two categories. Compared with the other two algorithms, the proposed algorithm has a better classification effect on these two categories. And except for some noise points and misclassification points at the boundary of the 10th and 5th categories, the noise points of other categories in this dataset are less and the boundary positioning is clearer. Compared with 1D-CNN, the noise points of the proposed algorithm are greatly reduced, and compared with 1D-S-CNN, there are fewer areas of error points. In KSC, the pixels are relatively discrete. Figure 13e,f shows that the main misclassification point of the algorithm is that the samples of the fifth class close to the fourth class are wrongly classified into the fourth class. The reason for this error is that the spectrum has the problem of the same spectrum including different objects and the same object scattering in a different spectrum, and the number of training samples is few. The classification results of our proposed method still have obvious advantages in the same region. It can be seen that the positive effect of AC-WGAN-GP data augmentation on classification.

From the Tables, it can be seen intuitively that our proposed method outperforms other methods on most of the three metrics OA, AA, Kappa, and most of the category classification accuracy.

Firstly, we observe that the method (i.e., 3D-RBF-SVM, EMP-SVM, 1D-CNN) uses the single pixel or image block of the original data as input, and their classification accuracy is lower than that of other methods (i.e., SVM, 1D-S-SVM, 1D-S-CNN, AC-WGAN-GP) that adopt gaussian smoothing processing. For example, as can be seen from Table 11, the OA of EMP-SVM is 18.97%, 21.94%, and 23.17% lower than 1D-S-SVM, 1D-S-CNN, and AC-WGAN-GP, respectively. Similar properties can be found in Table 12 and Table 13. The above phenomenon shows that gaussian smoothing can improve the classification accuracy, because gaussian smoothing not only simply filters hyperspectral pixels, but also adds neighboring information. At the same time, gaussian smoothing also makes the learning task easier.

Secondly, the classification accuracy of AC-WGAN-GP is higher than that of 1D-S- CNN with only original training samples. As shown in the experimental results of KSC dataset, OA, AA, and Kappa of AC-WGAN-GP are all higher than those of 1D-S-CNN, which are 1.36%, 2.03%, and 1.51% higher, respectively. The same results can be obtained in the Salinas dataset. On the Indian Pines dataset, OA and Kappa were significantly improved, while AA decreased slightly. Compared with 3D-CNN, the proposed method still has an advantage. The experimental results of the Indian Pines dataset, OA, AA, and Kappa of AC-WGAN-GP are all higher than those of 3D-CNN, which are 6.04%, 20.18% and 7.34% higher, respectively. In addition to the third category, we also outperform 3D-CNN in specific categories. For example categories 12, 13, 16, and 3D-CNN are far below the average due to poor training samples to learn and the proposed AC-WGAN-GP does not have this problem.

Thirdly, by comparing the 3D-Aug–GAN with our proposed AC-WGAN-GP method, it is observed from Table 12 that the OA, AA and Kappa of AC-WGAN-GP are 19.65%, 17.02% and 0.25% higher than 3D-Aug–GAN, respectively. In specific categories, our method is still leading. We can observe the same results from Indian pines and KSC data. The above analysis verifies that the proposed method has higher classification accuracy than that of 3D-Aug-GAN. We have made a little attribution on a GAN-based hyperspectral data augmentation and classifier compared with the above old models.

Fourthly, AML is a method that combines LSTM and attention and aims at HSI classification for small training size. On different proportion of training sets, we compare the AML with our AC-WGAN-GP. The result in Table 14 shows that the performance of our method is ahead of AML slightly.

Finally, we notice that high accuracy can be achieved using only 1D-CNN and the smoothing module on the KSC dataset. Only categories 3, 4 and 5 do not achieve 100.00 accuracy. Even in this case, the method using AC-WGAN-GP framework is still 1.36%, 2.03%, 1.51% higher on OA, AA, and Kappa, respectively. Specially, in Figure 14, we list distribution of generated samples from three categories. These samples have low quality and lead to low accuracy. In Alfalfa, we can see the distribution of real samples is discrete and irregular. So it is difficult for AC-WGAN-GP to learn a better distribution. The generated samples have obvious wrong. In Stone-Steel-Towers, the situation is similar. In OAK/Broadleaf, the generated samples conform to the distribution of the real samples to some extent, but the network has not learned the right sparse and density of real distribution. From the above instances, we find that some categories have complex and uneven distribution. This tests the performance of GAN. For AC-WGAN-GP proposed by us, the result is not ideal.

5. Conclusions

This paper discusses the feasibility of using labeled fake samples as a method of data augmentation in hyperspectral image classification with small sample sizes. Gaussian smoothing makes use of neighboring information and makes the learning task of the network simpler. The proposed AC-WGAN-GP model extends the traditional GAN framework based on the WGAN-GP and AC-GAN. Then, a new sampling method is introduced to generate labeled samples based online generation mechanism. Lastly, a sample selection method is designed. The LSR processing of fake labelled samples can make the use of fake samples more reasonable. The KNN method is used to select samples similar to the test samples from the generated samples and add them to the original training set. The combined training set is used to train the CNN and complete the hyperspectral images classification task with small samples. We verified the results of the proposed method on three popular well-known datasets by selecting few training samples with labels. When we only use 2.0% samples in Indian Pines set, 0.37% samples in Salinas set, 3.8% samples in KSC set, the classification accuracy obtained by our model is 92.51%, 96.86%, and 98.92%, respectively. Compared with the models based on 3DCNN, the proposed model in this paper increases by 6.04%, 8.71%, 3.29%, respectively. Compared with models based on 3DGAN, the proposed model in this paper increases by 1.41%, 3.19%, 0.8%, respectively. However, the complex distribution of original small samples is sometimes difficult for our framework to learn. In our future work, we will try to design more effective GAN to generate better samples or add other frameworks such as in [49].