Improving the Modeling of Sea Surface Currents in the Persian Gulf and the Oman Sea Using Data Assimilation of Satellite Altimetry and Hydrographic Observations
Abstract
:1. Introduction
2. Materials and Methods
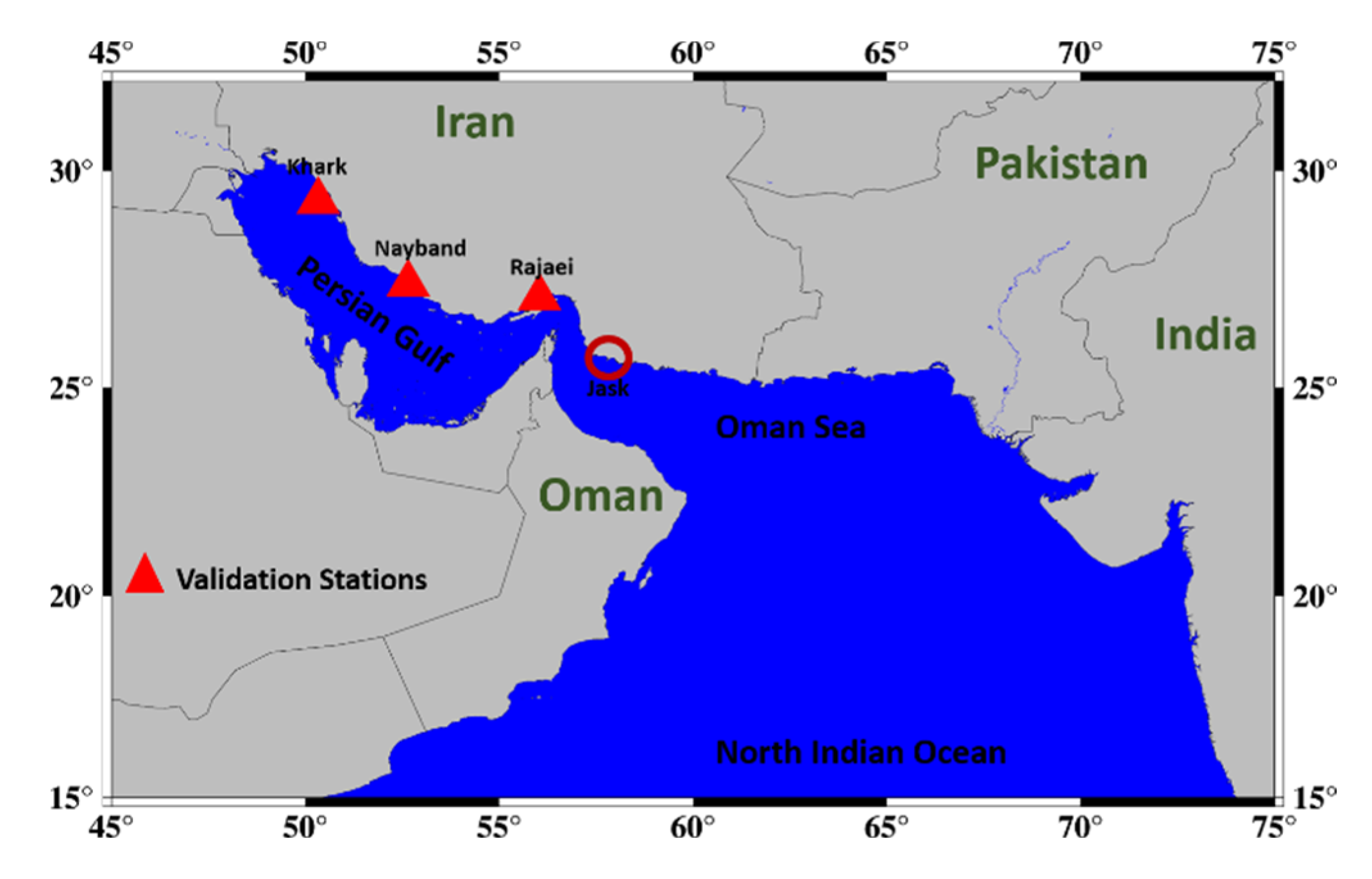
2.1. Data Description
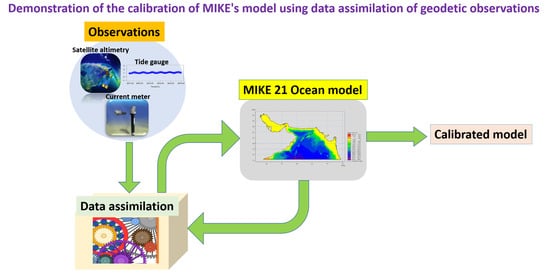
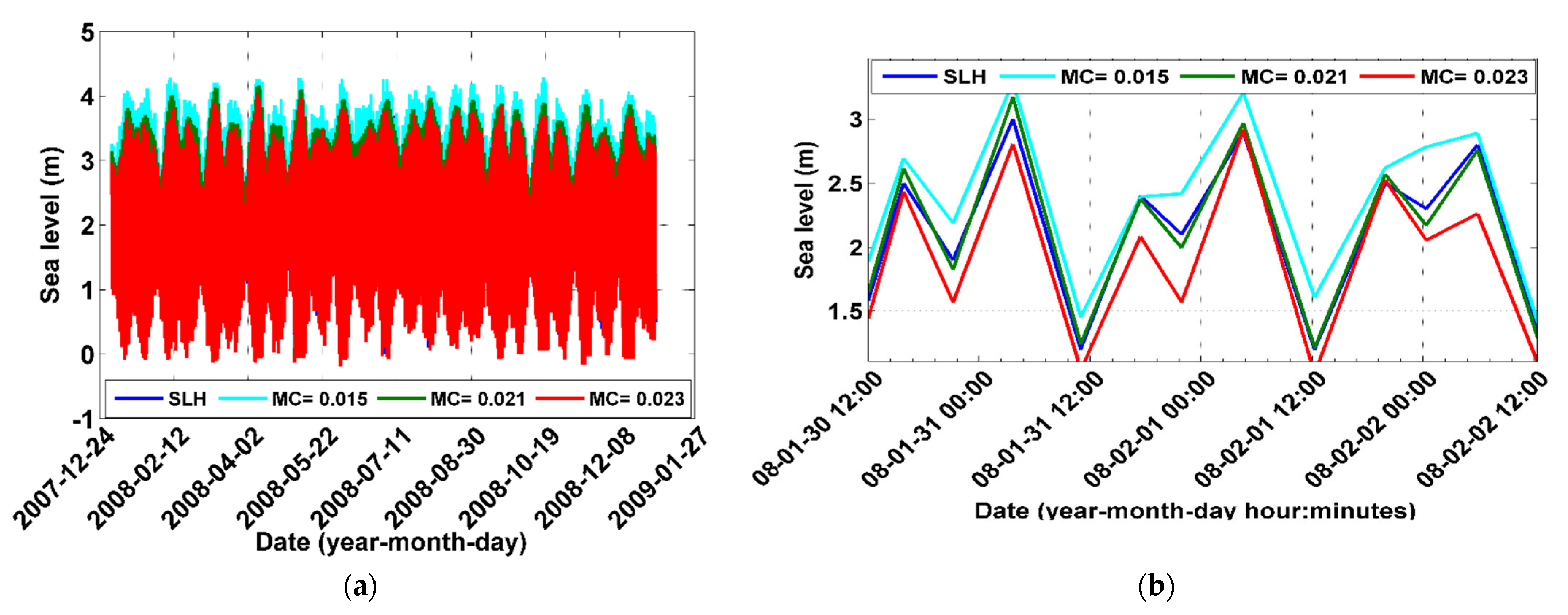
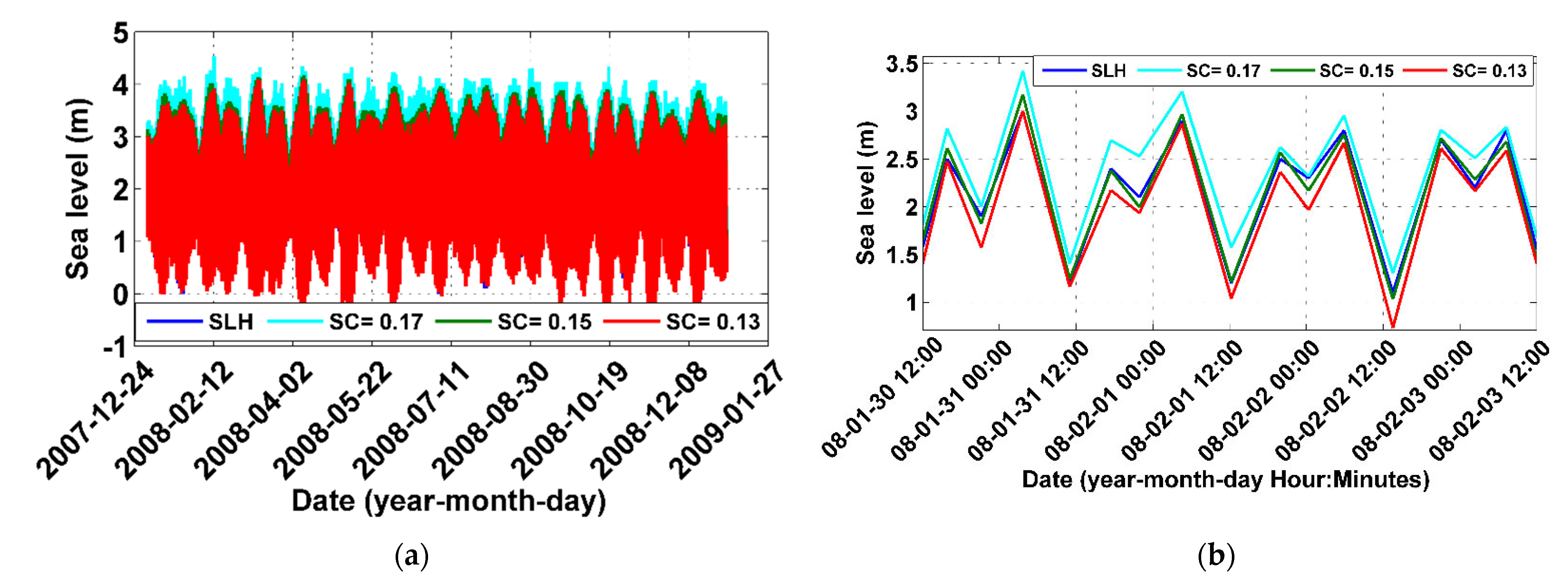
2.2. Methodology of Calibrating MIKE Model
- Selecting the equation solution as “discretization of equations with high degrees”;
- Considering density as a function of temperature and salinity;
- Variable Coriolis force in place;
- Variable wind force;
- Tidal force by applying TM-IR01 model tidal components;
- Precipitation and evaporation;
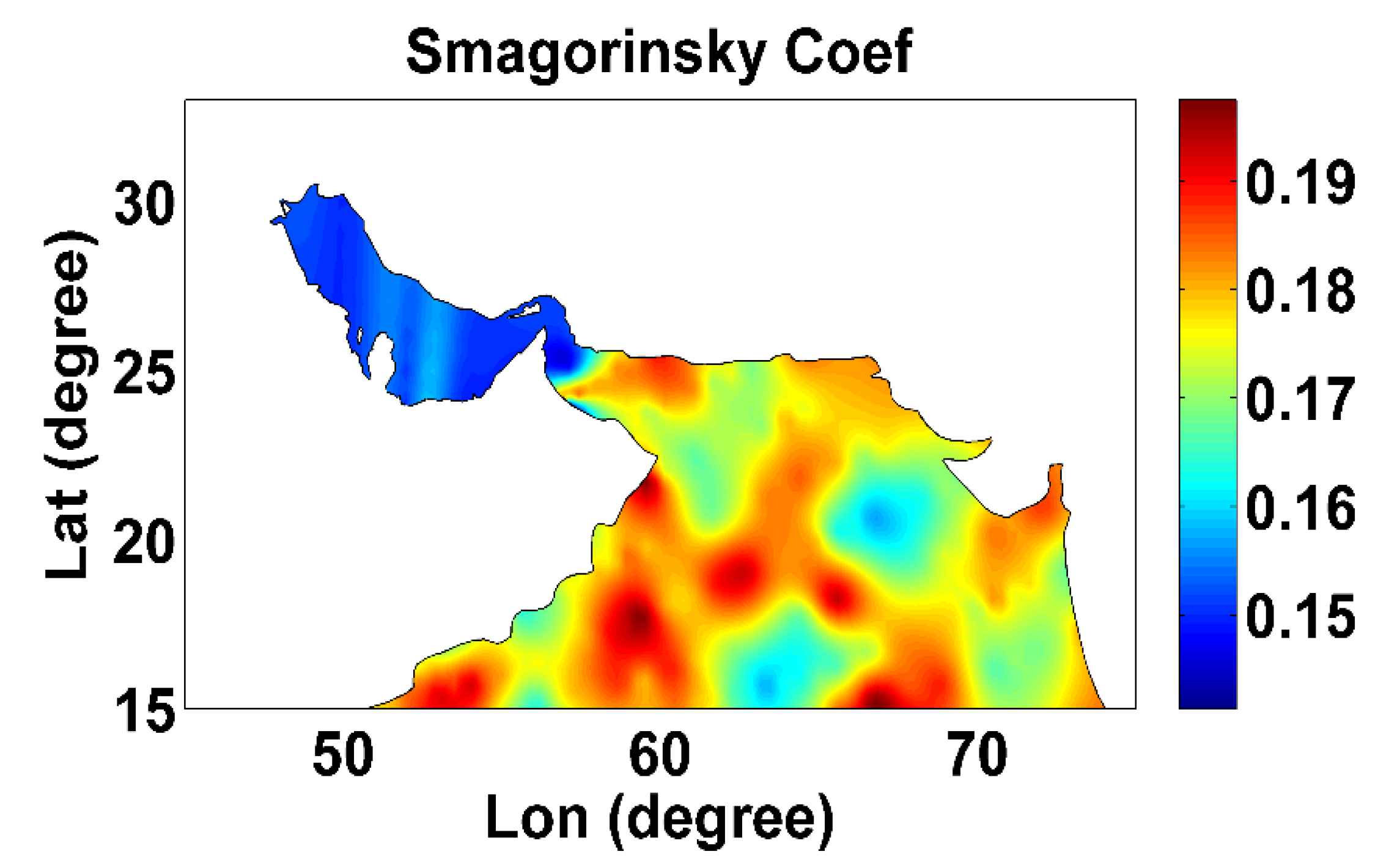
- The Smagorinsky formula was used for horizontal eddy viscosity [30], with a constant value of 0.28 for the Smagorinsky coefficient as the suggested number for the MIKE 21 model;
- In the MIKE 21 model, one of the most valuable features is the ability to dynamically adjust the domain of the computations. This enables one to calculate SSCs in areas that sometimes are dry and sometimes are wet, such as tidal zones;
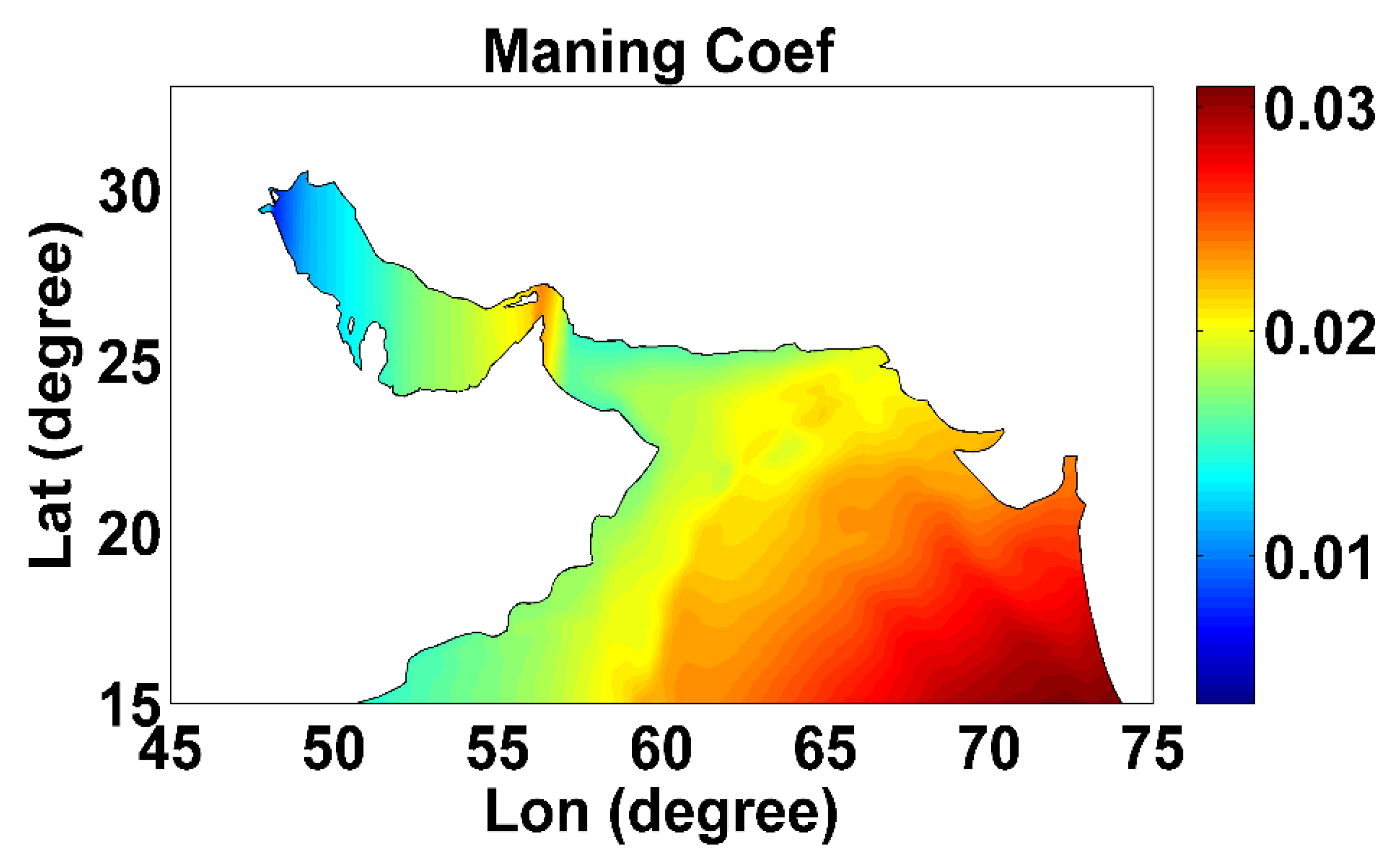
- Manning’s coefficient of 0.03 was applied for the bed resistance
3. Results
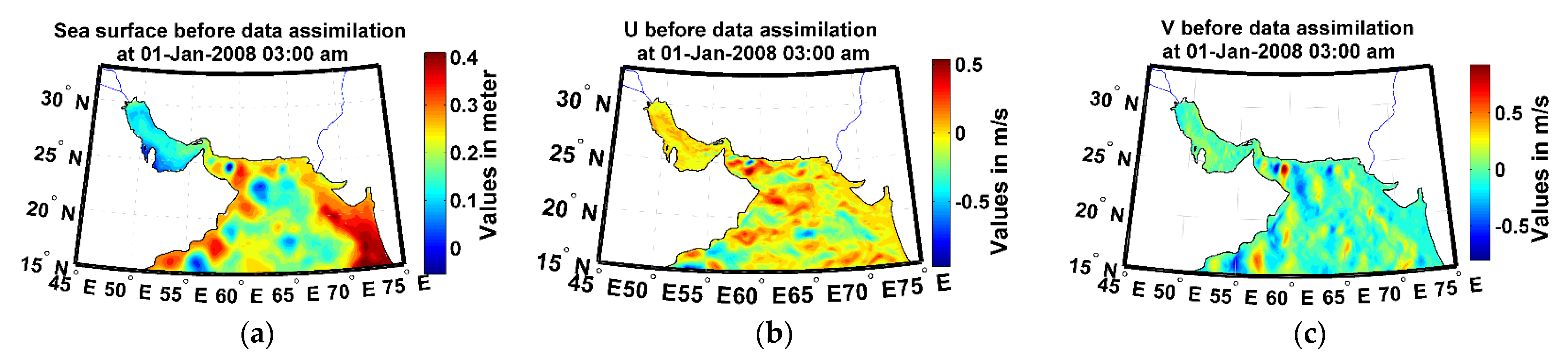
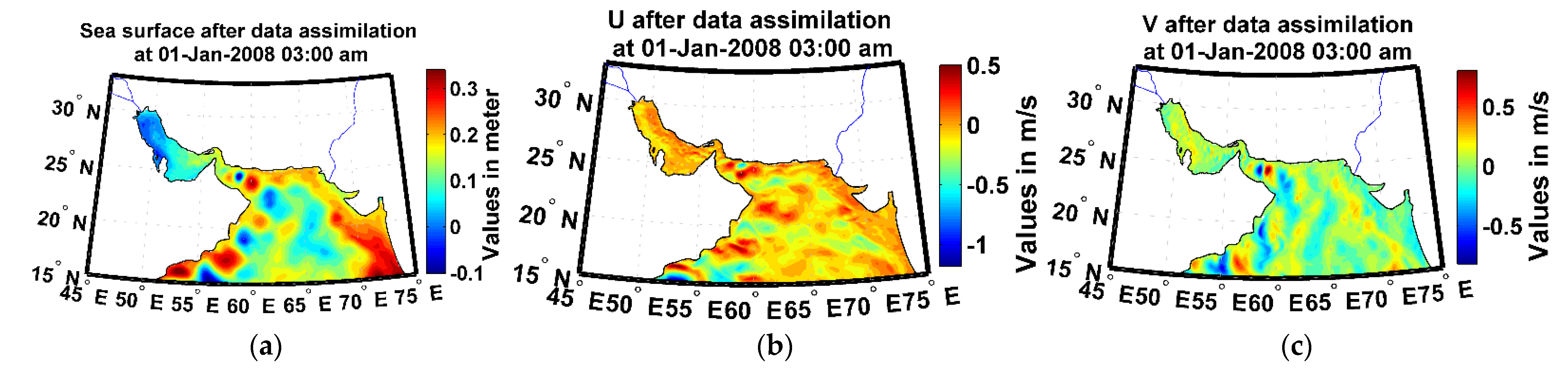
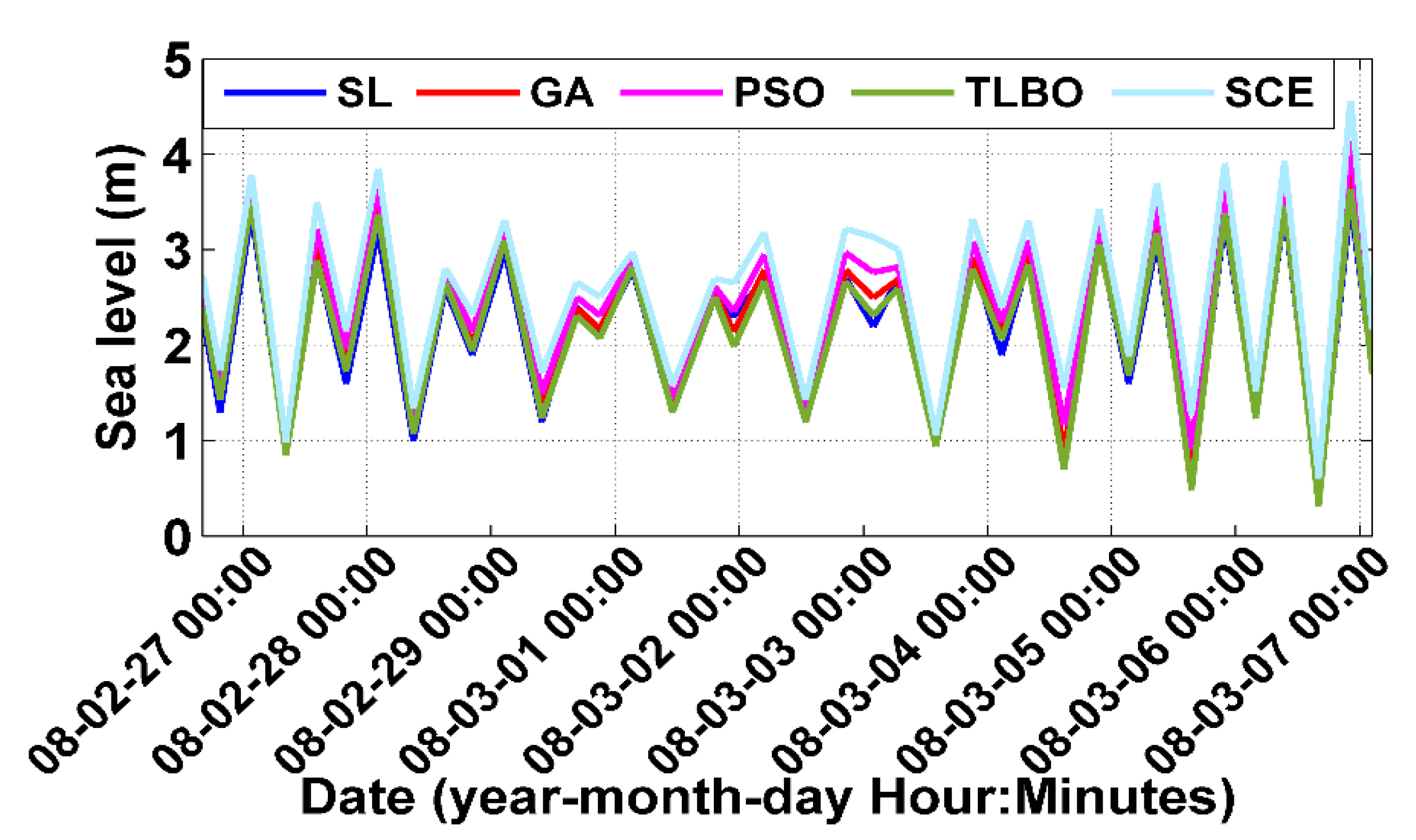
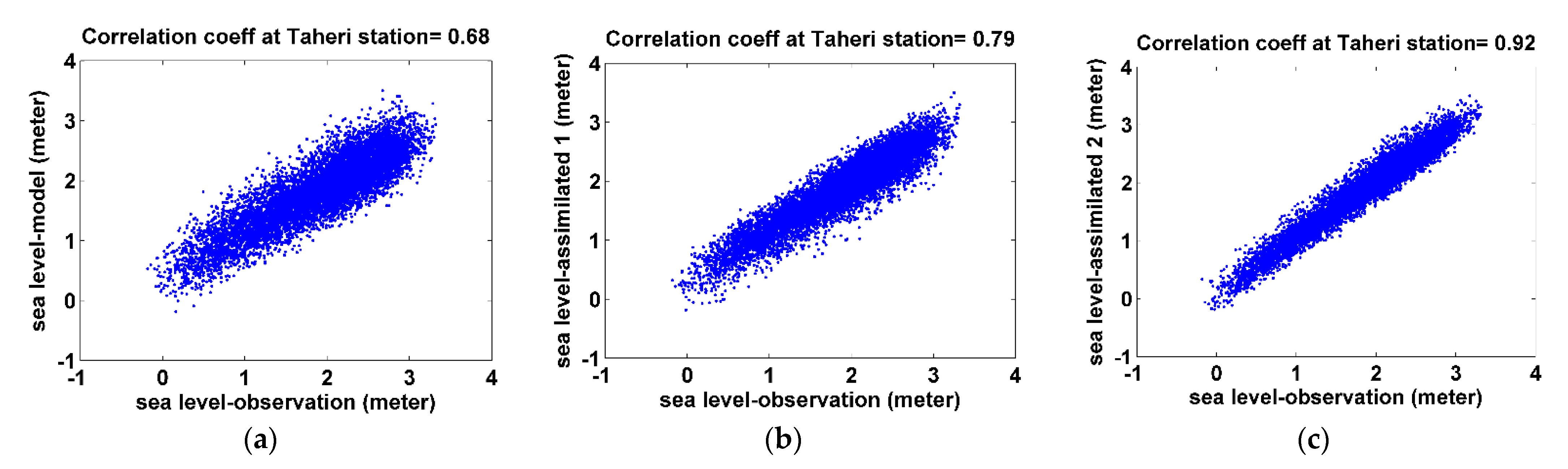
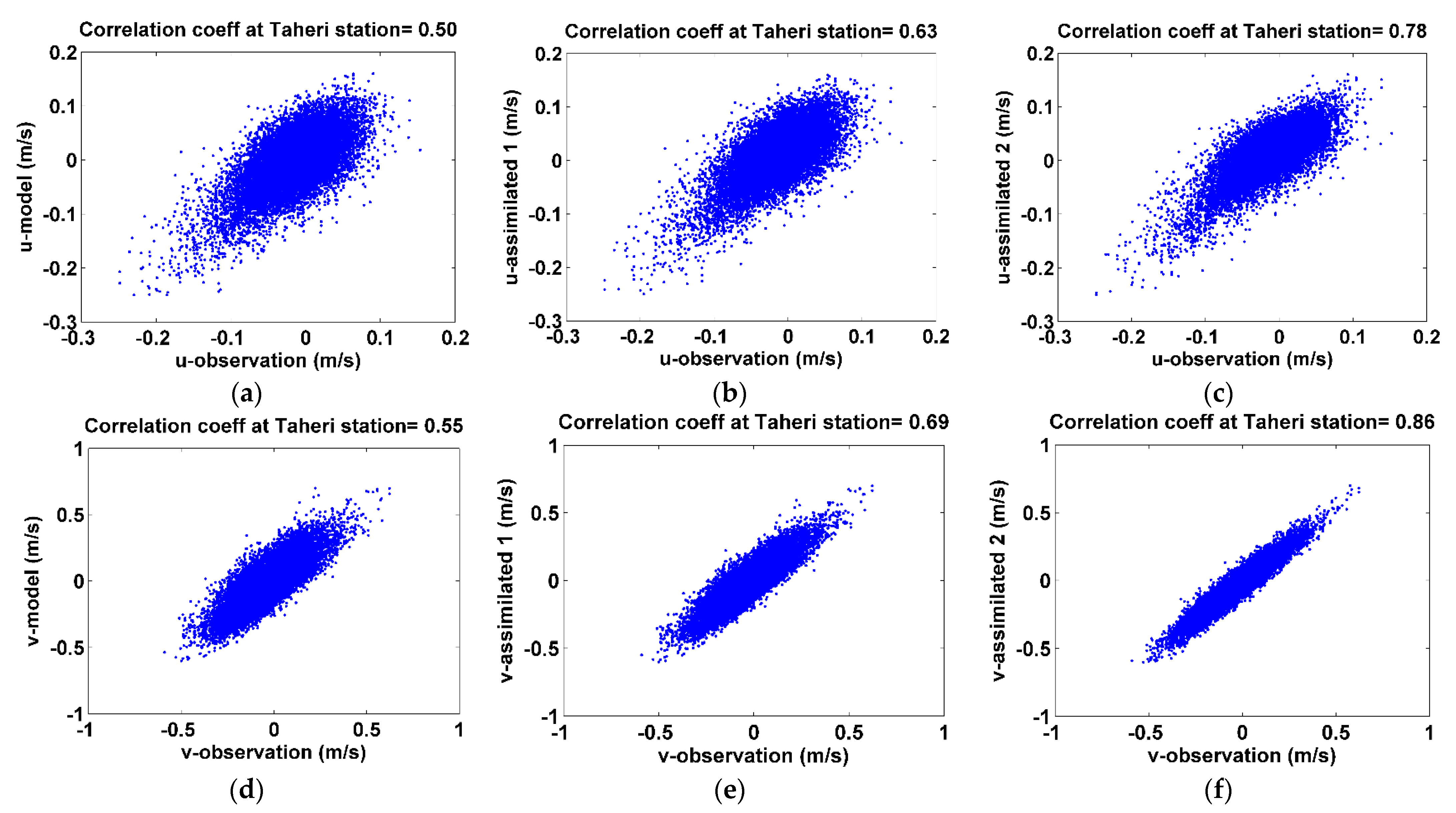
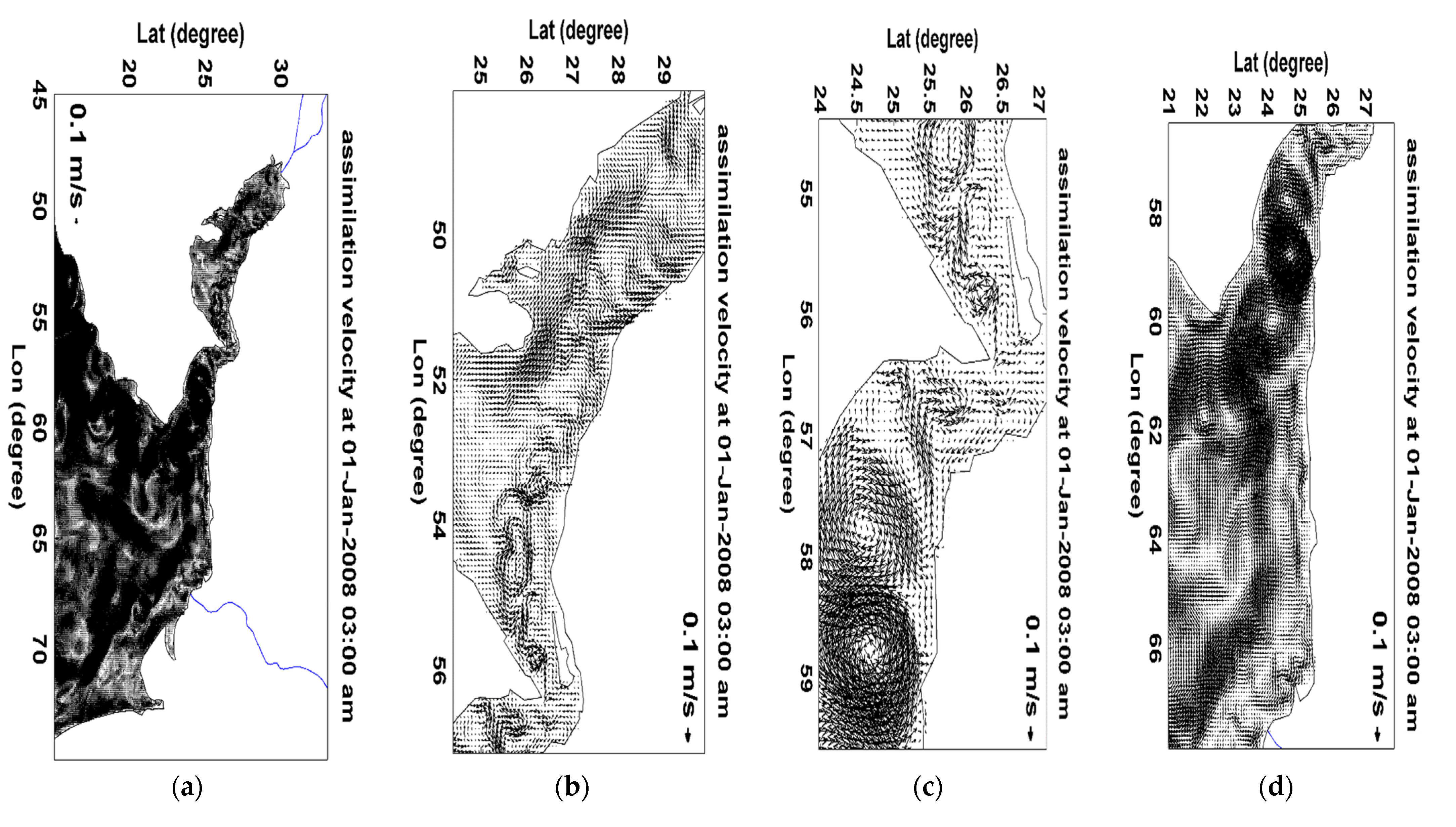
3.1. Numerical Ocean Model and Data Assimilation
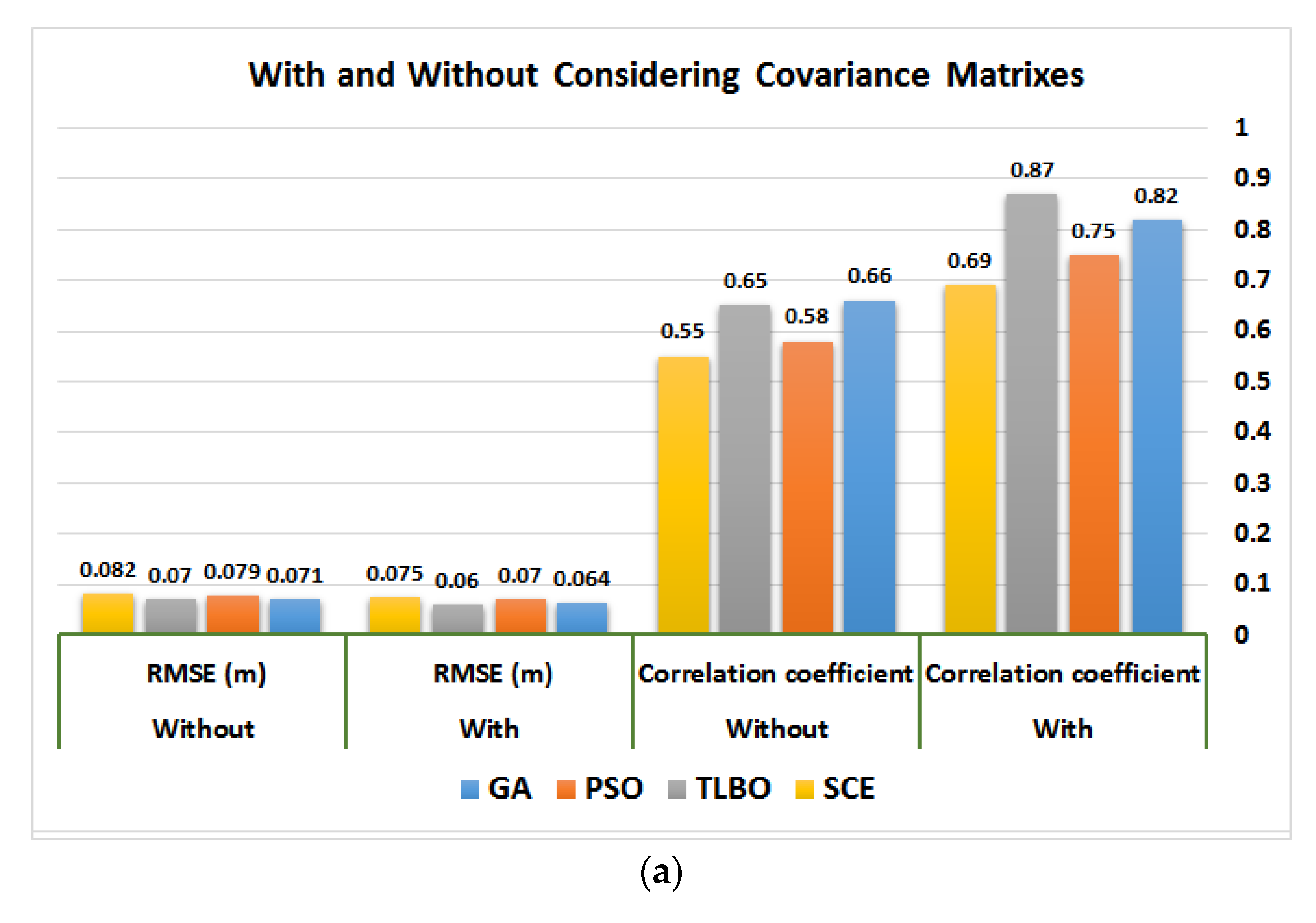
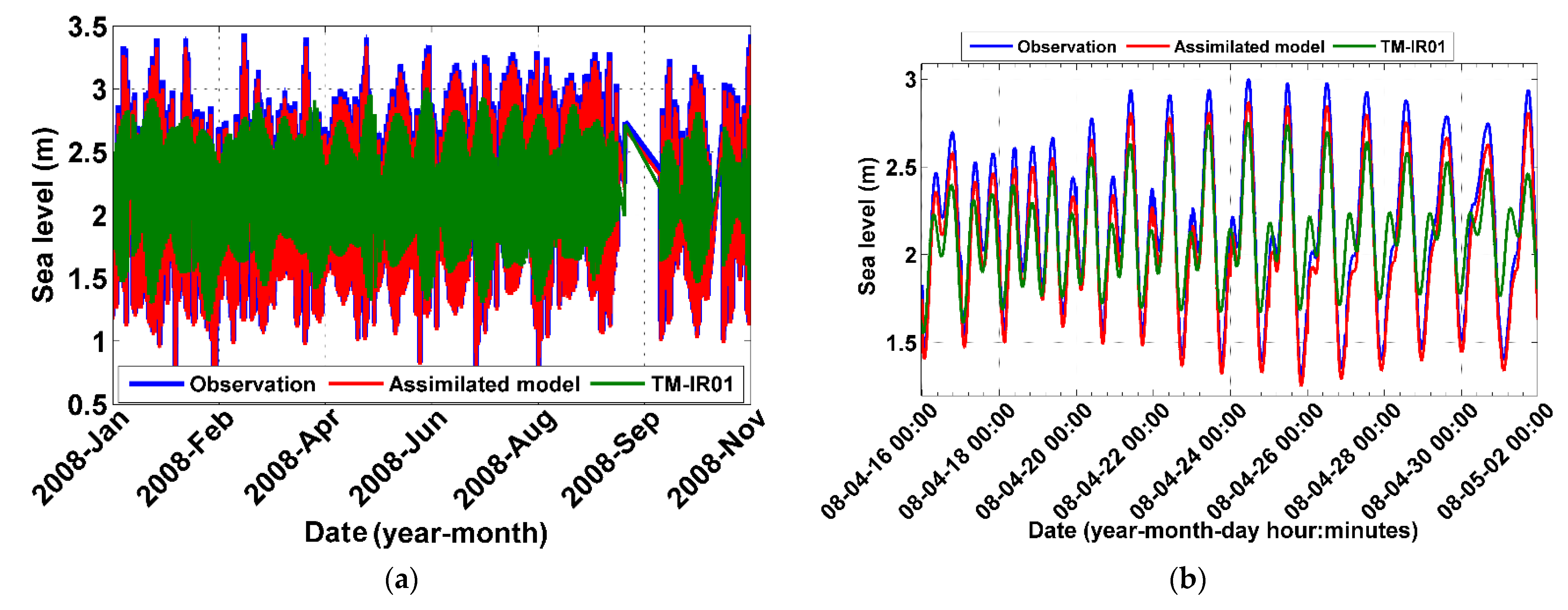
3.2. Validation and Control of Calibrated Model
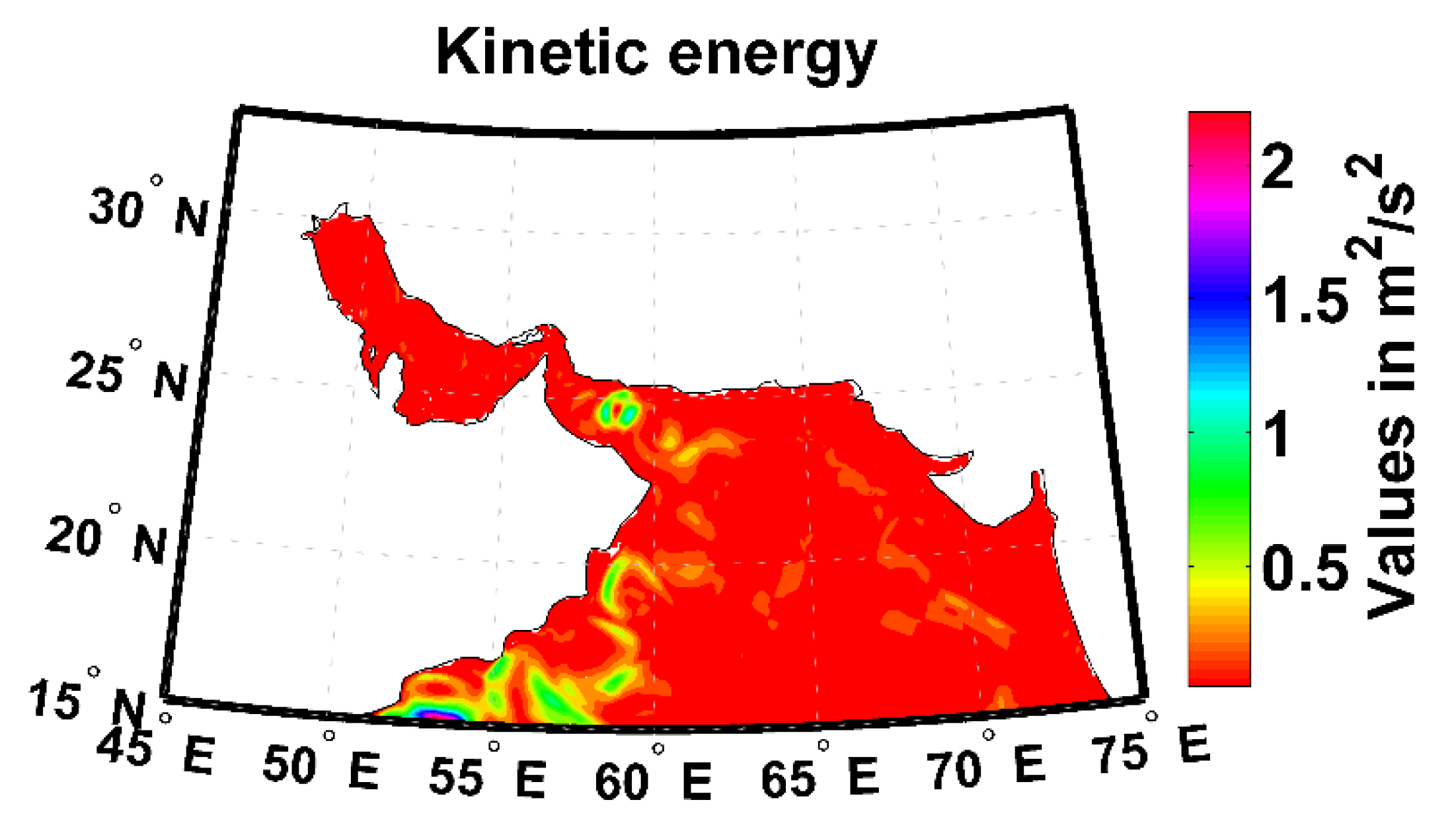
3.3. Analyzing the Results of the SSC and Its Application in Producing Renewable Energy
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dauji, S.; Deo, M.; Bhargava, K. Prediction of ocean currents with artificial neural networks. J. Hydraul. Eng. 2014, 21, 14–27. [Google Scholar] [CrossRef]
- Saha, D.; Deo, M.C.; Joseph, S.; Bhargava, K. A combined numerical and neural technique for short term prediction of ocean currents in the Indian Ocean. Environ. Syst. Res. 2016, 5, 4. [Google Scholar] [CrossRef]
- Sadrinasab, M. Three-dimensional flushing times of the Persian Gulf. Geophys. Res. Lett. 2004, 31, L24301. [Google Scholar] [CrossRef]
- Shchepetkin, A.; McWilliams, J. The regional oceanic modeling system (ROMS): A split-explicit free-surface topography-following-coordinate oceanic model. Ocean Model. 2005, 9, 347–404. [Google Scholar] [CrossRef]
- Bryan, K. A Numerical Method for the Study of the Circulation of the World Ocean. J. Comput. Phys. 1997, 135, 154–169. [Google Scholar] [CrossRef]
- Saputra, R.A.; Perdanawati, R.A.; Akhwadhy, R. Hydrodynamic modelling using software of MIKE 21 in the land reclamation of Jakarta Bay. Current condition and master plan. In Proceedings of the Built Environ Sci Technol International Conference, Surabaya, Indonesia, 18–19 September 2018. [Google Scholar] [CrossRef]
- Chao, S.; Kao, T.W.; Al-Hajri, K.R. A numerical investigation of circulation in the Arabian Gulf. J. Geophys. Res. 1992, 97, 11219–11236. [Google Scholar] [CrossRef]
- Saberi Najafi, S. Modeling Tide in Persian Gulf Using Dynamic Nesting. Ph.D. Thesis, University of Adelaide, Melbourne, Australia, 1997. [Google Scholar]
- Blain, C.A. Modeling three-dimensional thermohaline-driven circulation in the Arabian Gulf. In Estuarine and Coastal Modeling, Proceedings of the 6th International Conference, Stanford, CA, USA, 14–16 August 2000; American Society of Civil Engineers: Reston, VA, USA, 2000; pp. 74–92. [Google Scholar]
- Kämpf, J.; Sadrinasab, M. The circulation of the Persian Gulf: A numerical study. Ocean Sci. Discuss. 2005, 2, 129–164. [Google Scholar] [CrossRef]
- Sabbagh-Yazdi, S.R.; Zounemat-Kermani, M.; Kermani, A. Solution of depth averaged tidal currents in Persian Gulf on unstructured overlapping finite volumes. Int. J. Numer. Methods Fluids 2007, 55, 81–101. [Google Scholar] [CrossRef]
- Afshar-Kaveh, N.; Ghaheri, A.; Chegini, V.; Etemad-Shahidi, A.; Nazarali, M. Evaluation of different wind fields for storm surge modeling in the Persian Gulf. J. Coast. Res. 2017, 333, 596–606. [Google Scholar]
- Bertino, L.; Evensen, G.; Wackernagel, H. Sequential Data Assimilation Techniques in Oceanography. Int. Stat. Rev. 2007, 71, 223–241. [Google Scholar] [CrossRef]
- Peng, S.; Xie, L.; Pietrafesa, L.J. Correcting the errors in the initial conditions and wind stress in storm surge simulation using an adjoint optimal technique. Ocean Model. 2007, 18, 175–193. [Google Scholar] [CrossRef]
- Zalesny, V.; Agoshkov, V.; Shutyaev, V.; Parmuzin, E.; Zakharova, N. Numerical modeling of marine circulation with 4D variational data assimilation. J. Mar. Sci. Eng. 2020, 8, 503. [Google Scholar] [CrossRef]
- Sirkes, Z.; Tziperman, E.; Thacker, W. Combining data and a global primitive equation ocean general circulation model using the adjoint method. Elsevier Oceanogr. 1996, 61, 119–145. [Google Scholar] [CrossRef]
- Mayo, T.; Butler, T.; Dawson, C.; Hoteit, I. Data assimilation within the advanced circulation (ADCIRC) modeling framework for the estimation of manning’s friction coefficient. Ocean Model. 2014, 76, 43–58. [Google Scholar] [CrossRef]
- Stammer, D.; Ray, R.D.; Andersen, O.B.; Arbic, B.K.; Bosch, W.; Carrere, L.; Cheng, Y.; Chinn, D.S.; Dushaw, B.D.; Egbert, G.D. Accuracy assessment of global barotropic ocean tide models. Rev. Geophys. 2014, 52, 243–282. [Google Scholar] [CrossRef]
- Vrugt, J.A.; Gupta, H.V.; Bastidas, L.A.; Bouten, W.; Sorooshian, S. Effective and efficient algorithm for multiobjective optimization of hydrologic models. Water Resour. Res. 2003, 39, 8. [Google Scholar] [CrossRef]
- Lakshmi, V.R. Optimization of thinned dipole arrays using genetic algorithm. Int. J. Eng. Technol. 2011, 3, 658–662. [Google Scholar] [CrossRef]
- Gao, Y.; Zhu, K. Hybrid PSO-solver algorithm for solving optimization problems. J. Comput. Appl. 2012, 31, 1648–1651. [Google Scholar] [CrossRef]
- Rao, R.V. Optimization of multiple chiller systems using TLBO algorithm. In Teaching Learning Based Optimization Algorithm; Springer: Cham, Germany, 2016; pp. 115–128. [Google Scholar] [CrossRef]
- Sivamathi, C.; Vijayarani, S. Assimilation high utility itemsets using shuffled complex evolution of particle swarm optimization (SCE-PSO) optimization algorithm, 2017. In Proceedings of the International Conference on Inventive Computing and Informatics (ICICI), Coimbatore, India, 23–24 November 2017. [Google Scholar] [CrossRef]
- Yang, X.S. Metaheuristic Optimization. Scholarpedia 2011, 6, 11472. [Google Scholar] [CrossRef]
- Zhang, G.; Pan, L.; Neri, F.; Gong, M.; Leporati, A. Metaheuristic Optimization: Algorithmic Design and Applications. J. Optim. 2017, 2017, 1053145. [Google Scholar] [CrossRef]
- Soltanpour, A.; Pirooznia, M.; Aminjafari, S.; Zareian, P. Persian Gulf and Oman sea tide modeling using satellite altimetry and tide Gauge data (TM-IR01). Mar. Georesour. Geotechnol. 2017, 36, 677–687. [Google Scholar] [CrossRef]
- Hall, J.K. GEBCO Centennial special issue—Charting the secret world of the ocean floor. The GEBCO project 1903–2003. Mar. Geophys. Res. 2006, 27, 1–5. [Google Scholar] [CrossRef]
- Wang, Q.; Peng, W.; Dong, F.; Liu, X.; Ou, N. Simulating flow of an urban river course with complex cross sections based on the MIKE 21 FM model. Water 2020, 12, 761. [Google Scholar] [CrossRef]
- Manson, G.K. Configuration of MIKE 21 for the simulation of nearshore storm waves currents and sediment transport: Brackley bight Prince Edward Island. Geol. Surv. Can. 2012. [Google Scholar] [CrossRef]
- Uddin, M.; Mallik, M. Large eddy simulation of turbulent channel flow using Smagorinsky model and effects of Smagorinsky constants. Br. J Math. Comp. Sci. 2015, 7, 375–390. [Google Scholar] [CrossRef]
- Russell, T.F. Stability Analysis and Switching Criteria for Adaptive Implicit Methods Based on the CFL Condition; SPE Symposium on Reservoir Simulation: Houston, TX, USA, 1989. [Google Scholar]
- Zalesny, V.B.; Agoshkov, V.I.; Shutyaev, V.P.; Le Dimet, F.; Ivchenko, B.O. Numerical modeling of ocean hydrodynamics with variational assimilation of observational data. Izv.-Atmos. Ocean. Phys. 2016, 52, 431–442. [Google Scholar] [CrossRef]
- Chua, B.; Bennett, A. An inverse ocean modeling system. Ocean Model. 2001, 3, 137–165. [Google Scholar] [CrossRef]
- Mariella, L.; Tarantino, M. Spatial temporal conditional auto-regressive model: A new autoregressive matrix. Austrian J. Stat. 2016, 39, 223–244. [Google Scholar] [CrossRef]
- Pirooznia, M.; Raoofian Naeeni, M. The application of least-square collocation and variance component estimation in crossover analysis of satellite altimetry observations and altimeter calibration. J. Oper. Oceanogr. 2020, 13, 100–120. [Google Scholar] [CrossRef]
- Lee, J.C.; Huang, X. Modelling the Background Error Covariance Matrix: Applicability Over the Maritime Continent. In Data Assimilation for Atmospheric, Oceanic and Hydrologic Applications; Park, S.K., Xu, L., Eds.; Springer: Cham, Germany, 2021; Volume IV, pp. 599–627. [Google Scholar] [CrossRef]
- Wang, H.; Huang, X.; Sun, J.; Xu, D.; Zhang, M.; Fan, S.; Zhong, J. Inhomogeneous background error modeling for WRF-Var using the NMC method. J. Appl. Meteorol. Climatol. 2014, 53, 2287–2309. [Google Scholar] [CrossRef]
- DeChant, C. Hydrologic data assimilation: State estimation and model calibration. In Dissertations and Theses; Portland State University ProQuest Dissertations Publishing: Portland, OR, USA, 2000; p. 172. [Google Scholar] [CrossRef]
- Pirooznia, M.; Emadi, S.R.; Alamdari, M.N. The time series spectral analysis of satellite altimetry and coastal tide gauges and tide modeling in the coast of Caspian Sea. Open J. Mar. Sci. 2016, 6, 258–269. [Google Scholar] [CrossRef]
- Thoppil, P.G.; Hogan, P.J. A modeling study of circulation and eddies in the Persian Gulf. J. Phys. Oceanogr. 2010, 40, 2122–2134. [Google Scholar] [CrossRef]
- Dudhgaonkar, P.; Duraisamy, N.; Jalihal, P. Energy extraction from ocean currents using straight bladed cross-flow hydrokinetic turbine. Int. J. Ocean. Clim. Syst. 2017, 8, 4–9. [Google Scholar] [CrossRef]
- Shenoi, S.S.; Saji, P.K.; Almeida, A.M. Near-surface circulation and kinetic energy in the tropical Indian Ocean derived from lagrangian drifters. J. Mar. Res. 1999, 57, 885–907. [Google Scholar] [CrossRef]

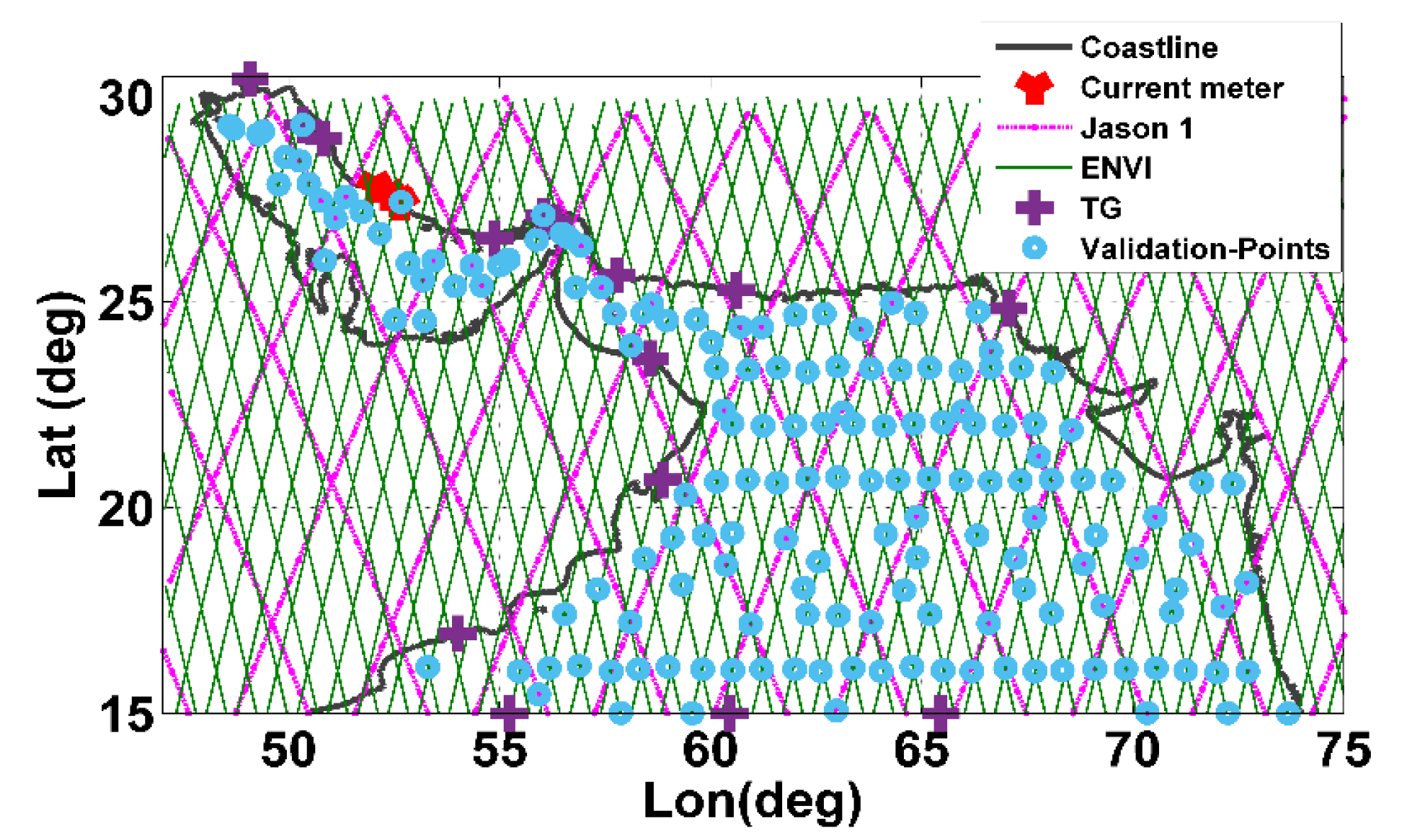


| Station | Country | Latitude [°] | Longitude [°] | Time Period | Data Source | Performance |
|---|---|---|---|---|---|---|
| Muscat | Oman | 23.633 | 58.567 | 2008–2009 | UHSLC 1 | modeling (CB 2) |
| Masirah | Oman | 20.683 | 58.867 | 2008–2009 | UHSLC | modeling (CB) |
| Salalah | Oman | 16.933 | 54.007 | 2008–2009 | UHSLC | data assimilation |
| Karachi | Pakistan | 24.85 | 67.067 | 2008–2009 | UHSLC | modeling (CB) |
| Khark | Iran | 29.31 | 50.33 | 2008–2009 | NCC 3 | validation |
| Jask | Iran | 25.66 | 57.77 | 2008–2009 | NCC | data assimilation |
| Chabahar | Iran | 25.296 | 60.603 | 2008–2009 | UHSLC | modeling (CB) |
| Rajaei | Iran | 27.1 | 56.04 | 2008–2009 | NCC | validation |
| Lengeh | Iran | 26.55 | 54.88 | 2008–2009 | NCC | modeling (CB) |
| Khomeini | Iran | 30.43 | 49.083 | 2008–2009 | NCC | data assimilation |
| Bushehr | Iran | 28.98 | 50.83 | 2008–2009 | NCC | data assimilation |
| Bahman | Iran | 26.95 | 56.28 | 2008–2009 | NCC | modeling (CB) |
| Point_1 | NIO 4 | 15 | 55.231 | 2008–2009 | TM-IR01 | data assimilation |
| Point_2 | NIO | 15 | 60.45 | 2008–2009 | TM-IR01 | modeling (OB 5) |
| Point_3 | NIO | 15 | 65.45 | 2008–2009 | TM-IR01 | modeling (OB) |
| Station | Instrument | Position | Period of Data | Source of Data | Performance |
|---|---|---|---|---|---|
| Taheri | ADCP | 27.63 52.36 | 2008–2009 | PMO 6 | Data assimilation |
| Nayband-Gulf | ADCP | 27.42 52.65 | 2008–2009 | PMO | validation |
| Nakhl-Taghi | ADCP | 27.49 52.57 | 2008–2009 | PMO | Data assimilation |
| Kangan | ADCP | 27.83 52.04 | 2008–2009 | PMO | Data assimilation |
| Mission | Period | Source | Performance |
|---|---|---|---|
| Jason 1 | 2008–2009 | NASA, AVISO | Creation of point-wise time series for data assimilation and validation |
| ENVISAT | 2008–2009 | ESA | Creation of point-wise time series for data assimilation and validation |
| Data | Description |
|---|---|
| Bathymetry | GEBCO, see: https://www.gebco.net/data_and_products/gridded_bathymetry_data/ (accessed on 1 January 2022). |
| Domain | GSHHG, see: https://www.ngdc.noaa.gov/mgg/shorelines/ (accessed on 1 January 2022). |
| Wind | ERA5 hourly data, see: https://cds.climate.copernicus.eu/cdsapp#!/dataset/reanalysis-era5-pressure-levels?tab=form (accessed on 1 January 2022). |
| Evaporation | Copernicus data center, see: https://cds.climate.copernicus.eu/cdsapp#!/dataset/reanalysis-era5-land?tab=overview (accessed on 1 January 2022); these data were used for climatology condition |
| Precipitation | Copernicus data center, see: https://cds.climate.copernicus.eu/cdsapp#!/dataset/satellite-precipitation?tab=overview (accessed on 1 January 2022); these data were used for climatology condition |
| Tidal potential | TM-IR01 from NCC [26]; these data were used for tidal force consideration |
| SLA 7 | Copernicus data center, see https://cds.climate.copernicus.eu/cdsapp#!/dataset/satellite-sea-level-global?tab=overview (accessed on 1 January 2022); these data were used for initial condition of modeling |
| SSC components | Copernicus data center, see:https://cds.climate.copernicus.eu/cdsapp#!/dataset/satellite-sea-level-global?tab=overview (accessed on 1 January 2022); these data were used for initial condition of modeling |
| Different State of Objective Function | ||||||
|---|---|---|---|---|---|---|
| Observations | ||||||
| SLH at Rajaei station (meter) | 0.071 | 0.079 | 0.087 | 0.098 | 0.118 | 0.124 |
| SLH at Khark station (meter) | 0.086 | 0.091 | 0.097 | 0.109 | 0.127 | 0.132 |
| The east–west component of SSC at Nayband station (U) (meters per second) | 0.069 | 0.076 | 0.088 | 0.091 | 0.105 | 0.114 |
| The north–south component of SSC at Nayband station (V) (meters per second) | 0.073 | 0.087 | 0.094 | 0.103 | 0.110 | 0.119 |
| Station | TM-IR01 Model | Assimilated Model |
|---|---|---|
| Muscat | 0.121 | 0.081 |
| Masirah | 0.112 | 0.084 |
| Salalah | 0.126 | 0.097 |
| Karachi | 0.109 | 0.078 |
| Khark | 0.132 | 0.094 |
| Jask | 0.113 | 0.081 |
| Chabahar | 0.132 | 0.075 |
| Rajaei | 0.129 | 0.088 |
| Lengeh | 0.115 | 0.079 |
| Khomeini | 0.127 | 0.082 |
| Bushehr | 0.131 | 0.081 |
| Bahman | 0.127 | 0.086 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pirooznia, M.; Raoofian Naeeni, M.; Atabati, A.; Tourian, M.J. Improving the Modeling of Sea Surface Currents in the Persian Gulf and the Oman Sea Using Data Assimilation of Satellite Altimetry and Hydrographic Observations. Remote Sens. 2022, 14, 4901. https://doi.org/10.3390/rs14194901
Pirooznia M, Raoofian Naeeni M, Atabati A, Tourian MJ. Improving the Modeling of Sea Surface Currents in the Persian Gulf and the Oman Sea Using Data Assimilation of Satellite Altimetry and Hydrographic Observations. Remote Sensing. 2022; 14(19):4901. https://doi.org/10.3390/rs14194901
Chicago/Turabian StylePirooznia, Mahmoud, Mehdi Raoofian Naeeni, Alireza Atabati, and Mohammad J. Tourian. 2022. "Improving the Modeling of Sea Surface Currents in the Persian Gulf and the Oman Sea Using Data Assimilation of Satellite Altimetry and Hydrographic Observations" Remote Sensing 14, no. 19: 4901. https://doi.org/10.3390/rs14194901
APA StylePirooznia, M., Raoofian Naeeni, M., Atabati, A., & Tourian, M. J. (2022). Improving the Modeling of Sea Surface Currents in the Persian Gulf and the Oman Sea Using Data Assimilation of Satellite Altimetry and Hydrographic Observations. Remote Sensing, 14(19), 4901. https://doi.org/10.3390/rs14194901