Detection of Carbon Use Efficiency Extremes and Analysis of Their Forming Climatic Conditions on a Global Scale Using a Remote Sensing-Based Model
Abstract
1. Introduction
2. Datasets and Methods
2.1. The BEPS Model
2.2. Datasets
2.2.1. Global Monthly GPP and NPP Datasets
2.2.2. Climate Data
2.3. Methods
2.3.1. Calculation of CUE
2.3.2. Detection of CUE Extremes
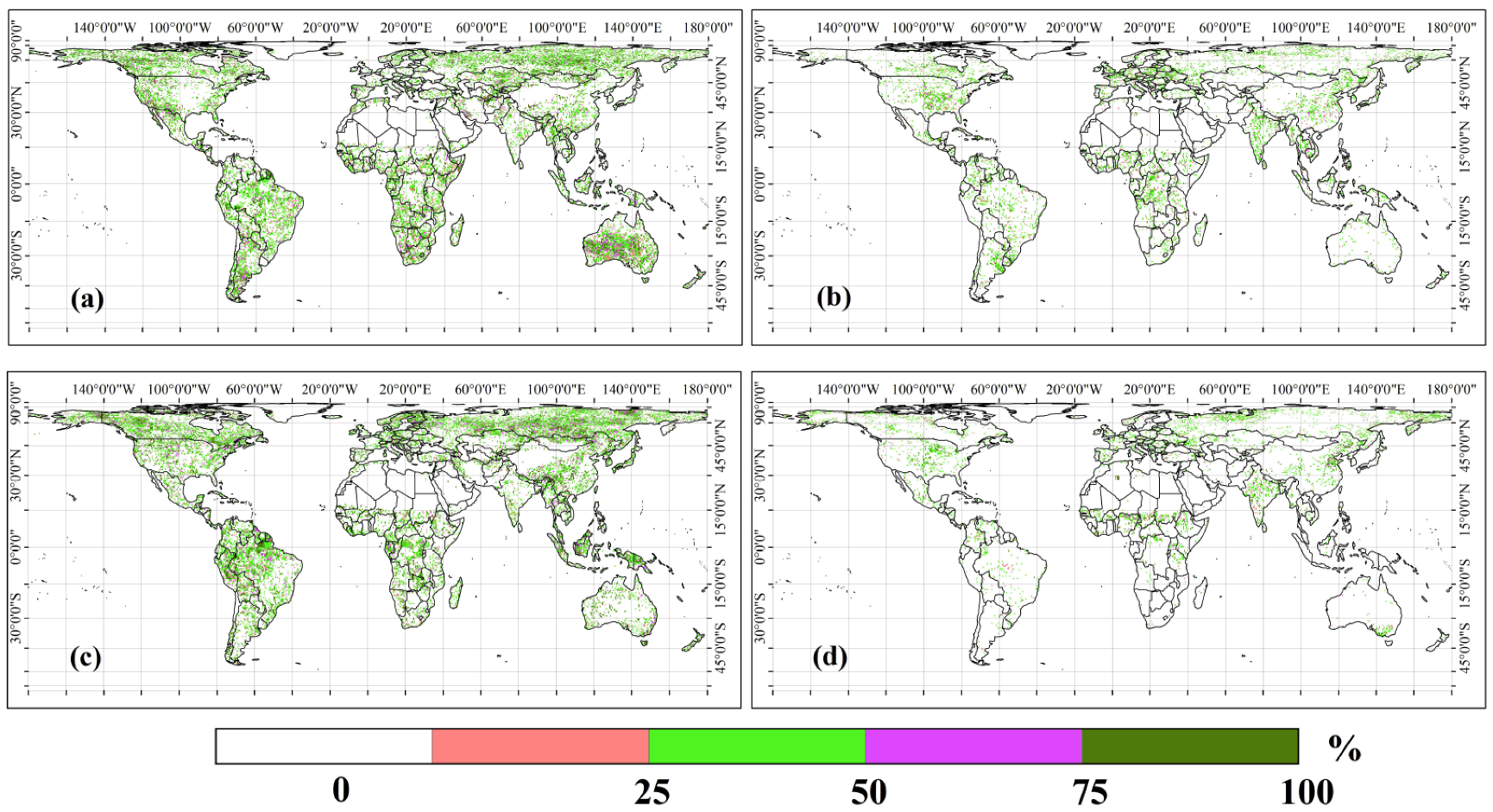
2.3.3. The Probabilities of GPP and Ra Extremes Contributed to CUE Extremes
2.3.4. Analysis of the Climate Conditions on the CUE Extremes
3. Results
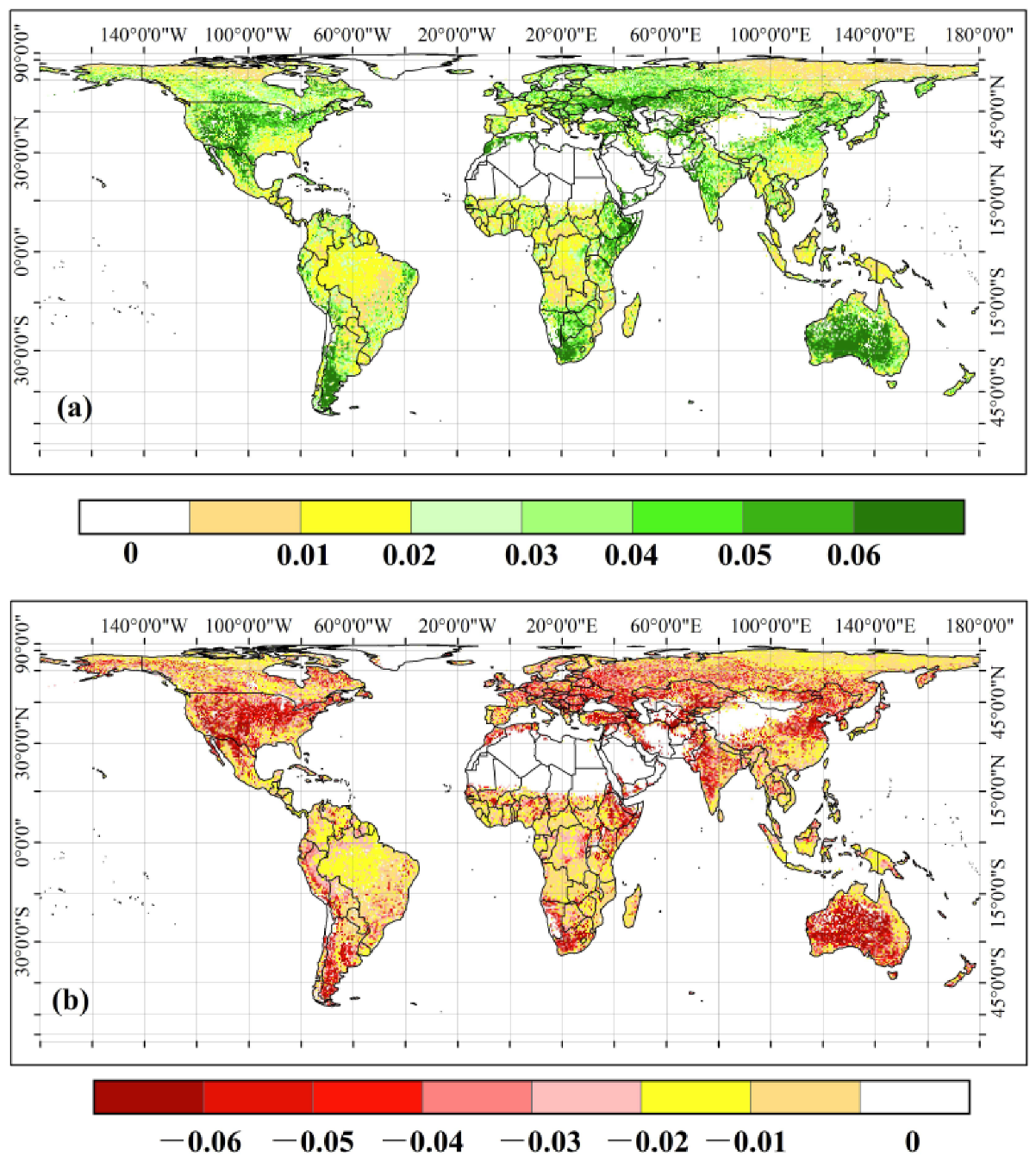
3.1. The Spatial Pattern of the CUE Extremes
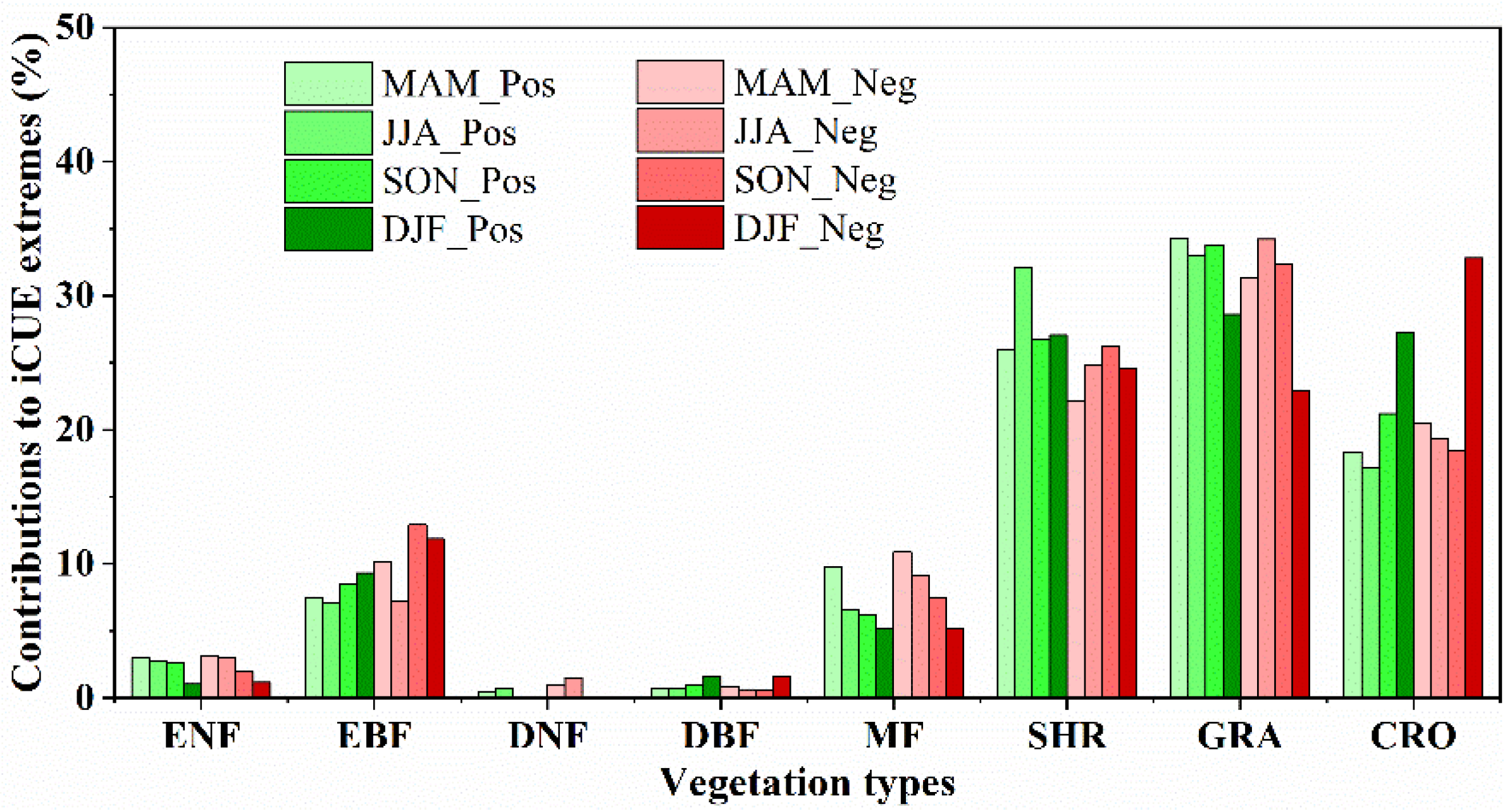
3.2. The PFTs and Seasonal Contribution to CUE Extremes
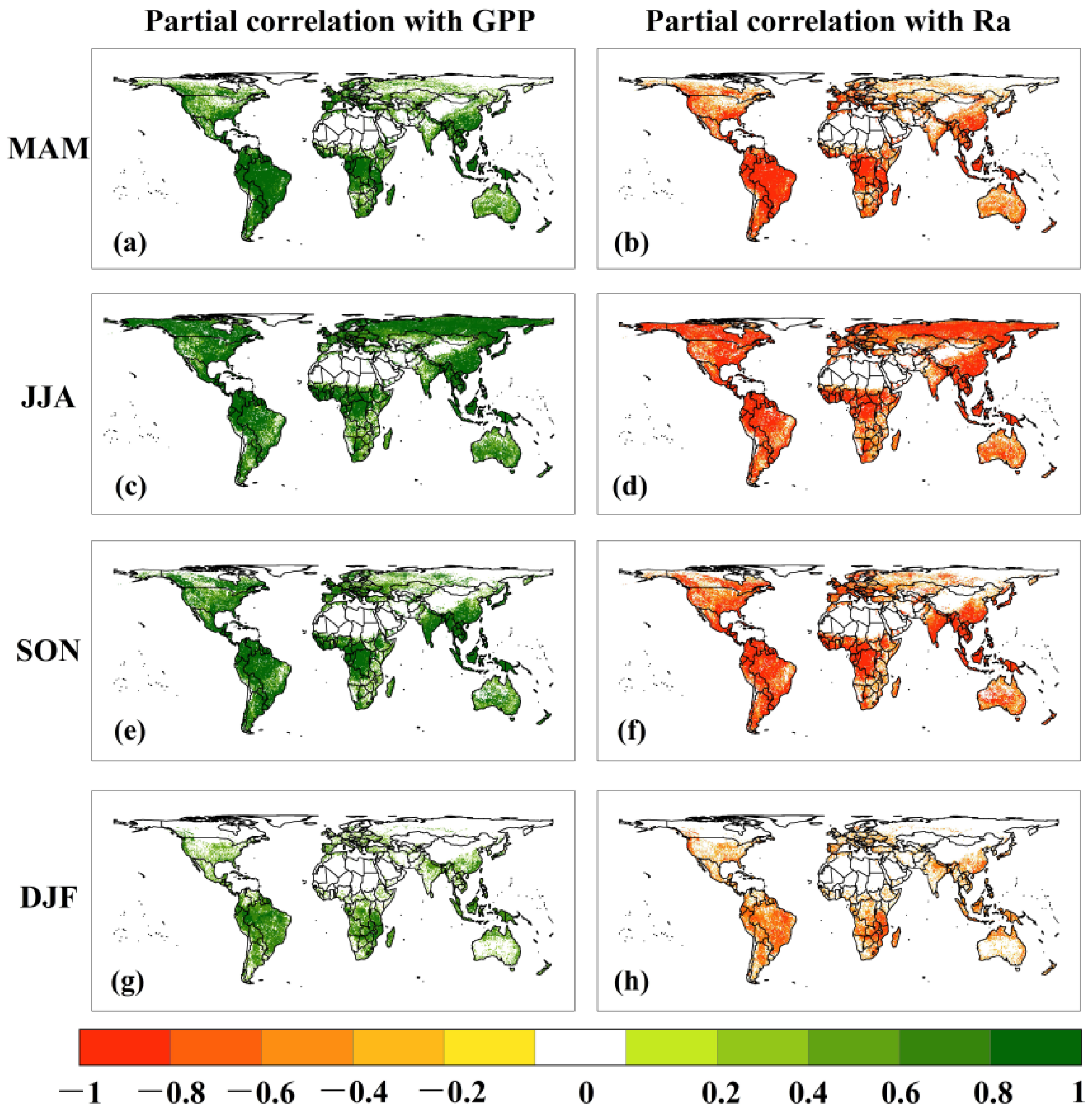
3.3. Correlation of CUE Extremes with GPP and Ra Extremes
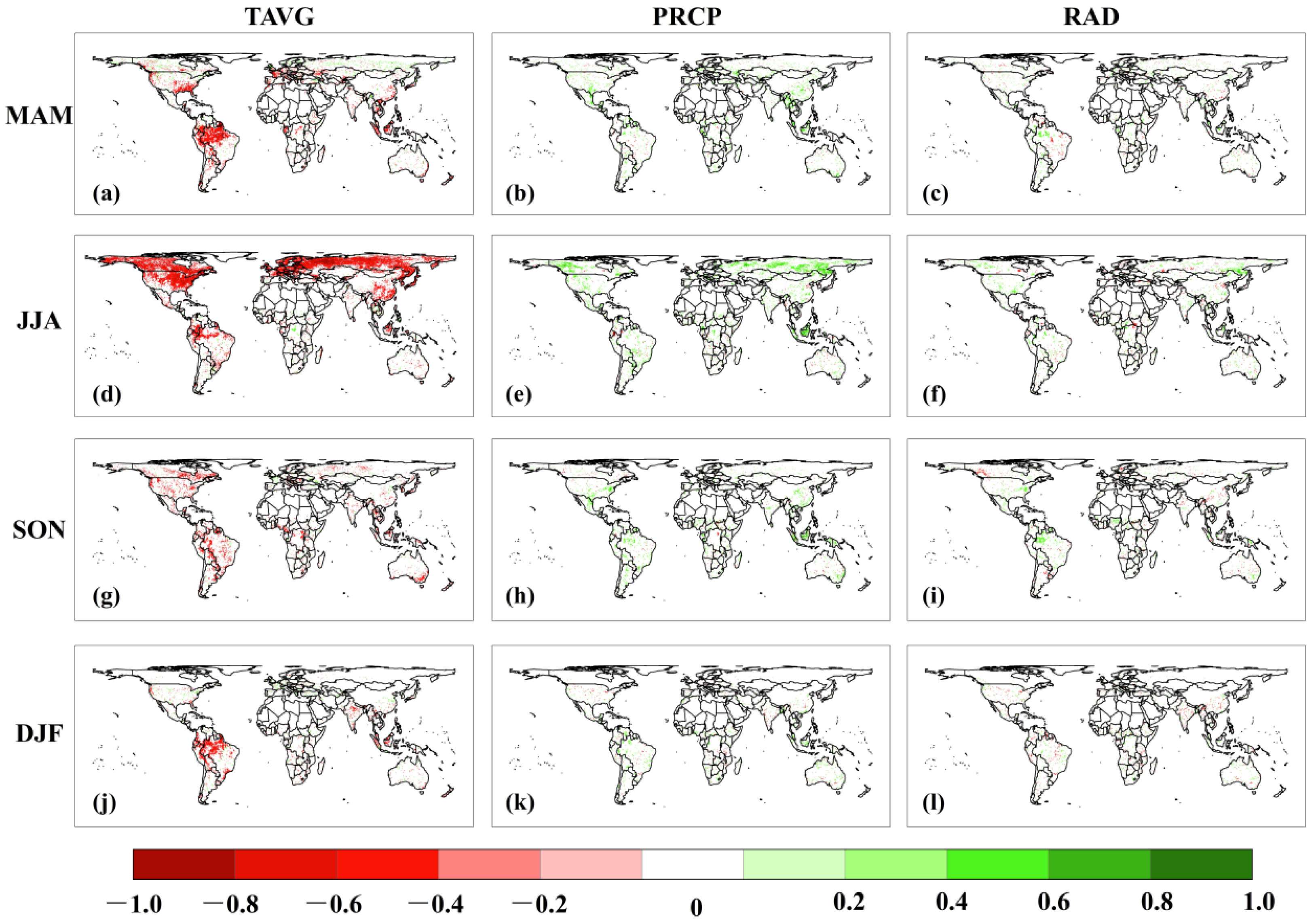
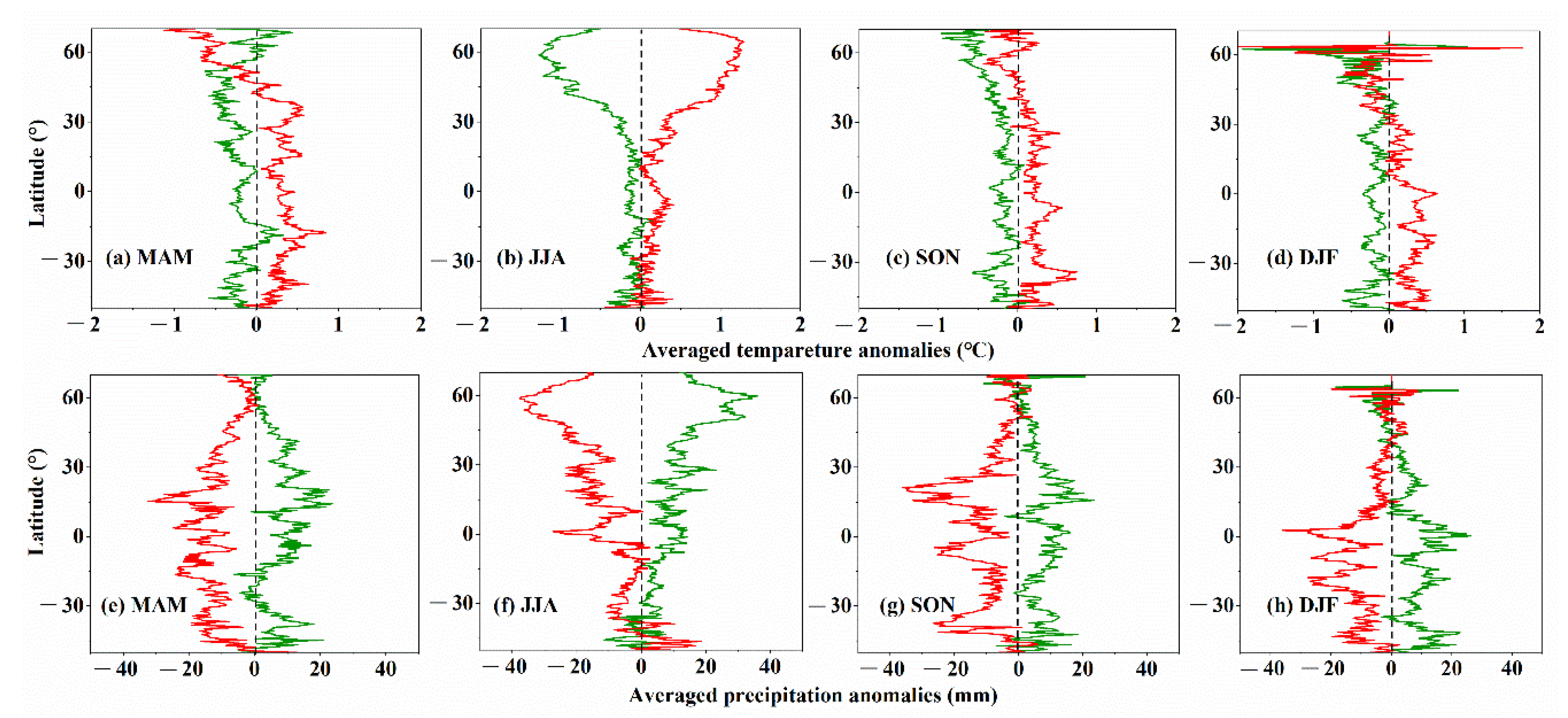
3.4. Climate Conditions for CUE Extremes
4. Discussion
4.1. The Different Contributions of PFTs and Seasonal to CUE Extremes
4.2. CUE Extremes Were Mainly Controlled by GPP Rather Than Ra Extremes
4.3. Cooler and Wetter Than the Current Climate Conditions Are Beneficial for Enhancing CUE in Global Terrestrial Ecosystems
4.4. Uncertainty Analysis
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Friedlingstein, P.; O’Sullivan, M.; Jones, M.W.; Andrew, R.M.; Hauck, J.; Olsen, A.; Peters, G.P.; Peters, W.; Pongratz, J.; Sitch, S.; et al. Global Carbon Budget 2020. Earth Syst. Sci. Data 2020, 12, 3269–3340. [Google Scholar] [CrossRef]
- Wang, M.; Zhao, J.; Wang, S.Q.; Chen, B. Regional Contributions and Climate Attributions to Interannual Variation of Global Net Ecosystems Production by an ECOSYSTEM Processed Model Driven by Remote Sensing Data over the Past 35 Years. Remote Sens. 2022, 14, 3208. [Google Scholar] [CrossRef]
- Collalti, A.; Trotta, C.; Keenan, T.; Ibrom, A.; Lamberty, B.; Grote, R.; Vicca, S.; Reyer, C.P.O.; Migliavacca, M.; Veroustraete, F.; et al. Thinning Can Reduce Losses in Carbon Use Efficiency and Carbon Stocks in Managed Forests Under Warmer Climate. J. Adv. Model. Earth Syst. 2018, 10, 2427–2452. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Yu, G. Spatial variations and controls of carbon use efficiency in China’s terrestrial ecosystems. Sci. Rep. 2019, 9, 19516. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Wang, G.; Mayes, M.A.; Allison, S.D.; Frey, S.D.; Shi, Z.; Hu, X.M.; Luo, Y.; Melillo, J.M. Reduced carbon use efficiency and increased microbial turnover with soil warming. Glob. Chang. Biol. 2019, 25, 900–910. [Google Scholar] [CrossRef] [PubMed]
- Geyer, K.M.; Snowman, K.; Grandy, A.S.; Frey, S.D. Microbial carbon use efficiency: Accounting for population, community, and ecosystem-scale controls over the fate of metabolized organic matter. Biogeochemistry 2016, 127, 173–188. [Google Scholar] [CrossRef]
- Campioli, M.; Vicca, S.; Luyssaert, S. Biomass production effciency controlled by management in temperate and boreal ecosystems. Nat. Genet. 2015, 8, 843–846. [Google Scholar]
- He, Y.; Piao, S.; Li, X.; Chen, A.; Qin, D. Global patterns of vegetation carbon use efficiency and their climate drivers deduced from MODIS satellite data and process-based models. Agric. For. Meteorol. 2018, 256–257, 150–158. [Google Scholar] [CrossRef]
- Mathias, J.M.; Trugman, A.T. Climate change impacts plant carbon balance, increasing mean future carbon use efficiency but decreasing total forest extent at dry range edges. Ecol. Lett. 2022, 25, 498–508. [Google Scholar] [CrossRef]
- Wang, M.M.; Wang, S.Q.; Wang, J.B.; Yan, H.; Mickler, R.A.; Shi, H.; He, H.L.; Huang, M.; Zhou, L. Detection of Positive Gross Primary Production Extremes in Terrestrial Ecosystems of China During 1982-2015 and Analysis of Climate Contribution. J. Geophys. Res.-Biogeosci. 2018, 123, 2807–2823. [Google Scholar] [CrossRef]
- Wang, M.; Zhao, J.; Wang, S.; Chen, B.; Li, Z. Detection and attribution of positive net ecosystem productivity extremes in China’s terrestrial ecosystems during 2000–2016. Ecol. Indic. 2021, 132, 108323. [Google Scholar] [CrossRef]
- Drake, J.E.; Furze, M.E.; Tjoelker, M.G.; Carrillo, Y.; Barton, C.V.M.; Pendall, E. Climate warming and tree carbon use efficiency in a whole-tree (13) CO2 tracer study. New Phytol. 2019, 222, 1313–1324. [Google Scholar] [CrossRef] [PubMed]
- Potter, C.; Randerson, J.T.; Field, C.B. Terrestrial ecosystem production: A process model based on global satellite and surface data. Glob. Biogeochem. Cycles 1993, 7, 811–841. [Google Scholar] [CrossRef]
- Running, S.W.; Coughlan, J.C. A General-Model of Forest Ecosystem Processes for Regional Applications I. Hydrologic Balance, Canopy Gas-Exchange and Primary Production Processes. Ecol. Model. 1988, 42, 125–154. [Google Scholar] [CrossRef]
- Piao, S.L.; Liu, Z.; Wang, T.; Peng, S.; Ciais, P.; Huang, M.; Ahlstrom, A.; Burkhart, J.F.; Chevallier, F.; Janssens, I.A.; et al. Weakening temperature control on the interannual variations of spring carbon uptake across northern lands. Nat. Clim. Chang. 2017, 7, 359–363. [Google Scholar] [CrossRef]
- Liu, D.; Li, Y.; Wang, T.; Peylin, P.; MacBean, N.; Clais, P.; Jia, G.; Ma, M.; Ma, Y.; Shen, M.; et al. Contrasting responses of grassland water and carbon exchanges to climate change between tibetan plateau and inner Mongolia. Agric. For. Meteorol. 2018, 249, 163–175. [Google Scholar] [CrossRef]
- Wu, D.; Ciais, P.; Viovy, N.; Knapp, A.K.; Wilcox, K.; Bahn, M.; Smith, M.D.; Vicca, S.; Fatichi, S.; Zscheischler, J.; et al. Asymmetric responses of primary productivity to altered precipitation simulated by ecosystem models across three long-term grassland sites. Biogeosci. Discuss. 2018, 15, 3421–3437. [Google Scholar] [CrossRef]
- Liu, J.; Chen, J.M.; Cihlar, J.; Park, W.M. A process-based boreal ecosystem productivity simulator using remote sensing inputs. Remote Sens. Environ. 1997, 62, 158–175. [Google Scholar] [CrossRef]
- Chen, J.M.; Ju, W.; Ciais, P.; Viovy, N.; Liu, R.; Liu, Y.; Lu, X. Vegetation structural change since 1981 significantly enhanced the terrestrial carbon sink. Nat. Commun. 2019, 10, 4259. [Google Scholar] [CrossRef]
- Chen, J.M.; Liu, J.; Cihlar, J.; Goulden, M.L. Daily canopy photosynthesis model through temporal and spatial scaling for remote sensing applications. Ecol. Model. 1999, 124, 99–119. [Google Scholar] [CrossRef]
- He, S.; Zheng, Z.; Zhu, R. Long-term tea plantation effects on composition and stabilization of soil organic matter in Southwest China. Catena 2021, 199, 105132. [Google Scholar] [CrossRef]
- He, H.; Wang, S.; Zhang, L.; Wang, J.; Ren, X.; Zhou, L.; Piao, S.; Yan, H.; Ju, W.; Gu, F.; et al. Altered trends in carbon uptake in China’s terrestrial ecosystems under the enhanced summer monsoon and warming hiatus. Nat. Sci. Rev. 2019, 6, 505–514. [Google Scholar]
- Matsushita, B.; Tamura, M. Integrating remotely sensed data with an ecosystem model to estimate net primary productivity in East Asia. Remote Sens. Environ. 2002, 81, 58–66. [Google Scholar] [CrossRef]
- Sprintsin, M.; Chen, J.M.; Desai, A.; Gough, C.M. Evaluation of leaf-to-canopy upscaling methodologies against carbon flux data in North America. J. Geophys. Res. Biogeosci. 2012, 117, 313–319. [Google Scholar] [CrossRef]
- Wang, Q.; Tenhunen, J.; Falge, E.; Bernhofer, C.H.; Granier, A.; Vesala, T. Simulation and scaling of temporal variation in gross primary production for coniferous and deciduous temperate forests. Glob. Chang. Biol. 2004, 10, 37–51. [Google Scholar] [CrossRef]
- Viovy, N. CRUNCEP Data Set. Available online: Ftp://nacp.ornl.gov/synthesis/2009/frescati/temp/landusechange/original/readme.htm (accessed on 11 August 2018).
- Du, L.; Gong, F.; Zeng, Y.; Ma, L.; Qiao, C.; Wu, H. Carbon use efficiency of terrestrial ecosystems in desert/grassland biome transition zone: A case in Ningxia province, northwest China. Ecol. Indic. 2021, 120, 106971. [Google Scholar] [CrossRef]
- Reichstein, M.; Bahn, M.; Ciais, P.; Frank, D.; Mahecha, M.D.; Seneviratne, S.I.; Zscheischler, J.; Beer, C.; Buchmann, N.; Frank, D.C.; et al. Climate extremes and the carbon cycle. Nature 2013, 500, 287–295. [Google Scholar]
- Frank, D.; Reichstein, M.; Bahn, M.; Thonicke, K.; Frank, D.; Mahecha, M.D.; Smith, P.; van der Velde, M.; Vicca, S.; Babst, F.; et al. Effects of climate extremes on the terrestrial carbon cycle: Concepts, processes and potential future impacts. Glob. Chang. Biol. 2015, 21, 2861–2880. [Google Scholar]
- Chen, C.; Riley, W.J.; Prentice, I.C.; Keenan, T.F. CO2 fertilization of terrestrial photosynthesis inferred from site to global scales. Proc. Natl. Acad. Sci. USA 2022, 119, e2115627119. [Google Scholar]
- FatFatichi, S.; Pappas, C.; Zscheischler, J.; Leuzinger, S. Modelling carbon sources and sinks in terrestrial vegetation. New Phytol. 2019, 221, 652–668. [Google Scholar] [CrossRef]
- Musavi, T.; Migliavacca, M.; Reichstein, M.; Kattge, J.; Wirth, C.; Black, T.A.; Janssens, I.; Knohl, A.; Loustau, D.; Roupsard, O.; et al. Stand age and species richness dampen interannual variation of ecosystem-level photosynthetic capacity. Nat. Ecol. Evol. 2017, 1, 0048. [Google Scholar] [CrossRef] [PubMed]
- Piao, S.L.; Ciais, P.; Huang, Y.; Shen, Z.H.; Peng, S.S.; Li, J.S.; Zhou, L.P.; Liu, H.Y.; Ma, Y.C.; Ding, Y.H.; et al. The impacts of climate change on water resources and agriculture in China. Nature 2010, 467, 43–51. [Google Scholar] [PubMed]
- Doughty, C.E.; Santos-Andrade, P.E.; Shenkin, A.; Goldsmith, G.R.; Bentley, L.P.; Blonder, B.; Diaz, S.; Salinas, N.; Enquist, B.J.; Martin, R.E.; et al. Tropical forest leaves may darken in response to climate change. Nat. Ecol. Evol. 2018, 2, 1918–1924. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Yu, G.; Yang, J.; Wimberly, M.C.; Zhang, X.; Tao, J.; Jiang, Y.; Zhu, J. Climate-driven global changes in carbon use efficiency. Ecol. Biogeogr. 2013, 23, 144–155. [Google Scholar]
- Dietze, M.C.; Sala, A.; Carbone, M.S.; Czimczik, C.I.; Mantooth, J.A.; Richardson, A.D.; Vargas, R. Nonstructural carbon in woody plants. Annu. Rev. Plant Biol. 2014, 65, 667–687. [Google Scholar]
- Collalti, A.; Prentice, I.C. Is NPP proportional to GPP? Waring’s hypothesis 20 years on. Tree Physiol. 2019, 39, 1473–1483. [Google Scholar]
- Fung, E.; Imbach, P.; Corrales, L.; Vilchez, S.; Zamora, N.; Argotty, F.; Hannah, L.; Ramos, Z. Mapping conservation priorities and connectivity pathways under climate change for tropical ecosystems. Clim. Chang. 2017, 141, 77–92. [Google Scholar]
- Chen, W.Z.; Zhu, D.; Huang, C.J.; Ciais, P.; Yao, Y.T.; Friedlingstein, P.; Sitch, S.; Haverd, V.; Jain, A.K.; Kato, E.; et al. Negative extreme events in gross primary productivity and their drivers in China during the past three decades. Agric. For. Meteorol. 2019, 275, 47–58. [Google Scholar] [CrossRef]
- Zscheischler, J.; Reichstein, M.; Harmeling, S.; Rammig, A.; Tomelleri, E.; Mahecha, M.D. Extreme events in gross primary production: A characterization across continents. Biogeosciences 2014, 11, 2909–2924. [Google Scholar] [CrossRef]
- Wang, M.; Wang, S.; Zhao, J.; Ju, W.; Hao, Z. Global positive gross primary productivity extremes and climate contributions during 1982–2016. Sci. Total Environ. 2021, 774, 145703. [Google Scholar]
- Beer, C.; Reichstein, M.; Tommelleri, E.; Ciais, P.; Jung, M.; Carvalhais, N.; Rodenbeck, C.; Arain, A.; Baldocchi, D.; Bonan, G.; et al. Terrestrial gross carbon dioxide uptake: Global distribution and covariation with climate. Science 2010, 329, 834–838. [Google Scholar] [PubMed]
- Xu, C.; McDowell, N.G.; Fisher, R.A.; Wei, L.; Sevanto, S.; Christoffersen, B.O.; Weng, E.; Middleton, R.S. Increasing impacts of extreme droughts on vegetation productivity under climate change. Nat. Clim. Chang. 2019, 9, 948–953. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, M.; Zhao, J.; Wang, S. Detection of Carbon Use Efficiency Extremes and Analysis of Their Forming Climatic Conditions on a Global Scale Using a Remote Sensing-Based Model. Remote Sens. 2022, 14, 4873. https://doi.org/10.3390/rs14194873
Wang M, Zhao J, Wang S. Detection of Carbon Use Efficiency Extremes and Analysis of Their Forming Climatic Conditions on a Global Scale Using a Remote Sensing-Based Model. Remote Sensing. 2022; 14(19):4873. https://doi.org/10.3390/rs14194873
Chicago/Turabian StyleWang, Miaomiao, Jian Zhao, and Shaoqiang Wang. 2022. "Detection of Carbon Use Efficiency Extremes and Analysis of Their Forming Climatic Conditions on a Global Scale Using a Remote Sensing-Based Model" Remote Sensing 14, no. 19: 4873. https://doi.org/10.3390/rs14194873
APA StyleWang, M., Zhao, J., & Wang, S. (2022). Detection of Carbon Use Efficiency Extremes and Analysis of Their Forming Climatic Conditions on a Global Scale Using a Remote Sensing-Based Model. Remote Sensing, 14(19), 4873. https://doi.org/10.3390/rs14194873






