Time Series Analysis-Based Long-Term Onboard Radiometric Calibration Coefficient Correction and Validation for the HY-1C Satellite Calibration Spectrometer
Abstract
1. Introduction
2. Materials and Methods
2.1. Overview of Onboard Calibration of HY-1C Sensor
2.1.1. Onboard Absolute Calibration of SCS
2.1.2. Cross-Calibration of HY-1C Sensors
2.2. Long-Term Calibration Coefficients of SCS and Data Preprocessing
2.3. Time Series Modeling and Analysis Method
2.3.1. Seasonal and Trend Decomposition Using Loess
2.3.2. Long Short-Term Memory (LSTM) Neural Network
3. Results
3.1. STL-Based SCS Calibration Coefficient Modeling and Analysis
3.1.1. STL Modeling Results
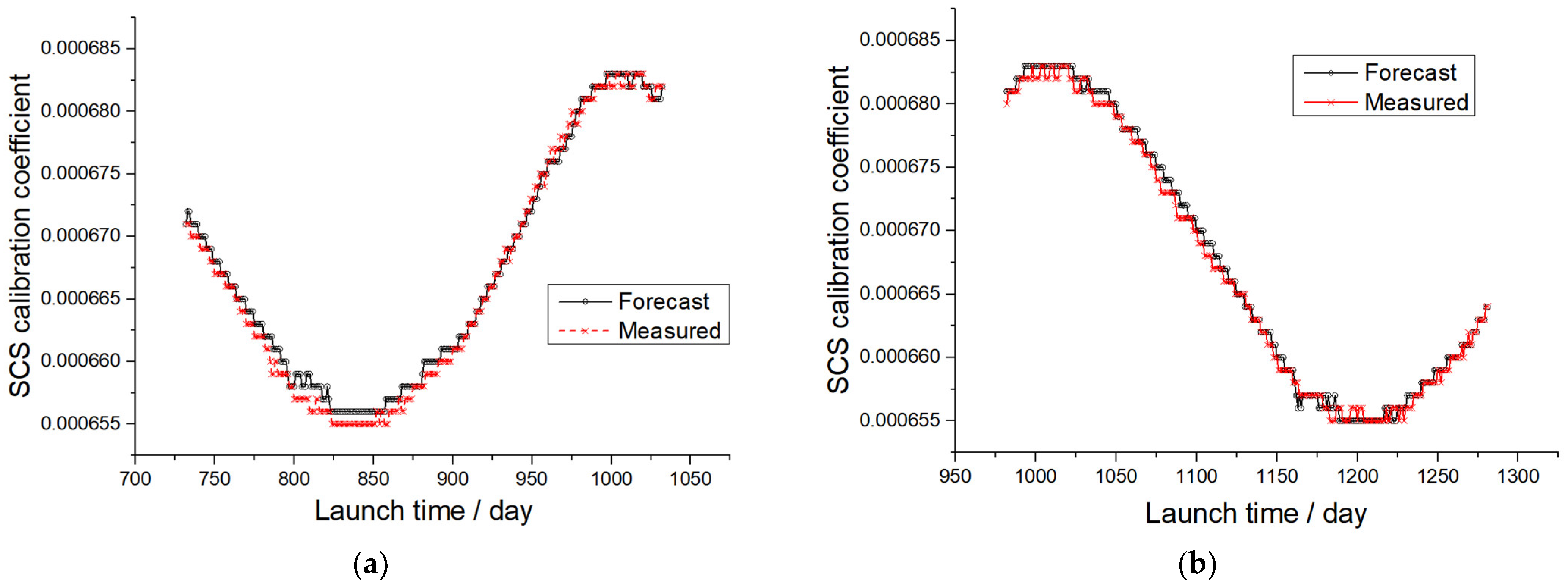
3.1.2. Forecast, Validation and Correction of Calibration Coefficients Using STL Model
- Calibration coefficient forecast
- 2.
- Anomaly calibration coefficient detection
- 3.
- Calibration coefficient correction
3.2. LSTM-Based SCS Calibration Coefficient Modeling and Analysis
4. Discussion
4.1. Discussion of the STL Decomposition Results
4.1.1. Trend Component
4.1.2. Seasonal Component
4.1.3. Remainder Component
4.1.4. Correlation of Different Spectral Band Calibration Coefficients
4.2. Discussion of the LSTM-Based SCS Calibration Coefficient Modeling and Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lewis, K.M.; Arrigo, K.R. Ocean color algorithms for estimating chlorophyll a, CDOM absorption, and particle backscattering in the Arctic Ocean. J. Geophys. Res. Oceans 2020, 125, e2019JC015706. [Google Scholar] [CrossRef]
- Tassan, S.; Sturm, R. An algorithm for the retrieval of sediment content in turbid coastal waters from CZCS data. Int. J. Remote Sens. 1986, 7, 643–655. [Google Scholar] [CrossRef]
- Ahn, Y.H.; Shanmugam, P. Detecting the red tide algal blooms from satellite ocean color observations in optically complex Northeast-Asia Coastal waters. Remote Sens. Environ. 2006, 103, 419–437. [Google Scholar] [CrossRef]
- Miguel, A.; Santos, P. Fisheries oceanography using satellite and arborne remote sensing methods: A review. Fish. Res. 2000, 49, 1–20. [Google Scholar]
- Waite, J.N.; Mueter, F.J. Spatial and temporal variability of chlorophyll-a concentrations in the coastal Gulf of Alaska, 1998–2011, using cloud-free reconstructions of SeaWiFS and MODIS-Aqua data. Prog. Oceanogr. 2013, 116, 179–192. [Google Scholar] [CrossRef]
- Frouin, R. In-Flight Calibration of Satellite Ocean-Colour Sensors. In Reports of the International Ocean-Colour Coordinating Group No. 14; IOCCG: Dartmouth, NS, Canada, 2013. [Google Scholar]
- Eplee, R.E.; Turpie, K.R.; Fireman, G.F.; Meister, G.; Stone, T.C.; Frederick, S.P.; Franz, B.A.; Bailey, S.W.; Robinson, W.D.; McClain, C.R. VIIRS on-orbit calibration for ocean color data processing. In Proceedings of the SPIE 8510, Earth Observing Systems XVII, San Diego, CA, USA, 15 October 2012. [Google Scholar]
- Mélin, F.; Zibordi, G. Vicarious calibration of satellite ocean color sensors at two coastal sites. Appl. Opt. 2010, 49, 798–810. [Google Scholar] [CrossRef]
- Xiong, X.; Wu, A.; Wenny, B.N.; Madhavan, S.; Wang, Z.; Li, Y.; Chen, N.; Barnes, W.L.; Salomonson, V.V. Terra and Aqua MODIS Thermal Emissive Bands in-orbit Calibration and Performance. IEEE Trans. Geosci. Remote Sens. 2015, 53, 5709–5721. [Google Scholar] [CrossRef]
- Cao, C.; de Luccia, F.J.; Xiong, X.; Wolfe, R.; Weng, F. Early in-orbit performance of the Visible Infrared Imaging Radiometer Suite onboard the Suomi National Polar-Orbiting Partnership (S-NPP) satellite. IEEE Trans. Geosci. Remote Sens. 2014, 52, 1142–1156. [Google Scholar] [CrossRef]
- Clark, D.; Feinholz, M.; Yarbrough, M.; Johnson, B.; Brown, S.; Kim, Y.; Barnes, R. Overview of the radiometric calibration of MOBY. In Proceedings of the SPIE 4483, Earth Observing Systems VI, San Diengo, CA, USA, 18 January 2002. [Google Scholar]
- Sun, J.; Wang, M. Radiometric calibration of the Visible Infrared Imaging Radiometer Suite reflective solar bands with robust characterizations and hybrid calibration coefficients. Appl. Opt. 2015, 54, 9331–9342. [Google Scholar] [CrossRef]
- Sun, J.; Xiong, X.; Barnes, W. MODIS solar diffuser stability monitor sun view modeling. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1845–1854. [Google Scholar]
- Xiong, X.; Sun, J.; Barnes, W.; Salomonson, V.; Esposito, J.; Erives, H.; Guenther, B. Multiyear in-orbit Calibration and Performance of Terra MODIS Reflective Solar Bands. IEEE Trans. Geosci. Remote Sens. 2007, 45, 879–889. [Google Scholar] [CrossRef]
- Meister, G.; Pattb, F.S.; Xiong, X.; Sun, J.; Xie, X.; McClain, C.R. Residual correlations in the solar diffuser measurements of the MODIS Aqua ocean color bands to the sun yaw angle. In Proceedings of the SPIE 5882, Earth Observing Systems X, Bellingham, WA, USA, 31 July 2005. [Google Scholar]
- Meister, G.; Sun, J.; Eplee, R.E., Jr.; Pattc, F.S.; Xiong, X.; McClain, C.R. Sun beta angle residuals in solar diffuser measurements of the MODIS ocean bands. In Proceedings of the SPIE 7081, Earth Observing Systems XIII, San Diengo, CA, USA, 10 August 2008. [Google Scholar]
- Xiong, X.; Angal, A.; Choi, T.; Sun, J.; Johnson, E. In-orbit Performance of MODIS Solar Diffuser Stability Monitor. In Proceedings of the SPIE 8510, Earth Observing Systems XVII, San Diengo, CA, USA, 10 August 2008. [Google Scholar]
- Eplee, R.E.; Meister, G.; Patt, F.S.; Barnes, R.A.; Bailey, S.W.; Franz, B.A.; McClain, C.R. In-orbit calibration of SeaWiFS. Appl. Opt. 2012, 51, 8702–8730. [Google Scholar] [CrossRef] [PubMed]
- Eplee, R.E., Jr.; Meister, G.; Patt, F.S.; McClain, C.R. The in-orbit Calibration of SeaWiFS: Functional Fits to the Lunar Time Series. In Proceedings of the SPIE 7081, Earth Observing Systems XIII, San Diengo, CA, USA, 10 August 2008. [Google Scholar]
- Bisoi, R.; Dash, P.K.; Parida, A.K. Hybrid Variational Mode Decomposition and evolutionary robus kernel extreme learning machine for stock price and movement prediction on daily basis. Appl. Soft Comput. 2018, 74, 652–678. [Google Scholar] [CrossRef]
- Eymen, A.; Köylü, U. Seasonal trend analysis and ARIMA modeling of relative humidity and wind speed time series around Yamula Dam. Meteorol. Atmos. Phys. 2019, 131, 601–612. [Google Scholar] [CrossRef]
- Sang, Y. A review on the applications of wavelet transform in hydrology time series analysis. Atmos. Res. 2013, 122, 8–15. [Google Scholar] [CrossRef]
- Li, R.; Jiang, P.; Yang, H.; Li, C. A novel hybrid forecasting scheme for electricity demand time series. Sustain. Cities Soc. 2020, 55, 102036. [Google Scholar] [CrossRef]
- Schmidt, M.; King, E.A.; Mcvicar, T.R. A method for operational calibration of AVHRR reflective time series data. Remote Sens. Environ. 2008, 112, 1117–1129. [Google Scholar] [CrossRef]
- Saadi, S.; Simonneaux, V.; Boulet, G.; Raimbault, B.; Mougenot, B.; Fanise, P.; Ayari, H.; Lili-Chabaane, Z. Monitoring Irrigation Consumption Using High Resolution NDVI Image Time Series: Calibration and Validation in the Kairouan Plain (Tunisia). Remote Sens. 2015, 7, 13005–13028. [Google Scholar] [CrossRef]
- Campbell, P.K.E.; Middleton, E.M.; Thome, K.J.; Kokaly, R.F. Eo-1 hyperion reflectance time series at calibration and validation sites: Stability and sensitivity to seasonal dynamics. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 276–290. [Google Scholar] [CrossRef]
- Xu, H.; Zhang, L.; Huang, W.; Li, X.; Si, X.; Xu, W.; Song, Q. On-board Absolute Radiometric Calibration and Validation Based on Solar Diffuser of HY-1C SCS. Acta Optica. Sin. 2020, 40, 181–190. [Google Scholar]
- Xu, H.; Zhang, L.; Huang, W.; Xu, W.; Si, X.; Chen, H.; Li, X.; Song, Q. Onboard absolute radiometric calibration and validation of the satellite calibration spectrometer on HY-1C. Opt. Express 2020, 28, 30015–30034. [Google Scholar] [CrossRef] [PubMed]
- Song, Q.; Chen, S.; Xue, C.; Lin, M.; Huang, X. Vicarious calibration of COCTS-HY1C at visible and near-infrared bands for ocean color application. Opt. Express 2019, 27, A1615–A1626. [Google Scholar] [CrossRef] [PubMed]
- Sović, A.; Seršić, D. Signal Decomposition Methods for Reducing Drawbacks of the DWT. Eng. Rev. Znan. Časopis Nove Tehnol. Stroj. Brodogr. Elektrotehnici 2012, 32, 70–77. [Google Scholar]
- Jie, W.; Wang, J. Forecasting stochastic neural network based on financial empirical mode decomposition. Neural Netw. 2017, 90, 8–20. [Google Scholar]
- Schuster, M.; Paliwal, K. Bidirectional recurrent neural networks. IEEE Trans. Signal Process. 1997, 45, 2673–2681. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Cleveland, R.; Cleveland, W.; McRae, J.; Terpenning, I. STL: A seasonal-trend decomposition procedure based on Loess. J. Off. Stat. 1990, 6, 3–73. [Google Scholar]
- Cleveland, W. Robust Locally Weighted Regression and Smoothing Scatterplots. Publ. Am. Stat. Assoc. 1979, 74, 829–836. [Google Scholar] [CrossRef]
- Ji, J.; Dong, M.; Lin, Q.; Tan, K.C. Forecasting Wind Speed Time Series via Dendritic Neural Regression. IEEE Comput. Intell. Mag. 2021, 16, 50–66. [Google Scholar] [CrossRef]
- Wu, Z.; Pan, S.; Long, G.; Jiang, J.; Chang, X.; Zhang, C. Connecting the Dots: Multivariate Time Series Forecasting with Graph Neural Networks. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining (KDD ′20), Association for Computing Machinery, New York, NY, USA, 20 August 2020. [Google Scholar]
- Newbold, P. ARIMA model building and the time series analysis approach to forecasting. J. Forecast. 1983, 2, 23–35. [Google Scholar] [CrossRef]
















| Uncertainty Sources | Measurement Uncertainty | |||
|---|---|---|---|---|
| Individual | Combined | |||
| CSD | CSD BRDF * measurement uncertainty | Light source stability | 0.2% | 0.84% |
| Stray light | 0.2% | |||
| Incident light angle | 0.2% | |||
| Light source to diffuser distance | 0.2% | |||
| Light source aperture | 0.2% | |||
| Incident light intensity signal | 0.3% | |||
| Reflectance light intensity signal | 0.5% | |||
| Uniformity (Considering the attenuation screen) | 0.4% | 0.4% | ||
| Mounting angle uncertainty | 0.35% | 0.35% | ||
| Spectral transmittance uncertainty of the attenuation screen | Light source stability | 0.2% | 0.58% | |
| Stray light | 0.2% | |||
| Measurement mechanism repeatability | 0.35% | |||
| Measurement noise | 0.1% | |||
| Aperture dimension accuracy | 0.2% | |||
| Fringe vignetting | 0.3% | |||
| Prelaunch calibration | Performance monitoring slice directional—hemispherical reflectance ratio measurement uncertainty | 0.5% | 0.5% | |
| RSD | Incident light angle inconsistency | 0.2% | 0.54% | |
| Reflectance ratio measurement stability | 0.5% | |||
| Solar spectral irradiance uncertainty | 1% | 1% | ||
| Spectral response function measurement uncertainty | 0.5% | 0.5% | ||
| Stray light and uncertain factors | 1% | 1% | ||
| Combined standard uncertainty | 2.0% | |||
| 16th | 32nd | 48th | 64th | 80th | s2s | |
|---|---|---|---|---|---|---|
| 16th | - | 0.999 | 0.990 | 0.997 | 0.993 | 0.973 |
| 32nd | 0.999 | - | 0.993 | 0.999 | 0.996 | 0.974 |
| 48th | 0.990 | 0.993 | - | 0.995 | 0.998 | 0.974 |
| 64th | 0.997 | 0.999 | 0.995 | - | 0.997 | 0.972 |
| 80th | 0.993 | 0.996 | 0.998 | 0.997 | - | 0.971 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, Q.; Ma, C.; Liu, J.; Wang, X.; Huang, Y.; Lin, G.; Li, Z. Time Series Analysis-Based Long-Term Onboard Radiometric Calibration Coefficient Correction and Validation for the HY-1C Satellite Calibration Spectrometer. Remote Sens. 2022, 14, 4811. https://doi.org/10.3390/rs14194811
Song Q, Ma C, Liu J, Wang X, Huang Y, Lin G, Li Z. Time Series Analysis-Based Long-Term Onboard Radiometric Calibration Coefficient Correction and Validation for the HY-1C Satellite Calibration Spectrometer. Remote Sensing. 2022; 14(19):4811. https://doi.org/10.3390/rs14194811
Chicago/Turabian StyleSong, Qingjun, Chaofei Ma, Jianqiang Liu, Xiaoxu Wang, Yu Huang, Guanyu Lin, and Zhanfeng Li. 2022. "Time Series Analysis-Based Long-Term Onboard Radiometric Calibration Coefficient Correction and Validation for the HY-1C Satellite Calibration Spectrometer" Remote Sensing 14, no. 19: 4811. https://doi.org/10.3390/rs14194811
APA StyleSong, Q., Ma, C., Liu, J., Wang, X., Huang, Y., Lin, G., & Li, Z. (2022). Time Series Analysis-Based Long-Term Onboard Radiometric Calibration Coefficient Correction and Validation for the HY-1C Satellite Calibration Spectrometer. Remote Sensing, 14(19), 4811. https://doi.org/10.3390/rs14194811






