The Approximate Analytical Solution for the Top-of-Atmosphere Spectral Reflectance of Atmosphere—Underlying Snow System over Antarctica
Abstract
1. Introduction
2. The Top-of-Atmosphere Reflectance Model
2.1. The Reflection of Light from Atmosphere—Underlying Surface System
2.2. The Atmospheric Path Reflectance
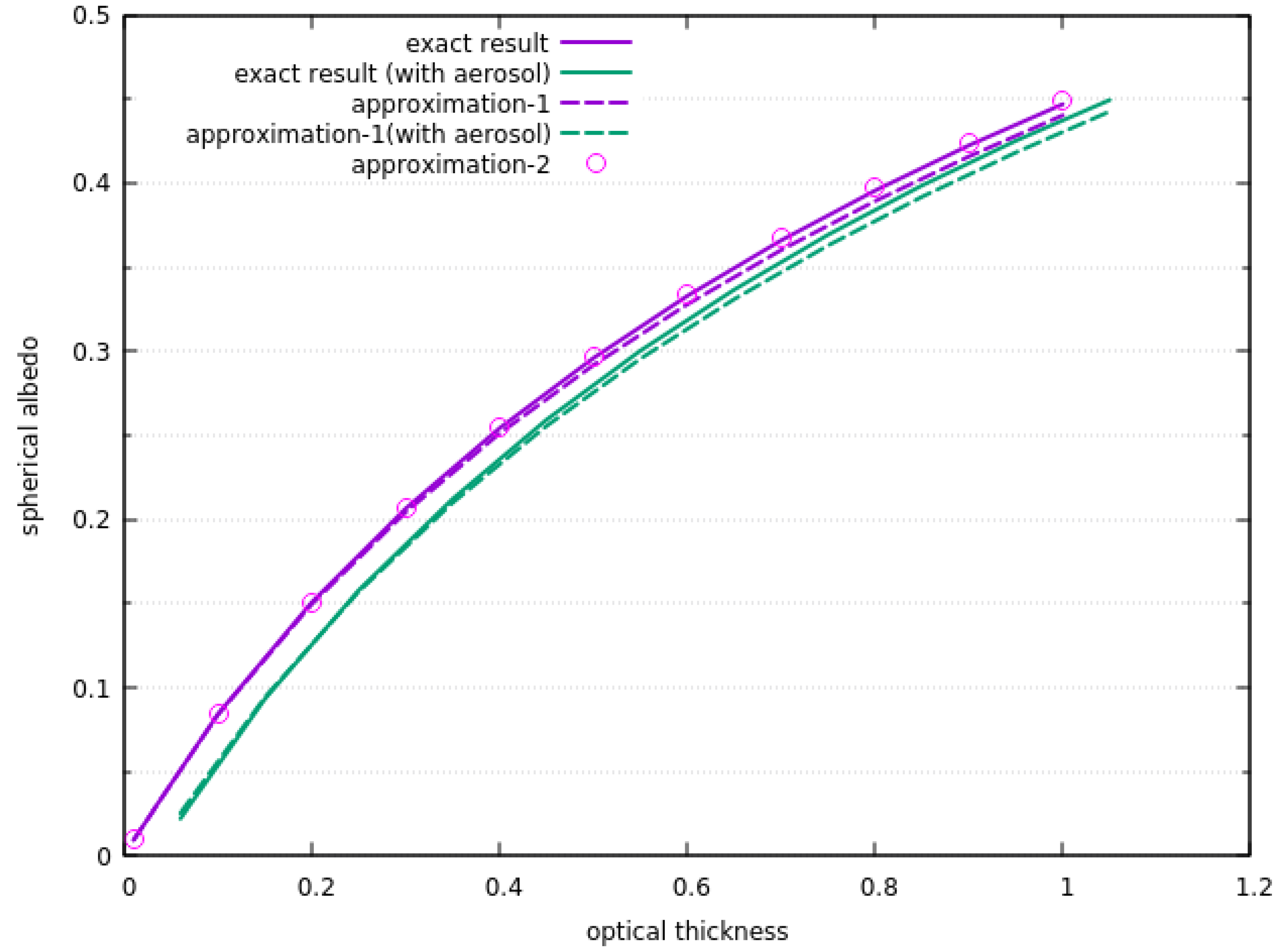
2.3. The Atmospheric Spherical Albedo
2.4. The Atmospheric Transmittance Outside Gaseous Absorption Bands
2.5. The Atmospheric Gaseous Transmittance
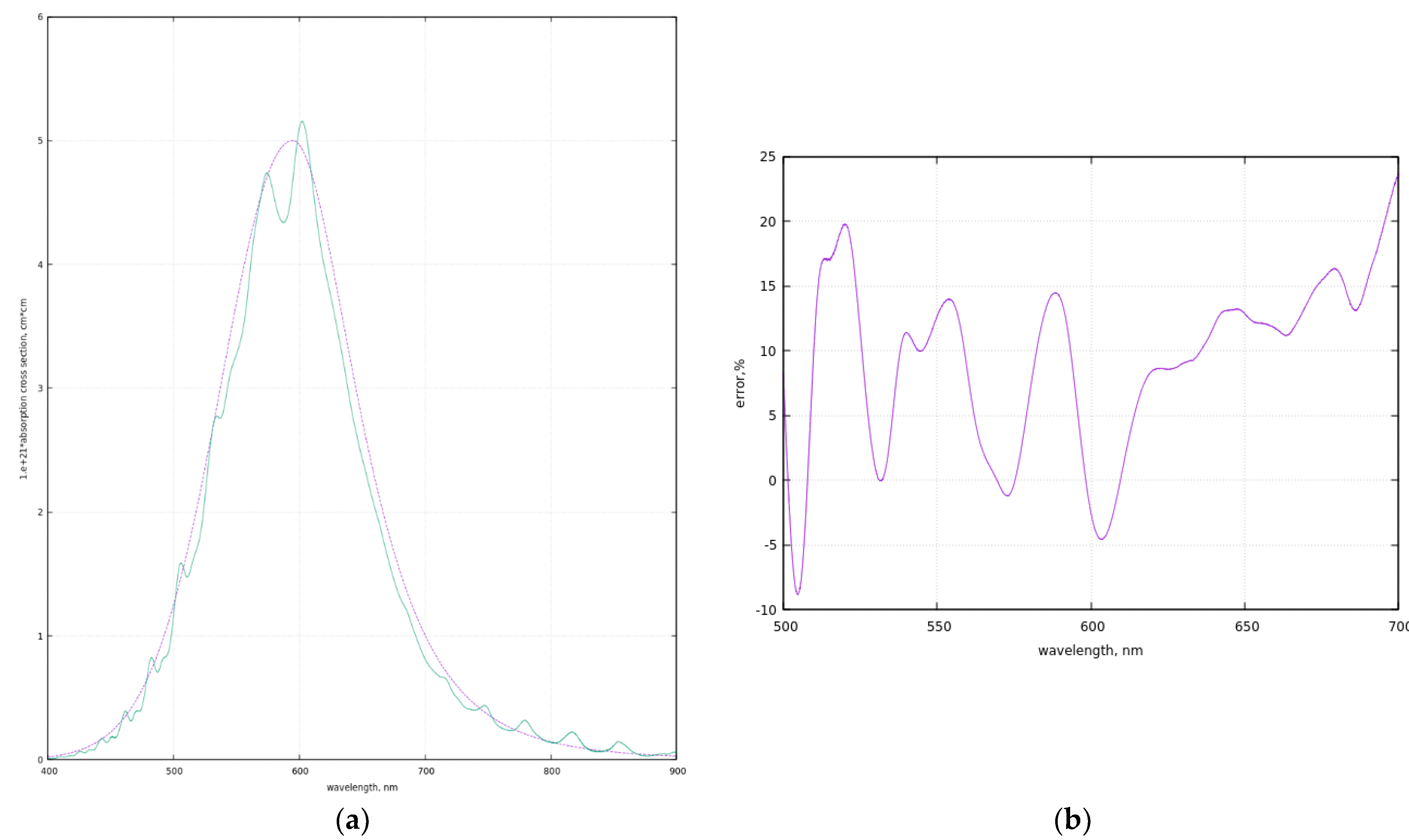
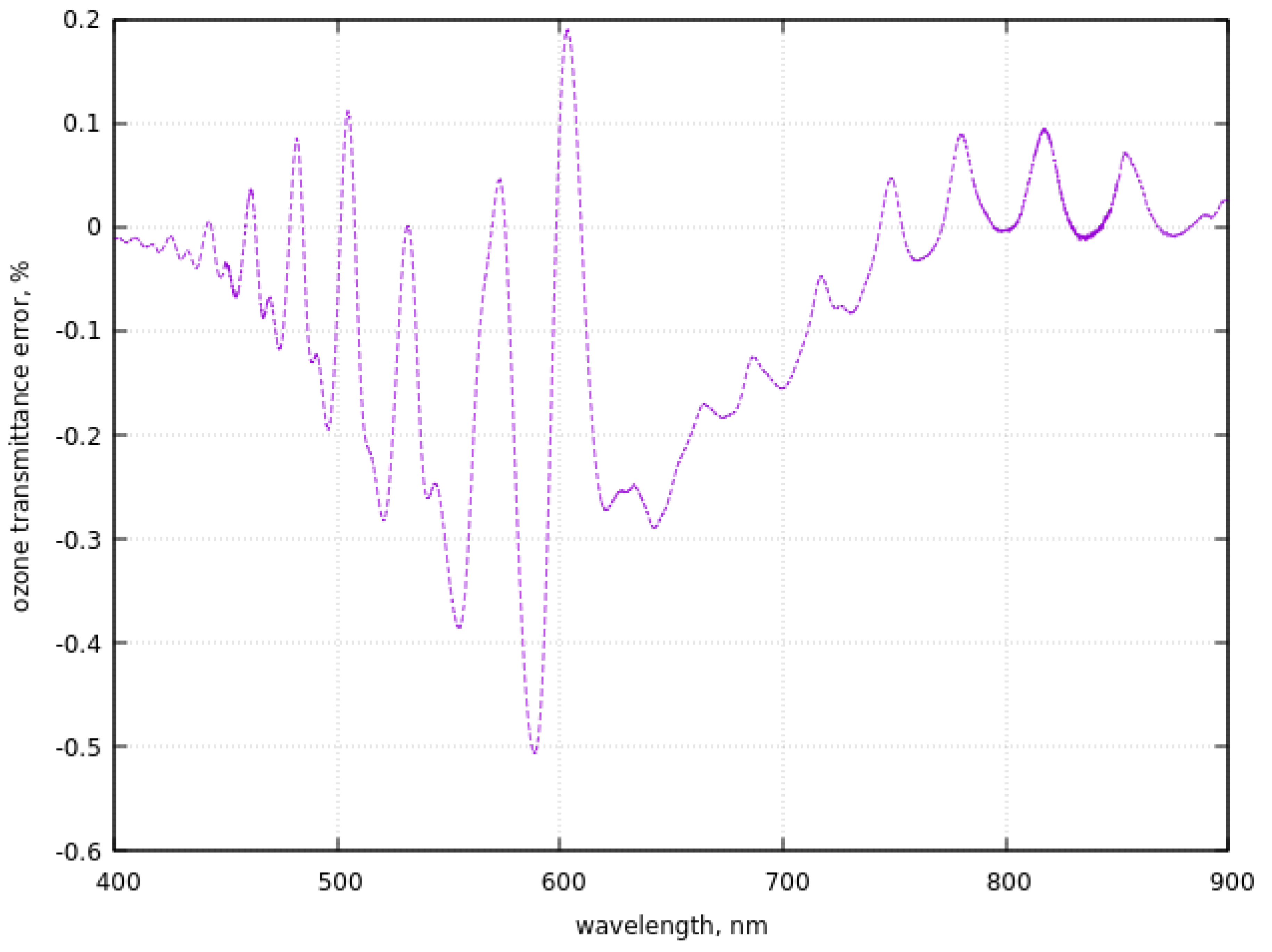
2.5.1. Ozone
2.5.2. Water Vapor
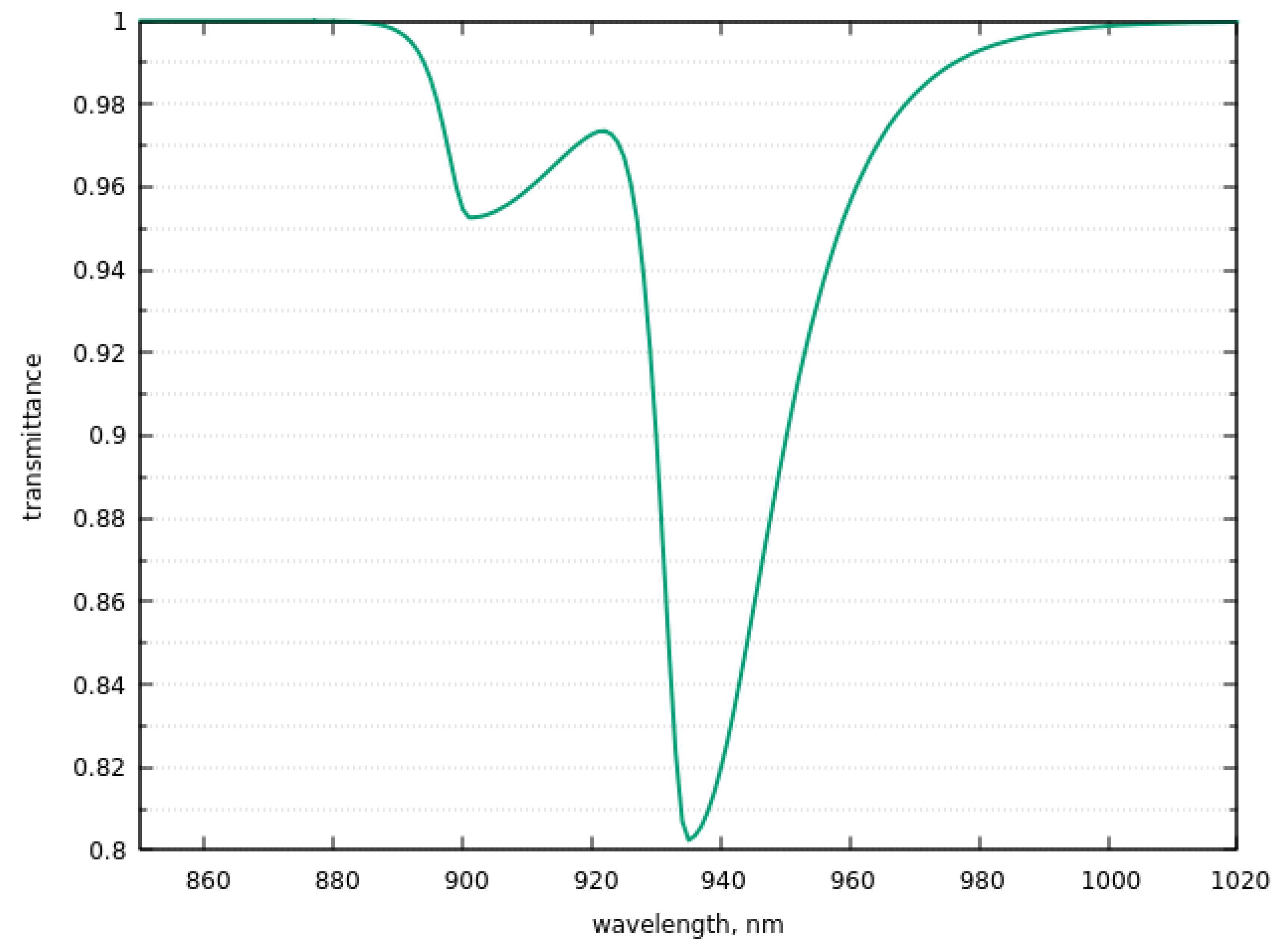
2.5.3. Oxygen
2.6. Reflectance of Solar Light from a Snow Surface
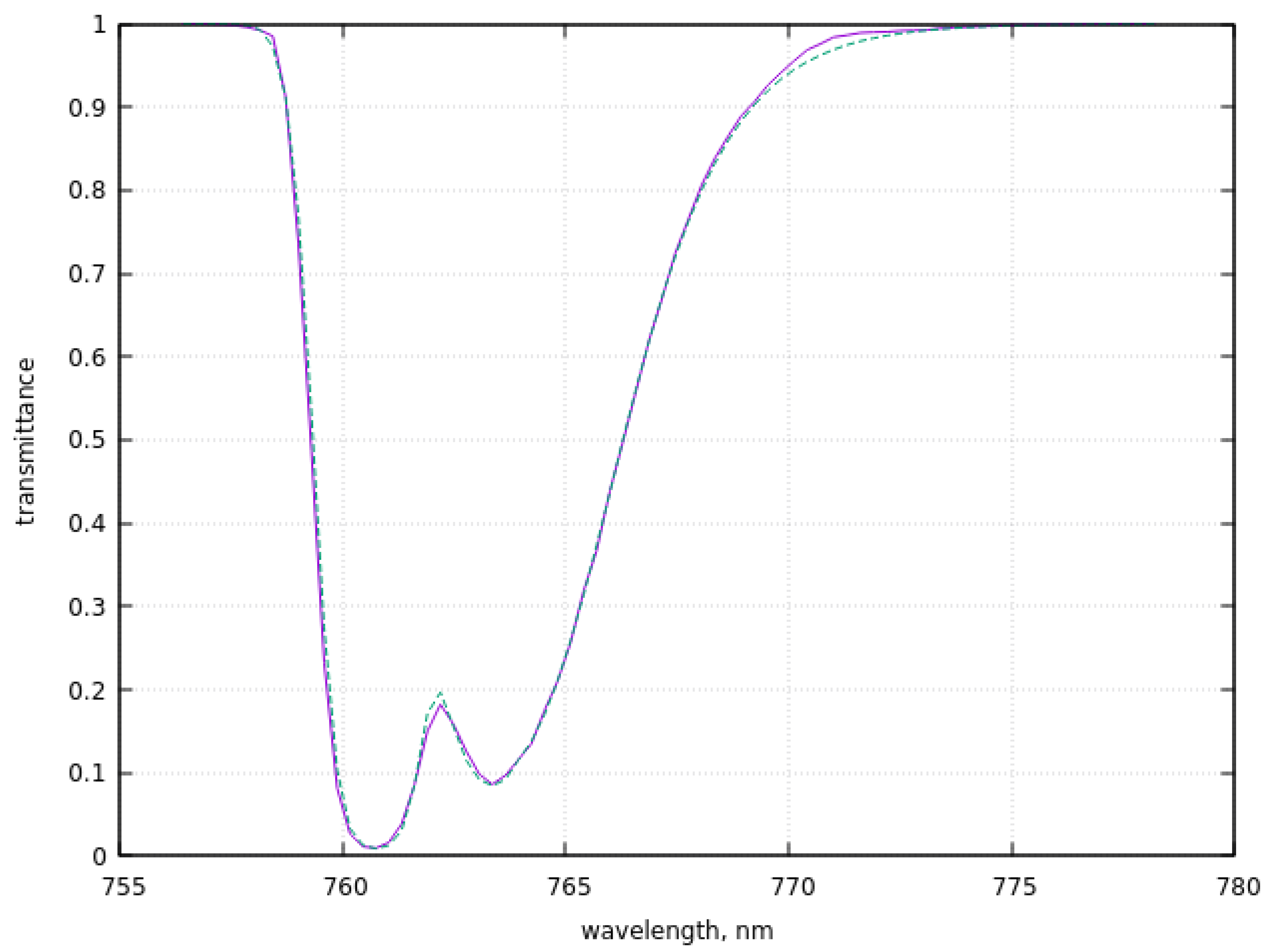
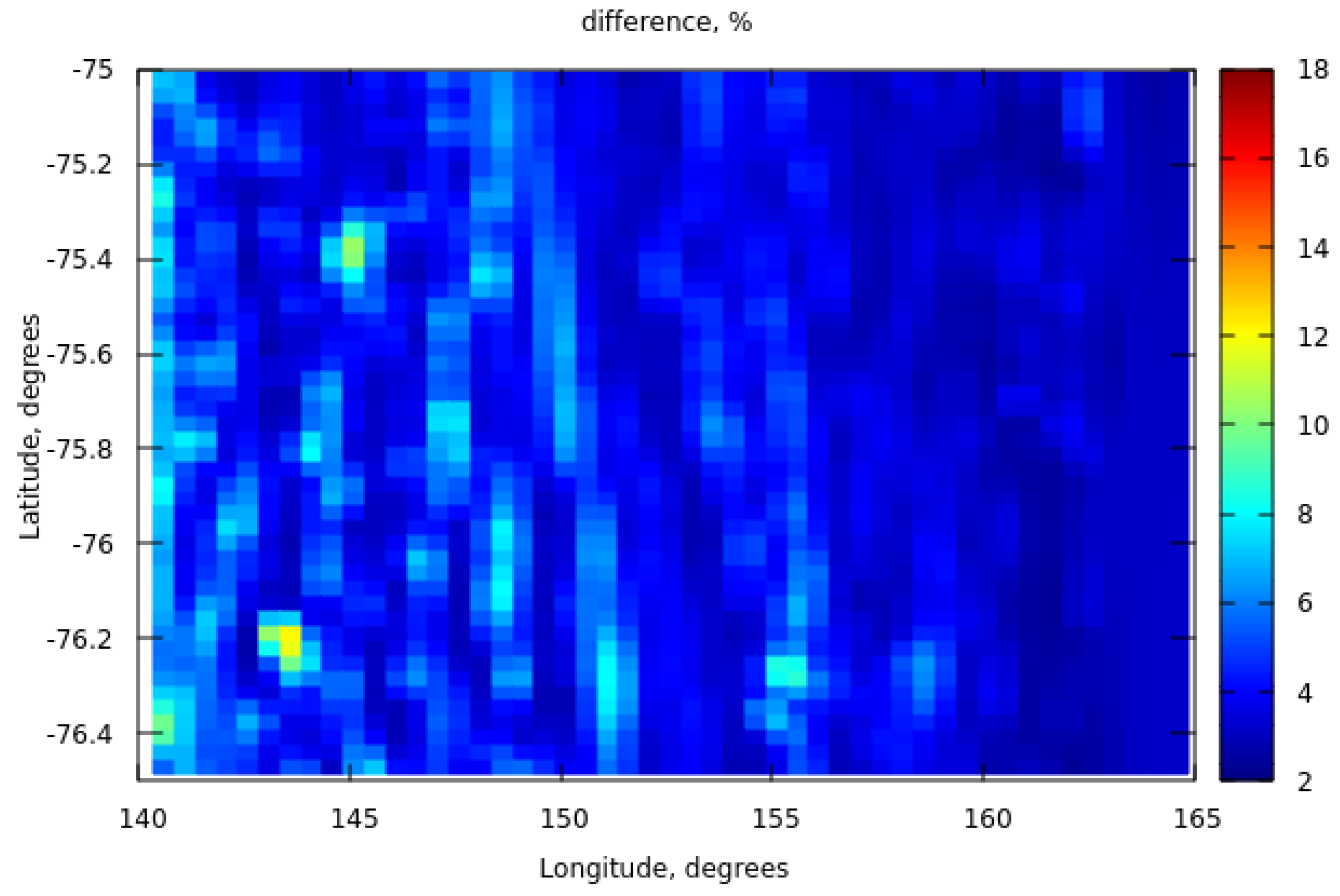
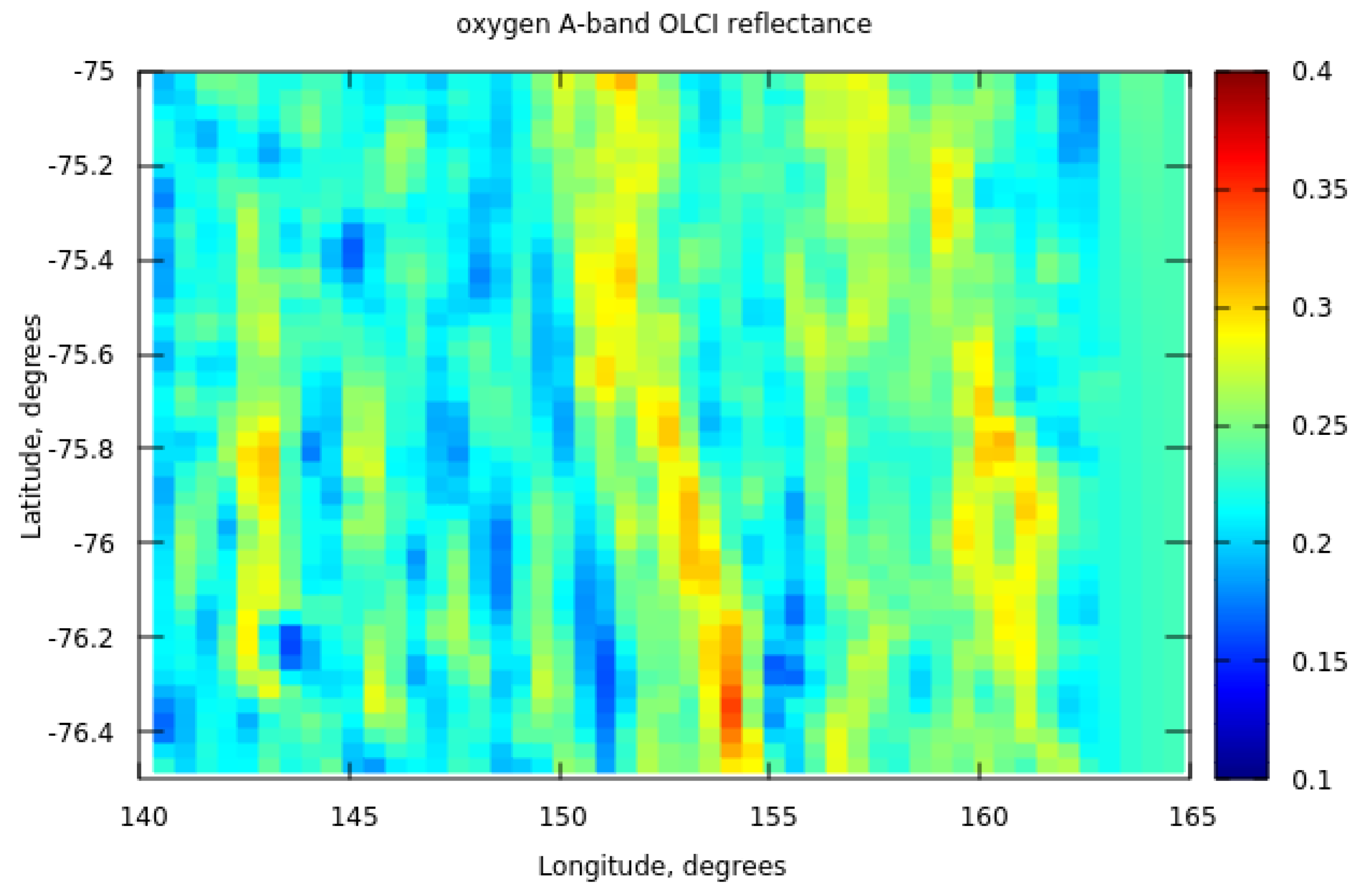
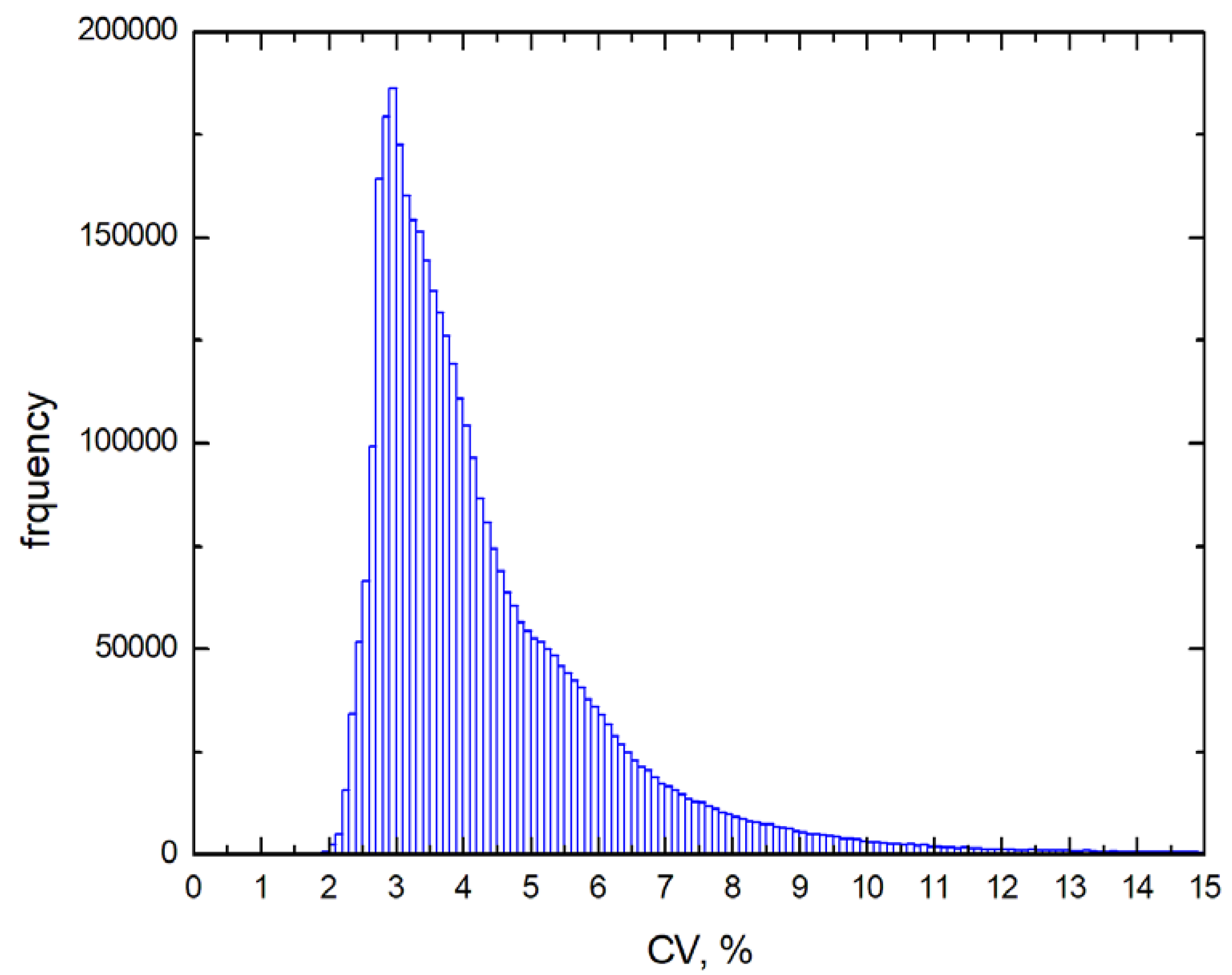
3. The Intercomparison of Derived Parameterisation with Spaceborne Measurements of Spectral Top-of-Atmosphere Reflectance
4. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Liou, K.-N. An Introduction to Atmopsheric Radiation; Academic Press: New York, NY, USA, 2002. [Google Scholar]
- Cachorro, V.E.; Antuña-Sanchez, J.C.; de Frutos, A.M. SSolar-GOA v1.0: A simple, fast, and accurate Spectral solar radiative transfer for clear skies. Geosci. Model Dev. 2022, 15, 1689–1712. [Google Scholar] [CrossRef]
- Mei, L.; Rozanov, V.; Burrows, J.P. A fast and accurate radiative transfer model for aerosol remote sensing. J. Quant. Spectrosc. Radiat. Transf. 2020, 256, 107270. [Google Scholar] [CrossRef]
- Mei, L.; Rozanov, V.; Jiao, Z.; Burrows, J.P. A new snow bidirectional reflectance distribution function model in spectral regions from UV to SWIR: Model development and application to ground-based, aircraft and satellite observations. ISPRS J. Photogramm. Remote Sens. 2022, 188, 269–285. [Google Scholar] [CrossRef]
- Kokhanovsky, A.A. Snow Optics; Springer Nature: Cham, Switzerland, 2021. [Google Scholar]
- Kokhanovsky, A.A. Reflection of light from particulate media with irregularly shaped particles. J. Quant. Spectrosc. Radiat. Transf. 2005, 96, 1–10. [Google Scholar] [CrossRef]
- Kokhanovsky, A.; Box, J.E.; Vandecrux, B.; Mankoff, K.D.; Lamare, M.; Smirnov, A.; Kern, M. The determination of snow albedo from satellite measurements using fast atmospheric correction technique. Remote Sens. 2020, 12, 234. [Google Scholar] [CrossRef]
- Malinka, A.V.; Zege, E.P.; Katsev, I.L.; Istomina, L. Accounting for atmospheric effects in the interpretation of satellite and ground-based optical measurements. J. Appl. Spectrosc. 2016, 83, 741–749. [Google Scholar] [CrossRef]
- Sobolev, V.V. Light Scattering in Planetary Atmospheres; Pergamon Press: Oxford, UK, 1975. [Google Scholar]
- Katsev, I.L.; Prikhach, A.S.; Zege, E.P.; Grudo, J.O.; Kokhanovsky, A.A. Speeding up the aerosol optical thickness retrieval using analytical solutions of radiative transfer theory. Atmos. Meas. Technol. 2010, 3, 1403–1422. [Google Scholar] [CrossRef]
- Katkovsky, L.V.; Martinov, A.O.; Siliuk, V.A.; Ivanov, D.A.; Kokhanovsky, A.A. Fast atmospheric correction method for hyperspectral data. Remote Sens. 2018, 10, 1698. [Google Scholar] [CrossRef]
- Avaste, O.A.; Atroshenko, V.S. The accuracy of the Sobolev approximation. Izv. Geophys. 1960, 3, 45–49. [Google Scholar]
- Busbridge, I.W.; Orchard, S.E. Reflection and transmission of light by a thick atmosphere according to a phase function 1+xcosυ. Astrophys. J. 1967, 149, 655–664. [Google Scholar] [CrossRef]
- Tomasi, C.; Petkov, B.H. Spectral calculations of Rayleigh-scattering optical depth at Arctic and Antarctic sites using a two-term algorithm. J. Geophys. Res. 2015, 120, 9514–9538. [Google Scholar] [CrossRef]
- Six, D.; Fily, M.; Blarel, L.; Goloub, P. First aerosol optical thickness measurements at Dome C (east Antarctica), summer season 2003–2004. Atmos. Env. 2005, 39, 5041–5050. [Google Scholar] [CrossRef]
- Ångström, A. On the atmospheric transmission of Sun radiation and on dust in the air. Geogr. Ann. 1929, 11, 156–166. [Google Scholar]
- Iqbal, M. An Introduction to Solar Radiation; Elsiever: Amsterdam, The Netherlands, 1983. [Google Scholar]
- Hansen, J.E.; Travis, L.D. Light scattering in planetary atmospheres. Space Sci. Rev. 1974, 16, 527–610. [Google Scholar] [CrossRef]
- Tomasi, C.; Petkov, B.; Stone, R.S.; Benedetti, E.; Vitale, V.; Lupi, A.; Mazzola, M.; Lanconelli, C.; Herber, A.; von Hoyningen-Huene, W. Characterizing polar atmospheres and their effect on Rayleigh-scattering optical depth. J. Geophys. Res. 2010, 115, D02205. [Google Scholar] [CrossRef]
- van de Hulst, H.C. Multiple Light Scattering; Academic Press: New York, NY, USA, 1980; Volume 1. [Google Scholar]
- Coakley, J.; Chylek, P. The two-stream approximation in radiative transfer: Including the angle of the incident radiation. J. Atmos. Sci. 1975, 32, 409–418. [Google Scholar] [CrossRef]
- Wiscombe, W.J.; Grams, G.W. The backscattered fraction in two-stream approximations. J. Atmos. Sci. 1976, 33, 2440–2451. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I. (Eds.) Handbook of Mathematical Functions and Formulas, Graphs, and Mathematical Tables. In National Bureau of Standards Applied Mathematics Series; U.S. Government Printing Office: Washington, DC, USA, 1964. [Google Scholar]
- Kokhanovsky, A.A.; Mayer, B.; Rozanov, V.V. A parameterization of the diffuse transmittance and reflectance for aerosol remote sensing problems. Atmos. Res. 2005, 73, 37–43. [Google Scholar] [CrossRef]
- Kokhanovsky, A.A.; Budak, V.P.; Cornet, C.; Duan, M.; Emde, C.; Katsev, I.L.; Klyukov, D.A.; Korkin, S.V.; C-Labonnote, L.; Mayer, B.; et al. Benchmark results in vector atmospheric radiative transfer. J. Quant. Spectrosc. Radiat. Transf. 2010, 111, 1931–1946. [Google Scholar] [CrossRef]
- Korkin, S.; Lyapustin, A.; Sinyuk, A.; Holben, B.; Kokhanovsky, A. Vector radiative transfer code SORD: Performance analysis and quick start guide. J. Quant. Spectrosc. Radiat. Transf. 2017, 200, 295–310. [Google Scholar] [CrossRef]
- Kokhanovsky, A.; Iodice, F.; Lelli, L.; Zschaege, A.; De Quattro, N.; Gasbarra, D.; Retscher, C. Retrieval of total ozone column using high spatial resolution top-of-atmosphere measurements by OLCI/S-3 in the ozone Chappuis absorption band over bright underlying surfaces. J. Quant. Spectrosc. Radiat. Transf. 2021, 276, 107903. [Google Scholar] [CrossRef]
- Green, A.E.; Wagner, J.C.; Mann, A. Analytic spectral functions for atmospheric transmittance calculations. Appl. Opt. 1988, 27, 2266–2272. [Google Scholar] [CrossRef]
- Gorshelev, V.; Serdyuchenko, A.; Weber, M.; Chehade, W.; Burrows, J.P. High spectral resolution ozone absorption cross-sections—Part 1: Measurements, data analysis and comparison with previous measurements around 293 K. Atmos. Meas. Technol. 2014, 7, 609–624. [Google Scholar] [CrossRef]
- Pierluissi, J.H.; Tsai, C.-M. Molecular transmission band model for oxygen in the visible. Appl. Opt. 1986, 25, 2458–2460. [Google Scholar] [CrossRef]
- Zege, E.P.; Ivanov, A.P.; Katsev, I.L. Image Transfer through Light Scattering Media; Springer: Berlin, Germany, 1991. [Google Scholar]
- Kokhanovsky, A.A.; Zege, E.P. Scattering optics of snow. Appl. Opt. 2004, 43, 1589–1602. [Google Scholar] [CrossRef]
- Kokhanovsky, A.; Lamare, M.; Di Mauro, B.; Picard, G.; Arnaud, L.; Dumont, M.; Tuzet, F.; Brockmann, C.; Box, J.E. On the reflectance spectroscopy of snow. Cryosphere 2018, 12, 2371–2382. [Google Scholar] [CrossRef]
- Kokhanovsky, A.; Lamare, M.; Danne, O.; Brockmann, C.; Dumont, M.; Picard, G.; Arnaud, L.; Favier, V.; Jourdain, B.; Meur, E.L.; et al. Retrieval of snow properties from the Sentinel-3 Ocean and Land Colour Instrument. Remote Sens. 2019, 11, 2280. [Google Scholar] [CrossRef]
- Kokhanovsky, A.; Di Mauro, B.; Garzonio, R.; Colombo, R. Retrieval of dust properties from spectral snow reflectance measurements. Front. Environ. Sci. Inform. Remote Sens. 2021, 9, 644551. [Google Scholar] [CrossRef]
- Picard, G.; Libois, Q.; Arnaud, L. Refinement of the ice absorption spectrum in the visible using radiance profile measurements in Antarctic snow. Cryosphere 2016, 10, 2655–2672. [Google Scholar] [CrossRef]
- Warren, S.; Brand, R.E. Optical constants of ice from the ultraviolet to the microwave: A revised compilation. J. Geophysical Research 2008, 113, D14. [Google Scholar] [CrossRef]
- Preusker, R.; Carbajal Henken, C.; Fischer, J. Retrieval of daytime total column water vapor from OLCI measurements over land surfaces. Remote Sens. 2021, 13, 932. [Google Scholar] [CrossRef]
- Mazeran, C.; Rueskas, A. Ocean Colour System Vicarious Calibration Tool Documentation; EUMETSAT: Darmstadt, Germany, 2020. [Google Scholar]
- Ricaud, P.; Gabard, B.; Derrien, S.; Chaboureau, J.-P.; Rose, T.; Mombauer, A.; Czekala, H. HAMSTRAD-Tropo, A 183-GHz Radiometer Dedicated to Sound Tropospheric Water vapor Over Concordia Station, Antarctica. IEEE Trans. Geosci. Remote Sens. 2010, 48, 1365–1380. [Google Scholar] [CrossRef]
- Kokhanovsky, A.A.; Di Mauro, B.; Colombo, R. Snow surface properties derived from PRISMA satellite data over the Nansen Ice Sheet (East Antarctica). Front. Environ. Sci 2022, 10, 904585. [Google Scholar] [CrossRef]
- Gay, M.; Fily, M.; Genthon, C.; Frezzotti, M.; Oerter, H.; Winther, J.-G. Snow grain-size measurements in Antarctica. J. Glaciol. 2002, 48, 527–535. [Google Scholar] [CrossRef][Green Version]
- Kokhanovsky, A.A. Cloud Optics; Springer: Berlin, Germany, 2006. [Google Scholar]
- van de Hulst, H.C. Light Scattering by Small Particles; Dover: New York, NY, USA, 1981. [Google Scholar]


| λ, nm | Comment | |||
|---|---|---|---|---|
| 910 (j = 1) | 0.744 | 11,099 | 23.4
73.8 | Weak absorption band |
| 940 (j = 2) | 7.560 | 10,697 | 23.1
110.2 | Strong absorption band |
| N | Parameter | Value | Comment |
|---|---|---|---|
| 1 | α | 0.008 | atmospheric aerosol |
| 2 | β | 1.3 | atmospheric aerosol |
| 3 | , cm-atm | oxygen | |
| 4 | , DU | 250 | ozone |
| 5 | , mm | 0.33 | water vapor |
| 6 | , hPa | 650 | surface pressure |
| 7 | , hPa | 325 | average pressure |
| 8 | , K | 233 | average temperature |
| 9 | L, mm | 2.24 | snow effective absorption length |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kokhanovsky, A. The Approximate Analytical Solution for the Top-of-Atmosphere Spectral Reflectance of Atmosphere—Underlying Snow System over Antarctica. Remote Sens. 2022, 14, 4778. https://doi.org/10.3390/rs14194778
Kokhanovsky A. The Approximate Analytical Solution for the Top-of-Atmosphere Spectral Reflectance of Atmosphere—Underlying Snow System over Antarctica. Remote Sensing. 2022; 14(19):4778. https://doi.org/10.3390/rs14194778
Chicago/Turabian StyleKokhanovsky, Alexander. 2022. "The Approximate Analytical Solution for the Top-of-Atmosphere Spectral Reflectance of Atmosphere—Underlying Snow System over Antarctica" Remote Sensing 14, no. 19: 4778. https://doi.org/10.3390/rs14194778
APA StyleKokhanovsky, A. (2022). The Approximate Analytical Solution for the Top-of-Atmosphere Spectral Reflectance of Atmosphere—Underlying Snow System over Antarctica. Remote Sensing, 14(19), 4778. https://doi.org/10.3390/rs14194778






