Anti-Jamming Method and Implementation for GNSS Receiver Based on Array Antenna Rotation
Abstract
:1. Introduction
2. Array Signal Reception and Anti-Jamming Model
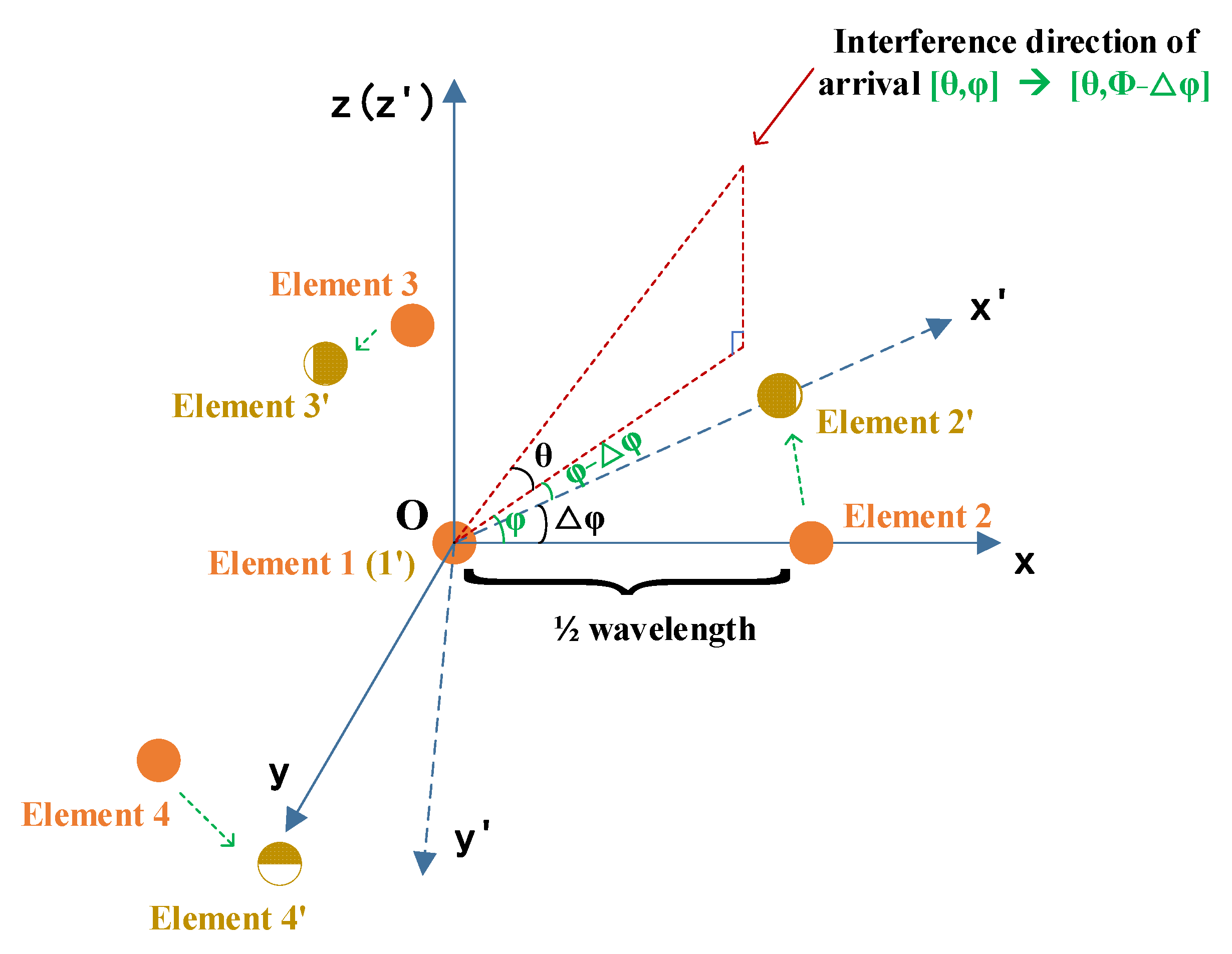
3. The Proposed Antenna Rotation Method
4. The Variable-Step Iteration Algorithm for Efficient Determination of Optimal Rotation Angle
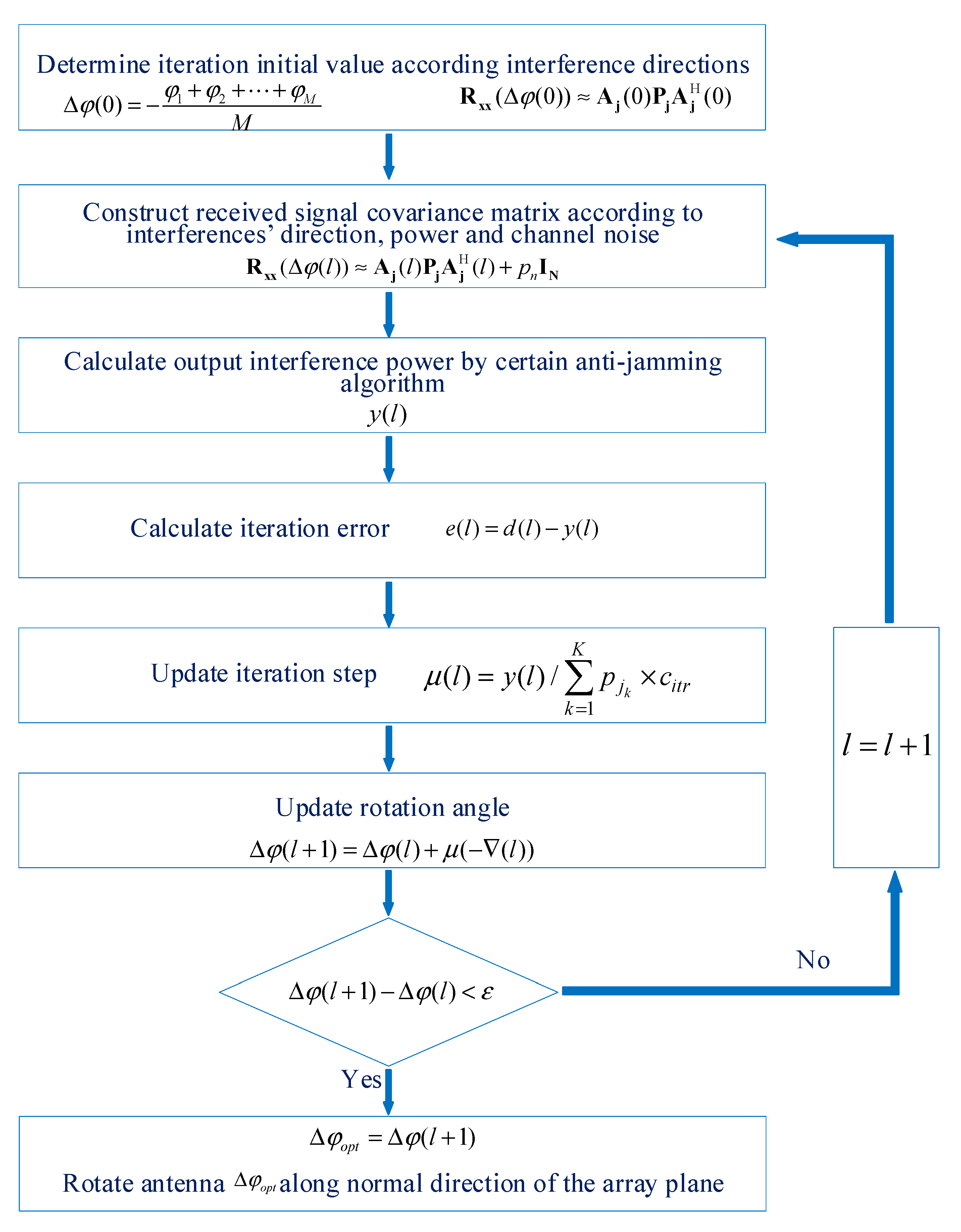
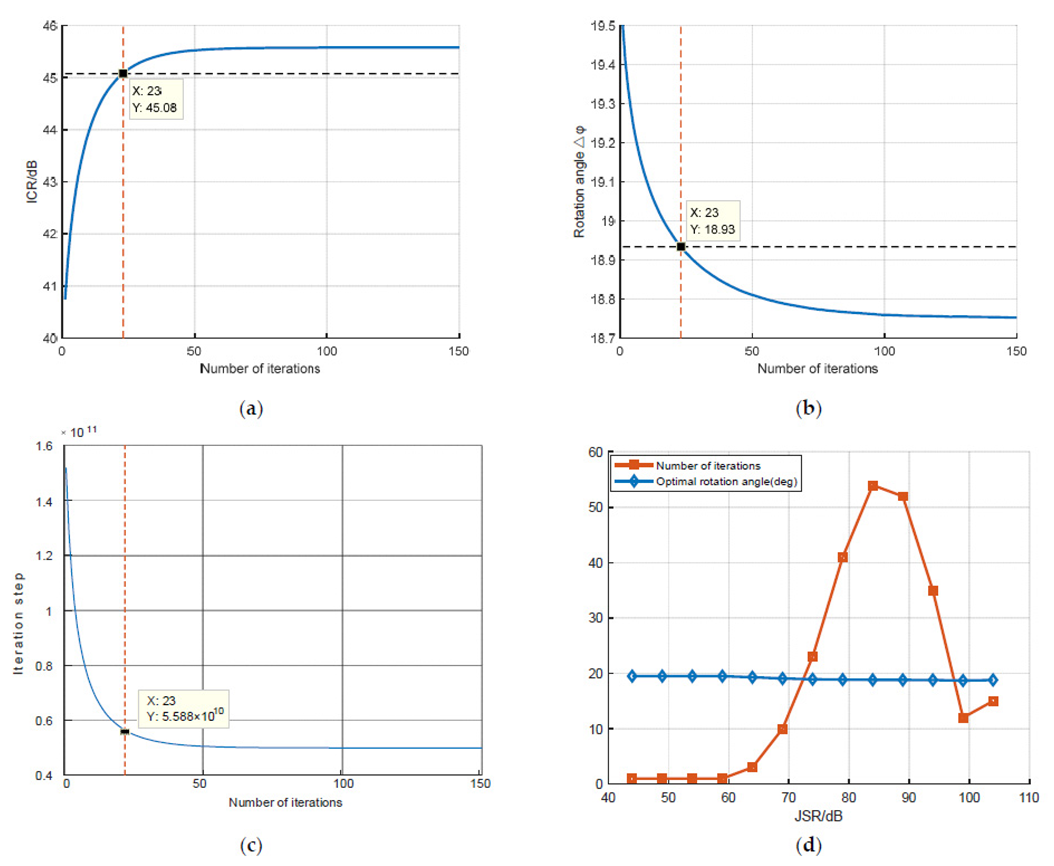
4.1. Iteration Process to Determine Optimal Rotation Angle
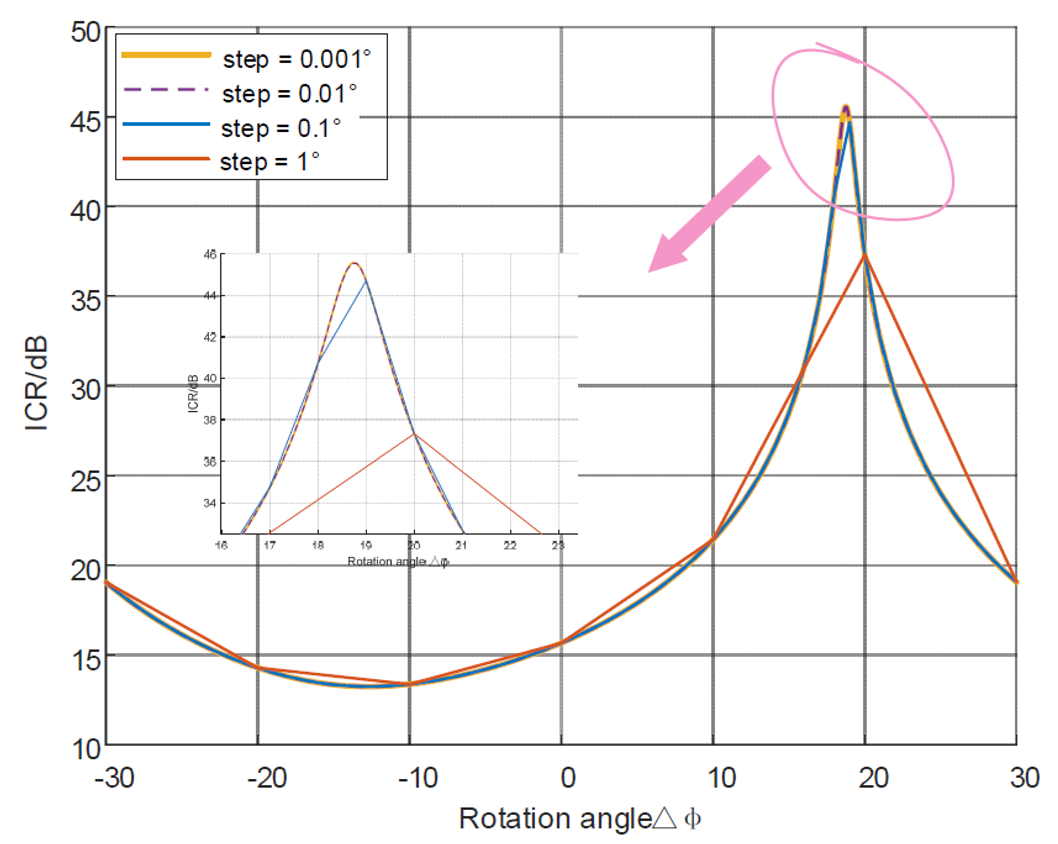
4.2. The Selection of Iteration Step
4.3. The Selection of Initial Iteration Value
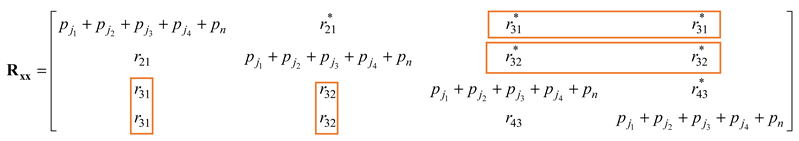
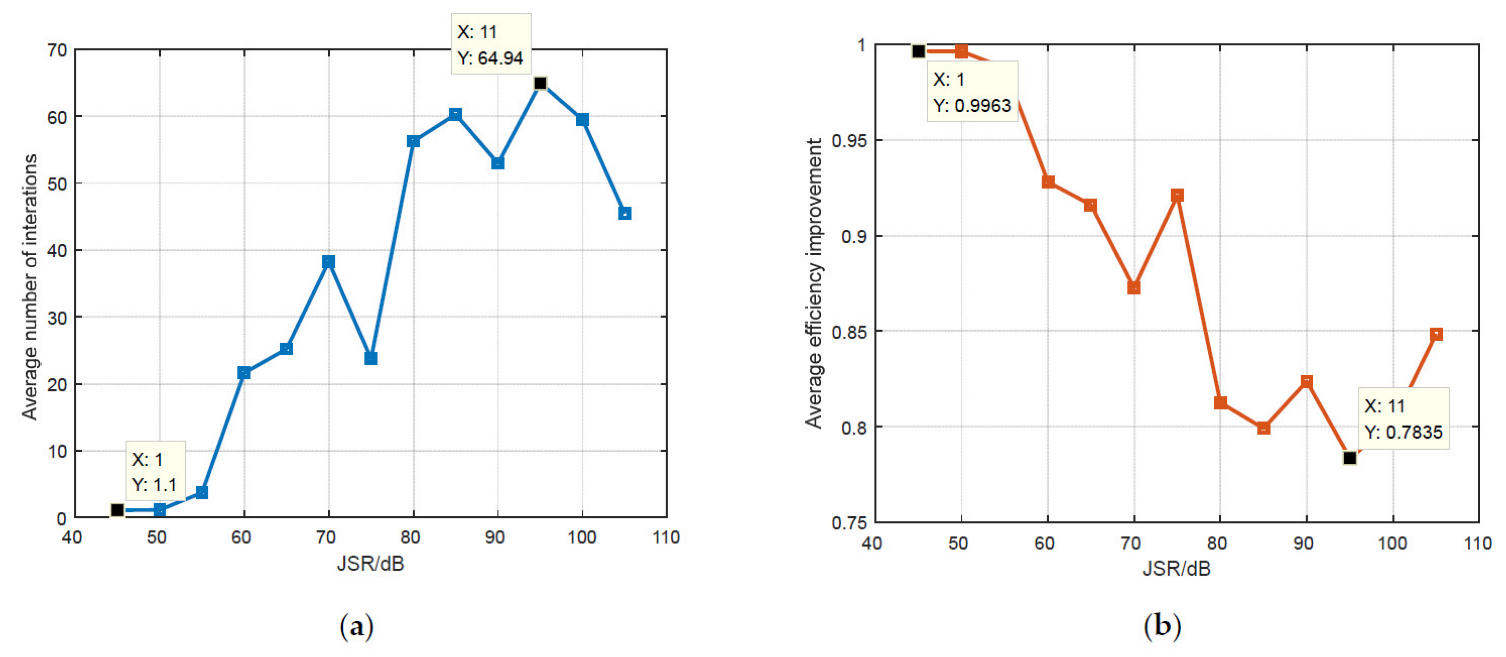
4.4. Evaluation of Iteration Efficiency
5. Simulation Results and Analysis
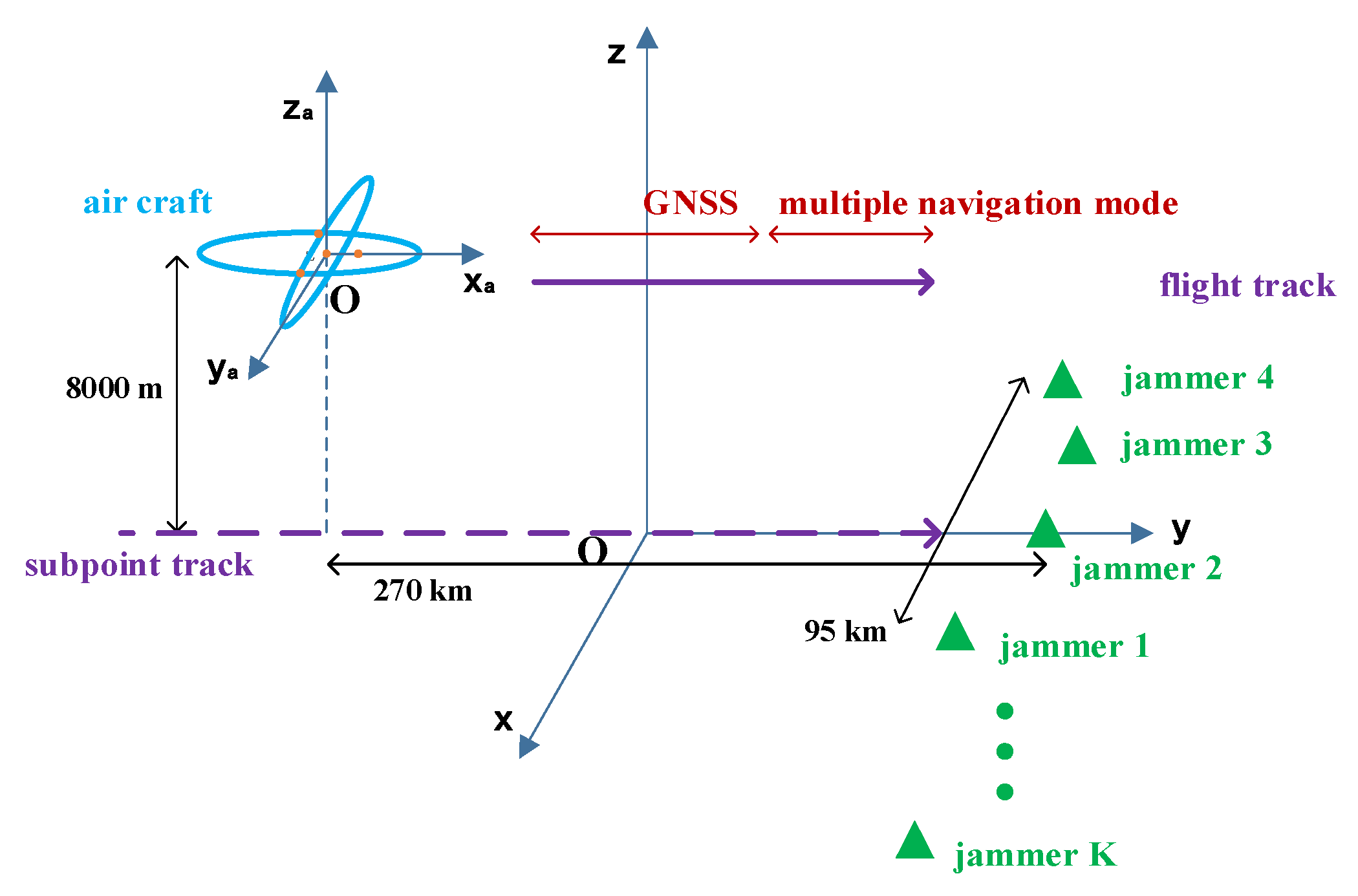
5.1. Simulation Scenario and Parameter Settings
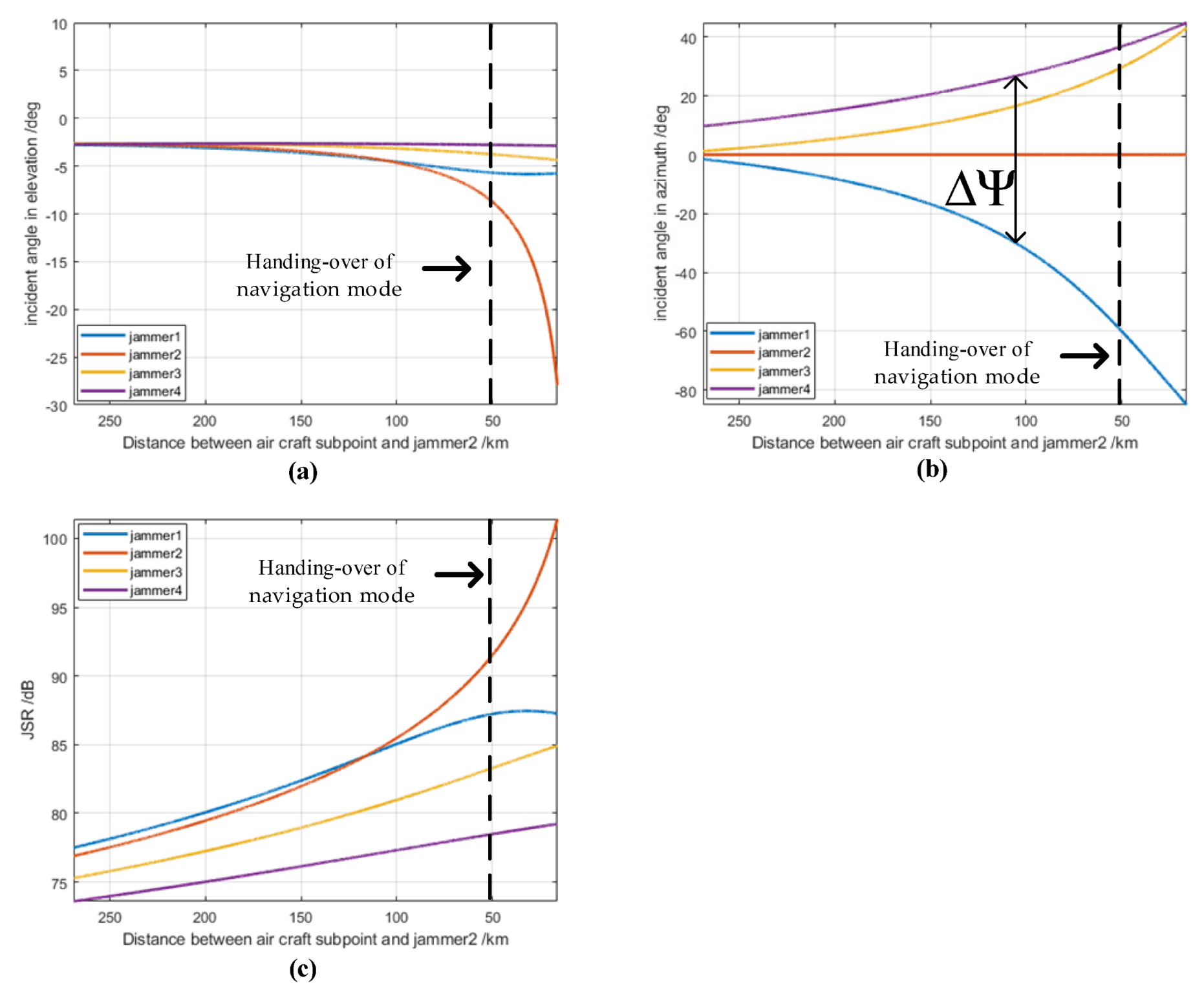
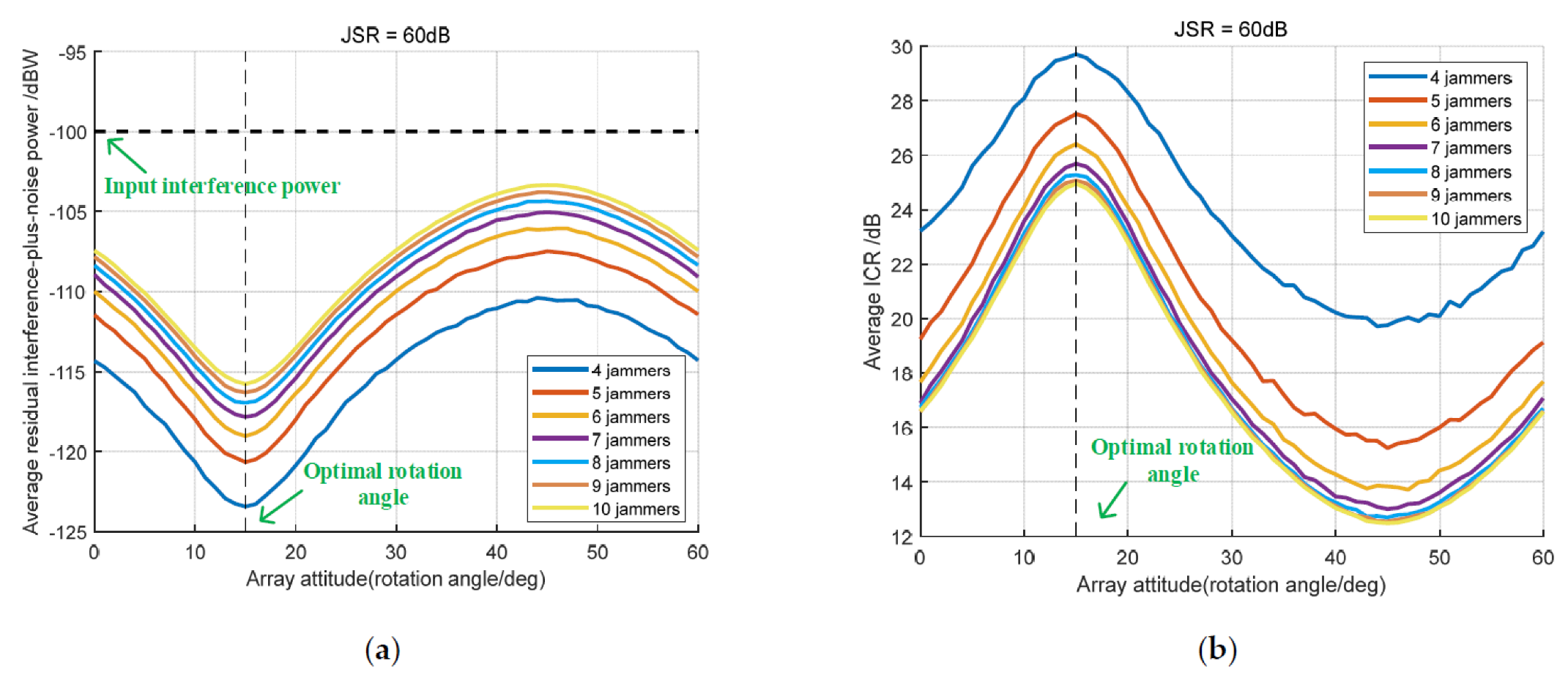
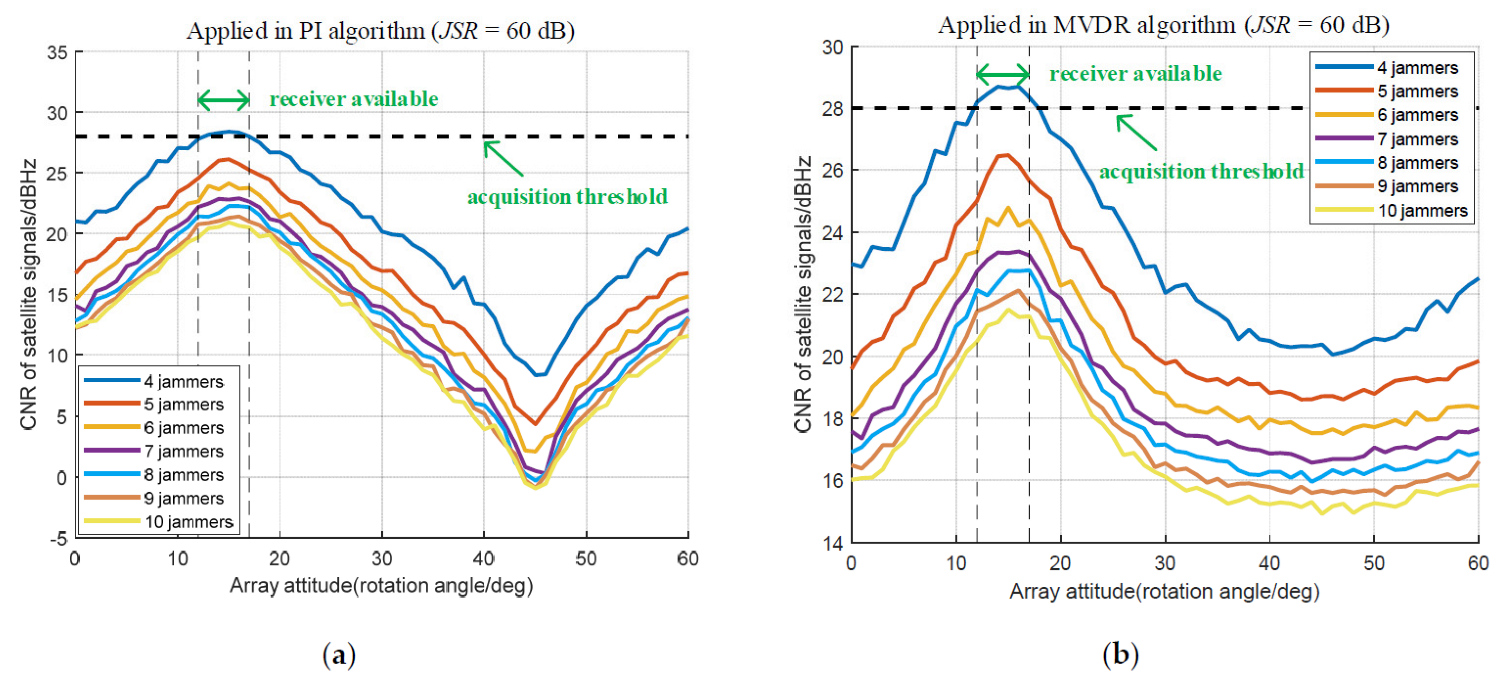
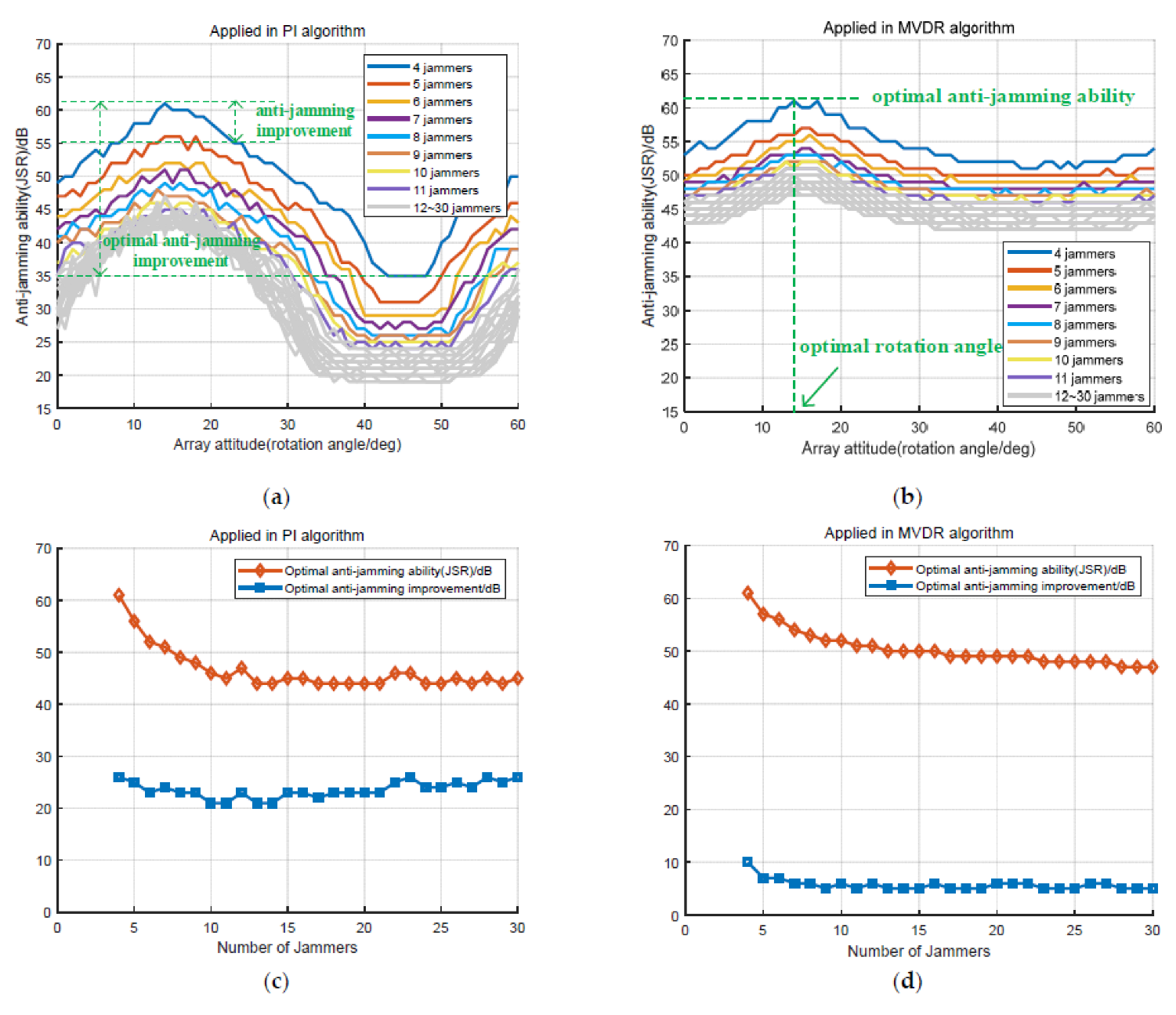
5.2. Effectiveness of Array Antenna Rotation Method
5.3. Efficiency Evaluation of the Variable-Step Iteration Algorithm Based on Gradient Descent
6. Conclusions
- (1)
- In term of sup-freedom anti-jamming performance, the characteristic of direction-sensitivity is revealed;
- (2)
- Making use of the direction-sensitivity, an anti-jamming method based on array antenna rotation is proposed showing in which interference suppression is improved by rotating the antenna at a certain angle.
- (3)
- In order to determine the optimal rotation angle efficiently, an implementation algorithm of variable-step iteration is proposed. Meanwhile, we derived the criteria of the iteration initial value and step selection, which improve the iteration efficiency by over 78.35%.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kaplan, E.D.; Hegarty, C.J. GPS Principle and Application; Electronic Industry Press: Beijing, China, 2002; pp. 1–15. [Google Scholar]
- Kohno, R.; Imai, H.; Hatori, M.; Pasupathy, S. Combinations of an adaptive array antenna and a canceller of interference for direct-sequence spread-spectrum multiple-access system. IEEE J. Sel. Areas Commun. 1990, 8, 675–682. [Google Scholar] [CrossRef]
- Bei, D. Navigation Satellite System Open Service Performance Standard (Version 3.0). Available online: http://www.beidou.gov.cn/xt/gfxz/202105/P020210526216231136238.pdf (accessed on 21 March 2021).
- Morton, Y.T.J.; van Diggelen, F.; Spilker, J.J., Jr.; Parkinson, B.W.; Lo, S.; Gao, G. Position, Navigation, and Timing Technologies in the 21st Century; Wiley-IEEE Press: Piscataway, NJ, USA, 2020; Volume 1, pp. 1121–1139. [Google Scholar]
- Gupta, I.J.; Weiss, I.M.; Morrison, A.W. Desired Features of Adaptive Antenna Arrays for GNSS Receivers. Proc. IEEE 2016, 104, 1195–1206. [Google Scholar] [CrossRef]
- Wang, J.; Ou, G.; Liu, W.; Chen, F. Characteristic Analysis on Anti-jamming Degrees of Freedom of GNSS Array Receiver. In Proceedings of the 13th China Satellite Navigation Conference, CSNC 2022, Beijing, China, 25–27 May 2022; pp. 463–472. [Google Scholar]
- Fernandez-Prades, C.; Arribas, J.; Closas, P. Robust GNSS Receivers by Array Signal Processing: Theory and Implementation. Proc. IEEE 2016, 104, 1207–1220. [Google Scholar] [CrossRef]
- Jie, W.; Wenxiang, L.; Feiqiang, C.; Zukun, L.; Gang, O. GNSS array receiver faced with overloaded interferences: Anti-jamming performance and the incident directions of interferences. J. Syst. Eng. Electron. 2022, 6, 1–7. [Google Scholar] [CrossRef]
- Gstar Anti-Jam Gps—Electronic Protection. Available online: https://www.lockheedmartin.com/content/dam/lockheed-martin/rms/documents/electronic-warfare/GSTAR%20Brochure.pdf (accessed on 25 April 2022).
- GPS Anti-Jam. Available online: https://www.mayflowercom.com/us/technology/gps-anti-jam/ (accessed on 25 April 2022).
- Mitch, R.H.; Dougherty, R.C.; Psiaki, M.L.; Steven, P.P. Signal characteristics of civil GPS jammers. In Proceedings of the 24th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS 2011), Portland, OR, USA, 20–23 September 2011; pp. 1907–1919. [Google Scholar]
- Gu, Y.; Goodman, N.A. Information-Theoretic Compressive Sensing Kernel Optimization and Bayesian Cramér–Rao Bound for Time Delay Estimation. IEEE Trans. Signal Process. 2017, 65, 4525–4537. [Google Scholar] [CrossRef]
- Moffet, A. Minimum-Redundancy Linear Arrays. Antennas and Propagation. IEEE Trans. Antennas Propag. 1968, 16, 172–175. [Google Scholar] [CrossRef]
- Xu, Y.; Liu, Z.; Gong, X. Signal Processing of Polarization Sensitive Array; National Defense Industry Press: Beijing, China, 2013. [Google Scholar]
- Ojeda, O.A.Y.; Grajal, J.; Lopez-Risueño, G. Analytical Performance of GNSS Receivers using Interference Mitigation Techniques. IEEE Trans. Aerosp. Electron. Syst. 2013, 49, 885–906. [Google Scholar] [CrossRef]
- Li, W.; Mao, X.; Yu, W.; Yue, C. An Effective Technique for Enhancing Direction Finding Performance of Virtual Arrays. Int. J. Antennas Propag. 2014, 2014, 1–7. [Google Scholar] [CrossRef]
- Brooks, D.H.; Nikias, C.L. The cross-bicepstrum: Definition, properties, and application for simultaneous reconstruction of three nonminimum phase signals. IEEE Trans. Signal Process. 1993, 41, 2389–2404. [Google Scholar] [CrossRef]
- Horn, R.A.; Johnson, C.R. Matrix Analysis, 2nd ed.; Cambridge University Press: Cambridge, UK, 2012; pp. 164–177. [Google Scholar]
- Mailloux, R.J. Covariance matrix augmentation to produce adaptive array pattern troughs. Electron. Lett. 1995, 31, 102–105. [Google Scholar] [CrossRef]
- Junwei, N. Research on Anti-Jamming Algorithm and Performance Evaluation Technology of GNSS Antenna Array. Ph.D. Dissertation, National University of Defense Technology, Changsha, China, 2012. [Google Scholar]
- Lu, Z.; Nie, J.; Chen, F.; Chen, H.; Ou, G. Adaptive Time Taps of STAP Under Channel Mismatch for GNSS Antenna Arrays. IEEE Trans. Instrum Meas 2017, 66, 2813–2824. [Google Scholar] [CrossRef]



| Symbol | Explanation |
|---|---|
| “H” means Hermitian Transpose | |
| “T” means transpose | |
| “min” means minimum value | |
| means norm of vector | |
| means the minimum eigen value of matrix |
| Number of Elements | X | Y | Z |
|---|---|---|---|
| element 1 | 0 | 0 | 0 |
| element 2 | 0 | 0 | |
| element 3 | − | − | 0 |
| element 4 | − | 0 |
| Parameter | Value |
|---|---|
| light speed | 3 × 108 m/s |
| carrier frequency | 1268.52 MHz |
| array geometry | four element central circular array |
| array element spacing | 1/2 wavelength |
| navigation signal power | −160 dBW |
| noise bandwidth | 20.48 MHz |
| interference type | wideband gaussian noise |
| jammer incident angles in elevation | 0°~−15°, uniform distribution |
| jammer incident angles in azimuth | 0°~360°, uniform distribution |
| of jammer incident angles in azimuth | 90° |
| satellite signal incident angles in elevation | 15°~90°, uniform distribution |
| satellite signal incident angles in azimuth | 0°~360°, uniform distribution |
| number of interferences | 4~30 |
| implementation of anti-jamming algorithm | Sampling Matrix Inversion |
| Interference Parameter | Angle in Elevation | Angle in Azimuth | JSR |
|---|---|---|---|
| Interference 1 | −15° | 28° | 65 dB |
| Interference 2 | −2° | 18° | 70 dB |
| Interference 3 | −6° | −42° | 62 dB |
| Interference 4 | −10° | −62° | 70 dB |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Y.; Chen, F.; Lu, Z.; Wang, F. Anti-Jamming Method and Implementation for GNSS Receiver Based on Array Antenna Rotation. Remote Sens. 2022, 14, 4774. https://doi.org/10.3390/rs14194774
Sun Y, Chen F, Lu Z, Wang F. Anti-Jamming Method and Implementation for GNSS Receiver Based on Array Antenna Rotation. Remote Sensing. 2022; 14(19):4774. https://doi.org/10.3390/rs14194774
Chicago/Turabian StyleSun, Yifan, Feiqiang Chen, Zukun Lu, and Feixue Wang. 2022. "Anti-Jamming Method and Implementation for GNSS Receiver Based on Array Antenna Rotation" Remote Sensing 14, no. 19: 4774. https://doi.org/10.3390/rs14194774
APA StyleSun, Y., Chen, F., Lu, Z., & Wang, F. (2022). Anti-Jamming Method and Implementation for GNSS Receiver Based on Array Antenna Rotation. Remote Sensing, 14(19), 4774. https://doi.org/10.3390/rs14194774







