Atmospheric Correction Model for Water–Land Boundary Adjacency Effects in Landsat-8 Multispectral Images and Its Impact on Bathymetric Remote Sensing
Abstract
1. Introduction
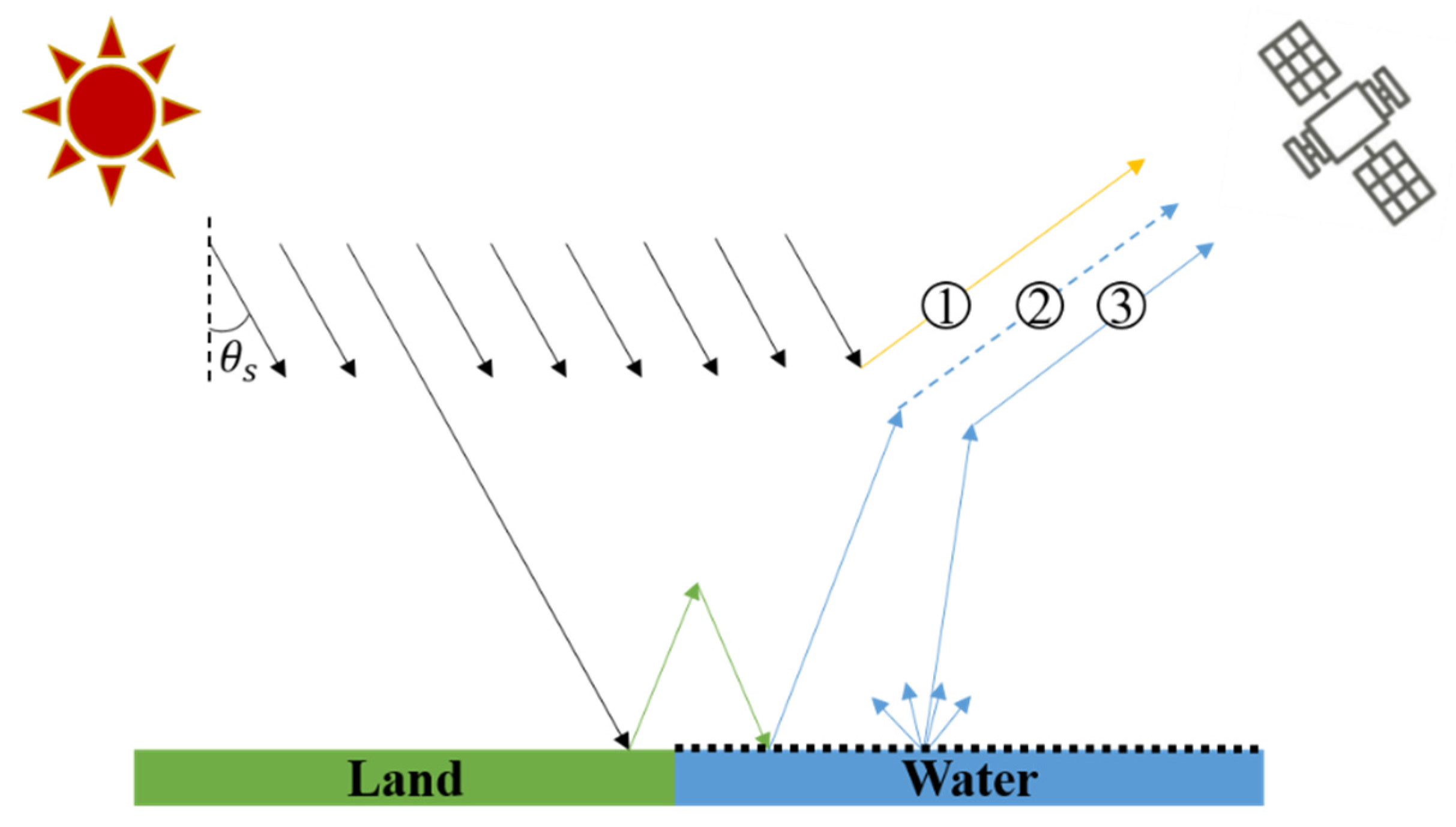
2. Correction Model for Water–Land Boundary AE
2.1. Composition of Remote Sensing Signals for Water Column
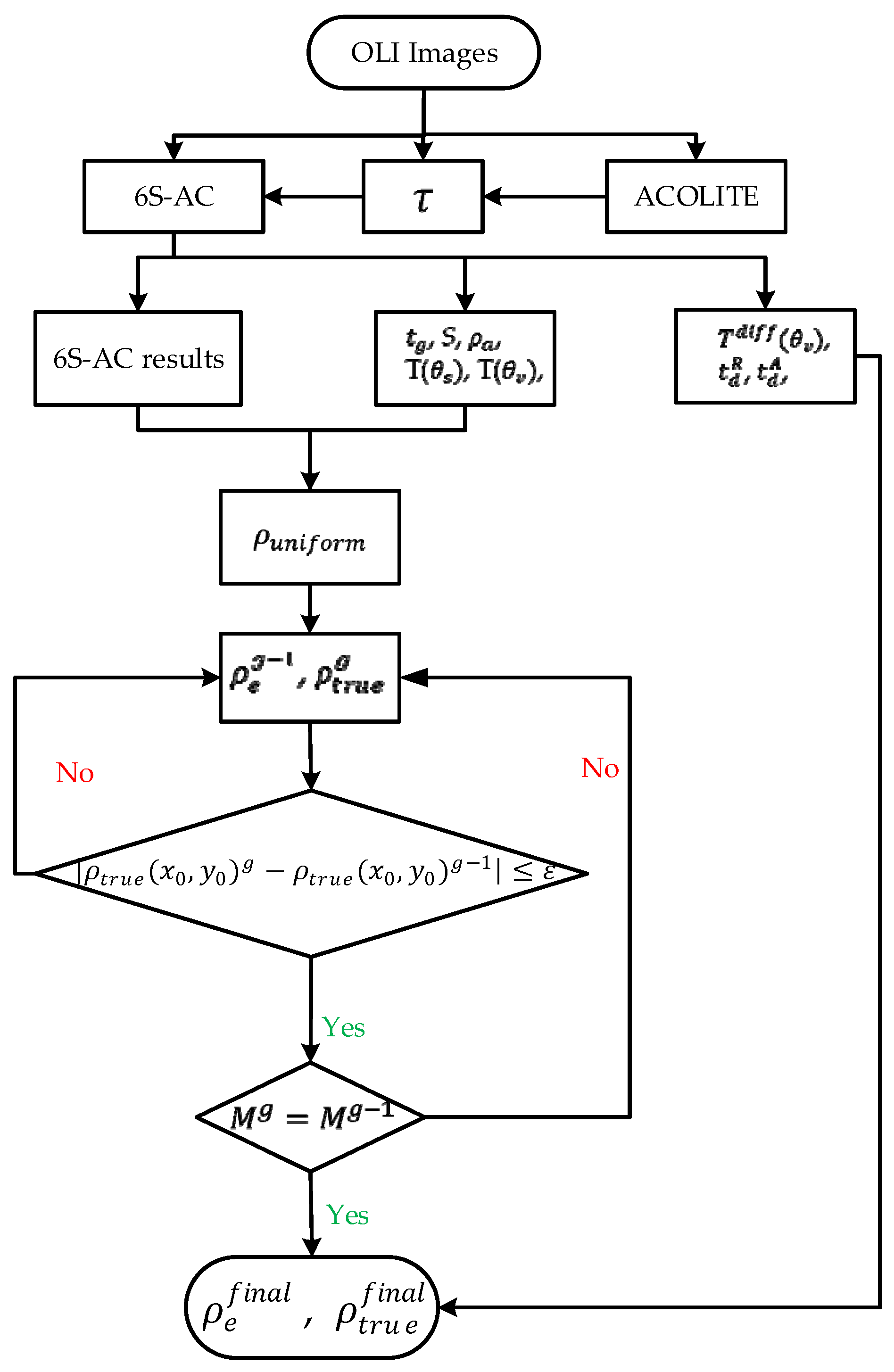
2.2. Proposed Model
3. Application and Analysis
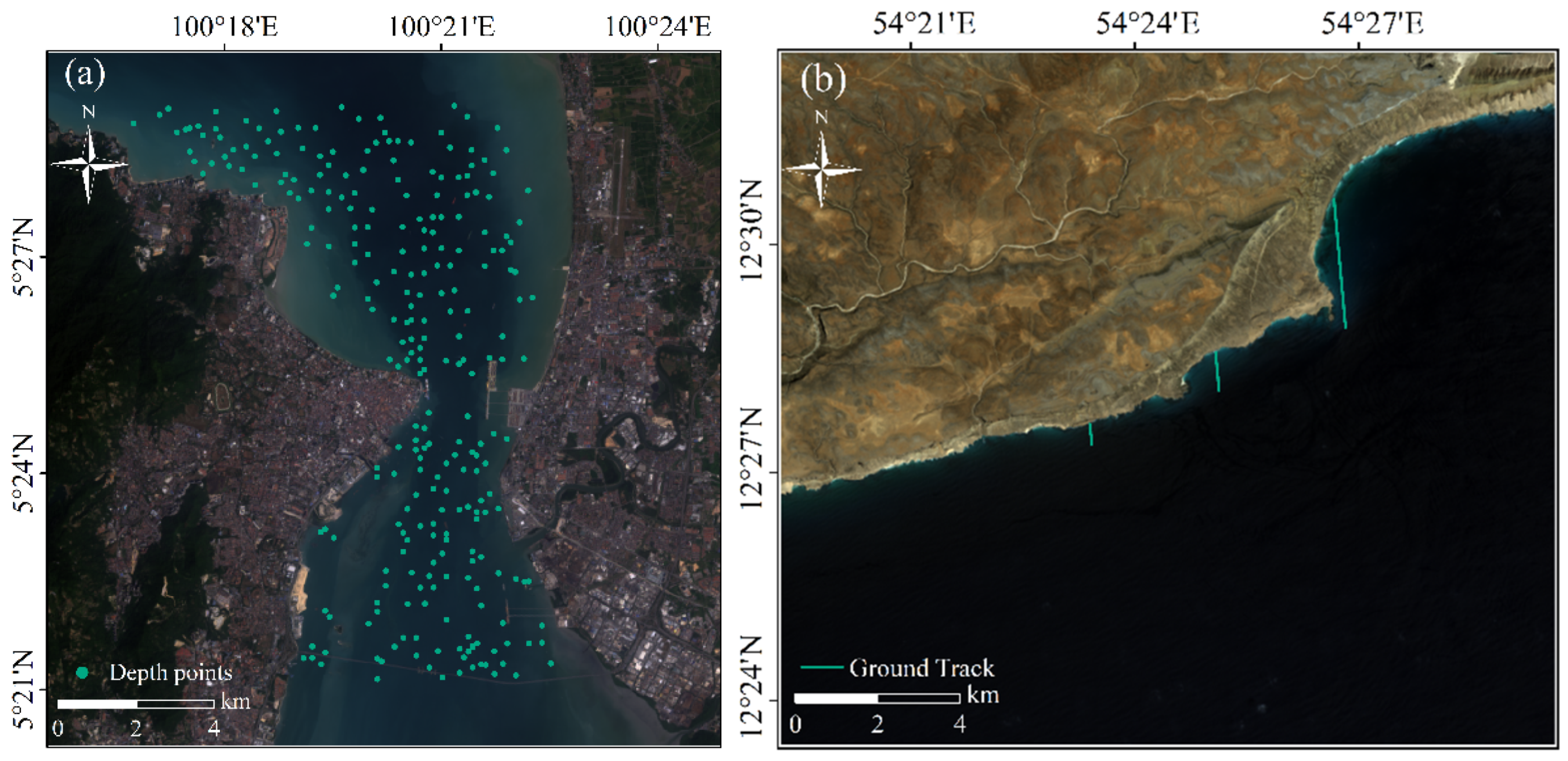
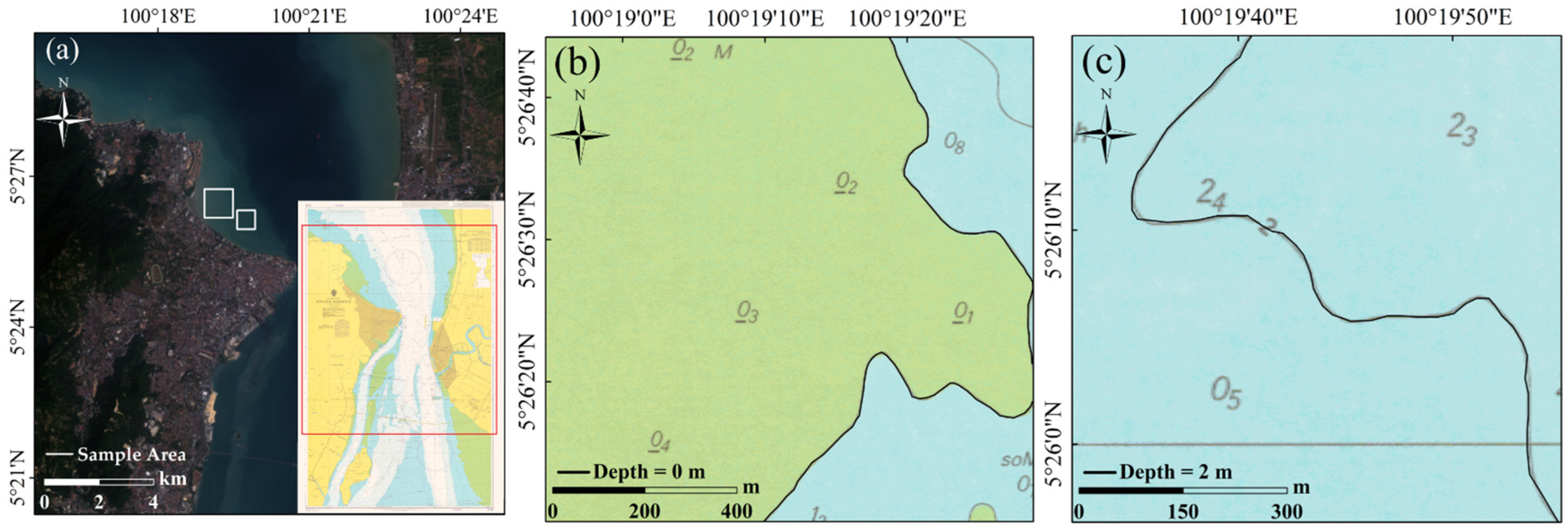
3.1. Data and Study Area
3.2. Data Preprocessing and Bathymetric Inversion
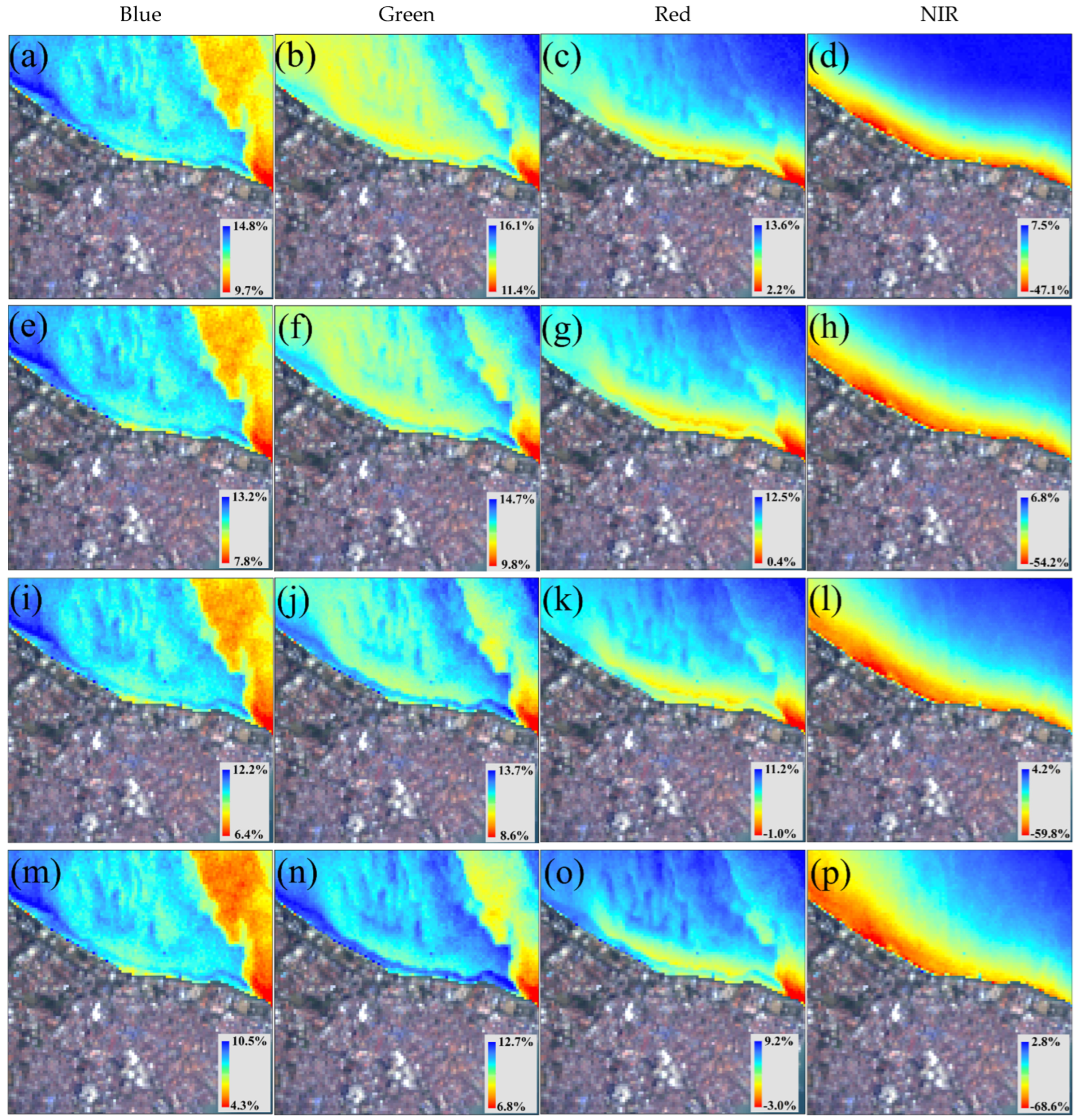
3.3. Analysis of the AC Results
3.3.1. Overall Quality Assessment
3.3.2. Regional Quality Assessment
3.4. Analysis of the Bathymetric Inversion Results
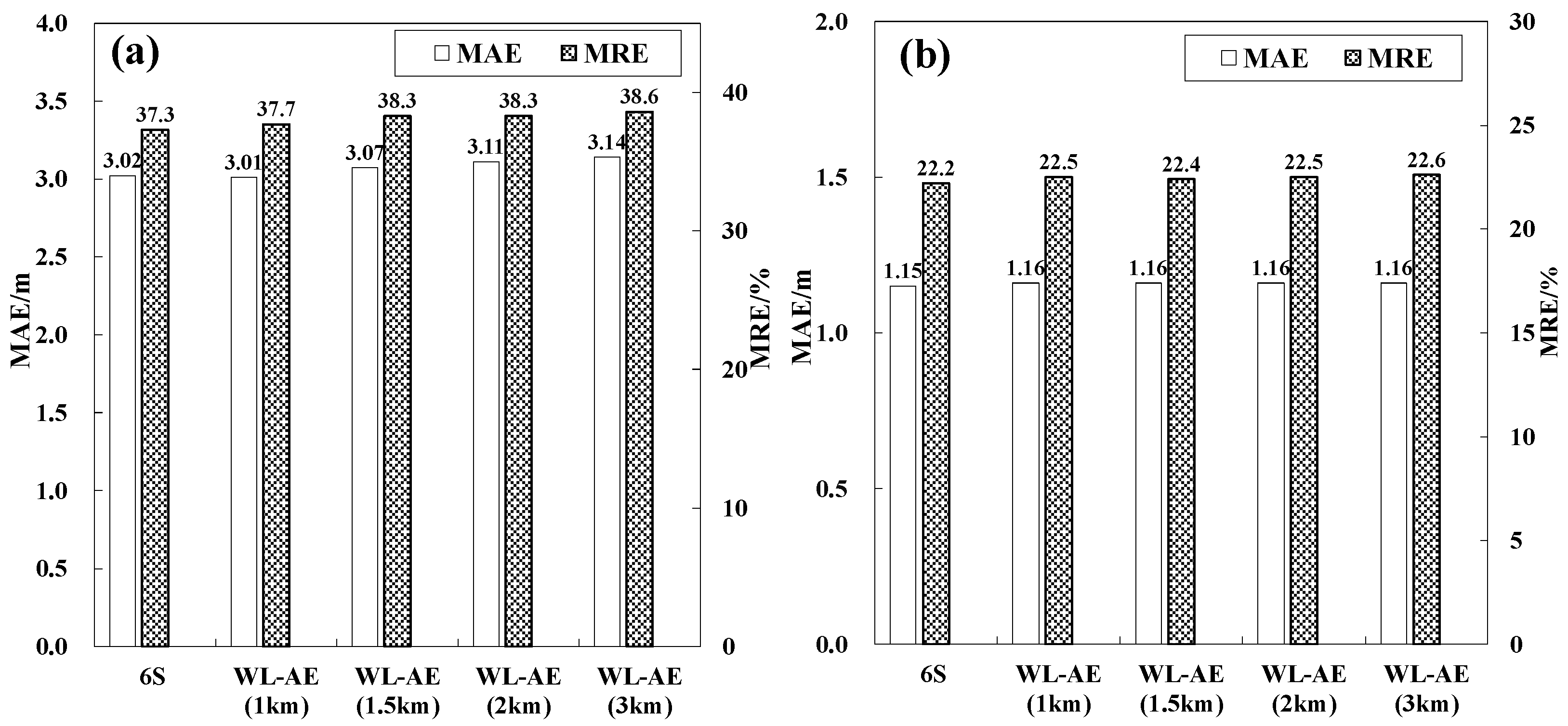
3.4.1. Assessment Analysis of the Overall Inversion Accuracy
3.4.2. Assessment Analysis of the Segmental Inversion Accuracy
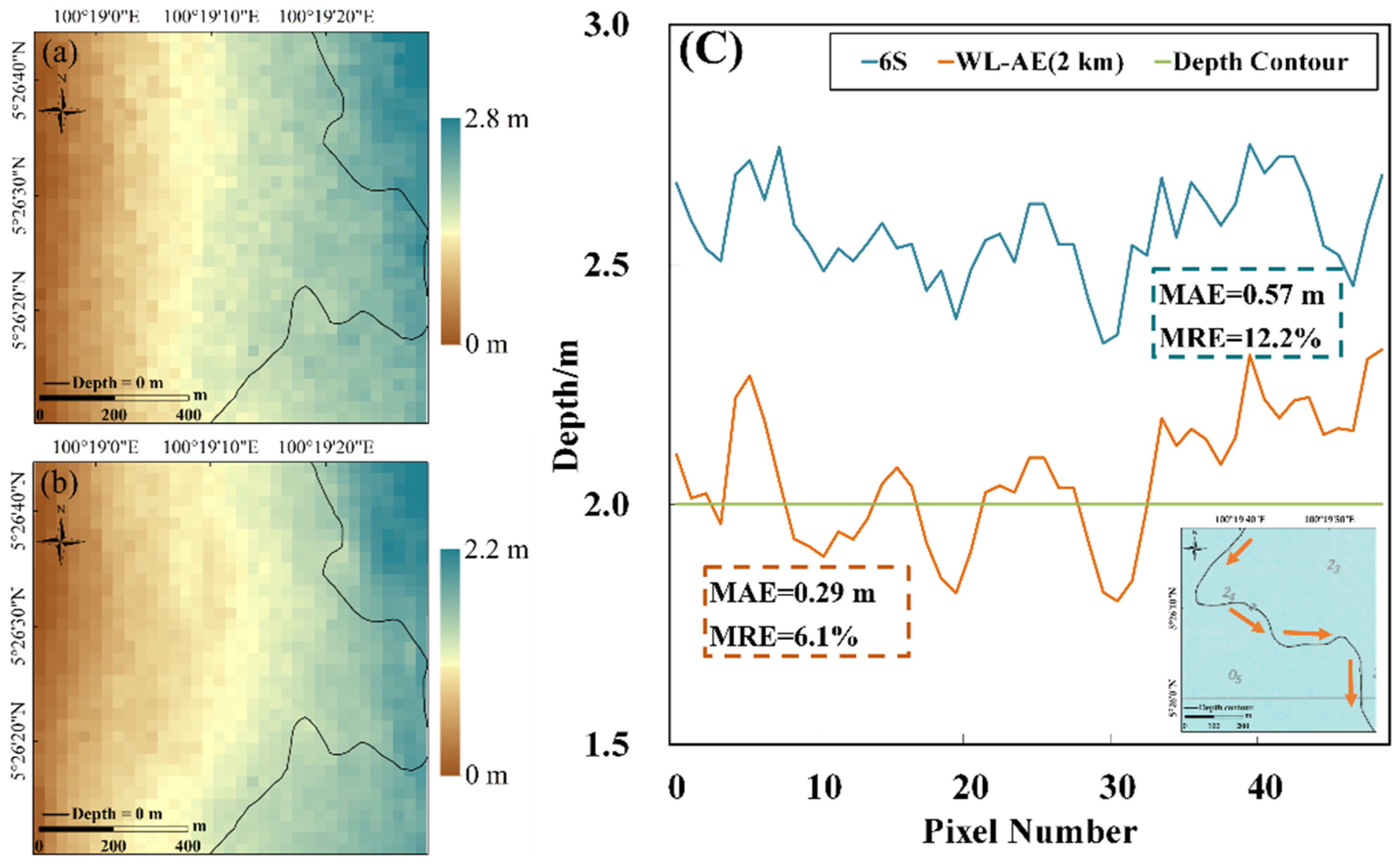
3.4.3. Influence Analysis of WL-AE Regarding Shallow Water Depth Inversion
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zheng, X.; Li, Z.-L.; Zhang, X.; Shang, G. Quantification of the adjacency effect on measurements in the thermal infrared region. IEEE Trans. Geosci. Remote Sens. 2019, 57, 321–331. [Google Scholar] [CrossRef]
- Vermote, E.F.; Tanre, D.; Deuze, J.L.; Herman, M.; Morcette, J.J. Second simulation of the satellite signal in the solar spectrum, 6S: An overview. IEEE Trans. Geosci. Remote Sens. 1997, 35, 675–686. [Google Scholar] [CrossRef]
- Bulgarelli, B.; Zibordi, G. On the detectability of adjacency effects in ocean color remote sensing of mid-latitude coastal environments by SeaWiFS, MODIS-A, MERIS, OLCI, OLI and MSI. Remote Sens. Environ. 2018, 209, 423–438. [Google Scholar] [CrossRef] [PubMed]
- Bulgarelli, B.; Kiselev, V.; Zibordi, G. Simulation and analysis of adjacency effects in coastal waters: A case study. Appl. Opt. 2014, 53, 1523. [Google Scholar] [CrossRef] [PubMed]
- Lyzenga, D.R. Passive remote sensing techniques for mapping water depth and bottom features. Appl. Opt. 1978, 17, 379. [Google Scholar] [CrossRef] [PubMed]
- Lyzenga, D.R. Shallow-water bathymetry using combined lidar and passive multispectral scanner data. Int. J. Remote Sens. 1985, 6, 115–125. [Google Scholar] [CrossRef]
- Lyzenga, D.R.; Malinas, N.P.; Tanis, F.J. Multispectral bathymetry using a simple physically based algorithm. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2251–2259. [Google Scholar] [CrossRef]
- Putsay, M. A simple atmospheric correction method for the short wave satellite images. Int. J. Remote Sens. 1992, 13, 1549–1558. [Google Scholar] [CrossRef]
- Sanders, L.C.; Schott, J.R.; Raqueño, R. A VNIR/SWIR atmospheric correction algorithm for hyperspectral imagery with adjacency effect. Remote Sens. Environ. 2001, 78, 252–263. [Google Scholar] [CrossRef]
- Tanré, D.; Deschamps, P.Y.; Duhaut, P.; Herman, M. Adjacency effect produced by the atmospheric scattering in thematic mapper data. J. Geophys. Res. Atmos. 1987, 92, 12000. [Google Scholar] [CrossRef]
- Guzzi, D.; Nardino, V.; Lastri, C.; Raimondi, V. A fast iterative procedure for adjacency effects correction on remote sensed data. Remote Sens. 2021, 13, 1799. [Google Scholar] [CrossRef]
- Richter, R. A spatially adaptive fast atmospheric correction algorithm. Int. J. Remote Sens. 1996, 17, 1201–1214. [Google Scholar] [CrossRef]
- Cooley, T.; Anderson, G.P.; Felde, G.W.; Hole, M.L.; Ratkowski, A.J.; Chetwynd, J.H.; Gardner, J.A.; Adlergolden, S.M.; Matthew, M.W.; Berk, A. FLAASH, a MODTRAN4-based atmospheric correction algorithm, its application and validation. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Toronto, ON, Canada, 24–28 June 2002; pp. 1414–1418. [Google Scholar] [CrossRef]
- Minomura, M.; Kuze, H.; Takeuchi, N. Adjacency effect in the atmospheric correction of satellite remote sensing data: Evaluation of the influence of aerosol extinction profiles. Opt. Rev. 2001, 8, 133–141. [Google Scholar] [CrossRef]
- Richter, R. A fast atmospheric correction algorithm applied to Landsat TM images. Int. J. Remote Sens. 1990, 11, 159–166. [Google Scholar] [CrossRef]
- Kiselev, V.; Bulgarelli, B.; Heege, T. Sensor independent adjacency correction algorithm for coastal and inland water systems. Remote Sens. Environ. 2015, 157, 85–95. [Google Scholar] [CrossRef]
- Bulgarelli, R.; Zibordi, G. Adjacency radiance around a small island: Implications for system vicarious calibrations. Appl. Opt. 2020, 59, C63–C69. [Google Scholar] [CrossRef] [PubMed]
- Feng, L.; Hu, C. Land adjacency effects on MODIS aqua top-of-atmosphere radiance in the shortwave infrared: Statistical assessment and correction. J. Geophys. Res. Oceans 2017, 122, 4802–4818. [Google Scholar] [CrossRef]
- Kaufman, Y.J.; Joseph, J.H. Determination of surface albedos and aerosol extinction characteristics from satellite imagery. J. Geophys. Res. Oceans 1982, 87, 1287. [Google Scholar] [CrossRef]
- Schäfer, M.; Bierwirth, E.; Ehrlich, A.; Jäkel, E.; Wendisch, E. Airborne observations and simulations of three-dimensional radiative interactions between Arctic boundary layer clouds and ice floes. Atmos. Chem. Phys. 2015, 15, 8147–8163. [Google Scholar] [CrossRef]
- Wang, T.; Du, L.; Yi, W.; Hong, J.; Zhang, L.; Zheng, J.; Li, C.; Ma, X.; Zhang, D.; Fang, W.; et al. An adaptive atmospheric correction algorithm for the effective adjacency effect correction of submeter-scale spatial resolution optical satellite images: Application to a WorldView-3 panchromatic image. Remote Sens. Environ. 2021, 259, 112412. [Google Scholar] [CrossRef]
- Wright, L.A.; Kindel, B.C.; Pilewskie, P.; Leisso, N.P.; Kampe, T.U.; Schmidt, K.S. Below-cloud atmospheric correction of airborne hyperspectral imagery using simultaneous solar spectral irradiance observations. IEEE Trans. Geosci. Remote Sens. 2020, 59, 1392–1409. [Google Scholar] [CrossRef]
- Harmel, T.; Chami, M.; Tormos, T.; Reynaud, N.; Danis, P.A. Sunglint correction of the multi-spectral instrument (msi)-sentinel-2 imagery over inland and sea waters from swir bands. Remote Sens. Environ. 2017, 204, 308–321. [Google Scholar] [CrossRef]
- Bulgarelli, B.; Zibordi, G. Seasonal Impact of Adjacency Effects on Ocean Color Radiometry at the AAOT Validation Site. IEEE Geosci. Remote Sens. Lett. 2018, 15, 488–492. [Google Scholar] [CrossRef]
- Ma, L.; Wang, N.; Liu, Y.; Zhao, Y.; Han, Q.; Wang, X.; Woolliams, E.R.; Bouvet, M.; Gao, C.; Li, C.; et al. An in-flight radiometric calibration method considering adjacency effects for high-resolution optical sensors over artificial targets. IEEE Trans. Geosci. Remote Sens. 2020, 60, 5600913. [Google Scholar] [CrossRef]
- Duan, S.B.; Li, Z.L.; Gao, C.; Zhao, W.; Wu, H.; Qian, Y.; Leng, P.; Gao, M. Influence of adjacency effect on high-spatial-resolution thermal infrared imagery: Implication for radiative transfer simulation and land surface temperature retrieval. Remote Sens. Environ. 2020, 245, 111852. [Google Scholar] [CrossRef]
- Yang, H.; Gordon, H.R.; Zhang, T. Island perturbation to the sky radiance over the ocean: Simulations. Appl. Opt. 1995, 34, 38354. [Google Scholar] [CrossRef]
- Santer, R.; Schmechtig, C. Adjacency effects on water surfaces: Primary scattering approximation and sensitivity study. Appl. Opt. 2000, 39, 361. [Google Scholar] [CrossRef]
- Ruddick, K.G.; Ovidio, F.; Rijkeboer, M. Atmospheric correction of SeaWiFS imagery for turbid coastal and inland waters. Appl. Opt. 2000, 39, 897–912. [Google Scholar] [CrossRef]
- Sei, A. Analysis of adjacency effects for two Lambertian half-spaces. Int. J. Remote Sens. 2007, 28, 1873–1890. [Google Scholar] [CrossRef]
- Zhang, H.; Ma, Y.; Zhang, J. Multi-dimensional analysis of atmospheric correction models on multi-spectral water depth inversion. Haiyang Xuebao 2022, 44, 145–160. [Google Scholar] [CrossRef]
- Bulgarelli, B.; Zibordi, G.; Kiselev, V. Modeling the adjacency effects at AERONET-OC sites. Am. Inst. Phys. 2013, 1531, 943–946. [Google Scholar] [CrossRef]
- Zhang, X.; Ma, Y.; Zhang, J. Shallow water bathymetry based on inherent optical properties using high spatial resolution multispectral imagery. Remote Sens. 2020, 12, 3027. [Google Scholar] [CrossRef]
- Pahlevan, N.; Mangin, A.; Balasubramanian, S.V.; Smith, B.; Alikas, K.; Arai, K.; Barbosa, C.; Bélanger, S.; Binding, C.; Bresciani, M.; et al. ACIX-Aqua: A global assessment of atmospheric correction methods for Landsat-8 and Sentinel-2 over lakes, rivers, and coastal waters. Remote Sens. Environ. 2021, 258, 112366. [Google Scholar] [CrossRef]
- Pahlevan, N.; Schott, J.R.; Franz, B.A.; Zibordi, G. Landsat 8 remote sensing reflectance (Rrs) products: Evaluations, intercomparisons, and enhancements. Remote Sens. Environ. 2017, 190, 289–301. [Google Scholar] [CrossRef]
- Lymburner, L.; Botha, E.; Hestir, E.; Anstee, J.; Sagar, S.; Dekker, A.; Malthus, T. Landsat 8: Providing continuity and increased precision for measuring multi-decadal time series of total suspended matter. Remote Sens. Environ. 2016, 185, 108–118. [Google Scholar] [CrossRef]
- López-Serrano, P.M.; Corral-Rivas, J.J.; Díaz-Varela, R.A.; Álvarez-González, J.G.; López-Sánchez, C.A. Evaluation of radiometric and atmospheric correction algorithms for aboveground forest biomass estimation using Landsat 5 TM data. Remote Sens. 2016, 8, 369. [Google Scholar] [CrossRef]
- Nazeer, M.; Nichol, J.E.; Yung, Y.K. Evaluation of atmospheric correction models and Landsat surface reflectance product in an urban coastal environment. Int. J. Remote Sens. 2014, 35, 6271–6291. [Google Scholar] [CrossRef]
- Hsu, H.J.; Huang, C.Y.; Jasinski, M.; Li, Y.; Gao, H.; Yamanokuchi, T.; Wang, C.G.; Chang, T.M.; Ren, H.; Kuo, C.Y.; et al. A semi-empirical scheme for bathymetric mapping in shallow water by ICESat-2 and Sentinel-2: A case study in the South China Sea. ISPRS J. Photogramm. Remote Sens. 2021, 178, 1–19. [Google Scholar] [CrossRef]
- Zhang, Y.; Gao, J.; Yan, G.U. A simple method for mapping bathymetry over turbid coastal waters from MODIS data: Possibilities and limitations. Int. J. Remote Sens. 2011, 32, 7575–7590. [Google Scholar] [CrossRef]
- Gardashov, R.H.; Eminov, M.S. Determination of sunglint location and its characteristics on observation from a METEOSAT 9 satellite. Int. J. Remote Sens. 2015, 36, 2584–2598. [Google Scholar] [CrossRef]
- Lafon, V.; Froidefond, J.M.; Lahet, F.; Castaing, P. SPOT shallow water bathymetry of a moderately turbid tidal inlet based on field measurements. Remote Sens. Environ. 2002, 81, 136–148. [Google Scholar] [CrossRef]

| Model | Blue | Green | Red | NIR |
|---|---|---|---|---|
| 6S | 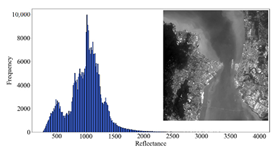 | 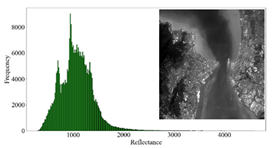 | 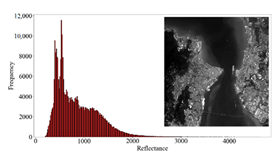 | 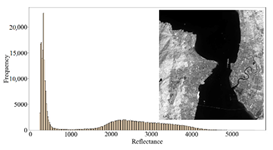 |
| WL-AE (1 km) |  | 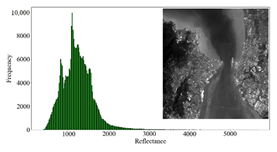 |  |  |
| WL-AE (1.5 km) |  | 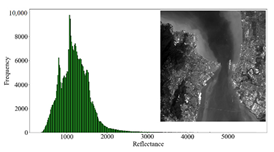 |  | 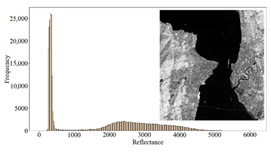 |
| WL-AE (2 km) | 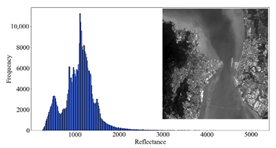 | 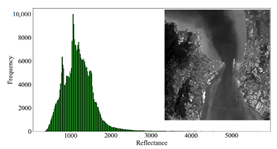 |  | 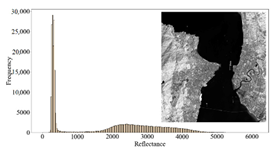 |
| WL-AE (3 km) | 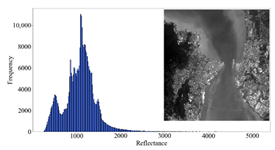 | 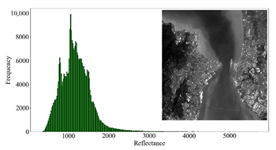 | 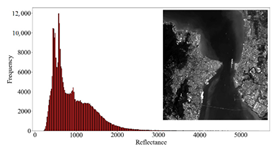 |  |
| Region | Band | Blue | Green | Red | NIR | ||||
|---|---|---|---|---|---|---|---|---|---|
| Model | Entropy | Contrast | Entropy | Contrast | Entropy | Contrast | Entropy | Contrast | |
| Penang | 6S | 2.045 | 0.880 | 2.067 | 0.883 | 2.051 | 0.924 | 2.010 | 0.922 |
| WL-AE (1 km) | 2.180 | 0.904 | 2.182 | 0.886 | 2.182 | 0.924 | 2.182 | 0.970 | |
| WL-AE (1.5 km) | 2.182 | 0.906 | 2.182 | 0.888 | 2.182 | 0.926 | 2.182 | 0.990 | |
| WL-AE (2 km) | 2.182 | 0.907 | 2.182 | 0.889 | 2.182 | 0.927 | 2.182 | 1.000 | |
| WL-AE (3 km) | 2.182 | 0.909 | 2.182 | 0.892 | 2.182 | 0.928 | 2.182 | 1.018 | |
| Socotra | 6S | 2.075 | 0.831 | 2.089 | 0.883 | 2.097 | 0.936 | 2.101 | 0.969 |
| WL-AE (1 km) | 2.182 | 0.856 | 2.182 | 0.881 | 2.182 | 0.934 | 2.182 | 1.047 | |
| WL-AE (1.5 km) | 2.182 | 0.859 | 2.182 | 0.881 | 2.182 | 0.934 | 2.182 | 1.063 | |
| WL-AE (2 km) | 2.182 | 0.861 | 2.182 | 0.882 | 2.182 | 0.939 | 2.182 | 1.076 | |
| WL-AE (3 km) | 2.182 | 0.864 | 2.182 | 0.883 | 2.182 | 0.948 | 2.182 | 1.093 | |
| Study Area | Samples | Mixed Zone | Water Zone | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Model | Index | Blue | Green | Red | NIR | Blue | Green | Red | NIR | |
| Penang | WL-AE (1 km) | /% | 12.5 | 14.2 | 10.3 | 8.2 | 11.5 | 16.5 | 13.9 | 7.3 |
| /% | 0.7 | 0.6 | 1.8 | 6.6 | 0.4 | 0.7 | 0.7 | 0.8 | ||
| WL-AE (1.5 km) | /% | 10.7 | 12.8 | 8.7 | 10.1 | 9.7 | 15.0 | 12.9 | 6.7 | |
| /% | 0.9 | 0.5 | 1.9 | 9.1 | 0.4 | 0.7 | 0.7 | 0.8 | ||
| WL-AE (2 km) | /% | 9.4 | 11.8 | 7.5 | 13.1 | 8.5 | 14.0 | 12.1 | 6.0 | |
| /% | 1.0 | 0.6 | 1.7 | 10.7 | 0.5 | 0.8 | 0.9 | 1.5 | ||
| WL-AE (3 km) | /% | 7.5 | 10.4 | 5.6 | 20.1 | 6.4 | 12.1 | 10.1 | 4.6 | |
| /% | 1.2 | 0.7 | 1.5 | 11.7 | 0.6 | 0.8 | 1.1 | 3.1 | ||
| Socotra | WL-AE (1 km) | /% | 4.4 | 7.8 | 5.0 | 5.4 | 3.8 | 11.0 | 10.1 | 4.8 |
| /% | 0.8 | 1.6 | 2.4 | 4.8 | 0.5 | 1.0 | 0.9 | 1.2 | ||
| WL-AE (1.5 km) | /% | 4.5 | 6.6 | 4.0 | 6.6 | 3.0 | 10.3 | 9.2 | 4.8 | |
| /% | 1.0 | 1.6 | 2.1 | 6.5 | 0.5 | 1.2 | 1.8 | 4.8 | ||
| WL-AE (2 km) | /% | 2.7 | 5.6 | 3.4 | 8.5 | 2.4 | 9.6 | 8.1 | 6.1 | |
| /% | 1.1 | 1.5 | 2.1 | 7.4 | 0.5 | 1.5 | 2.9 | 9.0 | ||
| WL-AE (3 km) | /% | 1.4 | 3.9 | 3.6 | 13.3 | 1.1 | 7.8 | 4.6 | 12.0 | |
| /% | 1.4 | 1.3 | 2.9 | 7.7 | 0.7 | 2.0 | 5.0 | 16.9 | ||
| Study Area | Depth/m | 0–5 | 5–10 | 10–15 | 15–20 | ||||
|---|---|---|---|---|---|---|---|---|---|
| Model | MAE/m | MRE/% | MAE/m | MRE/% | MAE/m | MRE/% | MAE/m | MRE/% | |
| Penang | 6S | 0.82 | 35.8 | 1.08 | 16.0 | 1.18 | 10.0 | 1.27 | 7.4 |
| WL-AE (1 km) | 0.85 | 37.7 | 1.09 | 16.1 | 1.19 | 9.6 | 1.14 | 6.6 | |
| WL-AE (1.5 km) | 0.82 | 36.0 | 1.05 | 15.6 | 1.08 | 9.0 | 1.10 | 6.4 | |
| WL-AE (2 km) | 0.93 | 32.4 | 1.04 | 15.4 | 1.05 | 8.8 | 1.02 | 5.9 | |
| WL-AE (3 km) | 0.82 | 35.7 | 1.06 | 15.7 | 1.01 | 8.4 | 1.02 | 6.0 | |
| Socotra | 6S | 0.91 | 36.8 | 0.36 | 4.4 | 0.62 | 5.4 | 0.91 | 5.5 |
| WL-AE (1 km) | 0.91 | 36.8 | 0.34 | 4.3 | 0.62 | 5.5 | 0.92 | 5.5 | |
| WL-AE (1.5 km) | 0.90 | 36.3 | 0.34 | 4.4 | 0.63 | 5.5 | 0.90 | 5.4 | |
| WL-AE (2 km) | 0.89 | 35.7 | 0.34 | 4.4 | 0.62 | 5.5 | 0.89 | 5.4 | |
| WL-AE (3 km) | 0.86 | 34.3 | 0.35 | 4.4 | 0.62 | 5.5 | 0.88 | 5.3 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Ma, Y.; Zhang, J.; Zhao, X.; Zhang, X.; Leng, Z. Atmospheric Correction Model for Water–Land Boundary Adjacency Effects in Landsat-8 Multispectral Images and Its Impact on Bathymetric Remote Sensing. Remote Sens. 2022, 14, 4769. https://doi.org/10.3390/rs14194769
Zhang H, Ma Y, Zhang J, Zhao X, Zhang X, Leng Z. Atmospheric Correction Model for Water–Land Boundary Adjacency Effects in Landsat-8 Multispectral Images and Its Impact on Bathymetric Remote Sensing. Remote Sensing. 2022; 14(19):4769. https://doi.org/10.3390/rs14194769
Chicago/Turabian StyleZhang, Huanwei, Yi Ma, Jingyu Zhang, Xin Zhao, Xuechun Zhang, and Zihao Leng. 2022. "Atmospheric Correction Model for Water–Land Boundary Adjacency Effects in Landsat-8 Multispectral Images and Its Impact on Bathymetric Remote Sensing" Remote Sensing 14, no. 19: 4769. https://doi.org/10.3390/rs14194769
APA StyleZhang, H., Ma, Y., Zhang, J., Zhao, X., Zhang, X., & Leng, Z. (2022). Atmospheric Correction Model for Water–Land Boundary Adjacency Effects in Landsat-8 Multispectral Images and Its Impact on Bathymetric Remote Sensing. Remote Sensing, 14(19), 4769. https://doi.org/10.3390/rs14194769







