Importance of Calibration for Improving the Efficiency of Data Assimilation for Predicting Forest Characteristics
Abstract
1. Introduction
- (1)
- An initial prediction of the variable of interest is made using a model obtained through regressing field reference data on RS metrics with the same spatial resolution.
- (2)
- A growth model is applied to predict the development of the state until the next RS data acquisition time point.
- (3)
- A new RS-based prediction is obtained, as described in step (1). This prediction is merged with the forecast from step (2) based on the uncertainty of the two predictions. With the standard Kalman filter, the two predictions are merged through a weighting procedure, which assigns weights inversely proportional to their variances.
- (4)
- Following the merger of the two predictions in step (3), the DA procedure continues by applying a growth model to the merged prediction to forecast the state to the next RS data acquisition time point.
- (5)
- A new RS-based prediction is merged with the forecasted prediction from step (4) through the procedure described in step (3). Steps (4) and (5) are repeated as many times as there are new predictions to assimilate.
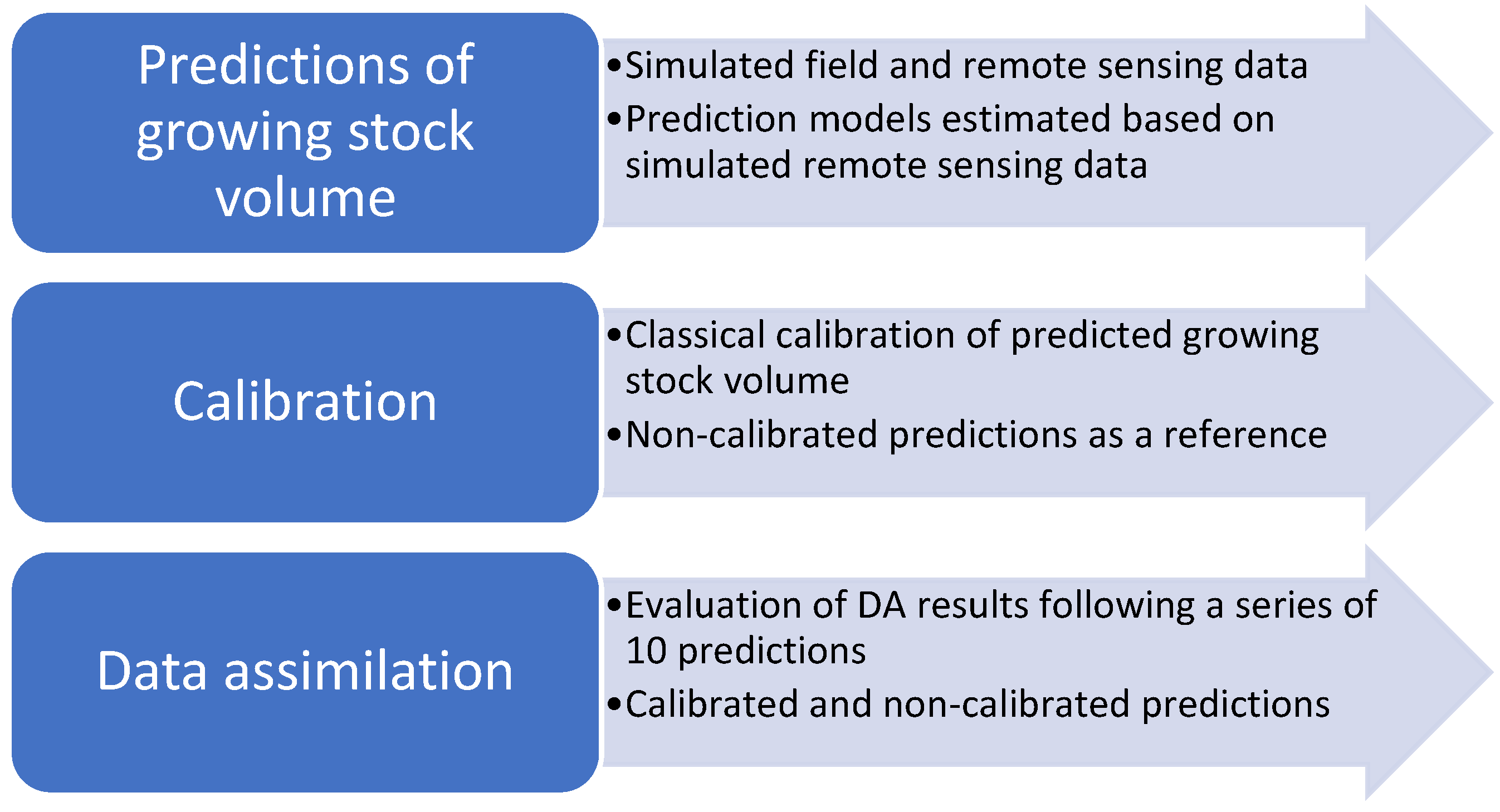
2. Materials and Methods
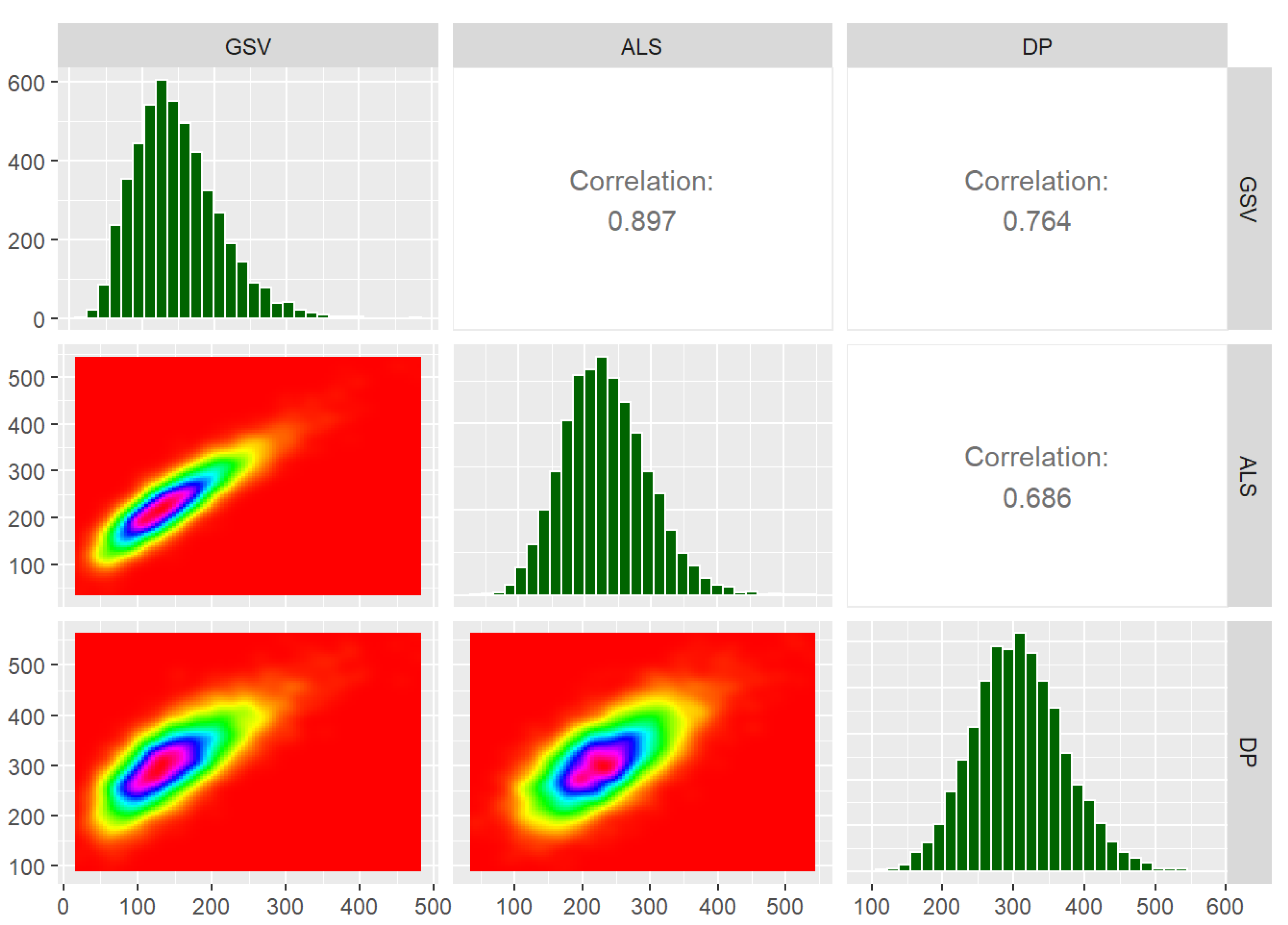
2.1. Simulating the Population
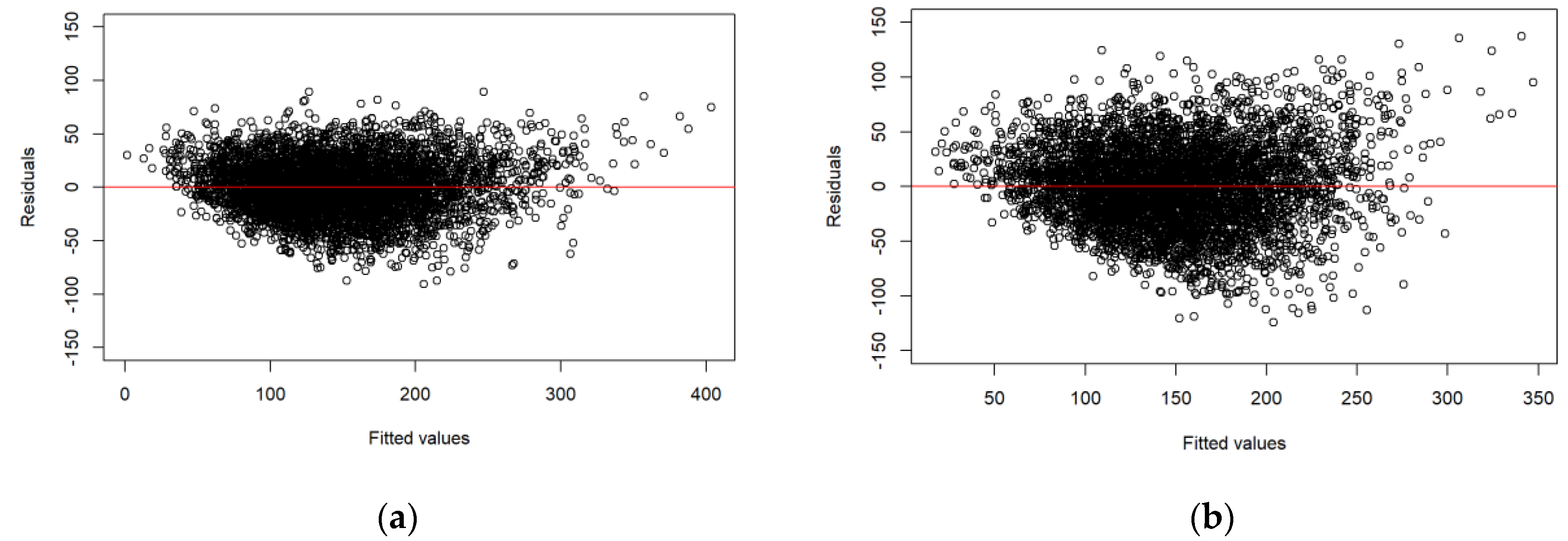
2.2. GSV Prediction Models
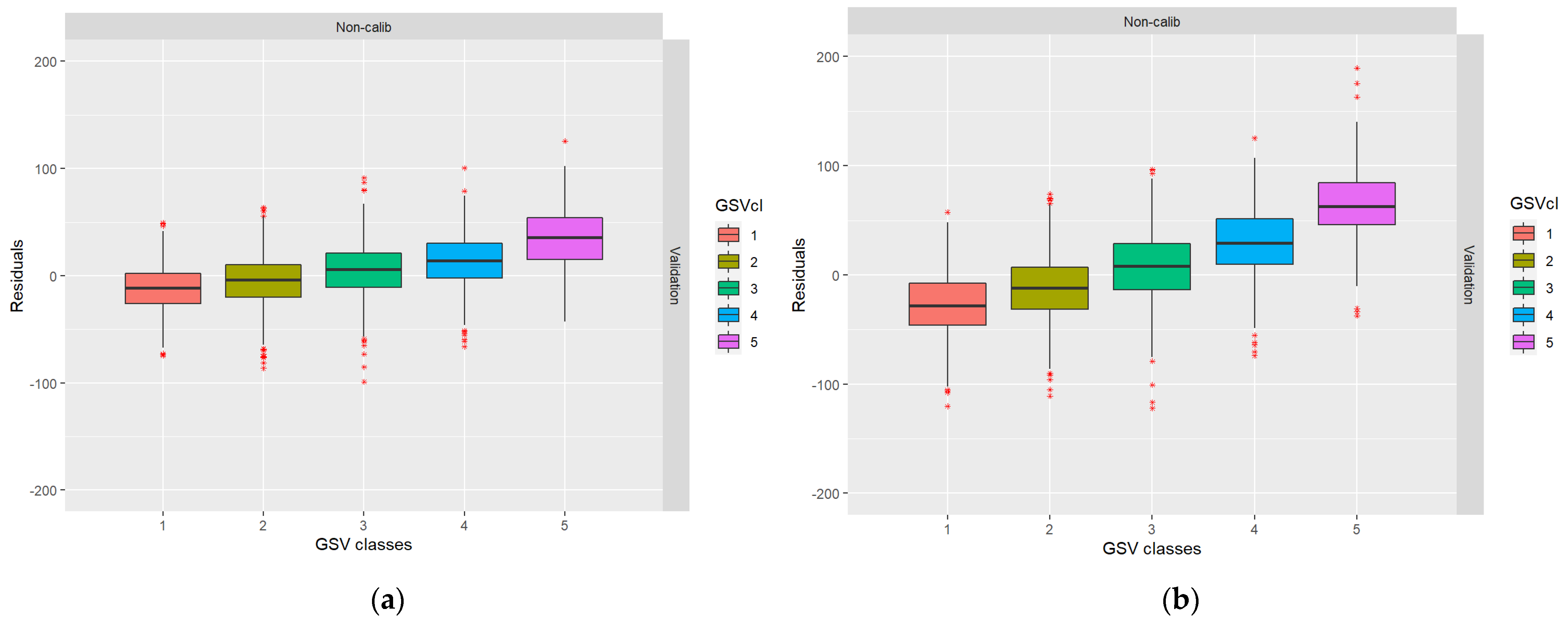
2.3. Calibration
2.4. Data Assimilation
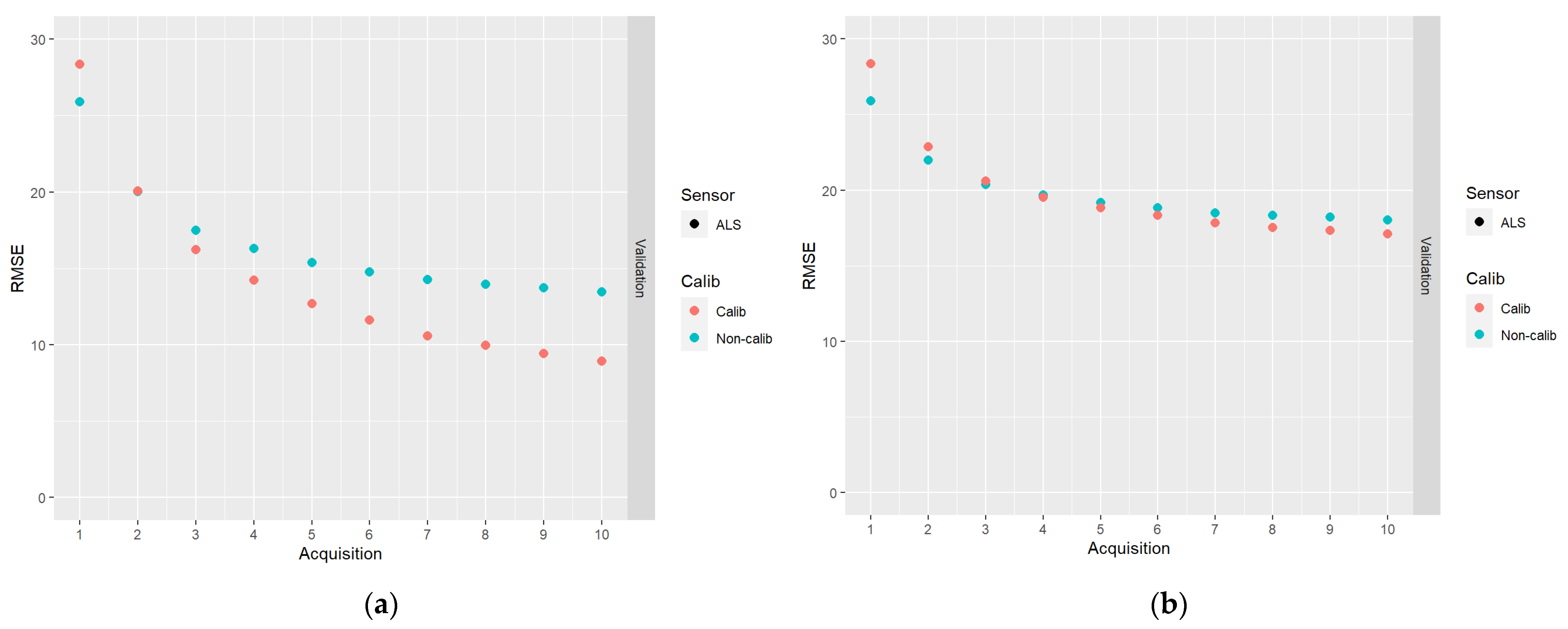
- (i)
- DA based on a series of 10 ALS-based predictions, using data with and without correlation between model residual errors in Equation (1).
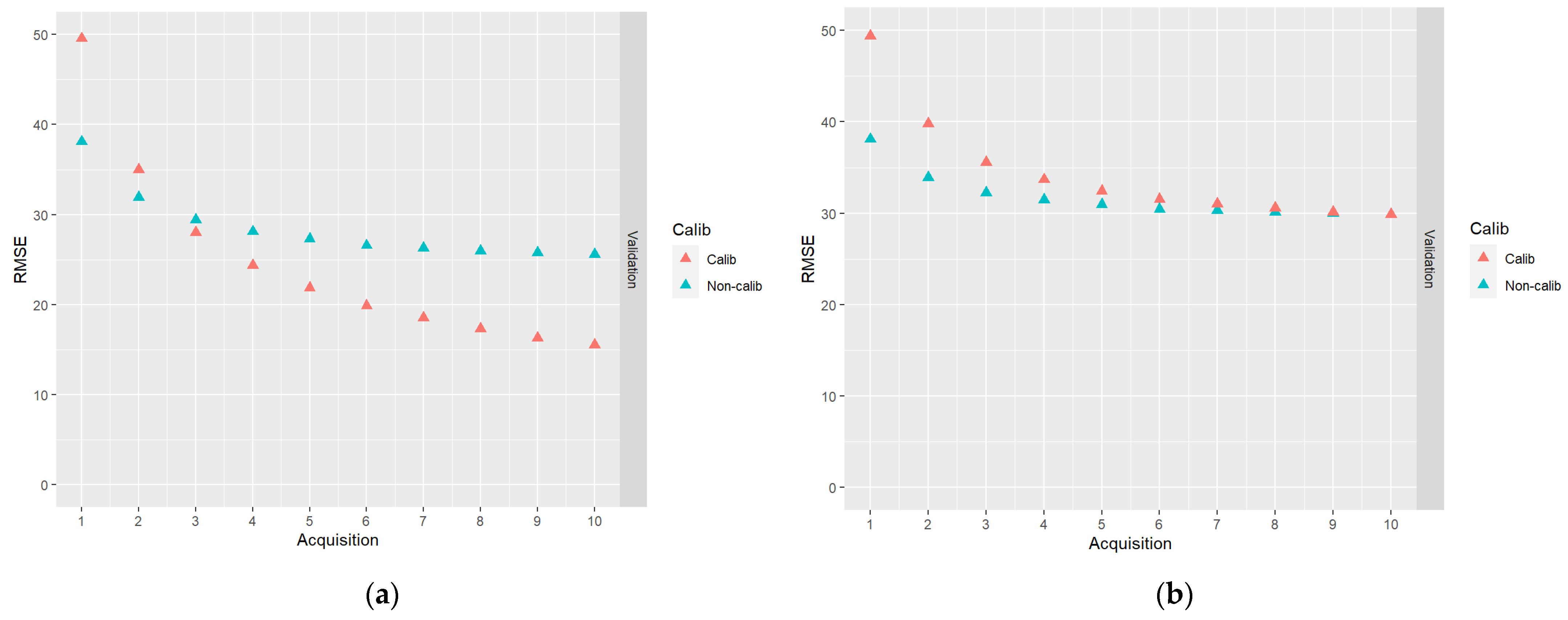
- (ii)
- DA based on a series of 10 DP-based predictions, using data with and without correlation between model residual errors in Equation (1).
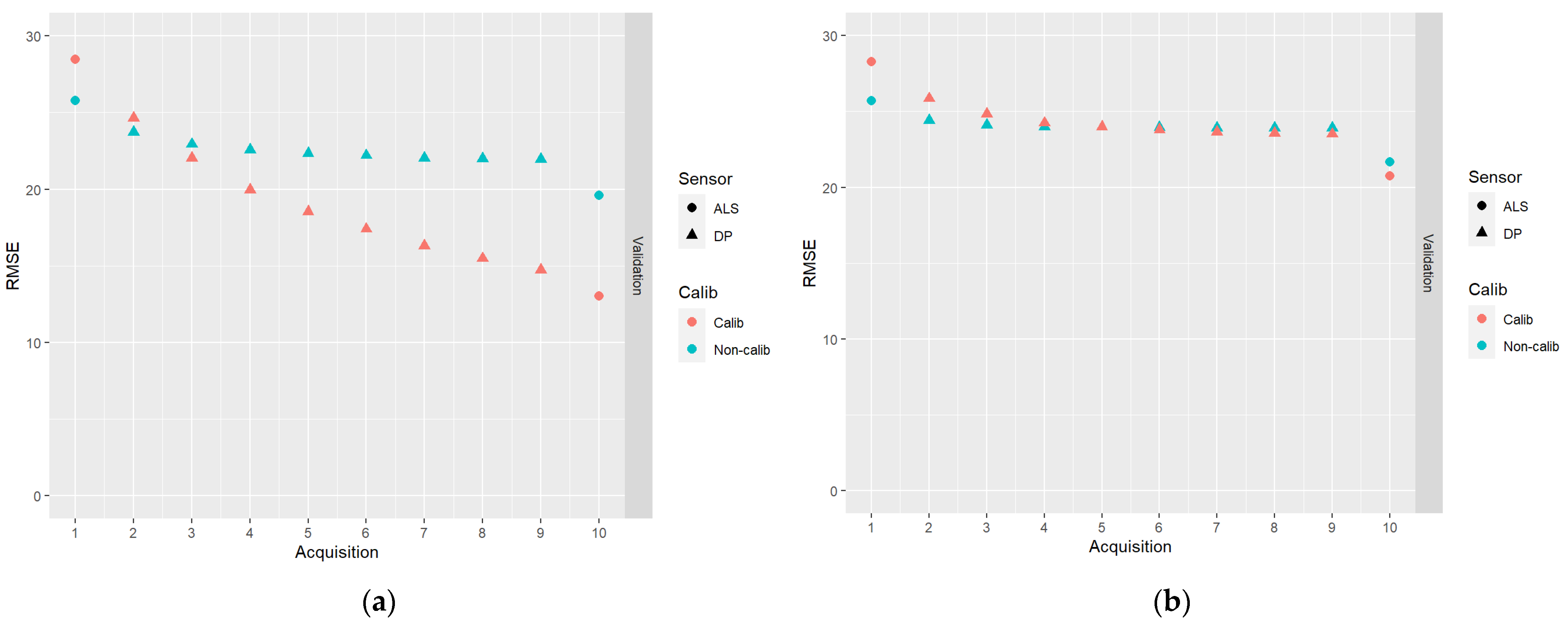
- (iii)
- DA based on a first ALS-based prediction, followed by a series of eight DP-based predictions, and ending with an ALS-based prediction, using data with and without model residual errors in Equation (1).
3. Results
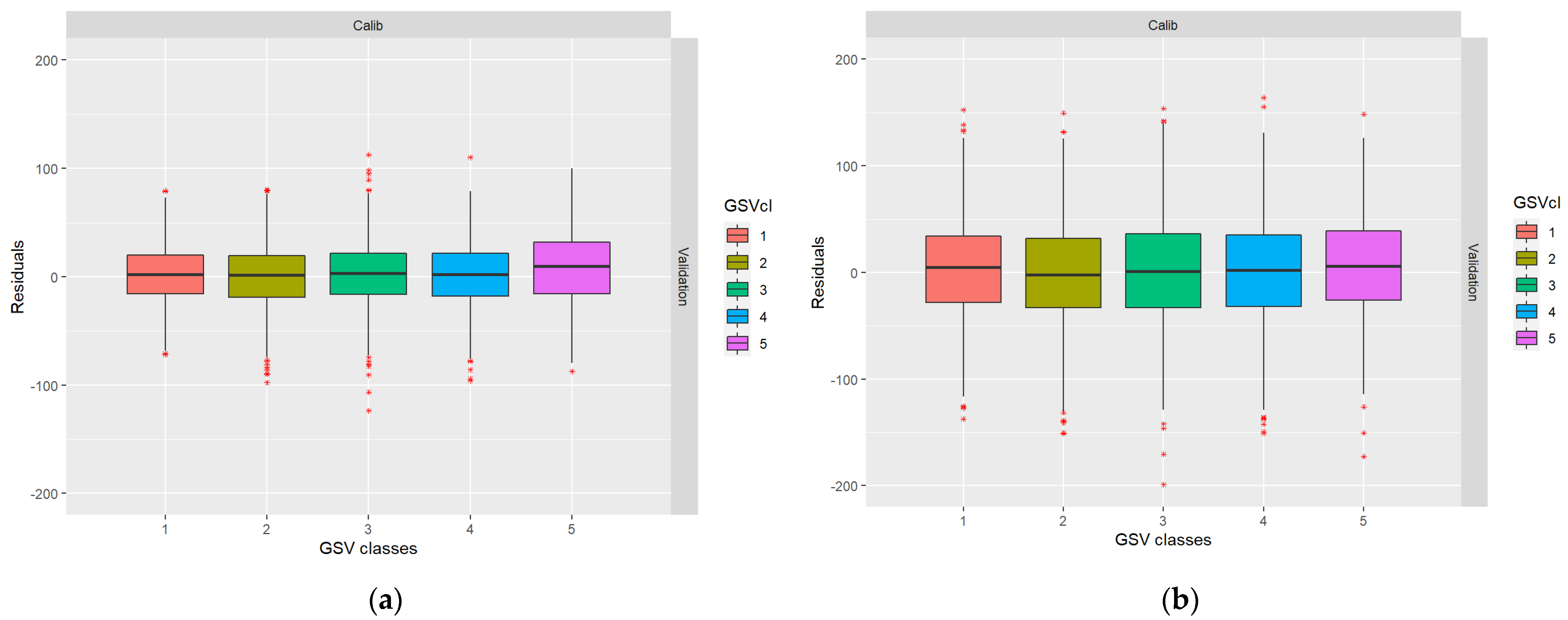
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ghil, M.; Malanotte-Rizzoli, P. Data Assimilation in Meteorology and Oceanography. In Advances in Geophysics; Elsevier: Amsterdam, The Netherlands, 1991; Volume 33, pp. 141–266. ISBN 978-0-12-018833-8. [Google Scholar]
- Rabier, F. Overview of Global Data Assimilation Developments in Numerical Weather-Prediction Centres. Q. J. R. Meteorol. Soc. 2005, 131, 3215–3233. [Google Scholar] [CrossRef]
- Dowd, M. Bayesian Statistical Data Assimilation for Ecosystem Models Using Markov Chain Monte Carlo. J. Mar. Syst. 2007, 68, 439–456. [Google Scholar] [CrossRef]
- Dixon, B.L.; Howitt, R.E. Continuous Forest Inventory Using a Linear Filter. For. Sci. 1979, 25, 675–689. [Google Scholar] [CrossRef]
- Czaplewski, R.L.; Alig, R.J.; Cost, N.D. Monitoring Land/Forest Cover Using the Kalman Filter: A Proposal. In Ek, Alan R.; Shifley, Stephen R.; Burk, Thomas E. Forest Growth Modelling and Prediction: Volume 2. Gen. Tech. Report NC-120; US Deptartment of Agriculture, Forest Service, North Central Forest Experiment Station: St. Paul, MN, USA, 1988; pp. 1089–1096. [Google Scholar]
- Kangas, A. Updated Measurement Data as Prior Information in Forest Inventory. Silva Fenn. 1991, 25, 181–191. [Google Scholar] [CrossRef]
- Kalman, R.E. A New Approach to Linear Filtering and Prediction Problems. J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef]
- Ehlers, S.; Grafström, A.; Nyström, K.; Olsson, H.; Ståhl, G. Data Assimilation in Stand-Level Forest Inventories. Can. J. For. Res. 2013, 43, 1104–1113. [Google Scholar] [CrossRef]
- Saad, R.; Eyvindson, K.; Gong, P.; Lämås, T.; Ståhl, G. Potential of Using Data Assimilation to Support Forest Planning. Can. J. For. Res. 2017, 47, 690–695. [Google Scholar] [CrossRef][Green Version]
- Nyström, M.; Lindgren, N.; Wallerman, J.; Grafström, A.; Muszta, A.; Nyström, K.; Bohlin, J.; Willén, E.; Fransson, J.; Ehlers, S.; et al. Data Assimilation in Forest Inventory: First Empirical Results. Forests 2015, 6, 4540–4557. [Google Scholar] [CrossRef]
- Lindgren, N.; Persson, H.J.; Nyström, M.; Nyström, K.; Grafström, A.; Muszta, A.; Willén, E.; Fransson, J.E.S.; Ståhl, G.; Olsson, H. Improved Prediction of Forest Variables Using Data Assimilation of Interferometric Synthetic Aperture Radar Data. Can. J. Remote Sens. 2017, 43, 374–383. [Google Scholar] [CrossRef]
- Ehlers, S.; Saarela, S.; Lindgren, N.; Lindberg, E.; Nyström, M.; Persson, H.; Olsson, H.; Ståhl, G. Assessing Error Correlations in Remote Sensing-Based Estimates of Forest Attributes for Improved Composite Estimation. Remote Sens. 2018, 10, 667. [Google Scholar] [CrossRef]
- Lindgren, N.; Olsson, H.; Nyström, K.; Nyström, M.; Ståhl, G. Data Assimilation of Growing Stock Volume Using a Sequence of Remote Sensing Data from Different Sensors. Can. J. Remote Sens. 2022, 48, 127–143. [Google Scholar] [CrossRef]
- Hou, Z.; Mehtätalo, L.; McRoberts, R.E.; Ståhl, G.; Tokola, T.; Rana, P.; Siipilehto, J.; Xu, Q. Remote Sensing-Assisted Data Assimilation and Simultaneous Inference for Forest Inventory. Remote Sens. Environ. 2019, 234, 111431. [Google Scholar] [CrossRef]
- Wallerman, J.; Holmgren, J. Estimating Field-Plot Data of Forest Stands Using Airborne Laser Scanning and SPOT HRG Data. Remote Sens. Environ. 2007, 110, 501–508. [Google Scholar] [CrossRef]
- Rahlf, J.; Breidenbach, J.; Solberg, S.; Næsset, E.; Astrup, R. Comparison of Four Types of 3D Data for Timber Volume Estimation. Remote Sens. Environ. 2014, 155, 325–333. [Google Scholar] [CrossRef]
- Yu, X.; Hyyppä, J.; Karjalainen, M.; Nurminen, K.; Karila, K.; Vastaranta, M.; Kankare, V.; Kaartinen, H.; Holopainen, M.; Honkavaara, E.; et al. Comparison of Laser and Stereo Optical, SAR and InSAR Point Clouds from Air- and Space-Borne Sources in the Retrieval of Forest Inventory Attributes. Remote Sens. 2015, 7, 15933–15954. [Google Scholar] [CrossRef]
- Tellinghuisen, J. Inverse vs. Classical Calibration for Small Data Sets. Fresenius J. Anal. Chem. 2000, 368, 585–588. [Google Scholar] [CrossRef] [PubMed]
- Persson, H.J.; Ståhl, G. Characterizing Uncertainty in Forest Remote Sensing Studies. Remote Sens. 2020, 12, 505. [Google Scholar] [CrossRef]
- Reese, H.; Nilsson, M.; Pahlén, T.G.; Hagner, O.; Joyce, S.; Tingelöf, U.; Egberth, M.; Olsson, H. Countrywide Estimates of Forest Variables Using Satellite Data and Field Data from the National Forest Inventory. AMBIO J. Hum. Environ. 2003, 32, 542–548. [Google Scholar] [CrossRef]
- Tomppo, E.; Olsson, H.; Ståhl, G.; Nilsson, M.; Hagner, O.; Katila, M. Combining National Forest Inventory Field Plots and Remote Sensing Data for Forest Databases. Remote Sens. Environ. 2008, 112, 1982–1999. [Google Scholar] [CrossRef]
- Næsset, E. Predicting Forest Stand Characteristics with Airborne Scanning Laser Using a Practical Two-Stage Procedure and Field Data. Remote Sens. Environ. 2002, 80, 88–99. [Google Scholar] [CrossRef]
- Næsset, E.; Gobakken, T.; Holmgren, J.; Hyyppä, H.; Hyyppä, J.; Maltamo, M.; Nilsson, M.; Olsson, H.; Persson, Å.; Söderman, U. Laser Scanning of Forest Resources: The Nordic Experience. Scand. J. For. Res. 2004, 19, 482–499. [Google Scholar] [CrossRef]
- Nilsson, M.; Nordkvist, K.; Jonzén, J.; Lindgren, N.; Axensten, P.; Wallerman, J.; Egberth, M.; Larsson, S.; Nilsson, L.; Eriksson, J.; et al. A Nationwide Forest Attribute Map of Sweden Predicted Using Airborne Laser Scanning Data and Field Data from the National Forest Inventory. Remote Sens. Environ. 2017, 194, 447–454. [Google Scholar] [CrossRef]
- Weisberg, S. Applied Linear Regression; John Wiley & Sons: Hoboken, NJ, USA, 2005; Volume 528, ISBN 0-471-70408-3. [Google Scholar]
- Eisenhart, C. The Interpretation of Certain Regression Methods and Their Use in Biological and Industrial Research. Ann. Math. Stat. 1939, 10, 162–186. [Google Scholar] [CrossRef]
- Osborne, C. Statistical Calibration: A Review. Int. Stat. Rev. Rev. Int. Stat. 1991, 59, 309. [Google Scholar] [CrossRef]
- Fridman, J.; Holm, S.; Nilsson, M.; Nilsson, P.; Ringvall, A.; Ståhl, G. Adapting National Forest Inventories to Changing Requirements—The Case of the Swedish National Forest Inventory at the Turn of the 20th Century. Silva Fenn. 2014, 48, 1095. [Google Scholar] [CrossRef]
- Chen, Q.; McRoberts, R.E.; Wang, C.; Radtke, P.J. Forest Aboveground Biomass Mapping and Estimation across Multiple Spatial Scales Using Model-Based Inference. Remote Sens. Environ. 2016, 184, 350–360. [Google Scholar] [CrossRef]
- Boucher, A.; Dimitrakopoulos, R. Block Simulation of Multiple Correlated Variables. Math. Geosci. 2009, 41, 215–237. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2022; Available online: https://www.R-project.org/ (accessed on 3 September 2022).
- Tian, Y.; Nearing, G.S.; Peters-Lidard, C.D.; Harrison, K.W.; Tang, L. Performance Metrics, Error Modeling, and Uncertainty Quantification. Mon. Weather Rev. 2016, 144, 607–613. [Google Scholar] [CrossRef]
- Hibbert, D.B.; Gooding, J.J. Data Analysis for Chemistry: An Introductory Guide for Students and Laboratory Scientists; Oxford University Press: New York, NY, USA, 2006; ISBN 0-19-516210-2. [Google Scholar]
- Grafström, A.; Ekström, M.; Jonsson, B.G.; Esseen, P.-A.; Ståhl, G. On Combining Independent Probability Samples. Surv. Methodol. 2019, 45, 349–364. [Google Scholar]
- Saarela, S.; Grafström, A. DatAssim: Data Assimilation; R Package Version 1.0. 2017. Available online: https://cran.r-project.org/package=DatAssim (accessed on 3 September 2022).
- Krutchkoff, R.G. Classical and Inverse Regression Methods of Calibration. Technometrics 1967, 9, 425–439. [Google Scholar] [CrossRef]
- Barth, A.; Lind, T.; Ståhl, G. Restricted Imputation for Improving Spatial Consistency in Landscape Level Data for Forest Scenario Analysis. For. Ecol. Manag. 2012, 272, 61–68. [Google Scholar] [CrossRef]
| Parameter | ALS | DP |
|---|---|---|
| 50.00 | 150.00 | |
| 3.40 | 2.90 | |
| 0.80 | 0.80 | |
| 28.33 | 41.47 |
| Sensor | Correlation | |
|---|---|---|
| Case I | Case II | |
| ALS | 0 | 0.30 |
| DP | 0 | 0.30 |
| Between ALS and DP | 0 | 0.15 |
| Parameter | Estimate | p-Value |
|---|---|---|
| —ALS | −6.24 | 2.56 × 10−8 |
| —ALS | 0.17 | <2.00 × 10−16 |
| —DP | −26.36 | <2.00 × 10−16 |
| —DP | 0.14 | <2.00 × 10−16 |
| Sensor | % RMSE | Correlation |
|---|---|---|
| ALS—case I | 17.02 | 0.18 |
| ALS—case II | 16.99 | 0.42 |
| DP—case I | 25.28 | 0.41 |
| DP—case II | 25.37 | 0.59 |
| Between ALS and DP—case I | -- | 0.27 |
| Between ALS and DP—case II | -- | 0.38 |
| Sensor | % RMSE | Correlation |
|---|---|---|
| ALS—case I | 18.83 | 0 |
| ALS—case II | 18.79 | 0.29 |
| DP—case I | 32.75 | 0 |
| DP—case II | 32.93 | 0.30 |
| Between ALS and DP—case I | -- | 0 |
| Between ALS and DP—case II | -- | 0.15 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lindgren, N.; Nyström, K.; Saarela, S.; Olsson, H.; Ståhl, G. Importance of Calibration for Improving the Efficiency of Data Assimilation for Predicting Forest Characteristics. Remote Sens. 2022, 14, 4627. https://doi.org/10.3390/rs14184627
Lindgren N, Nyström K, Saarela S, Olsson H, Ståhl G. Importance of Calibration for Improving the Efficiency of Data Assimilation for Predicting Forest Characteristics. Remote Sensing. 2022; 14(18):4627. https://doi.org/10.3390/rs14184627
Chicago/Turabian StyleLindgren, Nils, Kenneth Nyström, Svetlana Saarela, Håkan Olsson, and Göran Ståhl. 2022. "Importance of Calibration for Improving the Efficiency of Data Assimilation for Predicting Forest Characteristics" Remote Sensing 14, no. 18: 4627. https://doi.org/10.3390/rs14184627
APA StyleLindgren, N., Nyström, K., Saarela, S., Olsson, H., & Ståhl, G. (2022). Importance of Calibration for Improving the Efficiency of Data Assimilation for Predicting Forest Characteristics. Remote Sensing, 14(18), 4627. https://doi.org/10.3390/rs14184627







