Implementation of an Artificial Intelligence Approach to GPR Systems for Landmine Detection
Abstract
:1. Introduction
2. Statement of the Problem
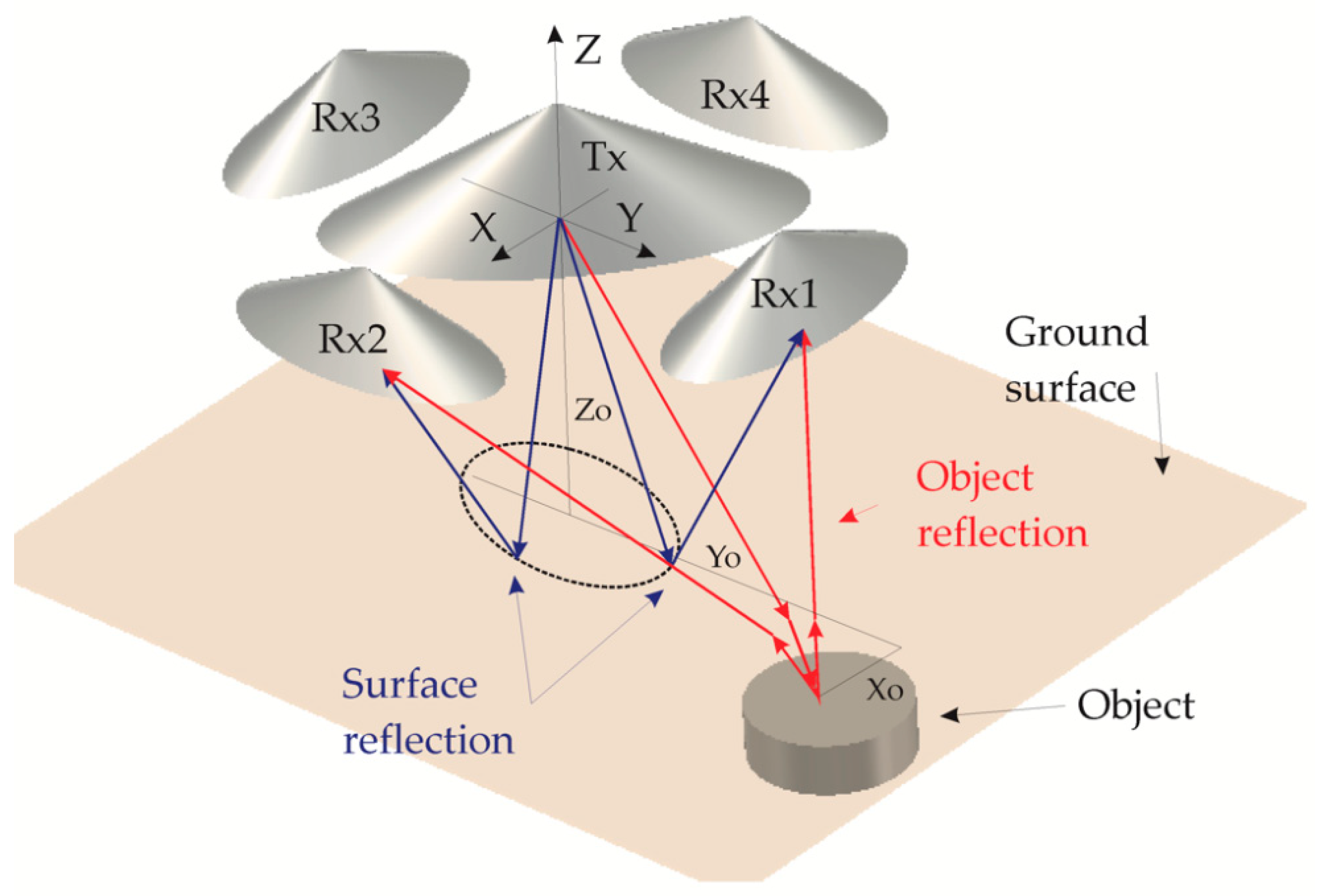
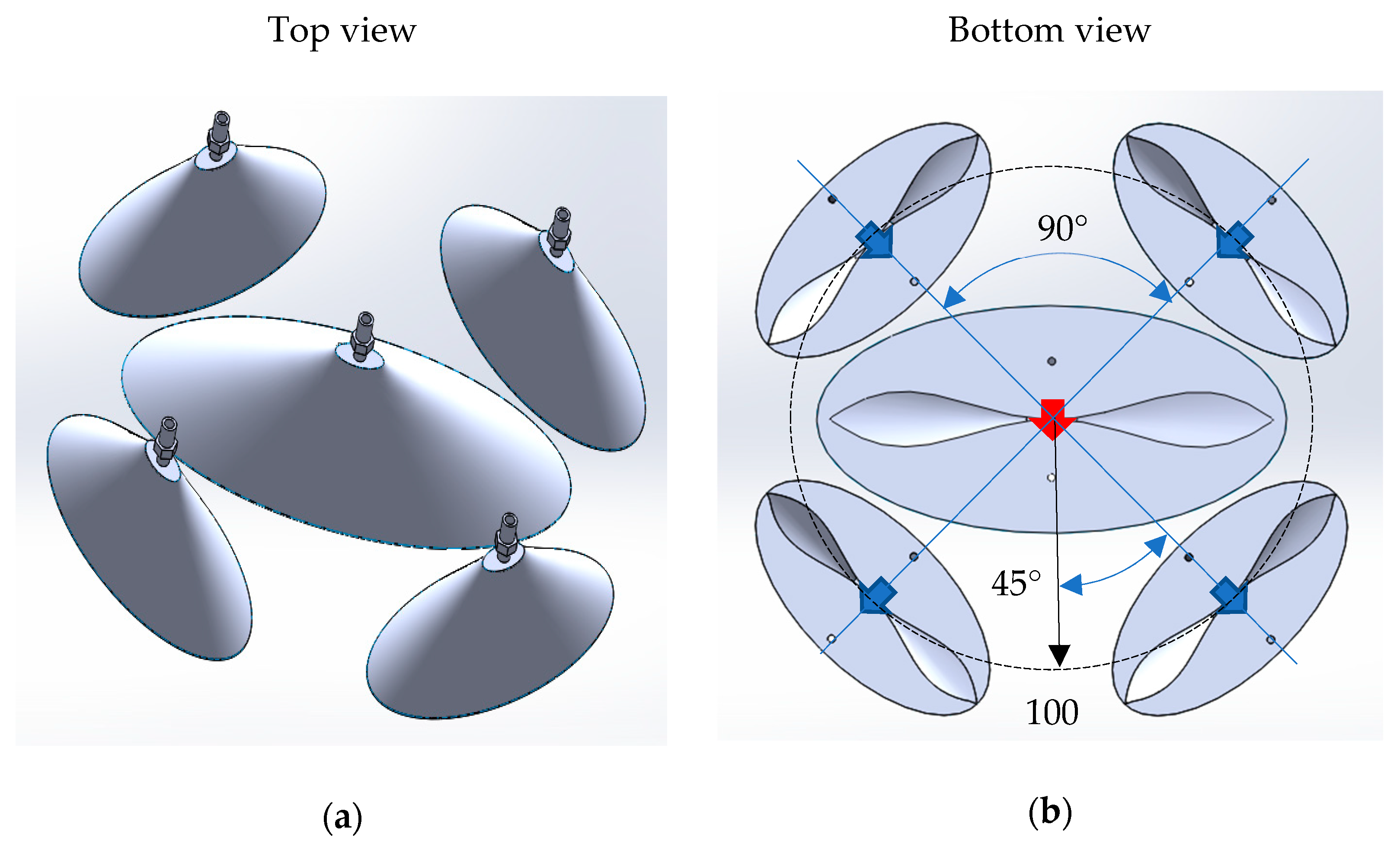
2.1. Description of the GPR and the Working Pipeline
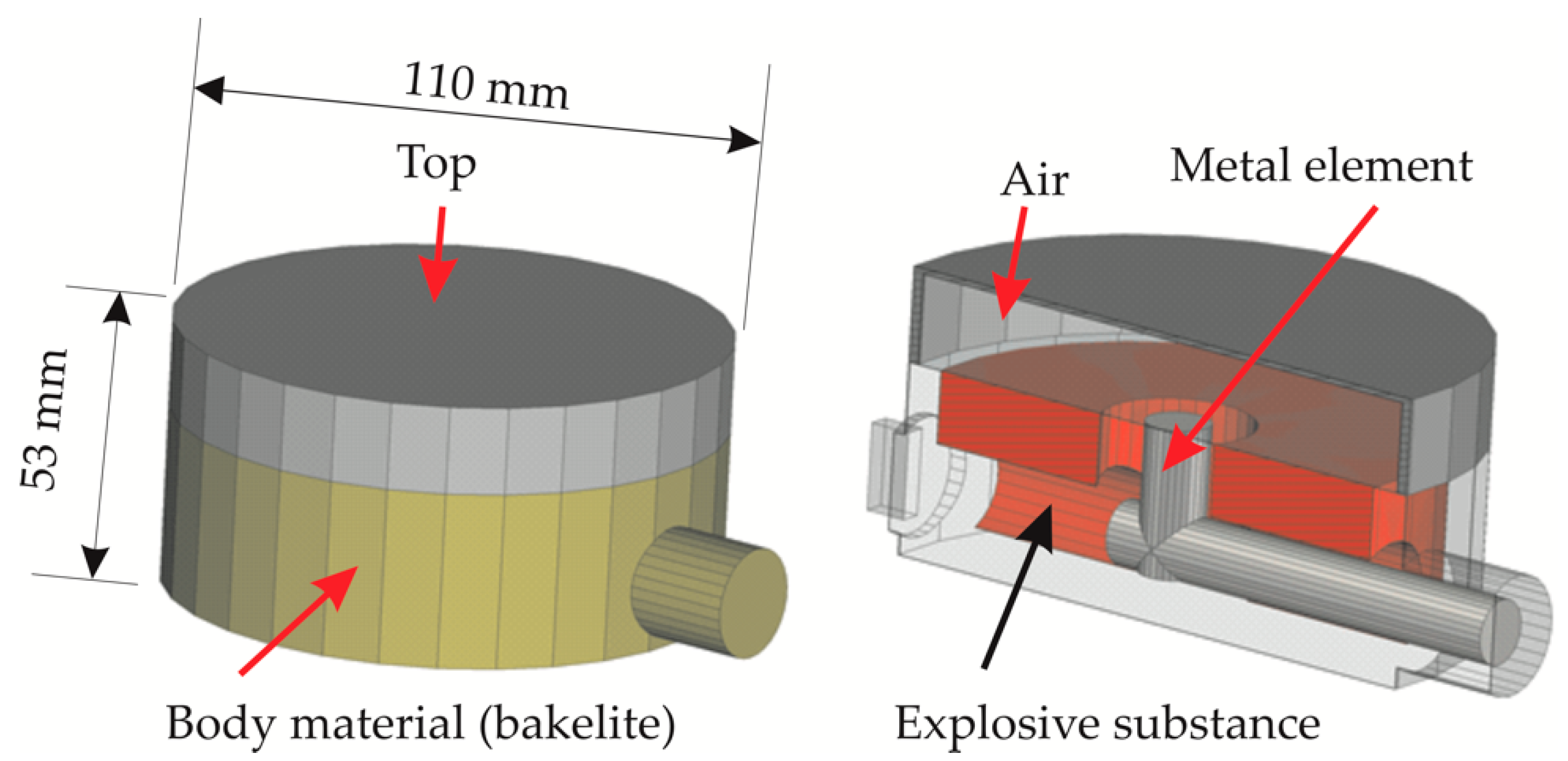
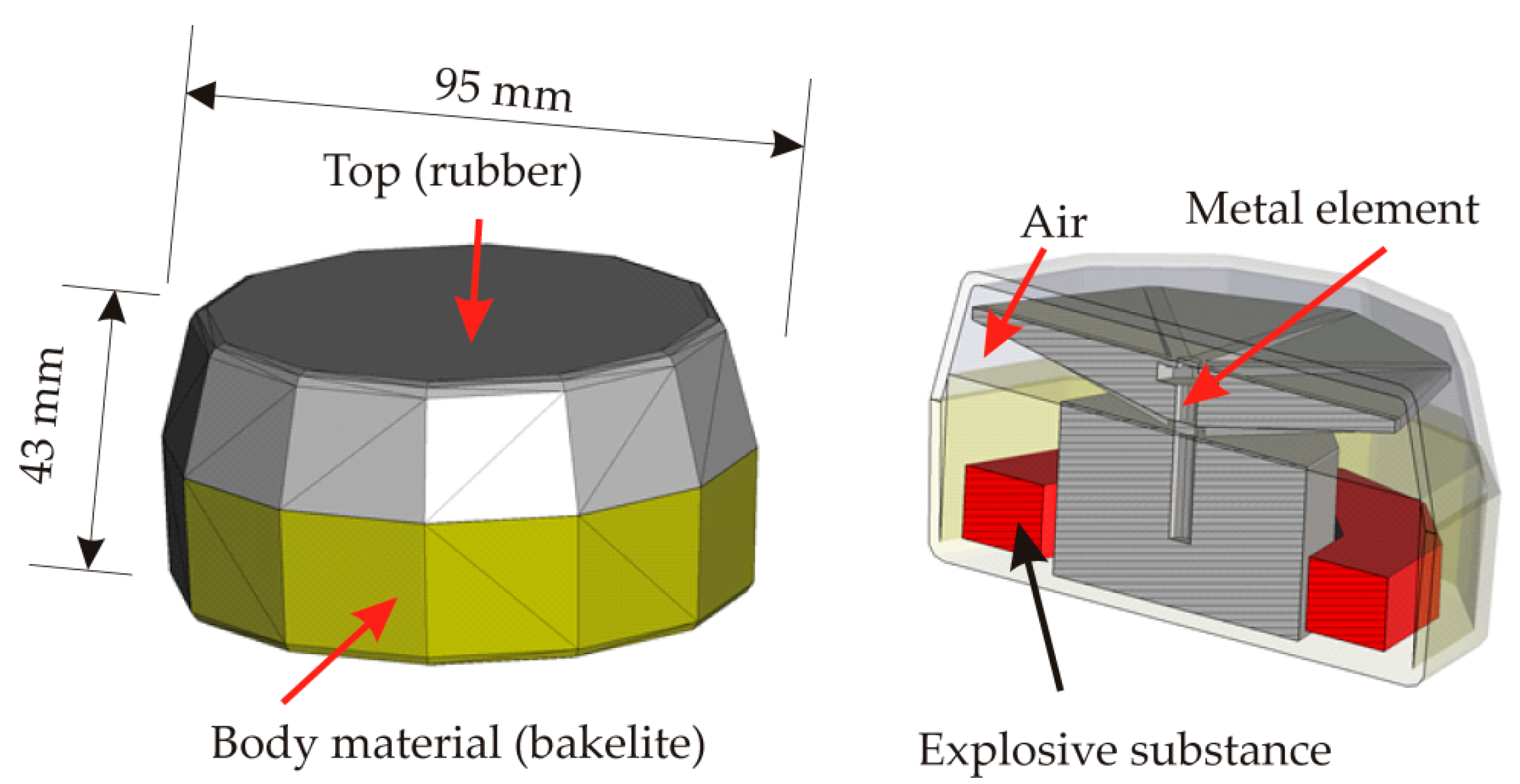
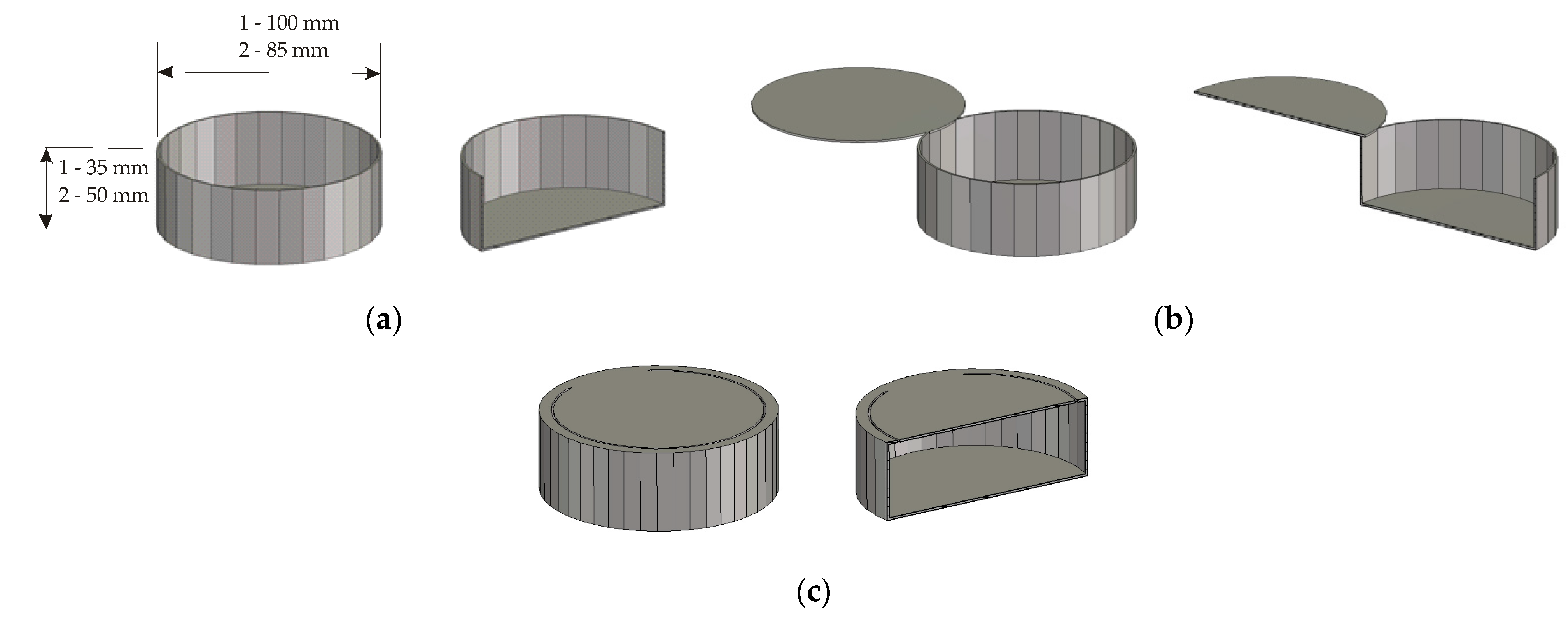
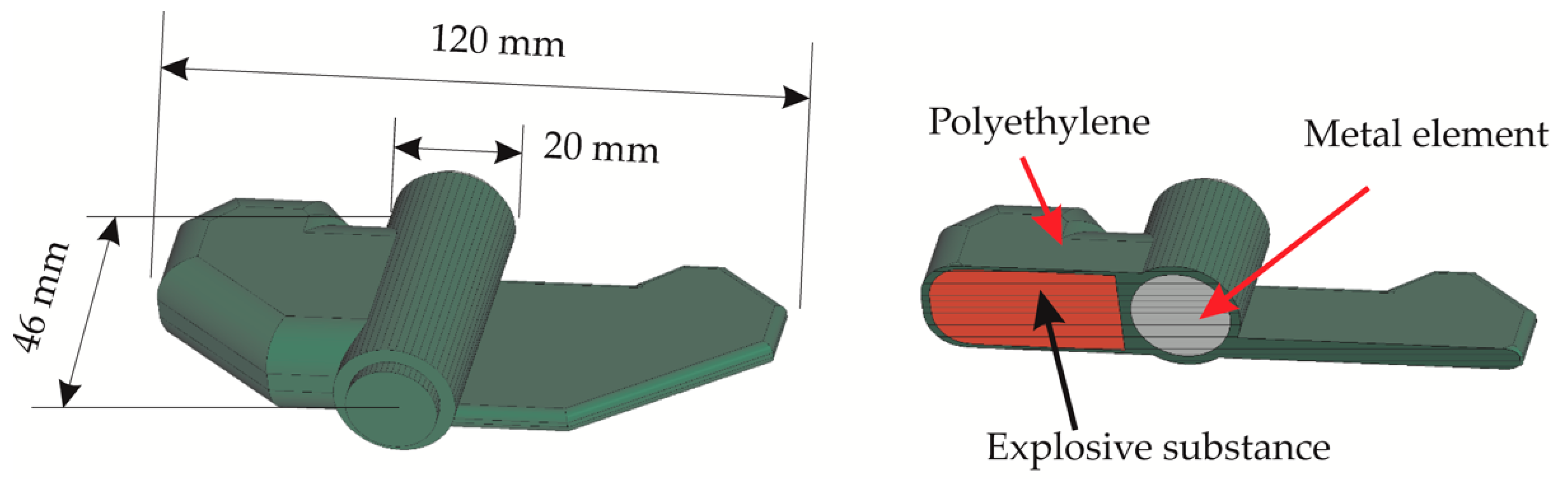
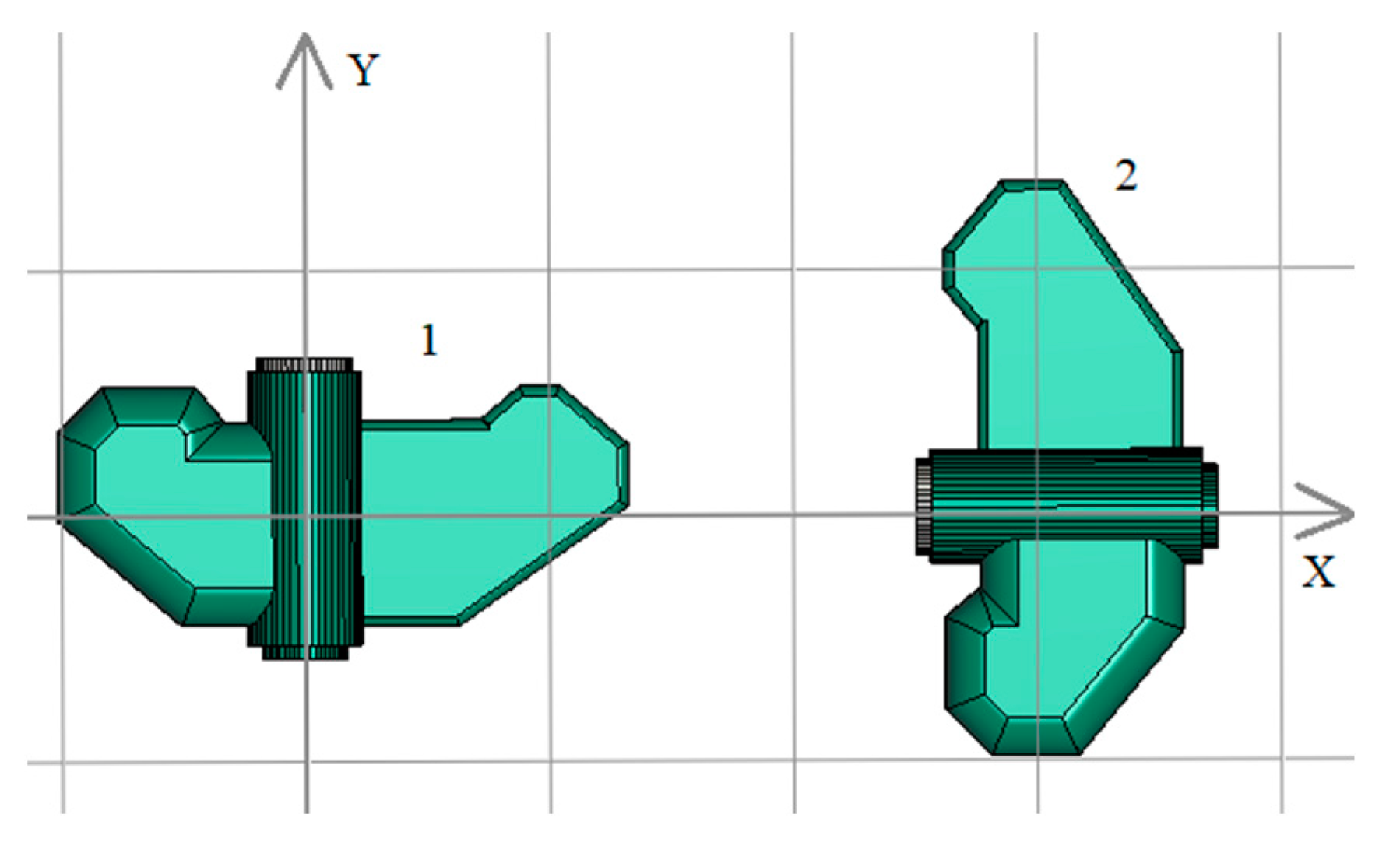
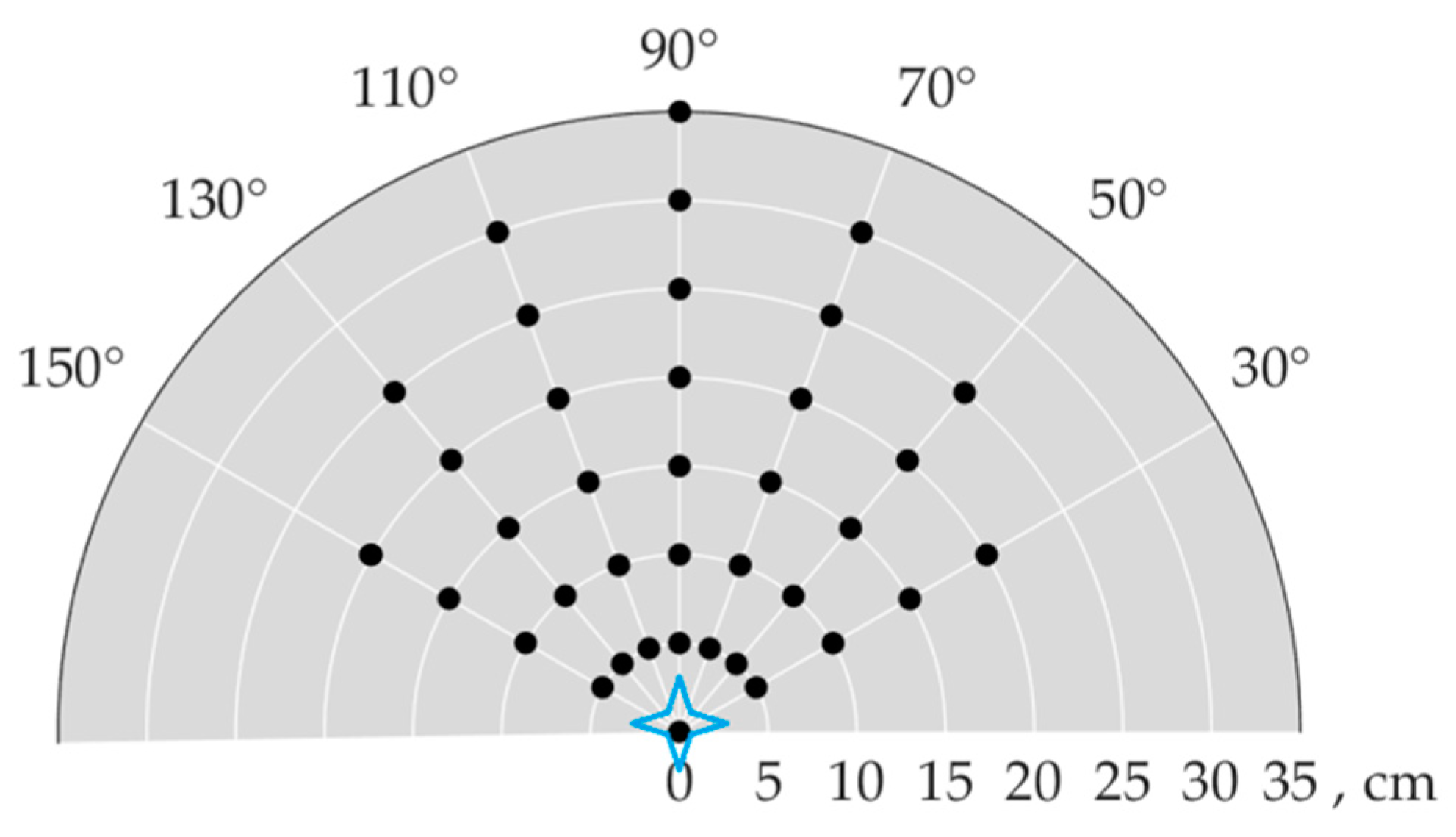
2.2. Description of Underground Objects
3. Results and Discussion
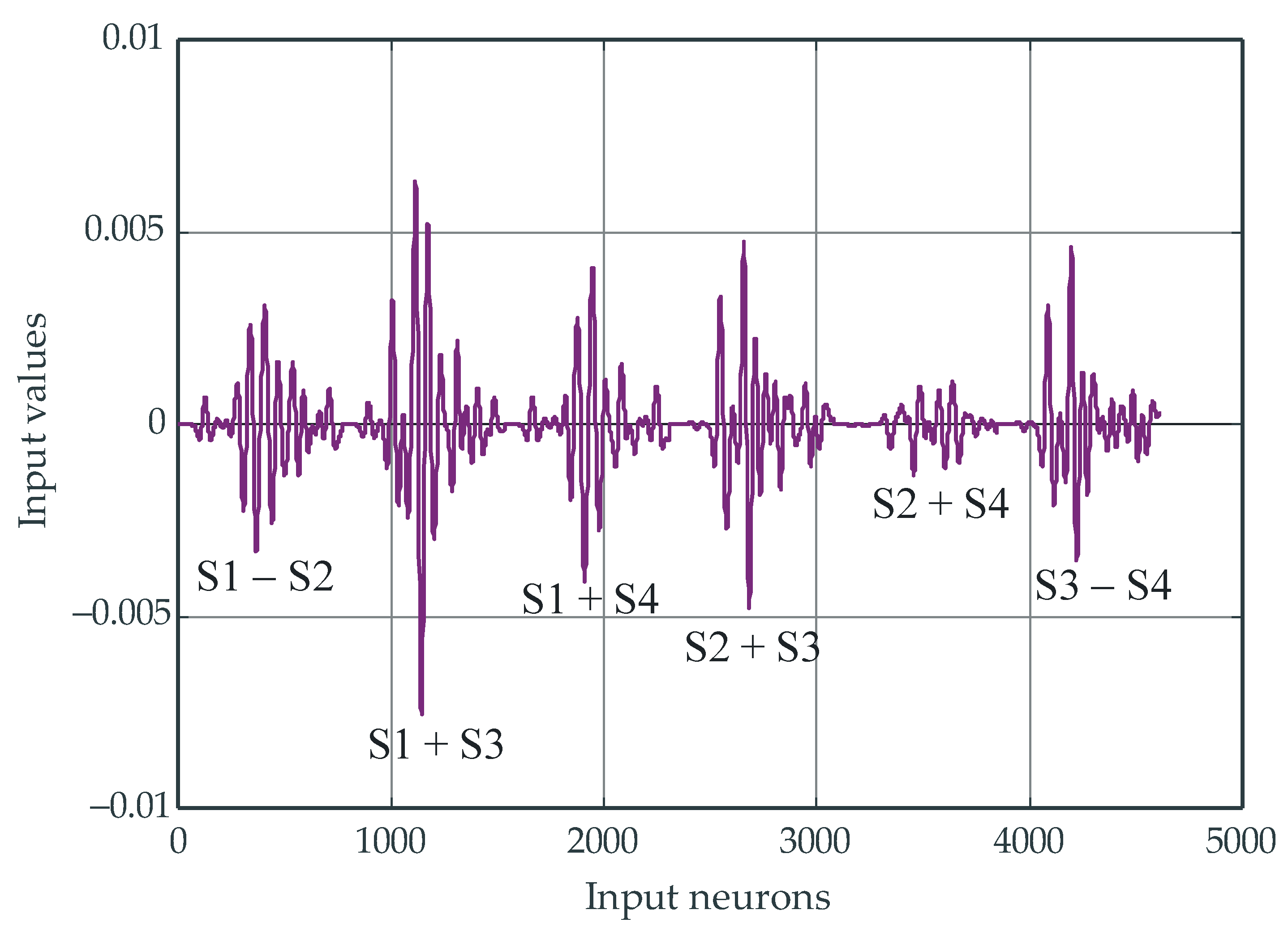
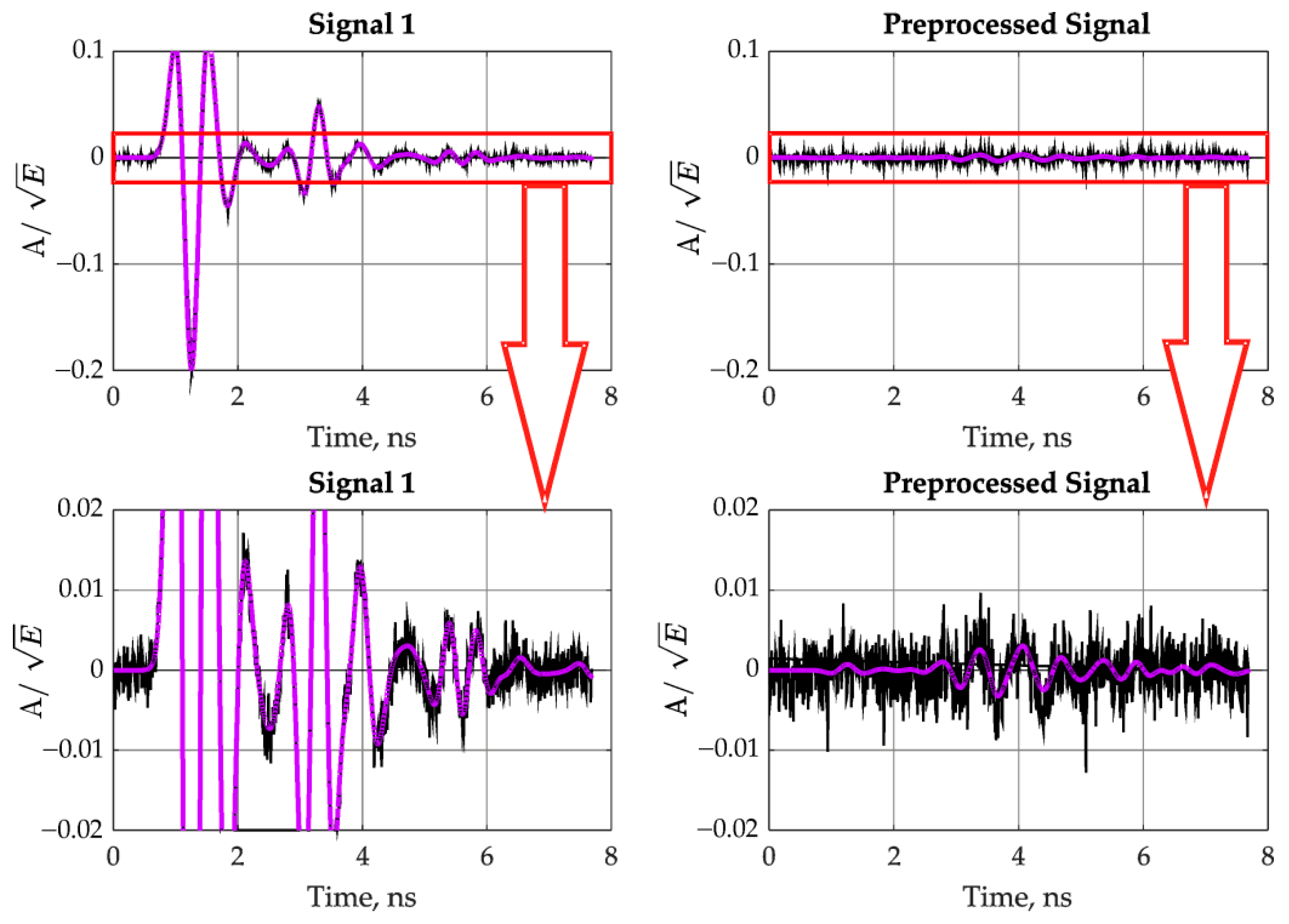
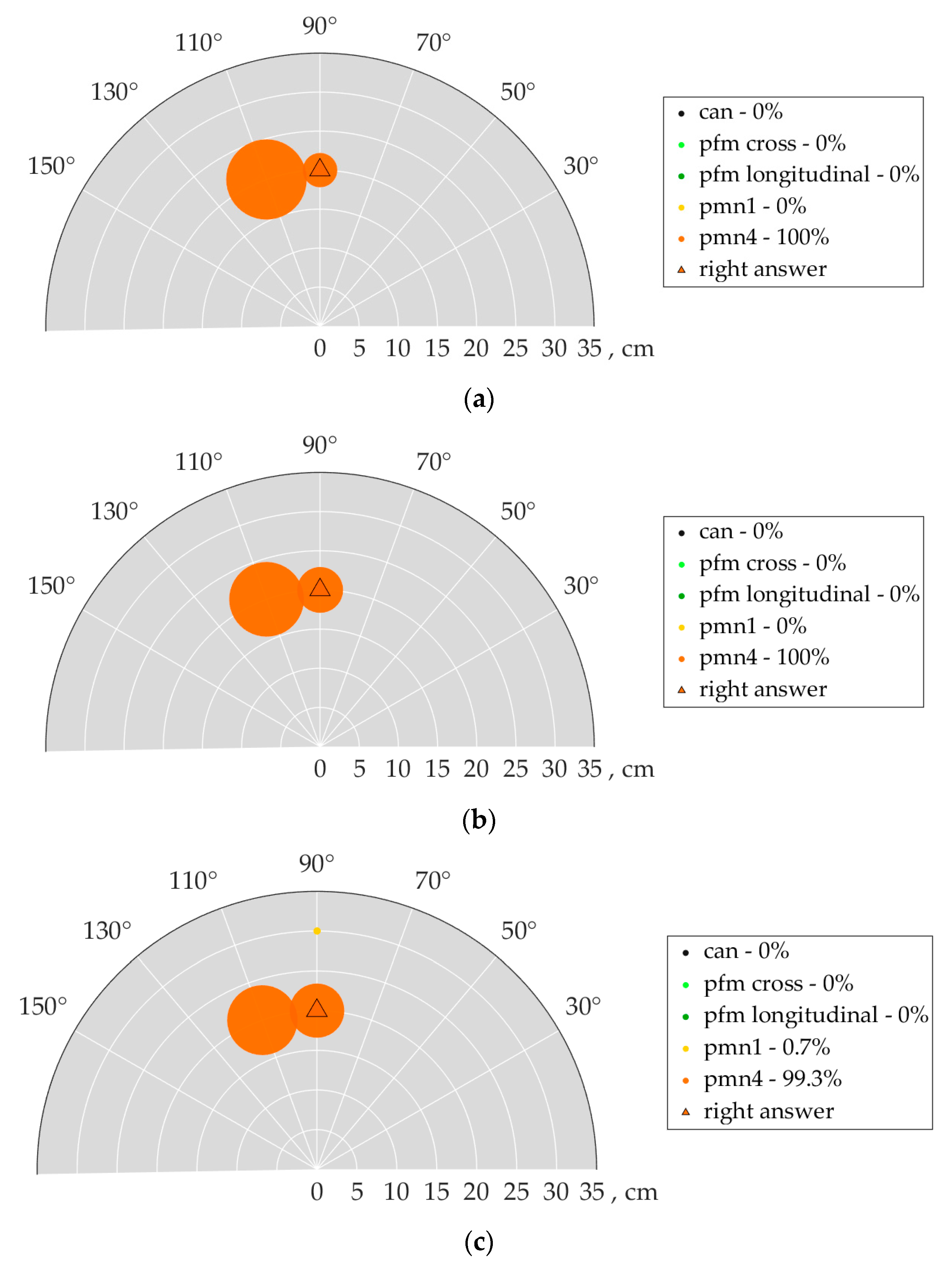
3.1. Mine Detection in Simulated Data
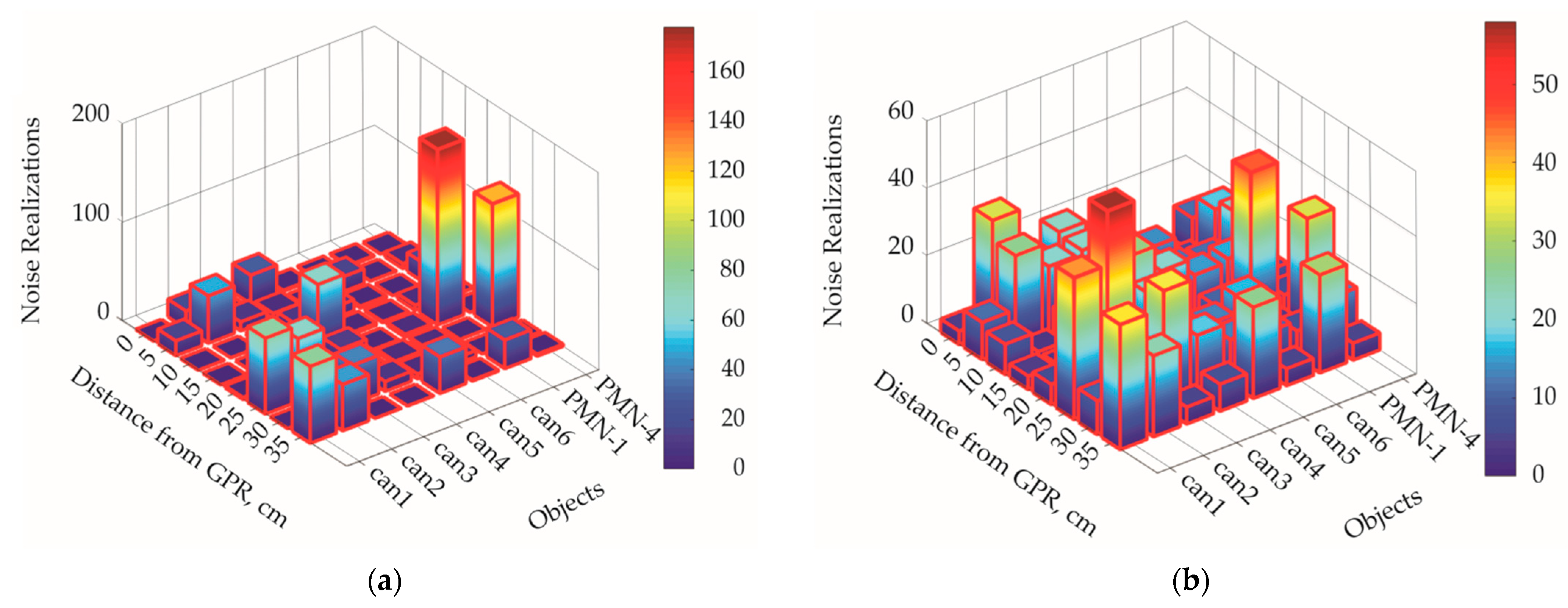
3.2. Mine Detection in Experimental Data
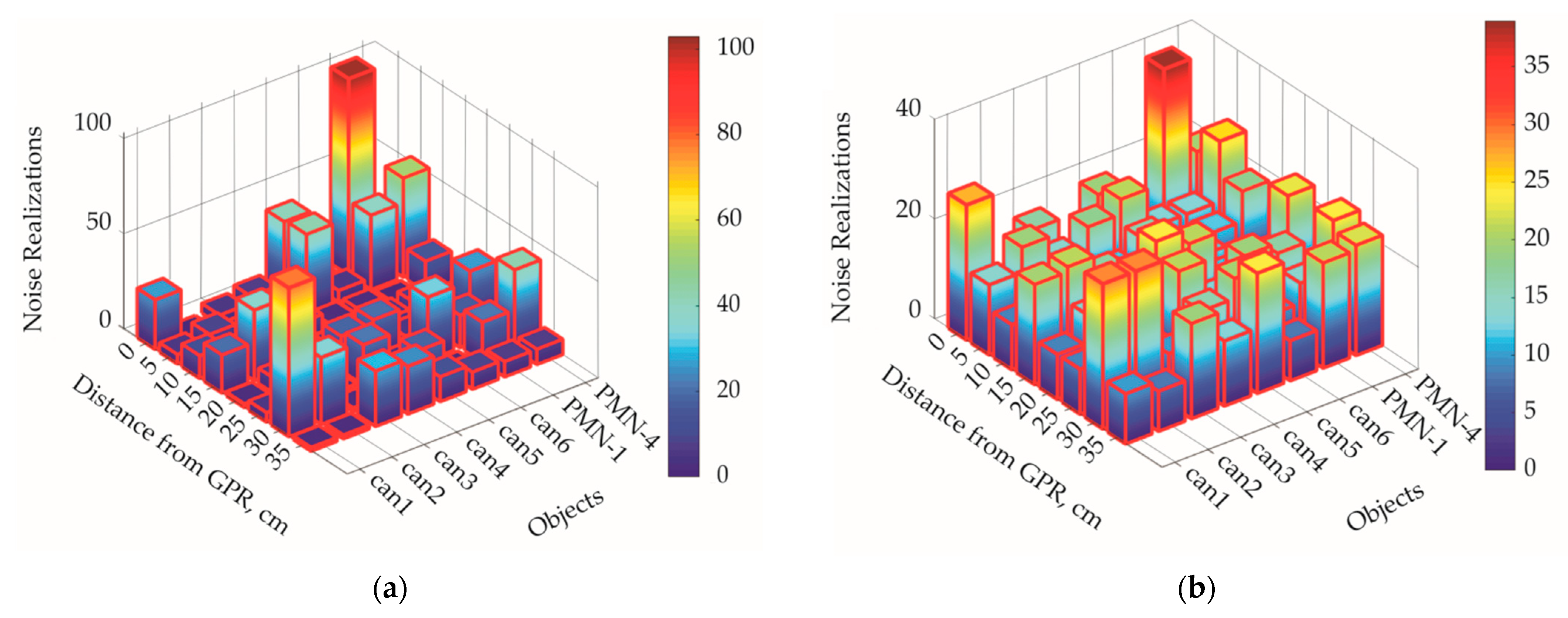
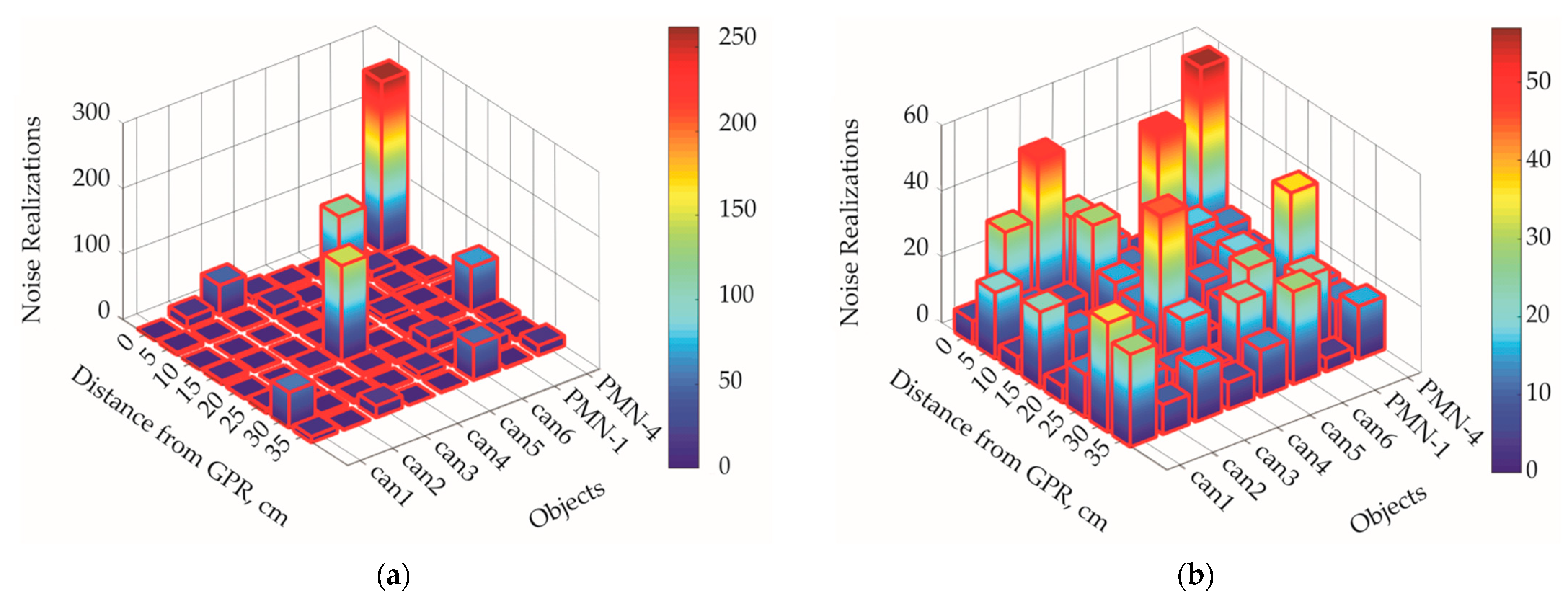
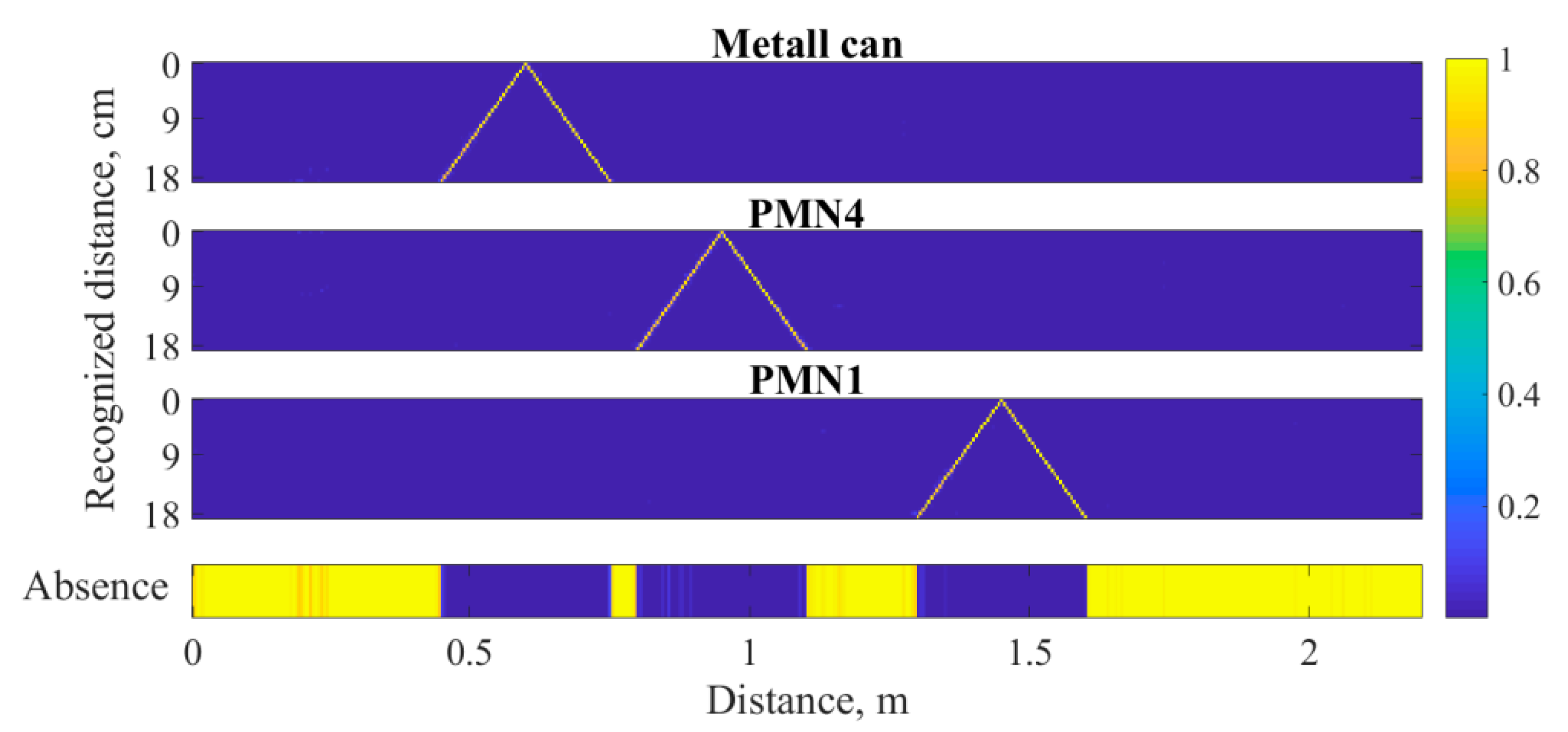
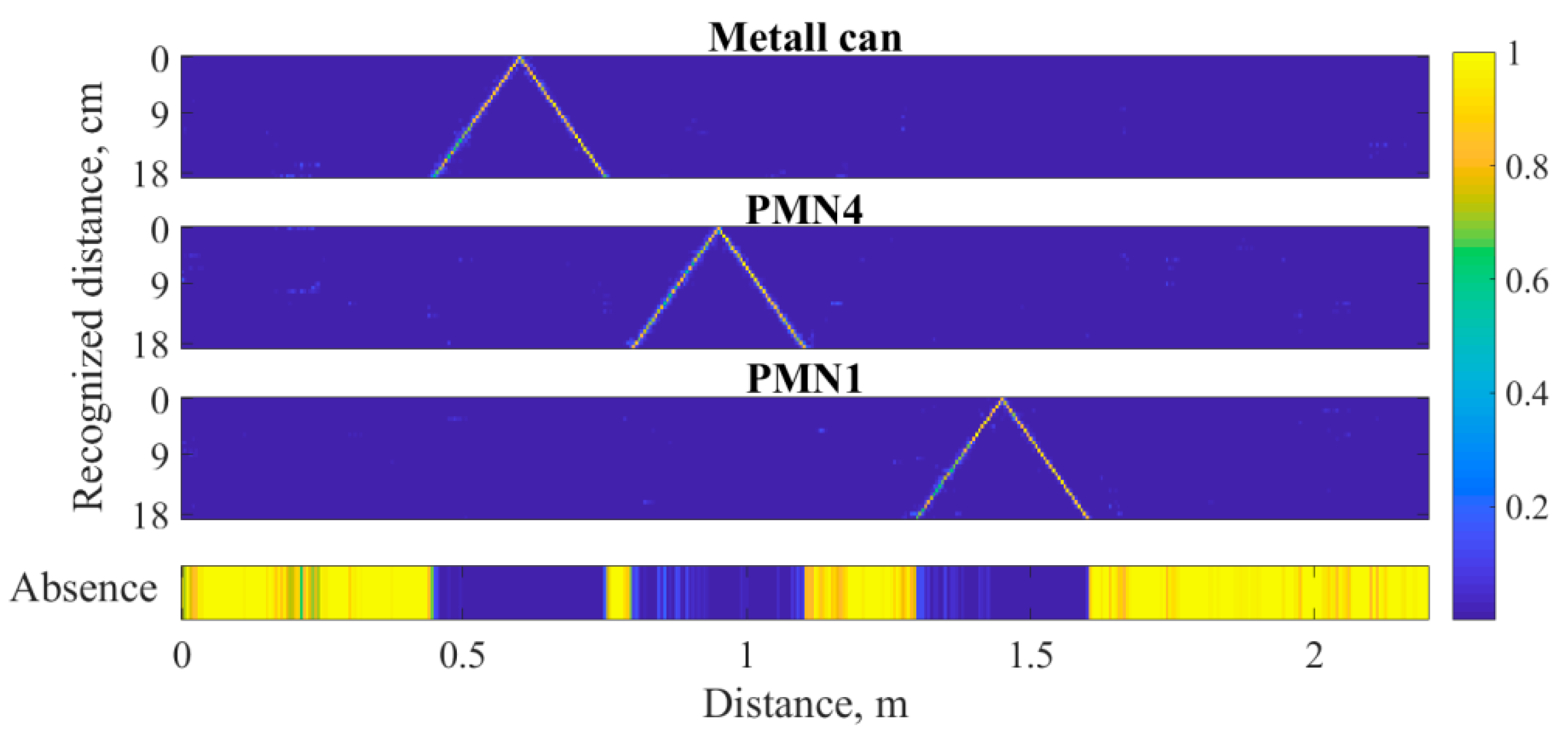
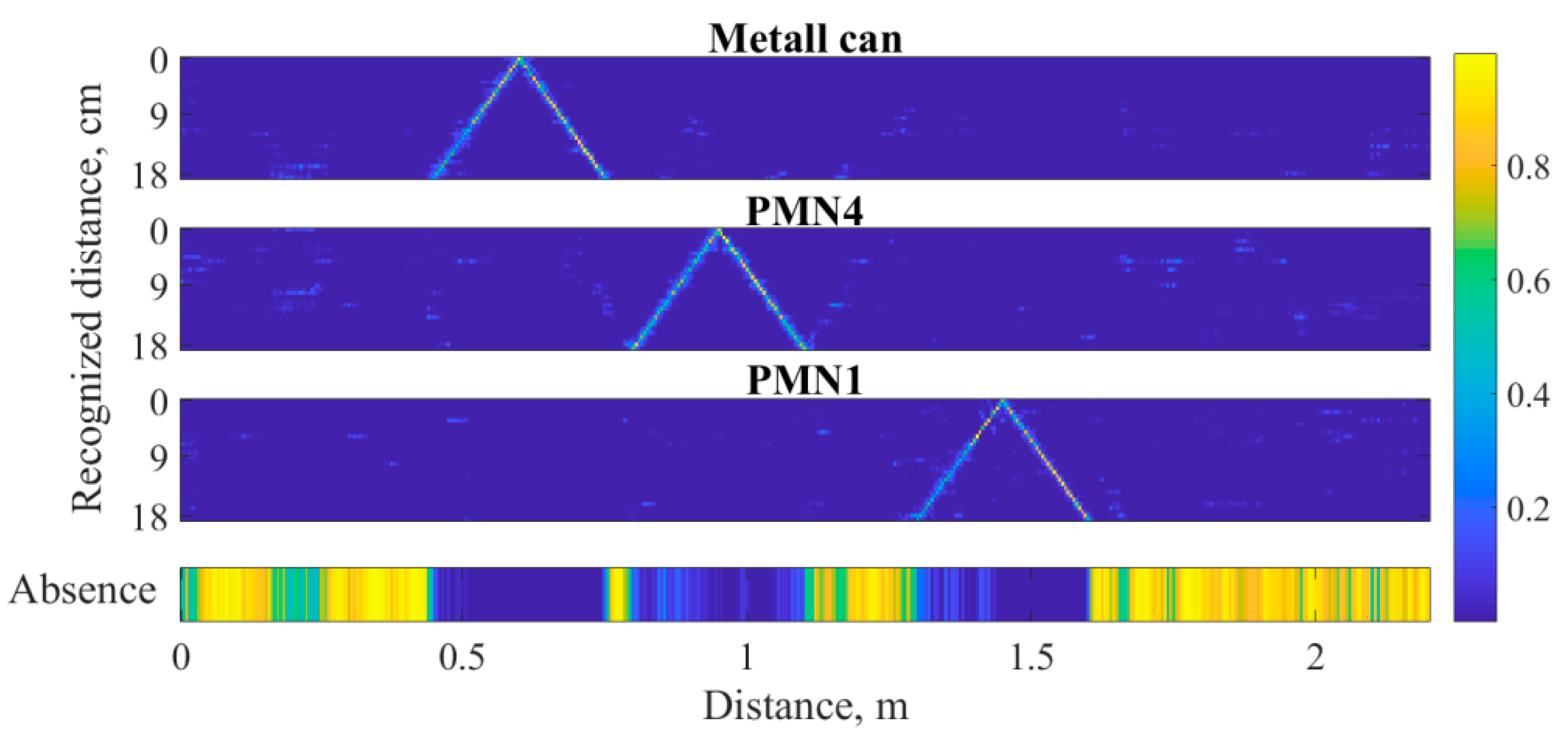
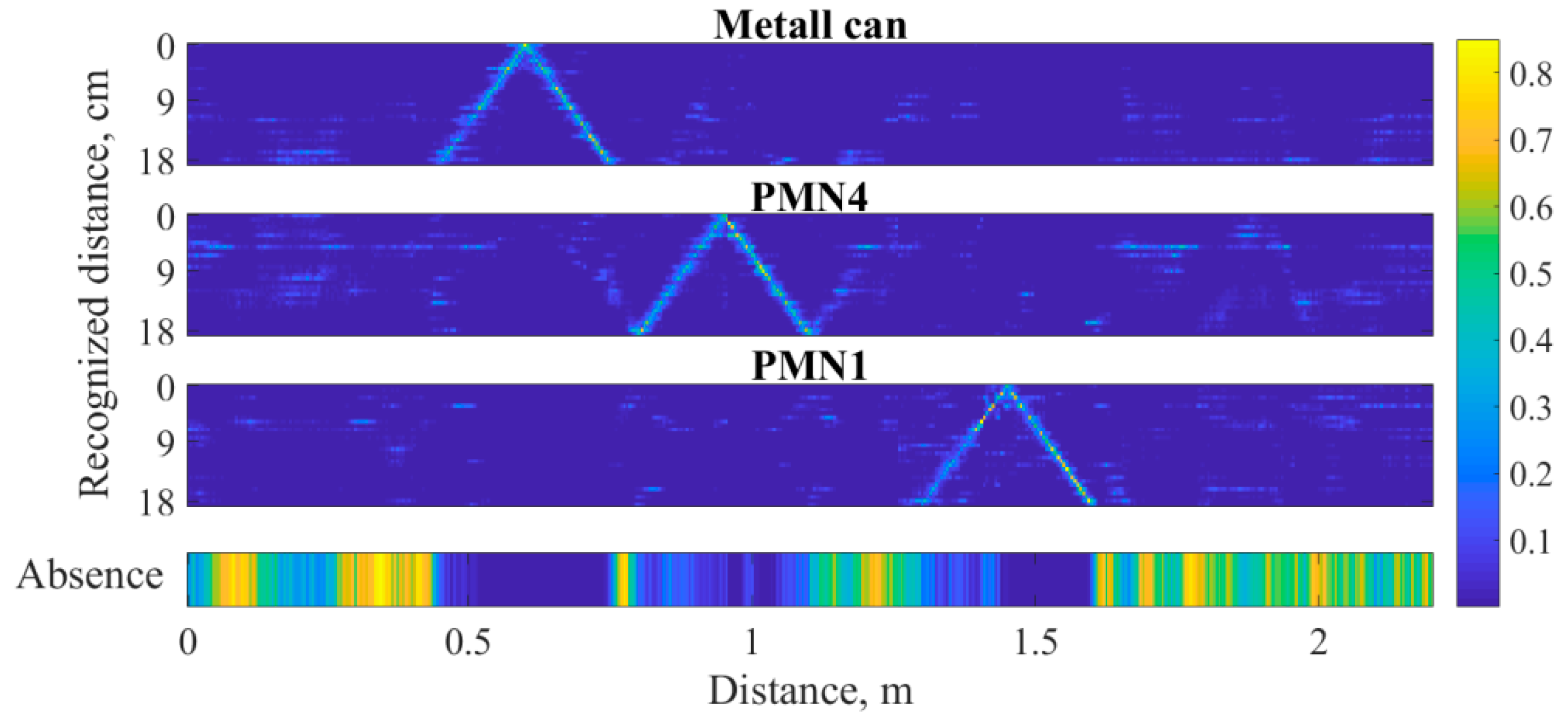
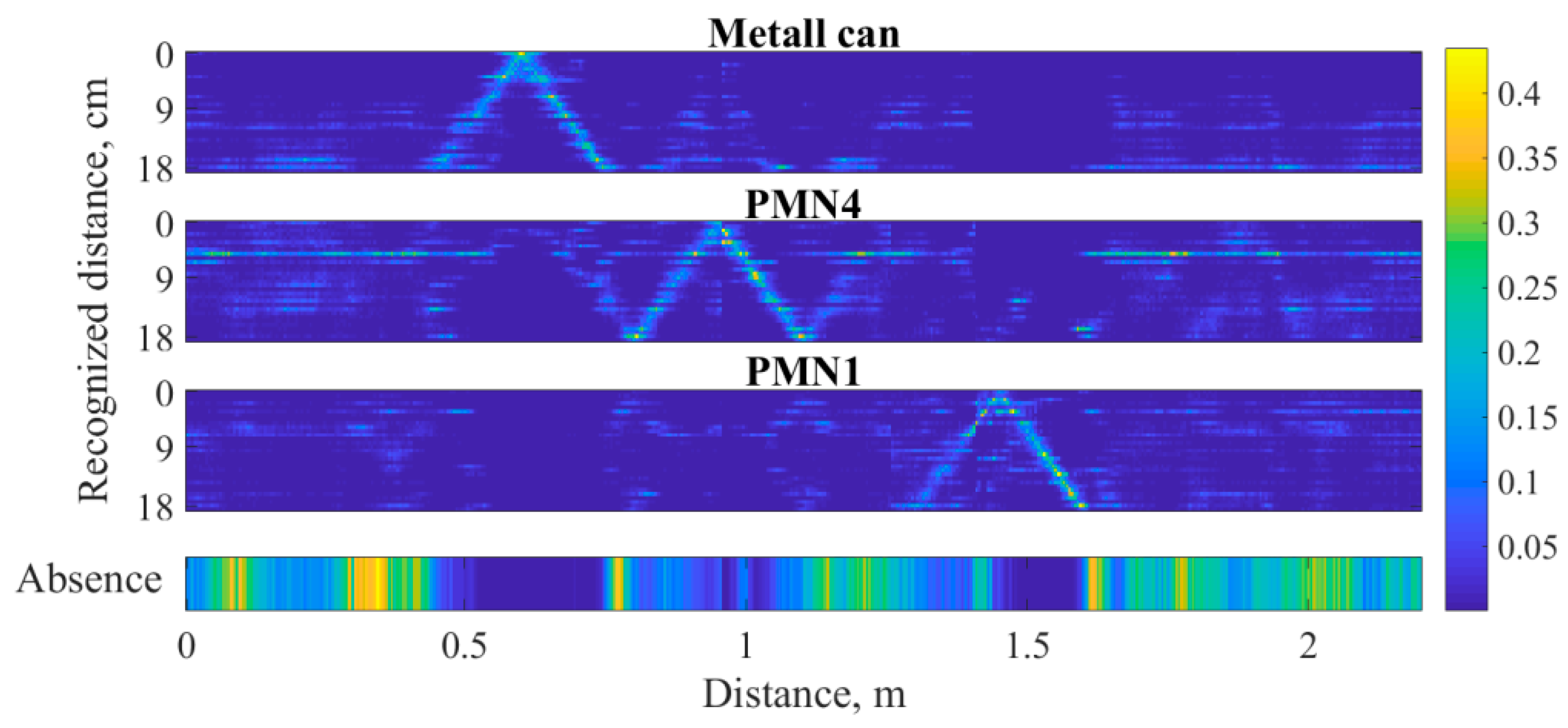
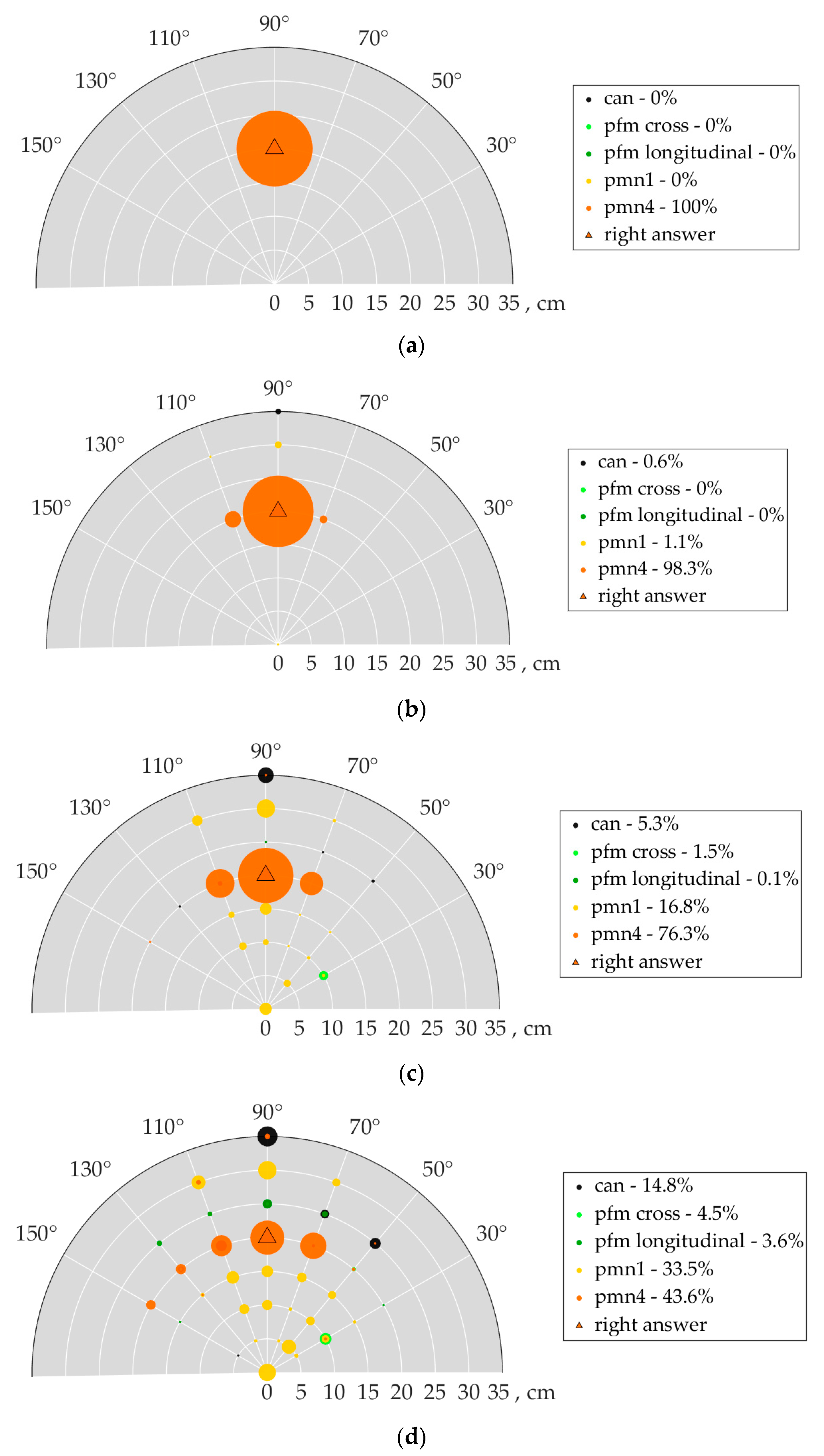
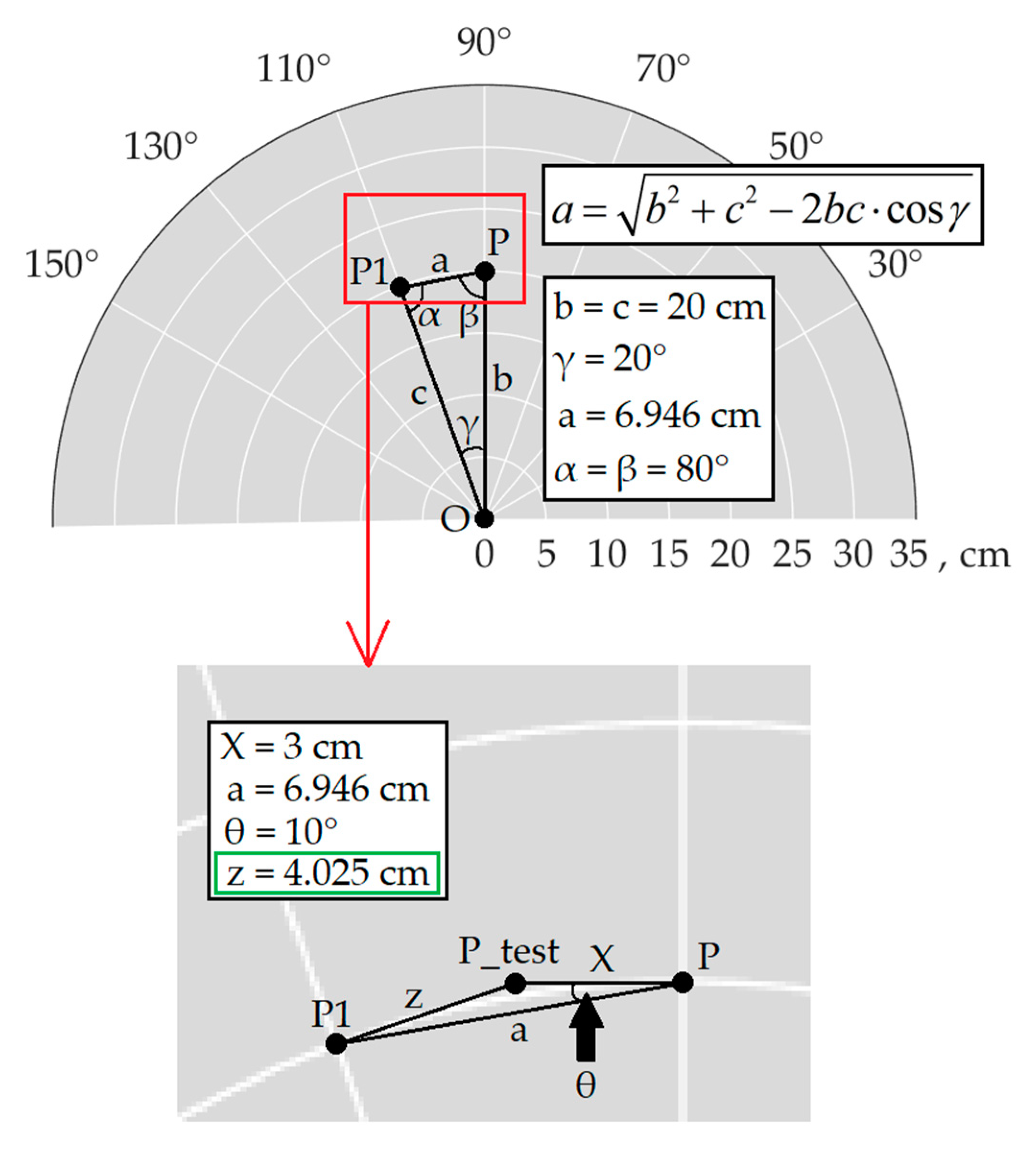
3.3. The Problem of Recognizing Dielectric Objects in the Sector of Angles
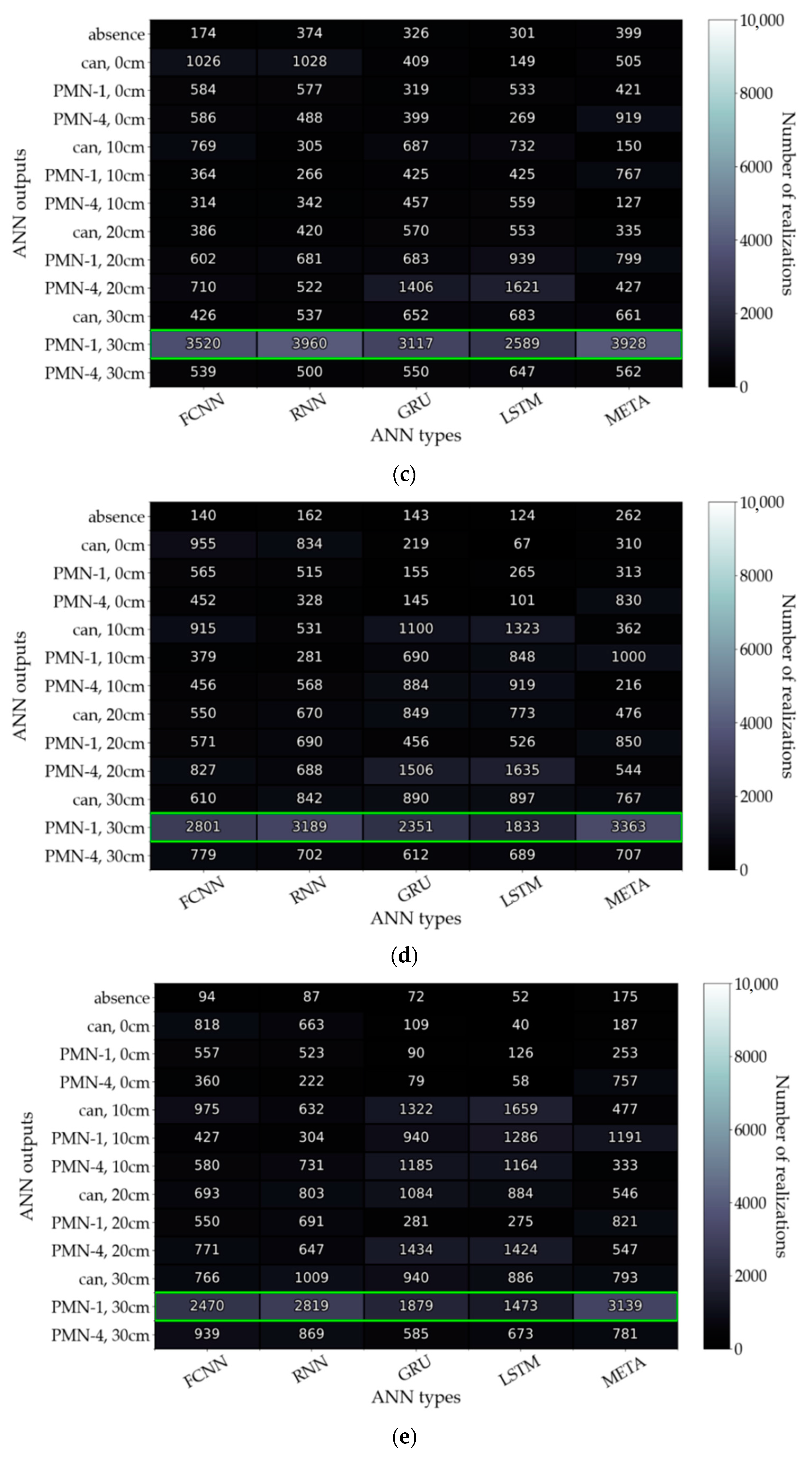
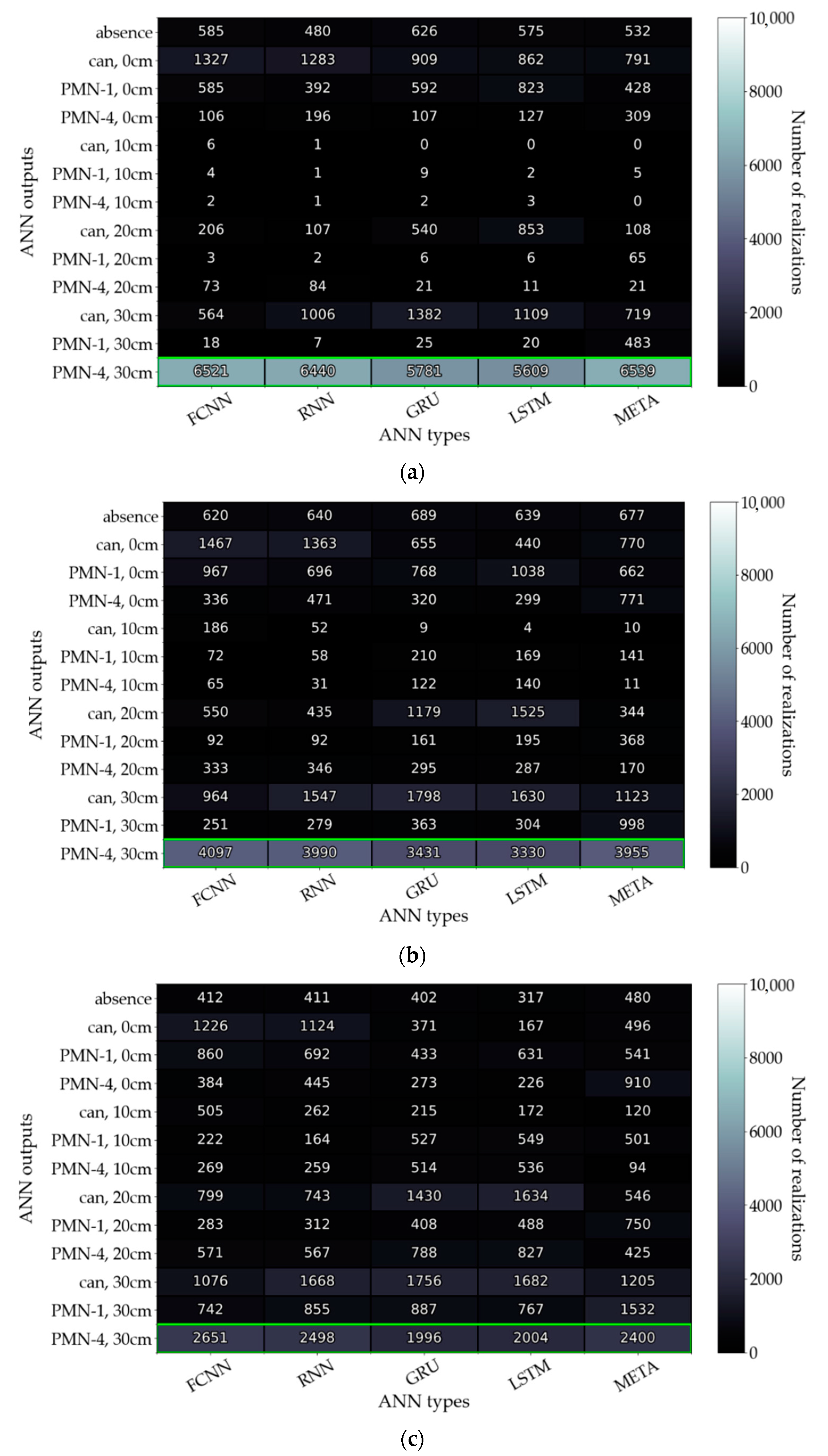
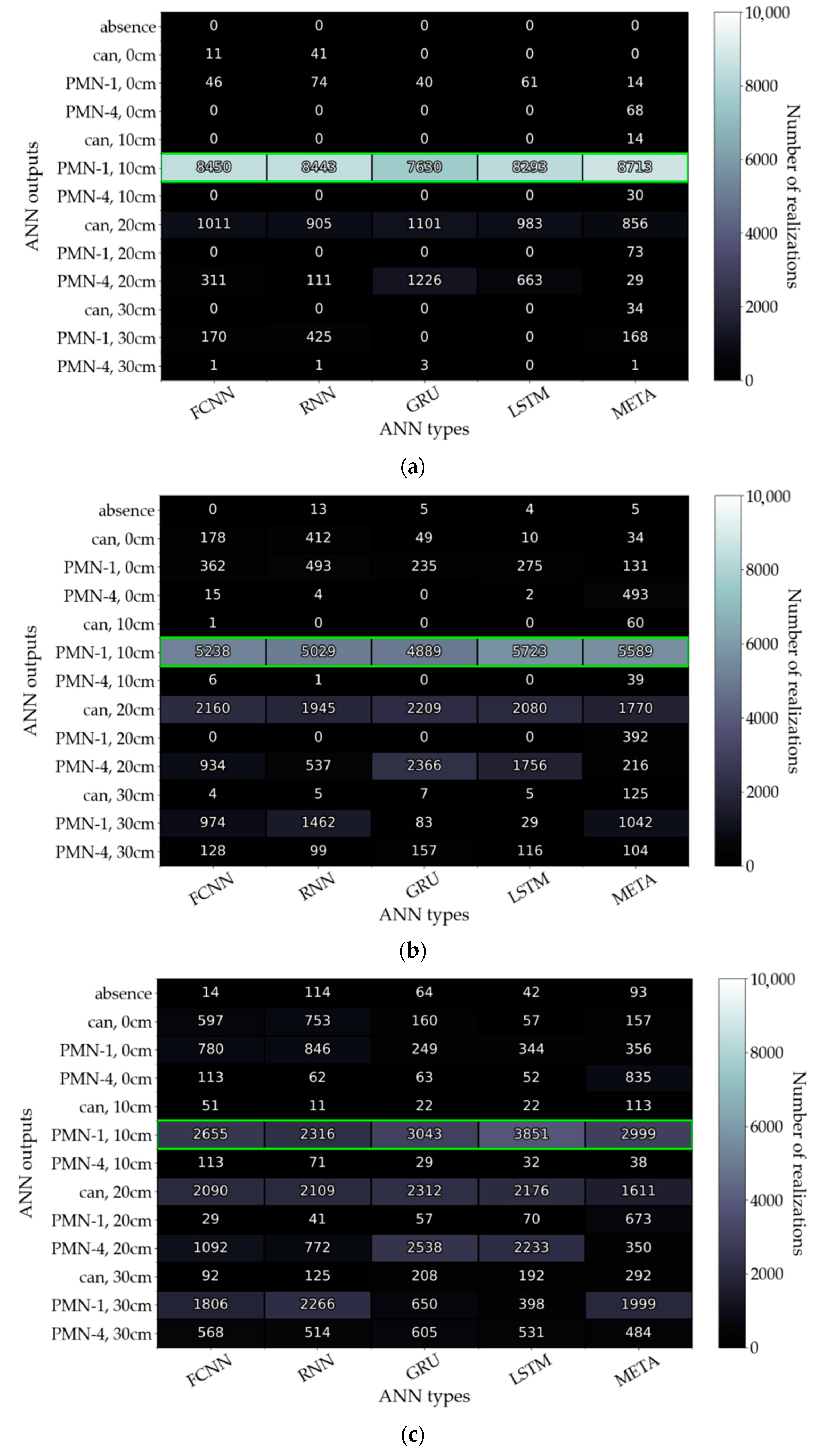
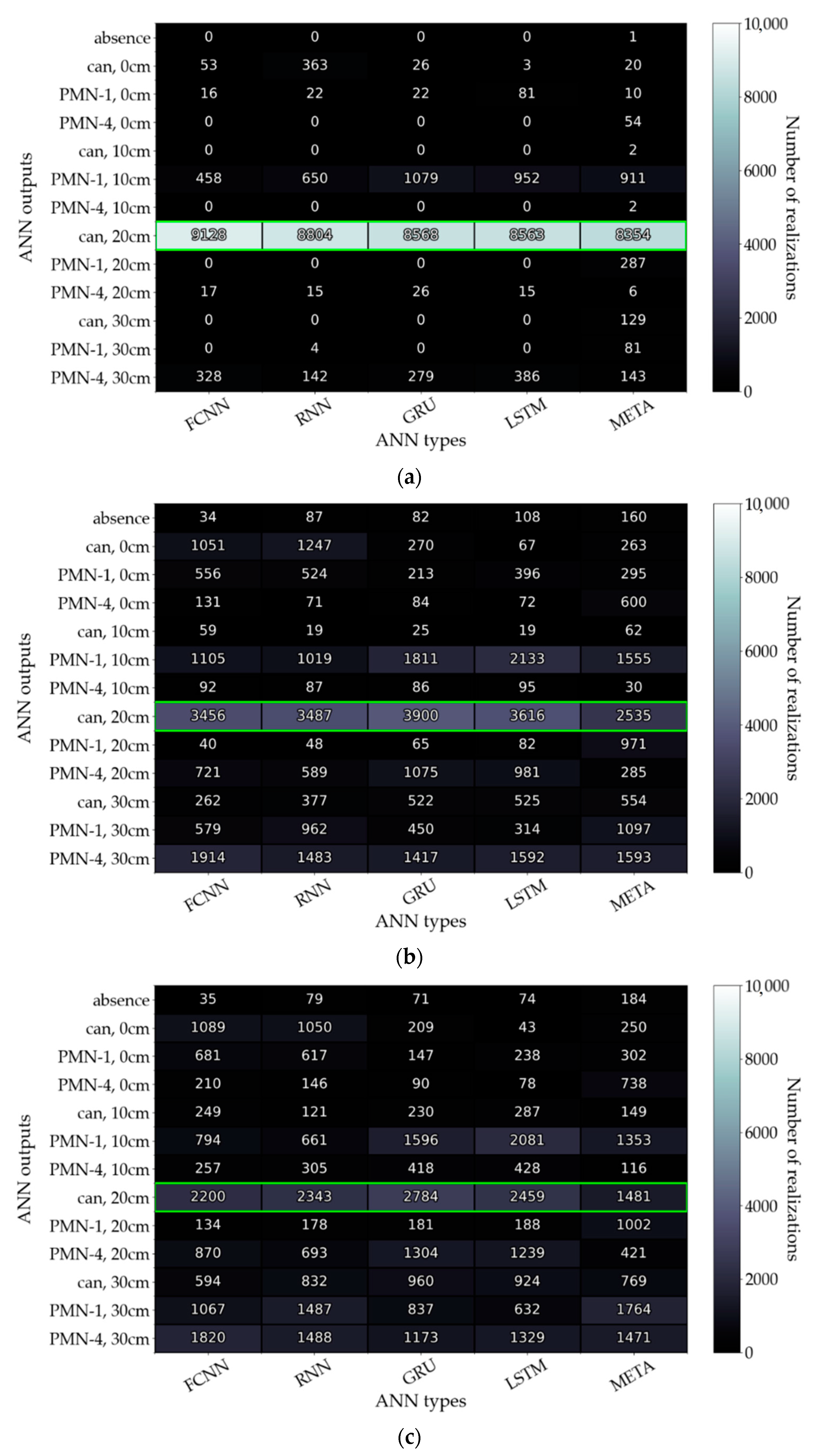
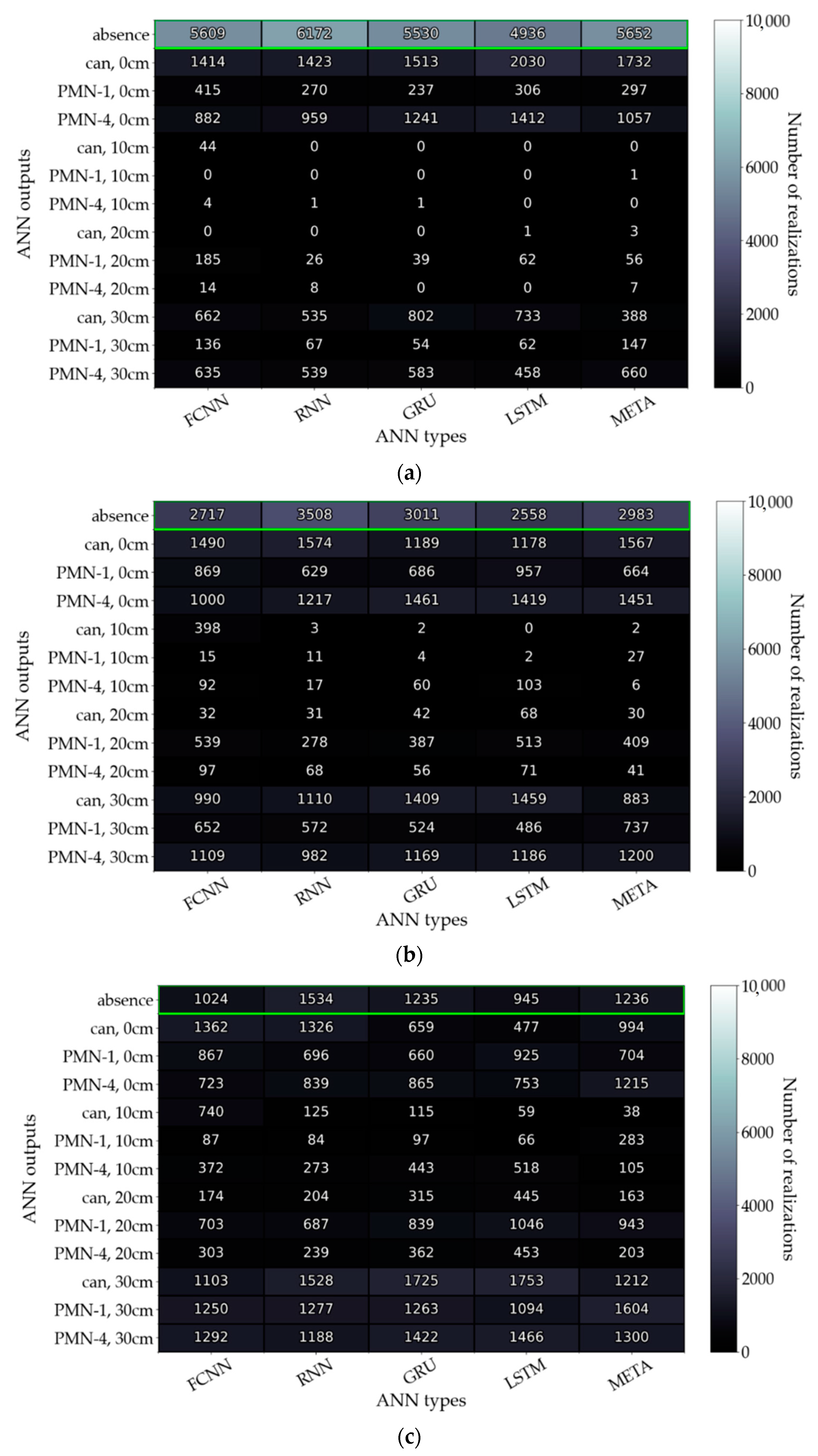
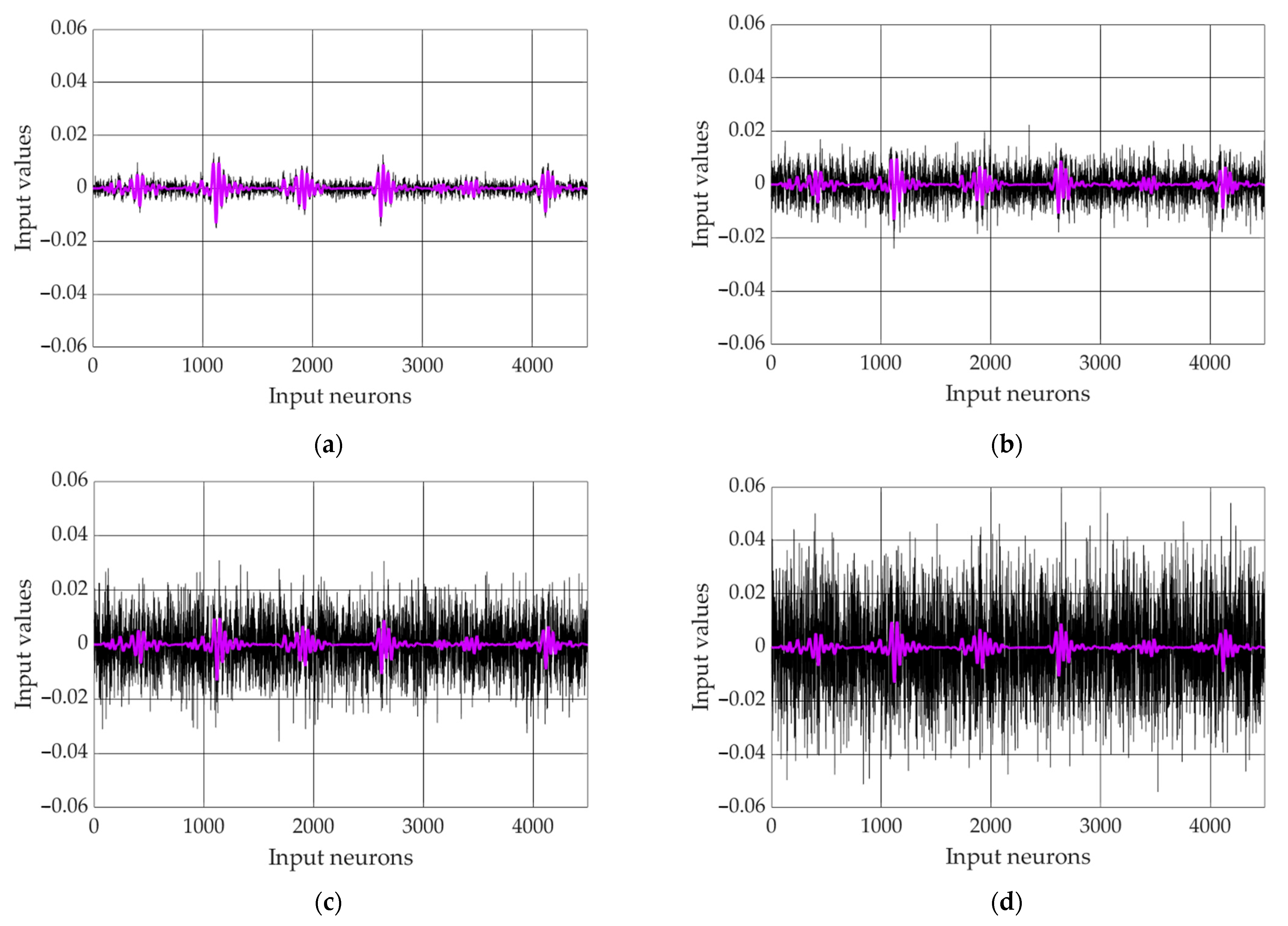
3.4. Improvement of the Data Processing Algorithm with a Neural Network Ensemble
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
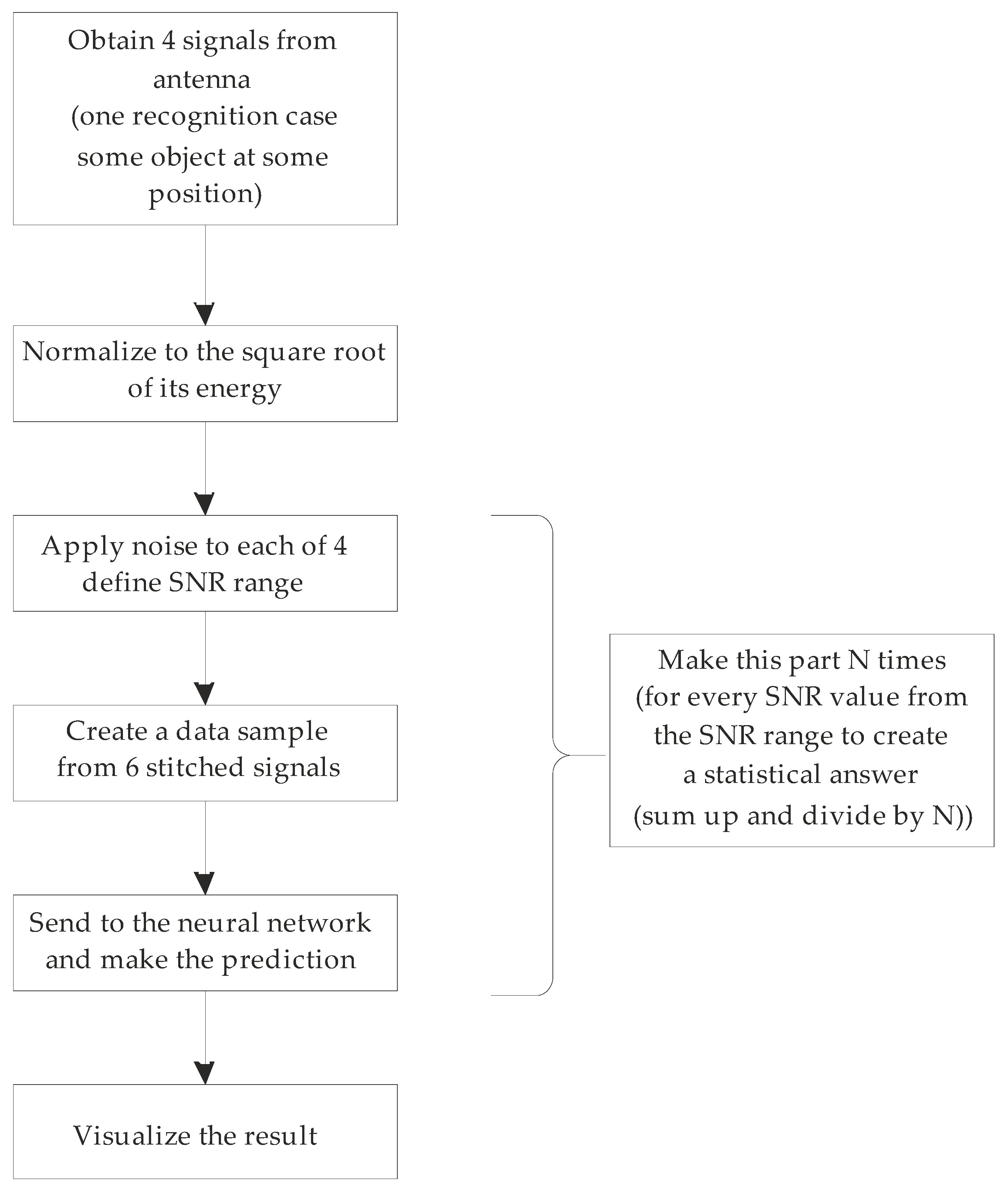

Appendix B
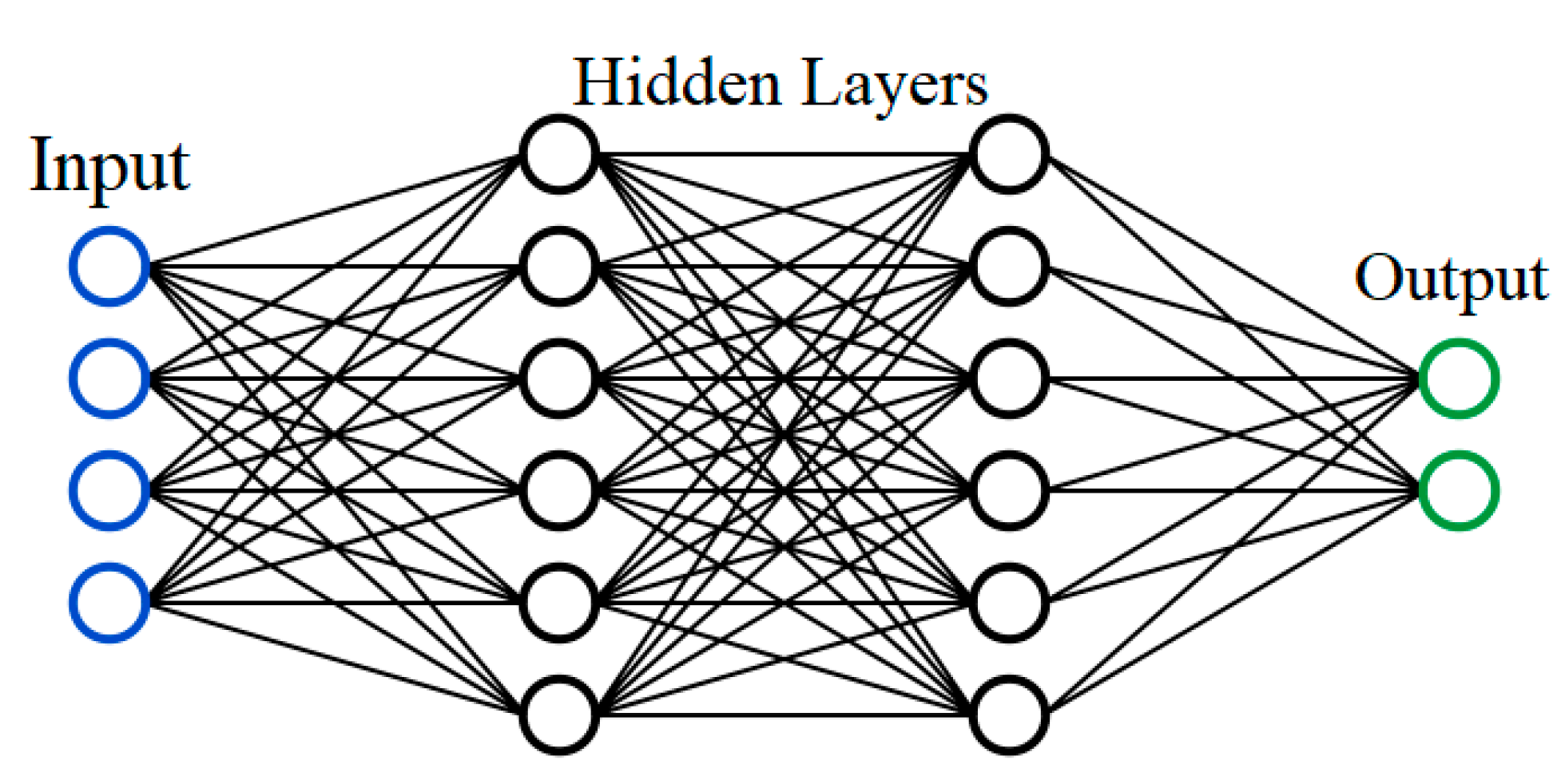
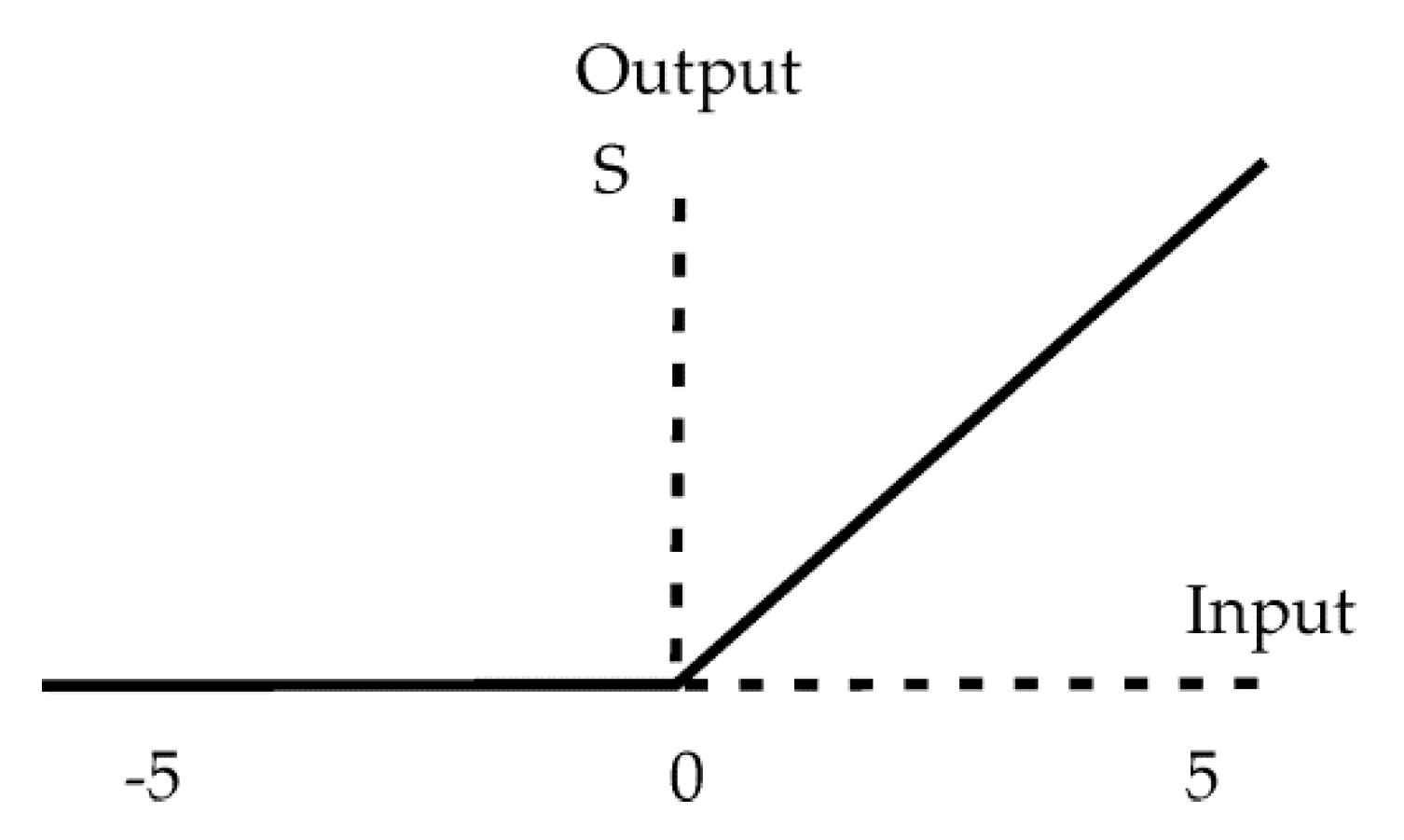
Appendix C
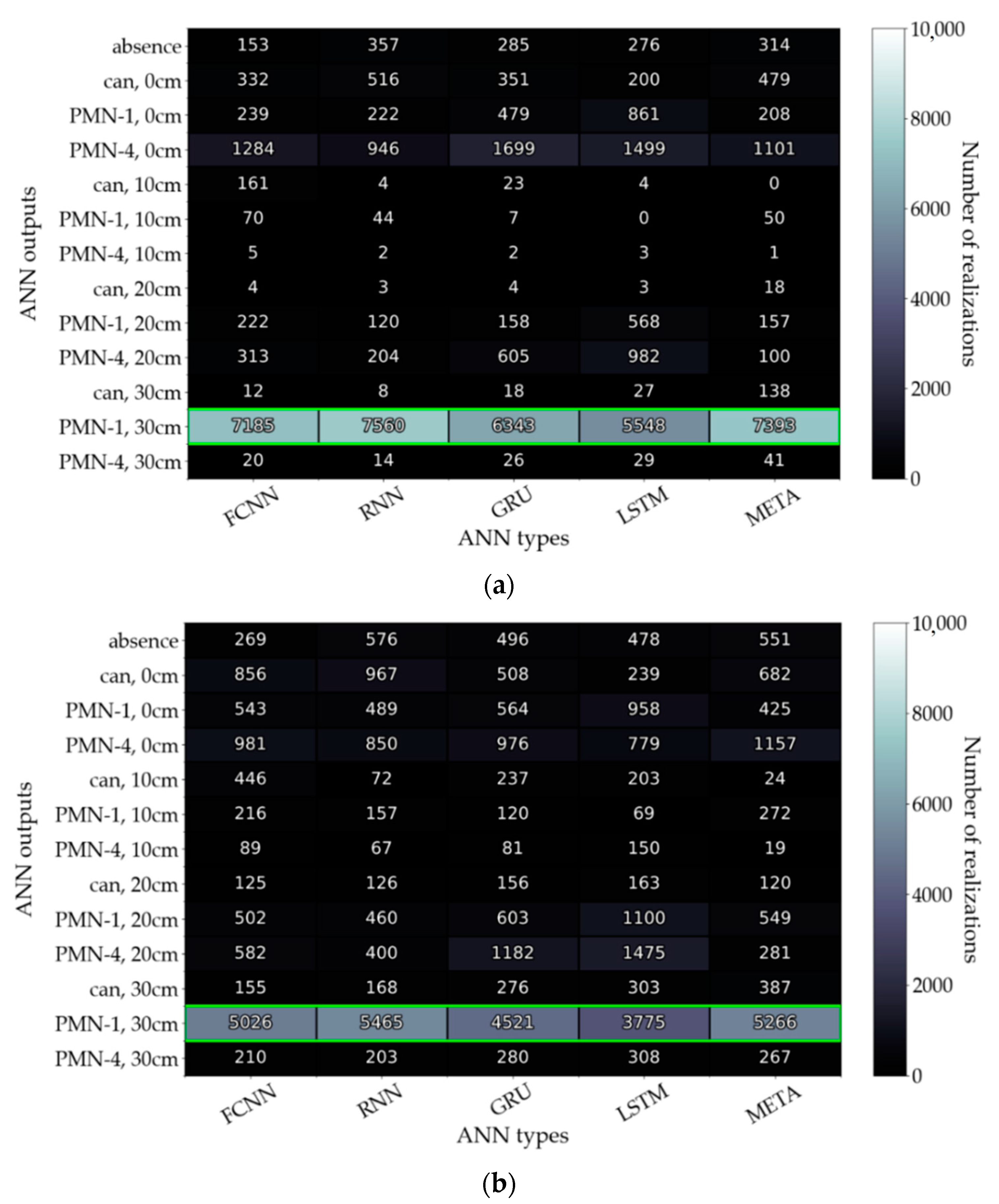

References
- EU Supports Demining Efforts in Ukraine. European Union News, 21 October 2020.
- Capineri, L.; Bechtel, T.; Pochanin, G.; Borgioli, G.; Bulletti, A.; Dimitri, M.; Falorni, P.; Simic, N.; Varyanitza-Roschupkina, L.; Ruban, V.; et al. Multi-Year Project: Holographic and Impulse Subsurface Radar for Landmine and IED Detection. In Explosives Detection; NATO Science for Peace and Security Series B; Capineri, L., Turmuş, E., Eds.; Physics and Biophysics; Springer: Dordrecht, The Netherlands, 2019; pp. 33–52. [Google Scholar]
- The 8-th Mine Action Technology Workshop. Available online: https://www.gichd.org/en/impact-stories/the-eighth-mine-action-technology-workshop/ (accessed on 1 February 2022).
- Sillerico-Justo, V. Control Scheme for Distributed Computing in Robot Networks Destined to Humanitarian Demining. In Proceedings of the IEEE XXV International Conference on Electronics, Electrical Engineering and Computing (INTERCON-2018), Lima, Peru, 8–10 August 2018; pp. 1–4. [Google Scholar]
- Sato, M.; Kikuta, K.; Bustemante, R.M. Evaluation of ALIS GPR for Humanitarian Demining in Colombia and Cambodia. In Proceedings of the International Conference on Electromagnetics in Advanced Applications (ICEAA-2018), Cartagena, Colombia, 10–14 September 2018; pp. 114–117. [Google Scholar]
- Pochanin, G.; Capineri, L.; Bechtel, T.; Ruban, V.; Falorni, P.; Crawford, F.; Ogurtsova, T.; Bossi, L. Radar Systems for Landmine Detection: Invited Paper. In Proceedings of the 2020 IEEE Ukrainian Microwave Week (UkrMW), Kharkiv, Ukraine, 21–25 September 2020; pp. 1118–1122. [Google Scholar]
- Daniels, D.J. Ground Penetrating Radar for Buried Landmine and IED Detection. In Unexploded Ordnance Detection and Mitigation; NATO Science for Peace and Security Series, B; Byrnes, J., Ed.; Physics and Biophysics; Springer: Dordrecht, The Netherlands, 2009; pp. 89–111. [Google Scholar]
- Taylor, J.D. Ultrawideband Radar: Applications and Design; CRC Press: Boca Raton, FL, USA; London, UK; New York, NY, USA, 2012; p. 536. [Google Scholar]
- Sytnik, O.; Masalov, S.; Kholod, P.; Pochanin, G.; Ruban, V. UWB Technology for Detecting Alive People Behind Optically Opaque Obstacles. In Proceedings of the 9th International Conference on Ultrawideband and Ultrashort Impulse Signals (UWBUSIS-2018), Odessa, Ukraine, 4–7 September 2018; pp. 110–114. [Google Scholar]
- Jaw, S.W.; Van Son, R.; Khoo Hock, V.; Schrotter, G.; Wei Kiah, R.; Teo Shen, S.; Yan, J. The Need for a Reliable Map of Utility Networks for Planning Underground Spaces. In Proceedings of the 17th International Conference on Ground Penetrating Radar (GPR-2018), Rapperswil, Switzerland, 18–21 June 2018; pp. 1–6. [Google Scholar]
- Pochanin, G.; Ruban, V.; Ogurtsova, T.; Orlenko, O.; Pochanina, I.; Kholod, P.; Capineri, L. Application of the Industry 4.0 Paradigm to the Design of a UWB Radiolocation System for Humanitarian Demining. In Proceedings of the 9th International Conference on Ultrawideband and Ultrashort Impulse Signals (UWBUSIS-2018), Odessa, Ukraine, 4–7 September 2018; pp. 50–56. [Google Scholar]
- Dumin, O.; Pryshchenko, O.; Plakhtii, V.; Pochanin, G. Landmine detection and classification using UWB antenna system and ANN analysis. In Proceedings of the IEEE Ukrainian Microwave Week (UkrMW-2020), Kharkiv, Ukraine, 21–25 September 2020; pp. 1030–1035. [Google Scholar]
- Badjou, S.; Kutrubes, D.; Montlouis, W. Low-Cost, Lightweight UWB Antenna Design for Humanitarian Drone-Launched GPR Surveys. In Proceedings of the IEEE Green Technologies Conference (GreenTech-2020), Oklahoma City, OK, USA, 1–3 April 2020; pp. 181–183. [Google Scholar]
- Ouadfeul, S.; Aliouane, L. Multiscale analysis of 3D GPR data using the continuous wavelet transform. In Proceedings of the XIII International Conference on Ground Penetrating Radar, Lecce, Italy, 21–25 June 2010; pp. 1–4. [Google Scholar]
- Morgenthaler, A.W.; Rappaport, C.M. Scattering from dielectric objects buried beneath random rough ground: Validating the semi-analytic mode matching algorithm with two-dimensional FDFD. In Proceedings of the International Geoscience and Remote Sensing Symposium. Taking the Pulse of the Planet: The Role of Remote Sensing in Managing the Environment, Honolulu, HI, USA, 24–28 July 2000; pp. 1634–1636. [Google Scholar]
- Hart, P.E. How the Hough transform was invented [DSP History]. IEEE Signal Process. Mag. 2009, 26, 18–22. [Google Scholar] [CrossRef]
- Ruban, V.; Capineri, L.; Bechtel, T.; Pochanin, G.; Falorni, P.; Crawford, F.; Ogurtsova, T.; Bossi, L. Automatic Detection of Subsurface Objects with the Impulse GPR of the UGO-1st Robotic Platform. In Proceedings of the IEEE Ukrainian Microwave Week (UkrMW), Kharkiv, Ukraine, 22–27 June 2020; pp. 1108–1111. [Google Scholar]
- Dumin, O.; Plakhtii, V.; Pryshchenko, O.; Pochanin, G. Comparison of ANN and Cross-Correlation Approaches for Ultra Short Pulse Subsurface Survey. In Proceedings of the 15th International Conference on Advanced Trends in Radioelectronics, Telecommunications and Computer Engineering (TCSET), Lviv-Slavske, Ukraine, 25–29 February 2020; pp. 381–386. [Google Scholar]
- Inagaki, M.; Bechtel, T.; Razevig, V. Experimental approach for determining the received pattern of a Rascan holographic radar antenna. In Proceedings of the XIII International Conference on Ground Penetrating Radar, Lecce, Italy, 21–25 June 2010; pp. 1–5. [Google Scholar]
- Song, X.; Su, Y.; Zhu, Y.; Huang, C.; Lu, M. Improving holographic radar imaging resolution via deconvolution. In Proceedings of the 15th International Conference on Ground Penetrating Radar, Brussels, Belgium, 30 June–4 July 2014; pp. 633–636. [Google Scholar]
- Dakrory, A.M.; Tawfik, M. Utilization of neural network and the discrepancy between it and modeling in quadcopter attitude. In Proceedings of the International Workshop on Recent Advances in Robotics and Sensor Technology for Humanitarian Demining and Counter-IEDs (RST), Cairo, Egypt, 27–30 October 2016; pp. 1–6. [Google Scholar]
- Liu, T.; Mei, H.; Sun, Q.; Zhou, H. Application of neural network in fault location of optical transport network. China Commun. 2019, 16, 214–225. [Google Scholar] [CrossRef]
- Uçkun, F.; Özer, H.; Nurbaş, E.; Onat, E. Direction Finding Using Convolutional Neural Networks and Convolutional Recurrent Neural Networks. In Proceedings of the 28th Signal Processing and Communications Applications Conference (SIU), Gaziantep, Turkey, 5–7 October 2020; pp. 1–4. [Google Scholar]
- Stoimenov, S.; Tsenov, G.; Mladenov, V. Face recognition system in Android using neural networks. In Proceedings of the 13th Symposium on Neural Networks and Applications (NEUREL), Belgrade, Serbia, 22–24 November 2016; pp. 1–4. [Google Scholar]
- Ruchkin, V.; Romanchuk, V.; Sulitsa, R. Clustering, restorability and designing of embedded computer systems based on neuroprocessors. In Proceedings of the 2nd Mediterranean Conference on Embedded Computing (MECO), Budva, Montenegro, 15–20 June 2013; pp. 58–61. [Google Scholar]
- Gu, J.; Wu, L.; Chen, J.; Cai, R.; Wan, H.; Shi, W.; Lv, X. Intelligent monitoring of subsidence cracks in underground power utility tunnel. In Proceedings of the SPIE 12166, Seventh Asia Pacific Conference on Optics Manufacture and 2021 International Forum of Young Scientists on Advanced Optical Manufacturing (APCOM and YSAOM 2021), Shanghai, China, 28–31 October 2021; Volume 121663D. [Google Scholar]
- Zhang, Y.; Yuen, K.V. Crack detection using fusion features-based broad learning system and image processing. Comput.-Aided Civ. Infrastruct. Eng. 2021, 36, 1568–1584. [Google Scholar] [CrossRef]
- Manan, A.; Kamal, K.; Abro, A.G.; Abdul Hussain Ratlamwala, T.; Fahad Sheikh, M.; Zafar, T. Failure Prediction and Classification in Natural Gas Pipe-Lines Using Artificial Intelligence. Energy Rep. 2021, 7, 7640–7647. [Google Scholar] [CrossRef]
- Dumin, O.; Prishchenko, O.; Pochanin, G.; Plakhtii, V.; Shyrokorad, D. Subsurface Object Identification by Artificial Neural Networks and Impulse Radiolocation. In Proceedings of the IEEE Second International Conference on Data Stream Mining & Processing (DSMP), Lviv, Ukraine, 21–25 August 2018; pp. 434–437. [Google Scholar]
- Dumin, O.; Prishchenko, O.; Plakhtii, V.; Shyrokorad, D. Application of UWB Electromagnetic Waves for Subsurface Object Location Classification by Artificial Neural Networks. In Proceedings of the 9th International Conference on Ultrawideband and Ultrashort Impulse Signals (UWBUSIS), Odessa, Ukraine, 4–7 September 2018; pp. 290–293. [Google Scholar]
- Uncini, A.; Cocchi, G. Subband neural networks for noisy signal forecasting and missing data reconstruction. In Proceedings of the International Joint Conference on Neural Networks, Honolulu, HI, USA, 12–17 May 2002; pp. 438–441. [Google Scholar]
- Juang, C.; Chiou, C.; Lai, C. Hierarchical Singleton-Type Recurrent Neural Fuzzy Networks for Noisy Speech Recognition. IEEE Trans. Neural Netw. 2007, 18, 833–843. [Google Scholar] [CrossRef] [PubMed]
- Phonsri, S.; Mukherjee, S.; Sellathurai, M. Computer vision and bi-directional neural network for extraction of communications signal from noisy spectrogram. In Proceedings of the IEEE Conference on Antenna Measurements & Applications (CAMA), Chiang Mai, Thailand, 30 November–2 December 2015; pp. 1–4. [Google Scholar]
- Plakhtii, V.; Dumin, O.; Prishchenko, O.; Shyrokorad, D.; Pochanin, G. Influence of Noise Reduction on Object Location Classification by Artificial Neural Networks for UWB Subsurface Radiolocation. In Proceedings of the XXIVth International Seminar/Workshop on Direct and Inverse Problems of Electromagnetic and Acoustic Wave Theory (DIPED), Lviv, Ukraine, 12–14 September 2019; pp. 64–68. [Google Scholar]
- Pathak, S.; Cai, X.; Rajasekaran, S. Ensemble Deep TimeNet: An Ensemble Learning Approach with Deep Neural Networks for Time Series. In Proceedings of the IEEE 8th International Conference on Computational Advances in Bio and Medical Sciences (ICCABS), Las Vegas, NV, USA, 18–20 October 2018; p. 1. [Google Scholar]
- Samat, A.; Du, P.; Liu, S.; Li, J.; Cheng, L. E2LMs: Ensemble Extreme Learning Machines for Hyperspectral Image Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 1060–1069. [Google Scholar] [CrossRef]
- Pang, W.; Fan, X. Chinese coreference resolution with ensemble learning. In Proceedings of the Asia-Pacific Conference on Computational Intelligence and Industrial Applications (PACIIA), Wuhan, China, 28–29 November 2009; pp. 377–380. [Google Scholar]
- Wijeratne, M.; Lakmal, R.; Geethadhari, W. Computer Vision and NLP based Multimodal Ensemble Attentiveness Detection API for E-Learning. In Proceedings of the IEEE Global Engineering Education Conference (EDUCON), Vienna, Austria, 21–23 April 2021; pp. 814–820. [Google Scholar]
- Mung, P.; Phyu, S. Effective Analytics on Healthcare Big Data Using Ensemble Learning. In Proceedings of the IEEE Conference on Computer Applications (ICCA), Yangon, Myanmar, 27–28 February 2020; pp. 1–4. [Google Scholar]
- Pochanin, G.; Capineri, L.; Bechtel, T.; Falorni, P.; Borgioli, G.; Ruban, V.; Orlenko, O.; Ogurtsova, T.; Pochanin, O.; Crawford, F.; et al. Measurement of Coordinates for a Cylindrical Target Using Times of Flight from a 1-Transmitter and 4-Receiver UWB Antenna System. IEEE Trans. Geosci. Remote Sens. 2020, 58, 1363–1372. [Google Scholar] [CrossRef]
- Capineri, L.; Falorni, P.; Borgioli, G.; Bossi, L.; Pochanin, G.; Ruban, V.; Pochanin, O.; Ogurtsova, T.; Crawford, F.; Bechtel, T. Background Removal for the Processing of Scans Acquired with the, “UGO-1st”, Landmine Detection Platform. In Proceedings of the 2019 Photonics & Electromagnetics Research Symposium—Spring (PIERS-Spring), Rome, Italy, 17–20 June 2019; pp. 3965–3973. [Google Scholar]
- Gutierrez, S.; Just, F.; Sachs, J.; Baer, C.; Vega, F. Field-Deployable System for the Measurement of Complex Permittivity of Improvised Explosives and Lossy Dielectric Materials. IEEE Sens. J. 2018, 18, 6706–6714. [Google Scholar] [CrossRef]
- Öztürk, T.; Sayinti, A.; Ünal, İ. Experimental studies based on classification of explosive and non-explosive liquids. In Proceedings of the 25th Signal Processing and Communications Applications Conference (SIU), Antalya, Turkey, 15–18 May 2017; pp. 1–4. [Google Scholar]
- Shi, X.; Cheng, D.; Song, Z.; Wang, C. A Real-time Method for Landmine Detection Using Vehicle Array GPR. In Proceedings of the 17th International Conference on Ground Penetrating Radar (GPR), Rapperswil, Switzerland, 18–21 June 2018; pp. 1–4. [Google Scholar]
- Pochanin, G.; Varianytsia-Roshchupkina, L.; Ruban, V.; Pochanina, I.; Falorni, P.; Borgioli, G.; Capineri, L.; Bechtel, T. Design and simulation of a “single transmitter—four-receiver” impulse GPR for detection of buried landmines. In Proceedings of the 2017 9th International Workshop on Advanced Ground Penetrating Radar (IWAGPR), Edinburgh, UK, 28–30 June 2017; pp. 1–5. [Google Scholar] [CrossRef]







Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pryshchenko, O.A.; Plakhtii, V.; Dumin, O.M.; Pochanin, G.P.; Ruban, V.P.; Capineri, L.; Crawford, F. Implementation of an Artificial Intelligence Approach to GPR Systems for Landmine Detection. Remote Sens. 2022, 14, 4421. https://doi.org/10.3390/rs14174421
Pryshchenko OA, Plakhtii V, Dumin OM, Pochanin GP, Ruban VP, Capineri L, Crawford F. Implementation of an Artificial Intelligence Approach to GPR Systems for Landmine Detection. Remote Sensing. 2022; 14(17):4421. https://doi.org/10.3390/rs14174421
Chicago/Turabian StylePryshchenko, Oleksandr A., Vadym Plakhtii, Oleksandr M. Dumin, Gennadiy P. Pochanin, Vadym P. Ruban, Lorenzo Capineri, and Fronefield Crawford. 2022. "Implementation of an Artificial Intelligence Approach to GPR Systems for Landmine Detection" Remote Sensing 14, no. 17: 4421. https://doi.org/10.3390/rs14174421
APA StylePryshchenko, O. A., Plakhtii, V., Dumin, O. M., Pochanin, G. P., Ruban, V. P., Capineri, L., & Crawford, F. (2022). Implementation of an Artificial Intelligence Approach to GPR Systems for Landmine Detection. Remote Sensing, 14(17), 4421. https://doi.org/10.3390/rs14174421





