Joint Flying Relay Location and Routing Optimization for 6G UAV–IoT Networks: A Graph Neural Network-Based Approach
Abstract
:1. Introduction
- High performance. In a 6G network, there will be a large amount of image and video monitoring tasks for IoT devices, and transmitting such data requires high communication rates [1]. It is usually required to jointly optimize the trajectories, relay paths, transmit powers, and so forth of the UAVs and IoT devices to maximize the communication rates. However, this joint optimization is generally not a convex problem, and it is challenging to find the optimal solution quickly [5]. In addition, traditional optimization methods such as alternating minimization (AM) algorithm usually fall into the false local optimal [14].
- High efficiency. In the 6G IoT network, the number of IoT devices can be very large, and thus the algorithm’s time complexity should be very low to deal with the large-scale optimization problem [15]. In addition, the ultra-low latency requirements of certain 6G services make the algorithm’s execution time significantly affect the quality of service (QoS), examples of which are mobile IoT services [16]. Therefore, the algorithm should be executed by the system in a very efficient way such that the QoS can be improved. Thus, exploiting traditional optimization and heuristic algorithms is challenging since they usually need a long time to generate a solution, especially when the network scale is large.
- High Robustness. As IoT devices may be moving, the algorithm should be robust to small changes in the locations of the IoT device, i.e., the optimization results can be directly inferred from the algorithm without iteration-based execution or re-training. Traditional optimization algorithms need to be executed again as long as the environment changes, resulting in extra delays when the environment is not sTable Unfortunately, using traditional neural network (NN) methods is challenging due to their low generalizability [17].
- High Scalability. In 6G networks, there will be many periodic hibernations and time-triggered switch-on IoT devices [18]. Thus, the scale of the network can be changed at different times. This requires the algorithm to be scalable to the increasing/decreasing number of users in the network. However, traditional multi-layer perception (MLP), convolutional neural networks (CNN), and recurrent neural networks (RNN), even attention-based transformer network has no such scalability [19].
- Low complexity. Usually, in UAV networks the optimization algorithm runs on the UAV’s processor. However, it is difficult for UAVs to carry high-performance computing chips due to limitations such as UAVs’ weight and energy consumption. Moreover, in 6G IoT networks, the number of users and UAVs might be very large, leading to a possible increase in the algorithm complexity [5]. Therefore, the algorithm should have low time complexity to improve the efficiency and low space complexity such that the algorithm can run on the UAV without memory overflow, even when it deals with very large IoT networks.
- (1)
- We model the problem of joint relay path selection and UAV location optimization in multi-user multi-UAV networks as a graph optimization problem and solve it using a GNN-based approach. Compared with traditional optimization-based methods and non-GNN neural network-based methods, GNN models have the benefits of flexible structure, lower computation requirement, and fast convergence, making them very suitable in dynamic environments of UAV networks and UAVs with low power and computation capabilities.
- (2)
- We propose a two-stage GNN-based optimization framework. The problem is decoupled into optimal relay path selection and UAV position optimization, each of which is solved by an individual GNN model. Through this, the complexity of the initial problem is significantly reduced, and the learning convergence and performance are improved.
- (3)
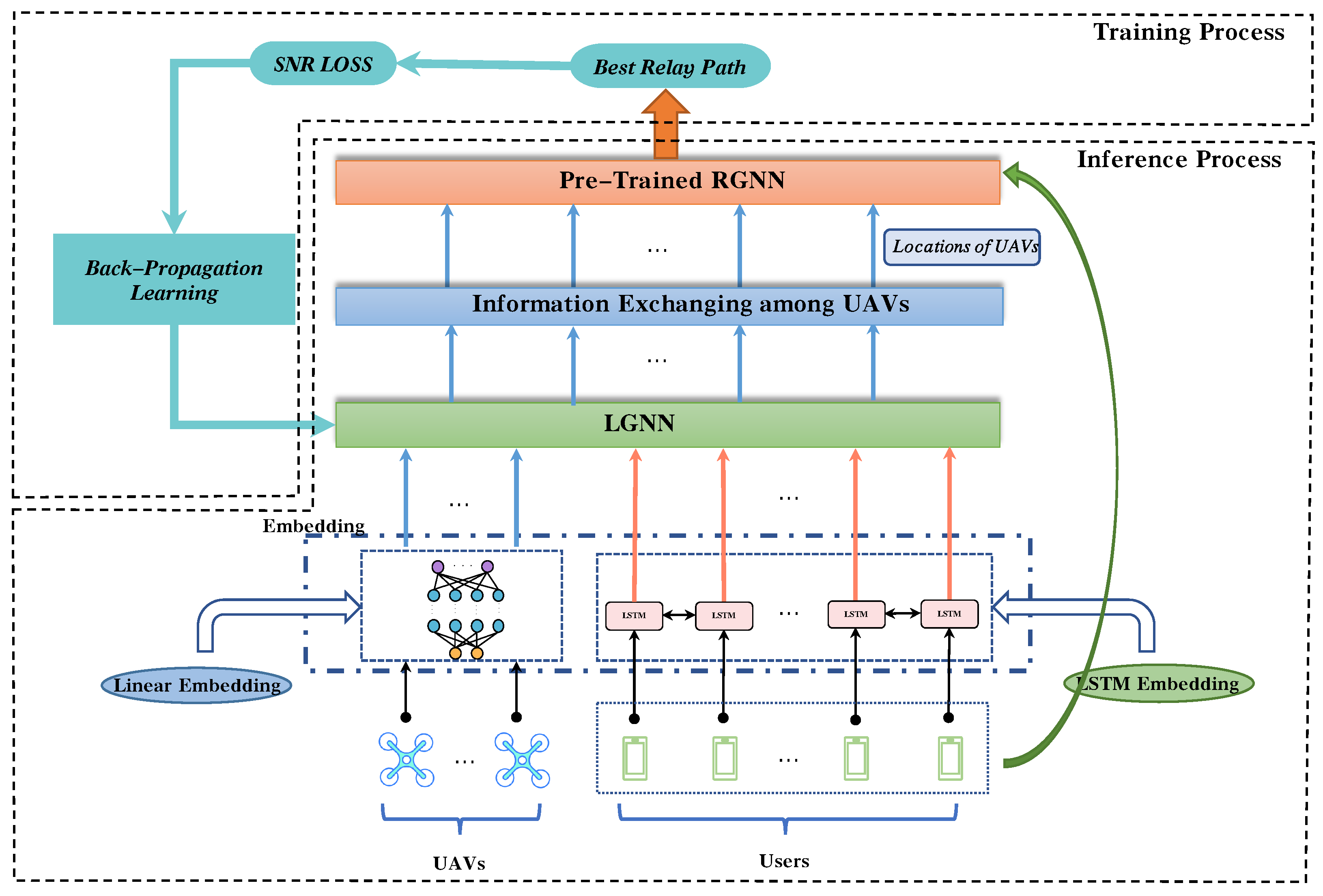
- With the two-stage framework, in the training procedure, a relay GNN (RGNN) is first trained to select the best relay path, and a location GNN (LGNN) is trained to optimize the locations of UAV relays with trained RGNN to select the paths such that the loss of LGNN can be calculated. Specifically, we exploit reinforcement learning and unsupervised learning to train RGNN and LGNN, respectively, which do not require any training data or knowledge of optimal solutions. In the inference procedure, LGNN is first used to optimize the location of UAVs, and then RGNN is used to select the best relay path based on the location of UAVs optimized by LGNN.
- (4)
- We evaluate the performance of the proposed method through extensive simulations. The results show that the proposed method achieves comparable performance to brute-force search with much lower time complexity. Furthermore, the proposed method is also scalable to very large networks and can adapt to environmental dynamics, which is significant in UAV–IoT networks.
2. Related Work and Preliminary
2.1. Related Work
2.2. Preliminary
2.2.1. Graph Neural Networks
2.2.2. Long Short Term Memory
3. System Model and Problem Formulation
3.1. System Model
3.2. Problem Formulation
- -
- A set of binary variables , where is set of relay path for sender s, and if node are used to transmit data from sender i, otherwise .
- -
- A set of continuous variables , where is the data flow from sender s, and is the amount of traffic from node i to node j to relay data from sender s.
- -
- A set of continuous variables , where is the location of UAVs u.
4. GNN-Based Efficient and Scalable Solution
4.1. Two-Stage Training and Inference Algorithm
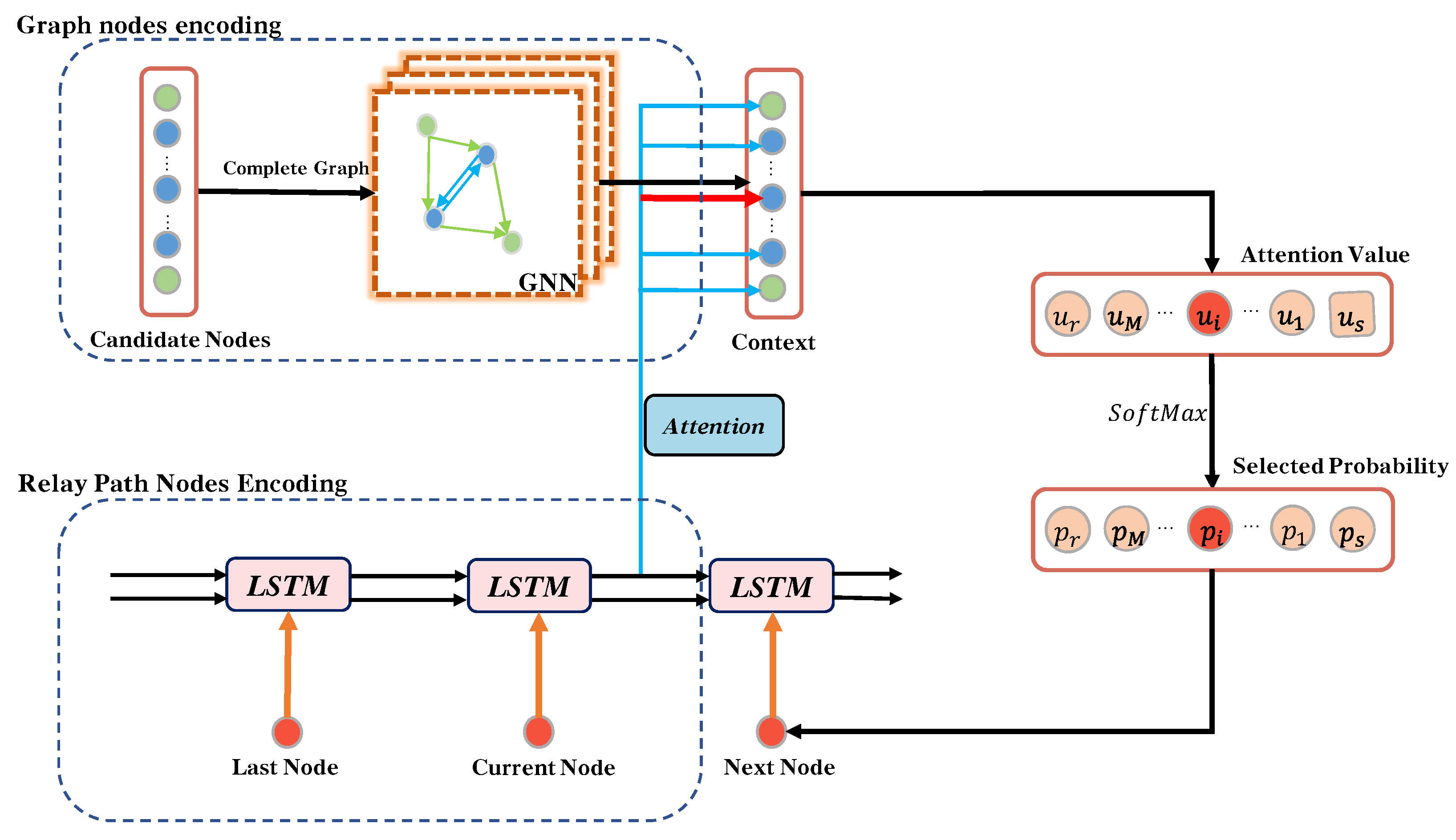
4.2. RGNN Based Relay Selection Method
4.2.1. Reinforcement Learning Based RGNN Training Method
4.2.2. Structure of RGNN
| Algorithm 1: Training procedure of LGNN-RGNN method |
|
| Algorithm 2: Inference procedure of LGNN-RGNN method |
|
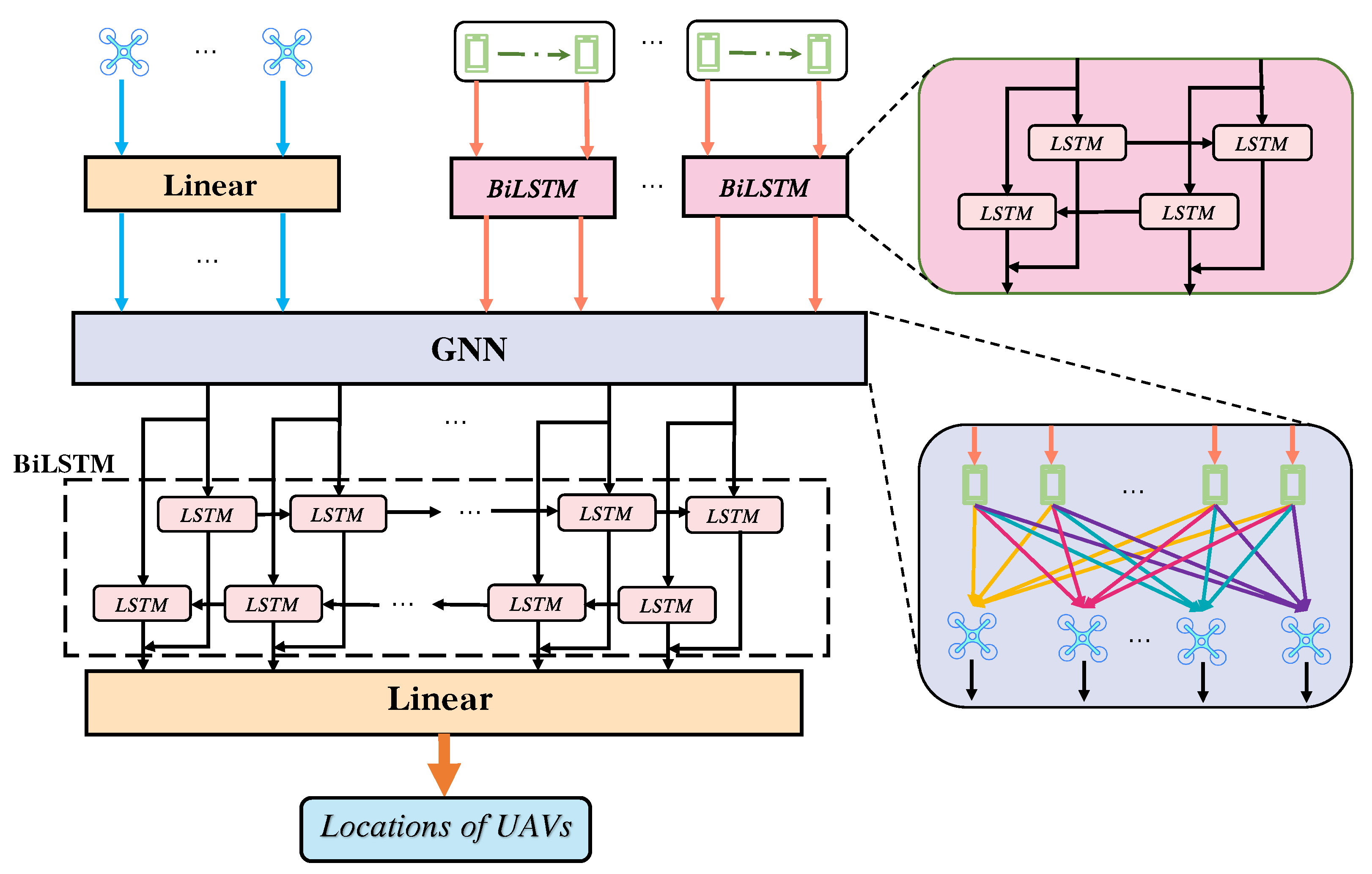
4.3. LGNN Based UAV Location Optimization
4.3.1. Unsupervised Learning-Based LGNN Training Method
4.3.2. Structure of LGNN
5. Performance Evaluation and Discussion
- LGNN-BF: In this scheme, the proposed LGNN is used to optimize the UAV-relay locations. However, the Bellman-Ford (BF) algorithm is used for relay path selection. The loss of LGNN is set as the opposite of the average Rate of relay paths calculated by BF algorithm.
- GA-RGNN: GA is used to optimize the locations of UAVs. GA generates a large population. Every individual in the population includes all the locations of UAVs. The fitness of individuals is set to the rate output from RGNN. In every iteration, the selection operator is used to keep individuals with higher rate alive and disuse other individuals with low rate. The crossover operator and mutation operator are applied to generate new individuals. The mutation rate of GA is set to 0.2, the scale of population is set as 100 and the multi-point crossover is taken as the crossover operator. The deterministic selection is taken as the selection operator to ensure the best individual could be kept and the top 30 percent of individuals are kept by GA while the left 70 percent individuals can be kept with a 0.3 probability.
- GA-BF: GA is set to optimize the locations of UAVs and the commucation rate output from Bellman-Ford algorithm is set as the fitness of individuals.
- MLP-RGNN: A MLP takes users’ locations as the input, indicating that the number of nodes in input layers is two times the number of users. There is one hidden layer with 128 nodes. The MLP outputs the locations of all UAVs in the output layer. ReLU is used as the activation function of the hidden layer. The opposite of the average rate calculated by RGNN is used as the loss value. The learning rate of MLP is 1e-4.
- MLP-BF: The hyper-parameters of MLP are the same as MLP-RGNN. Loss is set to the opposite of average rate calculated by the BF algorithm.
5.1. Simulation Configurations
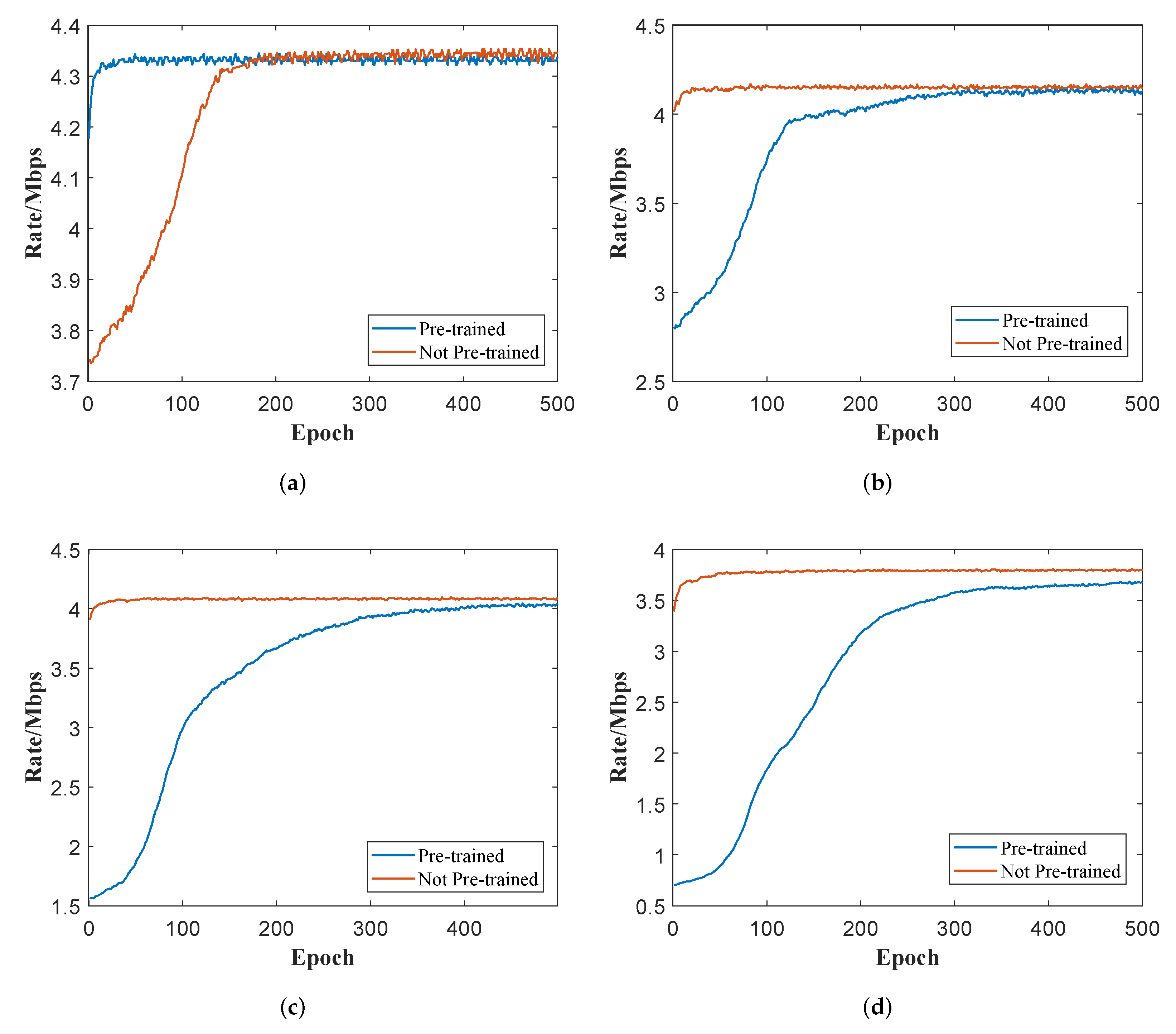
5.2. Performance of Pre-Trained RGNN and LGNN
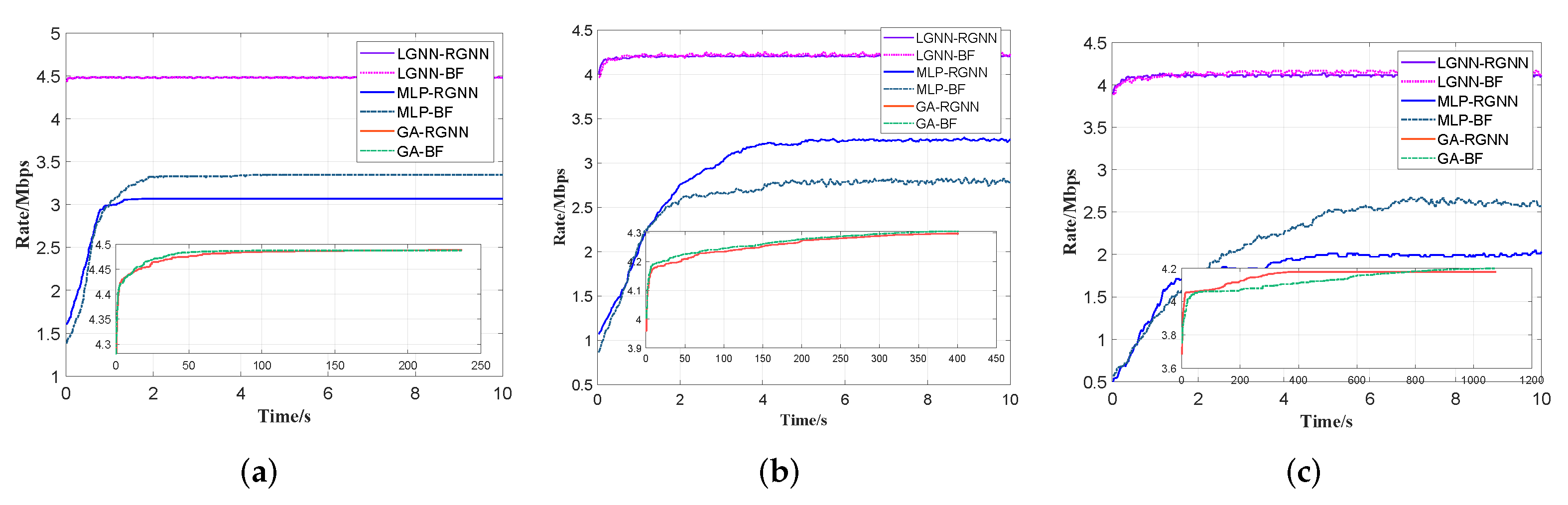
5.3. Optimality Analysis of the Proposed LGNN-RGNN Approach
5.4. Convergence Speed and Performance
5.5. Relation of and on Performance
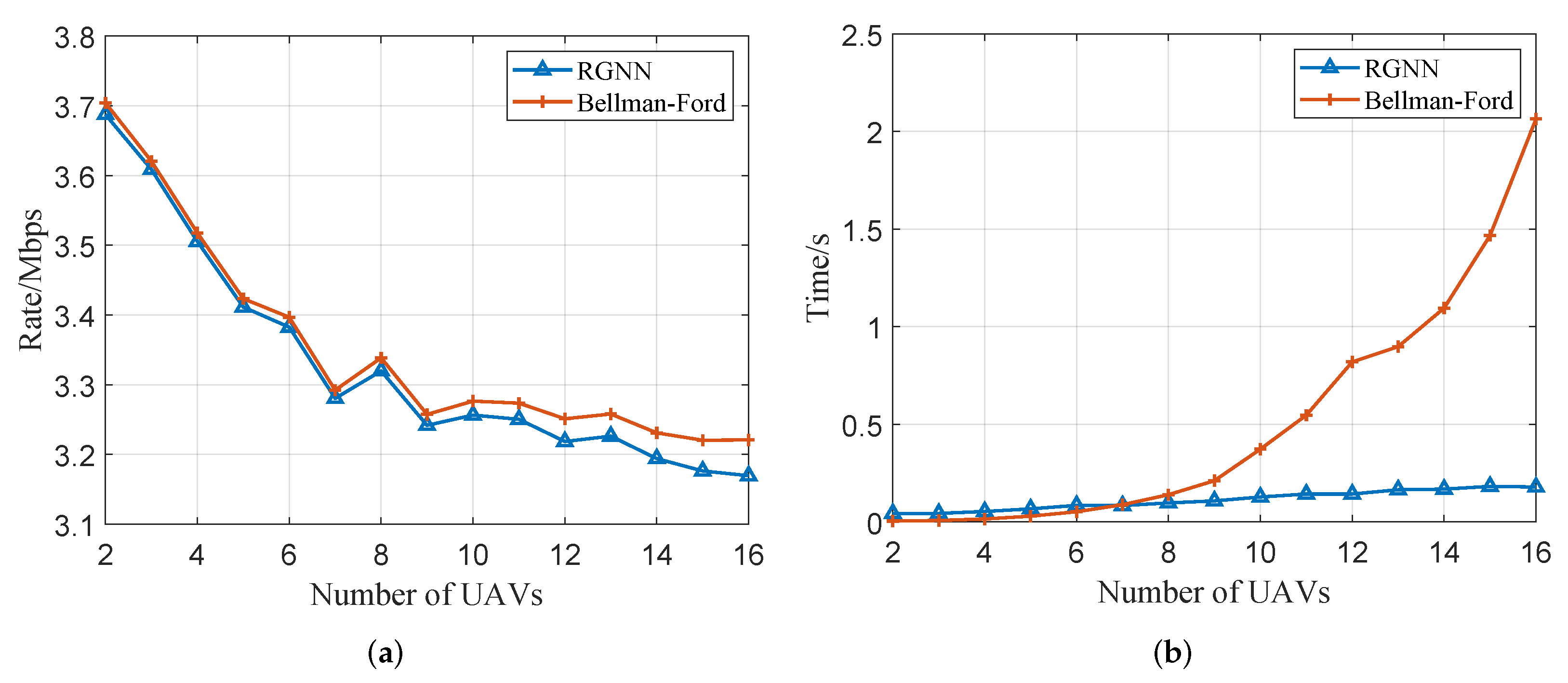
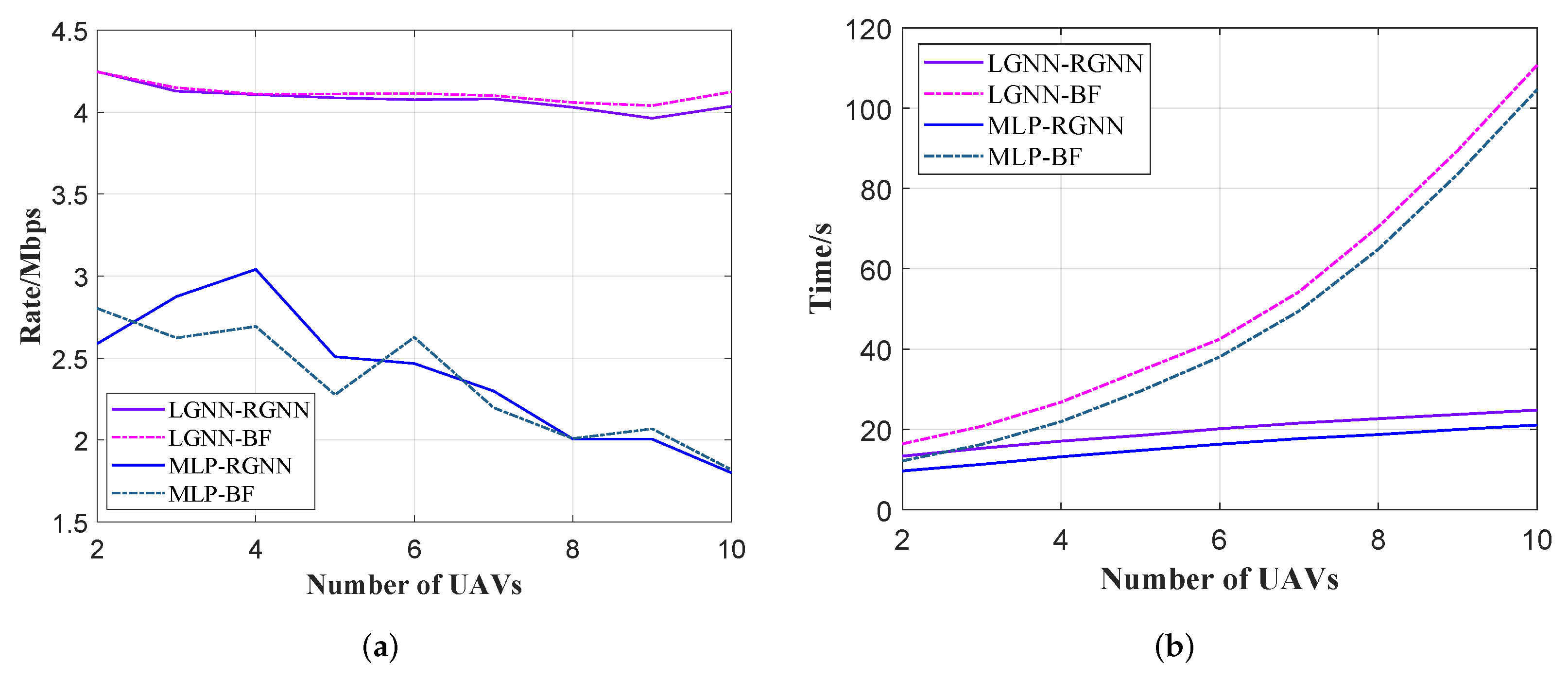
5.6. Performance in Large-Scale Networks
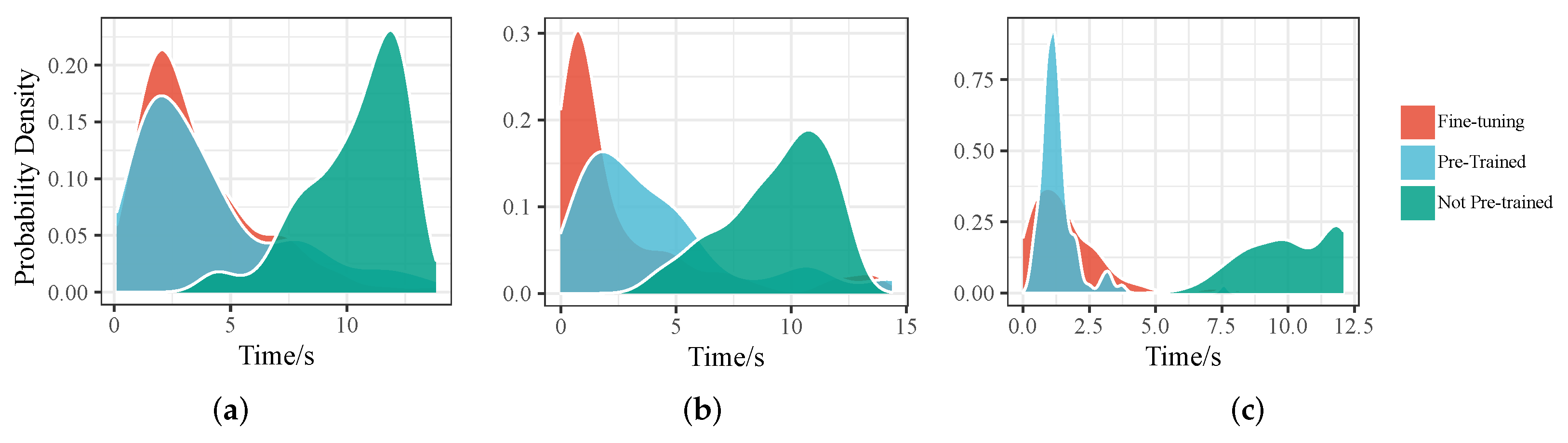
5.7. Performance on Robustness
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dang, S.; Amin, O.; Shihada, B.; Alouini, M.S. What should 6G be? Nat. Electron. 2020, 3, 20–29. [Google Scholar] [CrossRef]
- Alsamhi, S.H.; Ma, O.; Ansari, M.S.; Almalki, F.A. Survey on Collaborative Smart Drones and Internet of Things for Improving Smartness of Smart Cities. IEEE Access 2019, 7, 128125–128152. [Google Scholar] [CrossRef]
- Alsamhi, S.H.; Shvetsov, A.V.; Kumar, S.; Shvetsova, S.V.; Alhartomi, M.A.; Hawbani, A.; Rajput, N.S.; Srivastava, S.; Saif, A.; Nyangaresi, V.O. UAV Computing-Assisted Search and Rescue Mission Framework for Disaster and Harsh Environment Mitigation. Drones 2022, 6, 154. [Google Scholar] [CrossRef]
- Cheng, N.; Lyu, F.; Quan, W.; Zhou, C.; He, H.; Shi, W.; Shen, X. Space/Aerial-Assisted Computing Offloading for IoT Applications: A Learning-Based Approach. IEEE J. Sel. Areas Commun. 2019, 37, 1117–1129. [Google Scholar] [CrossRef]
- Gholami, A.; Torkzaban, N.; Baras, J.S.; Papagianni, C. Joint mobility-aware UAV placement and routing in multi-hop UAV relaying systems. In Proceedings of the International Conference on Ad Hoc Networks, Bari, Italy, 19–21 October 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 55–69. [Google Scholar]
- Zhong, X.; Guo, Y.; Li, N.; Chen, Y. Joint optimization of relay deployment, channel allocation, and relay assignment for UAVs-aided D2D networks. IEEE/ACM Trans. Netw. 2020, 28, 804–817. [Google Scholar] [CrossRef]
- Alsamhi, S.H.; Ma, O.; Ansari, M.S.; Gupta, S.K. Collaboration of Drone and Internet of Public Safety Things in Smart Cities: An Overview of QoS and Network Performance Optimization. Drones 2019, 3, 13. [Google Scholar] [CrossRef]
- Zeng, Y.; Zhang, R.; Lim, T.J. Wireless communications with unmanned aerial vehicles: Opportunities and challenges. IEEE Commun. Mag. 2016, 54, 36–42. [Google Scholar] [CrossRef]
- Yin, Z.; Jia, M.; Cheng, N.; Wang, W.; Lyu, F.; Guo, Q.; Shen, X. UAV-Assisted Physical Layer Security in Multi-Beam Satellite-Enabled Vehicle Communications. IEEE Trans. Intell. Transp. Syst. 2022, 23, 2739–2751. [Google Scholar] [CrossRef]
- Yin, Z.; Jia, M.; Wang, W.; Cheng, N.; Lyu, F.; Shen, X. Max-min secrecy rate for NOMA-based UAV-assisted communications with protected zone. In Proceedings of the 2019 IEEE Global Communications Conference (GLOBECOM), Waikoloa, HI, USA, 9–13 December 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Gupta, A.; Sundhan, S.; Gupta, S.K.; Alsamhi, S.; Rashid, M. Collaboration of UAV and HetNet for better QoS: A comparative study. Int. J. Veh. Inf. Commun. Syst. 2020, 5, 309–333. [Google Scholar] [CrossRef]
- Hou, T.; Liu, Y.; Song, Z.; Sun, X.; Chen, Y. Multiple antenna aided NOMA in UAV networks: A stochastic geometry approach. IEEE Trans. Commun. 2018, 67, 1031–1044. [Google Scholar] [CrossRef]
- Zhou, C.; Wu, W.; He, H.; Yang, P.; Lyu, F.; Cheng, N.; Shen, X. Deep reinforcement learning for delay-oriented IoT task scheduling in SAGIN. IEEE Trans. Wirel. Commun. 2020, 20, 911–925. [Google Scholar] [CrossRef]
- Xia, J.Y.; Li, S.; Huang, J.J.; Yang, Z.; Jaimoukha, I.M.; Gündüz, D. Metalearning-Based Alternating Minimization Algorithm for Nonconvex Optimization. IEEE Trans. Neural Netw. Learn. Syst. 2022. [Google Scholar] [CrossRef] [PubMed]
- Guo, F.; Yu, F.R.; Zhang, H.; Li, X.; Ji, H.; Leung, V.C. Enabling massive IoT toward 6G: A comprehensive survey. IEEE Internet Things J. 2021, 8, 11891–11915. [Google Scholar] [CrossRef]
- Ghaleb, S.M.; Subramaniam, S.; Zukarnain, Z.A.; Muhammed, A. Mobility management for IoT: A survey. Eurasip J. Wirel. Commun. Netw. 2016, 2016, 1–25. [Google Scholar] [CrossRef]
- Kandel, I.; Castelli, M. The effect of batch size on the generalizability of the convolutional neural networks on a histopathology dataset. ICT Express 2020, 6, 312–315. [Google Scholar] [CrossRef]
- Nguyen, D.C.; Ding, M.; Pathirana, P.N.; Seneviratne, A.; Li, J.; Niyato, D.; Dobre, O.; Poor, H.V. 6G Internet of Things: A comprehensive survey. IEEE Internet Things J. 2021, 359–383. [Google Scholar] [CrossRef]
- Shen, Y.; Shi, Y.; Zhang, J.; Letaief, K.B. Graph neural networks for scalable radio resource management: Architecture design and theoretical analysis. IEEE J. Sel. Areas Commun. 2020, 39, 101–115. [Google Scholar] [CrossRef]
- Wu, Z.; Pan, S.; Chen, F.; Long, G.; Zhang, C.; Philip, S.Y. A comprehensive survey on graph neural networks. IEEE Trans. Neural Netw. Learn. Syst. 2020, 32, 4–24. [Google Scholar] [CrossRef] [PubMed]
- Xu, K.; Hu, W.; Leskovec, J.; Jegelka, S. How powerful are graph neural networks? In Proceedings of the 7th International Conference on Learning Representations (ICLR 2019), New Orleans, LA, USA, 6–9 May 2019; pp. 1–17. [Google Scholar]
- Chen, Z.; Li, L.; Bruna, J. Supervised community detection with line graph neural networks. In Proceedings of the 7th International Conference on Learning Representations (ICLR 2019), New Orleans, LA, USA, 6–9 May 2019; pp. 1–24. [Google Scholar]
- Lim, J.; Ryu, S.; Park, K.; Choe, Y.J.; Ham, J.; Kim, W.Y. Predicting drug–target interaction using a novel graph neural network with 3D structure-embedded graph representation. J. Chem. Inf. Model. 2019, 59, 3981–3988. [Google Scholar] [CrossRef]
- Ma, Q.; Ge, S.; He, D.; Thaker, D.; Drori, I. Combinatorial optimization by graph pointer networks and hierarchical reinforcement learning. arXiv 2019, arXiv:1911.04936. [Google Scholar]
- Shen, Y.; Zhang, J.; Song, S.; Letaief, K.B. Graph neural networks for wireless communications: From theory to practice. arXiv 2022, arXiv:2203.10800. [Google Scholar]
- He, H.; Kosasihy, A.; Yu, X.; Zhang, J.; Song, S.; Hardjawanay, W.; Letaief, K.B. Graph neural network enhanced approximate message passing for MIMO detection. arXiv 2022, arXiv:2205.10620. [Google Scholar]
- Wang, H.; Wu, Y.; Min, G.; Miao, W. A graph neural network-based digital twin for network slicing management. IEEE Trans. Ind. Inform. 2020, 18, 1367–1376. [Google Scholar] [CrossRef]
- Sun, P.; Lan, J.; Li, J.; Guo, Z.; Hu, Y. Combining deep reinforcement learning with graph neural networks for optimal VNF placement. IEEE Commun. Lett. 2020, 25, 176–180. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Mozaffari, M.; Saad, W.; Bennis, M.; Debbah, M. Drone small cells in the clouds: Design, deployment and performance analysis. In Proceedings of the 2015 IEEE Global Communications Conference (GLOBECOM), San Diego, CA, USA, 6–10 December 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Saif, A.; Dimyati, K.; Noordin, K.A.; Shah, N.S.M.; Alsamhi, S.; Abdullah, Q. Energy-efficient tethered UAV deployment in B5G for smart environments and disaster recovery. In Proceedings of the 2021 IEEE 1st International Conference on Emerging Smart Technologies and Applications (eSmarTA), 10–12 August 2021; pp. 1–5. [Google Scholar]
- Galkin, B.; Kibilda, J.; DaSilva, L.A. Deployment of UAV-mounted access points according to spatial user locations in two-tier cellular networks. In Proceedings of the 2016 Wireless Days (WD), Toulouse, France, 23–25 March 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Huang, H.; Savkin, A.V. Reactive deployment of flying robot base station over disaster areas. In Proceedings of the 2018 IEEE International Conference on Robotics and Biomimetics (ROBIO), Kuala Lumpur, Malaysia, 12–15 December 2018; pp. 1665–1670. [Google Scholar] [CrossRef]
- Huang, H.; Savkin, A.V. A Method for Optimized Deployment of Unmanned Aerial Vehicles for Maximum Coverage and Minimum Interference in Cellular Networks. IEEE Trans. Ind. Inform. 2019, 15, 2638–2647. [Google Scholar] [CrossRef]
- Cicek, C.T.; Gultekin, H.; Tavli, B.; Yanikomeroglu, H. UAV base station location optimization for next generation wireless networks: Overview and future research directions. In Proceedings of the 2019 1st International Conference on Unmanned Vehicle Systems-Oman (UVS), Muscat, Oman, 5–7 February 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Sabzehali, J.; Shah, V.K.; Fan, Q.; Choudhury, B.; Liu, L.; Reed, J.H. Optimizing Number, Placement, and Backhaul Connectivity of Multi-UAV Networks. IEEE Internet Things J. 2022, 1. [Google Scholar] [CrossRef]
- Kang, Z.; You, C.; Zhang, R. Placement learning for multi-UAV relaying: A Gibbs sampling approach. In Proceedings of the ICC 2020–2020 IEEE International Conference on Communications (ICC), Dublin, Ireland, 7–11 June 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Košmerl, J.; Vilhar, A. Base stations placement optimization in wireless networks for emergency communications. In Proceedings of the 2014 IEEE International Conference on Communications Workshops (ICC), Sydney, Australia, 10–14 June 2014; pp. 200–205. [Google Scholar] [CrossRef]
- Kalantari, E.; Yanikomeroglu, H.; Yongacoglu, A. On the number and 3D placement of drone base stations in wireless cellular networks. In Proceedings of the 2016 IEEE 84th Vehicular Technology Conference (VTC-Fall), Montreal, QC, Canada, 18–21 September 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Plachy, J.; Becvar, Z.; Mach, P.; Marik, R.; Vondra, M. Joint Positioning of Flying Base Stations and Association of Users: Evolutionary-Based Approach. IEEE Access 2019, 7, 11454–11463. [Google Scholar] [CrossRef]
- Alsamhi, S.H.; Shvetsov, A.V.; Kumar, S.; Hassan, J.; Alhartomi, M.A.; Shvetsova, S.V.; Sahal, R.; Hawbani, A. Computing in the Sky: A Survey on Intelligent Ubiquitous Computing for UAV-Assisted 6G Networks and Industry 4.0/5.0. Drones 2022, 6, 177. [Google Scholar] [CrossRef]
- Chaudhri, S.N.; Rajput, N.S.; Alsamhi, S.H.; Shvetsov, A.V.; Almalki, F.A. Zero-padding and spatial augmentation-based gas sensor node optimization approach in resource-constrained 6G-IoT paradigm. Sensors 2022, 22, 3039. [Google Scholar] [CrossRef]
- Salh, A.; Audah, L.; Alhartomi, M.A.; Kim, K.S.; Alsamhi, S.H.; Almalki, F.A.; Abdullah, Q.; Saif, A.; Algethami, H. Smart Packet Transmission Scheduling in Cognitive IoT Systems: DDQN Based Approach. IEEE Access 2022, 10, 50023–50036. [Google Scholar] [CrossRef]
- Scarselli, F.; Gori, M.; Tsoi, A.C.; Hagenbuchner, M.; Monfardini, G. The Graph Neural Network Model. IEEE Trans. Neural Netw. 2009, 20, 61–80. [Google Scholar] [CrossRef] [PubMed]
- Greff, K.; Srivastava, R.K.; Koutník, J.; Steunebrink, B.R.; Schmidhuber, J. LSTM: A Search Space Odyssey. IEEE Trans. Neural Netw. Learn. Syst. 2017, 28, 2222–2232. [Google Scholar] [CrossRef] [PubMed]
- Graves, A.; Schmidhuber, J. Framewise phoneme classification with bidirectional LSTM and other neural network architectures. Neural Netw. 2005, 18, 602–610. [Google Scholar] [CrossRef] [PubMed]
- Yan-e, D. Design of intelligent agriculture management information system based on IoT. In Proceedings of the Fourth International Conference on Intelligent Computation Technology and Automation (ICICTA), Shenzhen, China, 28–29 March 2011; Volume 1, pp. 1045–1049. [Google Scholar] [CrossRef]
- Dan, L.; Xin, C.; Chongwei, H.; Liangliang, J. Intelligent agriculture greenhouse environment monitoring system based on IOT technology. In Proceedings of the 2015 International Conference on Intelligent Transportation, Big Data and Smart City, Halong Bay, Vietnam, 19–20 December 2015; pp. 487–490. [Google Scholar]
- Chiaraviglio, L.; Blefari-Melazzi, N.; Liu, W.; Gutiérrez, J.A.; Van De Beek, J.; Birke, R.; Chen, L.; Idzikowski, F.; Kilper, D.; Monti, P.; et al. Bringing 5G into rural and low-income areas: Is it feasible? IEEE Commun. Stand. Mag. 2017, 1, 50–57. [Google Scholar] [CrossRef]
- Maluleke, H.; Bagula, A.; Ajayi, O. Efficient airborne network clustering for 5G backhauling and fronthauling. In Proceedings of the 2020 16th International Conference on Wireless and Mobile Computing, Networking and Communications (WiMob), Thessaloniki, Greece, 12–14 October 2020; pp. 99–104. [Google Scholar]
- Liu, J.; Shi, Y.; Fadlullah, Z.M.; Kato, N. Space-air-ground integrated network: A survey. IEEE Commun. Surv. Tutor. 2018, 20, 2714–2741. [Google Scholar] [CrossRef]
- Gupta, L.; Jain, R.; Vaszkun, G. Survey of Important Issues in UAV Communication Networks. IEEE Commun. Surv. Tutor. 2016, 18, 1123–1152. [Google Scholar] [CrossRef]
- Wu, Q.; Zeng, Y.; Zhang, R. Joint Trajectory and Communication Design for Multi-UAV Enabled Wireless Networks. IEEE Trans. Wirel. Commun. 2018, 17, 2109–2121. [Google Scholar] [CrossRef]
- Mittal, S.; Bengio, Y.; Lajoie, G. Is a modular architecture enough? arXiv 2022, arXiv:2206.02713. [Google Scholar]
- Bellman, R. On a routing problem. Q. Appl. Math. 1958, 16, 87–90. [Google Scholar] [CrossRef]
- Schulman, J.; Moritz, P.; Levine, S.; Jordan, M.; Abbeel, P. High-dimensional continuous control using generalized advantage estimation. In Proceedings of the 4th International Conference on Learning Representations (ICLR), San Juan, Puerto Rico, 2–4 May 2016; pp. 1–14. [Google Scholar]
- Hendrycks, D.; Mazeika, M.; Kadavath, S.; Song, D. Using self-supervised learning can improve model robustness and uncertainty. In Proceedings of the Advances in Neural Information Processing Systems 32: Annual Conference on Neural Information Processing Systems 2019 (NeurIPS 2019), Vancouver, BC, Canada, 8–14 December 2019; pp. 1–13. [Google Scholar]
- Qiu, X.; Sun, T.; Xu, Y.; Shao, Y.; Dai, N.; Huang, X. Pre-trained models for natural language processing: A survey. Sci. China Technol. Sci. 2020, 63, 1872–1897. [Google Scholar] [CrossRef]
- Holland, J.H. Genetic algorithms. Sci. Am. 1992, 267, 66–73. [Google Scholar] [CrossRef]




| Parameter Definition | Notation | Value |
|---|---|---|
| Number of User Pairs in small-scale network | K (or ) | [2, 20] |
| Number of User Pairs in large-scale network | K (or ) | [50, 250] |
| Number of UAVs in small-scale network | M (or ) | [2, 10] |
| Number of UAVs in large-scale network | M (or ) | [10, 35] |
| Network area in small-scale network | ∖ | [100, 500] km2 |
| Network area in large-scale network | ∖ | [500, 1750] km2 |
| Learning rate of RGNN | 0.001 | |
| Learning rate of LGNN | 0.0001 | |
| Transmission Power | P | 0.1 w |
| Noise Power | −174 dBm/Hz | |
| Path-loss constant | −40 dB | |
| Path-loss exponent | 2 | |
| UAV communication coverage range | 5.0 km |
| (a) Performance onfor Different Algorithms | (b) Performance onfor Different Algorithms | ||||
| Algorithms | Rate/Mbps | Computation Time/s | Algorithms | Rate/Mbps | Computation Time/s |
| MLP | 2.24 | 10.59 | MLP | 2.31 | 20.03 |
| Greedy | 3.03 | 0.09 | Greedy | 3.00 | 0.13 |
| LGNN-RGNN (DI) | 3.79 | 0.05 | LGNN-RGNN (DI) | 3.44 | 0.06 |
| LGNN-RGNN (FT) | 3.88 | 7.98 | LGNN-RGNN (FT) | 3.65 | 15.72 |
| (c) Performance onfor Different Algorithms | (d) Performance onfor Different Algorithms | ||||
| Algorithms | Rate/Mbps | Computation Time/s | Algorithms | Rate/Mbps | Computation Time/s |
| MLP | 2.15 | 21.88 | MLP | 1.71 | 48.68 |
| Greedy | 2.67 | 0.17 | Greedy | 2.36 | 0.22 |
| LGNN-RGNN (DI) | 3.22 | 0.08 | LGNN-RGNN (DI) | 3.02 | 0.15 |
| LGNN-RGNN (FT) | 3.43 | 15.73 | LGNN-RGNN (FT) | 3.18 | 44.79 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Fu, L.; Cheng, N.; Sun, R.; Luan, T.; Quan, W.; Aldubaikhy, K. Joint Flying Relay Location and Routing Optimization for 6G UAV–IoT Networks: A Graph Neural Network-Based Approach. Remote Sens. 2022, 14, 4377. https://doi.org/10.3390/rs14174377
Wang X, Fu L, Cheng N, Sun R, Luan T, Quan W, Aldubaikhy K. Joint Flying Relay Location and Routing Optimization for 6G UAV–IoT Networks: A Graph Neural Network-Based Approach. Remote Sensing. 2022; 14(17):4377. https://doi.org/10.3390/rs14174377
Chicago/Turabian StyleWang, Xiucheng, Lianhao Fu, Nan Cheng, Ruijin Sun, Tom Luan, Wei Quan, and Khalid Aldubaikhy. 2022. "Joint Flying Relay Location and Routing Optimization for 6G UAV–IoT Networks: A Graph Neural Network-Based Approach" Remote Sensing 14, no. 17: 4377. https://doi.org/10.3390/rs14174377
APA StyleWang, X., Fu, L., Cheng, N., Sun, R., Luan, T., Quan, W., & Aldubaikhy, K. (2022). Joint Flying Relay Location and Routing Optimization for 6G UAV–IoT Networks: A Graph Neural Network-Based Approach. Remote Sensing, 14(17), 4377. https://doi.org/10.3390/rs14174377