Abstract
New scattering models are constantly emerging to extract the detailed polarization information of ground targets. They contribute to the refined interpretation of Polarimetric Synthetic Aperture Radar (PolSAR) images. However, an increasingly prominent problem lies ahead of model decomposition methods when there are similar scattering models for a decomposition scheme. It is difficult to separate the polarization power of similar scattering mechanisms reasonably and robustly. Therefore, in this paper, we first analyze the necessity of orthogonality between scattering models. Following this, we propose two mutually orthogonal rank-1 scattering models, which can degenerate to mostly current scattering models. The orthogonality and adaptability of scattering models are considered in the model derivation. Simulated PolSAR data, real ALOS-2/PALSAR-2, GF-3, and E-SAR data are selected to validate the proposed method. As shown by the results, first, the proposed method enhances the double-bounce scattering contribution in urban areas and maintains the volume-scattering contribution in vegetation areas because it separates the polarization power of different scattering mechanisms more reasonably. Second, the proposed method is powerful in the robust interpretation of different ground targets, resulting from the orthogonality of scattering models. These two characteristics of orthogonal scattering models are expected to play a positive role in large-scale applications, especially in land-cover classification.
1. Introduction
Polarimetric Synthetic Aperture Radar (PolSAR) is sensitive to the shape, orientation, and dielectric properties of ground targets, which can be effectively extracted by decomposition technology [1,2,3,4,5,6]. For decomposition technology, a key is to separate different scattering mechanisms of natural media [7]. To achieve this end, scholars have made many efforts, which can be mainly divided into two categories [8]. One is coherent decomposition based on scattering matrices. The other is incoherent decomposition based on coherency/covariance scattering matrices. Among them, the latter plays an essential role in parameter inversion for multilook PolSAR images.
An incoherent decomposition is based on eigenvalue/eigenvector. It interprets the echo signals from ground targets into three orthogonal scattering processes, which correspond to three orthogonal eigenvectors [9]. However, the interpretation of eigenvalues and eigenvectors is difficult because there is no guarantee that each eigenvector corresponds to a known scattering mechanism. In addition, an eigenvector cannot describe a scattering process with high polarization entropy [10].
The other incoherent decomposition is based on scattering models, which have been widely applied to parameter inversion, because of their clear physical meaning. A landmark work is the three-component decomposition proposed by Freeman and Durden [11]. It established three scattering models with consideration of the geometrical/physical properties of the illuminated targets. Subsequently, based on Freeman decomposition, some new scattering models have been proposed to promote the development of the PolSAR signal interpretation.
From the perspective of the non-reflection symmetry elements, Yamaguchi, Singh, and Han introduced helix, mixed dipole, and rotated dihedral scattering models to describe the scattering components recorded by polarization [12,13,14]. In addition, Singh et al. [15] proposed oriented dipole and compound dipole scattering models to interpret the scattering components associated with polarization . They visualize the interaction process between non-reflection symmetry targets and SAR signals. Furthermore, from the perspective of the diagonal elements, some cross-scattering models had been proposed to further account for and polarizations [16,17,18,19]. They characterize the scattering contribution generated by dihedral structures in the cross-polarization. However, it can be found that: (1) four scattering models—surface, double-bounce, oriented dipole, and compound dipole scattering models—account for the polarization; (2) six scattering models—surface, double-bounce, helix, mixed dipole, rotated dihedral, and cross-scattering models—account for the polarization; and (3) cross and the above rank-1 non-reflection scattering models all account for the polarization. It should be noted that many scattering models are not orthogonal to each other, and some are very similar. Furthermore, similar/same scattering models existing in a decomposition scheme also emerge. As a result, the polarization power is easy to misassign to similar scattering models, and the scattering mechanisms of ground targets are difficult to separate. For example, the combination of cross- and surface-scattering models can generate a similar/same form as the volume-scattering model. In such a case, the same/similar PolSAR response can sometimes be interpreted as a volume-scattering process, and sometimes as a combination of surface-scattering and cross-scattering processes. This obviously violates the original intention of polarization SAR decomposition [20].
In this paper, we assert that the above scattering models enrich the interpretation of PolSAR images. However, it is expected that when using these scattering models to interpret PolSAR images, the scattering mechanisms in the decomposition scheme should be as distinguishable from each other as possible. Therefore, the core idea of this paper is to investigate the negative impacts of a decomposition scheme with similar/same scattering models, and demonstrate the advantages of orthogonal scattering models. In detail, we try to propose two scattering models. Unlike most of the current scattering models, the proposed models are orthogonal to each other. The two scattering mechanisms can be well separated from each other. Furthermore, their generality is sufficient to degenerate into most existing scattering models, enabling them to explore the scattering properties of different targets.
The rest of this paper is organized as follows. In Section 2, the necessity of orthogonality between scattering models is analyzed. The derivation of general orthogonal scattering models is introduced in Section 3. In addition, this section presents a decomposition scheme incorporating orthogonal scattering models. In Section 4, some Monte Carlo simulations of PolSAR data are carried out and used to test the proposed method. In addition, real full polarization SAR datasets with different frequencies acquired over different areas are selected to validate the proposed method. The advantages of general orthogonal scattering models in separating the scattering mechanisms of natural media are demonstrated in this section. Further discussions and conclusions are given in Section 5 and Section 6.
2. The Advantages of Orthogonal Scattering Models
The PolSAR signals from distributed targets can be expressed by a coherency matrix [8]:
To simplify, (1) is re-expressed as
The coherency matrix reflects the dielectric properties and structural characteristics of ground targets. Model-based decompositions can extract the geometric and physical information contained in the coherency matrix [11]. They establish the mapping relationship between scattering models and the geometric and physical features of ground targets. We introduce the Freeman three-component decomposition and its extended decompositions in the following part. Furthermore, the advantages of orthogonal scattering models are analyzed.
2.1. Freeman Three-Component Decomposition and Its Extended Decompositions
In the Freeman three-component decomposition, the scattering processes of ground targets are described by three scattering models: volume, surface, and double-bounce scattering models. The forms of these three scattering models can be expressed by [21]:
where and are model parameters associated with the relative dielectric constant of the ground and vertical surfaces, respectively.
Based on the Freeman three-component decomposition, some novel scattering models have been proposed to account for the nine elements in the coherency matrix. For the non-reflection symmetry elements, the representative scattering models are helix, oriented dipole, compound dipole, and mixed dipole scattering models [12,13,15]. Their forms can be expressed as:
These models enrich the understanding of PolSAR signals coming from ground targets with non-reflection symmetry. For the diagonal elements, many novel cross-scattering models have been used to further interpret the scattering characteristics associated with and polarizations. These representative cross-polarization scattering models can be expressed as [16,17,18]:
where is the polarization orientation angle (POA). These models contribute to the interpretation of PolSAR images for urban areas. It can be found that, with the development of model-based decomposition, there are many scattering models to describe the nine elements in the coherency matrix. However, the ensuing concerns have not received enough attention. In the following, we focus on analyzing the necessity and advantages of scattering models being orthogonal to each other.
2.2. The Advantages of Orthogonal Scattering Models
For a decomposition scheme that incorporates the cross-scattering model into Freeman decomposition, the combination of surface- and the cross-scattering models can be expressed as [16,17,18,19]:
In many cases, the value of is small [22], and the value of is basically equal to one [16,17,18,19]. In such a case, it can be noted that (6) is similar to the volume-scattering model in (3). In addition, current works assume when the double-bounce scattering contribution is more significant than the surface-scattering contribution [11]. As a result, (6) has almost the same form as the volume-scattering model:
This shows that the same PolSAR response signal can be interpreted as a volume-scattering process, or a combination of surface- and cross-scattering processes, showing that the decomposition scheme cannot effectively separate these scattering contributions from the total polarization power. Furthermore, the volume-scattering process corresponds to random scatterers that are much smaller than the radar wavelength. The combination of surface- and cross-scattering processes corresponds to the combination of flat and random dihedral structures. The same PolSAR signal reflects two scatterers with entirely different geometric/physical properties, which significantly violates the original intention of model-based decomposition technology—separating different scattering mechanisms from PolSAR data and further analyzing the geometric and physical properties of ground targets [20].
Furthermore, a Cartesian coordinate consisting of three polarizations is used to further analyze this issue, as shown in Figure 1a. Without loss of generality, two similar and two orthogonal scattering models are shown in Figure 1b,c. The contributions of these two similar scattering models to the different polarizations are almost identical. This causes these two scattering mechanisms of natural media to not be separated well. However, the contributions of the orthogonal scattering models to the different polarizations are clearly differentiated, with one accounting for the and polarizations and the other for the polarization. This means that these two scattering mechanisms can be identified from PolSAR echo signals, showing the advantages of orthogonal scattering models.
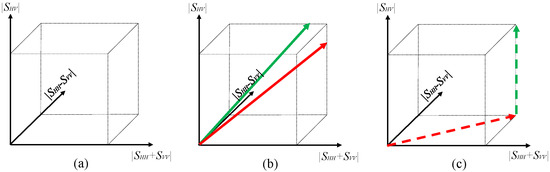
Figure 1.
Cartesian coordinates and the representation of scattering models in Cartesian coordinates. (a) Cartesian coordinate. (b) The representation of similar scattering models (solid line). (c) The representation of orthogonal scattering models (dashed line).
3. General Orthogonal Scattering Models
3.1. The Derivation of Orthogonal Scattering Models
There is a scatterer that is symmetrical about the horizontal or vertical direction. The scattering matrix corresponding to a scatterer can be expressed as [23]
and its corresponding coherency matrix is given by
where represents conjugation. The scatterer can generate a significant cross-polarization contribution when the scatterer is oriented with respect to the radar look direction, such as oriented buildings and terrain slopes [24,25]. To fit the actual situation, the coherency matrix is rotated by POA
where represents the conjugate transpose and represents the POA rotation matrix
Furthermore, researchers [26,27,28] found that when a scatterer is oriented with respect to the radar direction, and the scatterer is combining two structures separated by a radar distance, the helix angle (HA) is necessary to describe the scattering process of the scatterer. To make the scattering model (10) suitable for different environments, (10) is rotated by HA
with
where is the HA rotation matrix
Thus, one general scattering model is proposed. However, there are usually different scatterers in a common resolution, and only (12) is not sufficient to describe the scattering processes of ground targets. It is necessary to design the other scattering model. Here, to simplify the difficulty of model inversion, it is assumed that these two scatterers share the same POA and HA. We keep the orthogonality of scattering models in mind, and the other scattering model can then be expressed as
where
In such a case, two mutually orthogonal scattering models are proposed. For convenience, the two orthogonal scattering models presented in (12) and (14) are called orthogonal model 1 and orthogonal model 2. The characteristics of these two scattering models are further analyzed in the following.
3.2. Further Research on Orthogonal Scattering Models
First, we investigate the similarity degree between the two orthogonal scattering models. The similarity parameter proposed by Yang et al. is used to evaluate the similarity degree of the two proposed models. The similarity parameter can be expressed by [29]
where and are Pauli scattering vectors corresponding to orthogonal scattering models 1 and 2, respectively. represents the square sum of the absolute values of . It can be found that , which means that the similarity between the two scattering models, is zero. This supports the notion that the two scattering mechanisms can be effectively separated from each other [9].
Following this, the physical meaning of the proposed scattering models is investigated. The Pauli decomposition has been demonstrated to be a robust way to interpret the scattering process of ground targets [9]. When , orthogonal scattering models 1 and 2 degenerate to the first and second Pauli scattering components, respectively. The Pauli decomposition is an example to validate the proposed models.
In addition, as shown in Table 1, there is a significant connection between the orthogonal scattering models and surface and double-bounce scattering models. Correspondingly, without loss of generality, assuming and , the relative dielectric constant of the ground surface reflected by can be given by
where represents the local incidence angle on the ground surface. In addition, the relative dielectric constant of the vertical surface reflected by can be given by
with
where is the phase difference between horizontal and vertical polarization SAR signals, and represents the local incidence angle on a vertical surface.

Table 1.
Connections between orthogonal scattering models and surface and double-bounce scattering models.
Furthermore, in addition to describing the scattering characteristics of reflection symmetry targets, the scattering features of non-reflection symmetry targets can also be investigated by orthogonal scattering models. As shown in Table 2 (taking orthogonal scattering model 1 as an example), the proposed models can degenerate into current non-reflection symmetry scattering models with rank 1. It can be summarized that, being inherited from the existing scattering models, the orthogonal scattering models have high adaptability to different ground targets. They can be applied to homogeneous forests and anisotropic urban scenes. Meanwhile, the proposed scattering models are orthogonal to each other, guaranteeing that these two scattering mechanisms can be separated from each other.

Table 2.
Connections between orthogonal scattering models and non-reflection symmetry scattering models.
3.3. Two and Three-Component Decomposition Incorporating Orthogonal Scattering Models
Incorporating two general orthogonal scattering models, a two-component decomposition scheme is established as
This decomposition is only expected to be suitable for nonvegetated areas because the volume-scattering process is not considered in the decomposition scheme. However, the volume-scattering process plays a critical role in the interpretation of PolSAR images [30,31,32]. Therefore, to improve the applicability of the decomposition in vegetated areas, the Freeman volume-scattering model is added to (18), and a new three-component decomposition scheme can be proposed by
It can be found that the volume-scattering model is not orthogonal to the proposed models. In fact, it is difficult to achieve this goal because it is impossible to further derive one orthogonal scattering model in addition to the two proposed orthogonal scattering models [33]. However, the rank of the majority of volume-scattering models is three [30,31,32]. One scattering model with rank 1 cannot reflect volume-scattering characteristics. Therefore, the proposed decomposition separates the different scattering mechanisms as much as possible while considering the volume-scattering process.
Furthermore, it has been demonstrated that the orthogonal scattering models can describe the surface, double-bounce, and non-reflection symmetry scattering processes. However, for the proposed decomposition scheme (19), the orthogonal scattering models are mainly interpreted as surface and double-bounce scattering models, as shown in Table 1. The non-reflection symmetry components are regarded as generated by the rotation of orthogonal scattering models [27,28]. In such a case, without loss of generality, and are assumed to hold for the decomposition scheme (19). The orthogonal scattering models 1 and 2 degenerate to the surface and double-bounce scattering models.
To invert model parameters in (19), first, for simplicity, is estimated by the non-reflection symmetry elements of the coherency matrix [24,25,26,27,28]
Subsequently, there are four unknown parameters (note that ) and four equations derived by reflection symmetry elements:
In (21), to render the analytical solution of the proposed decomposition scheme easy to obtain and to provide it a simplified expression, without loss of generality, the parameter transformation of is carried out
Following this, from (21a) − (21b) + (21c)
To solve and , substitute (23) into (21d)
Subsequently, from (21b) − (21c)
To solve and , substitute (25) into (21d)
Finally, is estimated by
The scattering power of each scattering component can then be obtained as
Therefore, the analytical solution of the decomposition scheme can be obtained.
4. Results and Analysis
In this paper, simulation data and real data were used to test the advantages of the proposed decomposition. The Xiang five-component decomposition model (5XD) method [18] and the Singh seven-component decomposition model (7SD) [13] were selected for comparative analysis. Based on classic decomposition, 5XD adds a cross-scattering model to further account for the and polarizations, and 7SD adds four non-reflection symmetry scattering models to account for non-reflection symmetry polarization states. These two decompositions are effective and representative, so they were selected to verify the proposed scattering model. The Freeman volume-scattering model in [11] is employed by the above three decompositions.
4.1. Evaluation Based on Monte Carlo Simulation Data
The simulation of PolSAR data can use different approaches, under the limitation that simulation data are appropriate for evaluating various decomposition schemes. The Monte Carlo simulation method widely used elsewhere is adopted in this paper to simulate PolSAR data [8,34]. First, based on the Monte Carlo simulation method, coherency matrices were simulated by 5XD, 7SD, and the proposed decomposition. The simulated coherency matrices were then decomposed by the above three decompositions. The performance of different decompositions was evaluated by comparing the consistency of the simulation parameters and the decomposed results. During the simulation process, the geometry of the SAR system and the polarimetric properties of ground targets were provided, as listed in Table 3. The parameters of the simulated SAR system refer to the DLR E-SAR system [35]. The simulation procedure is as follows:

Table 3.
The geometry of the acquisition system and polarization properties of ground targets.
(1) Generation of the original coherency matrix. According to the assumed contributions of the different scattering mechanisms, and the geometrical/physical parameters provided in Table 3, the original coherency matrices can be simulated by the scattering models in 5XD, 7SD, and the proposed decomposition, denoted as , respectively.
(2) Add noise to the original coherency matrix. Randomly generate a complex vector that is complex distributed with zero mean and 0.5 variances [8]. Subsequently, multiply it with the triangular matrices derived by the Cholesky decomposition of the original coherency matrices. In such a case, the complex single-look vectors can be expressed as
(3) Generation of simulation data. Perform five-multilook processing on the generated complex single-look vector to generate simulated polarization SAR data
The mean ratios of different scattering mechanisms for simulation data and decomposition results are shown in Table 4, Table 5 and Table 6. To avoid the influence of rank deficiency on the evaluation results [18], the double-bounce scattering contribution in the simulation data of 5XD is fixed as zero. In addition, the relative ratio between surface, double-bounce, and volume-scattering contributions are similar for the simulation data of 7SD and the proposed decomposition. It can be seen that the decomposition results of 5XD and 7SD are significantly different from the simulated ratios. However, the results derived from the proposed decomposition are consistent with the simulation ratios, which strongly validates the proposed decomposition. This can be attributed to the two orthogonal scattering models with zero similarity in the proposed decomposition scheme. These two scattering processes can be separated from each other. Even if PolSAR data are affected by noise or other external environments, orthogonal scattering models will not excessively absorb the power unrelated to itself. In detail, for 5XD, the volume-scattering contribution is overestimated, but the cross and double-bounce scattering powers are underestimated, which is consistent with the above analysis. This phenomenon can be explained by the fact that the volume-scattering model is similar to the combination of surface and cross-scattering models, which causes the ambiguous allocation of the scattering power. This shows the negative impact of some similar scattering models on a decomposition scheme [36]. In addition, for 7SD, the difference between the original simulation ratio and decomposition results is caused by seven non-orthogonal scattering models. For example, it can be found that the combination of degenerated surface and helix (or mixed dipole) scattering models can formulate a similar form with the volume-scattering model on the diagonal elements. This causes a challenge for 7SD to separate the polarization power of different scattering mechanisms. This further confirms the necessity of establishing orthogonal scattering models.

Table 4.
The results of simulation data for 5XD (%).

Table 5.
The results of simulation data for 7SD (%).

Table 6.
The results of simulation data for the proposed method (%).
4.2. Evaluation Based on Images Dominated by Urban Building Areas
PolSAR data acquired over Changsha, China, by the ALOS-2/PALSAR-2 system were selected to further validate the proposed decomposition method. The color-coded SAR image of Pauli decomposition is shown in Figure 2, which covers various ground targets, such as moderately and highly oriented buildings, forests, and a wetland park. To reduce the impact of speckle noise on the decomposition results, and make the azimuth and range resolutions comparable (30 m × 30 m), the PolSAR image was processed with a multilook of 10 in the azimuth direction and 6 in the range direction.
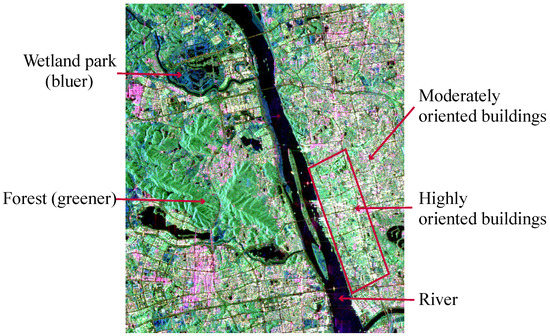
Figure 2.
The color-coded image of Pauli decomposition of the ALOS-2/PALSAR-2 dataset (red: , green: , blue: ).
The decomposition results derived by 5XD, 7SD, and the proposed method are shown in Figure 3. The surface and double-bounce scattering models are degenerated by the proposed orthogonal scattering models. It can be observed that the green building area in Figure 3a,b is decomposed into red or yellow in the image in Figure 3c. This can be attributed to the proposed decomposition allocating more scattering powers to the double-bounce scattering. For forest areas, the results of the proposed decomposition are greener than those of 5XD and 7SD. The above results demonstrate that the proposed method enhances the double-bounce scattering contribution for the building areas while maintaining the volume-scattering contribution in the forest areas. The reason for this observation is that, for the proposed decomposition, there are no similar scattering models with the double-bounce and volume-scattering models, which ensures that double-bounce and volume-scattering models can well absorb the scattering powers generated by dihedral structures and a cloud of dipoles, respectively.
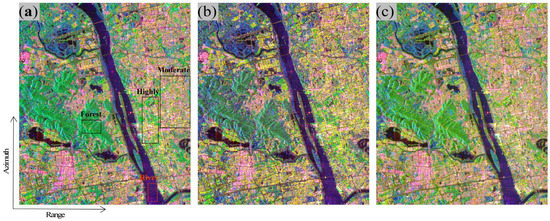
Figure 3.
The color-coded images of the decomposition results for the ALOS- 2/PALSAR-2 dataset (red: double-bounce; green: volume scattering; blue: surface scattering). (a) X5D decomposition method. (b) 7SD decomposition method. (c) Proposed decomposition method.
As shown in Figure 3a, four areas—moderately oriented buildings, highly oriented buildings, forests, and rivers—were selected for a quantitative comparison. Table 7 shows the mean ratios of scattering powers associated with different scattering mechanisms to the total scattering power. For moderately and highly oriented building areas, compared with 5XD and 7SD, the proposed method estimates the most double-bounce scattering contributions. The reason for this is that (1) for the proposed decomposition, the double-bounce scattering model degenerated from the orthogonal scattering model is significantly different from the other two scattering models, and (2) the double-bounce scattering model is general enough. It considers the orientations of the dihedral structures, including POA and HA. For forest areas, compared with 5XD and 7SD, the proposed decomposition estimates the most volume-scattering contributions. This is because, for 5XD, surface- and cross-scattering models can jointly formulate a similar form with the volume-scattering model. For 7SD, four non-orthogonal scattering models account for polarization. The above two shortcomings lead to the ambiguous interpretation of polarization. In addition, 5XD and 7SD allocate much power to the surface-scattering process (even higher than the building areas with pavement and roof structures for 7SD). The reason behind this is further analyzed. When the underestimation of volume-scattering contribution occurs, there is much residual power. In such a case, the surface contribution closely associated with is overestimated. The decomposition results of forest areas show that, when the power of a specific polarization channel is misallocated, the scattering-power estimation of all scattering mechanisms will be biased. This observation further emphasizes the necessity of orthogonality between different scattering models, because orthogonal scattering models mainly contribute to the different polarizations, as shown in Figure 1. As expected, the dominant scattering mechanism extracted by these three decompositions is the surface scattering for river areas. The above analysis indicates that the proposed decomposition can reasonably estimate the contribution of different scattering mechanisms, regardless of building, forest, and river areas.

Table 7.
The mean ratios of the different scattering powers for the different decomposition methods (%).
The performance of the proposed decomposition in separating the power of different scattering mechanisms is further analyzed. The ratio of the scattering power assigned to the different polarization channels of different scattering mechanisms to the total power is shown in Figure 4. It can be observed that the proposed decomposition allocates significant scattering power of polarization to surface scattering for river areas, and remarkable scattering power of polarization to double-bounce scattering for urban areas. In addition, basically all the scattering power is allocated to volume scattering for forest areas. These results are consistent with the morphological characteristics of the main scatterers in river, urban, and forest areas. This shows the potential of orthogonal scattering models in distinguishing different groundcover, which is worthy of further investigation.

Figure 4.
The ratio of the scattering power allocated to the different polarization channels of different scattering mechanisms to the total power. From left to right are the surface, double-bounce, and volume scattering. From top to bottom are the , , and polarizations. (a–c) Power distribution ratio derived with 5XD; (d–f) Power distribution ratio derived with 7SD; (g–i) Power distribution ratio derived with the proposed decomposition.
To further test the proposed decomposition, the other complementary PolSAR data acquired over Beijing, China, by the GF-3 SAR system were selected as shown in Figure 5. After multilook and filtering operations, the azimuth and range resolutions are about 13 m. The area at the bottom right of the image is covered by forest. The black portion of the image is water. Beyond those, most of the portions of this image are buildings. The results derived with different decomposition methods are shown in Figure 5. For urban areas, the “yellow” decomposition results of 5XD and 7SD are turned into “red” in the results of the proposed decomposition. In addition, for forest areas, the “green” color in the 7SD decomposition results is darker than those in the 5XD and proposed decomposition results. It can be concluded that, for PolSAR data with different frequencies and resolutions, urban buildings and forest canopies are well recognized into double-bounce and volume-scattering structures by the proposed method, respectively. This further demonstrates the powerful ability of orthogonal scattering models to separate the contributions of different scattering mechanisms.

Figure 5.
The color-coded images of the decomposition results for the GF-3 dataset (red: double-bounce scattering; green: volume scattering; blue: surface scattering). (a) 5XD decomposition method. (b) 7SD decomposition method. (c) Proposed decomposition method.
4.3. Evaluation Based on Image Dominated by Vegetation Areas
Here, we discuss whether different decompositions can robustly separate the contributions of different scattering mechanisms for similar ground covers. The L-band E-SAR dataset covering evenly sown crops was selected to test these models. The color-coded SAR image of Pauli decomposition and the ground truth map are shown in Figure 6. The corresponding incidence angle ranges from 25° to 55°. After multilook processing, the resolution of the slant range and azimuth direction is about 4 m. In addition, a refined Lee filter with a 5 × 5 window was applied to reduce the impact of speckle noise on the PolSAR image interpretation. This test site is covered with various crops, such as winter wheat, sugar beet, winter barley, rape, and maize. The SAR image was acquired on 3 May 2006, and the growth status of different crops is shown in Figure 7.
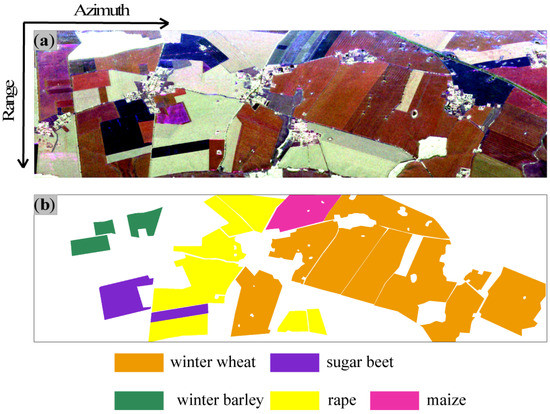
Figure 6.
(a) The color-coded image of Pauli decomposition of the AgriSAR dataset (red:
, green: , blue: ). (b) The ground truth map.

Figure 7.
Pictures of the growth status of five crops. (a) Winter wheat. (b) Sugar beet. (c) Winter barley. (d) Rape. (e) Maize.
The results of different decompositions are shown in Figure 8. It can be observed that the results of the three decompositions are similar. The volume-scattering contribution is significant in rape areas, and the surface-scattering contribution is dominant in maize areas. This is in line with their growth status, as shown in Figure 7. The “yellow” decomposition results indicate similar double-bounce and volume-scattering contributions in winter wheat and barley areas. The decomposition result for the sugar beet area is dark, which is caused by the Fresnel reflection on the ground surface.

Figure 8.
The color-coded images of the decomposition results for the E-SAR dataset (red: double-bounce; green: volume scattering; blue: surface scattering). (a) 5XD decomposition method. (b) 7SD decomposition method. (c) Proposed decomposition method.
After multilook and filter processing, the scattering process of a pixel should be a comprehensive manifestation of the scattering process of ground objects within a range of about 20 m. In such a case, a decomposition scheme with better decomposition performance should interpret the scattering process of different plots more robustly. It is observed that the result of the proposed decomposition is smoother than that of 5XD and 7SD, showing the stability of the orthogonal scattering models in separating the contributions of different scattering mechanisms. The reason for this phenomenon is that, for this area without terrain slope, the orthogonal scattering processes mainly account for the co-polarizations, and the cross-polarization is mainly interpreted by the volume-scattering process.
To quantitatively analyze the stability of the experimental results of different decomposition methods, five areas covering various crops were selected, as shown in Figure 8a. The standard deviations corresponding to different scattering contributions (dB) estimated by the three decomposition schemes are shown in Table 8. To make the evaluation index fair for 5XD and 7SD, cross-scattering and non-reflection symmetry scattering contributions are not analyzed. The standard deviations derived from the proposed decomposition are smaller than those derived from other decompositions. The reason for this observation is that (1) for 5XD, double-bounce and cross-scattering models account for polarization, and volume- and cross-scattering models account for polarization. There are two scattering models accounting for the and polarizations. In such a case, when the geometrical and physical characteristics of the ground targets in different pixels for the same plot are slightly different, unstable decomposition results are expected, which is consistent with the results shown in Table 8; and (2) for non-reflection symmetry elements, speckle results from a combination of multiplicative and additive noise components [37]. The polarization SAR echo signals from crop areas generally satisfy the assumption of reflection symmetry, and the correlation between co-polarization and cross-polarization is low, which results in the estimation of non-reflection symmetry power being susceptible to speckle noise. Meanwhile, 7SD has four non-reflection symmetry scattering models to account for polarization. Their unstable estimates all affect the estimation of the volume-scattering model. Importantly, they affect the volume-scattering power by a factor of four. It is therefore expected that the standard deviation of the volume-scattering power is larger, which is consistent with the result shown in Table 8. The unstable decomposition results derived by 5XD and 7SD show a negative impact when similar scattering models are used to describe the scattering process.

Table 8.
The standard deviations corresponding to different scattering contributions (dB) estimated by three decomposition schemes (%).
5. Discussion
5.1. The Orthogonality between Scattering Models Is Pursued by Current Model-Based Decomposition
In this paper, we suggest that the scattering models in a decomposition scheme should be as orthogonal as possible to each other. In fact, some current model-based decompositions are also potentially pursuing orthogonality between scattering models. For Freeman three-component decomposition, the surface and double-bounce scattering models have the same form [11]. Since there is no difference in their form, they are difficult to distinguish, which is further illustrated by Freeman’s two-component decomposition, where only one scattering model is used to describe the surface and double-bounce scattering processes [38]. To improve the distinguishability of surface and double-bounce scattering, model constraints and degenerations are performed in a three-component decomposition to pursue the orthogonality of these two scattering models:
(1) For the form of surface and double-bounce scattering models, as shown in (3), considering the physical boundaries of model parameters, both model parameters and are constrained to be less than one.
(2) Considering the rank deficit problem, these two scattering models will degenerate to the first or second scattering component of Pauli decomposition.
The above constraints and degenerations render the surface- and double-scattering models associated more with polarization and polarization, respectively. This improves the orthogonality of the surface model and double-bounce scattering models, making the two easier to distinguish. This further emphasizes the necessity of orthogonality between scattering models.
5.2. The Bridging Role of Orthogonal Scattering Models in Target Decompositions
There is a novel reflection symmetry approximation (RSA) algorithm proposed by An et al. [27]. Interestingly, when RSA-processed data are used as the input of the proposed decomposition, from the decomposition results, the proposed decomposition is equivalent to the nonnegative eigenvalue decomposition [39,40], which further validates the proposed decomposition. However, it is noted that these two decomposition methods are essentially different. The nonnegative eigenvalue decompositions emphasize that the scattering contributions of different scattering mechanisms should be nonnegative. The proposed method emphasizes that the scattering models in a decomposition scheme should be as orthogonal as possible. We believe that both decomposition schemes contribute to the interpretation of PolSAR images.
Furthermore, due to the volume-scattering process with high polarization entropy being difficult to describe by a model with rank 1, there are only two orthogonal scattering models. However, if a rank-1 scattering model orthogonal to the proposed scattering models is found to describe the “mean” scattering process of volume scattering, in this case, three orthogonal scattering models are used to interpret the PolSAR image. This is equivalent to eigenvalue/eigenvector decomposition. Orthogonal scattering model-based decomposition provides an opportunity to build a bridge between model-based decomposition and eigenvalue-based decomposition.
5.3. The Positive Role in Land-Cover Classification
For large-scale land-cover classification from PolSAR images, the key is to separate different scattering mechanisms robustly and accurately. This means that two requirements lie ahead of the model-based decomposition: (1) the decomposition scheme should allocate the power of varying polarization states reasonably in various scenarios, and (2) the decomposition scheme should be stable. However, to describe the complex scattering processes for different scenes, an increasing number of scattering models have been proposed. Many similar scattering models have even been introduced into a common decomposition scheme. Unfortunately, this runs counter to the above two requirements for model decomposition. We think a possible way to meet the above two requirements is to establish orthogonal scattering models. Different ground targets are expected to be sensitive to different polarizations, which promotes the development of land-cover classification. For example, surface, double-bounce, and volume-scattering processes are clearly distinguished for urban areas. This is expected to contribute to river, building, and forest classification. Furthermore, for agricultural areas, the robust decomposition result of the proposed method indicates robust classification results.
6. Conclusions
PolSAR is sensitive to the shape, orientation, and dielectric properties of ground targets. Model-based decomposition techniques extract the geometric/physical properties of ground targets by decomposing parameters, the key to which is that the scattering models can be effectively separated from each other, as this avoids the mutual interference between different scatterers in the same pixel. In such a case, the scattering models should be orthogonal to each other.
Therefore, in this paper, we propose two orthogonal scattering models. They can also degenerate to current scattering models with rank 1. The two orthogonal scattering models and the Freeman volume-scattering model are further combined into a three-component decomposition scheme. The simulation PolSAR data, real ALOS-2/PARSAR-2, and E-SAR data were selected to validate the proposed method. The results are consistent with the expectation:
(1) The proposed decomposition is superior in allocating scattering power to different scattering mechanisms.
(2) The proposed decomposition is stable in interpreting PolSAR images.
(3) The proposed method has powerful potential in land-cover classification.
Furthermore, the idea that the scattering models need to be orthogonal to each other provides new insight into understanding model-based and eigenvalue/eigenvector decomposition. In addition, the proposed method shows powerful ability in land-cover classification. This interesting point needs further investigation and confirmation.
Author Contributions
W.H. implemented and developed the proposed methodology, and wrote and revised the paper; H.F. contributed to designing the main idea, supervised the work, and revised the paper; J.Z. supervised the work, contributed some ideas; Q.X. revised the paper; and S.Z. contributed to the discussion of the results. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded in part by the National Natural Science Foundation of China under Grant 41820104005, Grant 41904004, Grant 42030112, Grant 42171387; and 41804004; and in part by the Natural Science Foundation of Hunan province under Grant 2021JJ30808.
Data Availability Statement
The ALOS2/PALSAR2 data are available from (https://gportal.jaxa.jp/gpr/index?lang=en); The GF-3 data are available from (https://osdds.nsoas.org.cn/); The AgriSAR data are available from (https://earth.esa.int/eogateway/campaigns/agrisar-2006).
Acknowledgments
The author would also like to thank the editors and anonymous reviewers for their constructive suggestions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Chen, S.W.; Li, Y.Z.; Wang, X.S.; Xiao, S.P.; Sato, M. Modeling and interpretation of scattering mechanisms in polarimetric synthetic aperture radar: Advances and perspectives. IEEE Signal Process. Mag. 2014, 31, 79–89. [Google Scholar] [CrossRef]
- Huang, X.D.; Wang, J.F.; Shang, J.L. An integrated surface parameter inversion scheme over agricultural fields at early growing stages by means of C-band polarimetric RADARSAT-2 imagery. IEEE Trans. Geosci. Remote Sens. 2016, 54, 2510–2528. [Google Scholar] [CrossRef]
- Li, D.; Zhang, Y. Adaptive Model-Based Classification of PolSAR Data. IEEE Trans. Geosci. Remote Sens. 2018, 56, 6940–6955. [Google Scholar] [CrossRef]
- Chen, S.; Wang, X.S.; Xiao, S.P.; Sato, M. General Polarimetric Model-Based Decomposition for Coherency Matrix. IEEE Trans. Geosci. Remote Sens. 2014, 52, 1843–1855. [Google Scholar] [CrossRef]
- Yin, Q.; Li, J.; Ma, F.; Xiang, D.; Zhang, F. Dual-Channel Convolutional Neural Network for Bare Surface Soil Moisture Inversion Based on Polarimetric Scattering Models. Remote Sens. 2021, 13, 4503. [Google Scholar] [CrossRef]
- Xie, Q.; Wang, J.; Liao, C.; Shang, J.; Lopez-Sanchez, J.M.; Fu, H.; Liu, X. On the Use of Neumann Decomposition for Crop Classification Using Multi-Temporal RADARSAT-2 Polarimetric SAR Data. Remote Sens. 2019, 11, 776. [Google Scholar] [CrossRef]
- Papathanassiou, K.P.; Cloude, S.R. Single-baseline polarimetric SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2001, 39, 2352–2363. [Google Scholar] [CrossRef]
- Lee, J.S.; Pottier, E. Polarimetric Radar Imaging: From Basics to Applications; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Cloude, S.R.; Fortuny, J.; Lopez-Sanchez, J.M.; Sieber, A.J. Wide-band polarimetric radar inversion studies for vegetation layers. IEEE Trans. Geosci. Remote Sens. 1999, 37, 2430–2441. [Google Scholar] [CrossRef]
- Van Zyl, J.J.; Kim, Y. Synthetic Aperture Radar Polarimetry; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar]
- Freeman, A.; Durden, S.L. A three-component scattering model for polarimetric SAR data. IEEE Trans. Geosci. Remote Sens. 1998, 36, 963–973. [Google Scholar] [CrossRef]
- Yamaguchi, Y.; Moriyama, T.; Ishido, M.; Yamada, H. Four-component scattering model for polarimetric SAR image decomposition. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1699–1706. [Google Scholar] [CrossRef]
- Singh, G.; Malik, R. Seven-Component Scattering Power Decomposition of POLSAR Coherency Matrix. IEEE Trans. Geosci. Remote Sens. 2019, 57, 8371–8382. [Google Scholar] [CrossRef]
- Han, W.T.; Fu, H.Q.; Zhu, J.J.; Wang, C.C.; Xie, Q.H. Polarimetric SAR Decomposition by Incorporating a Rotated Dihedral Scattering Model. IEEE Geosci. Remote Sens. Lett. 2022, 19, 4005505. [Google Scholar] [CrossRef]
- Singh, G.; Yamaguchi, Y. Model-based six-component scattering matrix power decomposition. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5687–5704. [Google Scholar] [CrossRef]
- Sato, A.; Yamaguchi, Y.; Singh, G.; Park, S.E. Four-component scattering power decomposition with extended volume scattering model. IEEE Geosci. Remote Sens. Lett. 2012, 9, 166–170. [Google Scholar] [CrossRef]
- Hong, S.H.; Wdowinski, S. Double-bounce component in cross polarimetric SAR from a new scattering target decomposition. IEEE Trans. Geosci. Remote Sens. 2014, 52, 3039–3051. [Google Scholar] [CrossRef]
- Xiang, D.L.; Ban, Y.; Su, Y. Model-based decomposition with cross scattering for polarimetric SAR urban areas. IEEE Geosci. Remote Sens. Lett. 2015, 12, 2496–2500. [Google Scholar] [CrossRef]
- Fan, H.; Quan, S.N.; Dai, D.H.; Wang, X.S.; Xiao, S.P. Seven-Component Model-Based Decomposition for PolSAR Data with Sophisticated Scattering Models. Remote Sens. 2019, 11, 2802. [Google Scholar] [CrossRef]
- Cloude, S.R.; Pottier, E. A review of target decomposition theorems in radar polarimetry. IEEE Trans. Geosci. Remote Sens. 1996, 34, 498–518. [Google Scholar] [CrossRef]
- Yamaguchi, Y.; Yajima, Y.; Yamada, H. A four-component decomposition of PolSAR images based on the coherency matrix. IEEE Geosci. Remote Sens. Lett. 2006, 3, 292–296. [Google Scholar] [CrossRef]
- Xie, Q.H.; Ballester-Berman, J.D.; Lopez-Sanchez, J.M.; Zhu, J.J.; Wang, C.C. Quantitative analysis of polarimetric model-based decomposition methods. Remote Sens. 2016, 8, 977. [Google Scholar] [CrossRef] [Green Version]
- Lee, J.S.; Ainsworth, T.L.; Wang, Y. Generalized Polarimetric model-based decompositions using incoherent scattering models. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2474–2491. [Google Scholar] [CrossRef]
- Yamaguchi, Y.; Sato, A.; Boerner, W.M.; Sato, R.; Yamada, H. Four-component scattering power decomposition with rotation of coherency matrix. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2251–2258. [Google Scholar] [CrossRef]
- Lee, J.S.; Ainsworth, T.L. The effect of orientation angle compensation on coherency matrix and polarimetric target decompositions. IEEE Trans. Geosci. Remote Sens. 2011, 49, 53–64. [Google Scholar] [CrossRef]
- Singh, G.; Yamaguchi, Y.; Park, S.E. General four-component scattering power decomposition with unitary transformation of coherency matrix. IEEE Trans. Geosci. Remote Sens. 2013, 51, 3014–3022. [Google Scholar] [CrossRef]
- An, W.T.; Lin, M.S. A Reflection Symmetry Approximation of Multilook Polarimetric SAR Data and its Application to Freeman–Durden Decomposition. IEEE Trans. Geosci. Remote Sens. 2019, 57, 3649–3660. [Google Scholar] [CrossRef]
- An, W.T.; Lin, M.S. An Incoherent Decomposition Algorithm Based on Polarimetric Symmetry for Multilook Polarimetric SAR Data. IEEE Trans. Geosci. Remote Sens. 2020, 58, 2383–2397. [Google Scholar] [CrossRef]
- Yang, J.; Peng, Y.N.; Lin, S.M. Similarity between two scattering matrices. Electron. Lett. 2001, 37, 193–194. [Google Scholar] [CrossRef]
- Neumann, M.; Ferro-Famil, L.; Reigber, A. Estimation of Forest Structure, Ground, and Canopy Layer Characteristics from Multibaseline Polarimetric Interferometric SAR Data. IEEE Trans. Geosci. Remote Sens. 2010, 48, 1086–1104. [Google Scholar] [CrossRef]
- Arii, M.; Van Zyl, J.J.; Kim, Y. A general characterization for polarimetric scattering from vegetation canopies. IEEE Trans. Geosci. Remote Sens. 2010, 48, 3349–3357. [Google Scholar] [CrossRef]
- An, W.T.; Cui, Y.; Yang, J. Three-component model-based decomposition for polarimetric SAR data. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2732–2739. [Google Scholar]
- Cui, Y.; Yamaguchi, Y.; Yamada, H.; Park, S.E. PolInSAR coherence region modeling and inversion: The best normal matrix approximation solution. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1048–1060. [Google Scholar] [CrossRef]
- Xie, Q.H.; Zhu, J.J.; Lopez-Sanchez, J.M.; Wang, C.C.; Fu, H.Q. A Modified General Polarimetric Model-Based Decomposition Method with the Simplified Neumann Volume Scattering Model. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1229–1233. [Google Scholar] [CrossRef]
- Lopez-Martinez, C.; Fabregas, X.; Pipia, L. Forest parameter estimation in the Pol-InSAR context employing the multiplicative–additive speckle noise model. ISPRS-J.Photogramm. Remote Sens. 2011, 66, 597–607. [Google Scholar] [CrossRef]
- Zhang, L.; Zou, B.; Cai, H.; Zhang, Y. Multiple-component scattering model for polarimetric SAR image decomposition. IEEE Geosci. Remote Sens. Lett. 2011, 5, 603–607. [Google Scholar] [CrossRef]
- López-Martínez, C.; Fàbregas, X. Polarimetric SAR speckle noise model. IEEE Trans. Geosci. Remote Sens. 2003, 41, 2232–2242. [Google Scholar] [CrossRef]
- Freeman, A. Fitting a two-component scattering model to polarimetric SAR data from forests. IEEE Trans. Geosci. Remote Sens. 2007, 45, 2583–2592. [Google Scholar] [CrossRef]
- Van Zyl, J.J.; Arii, M.; Kim, Y. Model-based decomposition of polarimetric SAR covariance matrices constrained for nonnegative eigenvalues. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3452–3459. [Google Scholar] [CrossRef]
- Cui, Y.; Yamaguchi, Y.; Yang, J.; Kobayashi, H.; Park, S.E.; Singh, G. On complete model-based decomposition of polarimetric SAR coherency matrix data. IEEE Trans. Geosci. Remote Sens. 2014, 52, 1991–2001. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).