Fast Distributed Multiple-Model Nonlinearity Estimation for Tracking the Non-Cooperative Highly Maneuvering Target

Abstract

The newly developed near-space vehicle has the characteristics of high speed and strong maneuverability, being able to perform vertical skips and a wide range of lateral maneuvers. Tracking this kind of target with ground-based radars is difficult because of the limited detection range caused by the curvature of the Earth. Compared with ground-based radars, satellite tracking platforms equipped with Synthetic Aperture Radars (SARs) have a wide detection range, and can keep the targets in custody, making them a promising approach to tracking near-space vehicles continuously. However, this approach may not work well, due to the unknown maneuvers of the non-cooperative target, and the limited computing power of the satellites. To enhance tracking stability and accuracy, and to lower the computational burden, we have proposed a Fast Distributed Multiple-Model (FDMM) nonlinearity estimation algorithm for satellites, which adopts a novel distributed multiple-model fusion framework. This approach first requires each satellite to perform local filtering based on its own single model, and the corresponding fusion factor derived by the Wasserstein distance is solved for each local estimate; then, after diffusing the local estimates, each satellite performs multiple-model fusion on the received estimates, based on the minimum weighted Kullback–Leibler divergence; finally, each satellite updates its state estimation according to the consensus protocol. Two simulation experiments revealed that the proposed FDMM algorithm outperformed the other four tracking algorithms: the consensus-based distributed multiple-model UKF; the improved consensus-based distributed multiple-model STUKF; the consensus-based strong-tracking adaptive CKF; and the interactive multiple-model adaptive UKF; the FDMM algorithm had high tracking precision and low computational complexity, showing its effectiveness for satellites tracking the near-space target.

1. Introduction

Target tracking has been extensively researched and widely used in areas such as situational awareness, precision navigation, and marine surveillance [1,2]. However, accurate non-cooperative target tracking remains challenging, due to the unknown maneuvers of the targets. Recently, newly developed high-speed near-space vehicles have been widely investigated [3,4,5]. Non-cooperative near-space vehicles can perform diverse maneuvering modes, including vertical skips and a wide range of lateral maneuvers, posing higher requirements for tracking technology.

Generally, observation platforms can be separated into two main categories in target tracking: ground-based radar [3,6] and satellites [7]. Although ground-based radars are widely used in target tracking, they cannot guarantee the near-space target to be in custody, due to the limited detection range caused by the curvature of the Earth. In contrast, satellites have the advantage of a wide detection range, and thus they are feasible for tracking near-space targets. Spaceborne Synthetic Aperture Radar (SAR) systems have large imaging coverage, and can provide high-quality measurements, which are suitable as detection devices for satellite tracking systems [8,9,10]. The techniques of satellite tracking systems whose objects are mainly space orbital targets have been researched in recent years [11,12,13], while few studies have been conducted for near-space targets. Unlike the tracking of space orbital targets, there are two main issues in tracking near-space targets: (1) the maneuvers of the target are unknown and diverse, and thus a high-precision and stable tracking algorithm is required; (2) the computing power of satellites is limited; hence, an algorithm with low computational complexity is demanded. It has been necessary, therefore, to develop a tracking algorithm with high tracking accuracy, strong stability, and high computational efficiency for satellites tracking non-cooperative near-space targets.

The frameworks of multiple satellites tracking algorithms can generally be divided into ‘centralized’ and ‘distributed’. In centralized tracking algorithms [14,15], a central satellite is required to communicate with the remaining satellites, i.e., to receive and process data from them. Centralized tracking algorithms therefore usually impose a substantial computational burden on the central satellite. Moreover, the centralized framework relies heavily on the central satellite, meaning that the tracking system will break down once the central satellite fails. In contrast, in the distributed framework, no central node is needed [16], and the computing tasks of the entire network can be allocated to each satellite, which significantly speeds up the computing efficiency of the tracking system. Each satellite only exchanges data with adjacent satellites [15]. Even if one satellite fails, the tracking system, as a whole, will not break down. Due to this high computing efficiency and high resistance to satellite faults, the distributed framework is therefore more appealing.

To improve tracking precision, numerous motion models have been developed in recent years, to more accurately describe the state transition of the target, such as the Constant Velocity (CV) model, the Constant Acceleration (CA) model, and the Singer model [17]. However, a single model may not work well when the target maneuvers. Various Multiple-Model (MM) methods have been proposed, to resist maneuvering uncertainty by using combinations of multiple models [1,2,18,19]. Unlike the mechanism in MM methods, where each elemental filter works individually, an Interactive Multiple Model (IMM) can adaptively track maneuvering targets via the efficient interaction of each filter, which assigns weights to each sub-model according to the model likelihood and mode probability at each moment [20,21,22]. MM methods are usually designed for centralized frameworks, and cannot be directly applied to distributed tracking.

In distributed tracking algorithms, consensus-based algorithms are widely used [15,16,23,24,25,26,27,28,29]. This enables state estimations or measurements from each node to attain the same value, through a consensus protocol, and guarantees global convergence [16]. To deal with the target maneuver, a Consensus-based Distributed Multiple Model UKF (CDMM-UKF) algorithm has been proposed, based on the IMM in [23]. However, when the model set mismatches the target motion, the competition between sub-models cannot be ignored. In addition, each satellite needs to run multiple filters in every filtering period, and to exchange data frequently to reach a consensus, which also creates a considerable communication and computational burden. The Strong Tracking Filter (STF) is suitable for dealing with model mismatches [6,24,30,31,32,33]. The STF can reduce the impact caused by the motion model error, by enlarging the predicted state covariance based on the innovation sequence orthogonal principle [30]. To eliminate the effect of the dynamics model error, a Consensus-based Strong Tracking Adaptive Cubature Kalman Filtering (CSTACKF) algorithm has been proposed in [24]. This distributed algorithm combines the advantages of consensus and adaptive filter, to resist maneuver uncertainty. However, as the CSTACKF algorithm adopts a single motion model, the tracking stability of the CSTACKF algorithm cannot be guaranteed when tracking non-cooperative targets with intense maneuvers.

To improve the stability and precision of satellite tracking systems, the aim of this paper was to develop a new distributed algorithm based on the MM approach and STF. To further cope with the computational burden brought about by the MM, a novel distributed MM framework was put forward for the algorithm, to reduce the computation complexity for each satellite. The proposed algorithm was termed the Fast Distributed Multiple-Model (FDMM) algorithm. The main idea of the FDMM algorithm is as follows: firstly, each satellite performs a local estimation, based on its single motion model and an adaptive CKF algorithm; then, the corresponding fusion factor derived by the Wasserstein distance is solved for each local estimate; secondly, after diffusing the local estimations, each satellite performs multiple-model fusion on the received estimations, based on the minimum weighted Kullback–Leibler (KL) divergence. Finally, each satellite updates its state estimation according to the consensus protocol. The contributions of this study are summarized as follows:

(1)

A novel distributed multiple-model fusion framework was proposed, to lower the computational burden for the satellites. Unlike the mechanism in a distributed MM [23,25], where each satellite needs to process multiple filters in the local estimation process, each satellite in the FDMM algorithm only needs to process one filter, based on one motion model in the local filtering process.

(2)

The Wasserstein distance with triangular inequality and symmetry is applied, to derive weight factors for each sub-model, to deal with the sub-model competition problem in MM.

The remainder of this paper is organized as follows: Section 2 presents the related works on the fading factor and topology; Section 3 gives the problem formulation; in Section 4, the proposed FDMM tracking algorithm is introduced in detail; the effectiveness and advantages of the FDMM algorithm are demonstrated in two simulation experiments in Section 5; finally, Section 6 concludes our study.

2. Related Works

2.1. Fading Factor

The STF is appealing, for tracking non-cooperative maneuvering targets. The core part of the STF is the fading factor, ${\alpha }_0$, which can reduce the impact caused by the motion model error. When a dynamics model mismatch occurs, the value of the fading factor, ${\alpha }_0$, is enlarged, and the prediction covariance matrix, $P_{k|k-1}$, is also enlarged by ${\alpha }_0$, in real time. This process reduces the contribution of the dynamics model, and improves the adaptability of the tracking algorithm to motion-modeling uncertainty [30].

Based on the mutual orthogonality between innovation sequences, the fading factor, ${\alpha }_0$, can be expressed as Equation (1):

$${\alpha }_0=\frac{tr\left[C_{0,k}-R_k\right]}{tr\left[P_{zz}-R_k\right]}$$

(1)

where $C_{0,k}$ denotes the covariance of the innovation vector, quantifying the dynamics error; this is usually estimated according to Equation (2):

$$C_{0,k}=\{\begin{array}{ll}{\mathsf{\nu }}_k{\mathsf{\nu }}_k^T& k=1\\ \frac{\lambda C_{0,k-1}+{\mathsf{\nu }}_k{\mathsf{\nu }}_k^T}{1+\lambda }& k>1\end{array}$$

(2)

where ${\mathsf{\nu }}_k$ is the innovation, and $\lambda$ is the forgetting factor, determined to be $0.95$.

2.2. Topology

The communication topology of the satellites at time $k$ can be represented by a graph, $G_k=\left(V,E\right)$, where vertexes $V=\left\{s_1,s_2,\dots ,s_n\right\}$ are the set of all satellites, and edges $E\subseteq V\times V$ present the communication connection between the satellites. The set of adjacent satellites of the satellite $s_i$ is expressed as $A_i$.

At time $k$, the communication protocol between satellite $s_i$ and its adjacent satellite, $s_j\in A_i$, is set as the Metropolis matrix, $W_{ij}$ [12], as shown in Equation (3):

$$W_{ij}=\{\begin{array}{cc}\frac{1}{1+\max \left\{A_i,A_j\right\}},\hfill & \left(s_j\in A_i\right)\\ 1-{\displaystyle \sum _{s_i,s_m\in A_i}}{W}_{im},\hfill & \left(i=j\right)\\ 0,\hfill & \left(others\right)\end{array}$$

(3)

where $i,j,m$ are indices of satellites.

3. Problem Formulation

3.1. Tracking Formulation

The dynamics and observation functions of the maneuvering target-tracking process are modeled as follows:

$${\mathit{X}}_{k+1}=f\left({\mathit{X}}_k\right)+{\mathit{w}}_k$$

(4)

$${\mathit{Z}}_{k+1}=h\left({\mathit{X}}_{k+1}\right)+{\mathsf{\epsilon }}_{k+1}$$

(5)

where ${\mathit{X}}_k\in {ℝ}^n$ and ${\mathit{Z}}_k\in {ℝ}^m$ are the state vector and measurement vector of the maneuvering target at time $k$, respectively; $f\left(·\right)$ is the state transition function; ${\mathit{w}}_k$ is the process noise; and $h\left(·\right)$ and ${\mathsf{\epsilon }}_k$ are the measurement function and the measurement noise, respectively.

3.2. Measurement Model

Satellites operating in low orbits are applied to detect the target. As shown in Figure 1, a single satellite can provide two measurements of the target through processing SAR images, consisting of the azimuth, $\varphi$, and the elevation angle, $\theta$. The detecting coordinate system is paralleled to the Earth-Centered Inertial (ECI) [34].

For satellite $s_i$, the measurement model at time $k$ is described as Equation (6):

$$\{\begin{array}{l}{\varphi }_k^i=\arctan \left(\frac{y-y_i}{x-x_i}\right)+{\epsilon }_k^{i,1}\\ {\theta }_k^i=\arctan \left(\frac{z-z_i}{\sqrt{{\left(x-x_i\right)}^2+{\left(y-y_i\right)}^2}}\right)+{\epsilon }_k^{i,2}\end{array}$$

(6)

where the position of satellite, $s_i$, and the target in ECI are $\left(x_i,y_i,z_i\right)$ and $\left(x,y,z\right)$, respectively; ${\epsilon }_k^{i,1}$ and ${\epsilon }_k^{i,2}$ are noises in the corresponding measurement channels.

If ${\mathit{z}}_k^i={\left[{\varphi }_k^i,{\theta }_k^i\right]}^T$, ${\mathsf{\epsilon }}_k^i={\left[{\epsilon }_k^{i,1},{\epsilon }_k^{i,2}\right]}^T$, Equation (6) can be further compacted into a measurement model of the standard form in Equation (7):

$${\mathit{z}}_k^i=h_k^i\left({\mathit{X}}_k\right)+{\mathsf{\epsilon }}_k^i$$

(7)

where $h_k^i\left(·\right)$ is the measurement function of satellite $s_i$. The measurement noise, ${\mathsf{\epsilon }}_k^i$, is modeled with the zero-mean Gaussian noise $\left({\mathsf{\epsilon }}_k^i~\mathcal{N}\left({\mathsf{\epsilon }}_k^i;0,{ℛ}_k^i\right)\right)$. The schematic diagram of multiple satellites tracking the target is shown in Figure 2.

4. Fast Distributed Multiple-Model Nonlinearity Estimation Algorithm

The traditional distributed multiple-model algorithms in [23,25] cannot track a non-cooperative highly maneuvering target stably, and impose a substantial computational burden on each satellite. Therefore, to reduce the computational burden and improve the tracking accuracy of the satellites, the Fast Distributed Multiple-Model (FDMM) nonlinearity estimation algorithm, combined with the adaptive Cubature Kalman filter, is put forward in this section.

In the FDMM algorithm, a novel distributed multi-model fusion framework is adopted to assign the computational tasks of MM filtering to each satellite. Unlike the framework in [23,25], where each node performs multiple filtering based on multiple-motion models, the FDMM algorithm allows each satellite to perform local filtering based only on a single but different motion model. After local filtering, the local estimates of each satellite are diffused to adjacent satellites, and then multiple-model fusion is performed on the obtained results in each satellite.

To deal with the motion model mismatches engendered by the non-cooperative target, the adaptive CKF algorithm, based on the fading factor for local filtering, is first introduced below. Next, the newly proposed fusion factor and the multiple-model fusion framework based on weighted KL divergence are introduced, to fuse each satellite’s obtained local estimation results.

4.1. Strong-Tracking Cubature Kalman Filter

Based on the fading factor, ${\alpha }_0$, shown in Equation (1), the strong-tracking CKF can be achieved by the following steps:

• Compute the cubature points at time $k-1$:

  $$P_{k-1|k-1}={\mathit{S}}_{k-1}{\mathit{S}}_{k-1}^T$$

  (8)

  $${\mathcal{X}}_{k-1|k-1}^a=X_{k-1|k-1}+{\mathit{S}}_{k-1}{\mathsf{\xi }}_a,a=1,2,\dots ,2n$$

  (9)

  $${\omega }_a=\frac{1}{2n}$$

  (10)

  where ${\mathit{S}}_{k-1}$ is the Cholesky factor of $P_{k-1|k-1}^i$; $n$ denotes the dimension of the state $X_{k-1|k-1}$; and ${\omega }_a$ represents weighted coefficients of the ${\mathsf{\xi }}_a$; the ${\mathsf{\xi }}_a$ being the $a$-th column of the following matrix:

  $${\left[\begin{array}{cccccccc}\sqrt{n}& 0& \cdots & 0& -\sqrt{n}& 0& \cdots & 0\\ 0& \sqrt{n}& \cdots & 0& 0& -\sqrt{n}& \cdots & 0\\ ⋮& ⋮& \ddots & 0& ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & \sqrt{n}& 0& 0& \cdots & -\sqrt{n}\end{array}\right]}_{n\times 2n}$$

  (11)
• Time update:

  $${\mathcal{X}}_{k|k-1}^a=F{\mathcal{X}}_{k-1|k-1}^a$$

  (12)

  $${\widehat{X}}_{k|k-1}={\displaystyle \sum }_{a=1}^{2n}{\omega }_a{\mathcal{X}}_{k|k-1}^a$$

  (13)

  $${\widehat{P}}_{k|k-1}={\displaystyle \sum }_{a=1}^{2n}{\omega }_a\left({\mathcal{X}}_{k|k-1}^a-{\widehat{X}}_{k|k-1}\right){\left({\mathcal{X}}_{k|k-1}^a-{\widehat{X}}_{k|k-1}\right)}^T+Q$$

  (14)

  $${\widehat{P}}_{k|k-1}={\mathit{S}}_{k|k-1}{\mathit{S}}_{k|k-1}^T$$

  (15)

  $${\widehat{\mathcal{X}}}_{k|k-1}^a={\widehat{X}}_{k|k-1}+{\mathit{S}}_{k|k-1}{\mathsf{\xi }}_a,a=1,2,\dots ,2n$$

  (16)

  $${\widehat{Z}}_{k|k-1}^a=H_k\left({\widehat{\mathcal{X}}}_{k|k-1}^a\right)$$

  (17)

  $${\widehat{Z}}_{k|k-1}={\displaystyle \sum }_{a=1}^{2n}{\omega }_a{\widehat{Z}}_{k|k-1}^a$$

  (18)

  $${\mathsf{\nu }}_k=Z_k-{\widehat{Z}}_{k|k-1}$$

  (19)

  where, ${\mathsf{\nu }}_k$ refers to the corresponding innovation sequence.
• Fading factor update:

  $${\mathit{C}}_{0,k}=\{\begin{array}{ll}{\mathsf{\nu }}_k{\mathsf{\nu }}_k{}^T,& k=1\\ \frac{\lambda {\mathit{C}}_{0,k-1}+{\mathsf{\nu }}_k{\mathsf{\nu }}_k{}^T}{1+\lambda },& k>1\end{array}$$

  (20)

  $${\alpha }_k=\{\begin{array}{ll}{\alpha }_0,& {\alpha }_0>1\\ 1,& {\alpha }_0\le 1\end{array}$$

  (21)

  $${\alpha }_0=\frac{tr\left[{\mathit{C}}_{0,k}-R_k\right]}{tr\left[{{\displaystyle \sum }}_{a=1}^{2n}{\omega }_a\left({\widehat{Z}}_{k|k-1}^a-{\widehat{Z}}_{k|k-1}\right){\left({\widehat{Z}}_{k|k-1}^a-{\widehat{Z}}_{k|k-1}\right)}^T\right]}$$

  (22)

  $${\widehat{P}}_{k|k-1}={\alpha }_k\left[{\displaystyle \sum }_{a=1}^{2n}{\omega }_a\left({\widehat{\mathcal{X}}}_{k|k-1}^a-{\widehat{X}}_{k|k-1}\right){\left({\widehat{\mathcal{X}}}_{k|k-1}^a-{\widehat{X}}_{k|k-1}\right)}^T\right]+Q$$

  (23)

  $$P_{xz}={\displaystyle \sum }_{a=1}^{2n}{\omega }_a\left({\widehat{\mathcal{X}}}_{k|k-1}^a-{\widehat{X}}_{k|k-1}\right){\left({\widehat{Z}}_{k|k-1}^a-{\widehat{Z}}_{k|k-1}\right)}^T$$

  (24)

  $$P_{zz}={\displaystyle \sum }_{a=1}^{2n}{\omega }_a\left({\widehat{Z}}_{k|k-1}^a-{\widehat{Z}}_{k|k-1}\right){\left({\widehat{Z}}_{k|k-1}^a-{\widehat{Z}}_{k|k-1}\right)}^T+R$$

  (25)
• Measurement update:

  $${\mathit{K}}_k=P_{xz}{P}_{zz}{}^{-1}$$

  (26)

  $$X_{k|k}={\widehat{X}}_{k|k-1}+{\mathit{K}}_k\left(Z_k-{\widehat{Z}}_{k|k-1}\right)$$

  (27)

  $$P_{k|k}={\widehat{P}}_{k|k-1}-{\mathit{K}}_k{P}_{zz}{\mathit{K}}_k^T$$

  (28)

4.2. Fusion Factor Derived from the Wasserstein Distance

As the detailed motion characteristics of the non-cooperative target cannot be obtained, a single model cannot work well when the target maneuvers. Considering that conventional distributed MM methods engender a substantial computational burden, we have proposed a new distributed multiple-model mechanism to cope with the target maneuvers, and to reduce the computational burden. Each satellite first performs local filtering based on a single but different motion model, then performs multiple-model fusion on the data obtained from adjacent satellites. By allocating the computing tasks of the MM filtering process to each satellite, the computational efficiency of the tracking system is significantly improved.

The distance function and fusion factor are introduced in this section. They are the core parameters for performing the fusion of distributed multiple-model estimations in the FDMM algorithm.

4.2.1. Distance Function

Before performing multiple-model fusion, it is necessary to evaluate the similarity of the current model to the actual motion mode of the target. In the traditional multiple-model algorithm, the model likelihood function, $L_k^i$, represents the Gaussian probability of classifying the current mode of the target to the i-th model based on the measurement $Z_k$, and $L_k^i$ is solved as shown in Equation (29):

$$L_k^i=\frac{1}{\sqrt{\det \left(2\pi S\right)}}\exp [-\frac{1}{2}{\mathsf{\nu }}^T{S}^{-1}\mathsf{\nu }]$$

(29)

where $\mathsf{\nu }$ is the innovation, and $S$ is the variance of the innovation.

In the proposed distributed algorithm, the measurements used by each satellite are different. Each satellite has different measurement errors. It is not appropriate to still use the model likelihood function, based on the respective measurements, to calculate the Gaussian probability of the model. Therefore, we introduced the Wasserstein distance [35,36], to evaluate the distance between the using model and the current motion mode.

Definition 1.

The$p^{th}$Wasserstein distance between two probability measures is defined as Equation (30) [35].

$$W_p{\left(P_1,P_2\right)}^p=inf\mathbb{E}\left[d{\left(X,Y\right)}^p\right]$$

(30)

where $\mathbb{E}\left[·\right]$ denotes the expected value, the infimum being taken over all joint distributions of the random variables, $X$ and $Y$, with marginals $P_1$ and $P_2$, respectively [35].

When $p\ge 1$, the $p^{th}$ Wasserstein distance has the following properties: symmetry and triangle inequality [35,36]. The properties of Wasserstein distance make it a good metric for evaluating the similarity between the used model and the target mode.

Specifically, for two Gaussian distributions, we can solve for their Wasserstein distance by Equation (31):

$$\begin{array}{c}dist=W_2\left(\mathcal{N}\left(\mu ;{\mu }_1,{\mathsf{\Sigma }}_1\right),\mathcal{N}\left(\mu ;{\mu }_2,{\mathsf{\Sigma }}_2\right)\right)\hfill \\ dis{t}^2=\parallel {\mu }_1-{\mu }_2{\parallel }_2^2+Tr\left({\mathsf{\Sigma }}_1+{\mathsf{\Sigma }}_2-2{\left({\mathsf{\Sigma }}_1^{\frac{1}{2}}{\mathsf{\Sigma }}_2{\mathsf{\Sigma }}_1^{\frac{1}{2}}\right)}^{\frac{1}{2}}\right)\hfill \end{array}$$

(31)

The measurement $Z_k^i$ that satellite $s_i$ obtains at time $k$ can be expressed as Equation (32):

$$Z_k^i=Z_k^{i,truth}+{\mathsf{\epsilon }}_k^i,\hspace{1em}{\mathsf{\epsilon }}_k^i~\mathcal{N}\left(\mathsf{\epsilon };0,R_k^i\right)$$

(32)

where $Z_k^{i,truth}$ represents the ideal measurement that does not contain noise.

The predicted measurement, ${\widehat{Z}}_{k|k-1}^i$, can be obtained according to Equation (18) at the satellite $s_i$, and ${\widehat{Z}}_{k|k-1}^i$ follows a Gaussian distribution, i.e., ${\widehat{Z}}_{k|k-1}^i~\mathcal{N}\left(Z;{\widehat{Z}}_{k|k-1}^i,P_{zz}\right)$. Therefore, the similarity between the using model and the current motion mode can be quantified by the Wasserstein distance between the predicted measurement, ${\widehat{Z}}_{k|k-1}^i$, of local filtering, and the ideal measurement, $Z_k^{i,truth}$, where $Z_k^{i,truth}~\mathcal{N}\left(Z;Z_k^i,R_k^i\right)$.

According to Equation (31), we can compute the Wasserstein distance, $D_k^i$, between the using model and the current motion mode as Equation (33):

$${(D_k^i)}^2=\parallel {\widehat{Z}}_{k|k-1}^i-Z_k^i{\parallel }_2^2+Tr\left(P_{zz}^i+R_k^i-2{\left({\left(P_{zz}^i\right)}^{\frac{1}{2}}{R}_k^i{\left(P_{zz}^i\right)}^{\frac{1}{2}}\right)}^{\frac{1}{2}}\right)$$

(33)

4.2.2. Fusion Factor

After local filtering, the local estimates of each satellite are diffused to adjacent satellites. Before performing multiple-model fusion on the data, it is necessary to assign weights to the data from each satellite. The Wasserstein distance, $D_k^i$, based on Equation (33), describes the distance between the model and the target motion mode. The smaller $D_k^i$ is, the closer the i-th model is to the target mode. In this paper, according to the characteristics of $D_k^i$, the fusion factor ${\beta }_k^i$ was introduced, to evaluate the similarity of each local estimate in the FDMM algorithm.

Definition 2.

Assuming that the Wasserstein distance between the i-th motion model and the current motion mode at time k is $D_k^i$, the fusion factor, ${\beta }_k^i$, in the FDMM algorithm is defined as Equation (34).

$${\beta }_k^i=\frac{1}{D_k^i}$$

(34)

The local estimates and the fusion factor of each satellite are simultaneously diffused to their adjacent satellites. According to the corresponding fusion factor, ${\beta }_k^i$, the weight of each estimation obtained at the satellite $s_i$ can be calculated by Equation (22):

$${\lambda }_k^{i,l_i}=\frac{{\beta }_k^{l_i}}{{{\displaystyle \sum }}_{l_i\in \left\{s_i,A_i\right\}}{\beta }_k^{l_i}}$$

(35)

where ${\lambda }_k^{i,l_i}$ refers to the weight of the estimation from the adjacent satellite, $s_{l_i}$ at the satellite $s_i$, so ${\displaystyle \sum }_{l_i\in \left\{s_i,A_i\right\}}{\lambda }_k^{i,l_i}=1$.

4.3. Multiple-Model Fusion Based on Weighted KL Divergence

After each satellite receives the local estimates and the corresponding fusion factor, the multiple-model fusion is performed. This section takes the satellite $s_i$ as an example, to introduce how each satellite performs multiple-model fusion on the received data. Firstly, the satellite $s_i$ obtains the local estimation $\left\{{\widehat{X}}_{k|k}^{j,Local},{\widehat{P}}_{k|k}^{j,Local}\right\},j\in A_j$ and corresponding fusion factor ${\beta }_k^j$ from the adjacent satellites. Secondly, based on the weighted sum minimization of the information entropy, a probability density function (PDF) is found, as the multiple-model fusion results that minimize the difference between the PDFs of the received estimations.

In order to solve the problem of multiple-state estimation fusion, combined with reference [37,38], the definition of weighted KL divergence is introduced.

Definition 3.

Given N PDFs$p^i\left(x\right)\in \mathcal{P}$, and relative weights${\lambda }_i$satisfying Equation (36),

$${\displaystyle \sum }_{i=1}^N{\lambda }_i=1,{\lambda }_i\ge 0$$

(36)

their weighted KL average (KLA) is defined by Equation (37):

$$\overline{p}\left(\mathit{x}\right)=\arg \underset{p\in \mathcal{P}}{\inf }{\displaystyle \sum }_{i=1}^N{\lambda }_i{D}_{KL}(p\parallel p^i)$$

(37)

Lemma 1.

The weighted KLA defined in Equation (37) is given by Equation (38):

$$\overline{p}\left(\mathit{x}\right)=\frac{{{\displaystyle \prod }}_{i=1}^N{\left[p^i\left(\mathit{x}\right)\right]}^{{\lambda }_i}}{{\displaystyle \int }{{\displaystyle \prod }}_{i=1}^N{\left[p^i\left(\mathit{x}\right)\right]}^{{\lambda }_i}d\mathit{x}}$$

(38)

Lemma 2.

If all the PDFs$p^i\left(\mathit{x}\right)$take the Gaussian PDF form, their weights${\lambda }_i$satisfying Equation (36), their weighted KLA in Equation (38) takes the form of Equation (39):

$$\overline{p}\left(\mathit{x}\right)=\mathcal{N}\left(\mathit{x};\overline{\mathit{x}},\overline{\mathit{P}}\right)$$

(39)

then the mean$\overline{\mathit{x}}$and the covariance$\overline{\mathit{P}}$can be computed from Equations (40) and (41):

$${\overline{\mathit{P}}}^{-1}={\displaystyle \sum }_{i=1}^{\mathit{N}}{\lambda }_i{\mathit{P}}_i^{-1}$$

(40)

$${\overline{\mathit{P}}}^{-\mathit{1}}\overline{\mathit{x}}={\displaystyle \sum }_{\mathit{i}=\mathit{1}}^{\mathit{N}}{\lambda }_{\mathit{i}}{\mathit{P}}_{\mathit{i}}^{-\mathit{1}}{\widehat{\mathit{x}}}_{\mathit{i}}$$

(41)

The proof of Lemmas 1 and 2 can be found in [37].

After filtering, each satellite ${\mathrm{s}}_i$ can obtain the local state estimation ${\widehat{X}}_{k|k}^{l_i,Local}$—where $l_i\in \{s_i,A_i\}$—the covariance ${\widehat{P}}_{k|k}^{l_i,Local}$, and the corresponding fusion factor, ${\beta }_k^j$, through communication. Then, we can obtain the weight of each estimate, ${\mathsf{\lambda }}_{{\mathit{l}}_{\mathit{i}}}$ according to Equation (35). Because each local estimate is a Gaussian distribution, with mean ${\widehat{X}}_{k|k}^{l_i,Local}$ and variance ${\widehat{P}}_{k|k}^{l_i,Local}$, we can approximate all obtained local estimates, $\mathcal{N}\left(X;{\widehat{X}}_{k|k}^{l_i,Local},{\widehat{P}}_{k|k}^{l_i,Local}\right)$, using a Gaussian distribution $\mathcal{N}\left(X;{\overline{X}}_{k|k}^i,{\overline{P}}_{k|k}^i\right)$ at satellite ${\mathrm{s}}_i$, based on lemma 1 and lemma 2. Then, we can get the multiple-model fusion results, ${\overline{\mathit{X}}}_{\mathit{k}|\mathit{k}}^{\mathrm{I}}$, ${\overline{\mathit{P}}}_{\mathit{k}|\mathit{k}}^{\mathit{i}}$, from Equations (42) and (43), based on Weighted KL Divergence:

$${\overline{\mathit{X}}}_{\mathit{k}|\mathit{k}}^{\mathrm{i}}=\left({\overline{\mathit{P}}}_{\mathit{k}|\mathit{k}}^{\mathit{i}}\right){\displaystyle \sum }_{l_i\in \left\{s_i,A_i\right\}}{\mathsf{\lambda }}_{{\mathit{l}}_{\mathit{i}}}{\left({\widehat{\mathit{P}}}_{\mathit{k}|\mathit{k}}^{{\mathit{l}}_{\mathit{i}},\mathit{Local}}\right)}^{-\mathit{1}}{\widehat{X}}_{\mathit{k}|\mathit{k}}^{{\mathit{l}}_{\mathit{i}},\mathit{Local}}$$

(42)

$${\left({\overline{\mathit{P}}}_{\mathit{k}|\mathit{k}}^{\mathit{i}}\right)}^{-\mathit{1}}={\displaystyle \sum }_{l_i\in \left\{s_i,A_i\right\}}{\mathsf{\lambda }}_{{\mathit{l}}_{\mathit{i}}}{\left({\widehat{\mathit{P}}}_{\mathit{k}|\mathit{k}}^{{\mathit{l}}_{\mathit{i}},\mathit{Local}}\right)}^{-\mathit{1}}$$

(43)

4.4. Fusion Framework

In the FDMM algorithm, a novel distributed multiple-model fusion framework is proposed, to reduce the computational burden of the tracking system by allocating tasks to each satellite. The fusion framework is introduced below. Each satellite performs local estimations, based on its own single-motion model. The motion model selecting rules that determine which satellite adopts which motion model are also discussed in this section.

4.4.1. Fusion Framework

The operation flow of satellite $s_i$, from time $k-1$ to time $k$, adopting the FDMM algorithm, is shown in Figure 3. Firstly, each satellite runs a different single-motion model, combined with the STCKF algorithm—based on the augmentation measurements from the adjacent satellites—and calculates the fusion factor, ${\beta }_k^i$, derived from the Wasserstein distance. Then, the local estimates, ${\widehat{X}}_{k|k}^{i,Local}$, ${\widehat{P}}_{k|k}^{i,Local}$, and ${\beta }_k^i$ are exchanged with the adjacent satellites via the topology net. Then, multiple-model fusion is performed, based on the weighted KL divergence for the received state estimates $\left\{{\widehat{X}}_{k|k}^{i,Local},{\widehat{P}}_{k|k}^{i,Local},{\beta }_k^i\right\},i\in \left\{s_i,A_i\right\}$ from different motion models. Finally, each satellite updates its state estimation according to the consensus protocol.

4.4.2. Motion Model Selecting Rules

When deciding which motion model to choose for which satellite, the following two aspects are mainly considered. Firstly, construct a suitable model set, which contains the motion models that will be used. The set needs to describe the maneuvers of the target as much as possible. The CV model describes targets without maneuverability, and the CA is modeled for targets with constant acceleration in each sampling interval. The Singer models with different parameters (the maneuvering frequency, $\alpha$, and the acceleration variance, ${\sigma }^2$) could represent the targets with different maneuvering capabilities [17]. Considering the characteristics of the models, the CA model, the CV model, and the Singer model were chosen as the element of the model set in this paper, to deal with the maneuvers of the non-cooperative target.

Secondly, the topology of satellites is a significant constraint to be aware of, when assigning the motion model to the satellite. In the FDMM algorithm, after the local filtering, each satellite performs multiple-model fusion on the received estimations solved by adjacent satellites. Therefore, the motion models used by adjacent satellites can affect this satellite’s multiple-model fusion results. If the neighbors of one satellite, and that satellite itself, all adopt the CV model, the multiple-model fusion results for that satellite will be at their worst when the target maneuvers. In addition, if the neighbors of one satellite, and that satellite itself, all adopt the CA model, the multiple-model fusion results of that satellite will also be poor when the target starts moving at a constant speed. Therefore, when assigning the motion model to each satellite, it is necessary to ensure that at least two models exist in each satellite and in its neighbors. One model is used to model the weak maneuvering or non-maneuvering situation of the target—such as the CV or the Singer with $\alpha \to \infty$—and the other is used to model the situation where the target performs maneuvers, such as the Singer with $\alpha \to 0$ or CA. Furthermore, after the multiple model fusion process, each satellite will update its state estimation according to the consensus protocol. In the consensus update process, each satellite can affect the outcome of the tracking system. Therefore, the satellite tracking system should use the motion models from the model set, as much as possible.

4.5. Implementation Steps of FDMM Algorithm

The FDMM algorithm applying to the satellite $s_i$, from time $k-1$ to time $k$, is shown in Algorithm 1.

Algorithm 1 Fast Distributed Multiple-Model (FDMM) Nonlinearity Estimation

Step 1. Local STCKF Filtering and Solving the fusion factor: Time update: ${\widehat{X}}_{k|k-1}^i={\displaystyle \sum _{a=1}^{2n}}{\omega }_a{\mathcal{X}}_{k|k-1}^{a,i}$ ${\widehat{P}}_{k|k-1}^i={\displaystyle \sum _{a=1}^{2n}}{\omega }_a\left({\mathcal{X}}_{k|k-1}^{a,i}-{\widehat{X}}_{k|k-1}^i\right){\left({\mathcal{X}}_{k|k-1}^{a,i}-{\widehat{X}}_{k|k-1}^i\right)}^T+Q_k^i$ Receive the measurements from adjacent satellites $A_i$, then perform measurement augmentation: $\left({\mathit{z}}_k^i,{ℛ}_k^i\right)\to \left(Z_k^i,R_k^i\right)$. Compute the fading factor, ${\alpha }_0$, utilizing Equations (21) and (22), then reformulate the predicted state covariance, ${\widehat{P}}_{k|k-1}^i$, as Equation (23) shows. Local filtering update: ${\widehat{X}}_{k|k}^{i,local}={\widehat{X}}_{k|k-1}^i+{\mathit{K}}_k\left(Z_k^i-{\widehat{Z}}_{k|k-1}^i\right)$ ${\widehat{P}}_{k|k}^{i,local}={\widehat{P}}_{k|k-1}^i-{\mathit{K}}_k{P}_{zz}^i{\mathit{K}}_k^T$ Compute the fusion factor ${\beta }_k^i$ of the local estimation: ${(D_k^i)}^2=\parallel {\mathsf{\nu }}_k^i{\parallel }_2^2+Tr\left(P_{zz}^i+R_k^i-2{\left({\left(P_{zz}^i\right)}^{\frac{1}{2}}{R}_k^i{\left(P_{zz}^i\right)}^{\frac{1}{2}}\right)}^{\frac{1}{2}}\right)$ ${\beta }_k^i=\frac{1}{D_k^i}$

Step 2. Multiple-Model Estimation Fusion based on Weighted KL Divergence: Send $\left\{{\widehat{X}}_{k|k}^{i,local},{\widehat{P}}_{k|k}^{i,local},{\beta }_k^i\right\}$ to the adjacent satellites $A_i$, and receive $\{{\widehat{X}}_{k|k}^{l_i,local},{\widehat{P}}_{k|k}^{l_i,local},{\beta }_k^{l_i}\}$ from adjacent satellites $A_i$. Compute the fusion weight $\left\{{\lambda }_k^{i,l_i}\right\}$ of received local estimations, $l_i\in \left\{i,A_i\right\}$: ${\lambda }_k^{i,l_i}=\frac{{\beta }_k^{l_i}}{{{\displaystyle \sum }}_{l_i\in \left\{i,A_i\right\}}{\beta }_k^{l_i}}$ Multiple-Model fusion: ${\overline{X}}_{k|k}^{\mathrm{i}}=\left({\overline{P}}_{k|k}^i\right){\displaystyle \sum _{l_i\in \left\{i,A_i\right\}}}{\lambda }_k^{i,l_i}{\left({\widehat{P}}_{k|k}^{l_i,Local}\right)}^{-1}{\widehat{X}}_{k|k}^{l_i,Local}$ ${\left({\overline{P}}_{k|k}^i\right)}^{-1}={\displaystyle \sum _{l_i\in \left\{i,A_i\right\}}}{\lambda }_k^{i,l_i}{\left({\widehat{P}}_{k|k}^{l_i,Local}\right)}^{-1}$

Step 3. State Update: Initialization: ${\overline{X}}_{k|k}^i\left[0\right]={\overline{X}}_{k|k}^i,{\overline{P}}_{k|k}^i\left[0\right]={\overline{P}}_{k|k}^i$ Consensus update: For $d=0:\left(N_d-1\right)$   ${\overline{X}}_{k|k}^i\left[d+1\right]={\overline{X}}_{k|k}^i\left[d\right]+{\displaystyle \sum _{j\in A_i}}{W}_{ij}({\overline{X}}_{k|k}^j\left[d\right]-{\overline{X}}_{k|k}^i\left[d\right])$   ${\overline{P}}_{k|k}^i\left[d+1\right]={\overline{P}}_{k|k}^i\left[d\right]+{\displaystyle \sum _{j\in A_i}}{W}_{ij}\left({\overline{P}}_{k|k}^j\left[d\right]-{\overline{P}}_{k|k}^i\left[d\right]\right)$ end for: State update: $X_{k|k}^i={\overline{X}}_{k|k}^i\left[N_d\right]$ $P_{k|k}^i={\overline{P}}_{k|k}^i\left[N_d\right]$

5. Simulation and Discussion

In this paper, we focused on tracking a non-cooperative target, which could perform maneuvers such as equilibrium glide and skip glide in near space. To verify the effectiveness and advantages of the proposed FDMM algorithm for satellites’ tracking systems, two simulation scenarios were established: Case 1 was designed to track an equilibrium gliding target, and Case 2 was for tracking the skip-gliding target. 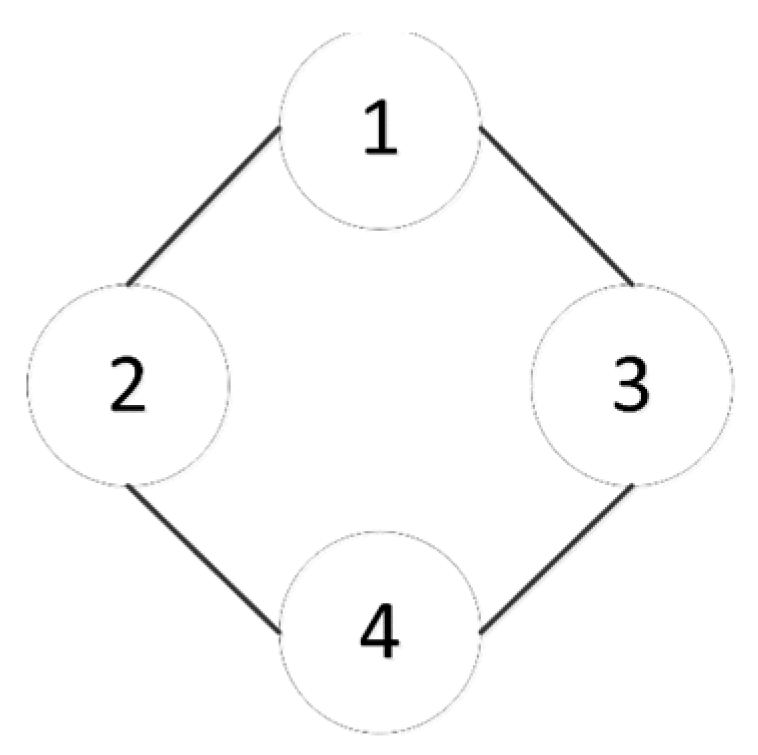The target trajectories in the two scenarios were designed according to [39]. Four LEO satellites were used as the tracking platform, and their communication topology is given in Figure 4.

Unlike a centralized framework, in the FDMM algorithm there is no need for a central satellite to communicate with and process data from the remaining satellites, and each satellite only exchanges data with its adjacent satellites. In both simulations, satellite 1 only communicated with satellite 2 and satellite 3; and satellite 2 only communicated with satellite 1 and satellite 4, as shown in Figure 4. In the centralized algorithms, one satellite was the central node to communicate with the others. In addition, in the FDMM algorithm, each satellite undertakes specific computing tasks, which is also different to a centralized framework, where most computational tasks are completed by the central satellite. By allocating the computing tasks of the MM filtering process to each satellite, the computational efficiency of the tracking system is significantly improved.

The initial orbital parameters of the satellites are shown in

Table 1. The initial orbital parameters of the satellites.

Parameters	$\mathit{a}$ (km)	$\mathit{e}$	$\mathit{i}\mathbf{ }\mathbf{(}\mathbf{°}\mathbf{)}$	$\mathbf{\Omega }\mathbf{ }\mathbf{(}\mathbf{°}\mathbf{)}$	$\mathit{\omega }\mathbf{ }\mathbf{(}\mathbf{°}\mathbf{)}$	$\mathit{M}\mathbf{ }\mathbf{(}\mathbf{°}\mathbf{)}$
Satellite 1	7,300,000	0.000001	80.030	0	0.041	345
Satellite 2	7,300,000	0.000001	75.030	15	0.041	345
Satellite 3	7,300,000	0.000001	85.030	20	0.041	345
Satellite 4	7,300,000	0.000001	70.030	5	0.041	345

. Each satellite was able to observe the azimuth and elevation of the non-cooperative target at each sampling moment. The sampling interval was set as $1s$ in this study.

Table 2. The detailed information of the used models.

Model	Parameter	Value
Singer 1 1	$\alpha$	$\frac{1}{20}$
	$a_{max}$	$20$
	$P_{max}$	$0.1$
	$P_0$	$0.3$
Singer 2	$\alpha$	1
	$a_{max}$	10
	$P_{max}$	0.01
	$P_0$	0.5
CV	$var\left(\omega \right)$ 2	100
CA	$S_{\omega }$ 3	20

¹ In the Singer model, $\alpha$ refers to the maneuvering frequency; $\alpha$, $a_{max}$, $P_{max}$ and $P_0$ are the design parameters for the different maneuvering modes; ² $var\left(\omega \right)$ refers to the variance of the white noise, $\omega$; ³ $S_{\omega }$ refers to the power spectral density of the white noise, $\omega$.

gives the detailed information of the model set in the multiple-model algorithm. In the FDMM algorithm, satellite 1 selects the Singer 2 model, satellite 2 selects the CA model, satellite 3 selects the CV model, and satellite 4 selects the Singer 1 model.

In the FDMM algorithm, the satellite tracking system tracks the target through a novel distributed multiple-model fusion framework, as shown in Figure 3. The communications between the four satellites in the FDMM algorithm, in the simulation, are presented below. Firstly, satellite 1, when it performed local filtering based on the Singer 2 model, needed to collect the measurements $\left(\left\{z_k^j,R_k^j\right\},j\in \left\{2,3\right\}\right)$ from satellites 2 and 3. After satellite 1 received the state estimates $\left\{{\widehat{X}}_{k|k}^{j,Local},{\widehat{P}}_{k|k}^{j,Local},{\beta }_k^j\right\},j\in \left\{2,3\right\}$ from satellites 2 and 3, it was able to perform the multiple-model fusion, based on the data $\left(\left\{{\widehat{X}}_{k|k}^{j,Local},{\widehat{P}}_{k|k}^{j,Local},{\beta }_k^j\right\},j\in \left\{1,2,3\right\}\right)$. Finally, satellite 1 exchanged the data $\left({\overline{X}}_{k|k}^i\left[d\right],{\overline{P}}_{k|k}^i\left[d\right]\right)$ with satellites 2 and 3, and updated its state estimation according to the consensus protocol. The other satellites followed a similar communication process to that of satellite 1.

To objectively compare the performance of the tracking algorithms, the experimental results of each algorithm were obtained through 100 Monte Carlo runs. The root mean-squared error (RMSE) [23,40] of the network, and the average CPU time per period of each satellite, were adopted as the performance index.

For the distributed algorithm, the RMSE of the Position estimate (PRMSE) at the satellite $s_i$, and at time $k$, is shown in Equation (44):

$$PRMS{E}_k^i=\sqrt{\frac{1}{M}{\displaystyle \sum }_{i=1}^M\left[{\left(x_k-{\widehat{x}}_{k|k}^i\right)}^2+{\left(y_k-{\widehat{y}}_{k|k}^i\right)}^2+{\left(z_k-{\widehat{z}}_{k|k}^i\right)}^2\right]}$$

(44)

where M refers to the number of the Monte Carlo experiments—which, in this study, was $M=100$. The RMSE of the Velocity estimate (VRMSE) at satellite $s_i$, and at time $k$, is shown in Equation (45):

$$VRMS{E}_k^i=\sqrt{\frac{1}{M}{\displaystyle \sum }_{i=1}^M\left[{\left({\dot{x}}_k-{\widehat{\dot{x}}}_{k|k}^i\right)}^2+{\left({\dot{y}}_k-{\widehat{\dot{y}}}_{k|k}^i\right)}^2+{\left({\dot{z}}_k-{\widehat{\dot{z}}}_{k|k}^i\right)}^2\right]}$$

(45)

The PRMSE and VRMSE of the overall nodes of the satellite network at time $k$ were respectively calculated as Equations (46) and (47):

$$PRMS{E}_k^{network}=\frac{1}{N}{\displaystyle \sum }_{i=1}^{N}PRMS{E}_k^i$$

(46)

$$VRMS{E}_k^{network}=\frac{1}{N}{\displaystyle \sum }_{i=1}^{N}VRMS{E}_k^i$$

(47)

where $N$ refers to the number of computing satellites. For the distributed algorithm in this study, $N=4$, and for the centralized algorithm, $N=1$.

In the distributed algorithm, the average CPU time per period referred to the average time consumed by each satellite for computing in each cycle; correspondingly, in the centralized algorithm, it referred to the average time the central satellite spent in calculations per cycle. This reflected the computational complexity of the algorithm. Both simulation experiments were run on a laptop equipped with an AMD Ryzen 7 4800H with Radeon Graphics 2.90 GHz CPU and the Windows 10 operating system.

5.1. Case 1: Tracking the Equilibrium Gliding Target

5.1.1. Simulation Introduction and Results

In Case 1, we focused on tracking the non-cooperative target in the equilibrium glide mode. The flight lasted for about $300\mathrm{s}$ during the gliding phase. The trajectory of the target is shown in Figure 5. This scenario aimed to study the performance of tracking algorithms for a target with wide-ranging lateral maneuvers in 3D space.

The initial position and velocity of the target in the ECI were $\left[6416\mathrm{km},0,0\right]$ and $\left[-9.7\mathrm{m}/\mathrm{s},4416.4\mathrm{m}/\mathrm{s},858.5\mathrm{m}/\mathrm{s}\right]$, respectively. In order to simulate a more realistic scenario, and to test the robustness of each tracking algorithm, an initial disturbance was given, where the position errors were $\left[1\mathrm{km},1\mathrm{km},1\mathrm{km}\right]$ and the velocity errors were $\left[1\mathrm{m}/\mathrm{s},1\mathrm{m}/\mathrm{s},1\mathrm{m}/\mathrm{s}\right]$.

In this experiment, the proposed Fast Distributed Multiple-Model algorithm (FDMM) was compared with the following algorithms: the Consensus-based Strong Tracking Cubature Kalman Filter algorithm (CSTACKF) proposed in [24]; the Consensus-based Distributed Multiple-Model algorithm (CDMM) proposed in [23]; the Improved CDMM algorithm (ICDMM) combined with STF; and the IMM algorithm combined with STF. Specifically, the CSTACKF algorithm was applied where the satellites took the same single-motion model as the global model, and utilized the STACKF. Here, the Singer 2 model in Table 2 was used as the global model for the CSTACKF algorithm. The CDMM algorithm represented the satellites’ employment of a distributed multiple-model approach to track the maneuvering target. Moreover, the ICDMM algorithm indicated that the satellites simultaneously used the multiple-model approach and STF method, to track the non-cooperative target. The IMM algorithm indicated that the satellites applied the interactive multiple-model approach and the STF under a centralized framework.

The RMSE of the position and velocity for the different algorithms are given in Figure 6 and Figure 7, respectively. Figure 8 gives the comparison of the average CPU time per period, and Figure 9 gives the comparison of the estimated trajectories with the true trajectory in one Monte Carlo run.

Table 3. The average tracking error of the total tracking process.

Algorithm	Average Position Error 1 (m)	Average Velocity Error 2 (m/s)
FDMM	35.9289	18.0141
ICDMM	63.5542	33.6745
IMM	70.9382	35.9268
CSTACKF	44.2134	19.9188
CDMM	1119.1594	294.4672

¹ The average position error is the average of $PRMS{E}_k^{network}$ over time. ² The average velocity error is the average of $VRMS{E}_k^{network}$ over time.

gives the average tracking error of the total tracking process in each algorithm.

5.1.2. Analysis and Discussion

Although each tracking algorithm was able to achieve tracking of the non-cooperative target, they exhibited different performances. In terms of the algorithm convergence rates, after being affected by the initial disturbance, the proposed FDMM algorithm showed a similar tracking convergence rate to the CSTACKF algorithm, while the rest of the multiple-model algorithms had slower convergence rates, as shown in Figure 6 and Figure 7. As there was no prior information on the target dynamics, model errors inevitably existed in the chosen model set of the multiple-model algorithms. Intense competition among the mismatched sub-models resulted in slower convergence. As the FDMM algorithm adopted a new multiple-model fusion framework, where the introduction of Wasserstein distance made the weight distribution between models more reasonable, the initial disturbance had little impact on the convergence of the FDMM algorithm, whereas it had a greater influence on the other three MM algorithms.

In terms of algorithm precision, the proposed FDMM algorithm exhibited the smallest position and velocity average tracking errors among all the employed algorithms. After the filtering process converged, it showed the smallest RMSE of position tracking, about 25 m, as shown in Table 3, Figure 6 and Figure 7. The CDMM algorithm adopted the UKF in the tracking process, which had poor adaptability. The initial disturbance engendered a more significant impact on the CDMM algorithm, compared to the ICDMM algorithm with the STUKF. Moreover, the wide-ranging lateral maneuver also made the filtering of the CDMM algorithm take a long time to converge, as shown in Figure 6 and Figure 9. For other algorithms, the CDMM algorithm without the STF showed the worst performance. After the filtering finally converged, the ICDMM and IMM algorithms, which adopted the MM method, and combined STF, showed higher filtering convergence precision than the CSTACKF algorithm, which adopted a single model and STF. The results indicated that the integration of the MM method and STFs was effective and exhibited higher performance.

In terms of the average CPU time per period, compared to other MM algorithms, the results illustrated that the FDMM algorithm required far less computation time, as shown in Figure 8, meaning that the FDMM algorithm had far less computational complexity than other MM methods. In addition, the average CPU time of the FDMM algorithm was close to the CSTACKF, which employed a single model, proving that the new proposed distributed multi-model fusion framework in the FDMM algorithm could significantly reduce the computational complexity of the MM algorithm.

In conclusion, the FDMM algorithm exhibited the best performance, in terms of convergence speed, tracking precision, and average CPU time per period. Case 1 demonstrated the advantages and effectiveness of the FDMM algorithm for satellites tracking non-cooperative targets with wide-ranging lateral maneuvers in 3D space.

5.2. Case 2: Tracking the Skip-Gliding Target

5.2.1. Simulation Introduction and Results

In Case 2, we focused on tracking a non-cooperative target in the skip-gliding mode. This experiment was conducted to study the tracking performance of algorithms for strong-maneuvering non-cooperative targets.

The initial position and velocity of the target in the ECI were $\left[6416.11\mathrm{km},0,0\right]$ and $\left[-12.8\mathrm{m}/\mathrm{s},4499.8\mathrm{m}/\mathrm{s},0\right]$, respectively. The initial altitude of the target was $45\mathrm{km}$, and the initial longitude and latitude were (0°, 0°). The trajectory is given in Figure 10.

The position and velocity RMSE of the algorithms are shown in Figure 11 and Figure 12, respectively. Figure 13 gives the comparison of the average CPU time per period, and Figure 14 gives the comparison of the estimated trajectories to the true trajectory in one Monte Carlo run. The average tracking error of the total tracking process is given in

Table 4. The average tracking error of the non-cooperative target in the skip-gliding mode.

Algorithm	Average Position Error 1 (m)	Average Velocity Error 2 (m/s)
FDMM	35.7261	15.9015
ICDMM	55.1157	29.2621
IMM	61.2298	30.5339
CSTACKF	56.2843	28.8910
CDMM	919.9887	239.1422

¹ The average position error is the average of $PRMS{E}_k^{network}$ over time. ² The average velocity error is the average of $VRMS{E}_k^{network}$ over time.

.

In Case 2, the proposed FDMM algorithm was also compared with the CSTACKF, the CDMM, the ICDMM, and the IMM algorithms. The initial disturbance was also given, where the position errors were $\left[1\mathrm{km},1\mathrm{km},1\mathrm{km}\right]$ and the velocity errors were $\left[1\mathrm{m}/\mathrm{s},1\mathrm{m}/\mathrm{s},1\mathrm{m}/\mathrm{s}\right]$. Since the target was non-cooperative, no relevant prior dynamics information could be obtained, to build an accurate motion model for the tracking algorithm. To verify the robustness of these tracking algorithms, the same set-up as in Case 1 was used in each multiple-model algorithm, despite tracking the highly maneuvering target in Case 2.

5.2.2. Analysis and Discussion

When tracking the non-cooperative target in the skip-gliding mode, the position RMSE and the velocity RMSE of the CSTACKF algorithm were not stable, as can be seen in Figure 11 and Figure 12. The CSTACKF algorithm took a single model, which mismatched the motion of the target. Affected by the skip-gliding maneuver of the target, it showed lower tracking process stability, and its tracking precision also fluctuated up and down. As there was no adaptive filter, the CDMM algorithm was greatly affected by the initial disturbance. In addition, the skip-gliding maneuver also made the filtering of the CDMM algorithm take a long time to converge, as shown in Figure 11, Figure 12 and Figure 14. In Case 2, the CDMM algorithm still showed the worst performance among the five algorithms.

The ICDMM and IMM algorithms, which incorporated STFs and MM methods, had relatively high tracking accuracy after the filtering converged. Although the STFs and MM methods improved their stability in tracking the non-cooperative target with strong maneuverability, inaccurate sub-models in the MM algorithms engendered problems with the convergence rate. Due to the sub-model competition, the convergence rate of the tracking process was relatively slow when it came to the initial disturbances, as shown in Figure 11 and Figure 12.

In contrast, the proposed FDMM algorithm, which also combines the STFs and MM methods, showed the best performance among the algorithms. By using the proposed fusion factors, the FDMM algorithm drastically reduced the competition among sub-models in the multiple model methods, and improved the ability to handle the disturbance. As shown in Figure 11 and Figure 12, and Table 4, the FDMM algorithm exhibited a relatively fast convergence rate, extremely high tracking accuracy, and a highly stable tracking process. After the filter converged, the position-tracking error was reduced to about $26\mathrm{m}$. Furthermore, the position-average-tracking error and the velocity-average-tracking error of the whole process were reduced to $35.7261\mathrm{m}$ and $15.9015\mathrm{m}/\mathrm{s}$, respectively.

The average computational costs per period of the ICDMM, CDMM, IMM, FDMM, and CSTACKF algorithms were assessed, as shown in Figure 13. This proved again that the FDMM algorithm had much lower algorithm computational complexity than other MM algorithms, and demonstrated the advantages of the newly proposed distributed multi-model fusion framework in the FDMM algorithm.

Overall, considering the performance of tracking-process stability, convergence rate, tracking precision, and the average CPU time per period, the FDMM algorithm demonstrated the best performance when tracking the target with a skip-gliding trajectory.

6. Conclusions

This paper puts forward a novel distributed multiple-model algorithm, the FDMM, for satellites tracking non-cooperative near-space targets. The FDMM algorithm had high robustness against disturbance, and high adaptability to the uncertainty modeling of non-cooperative targets. To improve the tracking precision, the strong-tracking CKF and the multiple-model methods were adopted in the FDMM algorithm, to cope with the intense maneuvers of the target. To reduce the computational burden, a new distributed multiple-model framework was developed. It first required each satellite to perform local filtering based on its own single model, and assigned corresponding weights to the local estimates based on the fusion factor; then, each satellite performed multiple-model fusion based on the minimum weighted KL divergence for the estimates from adjacent satellites; finally, the states of each satellite were updated based on the consensus protocol. The results of the two experiments demonstrated that the FDMM algorithm had higher tracking process stability, a faster convergence rate, higher tracking precision, and lower computational complexity, when compared with other multiple-model algorithms (e.g., the CDMM, the ICDMM, and the IMM algorithms). The effectiveness and advantages of the FDMM for satellites tracking non-cooperative near-space targets were thus validated.

In this paper, to reduce the computational burden and improve the accuracy of tracking a single non-cooperative near-space target, the FDMM algorithm was developed for satellite tracking systems equipped with SAR. A multi-target tracking scenario, employing the FDMM algorithm, has not yet been studied. In the future, we will develop the improved algorithm based on FDMM for multi-target tracking. Furthermore, the communication delay problem was not considered in this study. In the future, we will study the problem of satellites tracking non-cooperative targets in near-space with communication delays.