Modeling Evapotranspiration at Larger Temporal Scales: Effects of Temporal Aggregation and Data Gaps
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Description of Datasets
2.3. Brief Description of the Models
2.3.1. Priestley–Taylor Jet Propulsion Lab (PT-JPL)
2.3.2. Soil Plant Atmosphere and Remote Sensing Evapotranspiration (SPARSE)
2.3.3. Surface Temperature Initiated Closure (STIC)
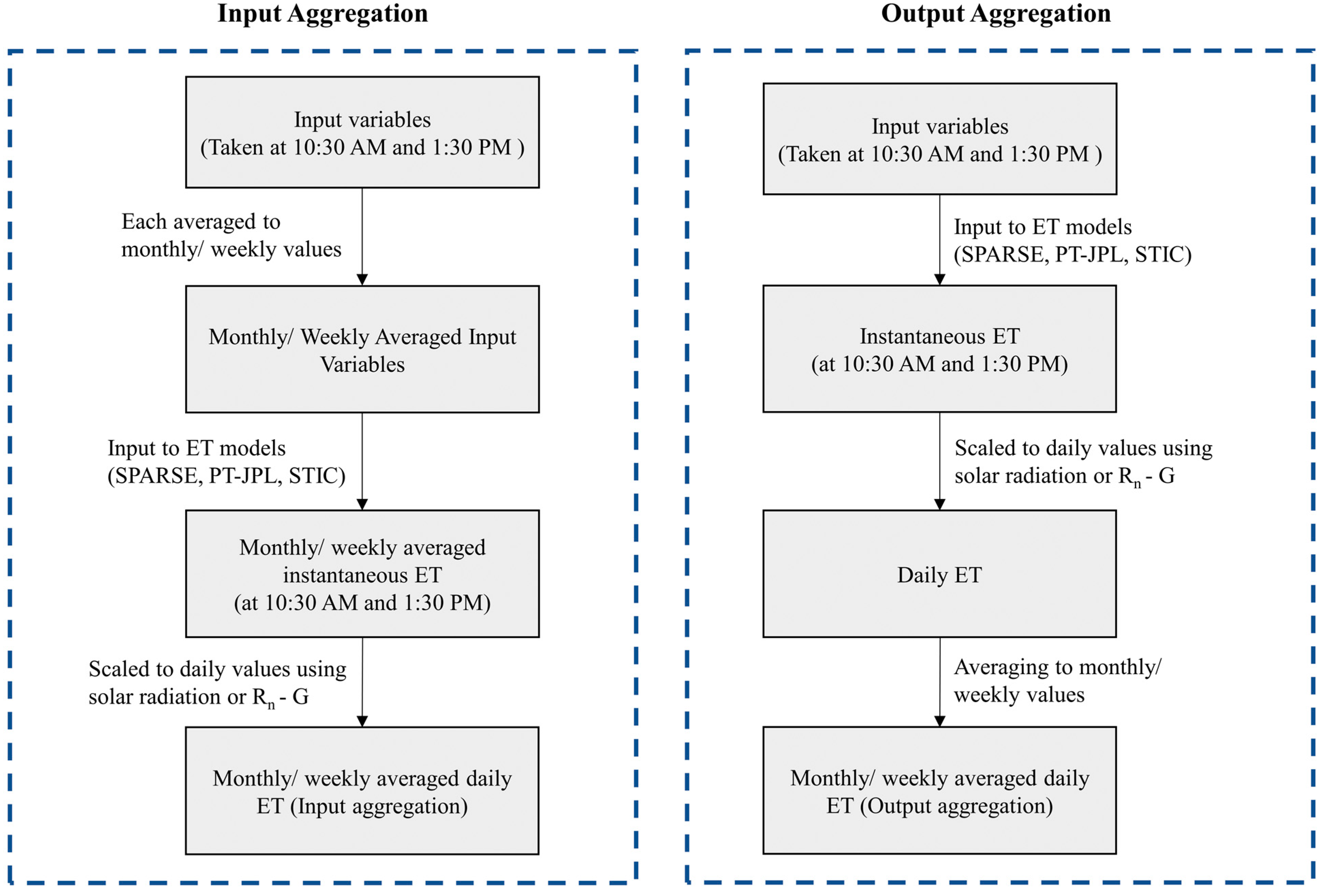
2.4. Methodology
2.4.1. Temporal Aggregation
2.4.2. Identifying Clear-Sky Days
2.4.3. Instantaneous to Daily ET
2.4.4. Effect of Missing Data
3. Results and Discussions
3.1. Temporal Aggregation
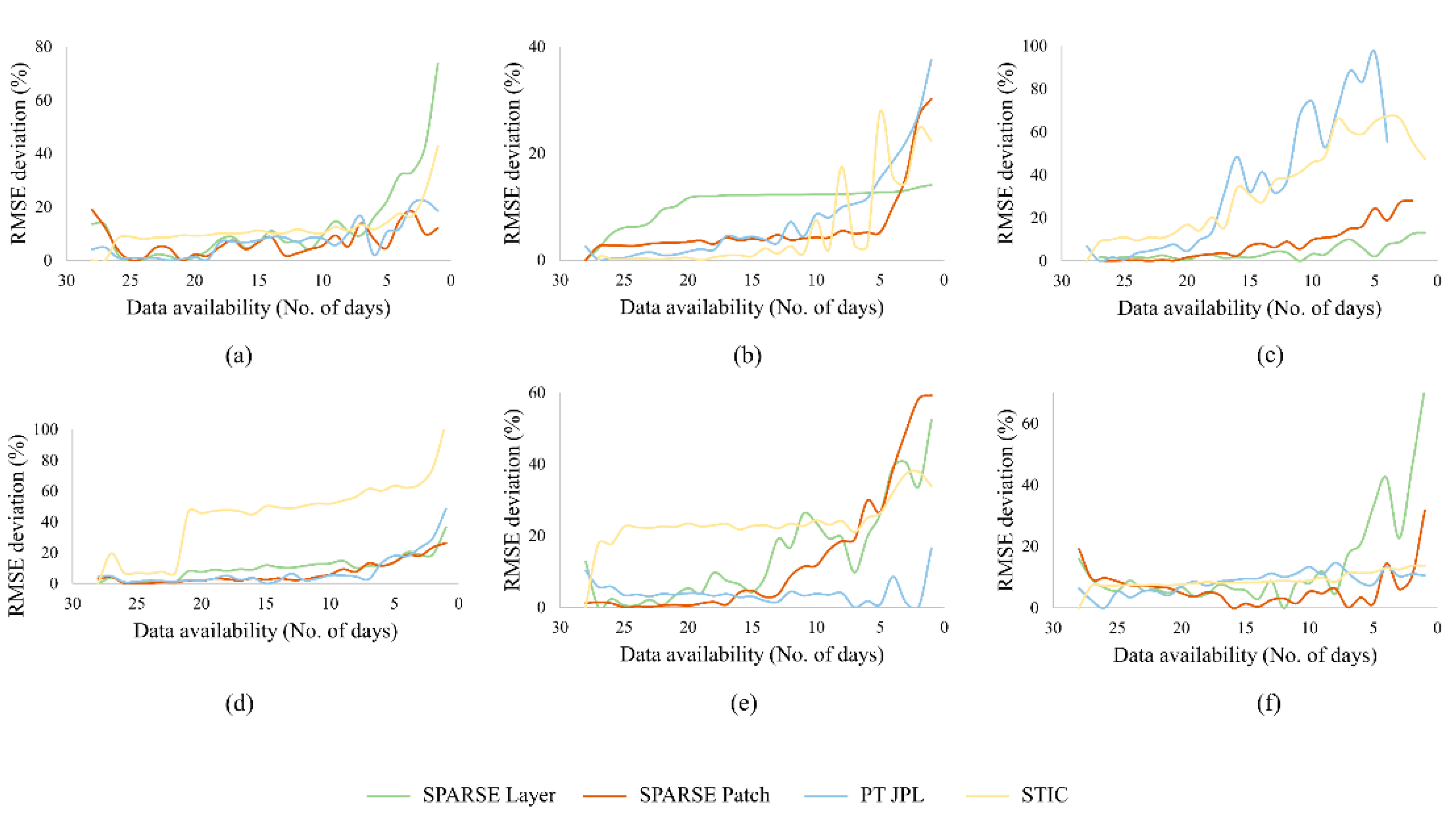
3.2. Effect of Missing Data
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, K.; Kimball, J.S.; Running, S.W. A Review of Remote Sensing Based Actual Evapotranspiration Estimation. WIREs Water 2016, 3, 834–853. [Google Scholar] [CrossRef]
- Chen, J.M.; Liu, J. Evolution of Evapotranspiration Models Using Thermal and Shortwave Remote Sensing Data. Remote Sens. Environ. 2020, 237, 111594. [Google Scholar] [CrossRef]
- Crago, R.; Brutsaert, W. Daytime Evaporation and the Self-Preservation of the Evaporative Fraction and the Bowen Ratio. J. Hydrol. 1996, 178, 241–255. [Google Scholar] [CrossRef]
- Delogu, E.; Boulet, G.; Olioso, A.; Coudert, B.; Chirouze, J.; Ceschia, E.; Le Dantec, V.; Marloie, O.; Chehbouni, G.; Lagouarde, J.-P. Reconstruction of Temporal Variations of Evapotranspiration Using Instantaneous Estimates at the Time of Satellite Overpass. Hydrol. Earth Syst. Sci. 2012, 16, 2995–3010. [Google Scholar] [CrossRef] [Green Version]
- Ryu, Y.; Baldocchi, D.D.; Black, T.A.; Detto, M.; Law, B.E.; Leuning, R.; Miyata, A.; Reichstein, M.; Vargas, R.; Ammann, C.; et al. On the Temporal Upscaling of Evapotranspiration from Instantaneous Remote Sensing Measurements to 8-Day Mean Daily-Sums. Agric. For. Meteorol. 2012, 152, 212–222. [Google Scholar] [CrossRef] [Green Version]
- Van Niel, T.G.; McVicar, T.R.; Roderick, M.L.; van Dijk, A.I.J.M.; Beringer, J.; Hutley, L.B.; van Gorsel, E. Upscaling Latent Heat Flux for Thermal Remote Sensing Studies: Comparison of Alternative Approaches and Correction of Bias. J. Hydrol. 2012, 468–469, 35–46. [Google Scholar] [CrossRef]
- Cammalleri, C.; Anderson, M.C.; Kustas, W.P. Upscaling of Evapotranspiration Fluxes from Instantaneous to Daytime Scales for Thermal Remote Sensing Applications. Hydrol. Earth Syst. Sci. 2014, 18, 1885–1894. [Google Scholar] [CrossRef] [Green Version]
- Xu, T.; Liu, S.; Xu, L.; Chen, Y.; Jia, Z.; Xu, Z.; Nielson, J. Temporal Upscaling and Reconstruction of Thermal Remotely Sensed Instantaneous Evapotranspiration. Remote Sens. 2015, 7, 3400–3425. [Google Scholar] [CrossRef] [Green Version]
- Alfieri, J.G.; Anderson, M.C.; Kustas, W.P.; Cammalleri, C. Effect of the Revisit Interval and Temporal Upscaling Methods on the Accuracy of Remotely Sensed Evapotranspiration Estimates. Hydrol. Earth Syst. Sci. 2017, 21, 83–98. [Google Scholar] [CrossRef] [Green Version]
- Guillevic, P.; Olioso, A.; Hook, S.; Fisher, J.; Lagouarde, J.-P.; Vermote, E. Impact of the Revisit of Thermal Infrared Remote Sensing Observations on Evapotranspiration Uncertainty—A Sensitivity Study Using AmeriFlux Data. Remote Sens. 2019, 11, 573. [Google Scholar] [CrossRef] [Green Version]
- Tang, R.; Li, Z.L.; Huo, X.; Jiang, Y.; Tang, B.; Wu, H. A re-examination of two methods for estimating daily evapotranspiration from remotely sensed instantaneous observations. Int. J. Remote Sens. 2019, 40, 1981–1995. [Google Scholar] [CrossRef]
- Liu, Z. The Accuracy of Temporal Upscaling of Instantaneous Evapotranspiration to Daily Values with Seven Upscaling Methods. Hydrol. Earth Syst. Sci. 2021, 25, 4417–4433. [Google Scholar] [CrossRef]
- Jiang, L.; Zhang, B.; Han, S.; Chen, H.; Wei, Z. Upscaling Evapotranspiration from the Instantaneous to the Daily Time Scale: Assessing Six Methods Including an Optimized Coefficient Based on Worldwide Eddy Covariance Flux Network. J. Hydrol. 2021, 596, 126135. [Google Scholar] [CrossRef]
- Fisher, J.B.; Lee, B.; Purdy, A.J.; Halverson, G.H.; Dohlen, M.B.; Cawse-Nicholson, K.; Wang, A.; Anderson, R.G.; Aragon, B.; Arain, M.A.; et al. ECOSTRESS: NASA’s Next Generation Mission to Measure Evapotranspiration from the International Space Station. Water Resour. Res. 2020, 56, e2019WR026058. [Google Scholar] [CrossRef]
- Fisher, J.B.; Tu, K.P.; Baldocchi, D.D. Global Estimates of the Land–Atmosphere Water Flux Based on Monthly AVHRR and ISLSCP-II Data, Validated at 16 FLUXNET Sites. Remote Sens. Environ. 2008, 112, 901–919. [Google Scholar] [CrossRef]
- Hong, S.; Hendrickx, J.M.H.; Borchers, B. Up-Scaling of SEBAL Derived Evapotranspiration Maps from Landsat (30 m) to MODIS (250m) Scale. J. Hydrol. 2009, 370, 122–138. [Google Scholar] [CrossRef]
- Ershadi, A.; McCabe, M.F.; Evans, J.P.; Walker, J.P. Effects of Spatial Aggregation on the Multi-Scale Estimation of Evapotranspiration. Remote Sens. Environ. 2013, 131, 51–62. [Google Scholar] [CrossRef]
- Sharma, V.; Kilic, A.; Irmak, S. Impact of Scale/Resolution on Evapotranspiration from Landsat and MODIS Images. Water Resour. Res. 2016, 52, 1800–1819. [Google Scholar] [CrossRef] [Green Version]
- Boulet, G.; Mougenot, B.; Lhomme, J.-P.; Fanise, P.; Lili-Chabaane, Z.; Olioso, A.; Bahir, M.; Rivalland, V.; Jarlan, L.; Merlin, O.; et al. The SPARSE Model for the Prediction of Water Stress and Evapotranspiration Components from Thermal Infra-Red Data and Its Evaluation over Irrigated and Rainfed Wheat. Hydrol. Earth Syst. Sci. 2015, 19, 4653–4672. [Google Scholar] [CrossRef] [Green Version]
- Mallick, K.; Jarvis, A.J.; Boegh, E.; Fisher, J.B.; Drewry, D.T.; Tu, K.P.; Hook, S.J.; Hulley, G.; Ardö, J.; Beringer, J.; et al. A Surface Temperature Initiated Closure (STIC) for Surface Energy Balance Fluxes. Remote Sens. Environ. 2014, 141, 243–261. [Google Scholar] [CrossRef]
- Delogu, E.; Olioso, A.; Alliès, A.; Demarty, J.; Boulet, G. Evaluation of Multiple Methods for the Production of Continuous Evapotranspiration Estimates from TIR Remote Sensing. Remote Sens. 2021, 13, 1086. [Google Scholar] [CrossRef]
- Bhat, G.S.; Morrison, R.; Taylor, C.M.; Bhattacharya, B.K.; Paleri, S.; Desai, D.; Evans, J.G.; Pattnaik, S.; Sekhar, M.; Nigam, R.; et al. Spatial and Temporal Variability in Energy and Water Vapour Fluxes Observed at Seven Sites on the Indian Subcontinent during 2017. Q. J. R. Meteorol. Soc. 2020, 146, 2853–2866. [Google Scholar] [CrossRef] [Green Version]
- Béziat, P.; Ceschia, E.; Dedieu, G. Carbon Balance of a Three Crop Succession over Two Cropland Sites in South West France. Agric. For. Meteorol. 2009, 149, 1628–1645. [Google Scholar] [CrossRef] [Green Version]
- Dare-Idowu, O.; Brut, A.; Cuxart, J.; Tallec, T.; Rivalland, V.; Zawilski, B.; Ceschia, E.; Jarlan, L. Surface Energy Balance and Flux Partitioning of Annual Crops in Southwestern France. Agric. For. Meteorol. 2021, 308–309, 108529. [Google Scholar] [CrossRef]
- Boulet, G.; Olioso, A.; Ceschia, E.; Marloie, O.; Coudert, B.; Rivalland, V.; Chirouze, J.; Chehbouni, G. An Empirical Expression to Relate Aerodynamic and Surface Temperatures for Use within Single-Source Energy Balance Models. Agric. For. Meteorol. 2012, 161, 148–155. [Google Scholar] [CrossRef] [Green Version]
- Priestley, C.H.B.; Taylor, R.J. On the Assessment of Surface Heat Flux and Evaporation Using Large-Scale Parameters. Mon. Weather Rev. 1972, 100, 81–92. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. FAO Irrigation and Drainage Paper No. 56; Food and Agriculture Organization of the United Nations: Rome, Italy, 1998.
- Anderson, M.C.; Allen, R.G.; Morse, A.; Kustas, W.P. Use of Landsat Thermal Imagery in Monitoring Evapotranspiration and Managing Water Resources. Remote Sens. Environ. 2012, 122, 50–65. [Google Scholar] [CrossRef]
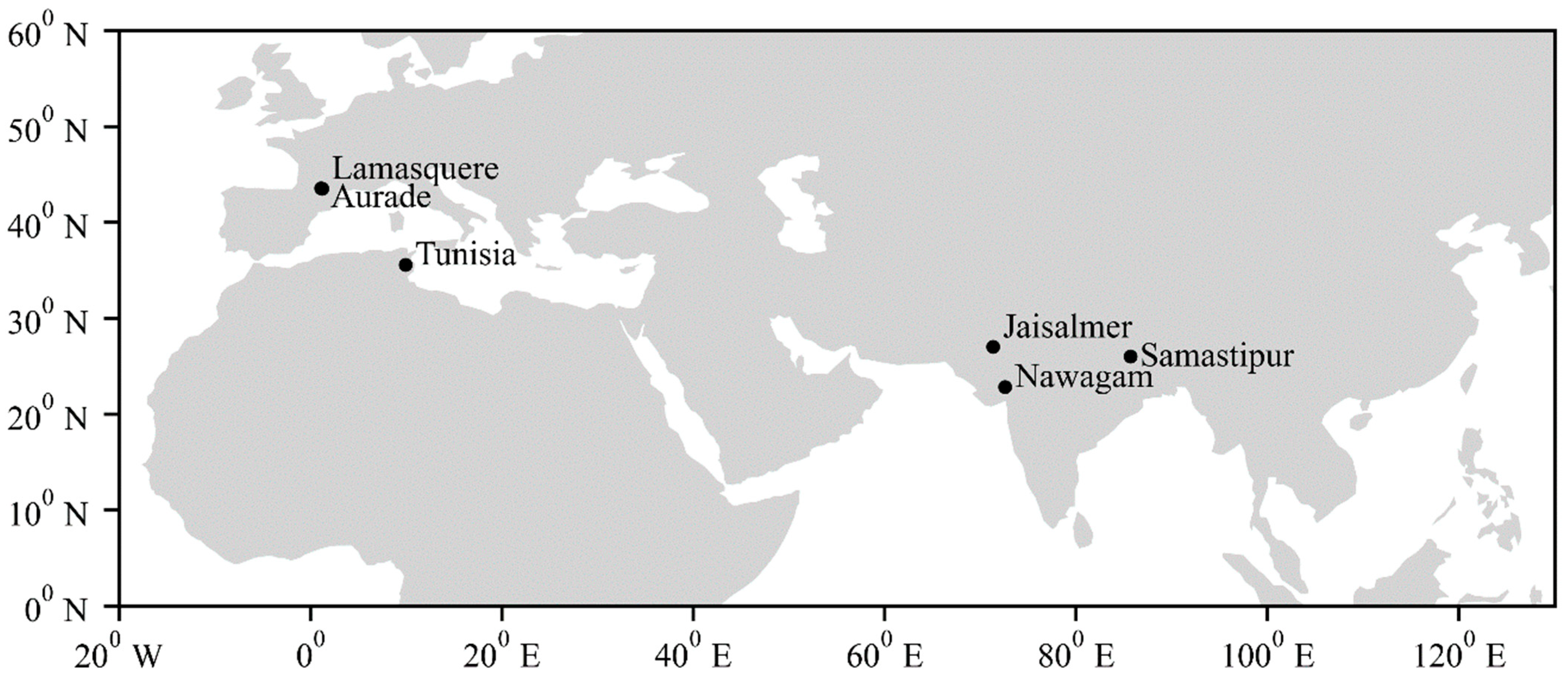

| Site | Location | Crop | Climate | Data Duration | References |
|---|---|---|---|---|---|
| Tunisia, North Africa | 35.56°N, 9.94°E | Wheat | Tropical semi-arid | January 2012–June 2012 | [19] |
| Auradé, France | 43.55°N, 1.11°E | Wheat | Temperate | January 2009–December 2010 | [21] |
| Lamasquère, France | 43.50°N, 1.24°E | Wheat | Temperate | January 2013–July 2013 | [21] |
| Nawagam, India | 22.80°N, 72.57°E | Rice | Semi-arid | August 2017–November 2018 | [22] |
| Samastipur, India | 26.00°N, 85.67°E | Rice and Wheat | Sub-humid | January 2018–September 2018 | [22] |
| Jaisalmer, India | 26.99°N, 71.34°E | Natural sewan grass | Arid | January 2018–December 2018 | [22] |
| Site | Evaporative Fraction | Solar Radiation | |||
|---|---|---|---|---|---|
| 10:30 a.m. | 1:30 p.m. | 10:30 a.m. | 1:30 p.m. | ||
| SPARSE-Layer | Tunisia | 2.39 (4.45) | 1.64 (3.05) | 2.77 (5.16) | 1.23 (2.3) |
| Auradé | 1.37 (3.16) | 1.92 (4.43) | 1.76 (4.08) | 2.48 (5.74) | |
| Lamasquère | 11.14 (9.83) | 3.26 (2.88) | 10.62 (9.37) | 4.84 (4.27) | |
| Nawagam | 1.11 (1.37) | 0.03 (0.03) | 0.22 (0.27) | 0.63 (0.78) | |
| Samastipur | 5.45 (5.81) | 5.03 (5.36) | 6.06 (6.46) | 4.9 (5.22) | |
| Jaisalmer | 4.49 (26.26) | 4.84 (28.32) | 4.2 (24.56) | 4.75 (27.81) | |
| SPARSE-Patch | Tunisia | 0.04 (0.07) | 0.72 (1.35) | 0.14 (0.26) | 2.53 (4.72) |
| Auradé | 0.04 (0.09) | 0.29 (0.66) | 0.78 (1.8) | 0.91 (2.1) | |
| Lamasquère | 0.96 (0.85) | 0.28 (0.24) | 0.3 (0.26) | 0.94 (0.83) | |
| Nawagam | 4.54 (5.63) | 1.73 (2.15) | 3.76 (4.66) | 0.3 (0.38) | |
| Samastipur | 0.13 (0.14) | 1.29 (1.38) | 0.31 (0.33) | 1.32 (1.41) | |
| Jaisalmer | 0.15 (0.86) | 0.12 (0.7) | 0.16 (0.95) | 0.13 (0.78) | |
| PT-JPL | Tunisia | 4.8 (8.96) | 6.08 (11.34) | 3.84 (7.16) | 3.52 (6.57) |
| Auradé | 4.43 (10.24) | 6.72 (15.53) | 4.05 (9.36) | 7.19 (16.61) | |
| Lamasquère | 40.01 (35.31) | 38.58 (34.05) | 48.08 (42.44) | 38.08 (33.61) | |
| Nawagam | 35.32 (43.78) | 30.35 (37.62) | 19.4 (24.04) | 31.07 (38.51) | |
| Samastipur | –18.14 (19.35) | –10.79 (11.5) | –22.11 (23.57) | –13.17 (14.04) | |
| Jaisalmer | –6.01 (35.16) | –26.43 (154.72) | –6.09 (35.67) | –26.98 (157.95) | |
| STIC | Tunisia | 0.34 (0.64) | 0.66 (1.23) | 0.63 (1.18) | 0.67 (1.24) |
| Auradé | 18.23 (42.13) | 0.18 (0.41) | 13.99 (32.33) | 0.73 (1.68) | |
| Lamasquère | 67.88 (59.9) | 22.19 (19.58) | 51.72 (45.65) | 21.21 (18.72) | |
| Nawagam | 2.83 (3.5) | 1.45 (1.79) | 2.51 (3.11) | 0.87 (1.08) | |
| Samastipur | 1.44 (1.54) | 1.83 (1.96) | 0.38 (0.41) | 2.33 (2.49) | |
| Jaisalmer | 16 (93.65) | 32.07 (187.77) | 17.89 (104.74) | 33.49 (196.1) | |
| Site | Evaporative Fraction | Solar Radiation | |||
|---|---|---|---|---|---|
| 10:30 a.m. | 1:30 p.m. | 10:30 a.m. | 1:30 p.m. | ||
| SPARSE-Layer | Tunisia | 0.35 (2.74) | 0.13 (0.99) | 0.43 (3.41) | 0.02 (0.15) |
| Auradé | 0.87 (9.83) | 0.81 (9.23) | 0.56 (6.32) | 0.1 (1.09) | |
| Lamasquère | 0.91 (3.48) | 1.4 (5.38) | 0.72 (2.75) | 0.63 (2.42) | |
| Nawagam | 0.33 (1.85) | 0.6 (3.38) | 0.17 (0.97) | 0.63 (3.52) | |
| Samastipur | 0.96 (4.42) | 0.74 (3.39) | 1.06 (4.87) | 0.8 (3.67) | |
| Jaisalmer | 0.24 (6.53) | 0.6 (16.46) | 0.19 (5.18) | 0.57 (15.38) | |
| SPARSE-Patch | Tunisia | 0.04 (0.29) | 0.16 (1.26) | 0.01 (0.06) | 0.04 (0.32) |
| Auradé | 0.49 (5.56) | 0.5 (5.7) | 0.18 (2.06) | 0.09 (1.01) | |
| Lamasquère | 1.88 (7.23) | 0.07 (0.25) | 0.03 (0.12) | 0.03 (0.1) | |
| Nawagam | 0.02 (0.09) | 0.48 (2.71) | 0.02 (0.14) | 0.14 (0.77) | |
| Samastipur | 0.33 (1.54) | 0.44 (2.04) | 0.31 (1.43) | 0.48 (2.2) | |
| Jaisalmer | 0.01 (0.32) | 0.03 (0.85) | 0.02 (0.42) | 0.02 (0.64) | |
| PT-JPL | Tunisia | 1.83 (14.5) | 2 (15.83) | 1.74 (13.78) | 1.28 (10.19) |
| Auradé | 0.44 (4.98) | 0.88 (9.96) | 0.24 (2.72) | 0.87 (9.9) | |
| Lamasquère | 3.24 (12.44) | 8.75 (33.57) | 3.58 (13.72) | 0.67 (2.57) | |
| Nawagam | 7.9 (44.19) | 6.28 (35.15) | 3.12 (17.48) | 4.82 (26.97) | |
| Samastipur | –3.46 (15.91) | 1.22 (5.59) | –4.05 (18.61) | 0.84 (3.87) | |
| Jaisalmer | –3.02 (82.08) | –3.59 (97.78) | –3.18 (86.65) | –3.73 (101.61) | |
| STIC | Tunisia | 0.05 (0.37) | 0.13 (1.02) | 0.05 (0.37) | 0.09 (0.69) |
| Auradé | 1.56 (17.67) | 0.37 (4.21) | 1.36 (15.44) | 0.42 (4.8) | |
| Lamasquère | 4.45 (17.08) | 2.1 (8.07) | 4.47 (17.15) | 15.94 (61.15) | |
| Nawagam | 0.61 (3.4) | 0.17 (0.96) | 0.37 (2.05) | 0.03 (0.19) | |
| Samastipur | 1.74 (7.99) | 5.61 (25.79) | 1.1 (5.08) | 5.69 (26.17) | |
| Jaisalmer | 2.4 (65.39) | 2.63 (71.65) | 2.72 (74.08) | 2.7 (73.55) | |
| Model | Site | 10:30 a.m. | 1:30 p.m. | ||
|---|---|---|---|---|---|
| Input | Output | Input | Output | ||
| SPARSE-Layer | Tunisia | 0.11 | 0.12 | 0.3 | 0.2 |
| Auradé | 0.35 | 0.4 | 0.31 | 0.36 | |
| Lamasquère | 0.09 | 0.19 | 0.09 | 0.15 | |
| Nawagam | 0.15 | 0.15 | 0.18 | 0.21 | |
| Samastipur | 0.06 | 0.06 | 0.1 | 0.09 | |
| Jaisalmer | 0.53 | 0.42 | 0.71 | 0.58 | |
| SPARSE-Patch | Tunisia | 0.47 | 0.31 | 0.28 | 0.32 |
| Auradé | 0.69 | 0.68 | 0.67 | 0.71 | |
| Lamasquère | 0.12 | 0.09 | 0.1 | 0.04 | |
| Nawagam | 0.42 | 0.33 | 0.35 | 0.31 | |
| Samastipur | 0.03 | 0.05 | 0.04 | 0.06 | |
| Jaisalmer | 0.88 | 0.94 | 0.87 | 0.93 | |
| PT-JPL | Tunisia | 0.54 | 0.65 | 0.63 | 0.79 |
| Auradé | 0.89 | 1 | 0.83 | 1 | |
| Lamasquère | 0.53 | 0.95 | 0.36 | 1 | |
| Nawagam | 0.14 | 0.65 | 0.35 | 0.66 | |
| Samastipur | 0.63 | 0.89 | 0.56 | 0.9 | |
| Jaisalmer | 0.92 | 1 | 0.94 | 0.91 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Athira, K.V.; Eswar, R.; Boulet, G.; Nigam, R.; Bhattacharya, B.K. Modeling Evapotranspiration at Larger Temporal Scales: Effects of Temporal Aggregation and Data Gaps. Remote Sens. 2022, 14, 4142. https://doi.org/10.3390/rs14174142
Athira KV, Eswar R, Boulet G, Nigam R, Bhattacharya BK. Modeling Evapotranspiration at Larger Temporal Scales: Effects of Temporal Aggregation and Data Gaps. Remote Sensing. 2022; 14(17):4142. https://doi.org/10.3390/rs14174142
Chicago/Turabian StyleAthira, K. V., R. Eswar, Gilles Boulet, Rahul Nigam, and Bimal K. Bhattacharya. 2022. "Modeling Evapotranspiration at Larger Temporal Scales: Effects of Temporal Aggregation and Data Gaps" Remote Sensing 14, no. 17: 4142. https://doi.org/10.3390/rs14174142
APA StyleAthira, K. V., Eswar, R., Boulet, G., Nigam, R., & Bhattacharya, B. K. (2022). Modeling Evapotranspiration at Larger Temporal Scales: Effects of Temporal Aggregation and Data Gaps. Remote Sensing, 14(17), 4142. https://doi.org/10.3390/rs14174142







