Seasonal Variation of Stratospheric Gravity Waves in the Asian Monsoon Region Derived from COSMIC-2 Data
Abstract
:1. Introduction
2. Data and Method
2.1. Data
2.2. Method
- (1)
- The observed temperature data are linearly interpolated onto equidistant points with a vertical interval of 100 m over heights 9–55 km.
- (2)
- (3)
- The background temperature for the gridded data is calculated using based on the following formula, where the coefficients are obtained by the least-squares method according to John and Kumar [31]:where is the background temperature at a specific height and latitude, is the longitude of the grid point. It can be seen from Equation (3) that the background temperature includes the temperature of planetary waves with zonal wavenumbers of 0 to 6, and is the temperature amplitude of the planetary wave. The temperature perturbation is the difference between the observed temperature and the background temperature, .
- (4)
- The temperature perturbation is filtered and smoothed in the vertical direction to obtain the GW temperature [13]. The temperature perturbation is first filtered with a bandwidth of 2–10 km according to Tsuda et al. [13] in the vertical direction, and each filtered temperature profile is then smoothed with a vertical height window of 2 km, as follows:where z1 and z2 are the upper and lower heights of the smoothing window, respectively.
- (5)
- Finally, the results of Equations (2) and (4) are inserted into Equation (1) to obtain the vertical profile of Ep. The Ep of the horizontal distribution is obtained by the IDW (inverse distance weight) [32].
3. Results and Discussion
3.1. Spatial Distribution and Seasonal Variation of Stratospheric GWs
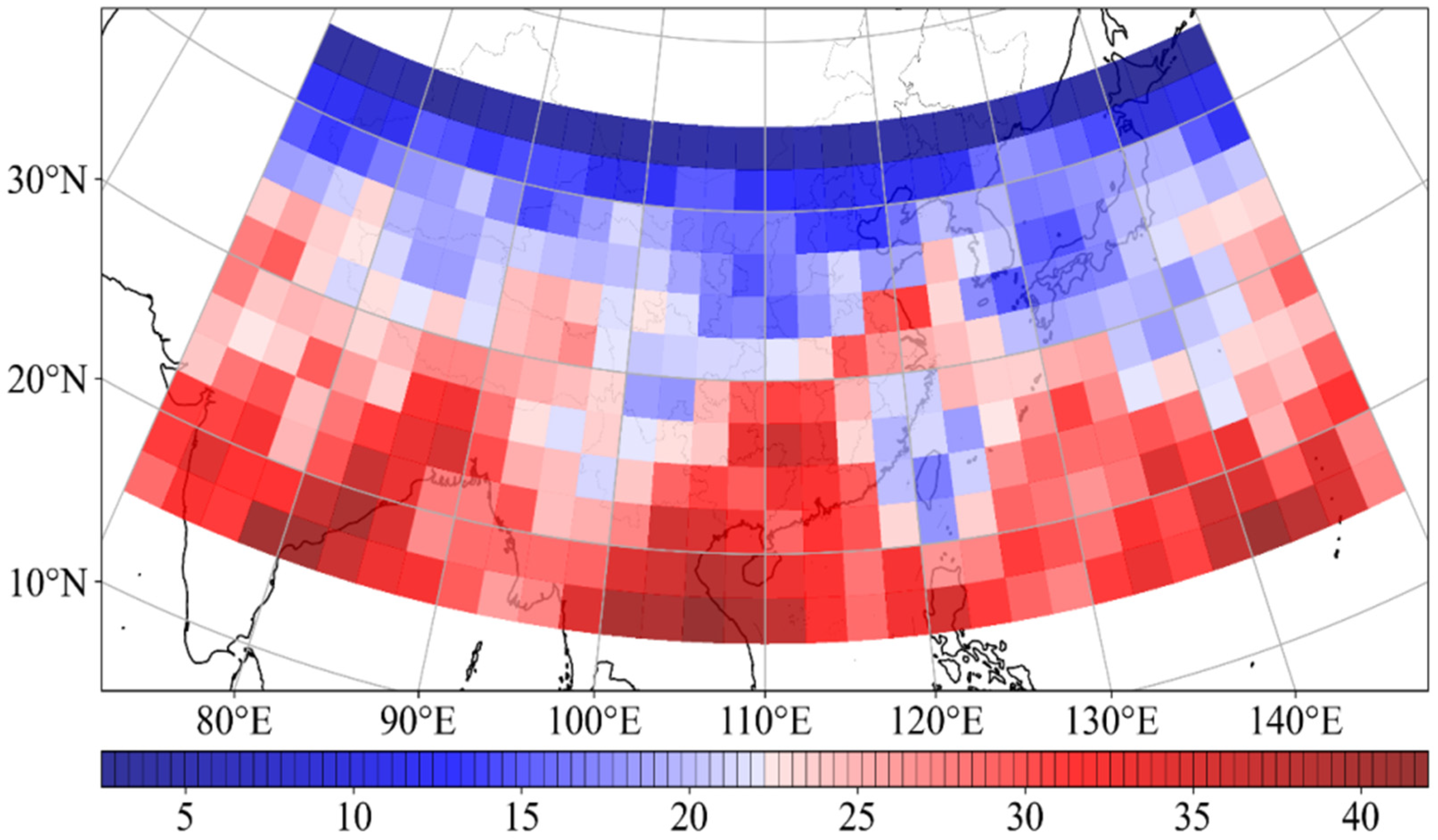
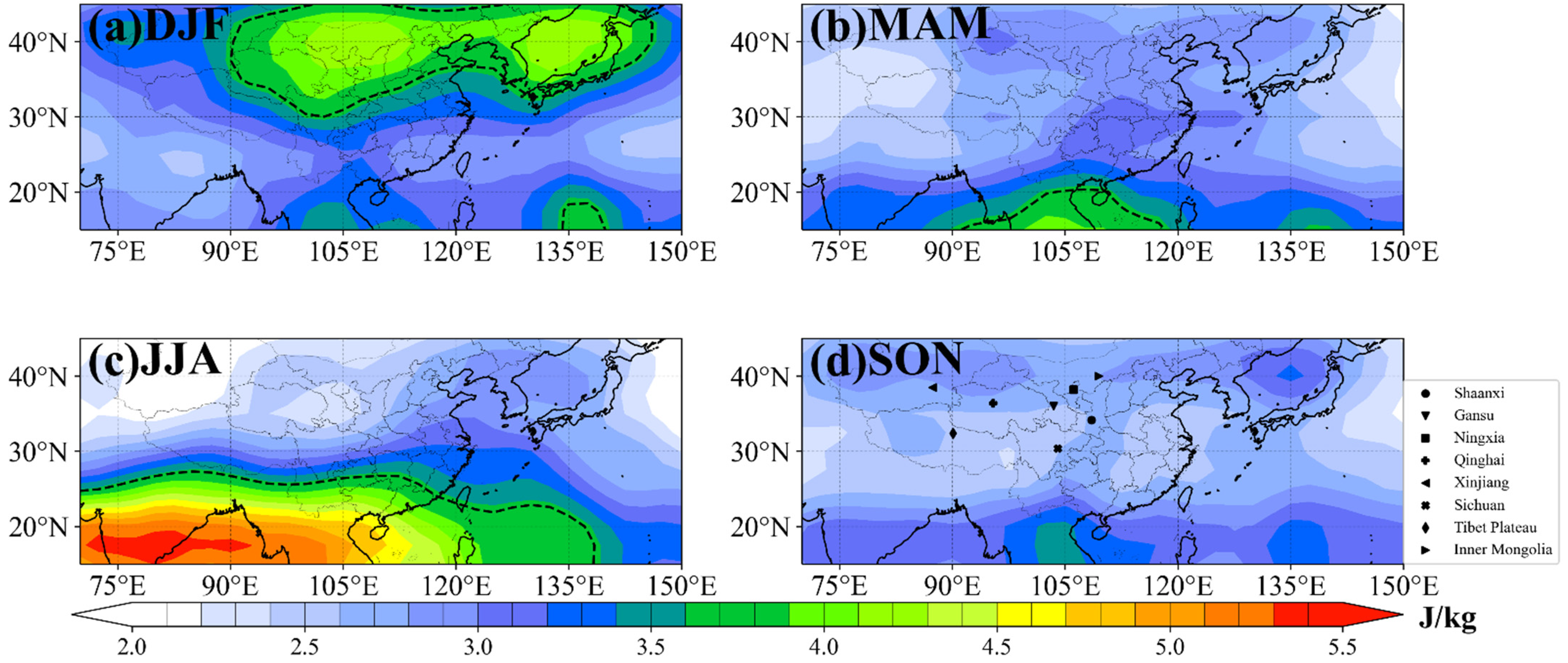
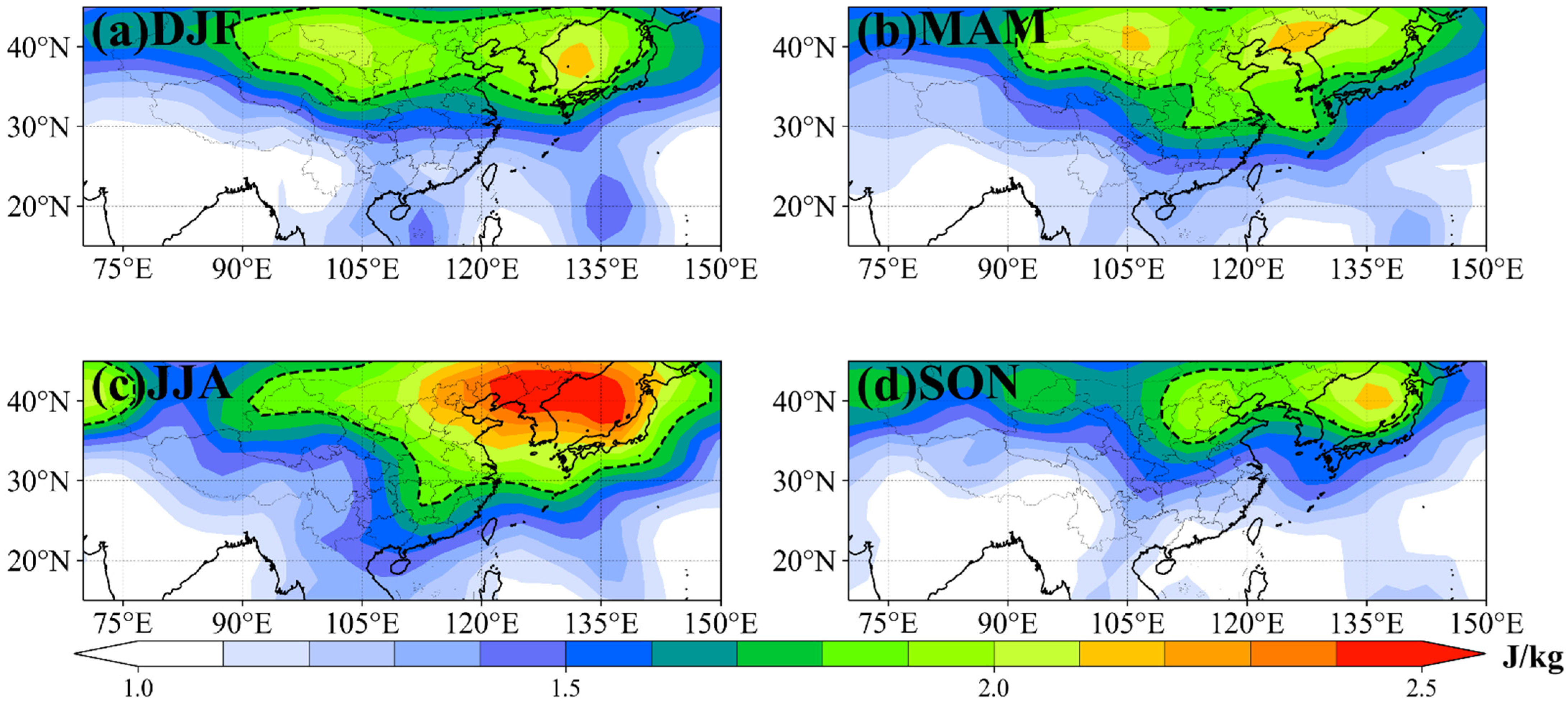
3.1.1. Horizontal Distribution and Seasonal Variation of Ep
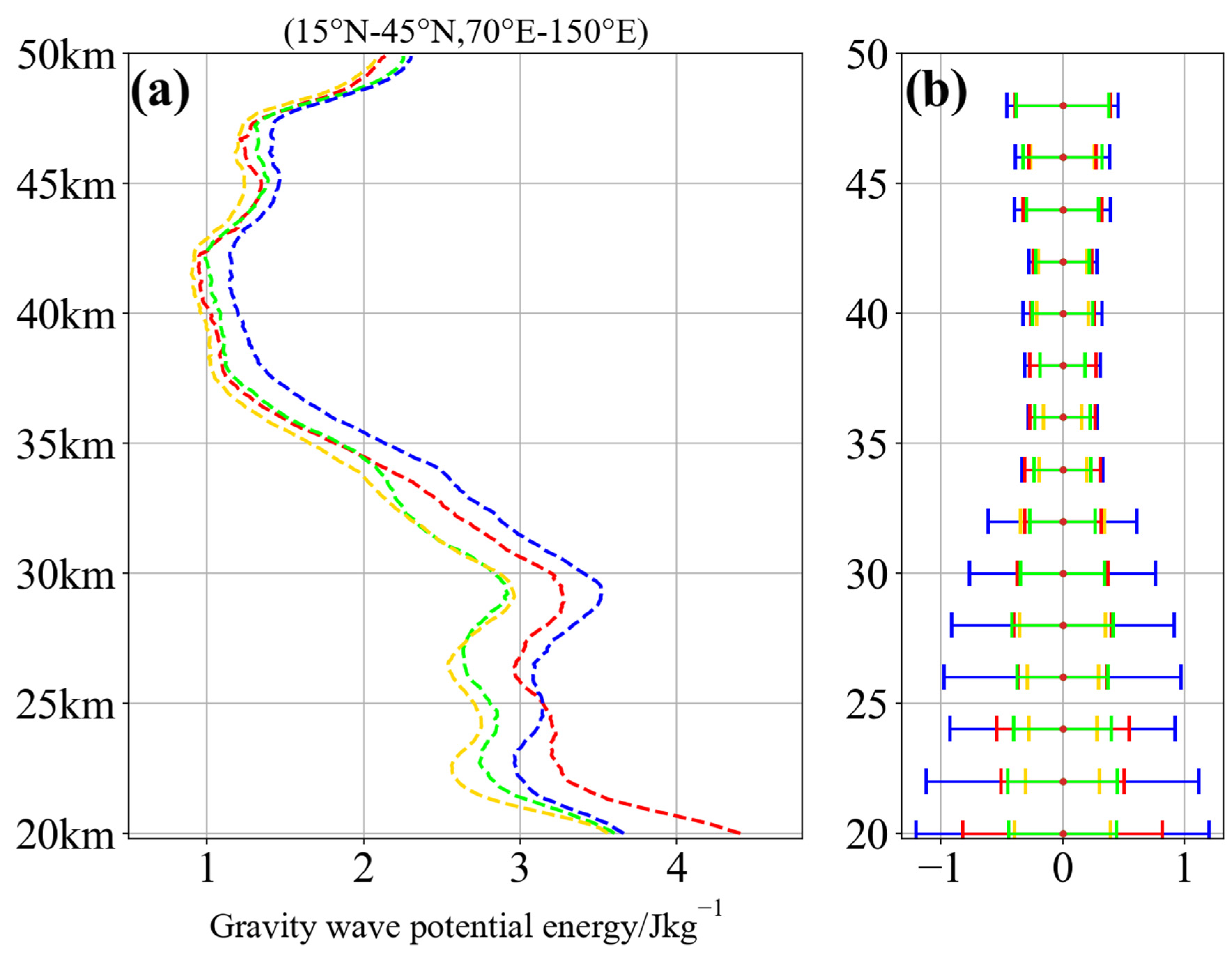
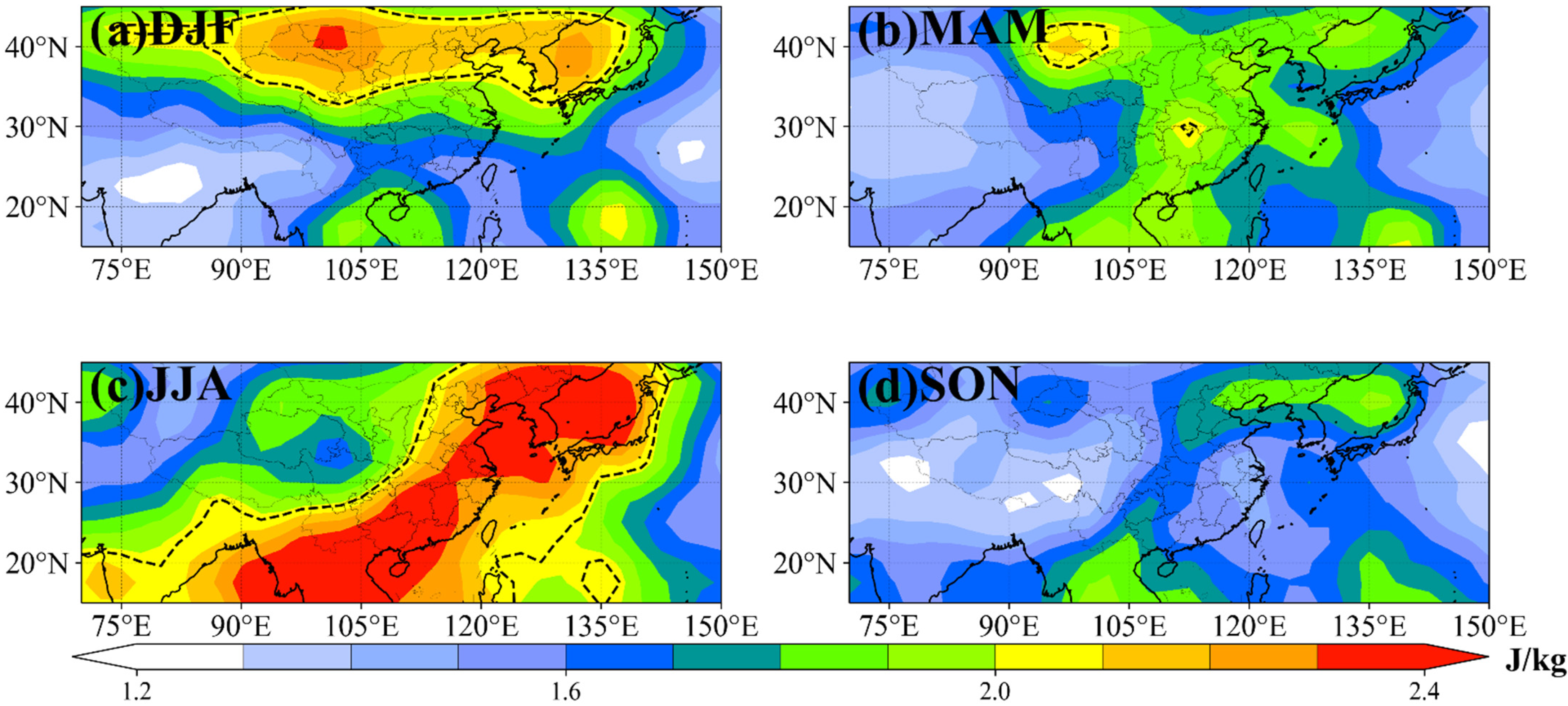
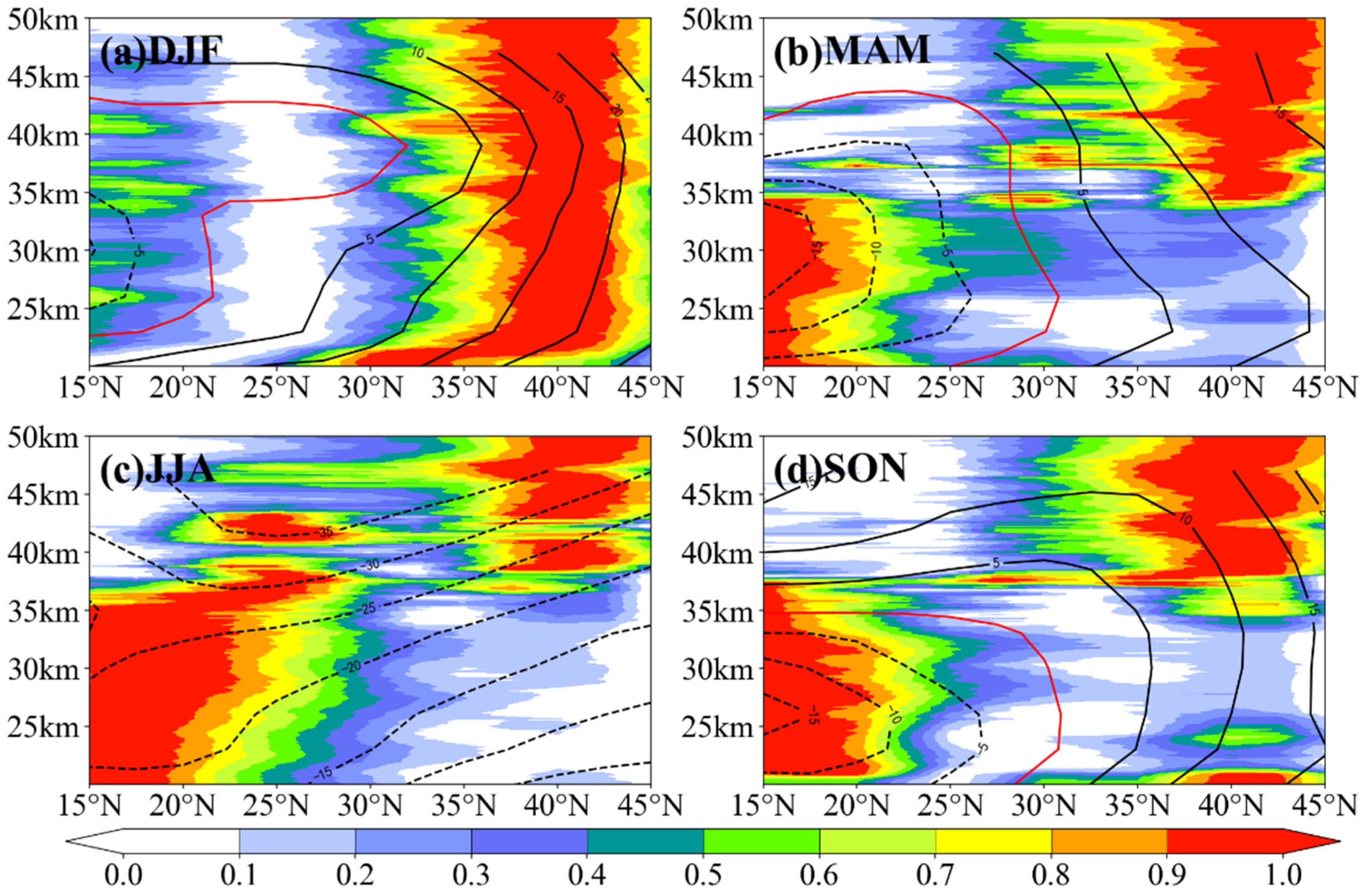
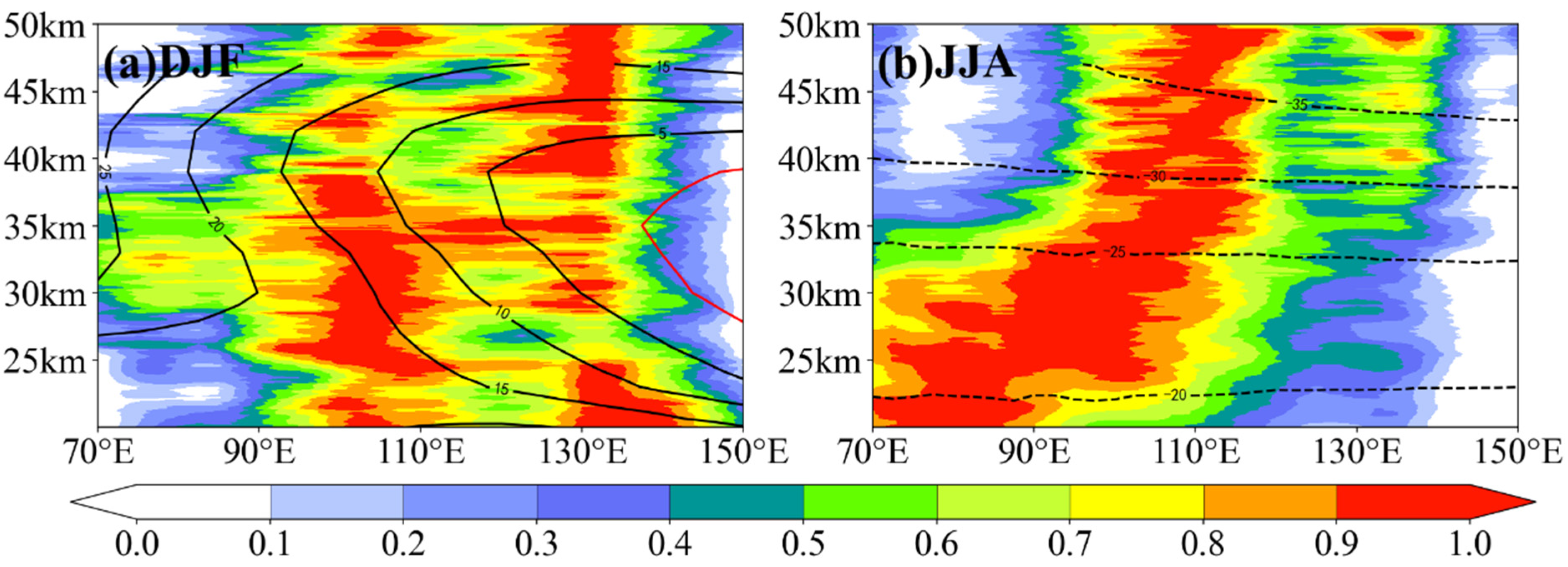
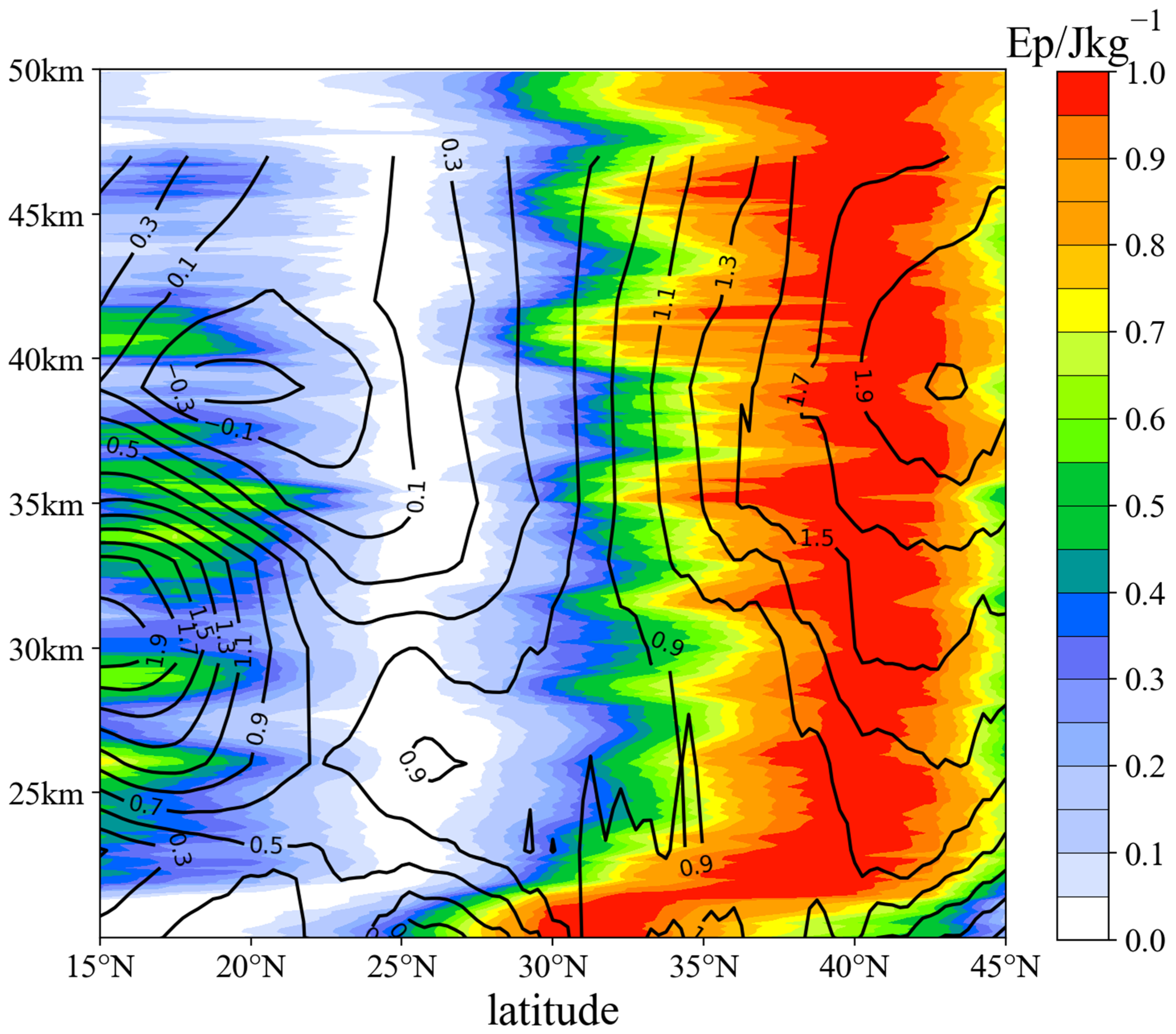
3.1.2. Vertical Distribution and Seasonal Variation of Ep
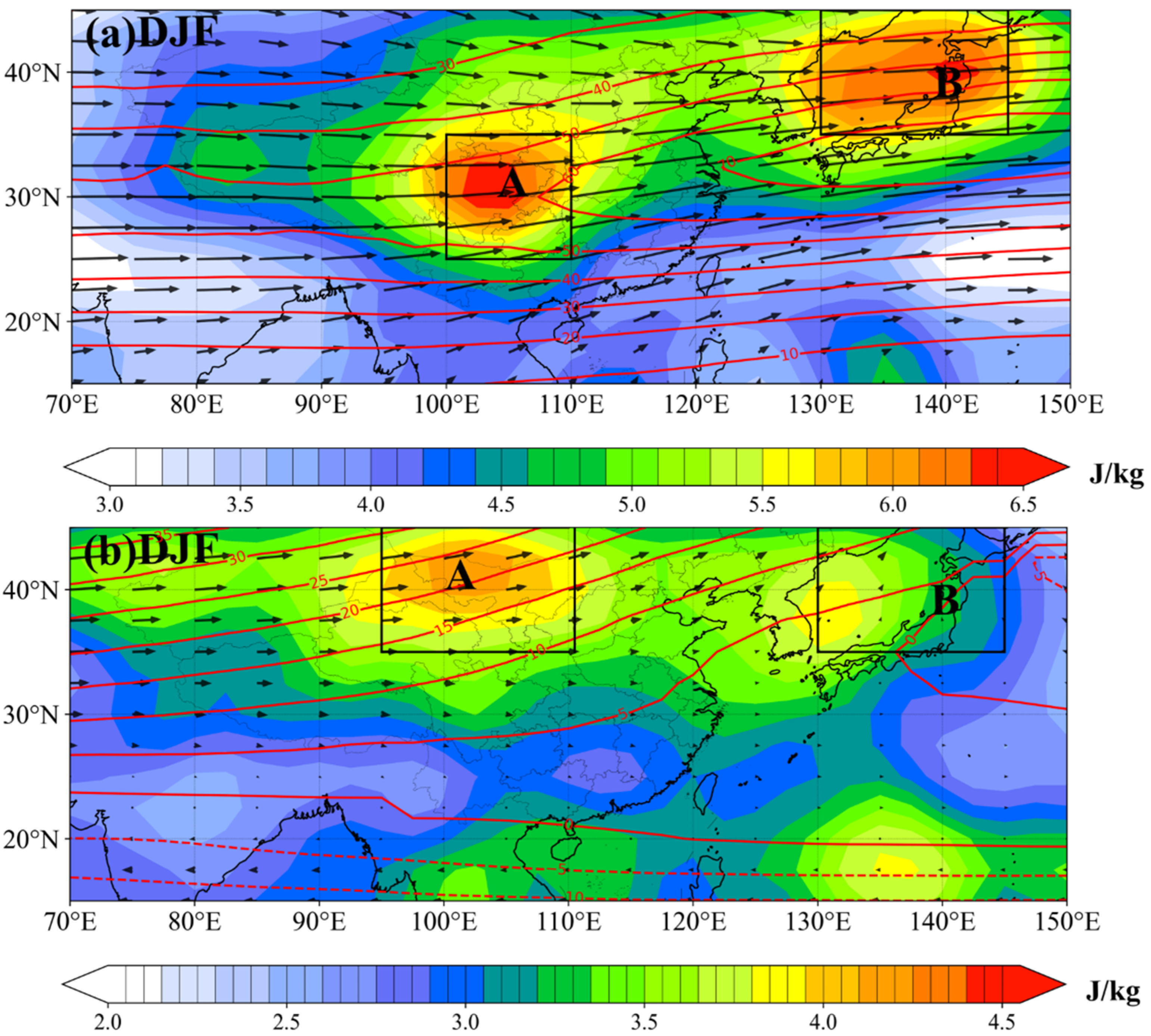
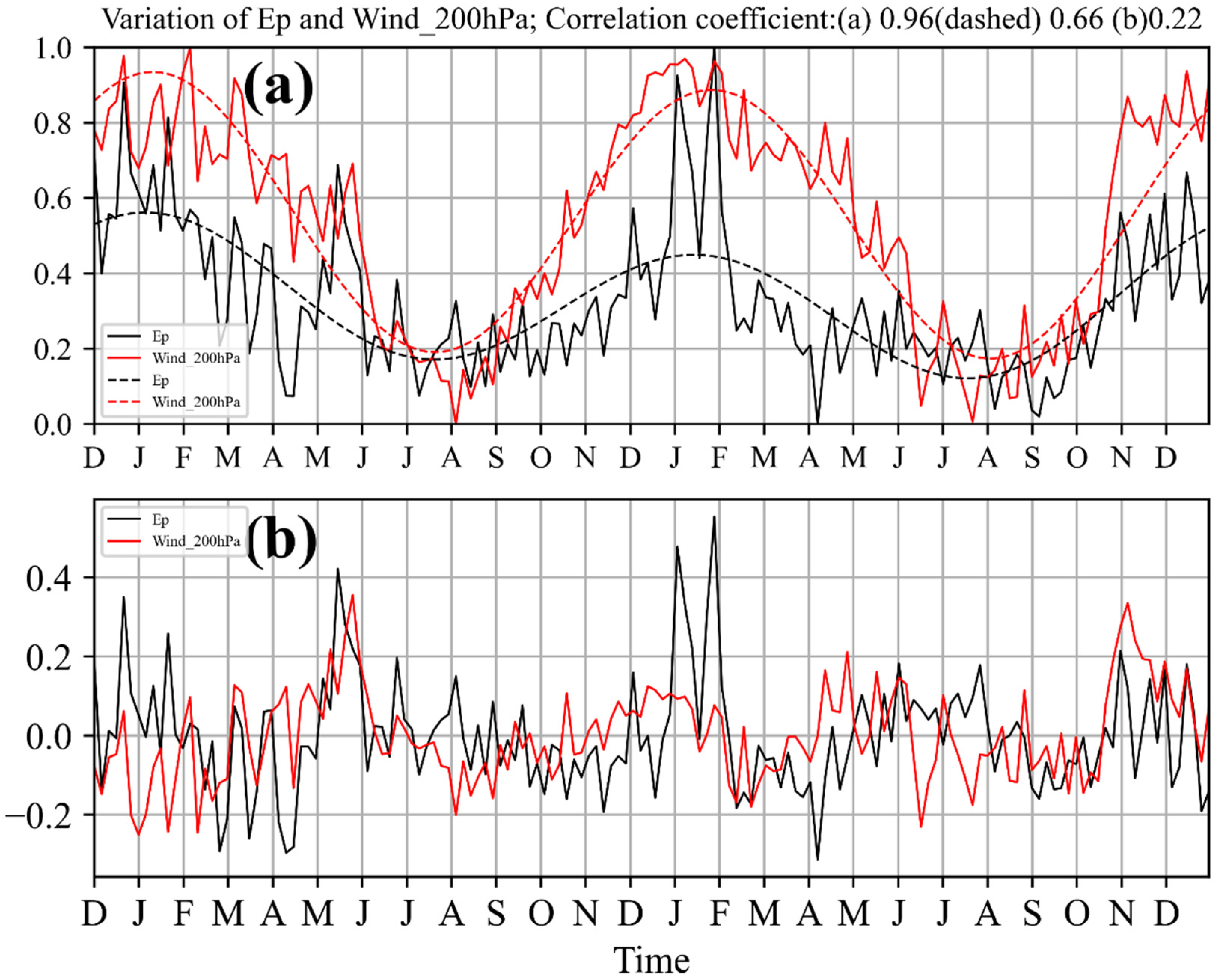
3.2. The Generation and Propagation Mechanisms of Middle-Latitude GWs in Winter
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fritts, D.C.; Alexander, M.J. Gravity wave dynamics and effects in the middle atmosphere. Rev. Geophys. 2003, 41, 1003. [Google Scholar] [CrossRef] [Green Version]
- Alexander, M.J.; Geller, M.; McLandress, C.; Polavarapu, S.; Preusse, P.; Sassi, F.; Sato, K.; Eckermann, S.; Ern, M.; Hertzog, A.; et al. Recent developments in gravity-wave effects in climate models and the global distribution of gravity-wave momentum flux from observations and models. Q. J. R. Meteorol. Soc. 2010, 136, 1103–1124. [Google Scholar] [CrossRef]
- Zhang, S.D.; Yi, F.; Huang, C.M.; Zhou, Q.J. Latitudinal and seasonal variations of lower atmospheric inertial gravity wave energy revealed by US radiosonde data. Ann. Geophys. 2010, 28, 1065–1074. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Geller, M.J. Morphology of gravity-wave energy as observed from 4 years (1998–2001) of high vertical resolution U.S. radiosonde data. J. Geophys. Res. Atmos. 2003, 108, 4489. [Google Scholar] [CrossRef]
- Tsuda, T.; Murayama, Y.; Yamamoto, M.; Kato, S.; Fukao, S. Seasonal variation of momentum flux in the mesosphere observed with the MU radar. Geophys. Res. Lett. 1990, 17, 725–728. [Google Scholar] [CrossRef]
- Hertzog, A.; Boccara, G.; Vincent, R.A.; Vial, F.; Cocquerez, P. Estimation of Gravity Wave Momentum Flux and Phase Speeds from Quasi-Lagrangian Stratospheric Balloon Flights. Part II: Results from the Vorcore Campaign in Antarctica. J. Atmos. Sci. 2008, 65, 3056–3070. [Google Scholar] [CrossRef]
- Hertzog, A.; Alexander, J.M.; Plougonven, R. On the intermittency of gravity wave momentum flux in the stratosphere (Article). J. Atmos. Sci. 2012, 69, 3433–3448. [Google Scholar] [CrossRef] [Green Version]
- Eckermann, S.D.; Hirota, I.; Hocking, W.K. Gravity wave and equatorial wave morphology of the stratosphere derived from long-term rocket soundings. Q. J. R. Meteorol. Soc. 1995, 121, 149–186. [Google Scholar] [CrossRef]
- Anthes, R.A.; Ector, D.; Hunt, D.C.; Kuo, Y.H.; Rocken, C.; Schreiner, W.S.; Sokolovskiy, S.V.; Syndergaard, S.; Wee, T.K.; Zeng, Z.J. The COSMIC/FORMOSAT-3 Mission: Early Results. Bull. Am. Meteorol. Soc. 2008, 89, 313–333. [Google Scholar] [CrossRef]
- Ware, R.; Rocken, C.; Solheim, F.; Exner, M.; Schreiner, W.; Anthes, R.; Feng, D.; Herman, B.; Gorbunov, M.; Sokolovskiy, S.J. GPS Sounding of the Atmosphere from Low Earth Orbit: Preliminary Results. Bull. Am. Meteorol. Soc. 1996, 77, 19–40. [Google Scholar] [CrossRef] [Green Version]
- Ratnam, V.M.; Tetzlaff, G.; Jacobi, C. Global and Seasonal Variations of Stratospheric Gravity Wave Activity Deduced from the CHAMP/GPS Satellite. J. Atmos. Sci. 2004, 61, 1610–1620. [Google Scholar] [CrossRef]
- Alexander, S.P.; Tsuda, T.; Kawatani, Y.; Takahashi, M. Global distribution of atmospheric waves in the equatorial upper troposphere and lower stratosphere: COSMIC observations of wave mean flow interactions. J. Geophys. Res. 2008, 113, D24115. [Google Scholar] [CrossRef]
- Tsuda, T.; Nishida, M.; Rocken, C.; Ware, R.H. A global morphology of gravity wave activity in the stratosphere revealed by the GPS occultation data (GPS/MET). J. Geophys. Res. 2000, 105, 7257–7273. [Google Scholar] [CrossRef]
- Xu, X.H.; Yu, D.C.; Luo, J. The Spatial and Temporal Variability of Global Stratospheric Gravity Waves and Their Activity during Sudden Stratospheric Warming Revealed by COSMIC Measurements. Adv. Atmos. Sci. 2018, 35, 1533–1546. [Google Scholar] [CrossRef]
- Wang, L.; Alexander, M.J. Global estimates of gravity wave parameters from GPS radio occultation temperature data. J. Geophys. Res. Atmos. 2010, 115. [Google Scholar] [CrossRef]
- Faber, A.; Llamedo, P.; Schmidt, T.; Torre, A.D.; Wickert, J. On the determination of gravity wave momentum flux from GPS radio occultation data. Atmos. Meas. Tech. 2013, 11, 3169–3180. [Google Scholar] [CrossRef] [Green Version]
- Hindley, N.P.; Wright, C.J.; Smith, N.D.; Mitchell, N.J. The southern stratospheric gravity-wave hot spot: Individual waves and their momentum fluxes measured by COSMIC GPS-RO. Atmos. Chem. Phys. Discuss. 2015, 15, 3173–3217. [Google Scholar] [CrossRef] [Green Version]
- Šacha, P.; Kuchař, A.; Jacobi, C.; Pišoft, P. Enhanced internal gravity wave activity and breaking over the northeastern Pacific-eastern Asian region. Atmos. Chem. Phys. 2015, 15, 13097–13112. [Google Scholar] [CrossRef] [Green Version]
- Fjeldbo, G.; Kliore, A.J.; Eshleman, V.R. The Neutral Atmosphere of Venus as Studied with the Mariner V Radio Occultation Experiments. Atmos. J. 1971, 76, 123. [Google Scholar] [CrossRef]
- Ho, S.P.; Zhou, X.; Shao, X.; Zhang, B.; Adhikari, L.; Kireev, S.; He, Y.; Yoe, J.G.; Xia-Serafino, W.; Lynch, E. Initial Assessment of the COSMIC-2/FORMOSAT-7 Neutral Atmosphere Data Quality in NESDIS/STAR Using in Situ and Satellite Data. Remote Sens. 2020, 12, 4099. [Google Scholar] [CrossRef]
- Schreiner, W.S.; Weiss, J.P.; Anthes, R.A.; Braun, J.; Chu, V.; Fong, J.; Hunt, D.; Kuo, Y.H.; Meehan, T.; Serafino, W.; et al. COSMIC-2 Radio Occultation Constellation: First Results. Geophys. Res. Lett. 2020, 47, e2019GL086841. [Google Scholar] [CrossRef]
- Zhang, S.D.; Yi, F. Latitudinal and seasonal variations of inertial gravity wave activity in the lower atmosphere over central China. J. Geophys. Res. Atmos. 2007, 112. [Google Scholar] [CrossRef] [Green Version]
- Bai, Z.X.; Bian, J.C.; Chen, H.B.; Chen, L. Inertial gravity wave parameters for the lower stratosphere from radiosonde data over China. Sci. China 2017, 60, 328–340. [Google Scholar] [CrossRef]
- Chen, L.; Bian, J.; Liu, Y.; Bai, Z.; Qiao, S. Statistical analysis of inertial gravity wave parameters in the lower stratosphere over Northern China. Clim. Dyn. 2019, 52, 563–575. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, L.; Zhang, Y.; Guan, J. Effects of Tropospheric Vertical Wind Shear on Gravity Waves Generated by Tropical Cyclones. Geophys. Res. Lett. 2019, 46, 4523–4530. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Zhang, L.; Wang, Y.; Zhang, Y. The Influencing Mechanism of a Mid-Latitude Westerly Trough on Stratospheric Gravity Waves Generated by Typhoon Lekima (2019). Geophys. Res. Lett. 2022, 49, e2021GL097544. [Google Scholar] [CrossRef]
- Randel, W.J.; Wu, F.; Podglajen, A. Equatorial Waves, Diurnal Tides and Small-Scale Thermal Variability in the Tropical Lower Stratosphere From COSMIC-2 Radio Occultation. J. Geophys. Res. 2021, 126, e2020JD033969. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Strelnikova, I.; Almowafy, M.; Baumgarten, G.; Baumgarten, K.; Ern, M.; Gerding, M.; Lubken, F.J. Seasonal Cycle of Gravity Wave Potential Energy Densities from Lidar and Satellite Observations at 54° and 69°N. J. Atmos. Sci. 2021, 78, 1359–1386. [Google Scholar] [CrossRef]
- Wang, L.; Alexander, M.J. Gravity wave activity during stratospheric sudden warmings in the 2007-2008 Northern Hemisphere winter(Article). J. Geophys. Res. Atmos. 2009, 114. [Google Scholar] [CrossRef]
- John, S.R.; Kumar, K.K. A discussion on the methods of extracting gravity wave perturbations from space-based measurements. Geophys. Res. Lett. 2013, 40, 2406–2410. [Google Scholar] [CrossRef]
- Chen, C.; Zhao, N.; Yue, T.; Guo, J. A generalization of inverse distance weighting method via kernel regression and its application to surface modeling. Arab. J. Geosci. 2015, 8, 6623–6633. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Zhang, L.; Wang, Y.; Zhang, Y. Influences of the Mid-Latitude Westerly Trough on Stratospheric Gravity Waves Generated by Typhoon Lekima (2019). J. Geophys. Res. Atmos. 2021, 126, e2021JD035399. [Google Scholar] [CrossRef]
- Zhang, S.; Yi, F.; Huang, C.; Huang, K.; Gan, Q.; Zhang, Y.; Gong, Y. Latitudinal and altitudinal variability of lower atmospheric inertial gravity waves revealed by U.S. radiosonde data(Article). J. Geophys. Res. Atmos. 2013, 118, 7750–7764. [Google Scholar] [CrossRef] [Green Version]
- Khan, A.; Jin, S. Gravity wave activities in Tibet observed by COSMIC GPS radio occultation(Article). Geod. Geodyn. 2018, 9, 504–511. [Google Scholar] [CrossRef]
- Zeng, X.; Xue, X.; Dou, X.; Liang, C.; Jia, M. COSMIC GPS observations of topographic gravity waves in the stratosphere around the Tibetan Plateau. Sci. China-Earth Sci. 2017, 60, 188–197. [Google Scholar] [CrossRef]
- Forbes, J.M.; Zhang, X.; Randall, C.E.; France, J.; Harvey, V.L.; Carstens, J.; Bailey, S.M. Troposphere-Mesosphere Coupling by Convectively Forced Gravity Waves During Southern Hemisphere Monsoon Season as Viewed by AIM/CIPS. J. Geophys. Res. Space Phys. 2021, 126, e2021JA029734. [Google Scholar] [CrossRef]
- Dunkerton, T.J. Inertia–Gravity Waves in the Stratosphere. J. Atmos. Sci. 1984, 41, 3396–3404. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qu, T.; Zhang, L.; Wang, Y.; Wang, X.; Guan, J. Seasonal Variation of Stratospheric Gravity Waves in the Asian Monsoon Region Derived from COSMIC-2 Data. Remote Sens. 2022, 14, 4096. https://doi.org/10.3390/rs14164096
Qu T, Zhang L, Wang Y, Wang X, Guan J. Seasonal Variation of Stratospheric Gravity Waves in the Asian Monsoon Region Derived from COSMIC-2 Data. Remote Sensing. 2022; 14(16):4096. https://doi.org/10.3390/rs14164096
Chicago/Turabian StyleQu, Tao, Lifeng Zhang, Yuan Wang, Xu Wang, and Jiping Guan. 2022. "Seasonal Variation of Stratospheric Gravity Waves in the Asian Monsoon Region Derived from COSMIC-2 Data" Remote Sensing 14, no. 16: 4096. https://doi.org/10.3390/rs14164096
APA StyleQu, T., Zhang, L., Wang, Y., Wang, X., & Guan, J. (2022). Seasonal Variation of Stratospheric Gravity Waves in the Asian Monsoon Region Derived from COSMIC-2 Data. Remote Sensing, 14(16), 4096. https://doi.org/10.3390/rs14164096





