Abstract
Knowledge of physical and mechanical properties of geomaterials is fundamental to characterise their response to external forcings (mechanical, climatic) at various scales. This is true, for instance, in slope stability assessments, civil engineering works, and agriculture. The direct evaluation of these properties in situ can be difficult, especially in inaccessible or vast areas, and so can be the sampling and subsequent testing in the laboratory—where ensuring the representativeness of the acquired data at the scale of analysis poses an additional challenge. Thus, empirical correlations with more readily determinable quantities remain a powerful and practical tool. Recently, several sensors, able to inform on various geomaterial properties, have been developed. However, applications have typically targeted rocks, while studies on uncemented geomaterials (soils, geotechnically speaking) are lacking. Here, we propose a simple method to evaluate the porosity and critical state friction angle of soils via infrared thermography, consisting of periodic acquisitions of images in infrared wavelengths. To demonstrate the method’s capability, we analysed the cooling behaviour of samples of bentonite, kaolin, and sand (for which an extensive characterisation exists in the literature), after compaction to different porosities and pre-heating in an oven. We interpreted the results by seeking the optimal time interval for which a cooling rate index (CRI) could be defined, which is best linked with the target property. We found that the CRI correlates very well with the critical state friction angle (R2 > 0.85) and that different materials show unique and strong (R2 = 0.86–0.99) relationships between their porosity and the CRI, which also varies in a material-specific fashion according to the explored time interval. Although a systematic investigation on a wide range of natural soils is warranted, we argue that our method can be highly informative and could be used to calibrate remote sensing-based full-scale implementations in situ for various purposes.
1. Introduction
An accurate characterisation of physical and mechanical properties of geomaterials, appropriate to the scale of analysis, is crucial in geotechnical and engineering geological problems, as well as in agriculture. As such, it remains the focus of extensive research despite decades of advances [1]. In fact, as the scale increases and homogeneous volumes leave the place to heterogeneous lands, slopes, and catchments, ensuring the representativeness of point measurements, while keeping their number reasonable, becomes progressively more challenging. In this situation, non-invasive, indirect testing methods become advantageous, and new instruments and methodologies come to aid [2,3]. Among them, strategies relying on remote sensing—via ground-based, airborne, and spaceborne sensors as the scale increases—seem the most promising [4,5,6,7]. In particular, sensors in the thermal infrared wavelength band (Table S1, Supplementary Materials) can record behaviours associated with intrinsic characteristics of rocks [4,8,9]. Notably, a similar approach for the investigation of soils is lacking, despite the absence of contra-indications. Note that we refer here to soils in a broad sense, including all uncemented geomaterials (that is, geomaterials with little to no cohesion in water-saturated condition). These typically entail mixtures of particles (mineral grains and aggregates resulting from weathering of rocks) and fluids (air, water), which are the object of study of soil mechanics [10]. As such, our methodological approach could also apply to regolith and debris covers on the one hand, and on the other hand on soils stricto sensu—mixtures with an important organic content, especially relevant in agriculture and life sciences.
Soil characteristics that can be determined in the laboratory range from “simple” grain-size distribution and plastic properties to mineral composition and mechanical strength that require more time-consuming testing. In general, values obtained in the laboratory are not directly applicable at the field scale [11], not only because of the aforementioned issue related with representativeness and spatial heterogeneity, but also because of the impossibility, in most cases, of precisely reproducing the site conditions in the laboratory. In fact, unless undisturbed sampling is performed, in situ mechanical stresses cannot be preserved; contextually, information on soil structure, total porosity, pore-size distribution, and degree of saturation can be lost. This is the reason why, often, field testing and monitoring are preferred over laboratory investigation, even though an optimal control of the experimental conditions in situ is hardly achievable. Yet, even in field testing, limitations arise concerning the number or spatial density of point measurements, which can even be unfeasible altogether, either because of their invasiveness (requiring physical distancing between measurements), or the inaccessibility of the medium to be tested (such as a very steep or unstable slope).
Thermal data, if acquired repeatedly over a suitable period of time, can inform on the readiness of a body to accumulate or release heat by evaluating the rate of change in its surface temperature [4,12]. In the field, this thermal forcing results from a complex interaction within the ground-vegetation-atmosphere system, which exchanges heat through radiation at the interface, conduction, convective air and water flows in discontinuities, changes in water phase, and mass transfers. In the light of these processes, it seems reasonable that a correlation should exist not only between a measurable thermal behaviour and the heat conduction/capacity characteristics of the geomaterial, but also between such behaviour and the characteristics, more specifically, of its voids (i.e., its pore and fracture networks) [13]. However, little research exists on the matter, which moreover mainly focuses on rock materials [9].
The other possible correlation we are exploring, which could prove rather useful in practice, is the one between a measurable thermal behaviour and a mechanical strength characteristic of soil. The critical state friction angle (or, equivalently, the critical state friction coefficient) seems a good candidate as it is a “robust” intrinsic parameter that relates with soil composition, rather than with its structure or mechanical history, and is relatively insensitive to the actual stress state. In fact, a critical state friction angle can be defined for most soils and does not vary significantly over a wide range of confining pressures typically encountered in land behaviour or slope stability problems.
Notably, the land-surface temperature (LST), quantified through spaceborne sensors, has recently been utilised [14] at the regional scale to evaluate spatio-temporal patterns of landslides. It has been shown that the role of LST was distinct from that of vegetation coverage both in terms of spatial patterns and nonlinear effects, suggesting the possibility of a thermo-mechanical control on surface/subsurface processes [5] in addition to the known hydrological mechanisms of soil-vegetation-atmosphere interaction. It may be hypothesised that this finding, obtained at a large scale, could stem from small-scale relationships between thermal behaviours and intrinsic properties of geomaterials, such as those that are investigated in this study.
In the field, temperature is most commonly monitored via meteorological stations (air temperature) and this information is generally only accounted for in hydrological models and not in mechanical models of soils [15]. Acquisition of temperature data within the ground to monitor the vertical temperature profile during the seasons is typically performed in cold regions, as freezing-thawing cycles can strongly affect the soil hydro-mechanical response. Similar analyses in agricultural land can provide clues on biological, chemical, and hydrological responses of shallow soil covers. Conversely, systematic use of thermal information in slope stability analysis remains uncommon [5,16,17], even though infrared thermography (IRT) is gaining popularity for a variety of purposes [8].
IRT is a remote-sensing technique by which the surface temperature of a body can be evaluated from its thermal radiation [18,19,20,21,22,23], for instance, by using a thermal camera mounted on a tripod or an unmanned aerial vehicle (UAV). Conceptually, the approach we present herein is a lab-scale IRT, which has the advantage of being performed in a controlled atmospheric condition, with a negligible sensor-object distance that overcomes the need of geometric corrections. IRT has been shown to provide useful results in field studies [8,24,25,26,27], with focuses on volcano monitoring [28,29,30,31], geothermal analyses [32], identification of preferential flow paths [33], but also of unstable/disrupted areas characterised by thermal anomalies compared with the surroundings [34].
2. Materials and Methods
We performed experiments on well-characterised, commercially available materials: a bentonite, a kaolin, and a sand. The bentonite, known as BCV (2017 batch) [35], is extracted from the Černý vrch deposit (Braňany, Czech Republic) and is distributed by Keramost Ltd., (Most, Czech Republic). It is being considered for use in the engineered barrier system of the Czech national geological repository of radioactive waste, currently under design. This bentonite has a liquid limit of ~130%, a specific surface area of ~90 m2/g, and a swelling pressure that increases from ~1 MPa to ~10 MPa as the dry density increases from ~1.3 g/cm3 to ~1.7 g/cm3 [35]. It is mainly composed of Ca- and Mg-montmorillonite (exchangeable interlayer cations: 38.7 meg/100 g of Mg2+ and 19.9 meg/100 g of Ca2+ with minor amounts of Na+ and K+) [35]. The kaolin is sold as FMC Kaolin and comes from Perak, Malaysia. It is composed by ~46 wt% kaolinite and ~48% wt% muscovite, with liquid and plastic limits of 65% and 38%, respectively, and a specific gravity of the solids of 2.71 [36,37]. The sand is a quartz sand from a quarry in Zbraslav, Czech Republic [38]. It has a specific gravity of the solids of 2.65, a mean particle size of 0.5 mm and coefficient of uniformity of 3.19. The choice of these materials was based on their well-constrained properties and their very different mineralogical compositions and mechanical responses (see also Table S2), hypothesising that these differences would correspond to easily discernible differences in thermal behaviour.
We prepared cylindrical samples with a diameter of 50 mm and height of 10 mm by compacting the sieved dry material in standardised moulds (±0.1 mm) under different loads (1, 3, or 5 tons, corresponding to ~5, 15, or 25 MPa, respectively, in quintuplicate; relative error < 0.1%). The values of porosity for kaolin and bentonite after compaction are reported in Figure 1a. The samples were then placed on a tray (Figure 1b) and heated in an oven at 105 ± 1 °C for 24 h. Then, they were extracted and left to cool to room temperature (20 ± 1 °C, relative humidity 35% ± 5%) while IRT monitoring was conducted.
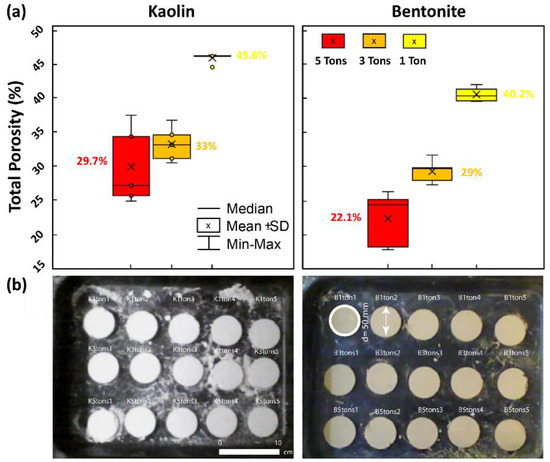
Figure 1.
(a) Box plot of porosity distribution for kaolin (left) and bentonite (right) samples after compaction; (b) photographs showing the samples placed on a tray, ready for oven-heating.
Thermal cameras contain a radiometric sensor, which enables the determination of the surface temperature of the imaged body according to the Stefan-Boltzmann law:
where J is the total energy emitted by the body, T is its surface temperature, ε is the emissivity, and θ is Stefan-Boltzmann’s constant [4,8,25]. A net heat transfer occurs to the air owing to its different temperature via irradiation, convection, and conduction.
J = εθT4,
Thermograms were acquired via a FLIR C2 camera, placed perpendicularly to the tray, at 5 min intervals (absolute error < 1 s) for 80 min (Table S3). Thus, seventeen thermal images were taken of each tray, and all pixels of each imaged disk were considered in the subsequent analysis. Air humidity and temperature were recorded through a weather station (Figure 2; Tables S4–S7) to calibrate the thermograms during image post-processing. Emissivity was assumed according to the literature data [39]. We filtered the raw input following two main operations: a radiometric correction and a geometric correction. The first is computed according to the atmospheric temperature and humidity [15,25], whereas the second is given by georeferencing the images [8,15]. The latter step, commonly used for images of distant objects, was skipped as the sample-object distance was only 0.5 m.
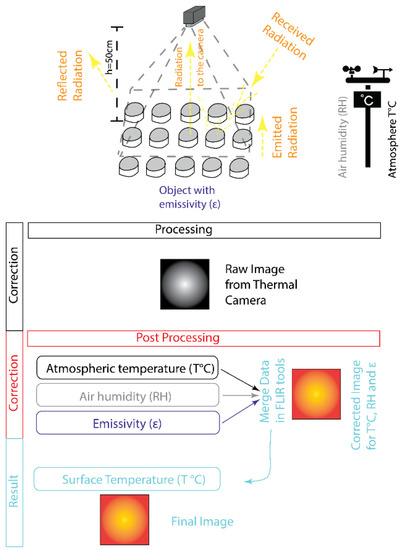
Figure 2.
(top) Sketch of the acquisition system and heat transfers between the samples and the atmosphere; (bottom) post-processing scheme.
3. Results
We calculated the mean, median, mode, standard deviation (SD), and range of porosity values for each sample (Table 1) using standard laboratory methods (entailing separate evaluations of volume and weight, e.g., the ASTM D7263-21 [40]). The mean was computed over all readings for each sample (5 readings per sample, 25 values per porosity). Minimum (MIN), first quantile (Q1), median (MED), third quantile (Q3), maximum (MAX), mean (MEAN), range (RA), and SD were computed over all readings.

Table 1.
Porosity number statistics of the samples. Data on critical state friction angle (see also Table S2) are included for comparison.
The different porosity values of kaolin and bentonite samples under comparable compaction levels depend on their physico-chemical characteristics, including their mineralogy. A clear symmetry in the data can be recognised from the median and mean values and the small SD. Overall, differences among the statistics are minor, and the estimated porosity values do not differ much across the samples of each material (SD < 0.050), suggesting high repeatability of the sample preparation procedure. In the subsequent analysis, the mean and SD were plotted, and the following mean porosity values were obtained and displayed in the graphs: kaolin compacted under 5 tons: 0.297; kaolinite under 3 tons: 0.330; kaolin under 1 ton: 0.456; bentonite under 5 tons: 0.221; bentonite under 3 tons: 0.290; bentonite under 1 ton: 0.402. Using the maximum and minimum values instead of the mean would not alter the first significant figure of the results.
The thermograms captured the cooling phase over a duration of 80 min (Figure 3). By observing the sample image displayed in Figure 4, it is apparent that zones located at the boundary are cooling more rapidly, while the samples placed at the centre of the tray remain warmer for a longer time. Moreover, cooling is shown to proceed more rapidly near the edges of each sample compared to their core, as reasonably expected. This spatial variability in temperature during cooling is not an issue, as comparisons across materials were made for the same geometrical setup. Notably, the use of a circular shape (axial symmetry of the disks) is beneficial in that it makes cooling more spatially homogeneous as it minimises edge effects, as opposed to a prismatic shape [41,42]. A spherical shape suspended at mid-air in a well-ventilated room would be even more advantageous, but it would not be easily implementable in practice. In addition to the shape, also the surface roughness and colour of the material can affect the cooling behaviour. As for the latter, the darker colour of the bentonite as opposed to the white kaolin samples makes the former resemble a black body more closely.
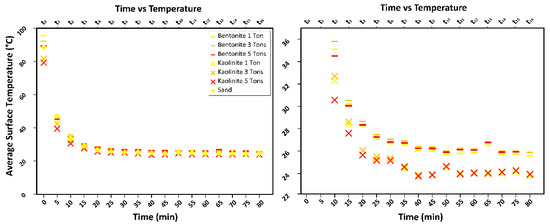
Figure 3.
(left) Cooling phases computed from thermograms over the first 80 min after taking the samples out of the oven. The data series refer to bentonite and kaolin samples having different porosities (because they were compacted under different loads, i.e., 1, 3, or 5 tons). The response of sand samples (not compacted) was also investigated for comparison. (right) Detail of the cooling phases, zoomed in to better display the decay to the room temperature.
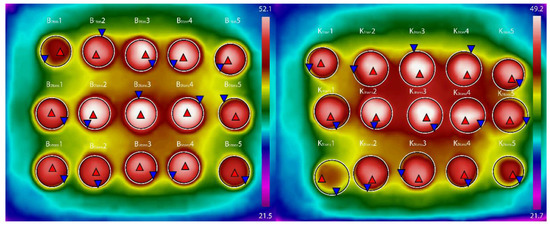
Figure 4.
Examples of thermograms recorded during the cooling phase of bentonite (left) and kaolin (right) samples, in which is possible to observe the inhomogeneous cooling of the disks, where samples located at the centre (red triangles) show higher temperatures than those at the borders (blue triangles).
First, we plotted the mean temperature as a function of time since the beginning of cooling for each sample (Figure 3). On a first, qualitative observation, samples with higher porosity seem to attain higher initial temperatures, but then rapidly cool down to values that, at the available resolution and considering the uncertainties, appear independent of porosity. Note that, in bentonite samples, an inversion is visible, as the more porous samples seem to release heat more efficiently and become slightly cooler than the less porous ones. This does not seem to occur in kaolin. With respect to material differences, not only the colour, but also the hygroscopic water content, which is larger for bentonite than for kaolin, should exert an effect on the cooling rate.
To obtain a quantitative insight, we then plotted the mean values of temperature, porosity, and critical state friction angle for each sample and performed a regression analysis (Figure 5 and Figure 6). In addition to evaluating distinct ranges of CRI values for the two clays, we find very good correlations between the porosity and CRI (Figure 5) and observe that the slopes of the correlations also are distinct. The coefficient of determination R2 is high for any time interval, but it is maximum for a cooling rate index (CRI = ΔT/Δt, where T is temperature and t is time) evaluated over the first 10 min of cooling (R2 = 0.97 for kaolin and 0.99 for bentonite). Interestingly, the correlation for the kaolin is negative during the first 5 min, then it turns positive, and the slope of the regression decreases as the time range increases. For the bentonite, the opposite holds true: the slope of the regression line increases for CRIs evaluated over longer time intervals. This observation seems worthy of further investigation as one could extract information on the nature of the material not only from the CRI value and the slope of the regression line, but also from how the latter changes with time during cooling. This value, in fact, is independent of the overall porosity and should only be influenced by some characteristics of the material itself (e.g., its mineralogy, pore size distribution, specific surface area) that could affect the cooling rate over time and/or as a function of the temperature difference between the material and the surrounding air or the air in the pores.
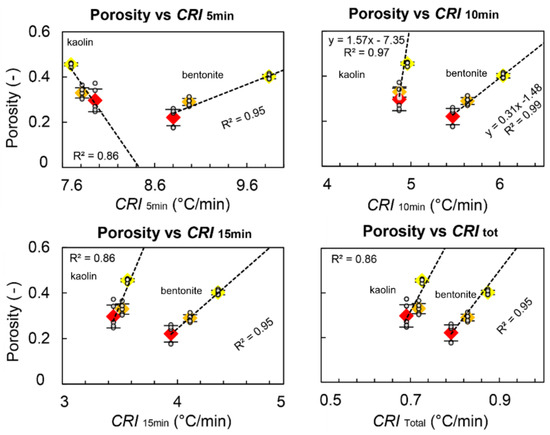
Figure 5.
Linear regression analysis between porosity and CRI according to different durations since the beginning of cooling: 5 min (top left); 10 min (top right); 15 min (bottom left); entire cooling phase (bottom right). Values for kaolin plot in th left portion of each graph (lower CRI), while those for bentonite plot in the right portion (higher CRI). The diamonds represent the mean values for disks, while small circles represent the distribution of values of all disks. Colours yellow, orange, and red, represent, respectively, samples compacted under 1 ton, 3 tons, and 5 tons.
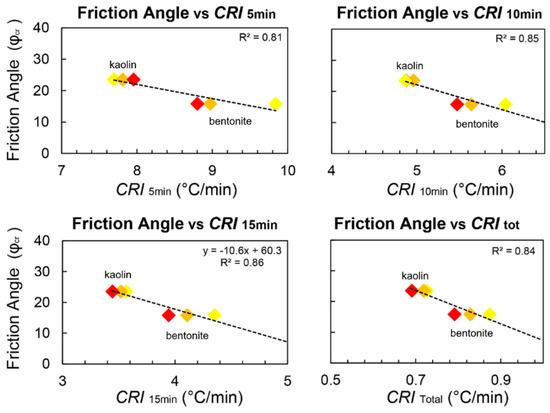
Figure 6.
Linear regression analysis between the critical state friction angle (φcr) and the CRI according to different time intervals since the beginning of cooling: 5 min (top left); 10 min (top right); 15 min (bottom left); entire cooling phase (bottom right). The markers represent the mean values for disks of bentonite and kaolin at different porosity. Note that the values for kaolin plot in th left portion of each graph (lower CRI), while those for bentonite plot in the right portion (higher CRI).
With respect to the correlation with the critical state friction angle, this has been explored less in the literature: in general, there are fewer examples of correlations between the CRI and mechanical parameters compared to those with basic or index properties [33,43]. Our results are shown in Figure 6. In this case, we performed a single regression for both materials, considering that the initial porosity has little effect on the friction angle at the critical state. In fact, the shear strength at the critical state is typically linearly and directly proportional to the effective confining stress, resulting in a constant friction angle across a wide range of initial porosity values. As a consequence, the difference in porosity across the samples only adds little variability to the regression, and high values of R2 can still be evaluated. In particular, the R2 is highest (0.86) for CRIs evaluated during the first 15 min of cooling but the value for the first 10 min is very close (0.84). A good correlation is also observed for the CRI evaluated over the entire cooling period (CRItot), similarly to what observed for the case of porosity (Figure 5). However, CRItot would be more time consuming to obtain without offering any advantage: the use of CRI10min is thus the most practical.
4. Discussion
The result delineated in the previous paragraphs, compared with experiences from the literature on empirical correlations between laboratory test results [1], suggest that while index properties (liquid limit, plasticity index) can be used to estimate strength parameters (with some significant degree of uncertainty), the thermal behaviour—which is even of more immediate evaluation—may inform on the nature of the material (its composition or possibly its microstructure), its porosity (an intrinsic characteristic, used as a state variable in physically-based modelling in geomechanics), and its mechanical strength (which is typically used as a parameter in modelling). What is more, the CRI seems able to explain the variability in the data almost entirely (R2 close to 1).
Therefore, we argue that the approach we propose is worthy of further development and tuning and could potentially lead to the formulation of a standard protocol of testing. Necessarily, a systematic investigation needs to be carried out, not only on materials with “simple” and well-constrained composition and structure (such as commercial clays and sands), but also on a wide range of natural soils, that are by nature far more complex and heterogeneous. Simple materials are useful for establishing the capability of the experimental method and its informativeness in a reduced-variables context; natural soils are fundamental for validation and for assessing usability in practice. We expect that, for the latter, the predictive capability of the CRI will be somewhat reduced, but the limitation could be overcome by introducing, in the empirical correlations, an additional variable (e.g., related to soil composition or grain size), selected, for instance, via a multivariate analysis of a large dataset of experimental results. The final step will be a comparison between laboratory results and field data (e.g., LST monitoring over 24 h), so as to evaluate to what extent the correlations obtained in a controlled, small-scale environment remain valid in situ.
5. Conclusions
We explored a new approach to the evaluation of geomechanical properties using infrared thermography by identifying correlations between the cooling rate index of oven-heated samples and conventionally determined porosity or critical state friction angle. These correlations may be useful for first assessments in the laboratory, but also for field evaluations (after proper validation) where geomechanical information is insufficient, while remote sensing imagery is readily available.
For laboratory samples, we identified the first ten minutes of cooling after the temperature peak as the most informative time interval for regression analysis with porosity data, while the first ten-fifteen minutes worked best for the critical state friction angle. We note that the size of the time interval is also sample size-dependent: field experiments on metre-scale blocks suggested the use of hours-long intervals for correlations with the compressive strength [4]. In fact, the cooling rate of a block of given shape and material under a given initial temperature difference should be proportional to its surface area-to-volume ratio (controlling the ratio between the radiative surface and heat capacity), which decreases as the block size increases.
The analysis of the thermograms also indicated that the nature of the geomaterial sample could be discerned, a possibility that was also suggested in the field [4,8,9,12,25,33,43,44]. Thus, this analysis can be a valid aid in both rock and soil classifications in the laboratory and in the field, as infrared thermography can be flexibly applied at various spatial scales and is non-destructive. However, limitations are still present that make lab-to-scale upscaling non-straightforward, partly related to the achievable resolution, the selective opacity of the atmosphere, and the anisotropy and heterogeneity of the material. Nonetheless, for laboratory-scale investigations, the methodology appears solid and further validation with natural soils is warranted.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/rs14164067/s1, additional information on methodological tools is provided in a separate file (Tables S1–S7 and Figure S1) [1,45,46].
Author Contributions
Conceptualisation and methodology, M.L. and G.S.; formal analysis, M.L. and G.S.; investigation, M.L.; data curation, and original draft preparation, M.L.; review and editing, M.L., G.S., J.B. and F.H.; visualisation, M.L.; supervision, G.S.; project administration, M.L. and G.S., funding acquisition, M.L. and G.S. All authors have read and agreed to the published version of the manuscript.
Funding
Data analysis: manuscript preparation and publication were funded by the Grant Agency of the Czech Republic (GAČR Grant No. 20-28853Y), the Charles University Grant Agency (GAUK; Project No. 337121), and the Fund for international mobility of researchers at Charles University (MSCA-IF IV; Project No. CZ.02.2.69/0.0/0.0/20_079/0017987).
Data Availability Statement
Elaborated data are presented in the manuscript. Raw experimental data can be provided by the authors upon reasonable request.
Acknowledgments
The authors are grateful to Tomáš Weiss for the use of the FLIR C2 camera.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Roháč, J.; Scaringi, G.; Boháč, J.; Kycl, P.; Najser, J. Revisiting Strength Concepts and Correlations with Soil Index Properties: Insights from the Dobkovičky Landslide in Czech Republic. Landslides 2020, 17, 597–614. [Google Scholar] [CrossRef]
- Bogena, H.R.; Huisman, J.A.; Güntner, A.; Hübner, C.; Kusche, J.; Jonard, F.; Vey, S.; Vereecken, H. Emerging Methods for Noninvasive Sensing of Soil Moisture Dynamics from Field to Catchment Scale: A Review. WIREs Water 2015, 2, 635–647. [Google Scholar] [CrossRef] [Green Version]
- Abdullah, A.Y.M.; Biswas, R.K.; Chowdhury, A.I.; Billah, S.M. Modeling Soil Salinity Using Direct and Indirect Measurement Techniques: A Comparative Analysis. Environ. Dev. 2019, 29, 67–80. [Google Scholar] [CrossRef]
- Loche, M.; Scaringi, G.; Blahůt, J.; Melis, M.T.; Funedda, A.; Da Pelo, S.; Erbì, I.; Deiana, G.; Meloni, M.A.; Cocco, F. An Infrared Thermography Approach to Evaluate the Strength of a Rock Cliff. Remote Sens. 2021, 13, 1265. [Google Scholar] [CrossRef]
- Scaringi, G.; Loche, M. A Thermo-Hydro-Mechanical Approach to Soil Slope Stability under Climate Change. Geomorphology 2022, 401, 108108. [Google Scholar] [CrossRef]
- Mineo, S.; Caliò, D.; Pappalardo, G. UAV-Based Photogrammetry and Infrared Thermography Applied to Rock Mass Survey for Geomechanical Purposes. Remote Sens. 2022, 14, 473. [Google Scholar] [CrossRef]
- Stead, D.; Donati, D.; Wolter, A.; Sturzenegger, M. Application of Remote Sensing to the Investigation of Rock Slopes: Experience Gained and Lessons Learned. ISPRS Int. J. Geo-Inf. 2019, 8, 296. [Google Scholar] [CrossRef] [Green Version]
- Melis, M.T.; Da Pelo, S.; Erbì, I.; Loche, M.; Deiana, G.; Demurtas, V.; Meloni, M.A.; Dessì, F.; Funedda, A.; Scaioni, M.; et al. Thermal Remote Sensing from UAVs: A Review on Methods in Coastal Cliffs Prone to Landslides. Remote Sens. 2020, 12, 1971. [Google Scholar] [CrossRef]
- Mineo, S.; Pappalardo, G. The Use of Infrared Thermography for Porosity Assessment of Intact Rock. Rock Mech. Rock Eng. 2016, 49, 3027–3039. [Google Scholar] [CrossRef]
- Mitchell, J.K.; Soga, K. Fundamentals of Soil Behavior; John Wiley & Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- Scaringi, G.; Fan, X.; Xu, Q.; Liu, C.; Ouyang, C.; Domènech, G.; Yang, F.; Dai, L. Some Considerations on the Use of Numerical Methods to Simulate Past Landslides and Possible New Failures: The Case of the Recent Xinmo Landslide (Sichuan, China). Landslides 2018, 15, 1359–1375. [Google Scholar] [CrossRef]
- Pappalardo, G.; Mineo, S.; Zampelli, S.P.; Cubito, A.; Calcaterra, D. InfraRed Thermography Proposed for the Estimation of the Cooling Rate Index in the Remote Survey of Rock Masses. Int. J. Rock Mech. Min. Sci. 2016, 83, 182–196. [Google Scholar] [CrossRef]
- Lu, Y.; Horton, R.; Zhang, X.; Ren, T. Accounting for Soil Porosity Improves a Thermal Inertia Model for Estimating Surface Soil Water Content. Remote Sens. Environ. 2018, 212, 79–89. [Google Scholar] [CrossRef]
- Loche, M.; Scaringi, G.; Yunus, A.P.; Catani, F.; Tanyaş, H.; Frodella, W.; Fan, X.; Lombardo, L. Surface Temperature Controls the Pattern of Post-Earthquake Landslide Activity. Sci. Rep. 2022, 12, 988. [Google Scholar] [CrossRef]
- Eccel, E.; Arman, G.; Zottele, F.; Gioli, B. Thermal Infrared Remote Sensing for High Resolution Minimum Temperature Mapping. Ital. J. Agrometeorol. 2008, 13, 52–61. [Google Scholar]
- Reichenbach, P.; Rossi, M.; Malamud, B.D.; Mihir, M.; Guzzetti, F. A Review of Statistically-Based Landslide Susceptibility Models. Earth-Sci. Rev. 2018, 180, 60–91. [Google Scholar] [CrossRef]
- Loche, M.; Alvioli, M.; Marchesini, I.; Bakka, H.; Lombardo, L. Landslide Susceptibility Maps of Italy: Lesson Learnt from Dealing with Multiple Landslide Types and the Uneven Spatial Distribution of the National Inventory. Earth-Sci. Rev. 2022, 232, 104125. [Google Scholar] [CrossRef]
- Shannon, H.R.; Sigda, J.M.; Van Dam, R.L.; Hendrickx, J.M.; McLemore, V.T. Thermal Camera Imaging of Rock Piles at the Questa Molybdenum Mine, Questa, New Mexico. In Proceedings of the 2005 National Meeting of the America Society of Mining and Reclamation, ASMR, Lexington, KY, USA, 19–23 June 2005; pp. 1015–1028. [Google Scholar]
- Prendes-Gero, M.B.; Suárez-Domínguez, F.J.; González-Nicieza, C.; Álvarez-Fernández, M.I. Infrared Thermography Methodology Applied to Detect Localized Rockfalls in Self-Supporting Underground Mines. In proceedings of the ISRM International Symposium-EUROCK 2013, Wrocław, Poland, 23–26 September 2013; OnePetro: Richardson, TX, USA, 2013. [Google Scholar]
- Teza, G.; Marcato, G.; Castelli, E.; Galgaro, A. IRTROCK: A MATLAB Toolbox for Contactless Recognition of Surface and Shallow Weakness of a Rock Cliff by Infrared Thermography. Comput. Geosci. 2012, 45, 109–118. [Google Scholar]
- Kuenzer, C.; Deck, S. Thermal Infrared Remote Sensing: Sensors, Methods, Applications; Springer: Dordrecht, The Netherlands, 2013; ISBN 978-94-007-6638-9. [Google Scholar]
- Mineo, S.; Pappalardo, G.; Rapisarda, F.; Cubito, A.; Di Maria, G. Integrated Geostructural, Seismic and Infrared Thermography Surveys for the Study of an Unstable Rock Slope in the Peloritani Chain (NE Sicily). Eng. Geol. 2015, 195, 225–235. [Google Scholar]
- Racek, O.; Blahůt, J.; Hartvich, F. Observation of the Rock Slope Thermal Regime, Coupled with Crackmeter Stability Monitoring: Initial Results from Three Different Sites in Czechia (Central Europe). Geosci. Instrum. Methods Data Syst. 2021, 10, 203–218. [Google Scholar] [CrossRef]
- Hudson, R.D. Infrared System Engineering; Wiley-Interscience: New York, NY, USA, 1969; Volume 1. [Google Scholar]
- Frodella, W.; Lazzeri, G.; Moretti, S.; Keizer, J.; Verheijen, F.G. Applying Infrared Thermography to Soil Surface Temperature Monitoring: Case Study of a High-Resolution 48 h Survey in a Vineyard (Anadia, Portugal). Sensors 2020, 20, 2444. [Google Scholar]
- Martino, S.; Mazzanti, P. Integrating Geomechanical Surveys and Remote Sensing for Sea Cliff Slope Stability Analysis: The Mt. Pucci Case Study (Italy). Nat. Hazards Earth Syst. Sci. 2014, 14, 831–848. [Google Scholar]
- Mazzanti, P.; Brunetti, A.; Bretschneider, A. A New Approach Based on Terrestrial Remote-Sensing Techniques for Rock Fall Hazard Assessment. In Modern Technologies for Landslide Monitoring and Prediction; Springer: Berlin/Heidelberg, Germany, 2015; pp. 69–87. [Google Scholar]
- Blackett, M. An Overview of Infrared Remote Sensing of Volcanic Activity. J. Imaging 2017, 3, 13. [Google Scholar]
- Oppenheimer, C.; Yirgu, G. Thermal Imaging of an Active Lava Lake: Erta’Ale Volcano, Ethiopia. Int. J. Remote Sens. 2002, 23, 4777–4782. [Google Scholar]
- Lagios, E.; Vassilopoulou, S.; Sakkas, V.; Dietrich, V.; Damiata, B.N.; Ganas, A. Testing Satellite and Ground Thermal Imaging of Low-Temperature Fumarolic Fields: The Dormant Nisyros Volcano (Greece). ISPRS J. Photogramm. Remote Sens. 2007, 62, 447–460. [Google Scholar]
- Spampinato, L.; Calvari, S.; Oppenheimer, C.; Boschi, E. Volcano Surveillance Using Infrared Cameras. Earth-Sci. Rev. 2011, 106, 63–91. [Google Scholar]
- Harvey, M.C.; Rowland, J.V.; Luketina, K.M. Drone with Thermal Infrared Camera Provides High Resolution Georeferenced Imagery of the Waikite Geothermal Area, New Zealand. J. Volcanol. Geotherm. Res. 2016, 325, 61–69. [Google Scholar]
- de Lima, J.L.; Abrantes, J.R.; Silva Jr, V.P.; Montenegro, A.A. Prediction of Skin Surface Soil Permeability by Infrared Thermography: A Soil Flume Experiment. Quant. InfraRed Thermogr. J. 2014, 11, 161–169. [Google Scholar]
- Morello, R. Potentialities and Limitations of Thermography to Assess Landslide Risk. Measurement 2018, 116, 658–668. [Google Scholar]
- Laufek, F.; Hanusová, I.; Svoboda, J.; Vašíček, R.; Najser, J.; Koubová, M.; Čurda, M.; Pticen, F.; Vaculíková, L.; Sun, H. Mineralogical, Geochemical and Geotechnical Study of BCV 2017 Bentonite—The Initial State and the State Following Thermal Treatment at 200 °C. Minerals 2021, 11, 871. [Google Scholar]
- Hong, Y.; Wang, L.Z.; Ng, C.W.; Yang, B. Effect of Initial Pore Pressure on Undrained Shear Behaviour of Fine-Grained Gassy Soil. Can. Geotech. J. 2017, 54, 1592–1600. [Google Scholar]
- Duque, J.; Ochmański, M.; Mašín, D.; Hong, Y.; Wang, L. On the Behavior of Monopiles Subjected to Multiple Episodes of Cyclic Loading and Reconsolidation in Cohesive Soils. Comput. Geotech. 2021, 134, 104049. [Google Scholar] [CrossRef]
- Duque, J. Contributions to the Experimental Investigation and Numerical Description of Soil Cyclic Behavior; Charles University: Prague, Czech Republic, 2021. [Google Scholar]
- Pivovarník, M.; Pikl, M.; Frouz, J.; Zemek, F.; Kopačková, V.; Notesco, G.; Ben Dor, E. A Spectral Emissivity Library of Spoil Substrates. Data 2016, 1, 12. [Google Scholar] [CrossRef] [Green Version]
- ASTM D7263-21; Standard Test Methods for Laboratory Determination of Density and Unit Weight of Soil Specimens. ASTM International: West Conshohocken, PA, USA, 2021; Volume 4.
- Pappalardo, G.; Mineo, S.; Marchese, G. Effects of Cubical Specimen Sizing on the Uniaxial Compressive Strength of Etna Volcanic Rocks (Italy). Ital. J. Eng. Geol. Environ. 2013, 10, 45–54. [Google Scholar] [CrossRef]
- Pappalardo, G.; Mineo, S. Investigation on the Mechanical Attitude of Basaltic Rocks from Mount Etna through InfraRed Thermography and Laboratory Tests. Constr. Build. Mater. 2017, 134, 228–235. [Google Scholar] [CrossRef]
- de Lima, J.L.M.P.; Abrantes, J.R.C.B.; Silva, V.P.; de Lima, M.I.P.; Montenegro, A.A.A. Mapping Soil Surface Macropores Using Infrared Thermography: An Exploratory Laboratory Study. Sci. World J. 2014, 2014, e845460. [Google Scholar] [CrossRef] [Green Version]
- Frodella, W.; Gigli, G.; Morelli, S.; Lombardi, L.; Casagli, N. Landslide Mapping and Characterization through Infrared Thermography (IRT): Suggestions for a Methodological Approach from Some Case Studies. Remote Sens. 2017, 9, 1281. [Google Scholar] [CrossRef] [Green Version]
- Wood, D.M. Soil Behaviour and Critical State Soil Mechanics, 1st ed.; Cambridge University Press: Cambridge, UK, 1991; ISBN 978-0-521-33249-1. [Google Scholar]
- Wu, T.H. Geotechnical Properties of Glacial Lake Clays. J. Soil Mech. Found. Div. 1958, 84. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).