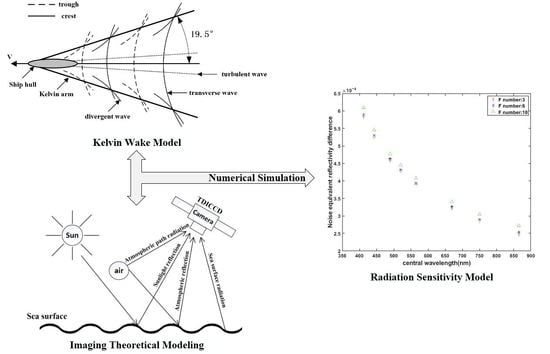
Radiation Sensitivity Analysis of Ocean Wake Information Detection System Based on Visible Light Remote Sensing
Abstract
:1. Introduction
2. Models and Methods
2.1. Kelvin Wake Model
2.2. Imaging Theoretical Modeling
2.2.1. TDICCD Imaging Principle
2.2.2. Noise Model
2.2.3. Wake Imaging Link Model
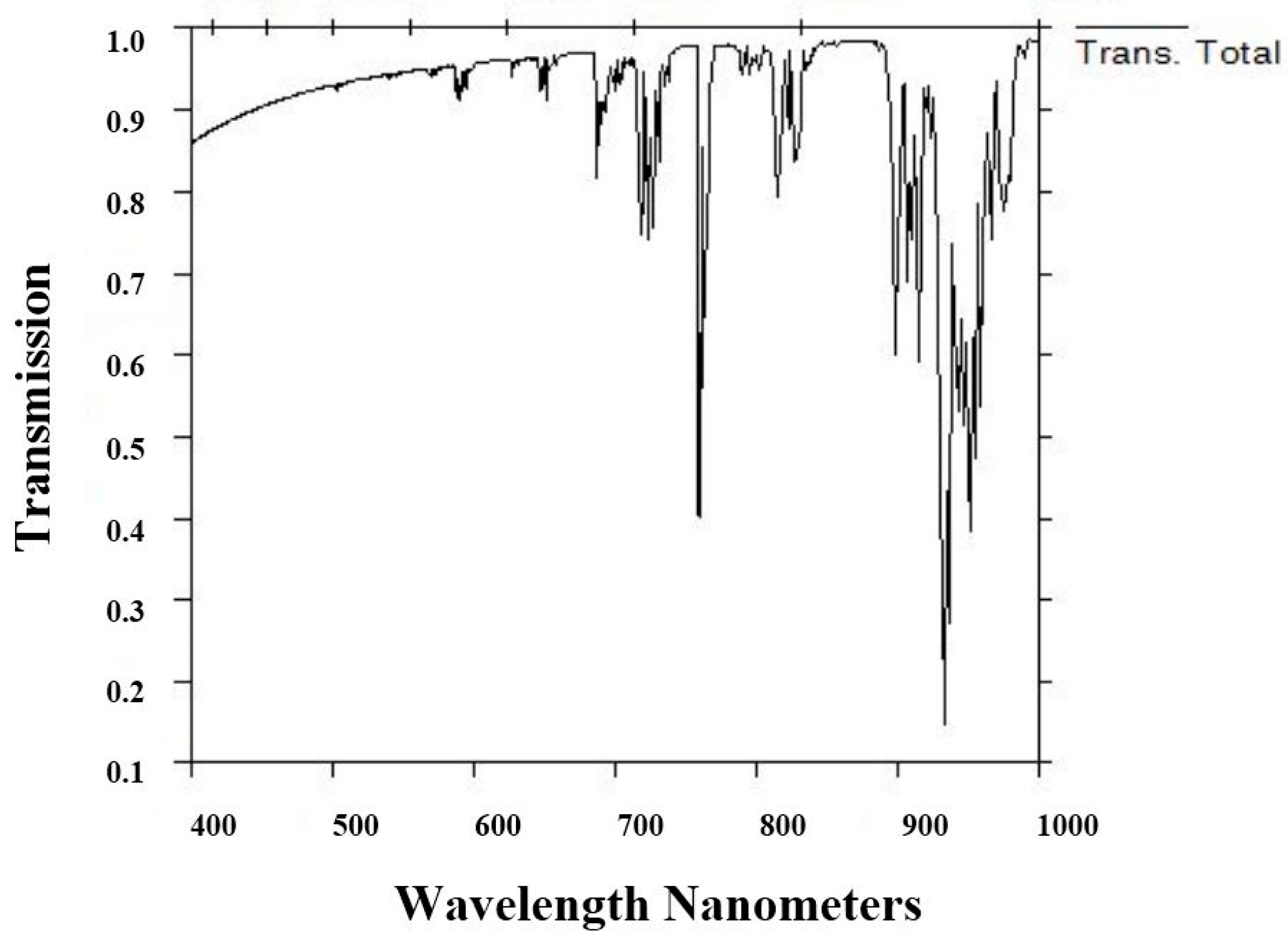
2.3. Radiative Sensitivity Modeling
3. Simulation
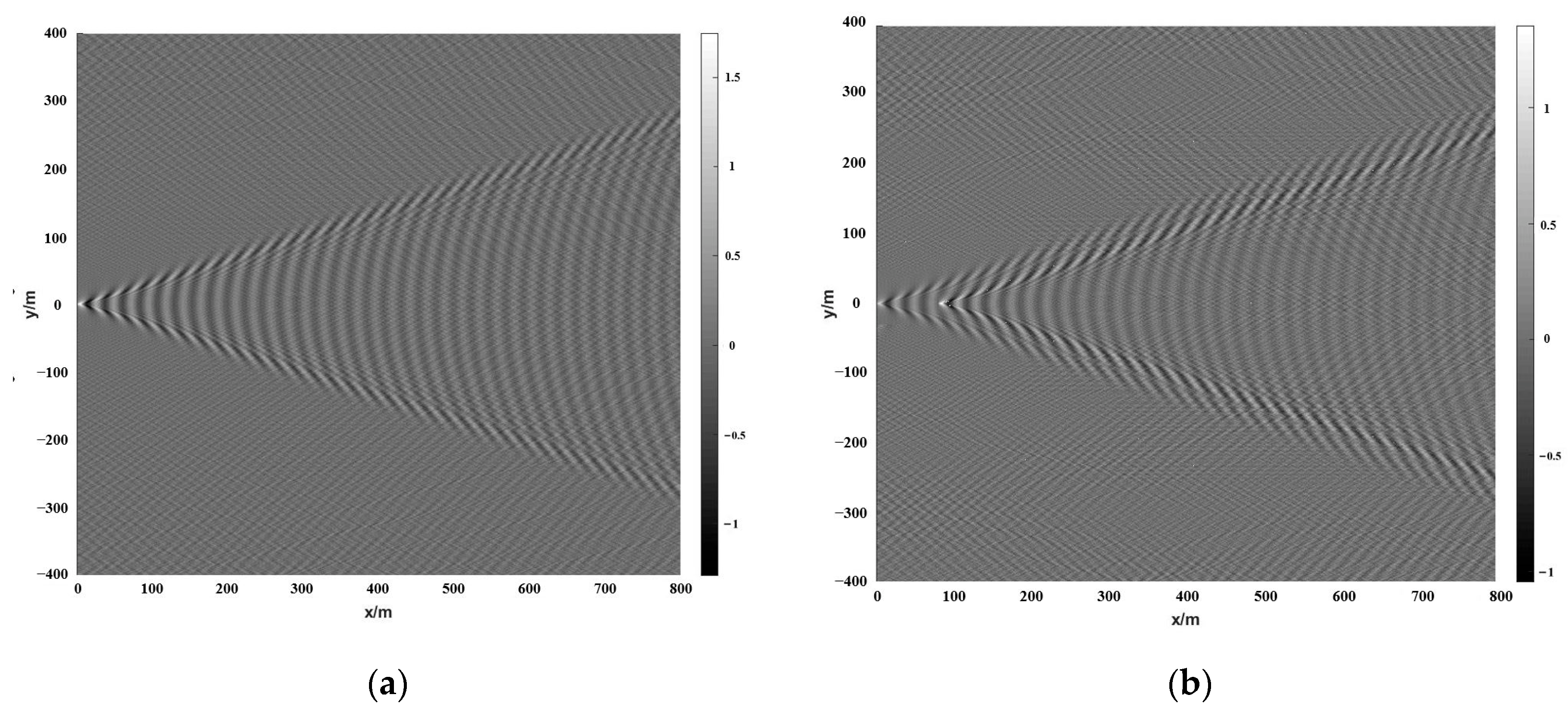
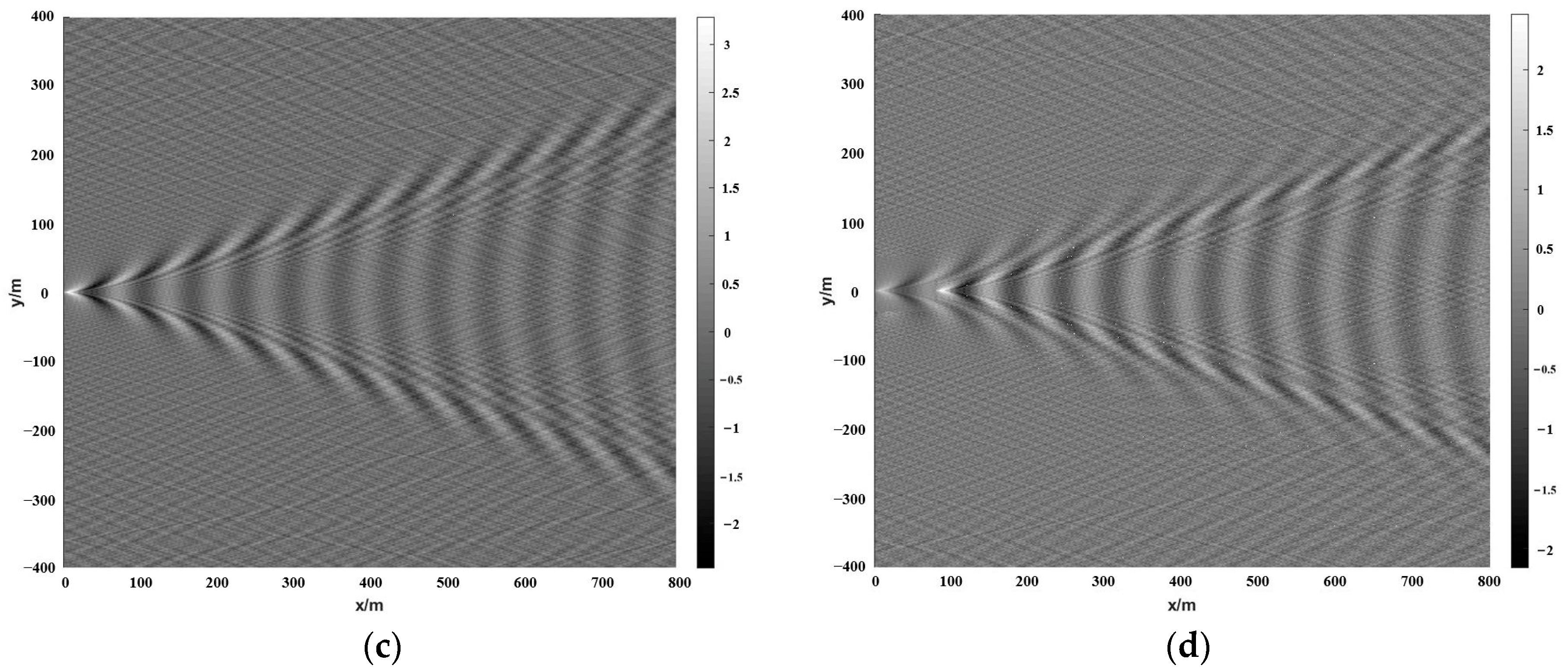
3.1. Kelvin Wake Model
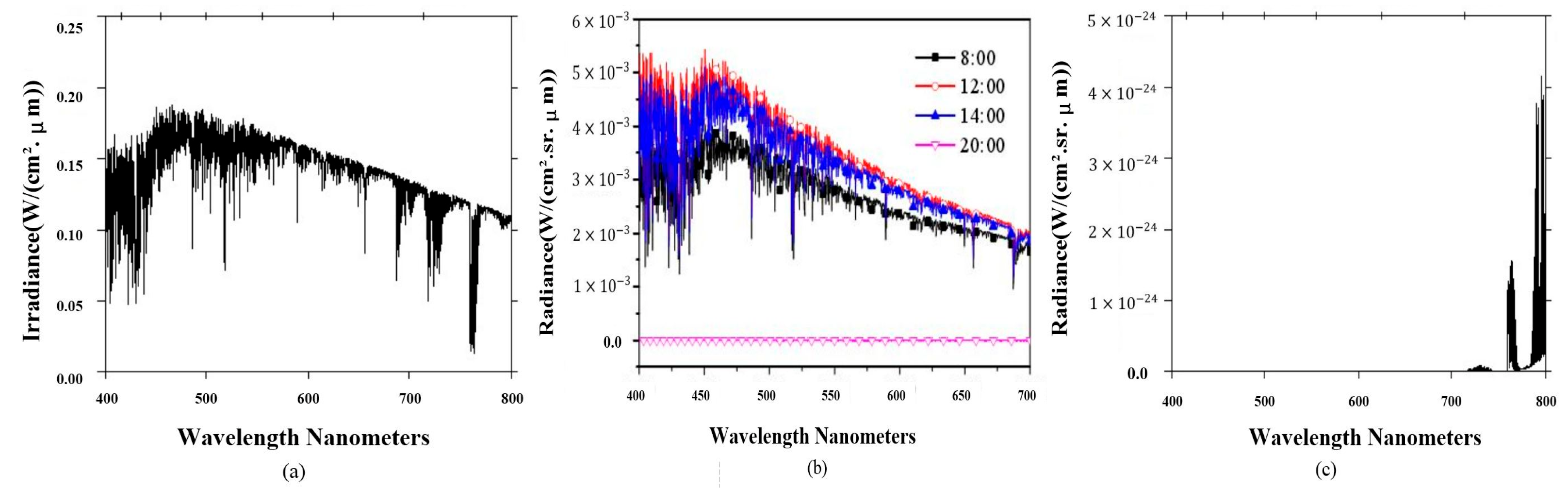
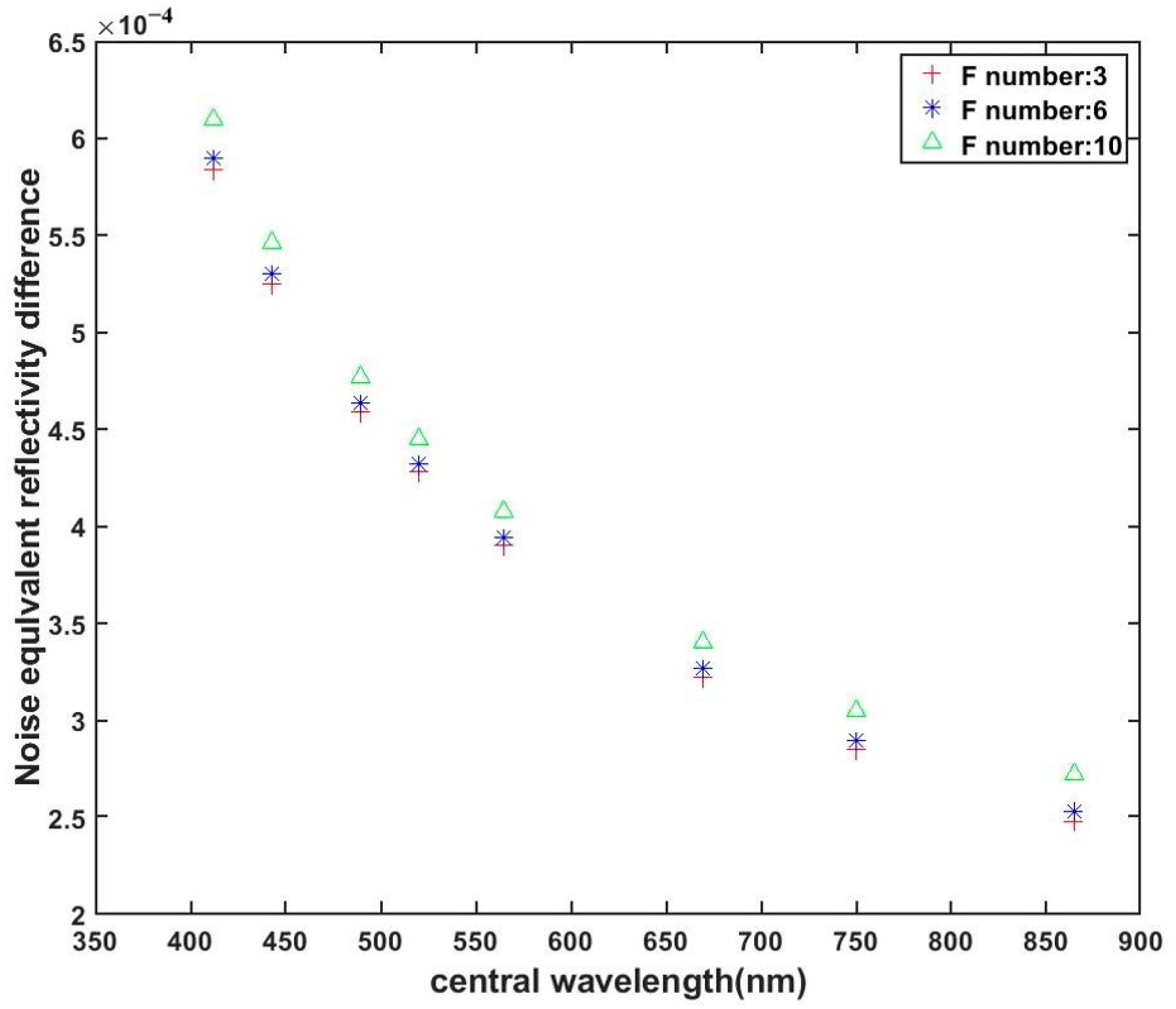
3.2. Radiative Sensitivity Model
4. Discussion
4.1. Improve the Optical System
4.2. Reduce Camera Noise
4.3. Increase the Pixel Area
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| TDICCD | Time delay and integration charge coupled devices |
| SNR | Signal-to-noise ratio |
| The noise equivalent reflectance difference | |
| The noise equivalent temperature difference |
Appendix A
References
- Tunaley, J.; Buller, E.; Wu, K.; Rey, M. The simulation of the SAR image of a ship wake. IEEE Trans. Geosci. Remote Sens. 1991, 29, 149–156. [Google Scholar] [CrossRef]
- Liu, Y.; Deng, R. Ship wakes in optical images. J. Atmos. Ocean. Technol. 2018, 35, 1633–1648. [Google Scholar] [CrossRef]
- Xue, F.; Jin, W.; Qiu, S.; Yang, J. Wake Features of Moving Submerged Bodies and Motion State Inversion of Submarines. IEEE Access 2020, 8, 12713–12724. [Google Scholar] [CrossRef]
- Xue, F.; Jin, W.; Qiu, S.; Yang, J. Airborne optical polarization imaging for observation of submarine Kelvin wakes on the sea surface: Imaging chain and simulation. ISPRS J. Photogramm. Remote Sens. 2021, 178, 136–154. [Google Scholar] [CrossRef]
- Zilman, G.; Zapolski, A.; Marom, M. On detectability of a ship’s Kelvin wake in simulated SAR images of rough sea surface. IEEE Trans. Geosci. Remote Sens. 2014, 53, 609–619. [Google Scholar] [CrossRef]
- Sun, X.; Cai, M.; Wang, J.; Liu, C. Numerical Simulation of the Kelvin Wake Patterns. Appl. Sci. 2022, 12, 6265. [Google Scholar] [CrossRef]
- Ahmadibebi, A.; Jones, B.; Shirkhodaie, A. Physics-based wake modeling for marine vehicles activity recognition based on simulated synthetic aperture radar. In Proceedings of the SPIE, Ocean Sensing and Monitoring XIV, Orlando, FL, USA, 3 April–13 June 2022; Volume 12118, pp. 107–119. [Google Scholar]
- Zhao, H.; Ji, Z.; Zhang, Y.; Sun, X.; Song, P.; Li, Y. Mid-infrared imaging system based on polarizers for detecting marine targets covered in sun glint. Opt. Express 2016, 24, 16396–16409. [Google Scholar] [CrossRef] [PubMed]
- Song, M.; Qu, H.; Zhang, G.; Tao, S.; Jin, G. variational model for sea image enhancement. Remote Sens. 2018, 10, 1313. [Google Scholar] [CrossRef]
- Zhu, S.; Chen, Z.; Kang, L. Satellite-borne SAR low-contrast signals wave wake image enhancement based on a bilateral rapid filtering visualization algorithm. In Proceedings of the 2019 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC), Dalian, China, 20–22 September 2019; pp. 1–3. [Google Scholar]
- Srivastava, R.; Christmas, J. Analysis of Sea Waves and Ship Wake Detection. In Proceedings of the OCEANS 2022-Chennai, Chennai, India, 21–24 February 2022; pp. 1–10. [Google Scholar]
- Wang, J.; Wang, Y.; Li, C. Noise model of hyperspectral imaging system and influence on radiation sensitivity. J. Remote Sens. 2010, 14, 607–620. [Google Scholar]
- Kelvin, L. On ship waves. Proc. Inst. Mech. Engrs. 1887, 38, 409–434. [Google Scholar]
- Oumansour, K.; Wang, Y.; Saillard, J. Multifrequency SAR observation of a ship wake. IEEE Proc. -Radar Sonar Navig. 1996, 143, 275–280. [Google Scholar] [CrossRef]
- Wang, H. Spectral comparisons of ocean waves and Kelvin ship waves. In Proceedings of the Seventh Offshore Mechanics and Arctic Engineering Symposium, New York, NY, USA; 1988; Volume 2, pp. 253–261. [Google Scholar]
- Liu, Y.; Deng, R.; Zhao, J. Simulation of Kelvin wakes in optical images of rough sea surface. Appl. Ocean. Res. 2019, 89, 36–43. [Google Scholar] [CrossRef]
- Cox, C.; Munk, W. Measurement of the roughness of the sea surface from photographs of the sun’s glitter. Josa 1954, 44, 838–850. [Google Scholar] [CrossRef]
- Song, M.; Wang, S.; Zhao, P.; Chen, Y.; Wang, J. Modeling Kelvin wake imaging mechanism of visible spectral remote sensing. Appl. Ocean. Res. 2021, 113, 102712. [Google Scholar] [CrossRef]
- Wang, Y. Influence of Infrared Detector Response Nonuniformity on System Sensitivity. Infrared Laser Eng. 2006, 3, 258–261. [Google Scholar]
- Wu, X.; Smith, W.L. Emissivity of rough sea surface for 8–13 µm: Modeling and verification. Appl. Opt. 1997, 36, 2609–2619. [Google Scholar] [CrossRef] [PubMed]
- Han, X. Calculation of radiation sensitivity for spaceborne multispectral scanner. Infrared Res. (Ser. A) 1988, 3, 213–217. [Google Scholar]





| Parameters | Value |
|---|---|
| Optical system total transmittance | 0.7 |
| Detector pixel size ) | 17.5 × 17.5 |
| Pixel number | 3072 |
| Quantum efficiency | 0.5 |
| Integration time (ms) | 4 |
| Central Wavelength (nm) | Irradiance |
|---|---|
| 412 | 1760 |
| 443 | 1877 |
| 490 | 1950 |
| 520 | 1933 |
| 565 | 1705 |
| 670 | 1456 |
| 750 | 1235 |
| 865 | 958 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ying, S.; Qu, H.; Tao, S.; Zheng, L.; Wu, X. Radiation Sensitivity Analysis of Ocean Wake Information Detection System Based on Visible Light Remote Sensing. Remote Sens. 2022, 14, 4054. https://doi.org/10.3390/rs14164054
Ying S, Qu H, Tao S, Zheng L, Wu X. Radiation Sensitivity Analysis of Ocean Wake Information Detection System Based on Visible Light Remote Sensing. Remote Sensing. 2022; 14(16):4054. https://doi.org/10.3390/rs14164054
Chicago/Turabian StyleYing, Shipeng, Hongsong Qu, Shuping Tao, Liangliang Zheng, and Xiaobin Wu. 2022. "Radiation Sensitivity Analysis of Ocean Wake Information Detection System Based on Visible Light Remote Sensing" Remote Sensing 14, no. 16: 4054. https://doi.org/10.3390/rs14164054
APA StyleYing, S., Qu, H., Tao, S., Zheng, L., & Wu, X. (2022). Radiation Sensitivity Analysis of Ocean Wake Information Detection System Based on Visible Light Remote Sensing. Remote Sensing, 14(16), 4054. https://doi.org/10.3390/rs14164054