Abstract
Hyperspectral images often have hundreds of spectral bands of different wavelengths captured by aircraft or satellites that record land coverage. Identifying detailed classes of pixels becomes feasible due to the enhancement in spectral and spatial resolution of hyperspectral images. In this work, we propose a novel framework that utilizes both spatial and spectral information for classifying pixels in hyperspectral images. The method consists of three stages. In the first stage, the pre-processing stage, the Nested Sliding Window algorithm is used to reconstruct the original data by enhancing the consistency of neighboring pixels and then Principal Component Analysis is used to reduce the dimension of data. In the second stage, Support Vector Machines are trained to estimate the pixel-wise probability map of each class using the spectral information from the images. Finally, a smoothed total variation model is applied to ensure spatial connectivity in the classification map by smoothing the class probability tensor. We demonstrate the superiority of our method against three state-of-the-art algorithms on six benchmark hyperspectral datasets with 10 to 50 training labels for each class. The results show that our method gives the overall best performance in accuracy even with a very small set of labeled pixels. Especially, the gain in accuracy with respect to other state-of-the-art algorithms increases when the number of labeled pixels decreases, and, therefore, our method is more advantageous to be applied to problems with a small training set. Hence, it is of great practical significance since expert annotations are often expensive and difficult to collect.
1. Introduction
Hyperspectral images (HSIs) often have hundreds of electromagnetic bands of reflectance collected by aircraft or satellites that contain rich spectral and spatial information. HSIs can be represented by a tensor , where are the numbers of rows and columns in each spectral band and B is the number of bands of the HSI [1]. In general, each distinct material has its own spectral signature owing to its unique chemical composition. The enhancement in spectral resolution makes it more feasible to explore the HSIs using machine learning approaches in various applications, such as land coverage mapping, change recognition, water quality monitoring, and mineral identification [2,3,4,5,6,7,8]. The rich information in HSIs enables the algorithms to distinguish more detailed categories for land cover clustering and classification, and thus HSIs play a vital role in detecting different natural resources and monitoring vegetation health [9,10,11,12,13,14,15,16]. These applications typically require the results to be as accurate as possible for subsequent analysis, assessments and actions. Therefore, HSI classification methods are always measured based on accuracies [17].
A variety of algorithms with and without manual annotations have been developed for pixel-wise classification of HSIs. Compared with unsupervised methods, semi-supervised methods require a few labeled data for training and produce considerable improvement in performance. The classical pixel-wise semi-supervised algorithms, such as support vector machines (SVMs) [18], k-nearest-neighbor (kNN) classifier [19], multinomial logistic regression [20], and random forest [21,22] were extensively studied in the past.
However, these classifiers only explore and analyze the spectral information of HSIs, whereas the spatial information is ignored, which leads to a poor classification result. For instance, for regions that are spatially homogeneous but with a variety in the spectra, these methods may produce a noisy classification map (see e.g., Figure 3d). A common theoretical assumption in HSI classification is local spatial connectivity in certain regions, which means spatially nearby pixels have a higher probability of belonging to the same class [23,24]. Thus, pixel-wise classification methods can be enhanced by incorporating the spatial dependency of the pixels. In recent years, the spatial features of HSI have been explored in the pre-processing and post-processing steps to provide more information for various classification or recognition tasks.
In the extreme sparse multinomial logistic regression framework, the extended multi-attribute profile is adopted for spatial feature extraction [25]. Gao et al. [26] propose a new approach that extracts spatial features by applying linear prediction error and the local binary pattern. It then combines the spatial and spectral information by using a vector stacking method before feeding into the Random Multi-Graphs model, which is proposed in [27]. The K-means algorithm and principal component analysis (PCA) are adopted in [28] to extract spatial features, and then an SVM is trained to produce the classification results. The authors in [29] redefine a pixel in both spectral domain and spatial domain by extracting features in its neighboring region. Then Mercer’s kernels are adopted in SVM to combine spectral and spatial information. Structural filtering methods, for instance, the Gabor filter, can extract spatial texture features of adjacent pixels in different scales and directions [30,31]. Mathematical morphology can be used to obtain the morphological profile, such as the orientation or size of the spatial structures of images [32]. Fang et al. [33] propose an adaptive sparse representation (MFASR) method based on four spatial and spectral features where spatial information is extracted by the Gabor filter, extended morphological profiles, and differential morphological profiles, resulting in an improved accuracy compared with several excellent classifiers in the field of both qualitative and quantitative results. Gan et al. [34] propose a multiple feature kernel sparse representation-based classifier, which transforms each feature into a low-dimensional space with a nonlinear kernel.
Chan et al. [35] incorporate segmentation techniques in their 2-stage method to incorporate spatial information in the post-processing step. After acquiring the class probability vector for each pixel by SVM, a convex variant of the Mumford-Shah method (equivalent to a smoothed total-variational method) is used to denoise the probability vectors. Their 2-stage method achieves good results, with better accuracy and relatively shorter time compared with five well-known methods. Experiments show that this method improves the accuracy significantly, see Figure 3f. Ren et al. [36] propose the Nested Sliding Window (NSW) pre-processing method to extract spatial information from original HSI data. The NSW algorithm determines the optimal sub-window position based on the largest average Pearson correlation coefficient of the target pixel and its neighboring pixels, and then the pixels are reconstructed depending on the pixels in the sub-window and their correlation coefficients. PCA is used to further process the reconstructed data for dimensionality reduction and denoising. Finally, the reconstructed data are fed into SVM for classification. In their experiments, the addition of NSW and PCA led to better accuracy in comparison with several SVM-based algorithms.
The convolutional neural network (CNN) is becoming popular these years which can extract spatial information internally by convolutional kernels. The original CNNs [37] learn spatial features naturally from the original images by applying convolutional layers. Gao et al. [38] employ a new CNN architecture that also takes the spatial features extracted from the original image as input and achieves a significant improvement of accuracy compared with the original CNN framework. Zhang et al. [39] created a diverse region-based CNN which learns spatial features based on inputs from different regions. The recurrent 2-D CNN and recurrent 3-D CNN achieve higher accuracies and faster convergence rates with its convolutional operators and the recurrent network structure [40]. Nonetheless, these CNNs have millions of parameters that need to be tuned. Thus they require powerful machines to train the model and a large number of expert labels that are expensive to get.
All the methods mentioned above explore both spatial and spectral information and have achieved quite good results with a certain number of labeled pixels. However, in practical classification tasks, the most difficult part is collecting the labeled points, which requires a lot of time and resources. The insufficient number of samples is an inherent challenge. Therefore, it is more feasible and preferable to only incorporate a few labeled pixels for training in the semi-supervised learning methods [36]. In this work, we propose a 3-stage method for HSI classification, which fully explores spatial and spectral information of HSI so that we only need a very small number of labeled pixels to obtain higher accuracy than other methods. The first stage is a pre-processing step where we first apply the NSW algorithm [36] to find the most correlated nested window and then reconstruct the data based on the Pearson correlation for each pixel. Then we use PCA to reduce the dimension of the reconstructed data. In the second stage, we train an SVM-type method SVC (-support vector classifier) [41] for semi-supervised classification and produce an estimated probability tensor consisting of the probability maps for all classes. In the last stage, to incorporate the spatial information, a smoothed total variation model [35] is applied to post-process the probability maps to remove isolated misclassified pixels.
To demonstrate the efficacy of our method, we test it against the classical SVM method and three state-of-the-art methods on six widely used benchmark hyperspectral datasets with 10 to 50 training labels for each class. The results show that our method gives the best overall accuracy on all six datasets with a very small number of labeled pixels. Besides, we emphasize that the gain in accuracy compared with the four algorithms is higher when the number of labeled pixels is smaller. Our method is therefore of great practical significance since expert annotations are often expensive and difficult to collect.
The superiority of our method stems from the fact that the spatial information of the image is extensively explored. The pre-processing step enhances the consistency of spectral signatures of adjacent pixels, especially for those pixels which are located in a large homogeneous area and have varying inner-class spectra. Through the reconstruction, the similarity of spectral information of the pixels in the same category can be utilized so that we only need a smaller set of training pixels for each class to achieve a pleasant result. This step is useful for datasets that do not have sufficiently good spectral information. The post-processing step further improves the classification result by ensuring connectivity across spatial homogeneous regions using the spatial positions of the pixels. The smoothed total variation model used here can simultaneously enhance the spatial homogeneity by denoising while segmenting the image into different classes.
2. The Proposed Method
The method proposed in this work comprises the following three stages: (i) pre-processing stage: the HSI dataset is reconstructed by NSW and then projected linearly to a lower-dimensional space by PCA. The step effectively uses spatial information and reduce the Gaussian white noise in HSIs [36,42]; (ii) pixel-wise classification stage: the SVC, which uses mainly the spectral information in the dataset, is applied to get the probability maps where each map gives the probability of the pixels belonging to a certain class [35,41,43,44,45]; (iii) smoothing stage: a smoothed total variation (STV) model is used to ensure local spatial connectivity in the probability maps to increase the classification accuracy [35,46]. In the following subsections, we introduce the three stages in detail. The outline of the whole method is illustrated in Figure 1.

Figure 1.
The outline of the proposed method, where d is the reduced dimension and c is the number of classes. Each color represents a class in the output classification map.
2.1. The Pre-Processing Stage
The pre-processing step of the HSI datasets can effectively improve the quality of the data, leading to a better performance in the classification with less number of training pixels [36]. In pre-processing, spatial features are usually extracted by analyzing the similarity between the spectral signatures of the pixels in local regions. Wu et al. [47] construct a shape-adaptive region for each target pixel by applying the LPA-ICI method [48,49], and then put them together into the joint sparse representation classifier, which effectively explores the spatial information. On this basis, in [50], a shape-adaptive reconstruction method is proposed to pre-process the data based on the shape-adaptive region. Bazine et al. [51] propose a CDCT-WF-SVM model where the original data is pre-processed by applying spectral Discrete Cosine Transform and spatial filtering adaptive Wiener filter to extract the most significant information before using SVM. The NSW method in [36] is to find the best nested sliding window for each pixel with the largest mean Pearson correlation coefficient and then reconstruct the given pixel’s spectral signature by weighting spectral information of pixels using normalized correlation coefficients in the best window. Then PCA is used to reduce the dimension of the reconstructed data. We adopt this approach in our pre-processing stage and explain it briefly in the following two subsections, see details in [36].
2.1.1. The Nested Sliding Window (NSW) Method
For two pixels in an HSI tensor , where represents the spatial size of HSI and B is the number of bands, the Pearson correlation coefficient is defined as:
where represents the covariance between and , and is the variance. We define the neighboring pixels of a target pixel with a window size as
where , and represents the distance between the target pixel and the window boundary. For target pixels on or near the boundary of the image, we use zero-padding to extend the image outside the boundary to obtain a window of the same size for these pixels.
Then we create a series of sliding windows inside to search for some neighboring pixels which are most similar to the target pixel . To calculate the correlation coefficients between the target pixel and its neighboring pixels, each sliding window should contain the target pixel; that is, the size of the sliding window should be ((),()). Then the neighboring pixels with a sliding window can be expressed as the 3-D tensor:
where and . Here determine the position of the sliding window; see the green window (tensor) in Figure 2.
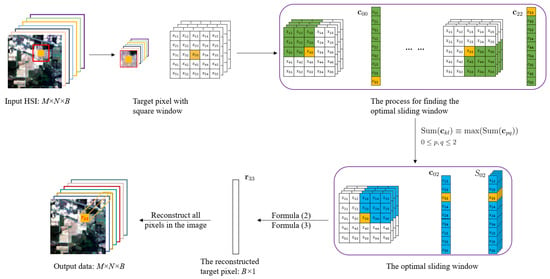
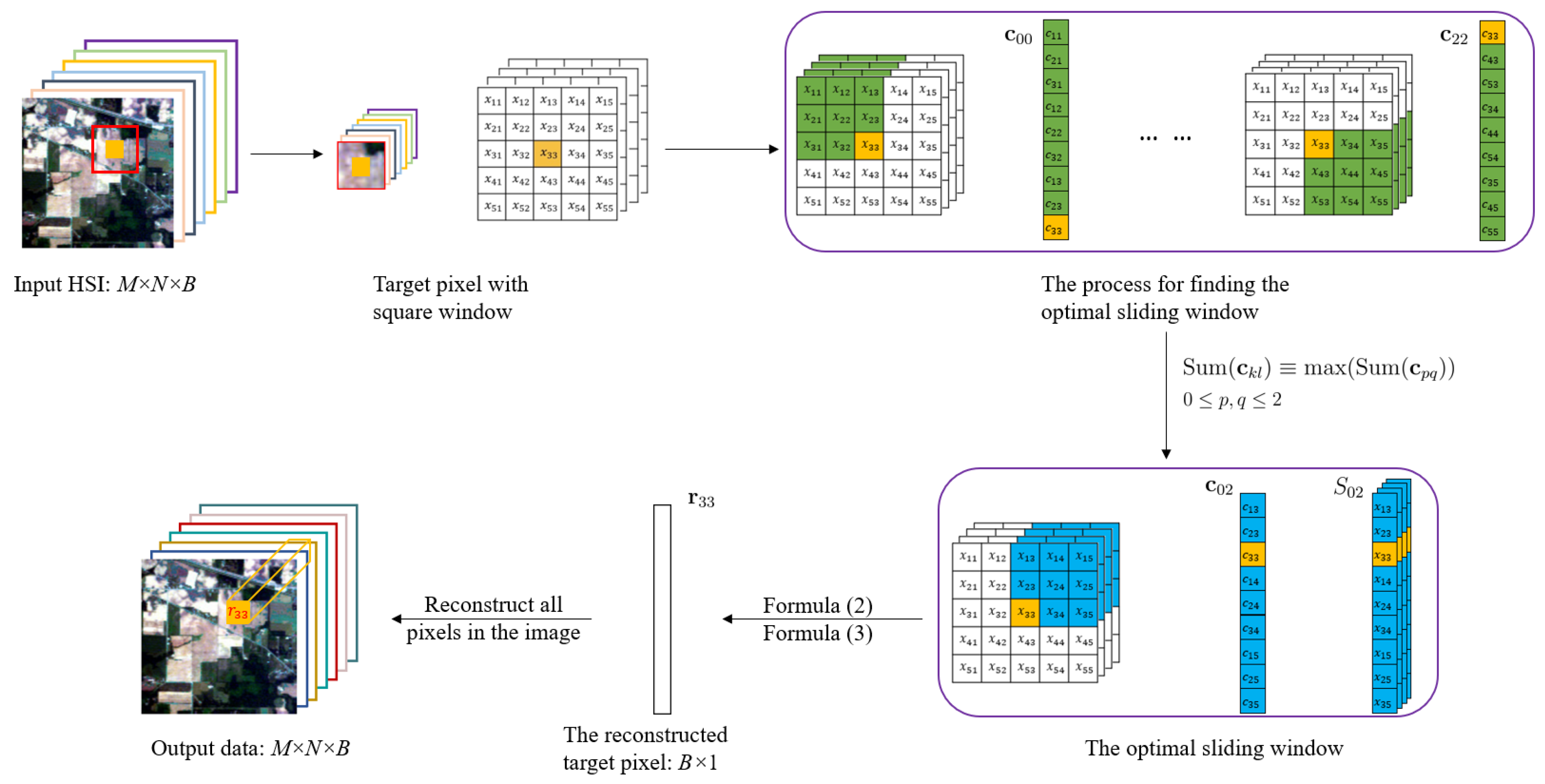
Figure 2.
The illustration diagram of the NSW method [36]. The yellow square represents the target pixel and the yellow square represents the correlation coefficient of with itself. The green squares represent the neighboring pixels in the sliding windows and their corresponding correlation coefficients. The blue squares represent the optimal sliding window and the corresponding correlation coefficients.
Thus, the Pearson correlation coefficient between the target pixel and each neighboring pixel in the sliding window can be computed by (1). Together, the correlation coefficients in each sliding window form a matrix, denote as :
It is reshaped as a vector with size . After going through all the sliding windows, we set where is the sum of the elements of the vector . The maximal correlation coefficient vector is then normalized by
Then the corresponding 3D tensor is re-shaped to a 2D matrix with size . The reconstruction of the pixel at the location is given by the B-vector:
We can view as a weighted spectrum of the target pixel from its nearby pixels’ spectra, with weights determined by the importance of the corresponding Pearson’s coefficients. After the reconstruction for all pixels in the HSI, we obtain a new tensor with vectors along the third axis being , representing the spectra of reconstructed pixels. In the following, we re-shape the tensor into a matrix .
Figure 2 illustrates the NSW method, where we assume the target pixel is with , , and the largest sum of Pearson’s coefficients is obtained at [36].
2.1.2. Principal Component Analysis (PCA)
PCA [52] is one of the most commonly used dimensionality reduction algorithms. Assume that we need to reduce the re-shaped data obtained by NSW algorithm from B dimensional to d dimensional, then the purpose of PCA is to find a 2D transformation matrix in where represents the trace of the matrix and . The maximization of W can be solved by using the Lagrangian multiplier method. Finally, we get the dimension-reduced data
2.2. The Pixel-Wise Classification Stage
Support vector machines (SVMs) have been used successfully in pattern recognition [53], object detection [54,55], and financial time series forecasting, [56,57] etc., to separate two classes of objects. SVM and SVC are two types of SVM classifiers. The main difference between the two classifiers is that SVM contains a parameter C, which determines the margin between two classes of training samples and C can take any positive value; while the parameter in SVC controls the number of support vectors, usually between 0 and 1. Here we adopt SVC for classification since the parameter C in SVM is difficult to choose optimally.
Suppose we have t labeled pixels, then the formulation of SVC is given as follows:
where is the column in the matrix D in (4), i represents the i-th labeled pixel, represents corresponding binary label. The function is a feature map that maps the data to a higher dimensional space to improve the separability between the two classes; and b are the normal vector and the bias of the hyperplane, respectively, is the upper bound for the error rate of training pixels and the lower bound of the fraction of support vectors, is the slack variable, which allows training errors, and is the distance between the hyperplane and the support vector.
Model (5) can be solved by its Lagrangian dual. Finally we obtain the hyperplane function which is then used to classify each test pixel (which are columns of D in (4)), see [58]. In the experiments, we follow [58] and use radial basis functions for where its parameter is determined by a 5-fold validation. Under the one-against-one strategy, there are such pairwise hyperplane functions where c is the number of classes. We use them to estimate the probability that a non-labeled pixel is in class k, see [44,45]. Finally, we obtain a 3D tensor where denotes the probability that the pixel at the location is in class k, and denotes the probability map for class k. In particular, if a pixel is a training pixel belonging to the l-th class, then while for all other k’s.
2.3. The Smoothing Stage
Post-processing the probability maps can further improve the performance. The Markov Random Field regularization is applied to post-process the classification results by considering spatial and edge information in [59]. In [60], the Fuzzy-Markov Random Field is adopted to smooth the classification result predicted by SVM. In our previous work [50], a smoothed total variation (STV) model is proposed to denoise the probability maps that SVC produces by ensuring local spatial connectivity in the maps. We adopt the same model here in our method.
Let . In this stage, we enforce the local connectivity by minimizing:
where and are the regularization parameters and denotes the training set so that the constraint can keep the classifications of the training pixels unchanged. The operator ∇ means the discrete gradient of the matrix when considering it as a 2-D image.
This is an - problem and can be solved by the alternating direction method of multipliers (ADMM) [61]. The minimizer is the enhanced probability map for class k. When the probability map for each class is obtained, we get a 3D tensor where each layer of the tensor is the corresponding 2D enhanced probability map, i.e., is the value of at the th location. The final classification for the pixel is then given by .
3. Experimental Results
In this section, we quantitatively compare our method with the classical SVC and three other state-of-the-art methods on six widely used datasets using three metrics. Besides, we also present heatmaps for different datasets under different methods to visually compare the classification results of classes with various shapes and sizes.
3.1. DataSets
To test the superiority of our method, six widely used publicly available hyperspectral datasets are chosen for testing. They are the Indian Pines, Salinas, Pavia Center, Kennedy Space Center (KSC), Botswana, and University of Pavia (PaviaU) datasets. They have different sizes and different numbers of spectral bands of different wavelengths, and they are commonly used these years in the study of hyperspectral images. In the following, we introduce them one by one.
The Indian Pines dataset was collected in the test site located in Northwest India by the AVIRIS sensor. It consists of 145 × 145 pixels and each pixel has 220 spectral reflectance bands with a wavelength from 0.4 to 2.5 m. After eliminating the effect of water absorption, the number of bands is finally 200. Its ground truth consists of 16 classes.
The Salinas dataset was collected over Salinas Valley in California by the AVIRIS sensor with a high spatial resolution of 3.7 m per pixel. The size is 512 × 217 pixels with 224 spectral reflectance bands. Same as the Indian Pines dataset, due to the water absorption, the number of band decreases to 204 after discarding the 108th–112th, 154th–167th, and 224th bands. There are 16 classes in the Salinas dataset.
The Pavia Center dataset and PaviaU dataset were acquired by the ROSIS sensor over Pavia in Italy with a spatial resolution of 1.3 m. The dataset sizes are 1096 × 715 × 102 and 610 × 340 × 103, respectively, where 102 and 103 represent the numbers of the spectral bands, respectively. Both datasets have 9 classes.
The KSC dataset was acquired over the Kennedy Space Center in Florida by the NASA AVIRIS sensor. It has 224 bands with wavelengths from 0.4 to 2.5 m, but after removing water absorption and low SNR bands, it has 176 bands totally. The size is 512 × 614 pixels and there are 13 classes. The sensor has a spatial resolution of 18 m.
The Botswana dataset was collected by the Hyperion sensor on NASA EO-1 satellite over Botswana with 30 m resolution. It has 145 bands after removing 97 bands because of water absorption and covers the wavelength from 0.4 to 2.5 m. The area is of size 1476 × 256, and there are 14 classes in the ground truth.
3.2. Comparison Methods and Evaluation Metrics
We compare our new method with several currently used methods: -support vector classifier (SVC) [41], multiple-feature-based adaptive sparse representation (MFASR) [33], the 2-stage method [35], and NSW-PCA-SVM [36]. We remark that, in [35,36], there are comprehensive comparisons of the last two methods with many other methods, which show the superiority of these two methods over others.
In this paper, we use Overall Accuracy (OA), Average Accuracy (AA), and kappa coefficient (kappa) [62] to evaluate the performance of these five methods quantitatively. These three metrics are all based on the confusion matrix G [63], where the element means the number of pixels that truly belong to class i are classified in class j. Thus OA represents the percentage of correctly classified pixels:
AA represents the average percentage of correctly classified pixels in each class:
and kappa represents the integrative reflections of OA and AA:
For each method, ten runs were conducted. To ensure the reliability of the experiments, the training set was randomly selected for each run and finally, the average of the results obtained from the ten runs was taken for comparison. In each figure, there is an error bar (the color bar) which represents the number of misclassification for each pixel in the image over the ten runs. As in [33,36], we assume the background pixels are given and we do not classify them. We only compare the accuracies on the non-background pixels.
All the tests were run on a computer with an Intel Core i7-9700 CPU, 32 GB RAM, and the software is MATLAB R2021b.
3.3. Classification Results
Table 1 shows the average classification results of each method for the Indian Pines dataset, which has large homogeneous regions with more regular shapes. In each experiment, 10 training pixels for each class were randomly selected and the remaining pixels were used for testing. The table shows the average accuracy over 10 runs, and we use boldface font to denote the best results among the methods. We see that our method generates the best results for all three metrics (OA, AA, and kappa) and is at least 2.65% higher than the results of all other methods. For some classes with a small number of pixels, like Alfalfa, Grass/pasture-mowed, and Oats, the results of our method achieve the highest accuracy, reaching 100%. For classes like Corn-no till and Soybeans-mill till with a higher misclassification rate under the 2-stage method, the rates are enhanced a lot in our method. This illustrates the power of the pre-processing stage in our method.

Table 1.
Average classification accuracies over 10 trials for the Indian Pines dataset with 10 random training pixels for each class. The boldface font represents the highest accuracy among the methods.
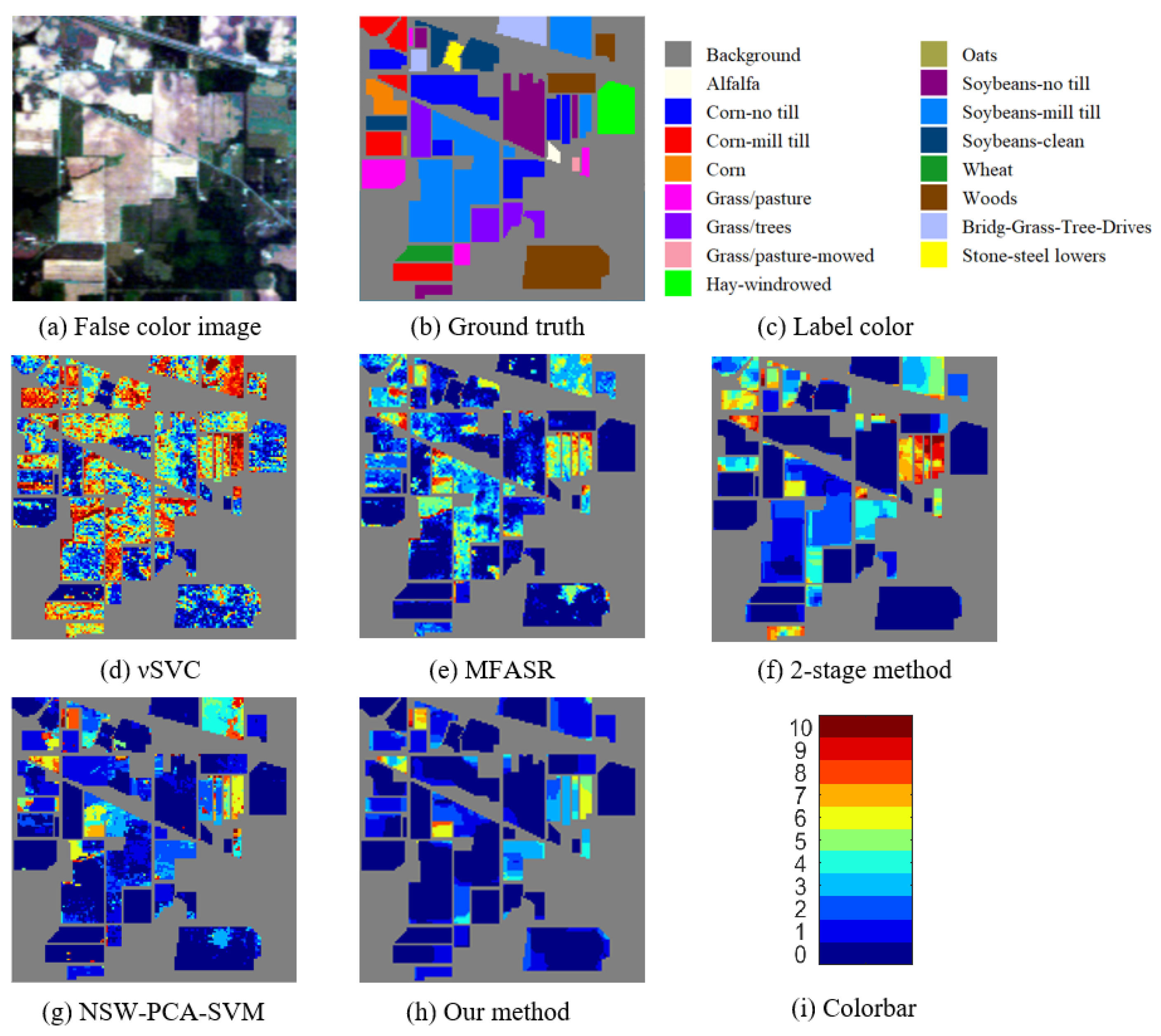
Figure 3 shows the ground-truth and error maps of misclassifications for the Indian Pines dataset. Among them, SVC, which uses only spectral information, produces the largest portion of misclassification and almost all classes have serious misclassification. The 2-stage method has poor classification results in the upper-left, upper-right, and bottom regions, and the corresponding materials of these regions are Corn-mill till, Corn-no till, Soybeans-mill till and Soybeans-no till, respectively. These classes have similar spectra, and the 2-stage method cannot distinguish them very well. MFASR method has a similar degree of misclassification as the 2-stage method. We see from Figure 3h that our method, with the pre-processing stage, produces the best result because it enhances the consistency of adjacent pixels, especially those pixels located in a large homogeneous area with various inner-class spectra. Finally, when compared with the NSW-PCA-SVM method, our method improves the result in most areas, especially for the Soybeans-mill till class. This shows that the smoothing TV step is very effective in enforcing spatial connectivity to increase the accuracy of the classification.
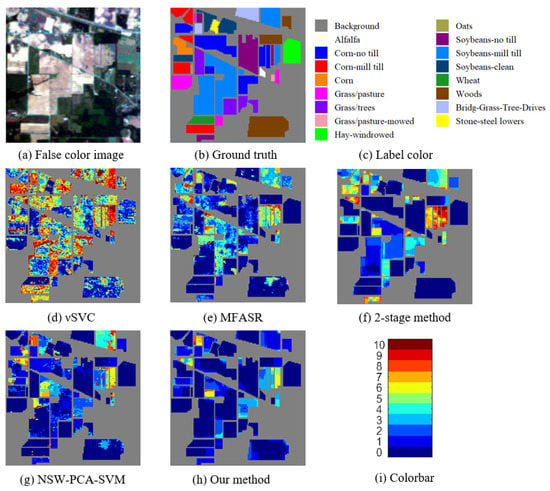
Figure 3.
Results for the Indian Pines dataset. (a) The false color image. (b,c) The ground truth and the corresponding label colors. (d–h) The misclassification counts of different methods. (i) The colorbar represents the misclassification counts.
Table 2 shows the average classification results over 10 trials on the Salinas dataset using 10 random pixels per class for training in each trial. Our method also achieves the best performance in OA, AA, and kappa when compared with the other four methods with a gain of at least 0.7% in the accuracies. For the Grapes-untrained class and Vinyard-untrained class, SVC yields less than 60% accuracy, indicating that the spectra of these two classes cannot provide enough information for discrimination. In comparison, the accuracies of our method for these two classes are enhanced a lot, nearly 40%.

Table 2.
Average classification accuracies over 10 trials for the Salinas dataset with 10 random training pixels for each class. The boldface font represents the highest accuracy among the methods.
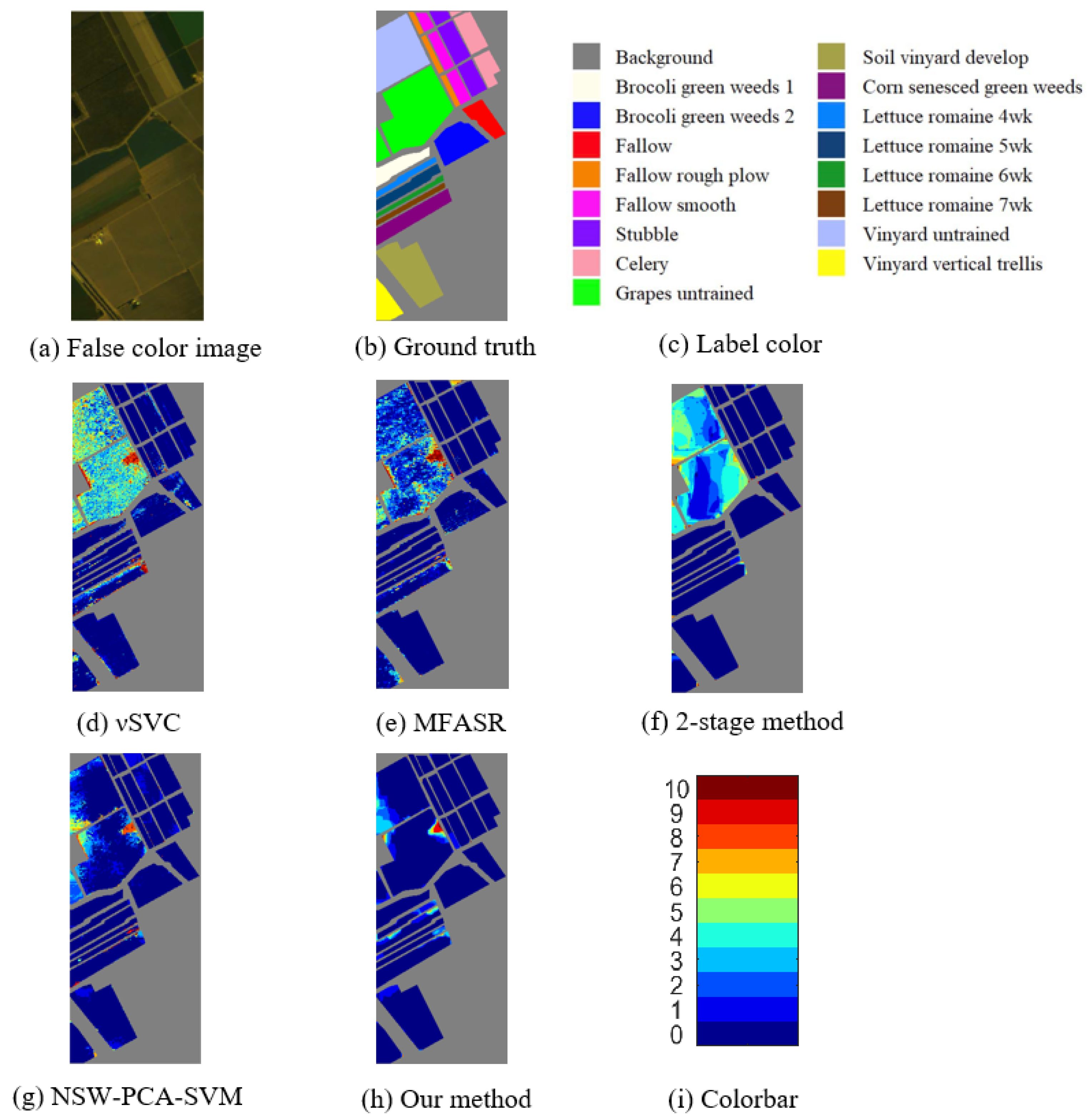
Figure 4 shows the ground-truth and error maps of misclassifications for the Salinas dataset. In Figure 4d–f, we see that the SVC, MFSAR, and the 2-stage method all have large areas of misclassification in the Salinas dataset. NSW-PCA-SVM method (Figure 4g) has a great improvement over the first three methods due to the pre-processing step, but there is still a serious misclassification in the Grapes-untrained class and Vinyard untrained class. Our method solves most of the problems by adding the denoising step to enhance local spatial homogeneity, see Figure 4h. As a whole, the results show that the pre-processing and post-processing stages have a great effect on those classes with large homogeneous regions and insufficient spectral information.
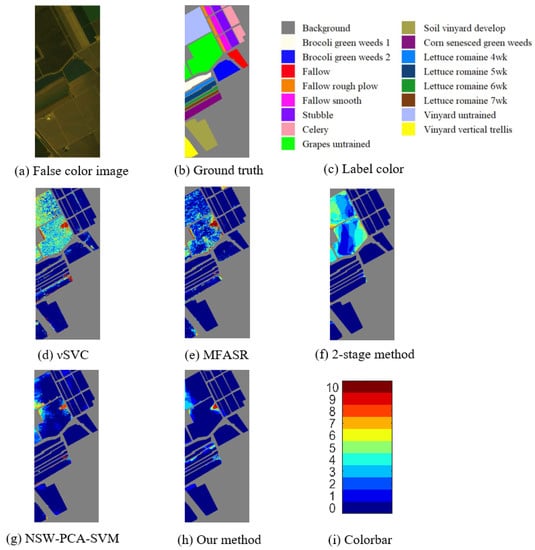
Figure 4.
Results for the Salinas dataset. (a) The false color image. (b,c) The ground truth and corresponding label colors. (d–h) The misclassification counts of different methods. (i) The colorbar represents the misclassification counts.
Table 3 shows the average classification results of the Pavia Center dataset over 10 trials with 10 random labeled pixels per class in each trial. It consists of more small regions and slender categories, see Figure 5b. Our method is also the best one in all OA, AA, and kappa coefficient. For those classes which do not have greatly ample spectral information, like the Bricks and Soil classes, our method earns the highest accuracies among these methods.

Table 3.
Average classification accuracies over 10 trials for the Pavia Center dataset with 10 random training pixels for each class. The boldface font represents the highest accuracy among the methods.
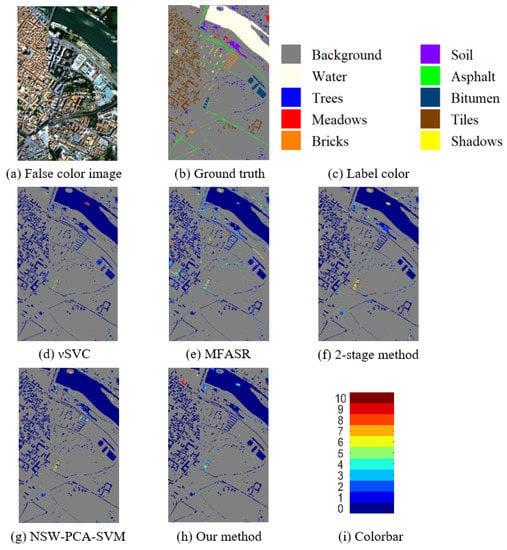
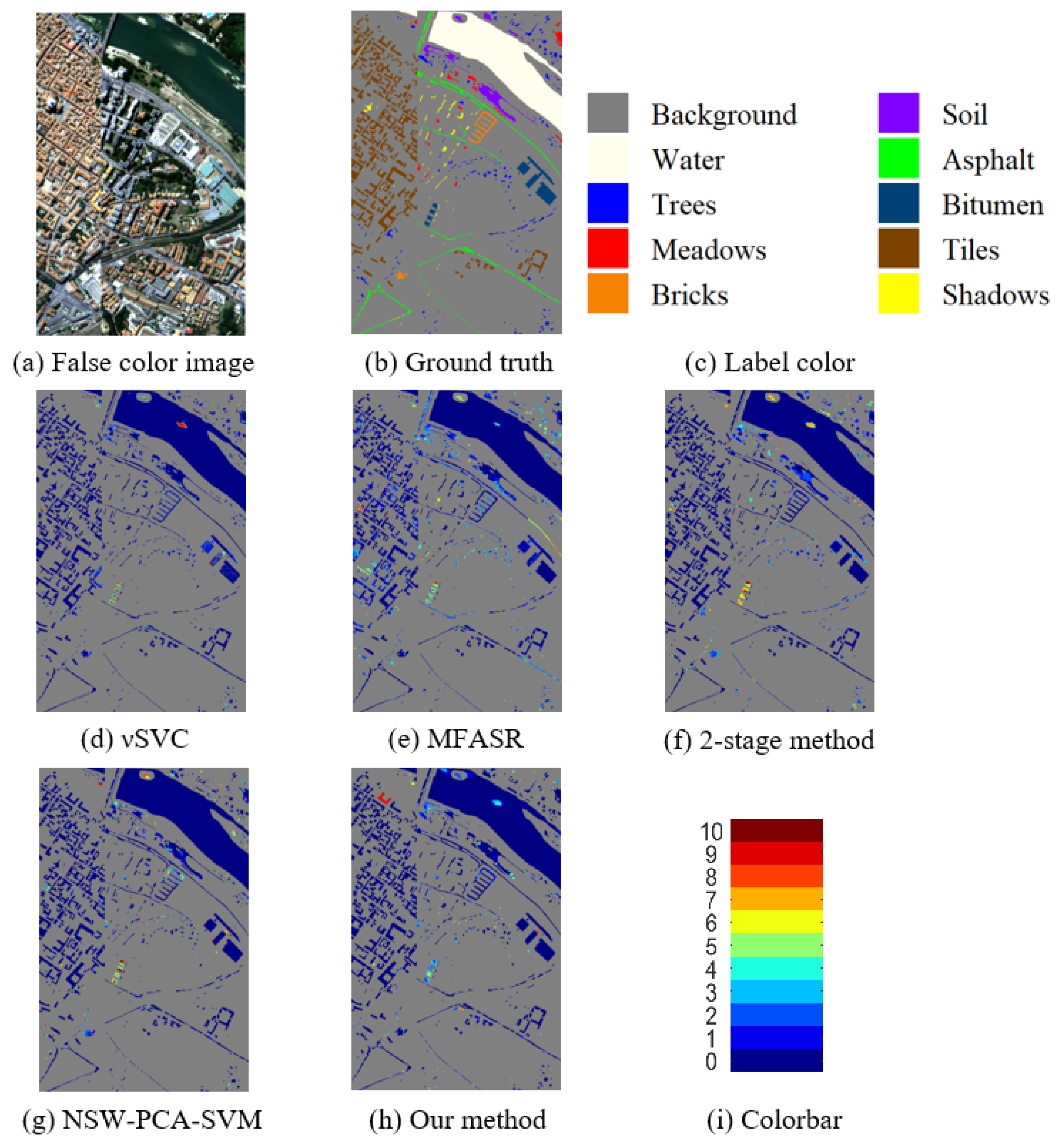
Figure 5.
Results for the Pavia Center dataset. (a) The false color image. (b,c) The ground truth and corresponding label colors. (d–h) The misclassification counts of different methods. (i) The colorbar represents the misclassification counts.
In Figure 5, which shows the misclassification map of the Pavia Center dataset, we see that SVC has distinct misclassification in the middle of the water class. Obviously, the MFASR method has a worse result in Trees class where SVC has great classification results only using spectral information. The 2-stage method and NSW-PCA-SVM method both have a higher degree of misclassification in the Bitumen class, mainly in the middle part of the image. Our method smooths the result, particularly for the water class and Bitumen class in the middle of the image, which again shows the strength of the pre-processing step and post-processing step.
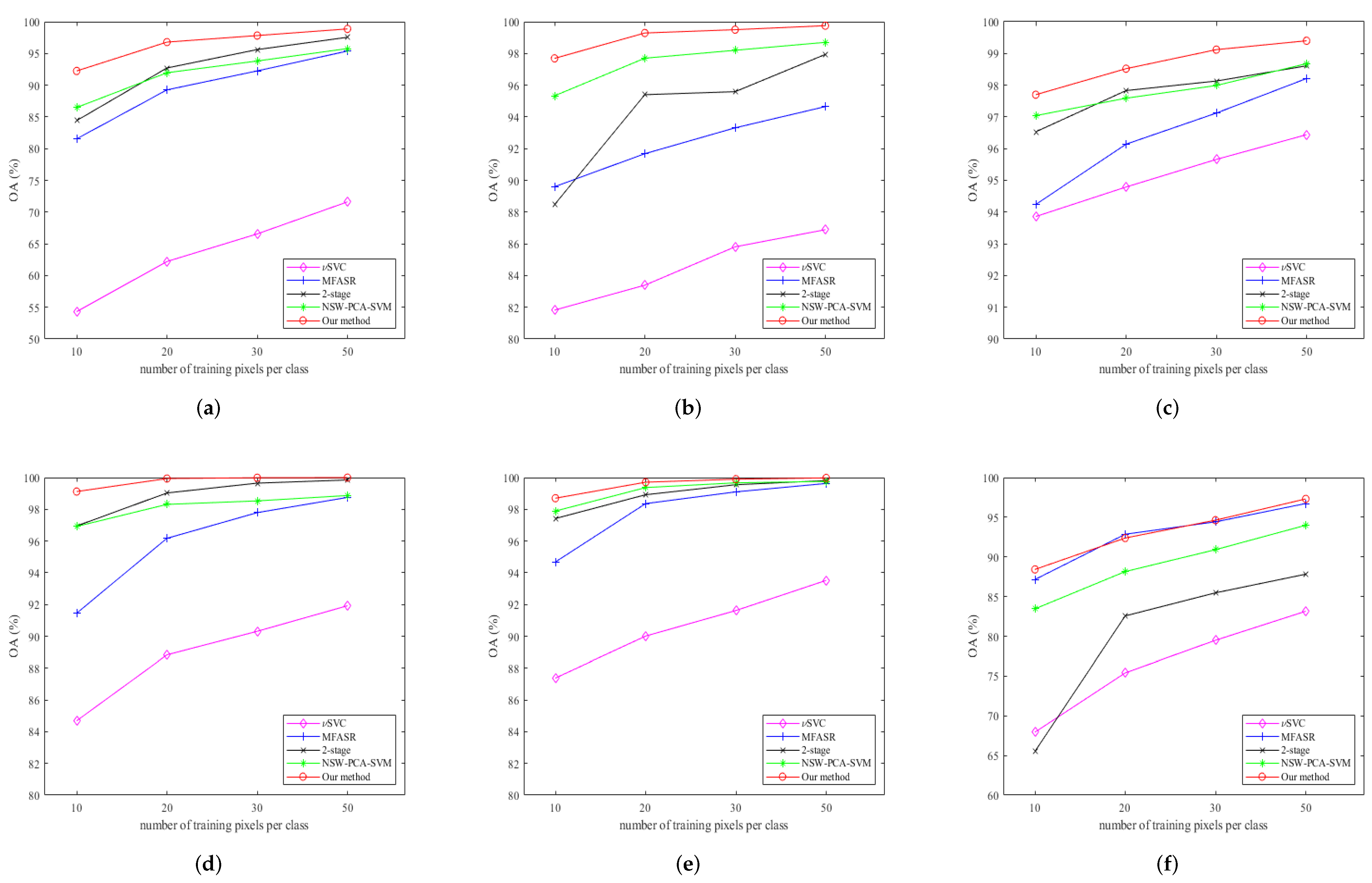
Figure 6 show the overall accuracy (OAs) of different methods on the six datasets with different numbers of training pixels. Our method achieves the best performance for all cases except for one situation, i.e., 20 pixels per class for the PaviaU dataset. Pavia Center, KSC, and Botswana datasets have more effective spectral information since SVC already reaches more than 80% accuracy. Our method is still enhanced a lot after adding steps for spatial information extraction, reaching more than 99% accuracy with the increment of the training pixels. One can see that the gain of the accuracy of our method over the other methods increases when the number of labeled pixels decreases. This shows the advantage of our method as getting labeled data is always the most difficult part of any HSI classification problem.
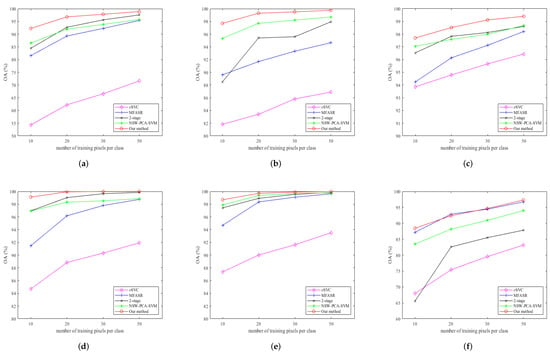
Figure 6.
OAs (y-axis) for different datasets with a different number of training pixels (x-axis). (a) OA on the Indian Pines dataset; (b) OA on the Salinas dataset; (c) OA on the Pavia Center dataset; (d) OA on the KSC dataset; (e) OA on the Botswana dataset; (f) OA on the PaviaU dataset.
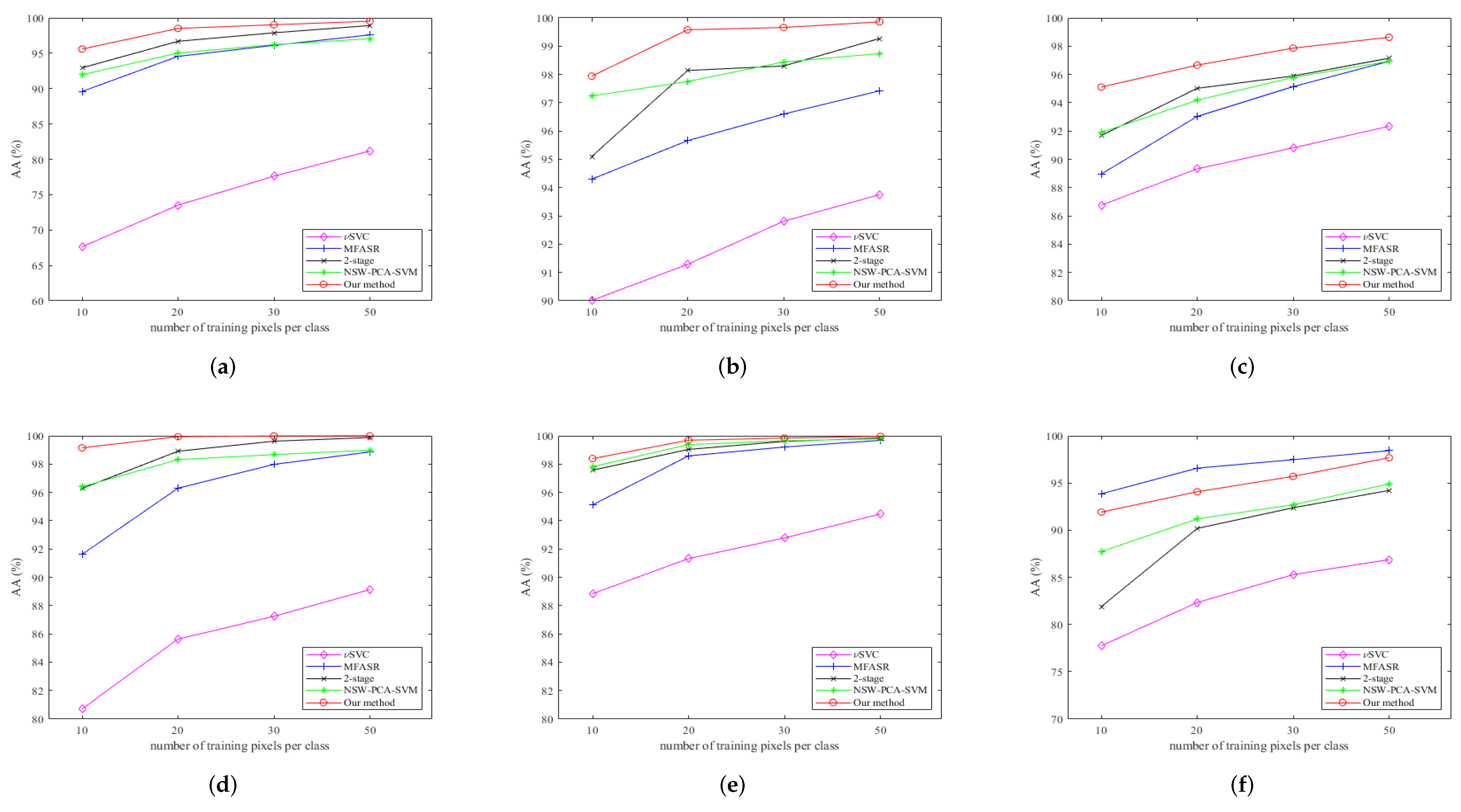
Figure 7 shows the average accuracy (AAs) of different methods on the six datasets with different numbers of training pixels. Our method performs the best on the first five datasets, no matter how many labeled pixels are used. For the Salinas, KSC, and Botswana datasets, the AAs are around 98% even in the case that 10 labeled pixels are available and attain more than 99% once there are more labeled pixels available for training. Only for the last dataset, the PaviaU dataset, see Figure 7f, our method attains the second highest accuracy, where the MFASR is the best. However, we note that MFASR generally fares only better than SVC in the other five datasets.
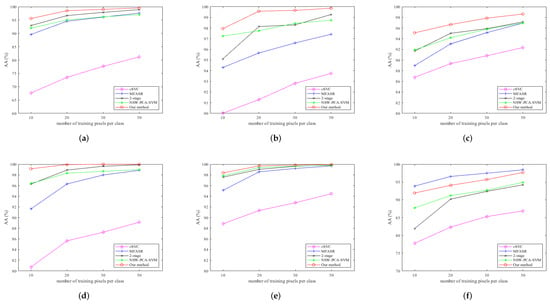
Figure 7.
AAs (y-axis) for different datasets with a different number of training pixels (x-axis). (a) AA on the Indian Pines dataset; (b) AA on the Salinas dataset; (c) AA on the Pavia Center dataset; (d) AA on the KSC dataset; (e) AA on the Botswana dataset; (f) AA on the PaviaU dataset.
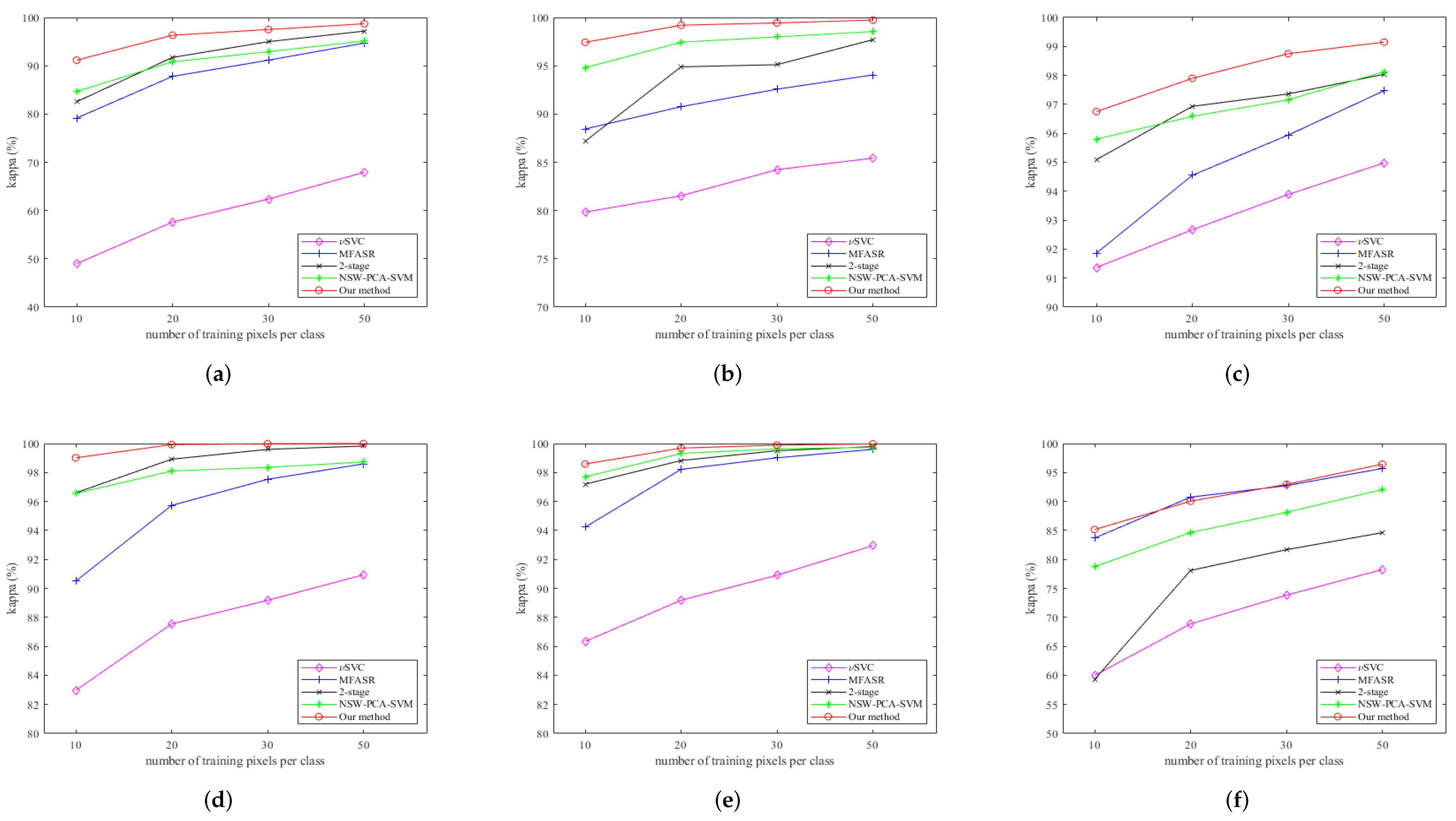
Figure 8 shows the kappas of different methods on the six datasets when different numbers of labeled pixels are used for training. Similar to the results of OAs, our method achieves the best performance for all cases except for one situation, i.e., 20 labeled pixels per class for the PaviaU dataset.
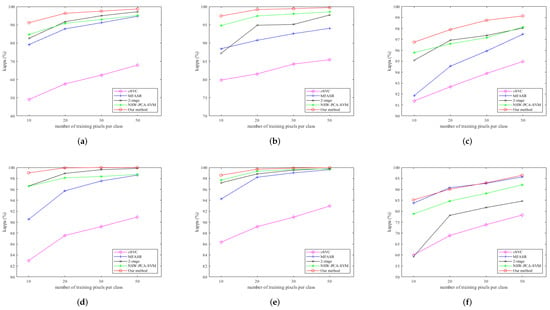
Figure 8.
Kappas (y-axis) for different datasets with a different number of training pixels (x-axis). (a) kappa on the Indian Pines dataset; (b) kappa on the Salinas dataset; (c) kappa on the Pavia Center dataset; (d) kappa on the KSC dataset; (e) kappa on the Botswana dataset; (f) kappa on the PaviaU dataset.
To sum up, these figures clearly show the advantages of our method over the other four methods on six datasets in three different error metrics (OA, AA, and kappa), especially for a smaller training set (10 pixels per class). Comparing the results of all the experiments, we are only second to MFASR in the PaviaU dataset. However, MFASR fares the worst for all the other five datasets except when compared to SVC. The figures also show that the gain of our method over the other methods increases as the number of training pixels decrease, which attest to the importance of our method.
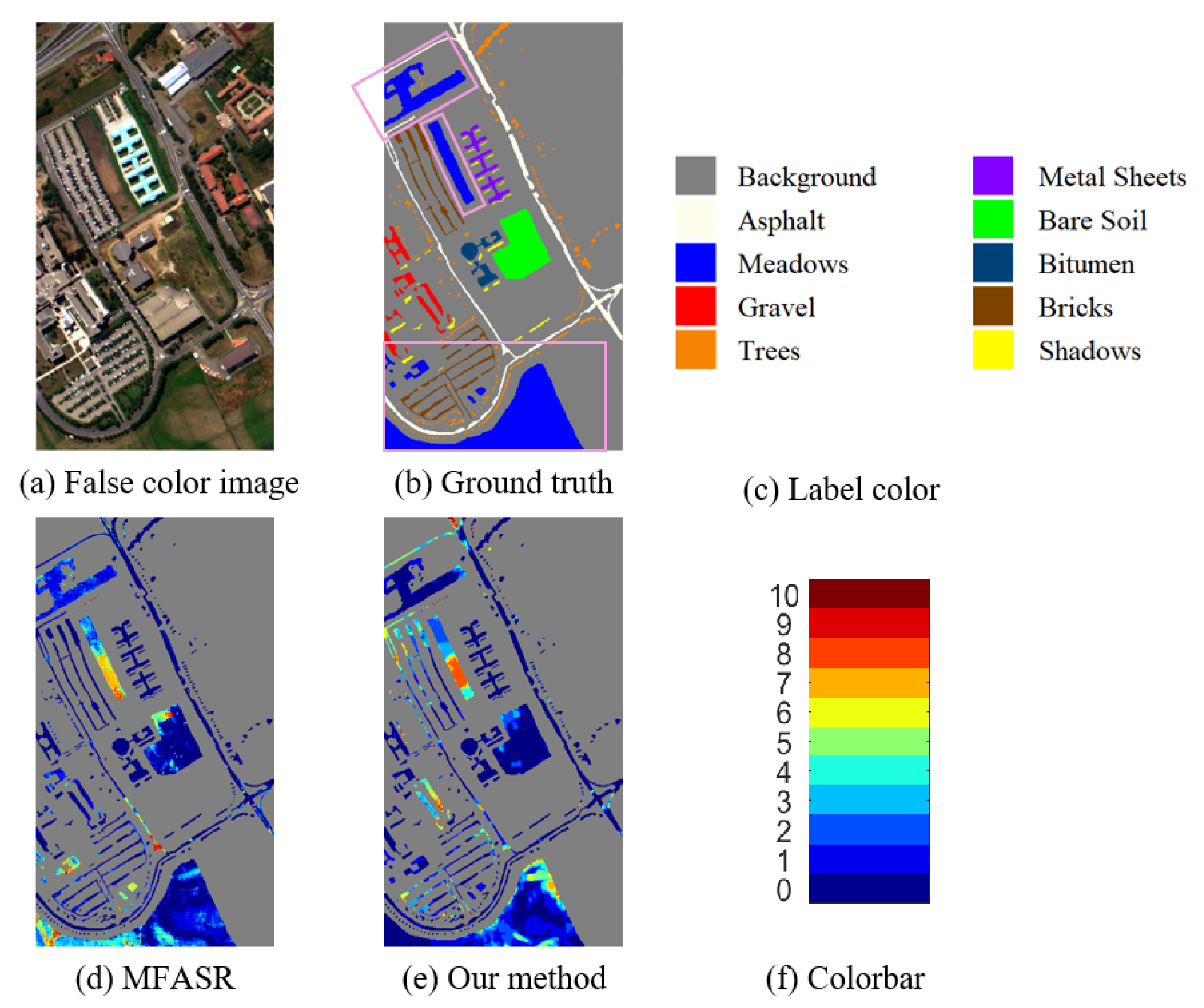
One may wonder what is so special about the PaviaU dataset. According to Figure 9b, in the PaviaU dataset, the distribution of the pixels in the same category is relatively scattered, especially for the classes of Asphalt, Meadows, Gravel, Bricks, and Shadows. In addition, the shapes of many regions are slender and long where MFASR performs better, see Figure 9d. Our method has a poor classification result in Gravel class and Bricks class while MFASR performs better, which leads to a lower AA.
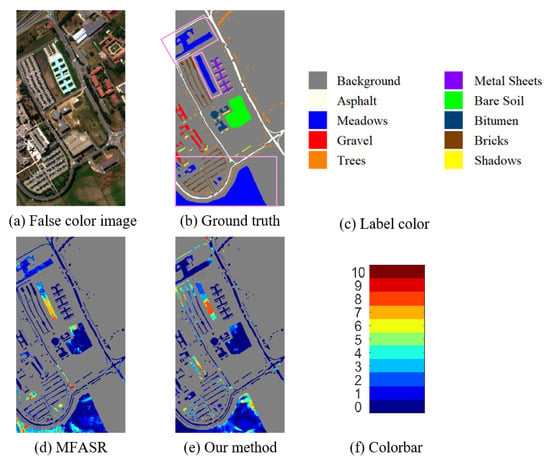
Figure 9.
Results for the PaviaU dataset. (a) The false color image. (b,c) The ground truth and the corresponding label colors. (d,e) The misclassification counts of MFASR and our method. (f) The colorbar represents the misclassification counts.
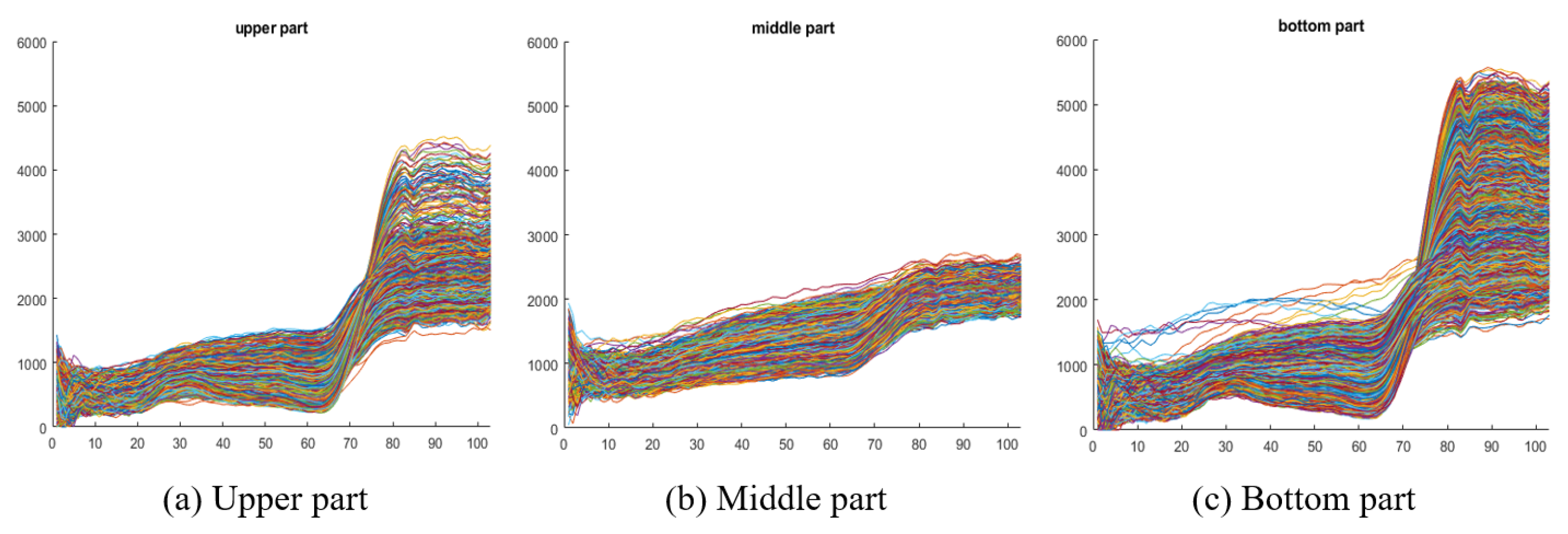
From Figure 9, we notice that no method has a good classification result for the Meadows class in the middle part of the image. Based on the ground truth in Figure 9b, Meadows are in three different locations in the image: upper, middle, and lower parts as marked by the pink boxes in the figure. Their corresponding spectra are shown in Figure 10 which shows that the spectra of the Meadow pixels in the middle part of the image vary greatly from the Meadow pixels in the other parts of the image, and this results in difficulty in correctly classifying them.
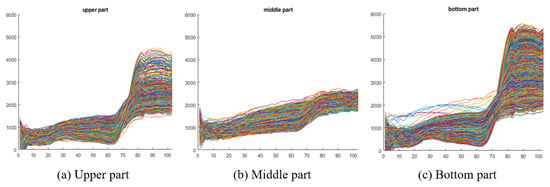
Figure 10.
The spectra of the Meadows class in the PaviaU dataset: (a) In the upper part of the image. (b) In the middle part of the image. (c) In the bottom part of the image. They show that the spectra of the Meadows class in the middle part of the image vary significantly from the spectra of the Meadows class in other parts of the image.
4. Discussion
In this section, we present a further explanation of our method and results, including the effect of the parameters on our results, the importance of the smoothing stage, and the execution time for all methods. Finally, we conclude the advantages and limitations of each method.
4.1. Parameters for Each Method
Table 4 shows the number of parameters for all methods mentioned in this paper. In the experiments, the parameters are chosen as follows. For SVC method and the first stage of the 2-stage method (which is also a SVC method), there are two parameters and they are obtained by a 5-fold cross validation [64]. For the 2-stage method, the remaining three parameters in the second stage are chosen by trial-and-error such that it gives the highest classification result. For the MFASR method, the ten optimal parameters are chosen by trial-and-error as mentioned in [33]. For the NSW-PCA-SVM method, the optimal window size and the optimal number of principal components are chosen by trial-and-error, while the parameters of SVM are chosen by a 5-fold cross-validation.

Table 4.
The number of parameters in different methods.
For our method, there are 7 parameters in total. The window size and the number of principal components d in the pre-processing stage are chosen by trial-and-error. The two parameters and in SVC (classification stage) are obtained automatically by a 5-fold validation. In the post-processing stage (see (6)), the regularization parameters and are fixed as 0.2 and 4, respectively, as the solution is robust against these parameters. When (6) is solved by ADMM, there is a parameter governing the convergence rate and we set it always to 5. Thus, in essence, there are only two parameters ( and d) in the pre-processing stage to be tuned by hand. Table 5 shows the values of two parameters for the different datasets with 10 training pixels per class.

Table 5.
The values of the parameters in our method for different datasets with 10 training pixels.
4.2. The Influence of the Two Parameters in the Pre-Processing Stage
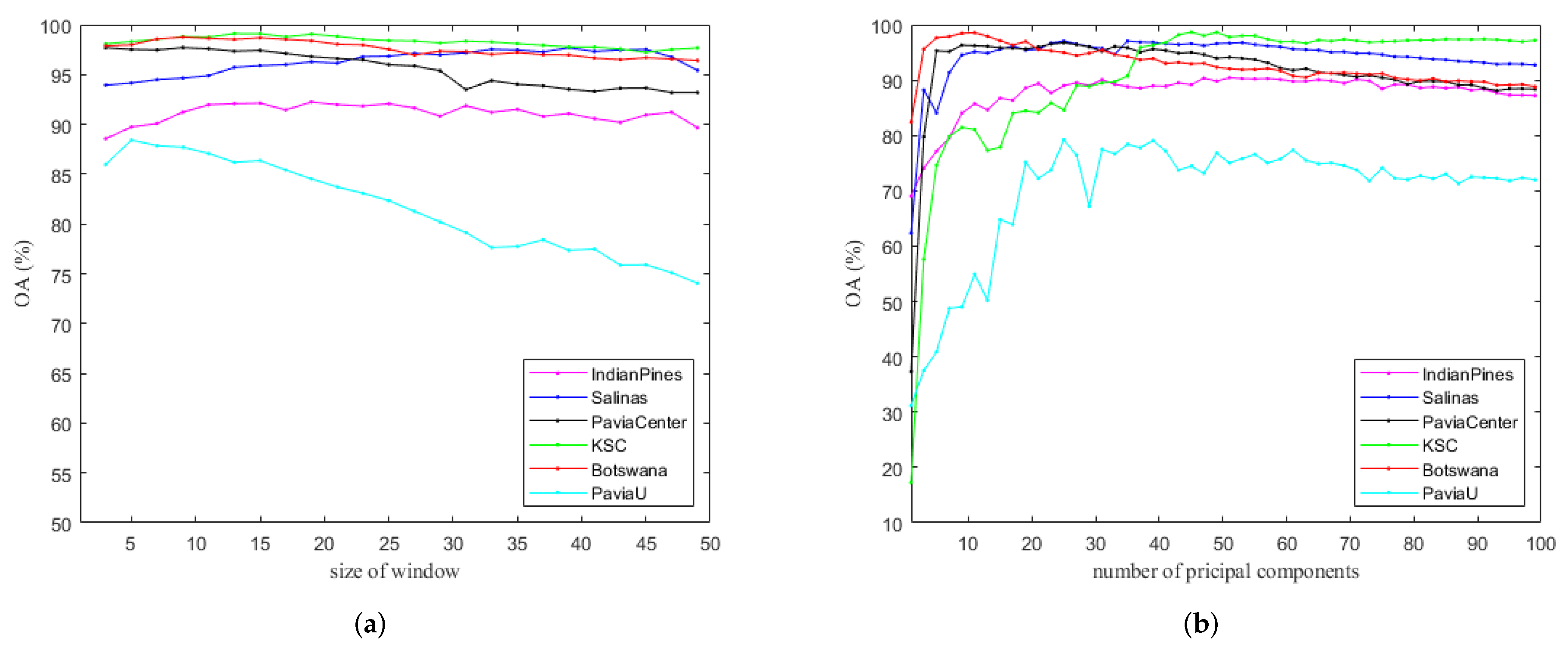
For our method, there are two parameters and d in the pre-processing stage, which can influence the classification result and the subsequent post-processing stage. The parameters introduced in Section 2.1, represent the size of the window and the number of principal components, respectively. In this section, we discuss how to choose them in practice.
Figure 11a shows the OAs of our method against different on the six datasets. Except for the PaviaU dataset, the curves in the figure are very flat, implying the accuracy is robust against . One can generally choose to get a good OA. According to Figure 9b, in the PaviaU dataset, the distribution of the pixels in the same category is relatively scattered, especially for the classes of Asphalt, Meadows, Gravel, Bricks, and Shadows. In addition, the shapes of many regions are slender and long, so a smaller window size fits the data better.
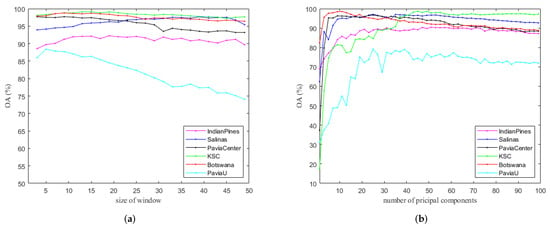
Figure 11.
Influence of parameters in the pre-processing stage on six datasets. (a) OA versus window size ; (b) OA versus number of principal components d.
To test the effect of d on the classification results, we fix for each dataset as the optimal value shown in Table 5. Figure 11b gives the OAs of our method versus d on the six datasets. It shows that OA increases sharply at first and then more or less flattens out after . Therefore, the accuracy is robust for large d, and in practice, one can choose d around 50 to ensure that the OA will be reasonably good.
4.3. The Quality of Post-Processing Step
The post-processing smoothed-TV stage is to smooth and denoise the probability tensor obtained by SVC. Thus we can use the peak signal-to-noise ratio (PSNR) to measure the quality of this stage:
where and are the k-th spectral bands of the true probability tensor and the predicted probability tensor , and MSE denotes the mean squares error. In Table 6, and represent the average PSNR value over c bands of and in 10 trials. A higher PSNR value means the probability tensor is closer to the true probability tensor. The gain is the difference between and . The gains clearly indicate the superb performance of the post-processing stage.

Table 6.
Quantitative comparisons of the probability tensors before and after the denoising stage in terms of the PSNR (in dB) value on the six datasets in ten trials.
4.4. Computation Times for Each Method
We test the computation times for all datasets with different methods, which only represent the running time of different algorithms and do not include the time needed to find the optimal parameters. All these tests were run on a computer with an Intel Core i7-9700 CPU, 32 GB RAM and the software is MATLAB R2021b, without applying parallelism.
Table 7 shows the computation time of six datasets in the case of 10 training pixels for each class. SVC requires the least amount of time when compared with the other four methods since it does not need to pre-process or post-process the data. The 2-stage method needs a little more extra time compared with SVC because of the denoising step. However, it has much higher accuracy than that of SVC, see Figure 6. MFASR needs a longer time, which is because of the inner product between feature dictionaries and feature matrices.

Table 7.
Comparison of computation times (in seconds) for 10 training pixels.
Relatively speaking, the most time-consuming part of the NSW-PCA-SVM method and our method is the pre-processing (NSW) step, where we need to calculate the correlation coefficients of pixels. Therefore, for the same window size , our method needs just a little more time than NSW-PCA-SVM because of the additional denoising stage. In general, the larger the window size selected, the more variance to be kept and the more pixels need to be reconstructed, and therefore the more time these two methods will take. For example, in the Salinas dataset, there are more large homogeneous areas, see Figure 4b; thus, a large window size is needed to achieve higher accuracy, which results in a much longer time for calculating the correlation coefficients in both methods. In Table 7, for those cases where our method requires less running time compared with NSW-PCA-SVM, it is because our method requires a smaller window to achieve the best accuracy. Regardless of time, the accuracy of our method is enhanced a lot once we add the pre-processing and post-processing stages, see Figure 6, Figure 7 and Figure 8.
We emphasize that although our method is not the fastest (the fastest is SVC), the accuracy of our method, especially for very small training datasets, can more than offset this drawback as the most time-consuming task in HSI classification is usually the labeling of the training pixels.
Further, it is worth mentioning that the reconstruction and classification stages in our method can be done in parallel to greatly reduce the running time. The NSW algorithm is to reconstruct pixels in their square neighborhoods; thus the reconstruction process of each target pixel is independent and can be done in parallel. In addition, in SVC, since we use the one-against-one strategy, the binary classifiers can be done in parallel too.
4.5. Summary of Each Method
In this subsection, we summarize the advantages and limitations of all five methods that were compared in this paper, see Table 8. In summary, the SVC method only considers the spectral information in HSI and thus produces the lowest accuracy. After adding the denoising second stage, the 2-stage method improves the result quite a lot and only a short time is required for the additional denoising stage. However, as the denoising process completely depends on the probability tensor, it can be greatly influenced by the misclassifications caused by the classification stage. MFASR needs more time to run and performs only better than SVC in most cases though it has relatively better results for PaviaU dataset. NSW-PCA-SVM and our method needs more time to obtain the results but generate better results compared with other methods. What’s more, the result of our method is the best and it is robust against the parameters in the method.

Table 8.
The advantages and limitations of five methods with a small set of training pixels available.
5. Conclusions
In this paper, we propose a new method that fully uses spatial and spectral information. Before classification, NSW and PCA are used to extract spatial information from the HSI and reconstruct the data. They enhance the consistency of the neighboring pixels so that we only need a smaller training set. After that, SVC is used to estimate the pixel-wise probability map of each class. Finally, a smoothed total variation model, which enhances spatial homogeneity in the probability tensor, is applied to classify the HSI into different classes. Compared with the other methods, our new method achieves the best overall accuracy, average accuracy, and kappa on six datasets except only for the PaviaU dataset, where we achieve the second best in some cases. The gain in accuracy of our method over the other methods increases when the number of training pixels available decreases. For many applications that need to use the classification results for research, analysis, and assessment, our method has obvious advantages and achieves better results with very limited labeled pixels. Our method is therefore of great practical significance since expert annotations are often expensive and difficult to collect.
The limitation of our method is that the pre-processing step extracts spatial information using square windows, which is not suitable for small-size datasets with long and thin regions, like the PaviaU dataset. In the future, we will try to improve and develop new methods for adaptively selecting neighborhood pixels, which will be more useful for those datasets that contain more irregular regions like the PaviaU dataset. In addition, different spatial filters will also be considered to extract spatial information and combine them with our method here.
Author Contributions
Conceptualization, R.H.C.; methodology, R.H.C. and R.L.; software, R.H.C. and R.L.; validation, R.H.C. and R.L.; formal analysis, R.L.; investigation, R.H.C. and R.L.; resources, R.H.C.; data curation, R.H.C. and R.L.; writing—original draft preparation, R.L.; writing—review and editing, R.L. and R.H.C.; visualization, R.L.; supervision, R.H.C.; project administration, R.H.C.; funding acquisition, R.H.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded in part by HKRGC Grants No. CUHK14301718, CityU11301120, C1013-21GF, CityU Grant 9380101.
Data Availability Statement
Publicly available datasets were analyzed in this study. This data can be found here: http://www.ehu.eus/ccwintco/index.php/Hyperspectral_Remote_Sensing_Scenes, accessed on 20 May 2021.
Acknowledgments
We would like to thank the authors of the paper [33,36] for providing the experimental codes, which help the part of method comparison.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Eismann, M.T. Hyperspectral Remote Sensing, 1st ed.; SPIE Press: Bellingham, WA, USA, 2012; pp. 1–33. [Google Scholar]
- Morchhale, S.; Pauca, V.P.; Plemmons, R.J.; Torgersen, T.C. Classification of Pixel-Level Fused Hyperspectral and Lidar Data Using Deep Convolutional Neural Networks. In Proceedings of the 2016 8th Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), Los Angeles, CA, USA, 21–24 August 2016; pp. 1–5. [Google Scholar]
- Liu, S.; Marinelli, D.; Bruzzone, L.; Bovolo, F. A Review of Change Detection in Multitemporal Hyperspectral Images: Current Techniques, Applications, and Challenges. IEEE Geosci. Remote Sens. Mag. 2019, 7, 140–158. [Google Scholar] [CrossRef]
- Khan, M.J.; Khan, H.S.; Yousaf, A.; Khurshid, K.; Abbas, A. Modern Trends in Hyperspectral Image Analysis: A Review. IEEE Access 2018, 6, 14118–14129. [Google Scholar] [CrossRef]
- Peyghambari, S.; Zhang, Y. Hyperspectral Remote Sensing in Lithological Mapping, Mineral Exploration, and Environmental Geology: An Updated Review. J. Appl. Remote Sens. 2021, 15, 1–25. [Google Scholar] [CrossRef]
- Polk, S.L.; Cui, K.; Plemmons, R.J.; Murphy, J.M. Diffusion and Volume Maximization-Based Clustering of Highly Mixed Hyperspectral Images. arXiv 2022, arXiv:2203.09992. [Google Scholar]
- Polk, S.L.; Cui, K.; Plemmons, R.J.; Murphy, J.M. Active Diffusion and VCA-Assisted Image Segmentation of Hyperspectral Images. arXiv 2022, arXiv:2204.06298. [Google Scholar]
- Camalan, S.; Cui, K.; Pauca, V.P.; Alqahtani, S.; Silman, M.; Chan, R.H.; Plemmons, R.J.; Dethier, E.N.; Fernandez, L.E.; Lutz, D. Change Detection of Amazonian Alluvial Gold Mining Using Deep Learning and Sentinel-2 Imagery. Remote Sens. 2022, 14, 1746. [Google Scholar] [CrossRef]
- Cui, K.; Plemmons, R.J. Unsupervised Classification of AVIRIS-NG Hyperspectral Images. In Proceedings of the 2021 11th Workshop on Hyperspectral Imaging and Signal Processing: Evolution in Remote Sensing (WHISPERS), Amsterdam, The Netherlands, 24–26 March 2021; pp. 1–5. [Google Scholar]
- Im, J.; Jensen, J.R.; Jensen, R.R.; Gladden, J.; Waugh, J.; Serrato, M. Vegetation Cover Analysis of Hazardous Waste Sites in Utah and Arizona Using Hyperspectral Remote Sensing. Remote Sens. 2012, 4, 327–353. [Google Scholar] [CrossRef]
- Hörig, B.; Kühn, F.; Oschütz, F.; Lehmann, F. HyMap Hyperspectral Remote Sensing to Detect Hydrocarbons. Int. J. Remote Sens. 2001, 22, 1413–1422. [Google Scholar] [CrossRef]
- Qin, Q.; Zhang, Z.; Chen, L.; Wang, N.; Zhang, C. Oil and Gas Reservoir Exploration Based on Hyperspectral Remote Sensing and Super-Low-Frequency Electromagnetic Detection. J. Appl. Remote Sens. 2016, 10, 1–18. [Google Scholar] [CrossRef]
- Jin, X.; Jie, L.; Wang, S.; Qi, H.J.; Li, S.W. Classifying Wheat Hyperspectral Pixels of Healthy Heads and Fusarium Head Blight Disease Using a Deep Neural Network in the Wild Field. Remote Sens. 2018, 10, 395. [Google Scholar] [CrossRef]
- Neupane, K.; Baysal-Gurel, F. Automatic Identification and Monitoring of Plant Diseases Using Unmanned Aerial Vehicles: A Review. Remote Sens. 2021, 13, 3841. [Google Scholar] [CrossRef]
- Chan, A.H.Y.; Barnes, C.; Swinfield, T.; Coomes, D.A. Monitoring Ash Dieback (Hymenoscyphus Fraxineus) in British Forests Using Hyperspectral Remote Sensing. Remote Sens. Ecol. Conserv. 2021, 7, 306–320. [Google Scholar] [CrossRef]
- Polk, S.L.; Chan, A.H.Y.; Cui, K.; Plemmons, R.J.; Coomes, D.; Murphy, J.M. Unsupervised Detection of Ash Dieback Disease (Hymenoscyphus Fraxineus) Using Diffusion-Based Hyperspectral Image Clustering. arXiv 2022, arXiv:2204.09041. [Google Scholar]
- Lv, W.; Wang, X. Overview of Hyperspectral Image Classification. J. Sens. 2020, 2020, 4817234. [Google Scholar] [CrossRef]
- Melgani, F.; Bruzzone, L. Classification of Hyperspectral Remote Sensing Images with Support Vector Machines. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1778–1790. [Google Scholar] [CrossRef]
- Kuo, B.; Yang, J.; Sheu, T.; Yang, S. Kernel-Based KNN and Gaussian Classifiers for Hyperspectral Image Classification. In Proceedings of the IGARSS 2008—2008 IEEE International Geoscience and Remote Sensing Symposium, Boston, MA, USA, 7–11 July 2008; pp. II-1006–II-1008. [Google Scholar]
- Li, J.; Bioucas-Dias, J.M.; Plaza, A. Semisupervised Hyperspectral Image Classification Using Soft Sparse Multinomial Logistic Regression. IEEE Geosci. Remote Sens. Lett. 2013, 10, 318–322. [Google Scholar]
- Ham, J.; Chen, Y.; Crawford, M.M.; Ghosh, J. Investigation of the Random Forest Framework for Classification of Hyperspectral Data. IEEE Trans. Geosci. Remote Sens. 2005, 43, 492–501. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Bo, C.; Lu, H.; Wang, D. Weighted Generalized Nearest Neighbor for Hyperspectral Image Classification. IEEE Access 2017, 5, 1496–1509. [Google Scholar] [CrossRef]
- Liu, J.; Wu, Z.; Wei, Z.; Xiao, L.; Sun, L. Spatial-Spectral Kernel Sparse Representation for Hyperspectral Image Classification. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2013, 6, 2462–2471. [Google Scholar] [CrossRef]
- Cao, F.; Yang, Z.; Ren, J.; Ling, W.-K.; Zhao, H.; Marshall, S. Extreme Sparse Multinomial Logistic Regression: A Fast and Robust Framework for Hyperspectral Image Classification. Remote Sens. 2017, 9, 1255. [Google Scholar] [CrossRef]
- Gao, F.; Wang, Q.; Dong, J.; Xu, Q. Spectral and Spatial Classification of Hyperspectral Images Based on Random Multi-Graphs. Remote Sens. 2018, 10, 1271. [Google Scholar] [CrossRef]
- Zhang, Q.; Sun, J.; Zhong, G.; Dong, J. Random Multi-Graphs: A Semi-supervised Learning Framework for Classification of High Dimensional Data. Image Vis. Comput. 2017, 60, 30–37. [Google Scholar] [CrossRef]
- Shu, L.; McIsaac, K.; Osinski, G.R. Learning Spatial-Spectral Features for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5138–5147. [Google Scholar] [CrossRef]
- Camps-Valls, G.; Gomez-Chova, L.; Muñoz-Marí, J.; Vila-Francés, J.; Calpe-Maravilla, J. Composite Kernels for Hyperspectral Image Classification. IEEE Geosci. Remote Sens. Lett. 2006, 3, 93–97. [Google Scholar] [CrossRef]
- Rajadell, O.; Garcia-Sevilla, P.; Pla, F. Spectral-Spatial Pixel Characterization Using Gabor Filters for Hyperspectral Image Classification. IEEE Geosci. Remote Sens. Lett. 2013, 10, 860–864. [Google Scholar] [CrossRef]
- Bau, T.C.; Sarkar, S.; Healey, G. Hyperspectral Region Classification Using a Three-Dimensional Gabor Filterbank. IEEE Trans. Geosci. Remote Sens. 2010, 48, 3457–3464. [Google Scholar] [CrossRef]
- Fauvel, M.; Tarabalka, Y.; Benediktsson, J.A.; Chanussot, J.; Tilton, J.C. Advances in Spectral-Spatial Classification of Hyperspectral Images. Proc. IEEE 2013, 101, 652–675. [Google Scholar] [CrossRef]
- Fang, L.; Wang, C.; Li, S.; Benediktsson, J.A. Hyperspectral Image Classification via Multiple-Feature-Based Adaptive Sparse Representation. IEEE Trans. Instrum. Meas. 2017, 66, 1646–1657. [Google Scholar] [CrossRef]
- Gan, L.; Xia, J.; Du, P.; Chanussot, J. Multiple Feature Kernel Sparse Representation Classifier for Hyperspectral Imagery. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5343–5356. [Google Scholar] [CrossRef]
- Chan, R.H.; Kan, K.K.; Nikolova, M.; Plemmons, R.J. A Two-Stage Method for Spectral–Spatial Classification of Hyperspectral Images. J. Math. Imaging Vis. 2020, 62, 790–807. [Google Scholar] [CrossRef]
- Ren, J.; Wang, R.; Liu, G.; Wang, Y.; Wu, W. An SVM-Based Nested Sliding Window Approach for Spectral-Spatial Classification of Hyperspectral Images. Remote Sens. 2021, 13, 114. [Google Scholar] [CrossRef]
- Yu, S.; Jia, S.; Xu, C. Convolutional Neural Networks for Hyperspectral Image Classification. Neurocomputing 2017, 219, 88–98. [Google Scholar] [CrossRef]
- Gao, Q.; Lim, S.; Jia, X. Hyperspectral Image Classification Using Convolutional Neural Networks and Multiple Feature Learning. Remote Sens. 2018, 10, 299. [Google Scholar] [CrossRef]
- Zhang, M.; Li, W.; Du, Q. Diverse Region-Based CNN for Hyperspectral Image Classification. IEEE Trans. Image Process. 2018, 27, 2623–2634. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.; Ye, Y.; Li, X.; Lau, R.Y.K.; Zhang, X.; Huang, X. Hyperspectral Image Classification With Deep Learning Models. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5408–5423. [Google Scholar] [CrossRef]
- Schölkopf, B.; Smola, A.J.; Williamson, R.C.; Bartlett, P.L. New Support Vector Algorithms. Neural Comput. 2000, 12, 1207–1245. [Google Scholar] [CrossRef]
- Luo, G.; Chen, G.; Tian, L.; Qin, K.; Qian, S. Minimum Noise Fraction versus Principal Component Analysis as a Preprocessing Step for Hyperspectral Imagery Denoising. Can. J. Remote Sens. 2016, 42, 106–116. [Google Scholar] [CrossRef]
- Hsu, C.-W.; Lin, C.-J. A Comparison of Methods for Multiclass Support Vector Machines. IEEE Trans. Neural Netw. 2002, 13, 415–425. [Google Scholar]
- Lin, H.-T.; Lin, C.-J.; Weng, R.C. A Note on Platt’s Probabilistic Outputs for Support Vector Machines. Mach. Learn. 2007, 68, 267–276. [Google Scholar] [CrossRef]
- Wu, T.-F.; Lin, C.-J.; Weng, R.C. Probability Estimates for Multi-Class Classification by Pairwise Coupling. J. Mach. Learn. Res. 2004, 5, 975–1005. [Google Scholar]
- Mumford, D.; Shah, J. Optimal Approximations by Piecewise Smooth Functions and Associated Variational Problems. Commun. Pure Appl. Math. 1989, 42, 577–685. [Google Scholar] [CrossRef]
- Fu, W.; Li, S.; Fang, L.; Kang, X.; Benediktsson, J.A. Hyperspectral Image Classification Via Shape-Adaptive Joint Sparse Representation. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2016, 9, 556–567. [Google Scholar] [CrossRef]
- Katkovnik, V.; Egiazarian, K.; Astola, J. Local Approximation Techniques in Signal and Image Processing, 1st ed.; SPIE Press: Bellingham, WA, USA, 2006; pp. 139–193. [Google Scholar]
- Foi, A.; Katkovnik, V.; Egiazarian, K. Pointwise shape-adaptive DCT for high-quality denoising and deblocking of grayscale and color images. IEEE Trans. Image Process 2007, 16, 1395–1411. [Google Scholar] [CrossRef]
- Li, R.; Cui, K.; Chan, R.H.; Plemmons, R.J. Classification of Hyperspectral Images Using SVM with Shape-adaptive Reconstruction and Smoothed Total Variation. arXiv 2022, arXiv:2203.15619. [Google Scholar]
- Bazine, R.; Wu, H.; Boukhechba, K. Spatial Filtering in DCT Domain-Based Frameworks for Hyperspectral Imagery Classification. Remote Sens. 2019, 11, 1405. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning, 1st ed.; MIT Press: Cambridge, MA, USA, 2016; pp. 492–502. [Google Scholar]
- Pontil, M.; Verri, A. Support Vector Machines for 3d Object Recognition. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 6, 637–646. [Google Scholar] [CrossRef]
- El-Naqa, I.; Yang, Y.; Wernick, M.N.; Galatsanos, N.P.; Nishikawa, R.M. A Support Vector Machine Approach for Detection of Microcalcifications. IEEE Trans. Med. Imaging 2002, 21, 1552–1563. [Google Scholar] [CrossRef]
- Osuna, E.; Freund, R.; Girosit, F.A. Training Support Vector Machines: An Application to Face Detection. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Juan, PR, USA, 17–19 June 1997; pp. 130–136. [Google Scholar]
- Tay, F.E.H.; Cao, L. Application of Support Vector Machines in Financial Time Series Forecasting. Omega 2001, 29, 309–317. [Google Scholar] [CrossRef]
- Kim, K.-J. Financial Time Series Forecasting Using Support Vector Machines. Neurocomputing 2003, 55, 307–319. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-Vector Networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Tarabalka, Y.; Fauvel, M.; Chanussot, J.; Benediktsson, J.A. SVM- and MRF-Based Method for Accurate Classification of Hyperspectral Images. IEEE Geosci. Remote Sens. Lett. 2010, 7, 736–740. [Google Scholar] [CrossRef]
- Chakravarty, S.; Banerjee, M.; Chandel, S. Spectral-Spatial Classification of Hyperspectral Imagery Using Support Vector and Fuzzy-MRF. In Proceedings of the International Conference on Intelligent, Secure, and Dependable Systems in Distributed and Cloud Environments, Vancouver, BC, Canada, 25–27 October 2017; pp. 151–161. [Google Scholar]
- Boyd, S.; Parikh, N.; Chu, E.; Peleato, B.; Eckstein, J. Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers. Found. Trends Mach. Learn. 2011, 3, 1–122. [Google Scholar] [CrossRef]
- Cohen, J. A Coefficient of Agreement for Nominal Scales. Educ. Psychol. Meas. 1960, 20, 37–46. [Google Scholar] [CrossRef]
- Story, M.; Congalton, R.G. Accuracy Assessment: A User’s Perspective. Photogramm. Eng. Remote Sens. 1986, 52, 397–399. [Google Scholar]
- Kohavi, R. A Study of Cross-Validation and Bootstrap for Accuracy Estimation and Model Selection. In Proceedings of the 14th International Joint Conference on Artificial Intelligence, Montreal, QC, Canada, 20–25 August 1995; pp. 1137–1143. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).