Characteristics and Applications of Summer Season Raindrop Size Distributions Based on a PARSIVEL² Disdrometer in the Western Tianshan Mountains (China)

Abstract

The summer season raindrop size distribution (DSD) characteristics and their important applications, based on a PARSIVEL² disdrometer installed in Zhaosu over the western Tianshan Mountains, China, in 2020–2021 are studied. Our analysis reveals that, for total rainfall and different rainfall types, the DSD in Zhaosu follows the normalized gamma distribution model, and convective rainfall has a higher raindrop concentration than stratiform rainfall at all diameters. For stratiform rainfall, the mean value of mass-weighted mean diameter (D_m) is lower than that of convective DSD, while the mean value of normalized intercept parameter (log₁₀ N_w) is higher than that of convective DSD, and the summer season convective rainfall in Zhaosu is continental convective rainfall according to the conventional classification, which is characterized by relatively larger D_m and lower log₁₀ N_w values. The derived µ–∧ relation in Zhaosu exhibits some differences from those reported in eastern, southern, and northern China and the Tibetan Plateau. Furthermore, derived Z–R relations for stratiform and convective rainfall in Zhaosu are compared with those from other regions. Analysis shows that the empirical relation of Z = 300R^1.4 (widely used), strongly overestimates the R of convective precipitation in Zhaosu. The C-band polarimetric radar rainfall estimation relations are derived, and the R(Z_h,Z_dr) and R(K_dp,Z_dr) relations perform the best in quantitative precipitation estimation. Moreover, the empirical D_m–Z_ku and D_m–Z_ka relations are derived, which are beneficial to the improvement of rainfall retrieval algorithms of the GPM DPR. Lastly, rainfall kinetic energy relations proposed in this study can be used to better assess rainfall erosivity. The empirical relationships of DSD evaluated in this study provide an opportunity to (1) improve rainfall retrieval algorithms for both ground-based and remote sensing radars and to (2) enhance rainfall kinetic energy estimates in rainfall erosivity studies based on disdrometer and GPM DPR.

1. Introduction

Raindrop size distribution (DSD) characteristics are critical for comprehending the microphysical process of precipitation [1,2]. Moreover, accurate estimation of the DSD variability is essential for improving quantitative precipitation estimates (QPE) for ground-based weather radar [3,4,5], space-borne radars [6,7,8,9], and microphysical parameterizations of numerical weather prediction models [10,11,12,13]. On top of that, the rainfall kinetic energy, obtained from the DSD is advantageous for evaluating the rainfall erosivity factor over the direct measuring instrument [14,15,16,17].

Previous studies have already confirmed that DSD not only changes with climatic regimes and geographical locations [18,19,20,21,22,23,24,25,26], but also exhibits different characteristics depending on the rain type [27,28,29,30,31,32,33,34,35,36]. Moreover, many other studies have also revealed seasonal and diurnal variations in the DSD [26,37,38,39,40,41,42]. To this end, for convective rainfall, Bringi et al. [20] have proposed a conventional classification of maritime and continental convective clusters, which is based on the normalized intercept parameter (log₁₀ N_w), and mass-weighted mean diameter (D_m). Wen et al. [39] have quantified the characteristics of DSD for different precipitation types as well as seasons in Nanjing (eastern China). Notably, they revealed a maritime convective nature for convective rainfall across seasons. Ma et al. [43] investigated the DSD characteristics of rainy seasons in Beijing, northern China, and reported that, for convective rainfall, both the average D_m and log₁₀ N_w are larger when compared to stratiform rainfall. Zhang et al. [38] studied the DSD characteristics in Zhuhai, southern China, and found, on average, the DSD in southern China contains a higher concentration of relatively small-sized drops, compared with that of eastern China and northern China. Fu et al. [31] analyzed the DSD characteristics over the middle reaches of the Yangtze River, central China, and revealed some dissimilarities between these characteristics and those over the lower reaches of the Yangtze River. Wang et al. [44] compared the differences in the DSD characteristics in two typical areas of the Tibetan Plateau (Mêdog and Nagqu). They concluded that convective rainfall in Nagqu belongs to continental convective rainfall category, while convective rainfall in Mêdog belongs to maritime convective rainfall category.

The Tianshan Mountains are located in the hinterland of the Eurasian continent and consist of a series of high mountains, intermountain basins and valleys [45]. The Tianshan Mountains are located far from the ocean in the arid region, which substantially differs from the monsoon region in climate [46,47]. Most of the Tianshan Mountains are in the Xinjiang Province (China), which accounts for about one-sixth of China’s land area and is affected by the topography of the Tianshan Mountains. Moreover, the Tianshan Mountains and the adjacent areas are the regions with the most abundant rainfall in Xinjiang [48]. Notably, the western Tianshan Mountains in China and its adjacent areas have become the main rainfall regions in the Tianshan Mountains due to the accumulation and uplift of the air flow, caused by the local topography of the bell mouth [49]. Heavy rainfall in the summer season near the western Tianshan Mountains in China is often accompanied by other disasters such as floods, debris flows and landslides [50]. Zeng et al. [51] studied the diurnal variation in spring season DSD near the western Tianshan Mountains and found that it is closely associated with the rainfall system and mountain-valley winds. The DSD of main rainfall period, lasting from April to October over the western Tianshan Mountains, have been elucidated by Zeng et al. [52]. They revealed a distinguishable border between stratiform and convective precipitation in terms of the scattergram of log₁₀ N_w versus D_m. However, the rainfall over western Tianshan Mountains mainly occurs in summer season. Moreover, studies about the QPE for dual-polarization radar and space-borne radar, and rainfall kinetic energy relations are still scanty for this area. It is also unclear whether the differences in summer season DSD characteristics of this region are significantly different from those of other regions, especially in the monsoon region of China. QPE relations that are specifically applicable for this region for a dual-polarization radar and space-borne radar are also unclear. Finally, the rainfall kinetic energy relations near the mountains, suitable for this area and regional applications, are unknown.

To alleviate these knowledge gaps, our study used a ground-based disdrometer, installed in Zhaosu (the western Tianshan Mountains, China), to investigate summer season DSD characteristics and their important applications in the western Tianshan Mountains (China) in 2020–2021. The study is organized as follows: the data and methodology are described in Section 2, Section 3 reveals the results on characteristics and applications of summer season DSD in the study region, A related discussion is given in Section 4, and Section 5 provides general conclusions of this study.

2. Data and Methodology

2.1. Data and Instruments

This research utilized two years of disdrometer observations, collected by using the second-generation OTT Particle Size Velocity (PARSIVEL²) disdrometer [51,52], during the summer season in Zhaosu (81.13°E/43.14°N, 1850.8 m ASL) over the western Tianshan Mountains (China) between 2020 and 2021. Figure 1 shows the locations of Zhaosu (the black dot) and the topographic map of Tianshan Mountains. Zhaosu is located in the topography of the bell mouth of the western Tianshan Mountains with the extremely arid Taklimakan Desert to the south.

The PARSIVEL² disdrometer is an optical disdrometer with an optical sensor, which can simultaneously measure particle size and the fall speed with 1 min temporal resolution [53,54]. The measured hydrometeors were separated into 32 non-uniform size bins (from 0.062 to 24.5 mm), and 32 non-uniform final velocity bins (from 0.05 to 20.8 m s⁻¹) [54]. The first two size classes were ignored due to their low signal-to-noise ratios [22,32]. There were some margin outliers, caused by raindrops not completely within the measuring area of disdrometers [54], as well as raindrops with unrealistically small final velocity, generated by splashing effects and strong winds during heavy rainfall [55]. The raindrops with final velocity within ±60% of the empirical fall speed-diameter relation [56] were retained, thereby removing unreal raindrops outside the range [55,57]. Before removing unreal raindrops, the empirical relation [56] was adjusted by considering the terrain height of Zhaosu (the correction factor of 1.07) [22,34,56]. Furthermore, 1-min samples with counts of raindrops of <10 or rain rates of <0.1 mm h⁻¹ were discarded [19,58]. After quality control, the distribution of drop final speeds-diameters is shown in Figure 2. Note that 14,609 1-min effective DSD data were used during the summer season from 2020 to 2021.

2.2. Raindrop Size Distribution

The raindrop concentration (N(D_i), m⁻³ mm⁻¹) for raindrop diameter can be derived [32,55,59] from Equation (1):

$$N\left(D_i\right)={\displaystyle \sum }_{j=1}^{32}\frac{n_{ij}}{A_{eff}\left(D_i\right)\cdot \mathsf{\Delta }t\cdot V\left(D_i\right)\cdot \mathsf{\Delta }{D}_i}$$

(1)

where n_ij is the drop number reckoned in the size bin i and velocity bin j; Δt (s) represents the sampling time (60 s); ΔD_i (mm) represents the interval of diameter for the ith size bin; A_eff (D_i) (m²) represents the effective sampling area [53,59,60], which can be expressed as:

$$A_{eff}\left(D_i\right)={10}^{-6}\cdot 180\cdot \left(30-\frac{D_i}{2}\right)$$

(2)

where V(D_i) (m s⁻¹) represents the drops velocity for the ith size bin [24,32,56,61], which is expressed as:

$$V\left(D_i\right)=\left(9.65-10.3\cdot exp(-0.6\cdot D_i\right))\cdot \delta \left(h\right)$$

(3)

where $\delta (h)$ is the correction factor (as mentioned above, 1.07), caused by the terrain height of Zhaosu.

The rain rate R (mm h⁻¹), rainwater content W (g m⁻³), and radar reflectivity factor Z (mm⁶ m⁻³) are expressed by Equations (4)–(6), respectively [55]:

$$R=\frac{6\pi }{{10}^4}\cdot {\displaystyle \sum }_{i=1}^{32}N\left(D_i\right)\cdot D_i{}^3\cdot V\left(D_i\right)\cdot \mathsf{\Delta }{D}_i$$

(4)

$$W=\frac{\pi }{6000}\cdot {\displaystyle \sum }_{i=1}^{32}N\left(D_i\right)\cdot D_i^3\cdot \mathsf{\Delta }{D}_i$$

(5)

$$Z={\displaystyle \sum }_{i=1}^{32}N\left(D_i\right)\cdot D_i^6\cdot \mathsf{\Delta }{D}_i$$

(6)

The gamma model, shown in Equation (7) below, is used to fit the observed DSD [18]:

$$N\left(D\right)=N_0\cdot D^{\mu }\cdot exp(-\Lambda \cdot D)$$

(7)

where N₀ (mm^−1-μ m⁻³) is the intercept parameter, μ (-) is the shape factor, and Λ (mm⁻¹) is the slope parameter [19]. The truncated moment method [62,63] was selected to calculate these three parameters with the third-fourth-sixth moments, according to [18,19,20,24,32,34], where the nth order moment M_n (mmⁿ m⁻³) can be calculated by:

$$M_n={\int }_0^{\infty }{D}^n\cdot N\left(D\right)\cdot dD$$

(8)

$$G=\frac{M_4^3}{M_3^2{M}_6}$$

(9)

$$N_0=\frac{M_3·{\wedge }^{\mu +4}}{\mathsf{\Gamma }\left(\mu +4\right)}$$

(10)

$$\mu =\frac{11·G-8+\sqrt{G·\left(G+8\right)}}{2\left(1-G\right)}$$

(11)

$$\Lambda =\left(\mu +4\right)\cdot \frac{M_3}{M_4}$$

(12)

To overcome the shortcoming of the non-independence of three parameters in the gamma function, the normalized gamma distribution has been proposed by [64,65,66,67,68], which is formalized in Equation (13):

$$N\left(D\right)=N_w\cdot f\left(\mu \right)\cdot {\left(\frac{D}{D_m}\right)}^{\mu }\cdot exp\left[-\left(4+\mu \right)\frac{D}{D_m}\right]$$

(13)

where

$$f\left(\mu \right)=\frac{6\cdot {(4+\mu )}^{4+\mu }}{4^4\cdot \mathsf{\Gamma }\left(4+\mu \right)}$$

(14)

N_w (mm⁻¹ m⁻³) represents the normalized intercept parameter, and D_m (mm) represents the mass-weighted mean diameter [67], which can be expressed by:

$$N_w=\frac{4^4}{\pi ·{\rho }_w}·\frac{{10}^3·W}{D_m^4}$$

(15)

$$D_m=\frac{{\sum }_{i=1}^{32}N\left(D_i\right)·D_i^4·\Delta D_i}{{\sum }_{i=1}^{32}N\left(D_i\right)·D_i^3·\Delta D_i}$$

(16)

Alongside the above-mentioned meteorological variables, the rainfall kinetic energy (including kinetic energy flux KE_time (J m⁻² h⁻¹), and kinetic energy content KE_mm (J m⁻² mm⁻¹)) [16,25,69,70] is formalized by Equations (17) and (18):

$$K{E}_{time}=\left(\frac{\pi }{12}\right)\cdot \left(\frac{1}{{10}^6}\right)\cdot \left(\frac{3600}{\Delta t}\right)\cdot \left(\frac{1}{A_{eff}\left(D_i\right)}\right){\displaystyle \sum }_{i=1}^{32}{n}_i\cdot D_i{}^3\cdot {(V\left(D_i\right))}^2$$

(17)

$$K{E}_{mm}=\frac{K{E}_{time}}{R}$$

(18)

2.3. Classification of Precipitation Types

Rainfall can be divided into stratiform and convective rainfalls with different microphysical characteristics [19,20,67]. To classify rainfall into stratiform and convective types, previous studies have utilized various classification criteria [19,20,27,29,67,71]. In this study, the classification criteria, based on R and the standard deviation (SD) of R were applied [20,29]. Specifically, when considering at least 10 min of consecutive rainfall, the rainfall was considered as stratiform rainfall if R was greater than 0.5 mm h⁻¹ and the SD of R was not greater than 1.5 mm h⁻¹. The rainfall was considered as convective if R was greater than 5 mm h⁻¹ and the SD of R was greater than 1.5 mm h⁻¹.

2.4. Calculated Polarimetric Radar Variables

Given their excellent performance in QPE, based on DSD derived relationships [23,42,72,73,74,75], polarimetric radars variables have been widely used in retrieving R. Three key polarimetric radars variables can be derived by:

$$Z_{h,v}=\left(\frac{4\cdot {\lambda }^4}{{\pi }^4\cdot {\left|K_w\right|}^2}\right)\cdot {\int }_{D_{min}}^{D_{max}}{\left|f_{hh,vv}\left(D\right)\right|}^2\cdot N\left(D\right)\cdot dD$$

(19)

$$Z_{dr}=10\cdot {\log }_{10}\left(\frac{Z_h}{Z_v}\right)$$

(20)

$$K_{dp}={10}^{-3}\cdot \frac{180}{\pi }\cdot \lambda \cdot Re\left\{{\int }_{Dmin}^{D_{max}}\left[f_h\left(D\right)-f_v\left(D\right)\right]\cdot N\left(D\right)\cdot dD\right\}$$

(21)

where Z_h,v (mm⁶ m⁻³) is radar reflectivity at horizontal or vertical polarization, Z_dr (dB) is differential reflectivity, and K_dp (° km⁻¹) is specific differential phase. λ (mm) and K_w are the radar wavelength (for the C-band, the value is 53.5 mm) and the dielectric factor of water, respectively, and f_hh,vv(D) and f_h,v(D) are the backscattering amplitude of a drop and the forward scattering amplitude for the horizontally or vertically polarized waves, respectively. In this study, the variables of dual-polarization radar were computed based on DSD data and the method of T-matrix scattering [76,77,78]. The temperature of the raindrop was assumed to be 10 °C. Moreover, raindrops assumingly followed the Brandes axis ratio relation [79].

3. Results

After the quality control according to the method mentioned in Section 2, 14,609 effective samples were obtained in this study. The variations of the mean raindrop concentration with raindrop size and the normalized gamma distribution model during summer season in Zhaosu are shown in Figure 3. As seen, the fitting results were certainly in good agreement with the observations. The mean and standard deviation (SD) values of several important DSD parameters for all the observations are summarized in

Table 1. Several important rainfall parameters for all samples.

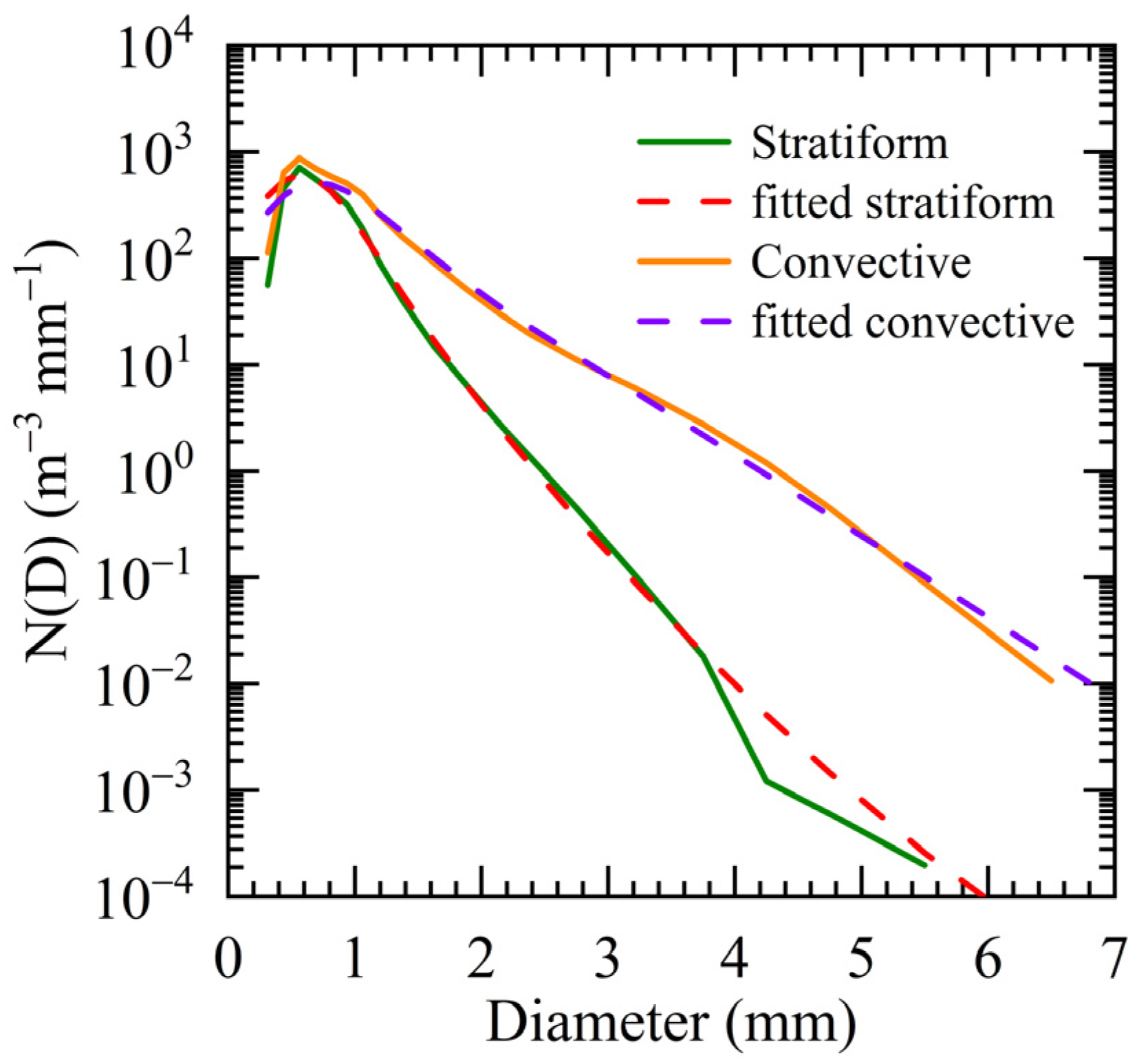
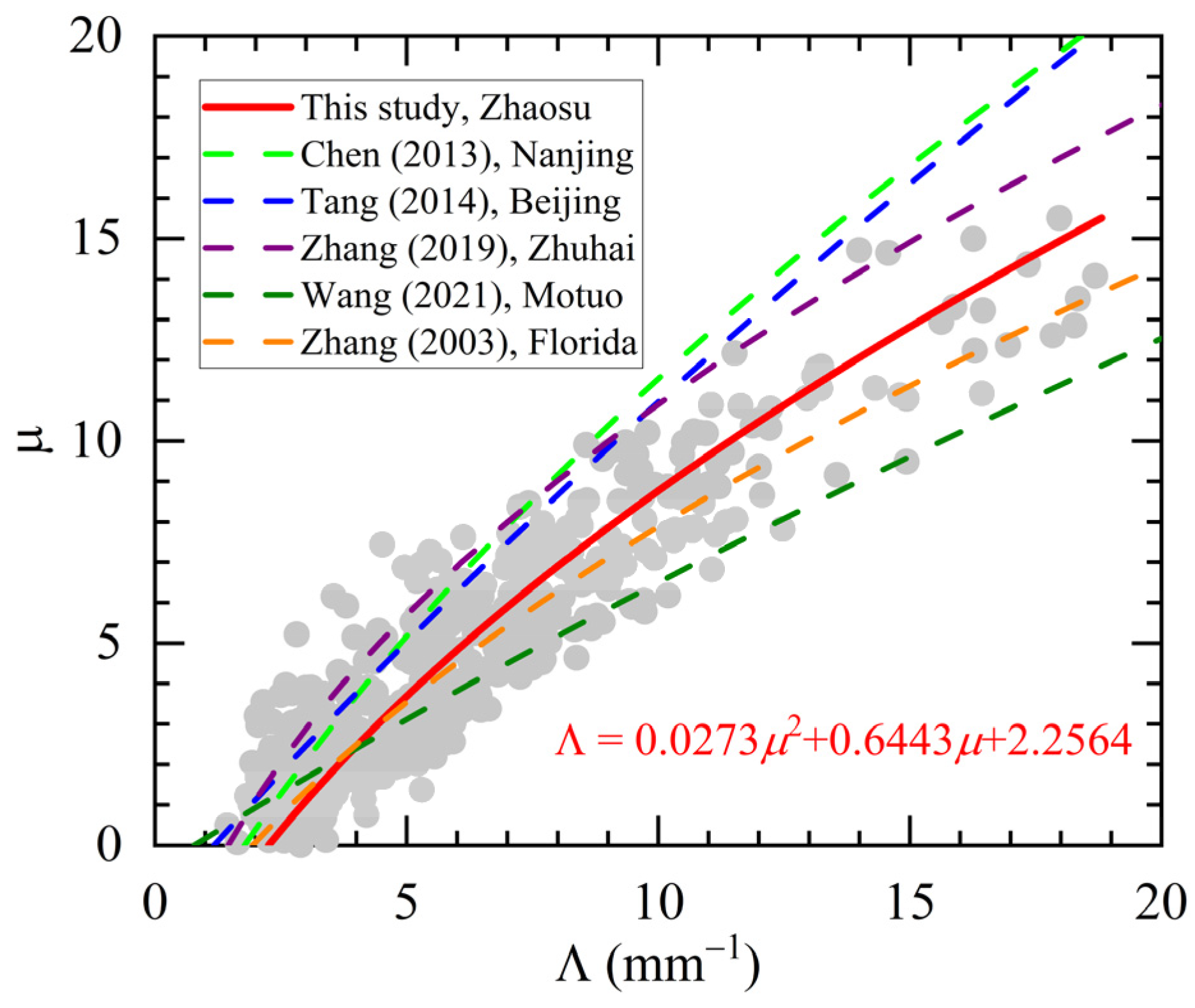
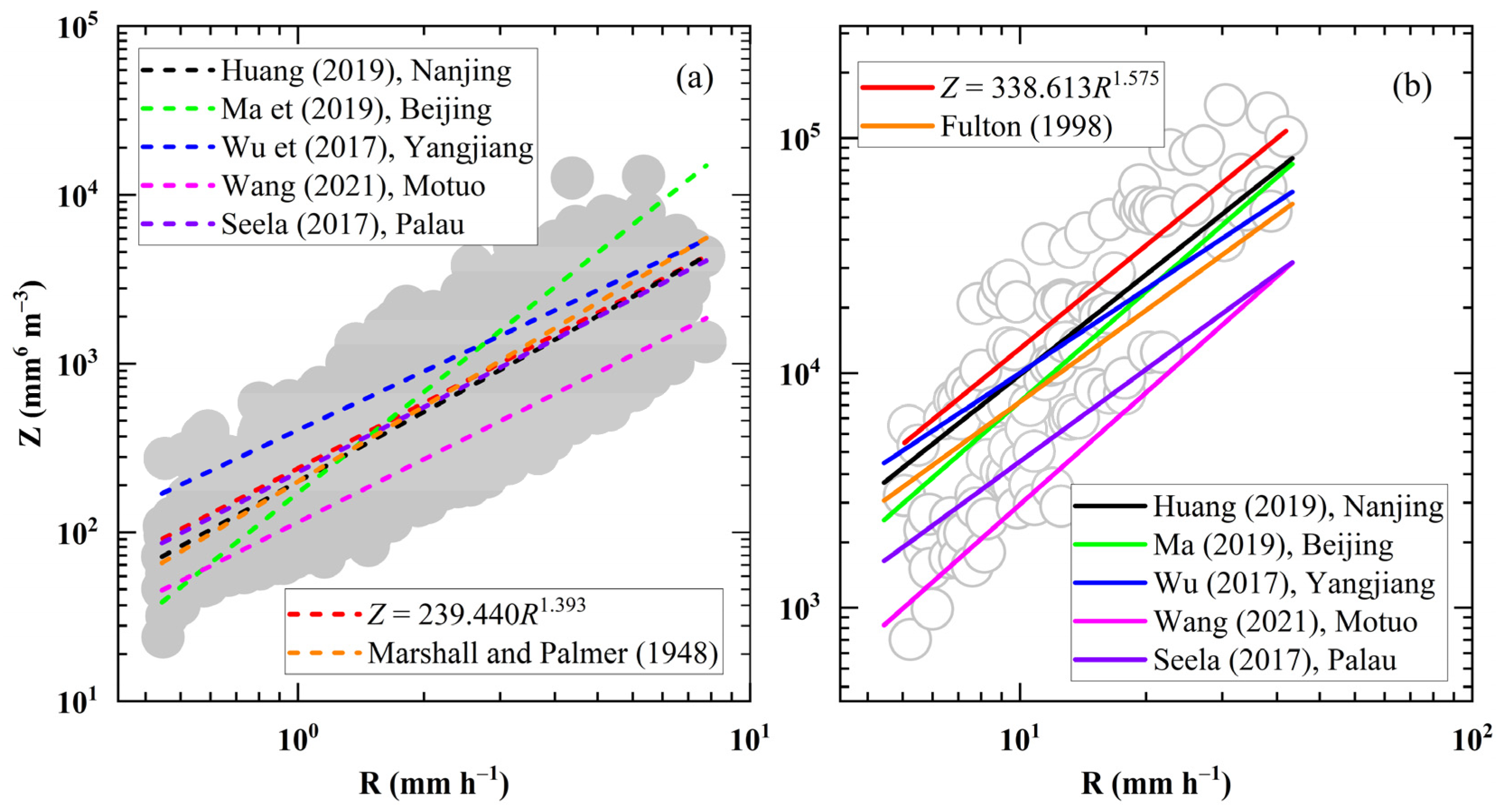
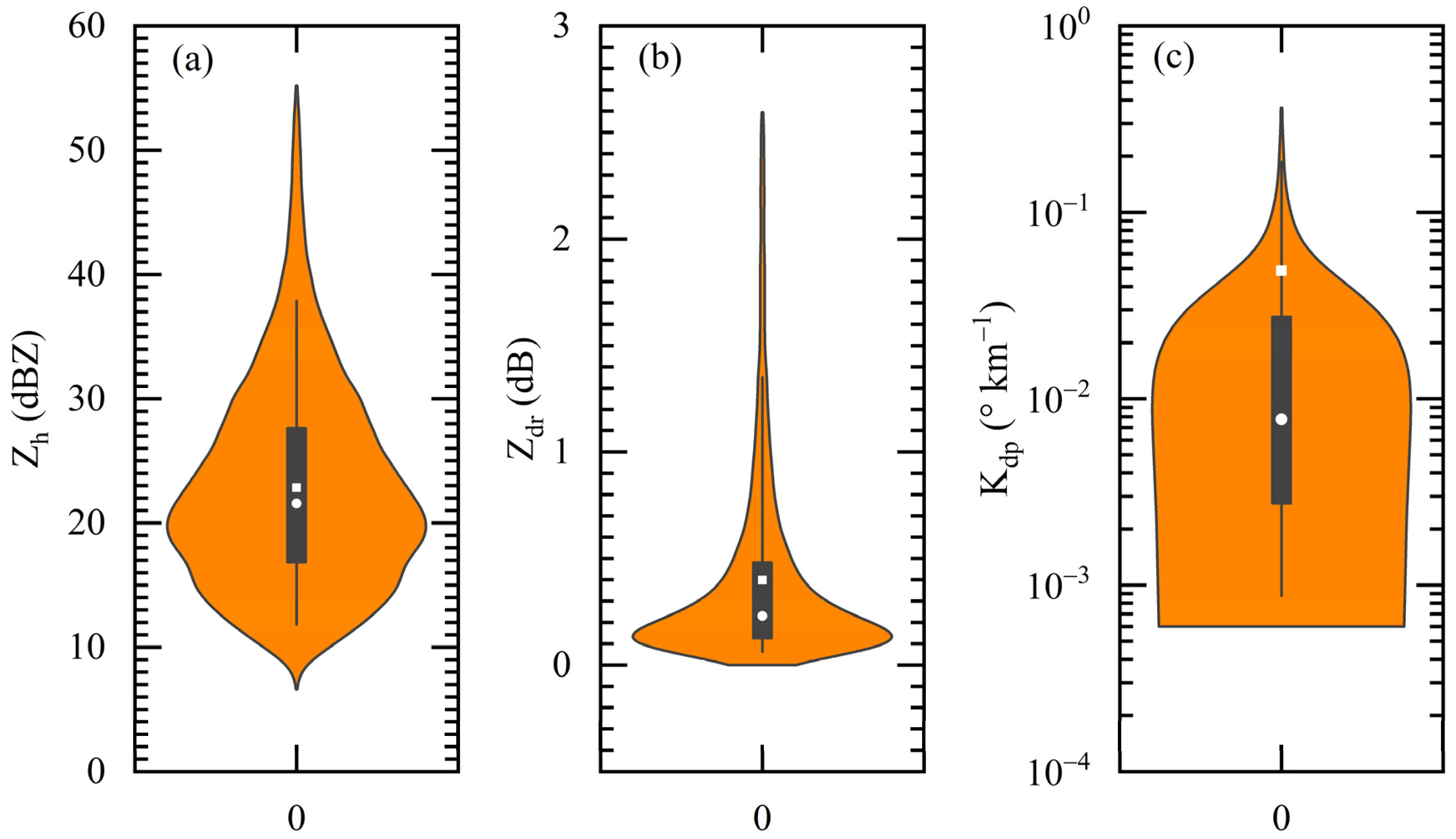
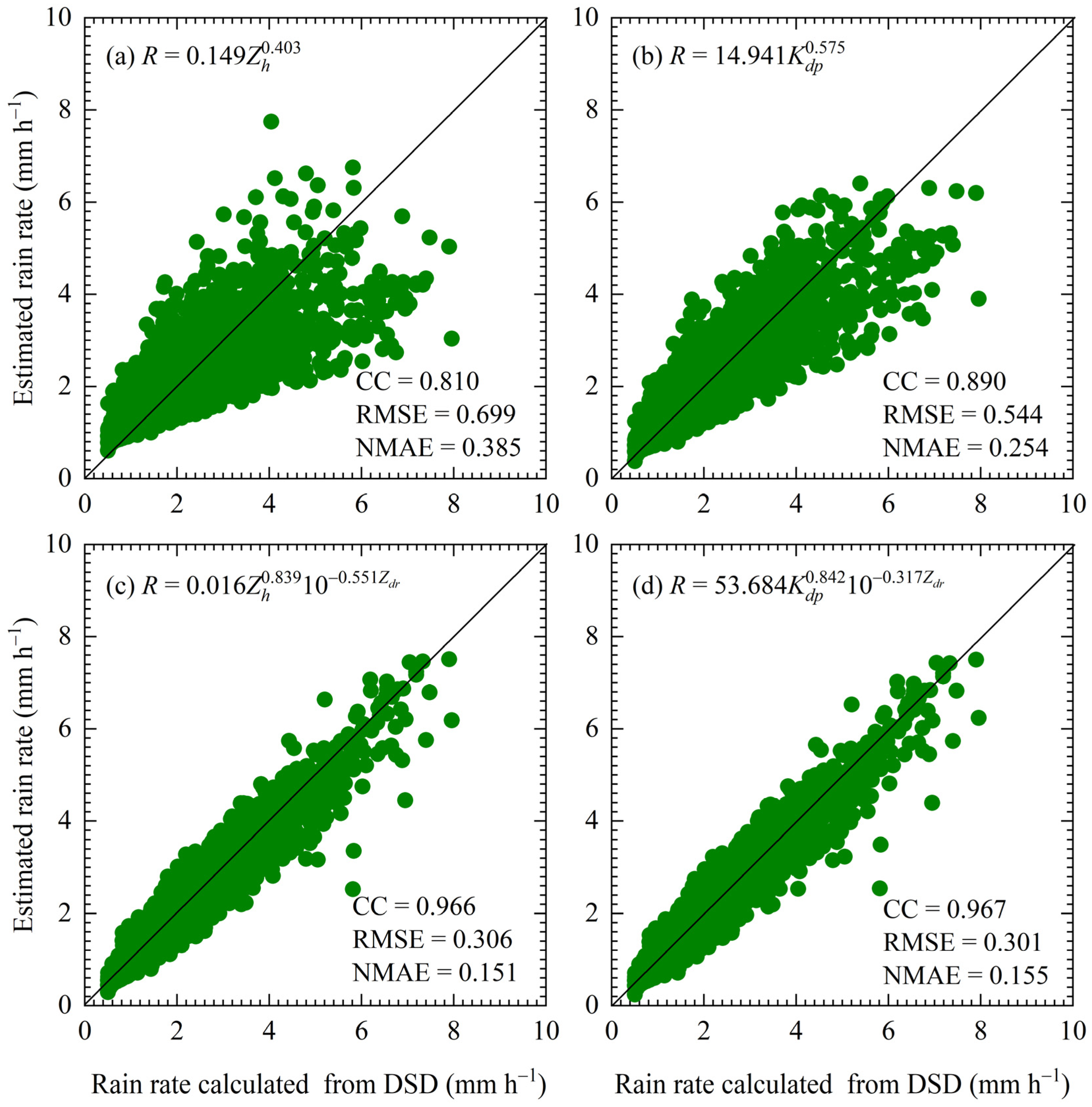
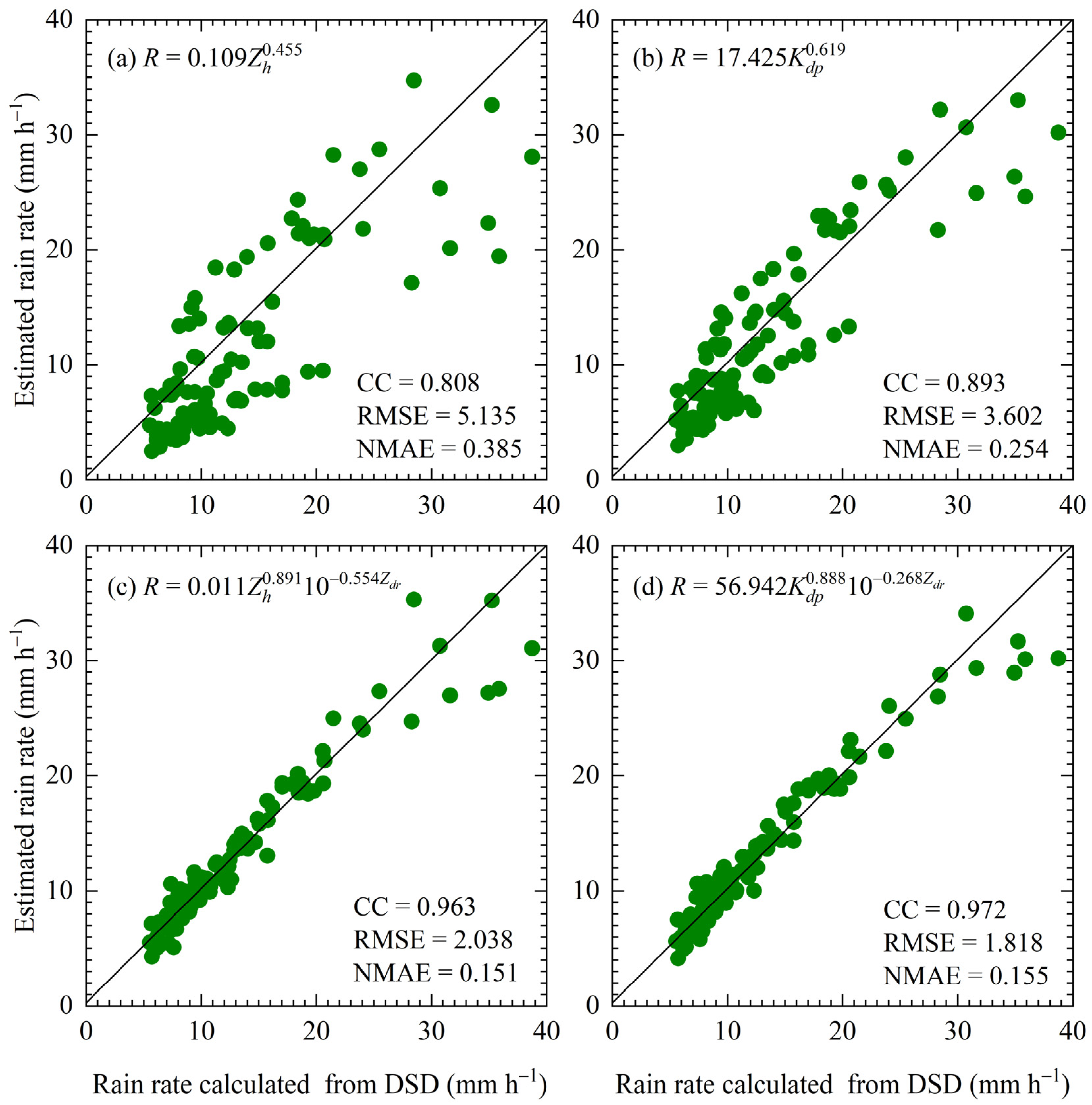
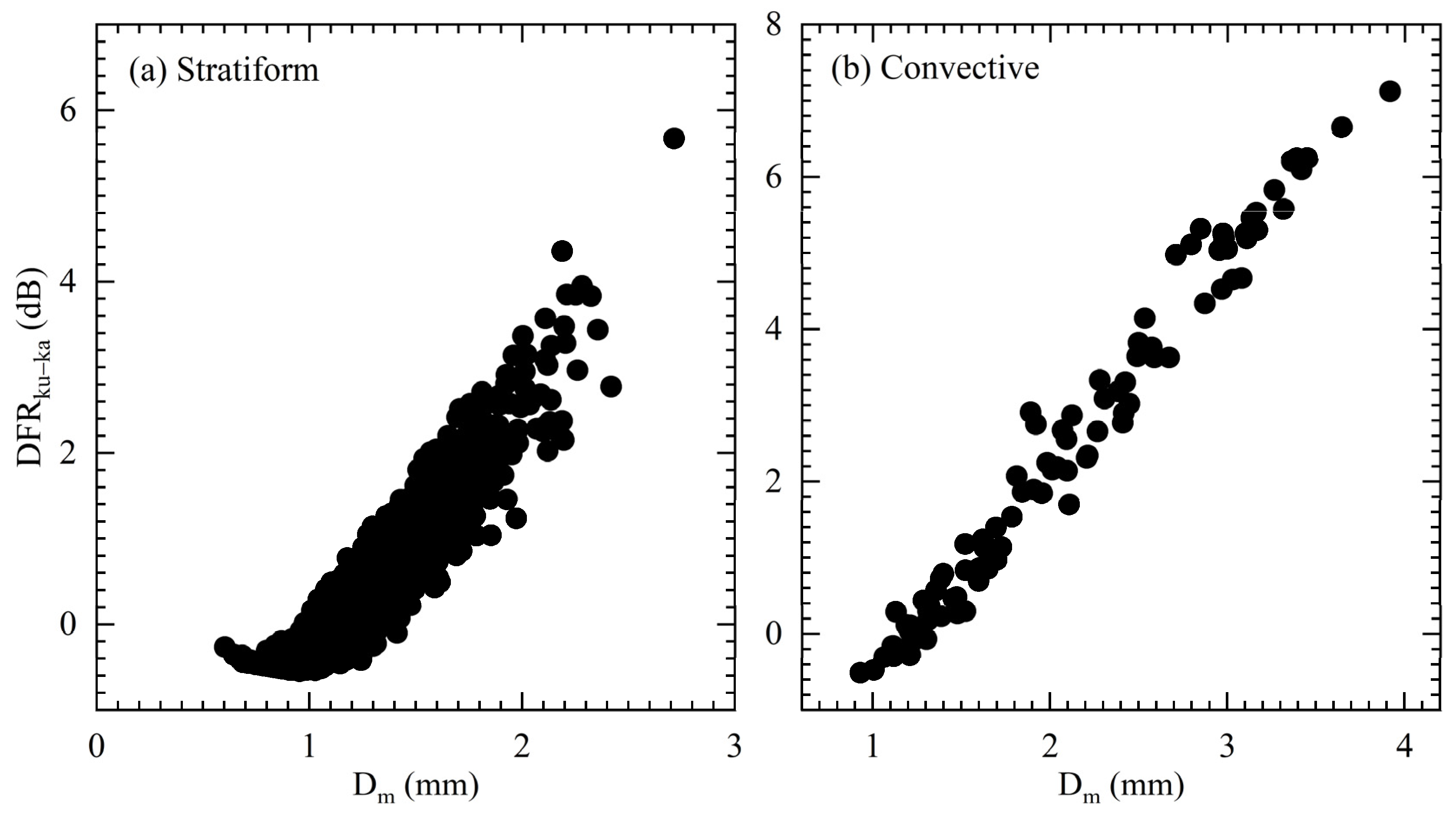
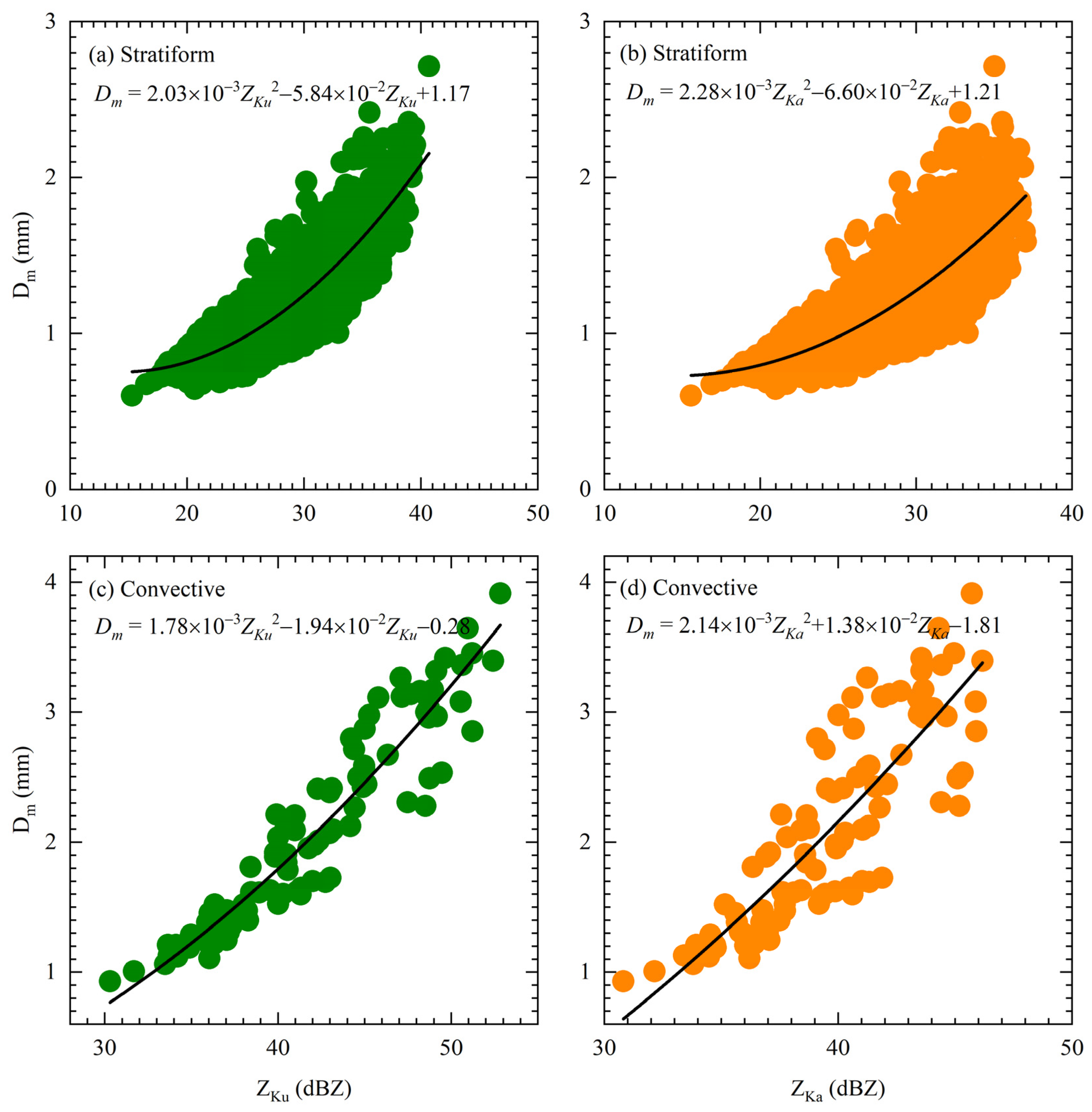
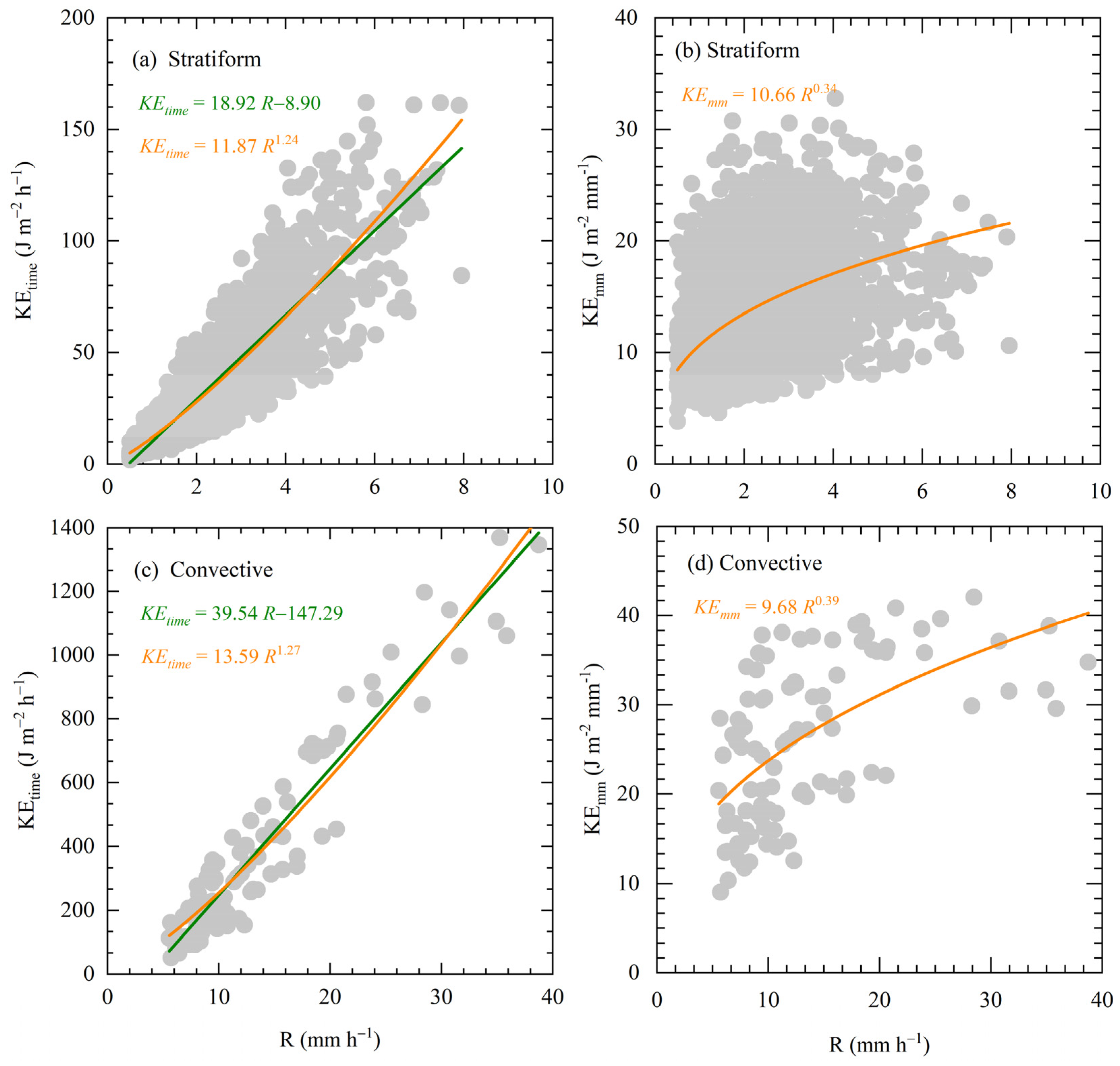
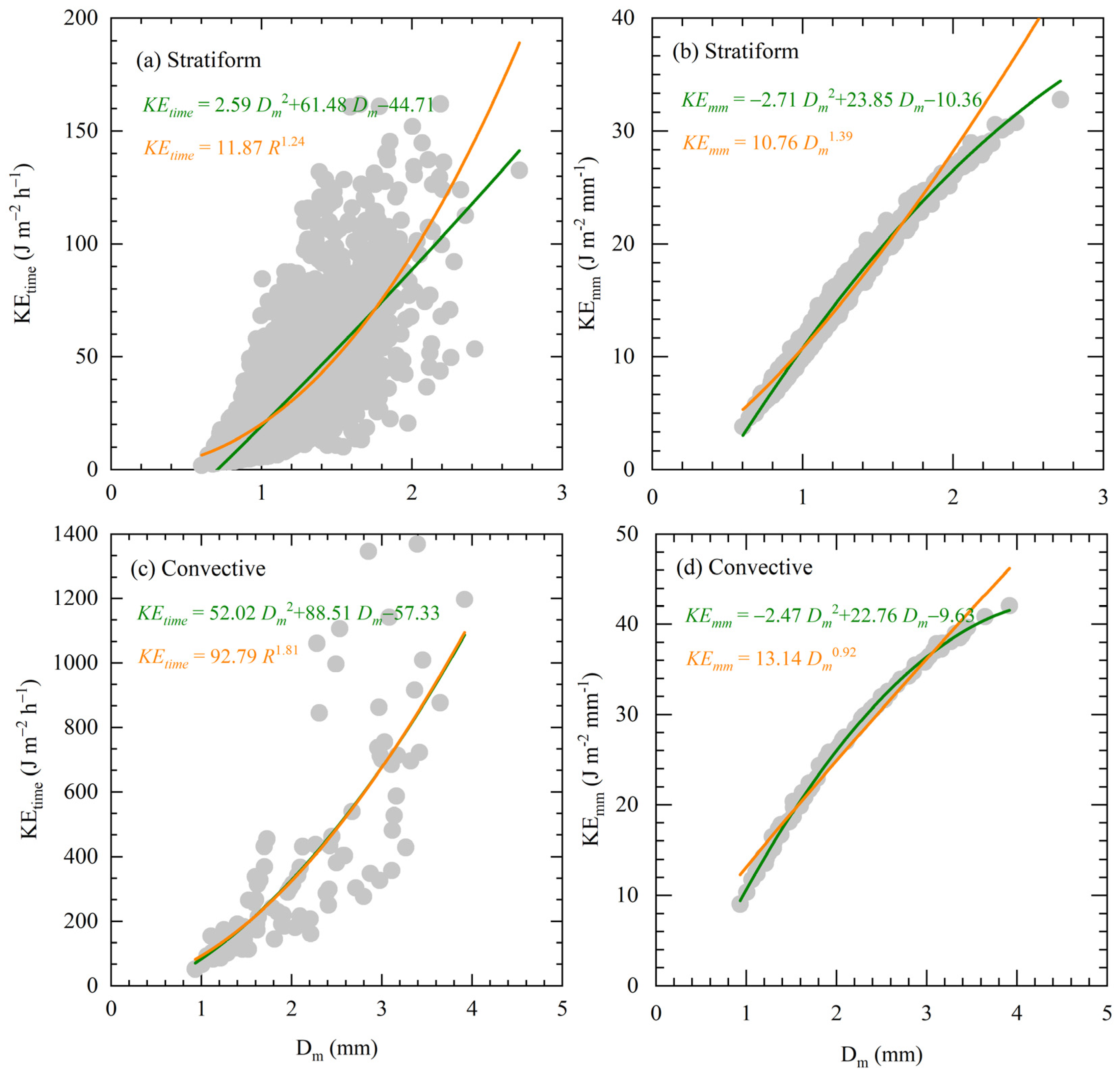
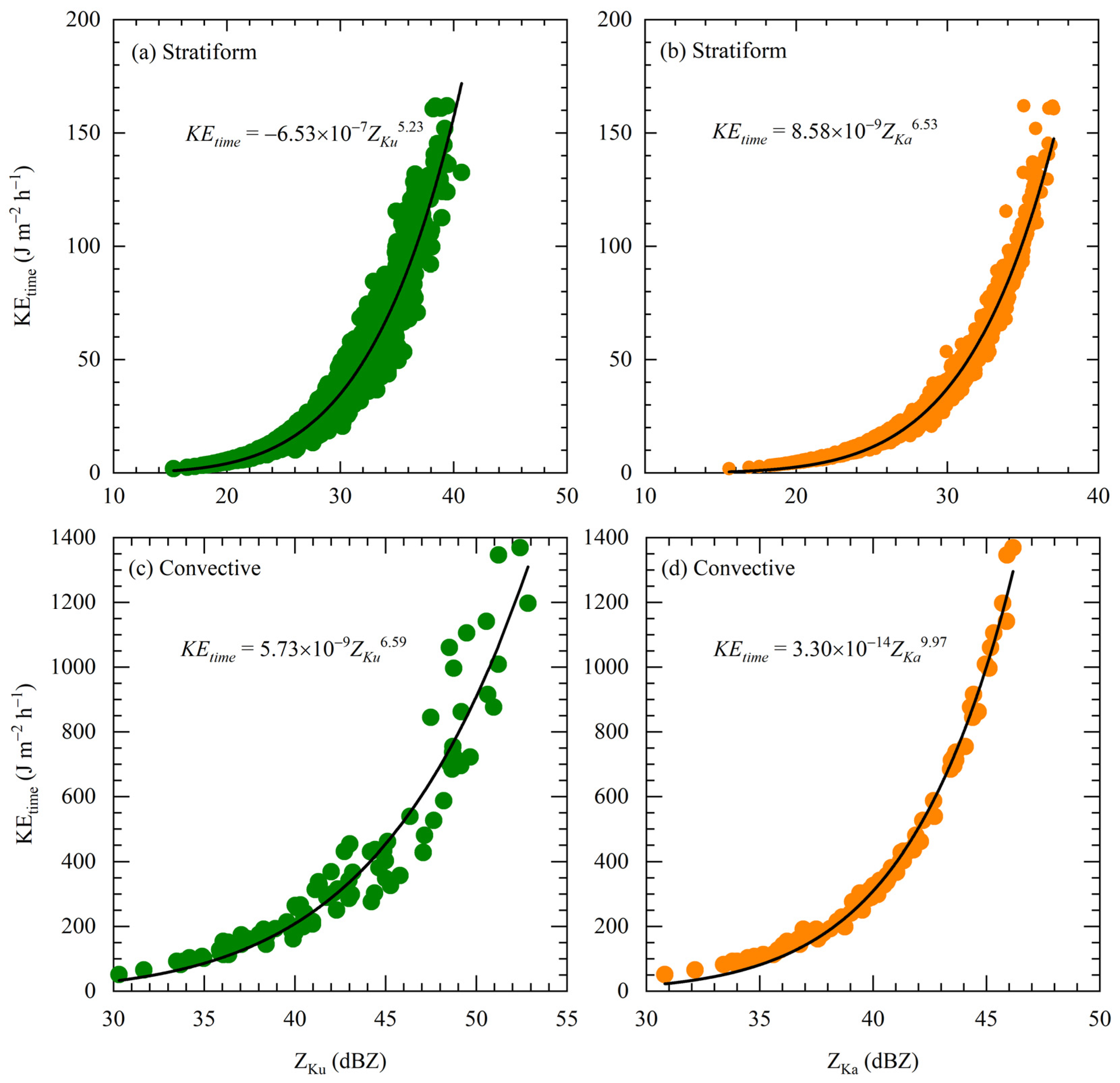
Parameters	R (mm h−1)	log10Nw (m−3 mm−1)	Dm (mm)	W (g m−3)	Z (dBZ)	μ	Λ (mm−1)
Mean	1.61	3.48	1.13	0.09	21.52	9.58	14.34
STD	2.96	0.52	0.45	0.12	7.92	7.54	10.35

. The mean values of D_m, log₁₀ N_w, and Z were 1.13 mm, 3.48 m⁻³ mm⁻¹, and 21.52 dBZ, respectively.

3.1. DSD in Stratiform and Convective Rainfall

The DSD variations for different types of rainfall (convective and stratiform rainfall) in Zhaosu are provided in Figure 4. Both peaks of the DSD of convective and stratiform rainfall were identified at 0.56 mm in diameter. A relatively high raindrop concentration was observed for convective rainfall, compared to that for stratiform rainfall at all size bins of raindrops. Meanwhile, the fitted normalized gamma distributions for convective and stratiform rainfall exhibited characteristics that were generally consistent with the observations. The mean value of R for convective rainfall was 13.57 mm h⁻¹, while that for stratiform rainfall was 1.97 mm h⁻¹. Other DSD parameters exhibited prominent differences, such as the mean values of D_m, which, for the two types of rainfall, were 2.11 mm and 1.13 mm, and their mean values of W were 0.56 g m⁻³ and 0.12 g m⁻³ as shown in

Table 2. Several important rainfall parameters for convective and stratiform precipitation.

Parameters		R (mm h−1)	log10Nw (m−3 mm−1)	Dm (mm)	W (g m−3)	Z (dBZ)	μ	Λ (mm−1)
Convective	Mean	13.57	3.44	2.11	0.56	40.22	4.75	4.85
	SD	7.57	0.62	0.75	0.25	5.51	2.52	2.81
Stratiform	Mean	1.97	3.77	1.13	0.12	25.67	5.90	9.84
	SD	1.19	0.40	0.28	0.06	4.54	4.51	6.10

.

Figure 5 illustrates the relative frequency histograms of D_m and log₁₀ N_w for the stratiform and convective rainfall, and their three important characteristic parameters including mean, SD, and skewness. The D_m of both types of rainfall exhibited positive skewness, as shown in Figure 5a, while the log₁₀ N_w of stratiform rainfall exhibited negative skewness, as demonstrated in Figure 5b. The mean values D_m of convective rainfall and stratiform rainfall were 2.11 and 1.13 mm, respectively. The mean values log₁₀ N_w of the two types of rainfall were 3.44 and 3.77, respectively. Moreover, the SD values of D_m and log₁₀ N_w for convective precipitation were larger when compared with stratiform precipitation, thereby indicating that convective rainfall exhibited stronger variability.

We further compared our data with the data from regions of China and other climatic regimes, reported by Bringi et al. [20]. Specifically, we compared the mean values of log₁₀ N_w versus the mean values of D_m for the stratiform and convective precipitation in Zhaosu and other regions of China with their results (see Figure 5c). The two gray rectangles correspond to the continental-like and maritime-like clusters for convective rainfall in Figure 5c [20]. The gray dashed line indicates the log₁₀ N_w–D_m relation of stratiform rainfall [20]. The results reveal that the convective rainfall in Zhaosu in the summer season was of continental convective rainfall type, characterized by relatively lower log₁₀ N_w (3.44 m⁻³ mm⁻¹) value and larger D_m (2.11 mm) value. Further, the comparison between Zhaosu and other regions in China was performed. The other regions here include Nanjing, East China [29], Beijing, North China [43], Zhuhai, South China [79], and Motuo, the Tibetan Plateau [34]. It was revealed that Zhaosu exhibited the lowest log₁₀ N_w and nearly largest D_m (outperformed only by Zhuhai), compared with those from other regions in China for convective rainfall. The stratiform rainfall analysis showed that the log₁₀ N_w in Zhaosu (3.77 m⁻³ mm⁻¹) was larger than that in the other regions in China except Zhuhai (4.36 m⁻³ mm⁻¹). Lastly, the D_m in Zhaosu (1.13 mm) was similar to that in Beijng (1.08 mm), larger than that in Motuo (0.84 mm), and lower than that in Nanjing (1.3 mm) and Zhuhai (1.53 mm).

3.2. Gamma Distribution Parameters

Numerous previous studies have reported that the µ–∧ constrained relations of gamma distribution parameters exhibited spatial variability, depending on a geographical location and a climatological regime [22,32,36,39,63,80,81,82]. In this study, the µ–∧ relation for rainfall in Zhaosu was derived according to the same criteria as in [82]. Considering the reliability of the results, the derived µ–∧ relation is applicable for the range of ∧ between 0 and 20 mm⁻¹ [63]. Figure 6 shows the scatterplots of µ and ∧, and the µ–∧ relation for rainfall in Zhaosu. For instance, the µ–∧ relations in Nanjing [29], Beijing [83], Zhuhai [79], Motuo [34], and Florida [63] are shown with corresponding colors in Figure 6. The µ–∧ relations in Tang et al. [83], Chen et al. [29], and Zhang et al. [79] were found to be close to each other. This implies much larger µ values for a given ∧ than the other µ–∧ relations. Compared with the µ–∧ relation in Wang et al. [34], the µ–∧ relation in this study of $\Lambda =0.0273{\mu }^2+0.6443\mu +2.2564$ was closer to that in Zhang et al. [63], despite some salient differences at ∧ > 7 mm⁻¹. The above comparison further reveals that the µ–∧ relations are dependent on geographical locations and climatological regimes.

3.3. Quantitative Precipitation Estimation

The Z–R relation is essential for QPE of a single polarized radar, and the Z–R relation heavily depends on the variability of DSD, which is associated with the climatic regime, geographical location, rain type/system, and season [19,29,30,31,32,34,84,85]. Figure 7 shows scatterplots of Z and R, and the fitted power law curves in red with corresponding equations for convective and stratiform rainfall in Zhaosu. For instance, the Z–R relations in Nanjing [86], Beijing [43], Yangjiang [87], Motuo [34], and Palau [24] are illustrated by dashed lines for stratiform rainfall. Note that the solid lines for convective rainfall are shown with the corresponding colors in Figure 7. Furthermore, Figure 7 also displays, in orange, the widely used Z–R relations, proposed by Marshall and Palmer [88] for stratiform rainfall and Fulton et al. [89] for convective rainfall. The convective rainfall analysis clearly revealed that the Z–R relation of Zhaosu in this study implies much higher Z value at the given R, compared with that of the other regions. At the same time, the stratiform rainfall analysis revealed some differences, while the Z–R relations in Huang et al. [86], Seela et al. [24], Marshall and Palmer [88], Zhaosu and from this study were close to each other. However, some significant differences with those estimates from Wu et al. [87], Ma et al. [43], and Wang et al. [34], were identified.

Furthermore, previous studies have indicated that polarimetric radar variables are useful for QPE given the comprehensive detection abilities of polarimetric radars. On this basis, numerous empirical relationships have been used in QPE [80,82,90,91]. More importantly, many other studies have recently demonstrated the advantages of using the DSD data to obtain polarimetric radar variables for QPE [23,42,72,73,74,92]. The China Meteorological Administration fully considered the distribution of heavy rainfall in China when setting up the Doppler weather radar network. The S-band radar was installed in eastern China, and the C-band radar was installed in northwestern China, including the western Tianshan Mountains, and the China Meteorological Administration plans to upgrade the Doppler weather radars to polarimetric radars in the future. Figure 8 shows the distribution of Z_h, Z_dr, and K_dp in Zhaosu for the C-band by using the T-matrix scattering method.

Table 3. The quantiles of variables for C-band polarization radar derived from DSD observations.

Parameters	5%	25%	Median	75%	95%	Mean
Zh	11.84	16.85	21.56	27.63	37.89	22.84
Zdr	0.06	0.13	0.23	0.48	1.35	0.40
Kdp	8.77 × 10−4	2.75 × 10−3	7.77 × 10−3	2.76 × 10−2	1.86 × 10−1	4.86 × 10−2

summarizes the details from boxplots in each panel. The mean and median values of Z_h were found to be close to ~22 dBZ, and ~75% of the values of Z_h were below 28 dBZ. The peak of the distribution of Z_dr was at ~0.15 dB. For K_dp. Notably, most values were <0.1 km⁻¹.

We also established the estimated polarimetric radar rainfall relationships of R(Z_h), R(K_dp), R(Z_h,Z_dr), and R(K_dp,Z_dr) for stratiform and convective rainfall as shown below:

R(Z_h) = 0.149 Z_h^0.403 (stratiform)

(22)

R(K_dp) = 14.941 K_dp^0.575 (stratiform)

(23)

R(Z_h,Z_dr) = 0.016 Z_h^0.83910^−0.551Zdr (stratiform)

(24)

R(K_dp,Z_dr) = 53.684 K_dp^0.84210^−0.317Zdr (stratiform)

(25)

R(Z_h) = 0.109 Z_h^0.455 (convective)

(26)

R(K_dp) = 17.425 K_dp^0.619 (convective)

(27)

R(Z_h,Z_dr) = 0.011 Z_h^0.89110^−0.554Zdr (convective)

(28)

R(K_dp,Z_dr) = 56.942 K_dp^0.88810^−0.268Zdr (convective)

(29)

To evaluate the accuracy of the derived polarimetric radar rainfall relations, we compared the estimated rainfall rate by various QPE relations based on polarimetric radar variables with the rain rate, directly derived from the DSD. To further evaluate the performance of each QPE relation, we used three evaluation indicators: (1) correlation coefficient (CC), (2) root mean square error (RMSE), and (3) normalized mean absolute error (NMAE), as recommended by Luo et al. [42]. Figure 9 and Figure 10 show these statistical results for stratiform and convective rainfall, respectively, indicating that three QPE relations (Figure 9b–d and Figure 10b–d) based on Z_dr and K_dp clearly exhibited better performance, compared to R(Z_h) (Figure 9a and Figure 10a). Moreover, the scatters were found to be more clustered with higher CC and lower RMSE and NMAE in the former. Specifically, of the four QPE relations for stratiform rainfall shown in Figure 9, the R(Z_h,Z_dr) and R(K_dp,Z_dr) exhibited the best performance in QPE. Their CC, RMSE, and NMAE were estimated to be 0.966 (0.967), 0.306 (0.301) mm h⁻¹, as well as 0.151 (0.155) mm h⁻¹, respectively. For the R(Z_h) relation, its CC, RMSE, and NMAE were found to be 0.810, 0.699 mm h⁻¹, as well as 0.385 mm h⁻¹, respectively, thereby indicating the worst performance among the four relations. The above conclusion was also true for the convective rainfall shown in Figure 10. Therefore, the QPE relations based on polarimetric radar parameters, mitigated the effect of the DSD variability on the rainfall estimation for the rainfall in Zhaosu, demonstrated in this study. Notably, these results are similar to some previous findings for Beijing [42,74], Nanjing [23,92], and Western Pacific [73]. More importantly, our study demonstrated for the first time the QPE algorithm, derived from polarimetric radar variables, obtained from the DSD data in the western Tianshan Mountains (China).

The GPM can retrieve rainfall rate based on normalized gamma distribution though the radar reflectivity (Ka and Ku bands) of the dual-frequency precipitation radar (DPR) [8,93]. The key to the rainfall retrieval algorithm for the GPM DPR is the difference in Ka and Ku bands (the dual-frequency ratio or DFR, dB), and the radar reflectivity (Z_Ka and Z_Ku) to obtain two key parameters (D_m and N_w), and then to estimate rainfall rates [94,95,96,97]. However, some observation gaps in GPM DPR summarized and proposed by Battaglia et al. [98] need to be filled and improved by ground-based observation equipment. Thus, we used the observations from Zhaosu to derive DFR, Z_Ka and Z_Ku according to the calculation procedure of [22,34,73]. Previous studies have indicated that positive values of DFR indicate a one-to-one relation between DFR and D_m, while negative values of DFR imply that D_m cannot be unambiguously retrieved because one value of DFR correlates with two values of D_m (e.g., the “dual value” problem) [8,94,95]. Figure 11 shows the scatterplots of DFR and D_m for stratiform and convective rainfall in Zhaosu. As seen, the “dual value” was clearly identified for the negative DFR values. Due to this, we derived the empirical relations between D_m and Z_Ku (Z_Ka) to avoid the “dual-value” trouble according to a similar way as in previous studies [22,34,73]. Figure 12 illustrates the scatterplots of D_m and Z_Ku (Z_Ka) for stratiform and convective rainfall, generated from the DSD data. As shown, the D_m increased with increasing Z_Ku (Z_Ka). Note that the corresponding equations of D_m–Z_Ku and D_m–Z_Ka for stratiform and convective rainfall were derived based on a least squares method:

D_m = 2.03 × 10⁻³ Z_Ku² − 5.84 × 10⁻² Z_Ku + 1.17 (stratiform)

(30)

D_m = 2.28 × 10⁻³ Z_Ka² − 6.60 × 10⁻² Z_Ka + 1.21 (stratiform)

(31)

D_m = 1.78 × 10⁻³ Z_Ku² − 1.94 × 10⁻² Z_Ku − 0.28 (convective)

(32)

D_m = 2.14 × 10⁻³ Z_Ka² + 1.38 × 10⁻² Z_Ka − 1.81 (convective)

(33)

3.4. Rainfall Kinetic Energy Relations

Rainfall kinetic energy (KE) is used to estimate the rainfall erosivity factor. It is done by establishing the empirical relation between rainfall KE and rainfall rate (KE–R relation) in soil erosion modeling studies [16,99,100,101]. Based on local DSD information, the KE–R relations, derived from previous studies, indicated that the KE–R relations strongly depended on geographical location, topographic condition, rainfall system, and rainfall type, thereby exhibiting strong variability [17,33,36,41,102,103]. Therefore, the KE–R relations are established by using the DSD information in Zhaosu. Figure 13 shows scatterplots of KE_time (KE_mm) and R, and the fitted curves with corresponding equations for stratiform and convective rainfall in Zhaosu. For the KE_time–R relation, the power fit relation exhibited a slightly better fitting effect, compared with the linear form (see Figure 13a,c). Likewise, the KE_mm–R relation for the two types of rainfall was also given in power form (see Figure 13b,d).

Besides providing Z_Ku (Z_Ka), mentioned in Section 3.3, GPM DPR also provides the drop size information (D_m) at global scales [6,104]. For mountainous areas, the ground observations are rather sparse. In such areas, it is essential to estimate rainfall KE, which can lay the foundation toward studying rainfall erosion factors by Z_Ku (Z_Ka) and D_m. Therefore, as in some previous studies [17,33,36,39], the empirical relations between rainfall KE and GPM DPR rain parameters (D_m, Z_Ku, and Z_Ka) were established based on DSD data. Figure 14 displays the scatterplots of KE_time (KE_mm) and D_m, and the fitted curves with the corresponding equations for stratiform and convective rainfall in Zhaosu. As seen, the fitted KE_mm–D_m relation clearly exhibited a better fitting effect than the fitted KE_time–D_m relation for both types of rainfall, based on the least square method. Furthermore, for the KE_mm–D_m relation, the second order polynomial fit relation exhibited slightly better fitting effect than the power fit relation for stratiform rainfall, while these two fit relations had almost the same fitting effect. Likewise, Figure 15 shows scatterplots of KE_time and Z_Ku (Z_Ka), and the fitted curves with corresponding equations for stratiform and convective rainfall in Zhaosu, based on the least square method. These results suggest that the power form fit relation can be utilized to estimate the rainfall KE.

4. Discussion

Numerous previous reports have revealed that the DSD varies with climatic regions, topography, seasons, and rainfall types [18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42]. However, most of these reports focused on monsoon areas with abundant water vapor, while less attention was paid to arid areas. For arid areas, precipitation is relatively scarce, vegetation coverage is low, and the ecological environment is fragile, so precipitation was of great significance to arid areas [49]. This study focused on Zhaosu near the western Tianshan Mountains (China), an area affected by terrain uplift which give these arid areas relatively rich precipitation [105]. On the other hand, heavy precipitation in mountainous areas can easily lead to secondary disasters such as floods, debris flows and landslides. Therefore, there are important theoretical and application value for the study on DSD characteristics, QPE and rainfall kinetic energy in areas near mountains in arid areas.

This study shed light on the characteristics of summer season DSD in the area (Zhaosu) near the western Tianshan Mountains in the arid area of China, and the results show that, for convective rainfall, Zhaosu had the lowest log₁₀ N_w and nearly largest D_m when compared with monsoon regions of China (East China [29], North China [43], South China [79], and the Tibetan Plateau [34]), which belonged to typical continental-like convective rainfall. The µ–∧and Z–R relations in this study also show a discernible difference from those in the monsoon regions. In addition, for the first time, we also give the rainfall retrieval algorithm of polarimetric radar and GPM DPR in the study area. Finally, we revealed the rainfall kinetic energy relations in the western Tianshan Mountains.

However, for readers, it should be noted that due to the limitations of the instrument itself, for small raindrops, the measured value is less than the actual value [58,106], meaning that the DSD we obtained for this study may not be complete. In addition to the PARSIVEL² used in this study, the other two commonly used instruments including 2DVD and JWD also have limitations, to a certain extent, in detecting small particles [79]. To overcome the shortcoming of these disdrometers, some efforts have been made [107,108,109]. Their methods improved the detection accuracy of small drops and were valuable for obtaining a more complete DSD of rainfall, especially for stratiform and light rainfall. In any case, it is necessary in the future to use more detection equipment to make joint observations, so as to obtain a comprehensive understanding of the microphysical process of rainfall over the western Tianshan Mountains.

5. Conclusions

Raindrop size distribution (DSD) characteristics and their key characteristics were investigated in this study by using a PARSIVEL² disdrometer in Zhaosu over the western Tianshan Mountains (China) during summer season in 2020–2021. For the first time, the characteristics of DSD, the dual-polarization radar and space-borne radar QPE relations, and the rainfall kinetic energy relations; all suitable for the western Tianshan Mountains, were analyzed. The analysis revealed that the DSD in Zhaosu basically followed the normalized gamma distribution model for both the total samples and the convective and stratiform cases. Although the peaks of the DSD of both stratiform rain and convective rain were identified at 0.56 mm in diameter, the raindrop concentration of convective rain was found to be relatively high, compared with that of stratiform rain of all the diameters. The mean value of D_m in stratiform rainfall was 1.13 mm, lower than convective rainfall which was 2.11 mm, whereas the mean value of log₁₀ N_w in stratiform rainfall was 3.77 m⁻³ mm⁻¹ higher than that in convective rainfall (3.44 m⁻³ mm⁻¹). Moreover, according to the continental-like and maritime-like convective clusters defined by [20], the summer season convective rainfall in Zhaosu was classified to be continental convective rainfall, characterized by relatively lower log₁₀ N_w value and larger D_mvalue.

The DSD data in Zhaosu were used to derive the µ–∧ relation, fitted with a second order polynomial distribution. We discerned significant differences between this derived distribution and those reported by previous studies from eastern, southern, and northern China and the Tibetan Plateau. For convective rainfall, the Z–R relation of Zhaosu in this study yielded higher Z value at the given R, compared with those in eastern, southern, and northern China and the Tibetan Plateau. Notably, the empirical relation of Z = 300R^1.4 from Fulton et al. [92] strongly overestimated the convective rainfall in Zhaosu. For stratiform rainfall, we identified some differences between our study and previous studies.

The C-band polarimetric radar rainfall estimation relations R(K_dp), R(Z_h,Z_dr), and R(K_dp,Z_dr) were derived and compared with the R(Z_h) relation by using the least squares method. We found that the R(Z_h,Z_dr) and R(K_dp,Z_dr) relations performed the best in QPE. Moreover, we derived empirical D_m–Z_Ku and D_m–Z_Ka relations based on the DSD data in Zhaosu. These relationships are vital for improving the rainfall retrieval algorithm of the GPM DPR in the Western Tianshan Mountains. Moreover, the rainfall kinetic energy relations (KE_time–R, KE_mm–R, KE_time–D_m, KE_mm–D_m, and KE_time–Z_Ku/Z_Ka), proposed in this study can be used for assessing rainfall erosivity.

The above empirical relationships based on DSD data provide a chance to improve rainfall retrieval algorithms for both ground-based and remote sensing radars; and enhance rainfall kinetic energy estimates based on DSD data and GPM DPR in rainfall erosivity studies. Despite the promising findings reported in this study, further research is needed to elucidate the seasonal and diurnal variations in the DSD over the western Tianshan Mountains (China) and to apply more vertical observation equipment for studying the rainfall process.