3D Convolutional Neural Network for Low-Light Image Sequence Enhancement in SLAM
Abstract
:1. Introduction
1.1. Overview
1.2. Conventional Image Enhancement
1.3. Image Enhancement Based on Deep Learning
1.4. Contributions
- In view of the image characteristics used by visual SLAM, we propose a low-light image enhancement method that considers time consistency by introducing a 3D convolution module.
- To satisfy requirements for feature point extraction and matching, we introduce a loss function for spatial consistency. By expanding the measurement range of the spatial consistency loss, texture features are preserved in the regions of the enhanced image, and the stability and repeatability of feature point extraction are improved.
- The proposed image enhancement method is integrated into the VINS-Mono estimator [10] and tested on low-light sequences. Among five evaluated methods, our proposal achieves the minimum positioning error, thus improving the robustness and positioning accuracy of SLAM in low-light environments.
2. Proposed Image Enhancement Method
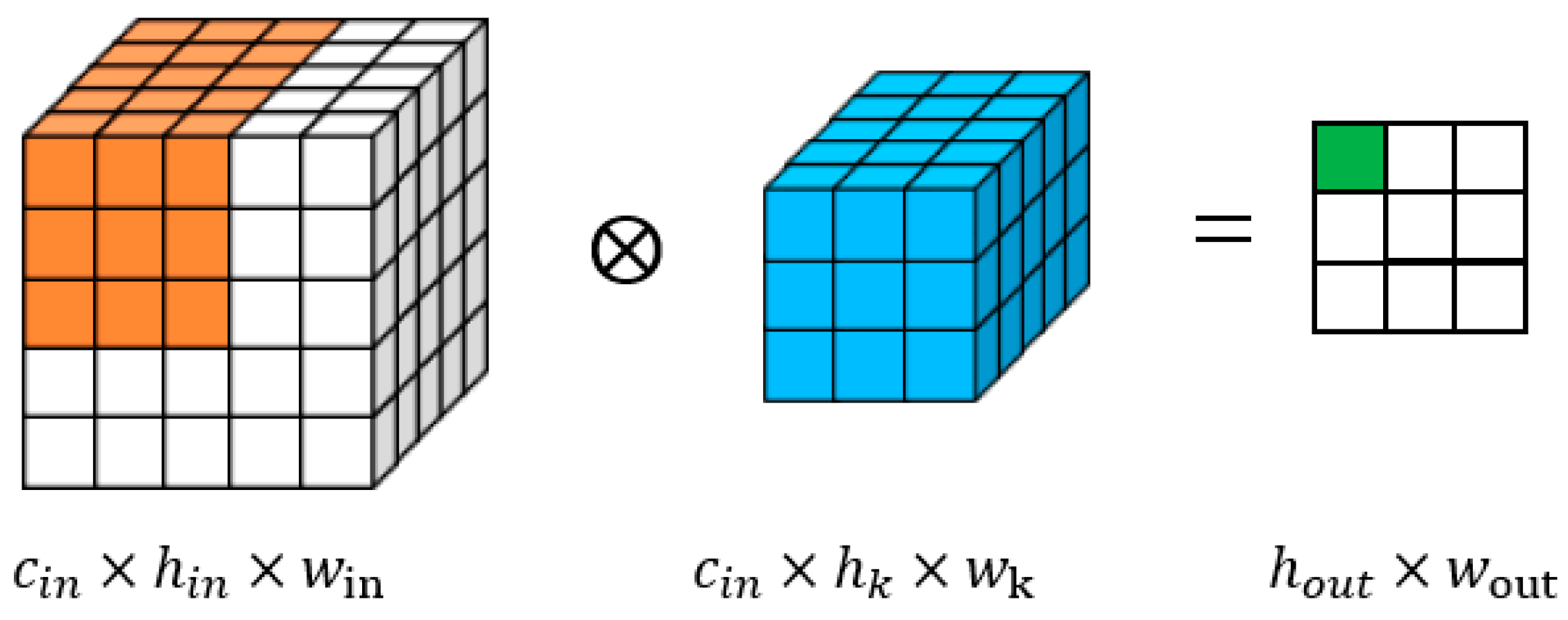
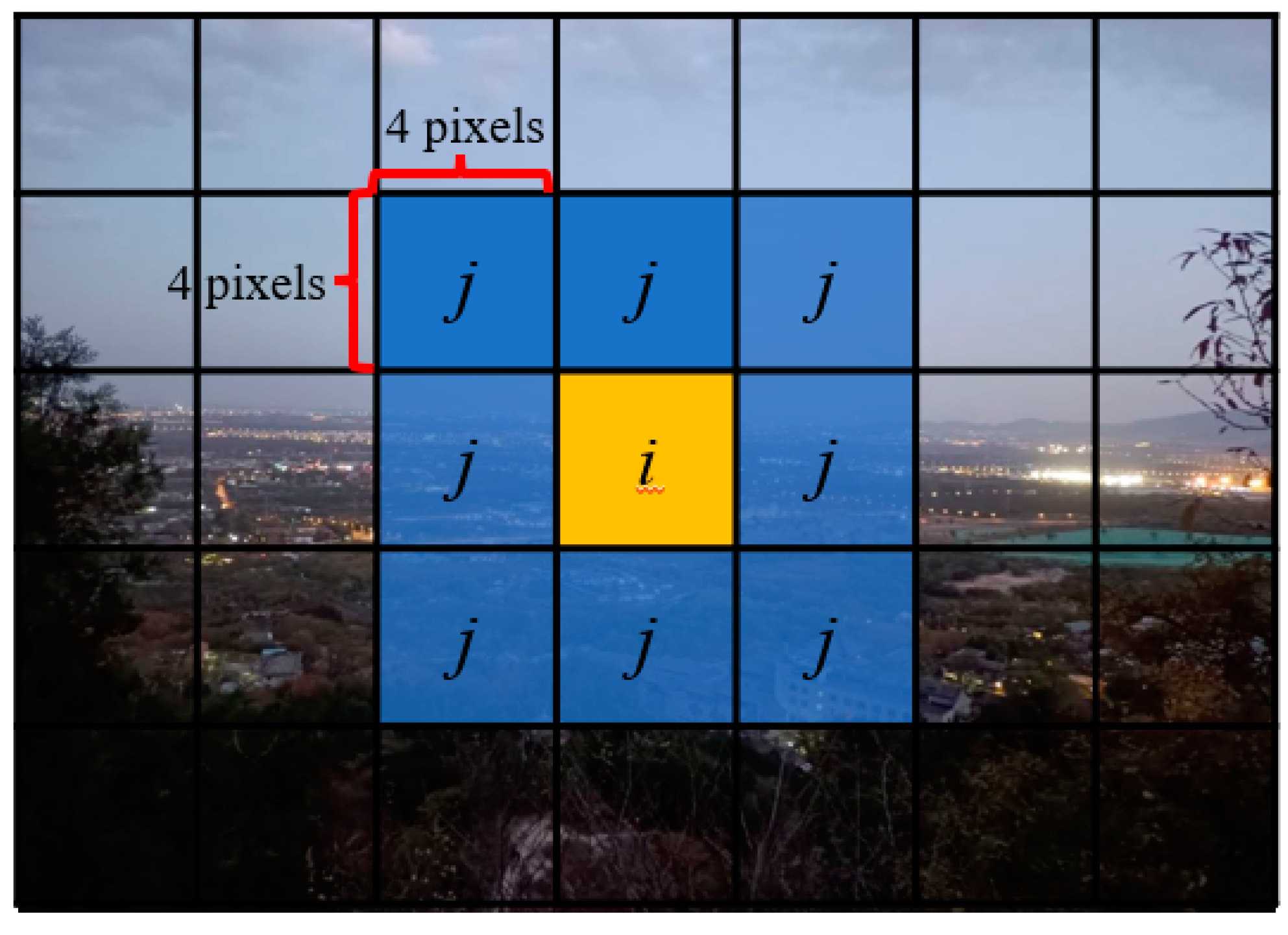
2.1. Two-Dimensional and Three-Dimensional Convolutions
2.1.1. Two-Dimensional Convolution
2.1.2. Three-Dimensional Convolution
2.1.3. Depthwise Separable Convolution
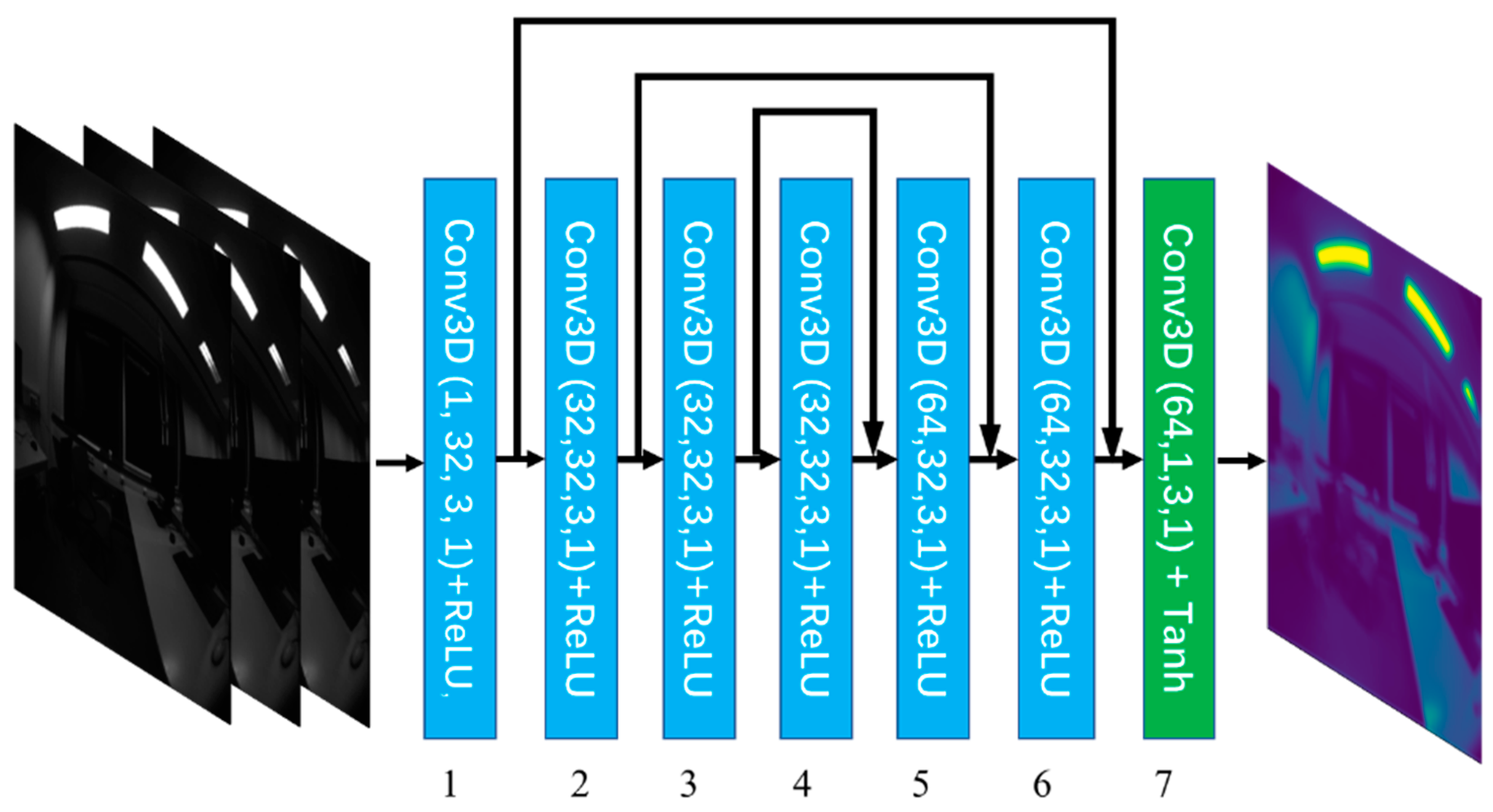
2.2. 3D-DCE++
2.2.1. Curve Parameter Estimation
2.2.2. Iterative Enhancement
2.2.3. Loss Function
3. Experiments and Results
3.1. Experimental Setup
3.2. Low-Light Image Enhancement
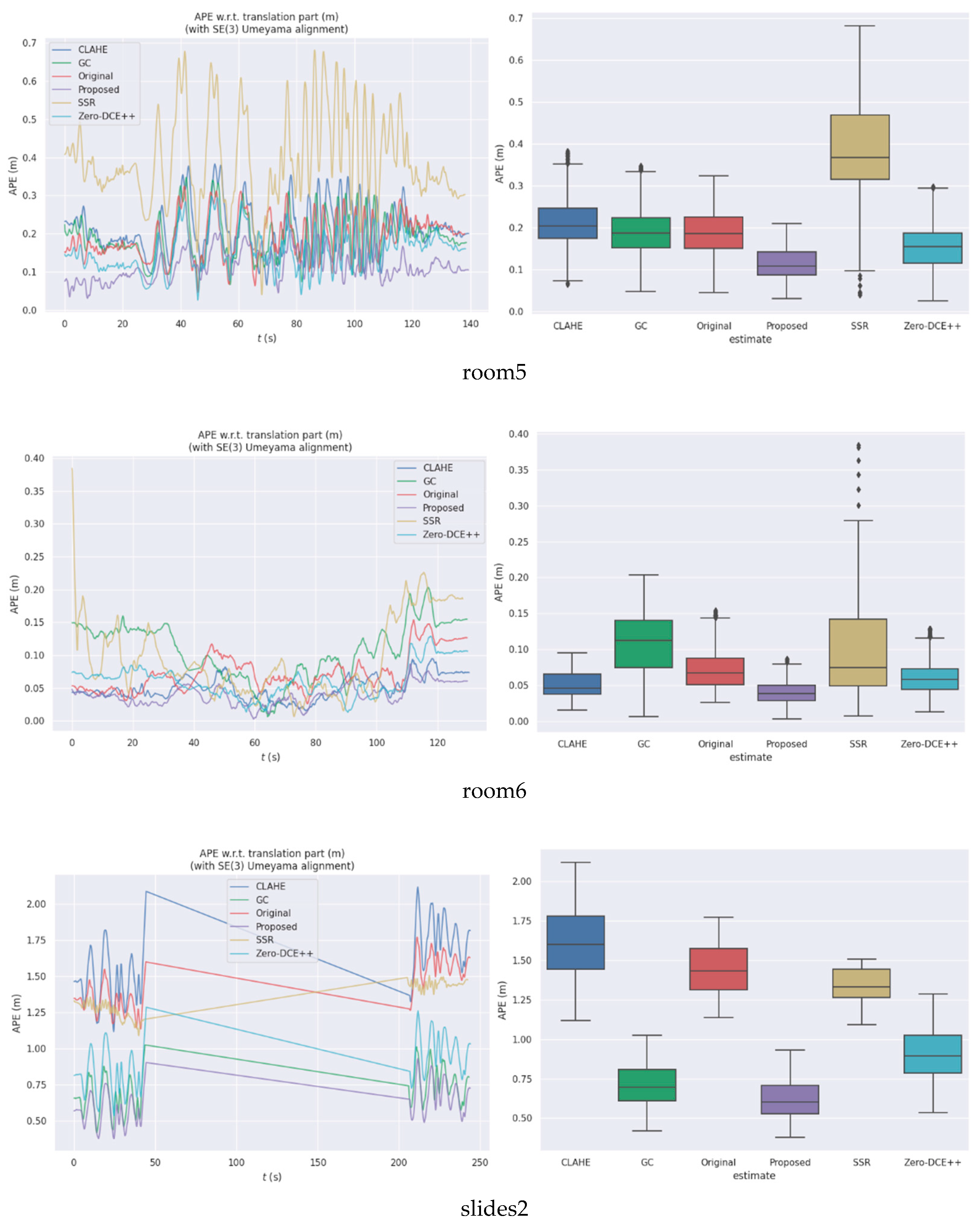
3.3. Sequence Positioning Error
4. Discussion
- Deep-learning-based methods have recently attracted significant attention in the SLAM research field. Due to the powerful feature representation ability of the data, a deep neural network can learn more general visual features. This property means a deep learning model can be used to relieve some challenges for geometry-based visual odometry, such as featureless areas, dynamic lighting conditions, and motion blur. Our research is aimed at combining the deep-learning-based low-light image enhancement methods with geometry-based visual odometry to improve the robustness of the visual SLAM system in a low-light environment. Zero-DCE++ employs zero-reference learning and a lightweight network to complete the low-light image enhancement task. These characteristics offer Zero-DCE++ the advantages of a flexible generalization capability and real-time inference speed. Moreover, we notice that the input data of the visual SLAM system have a strong temporal correlation. The ability to analyze a series of frames in context led to 3D convolution being used as a tool for spatiotemporal feature extractors in video analytics research. Therefore, we replaced the 2D convolution with 3D convolution to extract the temporal feature of the input image sequence. To improve the stability of feature point extraction, we abandoned the downsampling operation and strengthened the spatial consistency constraint. To evaluate the proposed method, we integrated different methods into VINS-Mono and compared their positioning error.
- The quantitative results in Table 2 show that both learning-based methods reduce the system’s positioning error on all sequences, while traditional methods increase positioning error on some sequences. We considered that the main reason may be that the parameters for image enhancement of traditional methods are fixed, while Zero-DCE++ and our method are constantly changing according to the input images. This also proves that the proposed method generalizes well to different lighting conditions.
- To analyze the computational complexity and model complexity increase by 3D convolution, we calculated the floating-point operations (FLOPs) and the number of parameters of Zero-DCE++ and our method. Following Section 3.2 and Section 3.3, we used the original size of the input image to calculate the FLOPs of Zero-DCE++ without downsampling. For an input image of size , the FLOPs and trainable parameters of the two methods are shown in Table 3. As shown in Table 3, the costs of introducing 3D convolution into Zero-DCE++ are that the FLOPs increased by two times and the number of parameters increased to 15K. Thankfully, for 15k, 7.89G FLOPs of 3D-DCE++ is still smaller than the technical specifications of existing NVIDIA edge platforms (Jetson Nano 4GB, 472G FLOPs; Jetson TX2: 8GB, 1.3T FLOPs) [43,44]. The proposed method can be deployed on specialized embedded devices.
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| SLAM | simultaneous localization and mapping |
| 2D | two-dimensional |
| IMU | inertial measurement unit |
| VINS | visual inertial system |
| 3D | three-dimensional |
| CLAHE | contrast-limited adaptive histogram equalization |
| GC | gamma correction |
| SSR | single-scale Retinex |
| RMSE | root-mean-squared error |
References
- Nguyen, H.; Mascarich, F.; Dang, T.; Alexis, K. Autonomous aerial robotic surveying and mapping with application to construction operations. arXiv 2020, arXiv:2005.04335. [Google Scholar] [CrossRef]
- Liu, Z.; Di, K.; Li, J.; Xie, J.; Cui, X.; Xi, L.; Wan, W.; Peng, M.; Liu, B.; Wang, Y.; et al. Landing site topographic mapping and rover localization for Chang’e-4 mission. Sci. China Inf. Sci. 2020, 63, 140901. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, H.; Lu, H.; Xiao, J.; Qiu, Q.; Li, Y. Robust SLAM System based on Monocular Vision and LiDAR for Robotic Urban Search and Rescue. In Proceedings of the 2017 IEEE International Symposium on Safety, Security and Rescue Robotics (SSRR), Shanghai, China, 11–13 October 2017; pp. 41–47. [Google Scholar] [CrossRef]
- Chiang, K.-W.; Tsai, G.-J.; Li, Y.-H.; Li, Y.; El-Sheimy, N. Navigation engine design for automated driving using INS/GNSS/3D LiDAR-SLAM and integrity assessment. Remote Sens. 2020, 12, 1564. [Google Scholar] [CrossRef]
- Kaichang, D.I.; Wenhui, W.A.; Hongying, Z.H.; Zhaoqin, L.I.; Runzhi, W.A.; Feizhou, Z.H. Progress and applications of visual SLAM. Acta Geod. Cartogr. Sin. 2018, 47, 770. [Google Scholar] [CrossRef]
- Cadena, C.; Carlone, L.; Carrillo, H.; Latif, Y.; Scaramuzza, D.; Neira, J.; Reid, I.D.; Leonard, J.J. Simultaneous localization and mapping: Present, future, and the robust-perception age. IEEE Trans. Robot. 2016, 32, 1309–1332. [Google Scholar] [CrossRef]
- Davison, A.J.; Reid, I.D.; Molton, N.D.; Stasse, O. MonoSLAM: Real-time single camera SLAM. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 29, 1052–1067. [Google Scholar] [CrossRef]
- Hartley, R.; Zisserman, A. Multiple View Geometry in Computer Vision; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Nützi, G.; Weiss, S.; Scaramuzza, D.; Siegwart, R.J. Fusion of IMU and vision for absolute scale estimation in monocular SLAM. J. Intell. Robot. Syst. 2011, 61, 287–299. [Google Scholar] [CrossRef]
- Qin, T.; Li, P.; Shen, S. Vins-mono: A robust and versatile monocular visual-inertial state estimator. IEEE Trans. Robot. 2018, 34, 1004–1020. [Google Scholar] [CrossRef]
- Campos, C.; Elvira, R.; Rodríguez, J.J.G.; Montiel, J.M.; Tardós, J.D. ORB-SLAM3: An accurate open-source library for visual, visual–inertial, and multimap SLAM. IEEE Trans. Robot. 2021, 37, 1874–1890. [Google Scholar] [CrossRef]
- Mourikis, A.I.; Roumeliotis, S.I. A Multi-State Constraint Kalman Filter for Vision-Aided Inertial Navigation. In Proceedings of the 2007 IEEE International Conference on Robotics and Automation, Roma, Italy, 10–14 April 2007; pp. 3565–3572. [Google Scholar] [CrossRef]
- Li, C.; Guo, C.; Han, L.-H.; Jiang, J.; Cheng, M.-M.; Gu, J.; Loy, C.C. Low-light image and video enhancement using deep learning: A survey. IEEE Trans. Pattern Anal. Mach. Intell. 2021. [Google Scholar] [CrossRef]
- Harris, C.; Stephens, M. A Combined Corner and Edge Detector. In Proceedings of the Alvey Vision Conference, Manchester, UK, 31 August–2 September 1988; pp. 147–151. [Google Scholar]
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Rublee, E.; Rabaud, V.; Konolige, K.; Bradski, G. ORB: An Efficient Alternative to SIFT or SURF. In Proceedings of the 2011 International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; pp. 2564–2571. [Google Scholar] [CrossRef]
- Abdullah-Al-Wadud, M.; Kabir, M.H.; Dewan, M.A.A.; Chae, O. A dynamic histogram equalization for image contrast enhancement. IEEE Trans. Consum. Electron. 2007, 53, 593–600. [Google Scholar] [CrossRef]
- Ibrahim, H.; Kong, N.S. Brightness preserving dynamic histogram equalization for image contrast enhancement. IEEE Trans. Consum. Electron. 2007, 53, 1752–1758. [Google Scholar] [CrossRef]
- Pisano, E.D.; Zong, S.; Hemminger, B.M.; DeLuca, M.; Johnston, R.E.; Muller, K.; Braeuning, M.P.; Pizer, S.M. Contrast limited adaptive histogram equalization image processing to improve the detection of simulated spiculations in dense mammograms. J. Digit. Imaging 1998, 11, 193–200. [Google Scholar] [CrossRef]
- Jeong, I.; Lee, C. An optimization-based approach to gamma correction parameter estimation for low-light image enhancement. Multimed. Tools Appl. 2021, 80, 18027–18042. [Google Scholar] [CrossRef]
- Li, C.; Tang, S.; Yan, J.; Zhou, T. Low-light image enhancement based on quasi-symmetric correction functions by fusion. Symmetry 2020, 12, 1561. [Google Scholar] [CrossRef]
- Xu, Q.; Jiang, H.; Scopigno, R.; Sbert, M. A novel approach for enhancing very dark image sequences. Signal Process. 2014, 103, 309–330. [Google Scholar] [CrossRef]
- Land, E.H. The retinex theory of color vision. Sci. Am. 1977, 237, 108–129. [Google Scholar] [CrossRef]
- Parihar, A.S.; Singh, K. A Study on Retinex Based Method for Image Enhancement. In Proceedings of the 2018 2nd International Conference on Inventive Systems and Control (ICISC), Coimbatore, India, 19–20 January 2018; pp. 619–624. [Google Scholar] [CrossRef]
- Zotin, A. Fast algorithm of image enhancement based on multi-scale retinex. Procedia Comput. Sci. 2018, 131, 6–14. [Google Scholar] [CrossRef]
- Fu, X.; Zeng, D.; Huang, Y.; Zhang, X.-P.; Ding, X. A Weighted Variational Model for Simultaneous Reflectance and Illumination Estimation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018; pp. 2782–2790. [Google Scholar] [CrossRef]
- Li, M.; Liu, J.; Yang, W.; Sun, X.; Guo, Z. Structure-revealing low-light image enhancement via robust retinex model. IEEE Trans. Image Process. 2018, 27, 2828–2841. [Google Scholar] [CrossRef]
- Lore, K.G.; Akintayo, A.; Sarkar, S. LLNet: A deep autoencoder approach to natural low-light image enhancement. Pattern Recognit. 2017, 61, 650–662. [Google Scholar] [CrossRef]
- Lv, F.; Lu, F.; Wu, J.; Lim, C. MBLLEN: Low-Light Image/Video Enhancement Using CNNs. In Proceedings of the 29th British Machine Vision Conference (BMVC), Northumbria University, Newcastle, UK, 3–6 September 2018; p. 4. [Google Scholar]
- Wei, C.; Wang, W.; Yang, W.; Liu, J.J. Deep retinex decomposition for low-light enhancement. arXiv 2018, arXiv:1808.04560. [Google Scholar]
- Zhang, Y.; Guo, X.; Ma, J.; Liu, W.; Zhang, J. Beyond brightening low-light images. Int. J. Comput. Vis. 2021, 129, 1013–1037. [Google Scholar] [CrossRef]
- Ren, W.; Liu, S.; Ma, L.; Xu, Q.; Xu, X.; Cao, X.; Du, J.; Yang, M.-H. Low-light image enhancement via a deep hybrid network. IEEE Trans. Image Process. 2019, 28, 4364–4375. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Zhang, L.; Liu, X.; Shen, Y.; Zhang, S.; Zhao, S. Zero-Shot Restoration of Back-Lit Images Using Deep Internal Learning. In Proceedings of the 2019 ACM International Conference on Multimedia (ACMMM), Nice, France, 21–25 October 2019; pp. 1623–1631. [Google Scholar] [CrossRef]
- Guo, C.; Li, C.; Guo, J.; Loy, C.C.; Hou, J.; Kwong, S.; Cong, R. Zero-Reference Deep Curve Estimation for Low-Light Image Enhancement. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Virtual, 14–19 June 2020; pp. 1780–1789. [Google Scholar]
- Li, C.; Guo, C.; Loy, C.C. Learning to enhance low-light image via zero-reference deep curve estimation. arXiv 2021, arXiv:2103.00860. [Google Scholar] [CrossRef]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going Deeper with Convolutions. In Proceedings of the 2015 the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Ji, S.; Xu, W.; Yang, M.; Yu, K. 3D convolutional neural networks for human action recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 35, 221–231. [Google Scholar] [CrossRef]
- Tran, D.; Bourdev, L.; Fergus, R.; Torresani, L.; Paluri, M. Learning Spatiotemporal Features with 3D Convolutional Networks. In Proceeding of the 2015 IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 13–16 December 2015; pp. 4489–4497. [Google Scholar]
- Schubert, D.; Goll, T.; Demmel, N.; Usenko, V.; Stückler, J.; Cremers, D. The TUM VI Benchmark for Evaluating Visual-Inertial Odometry. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 1680–1687. [Google Scholar] [CrossRef]
- Grupp, M. Evo: Python Package for the Evaluation of Odometry and SLAM; 2017. Available online: http://github.com/MichaelGrupp/evo (accessed on 1 July 2022).
- Sturm, J.; Engelhard, N.; Endres, F.; Burgard, W.; Cremers, D. A Benchmark for the Evaluation of RGB-D SLAM Systems. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Algarve, Portugal, 7–12 October 2012; pp. 573–580. [Google Scholar] [CrossRef]
- Süzen, A.A.; Duman, B.; Şen, B. Benchmark Analysis of Jetson tx2, Jetson Nano and Raspberry pi Using Deep-cnn. In Proceedings of the 2020 International Congress on Human-Computer Interaction, Optimization and Robotic Applications (HORA), Ankara, Turkey, 26–28 June 2020; pp. 1–5. [Google Scholar]
- Ullah, S.; Kim, D.-H. Benchmarking Jetson platform for 3D Point-Cloud and Hyper-Spectral Image Classification. In Proceedings of the 2020 IEEE International Conference on Big Data and Smart Computing (BigComp), Busan, Korea, 19–22 February 2020; pp. 477–482. [Google Scholar]

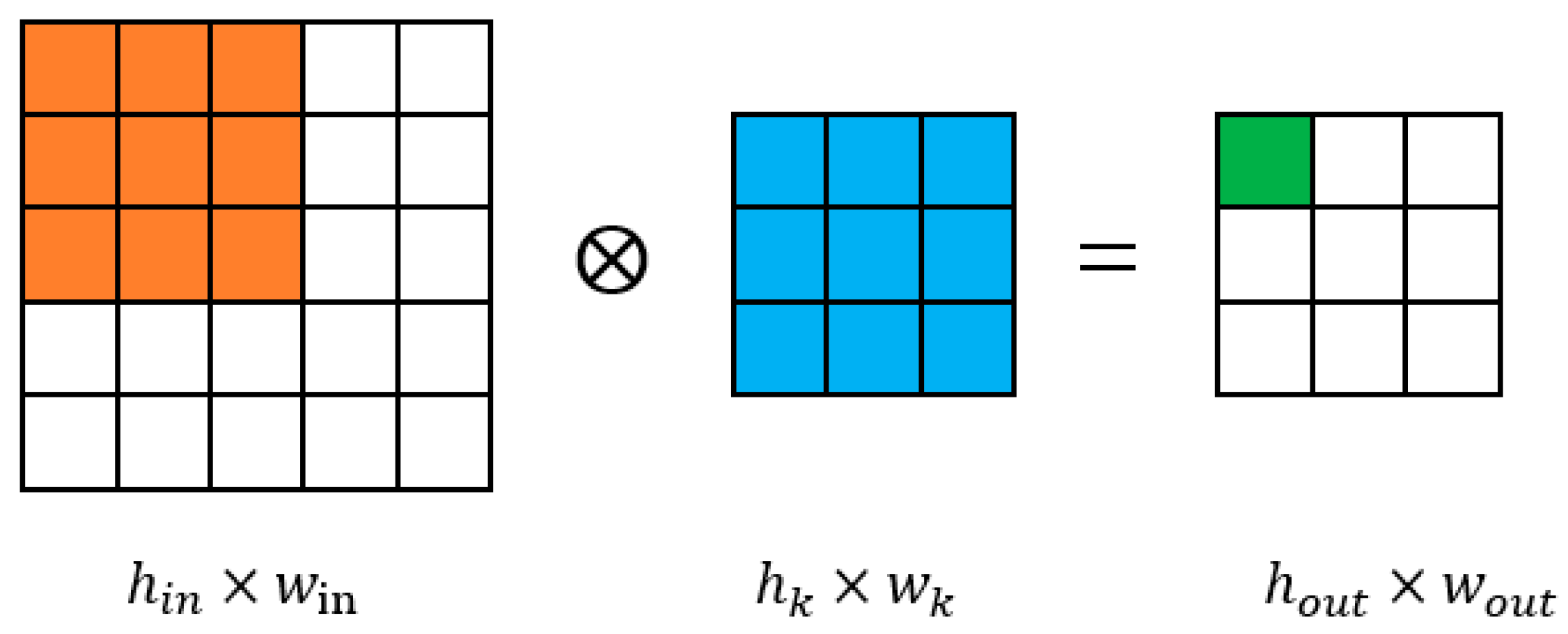
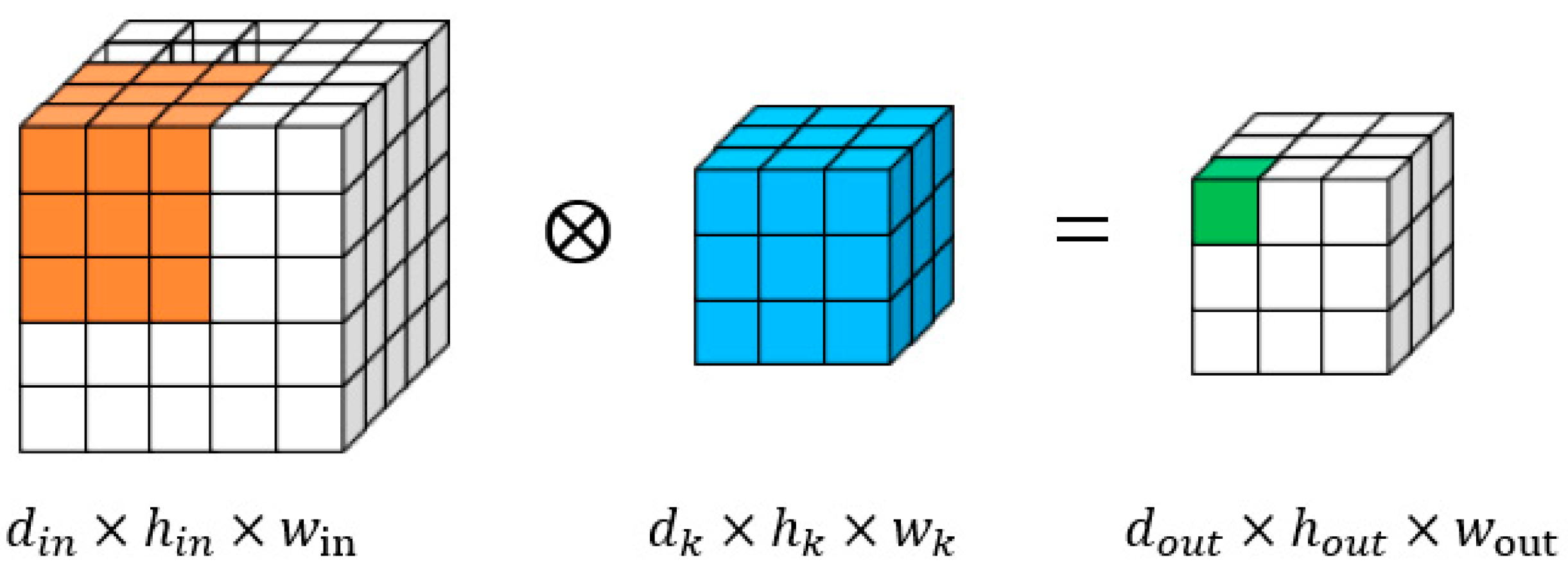







| Method | Computation Time per Frame (s) |
|---|---|
| CLAHE | 0.000150 |
| GC | 0.000800 |
| SSR | 0.032917 |
| Zero-DCE++ | 0.012503 |
| 3D-DCE++ (Ours) | 0.015070 |
| Sequence | Original | CLAHE | GC | SSR | Zero-DCE++ | 3D-DCE++ (Ours) | Compared with Zero-DCE++ |
|---|---|---|---|---|---|---|---|
| corridor1 | 2.3635 | 0.4137 | 0.7454 | 5.0429 | 0.4667 | 0.3913 | 16.15% |
| corridor5 | 0.3557 | 0.5608 | 0.6721 | 0.7177 | 0.3177 | 0.2547 | 19.83% |
| room1 | 0.0875 | 0.0521 | 0.0671 | 0.1212 | 0.0396 | 0.0395 | 0.18% |
| room2 | 0.1246 | 0.0792 | 0.1200 | 0.1571 | 0.0823 | 0.0696 | 15.38% |
| room5 | 0.1979 | 0.2224 | 0.2002 | 0.4092 | 0.1646 | 0.1215 | 26.18% |
| room6 | 0.0795 | 0.0532 | 0.1160 | 0.1130 | 0.0662 | 0.0423 | 36.18% |
| slides2 | 1.4485 | 0.6215 | 0.7181 | 1.3489 | 0.9114 | 0.6313 | 30.73% |
| Method | FLOPs | Number of Parameters |
|---|---|---|
| Zero-DCE++ | 2.65G | 10k |
| Ours | 7.89G | 15k |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Quan, Y.; Fu, D.; Chang, Y.; Wang, C. 3D Convolutional Neural Network for Low-Light Image Sequence Enhancement in SLAM. Remote Sens. 2022, 14, 3985. https://doi.org/10.3390/rs14163985
Quan Y, Fu D, Chang Y, Wang C. 3D Convolutional Neural Network for Low-Light Image Sequence Enhancement in SLAM. Remote Sensing. 2022; 14(16):3985. https://doi.org/10.3390/rs14163985
Chicago/Turabian StyleQuan, Yizhuo, Dong Fu, Yuanfei Chang, and Chengbo Wang. 2022. "3D Convolutional Neural Network for Low-Light Image Sequence Enhancement in SLAM" Remote Sensing 14, no. 16: 3985. https://doi.org/10.3390/rs14163985
APA StyleQuan, Y., Fu, D., Chang, Y., & Wang, C. (2022). 3D Convolutional Neural Network for Low-Light Image Sequence Enhancement in SLAM. Remote Sensing, 14(16), 3985. https://doi.org/10.3390/rs14163985






