Sensitivity Analysis of Ozone Profiles Retrieved from SCIAMACHY Limb Radiance Based on the Weighted Multiplicative Algebraic Reconstruction Technique
Abstract
:1. Introduction
2. Materials and Retrieval Method
2.1. Instrumentation Overview and Datasets Used for Experiments
2.2. Description of Retrieval Method
2.2.1. Radiance Normalization
2.2.2. Wavelength Pairing
2.2.3. Weighted Multiplicative Algebraic Reconstruction Technique
2.3. Radiative Transfer Model
3. Description of Sensitivity Analysis
3.1. Retrieval Error Method
3.2. Error Calculation
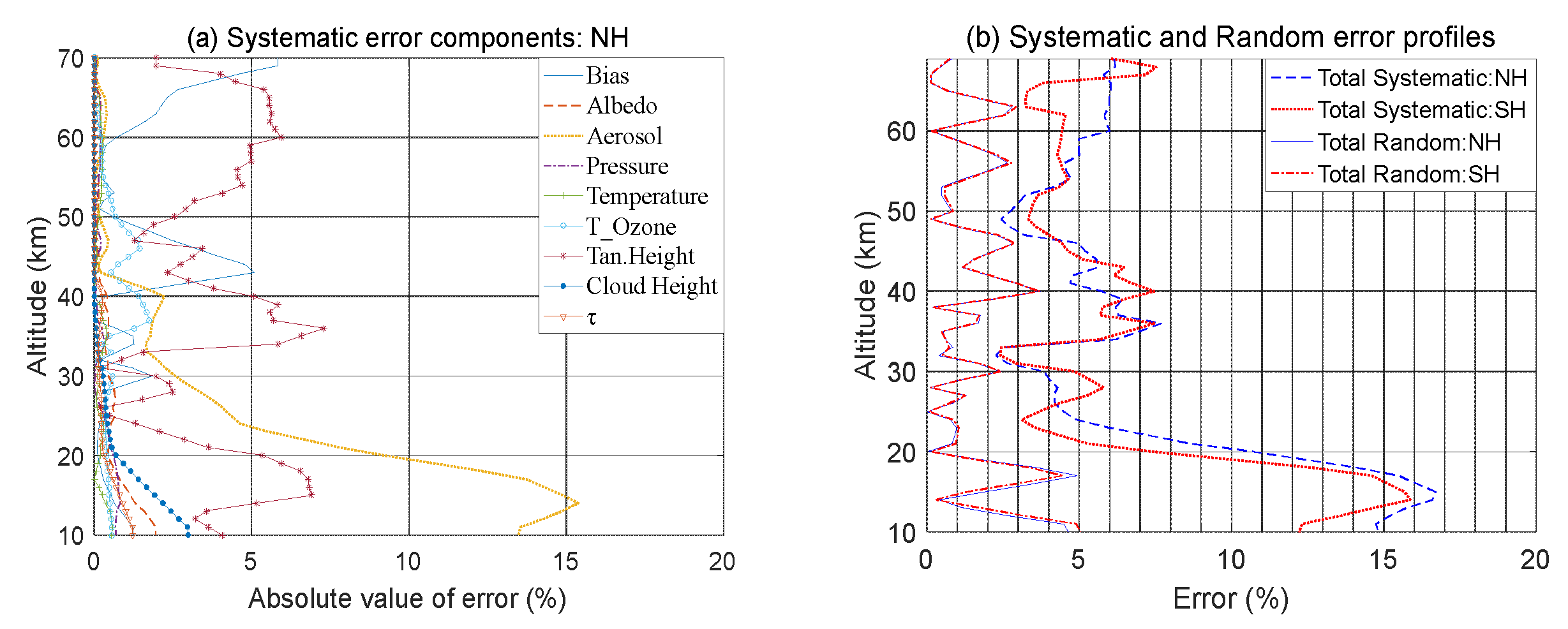
3.3. Systematic and Random Errors
4. Experiments and Results
4.1. Impact of Error Sources
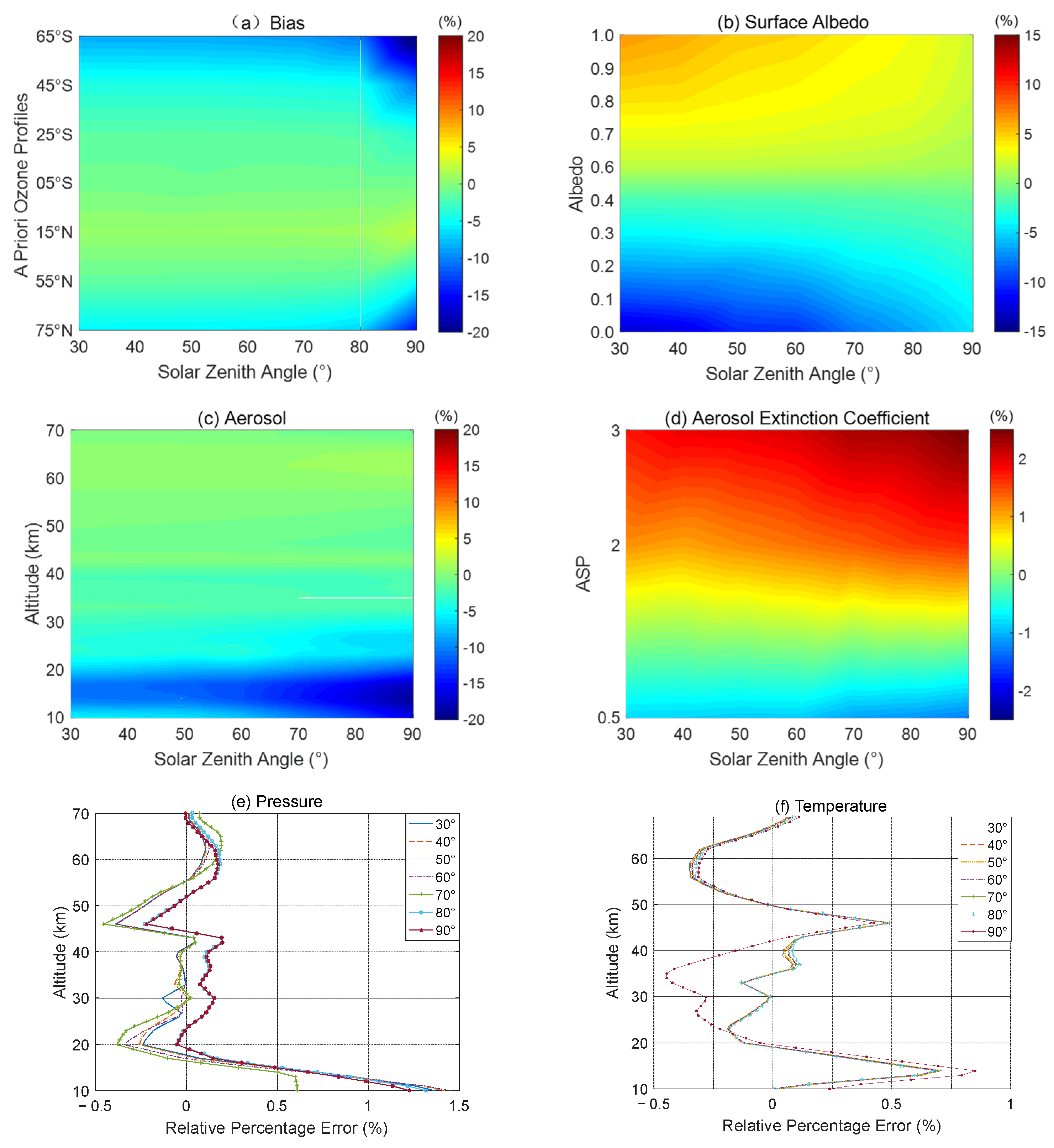
4.1.1. Bias and Smoothing Error
4.1.2. Parameters Errors in Forward Model
Surface Albedo
Aerosols
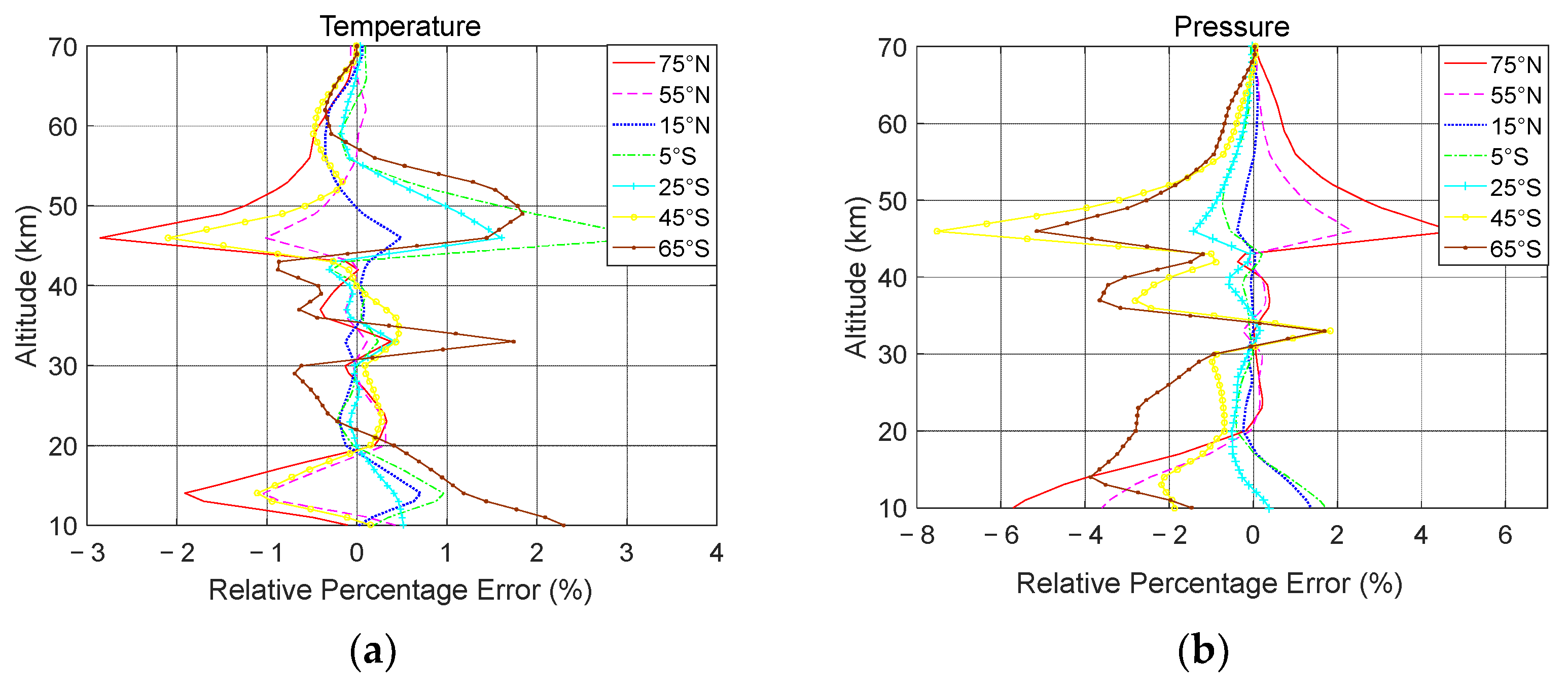
Pressure
Temperature
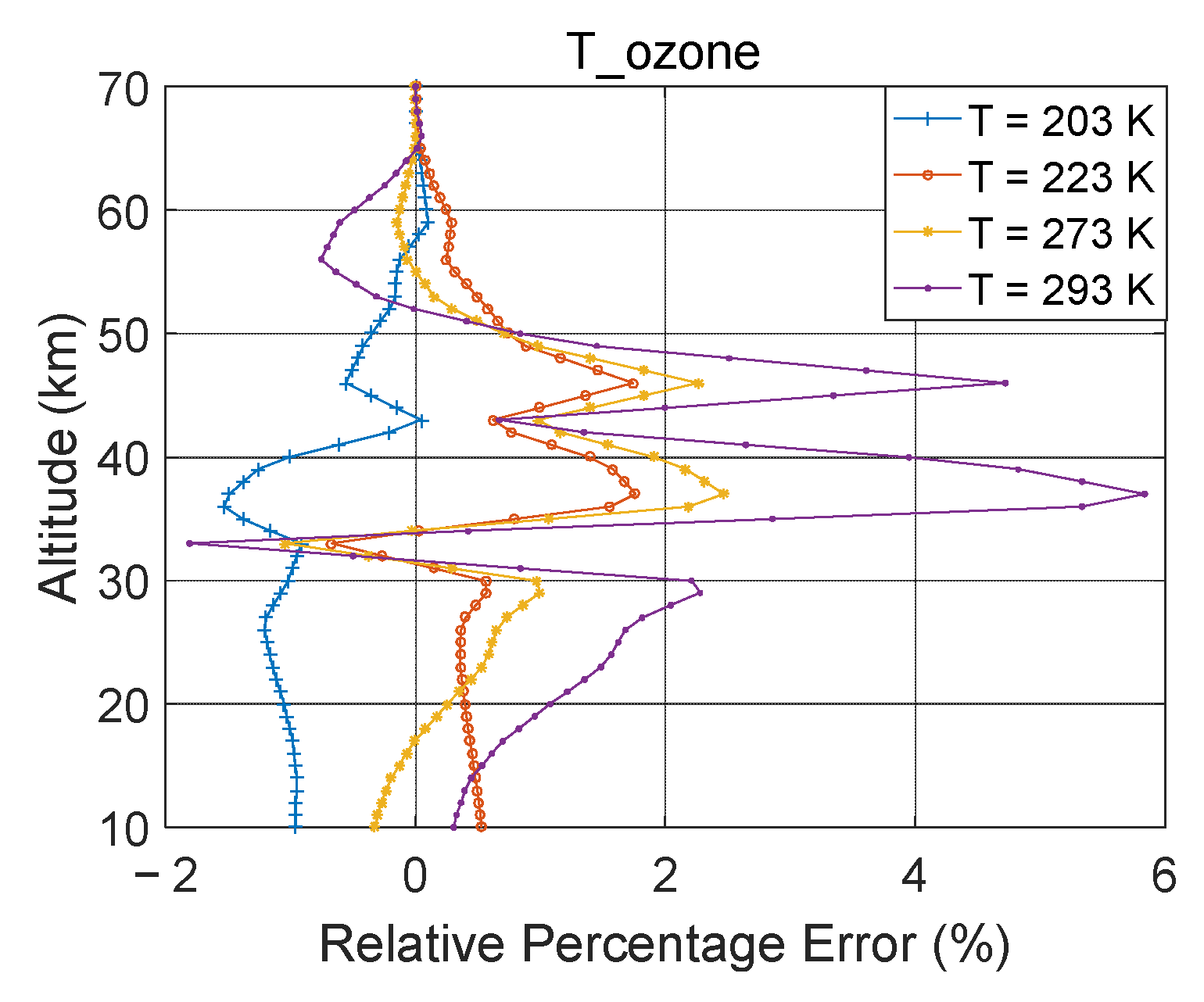
Ozone Absorption Cross Section
4.1.3. Measurement Error
Pointing Error
Noise Error
4.1.4. Cloud Error
Cloud Height
Cloud Optical Thickness
4.1.5. Total
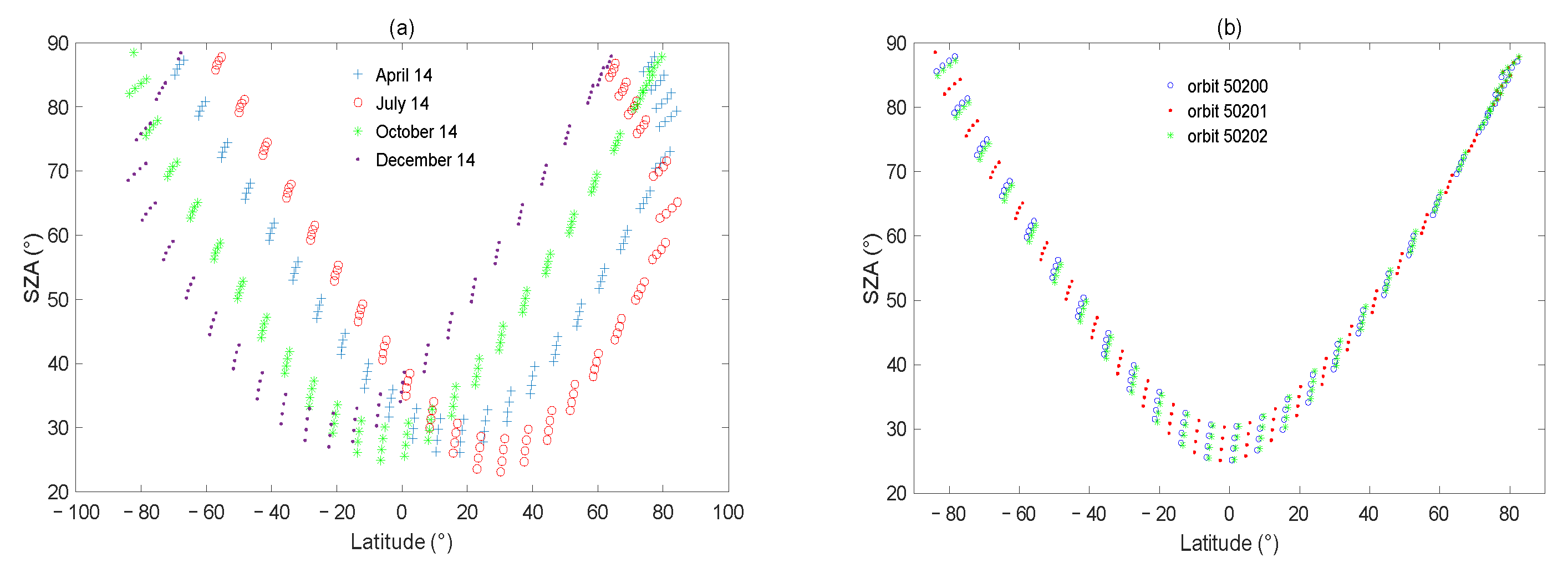
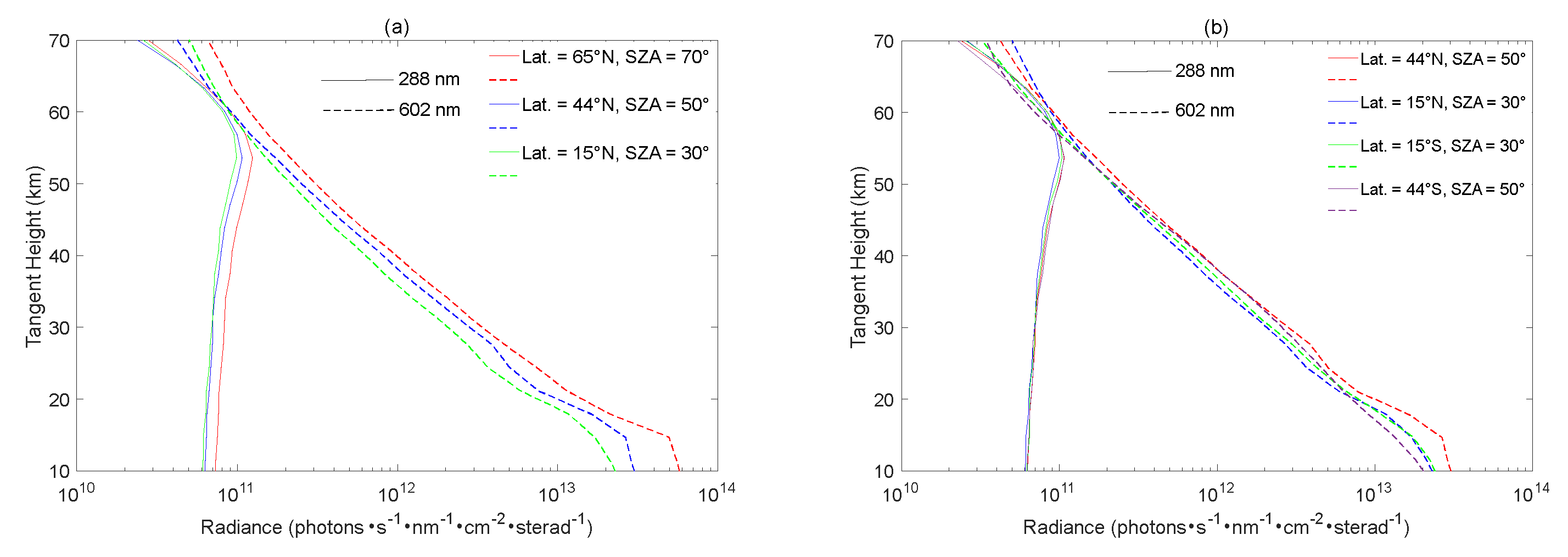
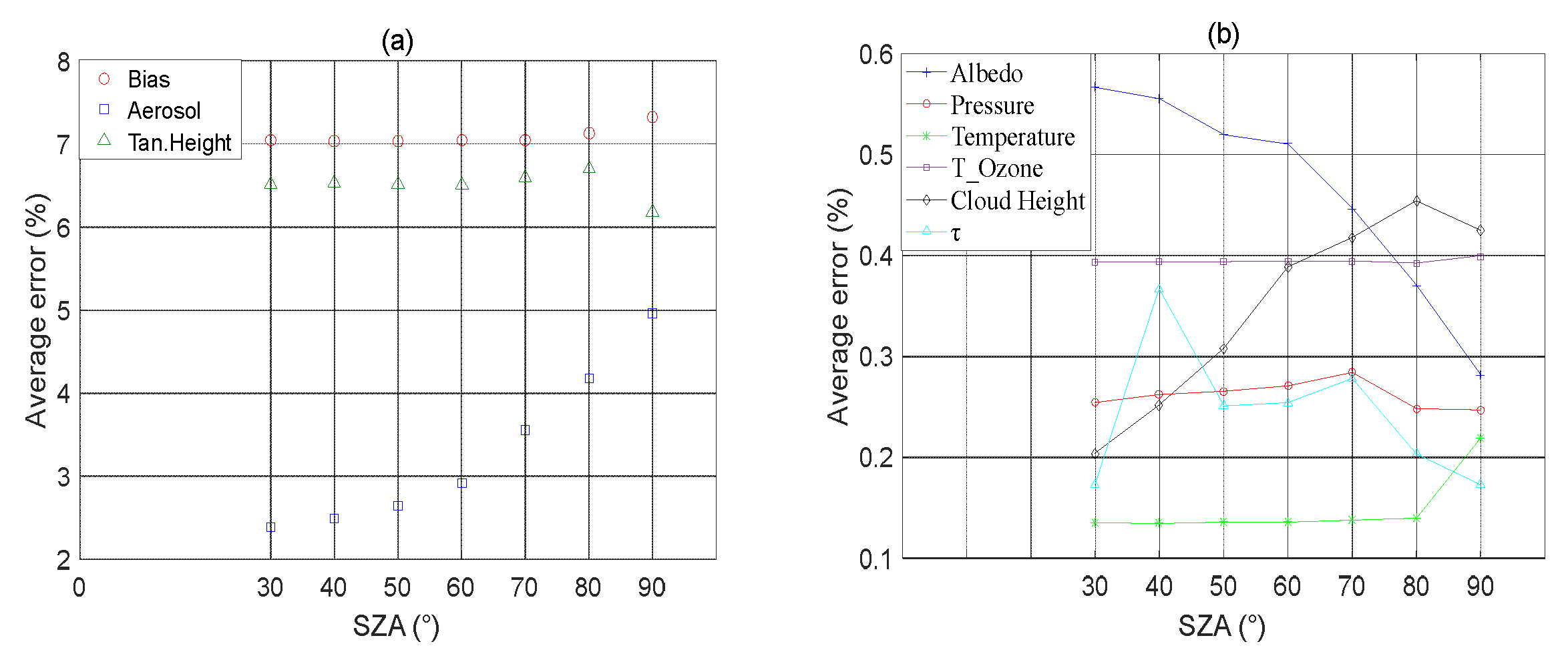
4.2. Impact of Solar Zenith Angle
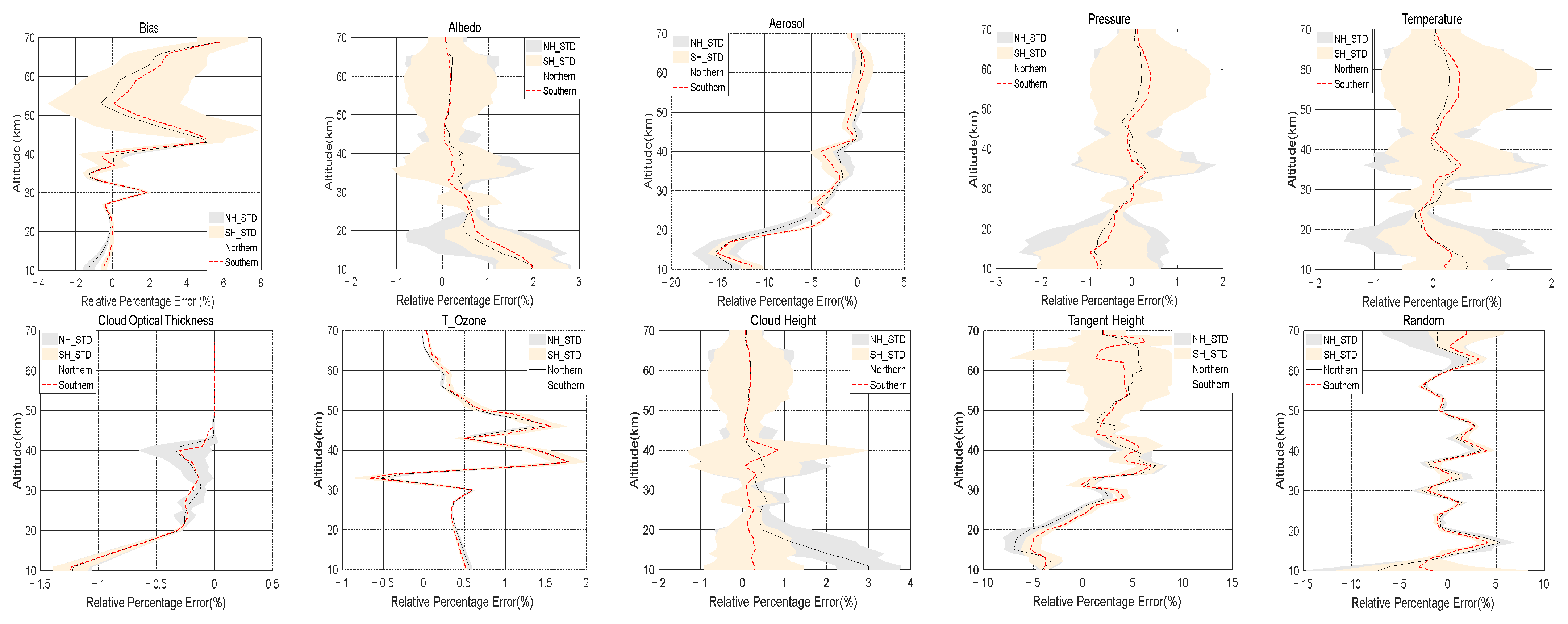
4.3. Differences between the Northern and Southern Hemispheres
5. Discussion
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
- 1.
- A Priori Averaging Kernel ()
- 2.
- Averaging Kernel ()
- 3.
- The Sensitivity of Model Parameters
- 4.
- The Vector/Retrieval Kernel ()
- 5.
- Random Radiance Vector
- 6.
- Cloud Sensitivity
References
- Arosio, C.; Rozanov, A.; Malinina, E.; Eichmann, K.-U.; von Clarmann, T.; Burrows, J.P. Retrieval of ozone profiles from OMPS limb scattering observations. Atmos. Meas. Tech. 2018, 11, 2135–2149. [Google Scholar] [CrossRef]
- Farman, J.C.; Gardiner, B.G.; Shanklin, J.D. Large Losses of Total Ozone in Antarctica Reveal Seasonal Clox/Nox Interaction. Nature 1985, 315, 207–210. [Google Scholar] [CrossRef]
- Cicerone, R.J.; Stolarski, R.S.; Walters, S. Stratospheric Ozone Destruction by Man-Made Chlorofluoromethanes. Science 1974, 185, 1165–1167. [Google Scholar] [CrossRef] [PubMed]
- Solomon, S.; Ivy, D.J.; Kinnison, D.; Mills, M.J.; Neely, R.R.; Schmidt, A. Emergence of healing in the Antarctic ozone layer. Science 2016, 353, 269–274. [Google Scholar] [CrossRef]
- Li, F.; Stolarski, R.S.; Newman, P.A. Stratospheric ozone in the post-CFC era. Atmos. Chem. Phys. 2009, 9, 2207–2213. [Google Scholar] [CrossRef]
- Hassler, B.; Petropavlovskikh, I.; Staehelin, J.; August, T.; Bhartia, P.K.; Clerbaux, C.; Degenstein, D.; De Maziere, M.; Dinelli, B.M.; Dudhia, A.; et al. Past changes in the vertical distribution of ozone—Part 1: Measurement techniques, uncertainties and availability. Atmos. Meas. Tech. 2014, 7, 1395–1427. [Google Scholar] [CrossRef]
- Van Peet, J.C.A.; van der, A.R.J.; de Laat, A.T.J.; Tuinder, O.N.E.; König-Langlo, G.; Wittig, J. Height resolved ozone hole structure as observed by the Global Ozone Monitoring Experiment-2. Geophys. Res. Lett. 2009, 36, 269–271. [Google Scholar] [CrossRef]
- Huang, F.; Liu, N.; Zhao, M.-X.; Wang, S.; Huang, Y. Vertical ozone profiles deduced from measurements of SBUS on FY-3 satellite. Chin. Sci. Bull. 2010, 55, 943–948. [Google Scholar] [CrossRef]
- Levelt, P.F.; Van den Oord, G.H.J.; Dobber, M.R.; Malkki, A.; Visser, H.; de Vries, J.; Stammes, P.; Lundell, J.O.V.; Saari, H. The Ozone Monitoring Instrument. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1093–1101. [Google Scholar] [CrossRef]
- Qian, Y.; Luo, Y.; Si, F.; Zhou, H.; Yang, T.; Yang, D.; Xi, L. Total Ozone Columns from the Environmental Trace Gases Monitoring Instrument (EMI) Using the DOAS Method. Remote Sens. 2021, 13, 2098. [Google Scholar] [CrossRef]
- Bertaux, J.L.; Kyrölä, E.; Fussen, D.; Hauchecorne, A.; Dalaudier, F.; Sofieva, V.; Tamminen, J.; Vanhellemont, F.; D’Andon, O.F.; Barrot, G.; et al. Global ozone monitoring by occultation of stars: An overview of GOMOS measurements on ENVISAT. Atmos. Chem. Phys. 2010, 10, 12091–12148. [Google Scholar] [CrossRef]
- Chateauneuf, F.J.; Fortin, S.Y.; Buijs, H.L.; Soucy, M.-A.A. On-orbit performance of the ACE-FTS instrument. Earth Obs. Syst. Ix 2004, 5542, 166–175. [Google Scholar]
- Adams, C.; Bourassa, A.E.; Bathgate, A.F.; McLinden, C.A.; Lloyd, N.D.; Roth, C.Z.; Llewellyn, E.J.; Zawodny, J.M.; Flittner, D.E.; Manney, G.L.; et al. Characterization of Odin-OSIRIS ozone profiles with the SAGE II dataset. Atmos. Meas. Tech. 2013, 6, 1447–1459. [Google Scholar] [CrossRef]
- McPeters, R.D.; Janz, S.J.; Hilsenrath, E.; Brown, T.L.; Flittner, D.E.; Heath, D.F. The retrieval of O-3 profiles from limb scatter measurements: Results from the Shuttle Ozone Limb Sounding Experiment. Geophys. Res. Lett. 2000, 27, 2597–2600. [Google Scholar] [CrossRef]
- Llewellyn, E.; Lloyd, N.D.; Degenstein, D.A.; Gattinger, R.L.; Petelina, S.V.; Bourassa, A.E.; Wiensz, J.T.; Ivanov, E.V.; McDade, I.C.; Solheim, B.H.; et al. The OSIRIS instrument on the Odin spacecraft. Can. J. Phys. 2004, 82, 411–422. [Google Scholar] [CrossRef]
- Bovensmann, H.; Burrows, J.P.; Buchwitz, M.; Frerick, J.; Noël, S.; Rozanov, V.V.; Chance, K.V.; Goede, A.P.H. SCIAMACHY: Mission objectives and measurement modes. J. Atmos. Sci. 1999, 56, 127–150. [Google Scholar] [CrossRef]
- Rault, D.F. Ozone, NO2 and aerosol retrieval from SAGE III limb scatter measurements. Remote Sens. Clouds Atmos. Ix 2004, 5571, 205–216. [Google Scholar]
- Rault, D.F.; Loughman, R.P. The OMPS Limb Profiler Environmental Data Record Algorithm Theoretical Basis Document and Expected Performance. IEEE Trans. Geosci. Remote Sens. 2013, 51, 2505–2527. [Google Scholar] [CrossRef]
- von Savigny, C.; Haley, C.S.; Sioris, C.E.; McDade, I.C.; Llewellyn, E.J.; Degenstein, D.; Evans, W.F.J.; Gattinger, R.L.; Griffioen, E.; Kyrölä, E.; et al. Stratospheric ozone profiles retrieved from limb scattered sunlight radiance spectra measured by the OSIRIS instrument on the Odin satellite. Geophys. Res. Lett. 2003, 30, 107–218. [Google Scholar] [CrossRef]
- Loughman, R.P.; Flittner, D.E.; Herman, B.M.; Bhartia, P.K.; Hilsenrath, E.; McPeters, R.D. Description and sensitivity analysis of a limb scattering ozone retrieval algorithm. J. Geophys. Res. Atmos. 2005, 110. [Google Scholar] [CrossRef]
- Roth, C.; Degenstein, D.; Bourassa, A.; Llewellyn, E. The retrieval of vertical profiles of the ozone number density using Chappuis band absorption information and a multiplicative algebraic reconstruction technique. Can. J. Phys. 2007, 85, 1225–1243. [Google Scholar] [CrossRef]
- Sonkaew, T.; Rozanov, V.V.; Von Savigny, C.; Rozanov, A.; Bovensmann, H.; Burrows, J.P. Cloud sensitivity studies for stratospheric and lower mesospheric ozone profile retrievals from measurements of limb-scattered solar radiation. Atmos. Meas. Tech. 2009, 2, 653–678. [Google Scholar] [CrossRef]
- von Savigny, C.; McDade, I.C.; Griffioen, E.; Haley, C.S.; Sioris, C.E.; Llewellyn, E.J. Sensitivity studies and first validation of stratospheric ozone profile retrievals from Odin/OSIRIS observations of limb-scattered solar radiation. Can. J. Phys. 2005, 83, 957–972. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, S.; Jin, L.; Yang, C. Ozone profiles retrieval from SCIAMACHY Chappuis-Wulf limb scattered spectra using MART. Sci. China-Phys. Mech. Astron. 2011, 54, 273–280. [Google Scholar] [CrossRef]
- Rahpoe, N.; von Savigny, C.; Weber, M.; Rozanov, A.; Bovensmann, H.; Burrows, J.P. Error budget analysis of SCIAMACHY limb ozone profile retrievals using the SCIATRAN model. Atmos. Meas. Tech. 2013, 6, 2825–2837. [Google Scholar] [CrossRef]
- Zhu, F.; Si, F.Q.; Zhan, K. Research on Ozone Profiles Retrieval Using Chappuis-Wulf Band Absorption Information from Limb Scattered Measurement. Acta Opt. Sin. 2021, 41, 39–48. [Google Scholar]
- von Clarmann, T.; Degenstein, D.A.; Livesey, N.J.; Bender, S.; Braverman, A.; Butz, A.; Compernolle, S.; Damadeo, R.; Dueck, S.; Eriksson, P.; et al. Overview: Estimating and reporting uncertainties in remotely sensed atmospheric composition and temperature. Atmos. Meas. Tech. 2020, 13, 4393–4436. [Google Scholar] [CrossRef]
- Wang, Z.J. Study on retrieval of atmospheric trace gas concentrations from satellite based limb radiance. In Earth Exploration Science and Technology; Jilin University: Changchun, China, 2011; p. 197. [Google Scholar]
- Degenstein, D.A.; Bourassa, A.E.; Roth, C.Z.; Llewellyn, E.J. Limb scatter ozone retrieval from 10 to 60 km using a multiplicative algebraic reconstruction technique. Atmos. Chem. Phys. 2009, 9, 6521–6529. [Google Scholar] [CrossRef]
- Flittner, D.E.; Bhartia, P.K.; Herman, B.M. O3 profiles retrieved from limb scatter measurements: Theory. Geophys. Res. Lett. 2000, 27, 2601–2604. [Google Scholar] [CrossRef]
- Chahine, M.T. General Relaxation Method for Inverse Solution of Full Radiative Transfer Equation. J. Atmos. Sci. 1972, 29, 741–747. [Google Scholar] [CrossRef]
- Roth, C.Z. Atmospheric Ozone Retrieval using Radiance Measurements from the Chappuis and Hartley-Huggins Absorption Bands. In Physics and Engineering Physics; University of Saskatchewan: Saskatoon, SK, Canada, 2007. [Google Scholar]
- Rozanov, V.; Dinter, T.; Wolanin, A.; Bracher, A.; Burrows, J.P. Radiative transfer modeling through terrestrial atmosphere and ocean accounting for inelastic processes: Software package SCIATRAN. J. Quant. Spectrosc. Radiat. Transf. 2017, 194, 65–85. [Google Scholar] [CrossRef]
- Rozanov, V.V.; Diebel, D.; Spurr, R.J.D.; Burrows, J.P. GOMETRAN: A radiative transfer model for the satellite project GOME, the plane-parallel version. J. Geophys. Res. Atmos. 1997, 102, 16683–16695. [Google Scholar] [CrossRef]
- Rozanov, A.; Rozanov, V.; Buchwitz, M.; Kokhanovsky, A.; Burrows, J.P. SCIATRAN 2.0—A new radiative transfer model for geophysical applications in the 175–2400 nm spectral region. Adv. Space Res. 2005, 36, 1015–1019. [Google Scholar] [CrossRef]
- Rodgers, C.D. Retrieval of Atmospheric-Temperature and Composition from Remote Measurements of Thermal-Radiation. Rev. Geophys. 1976, 14, 609–624. [Google Scholar] [CrossRef]
- Puliafito, E.; Bevilacqua, R.; Olivero, J.; Degenhardt, W. Retrieval Error Comparison for Several Inversion Techniques Used in Limb-Scanning Millimeter-Wave Spectroscopy. J. Geophys. Res. Atmos. 1995, 100, 14257–14267. [Google Scholar] [CrossRef]
- Bourassa, A.E.; Degenstein, D.A.; Gattinger, R.L.; Llewellyn, E.J. Stratospheric aerosol retrieval with optical spectrograph and infrared imaging system limb scatter measurements. J. Geophys. Res. Atmos. 2007, 112. [Google Scholar] [CrossRef]
- Rodgers, C.D. Inverse Methods for Atmospheric Sounding: Theory and Practice. Series on Atmospheric, Oceanic and Planetary Physics Volume 2; World Scientific: Singapore, 2000; p. 238. [Google Scholar]
- McLinden, C.A.; McConnell, J.C.; McElroy, C.T.; Griffioen, E. Observations of stratospheric aerosol using CPFM polarized limb radiances. J. Atmos. Sci. 1999, 56, 233–240. [Google Scholar] [CrossRef]
- Rault, D.F.; Taha, G. Validation of ozone profiles retrieved from Stratospheric Aerosol and Gas Experiment III limb scatter measurements. J. Geophys. Res. Atmos. 2007, 112. [Google Scholar] [CrossRef]






| Para. | 10 km | 15 km | 20 km | 25 km | 30 km | 35 km | 40 km | 45 km | 50 km | 55 km | 60 km | 65 km | 70 km | Rank | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Bias | 11.5 | 2.8 | 0.3 | 0.1 | 1.8 | 0.6 | 1.0 | 0.5 | 0.7 | 0.1 | 1.1 | 2.8 | 8.2 | 31.5 | 3 |
| Alb. | 2.8 | 1.8 | 1.0 | 0.6 | 0.4 | 0.3 | 0.2 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 7.1 | 5 |
| Aer. | 5.8 | 10.8 | 7.0 | 3.7 | 2.9 | 2.0 | 2.3 | 0.7 | 0.6 | 0.2 | 0.2 | 0.3 | 0.4 | 36.9 | 2 |
| Press. | 1.4 | 0.5 | 0.2 | 0.1 | 0.1 | 0.0 | 0.0 | 0.2 | 0.2 | 0.0 | 0.1 | 0.1 | 0.0 | 2.9 | 7 |
| Temp. | 0.0 | 0.6 | 0.1 | 0.1 | 0.0 | 0.0 | 0.0 | 0.4 | 0.0 | 0.3 | 0.3 | 0.2 | 0.1 | 2.1 | 8 |
| T_ozone | 0.5 | 0.5 | 0.4 | 0.4 | 0.6 | 0.8 | 1.4 | 1.4 | 0.7 | 0.3 | 0.2 | 0.0 | 0.0 | 7.2 | 4 |
| TH | 2.2 | 5.4 | 4.0 | 0.3 | 0.7 | 5.5 | 4.0 | 1.7 | 2.9 | 4.3 | 5.2 | 4.7 | 2.4 | 43.3 | 1 |
| CH | 1.6 | 0.5 | 0.8 | 0.4 | 0.0 | 0.1 | 0.1 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 3.5 | 6 |
| τ | 0.6 | 0.4 | 0.2 | 0.1 | 0.1 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.4 | 9 |
| 10 km | 15 km | 20 km | 25 km | 30 km | 35 km | 40 km | 45 km | 50 km | 55 km | 60 km | 65 km | 70 km | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Total systematic | NH | 14.81 | 16.70 | 10.72 | 4.49 | 3.85 | 6.98 | 5.75 | 5.21 | 2.75 | 4.58 | 6.01 | 6.05 | 6.16 |
| SH | 12.22 | 15.68 | 7.41 | 3.70 | 4.87 | 6.58 | 7.47 | 4.64 | 3.41 | 4.49 | 4.43 | 3.32 | 6.06 | |
| Total random | NH | 4.66 | 1.97 | 0.06 | 0.03 | 2.43 | 0.55 | 3.74 | 2.20 | 0.84 | 1.97 | 0.12 | 0.66 | 0.85 |
| SH | 5.04 | 1.31 | 0.15 | 0.07 | 2.45 | 0.49 | 3.70 | 2.23 | 0.87 | 2.07 | 0.16 | 0.69 | 0.77 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, F.; Si, F.; Zhou, H.; Dou, K.; Zhao, M.; Zhang, Q. Sensitivity Analysis of Ozone Profiles Retrieved from SCIAMACHY Limb Radiance Based on the Weighted Multiplicative Algebraic Reconstruction Technique. Remote Sens. 2022, 14, 3954. https://doi.org/10.3390/rs14163954
Zhu F, Si F, Zhou H, Dou K, Zhao M, Zhang Q. Sensitivity Analysis of Ozone Profiles Retrieved from SCIAMACHY Limb Radiance Based on the Weighted Multiplicative Algebraic Reconstruction Technique. Remote Sensing. 2022; 14(16):3954. https://doi.org/10.3390/rs14163954
Chicago/Turabian StyleZhu, Fang, Fuqi Si, Haijin Zhou, Ke Dou, Minjie Zhao, and Quan Zhang. 2022. "Sensitivity Analysis of Ozone Profiles Retrieved from SCIAMACHY Limb Radiance Based on the Weighted Multiplicative Algebraic Reconstruction Technique" Remote Sensing 14, no. 16: 3954. https://doi.org/10.3390/rs14163954
APA StyleZhu, F., Si, F., Zhou, H., Dou, K., Zhao, M., & Zhang, Q. (2022). Sensitivity Analysis of Ozone Profiles Retrieved from SCIAMACHY Limb Radiance Based on the Weighted Multiplicative Algebraic Reconstruction Technique. Remote Sensing, 14(16), 3954. https://doi.org/10.3390/rs14163954







