Efficient DOA Estimation for Wideband Sources in Multipath Environment

Abstract

A novel direction-of-arrival (DOA) estimator is proposed for the mixed uncorrelated and correlated wideband sources in the multipath environment. Firstly, the novel signal model is established using the aligned envelope technique. Next, the estimator can be divided into two parts. Theoretical analyses show that the correlated components cannot form peaks and only the DOA of uncorrelated signals can be acquired in the first part. Then, the correlated components are extracted from the corresponding covariance matrix and handled in the second part. Using the concept of linear search, the computational complexity of the algorithm is significantly reduced. Simulation results show the direction of uncorrelated and correlated wideband signals can be processed and distinguished effectively in the proposed method. Compared with previous DOA estimators for correlated wideband sources, the estimation accuracy has been improved.

1. Introduction

Recent developments in remote sensing, wireless communications, radar, and sonar have heightened the need for wideband signals. Due to the reflection and refraction from the atmosphere and objects such as mountains and buildings, multipath propagation is very common in practice. Highly correlated or coherent wideband signals could be received by antenna array when the multipath delays are less than the correlation time of wideband signals. For direction-of-arrival (DOA) estimation [1,2,3], previous studies about correlated wideband signals can be categorized into two types: sparse recovery (SR)-based algorithms and some subspace-based ones. The subspace-based methods contain the coherent signal subspace methods (CSM) [4] and some improved incoherent signal subspace methods, such as the coherent test of orthogonality of projected subspaces (CTOPS) [5]. CSM exploits the focusing operation to increase the rank of the covariance matrix associated with the reference frequency bin of correlated signals and CTOPS reconstructs the covariance matrix of correlated sources before the TOPS [6] method.

SR-based approaches often formulate wideband signals as the block sparsity problem and perform well in low signal-to-noise ratio (SNR) and limited snapshots [7,8]. However, not all the SR-based methods can deal with correlated wideband signals. On the one hand, if the sparse model is established after vectorization of the covariance matrix (e.g., underdetermined DOA estimation algorithms [9,10]), only diagonal elements of the covariance matrix are utilized, thus the correlated sources cannot be handled. On the other hand, the grid-less based sparse methods [11,12] can be viewed as the parameter estimation in the continuous range based on well-established covariance fitting criteria [13], but these criteria are not robust to the correlated sources.

The existing methods can only deal with correlated wideband signals in the frequency domain, the coexistence of both uncorrelated and correlated wideband signals in the multipath environment has not been considered, and there is still abundant room for further progress. Previous researches [14,15,16,17,18] about the estimation of mixed sources under multipath conditions only consider the narrowband sources. Although the wideband sources are used in [19], the information of sub-bands is not considered, and the wideband sources are processed in the same way as narrowband signals. In these studies, the delay in the envelope is ignored, which leads to two problems: (1) these methods cannot handle wideband sources appropriately owing to the nonignorable propagation delay in the envelope; (2) the existing models are limited to coherent signals because the multipath propagation delay is regarded as 0. Inspired by the data aligning concept used in uncorrelated noncircular wideband DOA estimation [20,21], a novel direction-finding approach for wideband sources is proposed in a multipath scenario to overcome the above drawbacks. To the best of our knowledge, this work is the pioneering one for the DOA estimation of the mixed wideband sources in multipath cases.

The contribution and novelty are reflected in the following aspects:

• Considering the propagation delay, a novel signal model with the coexistence of uncorrelated and correlated wideband signals is established in the time domain. Not only the coherent signals but also the partially correlated signals can be addressed.
• A wideband DOA estimation algorithm is proposed for the multipath environment, the uncorrelated and correlated components are estimated separately.
• The strategy of linear search is used to improve the proposed method and the operation speed is accelerated. Furthermore, the off-grid signals can be estimated without the Taylor approximation to the signal model.
• The Cramer–Rao bound (CRB) for DOA estimation of multipath wideband signals is derived in detail.

Throughout the paper, ${\left(·\right)}^{*}$, ${\left(·\right)}^T$ and ${\left(·\right)}^H$ represent conjugation, transposition, and conjugation transposition, respectively. $diag\left\{·\right\}$, $blkdiag\left\{·\right\}$, and $vec\left(·\right)$ mean the diagonal, the block diagonal, and the vectorization operators. $∥·∥$ denotes the matrix norm. $\mathbf{0}$ is the zero matrix, $\mathbf{I}$ is the identity matrix. ⊗ and ⊙ stand for the Kronecker product and Khatri–Rao product. $E\left\{·\right\}$ means the expectation. $\Re \left(·\right)$ and $\Im \left(·\right)$ mean the real and the imaginary parts. $\mathbb{R}$ and $\mathbb{C}$ denote the real set and complex set.

2. Problem Formulation

Suppose that K signals from $K_n$ far field statistically independent wideband sources impinging on the uniform linear array (ULA) with M sensors, where $K=K_u+K_m$ and $K_n=K_u+K_c$. The first $K_u$ ones are line of sight (LOS) uncorrelated signals without multipath components, the other $K_m$ correlated signals can be divided into $K_c$ groups with one LOS signal and $P_k-1$ multipath signals in each group, i.e., $K_m={\sum }_{k=1}^{K_c}{P}_k$. The baseband output of the mth sensor is:

$$x_m\left(t\right)=\sum _{k=1}^{K_u}{s}_k\left(t+{\tau }_{m,{\theta }_k}\right)e^{j{w}_0{\tau }_{m,{\theta }_k}}+\sum _{k=K_u+1}^{K_n}\sum _{i=1}^{P_k}{\rho }_{ki}{s}_k\left(t+{\tau }_{m,{\theta }_{ki}}+{\Delta }_{ki}\right)e^{j{w}_0\left({\tau }_{m,{\theta }_{ki}}+{\Delta }_{ki}\right)}+n_m\left(t\right),$$

(1)

where $s_k\left(t\right)$ is the complex envelope of the kth signal. ${\theta }_k$ is the DOA of kth source, $k\in \left\{1,2,\cdots ,K_u\right\}$. ${\theta }_{ki}$ and ${\rho }_{ki}$ are the direction and the complex fading coefficient corresponding to ith path of kth source, $k\in \left\{K_u+1,2,\cdots ,K_n\right\}$. ${\tau }_{m,{\theta }_k}$ is the propagation delay of kth source between mth sensor and the reference array element. ${\tau }_{m,{\theta }_{ki}}$ and ${\Delta }_{ki}$ are the propagation delay and multipath delay corresponding to the ith path of kth source. $n_m\left(t\right)$ is the zero-mean circular noise of mth sensor. Assuming that the noise is uncorrelated with signals, the signals are stationary zero-mean processes. Denote ${\mathbf{A}}_k=diag\left\{\mathbf{a}\left({\theta }_k\right)\right\}$ and ${\mathbf{A}}_{ki}=diag\left\{\mathbf{a}\left({\theta }_{ki}\right)\right\}$, where $\mathbf{a}\left({\theta }_k\right)={\left[e^{j{w}_0{\tau }_{1,{\theta }_k}},\cdots ,e^{j{w}_0{\tau }_{M,{\theta }_k}}\right]}^T$ is the array steering vector. Define the fading coefficient and multipath propagation delay matrices as ${\mathbf{\rho }}_{ki}={\rho }_{ki}\otimes {\mathbf{I}}_M$ and ${\Delta }_{ki}=e^{j{w}_0{\Delta }_{ki}}\otimes {\mathbf{I}}_M$, respectively. The array observation vector can be formulated as:

$$\mathbf{x}\left(t\right)=\sum _{k=1}^{K_u}{\mathbf{A}}_k{\mathbf{s}}_k\left(t\right)+\sum _{k=K_u+1}^{K_n}\sum _{i=1}^{P_k}{\mathbf{A}}_{ki}{\mathbf{\rho }}_{ki}{\Delta }_{ki}{\mathbf{s}}_{ki}\left(t\right)+\mathbf{n}\left(t\right),$$

(2)

where $\mathbf{x}\left(t\right)={\left[x_1\left(t\right),x_2\left(t\right),\cdots ,x_M\left(t\right)\right]}^T$, $\mathbf{n}\left(t\right)={\left[n_1\left(t\right),n_2\left(t\right),\cdots ,n_M\left(t\right)\right]}^T$, and ${\mathbf{s}}_k\left(t\right)={\left[s_k\left(t+{\tau }_{1,{\theta }_k}\right),\cdots ,s_k\left(t+{\tau }_{M,{\theta }_k}\right)\right]}^T$, ${\mathbf{s}}_{ki}\left(t\right)={\left[s_k\left(t+{\iota }_{1,{\theta }_{ki}}\right),\cdots ,s_k\left(t+{\iota }_{M,{\theta }_{ki}}\right)\right]}^T$, with ${\iota }_{m,{\theta }_{ki}}={\tau }_{m,{\theta }_{ki}}+{\Delta }_{ki}$. Through the discrete Fourier transform (DFT), we have

$$X_m\left(f\right)=\sum _{k=1}^{K_u}{S}_k\left(f\right)e^{j\left(w+w_0\right){\tau }_{m,{\theta }_k}}+\sum _{k=K_u+1}^{K_n}\sum _{i=1}^{P_k}{\rho }_{ki}{S}_k\left(f\right)e^{j\left(w+w_0\right)\left({\tau }_{m,{\theta }_{ki}}+{\Delta }_{ki}\right)}+N_m\left(f\right).$$

(3)

Based on the fact $x_m\left(t-{\tau }_{m,{\theta }_k}\right)=IDFT\left\{e^{-jw{\tau }_{m,{\theta }_k}}{X}_m\left(f\right)\right\}$, where $IDFT\left\{·\right\}$ means the inverse DFT, the delay term can be compensated in frequency domain by a matrix $\mathbf{T}\left(\theta \right)$ associated with the scan angle $\theta$ as ${\theta }_k$ is unknown, i.e.,

$${\mathbf{x}}_{\theta }\left(t\right)=IDFT\left\{\mathbf{T}\left(\theta \right)\mathbf{X}\left(f\right)\right\}=\sum _{k=1}^{K_u}{\mathbf{A}}_k{\mathbf{s}}_{k,\theta }\left(t\right)+\sum _{k=K_u+1}^{K_n}\sum _{i=1}^{P_k}{\mathbf{A}}_{ki}{\mathbf{\rho }}_{ki}{\Delta }_{ki}{\mathbf{s}}_{ki,\theta }\left(t\right)+{\mathbf{n}}_{\theta }\left(t\right),$$

(4)

where $\mathbf{T}\left(\theta \right)=diag\left\{e^{-jw{\tau }_{1,\theta }},\cdots ,e^{-jw{\tau }_{M,\theta }}\right\}$, ${\mathbf{x}}_{\theta }\left(t\right)={\left[x_1\left(t-{\tau }_{1,\theta }\right),\cdots ,x_M\left(t-{\tau }_{M,\theta }\right)\right]}^T$, ${\mathbf{n}}_{\theta }\left(t\right)={\left[n_1\left(t-{\tau }_{1,\theta }\right),\cdots ,n_M\left(t-{\tau }_{M,\theta }\right)\right]}^T$, ${\mathbf{s}}_{k,\theta }\left(t\right)={\left[s_k\left(t+{\tau }_{1,{\theta }_k}-{\tau }_{1,\theta }\right),\cdots ,s_k\left(t+{\tau }_{M,{\theta }_k}-{\tau }_{M,\theta }\right)\right]}^T$, ${\mathbf{s}}_{ki,\theta }\left(t\right)={\left[s_k\left(t+{\iota }_{1,{\theta }_{ki}}-{\tau }_{1,\theta }\right),\cdots ,s_k\left(t+{\iota }_{M,{\theta }_{ki}}-{\tau }_{M,\theta }\right)\right]}^T$.

3. Proposed Algorithm

In this section, the proposed algorithm for both uncorrelated and correlated wideband signals are discussed in detail.

3.1. Estimation for Uncorrelated Wideband Signals

The uncorrelated wideband signals are firstly estimated. Consider $\theta ={\theta }_k,k\in \left\{1,2,\cdots ,K_u\right\}$, which means the time delay is compensated with the DOA of uncorrelated signal. Using the complex envelope-aligned approach, one may have

$${\mathbf{x}}_{{\theta }_k}\left(t\right)=\mathbf{a}\left({\theta }_k\right)s_k\left(t\right)+{\mathbf{f}}_{{\theta }_k}\left(t\right)+{\mathbf{n}}_{{\theta }_k}\left(t\right),$$

(5)

where ${\mathbf{n}}_{{\theta }_k}\left(t\right)$ is the time-delayed noise and

$${\mathbf{f}}_{{\theta }_k}\left(t\right)=\sum _{\genfrac{}{}{0pt}{}{k^{\prime }=1\hfill }{k^{\prime }\ne k\hfill }}^{K_u}{\mathbf{A}}_{k^{\prime }}{\mathbf{s}}_{k^{\prime },{\theta }_k}\left(t\right)+\sum _{k^{\prime }=K_u+1}^{K_n}\sum _{i=1}^{P_{k^{\prime }}}{\mathbf{A}}_{k^{\prime }i}{\mathbf{\rho }}_{k^{\prime }i}{\Delta }_{k^{\prime }i}{\mathbf{s}}_{k^{\prime }i,{\theta }_k}\left(t\right).$$

(6)

The covariance matrix associated with ${\theta }_k$ can be formulated as:

$$\begin{array}{cc}\hfill {\mathbf{R}}_{\mathbf{x}}\left({\theta }_k\right)=E\left\{{\mathbf{x}}_{{\theta }_k}\left(t\right){\mathbf{x}}_{{\theta }_k}^H\left(t\right)\right\}& ={\sigma }_k^2\mathbf{a}\left({\theta }_k\right){\mathbf{a}}^H\left({\theta }_k\right)+{\mathbf{R}}_{\mathbf{f}}\left({\theta }_k\right)+{\sigma }_n^2\mathbf{I}\hfill \\ \hfill & =\sum _{m=1}^M{\lambda }_m\left({\theta }_k\right){\mathbf{e}}_m\left({\theta }_k\right){\mathbf{e}}_m^H\left({\theta }_k\right),\hfill \end{array}$$

(7)

and

$${\mathbf{R}}_{\mathbf{f}}\left({\theta }_k\right)=E\left\{{\mathbf{f}}_{{\theta }_k}\left(t\right){\mathbf{f}}_{{\theta }_k}^H\left(t\right)\right\}={\mathbf{V}}_{\mathbf{f}}\left({\theta }_k\right){\mathsf{\Sigma }}_{\mathbf{f}}\left({\theta }_k\right){\mathbf{V}}_{\mathbf{f}}^H\left({\theta }_k\right)+{\Xi }_{\mathbf{f}}\left({\theta }_k\right),$$

(8)

where ${\Xi }_{\mathbf{f}}\left({\theta }_k\right)={\sum }_{m=F_{{\theta }_k}}^M{\upsilon }_m\left({\theta }_k\right){\nu }_m\left({\theta }_k\right){\nu }_m^H\left({\theta }_k\right)$ and ${\lambda }_1\left({\theta }_k\right)\ge \cdots \ge {\lambda }_m\left({\theta }_k\right)\ge \cdots \ge {\lambda }_M\left({\theta }_k\right)$ are the ordered eigenvalues of ${\mathbf{R}}_{\mathbf{x}}\left({\theta }_k\right)$. The first $F_{u,{\theta }_k}$ ones are the dominant eigenvalues and the others are the subordinate eigenvalues. Similarly, ${\upsilon }_1\left({\theta }_k\right)\ge \cdots \ge {\upsilon }_m\left({\theta }_k\right)\ge \cdots \ge {\upsilon }_M\left({\theta }_k\right)$ are eigenvalues of ${\mathbf{R}}_{\mathbf{f}}\left({\theta }_k\right)$. Owing to the independence of sources, ${\mathbf{R}}_{\mathbf{f}}\left({\theta }_k\right)$ can be regarded as the covariance matrix of these signals after compensating the time delay except signal from ${\theta }_k$. Thus, the first $F_{u,{\theta }_k}-1$ ones are the dominant eigenvalues. ${\mathbf{e}}_m\left({\theta }_k\right)$ and ${\nu }_m\left({\theta }_k\right)$ are the eigenvectors related to ${\lambda }_m\left({\theta }_k\right)$ and ${\upsilon }_m\left({\theta }_k\right)$, respectively. Define two augmented matrices as ${\mathbf{H}}_{\mathbf{f}}\left({\theta }_k\right)=\left[\mathbf{a}\left({\theta }_k\right),{\mathbf{V}}_{\mathbf{f}}\left({\theta }_k\right)\right]$ and ${\mathbf{\Gamma }}_{\mathbf{f}}\left({\theta }_k\right)=blkdiag\left\{{\sigma }_k^2,{\mathsf{\Sigma }}_{\mathbf{f}}\left({\theta }_k\right)\right\}$, the rank of ${\mathbf{H}}_{\mathbf{f}}\left({\theta }_k\right)$ is $F_{u,{\theta }_k}$. From the above derivation, ${\mathbf{R}}_{\mathbf{x}}\left({\theta }_k\right)$ can be formulated as:

$${\mathbf{R}}_{\mathbf{x}}\left({\theta }_k\right)={\mathbf{H}}_{\mathbf{f}}\left({\theta }_k\right){\mathbf{\Gamma }}_{\mathbf{f}}\left({\theta }_k\right){\mathbf{H}}_{\mathbf{f}}^H\left({\theta }_k\right)+{\Xi }_{\mathbf{f}}\left({\theta }_k\right)+{\sigma }_n^2\mathbf{I}.$$

(9)

As the eigenvalue vector matrix of ${\mathbf{R}}_{\mathbf{x}}\left({\theta }_k\right)$ is unitary, ${\sum }_{m=1}^M{\mathbf{e}}_m\left({\theta }_k\right){\mathbf{e}}_m^H\left({\theta }_k\right)=\mathbf{I}$ and ${\mathbf{e}}_{m_1}^H\left({\theta }_k\right){\mathbf{e}}_{m_2}\left({\theta }_k\right)=0$ when $m_1\ne m_2$, thus

$${\mathbf{H}}_{\mathbf{f}}\left({\theta }_k\right){\mathbf{\Gamma }}_{\mathbf{f}}\left({\theta }_k\right){\mathbf{H}}_{\mathbf{f}}^H\left({\theta }_k\right){\mathbf{e}}_{m_2}\left({\theta }_k\right)=\sum _{m_1=1}^{F_{u,{\theta }_k}}\left[{\lambda }_{m_1}\left({\theta }_k\right)-{\sigma }_n^2\right]{\mathbf{e}}_{m_1}\left({\theta }_k\right){\mathbf{e}}_{m_1}^H\left({\theta }_k\right){\mathbf{e}}_{m_2}\left({\theta }_k\right)+{\epsilon }_f,$$

(10)

where ${\epsilon }_f={\sum }_{m_1=F_{u,{\theta }_k}+1}^M\left[{\lambda }_{m_1}\left({\theta }_k\right)-{\sigma }_n^2\right]{\mathbf{e}}_{m_1}\left({\theta }_k\right){\mathbf{e}}_{m_1}^H\left({\theta }_k\right){\mathbf{e}}_{m_2}\left({\theta }_k\right)-{\Xi }_{\mathbf{f}}\left({\theta }_k\right){\mathbf{e}}_{m_2}\left({\theta }_k\right)$, and $m_1\in \left\{1,\cdots ,M\right\}$, $m_2\in \left\{F_{u,{\theta }_k}+1,\cdots ,M\right\}$. Both ${\mathbf{H}}_{\mathbf{f}}\left({\theta }_k\right)$ and ${\mathbf{\Gamma }}_{\mathbf{f}}\left({\theta }_k\right)$ are full column rank matrices, ${\mathbf{H}}_{\mathbf{f}}\left({\theta }_k\right){\mathbf{\Gamma }}_{\mathbf{f}}\left({\theta }_k\right)$ is full column rank. When ${\epsilon }_f=\mathbf{0}$, ${\mathbf{H}}_{\mathbf{f}}\left({\theta }_k\right){\mathbf{\Gamma }}_{\mathbf{f}}\left({\theta }_k\right){\mathbf{H}}_{\mathbf{f}}^H\left({\theta }_k\right){\mathbf{e}}_{m_2}\left({\theta }_k\right)=\mathbf{0}$ and ${\mathbf{H}}_{\mathbf{f}}\left({\theta }_k\right){\mathbf{\Gamma }}_{\mathbf{f}}\left({\theta }_k\right){\mathbf{H}}_{\mathbf{f}}^H\left({\theta }_k\right)={\sum }_{m_1=1}^{F_{u,{\theta }_k}}\left[{\lambda }_{m_1}\left({\theta }_k\right)-{\sigma }_n^2\right]{\mathbf{e}}_{m_1}\left({\theta }_k\right){\mathbf{e}}_{m_1}^H\left({\theta }_k\right)\ne \mathbf{0}$, yielding

$${\mathbf{a}}^H\left({\theta }_k\right){\mathbf{e}}_{m_2}\left({\theta }_k\right)=0.$$

(11)

According to the subspace theory, ${\lambda }_m\left({\theta }_k\right)\to {\sigma }_n^2$ for $m\in \left\{F_{u,{\theta }_k}+1,\cdots ,M\right\}$, and ${\upsilon }_m\left({\theta }_k\right)\to 0$ for $m\in \left\{F_{u,{\theta }_k},\cdots ,M\right\}$ because the covariance matrix ${\mathbf{R}}_{\mathbf{f}}\left({\theta }_k\right)$ is noise-free. Thus, the error ${\epsilon }_f$ can be neglected. Clearly, the DOA of uncorrelated wideband signals can be found by searching the peak of the spectrum:

$$P_u\left({\theta }_k\right)=1/\phantom{1{∥{\mathbf{a}}^H\left({\theta }_k\right)\mathbf{E}\left({\theta }_k\right)∥}_2^2}{∥{\mathbf{a}}^H\left({\theta }_k\right)\mathbf{E}\left({\theta }_k\right)∥}_2^2,$$

(12)

where $\mathbf{E}\left({\theta }_k\right)=\left[{\mathbf{e}}_{F_{{\theta }_k}+1}\left({\theta }_k\right),\cdots ,{\mathbf{e}}_M\left({\theta }_k\right)\right]$.

When the compensated delay is associated with the DOA of correlated signal, ${\theta }_k={\theta }_{ki}$, $k\in \left\{K_u+1,\cdots ,K_n\right\}$, $i\in \left\{1,\cdots ,P_k\right\}$, the envelope aligned vector can be expressed as:

$${\mathbf{x}}_{{\theta }_k}\left(t\right)=\mathbf{a}\left({\theta }_k\right){\rho }_{ki}{e}^{j{w}_0{\Delta }_{ki}}{s}_k\left(t+{\Delta }_{ki}\right)+{\mathbf{g}}_{{\theta }_k}\left(t\right)+{\mathbf{n}}_{{\theta }_k}\left(t\right),$$

(13)

$${\mathbf{g}}_{{\theta }_k}\left(t\right)=\sum _{k^{\prime }=1}^{K_u}{\mathbf{A}}_{k^{\prime }}{\mathbf{s}}_{k^{\prime },{\theta }_k}\left(t\right)+\underset{k^{\prime }{i}^{\prime }\ne ki}{\sum _{k^{\prime }=K_u+1}^{K_n}\sum _{i^{\prime }=1}^{P_{k^{\prime }}}{\mathbf{A}}_{k^{\prime }{i}^{\prime }}}{\rho }_{k^{\prime }{i}^{\prime }}{\Delta }_{k^{\prime }{i}^{\prime }}{\mathbf{s}}_{k^{\prime }{i}^{\prime },{\theta }_k}\left(t\right),$$

(14)

yielding

$${\mathbf{R}}_{\mathbf{x}}\left({\theta }_k\right)={\sigma }_k^2{\left|{\rho }_{ki}\right|}^2\mathbf{a}\left({\theta }_k\right){\mathbf{a}}^H\left({\theta }_k\right)+{\mathbf{R}}_{\mathbf{g}}\left({\theta }_k\right)+{\sigma }_n^2\mathbf{I}.$$

(15)

Unlike the first condition, the first term in the envelope-aligned vector belongs to the kth group of multipath signals; it is coherent with other multipath signals coming from the same wideband source. Consequently, ${\mathbf{R}}_{\mathbf{g}}\left({\theta }_k\right)=E\left\{{\mathbf{g}}_{{\theta }_k}\left(t\right){\mathbf{g}}_{{\theta }_k}^H\left(t\right)\right\}$ cannot be taken as the covariance matrix of original signals excluding signal from ${\theta }_k$. Actually, ${\mathbf{R}}_{\mathbf{g}}\left({\theta }_k\right)$ may be written as

$${\mathbf{R}}_{\mathbf{g}}\left({\theta }_k\right)={\mathbf{V}}_{\mathbf{g}}\left({\theta }_k\right){\mathsf{\Sigma }}_{\mathbf{g}}\left({\theta }_k\right){\mathbf{V}}_{\mathbf{g}}^H\left({\theta }_k\right)+{\Xi }_{\mathbf{g}}\left({\theta }_k\right)+{\mathbf{\Pi }}_{\mathbf{g}}\left({\theta }_k\right),$$

(16)

$${\mathbf{\Pi }}_{\mathbf{g}}\left({\theta }_k\right)=E\left\{{\mathbf{\Pi }}_1\left({\theta }_k\right){\mathbf{\Pi }}_2^H\left({\theta }_k\right)+{\mathbf{\Pi }}_2\left({\theta }_k\right){\mathbf{\Pi }}_1^H\left({\theta }_k\right)\right\},$$

(17)

where ${\mathbf{\Pi }}_1\left({\theta }_k\right)=\mathbf{a}\left({\theta }_k\right){\rho }_{ki}{e}^{j{w}_0{\Delta }_{ki}}{s}_k\left(t+{\Delta }_{ki}\right)$, and ${\mathbf{\Pi }}_2\left({\theta }_k\right)={\sum }_{i^{\prime }=1,i^{\prime }\ne i}^{P_k}{\mathbf{A}}_{k{i}^{\prime }}{\mathbf{\rho }}_{k{i}^{\prime }}{\Delta }_{k{i}^{\prime }}{\mathbf{s}}_{k{i}^{\prime },{\theta }_k}\left(t\right)$.

Similar to the uncorrelated signals, let ${\mathbf{H}}_{\mathbf{g}}\left({\theta }_k\right)=\left[\mathbf{a}\left({\theta }_k\right),{\mathbf{V}}_{\mathbf{g}}\left({\theta }_k\right)\right]$, and ${\mathbf{\Gamma }}_{\mathbf{g}}\left({\theta }_k\right)=blkdiag\left\{{\sigma }_k^2{\left|{\rho }_{ki}\right|}^2,{\mathsf{\Sigma }}_{\mathbf{g}}\left({\theta }_k\right)\right\}$, ${\mathbf{R}}_{\mathbf{g}}\left({\theta }_k\right)-{\mathbf{\Pi }}_{\mathbf{g}}\left({\theta }_k\right)$ can be treated as the covariance matrix of original signals without the $ki$th multipath signal. Similar to (20), one can get:

$${\mathbf{H}}_{\mathbf{g}}\left({\theta }_k\right){\mathbf{\Gamma }}_{\mathbf{g}}\left({\theta }_k\right){\mathbf{H}}_{\mathbf{g}}^H\left({\theta }_k\right){\mathbf{e}}_{m_2}\left({\theta }_k\right)={\epsilon }_g-{\mathbf{\Pi }}_{\mathbf{g}}\left({\theta }_k\right){\mathbf{e}}_{m_2}\left({\theta }_k\right),$$

(18)

where ${\epsilon }_g={\sum }_{m_1=F_{{\theta }_k}+1}^M\left[{\lambda }_{m_1}\left({\theta }_k\right)-{\sigma }_n^2\right]{\mathbf{e}}_{m_1}\left({\theta }_k\right){\mathbf{e}}_{m_1}^H\left({\theta }_k\right){\mathbf{e}}_{m_2}\left({\theta }_k\right)-{\Xi }_{\mathbf{g}}\left({\theta }_k\right){\mathbf{e}}_{m_2}\left({\theta }_k\right)$. Despite ${\epsilon }_g$ can be ignored, (11) do not hold for correlated signals due to the presence of ${\mathbf{\Pi }}_{\mathbf{g}}\left({\theta }_k\right)$, which means the peak searching of $P_u$ can only obtain the DOA of uncorrelated wideband signals.

3.2. Estimation for Correlated Wideband Signals

In this subsection, the correlated components are extracted from the covariance matrix and the DOA can be acquired. To eliminate the uncorrelated components, the covariance matrices can be analyzed in a unified manner, i.e.,

$${\mathbf{R}}_{\mathbf{x}}\left({\theta }_k\right)={\mathbf{R}}_u\left({\theta }_k\right)+{\mathbf{R}}_c\left({\theta }_k\right)+{\sigma }_n^2\mathbf{I},$$

(19)

where

$${\mathbf{R}}_u\left({\theta }_k\right)=\sum _{k^{\prime }=1}^{K_u}{\mathbf{A}}_{k^{\prime }}E\left\{{\mathbf{s}}_{k^{\prime },{\theta }_k}\left(t\right){\mathbf{s}}_{k^{\prime },{\theta }_k}^H\left(t\right)\right\}{\mathbf{A}}_{k^{\prime }}^H,$$

(20)

$${\mathbf{R}}_c\left({\theta }_k\right)=\sum _{k^{\prime }=K_u+1}^{K_n}\sum _{i=1}^{P_{k^{\prime }}}\sum _{i^{\prime }=1}^{P_{k^{\prime }}}{\mathbf{A}}_{k^{\prime }i}{\mathbf{\rho }}_{k^{\prime }i}{\Delta }_{k^{\prime }i}E\left\{{\mathbf{s}}_{k^{\prime }i,{\theta }_k}\left(t\right){\mathbf{s}}_{k^{\prime }{i}^{\prime },{\theta }_k}^H\left(t\right)\right\}{\Delta }_{k^{\prime }{i}^{\prime }}^H{\mathbf{\rho }}_{k^{\prime }{i}^{\prime }}^H{\mathbf{A}}_{k^{\prime }{i}^{\prime }}^H.$$

(21)

The $\left(m,n\right)$th element in ${\mathbf{R}}_u\left({\theta }_k\right)$ and ${\mathbf{R}}_c\left({\theta }_k\right)$ are:

$${\mathbf{R}}_u{\left({\theta }_k\right)}_{m,n}=\sum _{k^{\prime }=1}^{K_u}{e}^{j{w}_0\left({\tau }_{m,{\theta }_{k^{\prime }}}-{\tau }_{n,{\theta }_{k^{\prime }}}\right)}E\left\{s_{k^{\prime }}\left(t+{\tau }_{m,{\theta }_{k^{\prime }}}-{\tau }_{m,{\theta }_k}\right)s_{k^{\prime }}^{*}\left(t+{\tau }_{n,{\theta }_{k^{\prime }}}-{\tau }_{n,{\theta }_k}\right)\right\},$$

(22)

$${\mathbf{R}}_c{\left({\theta }_k\right)}_{m,n}=\sum _{k^{\prime }=K_u+1}^{K_u+K_c}\sum _{i=1}^{P_{k^{\prime }}}\sum _{i^{\prime }=1}^{P_{k^{\prime }}}{\rho }_{k^{\prime }i}{\rho }_{k^{\prime }{i}^{\prime }}^{*}{e}^{j{w}_0\left({\Delta }_{k^{\prime }i}-{\Delta }_{k^{\prime }{i}^{\prime }}+{\tau }_{m,{\theta }_{k^{\prime }i}}-{\tau }_{n,{\theta }_{k^{\prime }{i}^{\prime }}}\right)}E\left\{s_{k^{\prime }}\left(t+{\iota }_{m,{\theta }_{k^{\prime }i}}-{\tau }_{m,{\theta }_k}\right)\right.\left.s_{k^{\prime }}^{*}\left(t+{\iota }_{n,{\theta }_{k^{\prime }{i}^{\prime }}}-{\tau }_{n,{\theta }_k}\right)\right\}.$$

(23)

The autocorrelation function of the stationary signal is an even function that depends only on the time lag, thus the elements on each diagonal of ${\mathbf{R}}_u\left({\theta }_k\right)$ are equal. From (39), ${\mathbf{R}}_u{\left({\theta }_k\right)}_{m,n}={\mathbf{R}}_u^{*}{\left({\theta }_k\right)}_{n,m}$, ${\mathbf{R}}_u\left({\theta }_k\right)$ is a Hermitian Toeplitz matrix. Affected by the exponential term and the coefficient term, ${\mathbf{R}}_c\left({\theta }_k\right)$ is not the Hermitian Toeplitz matrix. The noise covariance matrix is a Toeplitz matrix.

Define an exchange matrix $\mathbf{J}$ whose antidiagonal elements are ones and the other elements are zeros. For Hermitian Toeplitz matrix with real diagonals, ${\mathbf{R}}_u\left({\theta }_k\right)={\mathbf{JR}}_u^{*}\left({\theta }_k\right)\mathbf{J}$. Clearly, the uncorrelated and the noise components can be eliminated by ${\mathbf{R}}_{\mathbf{x}}\left({\theta }_k\right)-{\mathbf{JR}}_{\mathbf{x}}^{*}\left({\theta }_k\right)\mathbf{J}$. To deal with the correlated components, the spatial smoothing preprocessing scheme may be applied. Select L submatrices from ${\mathbf{R}}_{\mathbf{x}}\left({\theta }_k\right)$ and the lth submatrix can be defined as:

$${\mathbf{R}}_l\left({\theta }_k\right)={\mathbf{\Psi }}_l{\mathbf{R}}_{\mathbf{x}}\left({\theta }_k\right){\mathbf{\Psi }}_l^H,$$

(24)

where ${\mathbf{\Psi }}_l=\left[{\mathbf{0}}_{\left(M-L+1\right)\times \left(l-1\right)},{\mathbf{I}}_{M-L+1},{\mathbf{0}}_{\left(M-L+1\right)\times \left(L-l\right)}\right]$ is the selection matrix. The submatrices selected along the diagonal of ${\mathbf{R}}_u\left({\theta }_k\right)$ are theoretically the same Hermitian Toeplitz matrix thus the spatial differencing matrix can be denoted to remove the uncorrelated entries, i.e.,

$${\mathbf{R}}_d\left({\theta }_k\right)=\frac{1}{L}\sum _{l=1}^L\left({\mathbf{R}}_1\left({\theta }_k\right)-{\mathbf{JR}}_l^{*}\left({\theta }_k\right)\mathbf{J}\right)={\mathbf{\Psi }}_1{\mathbf{R}}_c\left({\theta }_k\right){\mathbf{\Psi }}_1^H-\frac{1}{L}\sum _{l=1}^L\mathbf{J}{\mathbf{\Psi }}_l{\mathbf{R}}_c^{*}\left({\theta }_k\right){\mathbf{\Psi }}_l^H\mathbf{J},$$

(25)

The eigenvalue decomposition (EVD) is:

$${\mathbf{R}}_d\left({\theta }_k\right)=\sum _{k^{\prime }=K_u+1}^{K_n}\sum _{i=1}^{P_{k^{\prime }}}\sum _{i^{\prime }=1}^{P_{k^{\prime }}}{\mathbf{A}}_{d{k}^{\prime }i}{\mathbf{R}}_{sd}{\mathbf{A}}_{d{k}^{\prime }i}^H=\sum _{m=1}^{M-L+1}{\eta }_m\left({\theta }_k\right){\mathit{\alpha }}_m\left({\theta }_k\right){\mathit{\alpha }}_m^H\left({\theta }_k\right),$$

(26)

where ${\eta }_1\left({\theta }_k\right)\ge \cdots \ge {\eta }_m\left({\theta }_k\right)\ge \cdots \ge {\eta }_{M-L+1}\left({\theta }_k\right)$ are the ordered eigenvalues of ${\mathbf{R}}_d\left({\theta }_k\right)$. The first $F_{c,{\theta }_k}$ ones are the dominant eigenvalues, and the others are the subordinate eigenvalues. ${\mathbf{a}}_d\left({\theta }_k\right)={\left[e^{j{w}_0{\tau }_{1,{\theta }_k}},\cdots ,e^{j{w}_0{\tau }_{M-L+1,{\theta }_k}}\right]}^T$ and ${{\mathbf{A}}_d}_{ki}=diag\left\{{\mathbf{a}}_d\left({\theta }_{ki}\right)\right\}$, ${\mathbf{R}}_{sd}$ can be formulated as:

$${\mathbf{R}}_{sd}=\sum _{k^{\prime }=K_u+1}^{K_n}\sum _{i=1}^{P_{k^{\prime }}}\sum _{i^{\prime }=1}^{P_{k^{\prime }}}\left({\mathbf{\rho }}_{k^{\prime }i}{\Delta }_{k^{\prime }i}E\left\{{\mathbf{s}}_{k^{\prime }i,{\theta }_k}\left(t\right){\mathbf{s}}_{k^{\prime }{i}^{\prime },{\theta }_k}^H\left(t\right)\right\}{\Delta }_{k^{\prime }{i}^{\prime }}^H{\mathbf{\rho }}_{k^{\prime }{i}^{\prime }}^H-{\mathsf{\Phi }}_l{\mathbf{\rho }}_{k^{\prime }i}^{*}{\Delta }_{k^{\prime }i}^{*}E\left\{{\mathbf{s}}_{k^{\prime }i,{\theta }_k}\left(t\right){\mathbf{s}}_{k^{\prime }{i}^{\prime },{\theta }_k}^H\left(t\right)\right\}{\Delta }_{k^{\prime }{i}^{\prime }}^T{\mathbf{\rho }}_{k^{\prime }{i}^{\prime }}^T{\mathsf{\Phi }}_l^H\right),$$

(27)

where ${\mathsf{\Phi }}_l=\left[{\mathbf{0}}_{\left(M-L+1\right)\times \left(l-1\right)},e^{j{w}_0{\tau }_{-M+L-l-1,{\theta }_{ki}}}\otimes {\mathbf{J}}_{M-L+1},{\mathbf{0}}_{\left(M-L+1\right)\times \left(L-l\right)}\right]$.

Consider ${\theta }_k={\theta }_{ki}$, one can extract the covariance of envelope aligned term from ${\mathbf{R}}_d\left({\theta }_k\right)$, i.e.,

$${\mathbf{R}}_d\left({\theta }_k\right)={\sigma }_k^2{\left|{\rho }_{ki}\right|}^2{\mathbf{a}}_d\left({\theta }_k\right){\mathbf{a}}_d^H\left({\theta }_k\right)+{\mathbf{R}}_h\left({\theta }_k\right),$$

(28)

$${\mathbf{R}}_h\left({\theta }_k\right)={\mathbf{V}}_h\left({\theta }_k\right){\mathsf{\Sigma }}_h\left({\theta }_k\right){\mathbf{V}}_h^H\left({\theta }_k\right)+{\Xi }_h\left({\theta }_k\right).$$

(29)

Let ${\mathbf{H}}_h\left({\theta }_k\right)=\left[{\mathbf{a}}_d\left({\theta }_k\right),{\mathbf{V}}_h\left({\theta }_k\right)\right]$ and ${\mathbf{\Gamma }}_h\left({\theta }_k\right)=blkdiag\left\{{\sigma }_k^2{\left|{\rho }_{ki}\right|}^2,{\mathsf{\Sigma }}_h\left({\theta }_k\right)\right\}$, yielding:

$${\mathbf{H}}_h\left({\theta }_k\right){\mathbf{\Gamma }}_h\left({\theta }_k\right){\mathbf{H}}_h^H\left({\theta }_k\right){\mathit{\alpha }}_m\left({\theta }_k\right)={\epsilon }_h,$$

(30)

where ${\epsilon }_h={\sum }_{m=F_{c,{\theta }_k}+1}^{M-L+1}{\eta }_m\left({\theta }_k\right){\mathit{\alpha }}_m\left({\theta }_k\right){\mathit{\alpha }}_m^H\left({\theta }_k\right)-{\Xi }_h\left({\theta }_k\right){\mathit{\alpha }}_m\left({\theta }_k\right)$. When ${\epsilon }_h=\mathbf{0}$, ${\mathbf{a}}_d\left({\theta }_k\right){\mathit{\alpha }}_m\left({\theta }_k\right)=0$. Because the noise has been removed, ${\eta }_m\left({\theta }_k\right)\to 0$ for $m\in \left\{F_{c,{\theta }_k}+1,\cdots ,M-L+1\right\}$ and ${\Xi }_h\left({\theta }_k\right)\to \mathbf{0}$. Consequently, ${\epsilon }_h$ is neglected and the correlated wideband signals can form peaks in the spectrum, i.e.,

$$P_c\left({\theta }_k\right)=1/\phantom{1{∥{\mathbf{a}}_d^H\left({\theta }_k\right){\mathbf{E}}_d\left({\theta }_k\right)∥}_2^2}{∥{\mathbf{a}}_d^H\left({\theta }_k\right){\mathbf{E}}_d\left({\theta }_k\right)∥}_2^2,$$

(31)

where ${\mathbf{E}}_d\left({\theta }_k\right)=\left[{\mathit{\alpha }}_{D_{{\theta }_k}+1}\left({\theta }_k\right),\cdots ,{\mathit{\alpha }}_{M-L+1}\left({\theta }_k\right)\right]$.

3.3. Efficient Implementation

Although the proposed approaches can acquire DOA of uncorrelated and correlated wideband signals, the computational complexity of operations (delay compensation, peak searching, etc.) corresponding to each scanning angle is prohibitive for the dense grid. Inspired by the linear search strategy, an efficient implementation is proposed.

For brevity, $\mathbf{E}\left({\theta }^{\left(i\right)}\right)$, ${\mathbf{E}}_d\left({\theta }^{\left(i\right)}\right)$, $\mathbf{a}\left({\theta }^{\left(i\right)}\right)$, and ${\mathbf{a}}_d\left({\theta }^{\left(i\right)}\right)$ are denoted as ${\mathbf{E}}_{{\theta }^{\left(i\right)}}$, ${\mathbf{E}}_{d{\theta }^{\left(i\right)}}$, ${\mathbf{a}}_{{\theta }^{\left(i\right)}}$, and ${\mathbf{a}}_{d{\theta }^{\left(i\right)}}$, respectively. Define the quantities for iteration i as:

$$z_{u1}\left({\theta }^{\left(i\right)}\right)={\mathbf{a}}_{{\theta }^{\left(i\right)}}^{″H}{\mathbf{E}}_{{\theta }^{\left(i\right)}}{\mathbf{E}}_{{\theta }^{\left(i\right)}}^H{\mathbf{a}}_{{\theta }^{\left(i\right)}}+2{\mathbf{a}}_{{\theta }^{\left(i\right)}}^{\prime H}{\mathbf{E}}_{{\theta }^{\left(i\right)}}{\mathbf{E}}_{{\theta }^{\left(i\right)}}^H{\mathbf{a}}_{{\theta }^{\left(i\right)}}^{\prime }+{\mathbf{a}}_{{\theta }^{\left(i\right)}}^H{\mathbf{E}}_{{\theta }^{\left(i\right)}}{\mathbf{E}}_{{\theta }^{\left(i\right)}}^H{\mathbf{a}}_{{\theta }^{\left(i\right)}}^{″},$$

(32)

$$z_{u2}\left({\theta }^{\left(i\right)}\right)={\mathbf{a}}_{{\theta }^{\left(i\right)}}^{\prime H}{\mathbf{E}}_{{\theta }^{\left(i\right)}}{\mathbf{E}}_{{\theta }^{\left(i\right)}}^H{\mathbf{a}}_{{\theta }^{\left(i\right)}}+{\mathbf{a}}_{{\theta }^{\left(i\right)}}^H{\mathbf{E}}_{{\theta }^{\left(i\right)}}{\mathbf{E}}_{{\theta }^{\left(i\right)}}^H{\mathbf{a}}_{{\theta }^{\left(i\right)}}^{\prime },$$

(33)

$$z_{c1}\left({\theta }^{\left(i\right)}\right)={\mathbf{a}}_{d{\theta }^{\left(i\right)}}^{″H}{\mathbf{E}}_{d{\theta }^{\left(i\right)}}{\mathbf{E}}_{d{\theta }^{\left(i\right)}}^H{\mathbf{a}}_{d{\theta }^{\left(i\right)}}+2{\mathbf{a}}_{d{\theta }^{\left(i\right)}}^{\prime H}{\mathbf{E}}_{d{\theta }^{\left(i\right)}}{\mathbf{E}}_{d{\theta }^{\left(i\right)}}^H{\mathbf{a}}_{d{\theta }^{\left(i\right)}}^{\prime }+{\mathbf{a}}_{d{\theta }^{\left(i\right)}}^H{\mathbf{E}}_{d{\theta }^{\left(i\right)}}{\mathbf{E}}_{d{\theta }^{\left(i\right)}}^H{\mathbf{a}}_{d{\theta }^{\left(i\right)}}^{″},$$

(34)

$$z_{c2}\left({\theta }^{\left(i\right)}\right)={\mathbf{a}}_{d{\theta }^{\left(i\right)}}^{\prime H}{\mathbf{E}}_{d{\theta }^{\left(i\right)}}{\mathbf{E}}_{d{\theta }^{\left(i\right)}}^H{\mathbf{a}}_{d{\theta }^{\left(i\right)}}+{\mathbf{a}}_{d{\theta }^{\left(i\right)}}^H{\mathbf{E}}_{d{\theta }^{\left(i\right)}}{\mathbf{E}}_{d{\theta }^{\left(i\right)}}^H{\mathbf{a}}_{d{\theta }^{\left(i\right)}}^{\prime },$$

(35)

where ${\mathbf{a}}^{\prime }\left(\theta \right)=\partial \mathbf{a}\left(\theta \right)/\phantom{\partial \mathbf{a}\left(\theta \right)\partial \theta }\partial \theta$, ${\mathbf{a}}^{″}\left(\theta \right)=\partial {\mathbf{a}}^{\prime }\left(\theta \right)/\phantom{\partial {\mathbf{a}}^{\prime }\left(\theta \right)\partial \theta }\partial \theta$, ${\mathbf{a}}_d^{\prime }\left(\theta \right)=\partial {\mathbf{a}}_d\left(\theta \right)/\phantom{\partial {\mathbf{a}}_d\left(\theta \right)\partial \theta }\partial \theta$, ${\mathbf{a}}_d^{″}\left(\theta \right)=\partial {{\mathbf{a}}^{\prime }}_d\left(\theta \right)/\phantom{\partial {\mathbf{a}}_d^{\prime }\left(\theta \right)\partial \theta }\partial \theta$. The initial approximations for directions can be found in (12) and (31) in the coarse grid. Then the accurate estimation result for each angle can be acquired using the following iteration:

$${\theta }_u^{\left(i+1\right)}={\theta }_u^{\left(i\right)}-z_{u1}\left({\theta }_u^{\left(i\right)}\right)/\phantom{z_{u1}\left({\theta }_u^{\left(i\right)}\right)z_{u2}\left({\theta }_u^{\left(i\right)}\right)}{z}_{u2}\left({\theta }_u^{\left(i\right)}\right),$$

(36)

$${\theta }_c^{\left(i+1\right)}={\theta }_c^{\left(i\right)}-z_{c1}\left({\theta }_u^{\left(i\right)}\right)/\phantom{z_{c1}\left({\theta }_u^{\left(i\right)}\right)z_{c2}\left({\theta }_u^{\left(i\right)}\right)}{z}_{c2}\left({\theta }_u^{\left(i\right)}\right).$$

(37)

The main cost of the proposed algorithm is the EVD, which requires $\mathrm{O}\left(M^3\right)$ computations for each scanning angle. Using (36) and (37), the number of grids is greatly reduced and the DOA results can be searched efficiently. In addition, the off-grid signals can also be estimated without the Taylor approximation to the signal model.

The detailed steps of the proposed algorithm are summarized in Algorithm 1.

Algorithm 1: Estimate the mixed uncorrelated and correlated wideband signals

Step 1: Set the coarse grid $\tilde{\theta }$.

Step 2: For each scanning angle ${\theta }_k\in \tilde{\theta }$, calculate ${\mathbf{x}}_{{\theta }_k}\left(t\right)$ by (4).

Step 3: Estimate the corresponding covariance matrix by ${\widehat{\mathbf{R}}}_{\mathbf{x}}\left({\theta }_k\right)=\frac{1}{T}{\sum }_{t=1}^T{\mathbf{x}}_{\theta }\left(t\right){\mathbf{x}}_{\theta }^H\left(t\right)$, perform EVD on ${\widehat{\mathbf{R}}}_{\mathbf{x}}\left({\theta }_k\right)$ to get $\widehat{\mathbf{E}}\left({\theta }_k\right)$.

Step 4: Estimate the corresponding differencing matrix ${\widehat{\mathbf{R}}}_d\left({\theta }_k\right)$ by (25) and obtain ${\widehat{\mathbf{E}}}_d\left({\theta }_k\right)$.

Step 5: Compute the approximate output $P_u$ by (12), find the largest $K_u$ peaks as the initial values for the accurate searching of uncorrelated wideband signals.

Step 6: Compute the approximate output $P_c$ by (31), find the largest $K_m$ peaks as the initial values for the accurate searching of correlated wideband signals.

Step 7: For each initial angle, repeat Step 2–Step 6.

Step 8: Obtain the next generation by (36) and (37) until convergence.

Step 9: Output the accurate results for mixed wideband signals.

4. Simulation Results

In this section, the proposed algorithm is compared with existing methods for correlated wideband sources such as the CSM [4], CTOPS [5], and the state-of-the-art sparse Bayesian learning based on off-grid methods in [7,8]. For brevity, we denote the off-grid methods in [7,8] as OG1 and OG2, respectively.

First of all, three uncorrelated off-grid wideband signals from $\left({-12.43}^{\circ },{22.56}^{\circ },{37.79}^{\circ }\right)$ and two groups of five off-grid wideband signals from $\left({-52.41}^{\circ },{-32.25}^{\circ },{2.48}^{\circ }\right)$ and $\left({32.78}^{\circ },{53.26}^{\circ }\right)$ impinging on the ULA with 12 sensors. The fading coefficients of the two groups of correlated signals are $\left(1,0.9e^{j{57.2}^{\circ }},0.8e^{j{98.5}^{\circ }}\right)$ and $\left(1,0.7e^{j{28.5}^{\circ }}\right)$. The multipath propagation delays are set as $\left(0,0.05,0.1\right)$ and $\left(0,0.2\right)$ times the correlation time $T_c$. The element spacing d equals the half wavelength at the center frequency. The carrier frequency is 2 GHz and the bandwidth is 400 MHz, which is $20\%$ of the center frequency. The sampling frequency is twice the highest frequency. The number of snapshots and SNR are 5000 and 10 dB. The number of submatrices L is 5. The step sizes for the subspace-based methods, the SR-based methods, and the proposed algorithm are set as ${0.01}^{\circ }$, $1^{\circ }$ and $5^{\circ }$, respectively. 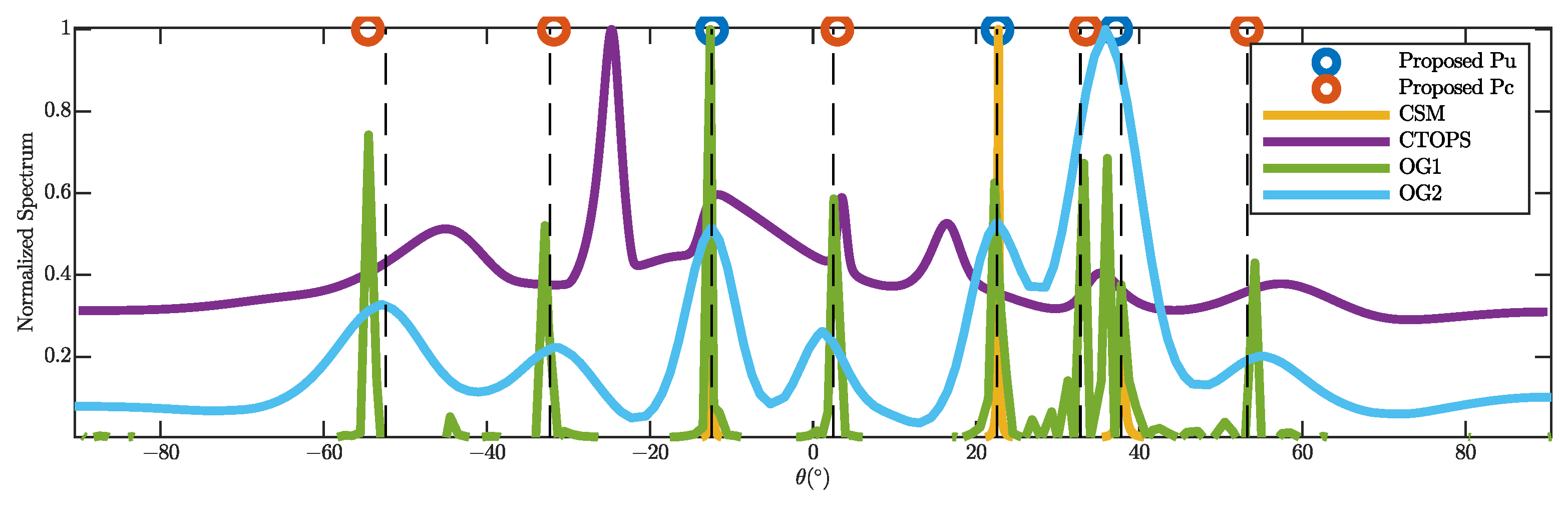Results in Figure 1 depict that the proposed algorithm can distinguish all the uncorrelated and correlated wideband signals extremely well. Figure 1 shows that CSM and CTOPS may miss part of the signals, the resolution performance of OG2 is not good enough, and OG1 forms some false peaks between the two close targets. Moreover, none of these algorithms can distinguish between uncorrelated and correlated signals.

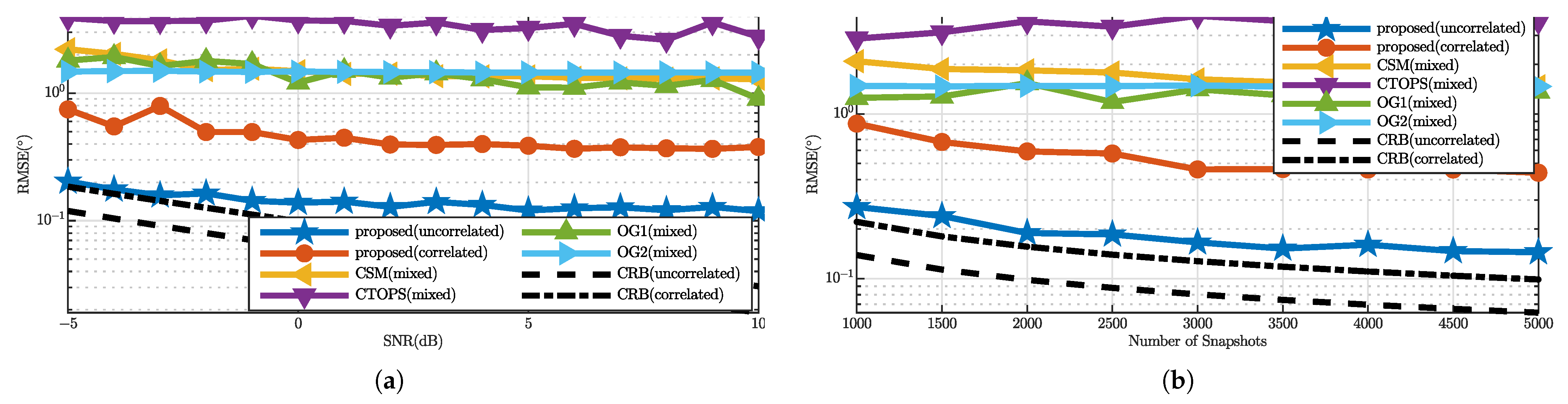
Next, the root-mean-square error (RMSE) of the above algorithms is compared. The RMSE can be defined as $RMS{E}_{\theta }=\sqrt{{\sum }_{i=1}^T{\sum }_{k=1}^K{\left({\widehat{\theta }}_{k,i}-\theta \right)}^2/KT}$, where the Monte Carlo trial number T is 100. Two uncorrelated wideband signals from $\left(-{41.32}^{\circ },-{22.76}^{\circ }\right)$ and a group of three wideband signals from $\left({2.59}^{\circ },{22.13}^{\circ },{41.88}^{\circ }\right)$ impinging on the ULA. The fading coefficients and the multipath propagation delays of the wideband correlated signals are $\left(1,0.9e^{j{57.2}^{\circ }},0.8e^{j{98.5}^{\circ }}\right)$ and $\left(0,0,0.02\right)$. $L=3$, other parameters remain unchanged. Let the SNR increases from $-5$ to 10 dB gradually and the number of snapshots is 5000; the results are shown in Figure 2a. Then snapshot number ranges from 1000 to 5000 and the SNR is 0 dB; results are displayed in Figure 2b. The CRB of the first $K_u$ uncorrelated LOS wideband signals can be found in [22]. For $K_m$ correlated multipath wideband signals, the CRB is deduced in detail (see Appendix A). It can be seen that the uncorrelated and correlated signals can be processed separately in the proposed algorithm. For correlated signals, it is not so close to CRB because the smoothing and spatial differencing sacrifices the array aperture and the power. However, the accuracy of the proposed algorithm is higher than that of other approaches in the multipath environment.

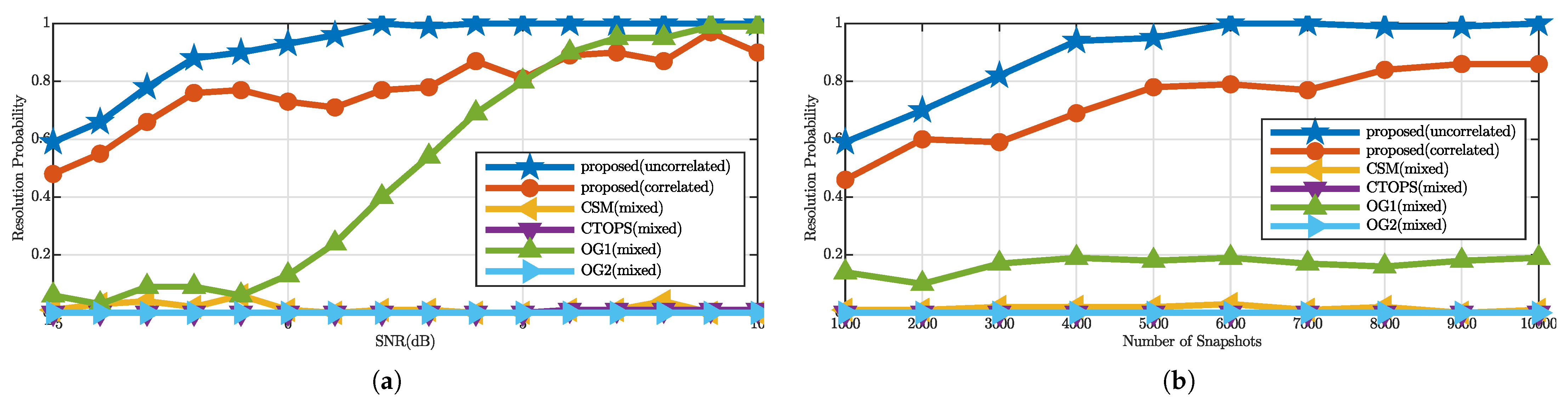
In the third case, the resolution probabilities of the above algorithms are compared to illustrate the performance further. Two correlated wideband signals and a group of two correlated wideband signals come from $\left(-{17.72}^{\circ },-{12.26}^{\circ }\right)$ and $\left({22.19}^{\circ },{27.53}^{\circ }\right)$, respectively. The step size is set as $2^{\circ }$ for the proposed method and the signals are resolved if the biases are smaller than $1^{\circ }$. Let the SNR increases from $-5$ to 10 dB gradually and the number of snapshots is 5000; results are shown in Figure 3a. Then snapshot number ranges from 1000 to 10,000 and the SNR is 0 dB; results are shown in Figure 3b. The resolution capability of the proposed algorithm is the best, and the resolution performance of the correlated components is inferior to that of the uncorrelated components. Although the off-grid algorithm can resolve two close directions in high SNR, many false peaks are formed between the targets.

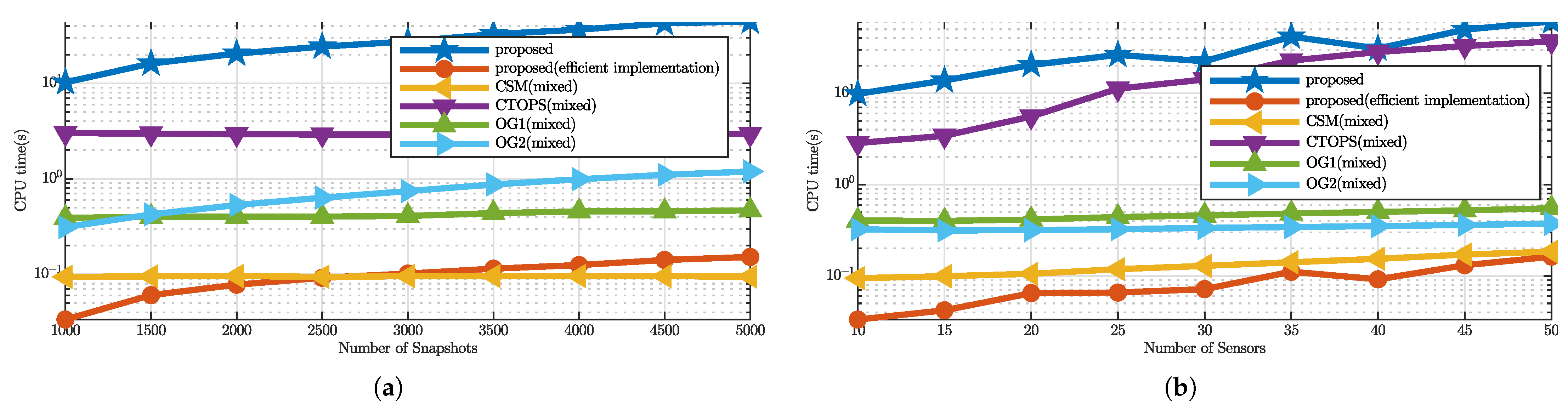
In the fourth case, we compare the computational cost of these algorithms. Figure 4a depicts the CPU time of the simulations in Figure 2b. Then the SNR and the snapshots number are set as 0 dB and 1000, respectively. Other parameters remain unchanged, Figure 4b shows the results when the number of sensors changes from 10 to 50. For other subspace-based methods, only one EVD is needed regardless of the number of scanning angles. However, for the proposed algorithm, EVD is required for each scanning angle because the delay in the envelope is compensated corresponding to the scanning angle. Consequently, the proposed algorithm before efficient implementation has the lowest performance compared with other algorithms. It is observed that the CPU time of the proposed algorithm has been shortened by more than three hundred times by the efficient implementation, because the number of scanning angles in efficient implementation is much less than that of the proposed algorithm without improvement. As the snapshots number increases, the operation time is longer than that of CSM due to the operations (delay compensation, EVD, peak searching, etc.) corresponding to each scanning angle but is much shorter than that of the other algorithms.

5. Conclusions

A novel efficient wideband DOA estimation algorithm is proposed to find the direction of uncorrelated and correlated wideband signals separately in the multipath environment. Furthermore, the CRB for DOA estimation of multipath wideband signals is derived in detail. Simulation results demonstrate the superiority of the presented algorithm.