Machine Learning in Extreme Value Analysis, an Approach to Detecting Harmful Algal Blooms with Long-Term Multisource Satellite Data
Abstract
:1. Introduction
2. Study Area and Data
2.1. Study Area
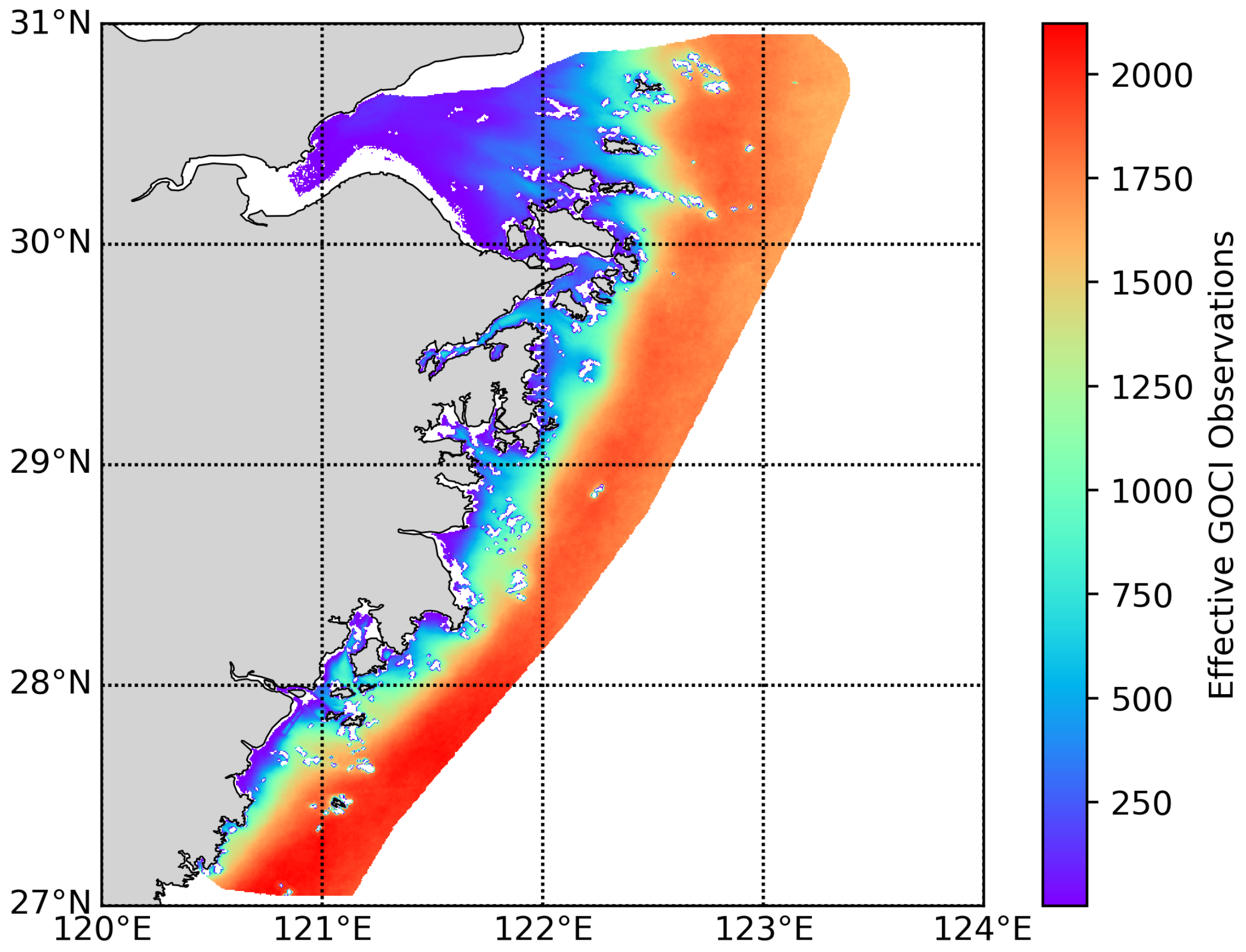
2.2. Long-Term Multisource Satellite Data
3. LSTM–EVA-Based Two-Step Detection Scheme
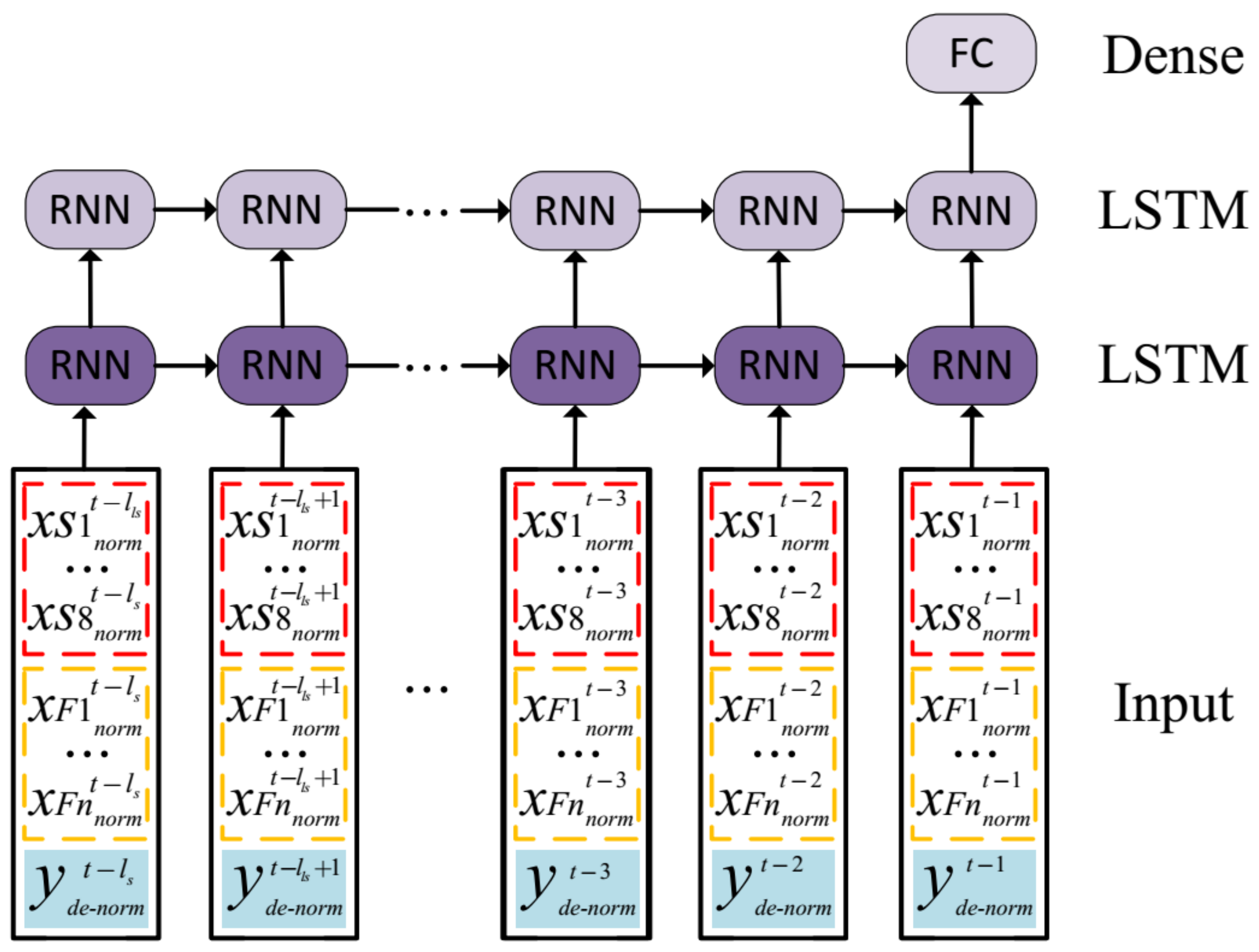
3.1. LSTM-Based Temporal Detection
3.2. EVA-Based Spatial Extraction
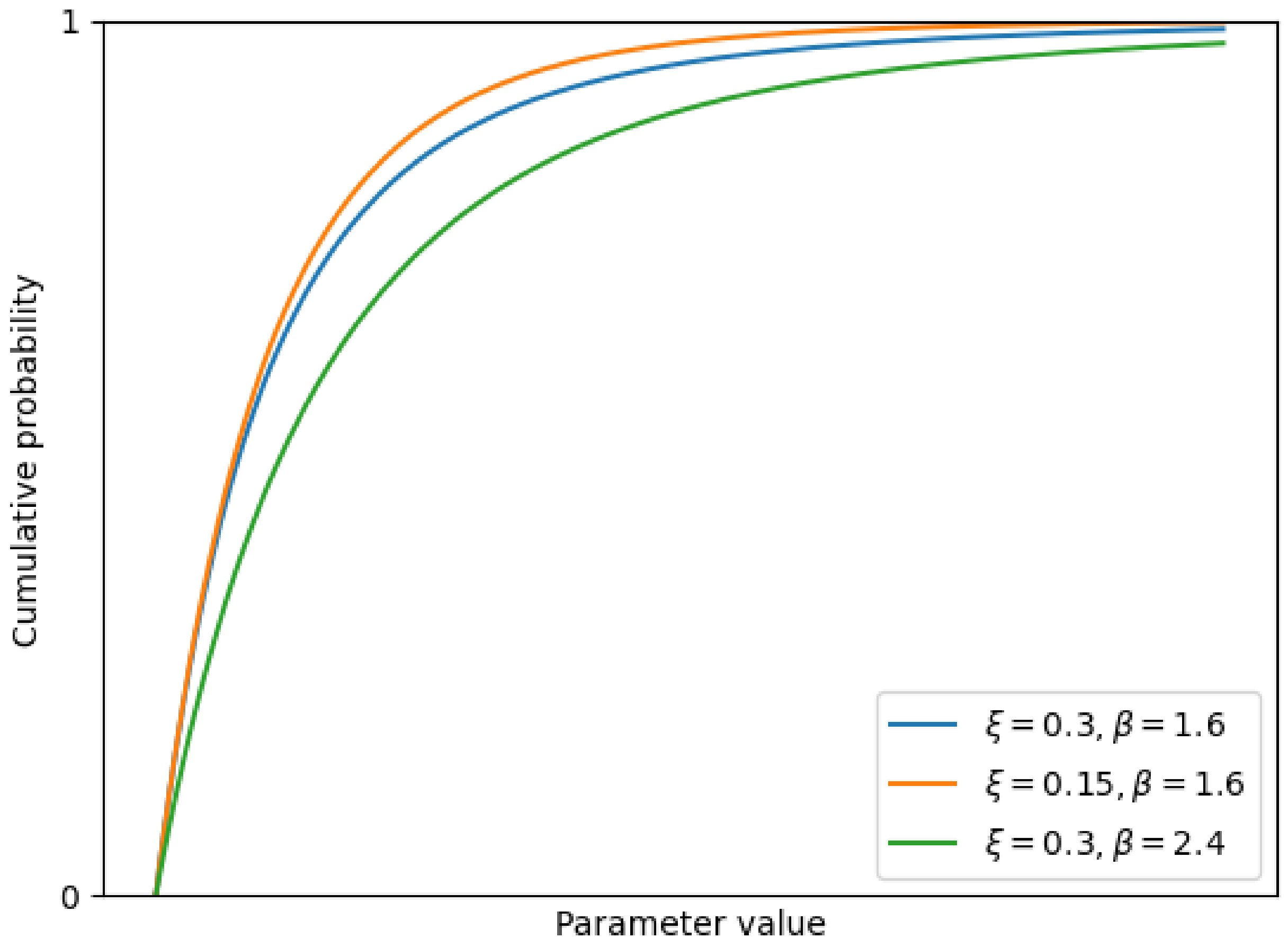
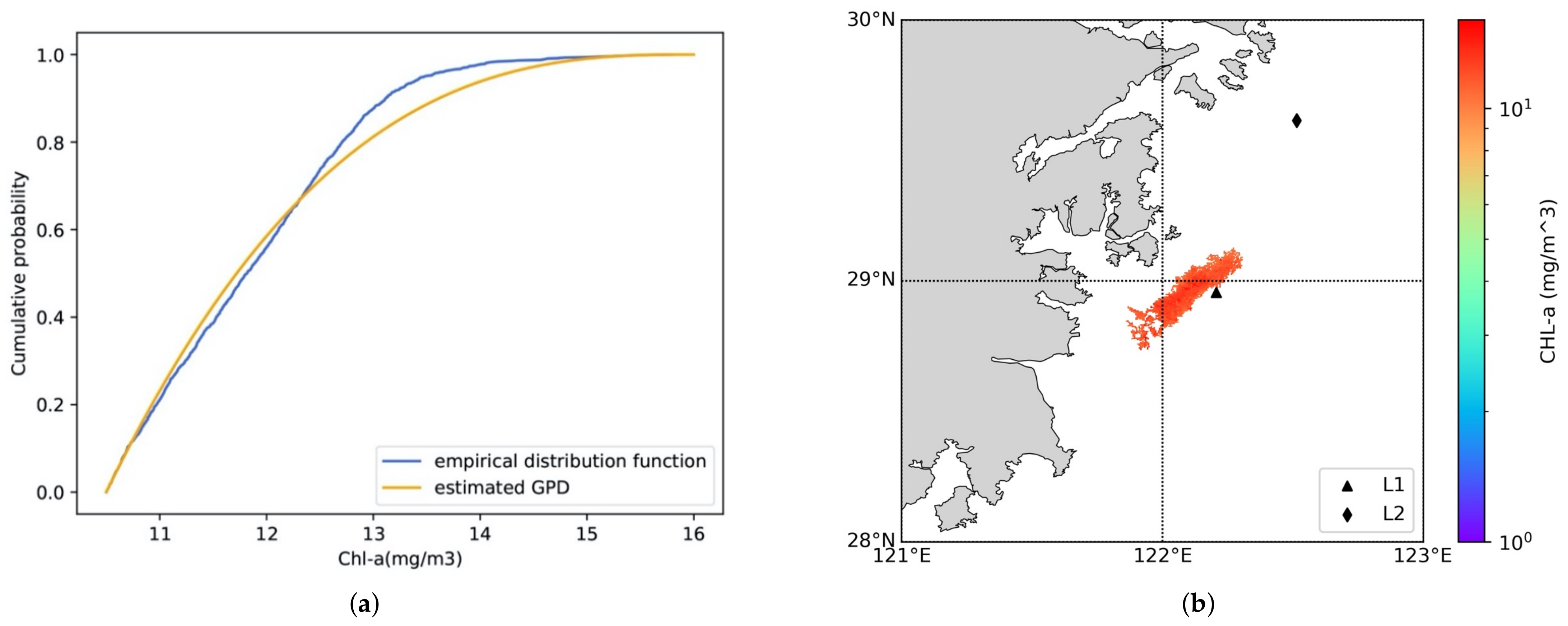
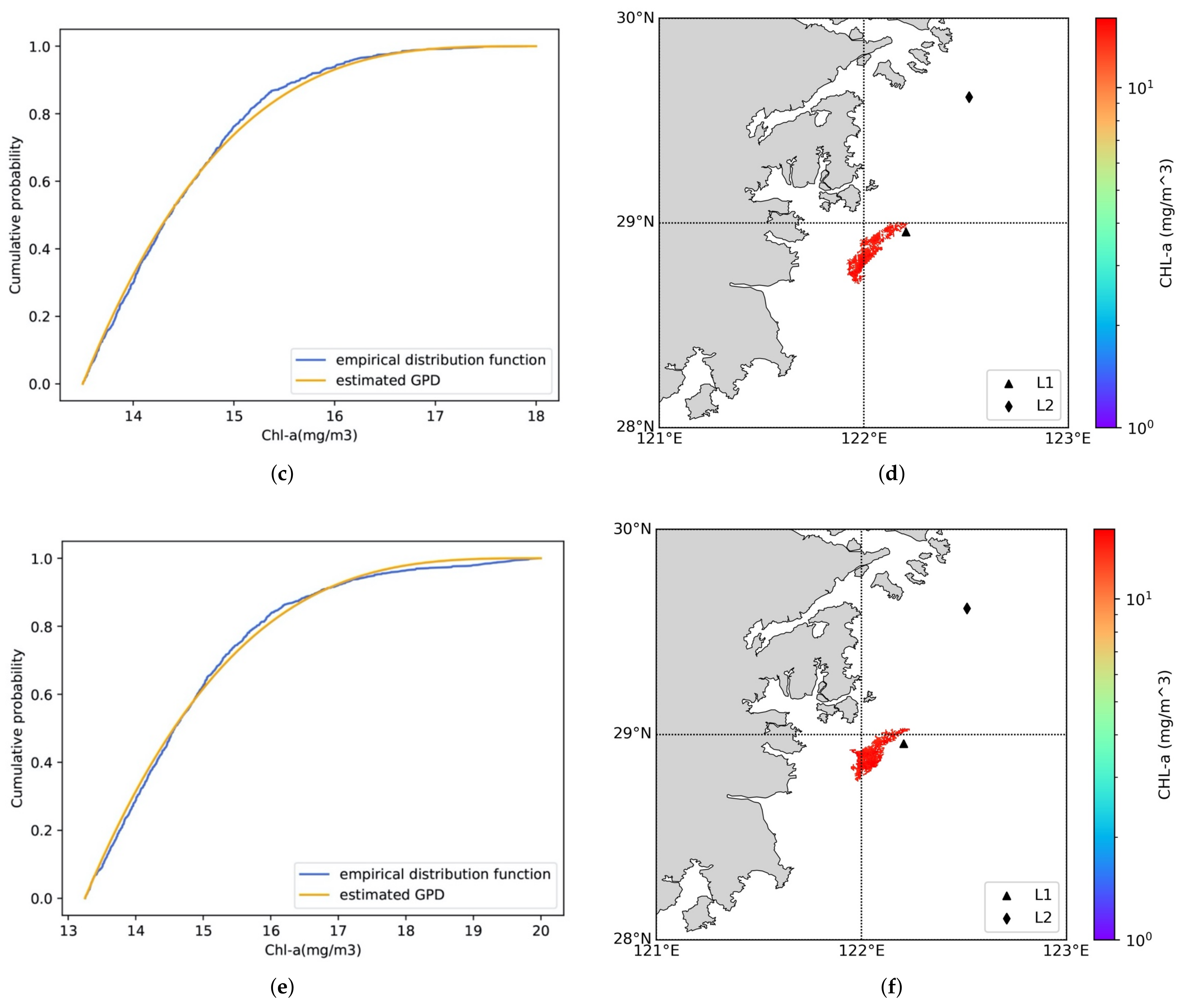
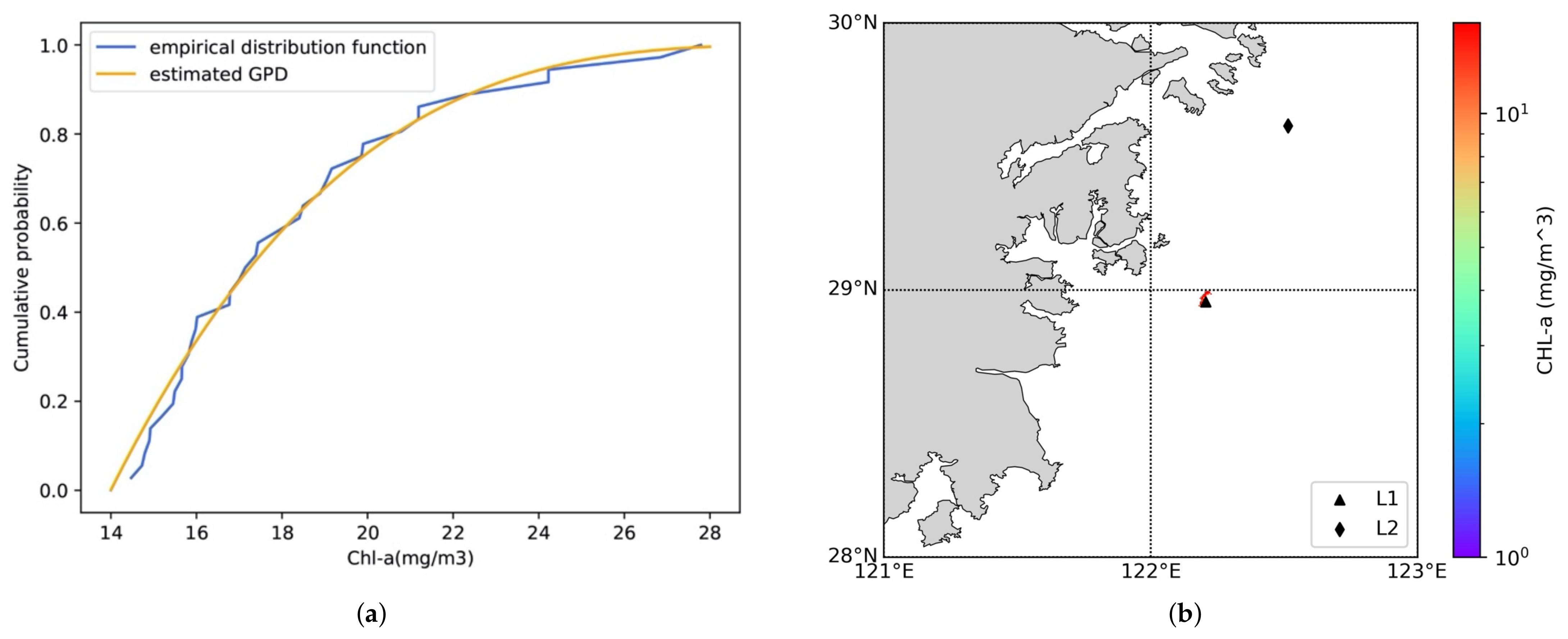
3.2.1. EVA Theory
3.2.2. Dynamic Thresholds
4. Experiment and Discussion
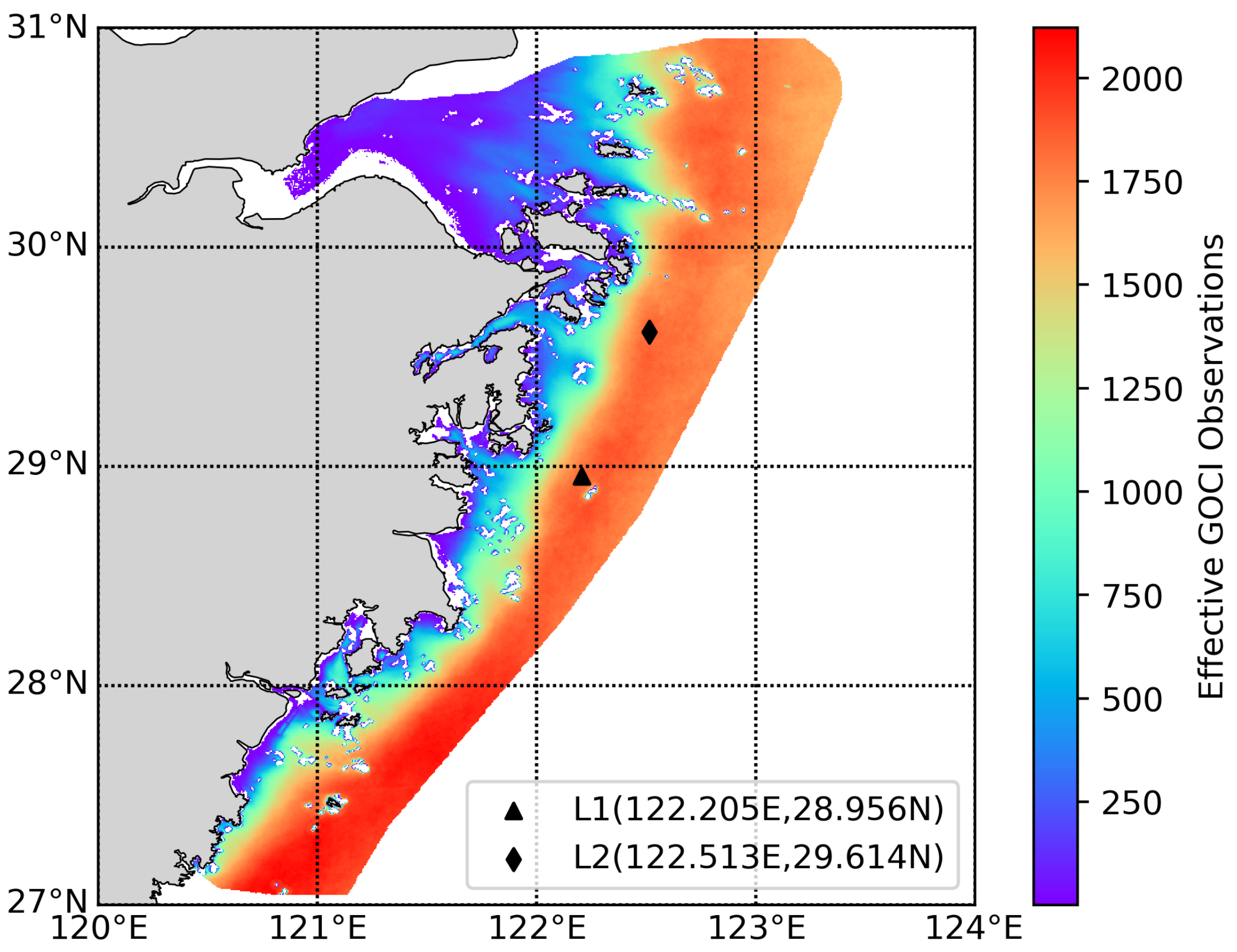
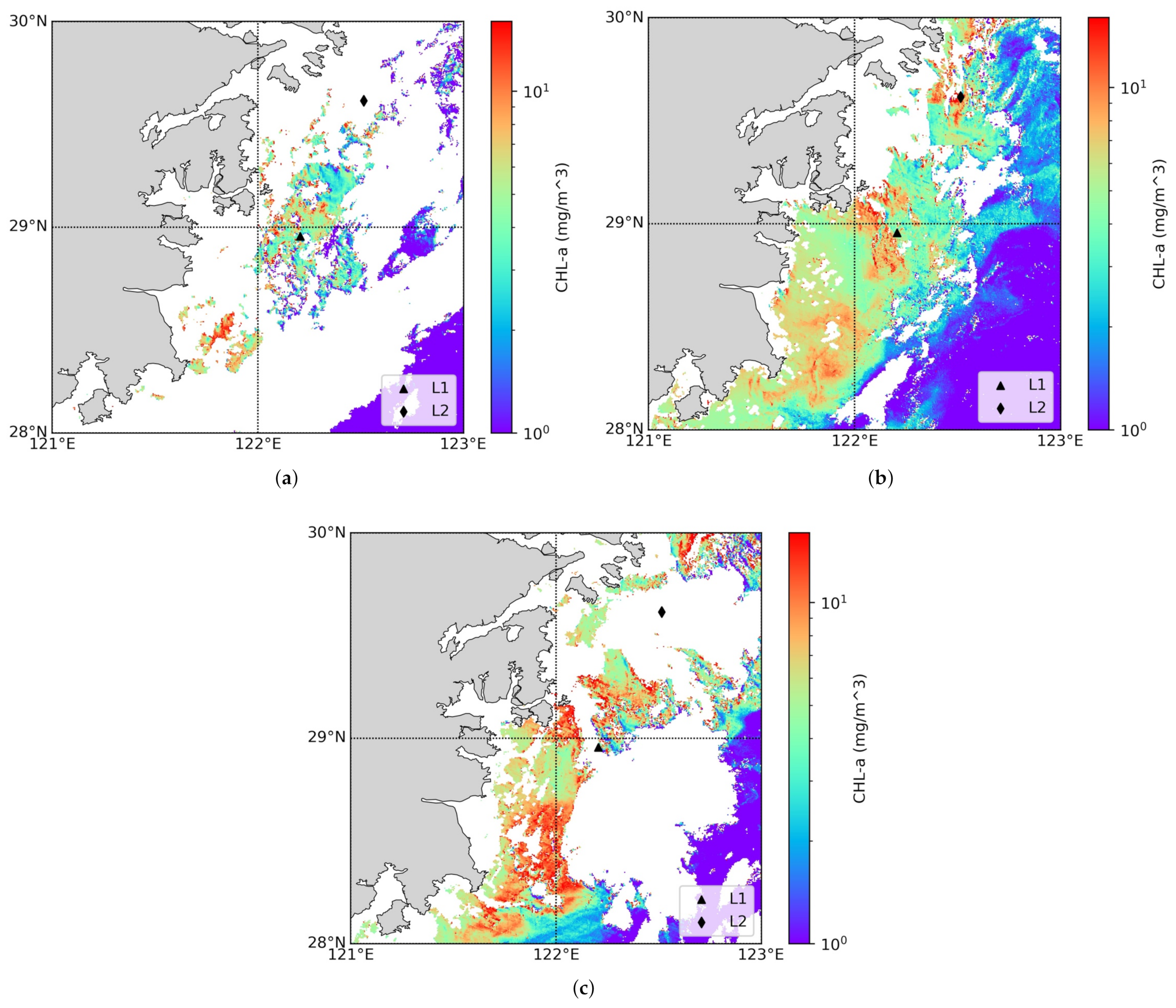
4.1. Representative Sites
4.2. Data Preprocessing
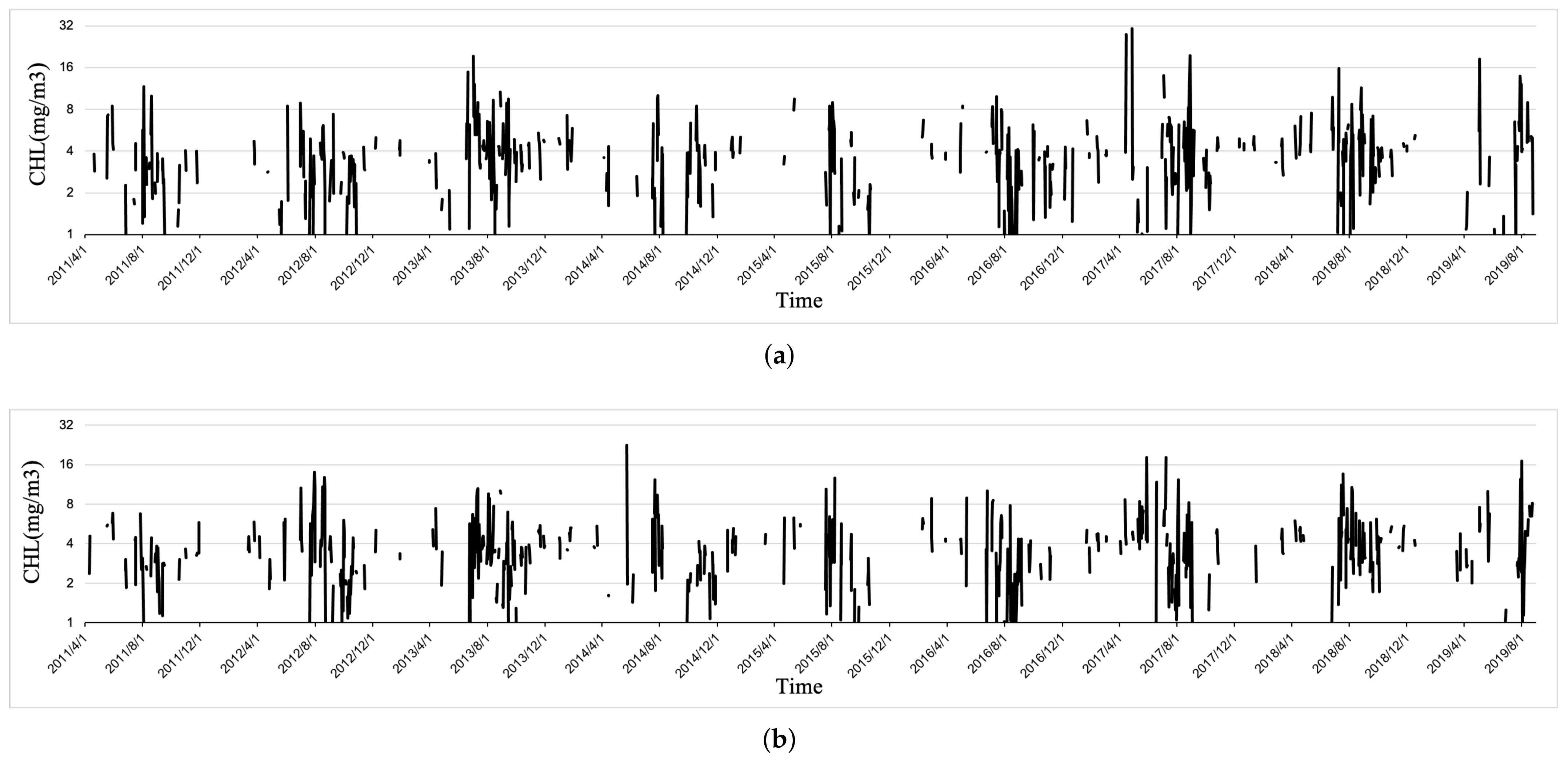
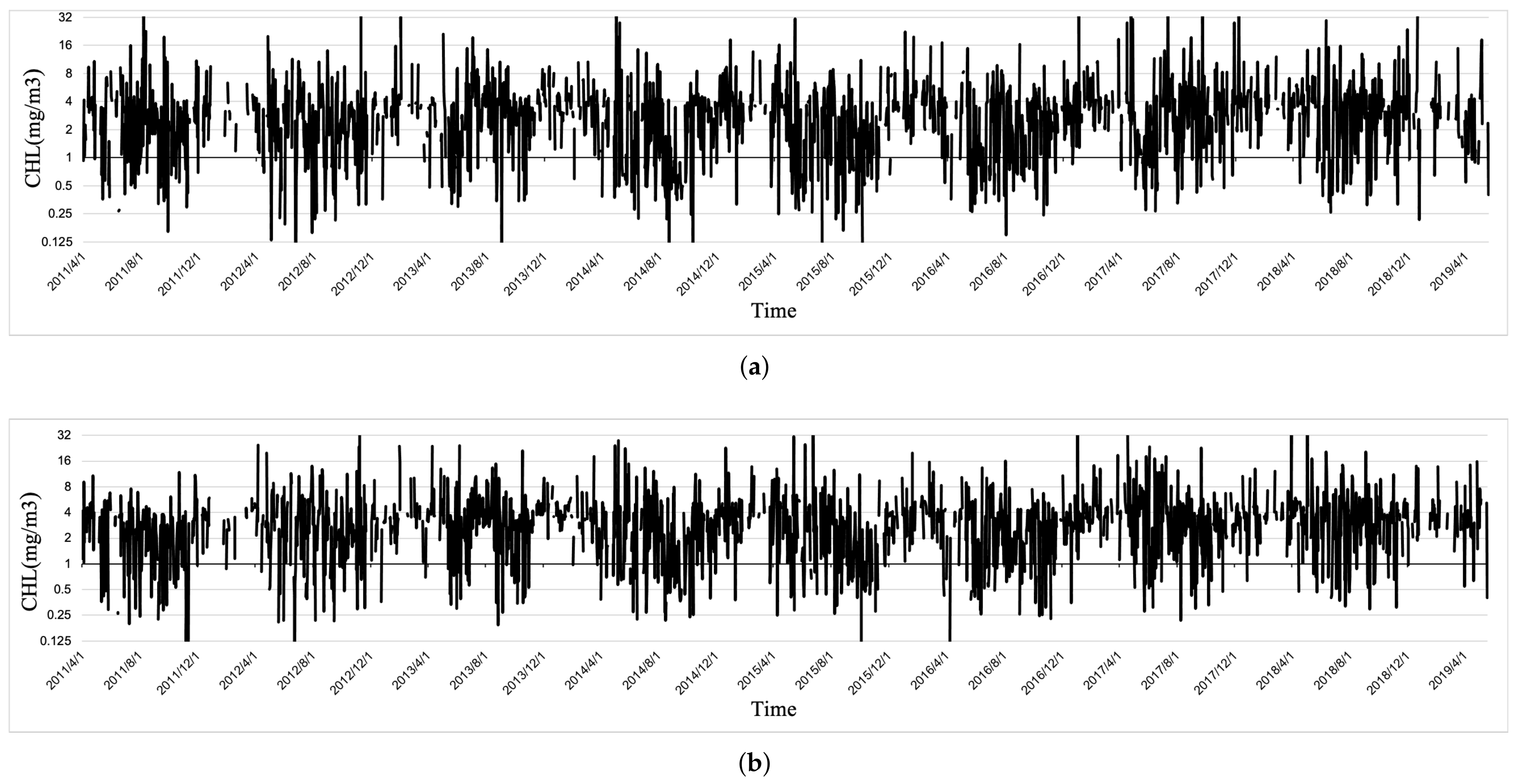
4.2.1. Time Series Extraction
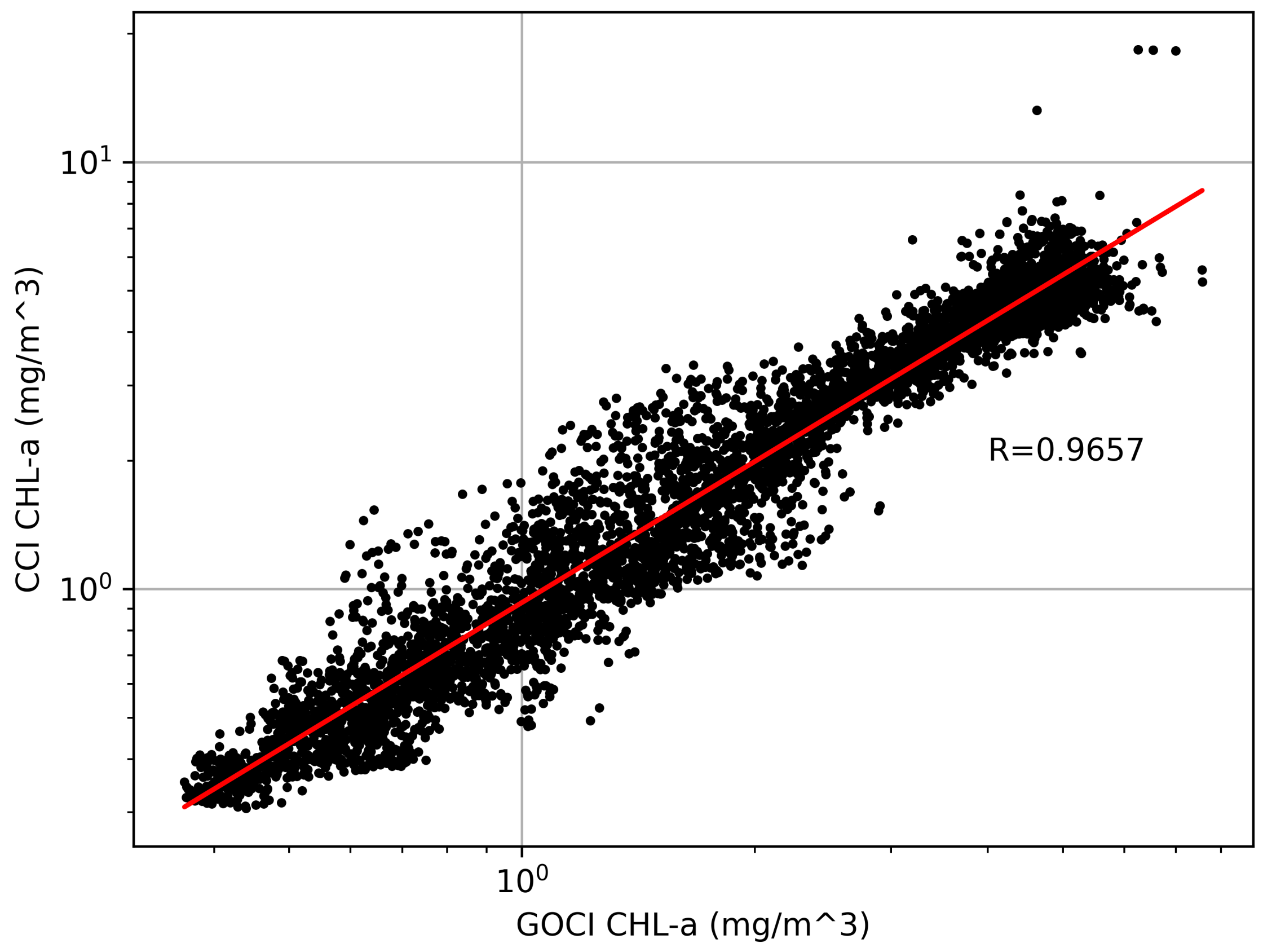
4.2.2. Interpolation of the GOCI CHL-a Time Series
4.2.3. Deseasonalization
4.2.4. Model Input and Parameters
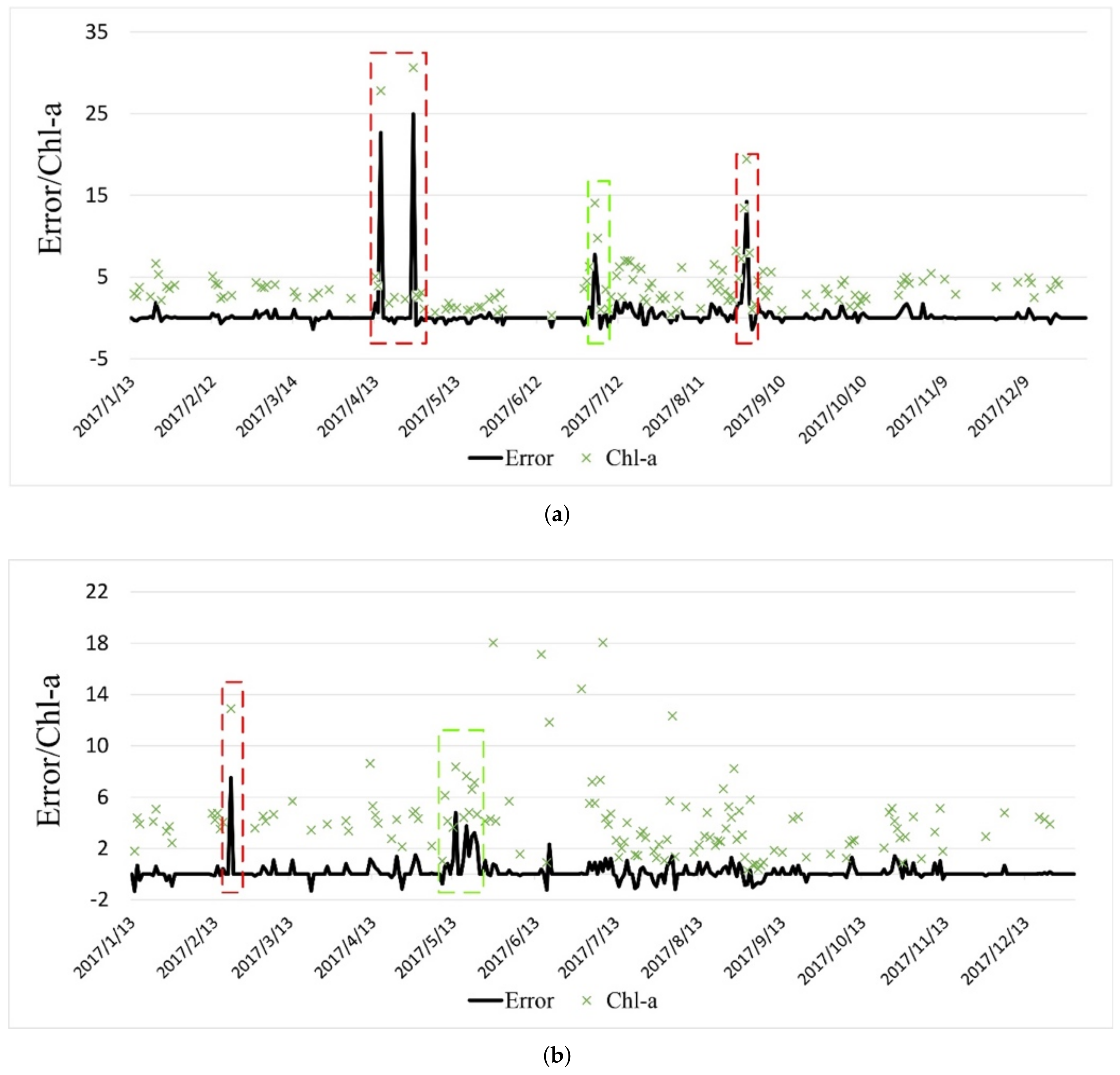
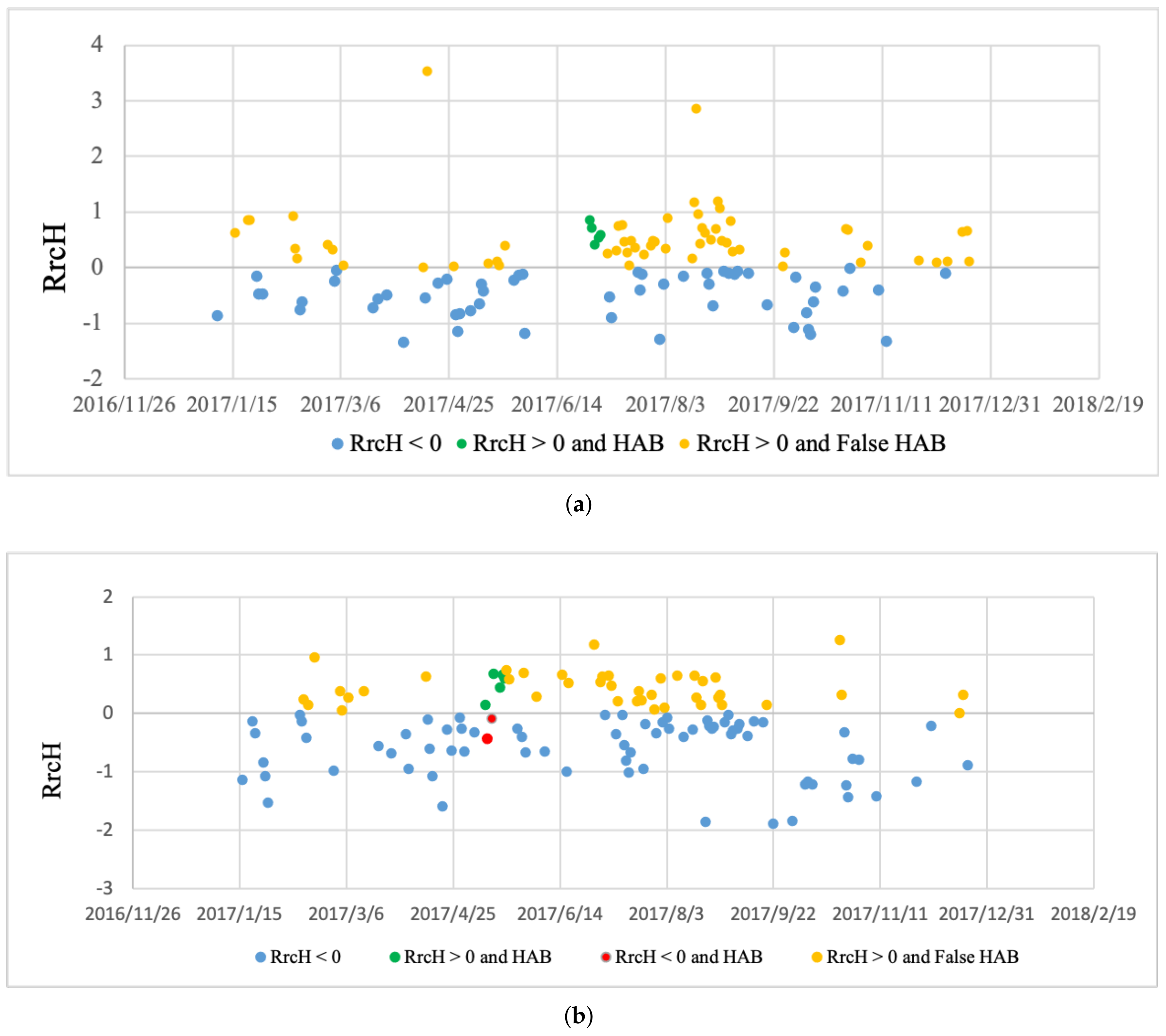
4.3. HAB Temporal Detection Results and Discussion
4.4. HAB Spatial Extraction Results and Discussion
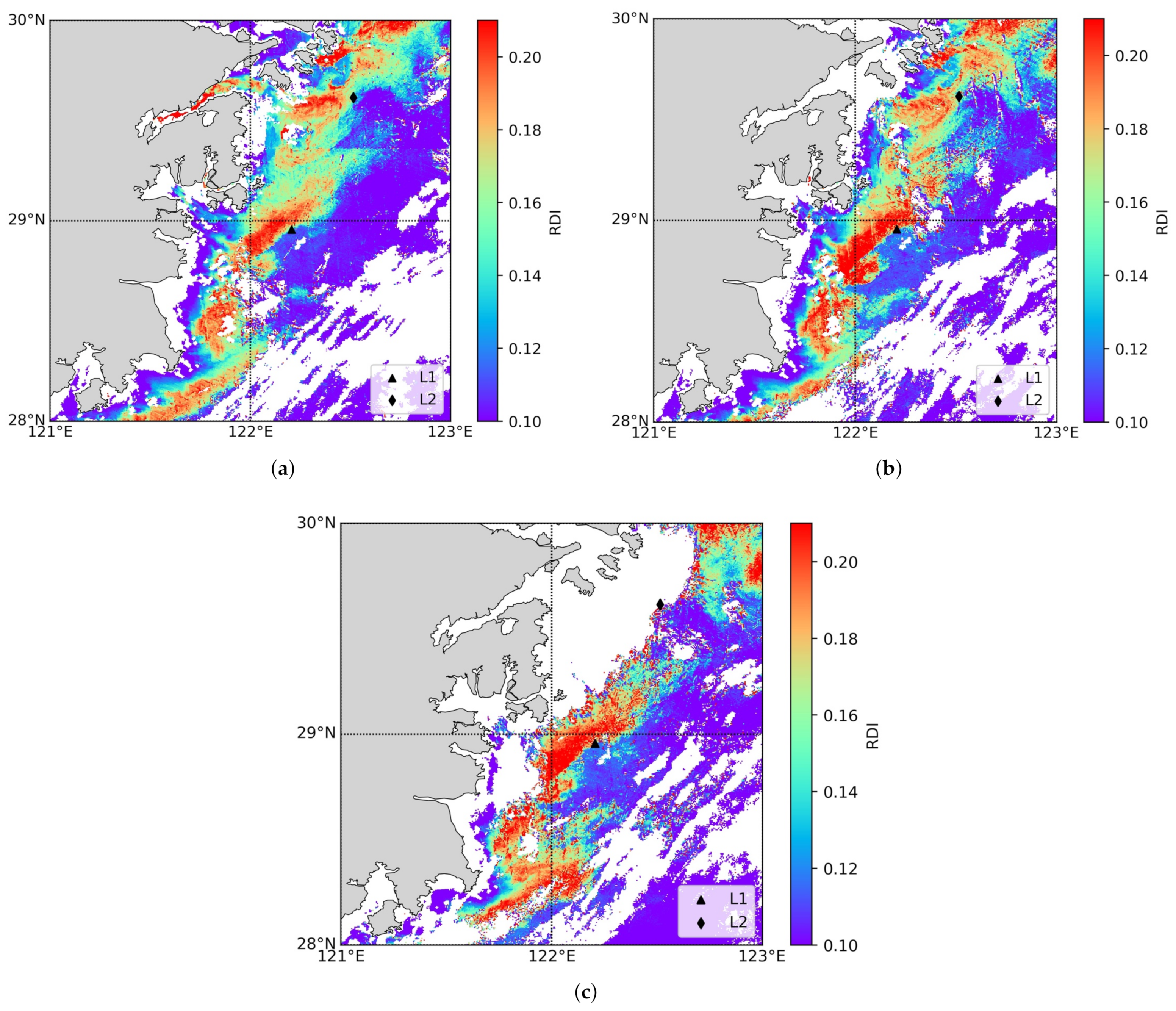
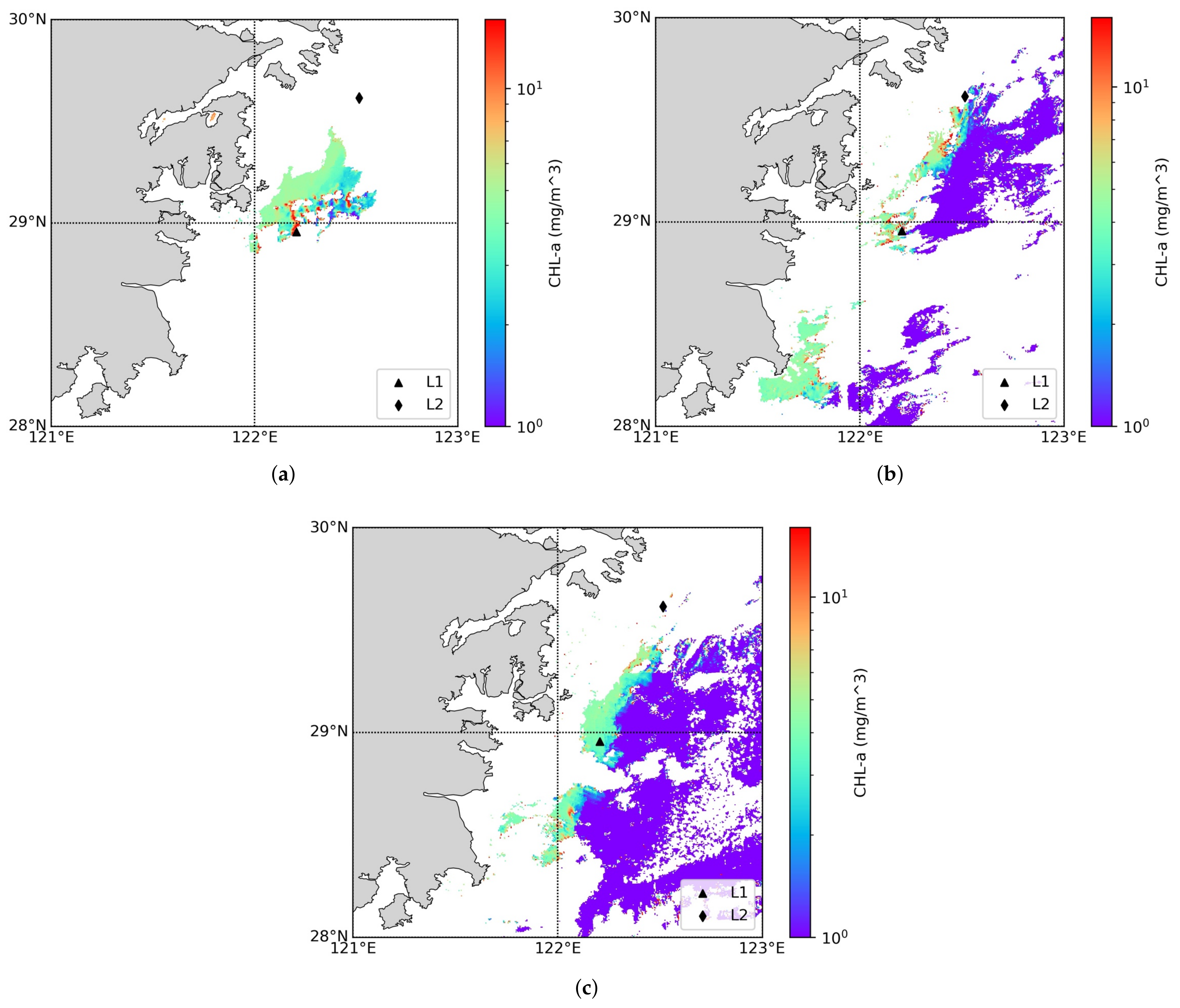
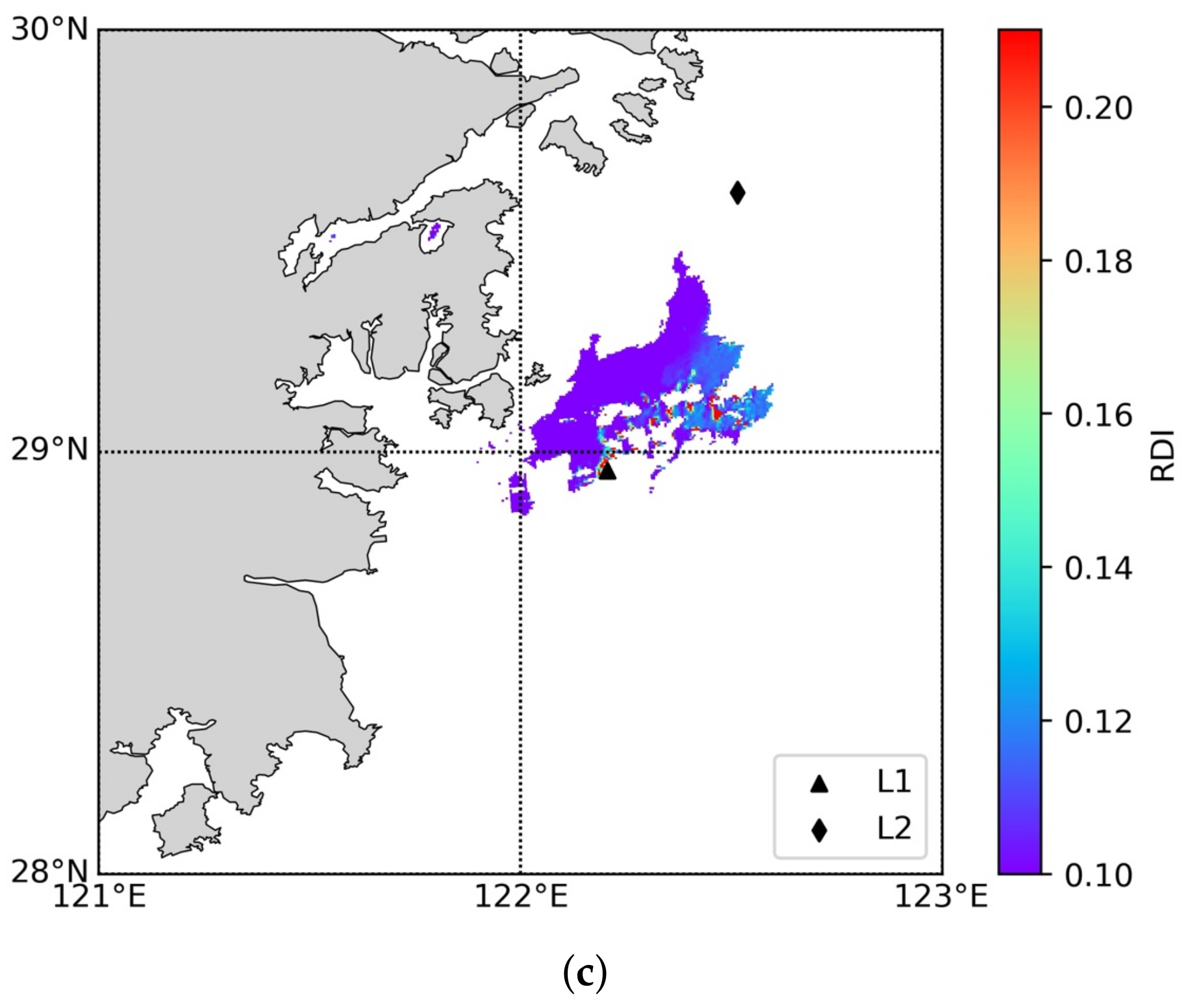
4.4.1. Recorded HAB Correctly Identified as Potential HAB Date
4.4.2. Unrecorded HAB Identified as Potential HAB Date
4.4.3. Recorded HAB Not Identified as Potential HAB Date
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Extreme Value Analysis
References
- Fleming, L.E.; McDonough, N.; Austen, M.; Mee, L.; Moore, M.; Hess, P.; Depledge, M.H.; White, M.; Philippart, K.; Bradbrook, P.; et al. Oceans and human health: A rising tide of challenges and opportunities for Europe. Mar. Environ. Res. 2014, 99, 16–19. [Google Scholar] [CrossRef] [PubMed]
- Anderson, D.M. Approaches to monitoring, control and management of harmful algal blooms (HABs). Ocean Coast. Manag. 2009, 52, 342–347. [Google Scholar] [CrossRef] [PubMed]
- Siswanto, E.; Ishizaka, J.; Tripathy, S.C.; Miyamura, K. Detection of harmful algal blooms of Karenia mikimotoi using MODIS measurements: A case study of Seto-Inland Sea, Japan. Remote Sens. Environ. 2013, 129, 185–196. [Google Scholar] [CrossRef]
- Stumpf, R.; Culver, M.; Tester, P.; Tomlinson, M.; Kirkpatrick, G.; Pederson, B.; Truby, E.; Ransibrahmanakul, V.; Soracco, M. Monitoring Karenia brevis blooms in the Gulf of Mexico using satellite ocean color imagery and other data. Harmful Algae 2003, 2, 147–160. [Google Scholar] [CrossRef]
- Tomlinson, M.; Wynne, T.; Stumpf, R. An evaluation of remote sensing techniques for enhanced detection of the toxic dinoflagellate, Karenia brevis. Remote Sens. Environ. 2009, 113, 598–609. [Google Scholar] [CrossRef]
- Hu, C.; Carder, K.L.; Muller-Karger, F.E. Atmospheric correction of SeaWiFS imagery over turbid coastal waters: A practical method. Remote Sens. Environ. 2000, 74, 195–206. [Google Scholar] [CrossRef]
- Siegel, D.A.; Wang, M.; Maritorena, S.; Robinson, W. Atmospheric correction of satellite ocean color imagery: The black pixel assumption. Appl. Opt. 2000, 39, 3582–3591. [Google Scholar] [CrossRef]
- Tao, B.; Mao, Z.; Lei, H.; Pan, D.; Shen, Y.; Bai, Y.; Zhu, Q.; Li, Z. A novel method for discriminating Prorocentrum donghaiense from diatom blooms in the East China Sea using MODIS measurements. Remote Sens. Environ. 2015, 158, 267–280. [Google Scholar] [CrossRef]
- Shen, F.; Tang, R.; Sun, X.; Liu, D. Simple methods for satellite identification of algal blooms and species using 10-year time series data from the East China Sea. Remote Sens. Environ. 2019, 235, 111484. [Google Scholar] [CrossRef]
- Ahn, Y.H.; Shanmugam, P. Detecting the red tide algal blooms from satellite ocean color observations in optically complex Northeast-Asia Coastal waters. Remote Sens. Environ. 2006, 103, 419–437. [Google Scholar] [CrossRef]
- Hu, C.; Muller-Karger, F.E.; Taylor, C.J.; Carder, K.L.; Kelble, C.; Johns, E.; Heil, C.A. Red tide detection and tracing using MODIS fluorescence data: A regional example in SW Florida coastal waters. Remote Sens. Environ. 2005, 97, 311–321. [Google Scholar] [CrossRef]
- Tester, P.A.; Steidinger, K.A. Gymnodinium breve red tide blooms: Initiation, transport, and consequences of surface circulation. Limnol. Oceanogr. 1997, 42, 1039–1051. [Google Scholar] [CrossRef]
- Neely, M.B.; Bartels, E.; Cannizzaro, J.; Carder, K.L.; Coble, P.; English, D.; Heil, C.; Hu, C.; Hunt, J.; Ivey, J.; et al. Florida’s Black Water Event. 2004. Available online: https://dspace.mote.org/handle/2075/3022 (accessed on 23 July 2020).
- Hu, C.; Luerssen, R.; Muller-Karger, F.E.; Carder, K.L.; Heil, C.A. On the remote monitoring of Karenia brevis blooms of the west Florida shelf. Cont. Shelf Res. 2008, 28, 159–176. [Google Scholar] [CrossRef]
- Gokaraju, B.; Durbha, S.S.; King, R.L.; Younan, N.H. A machine learning based spatio-temporal data mining approach for detection of harmful algal blooms in the Gulf of Mexico. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2011, 4, 710–720. [Google Scholar] [CrossRef]
- Gokaraju, B.; Durbha, S.S.; King, R.L.; Younan, N.H. Ensemble methodology using multistage learning for improved detection of harmful algal blooms. IEEE Geosci. Remote Sens. Lett. 2012, 9, 827–831. [Google Scholar] [CrossRef]
- Hill, P.R.; Kumar, A.; Temimi, M.; Bull, D.R. HABNet: Machine learning, remote sensing-based detection of harmful algal blooms. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 3229–3239. [Google Scholar] [CrossRef]
- Liu, W.; Pyrcz, M.J. A spatial correlation-based anomaly detection method for subsurface modeling. Math. Geosci. 2021, 53, 809–822. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Fisher, R.A.; Tippett, L.H.C. Limiting forms of the frequency distribution of the largest or smallest member of a sample. In Mathematical Proceedings of the Cambridge Philosophical Society; Cambridge University Press: Cambridge, UK, 1928; Volume 24, pp. 180–190. [Google Scholar]
- Li, X.; Shang, S.; Lee, Z.; Lin, G.; Zhang, Y.; Wu, J.; Kang, Z.; Liu, X.; Yin, C.; Gao, Y. Detection and Biomass Estimation of Phaeocystis globosa Blooms off Southern China From UAV-Based Hyperspectral Measurements. IEEE Trans. Geosci. Remote Sens. 2021, 60, 4200513. [Google Scholar] [CrossRef]
- Ministry of Natural Resources. Available online: https://www.mnr.gov.cn/sj/sjfw/hy/gbgg/zghyzhgb/ (accessed on 23 July 2022).
- Lou, X.; Hu, C. Diurnal changes of a harmful algal bloom in the East China Sea: Observations from GOCI. Remote Sens. Environ. 2014, 140, 562–572. [Google Scholar] [CrossRef]
- Blondeau-Patissier, D.; Gower, J.F.; Dekker, A.G.; Phinn, S.R.; Brando, V.E. A review of ocean color remote sensing methods and statistical techniques for the detection, mapping and analysis of phytoplankton blooms in coastal and open oceans. Prog. Oceanogr. 2014, 123, 123–144. [Google Scholar] [CrossRef]
- Sak, H.; Senior, A.W.; Beaufays, F. Long short-term memory recurrent neural network architectures for large scale acoustic modeling. In Proceedings of the 15th Annual Conference of the International Speech Communication Association, Singapore, 14–18 September 2014. [Google Scholar]
- Malhotra, P.; Vig, L.; Shroff, G.; Agarwal, P. Long short term memory networks for anomaly detection in time series. In Proceedings of the 23rd European Symposium on Artificial Neural Networks, Computational Intelligence and Machine Learning, ESANN 2015, Bruges, Belgium, 22–24 April 2015. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Chauhan, S.; Vig, L. Anomaly detection in ECG time signals via deep long short-term memory networks. In Proceedings of the 2015 IEEE International Conference on Data Science and Advanced Analytics (DSAA), Paris, France, 19–21 October 2015; pp. 1–7. [Google Scholar]
- Bontemps, L.; Cao, V.L.; McDermott, J.; Le-Khac, N.A. Collective anomaly detection based on long short-term memory recurrent neural networks. In Proceedings of the International Conference on Future Data and Security Engineering, Can Tho City, Vietnam, 23–25 November 2016; pp. 141–152. [Google Scholar]
- Malhotra, P.; Ramakrishnan, A.; Anand, G.; Vig, L.; Agarwal, P.; Shroff, G. LSTM-based encoder-decoder for multi-sensor anomaly detection. arXiv 2016, arXiv:1607.00148. [Google Scholar]
- Nanduri, A.; Sherry, L. Anomaly detection in aircraft data using Recurrent Neural Networks (RNN). In Proceedings of the 2016 Integrated Communications Navigation and Surveillance (ICNS), Herndon, VA, USA, 19–21 April 2016; p. 5C2-1. [Google Scholar]
- Padrón-Hidalgo, J.A.; Laparra, V.; Camps-Valls, G. Unsupervised Anomaly and Change Detection With Multivariate Gaussianization. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5513010. [Google Scholar] [CrossRef]
- Hundman, K.; Constantinou, V.; Laporte, C.; Colwell, I.; Soderstrom, T. Detecting spacecraft anomalies using lstms and nonparametric dynamic thresholding. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, London, UK, 19–23 August 2018; pp. 387–395. [Google Scholar]
- Smith, R.L. Extreme value analysis of environmental time series: An application to trend detection in ground-level ozone. Stat. Sci. 1989, 4, 367–377. [Google Scholar]
- Roberts, S.J. Novelty detection using extreme value statistics. IEE Proc.-Vision Image Signal Process. 1999, 146, 124–129. [Google Scholar] [CrossRef]
- Embrechts, P.; Klüppelberg, C.; Mikosch, T. Modelling Extremal Events: For Insurance and Finance; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 33. [Google Scholar]
- McNeil, A.; Embrechts, P.; Frey, R. Quantitative Risk Management: Concepts, Techniques and Tools; Princeton Series in Finance; New Age International: New Delhi, India, 2010. [Google Scholar]
- Pickands, J., III. Statistical inference using extreme order statistics. Ann. Stat. 1975, 3, 119–131. [Google Scholar]
- Maple, C. Geometric design and space planning using the marching squares and marching cube algorithms. In Proceedings of the 2003 International Conference on Geometric Modeling and Graphics, London, UK, 16–18 July 2003; pp. 90–95. [Google Scholar]
- Choi, J.K.; Park, Y.J.; Lee, B.R.; Eom, J.; Moon, J.E.; Ryu, J.H. Application of the Geostationary Ocean Color Imager (GOCI) to mapping the temporal dynamics of coastal water turbidity. Remote Sens. Environ. 2014, 146, 24–35. [Google Scholar] [CrossRef]
- Morel, A.; Huot, Y.; Gentili, B.; Werdell, P.J.; Hooker, S.B.; Franz, B.A. Examining the consistency of products derived from various ocean color sensors in open ocean (Case 1) waters in the perspective of a multi-sensor approach. Remote Sens. Environ. 2007, 111, 69–88. [Google Scholar] [CrossRef]
- Nelson, M.; Hill, T.; Remus, W.; O’Connor, M. Time series forecasting using neural networks: Should the data be deseasonalized first? J. Forecast. 1999, 18, 359–367. [Google Scholar] [CrossRef]
- Taylor, S.J.; Letham, B. Forecasting at scale. Am. Stat. 2018, 72, 37–45. [Google Scholar] [CrossRef]
- Feng, Z.; Xuying, Y.; Xiaoxiao, S.; Zhenhong, D.; Renyi, L. Developing Process Detection of Red Tide Based on Multi-Temporal GOCI Images. In Proceedings of the 2018 10th IAPR Workshop on Pattern Recognition in Remote Sensing (PRRS), Beijing, China, 19–20 August 2018; pp. 1–6. [Google Scholar]
- Balkema, A.A.; De Haan, L. Residual life time at great age. Ann. Probab. 1974, 2, 792–804. [Google Scholar] [CrossRef]
| Parameters | Source | Temporal Range | Temporal Resolution | Spatial Resolution |
|---|---|---|---|---|
| CHL-a | KOSC GOCI | 1 April 2011–31 August 2019 | Hourly | 500 m |
| PAR | NASA MODIS | Daily | 4 km | |
| G1SST | NOAA Multi-Sensor | 1 km | ||
| CHL-a | OCCCI Multi-Sensor | 6 September 1997–6 September 2017 | 4 km |
| Description | Value |
|---|---|
| Hidden layers | 2 |
| Units in hidden layers | 36,12 |
| Sequence length | 35 |
| Prediction length | 7 |
| Dropout | 0.3 |
| Optimizer | Adam |
| Thresholds | 8.00 | 8.25 | 8.50 | 8.75 | 9.00 | 9.25 | 9.50 | 9.75 |
| 1.6826 | 0 | 2.2630 | 0 | 2.2776 | 0 | 0 | 1.6782 | |
| Thresholds | 10.00 | 10.25 | 10.50 | 10.75 | 11.00 | 11.25 | 11.50 | |
| 2.4888 | 0 | 2.7136 | 2.4728 | 1.7894 | 1.5337 | 1.7710 |
| Thresholds | 10.50 | 10.75 | 11.00 | 11.25 | 11.50 | 11.75 | 12.00 | 12.25 | 12.50 | 12.75 |
| 0 | 1.9275 | 1.9948 | 1.5791 | 1.6360 | 1.8384 | 1.9096 | 1.5605 | 1.9004 | 1.5200 | |
| Thresholds | 13.00 | 13.25 | 13.50 | 13.75 | 14.00 | 14.25 | 14.50 | 14.75 | 15.00 | |
| 1.8892 | 1.4713 | 2.6471 | 1.7540 | 0 | 0.7941 | 0.3407 | 0 | 0.0550 |
| Thresholds | 10.75 | 11.00 | 11.25 | 11.50 | 11.75 | 12.00 | 12.25 | 12.50 | 12.75 |
| 1.5126 | 2.1054 | 1.5384 | 2.1111 | 2.0556 | 2.1176 | 2.0588 | 2.1250 | 1.9250 | |
| Thresholds | 13.00 | 13.25 | 13.50 | 13.75 | 14.00 | 14.25 | 14.50 | 14.75 | |
| 2.1239 | 2.2038 | 1.9898 | 0.4226 | 0.3581 | 0.1899 | 0.1114 | 0.0461 |
| Thresholds | 8.00 | 8.25 | 8.50 | 8.75 | 9.00 | 9.25 | 9.50 | 9.75 | 10.00 |
| 4.5000 | 6.0000 | 6.6667 | 6.3333 | 4.6667 | 5.8000 | 6.0000 | 5.4000 | 3.6667 | |
| Thresholds | 10.25 | 10.50 | 10.75 | 11.00 | 11.25 | 11.50 | 11.75 | 12.00 | 12.25 |
| 4.3846 | 6.0000 | 5.0000 | 4.2500 | 5.8000 | 5.4000 | 4.3750 | 2.0000 | 5.4444 | |
| Thresholds | 12.50 | 12.75 | 13.00 | 13.25 | 13.50 | 13.75 | 14.00 | 14.25 | 14.50 |
| 6.3333 | 4.8889 | 4.2500 | 5.8571 | 3.8333 | 14.0000 | 6.8889 | 4.4000 | 4.1000 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, W.; Zhang, F.; Du, Z. Machine Learning in Extreme Value Analysis, an Approach to Detecting Harmful Algal Blooms with Long-Term Multisource Satellite Data. Remote Sens. 2022, 14, 3918. https://doi.org/10.3390/rs14163918
Ye W, Zhang F, Du Z. Machine Learning in Extreme Value Analysis, an Approach to Detecting Harmful Algal Blooms with Long-Term Multisource Satellite Data. Remote Sensing. 2022; 14(16):3918. https://doi.org/10.3390/rs14163918
Chicago/Turabian StyleYe, Weiwen, Feng Zhang, and Zhenhong Du. 2022. "Machine Learning in Extreme Value Analysis, an Approach to Detecting Harmful Algal Blooms with Long-Term Multisource Satellite Data" Remote Sensing 14, no. 16: 3918. https://doi.org/10.3390/rs14163918
APA StyleYe, W., Zhang, F., & Du, Z. (2022). Machine Learning in Extreme Value Analysis, an Approach to Detecting Harmful Algal Blooms with Long-Term Multisource Satellite Data. Remote Sensing, 14(16), 3918. https://doi.org/10.3390/rs14163918






