Abstract
The accurate spatial positioning of the target in a fixed camera image is a critical sensing technique. Conventional visual spatial positioning methods rely on tedious camera calibration and face great challenges in selecting the representative feature points to compute the position of the target, especially when existing occlusion or in remote scenes. In order to avoid these deficiencies, this paper proposes a deep learning approach for accurate visual spatial positioning of the targets with the assistance of Global Navigation Satellite System (GNSS). It contains two stages: the first stage trains a hybrid supervised and unsupervised auto-encoder regression network offline to gain capability of regressing geolocation (longitude and latitude) directly from the fusion of image and GNSS, and learns an error scale factor to evaluate the regression error. The second stage firstly predicts regressed accurate geolocation online from the observed image and GNSS measurement, and then filters the predictive geolocation and the measured GNSS to output the optimal geolocation. The experimental results showed that the proposed approach increased the average positioning accuracy by 56.83%, 37.25%, 41.62% in a simulated scenario and 31.25%, 7.43%, 38.28% in a real-world scenario, compared with GNSS, the Interacting Multiple Model−Unscented Kalman Filters (IMM-UKF) and the supervised deep learning approach, respectively. Other improvements were also achieved in positioning stability, robustness, generalization, and performance in GNSS denied environments.
1. Introduction
Fixed cameras are widely deployed in outdoor areas to provide fine-grained information about the physical world. The accurate and reliable spatial positioning of the target in the fixed camera image is an important sensing technique in many promising applications, such as surveillance of autonomous vehicles, monitoring of mobile robots, digital twin, sea pilling, airport security surveillance and so on.
The current visual spatial positioning methods can be divided into two categories: calibrated methods [1,2,3] and uncalibrated methods [4,5,6]. The calibrated methods heavily rely on camera calibration. However, even with some matured camera calibration methods, the calibration procedure can be tedious and require a certain level of expertise [1]. The uncalibrated methods require no camera calibration, but highly rely on feature point selection and matching [5]. However, in many scenarios, for both calibrated and existing uncalibrated methods, choosing the representative positioning feature points in the image to compute the position of the target is challenging, especially in the occasion of occlusion or in remote scenes. For instance, for the large-size and complex-shaped airplane at an airport, as shown in Figure 1a, it is dramatically difficult to choose the representative positioning feature point (i.e., the landing gear tyre) in the image to compute the spatial position of the airplane, due to the mutual occlusion of its components and the difficulty of detecting the landing gear tyre of the small airplane object in far view field. Likewise, as shown in Figure 1b, it is difficult to choose a visual representative positioning feature point of Person 1 when his feet are occluded by Person 2. If we choose an inaccurate visual representative positioning feature point, the computed position of the target will deviate from the ground truth, especially in far view field, as shown in Figure 1c. Therefore, it is essential to explore an alternative visual spatial positioning method which requires no camera calibration (uncalibrated) and can overcome the feature point selection problem.
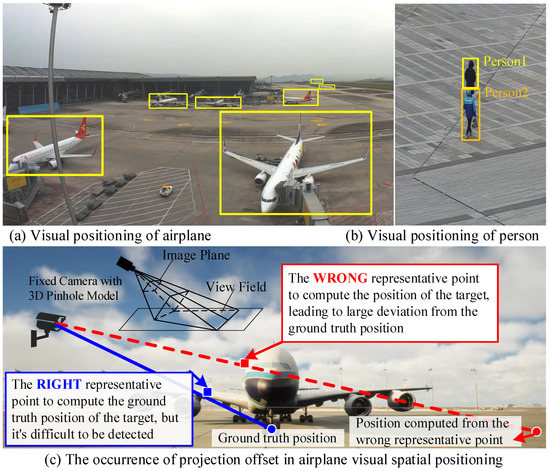
Figure 1.
(a,b): The difficulty of choosing visual representative positioning feature points. (c): The occurrence of projection offset in traditional visual spatial positioning methods, produced by the pinhole-based 3D camera model if choosing a wrong representative positioning feature point, which is difficult to be overcome in existing visual positioning methods.
In many occasions, the Global Navigation Satellite System (GNSS) devices are mounted on the targets, such as airplanes at airport and autonomous vehicles on the road. GNSS can provide external positioning information to the image. It enables us to explore a visual spatial positioning method which takes advantage of GNSS, to exempt from camera calibration and the positioning feature point selection problem. However, GNSS is always noisy and unstable due to various factors such as multi-path effect and signal blockage [7,8]. Fortunately, image and GNSS can be complementarily fused to improve the accuracy and stability of spatial positioning. Although some multi-sensor fusion approaches integrating image and GNSS have been presented [8,9,10], they rely on camera calibration, and cannot avoid the deficiencies of camera calibration and feature point selection problem mentioned above. If without camera calibration, since an uncalibrated image is high-dimensional, images and GNSS are highly heterogeneous, how to fuse them to obtain accurate spatial positions poses another great challenge.
To effectively address the above issues, this paper focuses on the fusion of an uncalibrated image and GNSS to obtain accurate spatial positions of the target from three considerations. Firstly, in order to avoid the deficiencies of camera calibration and feature point selection, a deep learning regression algorithm is presented to directly regress target’s accurate geolocation from the image, without camera calibration. Thanks to the advances of visual object detection techniques [11], the accurate visual location of the target can be obtained using a time-varying image bounding box, thus free from selecting fixed positioning feature points. Secondly, in order to improve the accuracy and stability of the spatial positioning result, the complementary information from image and GNSS are fused. Thirdly, in order to deal with high heterogeneity between image and GNSS, an auto-encoder based framework is proposed as the backbone of the deep learning regression algorithm.
To be specific, this paper proposes a two-stage approach to provide accurate spatial positions of the target. The first stage firstly obtains the accurate visual locations of the target using image bounding boxes. Then, it develops a hybrid supervised and unsupervised auto-encoder regression network to learn the spatial relationship between the image bounding boxes and GNSS. The supervised part of the regression network learns the relationship between the image bounding boxes and GNSS positions in a point-to-point manner. The unsupervised part of the regression network learns the relationship between the image bounding boxes and GNSS positions in a space-to-space manner. The hybrid supervised and unsupervised auto-encoder regression network can better filter out the noisy information in the training samples and increases the accuracy of the regressed positioning results comparing with the supervised learning method. After being trained offline, the regression network gains capability of regressing accurate geolocation directly from the fusion of image bounding box and GNSS. In addition, it designs an error scale factor to facilitate the evaluation of regression error. The second stage executes online fusion and filtering with two steps. The first step regresses a predictive accurate geolocation from the fusion of the observed image bounding box and GNSS measurement. The second step filters the predictive regressed geolocation and the GNSS measurement according to their estimation confidence levels, and outputs the optimal position estimation which is robust to errors of sensors. Experimental results in one simulated scenario and two real-world scenarios demonstrate the superiority of the proposed approach over GNSS, the well-known Interacting Multiple Model−Unscented Kalman Filters (IMM-UKF) and the state-of-the-art supervised learning approach.
The contributions of this paper are four-fold:
- (1)
- We present a novel accurate spatial positioning method based on uncalibrated fixed camera image and GNSS. As far as we know, it is the first time that accurate spatial geolocations from the fusion of fixed camera image and GNSS have been directly output, free from the highly calibration-error-sensitive 3D reconstruction and tricky positioning feature point selection;
- (2)
- We design a hybrid supervised and unsupervised auto-encoder fusion and regression framework for multi-sensor optimal position estimation. To the best of our knowledge, this is the first paper to optimize spatial positioning based on the fusion of image and GNSS using auto-encoder. We also mathematically prove that the proposed hybrid auto-encoder can yield optimal solution to the fusion and regression problem of multi-sensor position estimation;
- (3)
- Since our proposal is learning based, we make it possible that once the regression network is well trained offline with the assistance of GNSS, the camera itself can online automatically output the accurate geolocations of the targets in its view field. This function is significantly useful in some GNSS partially denied environments, where we first train a visual locator when GNSS is available, and then use it to predict the spatial positions of target when GNSS is not available;
- (4)
- We elaborately handcraft datasets which contain fixed camera images and GNSS in simulated and real-world scenes for the visual spatial positioning community. It is available at https://github.com/sculiang/image-spatial-localization (accessed on 23 April 2021).
The rest of this paper is organized as follows: Section 2 describes the related work about image-based and multi-sensor fusion based spatial positioning. Section 3 thoroughly introduces our two-stage approach for accurate spatial positioning. Section 4 shows the experimental results and discussion in terms of accuracy, robustness, generalization and the performance in GNSS denied environment. Section 5 draws the conclusion and suggests future work.
2. Related Work
2.1. Image-Based Spatial Positioning
The image-based spatial positioning has attracted a lot of attention over the years. Most of the conventional methods required camera calibration [12], which aimed to compute the intrinsic parameters (focal length, principal points, and lens distortion) and the extrinsic parameters (rotation and translation matrix related to the world coordinate system). Some methods were used for fixed camera calibration [1], and some methods were used for moving camera self-calibration [13]. In moving camera self-calibration, a series of images were taken from different views in the calibration process. For the calibration of fixed camera, an array of reference points with accurately known world coordinates were usually needed. Camera calibration in small-scale environments has been well studied [1,2,14], but camera calibration in large-scale environments still needs more research [3,12]. Reference points in large-scale environments are difficult to choose and their exact positions in the real world are difficult to ascertain. Some methods had supplemented camera calibration in large-scale environments with the assistance of GNSS [9]. However, the performance was quite sensitive to the GNSS accuracy at the chosen reference points, and the measuring process required two or three trained staff members to work together, which leaded to high labor costs and low efficiency. Several uncalibrated image-based positioning methods have been proposed, for the applications of visual servo [4,5,6] and stereo vision [15,16]. However, they usually used binocular vision system [15,16] or used moving monocular vision system [5] and were highly sensitive to the accuracy of feature points selection and matching in different views.
2.2. Multi-Sensor Fusion Based Spatial Positioning
There are many approaches that integrate multiple sensors to realize accurate spatial positioning [8,9,15,16,17,18,19,20,21,22,23,24,25,26]. The traditional methods of fusing GNSS with images firstly transformed the global GNSS coordinates to local camera coordinate system, and then fused them using optimization [8,9]. Min et al. [8] transformed the coordinates of GNSS to a local camera coordinate system, and the GNSS and visual tracks were calibrated with the improved weighted iterative closest point and least absolute deviation methods. However, these methods rely on camera calibration, and their positioning performances are impaired by the aforementioned deficiencies of camera calibration.
With respect to data fusion, most of the existing studies have been based on filtering methods. Kalman filter (KF) based algorithms have often been used for fusing data from different sources and has resulted in more accurate positioning [21,22]. However, KF based algorithms cannot directly process high-dimensional images and are limited in dealing with non-linearity and uncertainty. Alongside filtering, neural network (NN) based methods have been also studied for data fusion. In [23,24,25], artificial neural network-based fusion methods were proposed to learn the velocity or position errors between GNSS and inertial navigation system (INS) and compensate the INS when GNSS was denied. Images were not often considered by naive neural networks in fusion with GNSS, due to the difficulty to train.
Considering their great successes in computer vision, deep learning algorithms have also been used recently [16,26]. Sun et al. [26] proposed a method to train a geospatial deep neural network (Convolutional Neural Network + Long Short Term Memory) to predict the ego-positions of camera using only ordinary ground imagery and low accuracy cellphone-grade GPS. Although we both use deep learning to fuse image and GNSS for positioning purpose, our work obviously distinguishes from theirs. On the one hand, their work used a sequence of images captured by a moving camera mounted on a car for navigation purposes, whereas our work uses a single image from a fixed camera for surveillance purposes. It is worth mentioning that there is no literature about the image-aided accurate spatial positioning which requires no camera calibration for surveillance purpose. Our study fills this research gap. On the other hand, the output of their network was a location difference relative to the hand-picked ground control points, whereas our output is directly an accurate geolocation, with no need of ground control points. Mahmoud et al. [16] proposed an uncalibrated stereo vision method with deep learning for position estimation for a robot arm system. Their method is currently the most similar one to ours, because we both develop a deep learning regression network to directly regress positions of the target from uncalibrated fixed camera images. Our work extends that for theirs in two aspects. Firstly, the input of their network was the fusion of one camera image with another overlapped camera image (i.e., binocular), whereas ours are the fusion of target’s monocular image and GNSS. Secondly, their method used a 2D marker attached to the target to ease the detection and matching of the feature points, which would dramatically decrease the flexibility and practicality in actual situations. By comparison, our method can automatically and adaptively output the target’s image bounding box corner points, with no need of additional feature marker, free from feature points detection and matching, thus guarantees the high flexibility and practicality in actual situations.
3. Methodology
This paper provides accurate spatial positions of the target based on the fusion of uncalibrated image and GNSS. An overview of the proposal is illustrated in Figure 2. A fusion architecture with two stages is designed. Stage One is to train a hybrid supervised and unsupervised auto-encoder regression network offline before time . Stage Two is to output an optimally filtered position online at time . In Stage One, we prepare a lot of training samples which contain the target’s visual locations in images and their corresponding GNSS positions to train the hybrid auto-encoder regression network. The visual locations in the images are acquired by image target detection and tracking algorithm [27], and the GNSS data are standardized for the sake of better training. A regression error scale factor is created and learned to evaluate the scale of regression error. Stage Two is divided into two steps: the first step regresses a predictive accurate geolocation from the fusion of the observed visual location and the measured GNSS position using the trained hybrid auto-encoder regression network. The second step firstly evaluates the estimation confidences of the predictive regressed geolocation and the GNSS measurement, respectively, based on their errors, and then filters the predictive regressed geolocation and the GNSS measurement to compute the optimal geolocation according to their estimation confidence.
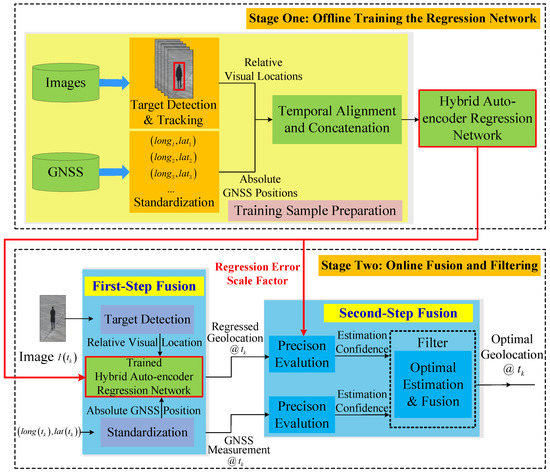
Figure 2.
Overview of the proposal.
3.1. Stage One: Offline Training the Regression Network
In this stage, we design a regression network which is trained offline. It takes a stacked auto-encoder as backbone. A stacked auto-encoder is an unsupervised learning architecture. If the input of a stacked auto-encoder includes information from multiple sources, the correlation of the sources will be encoded into the compressed feature, and the noisy information in sources will be filtered out [28]. In our study, the stacked auto-encoder fuses the relative visual locations with the global GNSS positions and compresses the fused high dimensional input tensor into 2D GNSS space to regress the geolocation. In addition to the unsupervised stacked auto-encoder backbone, we also introduce a supervised learning mechanism into its learning process: the regressed geolocation takes the GNSS position as the regression label. The hybrid of supervised learning and unsupervised learning, i.e., hybrid learning, enables the regressed geolocation to firstly approach the GNSS position by supervised learning, then filter out the noisy information in GNSS data by unsupervised learning. In this way, the positioning accuracy of the regressed geolocation can be improved.
The framework in Stage One is shown in Figure 3. Firstly, given a sequence of image training samples, the visual bounding boxes containing the target are cropped using state-of-the-art target detection and tracking algorithm [27]. An image can provide rich visual information of the target, including color, texture, location and size. Only the location and size are useful for spatial positioning. The location and size of the target can be accurately predicted using a bounding box. The bounding box in this paper is described as , where is the pixel coordinate of the top-left corner of the bounding box, and represent the pixel width and height of the bounding box, respectively. The longitude and latitude of the target are collected from GNSS sensors. In most occasions, the real-world spatial area corresponding to the camera view field is small. Its inside longitudes and latitudes at different locations have tiny differences, which will cause the vanishing gradient problem in the training process of the regression network. In order to better train the regression network, we standardize the longitude and latitude by normalizing them to 0–1 and multiplying a constant to improve their discriminability. The standardized longitude and latitude are denoted as a vector . The visual information and the longitude-latitude information are aligned by utilizing time stamp. If they have a same time stamp, they are concatenated as a 6D tensor . contains both the accurate location of the target in image space and in longitude-latitude space. Despite the fact that it has complementary information about targets’ positions compared to single GNSS or image, it also contains unexpected redundant information. In order to dig the accurate position information, we design a stacked auto-encoder architecture to refine .
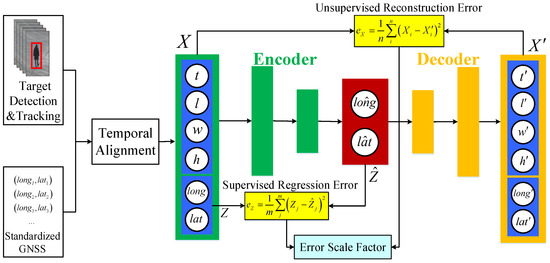
Figure 3.
Framework of Stage One, with a hybrid stacked auto-encoder backbone.
The stacked auto-encoder takes the tensor as input. After feed-forwarding through the encoder, a 2D regressed vector is obtained, and after feed-forwarding through the decoder, a 6D tensor is reconstructed. We train the stacked auto-encoder by minimizing the objective loss function using back propagation. The objective loss function is as follows:
where denotes the mean square error (MSE) between the input tensor and the reconstructed tensor . In our study, it is called “unsupervised reconstruction error” and computed as following:
where is the dimension of the input tensor , namely n = 6.
denotes the MSE between the GNSS measurement and the regressed vector . In our study, it is called “supervised regression error” and use the following equation to compute its value:
where is the dimension of , namely m = 2.
Minimizing ensures the overall good performance of the encoder and the decoder. It is an unsupervised learning process. It enables the stacked auto-encoder regression network to learn the spatial correlation between the visual location and the GNSS position . The correlation is latently encoded into the compressed 2D vector . It builds space-to-space mapping relationship between image bounding box tensor space and GNSS vector space by manifold learning. is a regularization item. Minimizing enforces the accurate mapping from 6D tensor to 2D vector . It is a supervised learning process, which builds point-to-point mapping relationship from a bounding box tensor to a geolocation vector. Appendix A proves that the hybrid auto-encoder with our objective loss function can yield an optimal solution to our problem.
are the weights of , respectively. determines the accuracy of space-to-space mapping and determines the accuracy of point-to-point mapping.
A regression error scale factor is created in our study to evaluate the ratio of the “supervised regression error” to the “unsupervised reconstruction error”. It can be learned in the training process as following:
where denotes the number of training samples. In practice, if we setup many iteration epochs in the training process, only the and in the last epoch are used to calculate . In the next fusion stage, the learned error scale factor is used to compute regression error from reconstruction error.
3.2. Stage Two: Online Fusion and Filtering
Stage Two is processed online at time , as shown in Figure 4. It is divided into two steps. The first step generates the predictive regressed geolocation at time . When the tensor is input into the trained hybrid auto-encoder regression network, the regressed longitude-latitude vector is predicted by the encoder, and is reconstructed online by the decoder.
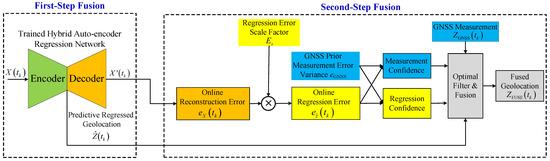
Figure 4.
Framework of Stage Two.
The second step finishes online filtering and optimization. If the online reconstruction error is computed as , then the online regression error at time is computed by multiplying the online reconstruction error with the learned regression error scale factor , i.e.,
After computing the online regression error, we then fuse the predictive regressed geolocation with the measured GNSS based on their estimation confidences. The estimation confidences are evaluated as follows:
where denotes the estimation confidence of the predictive regressed geolocation at time , and denotes the estimation confidence of GNSS measurement at time . denotes the priorly known GNSS measurement error variance, which is assumed as a constant intrinsic parameter of GNSS sensor. It is acquired by computing GNSS’s normal distribution from the statistics of many GNSS values at a fixed point according to the central-limit theorem.
The final optimal position at time is filtered as follows:
From Equations (6)–(8), we can observe that if an estimation has a smaller MSE, its estimation confidence is greater, and the result of the fused position will stay closer to it and thus improve the robustness to sensor errors.
4. Experiments and Results
4.1. Experimental Setup
We did not find any publicly available benchmark datasets which were able to meet our needs, so we handcrafted datasets covering a simulated scenario and two real-world scenarios to train and test our proposal. As shown in Figure 5, Scenario 1 simulated an airport scenario using the advanced virtual reality and digital twin 3D creation engine “UE4”, where a simulated airplane was taxing along the taxiway. We obtained the longitude and latitude ground truth positions of the airplane along the taxiway using UE4 and added position errors to simulate the noisy GNSS measurements of the airplane. In this scenario, 10,000 training samples and 400 test samples containing rendered images and simulated longitude-latitudes were collected. Scenario 2 and 3 were on a real-world urban square. A target person appeared in the camera view field with a low-cost cellphone-grade GNSS receiver. The target person walked back and forth along a polyline as shown in Scenario 3, and 10,000 training samples containing images and longitude-latitudes were collected. In Scenario 2, the target person stood still at a fixed point, and 450 test samples containing images and longitude-latitudes were collected. In Scenario 3, the target person walked back and forth along a polyline where some occlusions occurred between pedestrians, and 2000 test samples were collected. The ground truth locations in Scenario 2 and the ground truth line in Scenario 3 were acquired using an industrial-level accurate GNSS receiver. These three scenarios were cooperating. In Scenario 1, the rendered image block of the airplane could be tailored very precisely using UE4, thus there was no errors in image object detection. It could illustrate the performances of our proposal with no interference of visual noises. By contrast, Scenarios 2 and 3 had visual noises. They illustrated the performances of our proposal when dealing with a stationary target and a moving target, respectively, with both visual target detection noises and GNSS noises in real life. The simulated/real GNSS receivers and camera collected data simultaneously. We collected the GNSS at a frequency of 1 Hz and captured the video images at a frequency of 25 Hz. We choose the 13th image frame to pair the GNSS raw data at each second.
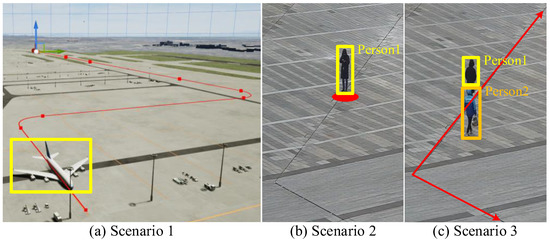
Figure 5.
Experimental scenarios. (a) In Scenario 1, the simulated airplane taxed along the taxiway (red). (b) In Scenario 2, the target Person 1 stood still at a fix point (red). (c) In Scenario 3, the target Person 1 walked back and forth along a polyline (red) where some occlusions occurred between pedestrians. The yellow and orange boxes represent the object detection bounding boxes.
Although there is no existing literature to fuse the fixed uncalibrated image with GNSS to directly output geolocation, in theory, the supervised Deep Neural Network (DNN) method proposed in [16], which is the currently most similar existing method to ours, can directly output geolocation from the fusion of image bounding box and GNSS. Moreover, the Interacting Multiple Model−Unscented Kalman Filters (IMM-UKF) [21,29] is a classical method to increase the GNSS positioning accuracy. In this paper, GNSS, IMM-UKF and the supervised DNN in [16] are chosen as the baseline methods. We conducted experiments with our approach, and compared with the three baselines, on a hardware platform of GPU NVIDIA GeForce 1080 Ti (USA) and CPU Intel Core i7-8700K (USA). By conducting many groups of tests, we found the best set of hyper-parameters to give the best positioning results: our stacked auto-encoder had 5 layers, of which encoder had 3 layers and decoder had 3 layers. The optimizer was Adam, and learning rate was 0.005, = 1, = 2000. The DNN in [16] had 5 layers, whose loss function was MSE, optimization algorithm was Adam, and learning rate was 0.001.
4.2. Experimental Results and Discussions
For description simplicity, the first step fusion in Stage Two is called “one-step fusion” method, and the combination of the first step and the second step in Stage Two is called “two-step fusion” method.
4.2.1. Accuracy
The accuracy performances were verified quantitatively in Scenario 1 and 2. The mean location errors of five methods, namely the GNSS, IMM-UKF, the supervised DNN in [16], our one-step fusion method and two-step fusion method, are listed in Table 1. It is worth mentioning that the location accuracy in Scenarios 1 and 2 were very different. This is because we added large GNSS noises to Scenario 1, on the one hand, to truly simulate the strong noise interference at large-scale airport in real life, and on the other hand, to increase the discrimination of each method’s positioning results along the long taxiway when plotting them in figures.

Table 1.
The mean location errors of four methods.
From Table 1, we can see that, in Scenario 1, our one-step fusion method achieved the smallest mean location error. In Scenario 2, our two-step fusion method achieved the smallest mean location error. From Figure 6, we can also see that, in these two scenarios, the location errors of our one-step fusion and two-step fusion methods were both smaller than GNSS, IMM-UKF and supervised DNN. The location errors of GNSS changed drastically, due to the unavoidable noisy errors coming from various negative factors. The IMM-UKF decreased the location errors, but still influenced by the drift of GNSS, so it also suffered from instability. With low-accuracy GNSS training data, the supervised DNN in [16] was difficult to learn the exact mapping relationship from image to geolocation, so its location errors were large. By contrast, our one-step and two-step methods outperformed GNSS, IMM-UKF and supervised DNN in term of accuracy. This is owing to that our proposed hybrid supervised and unsupervised auto-encoder regression network could regress geolocations accurately. Comparing with the supervised DNN in [16], our hybrid regression network can not only learn the accurate mapping relationship from image to geolocation, but also can dig the accurate position information from both image and GNSS, filter out noisy information in low-accuracy GNSS training data, therefore, our regressed geolocation can reach a high accuracy.
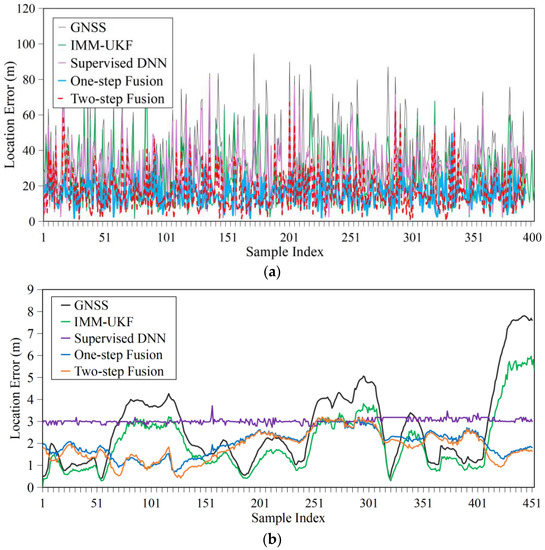
Figure 6.
Location error curves. (a). Location error curves in Scenario 1. (b). Location error curves in Scenario 2.
Besides, we can see from Figure 7 that the maximum location errors of our one-step fusion and two-step fusion methods were smaller than those of GNSS, IMM-UKF and supervised DNN, which indicates they are more reliable to avoid false warnings in applications such as collision warning at airports. The overall performances of our methods in both Scenarios 1 and 2 were much better than GNSS, IMM-UKF and supervised DNN, as our methods had obviously lower statistical location error value lines. By comparison, our one-step fusion method achieved better performance than our two-step fusion method in decreasing location errors in Scenario 1. This is because in Scenario 1, there was no image detection errors, so after offline training, our regressor gained capability of regressing accurate geolocations. In the online fusion stage, the regressed geolocation of one-step fusion method was not fused with low-accuracy GNSS, while that of the two-step fusion method was fused with low-accuracy GNSS, so the one-step fusion method achieved more accurate positioning result than two-step fusion method. In Scenario 2, they achieved almost the same accuracy performance when more or less image detection errors existed.
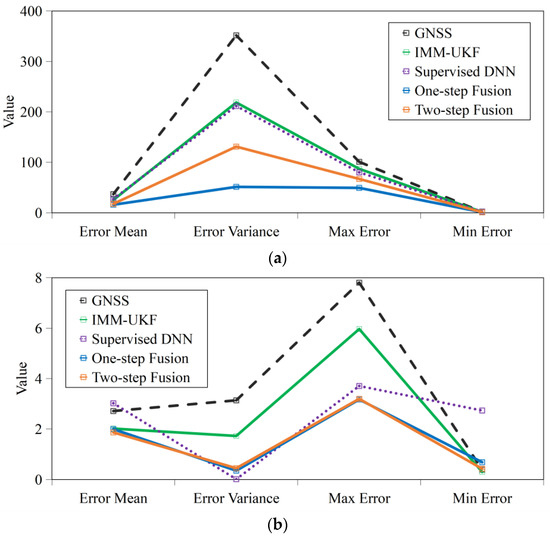
Figure 7.
Statistical parameters of location errors. (a). Statistical parameters of location errors in Scenario 1. (b). Statistical parameters of location errors in Scenario 2.
Figure 8 illustrates the cumulative percentage curves of five methods in each location error range in Scenario 1. We can see that our one-step fusion and two-step fusion methods had steepest cumulative percentage curves, which meant their location errors clustered within small error range. Specifically, 76.11%, 71.24% of the location errors of the one-step fusion, the two-step fusion methods were from 0–20 m. By contrast, only 28.54%, 48.01% and 40.71% of the location errors of GNSS, IMM-UKF and supervised DNN were from 0–20 m. It explicitly proves our methods outperformed other three baselines. Figure 9 illustrates that our one-step fusion and two-step fusion methods located more densely and closer to the ground truth than other three baselines in Scenario 1. By comparison, the one-step fusion method performed better than the two-step fusion method, and it was located more densely than the two-step fusion method.
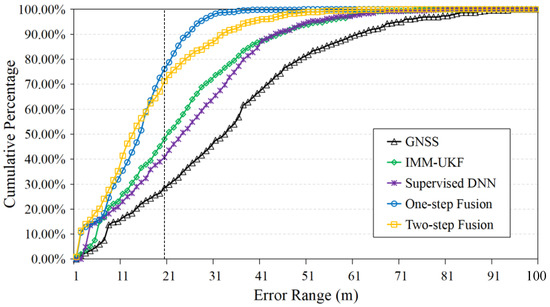
Figure 8.
Cumulative percentage curves in different location error range in Scenario 1.
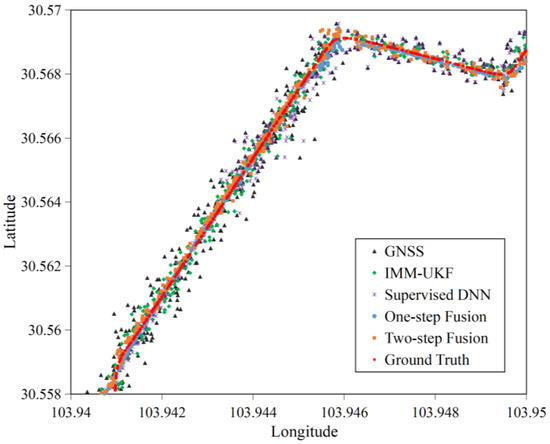
Figure 9.
Location distributions in Scenario 1.
Figure 10 also shows that locations in Scenario 2 generated by our one-step fusion and two-step fusion methods were closer to the ground truth than other three baselines and distributed much more densely than GNSS and IMM-UKF. This is because although GNSS positions drifted sharply, the relative locations of the target in images stayed almost unaltered in Scenario 2, which made the fused location results of our methods became stable. The supervised DNN could generate the densest location results but were far away from the ground truth.
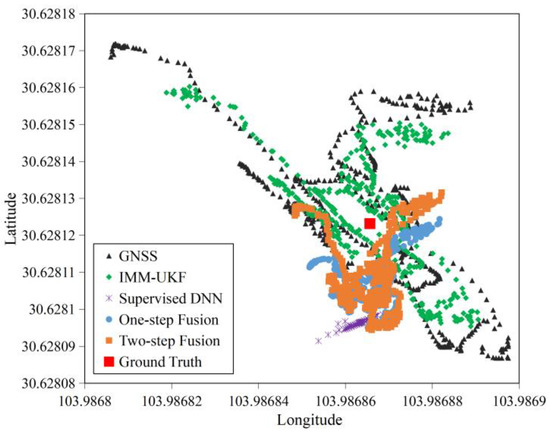
Figure 10.
Location distributions in Scenario 2.
Figure 11 shows that our methods located close to the ground truth line around the corner of the polyline in Scenario 3, where the two-step fusion method was better than the one-step fusion method. They both obviously outperformed GNSS and supervised DNN in term of positioning accuracy around the corner. Interestingly, our methods could respond correctly to the turning action of the target person, as they both produced correct walking trajectories with a same turning angle of the ground truth line. By comparison, supervised DNN had weak response to the turning action, while the trajectory produced by GNSS looked scattered with nearly no response to the turning action. The trajectory of IMM-UKF also located close to the ground truth line and responded correctly to the turning action of the target person. This is due to its well-known advance of locating and tracking a moving target. Encouragingly, our two-step fusion method achieved the same level of precision as IMM-UKF.
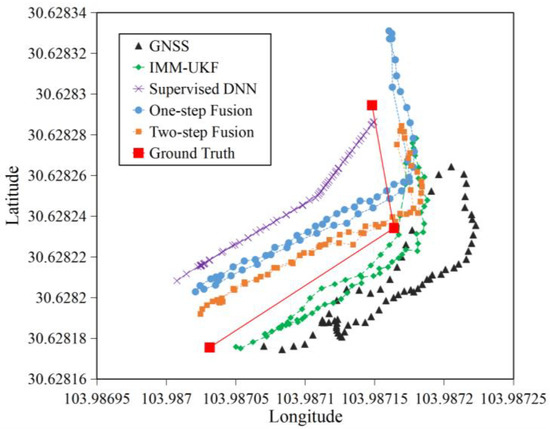
Figure 11.
Location distributions when the target person walked around a corner in Scenario 3.
4.2.2. Robustness
Object detection in images may suffer from negative effects such as illumination variation and occlusion, which brings about positioning errors of the image bounding boxes. In order to test the robustness of the methods to the object detection errors in uncalibrated images, we manually added positioning errors to the bounding box tensors in the test phase in Scenario 2. 10- and 30-pixel errors were, respectively, added to the width and height of the bounding boxes and expanded the bounding boxes toward top-left from right-bottom. Since IMM-UKF does not use visual information, it is not compared in this section.
From Figure 10 and Figure 12, we can see that our two-step fusion method had the strongest robustness to the uncalibrated image object detection errors, as it always located closest to the ground truth, regardless of how large the uncalibrated image object detection errors were. By comparison, supervised DNN and our one-step fusion method were sensitive to the uncalibrated image object detection errors, and their positioning accuracy dramatically degraded when the uncalibrated image object detection errors grew. This is because the growing errors in image bounding box tensors changed the inputs of supervised DNN, leading to its outputs increasingly deviating from the ground truth. In our one-step fusion method, when the errors of image bounding box tensors grew, the reconstruction errors of auto-encoder would increase, leading to the growth of regression errors, thus the regressed geolocations increasingly deviated from the ground truth. If the regression error was larger than GNSS error, the fused location result should stay closer to the GNSS estimation, and vice versa. This is a motivation to design the second step fusion of our two-step fusion method. Thanks to its online filtering mechanism, both the large regression errors and large GNSS errors were filtered, thus the fused location results in the two-step fusion method gaining robustness to image detection errors and GNSS measurement errors simultaneously.
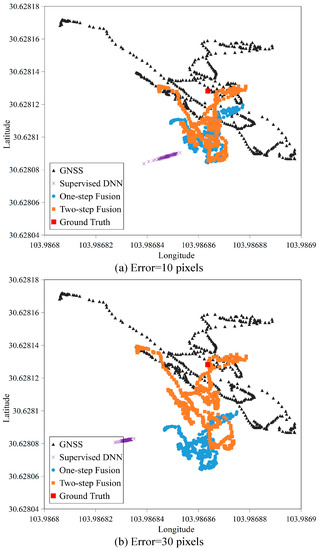
Figure 12.
Location distributions with different errors of image bounding box tensors in Scenario 2.
Scenario 3 allows us to further analyze the robustness of our methods when the uncalibrated image detection errors and GNSS measurement errors co-existed in real life. From Figure 13, we can see that the GNSS locations in Scenario 3 were scattered sharply on the two sides of the ground truth line. The supervised DNN had the smoothest location distribution, but the locations were far away from the ground truth line. By comparison, the location results of our one-step fusion method were much smoother than the ones of GNSS. The underlying reason is that in the concatenated 6D input of our regression network, the smoothly changed 4D image bounding box tensor had greater influences than the drifted 2D GNSS vector, hence improved the stability of positioning results of our one-step fusion method. However, because of the existence of the image detection errors and GNSS measurement errors, the regression network became hard train well, leading to the regressed geolocations derived from one-step fusion method still deviating from the ground truth line. The two-step fusion method mitigated the deviation and generated the closet location results to the ground truth line by fusing the regressed geolocations with GNSS measurements, but also bringing the GNSS drift errors into the fusion results, which caused some of the fused location results were drifting. However, the two-step fusion method achieved good trade-off between accuracy and smoothness, as its location results were closer to the ground truth line than the ones of the one-step fusion method, and at the same time were more converged than GNSS positions.
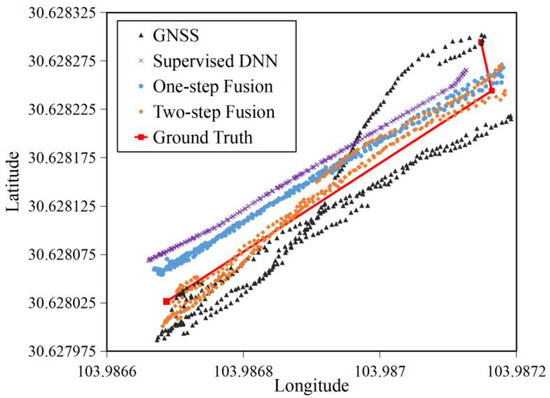
Figure 13.
Location distributions when the image detection errors and GNSS measurement errors co-exist in both training and test phases in Scenario 3.
4.2.3. Generalization
In order to validate the generalization performances of the machine learning methods, namely the supervised DNN and our methods, we collected completely new test samples along another different line in Scenario 3 (Red line in the right of Figure 14) which were dramatically different from the training samples in the training dataset (Collected along the yellow dash line in the right of Figure 14).
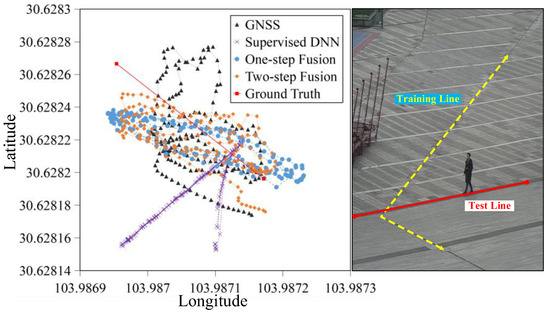
Figure 14.
Generalization performance of methods.
The results in the left of Figure 14 show that the positions of our methods were closer to the ground truth line than the ones of GNSS and supervised DNN, and located along the new testing line with correct direction. It infers that our methods successfully built correct space-to-space mapping relationship between image space and GNSS space, and managed to learn the spatial correlation between them, so it had the generalization capability to newly unseen test samples, as long as the unseen test samples were collected from the same image space and GNSS space of the training samples. The supervised DNN output completely wrong locations, indicating it had no generalizability, because it’s naive DNN could only build point-to-point mapping relationship from image training samples to GNSS training samples, and failed to learn the spatial correlation between the two spaces, thus it could not deal with completely different test samples.
4.2.4. Performance in GNSS Denied Environments
In many cases, GNSS is not available due to the lack of GNSS equipment or signal. In these cases, spatial positioning can rely solely on images, and only our one-step fusion method and supervised DNN can work. For applications under these conditions, we removed the GNSS longitude and latitude from the input tensor, decreased the input dimensions from 6 to 4. The training processes were re-run using a similar hybrid auto-encoder regression network and DNN neural network described in Section 4.1. Our retrained regression network and supervised DNN were then tested in Scenario 2.
Figure 15 and Table 2 show that our one-step fusion method achieved better performance than supervised DNN in positioning accuracy, as it had much lower location error mean, variance, and smaller maximum error.
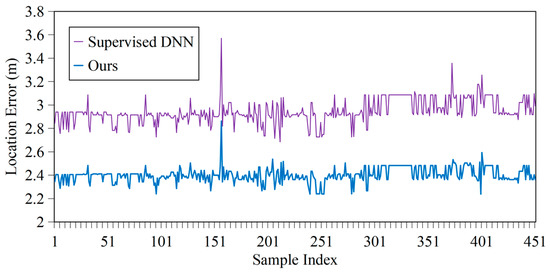
Figure 15.
Location error curves when GNSS is denied in Scenario 2.

Table 2.
Location error parameters in GNSS denied environments.
The retrained regression network of our approach and supervised DNN were also tested in Scenario 3. We can see from Figure 16 that the locations of our approach outperformed the ones of supervised DNN, as they located closer to the ground truth polyline, and could also respond correctly to the turning action of the target. It’s evident that our proposal performs well in environments where GNSS is denied.
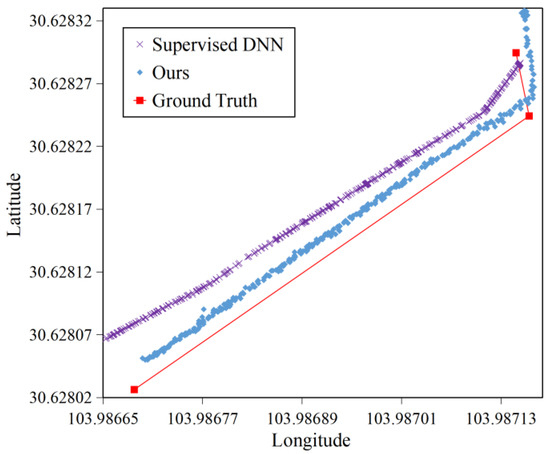
Figure 16.
Location distribution when GNSS is denied in Scenario 3.
4.2.5. Convergence Analysis of Regression Error Scale Factor
In order to analyze the convergence of the regression error scale factor , the curve of at each training epoch is illustrated in Figure 17. We can see that during the early epochs, was very unstable. This is because at the start of training, our auto-encoder network was searching for the direction of optimization. After several epochs, it could discover the optimization direction and achieved the equilibrium of “supervised regression error” and “unsupervised reconstruction error”. converged quickly at the 17th training epoch.
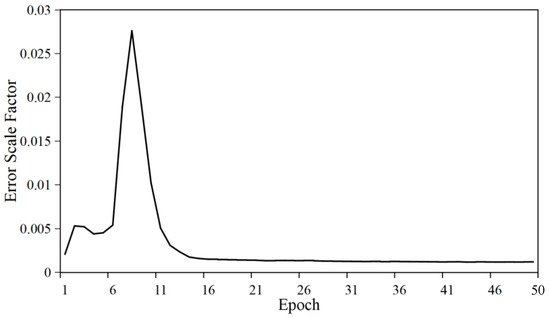
Figure 17.
The curve of error scale factor and epoch in the training phase.
4.2.6. Comparative Analysis of Different and
In order to analyze how different values of and influence the positioning results, we conducted a lot of comparative experiments with different values of and . We can see from Figure 18 that when the ratio of to is 1:2000, it achieved the best performance in term of location error. When was larger than , the errors became larger than those when was smaller than . This is because determines the accuracy of space-to-space mapping and determines the accuracy of point-to-point mapping. When was larger than , our auto-encoder network would focus on the space-to-space mapping, and decreased the point-to-point mapping accuracy, and vice versa. When was 1:2000, it achieved the best combination of space-to-space mapping and point-to-point mapping to solve our problem.
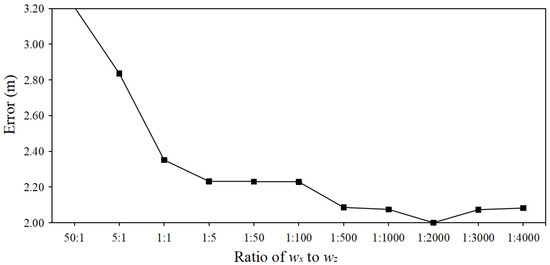
Figure 18.
The curve of error and ratio of to .
5. Conclusions
This paper proposed a two-stage deep learning approach for accurate spatial positioning of the target in fixed camera images based on the fusion of uncalibrated image and GNSS. It did not require the selection of representative positioning feature points. The first stage trained a hybrid supervised and unsupervised auto-encoder regression network offline and gained capability of regressing geolocation directly from the fusion of image and GNSS. The second stage finished online fusion and filtering to generate the optimal geolocation. Elaborate datasets were provided to train and test our approach. The experimental results in simulated and real scenarios demonstrated the effectiveness of the proposed approach in terms of positioning accuracy, stability, robustness, generalization, and performance in GNSS denied environment, much better than GNSS, the classical IMM-UKF and the state-of-the-art supervised deep learning approach. Although our approach achieved great success, its performance still can be further improved, especially when the GNSS training data are of a low accuracy. If the kinematic model-based position prediction is introduced to firstly filter the GNSS data, then use the filtered GNSS data to train our hybrid auto-encoder network, the positioning performance of our approach would become even better. Moreover, this paper fused single image and GNSS data to realize spatial positioning. If the temporal-spatial information within sequential video images is fully considered in algorithm, it would benefit our positioning performances. Future work will focus on these aspects.
Author Contributions
Conceptualization, B.L., S.H. and W.L.; methodology, B.L., S.H. and W.L.; software, B.L., D.F., R.H. and G.H.; validation, B.L., R.H. and G.H.; formal analysis, B.L., S.H. and W.L.; investigation, B.L.; resources, B.L. and D.F.; data curation, B.L., D.F. and R.H.; writing—original draft preparation, B.L.; writing—review and editing, S.H. and W.L.; visualization, B.L.; supervision, S.H. and W.L.; project administration, W.L.; funding acquisition, W.L. All authors have read and agreed to the published version of the manuscript.
Funding
This study was co-supported by the Key R&D project of Sichuan Province, China (No. 2022YFG0153), and the funding from Sichuan University (Nos. GSJDJS2021010 and 2020SCUNG205).
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Mathematical Derivation that Our Hybrid Auto-Encoder Can Yield Optimal Solution to Our Regression Problem
Generally, the model of a discrete system is:
State Model:
Measurement Model:
where is the system state at time tk, is the measurement at time tk.
In this paper, because we don’t know the exact motion process of the target, so we don’t know what the exact function is. However, we know that the state is a function of the measurement , so in our study, we modify the system model as follows:
State Model:
Measurement Model:
where is the system state at time tk, herein is the spatial position of the target. is the measurement at time tk, herein is the observation of the target’s image bounding box and GNSS. is the state estimation error, is the measurement error, and they are both supposed to follow the Gaussian distribution.
The accurate spatial position of the target can be estimated by maximizing a posterior (MAP) probability , namely, given an observation, the optimal spatial position estimation with the following greatest posterior probability is the spatial position of the target:
According to Bayesian rule,
However, the priori probability distribution is unknown, so we convert the objective function from maximizing a posterior probability to maximizing likelihood estimation, namely:
which means that the optimal spatial position estimation is the position that most probably to produce the measured observation of the target’s image bounding box and GNSS. Hence, our goal becomes to compute an optimal spatial position estimation which maximizes the likelihood estimation:
Because , , so
For a D-dimensional Gaussian variable ,
Likewise, for our goal with Gaussian distribution ,
where .
We can see that can be described by auto-encoder if we adopt an encoder to be and adopt a decoder to be , as derived mathematically in Equation (A13) and illustrated in Figure A1.
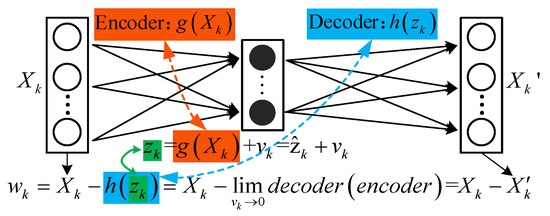
Figure A1.
Description of by auto-encoder.
So, our regression problem can be solved by auto-encoders, where we aim to minimize the measurement error and the state estimation error . We set the objective function of the auto-encoders in the overall training process as follows:
where N is the number of training samples, is the dimension of , is the dimension of . is the reconstruction error of the decoder, and is the regression error of the encoder. In order to facilitate auto-encoders learning from observable samples, we use to substitute , where is the measurement of GNSS.
By adding linear weights, the objective loss function of the auto-encoder is set as follows, which is the same one as described in Section 3:
References
- Zhang, Z. A flexible new technique for camera calibration. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 1330–1334. [Google Scholar] [CrossRef] [Green Version]
- Chuang, J.H.; Ho, C.H.; Umam, A.; Chen, H.Y.; Hwang, J.N.; Chen, T.A. Geometry- based camera calibration using closed-form solution of principal line. IEEE Trans. Image Processing 2021, 30, 2599–2610. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Zhang, B.; Tang, X.; Li, G.; Zhou, X.; Hu, L.; Dou, X. On-Orbit Geometric Calibration and Accuracy Validation for Laser Footprint Cameras of GF-7 Satellite. Remote Sens. 2022, 14, 1408. [Google Scholar] [CrossRef]
- Xu, F.; Wang, H.; Liu, Z.; Chen, W. Adaptive Visual Servoing for an Underwater Soft Robot Considering Refraction Effects. IEEE Trans. Ind. Electron. 2020, 67, 10575–10586. [Google Scholar] [CrossRef]
- Gong, Z.; Tao, B.; Yang, H.; Yin, Z.; Ding, H. An Uncalibrated Visual Servo Method Based on Projective Homography. IEEE Trans. Autom. Sci. Eng. 2018, 15, 806–817. [Google Scholar] [CrossRef]
- Liang, X.; Wang, H.; Liu, Y.H.; You, B.; Liu, Z.; Jing, Z.; Chen, W. Fully Uncalibrated Image-Based Visual Servoing of 2DOFs Planar Manipulators with a Fixed Camera. IEEE Trans. Cybern. 2021, 1–14. [Google Scholar] [CrossRef]
- Abosekeen, A.; Iqbal, U.; Noureldin, A.; Korenberg, M.J. A Novel Multi-Level Integrated Navigation System for Challenging GNSS Environments. IEEE Trans. Intell. Transp. Syst. 2021, 22, 4838–4852. [Google Scholar] [CrossRef]
- Min, H.; Wu, X.; Cheng, C.; Zhao, X. Kinematic and dynamic vehicle model-assisted global positioning method for autonomous vehicles with low-cost GPS/camera/in-vehicle sensors. Sensors 2019, 19, 5430. [Google Scholar] [CrossRef] [Green Version]
- Chen, X.; Hu, W.; Zhang, L.; Shi, Z.; Li, M. Integration of low-cost GNSS and monocular cameras for simultaneous positioning and mapping. Sensors 2018, 18, 2193. [Google Scholar] [CrossRef] [Green Version]
- Baldoni, S.; Battisti, F.; Brizzi, M.; Neri, A. A hybrid position estimation framework based on GNSS and visual sensor fusion. In Proceedings of the 2020 IEEE/ION Position, Location and Navigation Symposium (PLANS), Portland, OR, USA, 20–23 April 2020; pp. 979–986. [Google Scholar]
- Bochkovskiy, A.; Wang, C.; Liao, H. YOLOv4: Optimal speed and accuracy of object detection. arXiv 2020, arXiv:2004.10934. [Google Scholar]
- Wu, Y.; Tang, F.; Li, H. Image-based camera positioning: An overview. Vis. Comput. Ind. Biomed. Art. 2018, 1, 8. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Huang, W.; Jiang, S.; Jiang, W. Camera Self-Calibration with GNSS Constrained Bundle Adjustment for Weakly Structured Long Corridor UAV Images. Remote Sens. 2021, 13, 4222. [Google Scholar] [CrossRef]
- Zhang, J.; Zhu, J.; Deng, H.; Chai, Z.; Ma, M.; Zhong, X. Multi-camera calibration method based on a multi-plane stereo target. Appl. Optics. 2019, 58, 9353–9359. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, T.P.; Tran, T.H.P.; Jeon, J.W. MultiLevel Feature Pooling Network for Uncalibrated Stereo Rectification in Autonomous Vehicles. IEEE Trans. Ind. Inform. 2021, 68, 10281–10290. [Google Scholar] [CrossRef]
- Abdelaal, M.; Farag, R.M.; Saad, M.S.; Bahgat, A.; Emara, H.M.; El-Dessouki, A. Uncalibrated stereo vision with deep learning for 6-DOF pose estimation for a robot arm system. Robot. Auton. Syst. 2021, 145, 103847. [Google Scholar] [CrossRef]
- Wen, W.; Bai, X.; Kan, Y.C.; Hsu, L.T. Tightly coupled GNSS/INS integration via factor graph and aided by fish-eye camera. IEEE Trans. Veh. Technol. 2019, 68, 10651–10662. [Google Scholar] [CrossRef] [Green Version]
- Chang, L.; Niu, X.; Liu, T.; Tang, J.; Qian, C. GNSS/INS/LiDAR-SLAM integrated navigation system based on graph optimization. Remote Sens. 2019, 11, 1009. [Google Scholar] [CrossRef] [Green Version]
- Zheng, Z.; Li, X.; Sun, Z.; Song, X. A novel visual measurement framework for land vehicle positioning based on multimodule cascaded deep neural network. IEEE Trans. Ind. Inform. 2021, 17, 2347–2356. [Google Scholar] [CrossRef]
- Yuwen, X.; Chen, L.; Yan, F.; Zhang, H.; Tang, J.; Tian, B.; Ai, Y. Improved Vehicle LiDAR Calibration with Trajectory-Based Hand-Eye Method. IEEE Trans. Intell. Transp. Syst. 2022, 23, 215–224. [Google Scholar] [CrossRef]
- Xu, Q.; Li, X.; Chan, C.-Y. A Cost-Effective Vehicle Localization Solution Using an Interacting Multiple Model−Unscented Kalman Filters (IMM-UKF) Algorithm and Grey Neural Network. Sensors 2017, 17, 1431. [Google Scholar] [CrossRef]
- Chiang, K.W.; Le, D.T.; Duong, T.T.; Sun, R. The performance analysis of INS/GNSS/V-SLAM integration scheme using smartphone sensors for land vehicle navigation applications in gnss-challenging environments. Remote Sens. 2020, 12, 1732. [Google Scholar] [CrossRef]
- Yao, Y.; Xu, X.; Zhu, C.; Chan, C.Y. A hybrid fusion algorithm for GPS/INS integration during GPS outages. Measurement 2017, 103, 42–51. [Google Scholar] [CrossRef]
- Aslinezhad, M.; Malekijavan, A.; Abbasi, P. ANN-assisted robust GPS/INS information fusion to bridge GPS outage. EURASIP J. Wirel. Commun. Netw. 2020, 129. [Google Scholar] [CrossRef]
- Zhang, T.; Xu, X. A new method of seamless land navigation for GPS/INS integrated system. Measurement 2012, 45, 691–701. [Google Scholar] [CrossRef]
- Sun, S.; Sarukkai, R.; Kwok, J.; Shet, V. Accurate deep direct geo-positioning from ground imagery and phone-grade GPS. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Salt Lake City, UT, USA, 18–22 June 2018; pp. 1129–11297. [Google Scholar]
- Liu, X.; Zhang, Z. A Vision-Based Target Detection, Tracking, and Positioning Algorithm for Unmanned Aerial Vehicle. Wirel. Commun. Mob. Comput. 2021, 2021, 5565589. [Google Scholar] [CrossRef]
- Zhang, H.; Hu, B.; Xu, S.; Chen, B.; Li, M.; Jiang, B. Feature fusion using stacked denoising auto-encoder and GBDT for Wi-Fi fingerprint-based indoor positioning. IEEE Access 2020, 8, 114741–114751. [Google Scholar] [CrossRef]
- Zhu, F.; Zhang, Y.; Su, X.; Li, H.; Guo, H. GNSS position estimation based on unscented Kalman filter. In Proceedings of the 2015 International Conference on Optoelectronics and Microelectronics (ICOM), Changchun, China, 16–18 July 2015; pp. 152–155. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).