Finite-Region Approximation of EM Fields in Layered Biaxial Anisotropic Media
Abstract
1. Introduction
2. Theory
2.1. Spectral State Equation and Its Solution in Homogeneous Media
2.2. Solution of Mode-Waves in the Layered Media
2.2.1. Formal Solution of Mode-Waves in the Source Layer
2.2.2. Formal Solution of Mode-Waves in the Source-Free Layers
2.2.3. Spatial-Domain EM Fields
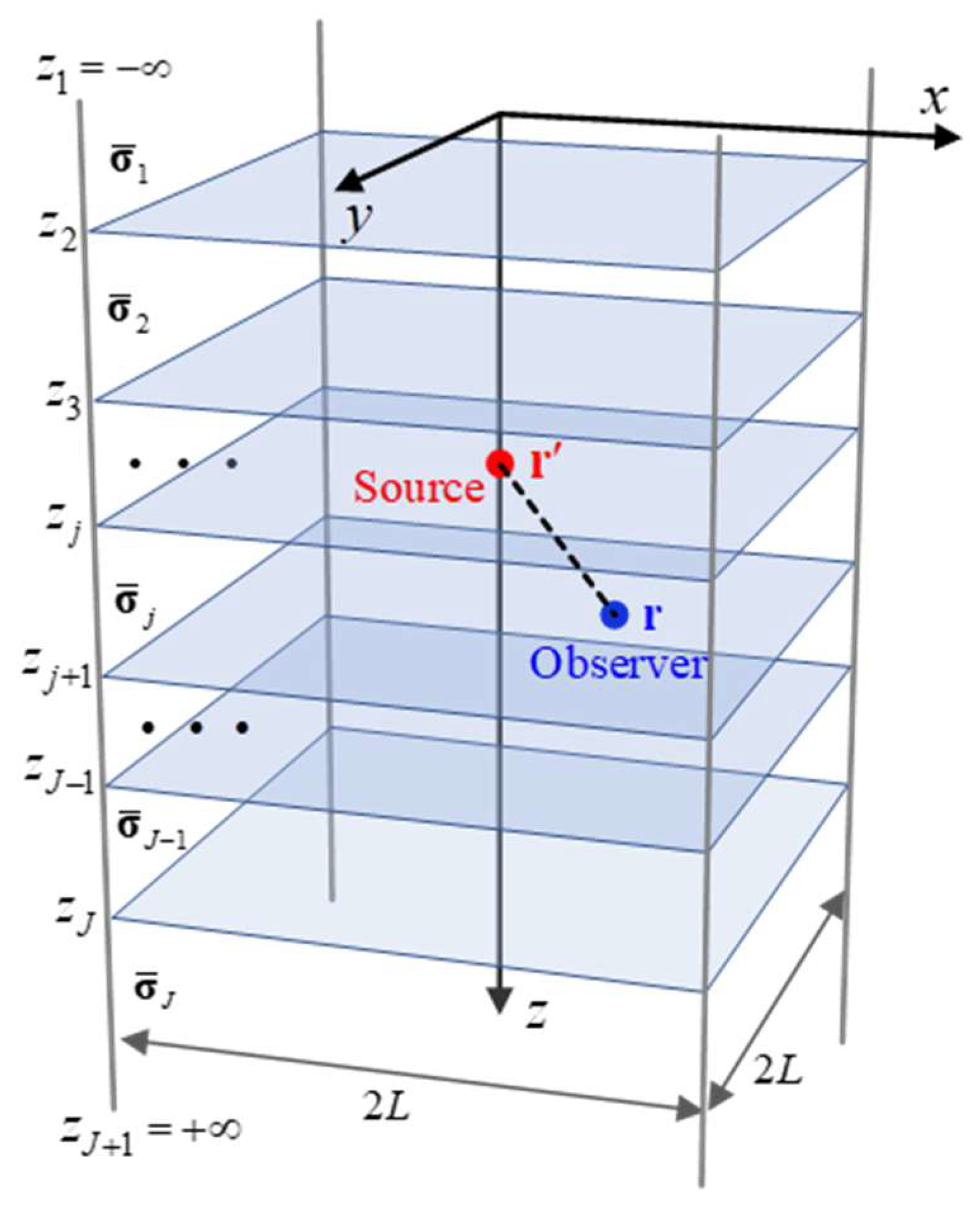
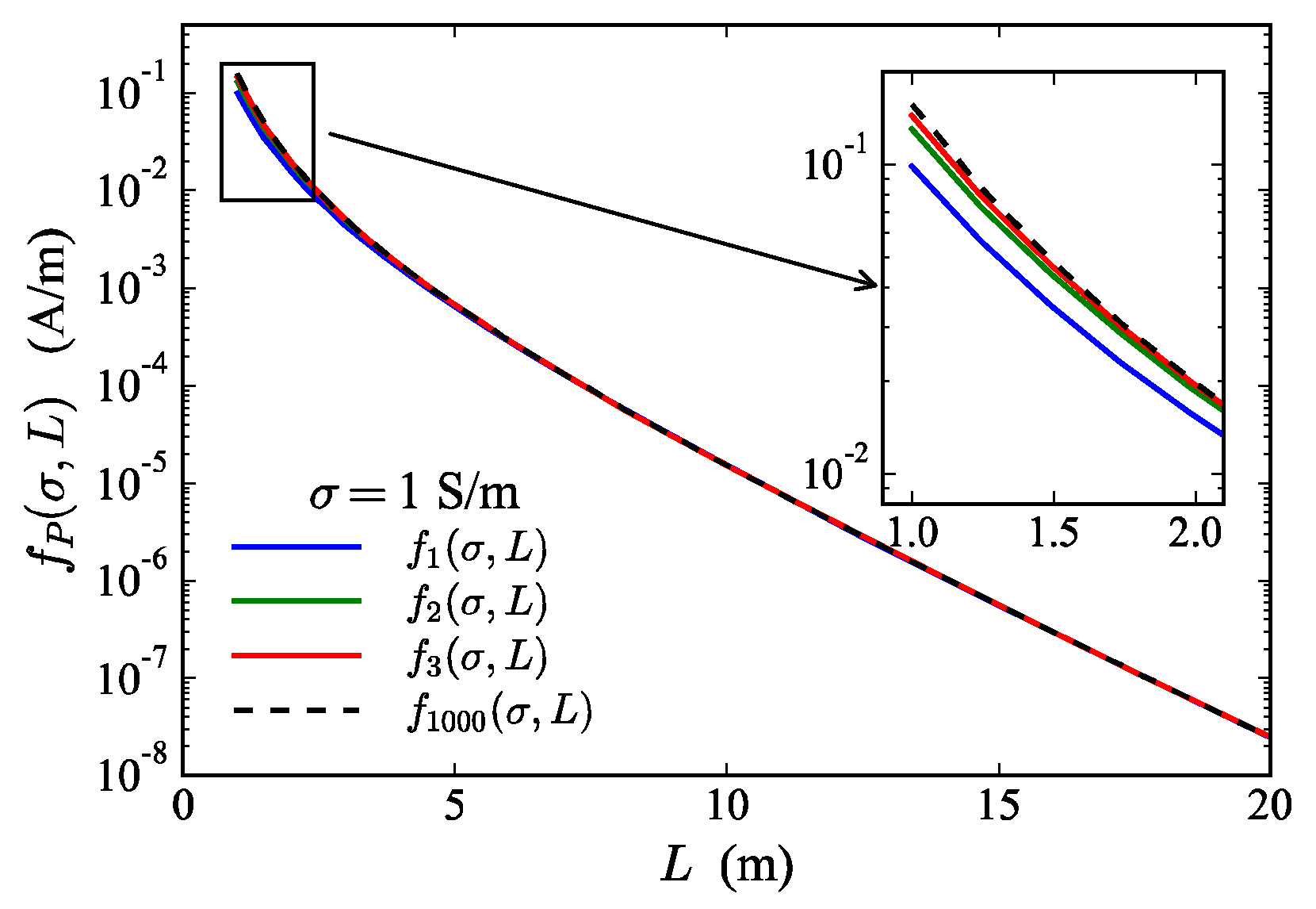
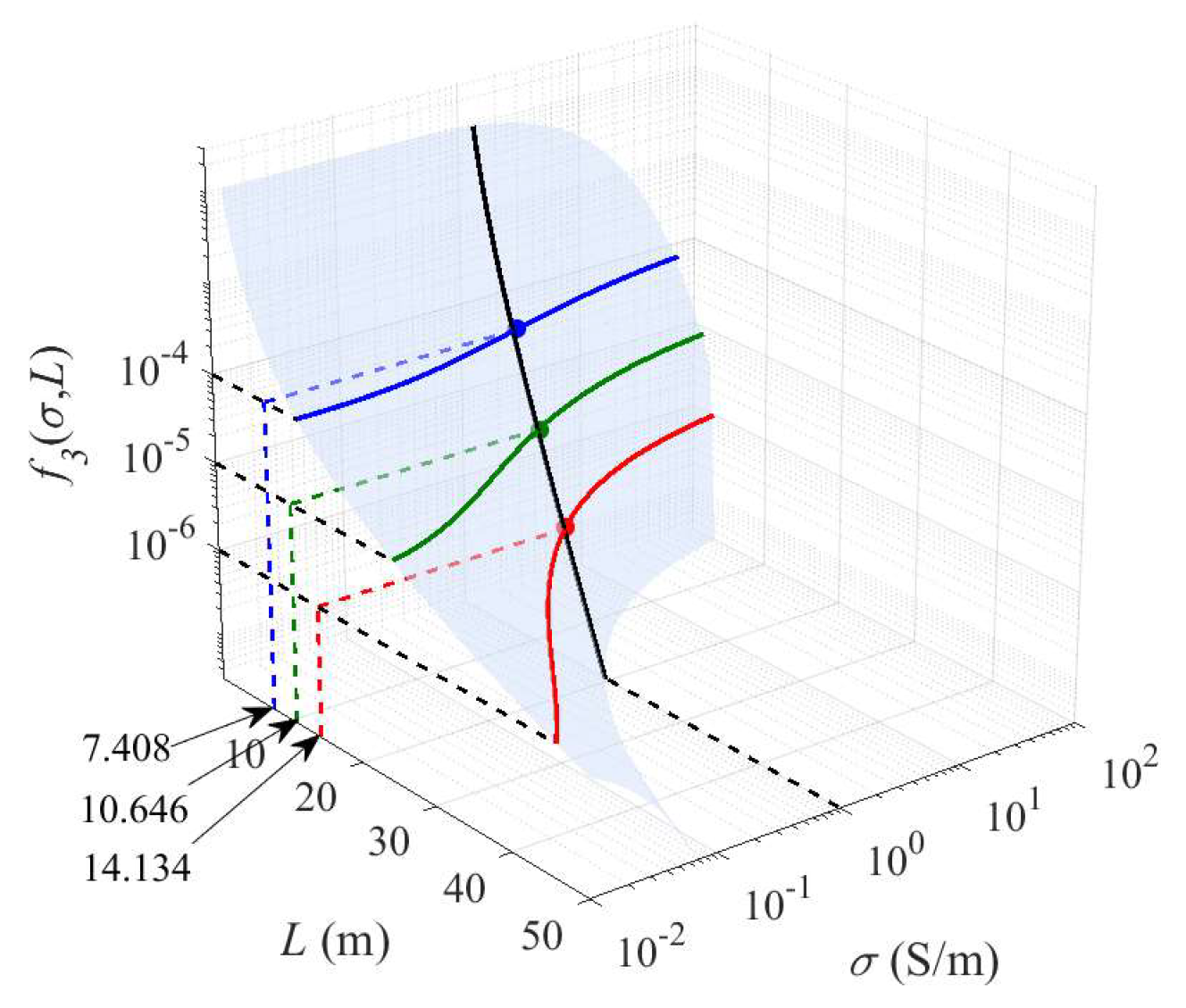
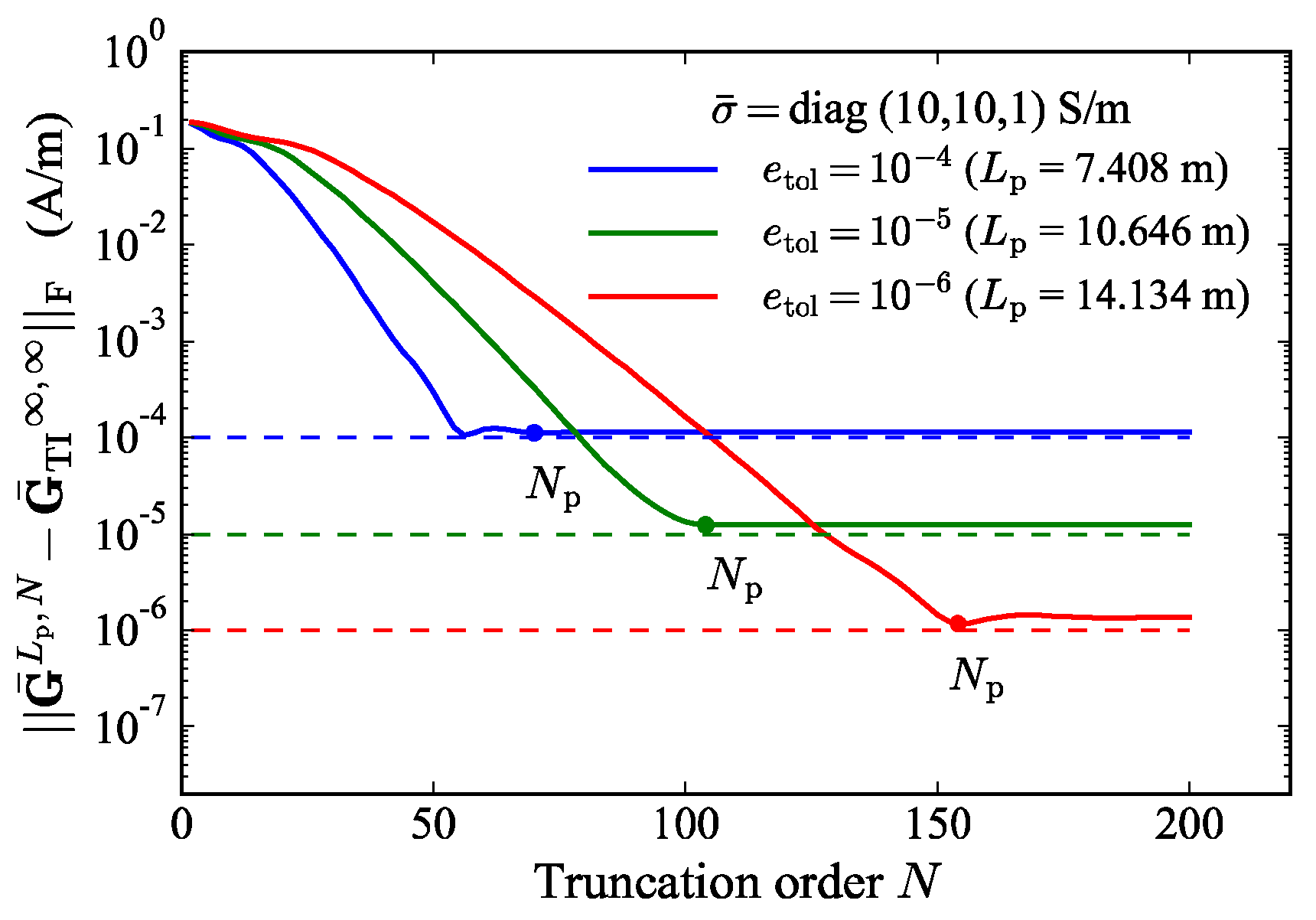
2.2.4. Tensor Green’s Function and the Choice of Region’s Size and Truncation Order
3. Results
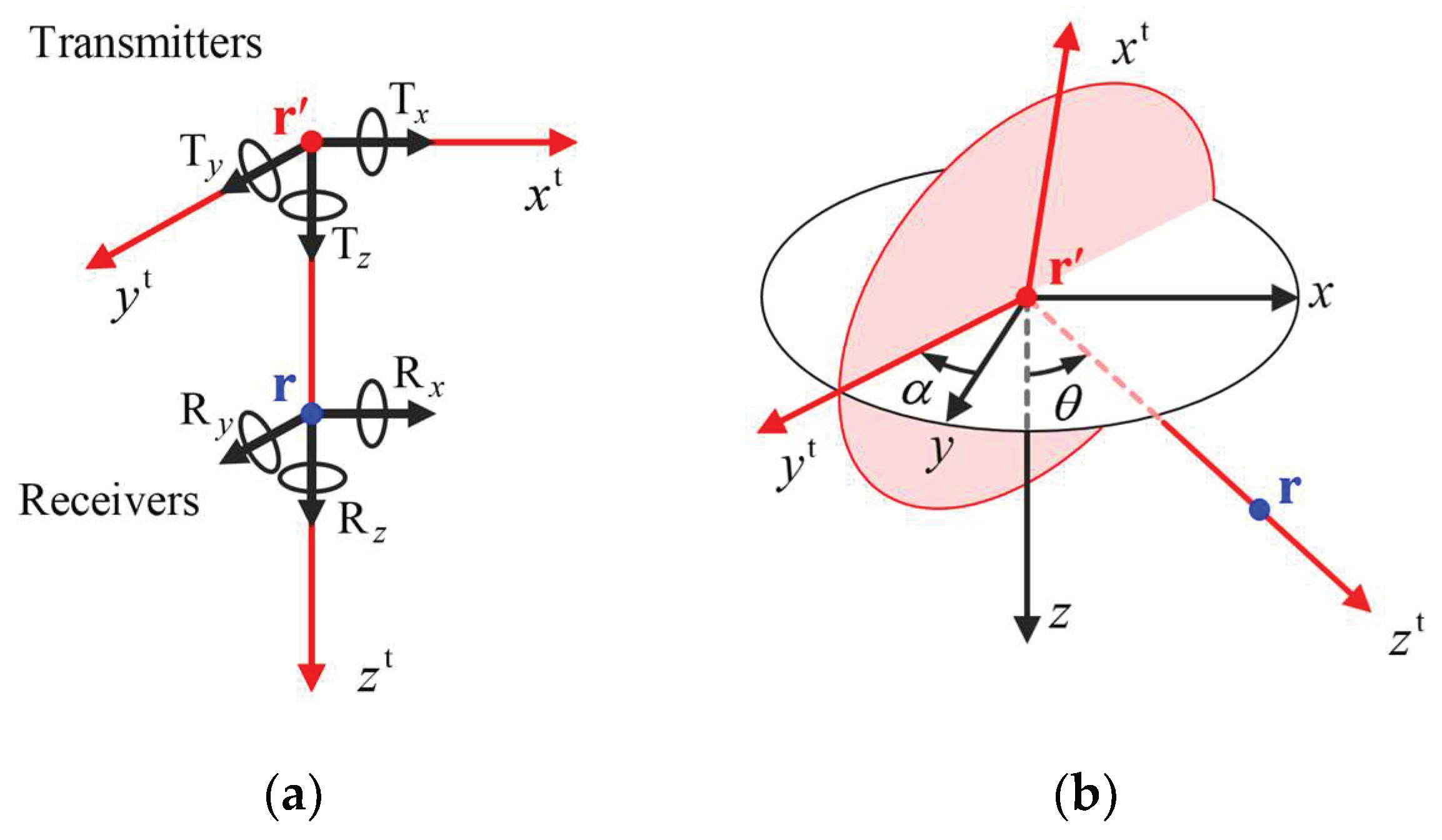
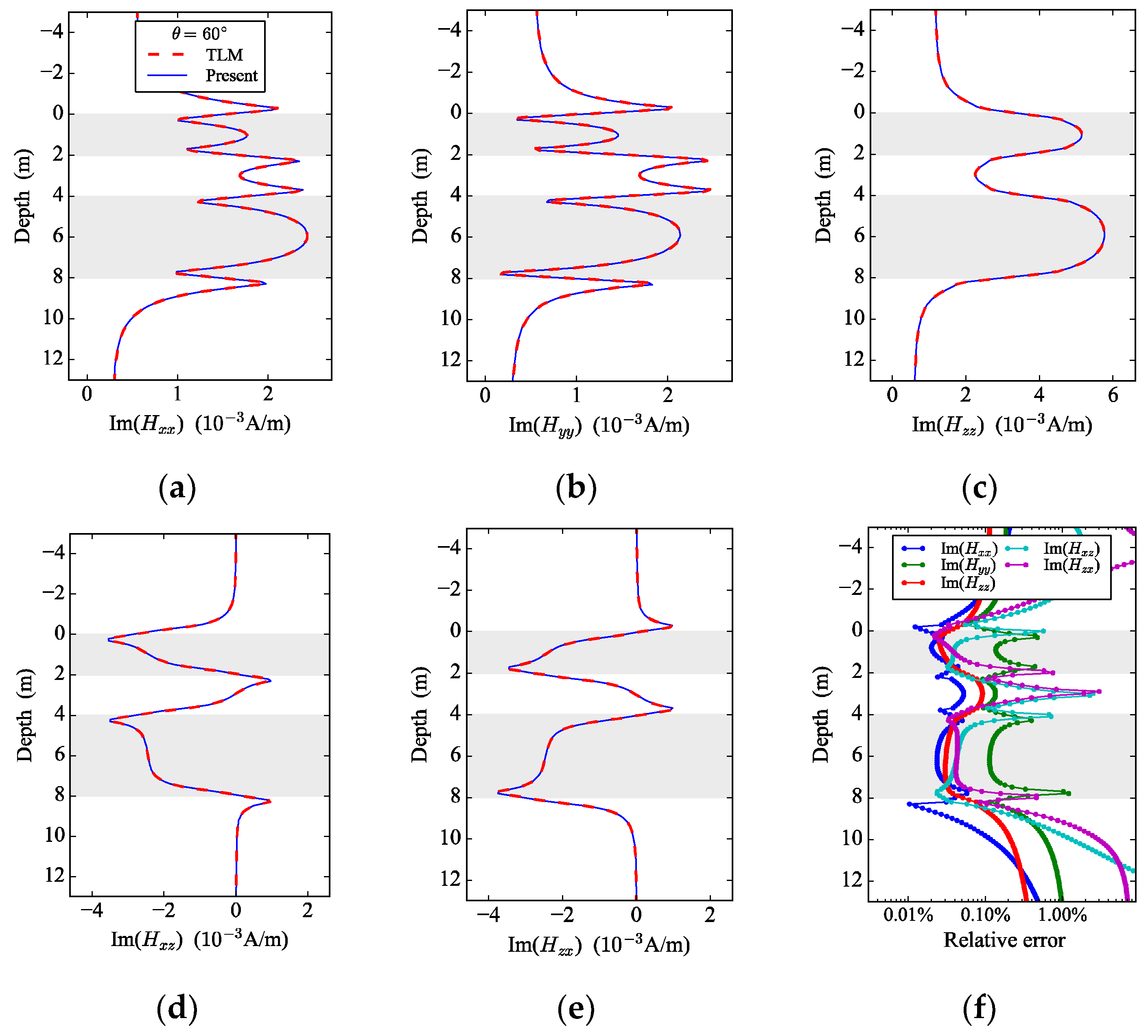
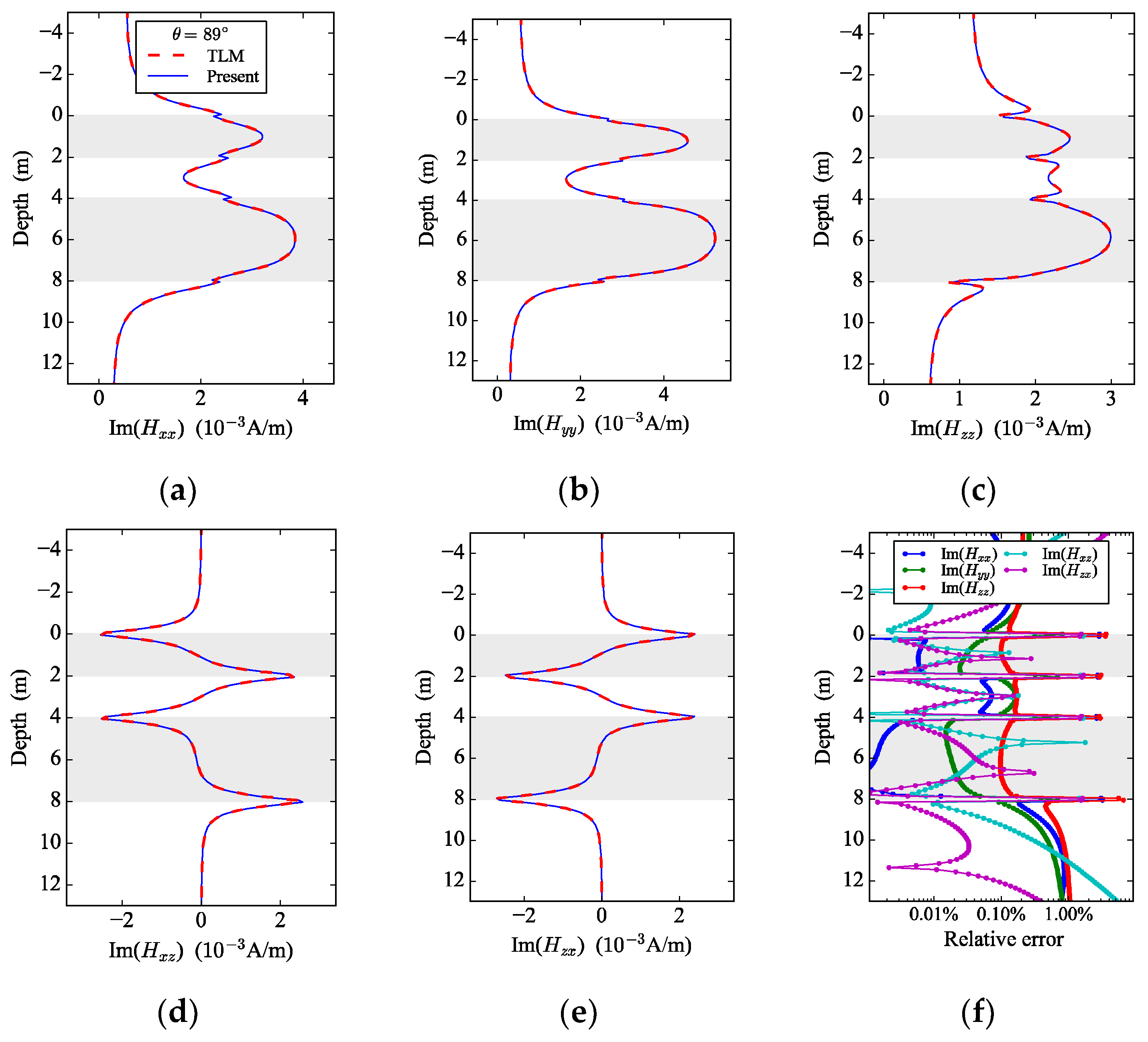
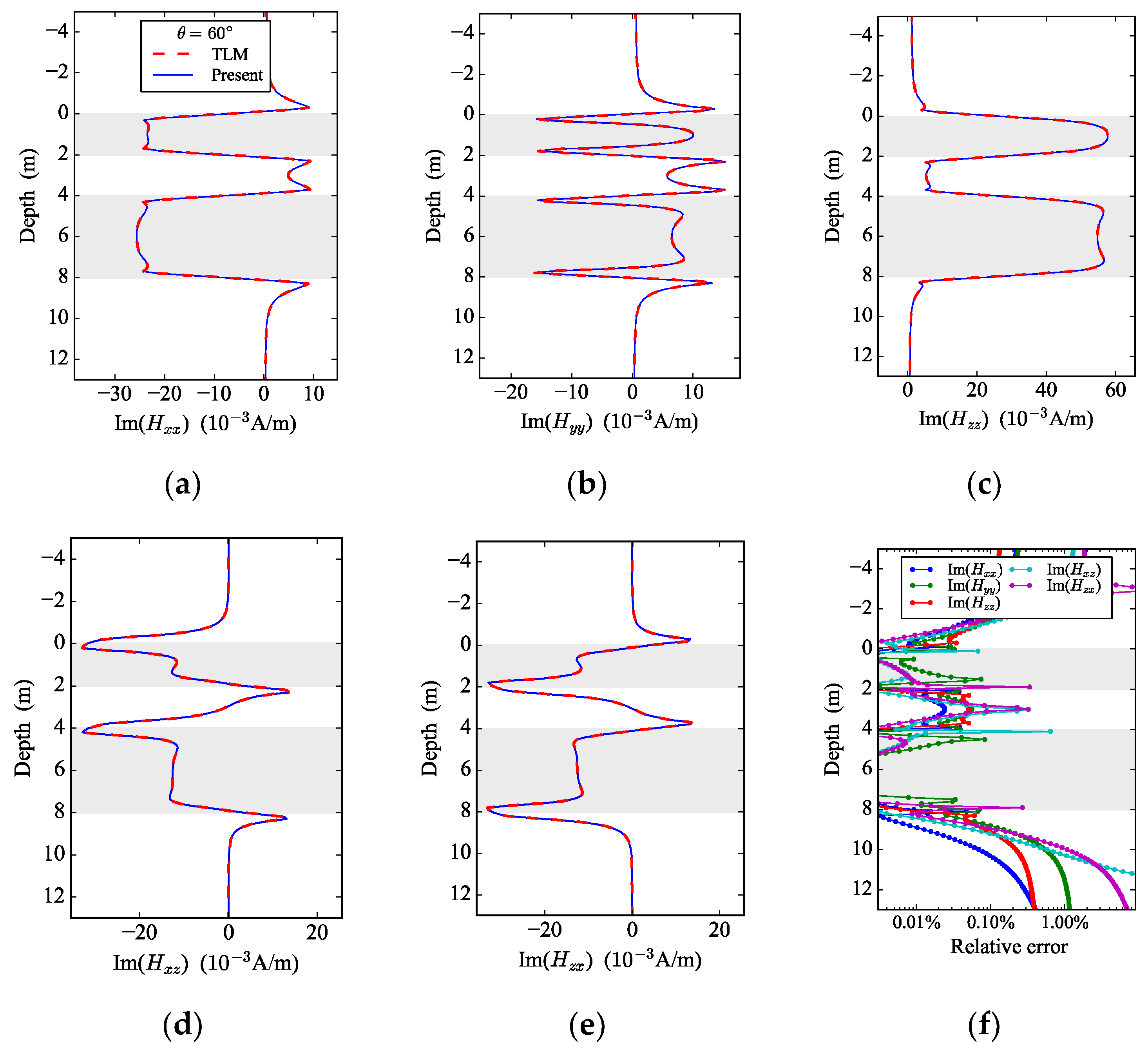
3.1. Triaxial Logging Responses in Layered TI Media
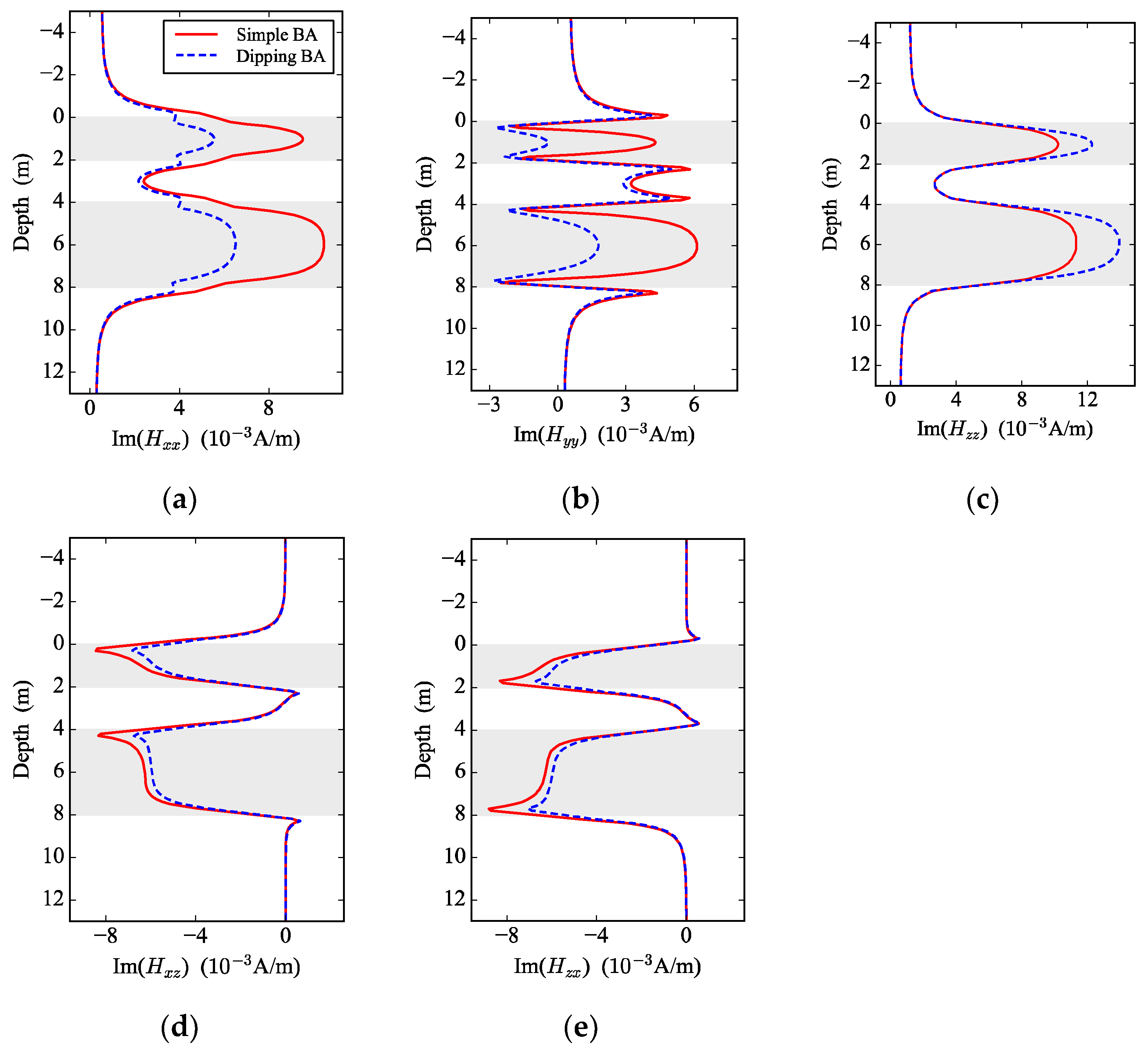
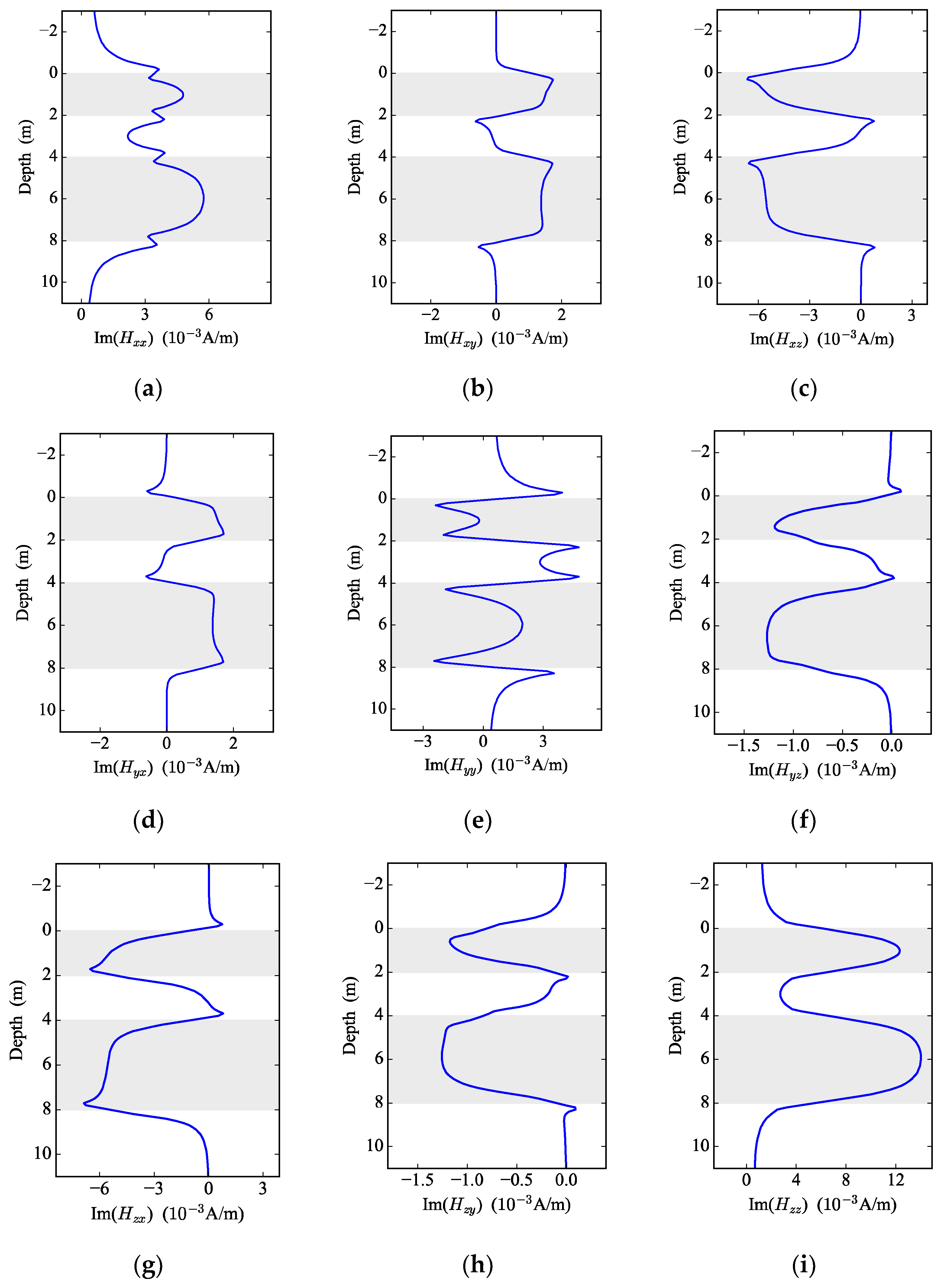
3.2. Triaxial Logging Responses in Layered BA Media
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Ursin, B. Review of elastic and electromagnetic wave propagation in horizontally layered media. Geophysics 1983, 48, 1063–1081. [Google Scholar] [CrossRef]
- Zhong, Y.; Lambert, M.; Lesselier, D.; Chen, X. Electromagnetic response of anisotropic laminates to distributed sources. IEEE Trans. Antennas Propag. 2014, 62, 247–256. [Google Scholar] [CrossRef]
- Yin, C. MMT forward modeling for a layered earth with arbitrary anisotropy. Geophysics 2006, 71, G115–G128. [Google Scholar] [CrossRef]
- Howard, A.Q. Petrophysics of magnetic dipole fields in an anisotropic earth. IEEE Trans. Antennas Propag. 2000, 48, 1376–1383. [Google Scholar] [CrossRef]
- Yu, L.; Wang, H.; Wang, H.; Yang, S.; Yin, C. 3-D finite volume modeling for LWD azimuthal propagation resistivity tool with multiple annular antenna recesses using coupled potentials on cylindrical grids. IEEE Trans. Antennas Propag. 2022, 70, 514–525. [Google Scholar] [CrossRef]
- Li, D.; Wilton, D.R.; Jackson, D.R.; Wang, H.; Chen, J. Accelerated computation of triaxial induction tool response for arbitrarily deviated wells in planar-stratified transversely isotropic formations. IEEE Geosci. Remote Sens. Lett. 2018, 15, 902–906. [Google Scholar] [CrossRef]
- Xing, G.; Zhang, X.; Teixeira, F.L. Computation of tensor Green’s functions in uniaxial planar-stratified media with a rescaled equivalent boundary approach. IEEE Trans. Antennas Propag. 2018, 66, 1863–1873. [Google Scholar] [CrossRef]
- Wang, H.N.; Yu, L.; Wang, H.S.; Yang, S.W.; Yin, C.C. A hybrid algorithm for LWD azimuthal electromagnetic responses with annular grooved drill collar. Chin. J. Geophys. 2021, 64, 1811–1829. [Google Scholar] [CrossRef]
- Lee, H.O.; Teixeira, F.L. Cylindrical FDTD analysis of LWD tools through anisotropic dipping-layered earth media. IEEE Trans. Geosci. Remote Sens. 2007, 45, 383–388. [Google Scholar] [CrossRef]
- Chew, W.C.; Chen, S.-Y. Response of a point source embedded in a layered medium. IEEE Antennas Wirel. Propag. Lett. 2003, 2, 254–258. [Google Scholar] [CrossRef][Green Version]
- Hong, D.; Xiao, J.; Zhang, G.; Yang, S. Characteristics of the sum of cross-components of triaxial induction logging tool in layered anisotropic formation. IEEE Trans. Geosci. Remote Sens. 2014, 52, 3107–3115. [Google Scholar] [CrossRef]
- Michalski, K.A.; Mosig, J.R. Multilayered media Green’s functions in integral equation formulations. IEEE Trans. Antennas Propagat. 1997, 45, 508–519. [Google Scholar] [CrossRef]
- Simsek, E.; Liu, Q.H.; Wei, B. Singularity subtraction for evaluation of Green’s functions for multilayer media. IEEE Trans. Microw. Theory Tech. 2006, 54, 216–225. [Google Scholar] [CrossRef]
- Chew, W.C. Waves and Fields in Inhomogenous Media; Wiley-IEEE Press: New York, NY, USA, 1995. [Google Scholar]
- Løseth, L.O.; Ursin, B. Electromagnetic fields in planarly layered anisotropic media. Geophys. J. Int. 2007, 170, 44–80. [Google Scholar] [CrossRef]
- Morgan, M.; Fisher, D.; Milne, E. Electromagnetic scattering by stratified inhomogeneous anisotropic media. IEEE Trans. Antennas Propag. 1987, 35, 191–197. [Google Scholar] [CrossRef]
- Yang, H.D. A spectral recursive transformation method for electromagnetic waves in generalized anisotropic layered media. IEEE Trans. Antennas Propag. 1997, 45, 520–526. [Google Scholar] [CrossRef]
- Hong, D.; Li, N.; Han, W.; Zhan, Q.; Zeyde, K.; Liu, Q.H. An analytic algorithm for dipole electromagnetic field in fully anisotropic planar-stratified media. IEEE Trans. Geosci. Remote Sens. 2021, 59, 9120–9131. [Google Scholar] [CrossRef]
- Hu, X.; Fan, Y.; Deng, S.; Yuan, X.; Li, H. Electromagnetic logging response in multilayered formation with arbitrary uniaxially electrical anisotropy. IEEE Trans. Geosci. Remote Sens. 2020, 58, 2071–2083. [Google Scholar] [CrossRef]
- Sainath, K.; Teixeira, F.L. Tensor Green’s function evaluation in arbitrarily anisotropic layered media using complex-plane Gauss-Laguerre quadrature. Phys. Rev. E 2014, 89, 053303. [Google Scholar] [CrossRef]
- Hu, Y.; Fang, Y.; Wang, D.; Zhong, Y.; Liu, Q.H. Electromagnetic waves in multilayered generalized anisotropic media. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5758–5766. [Google Scholar] [CrossRef]
- Li, N.; Hong, D.; Han, W.; Liu, Q.H. An analytic algorithm for electromagnetic field in planar-stratified biaxial anisotropic formation. IEEE Trans. Geosci. Remote Sens. 2020, 58, 1644–1653. [Google Scholar] [CrossRef]
- He, Z.; Huang, K.; Liu, R.C.; Guo, C.; Jin, Z.; Zhang, L. A semianalytic solution to the response of a triaxial induction logging tool in a layered biaxial anisotropic formation. Geophysics 2016, 81, D71–D82. [Google Scholar] [CrossRef]
- Kang, Z.Z.; Wang, H.N.; Wang, H.-S.; Yang, S.-W.; Yin, C.C. Study of multi-component induction logging in layered crossbedding formations by using propagation matrix method. Chin. J. Geophys. 2020, 63, 4277–4289. [Google Scholar] [CrossRef]
- Yao, D.H.; Wang, H.N.; Yang, S.W.; Yang, H.L. Study on the responses of multi-component induction logging tool in layered orthorhombic anisotropy formations by using propagator matrix method. Chin. J. Geophys. 2010, 53, 3026–3037. [Google Scholar]
- Wang, H.; Tao, H.; Yao, J.; Zhang, Y. Efficient and reliable simulation of multicomponent induction logging response in horizontally stratified inhomogeneous TI formations by numerical mode matching method. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3383–3395. [Google Scholar] [CrossRef]
- Wang, G.L.; Barber, T.; Wu, P.; Allen, D.; Abubakar, A. Fast inversion of triaxial induction data in dipping crossbedded formations. Geophysics 2017, 82, D31–D45. [Google Scholar] [CrossRef]
- Wang, H. Adaptive regularization iterative inversion of array multicomponent induction well logging datum in a horizontally stratified inhomogeneous TI formation. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4483–4492. [Google Scholar] [CrossRef]
- Kang, Z.; Wang, H.; Wang, Y.; Yin, C. Fourier series approximation of tensor Green’s function in biaxial anisotropic media. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Yang, S.; Wang, J.; Zhou, J.; Zhu, T.; Wang, H. An efficient algorithm of both Fréchet derivative and inversion of MCIL data in a deviated well in a horizontally layered TI formation based on TLM modeling. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6911–6923. [Google Scholar] [CrossRef]
- Kong, J.A. Electromagnetic Waves Theory; EMW Publishing: Cambridge, UK, 2000. [Google Scholar]
- Zhdanov, M.S.; Kennedy, W.D.; Peksen, E. Foundation of the tensor induction well logging. Petrophysics 2001, 42, 588–610. [Google Scholar]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kang, Z.; Wang, H.; Yin, C. Finite-Region Approximation of EM Fields in Layered Biaxial Anisotropic Media. Remote Sens. 2022, 14, 3836. https://doi.org/10.3390/rs14153836
Kang Z, Wang H, Yin C. Finite-Region Approximation of EM Fields in Layered Biaxial Anisotropic Media. Remote Sensing. 2022; 14(15):3836. https://doi.org/10.3390/rs14153836
Chicago/Turabian StyleKang, Zhuangzhuang, Hongnian Wang, and Changchun Yin. 2022. "Finite-Region Approximation of EM Fields in Layered Biaxial Anisotropic Media" Remote Sensing 14, no. 15: 3836. https://doi.org/10.3390/rs14153836
APA StyleKang, Z., Wang, H., & Yin, C. (2022). Finite-Region Approximation of EM Fields in Layered Biaxial Anisotropic Media. Remote Sensing, 14(15), 3836. https://doi.org/10.3390/rs14153836






