Abstract
The class imbalance problem has been reported to exist in remote sensing and hinders the classification performance of many machine learning algorithms. Several technologies, such as data sampling methods, feature selection-based methods, and ensemble-based methods, have been proposed to solve the class imbalance problem. However, these methods suffer from the loss of useful information or from artificial noise, or result in overfitting. A novel double ensemble algorithm is proposed to deal with the multi-class imbalance problem of the hyperspectral image in this paper. This method first computes the feature importance values of the hyperspectral data via an ensemble model, then produces several balanced data sets based on oversampling and builds a number of classifiers. Finally, the classification results of these diversity classifiers are combined according to a specific ensemble rule. In the experiment, different data-handling methods and classification methods including random undersampling (RUS), random oversampling (ROS), Adaboost, Bagging, and random forest are compared with the proposed double random forest method. The experimental results on three imbalanced hyperspectral data sets demonstrate the effectiveness of the proposed algorithm.
1. Introduction
Hyperspectral image (HSI) is one of the most important data types in the remote sensing field [1]. These images could provide rich information and have obtained lots of applications, including land use surveys, environmental monitoring, mineral development, and so on [2,3]. Machine learning, which automates analytical model building to find hidden insights, is a core sub-area of hyperspectral remote sensing research [4]. Generally speaking, classification approaches can be divided into unsupervised and supervised methods [5]. Unsupervised classification methods, such as K-means, graph-based methods, do not require labeled samples [6]. The relationship between clusters and classes with too little prior knowledge cannot be determined [7]. The supervised classification methods generally present better performance but need the class labels of the training data. However, many supervised classification methods suffer from the class imbalanced problem which exists when some classes (minority classes) are underrepresented as compared to the other classes (majority classes) [8,9,10]. For example, random forests (RF), which has been employed in many applicative domains, become intractable when an imbalance problem appears [10]. In addition, the “curse of dimensionality” makes imbalanced HSI processing face more challenges concerning other data classification tasks [11,12].
Dealing with imbalanced multi-class tasks is harder than dealing with binary ones [10,13,14,15,16]. In binary problems, the roles of classes are easily defined: one is majority and the other one is minority [17]. When dealing with multiple classes, a given class may be at the same time majority when compared to some, minority to others, and even in a relative balance with the rest [4]. This makes designing any balancing algorithms highly challenging, as they must take into account these various roles [17]. The purpose of multi-class imbalance learning is to provide high classification accuracy for the minority classes without heavily compromising the accuracy of the majority classes [10]. A larger number of methods have been proposed to solve the class imbalance problem. They can be divided into three categories: feature-level methods, data-level methods, and algorithm-level methods. Ensemble methods, which combine several base models to produce one strong predictive model [18,19,20], is one new method to deal with imbalanced data [10,21]. Different from the feature selection, data sampling, and normal algorithms, ensemble-based methods can combine multiple data sampling and classifier optimization algorithms, thus indirectly alleviating the effect of the data imbalance problem. For example, Ribeiro et al. [22] propose a multi-objective optimization design approach for imbalanced learning. This method has four steps: multi-objective ensemble member generation, multi-objective ensemble member selection, multi-objective ensemble member combination, and multi-objective ensemble member selection and combination. Wang et al. [23] developed a multi-matrices entropy discriminant ensemble learning method. This method introduced the multi-matrices approach and nearest entropy into the base classifier. Chen et al. [24] propose a method by combining ensemble learning with the union of a margin-based undersampling and diversity-enhancing oversampling. Wang et al. propose a hybrid ensemble learning strategy named Sample and Feature Selection Hybrid Ensemble Learning [25]. Qin et al. [26] combined the particle swarm optimization-based wrapper method and the dynamic oversampling approach with adaptive boosting to propose a hybrid multi-class imbalanced learning method. The wrapper method is utilized to adaptively select the optimal feature subset, and DySBoost is applied to solve the multi-class class imbalanced problem. Cmv et al. [27] designed a novel sequential ensemble learning framework. The method can divide the majority instances into multiple small and disjoint subsets for training multiple weak learners without compromising accuracy [27]. These researches prove that the problem of class imbalance can be effectively solved by ensemble learning. However, most of these methods do not consider the high dimension problems of imbalance learning.
According to the above presentation, hyperspectral data is commonly characterized by high dimension and multi-class imbalanced nature. This requires dedicated algorithms which use information about relationships among features and classes for multi-class imbalanced data. Most existing state-of-the-art solutions are designed for the binary problem and are not capable of processing multi-class data. This calls for developing efficient algorithms for handling multi-class imbalanced problems. Hence, this paper proposes a double random forest (DRF) method for multi-class imbalance learning by the idea of hybrid ensemble theory. This method firstly computes the feature importance values of the hyperspectral data, then produces several balanced data sets based on oversampling and builds a number of classifiers. Finally, the classification results of these diversity classifiers are combined according to a specific ensemble rule. In the experiment, different data handling methods and classification methods including random undersampling (RUS), random oversampling (ROS), Adaboost, Bagging, and random forest, are compared with the proposed double random forest method.
Thus, the contribution of this paper is to design a hybrid random forest framework that generates an ensemble and is biased toward the minority class(es). The rest of this paper is structured as follows. Section 2 briefly explains and reviews some of the related state-of-the-art approaches developed to tackle the class imbalance problem. Section 3 describes the proposed approach, DRF. Section 4 presents various measures for evaluating the DRF’s performance. Section 5 discusses the superior performance of the proposed work. Finally, Section 6 summarizes this paper.
2. Related Works
2.1. Feature-Level Methods
The main goal of the feature-level methods is to select a subset of K features from the original feature space, to increase the distinction between majority and minority classes. Then, redundancy and noisy information can be discarded; thus, this kind of method could reduce the risk of overfitting and lead to better classification performance. Moreover, the feature-level methods can be divided into embedded methods and filter methods. The approach integrates feature selection and classifier learning into a single process.
K-nearest neighborhood (KNN) and Principal Component Analysis (PCA)-based approaches are two well-known feature selection methods. The KNN-based method is a linear algorithm to evaluate the performance of feature subsets. Its shortcoming is that it cannot keep the geometric structure of the data in the originally high-dimensional space, when representing the data in a lower-dimensional space [28]. The PCA-based method is a category of dimensionality reduction approaches in discriminating directions in a data set and finding out the sensitive directions of maximal variance [28]. It is a linear transformation from a high-dimensional space to a lower-dimensional space, and is less effective in nonlinear data with a certain type of topological manifold [28]. However, PCA cannot reflect the true low-dimensional geometry of the manifold [28]. Hence, some nonlinear algorithms are proposed to avoid the above problems. For example, Richhariya et al. [29] propose a reduced Universum twin support vector machine (SVM) for class imbalance learning. This method is applicable for large-scale imbalanced datasets. The filtering methods compute the score or significance of each attribute for the purpose of ranking the input variables. Shahee et al. [30] proposes an effective distance-based feature selection method. This method employs a sophisticated distance measure to tackle the simultaneous occurrence of between and within-class imbalance.
2.2. Data-Level Methods
The random oversampling (ROS) method is a common method to deal with the problem of class imbalance [4]. ROS randomly tries to balance class distribution by randomly replicating minority class instances, thereby increasing the minority samples and creating a more balanced dataset. However, since the samples are randomly selected, over-fitting may be encountered in some cases. The random undersampling (RUS) method is the simplest class-balancing method. While oversampling appends instances to the original dataset, random undersampling eliminates instances from the original dataset. In the majority class data , instances are randomly selected and removed arbitrarily to create a balanced dataset. In this way, the number of total examples in is reduced by E, and the class distribution balance of S is adjusted accordingly. Finally, a balanced data set is generated. The undersampling method could be used in big data study. However, some rich and important instances of most classes may be discarded [10].
In addition, Chennuru et al. [31] propose a Simulated Annealing-based Under Sampling (SAUS) method. However, the method may remove potentially useful information. Different from undersampling, oversampling achieves rational distribution of samples by increasing the number of minority class samples of the imbalanced training set [4,32]. Chawla et al. [33] proposed the synthetic minority oversampling technique (SMOTE), which is a powerful algorithm and has enjoyed great success in various applications [4,34]. Engelmann et al. present a conditional Wasserstein Generative Adversarial Network-based oversampling method for imbalanced learning [35]. Xu et al. [36] proposed a cluster-based oversampling algorithm by combining SMOTE and k-means. Although oversampling has been proven effective for imbalanced data, most of these methods pay more attention to the binary problem and are very difficult in dealing with the multi class problem.
2.3. Algorithm-Level Methods
The methods of the algorithm level aim to modify the existing classification algorithm model appropriately according to the actual data distribution [4] Cost sensitive learning [37] and active learning [38] are representative algorithms. The core of cost-sensitive learning is to consider the classes with high misclassification costs. However, when dealing with data sets in the real world, the cost matrix is unknown in most cases, so it is difficult to accurately estimate the real error cost [39]. Although the active learning method could improve the classification performance by choosing more valuable instances and discarding those with less information, it is a large computation cost [40]. In addition, because algorithm-level solutions work directly within the training procedure of the considered classifier, they lack the flexibility offered by data-level approaches but compensate with a more direct and powerful way of reducing the bias of the certain learning algorithm [17]. They also require an in-depth understanding of how a given training procedure is conducted and what specific part of it may lead to bias towards the majority class [17].
Decomposition-based approaches transform multi-class problems into a series of binary ones. Then those binary problems are solved separately and later aggregated. The decomposition-based methods were developed from binary imbalanced classification. Those methods are often simple and allow the re-use of well-developed binary imbalanced algorithms [41]. The most popular algorithms rely on one-against-one (OAO) and one-against-all (OAA) ensemble schemes [4,10]. Most decomposition-based approaches are combined with data resampling techniques that modify the original dataset in a pre-processing step before learning the classifier. For example, Abdi et al. propose a Mahalanobis-distance oversampling (MDO) method [42]. SOUP integrates informed undersampling of majority classes and oversampling of minority ones [43]. However, those class decomposition-based schemes are not suitable when a large number of classes is considered [4]. In addition, decomposition methods are sometimes not as effective as some dedicated approaches for multi-class imbalanced data [41].
2.4. Ensemble-Based Imbalance Learning Methods
2.4.1. Adaboost
Boosting is one of the major ensemble learning methods. The term boosting refers to a family of algorithms that can convert weak learners to strong learners. Adaboost [44] is the most influential boosting algorithm, it is summarized in Algorithm 1 [45].
| Algorithm 1 Adaboost |
| Input: Data set ; Base learning algorithm ; Number of learning rounds T; Initialization: . Iterative process: for to T do 1. ; 2. ; 3. if then break 4. ; 5. Update: end Output: |
Adaboost.NC is the improved version of AdaBoost. Wang and Yao compared the performances of Adaboost.NC and Adaboost combined with random oversampling with or without using class decomposition for multi-class imbalanced data sets [46]. Their results in the case of class decomposition show AdaBoost.NC and Adaboost have similar performance.
2.4.2. Bagging
The Bagging came from the abbreviation of Bootstrap AGGregatING [47]. The two key ingredients of Bagging are bootstrap and aggregation [48]. Algorithm 2 summarizes the Bagging procedure. A bootstrap sample is obtained by uniformly subsampling the training data with replacement. To predict a test instance, Bagging feeds the sample to its base classifiers and collects all of their outputs, and then uses the most popular strategies voting to aggregate the outputs and takes the winner label as the prediction [48].
| Algorithm 2 Bagging |
|
Input: Data set ; Base learning algorithm ; Number of learning rounds T; Iterative process: for to T do ; end Output: |
Bagging outperforms boosting over imbalanced data [49]. Moreover, Bagging techniques are not only easy to develop but are also powerful when dealing with class imbalance if they are properly combined [50]. Most related works in the literature indicate good performance of Bagging extensions versus the other ensembles [51,52]. OverBagging [13] is a method for the management of class imbalance that merges Bagging and data preprocessing. It increases the cardinality of the minority class by replication of original examples (random oversampling), while the examples in the majority class can be all considered in each bag or can be resampled to increase the diversity. This method outperforms original Bagging in dealing with binary imbalanced data problems [50].
2.4.3. Random Forest
Illuminated by the Bagging algorithm [47], the random forest (RF) algorithm is proposed by Breiman [53]. A random forest is an ensemble of Classification and Regression Trees (CART) trees. Each tree represents a base classifier and the trainings of the base classifier are independent of each other. The core idea of RF is random sample selection and random feature selection, and the classification process is implemented by taking a majority vote. Let us suppose a dataset with m instances. Firstly, n samples are randomly chosen with replacement from the original data set to build a subset of samples. Secondly, f features are randomly selected from all the features of the selected instances. Then the best features are iteratively chosen based on the criterion of Gini impurity or mean squared error to construct a CART. Finally, the prediction results are obtained by repeating the above operation and employing the majority voting rule.
2.4.4. Ensemble-Based Methods
According to the different ensemble models, imbalance learning algorithms could contain boosting-based methods and Bagging/random forest-based methods [4].
Thanathamathee et al. proposed a class imbalance learning method by combining synthetic boundary data generation and boosting procedures [54]. The method outperforms KNN and AdaBoost.M1 but relies on boundary definition. Random balance boost [55] is proposed by training each classifier with a data set obtained via random balance. The random balance is designed by using both SMOTE and random undersampling to, respectively, increase or reduce the size of the classes to achieve the desired ratios. The combination could lead to better performance when compared with other state-of-the-art combined ensemble methods for binary-class imbalance problems [55]. However, most boosting-based methods face the threat of noise as the original boosting method [55]. In addition, most boosting-based imbalanced learning techniques only focus on two-class imbalance problems and are difficult to extend to multi-class imbalance problems [4].
Bagging significantly outperforms boosting over noisy and imbalanced data [49]. Moreover, Bagging techniques are not only easy to develop but also powerful when dealing with class imbalance if they are properly combined [4,50]. UnderBagging was first proposed by Barandela et al. [56]. In this method, the number of the majority class examples in each bootstrap sample is randomly reduced to the cardinality of the minority class. Simple versions of undersampling combined with Bagging are proved to work better than more complex solutions such as EasyEnsemble and BalanceCascade [51,57]. However, the performance of UnderBagging was not tested for multi-class imbalance learning in their work. OverBagging [13] is a famous class imbalance learning method that merges Bagging and data preprocessing. This method has been demonstrated to be effective in dealing with binary imbalanced data problems [50]. SMOTEBagging is the improved version of OverBagging [13]. The reported results show that SMOTEBagging can obtain better performance than OverBagging for both binary class problems [50,52].
Since the random forest is an improved version of Bagging, in theory, all class imbalance algorithms based on Bagging can be extended to the random forest. In addition, because the random forest has higher accuracy than Bagging, the imbalanced learning algorithm based on random forest should also have better performance in theory.
3. Proposed Method
This section presents the double random forest (DRF) which is a simple and effective method for high-dimensional data. DRF is motivated by the idea of combing the oversampling of the data level and ensemble random forest of the algorithm level. In other words, instead of increasing the minority instances in the data set before the classification, the proposed algorithm aims to oversample for all the ensemble models. In addition, before the class balancing operation, DRF employs the random forest to select the informative features for the imbalance classification. The overall structure of the DRF is shown in Algorithm 3. First, the random forest is adapted to identify the useful features of the data sets. Second, random oversampling, which contains all the majority instances, is operated to increase the number of the minority instances, then the bootstrap constructs several diversity training sets and generates a series of standard random forests. Third, the final results are obtained by combing all the outputs of separate random forests according to the major vote rule.
3.1. Feature Importance Determining Based on Random Forest
The random forest provides the measurement of feature importance. Let us note V as being the number of decision trees to induce. Rows of , figuring the training instances, are sampled with replacement. This is equivalent to the left multiplication of a matrix of size where each row contains only one component equal to 1 and its location in the row is evenly drawn from . The assigned labels are also transformed into . Moreover, a random G-sized subset of the -columns is selected. This is equivalent to the right multiplication of of size defined as the identity matrix deprived of a random set of columns. The labels remain unmodified. Finally, is used to train a decision tree using the Classification and Regression Trees methodology (CART). The trained decision tree maps any row-vector of size into an integer ; C is the number of classes. The above tasks are repeated V times, and the predictions of V decision trees are fused according to the majority rule.
where is a row vector, and is equal to one when is true and zero if not.
Let us consider the v-indexed decision tree trained with and denote the number of the internal nodes of the decision tree. If we assume a node indexed of the tree with n, then there are a set of samples and labels which are rows of and . We demote the set of these row indexes by and denote the components of and as and . At this node, samples are split with the feature and a cutting point .
Splitting modifies the class distribution into and . These class distributions are associated, respectively, to , and .
The importance value of a feature of the training set in node n is the amount by which splitting reduces entropy.
When averaging , the relative amount of samples dealt by each node is the weight value.
Thus, the measures of feature importance of random forest could be defined as
where is a normalization factor and can be defined as
Feature selection is used to avoid the curse of dimensionality and improve the performance of the random forest in the case of the class imbalance. The feature importance analysis results of the experiments are shown in Figure 1. The figure shows that the difference of the feature importance values for each band of each data is very obvious. This phenomenon is particularly evident on Indian Pines AVRIS and Salinas. Hence, the proposed method could filter out useless features, thereby reducing the impact of noise, which in turn reduces computational complexity of the learning model and improves the final classification accuracy.
| Algorithm 3 Oversampling-based double random forest methods. |
Inputs:
Process:
End |
Output: The ensemble E |
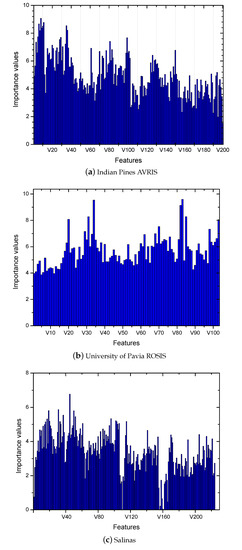
Figure 1.
Feature importance values of the hyperspectral data Indian, University and Salinas.
3.2. Over-Sampling Based Double Ensemble Methods
Let us denote as training samples. The first step of the proposed random forest method uses random oversampling to balance the class of the training set. Suppose L is the number of classes, then is the number of training instances of the ith class. is the training size of the biggest class L, and is the training size of the smallest class 1. For each class c, the resampling operation is used to increase the number of small class instances to contract a balanced data set. All the instances of the biggest class are kept. In the second phase, the bootstrap is employed to generate several diverse balanced training subsets. Random forest is as the base classifier. A series of classifiers are trained by the diverse datasets, and the ensemble results are obtained by a majority vote rule. The description of the proposal is presented in Algorithm 3. The flowchart of the double ensemble-based multi-class imbalanced data learning method is shown in Figure 2.
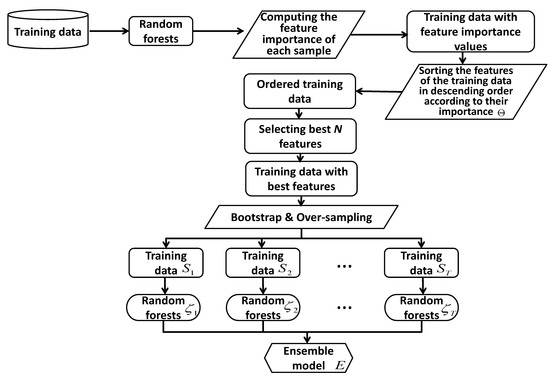
Figure 2.
Flowchart of the double ensemble-based multi-class imbalanced data learning method.
4. Experimental Study
To evaluate the performance of DRF, described in the previous section, Adaboost, Bagging, RF, data preprocessing involving random undersampling and random oversampling combined Adaboost, Bagging, and random forest are utilized in the comparative analysis. All ensembles are implemented with 100 trees. Other parameters of Adaboost, Bagging RF are kept to their default values in R-project packages, “randomForest” and “adabag”. All the presented results are averaged over 10 independent runs of the algorithm.
4.1. Evaluative Performance Metrics
Accuracy is commonly used as a performance metric for measuring the performance of a classifier model. However, overall accuracy has proven not suitable in class imbalance research. Therefore, we adopt , , , F— and G— as performance measures in our experiments [4].
- Overall accuracy(OA) measures the true prediction rate.where L stands for the number of classes and is the number of the training set. Recall is per class accuracy and can be defined as (10).
- Average accuracy(AA) gives the same weight to each of the classes of the problem. It can be calculated according to the following equation:
- F-Measure is one of the most popular methods to evaluate the performance of a classifier for imbalance data. It can be calculated according to the following equation.where can be computed by .
- G-mean is another method to evaluate the performance of a classifier for imbalance data.
4.2. Data Information
The proposed DRF is evaluated on three standard hyperspectral images, Indian Pines AVRIS, University of Pavia ROSIS, and Salinas.
- (1)
- Indian Pines AVRIS is highly imbalanced and composed of 145 × 145 pixels, with a spatial resolution of 20 m/pixel and 200 spectral bands. The reference data with 16 classes are composed of 10,249 samples.
- (2)
- University of Pavia ROSIS consists of 610 × 340 pixels, and 103 spectral bands. The spatial resolution of this data is 1.3 m/pixel. The reference data is with 9 classes and is composed of 42,776 instances.
- (3)
- Salinas consists of 512 × 217 pixels with a spatial resolution of 3.7 m/pixel. The data has 224 spectral bands. The reference data is with 16 classes and is composed of 54,129 instances.
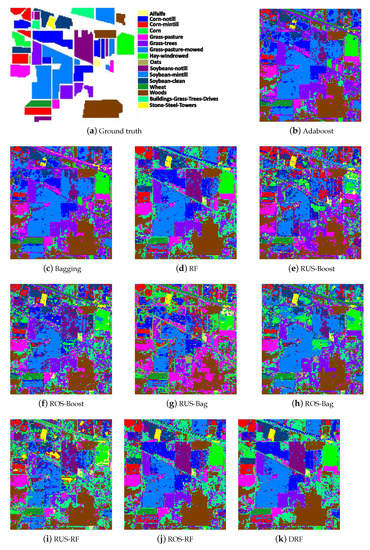
Figure 3.
Ground truth, classification maps of Adaboost, Bagging, random forest, random undersampling combined, random oversampling combined Adaboost, Bagging, and random forest, and the proposed double random forest DRF, on the hyperspectral data Salinas.

Figure 4.
Ground truth, classification maps of Adaboost, Bagging, random forest, random undersampling combined, random oversampling combined Adaboost, Bagging, and random forest, and the proposed double random forest DRF, on the hyperspectral data University.
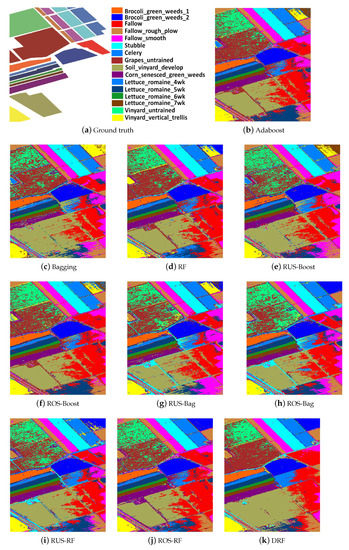
Figure 5.
Ground truth, classification maps of Adaboost, Bagging, random forest, random undersampling combined, random oversampling combined Adaboost, Bagging, and random forest, and the proposed double random forest DRF, on the hyperspectral data Salinas.
The data sampling is used to divide the reference data set into two non-overlapping parts: the training set and the test set. A total of 5% of their instances are selected randomly from original reference data to construct training sets. All the unselected instances are test sets. More details of the data information are presented in Table 1.

Table 1.
Data information.
4.3. Results and Analysis
This section shows the performance of the proposed DRF method. The objective of this section is as follows:
- 1
- Present the performance of DRF in dealing with the hyperspectral datasets.
- 2
- Compare the performance of DRF with data sampling methods.
- 3
- Analyze the parameter sensitivity of the proposed DRF methods.
Table 2, Table 3 and Table 4 present the AA, OA, F-measure, and Gmean results of the Adaboost, Bagging, traditional RF, two data sampling combined Adaboost, Bagging, and RF methods, as well as the proposed DRF on the hyperspectral images Indian Pines AVRIS, University of Pavia ROSIS and Salinas, respectively. The best results in all tables are highlighted in bold font. The experimental results in those tables show that Adaboost could obtain better results than the Bagging and the traditional RF. Both Bagging and RF biases in the classification of majority classes. In addition, resampling methods are useful to improve the performances of the ensemble models, especially Adaboost and Bagging, for the hyperspectral remote sensing data classification. Oversampling tends to outperform the undersampling reference strategies, which manifested in the average ranks concerning all of the performance metrics for oversampling-based methods. The undersampling can discard potentially useful data. Furthermore, The proposed DRF algorithm achieved a statistically significantly better performance than all the reference methods. In other means, DRF could obtain better results in dealing with high-dimensional imbalanced data than simple data sampling methods. The feature importance is helpful to improve the performance of the ensemble-based imbalance learning method. On the data set University of Pavia ROSIS, with respect to Adaboost, Bagging, RF, RUS-RF and ROS-RF, the best increases in AA are over 6%, 24%, 7%, 10%, 6%, and the best increases in OA are over 4%, 13% 6%, 22%, 4%. Moreover, the results of the F-measure and Gmean of three reference data also demonstrate the better performance of DRF when compared with other methods.

Table 2.
Classification results (%) of the Indian image, respectively, obtained by Adaboost, Bagging, RF, RUS + Adaboost, ROS + Adaboost, RUS + Bagging, ROS + Bagging, RUS-RF, ROS-RF, and the proposed DRF.

Table 3.
Classification results (%) of the University of Pavia ROSIS image, respectively, obtained by Adaboost, Bagging, RF, RUS + Adaboost, ROS + Adaboost, RUS + Bagging, ROS + Bagging, RUS-RF, ROS-RF, and the proposed DRF.

Table 4.
Classification results (%) of the Salinas image, respectively, obtained by Adaboost, Bagging, RF, RUS + Adaboost, ROS + Adaboost, RUS + Bagging, ROS + Bagging, RUS-RF, ROS-RF, and the proposed DRF.
For a more intuitive comparison of the proposed DRF algorithm and the other nine reference methods, the categorization map is adopted in our experiment. Figure 3, Figure 4 and Figure 5, respectively, exhibit the classification maps obtained by ten classification methods for Indian Pines AVRIS, University of Pavia ROSIS, and Salinas images. Those figures show that DRF could result in more accurate cartography with respect to Adaboost, Bagging, RF, and other improved ensemble methods. According to the map results, we find that the proposed algorithm can improve the classification accuracy of small class samples while maintaining the overall accuracy. This effect is especially pronounced in Indian data. This conclusion is consistent with the descriptions for the above tables.
The computational complexity of our proposal arises mainly from two sources: the feature importance calculation and the building of the double ensemble model. The computational cost of building a decision tree is where N is the number of the training set and D is the number of the features. The complexity of random forests with T base classifiers is . In the feature importance calculation process, only one random forest is built. Hence, the complexity of this step is . In double ensemble model building, because the individual classifiers are trained simultaneously, the computational complexity will be similar to that of a random forest. However, only features are used. Then the computational complexity of the second step is . In our proposal, because all of the positive patterns are used for training in each balanced individual training set, N is approximate twice the size of the positive samples. Therefore, the overall computational complexity of our proposal is . Although the training complexity of the framework is a little higher than the random forest, it is normal in dealing with the imbalanced data. In addition, because the produced training set is with low dimension, the proposed method has lower computational complexity than the reference imbalance learning method.
4.4. Parameter Analysis
In order to study the influence of feature size, we present in Figure 1b,c the evaluation of the average accuracy, overall accuracy, G-mean, and F-measure for the proposed method on the University of Pavia ROSIS and Salinas. In this experiment, the size T of the ensemble is still set to 100 and the tested number of feature set is set as (20, 40, 60, 80, 100) and (20, 40, 60, 80, 100, 120, 140, 160, 180, 200, 220). Figure 6 shows that DRF results in the best result when the feature size is 40 for University of Pavia ROSIS and 60 for Salinas. In other words, the proposed DRF could show superior performance with a small feature set, thus reducing the computation complexity obviously.
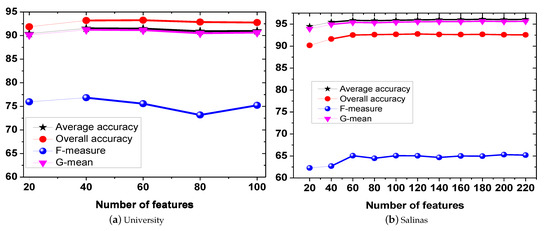
Figure 6.
Performances of the proposed method measured by , , F— and G— with respect to the number of features on hyperspectral data sets University and Salinas.
5. Discussion
- 1
- The proposed algorithm is effective for multi-class imbalanced hyperspectral remote sensing data. It could increase the robustness of the ensemble method to skewed distributions. Out of the examined methods, the proposed ensemble method, when combined with different information about instance-level difficulties, offers the best performance regardless of the used metric. The standard version of random forest is considered unsuitable for class imbalanced hyperspectral remote sensing data, as it underperformed when compared with random resampling methods.
- 2
- By analyzing the behaviors of single random undersampling or oversampling, we are able to identify the weak spot of the data level methods. As data in each base classifier is selected randomly, resampling performs locally correct oversampling that does not translate to the global characteristics of data. This could lead to increased overlapping among classes. Our proposed method used both feature selection and data sampling. This eliminated the drawbacks of single data resampling in the high dimensional data processing.
- 3
- The analysis of instance-level difficulties in multi-class imbalanced data allowed for a better understanding of each considered classification problem [17]. This paper adopts two popular data resampling methods and focuses on enhancing the presence of the most difficult instances. Although this could lead to improvements for the traditional random forest algorithm, the operation is unsuitable for hyperspectral remote sensing data.
- 4
- In our experiments, we analyzed the effect of feature parameters with the double ensemble algorithm. The results show that the proposed method is insensitive to the number of features. That means the proposed method has a good generalization ability.
6. Conclusions
In this paper, we proposed a novel double ensemble method to deal with multi-class imbalanced datasets. The proposed DRF method consists of two key steps: the feature importance measure of a balanced training dataset, and oversampling-based ensemble random forest model. The proposed DRF method aims to improve the classification performance in the case of high-dimensional multi-class imbalance problems. Experiments are conducted using two popular multi-class imbalanced hyperspectral datasets. The performance obtained by the proposed method is compared with five state-of-the-art techniques Experimental results demonstrated that the proposed DRF outperforms the other techniques in the multi-class imbalanced datasets and could decrease the computation complexity. The proposed method provides a direction for the big class imbalanced data learning.
Compared with random forest, the algorithm in this paper has slightly higher computational complexity. Therefore, in future work, we plan to optimize the structure of the algorithm to reduce the training time of the model.
Author Contributions
D.Q. and W.F. conceived and designed the experiments; W.F. performed the experiments. X.W. and M.X. edited the manuscript. G.D. and W.H. were responsible for validating the experimental conclusions and reviewing the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Natural Science Foundation of Zhejiang Province (LQ20F020021).
Acknowledgments
This work is supported by Zhejiang Provincial Natural Science Foundation (LQ20F020021).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Cao, X.; Yao, J.; Xu, Z.; Meng, D. Hyperspectral Image Classification with Convolutional Neural Network and Active Learning. IEEE Trans. Geosci. Remote Sens. 2020, 58, 4604–4616. [Google Scholar] [CrossRef]
- Li, S.; Song, W.; Fang, L.; Chen, Y.; Ghamisi, P.; Benediktsson, J. Deep Learning for Hyperspectral Image Classification: An Overview. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6690–6709. [Google Scholar] [CrossRef] [Green Version]
- Yang, J.; Wu, C.; Du, B.; Zhang, L. Enhanced Multiscale Feature Fusion Network for HSI Classification. IEEE Trans. Geosci. Remote Sens. 2021, 59, 10328–10347. [Google Scholar] [CrossRef]
- Feng, W.; Huang, W.; Ren, J. Class Imbalance Ensemble Learning Based on the Margin Theory. Appl. Sci. 2018, 8, 815. [Google Scholar] [CrossRef] [Green Version]
- Paoletti, M.; Haut, J.; Plaza, J.; Plaza, A. Deep learning classifiers for hyperspectral imaging: A review. ISPRS J. Photogramm. Remote Sens. 2019, 158, 279–317. [Google Scholar] [CrossRef]
- Tao, C.; Pan, H.; Li, Y.; Zou, Z. Unsupervised Spectral-patial Feature Learning with Stacked Sparse Autoencoder for Hyperspectral Imagery Classification. IEEE Geosci. Remote Sens. Lett. 2015, 12, 2438–2442. [Google Scholar] [CrossRef]
- He, Z.; Liu, H.; Wang, Y.; Hu, J. Generative Adversarial Networks-Based Semi-Supervised Learning for Hyperspectral Image Classification. Remote Sens. 2017, 9, 1042. [Google Scholar] [CrossRef] [Green Version]
- Garcia, S.; Zhang, Z.; Altalhi, A.; Alshomrani, S.; Herrera, F. Dynamic ensemble selection for multi-class imbalanced datasets. Inf. Sci. 2018, 445-446, 22–37. [Google Scholar] [CrossRef]
- Sun, T.; Jiao, L.; Feng, J.; Liu, F.; Zhang, X. Imbalanced Hyperspectral Image Classification Based on Maximum Margin. IEEE Geosci. Remote Sens. Lett. 2015, 12, 522–526. [Google Scholar] [CrossRef]
- Feng, W.; Huang, W.; Bao, W. Imbalanced Hyperspectral Image Classification with an Adaptive Ensemble Method Based on SMOTE and Rotation Forest with Differentiated Sampling Rates. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1879–1883. [Google Scholar] [CrossRef]
- Zhu, J.; Fang, L.; Ghamisi, P. Deformable Convolutional Neural Networks for Hyperspectral Image Classification. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1254–1258. [Google Scholar] [CrossRef]
- Roy, S.K.; Haut, J.M.; Paoletti, M.E.; Dubey, S.R.; Plaza, A. Generative Adversarial Minority Oversampling for Spectral-patial Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1695–1704. [Google Scholar] [CrossRef]
- Wang, S.; Yao, X. Diversity analysis on imbalanced data sets by using ensemble models. In Proceedings of the IEEE Symposium on Computational Intelligence and Data Mining, Nashville, TN, USA, 30 March–2 April 2009; pp. 324–331. [Google Scholar]
- Krawczyk, B. Learning from imbalanced data: Open challenges and future directions. In Progress in Artificial Intelligence; U.S. Department of Energy: Washington, DC, USA, 2016; pp. 221–232. [Google Scholar]
- Saez, J.A.; Krawczyk, B.; Wozniak, M. Analyzing the oversampling of different classes and types of examples in multi-class imbalanced datasets. Pattern Recognit. 2016, 57, 164–178. [Google Scholar] [CrossRef]
- Bi, J.; Zhang, C. An empirical comparison on state-of-the-art multi-class imbalance learning algorithms and a new diversified ensemble learning scheme. Knowl. Based Syst. 2018, 158, 81–93. [Google Scholar] [CrossRef]
- William, I.V.; Krawczyk, B. Multi-class imbalanced big data classification on Spark. Knowl. Based Syst. 2020, 212, 106598. [Google Scholar]
- Dietterich, T. Ensemble Methods in Machine Learning. In Proceedings of the 1st International Workshop on Multiple Classifier Systems, Cagliari, Italy, 21–23 June 2000; pp. 1–15. [Google Scholar]
- Feng, W.; Quan, Y.; Dauphin, G.; Li, Q.; Gao, L.; Huang, W.; Xia, J.; Zhu, W.; Xing, M. Semi-supervised rotation forest based on ensemble margin theory for the classification of hyperspectral image with limited training data. Inf. Sci. 2021, 575, 611–638. [Google Scholar] [CrossRef]
- Feng, W.; Quan, Y.; Dauphin, G. Label Noise Cleaning with an Adaptive Ensemble Method Based on Noise Detection Metric. Sensors 2020, 20, 6718. [Google Scholar] [CrossRef]
- Quan, Y.; Zhong, X.; Feng, W.; Chan, C.W.; Xing, M. SMOTE-Based Weighted Deep Rotation Forest for the Imbalanced Hyperspectral Data Classification. Remote Sens. 2021, 13, 464. [Google Scholar] [CrossRef]
- Ribeiro, V.; Reynoso-Meza, G. Ensemble learning by means of a multi-objective optimization design approach for dealing with imbalanced data sets. Expert Syst. Appl. 2020, 147, 113232. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, Z.; Zhu, Y.; Zhang, J.; Li, D. Multi-matrices entropy discriminant ensemble learning for imbalanced problem. Neural Comput. Appl. 2020, 32, 8245–8264. [Google Scholar] [CrossRef]
- Chen, Z.; Duan, J.; Kang, L.; Qiu, G. A Hybrid Data-Level Ensemble to Enable Learning from Highly Imbalanced Dataset. Inf. Sci. 2020, 554, 157–176. [Google Scholar] [CrossRef]
- Wang, Z.; Jia, P.; Xu, X.; Wang, B.; Li, D. Sample and feature selecting based ensemble learning for imbalanced problems. Appl. Soft Comput. 2021, 113, 107884. [Google Scholar] [CrossRef]
- Qin, W.; Zhuang, Z.L.; Guo, L.; Sun, Y. A hybrid multi-class imbalanced learning method for predicting the quality level of diesel engines. J. Manuf. Syst. 2021, 62, 846–856. [Google Scholar] [CrossRef]
- Cmv, A.; Jie, D.B. Accurate and efficient sequential ensemble learning for highly imbalanced multi-class data—ScienceDirect. Neural Netw. 2020, 128, 268–278. [Google Scholar]
- Chao, L.; Jiang, D.; Yang, W. Global geometric similarity scheme for feature selection in fault diagnosis. Expert Syst. Appl. 2014, 41, 3585–3595. [Google Scholar]
- Richhariya, B.; Tanveer, M. A reduced universum twin support vector machine for class imbalance learning. Pattern Recognit. 2020, 102, 107150. [Google Scholar] [CrossRef]
- Shahee, S.A.; Ananthakumar, U. An effective distance based feature selection approach for imbalanced data. Appl. Intell. 2020, 50, 717–745. [Google Scholar] [CrossRef]
- Chennuru, V.K.; Timmappareddy, S.R. Simulated annealing based undersampling (SAUS): A hybrid multi-objective optimization method to tackle class imbalance. Appl. Intell. 2021, 52, 2092–2110. [Google Scholar] [CrossRef]
- Lv, Q.; Feng, W.; Quan, Y.; Dauphin, G.; Gao, L.; Xing, M. Enhanced-Random-Feature-Subspace-Based Ensemble CNN for the Imbalanced Hyperspectral Image Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 3988–3999. [Google Scholar] [CrossRef]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic Minority Oversampling Technique. J. Artif. Intell. Res. 2004, 16, 321–357. [Google Scholar] [CrossRef]
- Feng, W.; Boukir, S.; Huang, W. Margin-Based Random Forest for Imbalanced Land Cover Classification. In Proceedings of the IGARSS 2019—2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019. [Google Scholar]
- Engelmann, J.; Lessmann, S. Conditional Wasserstein GAN-based Oversampling of Tabular Data for Imbalanced Learning. Expert Syst. Appl. 2021, 174, 114582. [Google Scholar] [CrossRef]
- Xu, Z.; Shen, D.; Nie, T.; Kou, Y.; Han, X. An oversampling algorithm combining SMOTE and k-means for imbalanced medical data. Inf. Sci. 2021, 572, 574–589. [Google Scholar] [CrossRef]
- Sun, Y.; Kamel, M.S.; Wong, A.K.; Wang, Y. Cost-sensitive boosting for classification of imbalanced data. Pattern Recognit. 2007, 40, 3358–3378. [Google Scholar] [CrossRef]
- Ertekin, S.; Huang, J.; Bottou, L.; Giles, C.L. Learning on the border: Active learning in imbalanced data classification. In Proceedings of the CIKM (Conference on Information and Knowledge Management); Silva, M.J., Laender, A.H.F., Baeza-Yates, R.A., McGuinness, D.L., Olstad, B., Olsen, H., Falcao, A.O., Eds.; ACM: New York, NY, USA, 2007; pp. 127–136. [Google Scholar]
- Feng, W.; Dauphin, G.; Huang, W.; Quan, Y.; Li, Q. Dynamic Synthetic Minority Over-Sampling Technique-Based Rotation Forest for the Classification of Imbalanced Hyperspectral Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, PP, 2159–2169. [Google Scholar] [CrossRef]
- Liu, W.; Zhang, H.; Ding, Z.; Liu, Q.; Zhu, C. A comprehensive active learning method for multiclass imbalanced data streams with concept drift—ScienceDirect. Knowl. Based Syst. 2021, 215, 106778. [Google Scholar] [CrossRef]
- Lango, M.; Stefanowski, J. What makes multi-class imbalanced problems difficult? An experimental study. Expert Syst. Appl. 2022, 199, 116962. [Google Scholar] [CrossRef]
- Abdi, L.; Hashemi, S. To combat multi-class imbalanced problems by means of oversampling and boosting techniques. Soft Comput. 2015, 19, 3369–3385. [Google Scholar] [CrossRef]
- Janicka, M.; Lango, M.; Stefanowski, J. Using Information on Class Interrelations to Improve Classification of Multiclass Imbalanced Data: A New Resampling Algorithm. Int. J. Appl. Math. Comput. Sci. 2019, 29, 769–781. [Google Scholar] [CrossRef] [Green Version]
- Freund, Y.; Schapire, R. A decision-theoretic generalization of on-line learning and an application to boosting. J. Comput. Syst. Sci. 1997, 55, 119–139. [Google Scholar] [CrossRef] [Green Version]
- Soui, M.; Mansouri, N.; Alhamad, R.; Kessentini, M.; Ghedira, K. NSGA-II as feature selection technique and AdaBoost classifier for COVID-19 prediction using patient’s symptoms. Nonlinear Dyn. 2021, 106, 1453–1475. [Google Scholar] [CrossRef]
- Wang, S.; Yao, X. Multiclass Imbalance Problems: Analysis and Potential Solutions. IEEE Trans. Syst. Man Cybern. Part Cybern. 2012, 42, 1119–1130. [Google Scholar] [CrossRef] [PubMed]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Z.H. Ensemble Methods: Foundations and Algorithms; Chapman and Hall/CRC: Boca Raton, FL, USA, 2012; p. 236. [Google Scholar]
- Khoshgoftaar, T.M.; Hulse, J.V.; Napolitano, A. Comparing Boosting and Bagging Techniques with Noisy and Imbalanced Data. IEEE Trans. Syst. Man Cybern. Part Syst. Humans 2011, 41, 552–568. [Google Scholar] [CrossRef]
- Galar, M.; Fernandez, A.; Barrenechea, E.; Bustince, H.; Herrera, F. A Review on Ensembles for the Class Imbalance Problem: Bagging-, Boosting-, and Hybrid-Based Approaches. IEEE Trans. Syst. Man Cybern. Part Appl. Rev. 2012, 42, 463–484. [Google Scholar] [CrossRef]
- Liu, X.Y.; Zhou, Z.H. Ensemble Methods for Class Imbalance Learning. In Imbalanced Learning: Foundations, Algorithms and Applications; He, H., Ma, Y., Eds.; Wiley-IEEE Press: River Street Hoboken, NJ, USA, 2013; pp. 61–82. [Google Scholar]
- Blaszczyński, J.; Stefanowski, J.; Idkowiak, L. Extending Bagging for Imbalanced Data. In Proceedings of the Eighth CORES (Core Ordering and Reporting Enterprise System); Springer: Berlin/Heidelberg, Germany, 2013; Volume 226, pp. 269–278. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Thanathamathee, P.; Lursinsap, C. Handling imbalanced data sets with synthetic boundary data generation using bootstrap re-sampling and AdaBoost techniques. Pattern Recognit. Lett. 2013, 34, 1339–1347. [Google Scholar] [CrossRef]
- Diez-Pastor, J.; Rodriguez, J.; Garcia-Osorio, C.; Kuncheva, L.I. Random Balance: Ensembles of variable priors classifiers for imbalanced data. Knowl. Based Syst. 2015, 85, 96–111. [Google Scholar] [CrossRef]
- Barandela, R.; Sanchez, J.S.; Valdovinos, R.M. New Applications of Ensembles of Classifiers. Pattern Anal. Appl. 2003, 6, 245–256. [Google Scholar] [CrossRef]
- Blaszczynski, J.; Stefanowski, J. Neighbourhood sampling in Bagging for imbalanced data. Neurocomputing 2015, 150, 529–542. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).