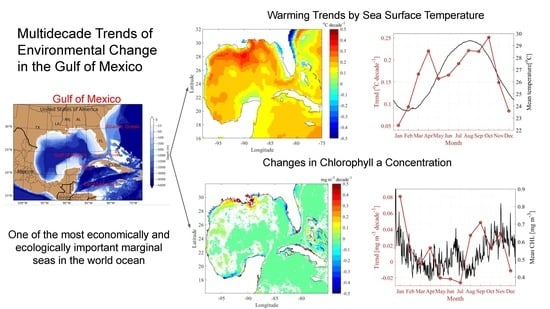
Multidecade Trends of Sea Surface Temperature, Chlorophyll-a Concentration, and Ocean Eddies in the Gulf of Mexico
Abstract
:1. Introduction
2. Materials and Methods
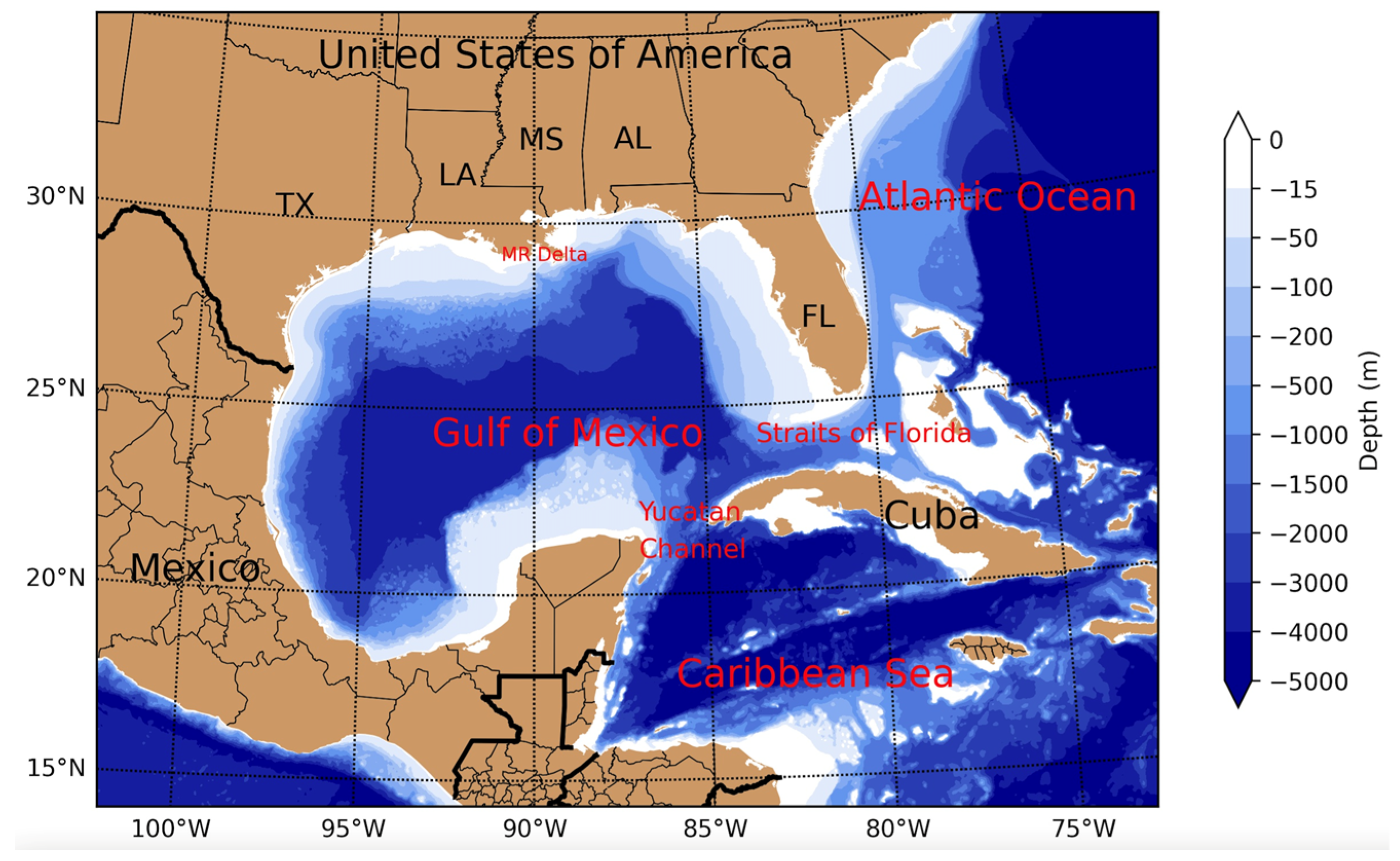
2.1. Study Area
2.2. Data
2.3. Method
2.3.1. Linear Regression and Monthly Downsample Analysis
2.3.2. Phenology Analysis
2.3.3. Energetic Features of Ocean Eddies
- (1)
- Vorticity:
- (2)
- Swirling strength [36]:
- (3)
- Okubo–Weiss parameter [38]:where and are normal and shear strain, respectively.
2.3.4. Source of Error
3. Results and Discussion
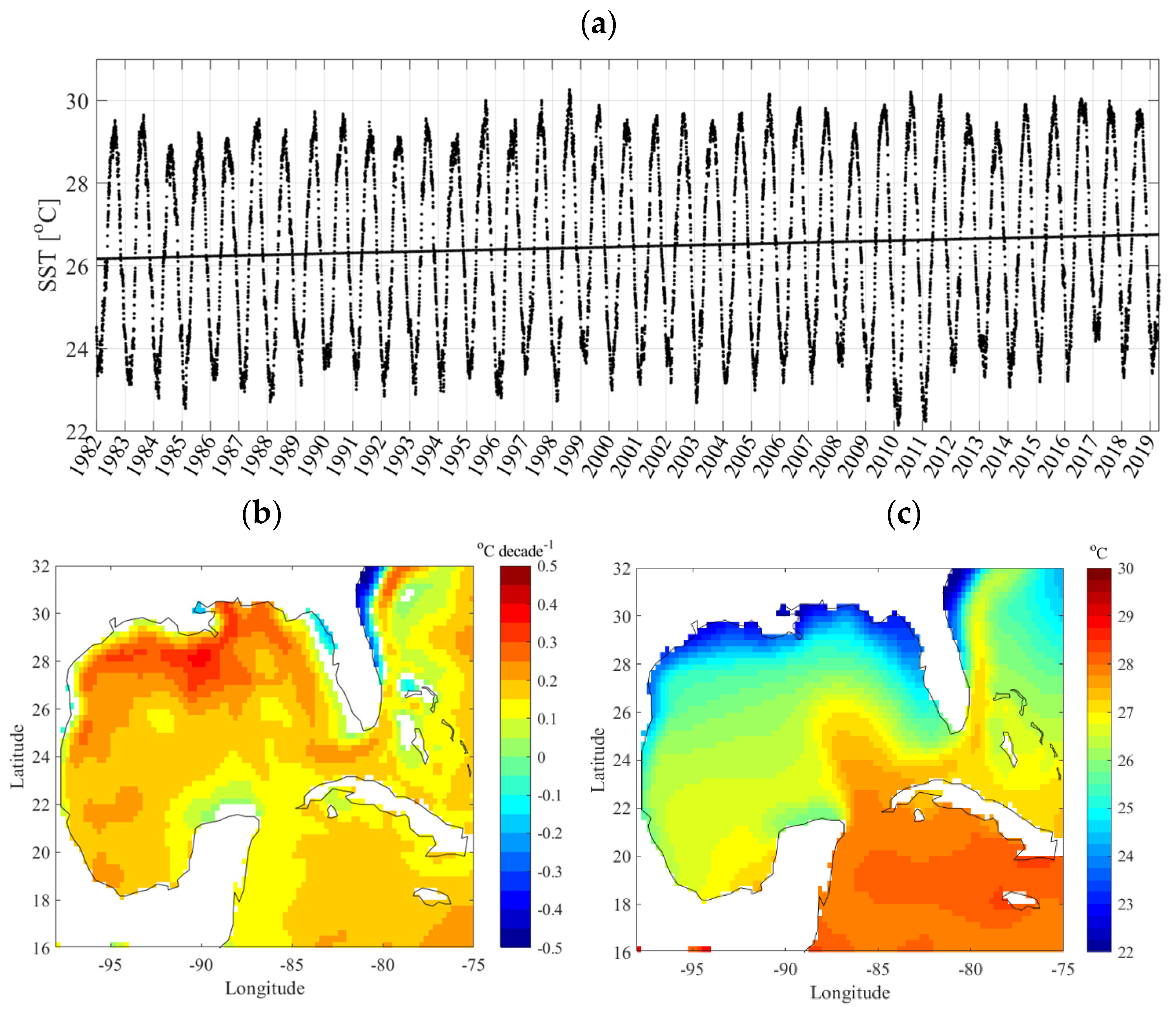
3.1. Sea Surface Temperature
3.1.1. Overall Linear Trend
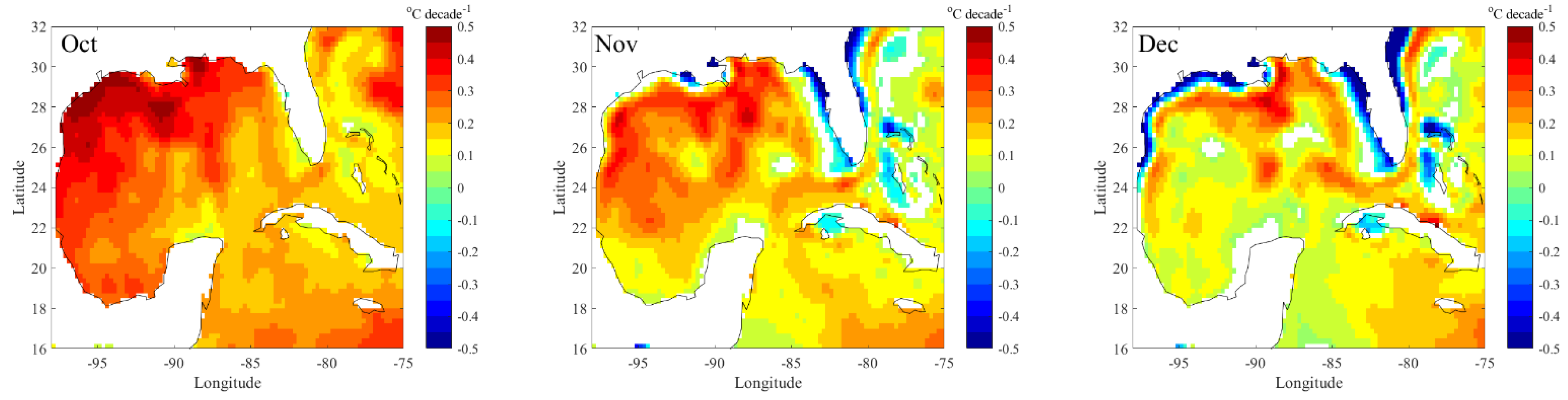
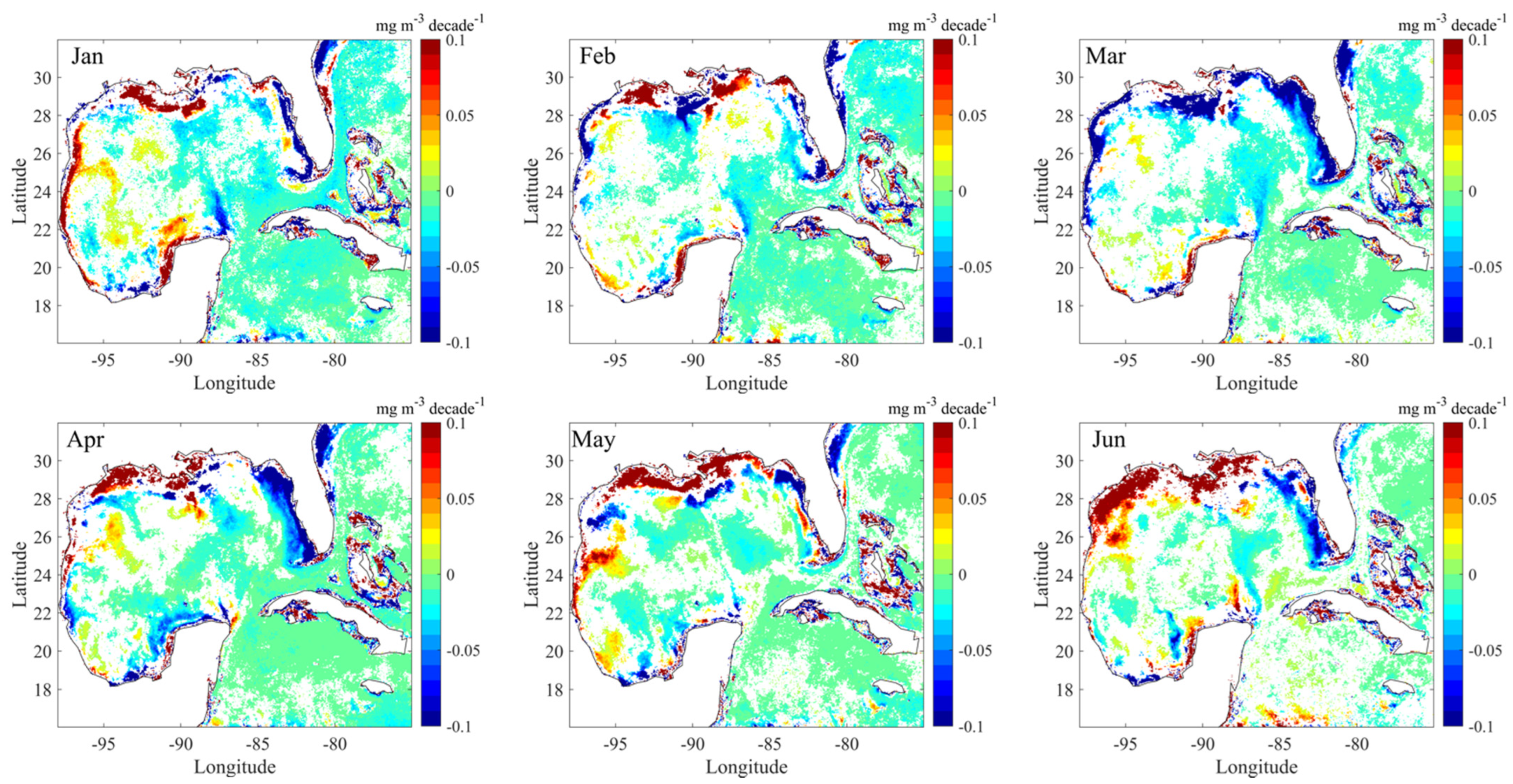
3.1.2. Month-Specific Trend
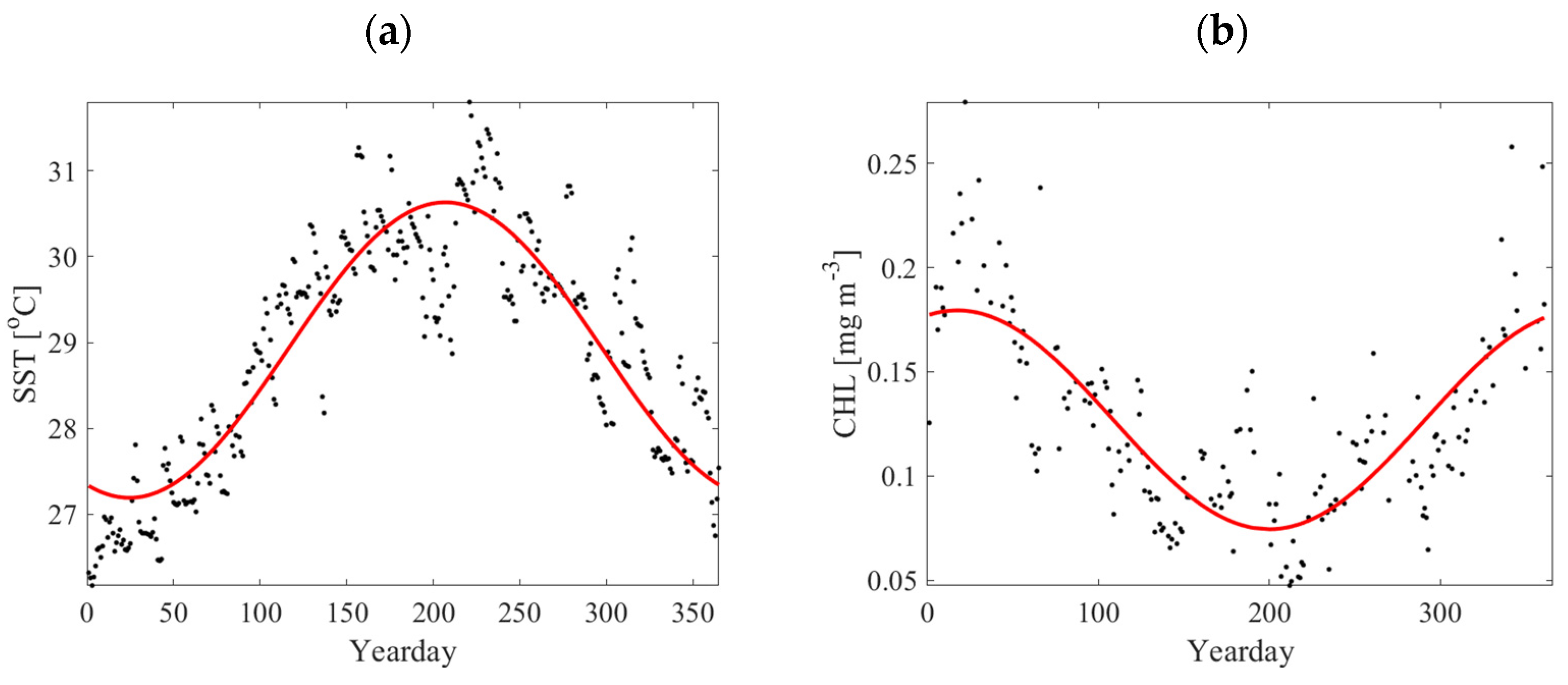
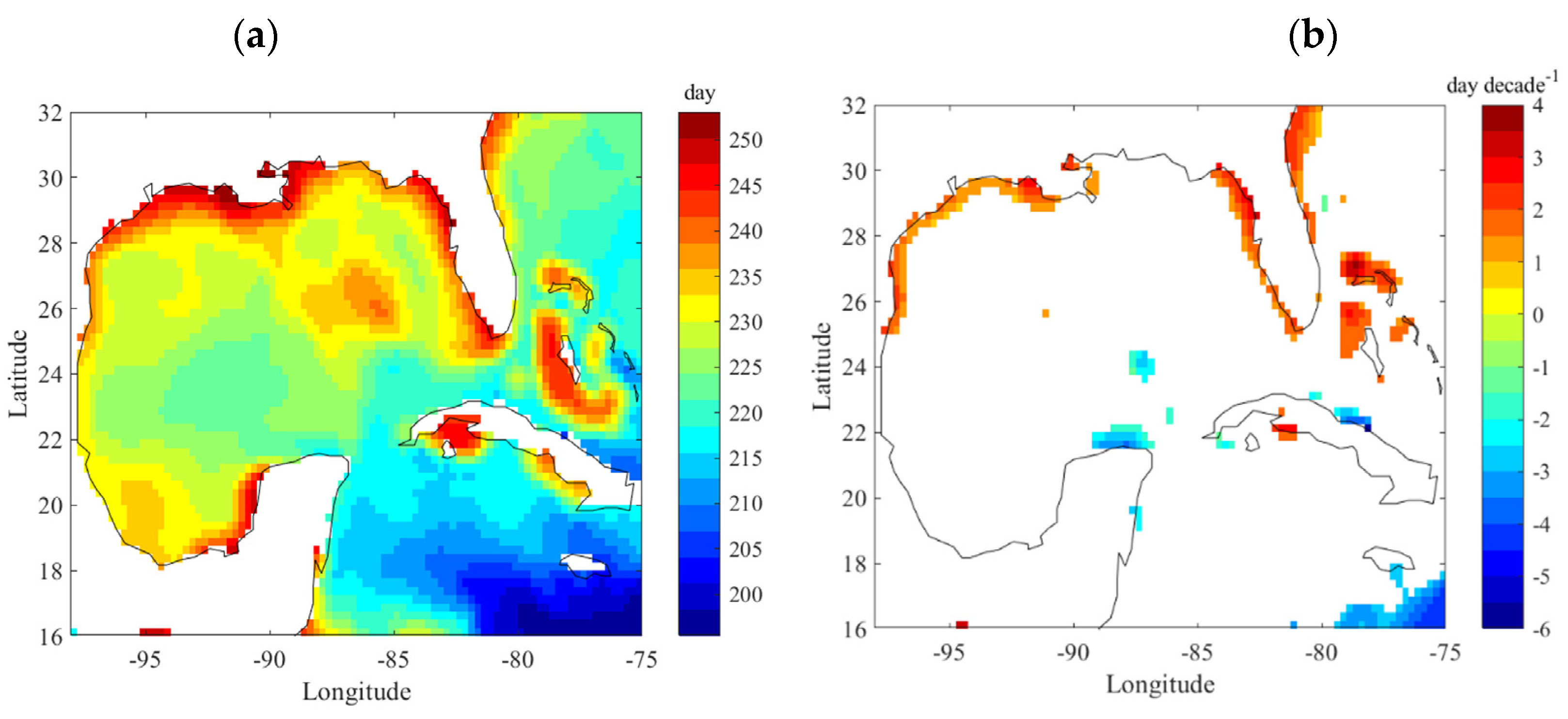
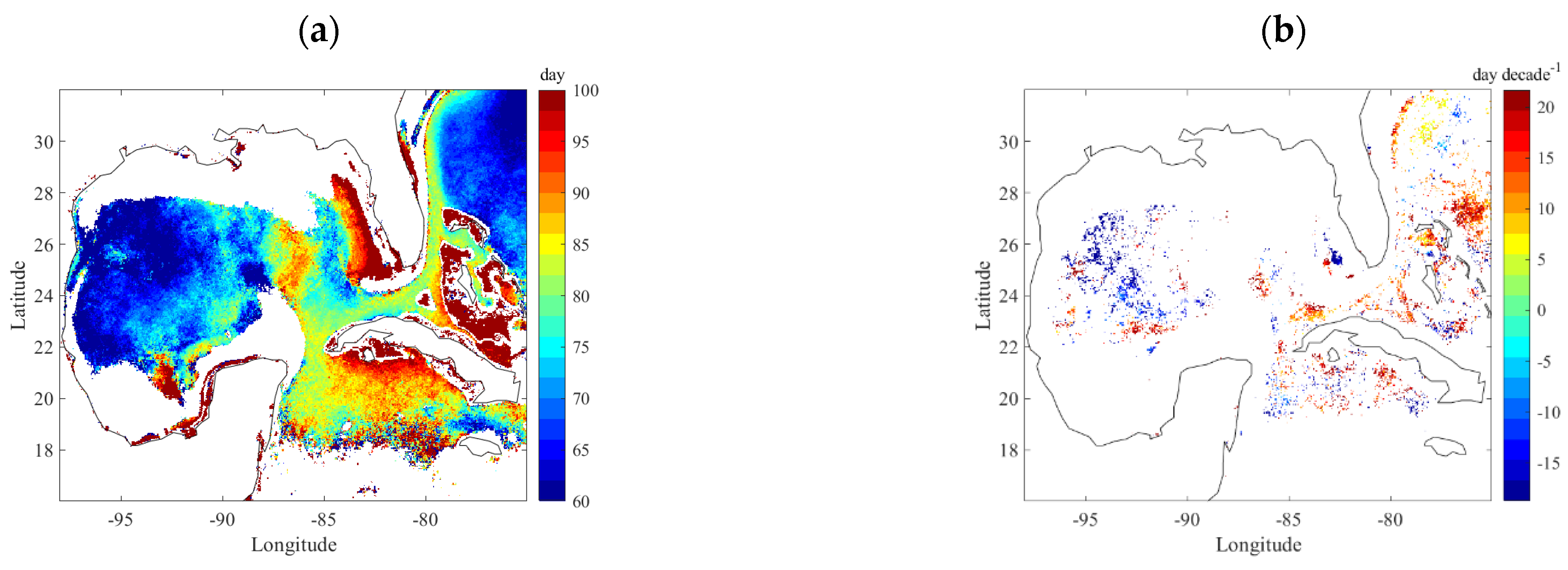
3.1.3. Phonology Changes
3.2. Chlorophyll-a
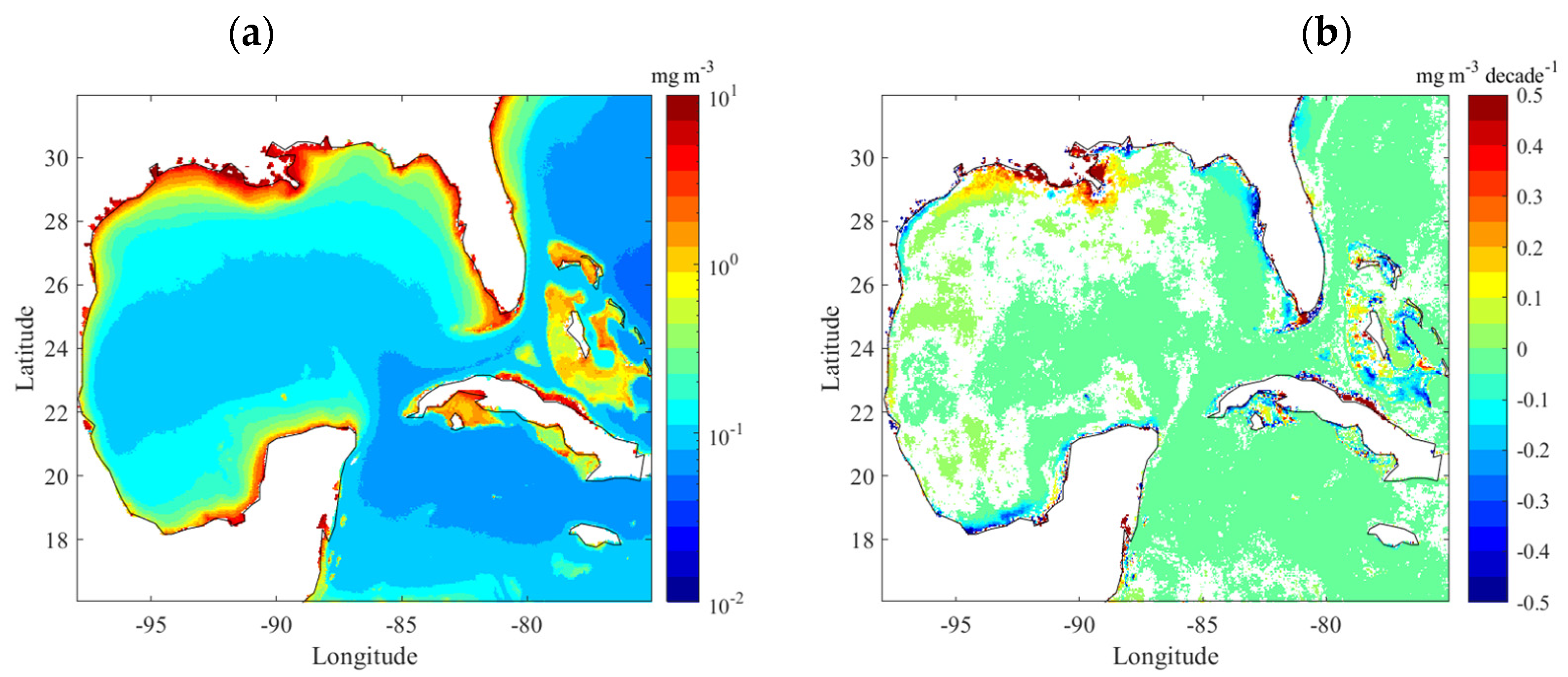
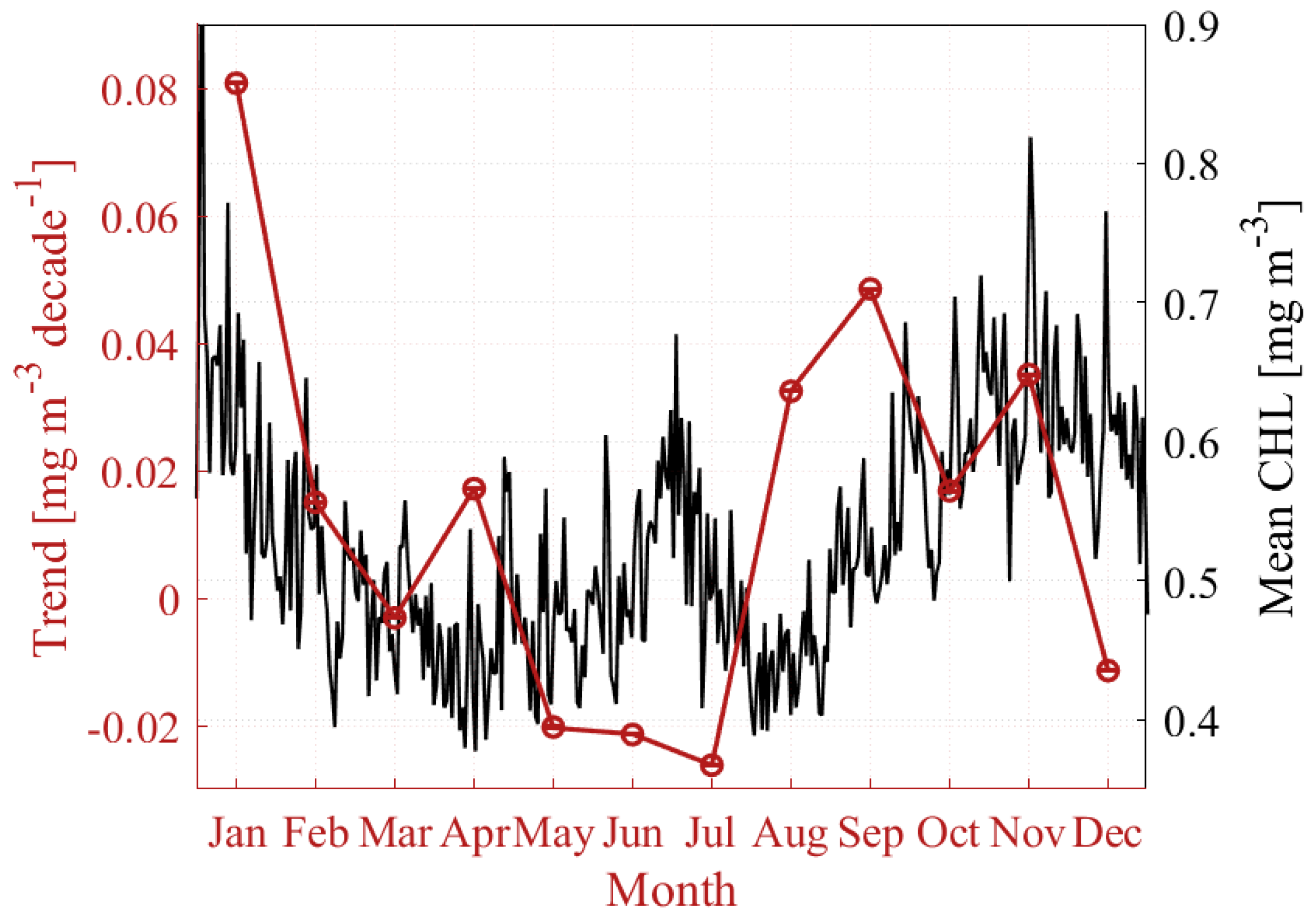
3.2.1. Mean Concentration and Trend
3.2.2. Phase and Phase Shift
3.3. Eddy-Related Energetic Features
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- McCarthy, G.D.; Haigh, I.D.; Hirschi, J.J.-M.; Grist, J.P.; Smeed, D.A. Ocean impact on decadal Atlantic climate variability revealed by sea-level observations. Nature 2015, 521, 508–510. [Google Scholar] [CrossRef] [Green Version]
- Spies, R.B.; Senner, S.; Robbins, C.S. An overview of the northern Gulf of Mexico ecosystem. Gulf Mex. Sci. 2016, 33, 9. [Google Scholar] [CrossRef]
- Saunders, M.A.; Lea, A.S. Large contribution of sea surface warming to recent increase in Atlantic hurricane activity. Nature 2008, 451, 557–560. [Google Scholar] [CrossRef]
- Dunstan, P.K.; Foster, S.D.; King, E.; Risbey, J.; O’Kane, T.J.; Monselesan, D.; Hobday, A.J.; Hartog, J.R.; Thompson, P.A. Global patterns of change and variation in sea surface temperature and chlorophyll a. Sci. Rep. 2018, 8, 14624. [Google Scholar] [CrossRef] [Green Version]
- Muhling, B.A.; Lee, S.-K.; Lamkin, J.T.; Liu, Y. Predicting the effects of climate change on bluefin tuna (Thunnus thynnus) spawning habitat in the Gulf of Mexico. ICES J. Mar. Sci. 2011, 68, 1051–1062. [Google Scholar] [CrossRef] [Green Version]
- Glenn, E.; Comarazamy, D.; González, J.E.; Smith, T. Detection of recent regional sea surface temperature warming in the Caribbean and surrounding region. Geophys. Res. Lett. 2015, 42, 6785–6792. [Google Scholar] [CrossRef]
- Muller-Karger, F.E.; Smith, J.P.; Werner, S.; Chen, R.; Roffer, M.; Liu, Y.; Muhling, B.; Lindo-Atichati, D.; Lamkin, J.; Cerdeira-Estrada, S.; et al. Natural variability of surface oceanographic conditions in the offshore Gulf of Mexico. Prog. Oceanogr. 2015, 134, 54–76. [Google Scholar] [CrossRef] [Green Version]
- Müller-Karger, F.E.; Walsh, J.J.; Evans, R.H.; Meyers, M.B. On the seasonal phytoplankton concentration and sea surface temperature cycles of the Gulf of Mexico as determined by satellites. J. Geophys. Res. Ocean. 1991, 96, 12645–12665. [Google Scholar] [CrossRef] [Green Version]
- Behrenfeld, M.J.; O’Malley, R.T.; Boss, E.S.; Westberry, T.K.; Graff, J.R.; Halsey, K.H.; Milligan, A.J.; Siegel, D.A.; Brown, M.B. Revaluating ocean warming impacts on global phytoplankton. Nat. Clim. Chang. 2016, 6, 323–330. [Google Scholar] [CrossRef]
- Wang, Z.; Boyer, T.; Reagan, J.; Hogan, P. Upper Oceanic Warming in the Gulf of Mexico between 1950 and 2020. In Proceedings of the GoMCon, Baton Rouge, LA, USA, 25–28 April 2022. [Google Scholar]
- Ochoa, J.; Ferreira-Bartrina, V.; Candela, J.; Sheinbaum, J.; López, M.; Pérez-Brunius, P.; Herzka, S.; Amon, R.M. Deep-Water Warming in the Gulf of Mexico from 2003 to 2019. J. Phys. Oceanogr. 2021, 51, 1021–1035. [Google Scholar] [CrossRef]
- Nowlin Jr, W.; Hubertz, J.; Reid, R. A detached eddy in the Gulf of Mexico. J. Mar. Res 1968, 26, 185–186. [Google Scholar]
- Brokaw, R.J.; Subrahmanyam, B.; Trott, C.B.; Chaigneau, A. Eddy surface characteristics and vertical structure in the Gulf of Mexico from satellite observations and model simulations. J. Geophys. Res. Ocean. 2020, 125, e2019JC015538. [Google Scholar] [CrossRef]
- Sturges, W.; Leben, R. Frequency of ring separations from the loop current in the Gulf of Mexico: A revised estimate. J. Phys. Oceanogr. 2000, 30, 1814–1819. [Google Scholar] [CrossRef]
- Leben, R.R. Altimeter-Derived Loop Current Metrics; Geophysical Monograph-American Geophysical Union: Washington, DC, USA, 2005. [Google Scholar]
- Chang, Y.L.; Oey, L.Y. Why does the Loop Current tend to shed more eddies in summer and winter? Geophys. Res. Lett. 2012, 39, L05605. [Google Scholar] [CrossRef]
- Fratantoni, P.S.; Lee, T.N.; Podesta, G.P.; Muller-Karger, F. The influence of Loop Current perturbations on the formation and evolution of Tortugas eddies in the southern Straits of Florida. J. Geophys. Res. Ocean. 1998, 103, 24759–24779. [Google Scholar] [CrossRef] [Green Version]
- Cochrane, J. Separation of an anticyclone and subsequent developments in the Loop Current (1969). Contrib. Phys. Oceanogr. Gulf Mex. 1972, 2, 91–106. [Google Scholar]
- Androulidakis, Y.; Kourafalou, V.; Le Hénaff, M. Influence of frontal cyclone evolution on the 2009 (Ekman) and 2010 (Franklin) Loop Current eddy detachment events. Ocean Sci. 2014, 10, 947–965. [Google Scholar] [CrossRef] [Green Version]
- Leben, R. Tracking Loop Current eddies with satellite altimetry. Adv. Space Res. 1993, 13, 325–333. [Google Scholar] [CrossRef]
- Liu, Y.; Weisberg, R.H.; Vignudelli, S.; Mitchum, G.T. Patterns of the loop current system and regions of sea surface height variability in the eastern Gulf of Mexico revealed by the self-organizing maps. J. Geophys. Res. Ocean. 2016, 121, 2347–2366. [Google Scholar] [CrossRef] [Green Version]
- Lewis, J.K.; Kirwan, A.D.; Forristall, G.Z. Evolution of a warm-core ring in the Gulf of Mexico: Lagrangian observations. J. Geophys. Res. 1989, 94, 8163–8178. [Google Scholar] [CrossRef]
- Hamilton, P.; Fargion, G.S.; Biggs, D.C. Loop Current eddy paths in the western Gulf of Mexico. J. Phys. Oceanogr. 1999, 29, 1180–1207. [Google Scholar] [CrossRef]
- Rivas, D.; Badan, A.; Sheinbaum, J.; Ochoa, J.; Candela, J. Vertical velocity and vertical heat flux observed within loop current eddies in the central Gulf of Mexico. J. Phys. Oceanogr. 2008, 38, 2461–2481. [Google Scholar] [CrossRef]
- Putrasahan, D.; Kamenkovich, I.; Le Hénaff, M.; Kirtman, B. Importance of ocean mesoscale variability for air-sea interactions in the Gulf of Mexico. Geophys. Res. Lett. 2017, 44, 6352–6362. [Google Scholar] [CrossRef] [Green Version]
- Brokaw, R.J.; Subrahmanyam, B.; Morey, S.L. Loop current and eddy-driven salinity variability in the Gulf of Mexico. Geophys. Res. Lett. 2019, 46, 5978–5986. [Google Scholar] [CrossRef]
- Damien, P.; Sheinbaum, J.; Pasqueron de Fommervault, O.; Jouanno, J.; Linacre, L.; Duteil, O. Do Loop Current eddies stimulate productivity in the Gulf of Mexico? Biogeosciences 2021, 18, 4281–4303. [Google Scholar] [CrossRef]
- Cardona, Y.; Bracco, A. Predictability of mesoscale circulation throughout the water column in the Gulf of Mexico. Deep Sea Res. Part II Top. Stud. Oceanogr. 2016, 129, 332–349. [Google Scholar] [CrossRef] [Green Version]
- Hamilton, P.; Lee, T.N. Eddies and jets over the slope of the northeast Gulf of Mexico. In Geophysical Monograph Series; American Geophysical Union: Washington, DC, USA, 2005; Volume 161, pp. 123–142. [Google Scholar]
- Androulidakis, Y.; Kourafalou, V.; Le Hénaff, M.; Kang, H.; Sutton, T.; Chen, S.; Hu, C.; Ntaganou, N. Offshore spreading of Mississippi waters: Pathways and vertical structure under eddy influence. J. Geophys. Res. Ocean. 2019, 124, 5952–5978. [Google Scholar] [CrossRef]
- Justić, D.; Kourafalou, V.; Mariotti, G.; He, S.; Weisberg, R.; Androulidakis, Y.; Barker, C.; Bracco, A.; Dzwonkowski, B.; Hu, C. Transport Processes in the Gulf of Mexico Along the River-Estuary-Shelf-Ocean Continuum: A Review of Research from the Gulf of Mexico Research Initiative. Estuaries Coasts 2021, 45, 621–657. [Google Scholar] [CrossRef]
- Sathyendranath, S.; Brewin, B.; Mueller, D.; Doerffer, R.; Krasemann, H.; Mélin, F.; Brockmann, C.; Fomferra, N.; Peters, M.; Grant, M. Ocean colour climate change initiative—Approach and initial results. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 2024–2027. [Google Scholar]
- Lian, T. Uncertainty in detecting trend: A new criterion and its applications to global SST. Clim. Dyn. 2017, 49, 2881–2893. [Google Scholar] [CrossRef] [Green Version]
- Kelly, K.A.; Beardsley, R.C.; Limeburner, R.; Brink, K.H.; Paduan, J.D.; Chereskin, T.K. Variability of the near-surface eddy kinetic energy in the California Current based on altimetric, drifter, and moored current data. J. Geophys. Res. Ocean. 1998, 103, 13067–13083. [Google Scholar] [CrossRef] [Green Version]
- Duran, R.; Nordam, T.; Serra, M.; Barker, C.H. Marine Hydrocarbon Spill Assessments; Makarynskyy, O., Ed.; Elsevier: Amsterdam, The Netherlands, 2021. [Google Scholar]
- Zhou, J.; Adrian, R.J.; Balachandar, S.; Kendall, T. Mechanisms for generating coherent packets of hairpin vortices in channel flow. J. Fluid Mech. 1999, 387, 353–396. [Google Scholar] [CrossRef]
- Adrian, R.; Christensen, K.; Liu, Z.-C. Analysis and interpretation of instantaneous turbulent velocity fields. Exp. Fluids 2000, 29, 275–290. [Google Scholar] [CrossRef]
- Vortmeyer-Kley, R.; Gräwe, U.; Feudel, U. Detecting and tracking eddies in oceanic flow fields: A Lagrangian descriptor based on the modulus of vorticity. Nonlinear Process. Geophys. 2016, 23, 159–173. [Google Scholar] [CrossRef] [Green Version]
- Reyes, O.; Manta, G.; Carrillo, L. Marine heatwaves and marine cold-spells on the Yucatan Shelf-break upwelling region. Cont. Shelf Res. 2022, 239, 104707. [Google Scholar] [CrossRef]
- Tavakol, A.; Rahmani, V.; Harrington Jr, J. Evaluation of hot temperature extremes and heat waves in the Mississippi River Basin. Atmos. Res. 2020, 239, 104907. [Google Scholar] [CrossRef]
- Martinez-Austria, P.F.; Bandala, E.R.; Patiño-Gómez, C. Temperature and heat wave trends in northwest Mexico. Phys. Chem. Earth Parts A/B/C 2016, 91, 20–26. [Google Scholar] [CrossRef]
- Gunter, G. Mass mortality and dinoflagellate blooms in the Gulf of Mexico. Science 1951, 113, 250–251. [Google Scholar] [CrossRef]
- Chang, Y.; Oey, L. Eddy and wind-forced heat transports in the Gulf of Mexico. J. Phys. Oceanogr. 2010, 40, 2728–2742. [Google Scholar] [CrossRef]
- Leipper, D.F. A sequence of current patterns in the Gulf of Mexico. J. Geophys. Res. 1970, 75, 637–657. [Google Scholar] [CrossRef]
- Sturges, W.; Evans, J.C. On the variability of the Loop Current in the Gulf of Mexico. J. Mar. Res. 1983, 41, 639–653. [Google Scholar] [CrossRef]
- Behringer, D.W.; Molinari, R.L.; Festa, J.F. The variability of anticyclonic current patterns in the Gulf of Mexico. J. Geophys. Res. 1977, 82, 5469–5476. [Google Scholar] [CrossRef]
- Liu, Y.; Weisberg, R.H.; Hu, C.; Kovach, C.; Riethmüller, R. Evolution of the Loop Current System during the Deepwater Horizon Oil Spill Event as Observed with Drifters and Satellites; American Geophysical Union: Washington, DC, USA, 2011; Volume 195, pp. 91–101. [Google Scholar] [CrossRef]
- Liu, Y.; Weisberg, R.H.; Mooers, C.N.K. Performance evaluation of the self-organizing map for feature extraction. J. Geophys. Res. 2006, 111, C05018. [Google Scholar] [CrossRef]
- Nickerson, A.K.; Weisberg, R.H.; Liu, Y. On the Evolution of the Gulf of Mexico Loop Current Through Its Penetrative, Ring Shedding and Retracted States. Adv. Space Res. 2022, 69, 4058–4077. [Google Scholar] [CrossRef]
- Yang, Y.; Weisberg, R.H.; Liu, Y.; San Liang, X. Instabilities and multiscale interactions underlying the loop current eddy shedding in the Gulf of Mexico. J. Phys. Oceanogr. 2020, 50, 1289–1317. [Google Scholar] [CrossRef]
- Stackpoole, S.; Sabo, R.; Falcone, J.; Sprague, L. Long-Term Mississippi River Trends Expose Shifts in the River Load Response to Watershed Nutrient Balances between 1975 and 2017. Water Resour. Res. 2021, 57, e2021WR030318. [Google Scholar] [CrossRef]
- González, N.M.; Müller-Karger, F.E.; Estrada, S.C.; Pérez de los Reyes, R.; del Río, I.V.; Pérez, P.C.; Arenal, I.M. Near-surface phytoplankton distribution in the western Intra-Americas Sea: The influence of El Niño and weather events. J. Geophys. Res. Ocean. 2000, 105, 14029–14043. [Google Scholar] [CrossRef]
- Pasqueron de Fommervault, O.; Perez-Brunius, P.; Damien, P.; Camacho-Ibar, V.F.; Sheinbaum, J. Temporal variability of chlorophyll distribution in the Gulf of Mexico: Bio-optical data from profiling floats. Biogeosciences 2017, 14, 5647–5662. [Google Scholar] [CrossRef] [Green Version]
- Gilbes, F.; Tomas, C.; Walsh, J.J.; Müller-Karger, F.E. An episodic chlorophyll plume on the West Florida Shelf. Cont. Shelf Res. 1996, 16, 1201–1224. [Google Scholar] [CrossRef]
- Martínez-López, B.; Zavala-Hidalgo, J. Seasonal and interannual variability of cross-shelf transports of chlorophyll in the Gulf of Mexico. J. Mar. Syst. 2009, 77, 1–20. [Google Scholar] [CrossRef]
- Meza-Padilla, R.; Enriquez, C.; Liu, Y.; Appendini, C.M. Ocean Circulation in the Western Gulf of Mexico Using Self-Organizing Maps. J. Geophys. Res. Ocean. 2019, 124, 4152–4167. [Google Scholar] [CrossRef]
- Shay, L.K.; Goni, G.J.; Black, P.G. Effects of a Warm Oceanic Feature on Hurricane Opal. Mon. Weather Rev. 2000, 128, 1366–1383. [Google Scholar] [CrossRef]
- Jacob, S.D.; Shay, L.K. The Role of Oceanic Mesoscale Features on the Tropical Cyclone–Induced Mixed Layer Response: A Case Study. J. Phys. Oceanogr. 2003, 33, 649–676. [Google Scholar] [CrossRef]
- Jaimes, B.; Shay, L.K. Near-Inertial Wave Wake of Hurricanes Katrina and Rita over Mesoscale Oceanic Eddies. J. Phys. Oceanogr. 2010, 40, 1320–1337. [Google Scholar] [CrossRef]
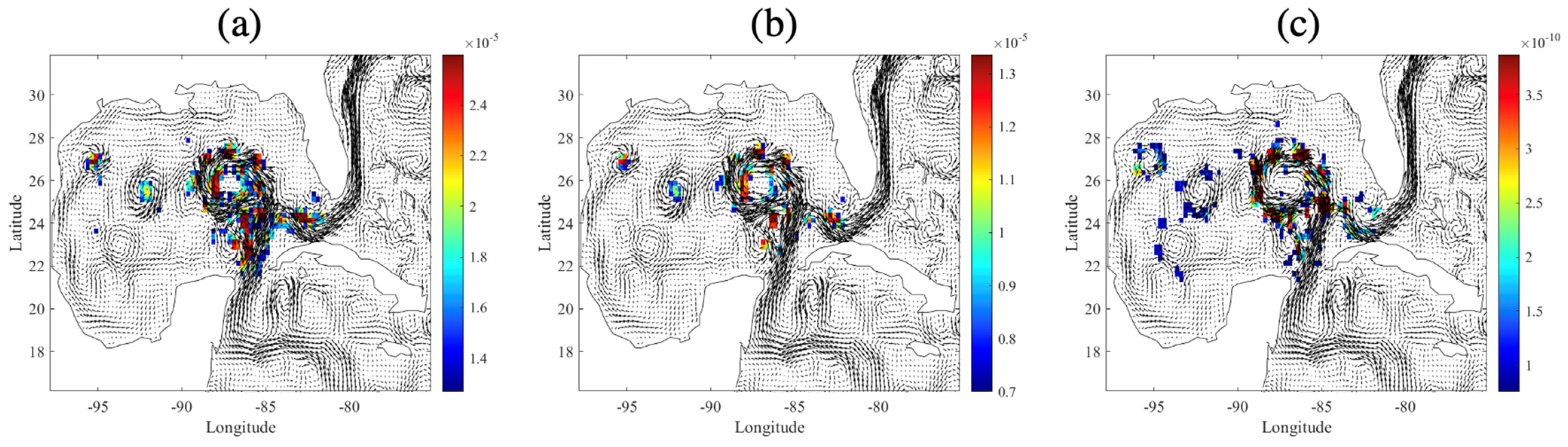


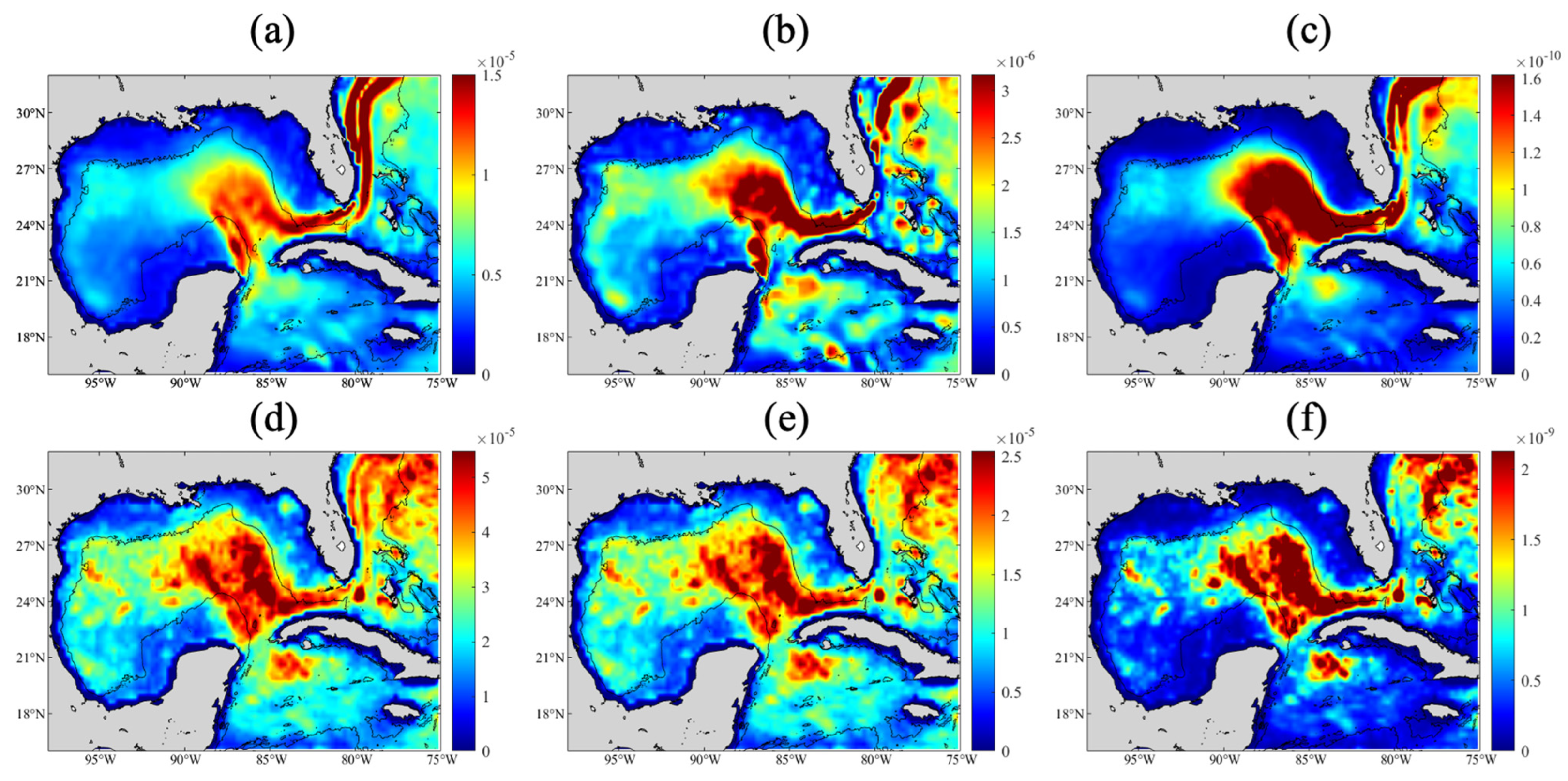
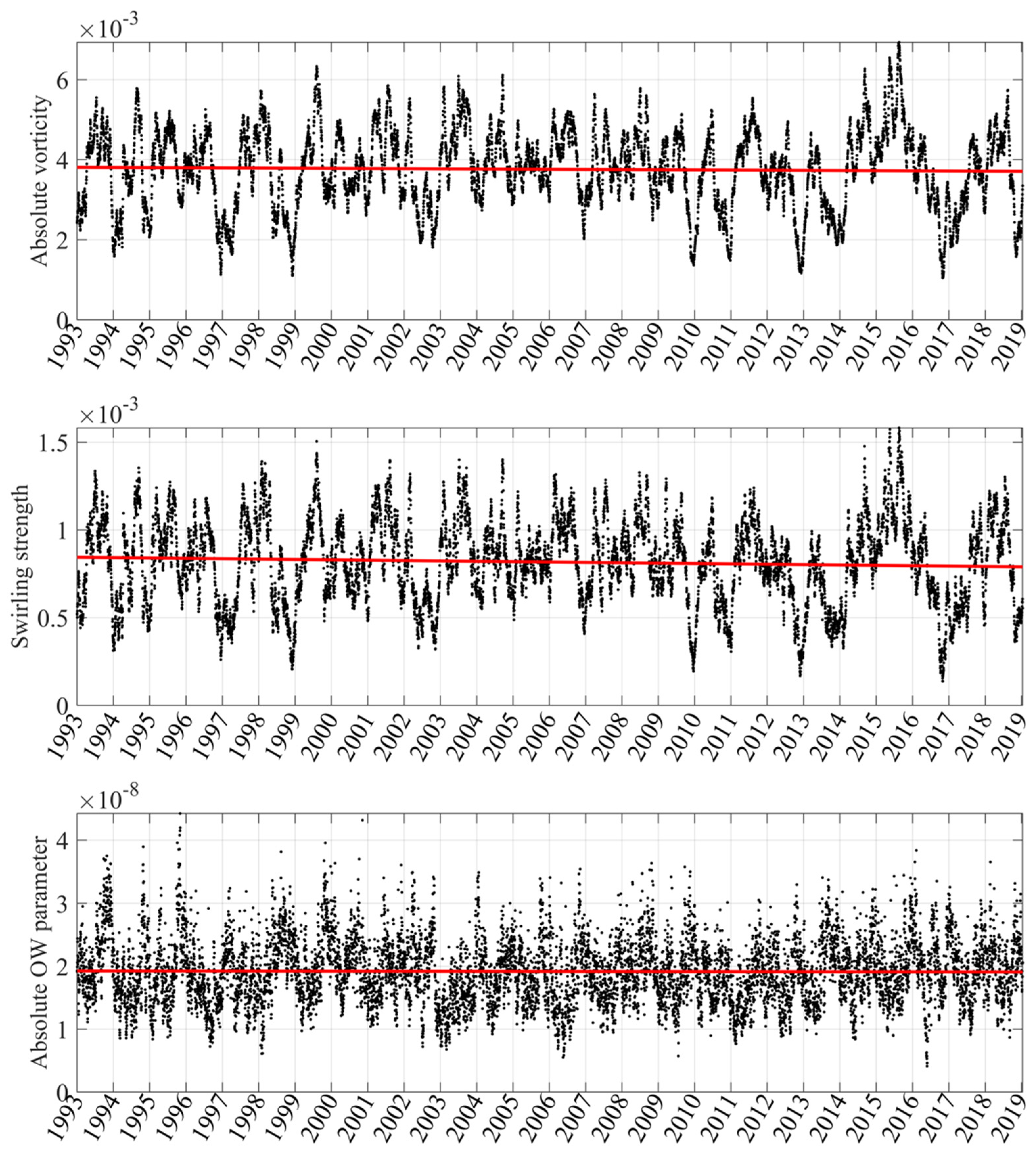
| Absolute Vorticity (s−1) | Swirling Strength (−) | Absolute Okubo–Weiss Parameter (s−2) | ||
|---|---|---|---|---|
| Area (km2) | Mean value | 1.3855 × 105 | 5.7026 × 104 | 2.7446 × 105 |
| Standard deviation | 3.2647 × 104 | 1.5544 × 104 | 4.9428 × 104 | |
| Slope of the regression (km2/decade) | −3.7065 × 102 | −9.0948 × 102 | −2.9844 × 103 | |
| p-value of regression | 0.4052 | 1.7725 × 10−5 | 9.4555 × 10−6 | |
| Strength | Mean value | 0.0038 | 8.1693 × 10−4 | 1.9182 × 10−8 |
| Standard deviation | 9.9937 × 104 | 2.4407 × 10−4 | 5.2887 × 10−9 | |
| Slope of the regression ([unit]/decade) | −3.8339 × 10−5 | −2.1015 × 10−5 | −6.1687 × 10−11 | |
| p-value of regression | 0.0049 | 2.6258 × 10−10 | 0.3924 | |
| Intensity | Mean value | 2.3900 × 10−8 | 1.3158 × 10−8 | 1.4849 × 10−13 |
| Standard deviation | 1.0894 × 10−9 | 6.5858 × 10−10 | 1.0234 × 10−14 | |
| Slope of the regression ([unit]/decade) | −1.0741 × 10−10 | −8.6675 × 10−11 | 4.6351 × 10−16 | |
| p-value of regression | 4.5467 × 10−13 | 3.9722 × 10−22 | 8.9413 × 10−4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, G.; Wang, Z.; Wang, B. Multidecade Trends of Sea Surface Temperature, Chlorophyll-a Concentration, and Ocean Eddies in the Gulf of Mexico. Remote Sens. 2022, 14, 3754. https://doi.org/10.3390/rs14153754
Li G, Wang Z, Wang B. Multidecade Trends of Sea Surface Temperature, Chlorophyll-a Concentration, and Ocean Eddies in the Gulf of Mexico. Remote Sensing. 2022; 14(15):3754. https://doi.org/10.3390/rs14153754
Chicago/Turabian StyleLi, Geng, Zhankun Wang, and Binbin Wang. 2022. "Multidecade Trends of Sea Surface Temperature, Chlorophyll-a Concentration, and Ocean Eddies in the Gulf of Mexico" Remote Sensing 14, no. 15: 3754. https://doi.org/10.3390/rs14153754
APA StyleLi, G., Wang, Z., & Wang, B. (2022). Multidecade Trends of Sea Surface Temperature, Chlorophyll-a Concentration, and Ocean Eddies in the Gulf of Mexico. Remote Sensing, 14(15), 3754. https://doi.org/10.3390/rs14153754