Landslide Displacement Prediction Based on a Two-Stage Combined Deep Learning Model under Small Sample Condition
Abstract
:1. Introduction
1.1. Background
1.2. Related Work
1.3. Article Arrangement
- A decomposition method based on first-order and second-order difference DDM (Difference decomposition method) is proposed for landslide displacement decomposition.
- A data enhancement method based on DTW (Dynamic Time Warping) method is proposed to enhance the few-shots GPS samples.
- A model enhancement method based on a two-stage CNN-attention-LSTM combined deep learning model named TC-DLDPM was built to extract the high non-linearity and complexity of spatial and temporal correlations in landslide displacement.
2. Materials and Methods
- (1)
- According to the Difference Decomposition Method (DDM), the cumulative landslide displacement is decomposed into trend displacement and periodic displacement components.
- (2)
- For the trend displacement component, the cubic curve fitting method is adopted for fitting and modeling in this paper to realize the trend prediction model of the displacement.
- (3)
- For the periodic displacement component, firstly, through analysis and evaluation of the related external factors which induced landslides, the displacement data of the monitoring station similar to the target dataset is fused together. Then, the data enhancement method DTW algorithm in the small sample learning is used to enhance the base dataset and the target datasets, respectively, to build an extensive base dataset.
- (4)
- Train the TC-DLDPM prediction model on the base and target datasets, and finally obtain the prediction result of periodic displacement components on the target testing dataset.
- (5)
- The predicted values of the trend displacement component and periodic displacement component are superimposed, and finally, the cumulative displacement prediction result can be obtained.
- (6)
- Compare and analyze the cumulative displacement prediction results with the observed data to evaluate the efficiency and performance of the model.
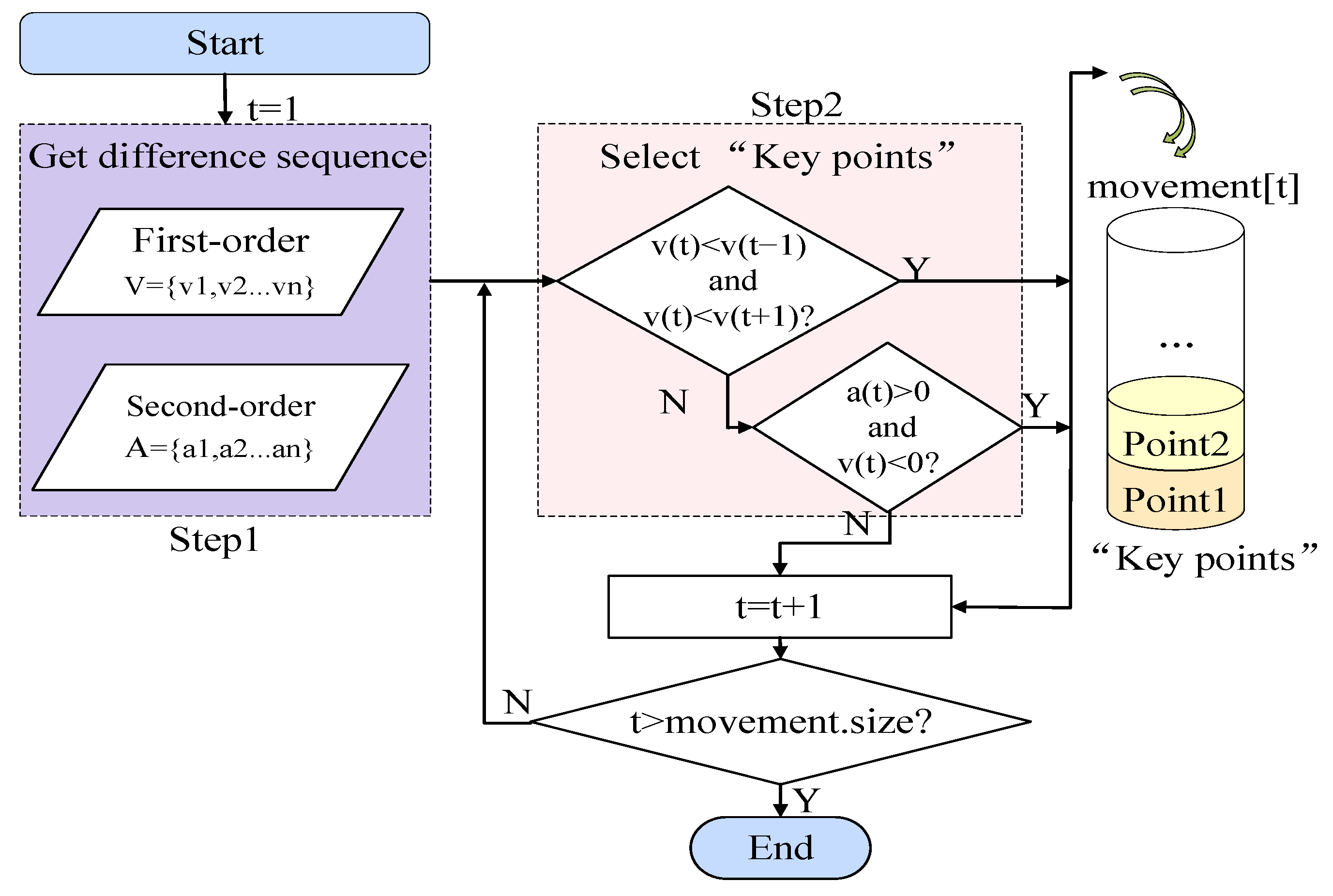
2.1. Difference Decomposition Method (DDM) for Landslide Displacement Decomposition
2.2. Enhancement Method Based on DTW of GPS Data
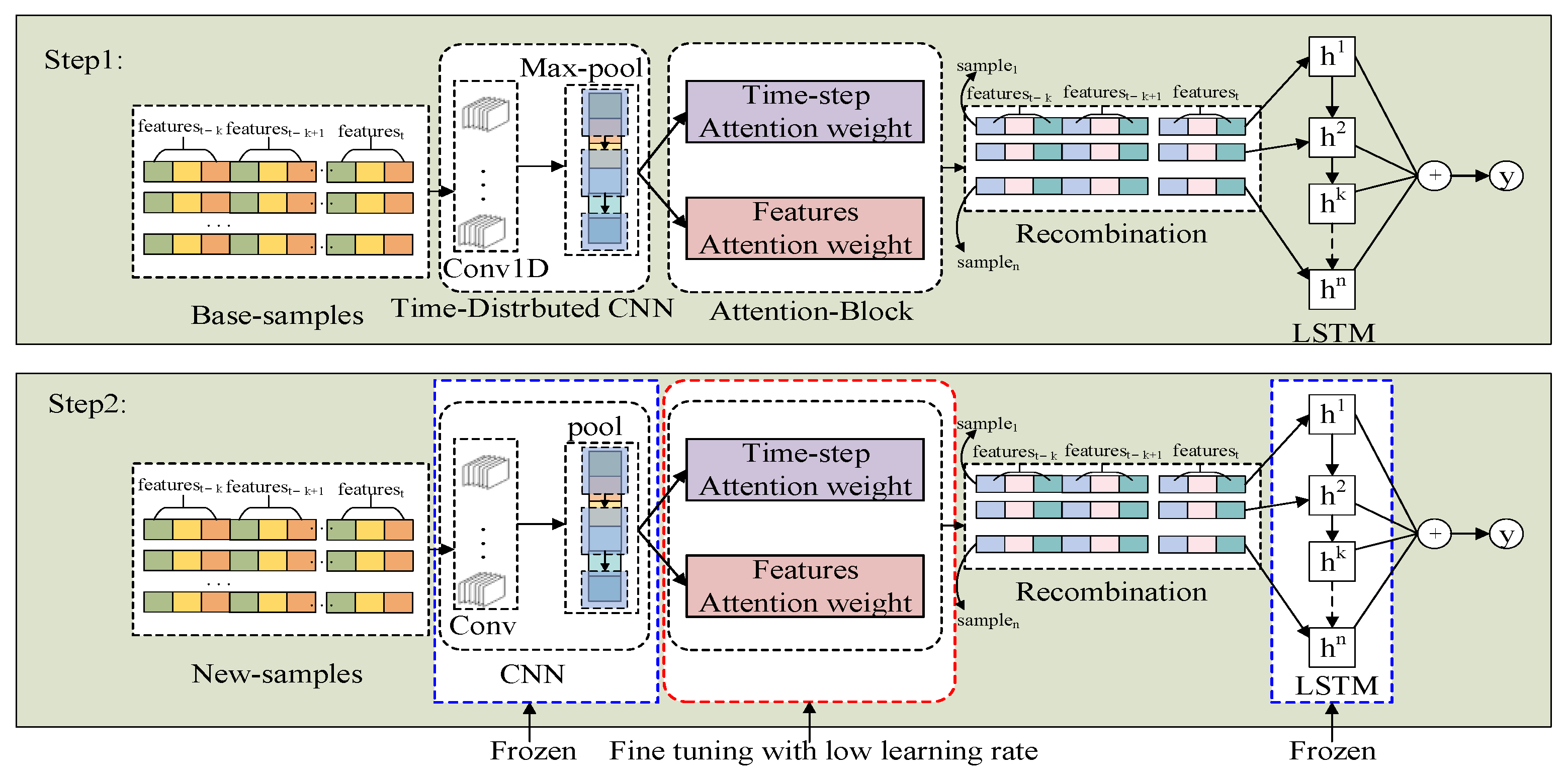
2.3. Two-Stage Combined Deep Learning Prediction Model TC-DLDPM
- CNN neural network
- 2.
- Attention layer
- 3.
- Long and Short-Term Memory (LSTM) neural network
2.4. Evaluation Indicators of Model Performance
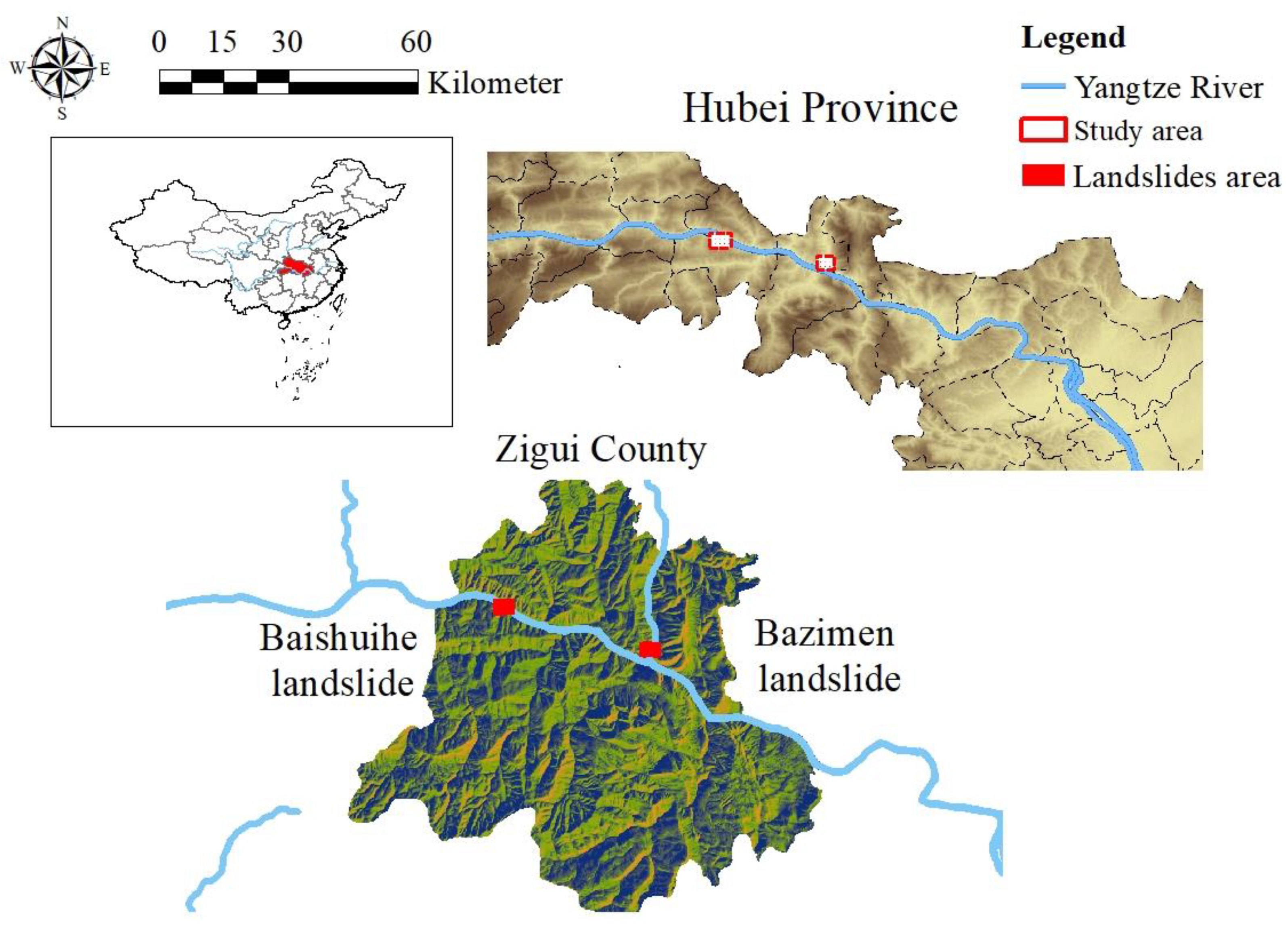
3. Study Area and the Landslide Displacement Data Set
3.1. Study Area
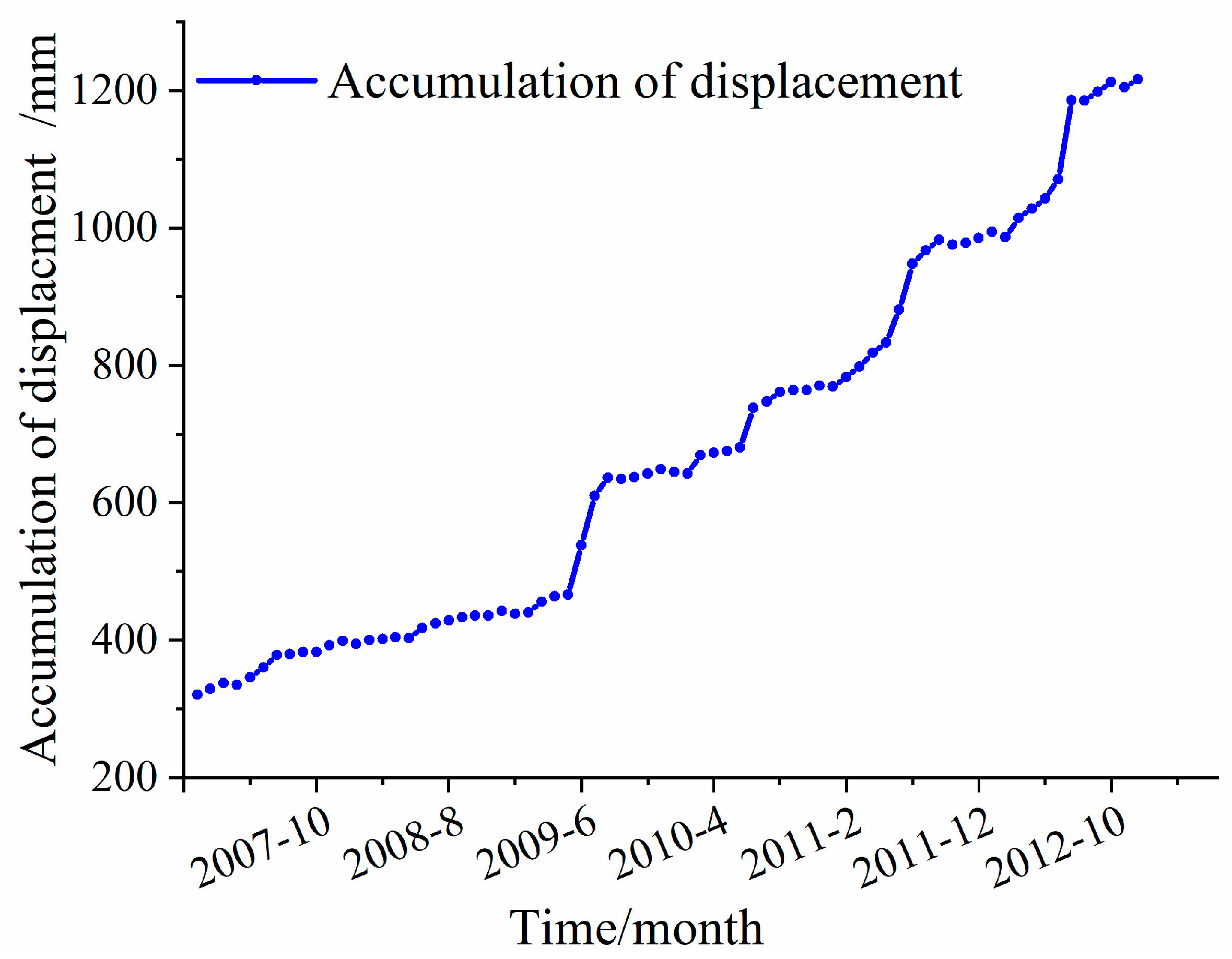
3.2. Landslide Displacement Dataset
4. Model Implementation
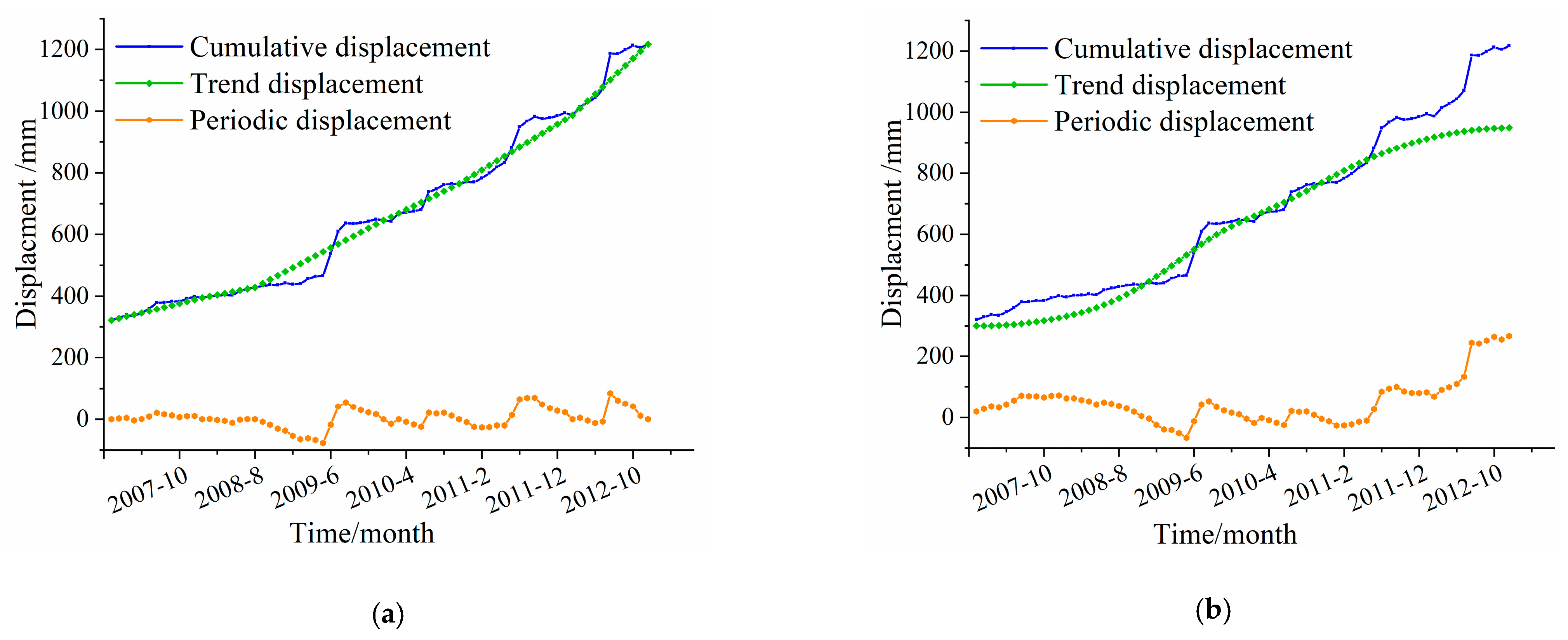
4.1. Decomposition of Landslide Displacement
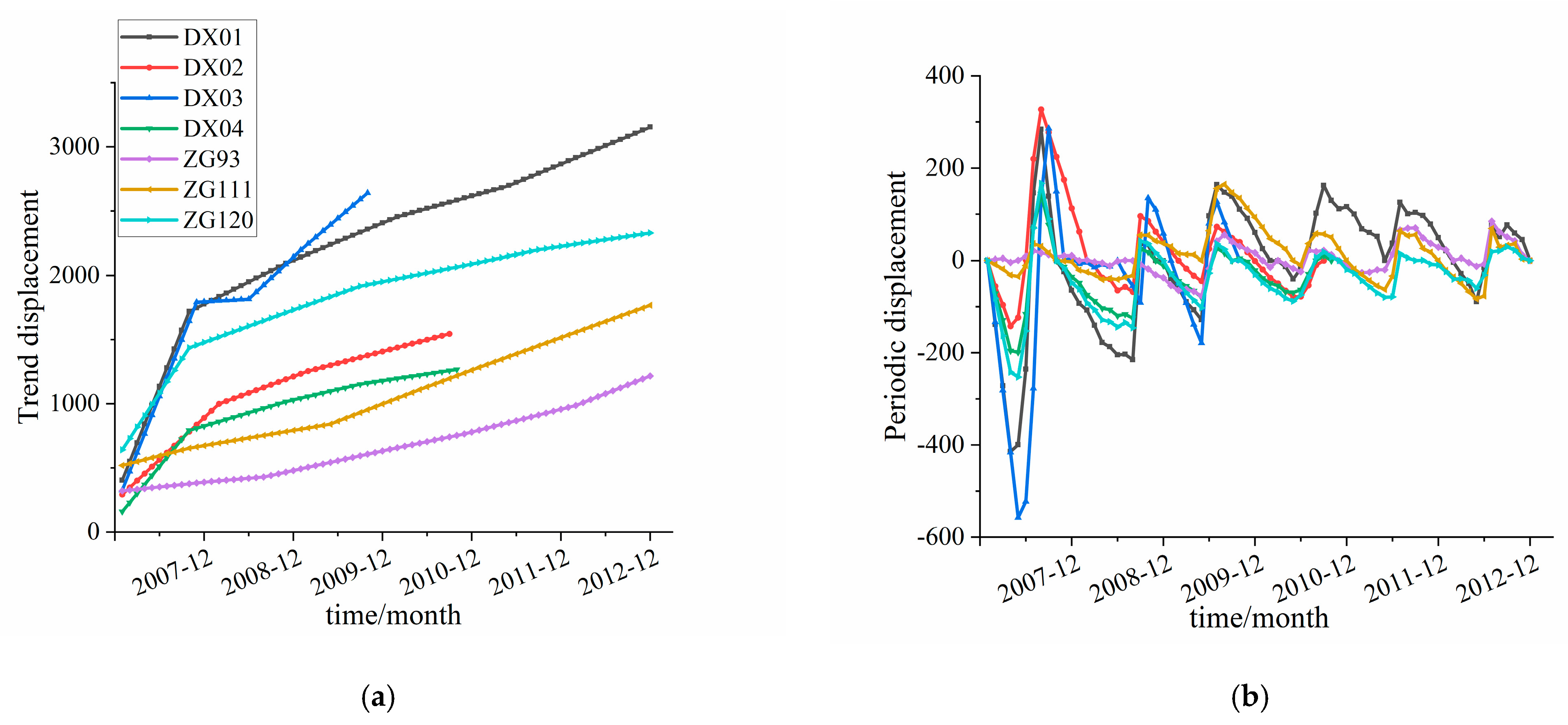
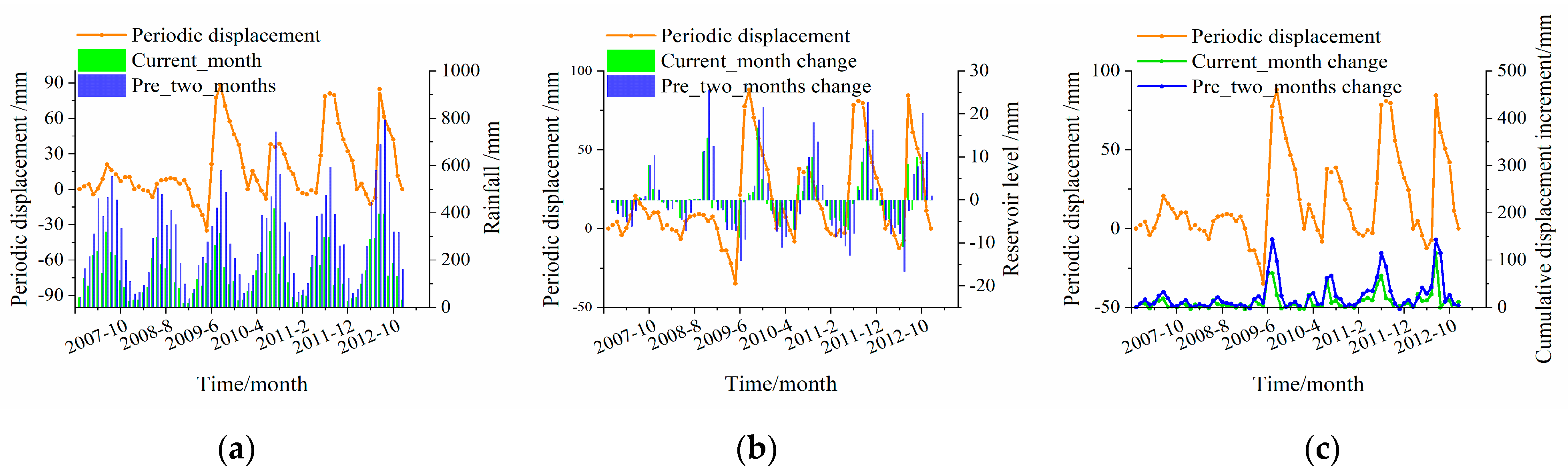
4.2. Selection of the Inducing Factors of the Periodic Displacement
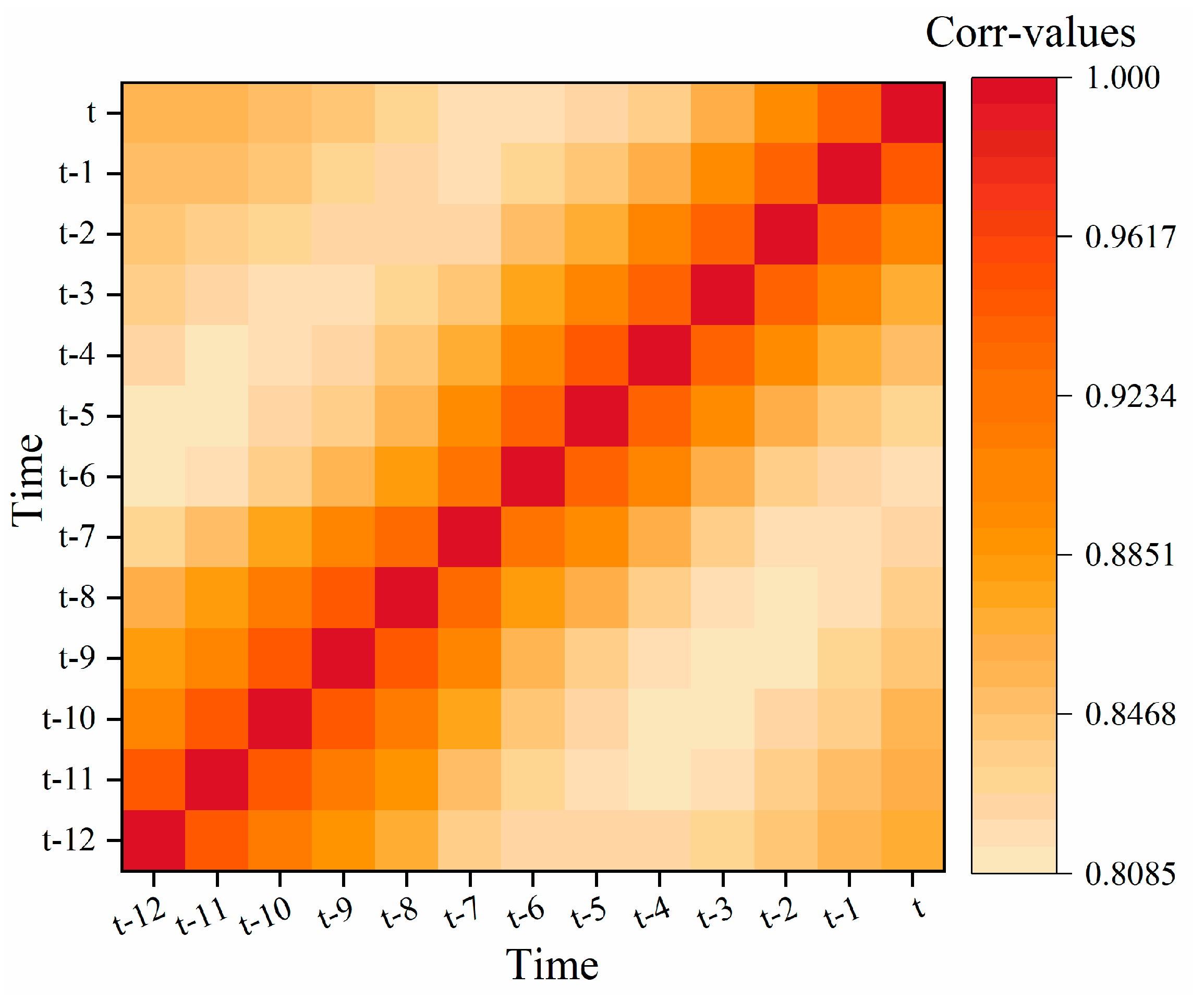
4.3. Feature Engineering of Periodic Displacement Based on Supervised Learning
4.4. Data Preparation
- 1.
- Construction of original base dataset and target dataset
- 2.
- Enhance Robustness of original base and target datasets
5. Discussion
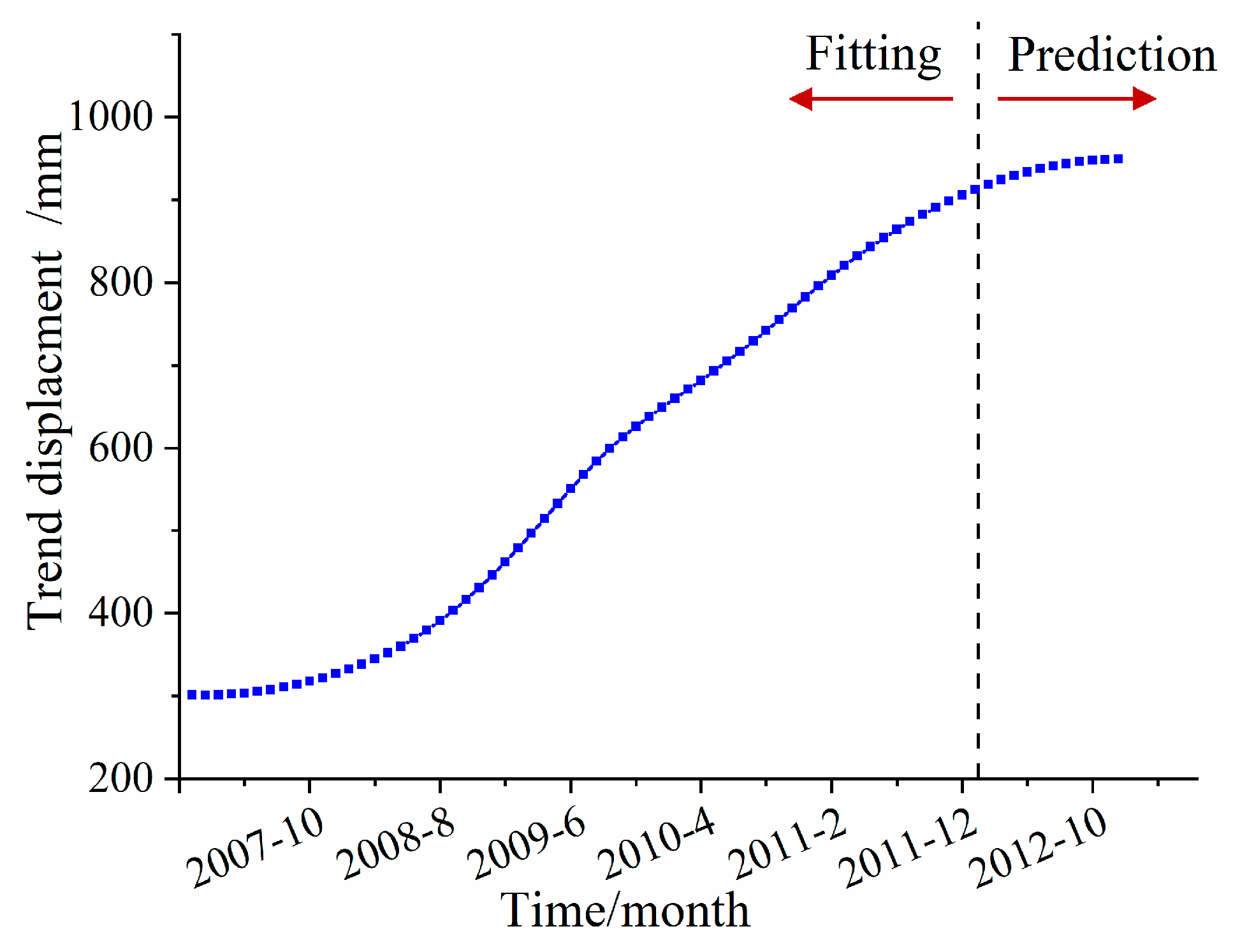
5.1. Prediction of Trend Displacement Component on ZG110
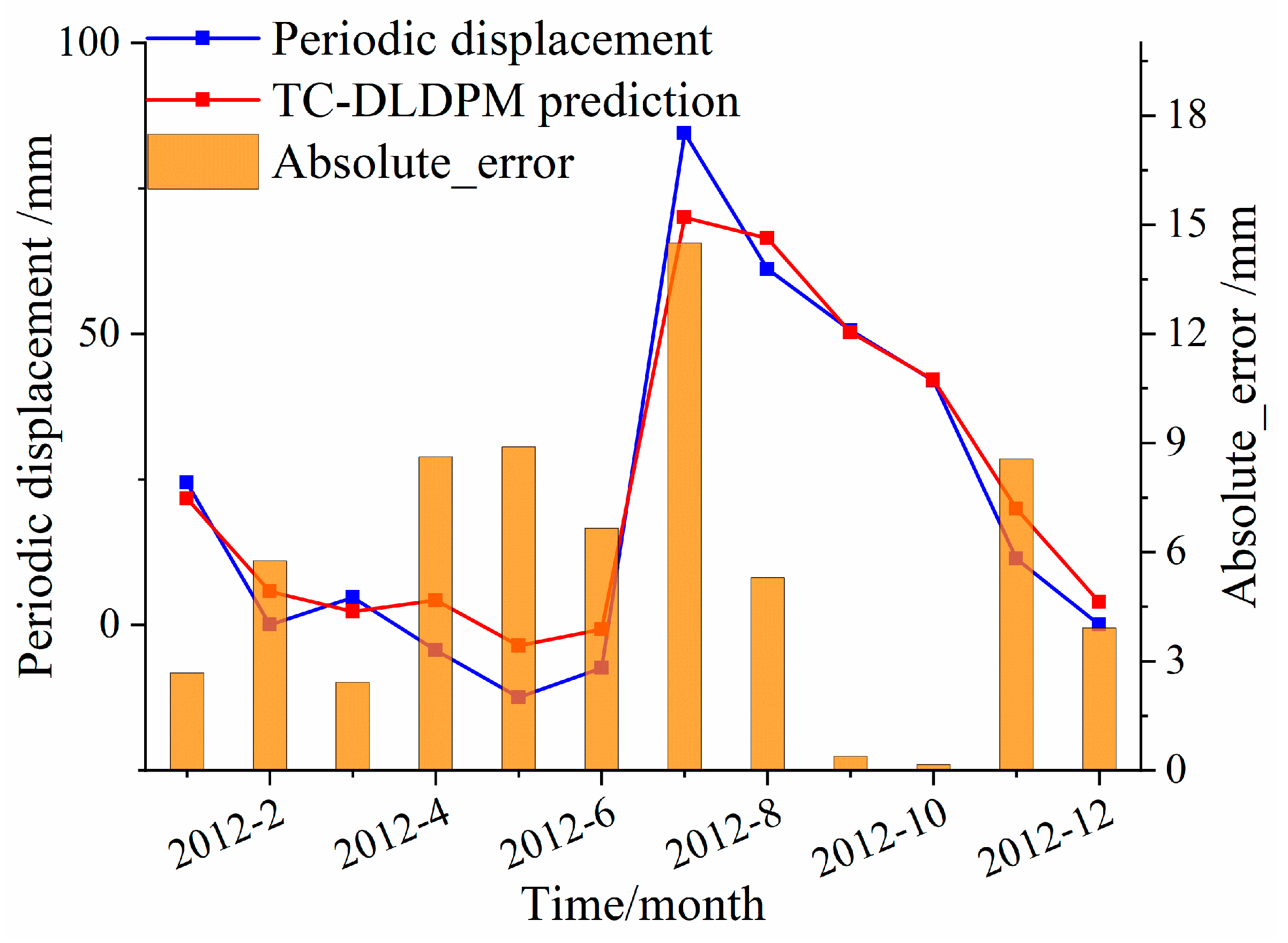
5.2. Prediction of Periodic Displacement Component on ZG110
- 1.
- Experimental environment and parameter selection of the TC-DLDPM model
- 2.
- Comparison and analysis of the prediction results of the periodic term displacement components
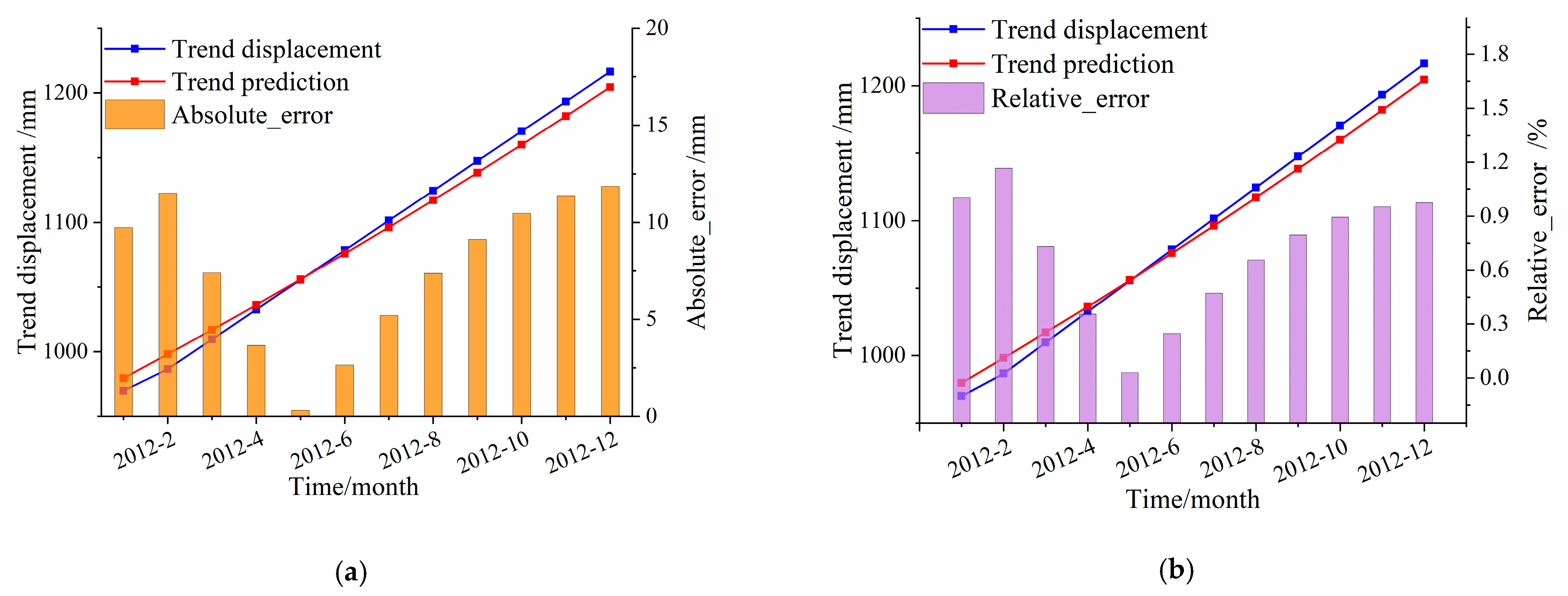
5.3. Prediction Experiments of the Landslide Cumulative Displacement
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, Y.-G.; Tang, J.; He, Z.-Y.; Tan, J.; Li, C. A novel displacement prediction method using gated recurrent unit model with time series analysis in the Erdaohe landslide. Nat. Hazards 2020, 105, 783–813. [Google Scholar] [CrossRef]
- Huang, D.; He, J.; Song, Y.; Guo, Z.; Huang, X.; Guo, Y. Displacement Prediction of the Muyubao Landslide Based on a GPS Time-Series Analysis and Temporal Convolutional Network Model. Remote Sens. 2022, 14, 2656. [Google Scholar] [CrossRef]
- Liu, S.; Liao, Q.; Xiao, M.; Zhao, D.; Huang, C. Spatial and Temporal Variations of Habitat Quality and Its Response of Landscape Dynamic in the Three Gorges Reservoir Area, China. Int. J. Environ. Res. Public Health 2022, 19, 3594. [Google Scholar] [CrossRef]
- Liu, Z.-Q.; Guo, D.; Lacasse, S.; Li, J.-H.; Yang, B.-B.; Choi, J.-C. Algorithms for intelligent prediction of landslide displacements. J. Zhejiang Univ. A 2020, 21, 412–429. [Google Scholar] [CrossRef]
- Xing, Y.; Yue, J.; Chen, C. Interval Estimation of Landslide Displacement Prediction Based on Time Series Decomposition and Long Short-Term Memory Network. IEEE Access 2019, 8, 3187–3196. [Google Scholar] [CrossRef]
- Ran, Q.-H.; Su, D.-Y.; Qian, Q.; Fu, X.-D.; Wang, G.-Q.; He, Z.-G. Physically-based approach to analyze rainfall-triggered landslide using hydraulic gradient as slide direction. J. Zhejiang Univ. A 2012, 13, 943–957. [Google Scholar] [CrossRef]
- Huang, F.; Yin, K.; Zhang, G.; Gui, L.; Yang, B.; Liu, L. Landslide displacement prediction using discrete wavelet transform and extreme learning machine based on chaos theory. Environ. Earth Sci. 2016, 75, 1376. [Google Scholar] [CrossRef]
- McDougall, S. 2014 Canadian Geotechnical Colloquium: Landslide runout analysis—Current practice and challenges. Can. Geotech. J. 2017, 54, 605–620. [Google Scholar] [CrossRef] [Green Version]
- Miao, S.; Hao, X.; Guo, X.; Wang, Z.; Liang, M. Displacement and landslide forecast based on an improved version of Saito’s method together with the Verhulst-Grey model. Arab. J. Geosci. 2017, 10, 53. [Google Scholar] [CrossRef]
- Tehrani, F.S.; Calvello, M.; Liu, Z.; Zhang, L.; Lacasse, S. Machine learning and landslide studies: Recent advances and applications. Nat. Hazards 2022, 1–49. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, Y.; Gu, X.; Wu, C.; Han, L. Application of Soft Computing, Machine Learning, Deep Learning and Optimizations in Geoengineering and Geoscience; Springer Nature: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
- Nandi, A.; Shakoor, A. A GIS-based landslide susceptibility evaluation using bivariate and multivariate statistical analyses. Eng. Geol. 2010, 110, 11–20. [Google Scholar] [CrossRef]
- Zhu, C.; Zhang, J.; Liu, Y.; Ma, D.; Li, M.; Xiang, B. Comparison of GA-BP and PSO-BP neural network models with initial BP model for rainfall-induced landslides risk assessment in regional scale: A case study in Sichuan. China. Nat. Hazards 2020, 100, 173–204. [Google Scholar] [CrossRef]
- Xu, F.; Fan, C.J.; Xu, X.J.; Li, L.; Ni, J.Y. Displacement prediction of landslide based on Variational mode decomposition and AMPSO-SVM coupling model. J. Shanghai Jiaotong Univ. 2018, 10, 1388–1395. [Google Scholar]
- Zhou, C.; Yin, K.L.; Cao, Y.; Ahmed, B. Application of time series analysis and PSO—SVM model in predicting the Bazimen landslide in the Three Gorges Reservoir, China J. Eng. Geol. 2016, 204, 108–120. [Google Scholar] [CrossRef]
- Bui, D.T.; Tuan, T.A.; Klempe, H.; Pradhan, B.; Revhaug, I. Spatial prediction models for shallow landslide hazards: A comparative assessment of the efficacy of support vector machines, artificial neural networks, kernel logistic regression, and logistic model tree. Landslides 2015, 13, 361–378. [Google Scholar] [CrossRef]
- Chang, K.-T.; Merghadi, A.; Yunus, A.P.; Pham, B.T.; Dou, J. Evaluating scale effects of topographic variables in landslide susceptibility models using GIS-based machine learning techniques. Sci. Rep. 2019, 9, 1–21. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, B.; Yin, K.; Lacasse, S.; Liu, Z. Time series analysis and long short-term memory neural network to predict landslide displacement. Landslides 2019, 16, 677–694. [Google Scholar] [CrossRef]
- Graves, A. Generating sequences with recurrent neural networks. arXiv 2013, arXiv:1308.0850. [Google Scholar] [CrossRef]
- Ma, X.; Tao, Z.; Wang, Y.; Yu, H.; Wang, Y. Long short-term memory neural network for traffic speed prediction using remote microwave sensor data. Transp. Res. Part C Emerg. Technol. 2015, 54, 187–197. [Google Scholar] [CrossRef]
- Xu, S.; Niu, R. Displacement prediction of Baijiabao landslide based on empirical mode decomposition and long short-term memory neural network in Three Gorges area, China. Comput. Geosci. 2018, 111, 87–96. [Google Scholar] [CrossRef]
- Wang, Y.; Yao, Q.; Kwok, J.T.; Ni, L.M. Generalizing from a Few Examples. ACM Comput. Surv. 2021, 53, 1–34. [Google Scholar] [CrossRef]
- Schwartz, E.; Karlinsky, L.; Shtok, J.; Harary, S.; Marder, M.; Kumar, A.; Feris, R.; Giryes, R.; Bronstein, A.M. Delta-encoder: An effective sample synthesis method for few-shot object recognition. In Proceedings of the 32nd International Conference on Neural Information Processing Systems, Montreal, QC, Canada, 3–8 December 2018; pp. 2850–2860. [Google Scholar]
- Kwitt, R.; Hegenbart, S.; Niethammer, M. One-shot learning of scene locations via feature trajectory transfer. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 78–86. [Google Scholar]
- Wu, Y.; Lin, Y.T.; Dong, X.Y.; Yan, Y.; Ouyang, W.L.; Yang, Y. Exploit the unknown gradually: One-shot video-based person re-identification by stepwise learning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 5177–5186. [Google Scholar]
- He, H.; Bai, Y.; Garcia, E.A.; Li, S. ADASYN: Adaptive synthetic sampling approach for imbalanced learning. In Proceedings of the IEEE International Joint Conference on Neural Networks, Hong Kong, China, 1–8 June 2008; pp. 1322–1328. [Google Scholar] [CrossRef] [Green Version]
- Berndt, D.J.; Clifford, J. Using dynamic time warping to find patterns in time series. KDD Workshop 1994, 10, 359–370. [Google Scholar]
- Zhang, Y.; Tang, H.; Jia, K. Fine-grained visual categorization using meta-learning optimization with sample selection of aux-iliary data. In Proceedings of the European conference on computer vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 233–248. [Google Scholar]
- Motiian, S.; Jones, Q.; Iranmanesh, S.M.; Doretto, G. Few-shot adversarial domain adaptation. In Proceedings of the 31st International Conference on Neural Information Processing Systems (NIPS’17); Curran Associates Inc.: New York, NY, USA, 2017; pp. 6673–6683. [Google Scholar]
- Xu, F.; Wang, Y.; Du, J.; Ye, J. Study of displacement prediction model of landslide based on time series analysis. Chin. J. Rock Mech. Eng. 2011, 30, 746–751. [Google Scholar]
- Lian, C.; Zeng, Z.; Yao, W.; Tang, H. Displacement prediction model of landslide based on a modified ensemble empirical mode decomposition and extreme learning machine. Nat. Hazards 2012, 66, 759–771. [Google Scholar] [CrossRef]
- Kim, S.; Kim, N.H.; Choi, J.-H. Prediction of remaining useful life by data augmentation technique based on dynamic time warping. Mech. Syst. Signal Process. 2019, 136, 106486. [Google Scholar] [CrossRef]
- Dynamic Time Warping. In Information Retrieval for Music and Motion; Springer: Berlin/Heidelberg, Germany, 2007; pp. 69–84. [CrossRef]
- Anantasech, P.; Ratanamahatana, C.A. Enhanced Weighted Dynamic Time Warping for Time Series Classification. In Third International Congress on Information and Communication Technology; Springer: Singapore, 2018; Volume 797, pp. 655–664. [Google Scholar] [CrossRef]
- Boulila, W.; Ghandorh, H.; Khan, M.A.; Ahmed, F.; Ahmad, J. A novel CNN-LSTM-based approach to predict urban expansion. Ecol. Informatics 2021, 64, 101325. [Google Scholar] [CrossRef]
- Gu, J.; Wang, Z.; Kuen, J.; Ma, L.; Shahroudy, A.; Shuai, B.; Liu, T.; Wang, X.; Wang, G.; Cai, J.; et al. Recent advances in convolutional neural networks. Pattern Recognit. 2018, 77, 354–377. [Google Scholar] [CrossRef] [Green Version]
- Niu, Z.; Zhong, G.; Yu, H. A review on the attention mechanism of deep learning. Neurocomputing 2021, 452, 48–62. [Google Scholar] [CrossRef]
- Yu, Y.; Si, X.; Hu, C.; Zhang, J. A Review of Recurrent Neural Networks: LSTM Cells and Network Architectures. Neural Comput. 2019, 31, 1235–1270. [Google Scholar] [CrossRef]
- Ye, R.Q.; Fu, X.L.; Guo, F.; Yi, Q.L.; Zhang, J.Y.; Li, X.M.; Hou, S.P.; Liu, N. Deformation characteristics and mechanism analysis of geological hazards during operation period of Three Gorges Reservoir. J. Eng. Geol. 2021, 29, 680–692. [Google Scholar] [CrossRef]
- Liu, S.; Segoni, S.; Raspini, F.; Yin, K.; Zhou, C.; Zhang, Y.; Casagli, N. Satellite InSAR as a New Tool for the Verification of Landslide Engineering Remedial Works at the Regional Scale: A Case Study in the Three Gorges Resevoir Area, China. Appl. Sci. 2020, 10, 6435. [Google Scholar] [CrossRef]
- Yang, H.P.; Wang, J.S. Geological features and cause analysis of Qianjiangping landslide of July 13, 2003 on Three Georges Reservoir. J. Eng. Geol. 2009, 2, 91–97. [Google Scholar]
- Zhao, M.; Yi, X.; Zhang, J.; Lin, C. PPP-BOTDA Distributed Optical Fiber Sensing Technology and Its Application to the Baishuihe Landslide. Front. Earth Sci. 2021, 9, 660918. [Google Scholar] [CrossRef]
- Lu, S.; Huang, B. Deforming tendency prediction study on typical accumulation landslide with step-like displacements in the Three Gorges Reservoir, China. Arab. J. Geosci. 2020, 13, 329. [Google Scholar] [CrossRef]
- Yi, W. Basic Characteristics and Monitoring Data of Bazimen Landslide at Three Gorges Reservoir, Zigui County, Yangtze River from 2007 to 2012, National Cryosphere Desert Data Center (NCDC). 2016. Available online: https://www.ncdc.ac.cn (accessed on 1 September 2021). [CrossRef]
- Yi, W. Basic Characteristics and Monitoring Data of Baishuihe Landslide in Zigui County, Three Gorges Reservoir Area, 2007–2012, National Cryosphere Desert Data Center (NCDC). 2016. Available online: https://www.ncdc.ac.cn (accessed on 1 September 2021). [CrossRef]
- Yang, B.B.; Yin, K.L.; Du, J. A model for predicting landslide displacement based on time series and long and short term memory neural network. Chin. J. Rock Mech. Eng. 2018, 37, 2334–2343. [Google Scholar]
- Yang, B.; Yin, K.; Xiao, T.; Chen, L.; Du, J. Annual variation of landslide stability under the effect of water level fluctuation and rainfall in the Three Gorges Reservoir, China. Environ. Earth Sci. 2017, 76, 564. [Google Scholar] [CrossRef]
- Xiao, T.; Yin, K.; Yao, T.; Liu, S. Spatial prediction of landslide susceptibility using GIS-based statistical and machine learning models in Wanzhou County, Three Gorges Reservoir, China. Acta Geochim. 2019, 38, 654–669. [Google Scholar] [CrossRef]
- Lin, Z.; Sun, X.; Ji, Y. Landslide Displacement Prediction Based on Time Series Analysis and Double-BiLSTM Model. Int. J. Environ. Res. Public Heath 2022, 19, 2077. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Tang, J.; Cheng, Y.; Huang, L.; Guo, F.; Yin, X.; Li, N. Prediction of landslide displacement with dynamic features using intelligent approaches. Int. J. Min. Sci. Technol. 2022, 32, 539–549. [Google Scholar] [CrossRef]





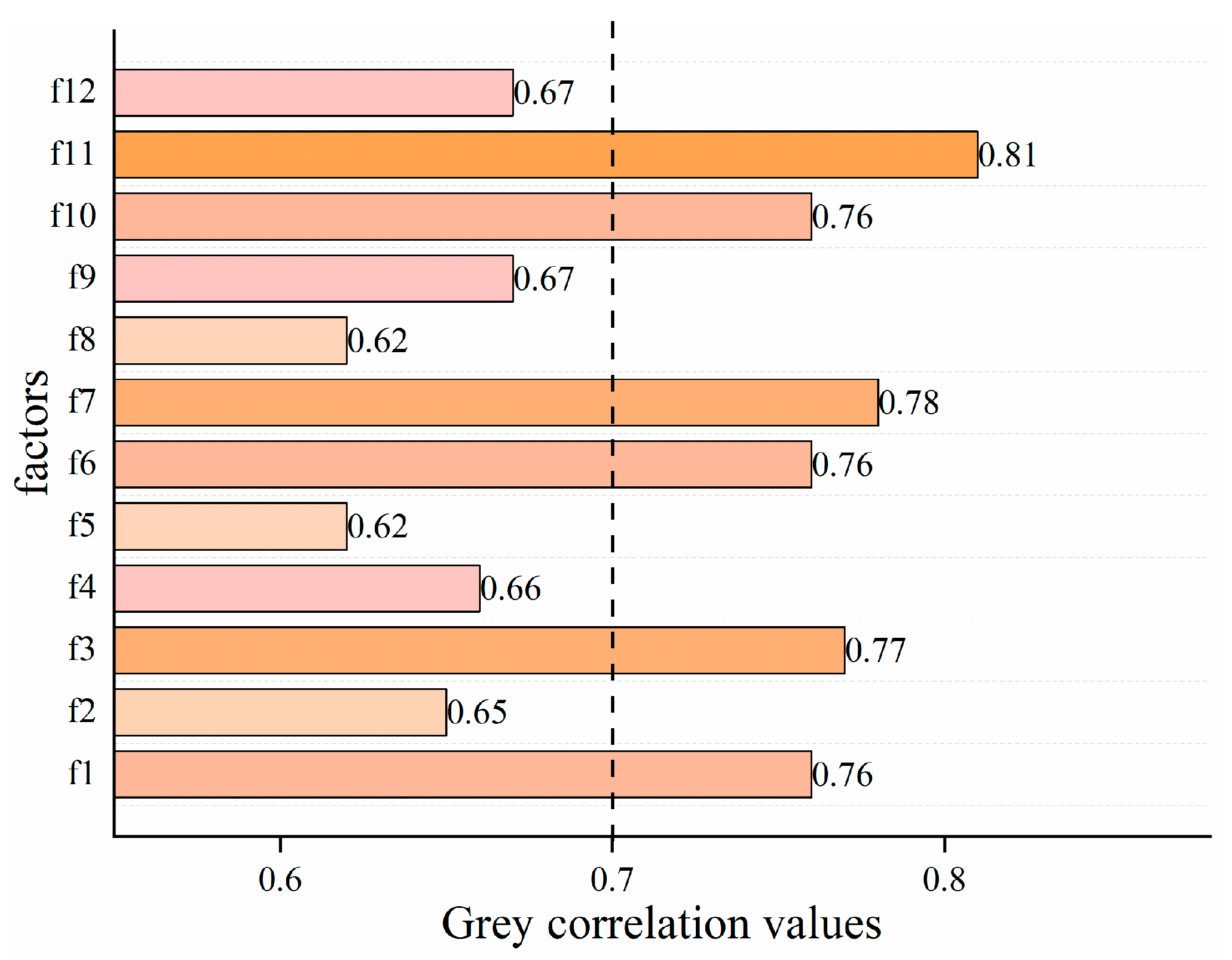

| Influencing Factor | Rainfall of the Current Month (f1) | Rainfall of the Previous Two Months (f3) | Reservoir of the Current Month (f6) | Reservoir of the Previous Two Months (f7) | Displacement Change of Current Month (f10) | Displacement Change of Previous Two Months (f11) |
|---|---|---|---|---|---|---|
| Correlation value | 0.76 | 0.77 | 0.76 | 0.78 | 0.76 | 0.81 |
| Models | Parameters | Values | Models | Parameters | Values |
|---|---|---|---|---|---|
| RF | Number of trees | 100 | GRU | hidden layers | 100 |
| maximum tree depth | 3 | Time-sliding window size | 12 | ||
| minimum number of samples | 20 | learning rate | 0.001 | ||
| minimum number of leaf nodes | 5 | batch_size | 64 | ||
| maximum number of features | 10 | training epochs | 500 | ||
| SVR | penalty factor C | 5.3 | Bi-LSTM | hidden layers | 100 |
| kernel function parameter Gamma | 0.01 | Time-sliding window size | 12 | ||
| BP | hidden layers | 160 | learning rate | 0.01 | |
| learning rate | 0.001 | batch_size | 64 | ||
| training epochs | 100 | training epochs | 500 | ||
| LSTM | hidden layers | 200 | CEEMDAN | hidden layers | 128 |
| Time-sliding window size | 12 | Time-sliding window size | 12 | ||
| learning rate | 0.001 | learning rate | 0.001 | ||
| batch_size | 64 | batch_size | 64 | ||
| training epochs | 500 | training epochs | 500 |
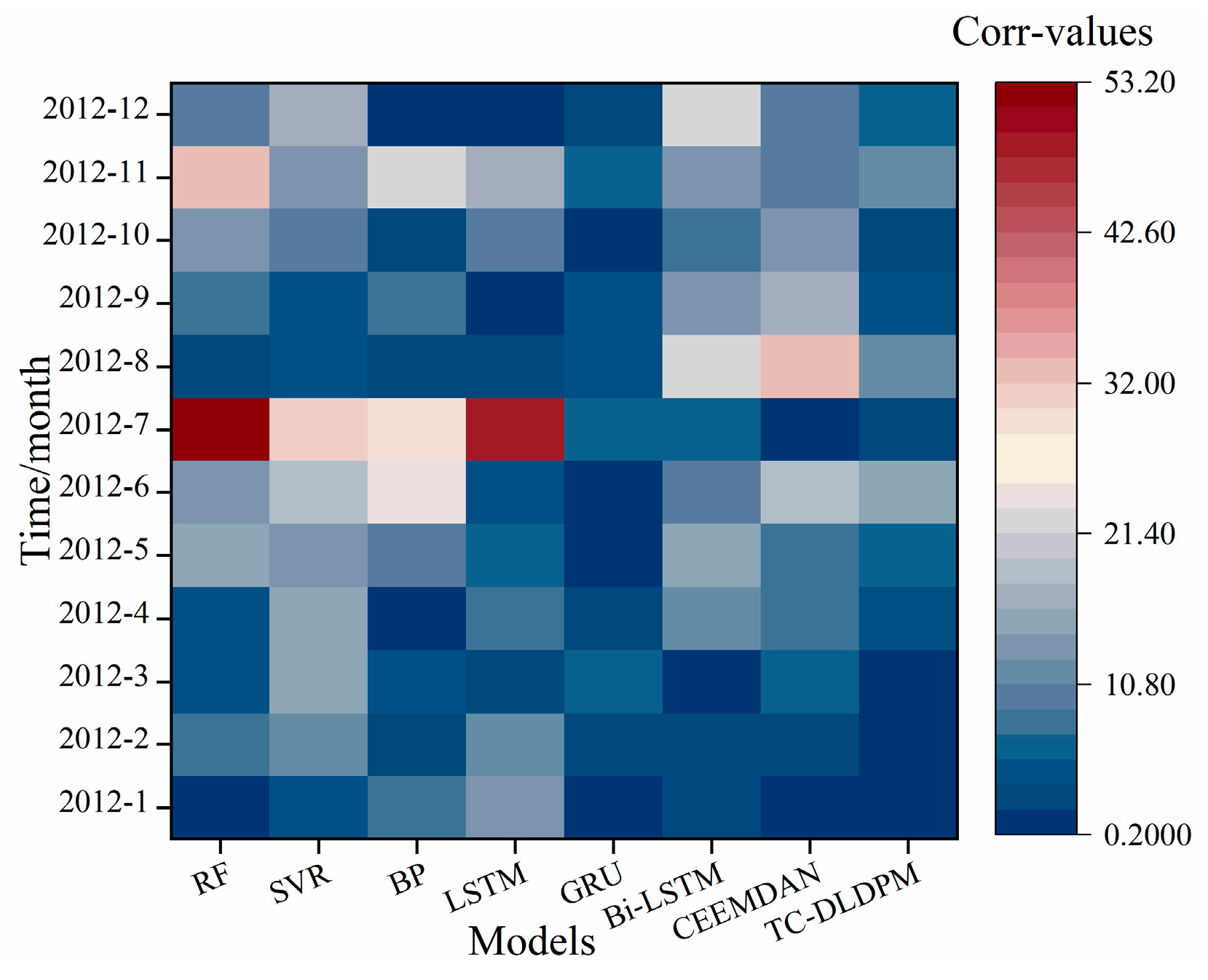
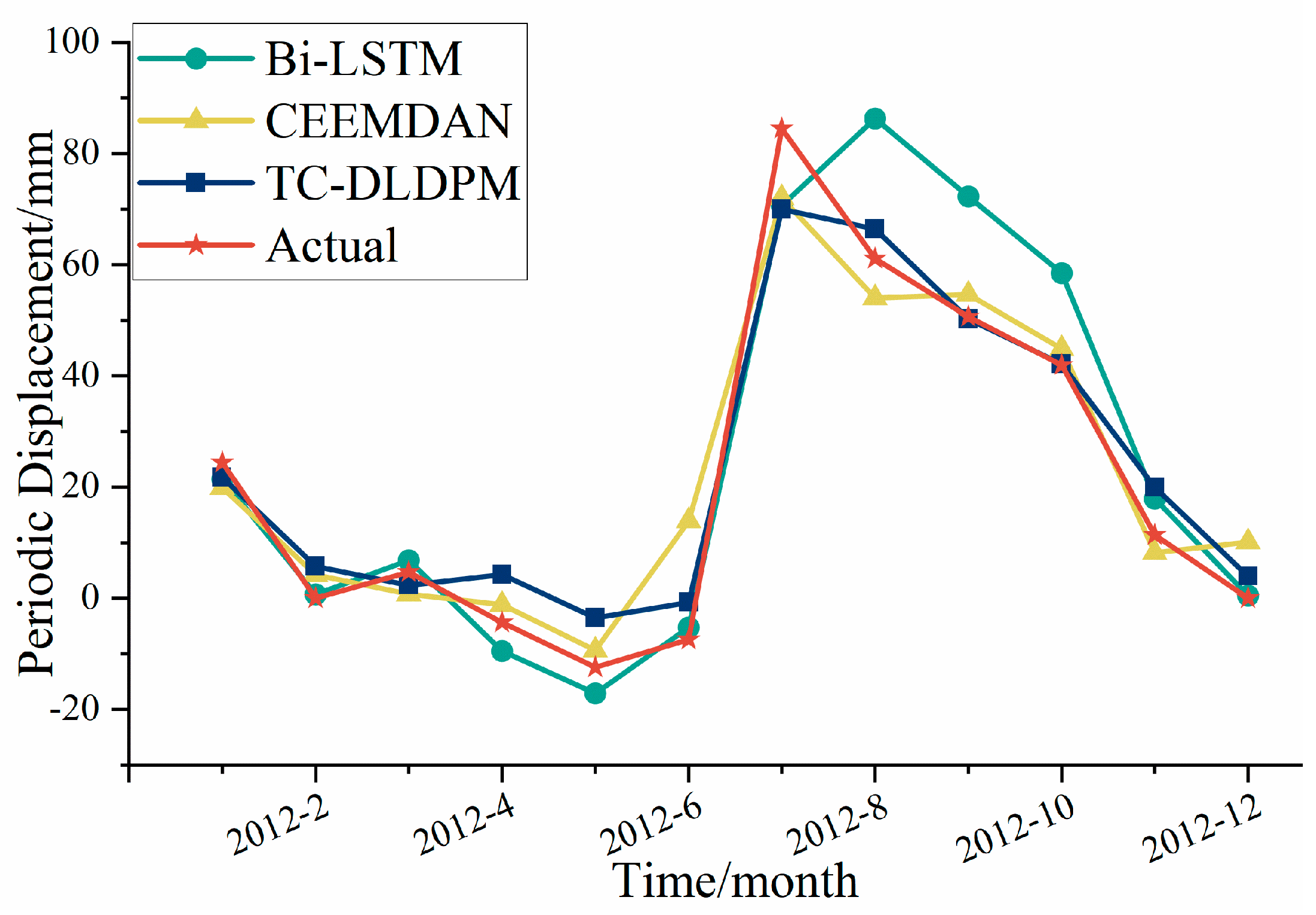
| Time Step | Real Data | RF | SVR | BP | LSTM | GRU | Bi-LSTM | CEEMDAN | TC-DLDPM |
|---|---|---|---|---|---|---|---|---|---|
| 2012/1 | 24.42 | 23.84 | 20.01 | 12.54 | 25.84 | 24.44 | 21.43 | 19.92 | 21.74 |
| 2012/2 | 0.00 | 8.43 | 19.96 | 17.57 | 6.75 | 4.35 | 0.68 | 4.20 | 5.76 |
| 2012/3 | 4.72 | −0.47 | 14.43 | 9.45 | 12.88 | 7.04 | 6.81 | 0.72 | 2.30 |
| 2012/4 | −4.36 | −0.27 | 14.17 | 12.48 | 5.19 | 1.75 | −9.51 | −1.16 | 4.26 |
| 2012/5 | −12.44 | 2.37 | 15.76 | 4.97 | −1.00 | −1.59 | −17.11 | −9.34 | −3.55 |
| 2012/6 | −7.42 | 6.28 | 24.37 | 0.71 | 5.78 | 4.63 | −5.25 | 13.90 | −0.76 |
| 2012/7 | 84.50 | 31.30 | 62.46 | 32.90 | 82.44 | 76.25 | 70.66 | 72.00 | 70.00 |
| 2012/8 | 61.12 | 58.20 | 62.53 | 64.70 | 68.16 | 64.01 | 86.30 | 54.00 | 66.42 |
| 2012/9 | 50.64 | 58.16 | 54.09 | 61.37 | 62.07 | 58.06 | 72.27 | 54.64 | 50.25 |
| 2012/10 | 41.96 | 54.64 | 44.78 | 42.22 | 51.33 | 50.31 | 58.50 | 44.86 | 42.13 |
| 2012/11 | 11.38 | 44.61 | 30.57 | 53.22 | 36.85 | 30.64 | 17.90 | 8.18 | 19.94 |
| 2012/12 | 0.00 | 9.55 | 25.73 | 26.45 | 27.00 | 23.27 | 0.46 | 10.10 | 3.92 |
| MAE/MM | 13.82 | 15.60 | 17.59 | 11.07 | 8.76 | 8.49 | 6.68 | 5.66 | |
| R2 | 0.56 | 0.61 | 0.61 | 0.80 | 0.87 | 0.91 | 0.93 | 0.95 |
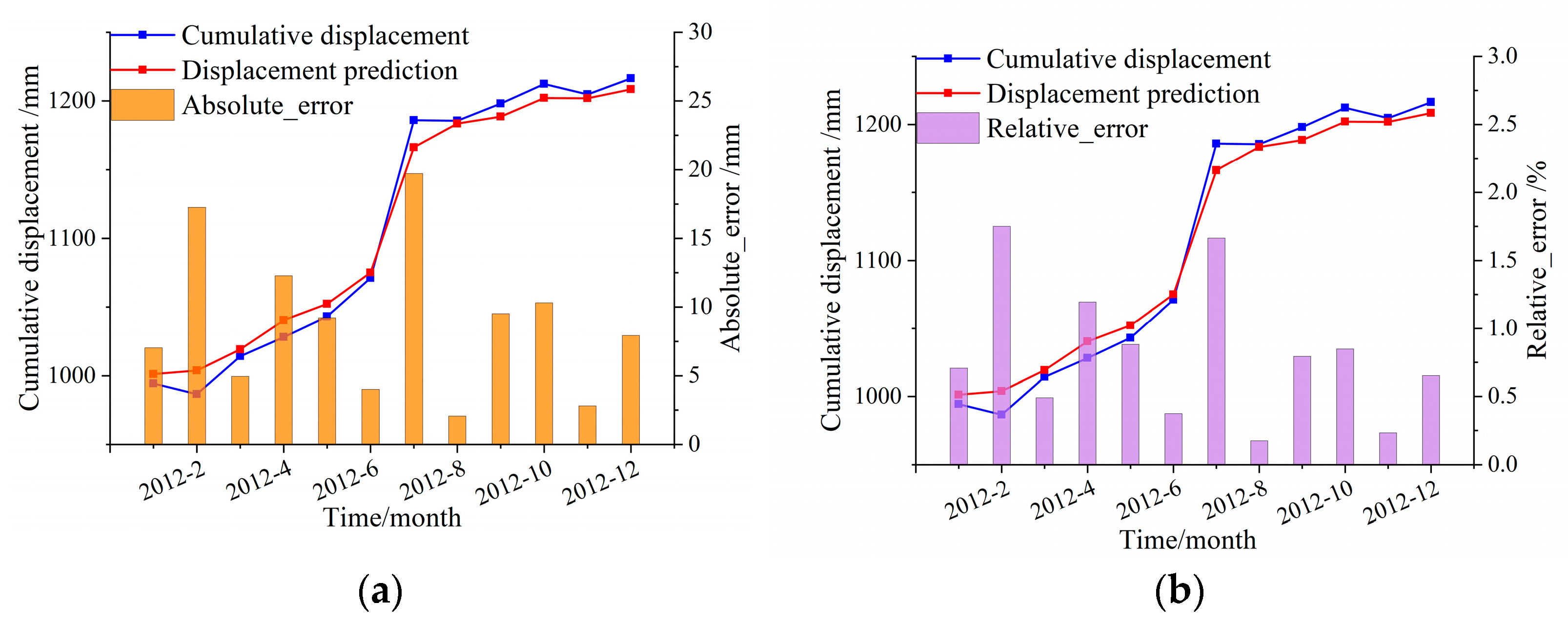
| Time Step | Trend Predicted Value (mm) | Periodic Predicted Value (mm) | Cumulative Predicted Value (mm) | Cumulative Real Value (mm) | Absolute Error (mm) | Relative Error (%) |
|---|---|---|---|---|---|---|
| 2012/1 | 979.60 | 21.74 | 1001.34 | 994.30 | 7.04 | 0.71 |
| 2012/2 | 998.10 | 5.76 | 1003.86 | 986.60 | 17.26 | 1.75 |
| 2012/3 | 1016.97 | 2.30 | 1019.27 | 1014.30 | 4.97 | 0.49 |
| 2012/4 | 1036.22 | 4.26 | 1040.47 | 1028.20 | 12.27 | 1.19 |
| 2012/5 | 1055.85 | −3.55 | 1052.30 | 1043.10 | 9.20 | 0.88 |
| 2012/6 | 1075.87 | −0.76 | 1075.11 | 1071.10 | 4.01 | 0.37 |
| 2012/7 | 1096.29 | 70.00 | 1166.28 | 1186.00 | 19.72 | 1.66 |
| 2012/8 | 1117.11 | 66.42 | 1183.53 | 1185.60 | 2.07 | 0.18 |
| 2012/9 | 1138.34 | 50.25 | 1188.59 | 1198.10 | 9.51 | 0.79 |
| 2012/10 | 1159.98 | 42.13 | 1202.11 | 1212.40 | 10.29 | 0.85 |
| 2012/11 | 1182.05 | 19.94 | 1201.99 | 1204.80 | 2.81 | 0.23 |
| 2012/12 | 1204.54 | 3.92 | 1208.46 | 1216.40 | 7.94 | 0.65 |
| Maximum error | 19.72 mm | |||||
| Minimum error | 2.07 mm | |||||
| Average error | 8.93 m | |||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, C.; Huo, J.; Li, C.; Zhang, Y. Landslide Displacement Prediction Based on a Two-Stage Combined Deep Learning Model under Small Sample Condition. Remote Sens. 2022, 14, 3732. https://doi.org/10.3390/rs14153732
Yu C, Huo J, Li C, Zhang Y. Landslide Displacement Prediction Based on a Two-Stage Combined Deep Learning Model under Small Sample Condition. Remote Sensing. 2022; 14(15):3732. https://doi.org/10.3390/rs14153732
Chicago/Turabian StyleYu, Chunxiao, Jiuyuan Huo, Chaojie Li, and Yaonan Zhang. 2022. "Landslide Displacement Prediction Based on a Two-Stage Combined Deep Learning Model under Small Sample Condition" Remote Sensing 14, no. 15: 3732. https://doi.org/10.3390/rs14153732
APA StyleYu, C., Huo, J., Li, C., & Zhang, Y. (2022). Landslide Displacement Prediction Based on a Two-Stage Combined Deep Learning Model under Small Sample Condition. Remote Sensing, 14(15), 3732. https://doi.org/10.3390/rs14153732






