Constructing High-Resolution (10 km) Daily Diffuse Solar Radiation Dataset across China during 1982–2020 through Ensemble Model
Abstract
:1. Introduction
2. Materials and Methods
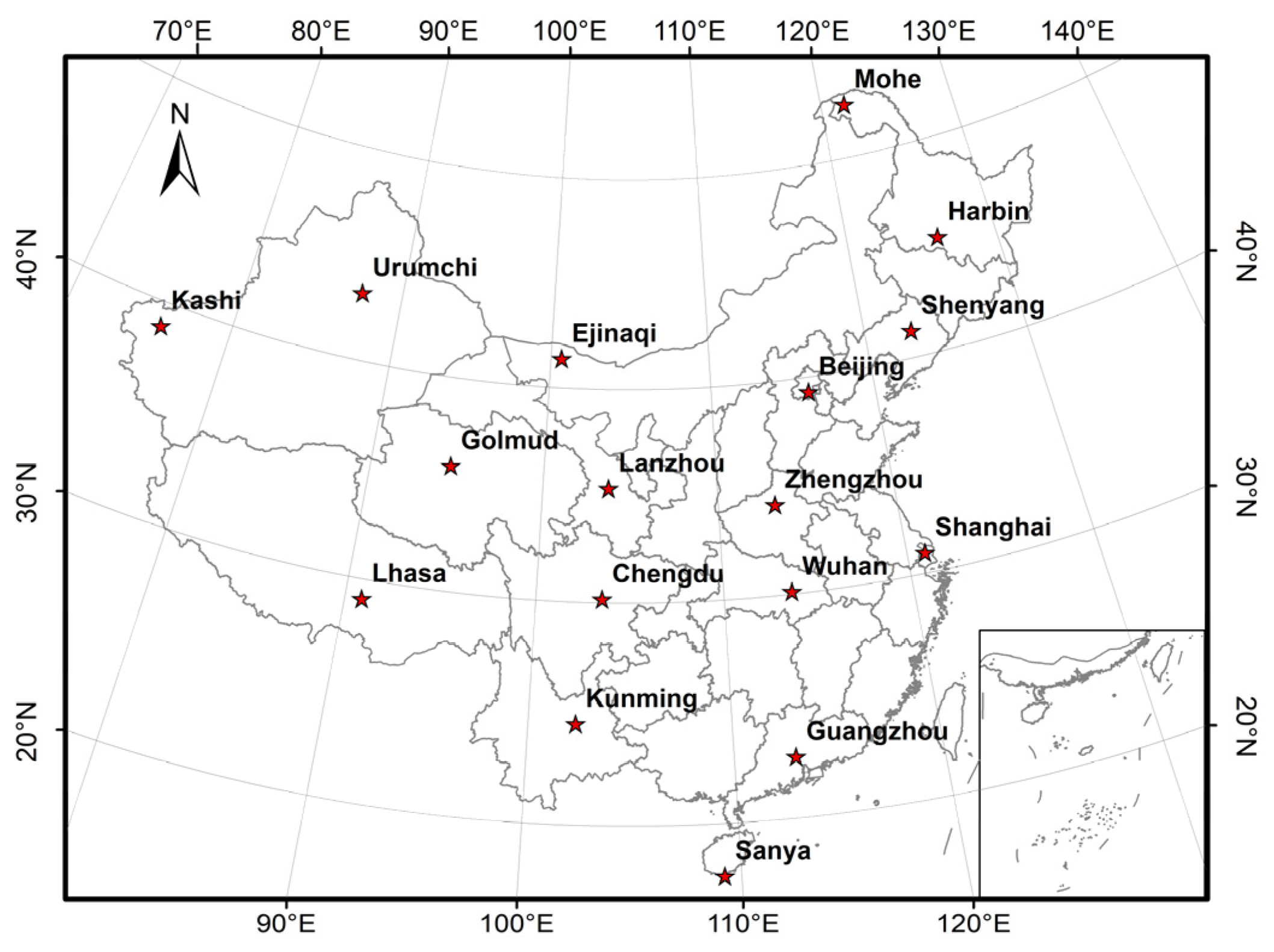
2.1. Study Region and Data
2.1.1. Ground-Level Daily Diffuse Solar Radiation Measurements
2.1.2. Reanalysis Data
2.1.3. Existing Diffuse Solar Radiation Products
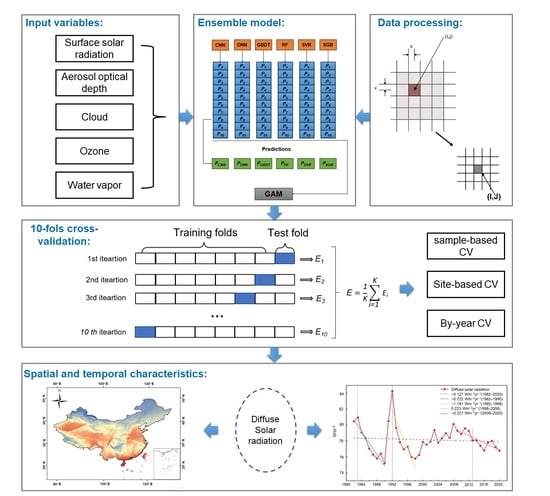
2.2. Methodology
2.2.1. Data Processing
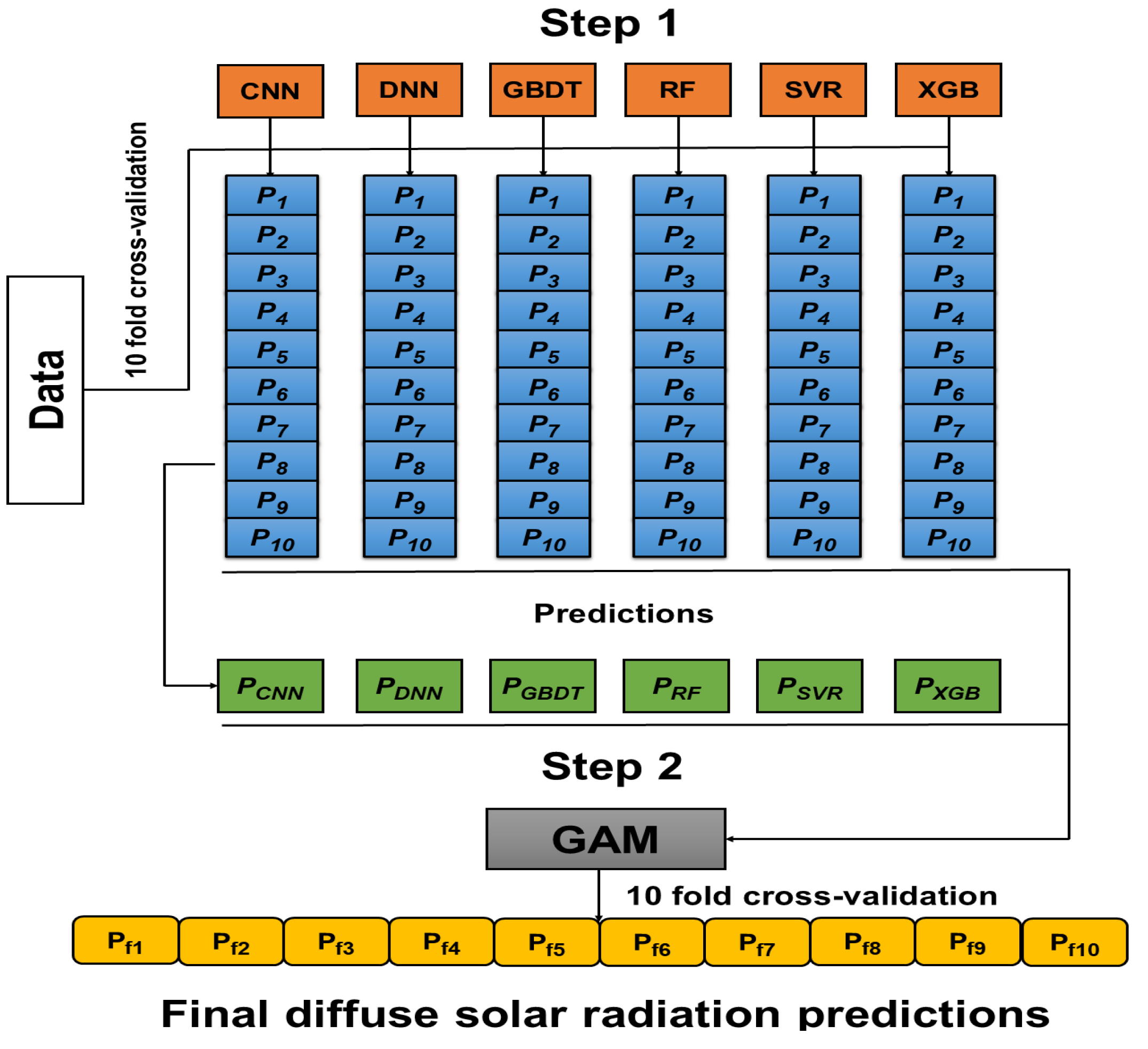
2.2.2. Base Learners and Ensemble Model
Deep Learning
Boosting Algorithm
Others
Generalized Additive Models
2.2.3. Model Development
3. Results
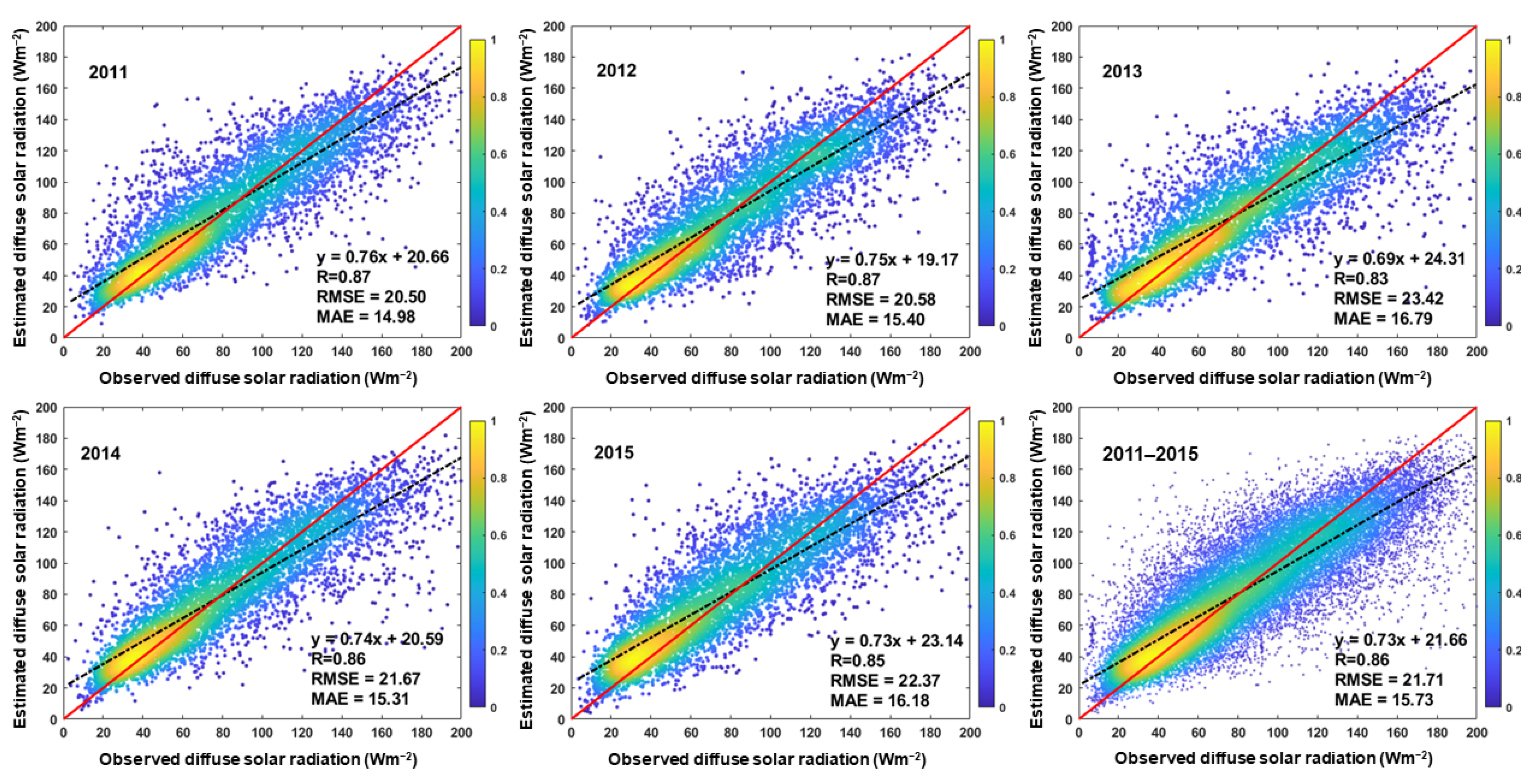
3.1. Evaluation of the Model Performance
3.2. Comparison with Other Diffuse Solar Radiation Products
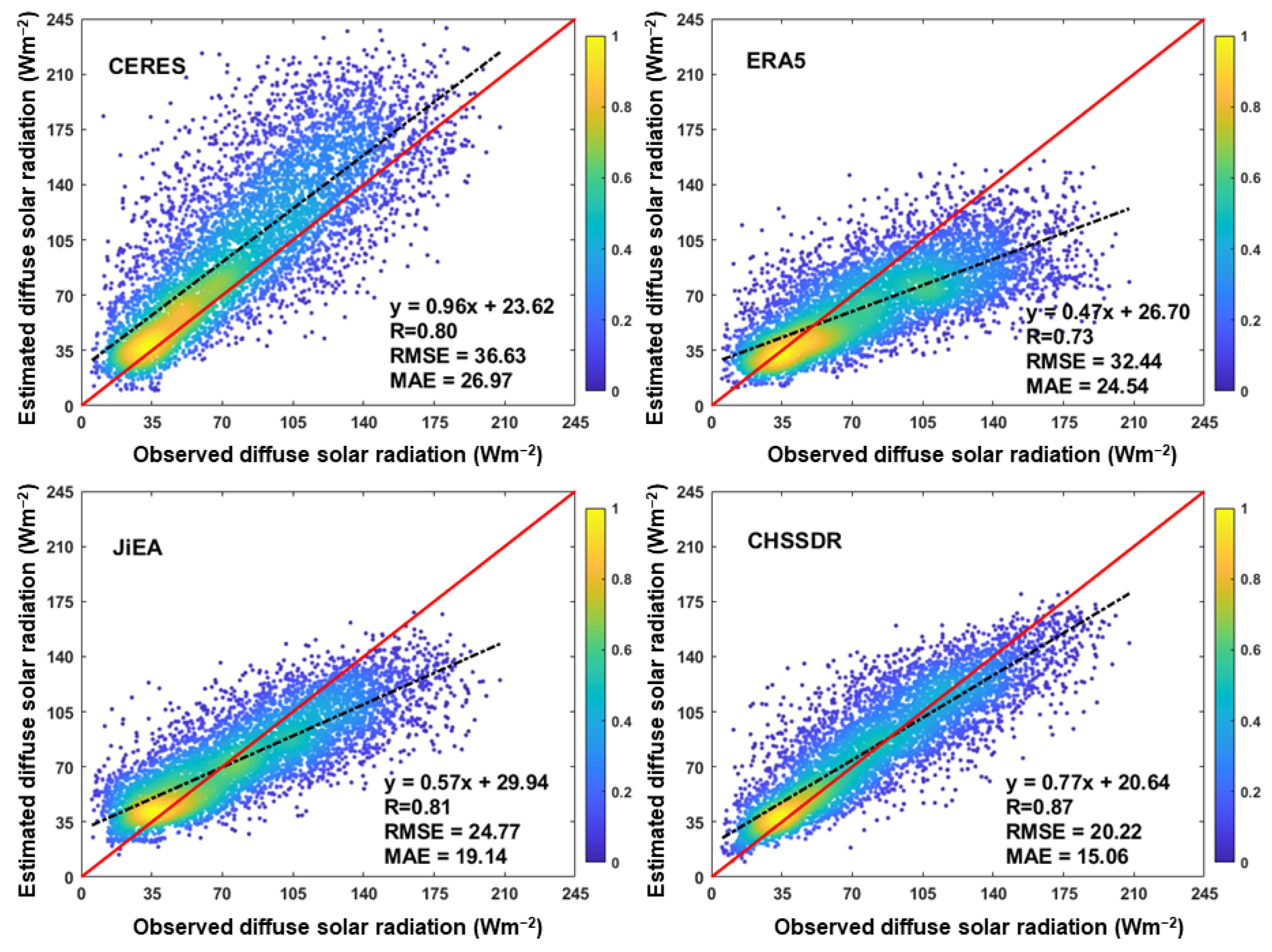
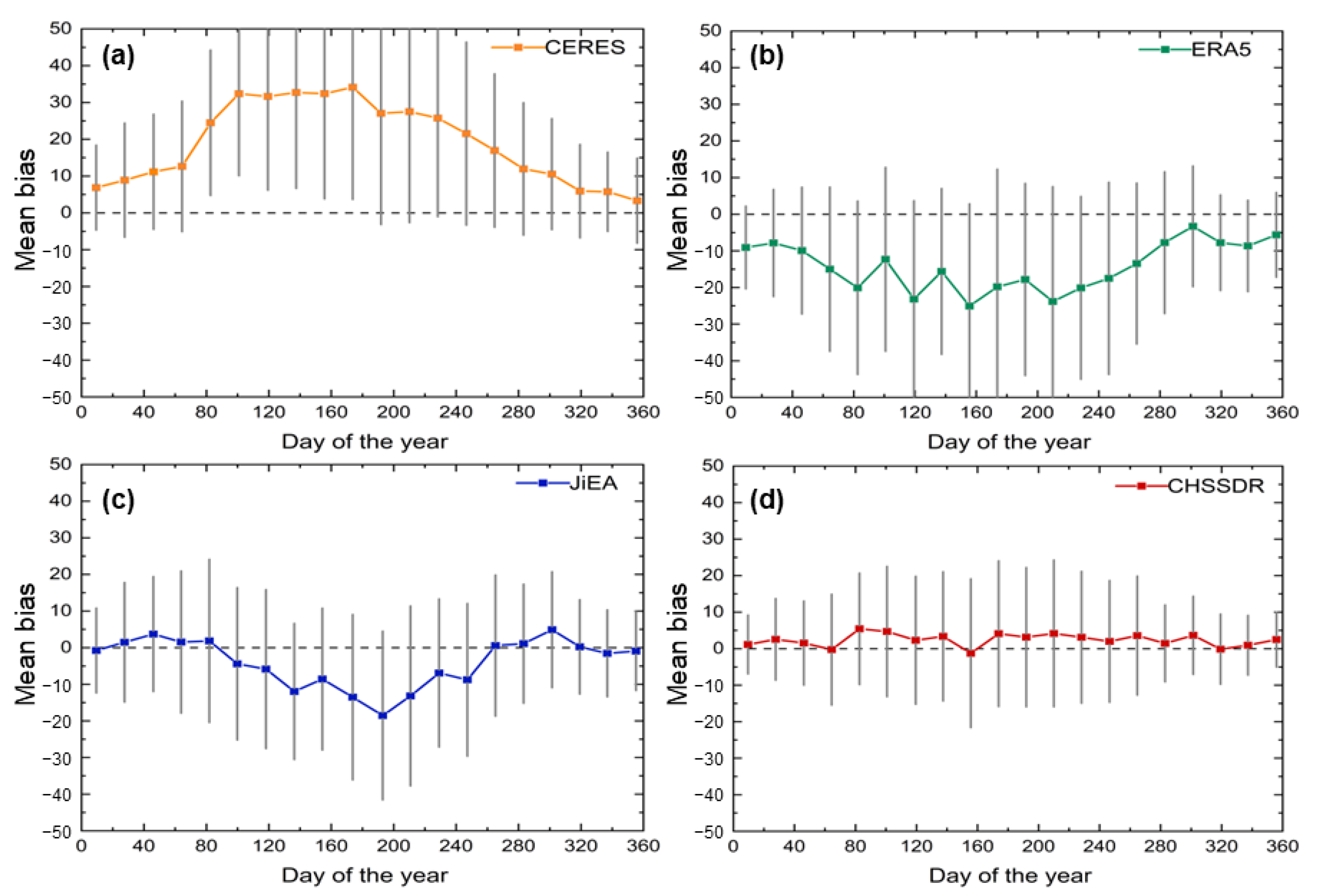
3.2.1. Validation between Diffuse Solar Radiation Products and Ground Observation Data
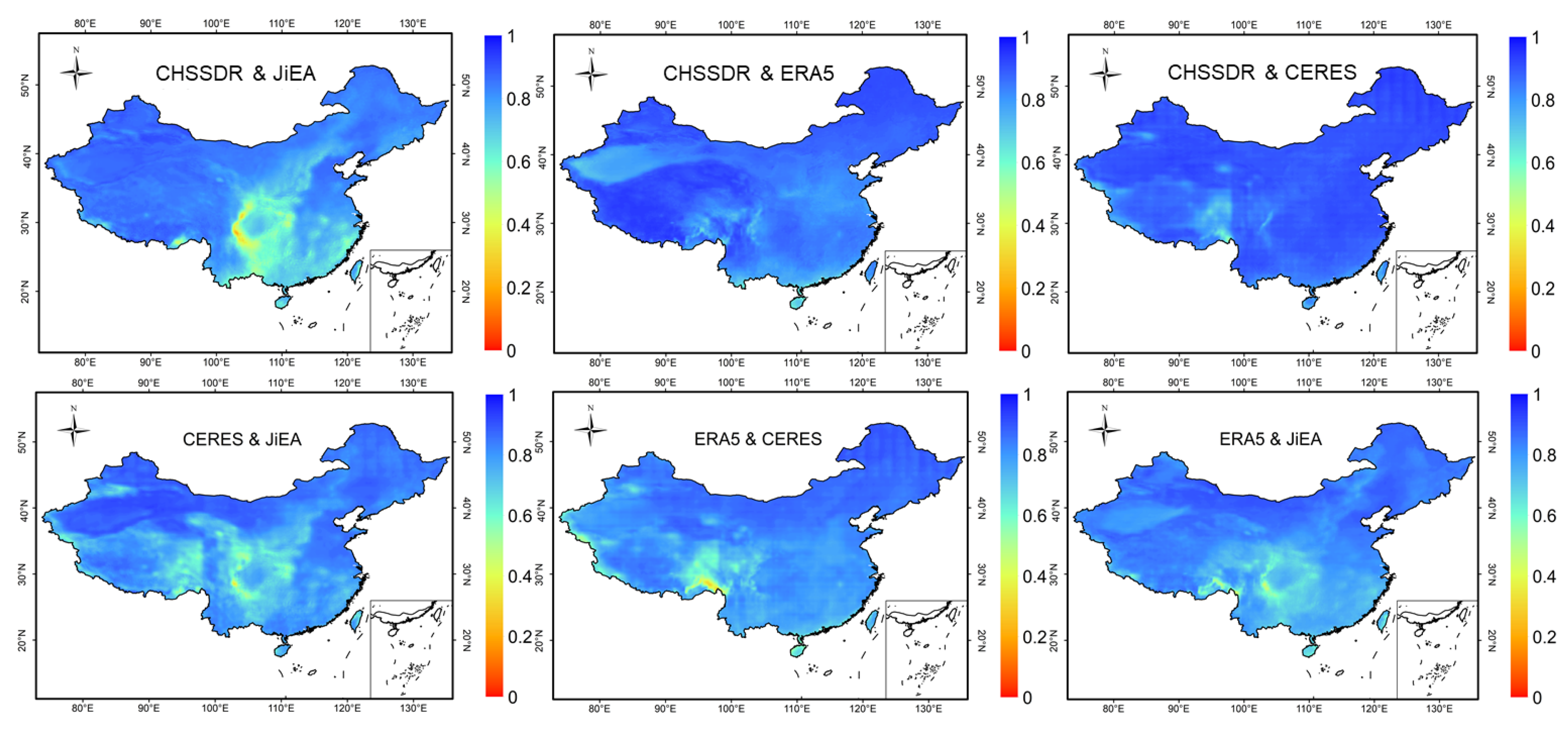
3.2.2. Intercomparison Analysis of Multiple Diffused Radiation Products
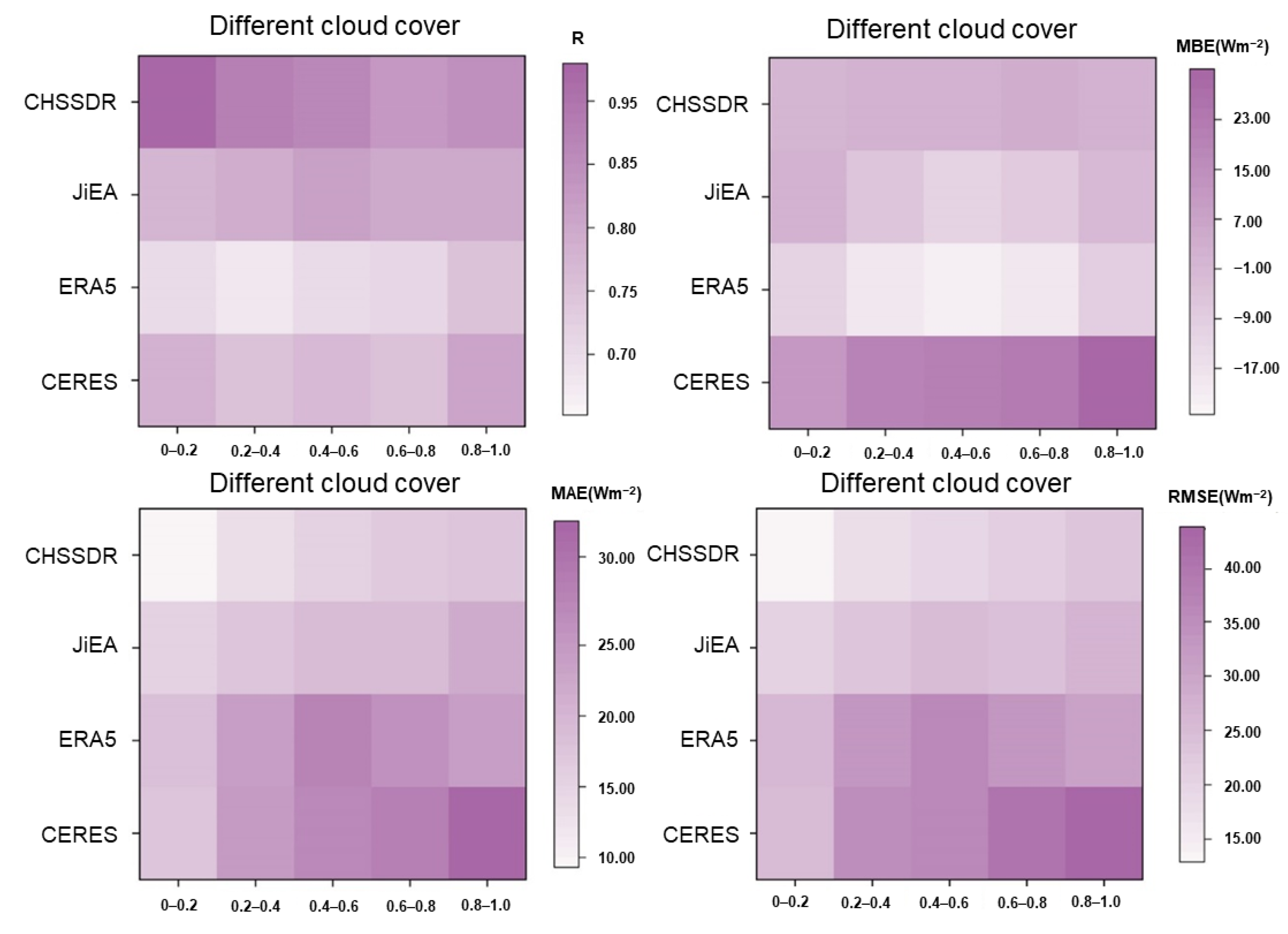
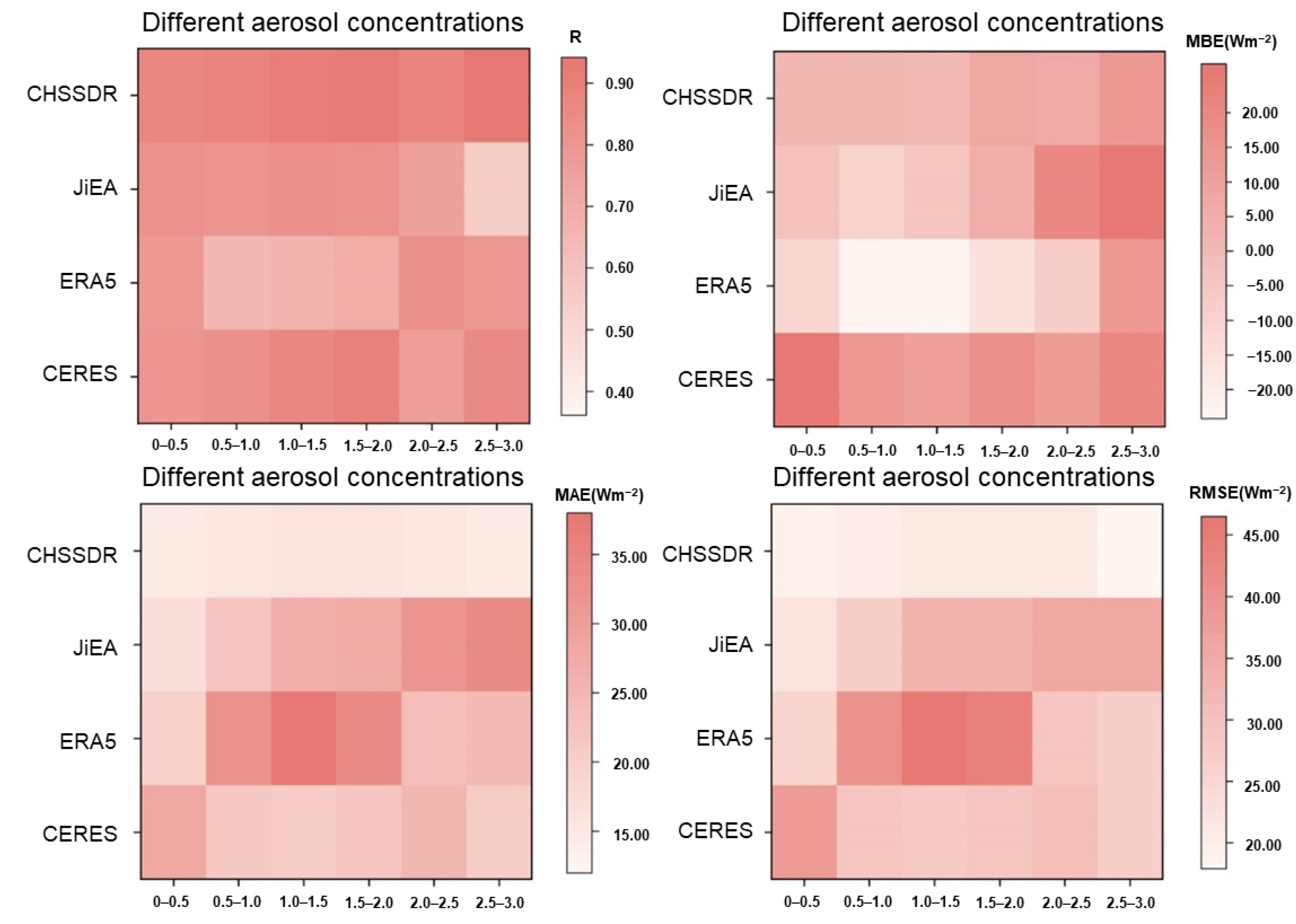
3.2.3. Error Comparison under the Different Conditions
3.3. Spatial and Temporal Distribution of Diffuse Solar Radiation
3.3.1. Dataset Availability
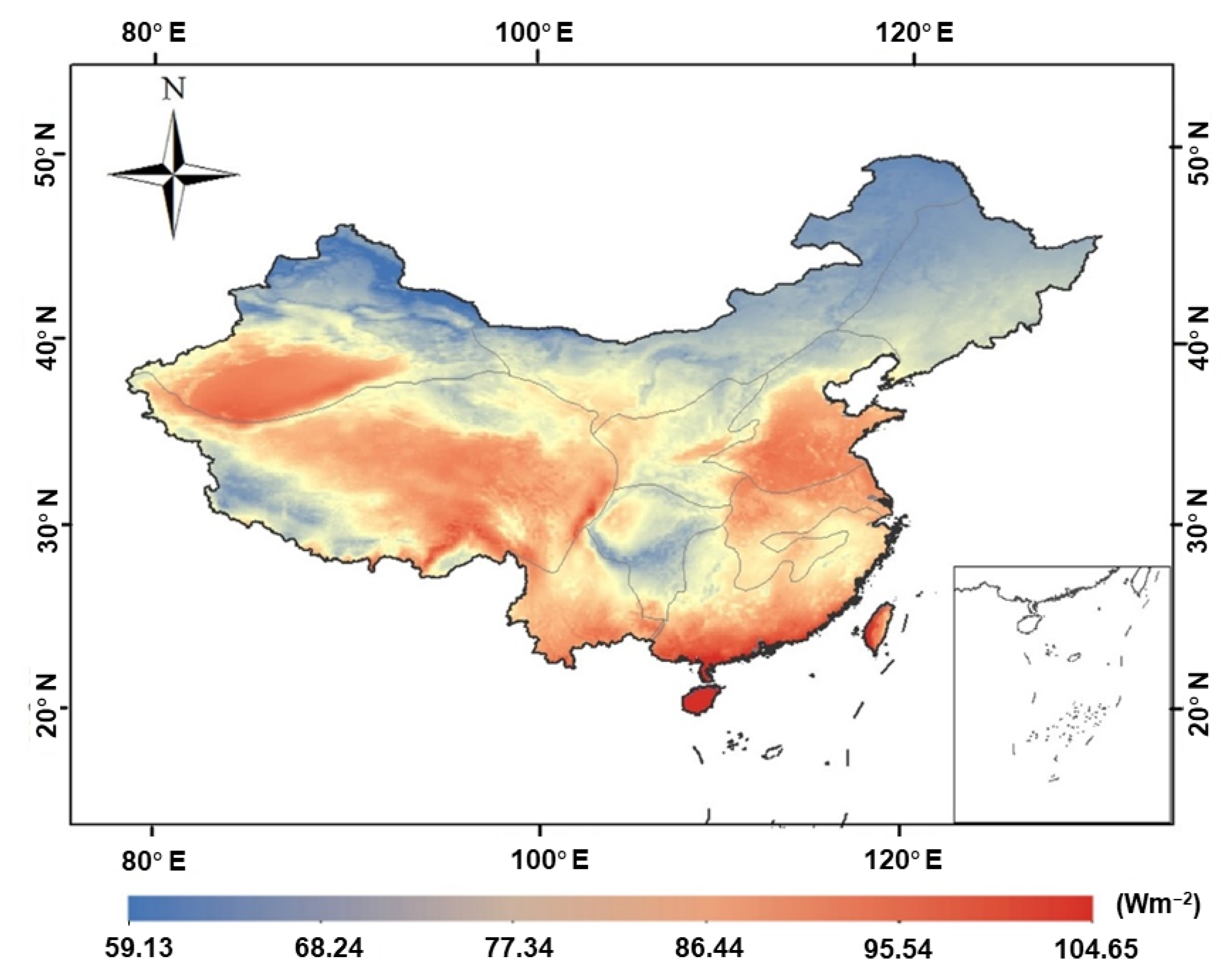
3.3.2. Annual Average Spatial Distribution of Diffuse Solar Radiation
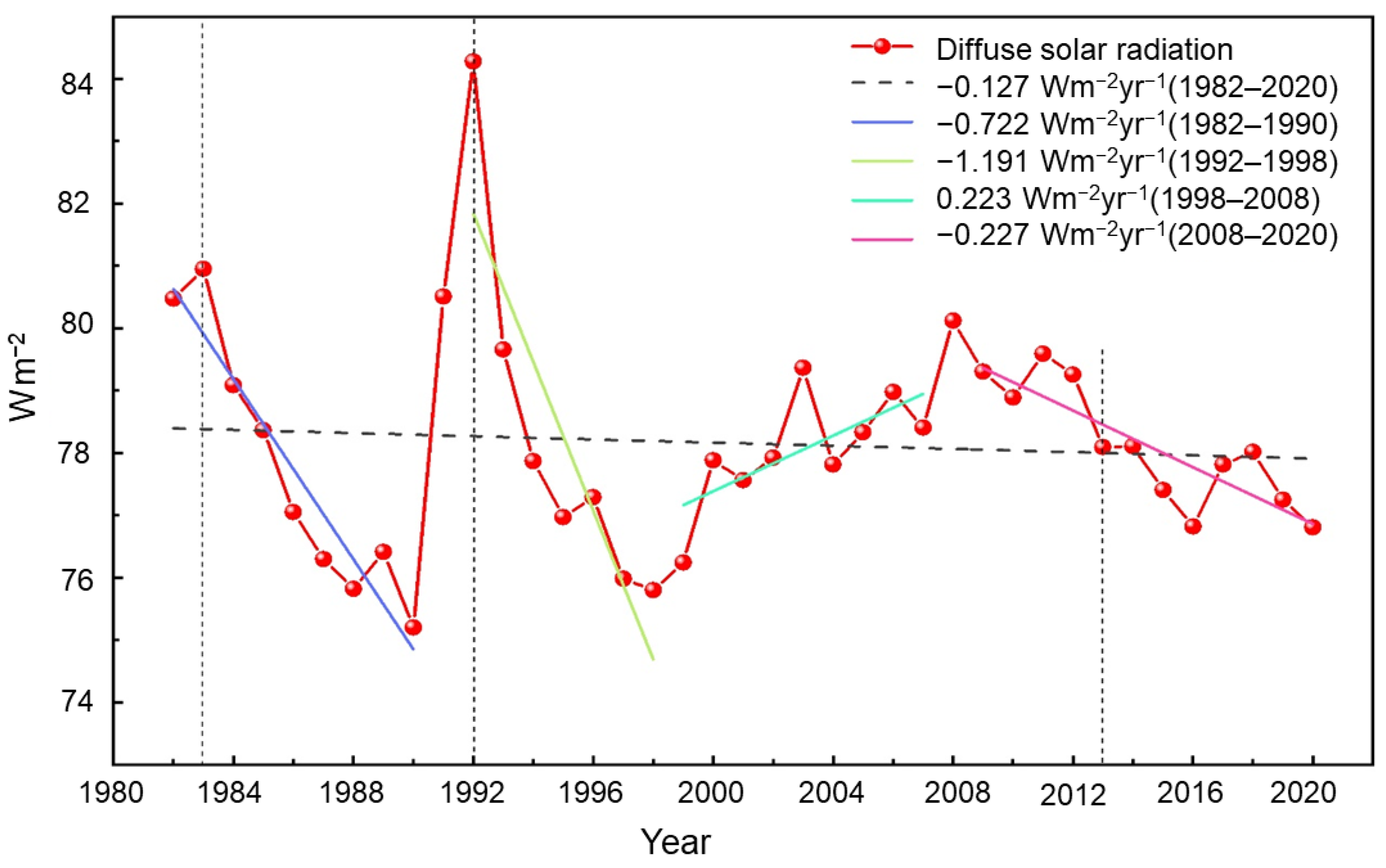
3.3.3. Interannual Variation Trend of Diffuse Solar Radiation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhu, T.; Li, J.; He, L.; Wu, D.; Tong, X.; Mu, Q.; Yu, Q. The improvement and comparison of diffuse radiation models in different climatic zones of China. Atmos. Res. 2021, 254, 105505. [Google Scholar] [CrossRef]
- Wang, L.; Lu, Y.; Zou, L.; Feng, L.; Wei, J.; Qin, W.; Niu, Z. Prediction of diffuse solar radiation based on multiple variables in China. Renew. Sustain. Energy Rev. 2019, 103, 151–216. [Google Scholar] [CrossRef]
- Alton, P.B.; North, P.R.; Los, S.O. The impact of diffuse sunlight on canopy light-use efficiency, gross photosynthetic product and net ecosystem exchange in three forest biomes. Global Change Biol. 2007, 13, 776–787. [Google Scholar] [CrossRef]
- Kanniah, K.D.; Beringer, J.; North, P.; Hutley, L. Control of atmospheric particles on diffuse radiation and terrestrial plant productivity: A review. Prog. Phys. Geog. 2012, 36, 209–237. [Google Scholar] [CrossRef]
- Mercado, L.M.; Bellouin, N.; Sitch, S.; Boucher, O.; Huntingford, C.; Wild, M.; Cox, P.M. Impact of changes in diffuse radiation on the global land carbon sink. Nature 2009, 458, 1014–1017. [Google Scholar] [CrossRef] [Green Version]
- Misson, L.; Lunden, M.; McKay, M.; Goldstein, A.H. Atmospheric aerosol light scattering and surface wetness influence the diurnal pattern of net ecosystem exchange in a semi-arid ponderosa pine plantation. Agr. Forest Meteorol. 2005, 129, 69–83. [Google Scholar] [CrossRef]
- Lee, M.S.; Hollinger, D.Y.; Keenan, T.F.; Ouimette, A.P.; Ollinger, S.V.; Richardson, A.D. Model-based analysis of the impact of diffuse radiation on CO2 exchange in a temperate deciduous forest. Agr. Forest Meteorol. 2018, 249, 377–389. [Google Scholar] [CrossRef] [Green Version]
- Prăvălie, R.; Patriche, C.; Bandoc, G. Spatial assessment of solar energy potential at global scale. A geographical approach. J. Clean. Prod. 2019, 209, 692–721. [Google Scholar] [CrossRef]
- Kim, C.K.; Kim, H.; Kang, Y.; Yun, C.; Kim, B.; Kim, J.Y. Solar Resource Potentials and Annual Capacity Factor Based on the Korean Solar Irradiance Datasets Derived by the Satellite Imagery from 1996 to 2019. Remote Sens. 2021, 13, 3422. [Google Scholar] [CrossRef]
- Sanchez-Lorenzo, A.; Enriquez-Alonso, A.; Wild, M.; Trentmann, J.; Vicente-Serrano, S.M.; Sanchez-Romero, A.; Posselt, R.; Hakuba, M.Z. Trends in downward surface solar radiation from satellites and ground observations over Europe during 1983–2010. Remote Sens. Environ. 2017, 189, 108–117. [Google Scholar] [CrossRef] [Green Version]
- Cano, D.; Monget, J.; Albuisson, M.; Guillard, H.; Regas, N.; Wald, L. A method for the determination of the global solar radiation from meteorological satellite data. Sol. Energy 1986, 37, 31–39. [Google Scholar] [CrossRef] [Green Version]
- Beyer, H.G.; Costanzo, C.; Heinemann, D. Modifications of the Heliosat procedure for irradiance estimates from satellite images. Sol. Energy 1996, 56, 207–212. [Google Scholar] [CrossRef]
- Laguarda, A.; Giacosa, G.; Alonso-Suárez, R.; Abal, G. Performance of the site-adapted CAMS database and locally adjusted cloud index models for estimating global solar horizontal irradiation over the Pampa Húmeda. Sol. Energy 2020, 199, 295–307. [Google Scholar] [CrossRef]
- Rusen, S.E.; Konuralp, A. Quality control of diffuse solar radiation component with satellite-based estimation methods. Renew. Energy 2020, 145, 1772–1779. [Google Scholar] [CrossRef]
- Oh, M.; Kim, C.K.; Kim, B.; Yun, C.; Kim, J.; Kang, Y.; Kim, H. Analysis of minute-scale variability for enhanced separation of direct and diffuse solar irradiance components using machine learning algorithms. Energy 2022, 241, 122921. [Google Scholar] [CrossRef]
- Qin, J.; Tang, W.; Yang, K.; Lu, N.; Niu, X.; Liang, S. An efficient physically based parameterization to derive surface solar irradiance based on satellite atmospheric products. J. Geophys. Res. Atmos. 2015, 120, 4975–4988. [Google Scholar] [CrossRef]
- Jiang, H.; Lu, N.; Qin, J.; Yao, L. Hourly 5-km surface total and diffuse solar radiation in China, 2007–2018. Sci. Data 2020, 7, 1–12. [Google Scholar] [CrossRef]
- Tang, W.; Qin, J.; Yang, K.; Liu, S.; Lu, N.; Niu, X. Retrieving high-resolution surface solar radiation with cloud parameters derived by combining MODIS and MTSAT data. Atmos. Chem. Phys. 2016, 16, 2543–2557. [Google Scholar] [CrossRef] [Green Version]
- Jiang, H.; Lu, N.; Qin, J.; Tang, W.; Yao, L. A deep learning algorithm to estimate hourly global solar radiation from geostationary satellite data. Renew. Sustain. Energy Rev. 2019, 114, 109327. [Google Scholar] [CrossRef]
- Tang, W.; Yang, K.; Qin, J.; Li, X.; Niu, X. A 16-year dataset (2000–2015) of high-resolution (3 h, 10 km) global surface solar radiation. Earth Syst. Sci. Data 2019, 11, 1905–1915. [Google Scholar] [CrossRef] [Green Version]
- Şenkal, O.; Kuleli, T. Estimation of solar radiation over Turkey using artificial neural network and satellite data. Appl. Energ. 2009, 86, 1222–1228. [Google Scholar] [CrossRef]
- Ouarda, T.B.M.J.; Charron, C.; Marpu, P.R.; Chebana, F. The Generalized Additive Model for the Assessment of the Direct, Diffuse, and Global Solar Irradiances Using SEVIRI Images, With Application to the UAE. IEEE J. Stars. 2016, 9, 1553–1566. [Google Scholar] [CrossRef] [Green Version]
- Cornejo-Bueno, L.; Casanova-Mateo, C.; Sanz-Justo, J.; Salcedo-Sanz, S. Machine learning regressors for solar radiation estimation from satellite data. Sol. Energy. 2019, 183, 768–775. [Google Scholar] [CrossRef]
- Yang, L.; Zhang, X.; Liang, S.; Yao, Y.; Jia, K.; Jia, A. Estimating surface downward shortwave radiation over china based on the gradient boosting decision tree method. Remote Sens. 2018, 10, 185. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Jiang, B.; Liang, S.; Wang, D.; He, T.; Wang, Q.; Zhao, X.; Xu, J. Surface Shortwave net radiation estimation from Landsat TM/ETM+ data using four machine learning algorithms. Remote Sens. 2019, 11, 2847. [Google Scholar] [CrossRef] [Green Version]
- Letu, H.; Yang, K.; Nakajima, T.Y.; Ishimoto, H.; Nagao, T.M.; Riedi, J.; Baran, A.J.; Ma, R.; Wang, T.; Shang, H. High-resolution retrieval of cloud microphysical properties and surface solar radiation using Himawari-8/AHI next-generation geostationary satellite. Remote Sens. Environ. 2020, 239, 111583. [Google Scholar] [CrossRef]
- Jamil, B.; Akhtar, N. Comparative analysis of diffuse solar radiation models based on sky-clearness index and sunshine period for humid-subtropical climatic region of India: A case study. Renew. Sustain. Energy Rev. 2017, 78, 329–355. [Google Scholar] [CrossRef]
- Jamil, B.; Akhtar, N. Comparison of empirical models to estimate monthly mean diffuse solar radiation from measured data: Case study for humid-subtropical climatic region of India. Renew. Sustain. Energy Rev. 2017, 77, 1326–1342. [Google Scholar] [CrossRef]
- Mubiru, J.; Banda, E. Performance of empirical correlations for predicting monthly mean daily diffuse solar radiation values at Kampala, Uganda. Theor. Appl. Climatol. 2007, 88, 127–131. [Google Scholar] [CrossRef]
- Sabzpooshani, M.; Mohammadi, K. Establishing new empirical models for predicting monthly mean horizontal diffuse solar radiation in city of Isfahan, Iran. Energy 2014, 69, 571–577. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, D.; Liu, Y.; Liu, J. Diffuse solar radiation models for different climate zones in China: Model evaluation and general model development. Energ. Convers. Manage. 2019, 185, 518–536. [Google Scholar] [CrossRef]
- Gueymard, C.A. Parameterized transmittance model for direct beam and circumsolar spectral irradiance. Sol. Energy 2001, 71, 325–346. [Google Scholar] [CrossRef]
- Lemos, L.F.; Starke, A.R.; Boland, J.; Cardemil, J.M.; Machado, R.D.; Colle, S. Assessment of solar radiation components in Brazil using the BRL model. Renew. Energy 2017, 108, 569–580. [Google Scholar] [CrossRef]
- Iqbal, M. An Introduction to Solar Radiation; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Gueymard, C.A. REST2: High-performance solar radiation model for cloudless-sky irradiance, illuminance, and photosynthetically active radiation–Validation with a benchmark dataset. Sol. Energy 2008, 82, 272–285. [Google Scholar] [CrossRef]
- Gueymard, C. A two-band model for the calculation of clear sky solar irradiance, illuminance, and photosynthetically active radiation at the earth’s surface. Sol. Energy 1989, 43, 253–265. [Google Scholar] [CrossRef]
- Rehman, S.; Mohandes, M. Estimation of diffuse fraction of global solar radiation using artificial neural networks. Energy Sources Part A 2009, 31, 974–984. [Google Scholar] [CrossRef]
- Feng, Y.; Cui, N.; Zhang, Q.; Zhao, L.; Gong, D. Comparison of artificial intelligence and empirical models for estimation of daily diffuse solar radiation in North China Plain. Int. J. Hydrogen Energ. 2017, 42, 14418–14428. [Google Scholar] [CrossRef]
- Mellit, A.; Eleuch, H.; Benghanem, M.; Elaoun, C.; Pavan, A.M. An adaptive model for predicting of global, direct and diffuse hourly solar irradiance. Energ. Convers. Manage. 2010, 51, 771–782. [Google Scholar] [CrossRef]
- Schulz, K.; Hänsch, R.; Sörgel, U. Machine learning methods for remote sensing applications: An overview. Earth Resour. Environ. Remote. Sens./GIS Appl. IX 2018, 10790, 1079002. [Google Scholar]
- Letu, H.; Shi, J.; Li, M.; Wang, T.; Shang, H.; Lei, Y.; Ji, D.; Wen, J.; Yang, K.; Chen, L. A review of the estimation of downward surface shortwave radiation based on satellite data: Methods, progress and problems. Sci. China Earth Sci. 2020, 63, 774–789. [Google Scholar] [CrossRef]
- Bamisile, O.; Oluwasanmi, A.; Ejiyi, C.; Yimen, N.; Obiora, S.; Huang, Q. Comparison of machine learning and deep learning algorithms for hourly global/diffuse solar radiation predictions. Int. J. Energ. Res. 2021, 46, 10052–10073. [Google Scholar] [CrossRef]
- Aler, R.; Galván, I.M.; Ruiz-Arias, J.A.; Gueymard, C.A. Improving the separation of direct and diffuse solar radiation components using machine learning by gradient boosting. Sol. Energy 2017, 150, 558–569. [Google Scholar] [CrossRef]
- Fan, J.; Wang, X.; Zhang, F.; Ma, X.; Wu, L. Predicting daily diffuse horizontal solar radiation in various climatic regions of China using support vector machine and tree-based soft computing models with local and extrinsic climatic data. J. Clean. Prod. 2020, 248, 119264. [Google Scholar] [CrossRef]
- Jia, D.; Yang, L.; Lv, T.; Liu, W.; Gao, X.; Zhou, J. Evaluation of machine learning models for predicting daily global and diffuse solar radiation under different weather/pollution conditions. Renew. Energy 2022, 187, 896–906. [Google Scholar] [CrossRef]
- Benali, L.; Notton, G.; Fouilloy, A.; Voyant, C.; Dizene, R. Solar radiation forecasting using artificial neural network and random forest methods: Application to normal beam, horizontal diffuse and global components. Renew. Energy 2019, 132, 871–884. [Google Scholar] [CrossRef]
- Shamshirband, S.; Mohammadi, K.; Khorasanizadeh, H.; Yee, P.L.; Lee, M.; Petković, D.; Zalnezhad, E. Estimating the diffuse solar radiation using a coupled support vector machine–wavelet transform model. Renew. Sustain. Energy Rev. 2016, 56, 428–435. [Google Scholar] [CrossRef]
- Jović, S.; Aničić, O.; Marsenić, M.; Nedić, B. Solar radiation analyzing by neuro-fuzzy approach. Energ. Build. 2016, 129, 261–263. [Google Scholar] [CrossRef]
- Landeras, G.; López, J.J.; Kisi, O.; Shiri, J. Comparison of Gene Expression Programming with neuro-fuzzy and neural network computing techniques in estimating daily incoming solar radiation in the Basque Country (Northern Spain). Energy Convers. Manage. 2012, 62, 1–13. [Google Scholar] [CrossRef]
- Sanchez-Lorenzo, A.; Calbó, J.; Wild, M. Global and diffuse solar radiation in Spain: Building a homogeneous dataset and assessing their trends. Global Planet. Change 2013, 100, 343–352. [Google Scholar] [CrossRef]
- Yang, D.; Bright, J.M. Worldwide validation of 8 satellite-derived and reanalysis solar radiation products: A preliminary evaluation and overall metrics for hourly data over 27 years. Sol. Energy 2020, 210, 3–19. [Google Scholar] [CrossRef]
- Huang, G.; Li, Z.; Li, X.; Liang, S.; Yang, K.; Wang, D.; Zhang, Y. Estimating surface solar irradiance from satellites: Past, present, and future perspectives. Remote Sens. Environ. 2019, 233, 111371. [Google Scholar] [CrossRef]
- Jiang, H.; Yang, Y.; Wang, H.; Bai, Y.; Bai, Y. Surface Diffuse Solar Radiation Determined by Reanalysis and Satellite over East Asia: Evaluation and Comparison. Remote Sens. 2020, 12, 1387. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. Roy. Meteor. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Qin, W.; Wang, L.; Wei, J.; Hu, B.; Liang, X. A novel efficient broadband model to derive daily surface solar Ultraviolet radiation (0.280–0.400 μm). Sci. Total Environ. 2020, 735, 139513. [Google Scholar] [CrossRef] [PubMed]
- Wielicki, B.A.; Barkstrom, B.R.; Harrison, E.F.; III, R.B.L.; Smith, G.L. Clouds and the Earth’s Radiant Energy System (CERES): An Earth Observing System Experiment. Bull. Am. Meteorol. Soc. 1996, 77, 853–868. [Google Scholar] [CrossRef] [Green Version]
- Jiang, H.; Yang, Y.; Bai, Y.; Wang, H. Evaluation of the Total, Direct, and Diffuse Solar Radiations from the ERA5 Reanalysis Data in China. IEEE Geosci. Remote S. 2020, 17, 47–51. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- LeCun, Y.; Boser, B.; Denker, J.; Henderson, D.; Howard, R.; Hubbard, W.; Jackel, L. Handwritten digit recognition with a back-propagation network. Adv. Neural Inf. Process. Syst. 1989, 2, 396–404. [Google Scholar]
- Cui, L.; Wang, S. Mapping the daily nitrous acid (HONO) concentrations across China during 2006–2017 through ensemble machine-learning algorithm. Sci. Total Environ. 2021, 785, 147325. [Google Scholar] [CrossRef]
- Chen, T.; He, T.; Benesty, M.; Khotilovich, V.; Tang, Y.; Cho, H.; Chen, K. Xgboost: Extreme gradient boosting. R Package Version 0.4-2. 2015, 1, 1–4. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Fan, J.; Wu, L.; Zhang, F.; Cai, H.; Zeng, W.; Wang, X.; Zou, H. Empirical and machine learning models for predicting daily global solar radiation from sunshine duration: A review and case study in China. Renew. Sustain. Energy Rev. 2019, 100, 186–212. [Google Scholar] [CrossRef]
- Di, Q.; Amini, H.; Shi, L.; Kloog, I.; Silvern, R.; Kelly, J.; Sabath, M.B.; Choirat, C.; Koutrakis, P.; Lyapustin, A.; et al. An ensemble-based model of PM2.5 concentration across the contiguous United States with high spatiotemporal resolution. Environ. Int. 2019, 130, 104909. [Google Scholar] [CrossRef] [PubMed]
- Hastie, T.; Tibshirani, R. Generalized additive models: Some applications. J. Am. Stat. Assoc. 1987, 82, 371–386. [Google Scholar] [CrossRef]
- Lukas, M.A.; de Hoog, F.R.; Anderssen, R.S. Efficient algorithms for robust generalized cross-validation spline smoothing. J. Comput. Appl. Math. 2010, 235, 102–107. [Google Scholar] [CrossRef] [Green Version]
- Zheng, M.; Cass, G.R.; Schauer, J.J.; Edgerton, E.S. Source Apportionment of PM2.5 in the Southeastern United States Using Solvent-Extractable Organic Compounds as Tracers. Environ. Sci. Technol. 2002, 36, 2361–2371. [Google Scholar] [CrossRef]
- Che, H.Z.; Shi, G.Y.; Zhang, X.Y.; Arimoto, R.; Zhao, J.Q.; Xu, L.; Wang, B.; Chen, Z.H. Analysis of 40 years of solar radiation data from China, 1961–2000. Geophys. Res. Lett. 2005, 32, L06803. [Google Scholar] [CrossRef]
- Hay, J.E.; Darby, R. El Chichón–influence on aerosol optical depth and direct, diffuse and total solar irradiances at Vancouver, BC. Atmos. Ocean. 1984, 22, 354–368. [Google Scholar] [CrossRef]
- Nagel, D.; Herber, A.; Thomason, L.W.; Leiterer, U. Vertical distribution of the spectral aerosol optical depth in the Arctic from 1993 to 1996. J. Geophys. Res. Atmos. 1998, 103, 1857–1870. [Google Scholar] [CrossRef]
- Streets, D.G.; Yan, F.; Chin, M.; Diehl, T.; Mahowald, N.; Schultz, M.; Wild, M.; Wu, Y.; Yu, C. Anthropogenic and natural contributions to regional trends in aerosol optical depth, 1980–2006. J. Geophys. Res. Atmos. 2009, 114, D00D18. [Google Scholar] [CrossRef]
- He, Q.; Zhang, M.; Huang, B. Spatio-temporal variation and impact factors analysis of satellite-based aerosol optical depth over China from 2002 to 2015. Atmos. Environ. 2016, 129, 79–90. [Google Scholar] [CrossRef]

| Dataset | Parameters Used in This Study | Spatial Resolution | Temporal Resolution |
|---|---|---|---|
| ERA5-single | TOA incident solar radiation (TISR), surface solar radiation downward clear sky (SSRDC), boundary layer height (BLH), total column ozone (TCO), low cloud cover (LCC), high cloud cover (HCC), medium cloud cover (MCC), total column cloud ice water (TCCIW), total column cloud liquid water (TCCLW), total cloud cover (TCW), total column water (TCW) | 0.25° × 0.25° | Hourly |
| ERA5-land | 2m Temperature (T2m), forecast albedo (FA), total precipitation (TP), surface solar radiation downwards (SSRD), surface pressure (SP) | 0.1° × 0.1° | Hourly |
| MERRA-2 | Aerosol optical depth (AOD) | 0.625° × 0.5° | Hourly |
| Products | Parameters | Spatial Resolution | Temporal Resolution |
| CERES-SYN1deg | Surface shortwave diffuse flux | 1° × 1° | Daily |
| JiEA | Diffuse solar radiation | 0.05° × 0.05° | Daily |
| ERA5 | Surface solar radiation downwards, total sky direct solar radiation at surface | 0.25° × 0.25° | Hourly |
| CHSSDR | Diffuse solar radiation | 0.1° × 0.1° | Daily |
| Stations | R | RMSE (Wm−2) | MAE (Wm−2) |
|---|---|---|---|
| Sanya | 0.65 | 24.11 | 18.81 |
| Guangzhou | 0.84 | 19.77 | 15.17 |
| Kunming | 0.80 | 23.24 | 16.71 |
| Lhasa | 0.83 | 26.06 | 18.55 |
| Wuhan | 0.87 | 23.09 | 17.01 |
| Chengdu | 0.84 | 22.97 | 17.91 |
| Shanghai | 0.89 | 18.51 | 13.90 |
| Zhengzhou | 0.92 | 18.50 | 13.73 |
| Lanzhou | 0.83 | 21.17 | 15.46 |
| Golmud | 0.87 | 21.40 | 16.18 |
| Kashi | 0.84 | 20.49 | 15.25 |
| Beijing | 0.91 | 18.04 | 13.03 |
| Shenyang | 0.84 | 24.20 | 16.08 |
| Ejinaqi | 0.77 | 25.13 | 18.37 |
| Urumchi | 0.79 | 19.53 | 14.79 |
| Harbin | 0.90 | 17.71 | 12.83 |
| Mohe | 0.85 | 23.21 | 13.86 |
| Overall | 0.84 | 21.60 | 15.74 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, J.; Fang, H.; Qin, W.; Wang, L.; Song, Y.; Su, X.; Zhang, Y. Constructing High-Resolution (10 km) Daily Diffuse Solar Radiation Dataset across China during 1982–2020 through Ensemble Model. Remote Sens. 2022, 14, 3695. https://doi.org/10.3390/rs14153695
Wu J, Fang H, Qin W, Wang L, Song Y, Su X, Zhang Y. Constructing High-Resolution (10 km) Daily Diffuse Solar Radiation Dataset across China during 1982–2020 through Ensemble Model. Remote Sensing. 2022; 14(15):3695. https://doi.org/10.3390/rs14153695
Chicago/Turabian StyleWu, Jinyang, Hejin Fang, Wenmin Qin, Lunche Wang, Yan Song, Xin Su, and Yujie Zhang. 2022. "Constructing High-Resolution (10 km) Daily Diffuse Solar Radiation Dataset across China during 1982–2020 through Ensemble Model" Remote Sensing 14, no. 15: 3695. https://doi.org/10.3390/rs14153695
APA StyleWu, J., Fang, H., Qin, W., Wang, L., Song, Y., Su, X., & Zhang, Y. (2022). Constructing High-Resolution (10 km) Daily Diffuse Solar Radiation Dataset across China during 1982–2020 through Ensemble Model. Remote Sensing, 14(15), 3695. https://doi.org/10.3390/rs14153695