Abstract
Correntropy has been proved to be effective in eliminating the adverse effects of impulsive noises in adaptive filtering. However, correntropy is not desirable when the error between the two random variables is asymmetrically distributed around zero. To address this problem, asymmetric correntropy using an asymmetric Gaussian function as the kernel function was proposed. However, an asymmetric Gaussian function is not always the best choice and can be further expanded. In this paper, we propose a robust adaptive filtering based on a more flexible definition of asymmetric correntropy, which is called generalized asymmetric correntropy that adopts a generalized asymmetric Gaussian density (GAGD) function as the kernel. With the shape parameter properly selected, the generalized asymmetric correntropy may get better performance than the original asymmetric correntropy. The steady-state performance of the adaptive filter based on the generalized maximum asymmetric correntropy criterion (GMACC) is theoretically studied and verified by simulation experiments. The asymmetric characteristics of queue delay in satellite networks is analyzed and described, and the proposed algorithm is used to predict network delay, which is essential in space telemetry. Simulation results demonstrate the desirable performance of the new algorithm.
1. Introduction
Traditional adaptive filtering builds cost functions based on the minimum mean square error (MMSE) criterion, which is desirable under the assumption that the system noise follows a Gaussian distribution [1,2]. However, when the system noise contains impulsive components, the performance of the MMSE criterion is severely degraded [3]. To solve the problem and reduce the impact of impulsive noise, robust adaptive filtering has been studied, adopting criteria beyond MMSE to construct robust cost functions, such as M-estimation statistics [4,5], least mean p-power [6,7], etc. In recent years, inspired by information learning theory [8], the maximum correntropy criterion (MCC) and its extensions have been studied extensively and considered to be effective when dealing with non-Gaussian system noise [9,10,11,12,13].
Correntropy in the MCC is a measure of the distance between two random variables based on a Gaussian kernel function. The distance can be also called correntropy induced metric (CIM) in the input space and CIM behaves like different norms from L2-norm to L1-norm depending on the distance between the two inputs [14,15]. With the above property, correntropy can stay insensitive to data outliers when set with a small kernel bandwidth, which diminishes the influence of impulsive noise in adaptive filtering and ensures robustness. One classic extension of the MCC is the generalized maximum correntropy criterion (GMCC) based on a generalized Gaussian kernel, which adds a shape parameter to the Gaussian kernel and improves the adaptability faced with different kinds of non-Gaussian system noises [11,12,13]. The MCC and GMCC have been extensively studied and applied to many applications in system parameter identification and state estimation, such as channel estimation [16,17,18], blind multiuser detection [19], SINS/GPS-integrated system estimation [20], spacecraft relative state estimation [21], acoustic echo cancellation [22], etc.
The above criteria are based on a symmetric Gaussian kernel and are desirable when dealing with symmetric distributed system noises. However, an asymmetric signal or noise exists in many areas of data analysis and signal processing, such as in insurance analysis [23], finance analysis [24,25], image processing [26], etc. Under an asymmetric noise environment, the estimation error follows a skewed distribution, thus the MCC and GMCC based on a symmetric Gaussian kernel are no longer suitable. In [27], a very enlightening idea was proposed where a maximum asymmetric correntropy criterion (MACC) was obtained by replacing the Gaussian kernel in the MCC with an asymmetric Gaussian kernel. An asymmetric Gaussian kernel can process positive and negative estimation errors with different kernel widths, respectively, so that it can better adapt to asymmetric noise. Similar to the expansion from the MCC to the GMCC [11], this paper adds a shape parameter to MACC leading to a generalized maximum asymmetric correntropy criterion (GMACC), which is based on a generalized asymmetric Gaussian (GAG) kernel [28,29,30,31] and is more flexible than MACC. Ref. [28] used finite asymmetric generalized Gaussian mixture model learning to improve the effect of infrared object detection. Ref. [29] presented an image segmentation method based on a parametric and unsupervised histogram, which was assumed to be a mixture of asymmetric generalized Gaussian distributions. In [31], an asymmetric generalized Gaussian density was used to deal with the asymmetric shape property of certain texture classes. Ref. [30] expanded the concept of a generalized Gaussian distribution to include asymmetry so as to model distributions of different tail lengths as well as different degrees of asymmetry. The above research works on the GAG kernel mostly used the kernel function to build data models, while this paper is inspired by the GMACC to construct the cost function of robust adaptive filtering, so as to improve the research framework as an extension of MACC-based adaptive filtering. More specifically, this paper improves the adaptability of MACC-based adaptive filtering by working out a generalized form of the algorithm. The adjustment of the shape parameter can balance the steady-state performance and convergence rate of the GMACC algorithm.
In practical data of regression analysis or adaptive filtering, there are noises distributed with asymmetric heavy tails extending out towards positive or negative values. For example, Ref. [23] applied a robust regression in automobile insurance premium estimation that figured out the risk of a driver given a profile (age, type of car, etc.), and revealed the asymmetric heavy-tail noise problem that the premium had to take into account the tiny fraction of well-behaved drivers who cause serious accidents and large claim amounts. Moreover, the asymmetric heavy-tail noise problem could not be neglected in time series analysis such as oil-price-related stock analysis [24]. This paper studies robust adaptive filtering based on GMACC and applies it to network delay prediction. As far as the authors know, although the network delay prediction is very important in remote tasks such as space telemetry [32] and satellite link handover management [33], the asymmetric property of the network delay, especially of the queue delay, has not been discovered and described so far.
The main contributions of this paper are as follows: (1) The GMACC is obtained by the expansion of MACC, and the relationship of different robust criteria is discussed. GMACC-based robust adaptive filtering is proposed and its properties are analyzed. (2) The steady-state performance of GMACC-based robust adaptive filtering is analyzed theoretically and verified by simulation experiments. (3) The asymmetric property of the satellite network delay is discovered and described. (4) Simulations verify the effectiveness of the GMACC-based adaptive filter in satellite network delay prediction.
2. Methodology
2.1. Generalized Asymmetric Correntropy
First, a brief review of the correntropy and the asymmetric correntropy is given.
Correntropy in information-theoretic learning (ITL) [8] is used to measure the similarity of two random variables, and is defined as:
where denote two random variables; is the expectation operator; represents the joint distribution function of ; and stands for a Mercer kernel which is in general the Gaussian kernel defined as:
where is the Gaussian kernel width, , and is the normalization parameter.
In practical adaptive filtering, the available data of are discrete and the joint distribution is unknown. So the cost function based on correntropy can be presented as the sample mean estimator:
For some asymmetric noise, the maximum correlation entropy criterion based on a Gaussian kernel is no longer applicable. MACC replaces the Gaussian kernel in the maximum correntropy criterion with the asymmetric Gaussian kernel, in which different kernel widths are used to deal with the different distributions on both sides of the asymmetric noise peak.
The expression of an asymmetric Gaussian kernel is
where k of stands for the time subscript.
To enhance the adaptability of the asymmetric correntropy-based robust adaptive filtering, this paper builds the cost function based on a new generalized maximum asymmetric correntropy criterion by adding a shape parameter to the asymmetric Gaussian kernel and extending the asymmetric Gaussian kernel to the generalized asymmetric Gaussian (GAG) kernel.
By combining the definitions of the Gaussian kernel, generalized Gaussian kernel, and asymmetric Gaussian kernel, the generalized asymmetric Gaussian kernel is obtained as
where is the shape parameter of the kernel function.
2.2. Robust Adaptive Filtering Based on GMACC
Robust adaptive filters build cost functions using statistics that can reduce the impact of impulsive noise, such as Huber statistics, fractional lower-order statistics, correntropy-induced metric statistics, etc. In the discussed situation of this paper, the system noise is not only impulsive but also asymmetric. In order to deal with this kind of system noise, this paper uses a generalized asymmetric correntropy as the cost function to build a robust linear adaptive filter.
Based on the proposed generalized asymmetric Gaussian kernel, the cost function of the adaptive filter can be presented as:
where the estimation error can be expressed as
with being the desired output at time k, being the output of the linear adaptive filter, being the system parameter vector, and being the input vector, which is composed by the sample value of the input x of the previous n times:
The solution of the adaptive filter is the system parameter vector that maximizes the cost function:
where the cost function is the expectation of the generalized asymmetric Gaussian kernel function, , which is equal to the average value of the kernel function at each time in the case of a discrete sample input, .
We use the gradient ascent method to solve the problem (9), which is similar to the gradient descent method. To simplify computation, the gradient of the kernel function corresponding to the instantaneous estimation error at each time is used as the instantaneous gradient. Then, the instantaneous-gradient-based adaptive algorithm, called in this work the GMACC algorithm, can be derived as
where the weighting function corresponding to the generalized maximum asymmetric correntropy criterion can be presented as
One can observe that:
(1) When , the GMACC algorithm becomes the MACC algorithm, which can be presented as:
where the weighting function corresponding to the generalized maximum asymmetric correntropy criterion is
(2) When , the GMACC algorithm becomes the GMCC algorithm [11]. When the two conditions and are both satisfied, the GMACC algorithm becomes the MCC algorithm. Furthermore, according to the properties of the GMCC, when , the GMACC algorithm becomes the least mean p-norm algorithm (LMP), while when and , the GMACC algorithm becomes the LMS algorithm. It can be found that GMACC is a broad concept, which includes many algorithms as its special cases. The relationship between the GMACC and other algorithms as its special cases are presented in Figure 1.
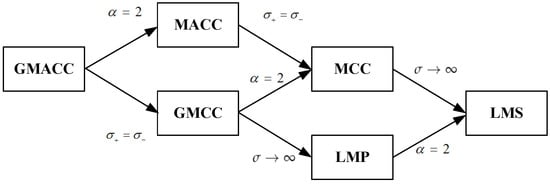
Figure 1.
Relationship between the GMACC and other algorithms.
(3) The kernel width controls the balance between convergence rate and robustness. When the kernel size is small, the estimation error can affect the value of the weighting function significantly, thus reducing the effect of the input data that cause larger estimation error. In contrast, when the kernel size is large, the weighting function stays close to , and the convergence occurs at a high rate.
Moreover, the kernel widths corresponding to the positive and negative parts of the error variable, and , determine the robustness and convergence rate of the algorithm faced with a positive and negative error, respectively. Compared with the symmetric Gaussian kernel, the asymmetric Gaussian kernel can flexibly choose the widths of the kernel, and , so as to deal with asymmetric noise better. For example, the system noise in a network delay prediction follows a right-skewed distribution due to the sharp increase of queuing delay caused by a user’s burst request, in which case a small is needed because data that bring about large positive errors are usually corrupted by impulsive noise.
(4) The GMACC algorithm can be considered as one kind of least mean square algorithm with variable step size, , which can be presented as
(5) The difference between the GMACC and other algorithms can be also attributed to the difference of the weighting functions of the algorithms. The weighting functions of robust adaptive filters usually assign less weight to data outliers or large estimation error caused by impulsive noise, which keeps the algorithm robust in a non-Gaussian noise environment. The weighting functions of different algorithms are presented in Figure 2, which shows that ITL-inspired criteria assign very little weight on sample data that cause a large estimation error compared with the MMSE criterion and least p-norm criterion, and the asymmetric criteria assign different weights on the positive and negative estimation errors even though they have the same absolute value.
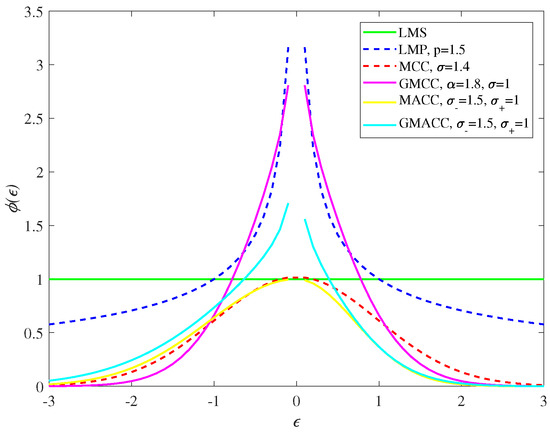
Figure 2.
The weighting functions of different algorithms.
(6) The computational complexity of the proposed GMACC algorithm is almost the same as that of the LMS algorithm, and the only extra computational effort needed is to calculate the weighting function (11), which is obviously not expensive. For a detailed description of the computational complexity of the algorithm, we analyzed the number of operations per iteration, which is presented in Table 1. One can conclude that the computational complexity of the GMACC is .

Table 1.
Computational complexity (per iteration) of LMS and GMACC algorithms.
2.3. Steady-State Performance Analysis
2.3.1. Stability Analysis
The error vector of the filter parameter estimation is the difference between the estimated value and the optimal value of adaptive filter parameters, which can be expressed as
It is known that
According to the energy conservation relation (ECR) [34,35,36], we can get
In order to ensure the algorithm finally come to the steady state, the error vector norm must satisfy:
So, we can derive that
Then, we can deduce that the step size should satisfy the following condition
so that the expectation sequence of the power of the estimation error monotonously decreases, hence the adaptive filter converges to the steady state after some iterations.
As one can see from (21), the threshold value of the step size depends on many factors such as the error size, the variance of the system noise, the kernel width, and the shape parameter. Therefore, the threshold value is hard to tell before the experiment, because the steady-state error is previously unknown. Usually, a small step size can help the algorithm to converge to a low steady-state MSD. Thus, one can just set a small step size at the beginning of the simulation and carefully try a larger step size to get a faster convergence speed. By running a simulation, we can provide an empirical value of the threshold. For example, in experiment 1, the empirical value of the step size was less than 2.5.
2.3.2. Steady-State Performance
Before the analysis of the steady-state performance of the algorithm, the following assumptions are given.
Assumption 1.
The additive noise sequence with variance is independent and identically distributed (i.i.d) and is independent of the input sequence .
Assumption 2.
The order of the adaptive filter is long enough that the prior error accords with the Gaussian distribution with a mean value of 0 and is independent of the background noise .
We define prior and posterior errors as
and
According to the previous definitions, the relationship between the estimation error and the prior error at the kth moment can be presented as:
We define the steady-state mean square error (MSE) as:
Then the excess mean square error (EMSE) can be presented as:
Furthermore, the relationship between MSE and EMSE can be presented as:
In the steady-state performance analysis of adaptive filtering, EMSE is widely used as a measure of steady-state performance, because it can filter out the direct influence of noise on the steady-state performance.
For an adaptive filtering algorithm which can converge to a steady state, when the number of iterations becomes very large, the estimation error of the filter parameters gets very close. In other words, when , we can get . According to (17) and (18), one can obtain:
Assume
Then, the above equation can be written as
In steady state, the distribution of and is independent of time k. In order to simplify the expression of the derivation process, the time subscript is omitted in the following derivation.
The Taylor expansion of is [22,34]:
According to the properties of the expected operator, we can further derive that
and
Substituting (32) and (33) into (30), we can get
where represents the trace operator of the matrix, and represents the autocorrelation matrix of the input signal. The expressions of , , and can be expressed as:
According to the above formulas, the closed-form solution of the EMSE can be obtained given the input sample data. It can be seen that the parameters that affect the steady-state EMSE are step size, noise variance, width and shape parameters of the generalized asymmetric Gaussian kernel.
3. Experiments and Results
In this section, we firstly compare the theoretical derived EMSE in Section 2.3 with the simulated one to confirm the theoretical result. Then, we describe the asymmetry of queuing delay in a satellite network and verify the robustness and the adaptability of the GMACC in a satellite network delay prediction. Note that the experiments in this section are all computer simulations.
3.1. Experimental Verification of Theoretical Analysis of Steady-State Performance
The steady-state performance of the GMACC algorithm under different step sizes and noise distributions were simulated. The noise in the simulation was a uniform noise distributed in [−m, m]. When the step size and noise variance were changed, the other parameters were kept unchanged, that is, the kernel width was set to 0.5, and the shape parameter was set to 2. For each simulation under a certain parameter setting, 100 Monte Carlo runs were executed to get the average simulation result of the EMSE. When calculating the steady-state results of the EMSE, the mean value of the EMSE of the last 500 iterations was taken as its steady-state value. In order to ensure that the algorithm could converge to the steady state in the last few hundred iterations, 5000 iterations were set in each Monte Carlo simulation. Considering that too small a step size leads to too slow a convergence of the algorithm, the step size should be adjusted appropriately to avoid too small a step size. The comparison between theoretical analysis results and experimental results is shown in Figure 3 and Figure 4.
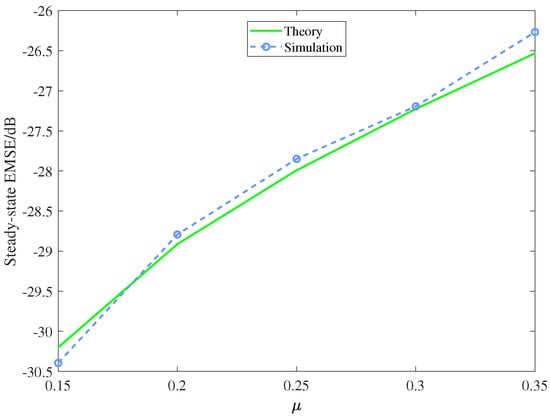
Figure 3.
Theoretical and simulated steady-state EMSEs with different step sizes.
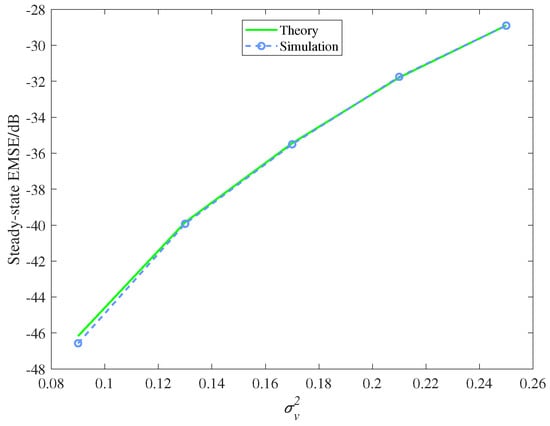
Figure 4.
Theoretical and simulated steady-state EMSEs with different variances.
It can be observed that: (1) when the step size and noise variance increase, the steady-state EMSE also increases and (2) the theoretical analysis shows the relationship between the steady-state performance of the algorithm and the step size and noise, and the theoretical analysis results agree well with the experimental results.
3.2. Satellite Network Delay Prediction Based on GMACC
In most ground network research, the network delay is directly measured, but in the large-scale propagation space of a satellite network, the time difference between the measured delay and the actual delay cannot be ignored. If the measured delay is used in a link-switching mechanism, remote control, and other scenarios, the accuracy of these algorithms is reduced, so it is necessary to predict the delay of the satellite network in these scenarios. In this paper, the autoregressive (AR) model was used to model the time series of the satellite network delay, and the adaptive filter was used to estimate the model parameters, so as to predict the network delay.
Generally speaking, the satellite network delay includes four parts: processing delay, queuing delay, transmission delay, and propagation delay. Figure 5 shows the components of the delay in the satellite network. The processing delay includes the time that the node checks the packet header and determines how to send or process the packet according to the packet header information, as well as the time to check whether the packet is misplaced, etc. The processing time is usually negligibly small. The transmission delay refers to the time required for the router to send packets onto the wire. The time is related to the length of the packets and the speed of the router to send packets. According to the actual packet length and network bandwidth parameter level, the transmission delay is small, and accounts for a low proportion in the overall network delay. The propagation delay refers to the time spent by an electromagnetic wave carrying data information going through the propagation channel, which can be calculated by dividing the channel length by the propagation rate of the electromagnetic wave in the channel. In the long-distance and dynamic channel of a satellite network, the influence of the propagation delay is obvious, while in the medium- and short-distance channel of a ground network, the influence of the propagation delay on the overall delay is limited. In most networks, the queuing delay accounts for a high proportion of the total network delay and is the decisive factor of the network delay variation. The queuing delay refers to the time that a packet is waiting to be sent in the router queue after it arrives at the router. For a specific packet, the queuing delay depends on the length of the queue in which the packet is located and the speed at which the router processes and sends the packet. For a specific queue, the queuing delay depends on the arrival strength and distribution characteristics of packets. Studies have shown that if there are 10 IP packets queued by 10 routers on average, the queuing delay on this path can reach hundreds of milliseconds [37,38].
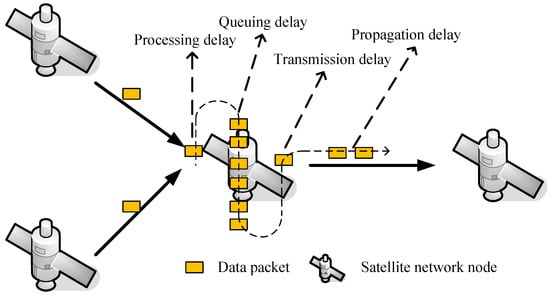
Figure 5.
All kinds of delay in a satellite network.
In most time series analyses, an AR model or autoregressive moving average (ARMA) model and autoregressive integrated moving average (ARIMA) are very useful models, which can well reflect the autocorrelation of time series and is very suitable for modeling the time series of the network delay or its differential variation [39,40]. In this paper, considering that the delay time series may not satisfy the stationary condition, we refer to the idea of ARIMA, and take the first-order difference of the network delay time series to build the AR model.
The AR model of the satellite network delay can be expressed as
where n is the order of the AR model, is the weight vector or the system parameter of the model, and is the measured value of a continuous p delay before time k. is the disturbance term of time k and represents the unpredictable part of the network delay time series.
In the autoregressive modeling of time series delay, there is a certain error between the measured delay and the real delay. Moreover, because the queuing delay is closely related to the unpredictable network traffic, the change of queuing delay also causes noise in the overall network delay modeling. The above two unpredictable signals are regarded as the disturbance term in the autoregressive model. In the ordinary autoregressive model, the disturbance term is assumed to be Gaussian distributed. However, due to the burst of network traffic and the queue features of network nodes, the network traffic shows explosive and asymmetric characteristics. When a node suddenly receives a large number of data packets, the queuing delay rises abruptly in a short time. However, due to the limited processing capacity of nodes, the speed of the queuing delay reducing is limited. Thus, the probability distribution of the sudden rise and fall of the queuing delay are quite different, showing an obvious asymmetry.
To make the discussion more convincing, this paper simulated the queue delay in MATLAB software (version 9.3) [41] and described its specific asymmetric characteristics inspired by the idea of queuing theory. According to the previous discussion, the arrival packet traffic in a network node queue is sudden and unpredictable, and the speed of packets leaving the node queue is constant. Suppose that there are two kinds of service packets passing through one certain network node in a period of time. The packet arrival process of one service is relatively stable, while the arrival process of the other service is very sudden and explosive. The speed of the network node processing a data packet is constant. According to the above settings, the number of packets arriving at each time and the number of packets processed can be simulated and calculated in MATLAB. Then, a time series can be generated to represent the change of the number of packets in the node queue over time. It should be noted that this paper assumed that the upper limit of the simulated queue length was large enough, so there was no packet loss. In the case of a constant processing speed, the queue length is proportional to the queue delay, so the change of the queue length can also represent the change of the queue delay. In this simulation, the queue length of nodes, the first-order difference of the queue length (i.e., the change of queue length), and the statistical distribution of the first-order difference are shown in Figure 6, Figure 7 and Figure 8, respectively.
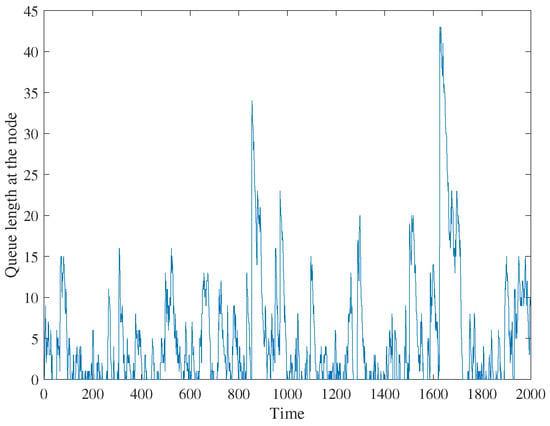
Figure 6.
Queue length at one node.
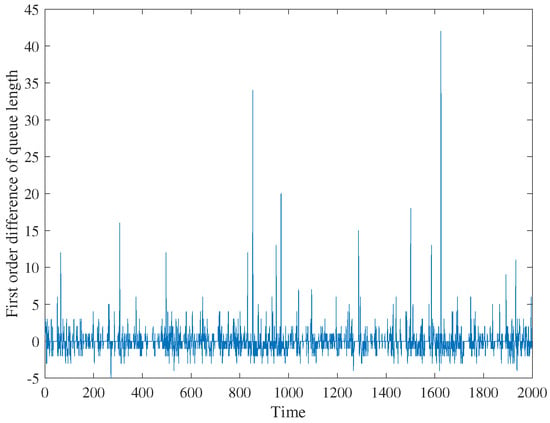
Figure 7.
The first-order difference of queue length.
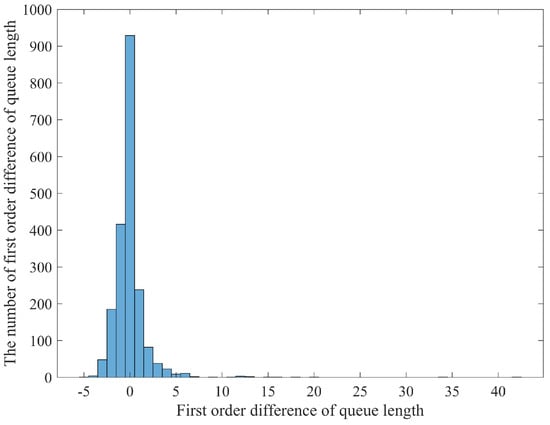
Figure 8.
Statistical distribution of first-order difference of queue length.
It can be observed from Figure 6 that the rising slope of the queue length time series is usually larger than the falling slope, which indicates that in the packet queuing simulation, the queue growth rate is faster than the queue reduction rate. From Figure 7, one can observe that the distribution range of the first-order difference of the node queue length on the positive axis and the negative axis are quite different. The maximum value on the positive axis can reach dozens, while the minimum value on the negative axis is not less than −5. Figure 8 shows that the distribution of the first-order difference of the node queue length is unimodal, and the mean value is approximately equal to 0. In addition, there are some outliers in the right tail, which is thicker than the tails of an exponential distribution. Thus, it is a heavy-tail distribution. Because the right tail is much longer than the left tail, the distribution can be described as a right-skewed distribution.
Next, we simulated the satellite network delay prediction in MATLAB. In the simulation, all criteria related to the GMACC were included in the comparison algorithms. Because the optimization method was a gradient descent method, only the names of the criteria were used to represent the algorithms in order to simplify the expression. The algorithms compared in the simulation included the LMS based on the minimum mean square error criterion, the MCC based on the maximum correntropy criterion, the MACC based on the maximum asymmetric correntropy criterion, and the GMACC based on the generalized maximum asymmetric correntropy criterion. The performance was measured by the mean squared deviation (MSD):
where is the estimated AR weight vector at time k, and is the optimal value of the parameter vector.
To discuss the performance of the proposed algorithm under a symmetric and asymmetric noise, we first carried out a simulation under a non-Gaussian noise and asymmetric Gaussian noise, then conducted a simulation with an asymmetric non-Gaussian noise. The noise parameters settings of the simulations are shown in Table 2. The parameters selection of simulation 1 and simulation 2 are the same and are all shown in Table 3.

Table 2.
Parameters of alpha stable noise.

Table 3.
Parameters and steady-state MSD of the algorithms in simulation 1 and simulation 2.
Simulation 1: Under the condition that the disturbance term of the network delay time series was small and close to Gaussian distribution, the MSD performance of the LMS, MCC, MACC, and GMACC algorithms were simulated and compared. In this simulation, we first set the disturbance term of the time delay series to obey a symmetric non-Gaussian distribution with shape parameter 1.98, which is close to a Gaussian distribution but contains impulsive components. Figure 9 presents the noise time series. The steady-state performance of the algorithms is shown in Figure 10.
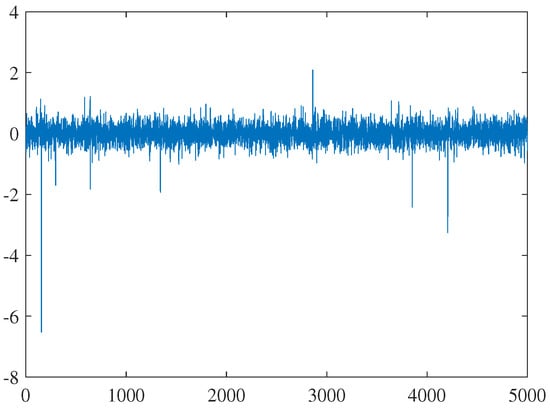
Figure 9.
Noise signal in simulation 1.
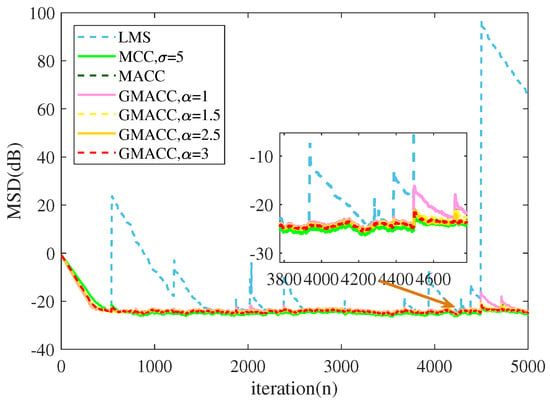
Figure 10.
Steady-state performance comparison of different algorithms under the perturbation term of a symmetric non-Gaussian distribution close to a Gaussian distribution.
It can be observed from Figure 10 that almost all the listed algorithms converge with the increase of iterations. However, as long as there is a little impact noise, the convergence process of the LMS is seriously affected. In contrast, the other algorithms can suppress the impact of the impulsive noise and show a good robustness.
Simulation 2: Then, we simulated the comparison between different algorithms when the disturbance term followed asymmetric Gaussian distribution. The skew index of the asymmetric distribution function was set to 0.4, the shape parameter was set to 2, and the interference term obeyed the asymmetric Gaussian distribution. The MSD performance of different algorithms are shown in Figure 11.
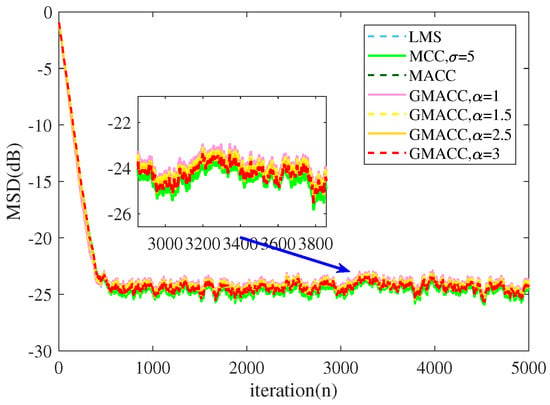
Figure 11.
Steady-state performance comparison of different algorithms under asymmetric Gaussian distribution disturbance.
As can be seen from Figure 11, all algorithms including the LMS show good convergence and steady-state performance when the disturbance term follows an asymmetric Gaussian distribution.
The steady-state MSD in simulation 1 and simulation 2 are presented in Table 3, from which one can observe that the asymmetric-correntropy-criteria-based algorithms deal with asymmetric Gaussian noise and non-Gaussian noise well, and the LMS as well as MCC algorithms also perform well in an asymmetric Gaussian noise.
Simulation 3: Next, we simulated the comparison among the MCC, MACC, and LMS when the disturbance term followed an asymmetric non-Gaussian distribution. It has been described that the queue delay is asymmetric due to the sudden increase of user request and the limited processing speed of the network nodes. According to the above characteristics of the queue delay, an asymmetric alpha-stable noise [42] with a lower bound was generated in this simulation, so as to simulate the disturbance term in the network delay time series. The noise parameters are shown in Table 2. The performance of the MACC and MCC with different kernel widths was compared under the condition of asymmetric noise. For a fair comparison, the initial convergence speed of the algorithms were set to be the same, which is similar to the simulation in [43]. For one algorithm, the faster the initial convergence speed was, the less optimal the convergence step was. The parameters of the algorithms are presented in Table 4. We took the mean MSD of the last 1000 iterations as the steady-state MSD and present the results in Table 4. The convergence process and the steady-state performance results are shown in Figure 12.

Table 4.
Parameters and steady-state MSD of MCC and MACC in simulation 3.
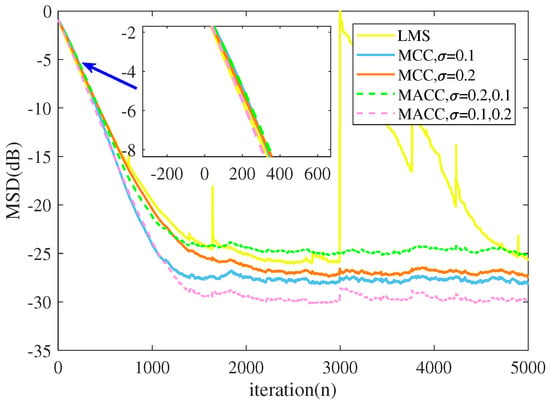
Figure 12.
Steady-state performance comparison of different algorithms under asymmetric and non-Gaussian distribution disturbance.
It can be observed from Figure 12 that the asymmetric Gaussian kernel with properly selected kernel widths has better steady-state performance than the symmetric Gaussian kernel when dealing with asymmetric noise, which has a heavy tail component in the positive range and a lower limit in the negative range. However, the asymmetric Gaussian kernel with wrong kernel widths has even worse steady-state performance than the symmetric Gaussian kernel. The steady-state MSD in Table 4 also clearly shows the difference of steady-state performance between algorithms.
Comparing the two simulation results in simulation 2 and simulation 3, one can observe that the asymmetric non-Gaussian noise is the real test of the algorithms, while the asymmetric Gaussian noise is not challenging.
Simulation 4: The following simulation compared the MACC and MCC with the GMACC under different shape parameters. The kernel widths of the GMACC were the same as those of the MACC. The step sizes were set to unify the convergence rate of the algorithms. The noise was set to follow an asymmetric and non-Gaussian distribution of which the parameters were the same as those of simulation 3, and they are shown in Table 2. The simulation results are shown in Figure 13.
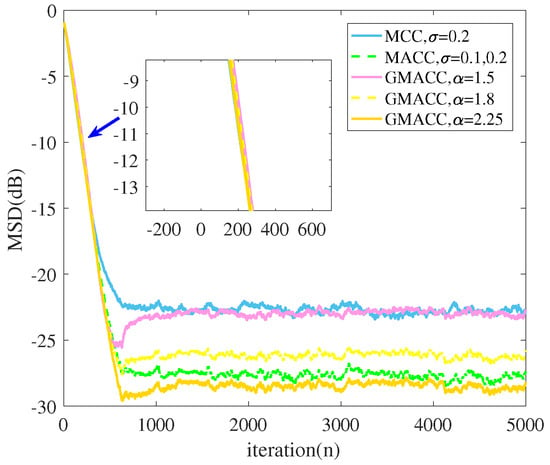
Figure 13.
Performance comparison of GMACC, MACC and MCC algorithms with different shape parameters.
It can be observed from Figure 13 that the GMACC with a proper shape parameter can outperform the MACC in terms of the steady-state MSD under the same convergence rate.
Simulation 5: In this simulation, the GMACC was compared with other robust adaptive filtering algorithms such as Llncosh [44], least p-norm [7], and Huber algorithm [45]. The system noise was set the same as that of simulation 3 and 4. The parameters setting and steady-state MSD of the algorithms are shown in Table 5, and the simulation results are shown in Figure 14.

Table 5.
Parameters and steady-state MSD of the algorithms in simulation 5.
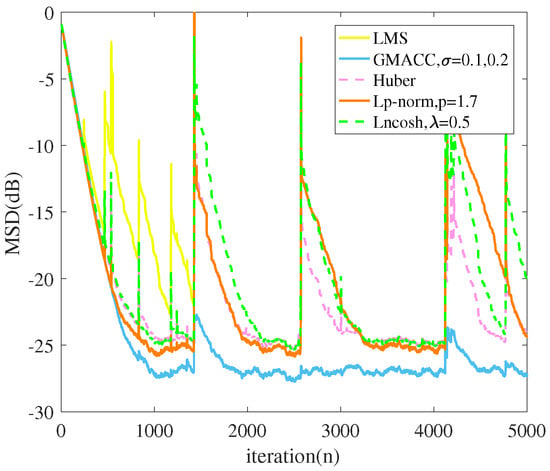
Figure 14.
Steady-state performance comparison of GMACC and other robust algorithms under asymmetric and non-Gaussian distribution disturbance.
One can observe that the GMACC algorithm outperforms classic or recently proposed robust algorithms under an asymmetric non-Gaussian distribution disturbance in terms of the steady-state MSD. Concretely, the steady-state MSD of the GMACC algorithm is significantly lower than that of classic or recently proposed robust algorithms in the presence of asymmetric non-Gaussian noise under the condition that the initial convergence rate is consistent. Moreover, the robustness of the GMACC is the best among the compared algorithms since the GMACC is least affected by impact noise.
4. Discussion
The result of simulation 2 that the LMS and MCC with a symmetric Gaussian kernel can deal with asymmetric Gaussian noise well is beyond expectation. However, that could be explained. It is because the criteria selected by the several algorithms in this simulation can well describe the second-order statistics of the error contained in the asymmetric Gaussian distribution.
Combining the two simulation results in simulation 2 and simulation 3, one can observe that the asymmetric non-Gaussian noise is the real test of the algorithms, while the asymmetric Gaussian noise is not challenging.
The result in simulation 3 shows the desirable performance of the asymmetric Gaussian kernel, for which the underlying reason is that the asymmetric Gaussian kernel can flexibly select the kernel widths of positive and negative axes, so it can adapt to the asymmetric noise. In simulation 3, the noise is in accordance with the right-skewed distribution, and the distribution in the positive axis has impact characteristics. Therefore, the MACC with a small positive kernel width performs well and can suppress the impact component of the noise in the positive axis.
The result in simulation 4 shows that the shape parameter of GMACC can improve the adaptability and the robustness of the algorithm. The adjustment of the shape parameter can not only balance the steady-state performance and convergence rate of the GMACC algorithm, but also help to achieve better performance under an asymmetric and non-Gaussian noise. Furthermore, that is the advantage of GMACC.
According to the results of simulation 3 and simulation 4, the GMACC has an enhanced adaptability because of the flexible selection of the shape and kernel width parameters. The GMACC with a small positive kernel width performs well under a right-skew-distributed system noise while the GMACC with a small negative kernel width is suitable for dealing with a left-skew-distributed system noise. This could be considered as a reference for the selection of the kernel width parameters. According to the stability analysis presented in Section 2.3.1, the step size should be set smaller than a threshold value, which is uncertain before an experiment, as the steady-state error is unknown in advance. Therefore, to make the algorithm converge to the steady state, one can just set a small step size at the beginning of the simulation, and carefully try larger step sizes to get a faster convergence speed if necessary. By running the simulations, we can provide the empirical value of the step size threshold. For example, in simulation 1, the empirical value of step size was less than 2.5. The shape parameter of the GMACC ranged from 1 to 3.5. With the other parameters unchanged, the larger the shape parameter is, the better the GMACC algorithms perform in terms of the steady-state MSD. In contract, larger shape parameters lead to a lower convergence rate. Furthermore, that could be the reference for the selection of the shape parameter. According to our experimental experience, the GMACC algorithm achieves the best performance under an asymmetric non-Gaussian noise when the shape parameter is set to around 2.25.
5. Conclusions
Symmetric Gaussian kernel based criteria such as the MCC and GMCC are not desirable when dealing with asymmetric heavy-tailed system noise in adaptive filtering. This paper proposed the GMACC to build the cost function of robust adaptive filtering, which was the expansion of traditional ITL-based adaptive filtering and included the original algorithms as special cases. The flexible values of the parameters brought many benefits. The different kernel widths in positive and negative axes made the GMACC suitable to deal with asymmetric noise. The shape parameter of the GMACC could balance the steady-state performance and convergence rate of the algorithm. The steady-state performance of the algorithm was analyzed theoretically and verified by experiment. The asymmetric property of a satellite network delay was discovered and described. Simulations verified the effectiveness of the GMACC-based adaptive filter in a satellite network delay prediction. The proposed GMACC-based adaptive filtering performed well under an asymmetric non-Gaussian system noise environment, and improved the research framework of robust adaptive filtering.
The proposed GMACC algorithm in this paper was tested in simulation environments only, but it has application prospects in satellite network delay prediction, oil price prediction, etc., where asymmetric non-Gaussian noise exists. Moreover, the adaptability of the GMACC under different types of noise needs more studying in the future.
Author Contributions
Conceptualization, P.Y. and H.Q.; methodology, P.Y. and M.W.; software, M.W.; validation, P.Y., H.Q. and J.Z.; formal analysis, M.W., P.Y. and J.Z.; investigation, P.Y. and M.W.; resources, M.W.; data curation, M.W.; writing—original draft preparation, P.Y.; writing—review and editing, M.W., P.Y., S.Z., T.L. and J.Z.; supervision, S.Z., T.L. and H.Q.; funding acquisition, H.Q. and J.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by National Key Research and Development Project under Grant 2018YFB18003600 and National Natural Science Foundation of China under Grant 61531013.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Widrow, B.; Stearns, S.D. Adaptive Signal Processing; Prentice Hall: Hoboken, NJ, USA, 2008. [Google Scholar]
- Haykin, S. Adaptive Filter Theory; Prentice Hall: Upper Saddle River, NJ, USA, 2002; Volume 4. [Google Scholar]
- Rousseeuw, P.J.; Leroy, A.M. Robust Regression and Outlier Detection; John Wiley & Sons: Hoboken, NJ, USA, 2005; Volume 589. [Google Scholar]
- Zou, Y.; Chan, S.C.; Ng, T.S. Least mean M-estimate algorithms for robust adaptive filtering in impulse noise. IEEE Trans. Circuits Syst. II Analog. Digit. Signal Process. 2000, 47, 1564–1569. [Google Scholar]
- Chan, S.C.; Zou, Y.X. A recursive least M-estimate algorithm for robust adaptive filtering in impulsive noise: Fast algorithm and convergence performance analysis. IEEE Trans. Signal Process. 2004, 52, 975–991. [Google Scholar] [CrossRef]
- Tahir Akhtar, M. Fractional lower order moment based adaptive algorithms for active noise control of impulsive noise sources. J. Acoust. Soc. Am. 2012, 132, EL456–EL462. [Google Scholar] [CrossRef] [Green Version]
- Navia-Vazquez, A.; Arenas-Garcia, J. Combination of recursive least p-norm algorithms for robust adaptive filtering in alpha-stable noise. IEEE Trans. Signal Process. 2011, 60, 1478–1482. [Google Scholar] [CrossRef]
- Principe, J.C. Information Theoretic Learning: Renyi’s Entropy and Kernel Perspectives; Springer Science & Business Media: Berlin, Germany, 2010. [Google Scholar]
- Singh, A.; Principe, J.C. A closed form recursive solution for maximum correntropy training. In Proceedings of the 2010 IEEE International Conference on Acoustics, Speech and Signal Processing, Dallas, TX, USA, 14–19 March 2010; pp. 2070–2073. [Google Scholar]
- Zhao, S.; Chen, B.; Principe, J.C. Kernel adaptive filtering with maximum correntropy criterion. In Proceedings of the 2011 International Joint Conference on Neural Networks, San Jose, CA, USA, 31 July–5 August 2011; pp. 2012–2017. [Google Scholar]
- He, Y.; Wang, F.; Yang, J.; Rong, H.; Chen, B. Kernel adaptive filtering under generalized maximum correntropy criterion. In Proceedings of the 2016 International Joint Conference on Neural Networks (IJCNN), Vancouver, BC, Canada, 24–29 July 2016; pp. 1738–1745. [Google Scholar]
- Hakimi, S.; Abed Hodtani, G. Generalized maximum correntropy detector for non-Gaussian environments. Int. J. Adapt. Control Signal Process. 2018, 32, 83–97. [Google Scholar] [CrossRef]
- Zhao, J.; Zhang, H. Kernel recursive generalized maximum correntropy. IEEE Signal Process. Lett. 2017, 24, 1832–1836. [Google Scholar] [CrossRef]
- Seth, S.; Principe, J.C. Compressed signal reconstruction using the correntropy induced metric. In Proceedings of the 2008 IEEE International Conference on Acoustics, Speech and Signal Processing, Las Vegas, ND, USA, 31 March–4 April 2008; pp. 3845–3848. [Google Scholar] [CrossRef]
- Liu, W.; Pokharel, P.P.; Principe, J.C. Correntropy: Properties and Applications in Non–Gaussian Signal Processing. IEEE Trans. Signal Process. 2007, 55, 5286–5298. [Google Scholar] [CrossRef]
- Yue, P.; Qu, H.; Zhao, J.; Wang, M. An Adaptive Channel Estimation Based on Fixed-Point Generalized Maximum Correntropy Criterion. IEEE Access 2020, 8, 66281–66290. [Google Scholar] [CrossRef]
- Ma, W.; Qu, H.; Gui, G.; Xu, L.; Zhao, J.; Chen, B. Maximum correntropy criterion based sparse adaptive filtering algorithms for robust channel estimation under non-Gaussian environments. J. Frankl. Inst. 2015, 352, 2708–2727. [Google Scholar] [CrossRef] [Green Version]
- Ma, W.; Chen, B.; Qu, H.; Zhao, J. Sparse least mean p-power algorithms for channel estimation in the presence of impulsive noise. Signal Image Video Process. 2015, 10, 503–510. [Google Scholar] [CrossRef]
- Yue, P.; Qu, H.; Zhao, J.; Wang, M.; Liu, X. A robust blind adaptive multiuser detection based on maximum correntropy criterion in satellite CDMA systems. Trans. Emerg. Telecommun. Technol. 2019, 30, e3605. [Google Scholar] [CrossRef]
- Liu, X.; Qu, H.; Zhao, J.; Yue, P. Maximum correntropy square-root cubature Kalman filter with application to SINS/GPS integrated systems. ISA Trans. 2018, 80, 195–202. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Qu, H.; Zhao, J.; Yue, P.; Wang, M. Maximum Correntropy Unscented Kalman Filter for Spacecraft Relative State Estimation. Sensors 2016, 16, 1530. [Google Scholar] [CrossRef] [PubMed]
- Yue, P.; Qu, H.; Zhao, J.; Wang, M. Newtonian-Type Adaptive Filtering Based on the Maximum Correntropy Criterion. Entropy 2020, 22, 922. [Google Scholar] [CrossRef] [PubMed]
- Takeuchi, I.; Bengio, Y.; Kanamori, T. Robust Regression with Asymmetric Heavy-Tail Noise Distributions. Neural Comput. 2002, 14, 2469–2496. [Google Scholar] [CrossRef] [PubMed]
- You, W.; Guo, Y.; Zhu, H.; Tang, Y. Oil price shocks, economic policy uncertainty and industry stock returns in China: Asymmetric effects with quantile regression. Energy Econ. 2017, 68, 1–18. [Google Scholar] [CrossRef]
- Amudha, R.; Muthukamu, M. Modeling symmetric and asymmetric volatility in the Indian stock market. Indian J. Financ. 2018, 12, 23–36. [Google Scholar] [CrossRef]
- Sun, H.; Yang, X.; Gao, H. A spatially constrained shifted asymmetric Laplace mixture model for the grayscale image segmentation. Neurocomputing 2019, 331, 50–57. [Google Scholar] [CrossRef]
- Chen, B.; Li, Z.; Li, Y.; Ren, P. Asymmetric correntropy for robust adaptive filtering. arXiv 2019, arXiv:1911.11855. [Google Scholar] [CrossRef]
- Elguebaly, T.; Bouguila, N. Finite asymmetric generalized Gaussian mixture models learning for infrared object detection. Comput. Vis. Image Underst. 2013, 117, 1659–1671. [Google Scholar] [CrossRef]
- Nacereddine, N.; Tabbone, S.; Ziou, D.; Hamami, L. Asymmetric Generalized Gaussian Mixture Models and EM Algorithm for Image Segmentation. In Proceedings of the 2010 20th International Conference on Pattern Recognition, Istanbul, Turkey, 23–26 August 2010; pp. 4557–4560. [Google Scholar] [CrossRef]
- Nandi, A.K.; Mämpel, D. An extension of the generalized Gaussian distribution to include asymmetry. J. Frankl. Inst. 1995, 332, 67–75. [Google Scholar] [CrossRef]
- Lasmar, N.E.; Stitou, Y.; Berthoumieu, Y. Multiscale skewed heavy tailed model for texture analysis. In Proceedings of the 2009 16th IEEE International Conference on Image Processing (ICIP), Cairo, Egypt, 7–10 November 2009; pp. 2281–2284. [Google Scholar] [CrossRef] [Green Version]
- Berner, J.B.; Bryant, S.H.; Kinman, P.W. Range Measurement as Practiced in the Deep Space Network. Proc. IEEE 2007, 95, 2202–2214. [Google Scholar] [CrossRef]
- Yue, P.C.; Qu, H.; Zhao, J.H.; Wang, M.; Wang, K.; Liu, X. An inter satellite link handover management scheme based on link remaining time. In Proceedings of the 2016 2nd IEEE International Conference on Computer and Communications (ICCC), Chengdu, China, 14–17 October 2016; pp. 1799–1803. [Google Scholar]
- Chen, B.; Xing, L.; Liang, J.; Zheng, N.; Principe, J.C. Steady-state mean-square error analysis for adaptive filtering under the maximum correntropy criterion. IEEE Signal Process. Lett. 2014, 21, 880–884. [Google Scholar]
- Wang, W.; Zhao, J.; Qu, H.; Chen, B.; Principe, J.C. Convergence performance analysis of an adaptive kernel width MCC algorithm. AEU-Int. J. Electron. Commun. 2017, 76, 71–76. [Google Scholar] [CrossRef]
- Qu, H.; Shi, Y.; Zhao, J. A Smoothed Algorithm with Convergence Analysis under Generalized Maximum Correntropy Criteria in Impulsive Interference. Entropy 2019, 21, 1099. [Google Scholar] [CrossRef] [Green Version]
- Nichols, K.; Jacobson, V. Controlling Queue Delay. Commun. ACM 2012, 55, 42–50. [Google Scholar] [CrossRef]
- Chang, C.S. Stability, queue length, and delay of deterministic and stochastic queueing networks. IEEE Trans. Autom. Control 1994, 39, 913–931. [Google Scholar] [CrossRef] [Green Version]
- Trindade, A.A.; Zhu, Y.; Andrews, B. Time series models with asymmetric Laplace innovations. J. Stat. Comput. Simul. 2010, 80, 1317–1333. [Google Scholar] [CrossRef]
- Arnold, M.; Milner, X.; Witte, H.; Bauer, R.; Braun, C. Adaptive AR modeling of nonstationary time series by means of Kalman filtering. IEEE Trans. Biomed. Eng. 1998, 45, 553–562. [Google Scholar] [CrossRef]
- Etter, D.M.; Kuncicky, D.C.; Hull, D.W. Introduction to MATLAB; Prentice Hall: Hoboken, NJ, USA, 2002. [Google Scholar]
- Janicki, A.; Weron, A. Simulation and Chaotic Behavior of Alpha-Stable Stochastic Processes; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar]
- Chen, B.; Xing, L.; Zhao, H.; Zheng, N.; Principe, J.C. Generalized correntropy for robust adaptive filtering. IEEE Trans. Signal Process. 2016, 64, 3376–3387. [Google Scholar] [CrossRef] [Green Version]
- Liu, C.; Jiang, M. Robust adaptive filter with lncosh cost. Signal Process. 2020, 168, 107348. [Google Scholar] [CrossRef]
- Huber, P.J. Robust Statistics; John Wiley & Sons: Hoboken, NJ, USA, 2004; Volume 523. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).