Abstract
In this study, the annual and seasonal climatology of cloud fraction (CF) and cloud type simulated by the Canadian Environmental System Models (CanESMs) version 5 (CanESM5) and version 2 (CanESM2) at their fully coupled and AMIP configurations were validated against the CALIPSO-GOCCP-based CF. The CFs produced using the CALIPSO-COSP simulator based on the CanESMs data at their atmospheric (AMIP) configuration are also evaluated. The simulated shortwave, longwave, and net cloud radiative forcing using the AMIP version of the CanESM5 were also validated against satellite observations based on the recent CERES radiation satellite products. On average, all models have a negative bias in the total CF with global mean biases (MBs) of 2%, 2.4%, 3.9%, 6.4%, 5.6%, and 7.1% for the coupled-CanESM5, AMIP-CanESM5, COSP-AMIP-CanESM5, coupled-CanESM2, AMIP-CanESM2, and COSP-AMIP-CanESM2, respectively, indicating that the CanESM5 has a smaller MB. There were no significant differences between AMIP and coupled versions of the model, but the COSP-based model-simulated data showed larger biases. Although the models captured well the climatological features of CF, they also exhibited a significant bias in CF reaching up to 40% over some geographical locations. This is particularly prevalent over the low level (LL) marine stratocumulus/cumulus, convectively active tropical latitudes that are normally dominated by high level (HL) clouds and at the polar regions where all models showed negative, positive, and positive bias corresponding to these locations, respectively. The AMIP-CanESM5 model performed reasonably well simulating the global mean cloud radiative forcing (CRF) with slight negative biases in the NetCRF at the TOA and surface that would be expected if the model has a positive bias in CF. This inconsistent result may be attributed to the parameterization of the optical properties in the model. The geographical distributions of the model bias in the NetCRF, however, can be significant reaching up to ±40 Wm−2 depending on the location and atmospheric level. The Pearson correlation showed that there is a strong correlation between the global distribution of model bias in NetCRF and CF and it is significantly influenced by the LL and HL clouds.
1. Introduction
Clouds play important role in the Earth’s climate and weather by controlling the radiative and hydrological balance. They act as a greenhouse that warms the Earth by trapping the outgoing longwave radiation and reflect the shortwave radiation that tends to cool the Earth. The net cloud radiative effects or forcing (NetCRF) depend on the type, height, and optical properties of the cloud [1]. It is generally accepted that the dominant source of uncertainty in climate projections for the current general circulation models (GCMs) is largely related to the representation of clouds [2,3]. The most recent results based on several current Earth system models (ESM) participated in the Sixth Couple Model Intercomparison Project (CMIP6) revealed a greater range of climate sensitivity to increased CO2 concentration. These models suggests that the Earth’s atmosphere could be warming faster than previously thought according to some of the models, including the Canadian ESM version 5 (CanESM5) [4,5,6,7]. The most likely cause of this was attributed to the difficulty related to simulation of clouds and the associated impact on the radiative balance.
One of the problems is related to the coarse resolution of the most current GCMs that fail to resolve the cloud microphysical and small-scale dynamical processes. As a result, these processes need to be parameterized. The parameterization schemes used vary from model to model and hence some of the differences revealed in these studies could be attributed to these differences. Previous studies also showed that the vertical variability and type of cloud could have a significant impact on the Earth’s radiation budget [8,9,10,11,12] and hence accurate prediction of cloud structure and type is critical for improving the GCMs. Therefore, validation of the performance of these models using observation data is the critical step.
Evaluation of model-simulated cloud fraction (CF) or cloud radiative forcing (CRF) against satellite-based data obtained using remote sensing instruments is difficult because of the difference in representation of cloud properties in models as compared to satellite observations as well as uncertainties associated with the satellite retrievals. To narrow the gap and better facilitate comparisons of GCM output with satellite data, an integrated satellite simulator referred to as the Cloud Feedback Model Intercomparison Project (CFMIP) Observation Simulator Package (COSP) is used (e.g., [13,14]). The COSP software emulates cloud properties from both active sensors such as the Aerosol Lidar and Infrared Pathfinder Satellite Observations (CALIPSO) and passive sensors used in the International Satellite Cloud Climatology Project (ISCCP) using as input cloud-related fields simulated in the GCM. There have been a number of studies focusing on evaluation of GCM-simulated clouds against satellite observations by employing the CALIPSO and ISCCP simulators (e.g., [8,15,16,17]). The authors of [15] compared the ECHAM5 model with the LIDAR simulator and found that the model overestimates high-level clouds (HLC), particularly optically thin clouds. Their study also demonstrated that the model significantly underestimates mid-level cloud (MLC) and sub-tropical low-level clouds (LLC). Ref. [17] used simulated cloud properties based on two generations of GCMs including the CanESM Version 2 model by employing the ISCCP simulator and compared that against the ISCCP cloud datasets. Based on this study, generally the models underestimate the total CF in regions of marine stratocumulus on the eastern sides of subtropical ocean basins and over middle latitudes. The models also underestimate the amount of ML and LL clouds, but on average, the HLC were predicted reasonably well as compared to the ISCCP data. The underestimation of LLCs is attributed to the lack of marine stratocumulus within mid-latitude regions, but the absence of MLCs from the prospective of the ISCCP data is rather not so trivial to interpret since ISCCP under some conditions may be misinterpreted as MLC when thin cirrus and boundary layer clouds are present [18,19]. Passive sensors such as those used for obtaining the ISCCP data normally have difficulty detecting optically thin HLC and as discussed in [20], these sensors generally underestimate the CF as compared to those obtained using active sensors such as the CALIPSO and hence some cautions are required interpreting these results. The authors of [21] evaluated several Atmospheric Model Inter-comparison (AMIP) versions of GCMs that participated in the Coupled Model Intercomparison Project Phase 5 (CMIP5) experiment including the Canadian Atmospheric Model version 4 (CanAM4) against the GCM-Oriented CALIPSO Cloud Product (CALIPSO-GOCCP) [22]. Based on their annual and zonal mean CF, analysis showed that the total cloud fraction (TCF), mid-level cloud fraction (MLCF), and low-level cloud fraction (LLCF) are underestimated by most GCMs including the CanAM4. Using the ISCCP-H satellite data, the authors [7] have evaluated the TCF simulated using the CanESM5 model and found a positive bias in TCF along the equator, including over eastern tropical Pacific Antarctica and the Arctic. Their finding also showed that the model underestimates the TCF over most other land areas.
Accurate representation of clouds in GCM is necessary to predict the CRF and quantify the Earth’s radiation budget. The CRF is normally considered separately for the shortwave and longwave portion of the radiation spectrum, and they are computed based on the difference between cloudy and cloud-free parts of upwelling radiation in the atmosphere [1,23,24,25]. These will be discussed in more detail later. The CRF at the top of the atmosphere (TOA) can be calculated using satellite observations of radiative fluxes [25,26]. At the surface level, the CRF normally computed based on radiative fluxes is determined using radiative transfer code and satellite-derived cloud and aerosol properties as well as model-based temperature and humidity profiles [27], and as a result it is much more susceptible to errors. To minimize these errors, the radiances measured at TOA are used to constrain the radiances determined at the surface level [27,28]. The values of the calculated global mean shortwave CRF (SWCRF), longwave CRF (LWCRF), and NetCRF can vary depending on the data used [25,29]. The calculated global mean values for LWCRF, SWCRF, and NetCRF based on the latest Clouds and the Earth’s Radiant Energy System (CERES) energy balanced and filled (EBAF) Edition 4 (EBAF4) radiation data are 27.9, −45.8, and −17.9 Wm−2, respectively [29] showing on average that the net effect of clouds is cooling the Earth’s atmosphere. After introducing some adjustment factors to the EBAF4 radiation data for computing clear-sky flux that are more consistent with climate models, the re-calculated global mean values for these quantities were 25.7, −45.3, and −19.6 Wm−2, respectively [30,31]. Similar reports of calculations of these parameters on a global scale at the surface and in the atmosphere based on the most recent CERES satellite products are not currently available in the scientific literature. However, based on the NASA Surface Radiation Budget datasets, ref. [24] reported that the global mean values of CRFs at the surface for LWCRF, SWCRF, and NetCRF were 32.7, −52.8, −20.1 Wm−2, respectively and the corresponding values in the atmosphere were 4.3, −5.5, and −1.2 Wm−2, respectively. Based on the CERES EBAF surface data [28], more recently [32] reported CRF at the surface level as −52.0, 28.9, and −23.1 Wm−2 corresponding to LWCRF, SWCRF, and NetCRF, respectively. According to these results, the effects of clouds at the surface level are similar to the TOA case, but in the atmosphere, the SWCF on average warms the atmosphere and the opposite is true for the LWCRF, and the net effect is slight cooling of the atmosphere. The NetCRF at the surface level reported by Hinkelman [32], however, suggests more cooling. The most recent CERES datasets [27,30], particularly with adjusted clear-sky flux can be used to compute more reliable cloud radiative effects and hence more suited for evaluation of the current GCMs.
The main objectives of this study include using up-to-date versions of the satellite datasets to evaluate the new CanESM5 model’s ability to simulate clouds and radiation. The simulated clouds at different model configurations, coupled and Atmospheric Model Inter-comparison (AMIP) are also compared and validated. The simulated clouds and types using the CanESM5 model are compared to the older version of the mode, namely CanESM2. The COSP software-based emulated CF data are also investigated and compared to satellite observations. To conduct these tests, satellite cloud products based on CALIPSO-GOCCP and for radiation the latest versions of the CERES Edition 4.1 (EBAF4.1) datasets will be used, and the results will be summarized. The data and methods are described in Section 2, the results of the analysis are given in Section 3, and summary and conclusions are given in Section 4.
2. Materials and Methods
2.1. Descriptions of the Satellite Cloud Products
The satellite datasets used are described in Boudala and Milbrandt (2021) [20] and references therein. Here, brief descriptions of the datasets are given. The datasets and abbreviations used in this paper are given in Table A1 (Appendix A).
CAPLISO-GOCCP
These are observation-based cloud products geared towards validating GCM-simulated datasets and hence normally referred to as the GCM Oriented Cloud CALIPSO Product (GOCCP) [21]. The data are fully compatible with the GCM-LIDAR simulator data produced using the COSP (e.g. [13,14]). These datasets are derived using the CALIPSO products and are fully consistent with the ones simulated by the ensemble GCM + LIDAR simulator [21] and can be found (see https://climserv.ipsl.polytechnique.fr/cfmip-obs/, accessed on 25 July 2022. Based on [21], the cloud cover data are processed using a Cloud-Aerosol Lidar with Ortho gonal Polarization following the identical steps as would be followed in the LIDAR simulator aimed at diagnosing the model cloud cover that CALIPSO would see from space. The CF is determined using the observed LIDAR backscattered ratio (SR) of total attenuated backscattered (ATB) signal to gas molecular ATB without consideration of aerosols at high horizontal resolution of 330 m by keeping the vertical resolution similar to the current GCMs. The cloudy pixels are identified based on SR thresholds of SR > 5, 0.01 > SR < 1.2, and 1.2 < SR < 5 considered as cloudy, clear, and unclassified, respectively [21,33]. The CF at a given height is defined as the number of cloudy pixels divided by the total number of pixels by ignoring the totally attenuated pixels (SR < 0.01). The cloud phases are identified based on the relationship between ATB and cross-polarized ATB (ATB┴) [33]. Based on this relationship, the CF is classified as liquid, ice, or unidentified. The undefined clouds are estimated to be about 10% of the total CF [33]. Studies show that highly reflective layers in lidar imagery and low depolarization ratio (e.g., [34,35]) characterize super-cooled mixed phase clouds; thus, most of these undefined cloud layers may be related to mixed phase clouds. The CALIPSO-GOCCP data used here range from year 2007 to 2019 (close to 13 years). The 3D version of the data has 40 vertical levels and a grid resolution of 2° × 2°. The cloud types are identified using a methodology given in Table A2 (Appendix A).
2.2. Radiation
The Clouds and the Earth’s Radiant Energy System (CERES) radiation data including the Edition 4.1 datasets are described elsewhere [27,29,31], here only brief descriptions are given.
2.2.1. At the Top of the Atmosphere (TOA)
The CERES instruments fly on board the Terra and Aqua satellites. Each satellite carries on board identical CERES instruments that measure filtered radiances in the shortwave (SW) (0.3–5 μm), total (0.3–200 μm), and window (WIN) (8–12 μm) regions and including Moderate Resolution Imaging Spectrometer (MODIS) that measures radiation at 36 spectra bands covering the wavelengths between 0.4 and 14.4 μm. The unfiltered SW, longwave (LW), and WIN radiances are determined following [36]. These radiances are converted to radiative fluxes using empirical angular distribution models (EADM) [37,38,39,40]. The CERES instruments provide global coverage daily, and monthly mean regional fluxes based on complete daily samples. Although there have been considerable improvements in satellite-based measurements due to better instrument calibration and retrieval algorithms, there are still two significant problems in CERES L3 products. One is the persistence of significant imbalance in the calculated mean global net radiation at the top of the atmosphere (TOA) and the second is the occurrence of gaps in monthly mean clear-sky TOA flux maps due to the absence of cloud-free areas. The observed global net energy imbalance (GNEI) in CERES data is estimated to be between 3.4 and 4.3 Wm−2 [41,42]. This is normally compared to the expected ocean-heating rate based on independent in situ measurements that varies between 0.58 and 0.71 Wm−2 [41]. Assuming that most of the GNEI at the TOA (>90%) goes to warming the ocean, the GNEI based on CERES data is significantly larger than the observed values and thus can have a significant impact on the validation of global climate models (GCM) by using these datasets. The CERES energy balanced and filled (CERES-EBAF) products address some of these problems by using an algorithm that adjusts SW and LW TOA fluxes to remove the imbalance between the average global net TOA flux and heat storage in the Earth–atmosphere system. In the most recent edition of EBAF (EBAF4.1), an averaged GNEI close to 0.7 Wm−2 has been applied. To address the problem of gaps in clear-sky TOA flux, the EBAF algorithm that uses clear-sky fluxes from both CERES and MODIS measurements is used to produce a new clear-sky TOA flux climatology that provides TOA fluxes in each 1° × 1° region every month. The regional monthly mean uncertainty in net shortwave cloud radiative forcing (SWCRF), longwave cloud radiative (LWCRF), and net cloud radiative forcing (NetCRF), at the top of the atmosphere (TOA) in the EBAF4.1 radiation data are estimated to be 5.9, 4.5, and 7.4 Wm−2, respectively [31]. The data summary does not include the global annual mean uncertainties in these cloud properties. The annual mean values are smaller and estimated to be in the range 2–3 Wm−2 (Norman Loeb personal communication).
2.2.2. Surface Measurements
The summary of the data quality and associated retrieval methods of the radiation flux at the surface can be found in two references [27,31]. The algorithms employed to derive the radiation flux at the surface level uses two datasets: the EBAF Edition (Ed) 4.1 (EBAF_Ed4.1) that is based on satellite observations [29] and the Synoptic Ed 4.1 (SYN-Ed4.1) that uses a radiative transfer model to compute the radiative flux at various atmospheric levels including at the TOA and surface. The computed surface radiative fluxes (shortwave and longwave) are adjusted by adjusting the bias between the computed (SYN-Ed4.1) and observed (EBAF-Ed4.1) radiative flux at the TOA and by adjusting the CF bias using CALIPSO and CloudSat measurements [27]. Error covariance is derived from surface irradiance sensitivity to surface, atmospheric, cloud, and aerosol property perturbations. The regional monthly mean uncertainties in longwave, shortwave, and net cloud radiative forcing at the surface (), (), and () are estimated to be 18, 16, and 26 Wm−2 [31] indicating the much more significant uncertainties are associated with these datasets as compared to the radiation at the TOA. The global and annual mean uncertainty in shortwave, longwave, and total irradiances at the surface are 5.7, 6.7, and 9.7 Wm−2, respectively [43]. The uncertainties in cloud radiative forcing at the surface is not reported, but it is expected to be larger than the uncertainties at the TOA.
2.2.3. Derivation of the Cloud Radiative Forcing
Using the model and satellite data, the longwave cloud radiative forcing (LWCRF), shortwave cloud radiative forcing (SWCRF), and net cloud radiative forcing (NetCRF) at the TOA are derived as
where and are all sky shortwave and longwave upward fluxes at the TOA and and are the corresponding upward clear sky shortwave and longwave clear sky (cs) fluxes, respectively. In these calculations, clear sky is defined to be compatible with the way it is defined in GCMs.
The cloud forcing at the surface (surf) level are calculated following [24] as
where , and and are all sky downward and upward longwave and shortwave fluxes at the surface, respectively, and the symbol “cs” denotes clear sky conditions. The modeled upward clear sky longwave radiation () is estimated using surface temperature (Ts) as
where is the surface emissivity approximated close to 1 and is the Stefan–Boltzmann constant (5.67 × 10−8 Wm−2K−4). The longwave cloud radiative forcing in the atmosphere () and shortwave cloud radiative forcing in the atmosphere () and net forcing () are calculated using the following equations by taking the difference between cloud radiative forcing at the TOA given in Equations (1)–(3) and surface (Equations (4) and (5)).
2.3. Descriptions of the Models and Satellite Simulators
The detailed description of the CanESM version 5 model is given in [7]. The atmospheric component of the model implemented in this model is an improved version of the Canadian Atmospheric Model version 4 (CanAM4). The detailed description of the CanAM4 can be found in [44]. The older version of CanESM (CanESM2) is based on the CanAM4 scheme. The cloud microphysics scheme used for simulating both ice and liquid phase stratiform cloud is based on prognostic equations described by [45,46]. It is a fully coupled model that incorporates various systems including ocean, land surface, sea ice, and atmosphere [7]. The deep moist convection is based on a spectral mass flux scheme introduced by [47]. The CF is diagnosed based on a grid-scale condensate-mixing ratio [44].
In CanESM2, the single scattering properties of cloud particles are parameterized in terms of cloud water content and the mean effective cloud particle size depending on cloud phase. For ice clouds, the mean ice particle effective size is defined following [48], as a generalized effective size (Dge) that considers the ice particle shapes [49,50]. For the liquid phase case, the parameterizations developed by [51] in the visible spectrum (0.25–4 µm) and [52] for the infrared spectrum (4–100 µm) were used. For the solid phase case in both the solar and infrared spectrums, the [48,53] parameterizations, respectively, were used. In CanESM5, for the solid phase case in both the solar and infrared spectrums, the parameterizations developed by [54] were used (Jason Cole personal communication). In this study, both the Atmospheric Model Intercomparison Project (AMIP) and coupled model historical simulations were used. The AMIP configuration is based on prescribed sea surface temperature (SST) and sea ice extent [55].
To facilitate the comparisons of GCM data with satellite data, an integrated satellite simulator referred to as COSP was developed (e.g., [13,14]). The COSP software emulates cloud properties from both active and passive sensors using grid and sub-grid scale model data. The simulator used in this study is based on the COSP version 1.4 (personal communication, Jason Cole). The more detailed technical description of the COSP software can be found in the references given previously. The available model data used for this validation study range from 1995 to 2014, as indicated in Table A1. There is a time mismatch between the models themselves and satellite observations but based on earlier studies such comparisons are possible as long as the number of years used to create the climatology exceeds 5 years [56], which would be satisfied in this case. The CALIPSO satellite-based emulated CF datasets are only available for the AMIP configuration. All the satellite datasets are remapped into the model grid using a technique that is referred to as the first-order conservative remapping method [57].
3. Results
3.1. Satellite and Model Total Cloud Cover Comparisons
Since one of the main objectives of this study is to evaluate the simulated CF using the Canadian Environmental System Models (CanESMs) and the most recent satellite products, the CALIPSO-GOCCP (referred to GOCCP from here on) data was chosen for this evaluation since active sensors are more reliable than the passive sensors, particularly at higher latitudes where the passive sensors have more limitations [20]. Figure 1 shows 2D density plot monthly averaged total cloud fraction (TCF) obtained from GOCCP and several versions of the CanESM and the associated mean difference (MD). The first two panels show the CanESM5 at its fully coupled model configuration represented here as CanESM5 (Figure 1a) and Atmospheric Model Intercomparison Project (AMIP) configuration () (Figure 1b). Both models have similar discrepancy at the observed TCF values (TCF < 60%) where both models underestimate and overestimate the cloud cover depending on the geographical location and this will be discussed in more detail later. Nonetheless, the model data are reasonably correlated with the GOCCP data with a correlation coefficient of 0.8 for both models, but both models have negative bias with an MD for the CanESM5 of −1.8%, whereas the has an MD of −2.4 % which is slightly higher. The CanESM2 model shows similar discrepancies (Figure 1c,d) as compared to the CanESM5 (Figure 1a,b), but the MD values for CanESM2 models are a factor of 3 higher than the CanESM5 models (see Figure 1c,d). From a perspective of the 2D density plots (Figure 1f,g), the two versions of the CanESM5 and CanESM2 show excellent agreement with their counterparts the and , respectively, with a correlation coefficient of 0.97. The CanESM5 is slightly higher than with an MD of 0.6% and CanESM2 is slightly lower than with an MD of 0.8%. The area weighted global mean values of TCF were 65.4%, 64.8%, 61%, and 61.6% for CanESM5, CanESM2, and , respectively. These values are relatively smaller as compared to the GOCCP global mean value of 67%. On the basis of the area-weighted global mean TCF data perspective, the CanESM5 is closer to the satellite data, and thus the new version shows some improvements.
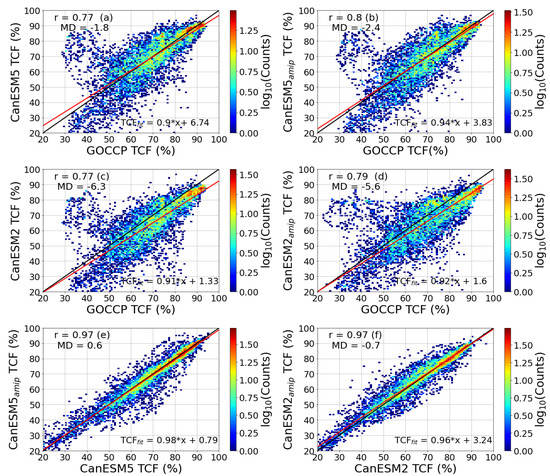
Figure 1.
The 2D density plots of monthly averaged total cloud fraction (TCF) based on the GOCCP and model data (CanESM5 (a), CanESM5amip (b), CanESM2 (c), CanESM2amip (d)), and based on model data (CanESM5amip and CanESM5 (e); CanESM2amip and CanESM2 (f)). The red solid lines represent the best-fit equations (x represents the variable on the x-axis) and the solid black line represents the 1:1 line. The correlation coefficients (r) and the mean difference (MD) values are given.
Figure 2 shows the global maps of the bias in annually averaged TCF and RMSE between the model and GOCCP data (Figure 2a–f)) and between the different versions of the model (Figure 2g–i). The COSP software-based CALIPSO lidar emulated CF data are only available for the AMIP configuration and here they are represented as and (Figure 2e,f). The first three panels show the bias for CanESM5 (Figure 2a), (Figure 2b), and (Figure 1c). All versions of the model overestimate TCF (positive bias) mainly over the oceanic tropical region within the intertropical convergence zone (ITCZ) that includes western and eastern Pacific Ocean, Atlantic and Indian Ocean near the equator, and including over the Atlantic Ocean situated at the northern mid-latitude region as well as polar regions, particularly in the southern hemisphere. A similar bias for the CanESM5 model based on the ISCCP satellite has been reported [7]. The models, however, underestimate the TCF (negative bias) over the rest of the globe; particularly over Sahelian dry regions of northern Africa and southern Europe and Asia, and eastern shores of South and North America and Africa. The and data appear to remove some of the positive bias over the eastern side of the Pacific Ocean near the eastern coasts of South America with RSME values of 10.7 % and 10.2%, respectively, as compared to 11.1% for CanESM5 which is slightly higher (Figure 1b,c). It should be noted here that the COSP-based simulated models and ) have larger mean negative bias as compared to the models without the COSP simulator and ), particularly for the model (Figure 2b,c). The model (all versions) generally has a negative bias indicating underestimation of the cloud cover except over the west side of the Pacific Ocean and the northern Indian Ocean where the model overestimates the cloud cover (Figure 2d–f). The (both the AMIP and coupled versions) has relatively higher RMSE values of 12.2% and 11.6% (Figure 1c,d) as compared to the models (Figure 1a,b). Similar to the AMIP versions of the model, the AMIP versions of slightly improve the bias over some oceanic regions. The globally averaged MD of the model bias values varied from −1.8% to −3.8% for CanESM5 and from −6.3% to −7.1% for CanESM2 indicating that, on average, both models underestimate clouds. The predicted higher TCF as compared to the model over most of the globe, particularly over the Pacific Ocean potentially associated with low-level marine clouds and northern South America where high-level convective clouds are prevalent. On average, the overpredicts TCF as compared to with an MD of 4.6% and RMSE value of 6.2%. The difference between the fully coupled and the corresponding AMIP version of the model is relatively small (Figure 2h,i) except within the tropical regions where the fully coupled model version overpredicts the TCF mainly over the tropical oceanic regions and underpredicts the TCF over continental regions. The global mean differences between the AMIP and coupled are 0.6% and −0.7% for and , respectively (Figure 2h,i). The variation in spatial distribution of the model bias for a given model depicted in Figure 2 could be connected to weakness of simulating certain cloud types over a given location in the globe and this will be discussed in Section 3.2.
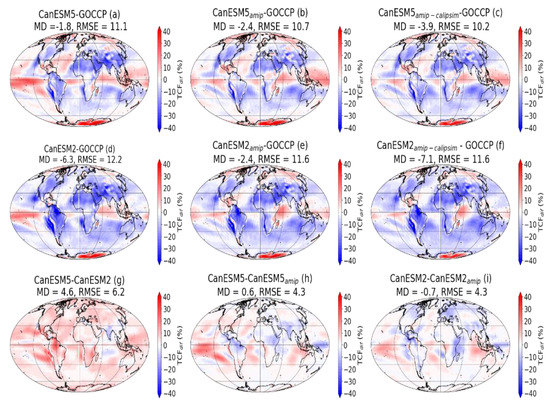
Figure 2.
The global maps of model bias in annually averaged total cloud fraction (TCF). The root mean square error (RMSE) and mean difference (MD) values are also given.
The global maps of bias in annually and seasonally averaged TCF for some selected datasets are shown in Figure 3. The first column shows the northern hemisphere summer season (JJA) and the second column shows the northern hemisphere winter season (DJF). On average, the models underestimate the TCF in the JJA season as compared to the DJF season, but the distribution of the bias shows spatial and seasonal variability following typical general atmospheric circulations. During the JJA season, convectively active regions associated with the ascending branches of the Hadley circulations in the tropics are normally present and the circulation associated with Ferrel Cell at higher latitudes is expected to shift towards the northern hemisphere and the opposite happens during the DJF season. This seasonal variability in the atmospheric circulation is also reflected in the distribution of the model bias as depicted in Figure 3. Generally, over the tropical oceanic regions where convection activities are prevalent, such as the Atlantic and Pacific, all the models have a significant positive bias. Over the oceanic regions where persistent LL marine stratocumulus/cumulus clouds are expected, the models have significant negative bias. The continental regions including the Arctic are mostly characterized by a negative bias but in the Antarctic regions, the bias is positive. This positive bias in the DJF season (summer in southern hemisphere) propagates to the northern hemisphere during the JJA season following the Hadley circulation and this is particularly true for the model (Figure 3a,b). This negative bias over the Arctic regions in the JJA season shifts to a positive bias in DJF. The JJA season is also characterized by higher RMSE values as compared to the DJF season. The positive bias over the western Pacific Ocean near the equator is persistent during both seasons ((a) and (b)) and it becomes wider during the northern hemisphere winter season (panel b). The model agrees reasonably well over the southern oceans between 30°S and 60°S during both seasons (DJF and JJA).
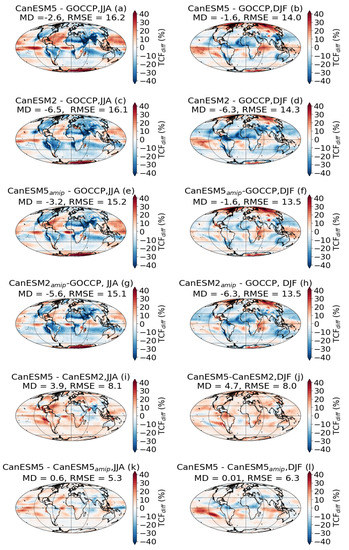
Figure 3.
The global maps of model bias in annually and seasonally averaged total cloud fraction (TCF). The mean difference (MD) and root mean square error (RMSE) values are also given.
The data shows a similar geographical bias distribution as the model, but the model has a mostly negative bias during both seasons, which implies underestimation of the CF (Figure 3c,d). The AMIP versions of the and models (Figure 3e,f) behave very similar to their counter parts (Figure 3a–d) and remove some of the positive bias over the western Pacific Ocean near the equator as mentioned previously and are characterized by relatively smaller RMSE values. The comparison of the coupled version of the Canadian models ( and ) and AMIP versions () are shown in the last two rows (Figure 3i–l). When the two coupled models are compared during the JJA season, the generally predicts smaller CF as compared to the model except over localized regions of India and the Indian Ocean where the overestimated the CF (negative bias (Figure 3i)). This negative bias changes to positive bias during the DJF season (j), but no significant seasonal north–south shifts in the bias or MD values (Figure 3i,j). The difference between the coupled and AMIP versions of the is most pronounced over the tropical latitudes (30°S and 30°N) during both seasons (Figure 3k,l). During the JJA season, the coupled model mostly overestimates CF over the Pacific and Atlantic Oceans, and underestimates the CF over India, the Indian Ocean, and the western Pacific Islands (k). During the DJF season, the coupled model underestimated the cloud over the Tropics in the northern hemisphere and the opposite is true in the southern hemisphere (l). On average, however, the two versions agreed well with MD values of 0.01% and 0.6% in the DJF and JJA seasons, respectively.
3.2. The Model, Satellite, and Cloud Type Comparisons
3.2.1. GOCCP and CALIPSO Emulated (COSP) Model Data
In this part of the analysis, only the AMIP version of the model datasets were used in the CALIPSO-COSP simulator since the coupled model versions of the datasets were not available. As before, these datasets are represented as and corresponding to the two versions of the Canadian models. Figure 4 shows annually and globally averaged low-level cloud (LLC) cover, mid-level cloud (MLC) cover, and high-level cloud (HLC) cover based on the GOCCP data (Figure 4a,d,g), (Figure 4b,e,h), and (Figure 4c,f,i). According to the observed GOCCP data, the LLCs are prevalent mostly over the oceanic regions of the globe, particularly over the south-eastern Pacific (SEP), Atlantic (SEA), Indian (SEI), and north-eastern Pacific (NEP) oceans near the west coasts of South America, Africa, Australia, and North America, respectively. These locations are normally dominated by persistent decks of subtropical low marine stratocumulus clouds (MSC) that are characterized by upwelling of cold ocean water near the coast, strong subsidence, boundary layer temperature inversion, and high atmospheric stability [58,59]. The LLC clouds are also found over mid-latitude oceanic storm track regions, predominantly over the southern hemisphere potentially related to shallow convective activities [60], and in the Arctic oceans east of Greenland. The MLCs constitute a relatively small portion of the total cloud cover and are found mainly over the continents of South America and in the Tropics and over the high-latitude regions (both hemispheres). On the other hand, the HLCs are largely found over the continental regions of South America and Africa within the ITCZ and over the Indo-Pacific warm pool where deep convective activities are prevalent [61,62]. The HLCs are also found at the high-latitude regions but constitute a relatively smaller portion of the total HLC in comparison to the tropical regions.
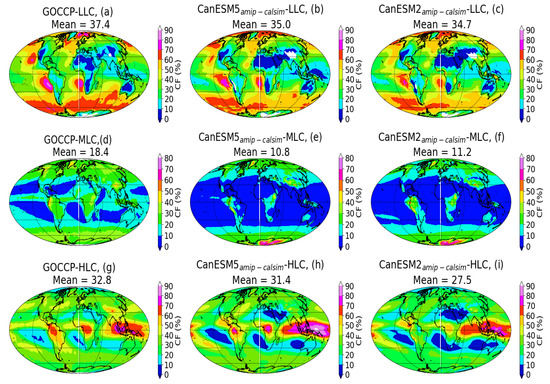
Figure 4.
Annually averaged global distribution of cloud fraction (CF) of low-level clouds (LLC), mid-level clouds (MLC), and high-level clouds (HLC) based on GOCCP and CanESM models.
Based on a visual inspection of Figure 4, the model reasonably captured the climatological distribution of the LLC and HLC cover (Figure 4a,b,g,h). It can also be seen, however, that the HLC clouds are particularly overpredicted over the Indo-Pacific warm pool regions and over the Western North Atlantic Ocean (WNAO) near the southeastern coasts of North America (Figure 4g). It is also worth noting that the model totally missed the HLC over South America (Figure 4g,i). The most notable differences between the GOCCP and the models is the absence of MLCs in the model data (Figure 4e,f). The area-weighted global mean CF for LLC varied from 34.7% to 37.4%, the lowest being for the model. From the perspective of the global mean values, the models underestimated the LLC as compared to the GOCCP data, but both models simulated similar LLCs (Figure 4b,c). The models also underestimated the HLCs, and the mean values varied from 27.5% to 32.8% (Figure 4g,h,i) and the lowest global mean value in this case was simulated by the . The models simulated significantly lower (by a factor of ≈2) MLCs as compared to satellite-based data.
The difference in spatial distribution of model bias in CF and type are better illustrated using Figure 5. According to results shown, all the models including the underestimate the LLC CF (negative bias) over a majority of the oceanic regions including the LL MSC cover over the oceanic locations of the SEP, SEA, SEI, NEP, Indo-Pacific, and southern oceans mentioned previously. The results also show that there are sporadic patches of positive bias over the eastern Pacific Ocean near the equator and Atlantic Ocean, and over most of the continents. The model overestimated the HLC fraction over the western Pacific and Indian Oceans within the tropics where deep convective clouds are expected, and over the tropical and sub-tropical regions of the WNAO mentioned previously. The WNAO region is characterized by both convective and synoptic scale weather systems and climatologically it is mainly dominated by LL shallow cumulus and stratocumulus clouds [63] as also confirmed in Figure 4a,g. The model also underestimates the HLC clouds over southern oceans and over most of the continental regions except over the areas normally characterized by relatively large amounts of HL clouds (Figure 4g–i) where the model slightly overestimated the HLC in the case of the . Comparisons of these results and the results given in Figure 2c where it shows the spatial distribution of model bias in TCF, it can be seen that the overestimation of TCF near the equator and Atlantic Ocean within the tropics are largely associated with LL marine clouds. On the other hand, overestimation of TCF over the Indo-Pacific warm pool appears to be largely associated with overestimation of HLCs. The overestimation of TCF over Antarctica appears to be related to the overestimation MLC. However, as indicated in the plots, the models significantly underestimate the MLC over most of the globe except over northern Ethiopia, central Europe, and the western coast of continental South America. The distribution bias in CF and type associated with the model is qualitatively similar to the model, but the model more severely underestimated the HL clouds, particularly over continental regions. Generally, on average, the models underestimate all the cloud types with MDs of −2.4%, −7.6%, and −1.4% corresponding to LLC, MLC, and HLC for and −2.7%, −7.2%, and −5.4% for indicating that both models more significantly underestimate the MLC, but the model more significantly underestimated the HL clouds as compared to the model. Studies show that the HLCs have a strong tendency to suppress the outgoing IR radiation and warm the atmosphere, particularly in the Tropics (e.g., [64]), and net radiative forcing or cooling is strongly correlated with the proportion of the LLC cover (e.g., [65]). Thus, such discrepancies in the model can have a significant impact on the climate simulation. The cloud radiative effects will be discussed later in more detail.
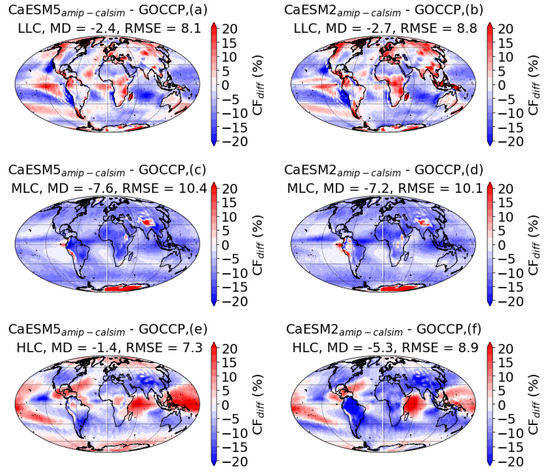
Figure 5.
The model bias in annually averaged global distribution of CF for low-level cloud (LLC) (a,b), mid-level cloud (MLC) (c,d), and high-level cloud (HLC) (e,f).
Figure 6 shows annually and zonally averaged CFs shown in Figure 5 and CF data from all the models. As indicated in Figure 5a, the models generally captured the zonal variation in the LLC, which is consistent with the discussion given previously. However, the models have some discrepancies in the tropics and high latitude (near 60°S) where, on average, they underestimated the LLC cover as compared to the GOCCP data. The models generally underestimated the zonal mean MLC cover over all latitudes (Figure 6b) as would be expected based on Figure 5. From the zonal mean perspective, only the overestimated the HLC fraction in the tropics between approximately 15°N and 15°S latitudes and high-latitude regions (lat > 60°) in both hemispheres, outside these limits both models underestimate the HLC CF, particularly the (Figure 6c). The models generally understated the TCF as compared to GOCCP, particularly in the Tropics within the region between 10° and 40° latitude over both hemispheres where it is dominated by subsiding air (Figure 6d). As can be seen in the figure, the new version of the model, CanESM, is slightly better than the older version of the model (), but it can also be seen that the model overestimated CF within the narrow region of the globe near the equator and this may be related to the overestimation of the HLCs (Figure 6c).
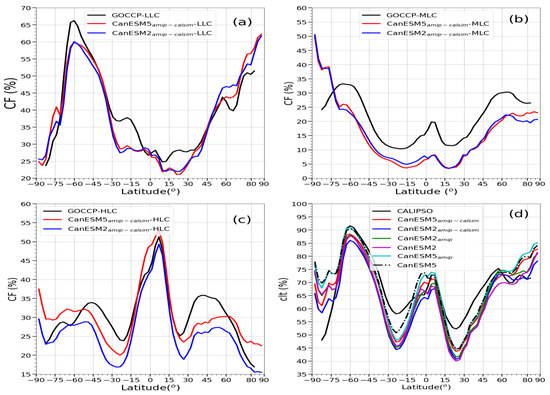
Figure 6.
Annually and zonal averaged low-level cloud (LLC) (a), mid-level cloud (MLC) (b), high level cloud (HLC) (c), and total cloud cover (d) based on the models, GOCCP.
Figure 7 shows a latitudinal dependence of ratios (Model/GOCCP) of the zonally averaged CF for each cloud type shown in Figure 6. According to the results shown in the figure, the models underestimate the MLCs more significantly than the rest of the cloud types over all latitudes reaching up to a factor 3 in the Tropics near the equator (within ±30° lat) where both the sinking and rising branches of the Hadley cell are expected. The exception is south of 72°S over Antarctica where both models overestimate the MLCs as also demonstrated in Figure 5c,d. The model underestimation of LLC is generally confined between 10° and 30° latitude over both hemispheres having two minima (near ±20° lat) where the total cloud fractions were significantly underestimated as a result of subsiding relatively dry air (Figure 6d). The LLC fraction is slightly overestimated by both and near the equator in the southern hemisphere. As discussed above, from a perspective of the zonally averaged data, the simulated HLC fraction was only slightly overestimated over the regions near the equator (within ±15° lat) by the model. In contrast, the model reasonably agreed with the GOCCP data in this region. The models, however, significantly underestimated the HLCs over the regions where the subsiding branches of the Hadley cell are expected, particularly by the model. According to Figure 6, the HL and LL clouds constitute the larger portion of the total cloud cover at lower latitudes; thus, the underestimation of the total cloud cover by the models within ±30° lat (see Figure 6d) could be mostly related to these clouds. However, the MLC fractions are comparable to the HLCs at the higher latitudes and hence are expected to make comparable contributions to the total cloud over these regions.
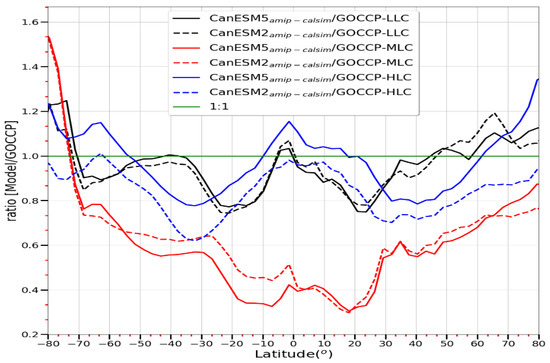
Figure 7.
Ratios (Model/GOCCP) of the annually and zonally averaged modeled low-level, mid-level, and high-level CFs to the corresponding observed values.
3.2.2. GOCCP and Model Vertical Profiles
Figure 8 shows annually and zonally averaged vertical cross-sections of CF based on the GOCCP, , and (Figure 8a–c)) and the bias (model-GOCCP) (Figure 8d,e), and difference (-) (panel f). Based on the GOCCP data (Figure 8a), the distinct climatological regions of the HLCs in the Tropics, the cloud-free subsiding and cloudy rising branches of the Hadley cell, and boundary layer clouds can be identified. The models are generally able to identify these climatological regions as compared to the GOCCP data (Figure 8b,c), but the most striking difference based on visual sections (Figure 8b,c) is the lack of mid-level clouds in the model-simulated data in the Tropics and mid-latitude regions and this fact has been already noted in the previous discussions. This cloud-free region becomes vertically wider in the Tropics where it extends from 2 km to about 10 km height. The model biases shown in the figure (Figure 8d,e) generally illustrate the previous discussions that the models generally underestimate the LLC (z < 3.2 km) cover over all latitudes, particularly over high-latitude regions near 60° in both hemispheres where the bias reaches over −10% to −15% (Figure 8d,f). It can also be seen that the models overestimate HLC (z > 6.5 km) over all latitudes particularly near the Tropics and higher latitude regions of both hemispheres. The model has a larger positive bias in HLC close to 12.5 % over the northern high-latitude regions (Figure 8d) as compared to the bias of close to 5% (Figure 8e). As illustrated in (Figure 8f) of the figure, the difference between the and generally ranges from −2.5% to 2.5% except at higher attitudes in the Tropics and lower levels at higher latitudes over the southern hemisphere where the predicts generally higher cloud amounts as compared to the . On the other hand, the model slightly predicts lower mid-level cloud amounts.
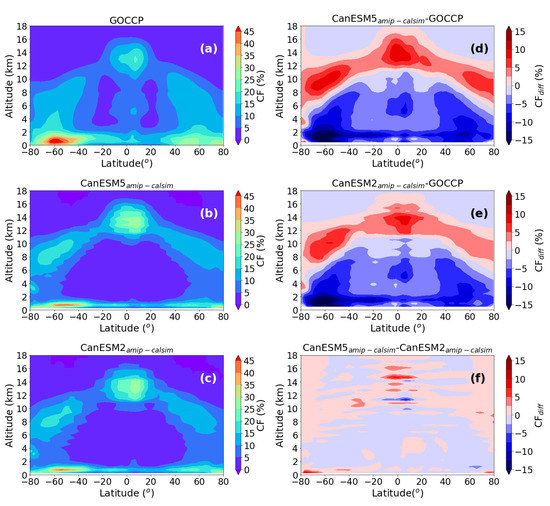
Figure 8.
Annually and zonally average vertical cross-section of CF based on CALIPSO (panel (a)), (b), (c) and the difference (model-CALIPSO) for CanESM5amip-calsim (d), CanESM2amip-calsim (e), and CanESM5 and - (f).
The differences between the model and satellite data discussed above are better illustrated using the vertical profile of CF and phase based on CALIPSO and model data given in Figure 9. Here, we show only the data since data was not available. The first two panels (Figure 9a,d) are similar to the ones given in Figure 8a,b. The remaining four panels show ice ((c) and (d)) and liquid (Figure 9e,f) phase clouds based on the GOCCP and data. According to the GOCCP data, the LLCs (z < 3.2 km) are largely associated with the liquid phase clouds, increasing with increasing latitude having more liquid phase clouds over the high-latitude regions where the temperature is expected to be colder, and the southern high-latitude regions particularly have higher liquid phase clouds (see panel c). Previous studies also found similar results [66,67]. The model data are consistent with the GOCCP data in this sense, but the model-based low-level liquid phase clouds are vertically shallower as compared to the CALIPSO data (Figure 9e,f). According to the results found by [67] for a given subzero temperature (T = −20 °C in this case), the proportion of the super-cooled liquid phase cloud is negatively correlated with relative dust particle frequency suggesting that enhanced glaciation may occur over lower latitudes where these lifted dust particles are more frequent, particularly over the northern hemisphere. This suggests that although the cloud phase is strongly linked to local atmospheric temperature, it may be misleading to assume that a single-phase fraction and temperature relationship is applicable for the entire globe as has been done in some models. As indicated in the plots, the model overpredicted the ice phase cloud cover (HLCs) (Figure 9c,d), particularly in the Tropics. The model also shows glaciated clouds near the surface level at higher latitudes that are not found in the CALIPSO data. Comparisons of the first two panels and the rest suggest that most of the missing mid-level clouds in the model are probably associated with mixed phase clouds. Note also that the current GOCCP data does not classify mixed phase clouds. However, by comparing the all-phase CF (a) and the rest suggests that most of the unclassified clouds could be associated with mid-level clouds. The previous studies using active sensors also indicated that the MLCs particularly over the Tropics are mostly associated with mixed phase clouds [68,69].
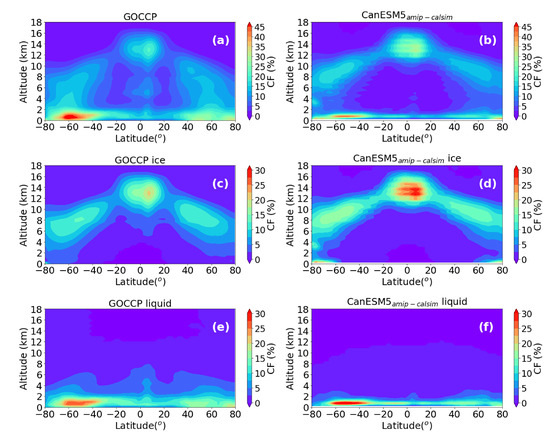
Figure 9.
Annually and zonally average vertical cross-section of CF GOCCP (all phase (a), ice (c), liquid (e)) and (all phase (b), ice (d), and liquid (f)).
Figure 10 shows a horizontally averaged version of the data given in Figure 9. In the figure, the data for the tropical regions (±30° latitude) are also shown (Figure 10a). It can be seen in the figure that a significant portion of the mid-level clouds are missing in the model and high-level ice clouds are overpredicted, particularly in the tropical regions (Figure 10a,b). Note that the GOCCP data shows three CF peaks at high, mid, and low altitudes corresponding to potentially two detrainment levels of tropical deep convective and low-level boundary layer clouds (a). The mid-level peak, however, is missing in the model data. The authors of [15] compared CF simulated using the ECHAM5 GCM with a LIDAR simulator and found that the model overestimated the HLCs in the Tropics similar to this study. They attributed this discrepancy to overestimation of mass flux by the convective parameterization scheme [70] used in the model and underestimation of detrainment at mid-level that led to formation of excessive clouds at a higher level that normally takes a longer time to sediment and dissipate via evaporation. Relatively enhanced ice cloud cover at higher altitude and missing mid-level (possibly mixed phase clouds) in the models found in this study may be also partly linked to the treatment of deep convection in the model which is based on the spectral mass flux scheme introduced by [46] (from here on ZM95). This scheme has been also implemented in the NCAR CAM3 model. By comparing the NCAR CAM3 model results with 3D WRF high-resolution simulation, the authors of [71] found that the ZM95 parameterization scheme underestimates the cloud entrainment rate at the lower level and as a result excess moisture and heat is transported to the higher level producing unrealistic HLCs. As mentioned previously, the type of aerosol particles included in the ice nucleation process may also have a significant impact on the observed cloud phase distribution, but many of the current GCMs and NWP models, including the CanESM model, do not explicitly include aerosol type in their cloud microphysical parameterization schemes. The increase in ice CF near the surface shown in the model data may be associated with the polar regions discussed previously. As mentioned previously, the liquid phase clouds predicted by the model near the surface are confined to vertically narrow regions as compared to the GOCCP data, but also slightly higher than the GOCCP data at about the 1 km level.
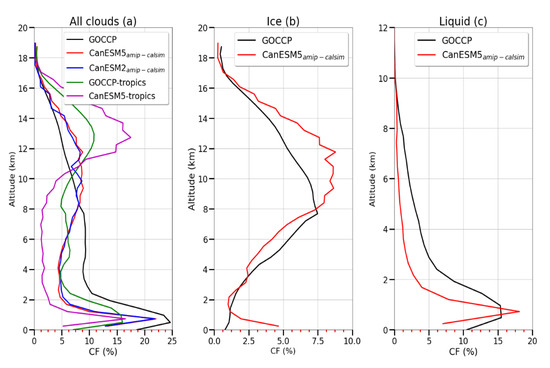
Figure 10.
Annually, globally, and horizontally averaged CF for all phase (a), ice phase (b), and liquid phase clouds (c).
The seasonal climatology of the data shown in Figure 9 is given in Figure 11 and Figure 12 for JJA and DJF, respectively. The main differences between the JJA and DJF climatology includes shifting of the high-level ice cloud cover maximum towards the summer hemisphere, but there is no such shifting of the low-level liquid phase clouds (see Figure 11 and Figure 12c,b). It is interesting that higher liquid phase low-level clouds are detected over the high-latitude southern hemispheric regions during the JJA season (Figure 11c) which is a winter season in the southern hemisphere. On the other hand, in the northern hemisphere, relatively higher liquid clouds were formed during the summer season (JJA). As compared to the satellite observation, the model does not show any significant seasonal variability in the low-level liquid phase clouds (Figure 11 and Figure 12). It can be also noted that based on the satellite data more mid-level clouds are formed during the summer season in both hemispheres (see Figure 11 and Figure 12), but the model data does not show such seasonal variability.
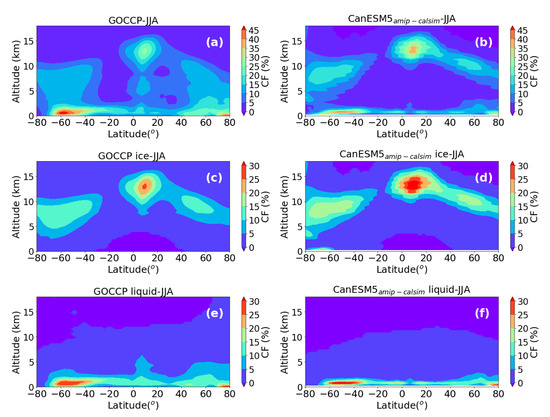
Figure 11.
Annually and zonally average vertical cross-section of CF in JJA for GOCCP (TCF (a), ice (c), and liquid (e)), and (b,d,f).
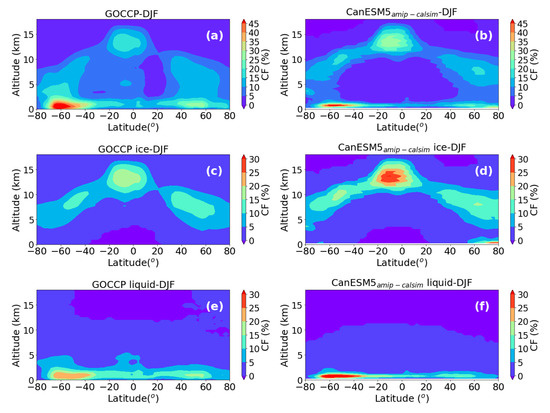
Figure 12.
Similar to Figure 11, but the DJF season.
3.3. Cloud Radiative Forcing
The annually averaged global distributions of SWCRF, LWCRF, and NetCRF at the TOA, surface, and in the atmosphere derived based on the satellite (EBAF4.1) and CanESM5 model data are given in Figure 13. Based on the satellite data, the LWCRF at the TOA and surface has a strong link to the cloud cover and the effect is positive (warming) with global mean values of 26 and 27.6 Wm−2, respectively. At the TOA, the warming effect of the LWCRF is more sensitive to the HLC and hence the warming effect is large in the Tropics, particularly over the Indo-Pacific warm pool, central Africa, and northern South America. At the TOA, the warming effect of the LWCRF over the poles is relatively weaker than the lower latitudes. At the surface level, the warming effect is larger in the areas of LLC such as in high-latitude regions and in the Tropics where the LL marine stratocumulus clouds are prevalent (Figure 4). Thus, from the perspective of LWCRF at the surface, clouds relatively warm the high-latitude regions as compared to the tropical region that may weaken the near-surface meridional air flow. On the other hand, the LWCRF within the atmosphere appears to have opposite effects that tend to enhance the meridional circulation by warming the Tropics and cooling the high-latitude regions.
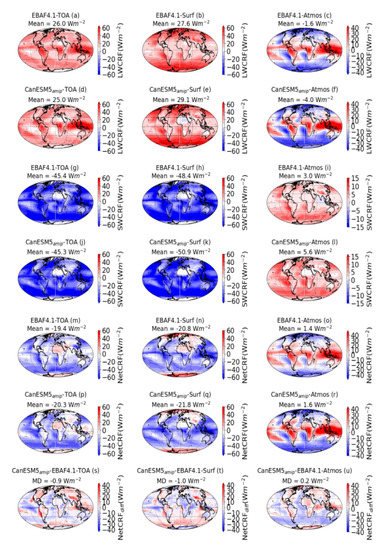
Figure 13.
The annually averaged global distributions of SWCRF, LWCRF, and NetCRF at the TOA, surface, and in the atmosphere derived based on the satellite (EBAF4.1) and CanESM5 model data.
In contrast to the LWCF, the SWCF at the TOA and surface is negative (cooling) with global means values of −45.4 and −48.4 Wm−2, respectively. The spatial distribution of the SWCRF at the TOA and surface is largely connected to variation in cloud cover as shown in Figure 4. With more cloud cover, the reflection in shortwave radiation is higher and hence there is enhanced cooling both at the TOA and the surface. This cooling effect is particularly sensitive to the LLC cover amount (Figure 4), particularly over oceanic, mid-latitude storm-track regions, the tropical warm pool, and the ITCZ. The diminished cooling regions are associated with the areas of lower cloud cover amount such as over the Sahel region in northern Africa and over the Middle East, as well as over the Antarctic and Arctic regions. It should be noted here that over the Antarctic and Arctic regions the surface is covered by snow characterized by high albedo and high solar zenith angle and thus it is hard to distinguish between clear and cloudy scenes over the bright ice and snow-covered regions, and, therefore, the slight negative SWCRF results in the figure are probably less accurate than elsewhere. Recent studies based on airborne measurements suggests that clouds in the Arctic probably have a stronger cooling effect by enhancing surface albedo over highly reflective snow and ice surfaces [72]. Earlier studies also indicated that over Antarctica, the shortwave cloud forcing was negative (cooling) at the surface [73,74] and positive (heating) at the TOA [71]. However, on average, the SWCRF in the atmosphere is positive (near 3.0 Wm−2), which implies a warming effect, and this effect increases with increasing LLC cover amount (Figure 4).
The net radiative effect of clouds at the TOA and surface is cooling with corresponding global mean values of −19.4 and −20.8 Wm−2, respectively, and these values are very close to the values given in [24,30], respectively. In the atmosphere, the global mean net cloud radiative effect is positive and relatively small (1.4 Wm−2) as a result of cancelation effects due to strong warming over the Tropics, potentially related to HL clouds and strong cooling over the high-latitude regions and some areas within the Tropics were dominated by LL marine clouds (Figure 4). Generally, the NetCRF at the TOA associated with deep convective clouds such as those found in the Tropics is expected to be small because of cancelation effects, but over the areas dominated by LLCs the cooling effect dominates (Figure 13m). The NetCRF at the surface appears to be stronger (more negative) over regions where HL convective clouds are expected.
Based on visual inspections of the plots, the model generally captured the spatial distribution of the cloud radiative forcing or effect, although the degree of the forcing varies from region to region as compared to the satellite data. The modeled global mean SWCRF TOA is −45.4 Wm−2, which is identical to the value obtained using the satellite data, but at the surface level, the modeled SWCRF is −50.9 Wm−2, which suggests more cooling. Based on the global mean values perspective, the warming effect due to the LWCRF at the TOA is slightly smaller for the modeled data having an MD of −1 Wm−2 (Figure 13a,d) and slightly warmer with an MD of 1.5 Wm−2 at the surface as compared to the EBAF4.1 data (Figure 13b,e). In the atmosphere, the modeled global mean LWCRF is more negative −4.0 Wm−2 with an MD of −2.5 Wm−2 as compared to the satellite data (Figure 13c,f). The global mean net model radiative forcing at the TOA, surface, and in the atmosphere are −20.3, −21.8, and 1.6 Wm−2, respectively, indicating more cooling at the TOA and surface, and slightly more warming in the atmosphere as compared to the satellite data ((m), (n) and (o)). The corresponding global mean bias or the MD between the model and satellite-based NetCRF are −0.9, −1, and 0.2 Wm−2 ((s), (t), and (u)). Thus, from a global mean data perspective, the model has a negative bias or more cooling both at the TOA and surface, but in the atmosphere the bias is negligibly small. Thus, when the model is compared against the satellite data using global mean values of NetCRF, the biases are within the uncertainties of the radiation measurements.
As depicted on the last row of Figure 13s–u, however, the model bias distribution in NetCRF can be quite high over some geographical locations. The model has a negative bias at the TOA and in the atmosphere over most of the oceans reaching over −40 Wm−2 and a positive bias over the continents and including high-latitude regions, particularly in the southern hemisphere (Figure 13s,u) with a bias reaching over 40 Wm−2. At the surface level, the model bias is similar to the TOA, but over the Southern Ocean, south of 30°S the biases tend to be positive. These differences could be related to both the difference in cloud cover and type distributions as discussed previously and due to parameterization of the cloud optical properties in the model. Visual comparisons of the model bias in TCC (Figure 2c), LLC, and HLC (Figure 5a,c,e) and the biases in NetCRF at the TOA, surface, and atmosphere (Figure 13s–u) show that the positive model bias in TCF mainly over the tropical eastern Pacific and Atlantic Oceans near the equator are associated with a negative model bias in NetCRF. This can be interpreted as the negative model bias in NetCRF was caused by the positive model bias in LL clouds (Figure 5a). However, over the western Pacific and northern Indian Oceans, the positive bias in NetCRF implies more warming and may be associated with enhanced HL deep convective model clouds and this is particularly prevalent in the atmosphere (Figure 13u). Outside the tropical regions, particularly over the continents, where the LLCs are underestimated by the model are also generally characterized by positive model bias in NetCRF at the TOA and the surface, which is consistent with the fact that the models reflect less visible radiation. The only difference is that the role of enhanced HL deep convective model clouds over the western Pacific Ocean that led to a slight negative bias in NetCRF. In the atmosphere, the model bias in NetCRF is negative over the oceanic regions and positive over the continents, in this case it appears that both negative and positive model bias in LLC and HLC, respectively, led to corresponding negative and positive bias in NetCRF.
To better understand the effects of cloud and cloud type, statistical Pearson correlation using a time series data covering years 2006–2014 was also calculated between the biases in NetCRF and cloud fraction for given cloud type, in this case HLC, LLC, and TCF shown in Figure 2 and Figure 5. These statistical results are given in Figure 14. As indicated in the figure, at the TOA there are mainly negative correlations between the model bias in LLC and NetCRF at the TOA (Figure 14a), and the opposite is true between model bias in HLC and NetCRF (Figure 14d). The correlation between the model bias in TCF and NetCRF shows the net effects of the bias in both LL and HL clouds (Figure 14g). These areas of the negative correlations are normally related to the negative model bias in LCC (Figure 5a) and positive bias in NetCRF. Over the areas where positive model bias in HLC is present at locations such as the western Pacific and northern Indian Oceans and over the Sahelian desert in northern Africa where the model underestimated both LL and HLC (Figure 5a,e), the calculated Pearson correlations are positive at the TOA (Figure 14g). There is also slight positive correlation over Antarctica (Figure 14a) where both MLC and HLC are underestimated by the model (Figure 5c,e). In the atmosphere, the global distribution of the correlation between the model bias in LLC and NetCRF is negative (Figure 14b), but positive when the bias in HLC is used similar to the TOA case (Figure 14e). This is because the positive bias in HLC leads to a positive bias in NetCRF and the negative bias in HLC leads to a negative bias in NetCRF in the atmosphere (Figure 5e and Figure 13u). The net effects of the model bias in both LL and HLC (TCF) on the biases in NetCRF are a strong positive correlation over the tropical regions and relatively weaker negative correlation over the higher latitudes as illustrated in Figure 14h. At the surface level, clouds play both warming and cooling effects by trapping the outgoing longwave radiation and reflecting the visible portion of the radiation and hence interpretation is difficult. As shown in Figure 5a and Figure 13b, at this level, where the model underestimates the LLC (negative bias), generally the model bias in NetCRF is positive and the opposite is true when the model bias in LLC is positive. The correlation between these biases leads to relatively strong negative bias where LLC are prevalent, particularly over the tropical Atlantic and eastern Pacific Oceans and the correlation is rather positive where the LLC are also understated, but the model normally overestimated the HLC (Figure 14c). Outside of these regions, the correlations are relatively weak. The impacts of the model bias in HLCs on the NetCRF at surface is also negatively correlated (Figure 14f) except over Antarctica where the model overestimated both HL and MD clouds and the correlation is positive. This is particularly stronger where the model overestimated the HLCs in the Tropics (Figure 5e). Overall impacts of the model bias in TCF are a strong negative correlation in the Tropics, and relatively weaker correlation in the high-latitude regions except in Antarctica where the correlation is positive that may be mainly due to the fact that the model significantly overestimated the MLCs (Figure 5 and Figure 7).
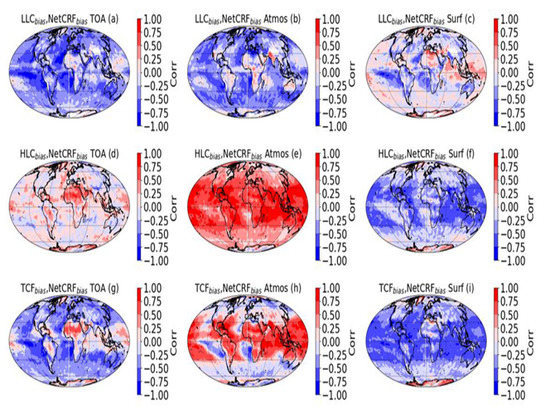
Figure 14.
The global distribution of temporal (2006–2014) Pearson correlation of model bias in LLC, HLC, and TCF, and the bias in NetCRF TOA (a,d,g), atmosphere (b,e,h), and surface (c,f,i).
As demonstrated in Figure 13 and Figure 14, the model bias in NetCRF can be spatially correlated to the model bias in clouds. However, on the bases of zonal mean CF and NetCRF given in Figure 6 and Figure 15, although there are significant discrepancies in CF between the model and satellite observation, there are no significant differences in NetCRF, even over the areas where the model significantly underestimated the CF such as oceanic regions potentially associated with subsiding air. These agreements between the model and satellite data, could be partly related to the parameterization of the cloud optical properties in order to match the radiation balance at the TOA. The SWCR largely depends on the cloud optical thickness, water content, and particle spectra. In most climate models including the CanESMs, the cloud optical properties are parameterized in terms of some bulk cloud properties such as cloud water path and effective particle size. Adjusting any of these parameters could affect the optical properties of clouds and could be used to adjust the radiative balance even without significantly altering the distribution of the cloud fraction. The LWCRF largely depends on the height and thickness of the cloud and background moisture.
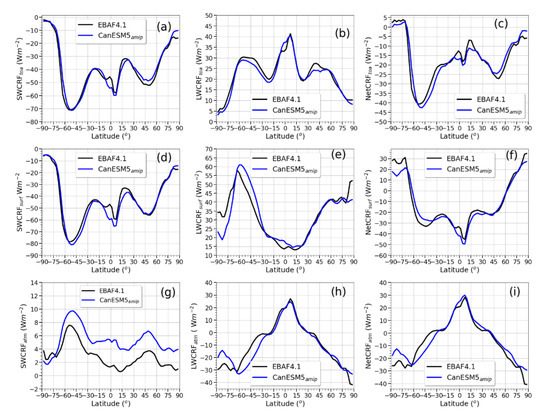
Figure 15.
Zonally and annually averaged SWCRF, LWCRF, and NetCRF TOA (a–c), at the surface (d–f) and atmosphere (g–i).
As shown in Figure 15, based on zonally and annually averaged data, the SWCRF at the TOA and surface is negative (cooling effect) and generally, follows the climatology of the total cloud fraction showing stronger cooling where the cloud fraction is larger (Figure 15a). In the atmosphere, the SWCRF is positive, because of the absorption of solar radiation by the atmosphere above low-altitude cloud decks [24] and hence the heating effect is more prominent where the low-level clouds are dominant (Figure 6). The model predicts slightly higher SWCRF in the atmosphere and this could be related to the fact that the model predicted more negative SWCRF at the surface than the satellite data. The LWCRF at the TOA is positive, generally increasing with increasing CF, but it is much stronger in the Tropics where it is dominated by high-level convective clouds (Figure 15b). This is because colder cloud tops are normally associated with high-level clouds and hence the loss of the longwave radiation is weaker than the loss above the low-level clouds found elsewhere. The LWCRF at the surface differs from the TOA mainly in the Tropics which is dominated by high-level convective clouds and the heating effect is weaker (Figure 15e). This cloud be due to weaker downward emission of the longwave radiation from relatively higher cloud base heights and hence colder temperature in the tropical regions. It can be seen also that there are some discrepancies in LWCRF at the surface between the model and the satellite data in the southern hemisphere indicating that the model underestimated the LWCRF (heating effects) near the poles and overestimated the heating over the southern oceans. The LWCRF in the atmosphere, on average, is warming the atmosphere over the tropical regions and cooling the atmosphere outside of these regions (Figure 15h). This zonal structure of the LWCRF in the atmosphere is formed because of the difference between the LWCRF at the TOA and the surface, and hence some differences between the model and satellite data are visible particularly over the high-latitude regions. According to these results, the LWCRF effect of the model is less cooling in the Polar regions (Figure 14i).
According to the zonally and annually averaged data, the NetCRF at the TOA is generally negative, and it is particularly stronger (more cooling) where the total cloud fraction is climatologically larger except over the topical regions where high-level convective clouds are dominant (Figure 15c). The model-predicted values of the NetCRF at the TOA near the pole in the northern hemisphere are near zero, but in contrast, the satellite data shows a cooling effect. In the southern hemisphere, the opposite is true. It should be mentioned here that the uncertainty in calculation of these results in this part of globe is much greater and hence further confirmation is required. Cooling effects similar to the TOA case dominate the NetCRF at the surface, but at the surface stronger cooling occurs in the Tropics, and the cooling effect is decreasing towards the poles and turning to positive (heating effect) after about 60° in both hemispheres (Figure 15f). In this case, the NetCRF at the surface is to cool lower latitudes and warm the high-latitude regions that would potentially diminish the north–south temperature gradient and hence weaker meridional air circulation. This can have a very important implication in potential amplification of the warming trends of these regions because of the expected increase in cloud fraction following global warming [75,76]. Similar to the NetCRF at TOA, there are some discrepancies in the NetCRF at the surface between the model and the satellite data, particularly at the polar regions where the satellite data indicates a stronger net warming effect with the maximum difference reaching close to 10 Wm−2. These discrepancies appear to be mainly related to the discrepancy in the LWCRF discussed previously. The NetCRF in the atmosphere is opposite to the NetCRF at the surface, where the atmosphere is warming the tropical region, but cooling the high-latitude regions that may enhance the meridional circulation. In case of the NetCRF in the atmosphere, the model cools the atmosphere over the polar region at a slower rate than the satellite data (Figure 15i).
4. Summary and Conclusions
In this study, cloud fraction (CF) and cloud type simulated using the Canadian Environmental System Models (CanESMs) version 5 (CanESM5) and the older version 2 (CanESM2) at their fully coupled and AMIP ( and ) configurations were validated against the GOCCP-based cloud products. Cloud products produced using the CALIPSO satellite simulator based on relevant cloud related parameters from CanESM5 and CanESM2 models at their AMIP configuration ( and were also evaluated including vertical profiles. The simulated cloud radiative forcings at the TOA, surface, and atmosphere using the AMIP version of the CanESM5 model were also evaluated using the most recent Edition 4.1 of the CERES radiation satellite datasets. The main findings in this study are summarized below.
The summary of the statistics of the global mean of CF, mean difference (MD) or bias, and the root mean square error (RMSE) of the simulated total cloud fraction (TCF), the CF associated with low-level cloud (LLC), mid-level cloud (MLC), and high-level cloud (HLC) are given in Table A3 (Appendix A). From the perspective of global mean values given in Table A3 (Appendix A), all the models underestimated the cloud amount. The model bias or MD values for TCF ranged from −1.8% to −7.1% and the RMSE values ranged from 11% to 12%. The smallest MD and RMSE were calculated for and the opposite is true for the CanESM2. The RSME values for the and were 10.7 % and 10.2%, respectively, as compared to the 11.2% for which is slightly higher. The has a slightly lower RMSE as compared to the , but no significant difference can be observed because of the use of the simulator. The difference between coupled and AMIP versions of the models is very small with an MD of 0.6% and −0.7% for and , respectively. This suggests that much of the model discrepancies in simulated clouds could be related to atmospheric dynamics and cloud microphysical processes, which is consistent with earlier studies [77,78]. As indicated in Table A3, the COSP-CALIPSO-simulated LLC, MLC, and HLC are also underestimated as compared to the GOCCP satellite data. The globally averaged bias values for are −2.4%, −7.6%, and −1.4% for LLC, MLC, and HLC, respectively, indicating that the bias for MLC is the largest. The bias values for CanESM2 are higher for HL and LL clouds. The COSP-based simulated models and revealed even higher underestimation of the TFC, particularly the model as compared to the models without the COSP simulation.
Although the models have negative bias based on the global mean CF. This study also showed significant spatial variability in the CF bias and the sign of the bias depends on the geographical location. Over the oceanic regions, all the models have positive bias in TCF mainly within the intertropical convergence zone (ITCZ) which are mostly dominated by ascending air possibly related to high-level ice clouds. These biases are much larger than the global mean values mentioned previously exceeding 40% over some regions. These oceanic regions include the eastern Pacific and Atlantic Oceans near the equator and the Indo-Pacific warm pool where the HLCs are also overestimated by the models. This was confirmed using vertical cross-sections of the model bias in CF that showed that the models overestimated the HL ice clouds particularly over the Tropics. Positive model bias is also noted over the Atlantic Ocean situated at the northern mid-latitude region. The CanESM5 model exhibited relatively higher positive bias over these oceanic locations and compared to the CanESM2 model. The models also have positive bias in TCF over the Polar regions, particularly over Antarctica that is potentially related to the overestimation of the MLC. The models, however, generally have negative bias in total CF over the rest of the globe, particularly over the oceanic regions associated with enhanced marine LL stratocumulus clouds such as over the southeastern Pacific, Atlantic, and Indian Oceans, and northeastern Pacific Ocean near the west coasts of the continent, and this is more pronounced in the data. The model predicted significantly higher TCF as compared to the CanESM2 over most of the geographical locations of the globe.
The seasonal variability of the model bias for all models follows the general atmospheric circulation patterns. Over the tropical oceanic regions, the positive model bias of the CanESM models in the DJF season (summer in southern hemisphere) move to the northern hemisphere during the JJA season following the Hadley circulation and this is particularly more pronounced in data. During the northern summer (JJA), the model has a significant negative and positive bias over the northern hemisphere oceanic and continental regions, respectively, and characterized by a higher RMSE value as compared to the northern hemisphere winter (DJF). Most of the negative bias in the tropical southern hemisphere during the JJA season shifts to a positive bias during the DJF season (southern hemisphere summer). The positive bias over the western Pacific Ocean near the equator is persistent during both seasons and it becomes wider during the northern hemisphere winter season. The model agrees reasonably well over the southern oceans between 30°S and 60°S during both seasons (DJF and JJA). The data shows a similar geographical bias distribution as the model, but the model has a mostly negative bias during both seasons, which implies underestimation of the CF. The AMIP versions of the and models behave very similar to their counter parts and remove some of the negative bias over the western Pacific Ocean near the equator and are characterized by relatively smaller RMSE values. Generally, the RSME values are smaller during the northern hemisphere winter when the models are compared to the CALIPSO data.
The GOCCP data showed that the LLCs are mainly associated with liquid phase clouds having more liquid phase clouds at higher latitudes (particularly in the southern hemisphere) where the atmospheric temperatures are relatively colder than the lower latitudes. The model data are consistent with the GOCCP data in this sense, but the model-based low-level liquid phase clouds are vertically shallower as compared to the GOCCP data. Previous studies (e.g., [67]) suggest that this variability could be related to glaciation of supercoiled clouds initiated by dust particles in the atmosphere that are frequently found at lower latitudes and this needs to be investigated further.
According to the CERES EBAF4.1 radiation data, the calculated global mean NetCRF at the TOA, surface, and atmosphere were −19.4, −20.4, and 1.4 Wm−2, respectively, with corresponding mean model bias of −0.9, −1, and 0.2 Wm−2 indicating that the model is predicting slightly more cooling at the TOA and the surface, and more heating in the atmosphere. On the global scale, the NetCRF at the TOA and surface is negative (cooling) and the degree of cooling is expected to increase with increasing CF. Provided that the model predicted lower CF, these differences in NetCRF cannot be explained based on the difference in global mean CF. This may be related to the parameterization of cloud optical properties. Nonetheless, these differences are within the uncertainty of the measurements.
Based on the annual mean global distribution of satellite data (both radiation and clouds), the LWCRF effects at the TOA and surface (mainly heating) are strongly connected to HL and LL clouds, respectively. In the atmosphere, however, the LWCRF is negative (cooling) at higher latitudes and positive (warming) in the Tropics. These are well captured by the model, although the model data showed slightly weaker and stronger warming at the TOA and the surface, respectively, that led to relatively higher cooling in the atmosphere. Similarly, the satellite data showed that the SWCRF effects at the TOA and surface are related to the TCF, but at the surface the LLC appears to have stronger cooling effects, which led to stronger warming effects in the atmosphere where the LLC dominates. The model also captured these reasonably well, but the model predicted relatively stronger cooling effects of the LLCs that led to relatively warmer effects in the atmosphere as compared to the satellite data. The satellite data showed that the LL clouds including the marine stratocumulus clouds appear to have stronger net cooling effects at the TOA, but at the surface level both LL and HL clouds may play some roles controlling the net effects of radiation, depending on the geographical location, and these are also well captured by the model. The model shows strong positive bias in NetCRF at the TOA associated with LL marine stratocumulus clouds over the eastern coasts of North and South America, HLC over the Indo-Pacific warm pool region, over most of the continents, and over the southern edge of southern oceans. The model bias at the surface level is similar, but the positive bias over the southern oceans is more pronounced and the bias over the Indo-Pacific warm pool region is relatively diminished as compared to the TOA case and this led to stronger negative and positive bias in NetCRF in the atmosphere over oceanic and continental regions, respectively. It is rather complex to know the exact cause of the source of the spatial variability of the model bias when compared to the bias in CF. The Pearson correlations performed between the bias in CF and NetCRF showed that there is a strong negative correlation between the bias in LLC and NetCRF at the TOA and atmosphere, particularly where the LLC dominates. This implies that increasing or decreasing model bias in LLC always negatively impacts the NetCRF at the TOA and in the atmosphere and the results also show that the opposite is true for the HLC, particularly in the Tropics, and these combined effects led to a positive correlation in the Tropics and negative correlation at higher latitudes. At the surface level, the model bias in TCF is significantly influenced by the model bias in HLC and it is negatively correlated with the model bias in NetCRF except for Antarctica.
Overall, this study shows that all the CanESM models generally underestimate the TCF (negative bias), particularly the LL marine stratocumulus and cumulus clouds over the tropical oceans. The areas are normally characterized by low cloud cover because of subsiding relatively dry air because of the Hadley circulation and persistent cloudy coastal regions associated with upwelling of cold water that produces LL atmospheric temperature inversion and hence strong ocean and atmospheric interaction or coupling. The use of the detailed modeling of ocean and atmospheric coupling does not seem to significantly improve the bias when compared to the AMIP version of the model, but further specific studies targeting these regions can give better insights. This negative bias in CF is particularly more prevalent in the CanESM2 data. This is a common problem in many of the current GCMs [6,16,79] and this may be associated with a poor treatment of shallow convection and parameterization of ocean and atmospheric coupling. The models also underestimate and overestimate the ML and HL CF, respectively, particularly over the Tropics. These biases are particularly more pronounced in the CanESM5 data. The AMIP version of the model appears to reduce this bias as compared to the coupled version of the model. These types of problems are also common in many of the current GCMs as discussed previously and this has been mainly attributed to the poor treatment of deep convection in these models [15,71]. The CanESM models also employ a similar deep convection parameterization scheme and hence the results strongly suggest that the deep convection parameterization scheme employed in these models needs to be examined and improved. Generally, all the models overpredict LL and ML clouds over the Antarctic and Arctic regions and Antarctic region, respectively. The CanESM5 model also overestimates the HL clouds over both locations. A similar positive bias in LL clouds in the Arctic region has been reported [80] who attributed the discrepancy to overprediction of liquid phase clouds because of insufficient efficiency of the Wegener–Bergeron–Findeisen process. Further detailed studies are required to better understand the nature of these discrepancies.
The new version of the CanESM model performed reasonably well simulating the global mean CRF with very small negative biases in NetCRF at the TOA and surface. These model biases in NetCRF, however, cannot be directly linked to the global mean model bias in CF and this may be partly attributed to the parameterization of the optical properties in the model. However, as discussed previously, the geographical distribution of the model bias in CRF can be very significant depending on the location and atmospheric level. The cause of these biases based on a visual inspection of model bias in CF is not immediately obvious, but a statistical analysis performed using the Pearson correlation showed that there is a strong correlation between the global distribution of model bias in NetCRF and CF and it is significantly influenced by the LL and HL clouds. Further improvements in representation of clouds in the model, which is more consistent with radiation, can remedy these discrepancies.
Author Contributions
Methodology, validation, formal analysis, visualization, data curation, writing—original draft preparation, F.S.B.; writing—review and editing, J.A.M. and G.A.I. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The satellite dataset used in this study is publicly available; the authors did not report any newly generated satellite data. The model data can be obtained upon request from the authors.
Acknowledgments
The authors would like to thank Jason Cole for providing the model data and useful comments during the earlier part of this work.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
The satellite cloud products, models, and abbreviations used in this study.
Table A1.
The satellite cloud products, models, and abbreviations used in this study.
| Abbreviations | Description | ||
|---|---|---|---|
| AMIP | Atmospheric Model Intercomparison Project (configuration). The configuration is based on prescribed sea surface temperature (SST) and sea ice extent. | ||
| CAPLISO | Cloud–Aerosol Lidar and Infrared Pathfinder Satellite Observation | ||
| CanESM | Canadian Environmental System Model | ||
| CERES | The Clouds and the Earth’s Radiant Energy System | ||
| GCM | General Circulation Model | ||
| Satellite data | Descriptions | Res | Period |
| GOCCP | GCM Oriented CALIPSO Cloud Products | 2° × 2° | 2007–2019 |
| EBAF4.1 | CERES energy balanced and filled Edition 4.1 | 1° × 1° | 2000–2019 |
| Model names | Descriptions | ||
| CanESM5 | CanESM version 5 (coupled) | 2.8° × 2.8° | 1995–2005 |
| CanESM5amip | CanESM version 5 (AMIP) | - | 2000–2014 |
| CanESM5amip-calsim | CanESM5amip + CALIPSO simulator | - | - |
| CanESM5amip-iscsim | CanESM5amip + ISCCP simulator | - | - |
| CanESM2 | CanESM version 2 (coupled) | - | 1995–2009 |
| CanESM2amip | CanESM2 (AMIP) | - | - |
| CanESM2amip-calsim | CanESM2amip + CALIPSO simulator | - | - |
| CanESM2amip-iscsim | CanESM2amip + ISCCP simulator | - | |

Table A2.
The cloud classification scheme based on pressure (P) and height (Z) in CALIPSO-GOCCP data.
Table A2.
The cloud classification scheme based on pressure (P) and height (Z) in CALIPSO-GOCCP data.
| Low-level clouds (LLC) | P > 680 hPa | Z < 3.2 km |
| Mid-level clouds (MLC) | 680 > P > 440 hPa | 3.2 km < Z < 6.5 km |
| High level clouds (HLC) | P < 440 hPa | Z > 6.5 km |

Table A3.
Summary of the calculated statistics for the models and satellite-based data used in this study. The annually averaged global mean cloud fraction (CF), model bias (mean difference = MD (model-GOCCP)), and RMSE (GOCCP, model) of total cloud fraction (TCF) and low-level clouds (LLC), mid-level clouds (MLC), and high-level clouds (HLC) are shown in the table.
Table A3.
Summary of the calculated statistics for the models and satellite-based data used in this study. The annually averaged global mean cloud fraction (CF), model bias (mean difference = MD (model-GOCCP)), and RMSE (GOCCP, model) of total cloud fraction (TCF) and low-level clouds (LLC), mid-level clouds (MLC), and high-level clouds (HLC) are shown in the table.
| Source | TCF (%) | LLC (%) | MLC (%) | HLC (%) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | MD | RMSE | Mean | MD | RMSE | Mean | MD | RMSE | Mean | MD | RMSE | |
| GOCCP | 67.2 | 37.4 | 18.4 | 32.8 | ||||||||
| CanESM5 | 65.4 | −1.8 | 11.1 | |||||||||
| CanESM5amip | 64.8 | −2.4 | 10.7 | |||||||||
| CanESM2 | 61 | −6.3 | 12.2 | |||||||||
| CanESM2amip | 61.6 | −5.6 | 11.6 | |||||||||
| CanESM5amip-calsim | 63.3 | −3.9 | 10.2 | 35 | −2.4 | 8.1 | 10.8 | −7.6 | 10.4 | 31.4 | −1.4 | 7.3 |
| CanESM2amip-calsim | 60.1 | −7.1 | 11.6 | 34.7 | −2.7 | 8.8 | 11.2 | −7.2 | 10.1 | 27.5 | −5.3 | 8.9 |
References
- Hartmann, D.L.; Doelling, D.E. On the net radiative effectiveness of clouds. J. Geophys. Res. 1991, 96, 869–891. [Google Scholar] [CrossRef]
- Boucher, O.; Randall, D.; Artaxo, P.; Bretherton, C.; Feingold, G.; Forster, P.; Kerminen, V.-M.; Kondo, Y.; Liao, H.; Lohmann, U.; et al. Clouds and Aerosols. In Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013. [Google Scholar]
- IPCC. Climate Change 2014: Synthesis Report. Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Core Writing Team, Pachauri, R.K., Meyer, L.A., Eds.; IPCC: Geneva, Switzerland, 2014; 151p. [Google Scholar]
- Huntingford, C.; Williamson, M.S.; Nijsse, F.J.M.M. CMIP6 climate models imply high committed warming. Clim. Chang. 2020, 162, 1515–1520. [Google Scholar] [CrossRef] [PubMed]
- Zelinka, M.D.; Myers, T.A.; McCoy, D.T.; Po-Chedley, S.; Caldwell, P.M.; Ceppi, P.; Klein, S.A.; Taylor, K.E. Causes of higher climate sensitivity in CMIP6 models. Geophys. Res. Lett. 2020, 47, e2019GL085782. [Google Scholar] [CrossRef]
- Meehl, G.A.; Senior, C.A.; Eyring, V.; Flato, G.; Lamarque, J.-F.; Stouffer, R.J.; Taylor, K.E.; Schlund, M. Context for interpreting equilibrium climate sensitivity and transient climate response from the CMIP6 Earth system models. Sci. Adv. 2020, 6, eaba1981. [Google Scholar] [CrossRef]
- Swart, N.C.; Cole, J.N.; Kharin, V.V.; Lazare, M.; Scinocca, J.F.; Gillett, N.P.; Anstey, J.; Arora, V.; Christian, J.R.; Hanna, S.; et al. The Canadian Earth System Model version 5 (CanESM5.0.3). Geosci. Model Dev. 2019, 12, 4823–4873. [Google Scholar] [CrossRef]
- Lee, D.; Oreopoulos, L.; Cho, N. An evaluation of clouds and radiation in a large-scale atmospheric model using a cloud vertical structure classification. Geosci. Model Dev. 2020, 13, 673–684. [Google Scholar] [CrossRef]
- Kato, S.; Rose, F.G.; Ham, S.H.; Rutan, D.A.; Radkevich, A.; Caldwell, T.E.; Sun-Mack, S.; Miller, W.F.; Chen, Y. Radiative heating rates computed with clouds derived from satellite-based passive and active sensors and their effects on generation of available potential energy. J. Geophys. Res. Atmos. 2019, 124, 1720–1740. [Google Scholar] [CrossRef]
- Chen, T.; Rossow, W.B.; Zhang, Y. Radiative Effects of Cloud-Type Variations. J. Clim. 2000, 13, 264–286. [Google Scholar] [CrossRef]
- Aebi, C.; Gröbner, J.; Kämpfer, N.; Vuilleumier, L. Cloud radiative effect. cloud fraction and cloud type at two stations in Switzerland using hemispherical sky cameras. Atmos. Meas. Tech. 2017, 10, 4587–4600. [Google Scholar] [CrossRef]
- Lin, B.; Minnis, P.; Fan, T.-F.; Hu, Y.; Sun, W. Radiation characteristics of low and high clouds in different oceanic regions observed by CERES and MODIS. Int. J. Remote Sens. 2010, 31, 6473–6492. [Google Scholar] [CrossRef]
- Swales, D.J.; Pincus, R.; Bodas-Salcedo, A. The Cloud Feedback Model Intercomparison Project Observational Simulator Package: Version 2. Geosci. Model Dev. 2018, 11, 77–81. [Google Scholar] [CrossRef]
- Bodas-Salcedo, A.; Webb, M.J.; Bony, S.; Chepfer, H.; Dufresne, J.-L.; Klein, S.; Zhang, Y.; Marchand, R.; Haynes, J.M.; Pincus, R.; et al. COSP: Satellite simulation software for model assessment. Bull. Am. Meteorol. Soc. 2011, 92, 1023–1043. [Google Scholar] [CrossRef]
- Nam, C.C.; Quaas, J. Evaluation of Clouds and Precipitation in the ECHAM5 General Circulation Model Using CALIPSO and CloudSat Satellite Data. J. Clim. 2012, 25, 4975–4992. [Google Scholar] [CrossRef]
- Zhang, M.H.; Lin, W.Y.; Klein, S.; Bacmeister, J.T.; Bony, S.; Cederwall, R.T.; Del Genio, A.D.; Hack, J.J.; Loeb, N.G.; Lohmann, U.; et al. Comparing clouds and their seasonal variations in 10 atmospheric general circulation models with satellite measurements. J. Geophys. Res. 2005, 110, D15S02. [Google Scholar] [CrossRef]
- Klein, S.A.; Zhang, Y.; Zelinka, M.D.; Pincus, R.; Boyle, J.; Gleckler, P.J. Are climate model simulations of clouds improving? An evaluation using the ISCCP simulator. J. Geophys. Res. Atmos. 2013, 118, 1329–1342. [Google Scholar] [CrossRef]
- Marchand, R.; Ackerman, T.; Smyth, M.; Rossow, W.B. A review of cloud top height and optical depth histograms from MISR, ISCCP and MODIS. J. Geophys. Res. 2010, 115, D16206. [Google Scholar] [CrossRef]
- Mace, G.G.; Houser, S.; Benson, S.; Klein, S.A.; Min, Q. Critical Evaluation of the ISCCP Simulator Using Ground-Based Remote Sensing Data. J. Clim. 2011, 24, 1598–1612. [Google Scholar] [CrossRef]
- Boudala, F.S.; Milbrandt, J.A. Evaluations of the Climatologies of Three Latest Cloud Satellite Products Based on Passive Sensors (ISCCP-H, Two CERES) against the CALIPSO-GOCCP. Remote Sens. 2021, 13, 5150. [Google Scholar] [CrossRef]
- Cesana, G.; Chepfer, H. How well do climate models simulate cloud vertical structure? A comparison between CALIPSO-GOCCP satellite observations and CMIP5 models. Geophys. Res. Lett. 2012, 39, L20803. [Google Scholar] [CrossRef]
- Chepfer, H.; Bony, S.; Winker, D.; Cesana, G.; Dufresne, J.-L.; Minnis, P.; Stubenrauch, C.J.; Zeng, S. The GCM Oriented CALIPSO Cloud Product (CALIPSO-GOCCP). J. Geophys. Res. 2010, 115, D00H16. [Google Scholar] [CrossRef]
- Ramanathan, V.; Cess, R.D.; Harrison, E.F.; Minnis, P.; Barikstrom, B.R.; Ahmad, E.; Hartmann, D. Cloud-Radiative Forcing and Climate: Results from the Earth Radiation Budget Experiment. Science 1989, 243, 57–63. [Google Scholar] [CrossRef]
- Allan, P.R. Combining satellite data and models to estimate cloud radiative effect at the surface and in the atmosphere. Meteorol. Appl. 2011, 18, 324–333. [Google Scholar] [CrossRef]
- Loeb, N.G.; Wielicki, B.A.; Doelling, D.R.; Smith, G.L.; Keyes, D.F.; Kato, S.; Manalo-Smith, N.; Wong, T. Toward optimal closure of the Earth’s top-of-atmosphere radiation budget. J. Clim. 2009, 22, 748–766. [Google Scholar] [CrossRef]
- Loeb, N.G.; Manalo-Smith, N.; Su, W.; Shankar, M.; Thomas, S. CERES top-of- atmosphere earth radiation budget climate data record: Accounting for in-orbit changes in instrument calibration. Remote Sens. 2016, 8, 182. [Google Scholar] [CrossRef]
- Kato, S.; Rose, F.G.; Rutan, D.A.; Thorsen, T.; Loeb, N.G.; Doelling, D.R.; Huang, X.; Smith, W.L.; Su, W.; Ham, S.-H. Surface irradiances of Edition 4.0 Clouds and the Earth’s Radiant Energy System (CERES) Energy Balanced and Filled (EBAF) data product. J. Clim. 2018, 31, 4501–4527. [Google Scholar] [CrossRef]
- Kato, S.; Loeb, N.G.; Rose, F.G.; Doelling, D.R.; Rutan, D.A.; Caldwell, T.E.; Yu, L.; Weller, R.A. Surface irradiances consistent with CERES-derived top-of-atmosphere shortwave and longwave irradiances. J. Clim. 2013, 26, 2719–2740. [Google Scholar] [CrossRef]
- Loeb, N.G.; Doelling, D.R.; Wang, H.; Su, W.; Nguyen, C.; Corbett, J.G.; Liang, L.; Mitrescu, C.; Rose, F.G.; Kato, S. Clouds and the Earth’s Radiant Energy System (CERES) Energy Balanced and Filled (EBAF) Top-of-Atmosphere (TOA) Edition-4.0 Data Product. J. Clim. 2018, 31, 895–918. [Google Scholar] [CrossRef]
- Loeb, N.G.; Rose, F.G.; Kato, S.; Rutan, D.A.; Su, W.; Wang, H.; Doelling, D.R.; Smith, W.L.; Gettelman, A. Towards a consistent definition between satellite and model clear-sky radiative fluxes. J. Clim. 2019, 33, 61–75. [Google Scholar] [CrossRef]
- CERES EBAF4.1 Data Quality Summary. 2021. Available online: https://ceres.larc.nasa.gov/documents/DQ_summaries/CERES_EBAF_Ed4.1_DQS.pdf (accessed on 25 July 2022).
- Hinkelman, L.M. The global radiative energy budget in MERRA Version 1 and Version 2: Evaluation with respect to CERES EBAF data. J. Clim. 2019, 32, 1973–1994. [Google Scholar] [CrossRef]
- Cesana, G.; Chepfer, H. Evaluation of the cloud thermodynamic phase in a climate model using CALIPSO-GOCCP. J. Geophys. Res. Atmos. 2013, 118, 7922–7937. [Google Scholar] [CrossRef]
- Hogan, R.J.; Francis, P.N.; Flentje, H.; Illingworth, A.J.; Quante, M.; Pelon, J. Characteristics of mixed-phase clouds. I: Li-dar, radar and aircraft observations from CLARE’98. Q. J. R. Meteorol. Soc. 2003, 129, 2089–2116. [Google Scholar] [CrossRef]
- Heike Kalesse-Los, H.; Schimmel, W.; Luke, E.; Seifert, P. Evaluating cloud liquid detection against Cloudnet using cloud radar Doppler spectra in a pre-trained artificial neural network. Atmos. Meas. Tech. 2022, 15, 279–295. [Google Scholar] [CrossRef]
- Loeb, N.G.; Priestley, K.J.; Kratz, D.P.; Geier, E.B.; Green, R.N.; Wielicki, B.A.; Hinton, P.O.R.; Nolan, S.K. Determination of unfiltered radiances from the Clouds and the Earth’s Radiant Energy System (CERES) instrument. J. Appl. Meteorol. 2001, 40, 822–835. [Google Scholar] [CrossRef]
- Loeb, N.G.; Manalo-Smith, N.; Kato, S.; Miller, W.F.; Gupta, S.K.; Minnis, P.; Wielicki, B.A. Angular distribution models for top-of-atmosphere radiative flux estimation from the Clouds and the Earth’s Radiant Energy System instrument on the Tropical Rainfall Measuring Mission Satellite. Part I: Methodology. J. Appl. Meteorol. 2003, 42, 240–265. [Google Scholar] [CrossRef]
- Loeb, N.G.; Kato, S.; Loukachine, K.; Manalo-Smith, N. Angular distribution models for top-of-atmosphere radiative flux estimation from the Clouds and the Earth’s Radiant Energy System instrument on the Terra satellite. Part I: Methodology. J. Atmos. Ocean. Technol. 2005, 22, 338–351. [Google Scholar] [CrossRef]
- Su, W.; Corbett, J.; Eitzen, Z.; Liang, L. Next-generation angular distribution models for top-of- atmosphere radiative flux calculation from the CERES instruments: Methodology. Atmos. Meas. Tech. 2015, 8, 611–632. [Google Scholar] [CrossRef]
- Su, W.; Corbett, J.; Eitzen, Z.; Liang, L. Next-generation angular distribution models for top-of- atmosphere radiative flux calculation from the CERES instruments: Validation. Atmos. Meas. Tech. 2015, 8, 3297–3313. [Google Scholar] [CrossRef]
- Johnson, G.C.; Lyman, J.M.; Loeb, N.G. Improving estimates of Earth’s energy imbalance. Nat. Clim. Chang. 2016, 6, 639–640. [Google Scholar] [CrossRef]
- Loeb, N.G.; Lyman, J.M.; Johnson, G.C.; Allan, R.; Doelling, D.R.; Wong, T.; Soden, B.; Stephens, G.L. Observed changes in top-of-the-atmosphere radiation and upper-ocean heating consistent within uncertainty. Nat. Geosci. 2012, 5, 110–113. [Google Scholar] [CrossRef]
- Kato, S.; Rutan, D.A.; Rose, F.G.; Caldwell, T.E.; Ham, S.-H.; Radkevich, A.; Thorsen, T.J.; Viudez-Mora, A.; Fillmore, D.; Huang, X. Uncertainty in Satellite-Derived Surface Irradiances and Challenges in Producing Surface Radiation Budget Climate Data Record. Remote Sens. 2020, 12, 1950. [Google Scholar] [CrossRef]
- von Salzen, K.; Scinocca, J.F.; McFarlane, N.A.; Li, J.; Cole, J.N.; Plummer, D.; Verseghy, D.; Reader, M.C.; Ma, X.; Lazare, M.; et al. The Canadian Fourth Generation Atmospheric Global Climate Model (CanAM4). Part I: 1346 Representation of Physical Processes. Atmos. Ocean 2013, 51, 104–125. [Google Scholar] [CrossRef]
- Lohmann, U. Sensitivität des Modellklimas Eines Globalen Zirkulationsmodells der Atmosphäre Gegenüber Änderungen der Wolkenmikrophysik; Examensarbeit Nr. 41; Max-Planck-Institut für Meteorologie: Hamburg, Germany, 1996. [Google Scholar]
- Lohmann, U.; Roeckner, E. Design and performance of a new cloud microphysics scheme developed for the ECHAM general circulation model. Clim. Dyn. 1996, 12, 557–572. [Google Scholar] [CrossRef]
- Zhang, G.J.; McFarlane, N.A. Sensitivity of climate simulations to the parameterization of cumulus convection in the Canadian Climate Centre general circulation model. Atmos. Ocean 1995, 33, 407–446. [Google Scholar] [CrossRef]
- Fu, Q. An accurate parameterization of the solar radiative properties of cirrus clouds for climate models. J. Clim. 1996, 9, 2058–2082. [Google Scholar] [CrossRef]
- Boudala, F.S.; Isaac, G.A.; McFarlane, N.A.; Li, J. The Sensitivity of the Radiation Budget in a Climate Simulation to Neglecting the Effect of Small Ice Particles. J. Clim. 2007, 20, 3527–3541. [Google Scholar] [CrossRef][Green Version]
- Boudala, F.S.; Isaac, G.A.; Fu, Q.; Cober, S.G. Parameterization of effective ice particle sizes for high latitude clouds. Int. J. Climatol. 2002, 22, 1267–1284. [Google Scholar] [CrossRef]
- Dobbie, J.S.; Li, J.; Chýlek, P. Two and four stream optical properties for water clouds and solar wavelengths. J. Geophys. Res. 1999, 104, 2067–2079. [Google Scholar] [CrossRef]
- Lindner, T.H.; Li, J. Parameterization of the Optical Properties for Water Clouds in the Infrared Notes and Correspondence. J. Clim. 2000, 13, 1797–1805. [Google Scholar] [CrossRef]
- Fu, Q.; Yang, P.; Sun, W.B. An accurate parameterization of the infrared radiative properties of cirrus clouds for climate models. J. Clim. 1998, 11, 2223–2237. [Google Scholar] [CrossRef]
- Yang, P.; Bi, L.; Baum, B.A.; Liou, K.-N.; Kattawar, G.W.; Mishchenko, M.I.; Cole, B. Spectrally Consistent Scattering, Absorption, and Polarization Properties of Atmospheric Ice Crystals at Wavelengths from 0.2 to 100 mm. J. Atmos. Sci. 2013, 70, 330–347. [Google Scholar] [CrossRef]
- Arora, V.K.; Scinocca, J.F.; Boer, G.J.; Christian, J.R.; Denman, K.L.; Flato, G.M.; Kharin, V.V.; Lee, W.G.; Merryfield, W.J. Carbon emission limits required to satisfy future representative concentration pathways of greenhouse gases. Geophys. Res. Lett. 2011, 38, L05805. [Google Scholar] [CrossRef]
- Pincus, R.; Batstone, C.P.; Hofmann, R.J.P.; Taylor, K.E.; Glecker, P.J. Evaluating the present-day simulation of clouds, precipitation, and radiation in climate models. J. Geophys. Res. 2008, 113, D14209. [Google Scholar] [CrossRef]
- Jones, P.W. First- and second-order conservative remapping schemes for grids in spherical coordinates. Mon. Weather Rev. 1999, 127, 2204–2210. [Google Scholar] [CrossRef]
- Klein, S.A.; Hartmann, D.L. The Seasonal Cycle of Low Stratiform Clouds. J. Clim. 1993, 6, 1587–1606. Available online: http://www.jstor.org/stable/26198436 (accessed on 25 July 2022). [CrossRef]
- Muhlbauer, A.; McCoy, I.L.; Wood, R. Climatology of stratocumulus cloud morphologies: Microphysical properties and radiative effects. Atmos. Chem. Phys. 2014, 14, 6695–6716. [Google Scholar] [CrossRef]
- Lang, F.; Huang, Y.; Protat, A.; Truong, S.C.H.; Siems, S.T.; Manton, M.J. Shallow convection and precipitation over the Southern Ocean:A case study during the CAPRICORN 2016 field campaign. J. Geophys. Res. Atmos. 2021, 126, e2020JD034088. [Google Scholar] [CrossRef]
- Gettelman, A.; Salby, M.L.; Sassi, F. Distribution and influence of convection in the tropical tropopause region. J. Geophys. Res. 2002, 107, 4080. [Google Scholar] [CrossRef]
- De Deckker, P. The Indo-Pacific Warm Pool: Critical to world oceanography and world climate. Geosci. Lett. 2016, 3, 20. [Google Scholar] [CrossRef]
- Painemal, D.; Corral, A.F.; Sorooshian, A.; Brunke, M.A.; Chellappan, S.; Rooh, V.A.G.; Ham, S.; O’Neill, L.; Smith, W.L.; Tselioudis, G.; et al. An overview of atmospheric features over the Western North Atlantic Ocean and North American East Coast—Part Circulation, boundary layer, and clouds. J. Geophys. Res. Atmos. 2021, 126, e2020JD033423. [Google Scholar] [CrossRef]
- Kang, H.; Choi, Y.-S.; Hwang, J.; Kim, H.-S. On the cloud radiative effect for tropical high clouds overlying low clouds. Geosci. Lett. 2020, 7, 7. [Google Scholar] [CrossRef]
- Fermepin, S.; Bony, S. Influence of low-cloud radiative effects on tropical circulation and precipitation. J. Adv. Model. Earth Syst. 2014, 6, 513–526. [Google Scholar] [CrossRef]
- Guo, Z.; Wang, M.; Peng, Y.; Luo, Y. Evaluation on the vertical distribution of liquid and ice phase cloud fraction in Community Atmosphere Model version 5.3 using spaceborne LIDAR observations. Earth Space Sci. 2020, 7, e2019EA001029. [Google Scholar] [CrossRef]
- Choi, Y.S.; Lindzen, R.S.; Ho, C.H.; Kim, J. Space observations of cold-cloud phase change. Proc. Natl. Acad. Sci. USA 2010, 107, 11211–11216. [Google Scholar] [CrossRef]
- Riihimaki, L.D.; McFarlane, S.A.; Comstock, J.M. Climatology and Formation of Tropical Midlevel Clouds at the Darwin ARM Site. J. Clim. 2012, 25, 6835–6850. [Google Scholar] [CrossRef]
- Zhang, D.; Wang, Z.; Liu, D. A global view of midlevel liquid-layer topped stratiform cloud distribution and phase partition from CALIPSO and CloudSat measurements. J. Geophys. Res. 2010, 115, D00H13. [Google Scholar] [CrossRef]
- Tiedtke, M. A Comprehensive Mass Flux Scheme for Cumulus Parameterization in Large Scale Models. Mon. Weather Rev. 1989, 117, 1779–1800. [Google Scholar] [CrossRef]
- Wang, W.; Liu, X. Evaluating deep updraft formulation in NCAR CAM3 with high-resolution WRF simulations during ARM TWP-ICE. Geophys. Res. Lett. 2009, 36, L04701. [Google Scholar] [CrossRef]
- Stapf, J.; Ehrlich, A.; Jäkel, E.; Lüpkes, C.; Wendisch, M. Reassessment of shortwave surface cloud radiative forcing in the Arctic: Consideration of surface-albedo–cloud interactions Atmos. Chem. Phys. 2020, 20, 9895–9914. [Google Scholar] [CrossRef]
- Pavolonis, M.J.; Key, J.R. Antarctic Cloud Radiative Forcing at the Surface Estimated from the AVHRR Polar Pathfinder and ISCCP D1 Datasets, 1985–1993. J. Appl. Meteorol. 2003, 42, 827–840. [Google Scholar] [CrossRef]
- Aoki, T.; Yamanouchi, T. Cloud-Radiative Forcing Over the Snow-Covered Surface Around Asuka Station, Antarctica. Proc. NIPR Symp. Polar Meteorol. Glaciol. 1992, 5, 76–89. [Google Scholar]
- Liu, Y.; Shupe, M.D.; Wang, Z.; Mace, G. Cloud vertical distribution from combined surface and space radar–LIDAR observations at two Arctic atmospheric observatories. Atmos. Chem. Phys. 2017, 17, 5973–5989. [Google Scholar] [CrossRef]
- Norris, J.R.; Allen, R.J.; Evan, A.T.; Zelinka, M.D.; O’Dell, C.W.; Klein, S.A. Evidence for climate change in the satellite cloud record. Nature 2016, 536, 72–75. [Google Scholar] [CrossRef] [PubMed]
- Manaster, A.; O’Dell, C.W.; Elsaesser, G. Evaluation of Cloud Liquid Water Path Trends Using a Multi-Decadal Record of Passive Microwave Observations. J. Clim. 2017, 30, 5871–5884. [Google Scholar] [CrossRef] [PubMed]
- Lauer, A.; Hamilton, K. Simulating clouds with global climate models: A comparison of CMIP5 results with CMIP3 and satellite data. J. Clim. 2013, 26, 3823–3845. [Google Scholar] [CrossRef]
- Rotstayn, L.D.; Ryan, B.F.; Katzfey, J.J. A scheme for calculation of the liquid fraction in mixed-phase stratiform clouds in large-scale models. Mon. Weather Rev. 2000, 128, 1070–1088. [Google Scholar] [CrossRef]
- Kretzschmar, J.; Salzmann, M.; Mülmenstädt, J.; Quaas, J. Arctic clouds in ECHAM6 and their sensitivity to cloud microphysics and surface fluxes. Atmos. Chem. Phys. 2019, 19, 10571–10589. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).