Chinese High Resolution Satellite Data and GIS-Based Assessment of Landslide Susceptibility along Highway G30 in Guozigou Valley Using Logistic Regression and MaxEnt Model
Abstract
:1. Introduction
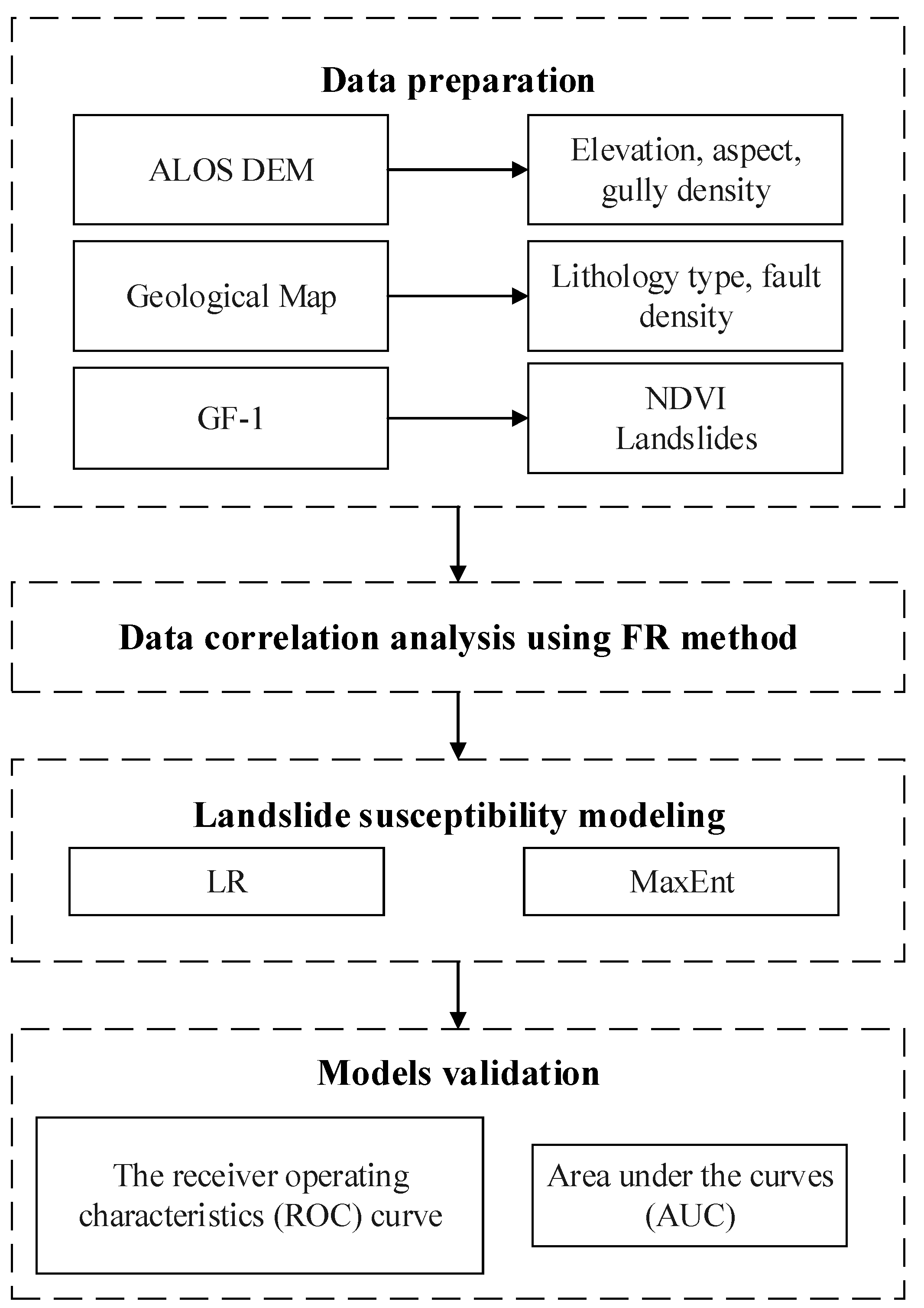
2. Materials and Methods
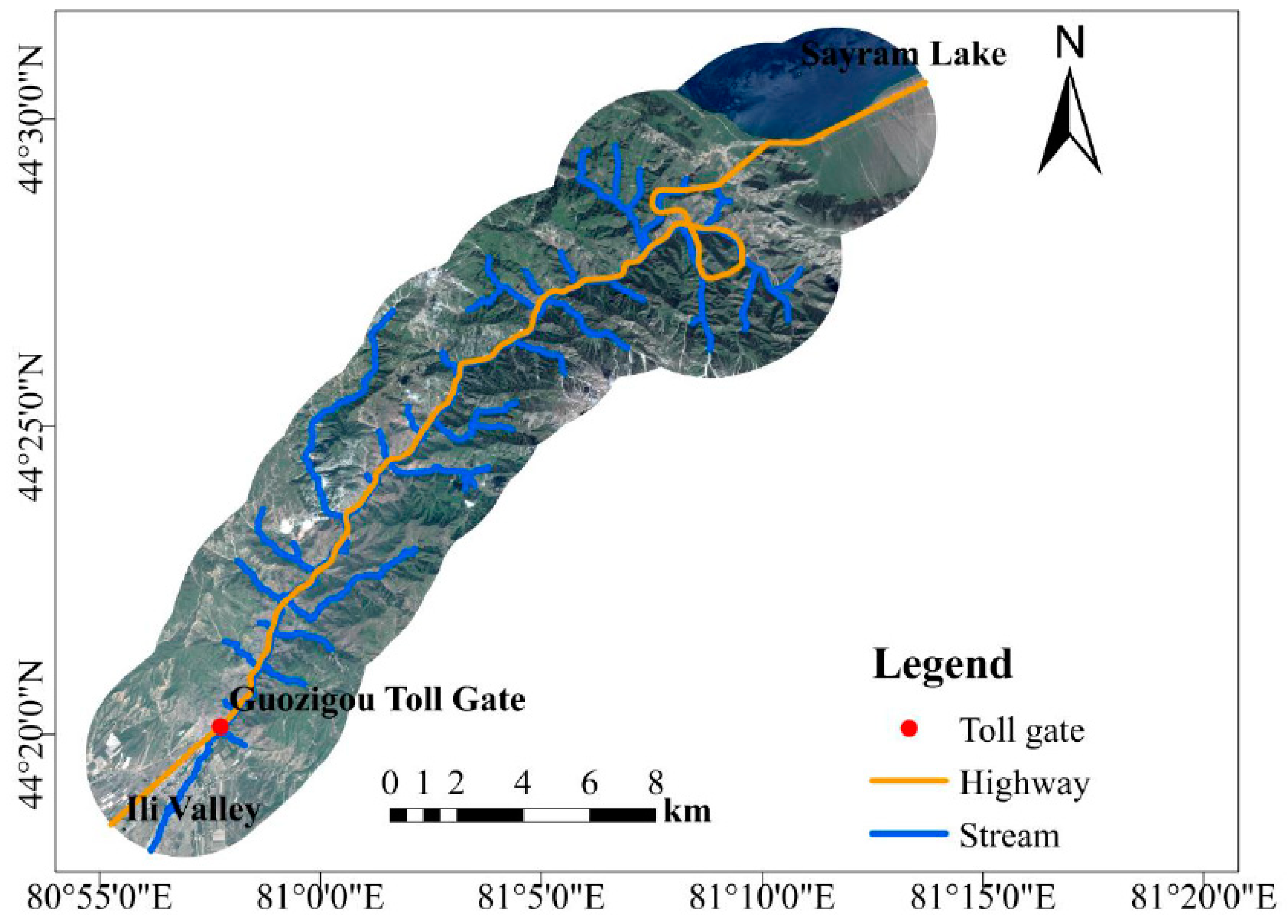
2.1. Study Area
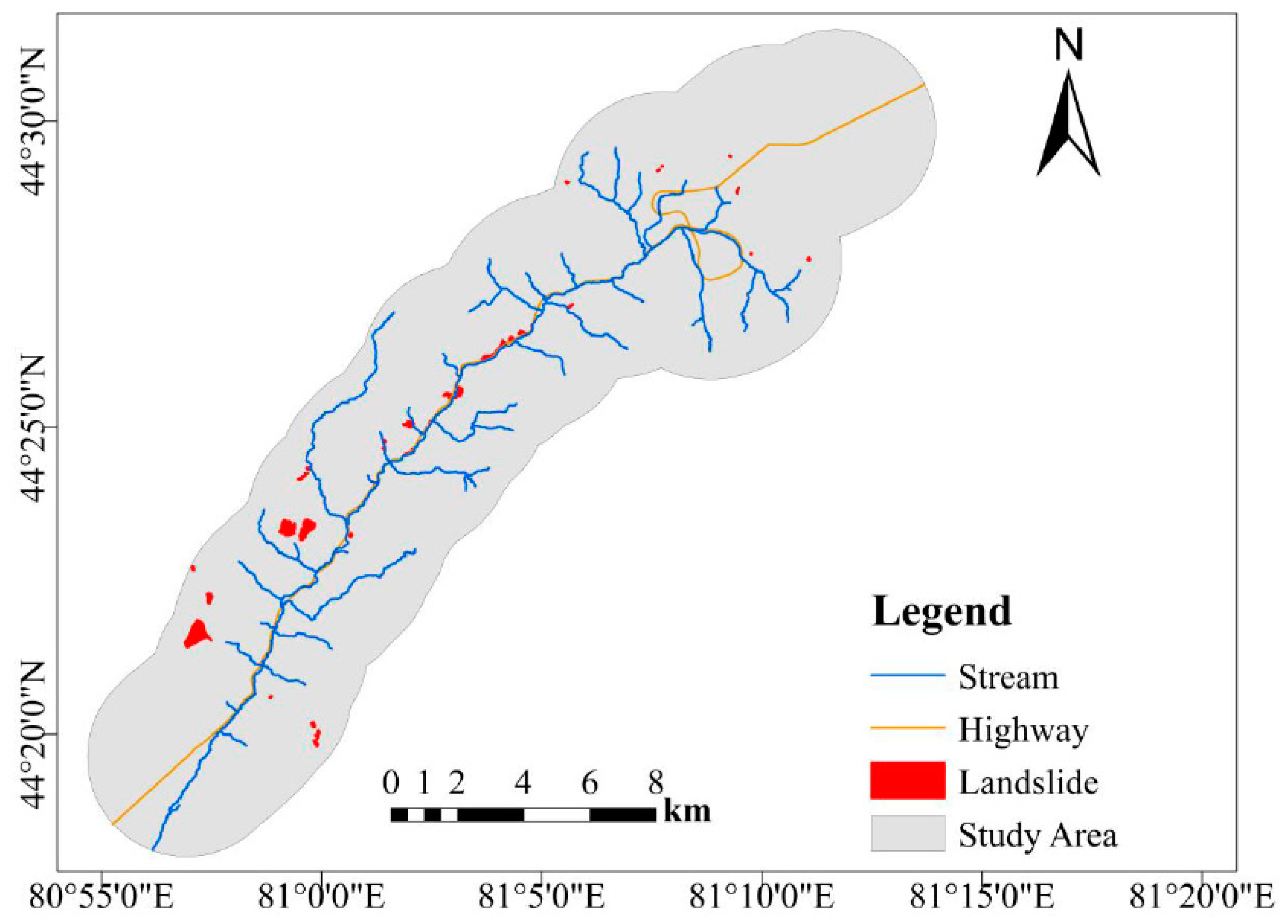
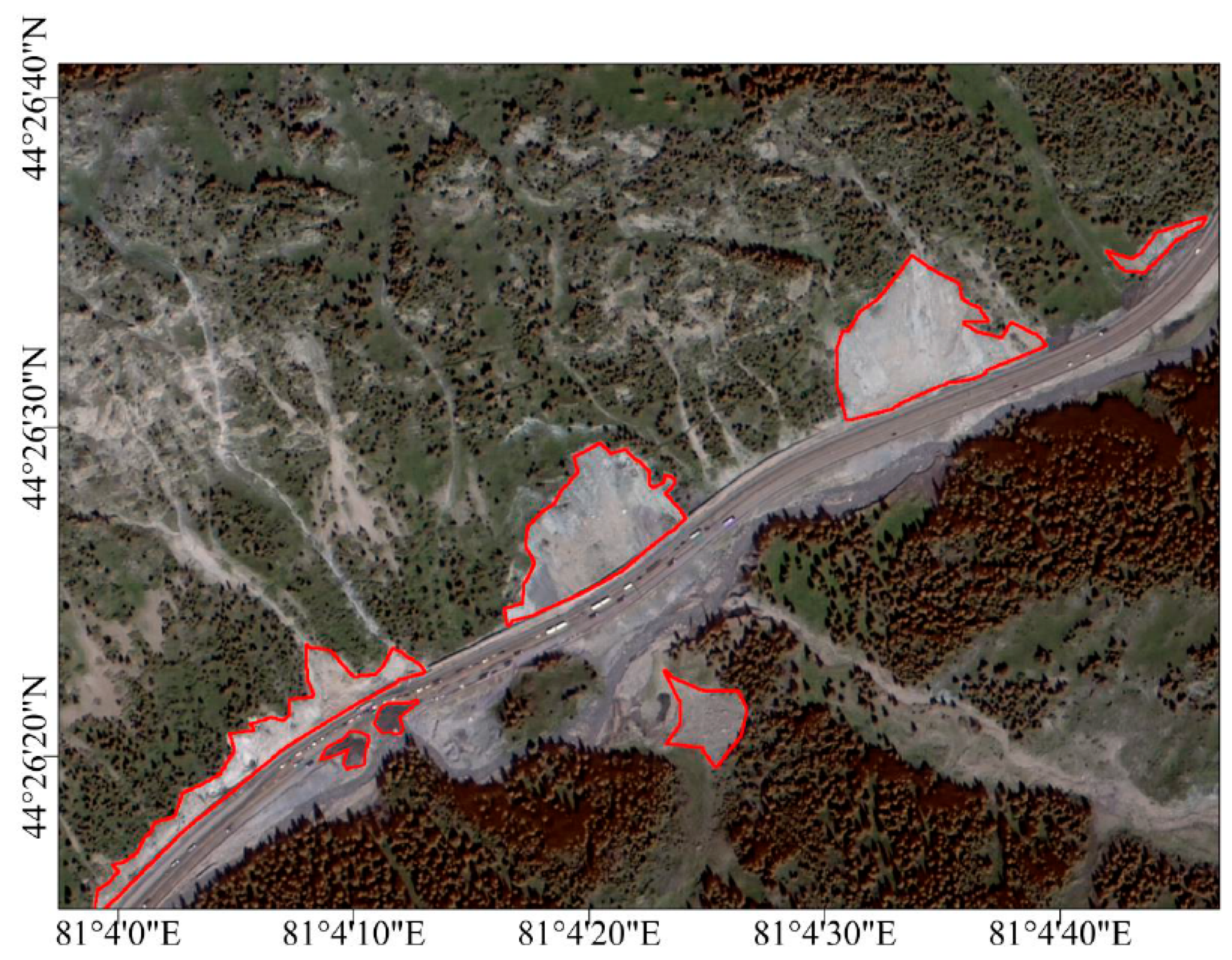
2.2. Landslide Inventory
2.3. Landslide Conditioning Factors
2.3.1. Elevation
2.3.2. Aspect
2.3.3. Slope
2.3.4. Gully Density
2.3.5. Lithology
2.3.6. Fault Density
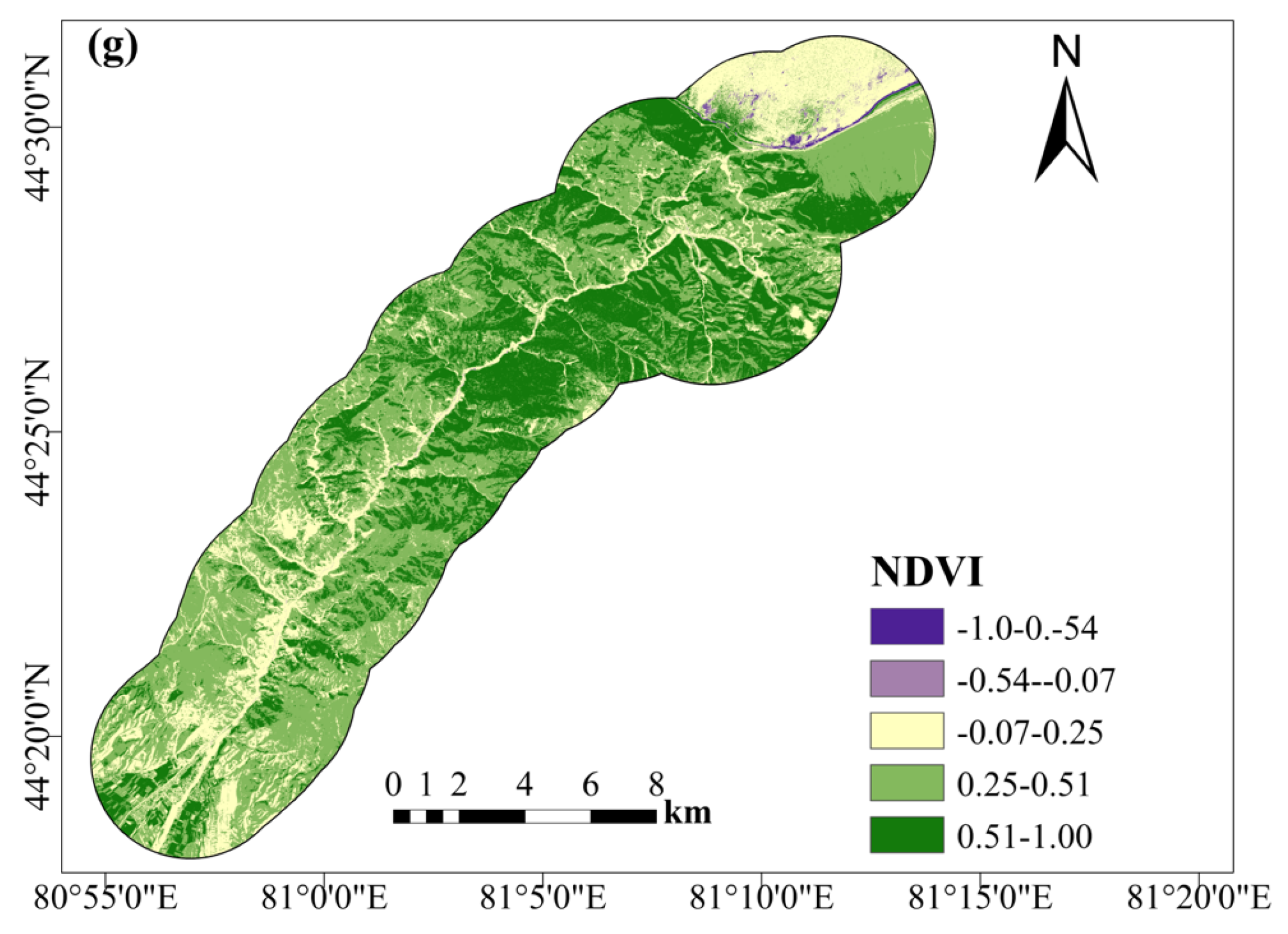
2.3.7. Normalized Difference Vegetation Index (NDVI)
2.4. Bivariate Method: Frequency Ratio
2.5. Landslide Susceptibility Models
2.5.1. Logistic Regression
2.5.2. MaxEnt
2.6. Landslide Susceptibility Maps
2.7. Model Performance
3. Results
3.1. Bivariate Frequency Ratio
3.2. Logistic Regression
3.3. MaxEnt
4. Discussion
4.1. Causes of Landslide along Highway in Mountainous Area
4.2. Comparison of LR and MaxEnt
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Das, I.; Stein, A.; Kerle, N.; Dadhwal, V.K. Landslide susceptibility mapping along road corridors in the Indian Himalayas using Bayesian logistic regression models. Geomorphology 2012, 179, 116–125. [Google Scholar] [CrossRef]
- Raja, N.B.; Çiçek, I.; Türkoğlu, N.; Aydin, O.; Kawasaki, A. Landslide susceptibility mapping of the Sera River basin using logistic regression model. Nat. Hazards 2017, 85, 1323–1346. [Google Scholar] [CrossRef] [Green Version]
- Choi, J.; Oh, H.J.; Lee, H.J.; Lee, C.; Lee, S. Combining landslide susceptibility maps obtained from frequency ratio, logistic regression, and artificial neural network models using ASTER images and GIS. Eng. Geol. 2012, 124, 12–23. [Google Scholar] [CrossRef]
- Kaczmarek, Ł.D.; Popielski, P. Selected components of geological structures and numerical modelling of slope stability. Open Geosci. 2019, 11, 208–218. [Google Scholar] [CrossRef]
- Dai, F.C.; Lee, C.F.; Ngai, Y.Y. Landslide risk assessment and management: An overview. Eng. Geol. 2002, 64, 65–87. [Google Scholar] [CrossRef]
- Das, I.; Sahoo, S.; Van Westen, C.J.; Stein, A.; Hack, R. Landslide susceptibility assessment using logistic regression and its comparison with a rock mass classification system, along a road section in the northern Himalayas (India). Geomorphology 2010, 114, 627–637. [Google Scholar] [CrossRef]
- Goetz, J.N.; Guthrie, R.H.; Brenning, A. Integrating physical and empirical landslide susceptibility models using generalized additive models. Geomorphology 2011, 129, 376–386. [Google Scholar] [CrossRef]
- Strauch, R.L.; Raymond, C.L.; Rochefort, R.M.; Hamlet, A.F.; Lauver, C. Adapting transportation to climate change on federal lands in Washington State, U.S.A. Clim. Chang. 2015, 130, 185–199. [Google Scholar] [CrossRef]
- Van Westen, C.J.; van Asch, T.W.J.; Soeters, R. Landslide hazard and risk zonation—Why is it still so difficult? Bull. Eng. Geol. Env. 2006, 65, 167–184. [Google Scholar] [CrossRef]
- Banerjee, P.; Ghose, M.K. Spatial analysis of environmental impacts of highway projects with special emphasis on mountainous area: An overview. Impact Assess. Proj. Apprais. 2016, 34, 279–293. [Google Scholar] [CrossRef] [Green Version]
- Corominas, J.; Moya, J. A review of assessing landslide frequency for hazard zoning purposes. Eng. Geol. 2008, 102, 193–213. [Google Scholar] [CrossRef]
- Ayalew, L.; Yamagishi, H. The application of GIS-based logistic regression for landslide susceptibility mapping in the Kakuda-Yahiko Mountains, Central Japan. Geomorphology 2005, 65, 15–31. [Google Scholar] [CrossRef]
- Lee, S. Application of logistic regression model and its validation for landslide susceptibility mapping using GIS and remote sensing data. Int. J. Remote Sens. 2005, 26, 1477–1491. [Google Scholar] [CrossRef]
- Shahabi, H.; Hashim, M.; Ahmad, B.B. Remote sensing and GIS-based landslide susceptibility mapping using frequency ratio, logistic regression, and fuzzy logic methods at the central Zab basin, Iran. Environ. Earth Sci. 2015, 73, 8647. [Google Scholar] [CrossRef]
- Trigila, A.; Iadanza, C.; Esposito, C.; Scarascia-Mugnozza, G. Comparison of logistic regression and random forests techniques for shallow landslide susceptibility assessment in Giampilieri (NE Sicily, Italy). Geomorphology 2015, 249, 119–136. [Google Scholar] [CrossRef]
- Reichenbach, P.; Rossi, M.; Malamud, B.D.; Mihir, M.; Guzzetti, F. A review of statistically based landslide susceptibility models. Earth-Sci. Rev. 2018, 180, 60–91. [Google Scholar] [CrossRef]
- Youssef, A.M.; Pourghasemi, H.R. Landslide susceptibility mapping using machine learning algorithms and comparison of their performance at Abha Basin, Asir Region, Saudi Arabia. Geosci. Front. 2021, 12, 639–655. [Google Scholar] [CrossRef]
- Yalcin, A. GIS-based landslide susceptibility mapping using analytical hierarchy process and bivariate statistics in Ardesen (Turkey): Comparisons of results and confirmations. Catena 2008, 72, 1–12. [Google Scholar] [CrossRef]
- Youssef, A.M.; Al-Kathery, M.; Pradhan, B. Landslide susceptibility mapping at Al-Hasher Area, Jizan (Saudi Arabia) using GIS-based frequency ratio and index of entropy models. Geosci. J. 2015, 19, 113–134. [Google Scholar] [CrossRef]
- Lee, S.; Ryu, J.H.; Won, J.S.; Park, H.J. Determination and application of the weights for landslide susceptibility mapping using an artificial neural network. Eng. Geol. 2004, 71, 289–302. [Google Scholar] [CrossRef]
- Tien Bui, D.; Tuan, T.A.; Klempe, H.; Pradhan, B.; Revhaug, I. Spatial prediction models for shallow landslide hazards: A comparative assessment of the efficacy of support vector machines, artificial neural networks, kernel logistic regression, and logistic model tree. Landslides 2016, 13, 361–378. [Google Scholar] [CrossRef]
- Huang, Y.; Zhao, L. Review on landslide susceptibility mapping using support vector machines. Catena 2018, 165, 520–529. [Google Scholar] [CrossRef]
- Chen, W.; Zhang, S.; Li, R.W.; Shahabi, H. Performance evaluation of the GIS-based data mining techniques of best-first decision tree, random forest, and naïve Bayes tree for landslide susceptibility modeling. Sci. Total Environ. 2018, 644, 1006–1018. [Google Scholar] [CrossRef]
- Convertino, M.; Troccoli, A.; Catani, F. Detecting fingerprints of landslide drivers: A MaxEnt model. J. Geophys. Res. Earth Surf. 2013, 118, 1367–1386. [Google Scholar] [CrossRef] [Green Version]
- Park, N.W. Using maximum entropy modeling for landslide susceptibility mapping with multiple geoenvironmental data sets. Environ. Earth Sci. 2015, 73, 937–949. [Google Scholar] [CrossRef]
- Kornejady, A.; Ownegh, M.; Bahremand, A. Landslide susceptibility assessment using maximum entropy model with two different data sampling methods. Catena 2017, 152, 144–162. [Google Scholar] [CrossRef]
- Ngo, P.T.T.; Panahi, M.; Khosravi, K.; Ghorbanzadeh, O.; Kariminejad, N.; Cerda, A.; Lee, S. Evaluation of deep learning algorithms for national scale landslide susceptibility mapping of Iran. Geosci. Front. 2021, 12, 505–519. [Google Scholar] [CrossRef]
- Pham, B.T.; Nguyen-Thoi, T.; Qi, C.; Phong, T.V.; Dou, J.; Ho, L.S.; Le, H.V.; Prakash, I. Coupling RBF neural network with ensemble learning techniques for landslide susceptibility mapping. Catena 2020, 195, 104805. [Google Scholar] [CrossRef]
- Zhou, X.Z.; Wen, H.J.; Zhang, Y.L.; Xu, J.H.; Zhang, W.G. Landslide susceptibility mapping using hybrid random forest with GeoDetector and RFE for factor optimization. Geosci. Front. 2021, 12, 101211. [Google Scholar] [CrossRef]
- Chen, W.; Pourghasemi, H.R.; Kornejady, A.; Zhang, N. Landslide spatial modelling: Introducing new ensembles of ANN, MaxEnt, and SVM machine learning techniques. Geoderma 2017, 305, 314–327. [Google Scholar] [CrossRef]
- Dehnavi, A.; Aghdam, I.N.; Pradhan, B.; Varzandeh, M.H.M. A new hybrid model using step-wise weight assessment ratio analysis (SWARA) technique and adaptive neuro-fuzzy inference system (ANFIS) for regional landslide hazard assessment in Iran. Catena 2015, 135, 122–148. [Google Scholar] [CrossRef]
- Zhu, A.X.; Miao, Y.M.; Yang, L.; Bai, S.B.; Liu, J.Z.; Hong, H.Y. Comparison of the presence-only method and presence-absence method in landslide susceptibility mapping. Catena 2018, 171, 222–233. [Google Scholar] [CrossRef]
- Felicísimo, Á.M.; Cuartero, A.; Remondo, J.; Quirós, E. Mapping landslide susceptibility with logistic regression, multiple adaptive regression splines, classification and regression trees, and maximum entropy methods: A comparative study. Landslides 2012, 10, 175–189. [Google Scholar] [CrossRef]
- Zhao, L.J.; Li, H.; Liu, Y.F.; Chen, D.H.; Li, J.L. Evaluation on geological hazard risk and disaster-causing factors in the Guozigou Valley in Ili, Xinjiang. Arid. Zone Res. 2017, 34, 693–700. [Google Scholar]
- Zhao, L.J.; Chen, D.H.; Li, H.; Liu, Y.F. A method to assess landslide susceptibility by using logistic regression model for Guozigou Region, Xinjinag. Mt. Res. 2017, 32, 203–211. [Google Scholar]
- Guzzetti, F.; Carrara, A.; Cardinali, M.; Reichenbach, P. Landslide hazard evaluation: A review of current techniques and their application in a multiscale study, Central Italy. Geomorphology 1999, 31, 181–216. [Google Scholar] [CrossRef]
- Guzzetti, F.; Mondini, A.C.; Cardinali, M.; Fiorucci, F.; Santangelo, M.; Chang, K.T. Landslide inventory maps: New tools for an old problem. Earth-Sci. Rev. 2012, 112, 42–66. [Google Scholar] [CrossRef] [Green Version]
- Tanyas, H.; van Westen, C.J.; Persello, C.; Alvioli, M. Rapid prediction of the magnitude scale of landslide events triggered by an earthquake. Landslides 2019, 16, 661–676. [Google Scholar] [CrossRef] [Green Version]
- Dai, F.C.; Lee, C.F. Landslide characteristics and slope instability modelling using GIS, Lantau Island, Hong Kong. Geomorphology 2002, 42, 213–228. [Google Scholar] [CrossRef]
- Devkota, K.C.; Regmi, A.D.; Pourghasemi, H.R.; Yoshida, K.; Pradhan, B.; Ryu, I.C.; Dhital, M.R.; Althuwaynee, O.F. Landslide susceptibility mapping using certainty factor, index of entropy and logistic regression models in GIS and their comparison at Mugling-Narayanghat road section in Nepal Himalaya. Nat. Hazards 2013, 65, 135–165. [Google Scholar] [CrossRef]
- Hong, H.; Naghibi, S.A.; Pourghasemi, H.R.; Pradhan, B. GIS-based landslide spatial modeling in Ganzhou City, China. Arab. J. Geosci. 2016, 9, 112. [Google Scholar] [CrossRef]
- Yang, J.T.; Song, C.; Yang, Y.; Xu, C.D.; Guo, F.; Xie, L. New method for landslide susceptibility mapping supported by spatial logistic regression and GeoDetector: A case study of Duwen Highway Basin, Sichuan Province, China. Geomorphology 2019, 324, 62–71. [Google Scholar] [CrossRef]
- Kawabata, D.; Bandibas, J. Landslide susceptibility mapping using geological data, a DEM from ASTER images and an Artificial Neural Network (ANN). Geomorphology 2009, 113, 97–109. [Google Scholar] [CrossRef]
- Sidle, R.C.; Ochiai, H. Landslides: Processes, Prediction, and Land Use; American Geophysical Union: Washington, DC, USA, 2006. [Google Scholar]
- Lee, S.; Min, K. Statistical analysis of landslide susceptibility at Yongin, Korea. Environ. Geol. 2001, 40, 1095–1113. [Google Scholar] [CrossRef]
- He, Y.; Beighley, E. GIS-based regional landslide susceptibility mapping: A case study in southern California. Earth Surf. Proc. Land. 2008, 33, 380–393. [Google Scholar] [CrossRef]
- Van Den Eeckhaut, M.; Vanwalleghem, T.; Poesen, J.; Govers, G.; Verstraeten, G.; Vandekerckhove, L. Prediction of landslide susceptibility using rare events logistic regression: A case-study in the Flemish Ardennes (Belgium). Geomorphology 2006, 76, 392–410. [Google Scholar] [CrossRef]
- Brenning, A. Spatial prediction models for landslide hazards: Review, comparison and evaluation. Nat. Hazards Earth Syst. Sci. 2005, 5, 853–862. [Google Scholar] [CrossRef]
- Phillips, S.J.; Anderson, R.P.; Schapire, R.E. Maximum entropy modeling of species geographic distributions. Ecol. Model. 2006, 190, 231–259. [Google Scholar] [CrossRef] [Green Version]
- Phillips, S.J.; Dudík, M.; Schapire, R.E. Maxent Software for Modeling Species Niches and Distributions (Version 3.4.1). 2021. Available online: http://biodiversityinformatics.amnh.org/open_source/maxent/ (accessed on 25 July 2021).
- Beguería, S. Validation and evaluation of predictive models in hazard and risk assessment. Nat. Hazards 2006, 37, 315–329. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.M.; Feng, L.W.; Li, S.J.; Ren, F.; Du, Q.Y. A hybrid model considering spatial heterogeneity for landslide susceptibility mapping in Zhejiang Province, China. Catena 2020, 188, 104425. [Google Scholar] [CrossRef]
- Swanson, F.J. Impact of clear-cutting and road construction on soil erosion by landslides in the western Cascade Range, Oregon. Geology 1975, 3, 393–396. [Google Scholar] [CrossRef]
- Sidle, R.C.; Furuichi, T.; Kono, Y. Unprecedented rates of landslide and surface erosion along a newly constructed road in Yunnan, China. Nat. Hazards 2011, 57, 313–326. [Google Scholar] [CrossRef]
- Muenchow, J.; Brenning, A.; Richter, M. Geomorphic process rates of landslides along a humidity gradient in the tropical Andes. Geomorphology 2012, 139, 271–284. [Google Scholar] [CrossRef]
- Brenning, A.; Schwinn, M.; Ruiz-Páez, A.P.; Muenchow, J. Landslide susceptibility near highways is increased by 1 order of magnitude in the Andes of southern Ecuador, Loja province. Nat. Hazards Earth Syst. Sci. 2015, 15, 45–57. [Google Scholar] [CrossRef] [Green Version]
- Mokhtari, M.; Abedian, S. Spatial prediction of landslide susceptibility in Taleghan basin, Iran. Stoch. Environ. Res. Risk Assess. 2019, 33, 1297–1325. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Kornejady, A.; Kerle, N.; Shabani, F. Investigating the effects of different landslide positioning techniques, landslide partitioning approaches, and presence-absence balances on landslide susceptibility mapping. Catena 2020, 187, 104364. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Mohammady, M.; Pradhan, B. Landslide susceptibility mapping using index of entropy and conditional probability models in GIS: Safarood Basin, Iran. Catena 2012, 97, 71–84. [Google Scholar] [CrossRef]
- Shirani, K.; Pasandi, M.; Arabameri, A. Landslide susceptibility assessment by Dempster–Shafer and Index of Entropy models, Sarkhoun basin, Southwestern Iran. Nat. Hazards 2018, 93, 1379–1418. [Google Scholar] [CrossRef]
- Jiao, Y.M.; Zhao, D.M.; Ding, Y.P.; Liu, Y.; Xu, Q.; Qiu, Y.M.; Liu, C.J.; Liu, Z.L.; Zha, Z.Q.; Li, R. Performance evaluation for four Gis-based models purposed to predict and map landslide susceptibility: A case study at a World Heritage site in Southwest China. Catena 2019, 183, 104221. [Google Scholar] [CrossRef]
- Pradhan, A.; Kang, H.S.; Lee, J.S.; Kim, Y.T. An ensemble landslide hazard model incorporating rainfall threshold for Mt. Umyeon, South Korea. Bull. Eng. Geol. Environ. 2019, 78, 131–146. [Google Scholar] [CrossRef]
- Sheikh, V.; Kornejady, A.; Ownegh, M. Application of the coupled TOPSIS–Mahalanobis distance for multi-hazard-based management of the target districts of the Golestan Province, Iran. Nat. Hazards 2019, 96, 1335–1365. [Google Scholar] [CrossRef]
- Javidan, N.; Kavian, A.; Pourghasemi, H.R.; Conoscenti, C.; Jafarian, Z.; Rodrigo-Comino, J. Evaluation of multi-hazard map produced using MaxEnt machine learning technique. Sci. Rep. 2021, 11, 6496. [Google Scholar] [CrossRef] [PubMed]
- Teimouri, M.; Kornejady, A. The dilemma of determining the superiority of data mining models: Optimal sampling balance and end users’ perspectives matter. Bull. Eng. Geol. Environ. 2019, 79, 1707–1720. [Google Scholar] [CrossRef]
- Mirzaei, G.; Soltani, A.; Soltani, M.; Darabi, M. An integrated data-mining and multi-criteria decision-making approach for hazard-based object ranking with a focus on landslides and floods. Environ. Earth Sci. 2018, 77, 581. [Google Scholar] [CrossRef]
- Phillips, S.J.; Dudık, M.; Elith, J.; Graham, C.H.; Lehmann, A.; Leathwick, J.; Ferrier, S. Sample selection bias and presence-only distribution models: Implications for background and pseudo-absence data. Ecol. Appl. 2009, 19, 181–197. [Google Scholar] [CrossRef] [PubMed] [Green Version]

| Conditioning Factors | Data Type | Source |
|---|---|---|
| Elevation | Continuous | Digital Elevation Model (DEM) |
| Aspect | Categorical (9 classes) | DEM |
| Slope | Continuous | DEM |
| Gully Density | Continuous | DEM |
| Lithology Type | Categorical (5 classes) | Geology Map |
| Fault Density | Continuous | Geology Map |
| NDVI | Continuous | GF-1 satellite image |
| Conditioning Factors | Categories | Pixels of Land Area | Percentage of Domain (%) | Pixels of Landslide Area | Percentage of Landslides (%) | FR |
|---|---|---|---|---|---|---|
| Elevation (m) | 941–1255 | 298,868 | 13.90 | 32 | 0.35 | 0.03 |
| 1255–1592 | 418,538 | 19.47 | 7932 | 86.22 | 4.43 | |
| 1592–1897 | 458,777 | 21.34 | 1084 | 11.78 | 0.55 | |
| 1897–2211 | 749,941 | 34.89 | 137 | 1.49 | 0.04 | |
| 2211–2940 | 223,542 | 10.40 | 15 | 0.16 | 0.02 | |
| Aspect | Flat | 174,720 | 8.13 | 0.00 | 0.00 | |
| North | 270,356 | 12.58 | 200 | 2.17 | 0.17 | |
| Northeast | 194,573 | 9.05 | 262 | 2.85 | 0.31 | |
| East | 199,082 | 9.26 | 1397 | 15.18 | 1.64 | |
| Southeast | 207,236 | 9.64 | 2627 | 28.55 | 2.96 | |
| South | 272,025 | 12.65 | 2974 | 32.33 | 2.55 | |
| Southwest | 293,547 | 13.66 | 792 | 8.61 | 0.63 | |
| West | 304,150 | 14.15 | 681 | 7.40 | 0.52 | |
| Northwest | 233,977 | 10.88 | 267 | 2.90 | 0.27 | |
| Slope | 0–10 | 530,643 | 24.68 | 709 | 7.71 | 0.31 |
| 10–20 | 481,847 | 22.41 | 2424 | 26.35 | 1.18 | |
| 20–30 | 506,654 | 23.57 | 2428 | 26.39 | 1.12 | |
| 30–40 | 386,096 | 17.96 | 1764 | 19.17 | 1.07 | |
| 40–90 | 244,426 | 11.37 | 1875 | 20.38 | 1.79 | |
| Gully Density | 0–2.08 | 130,320 | 6.06 | 0.00 | 0.00 | |
| 2.08–4.32 | 636,067 | 29.59 | 2241 | 24.36 | 0.82 | |
| 4.32–5.42 | 767,112 | 35.68 | 3468 | 37.70 | 1.06 | |
| 5.42–6.86 | 437,781 | 20.36 | 2950 | 32.07 | 1.57 | |
| 6.86–9.67 | 178,517 | 8.30 | 541 | 5.88 | 0.71 | |
| Lithology Type | Loose Rock | 531,449 | 24.72 | 3479 | 37.82 | 1.53 |
| Softer Rock | 288,595 | 13.42 | 1749 | 19.01 | 1.42 | |
| Soft Rock | 227,049 | 10.56 | 73 | 0.79 | 0.08 | |
| Hard Rock | 764,054 | 35.54 | 3737 | 40.62 | 1.14 | |
| Harder Rock | 176,922 | 8.23 | 162 | 1.76 | 0.21 | |
| Other | 161,728 | 7.52 | 0.00 | 0.00 | ||
| Fault Density | 0–4.09 | 334,277 | 15.55 | 65 | 0.71 | 0.05 |
| 4.09–9.55 | 279,183 | 12.99 | 1344 | 14.61 | 1.12 | |
| 9.55–13.08 | 843,030 | 39.21 | 3439 | 37.38 | 0.95 | |
| 13.08–17.17 | 530,926 | 24.70 | 4273 | 46.45 | 1.88 | |
| 17.17–29.00 | 162,380 | 7.55 | 79 | 0.86 | 0.11 | |
| NDVI | −1.00–0.54 | 6532 | 0.30 | 0.00 | 0.00 | |
| −0.54–0.07 | 6671 | 0.31 | 28 | 0.30 | 0.98 | |
| −0.07–0.25 | 433,388 | 20.16 | 6324 | 68.74 | 3.41 | |
| 0.25–0.51 | 1,040,774 | 48.41 | 2677 | 29.10 | 0.60 | |
| 0.51–1.00 | 662,432 | 30.81 | 171 | 1.86 | 0.06 |
| −2 Log Likelihood | Cox and Snell R Square | Nagelkerke R Square | Overall Percentage |
|---|---|---|---|
| 109.651 a | 0.283 | 0.415 | 82.2 |
| Models | Study Region | Landslide Areas | Landslide-Free Areas |
|---|---|---|---|
| LR | 0.167 | 0.503 | 0.166 |
| MaxEnt | 0.096 | 0.537 | 0.094 |
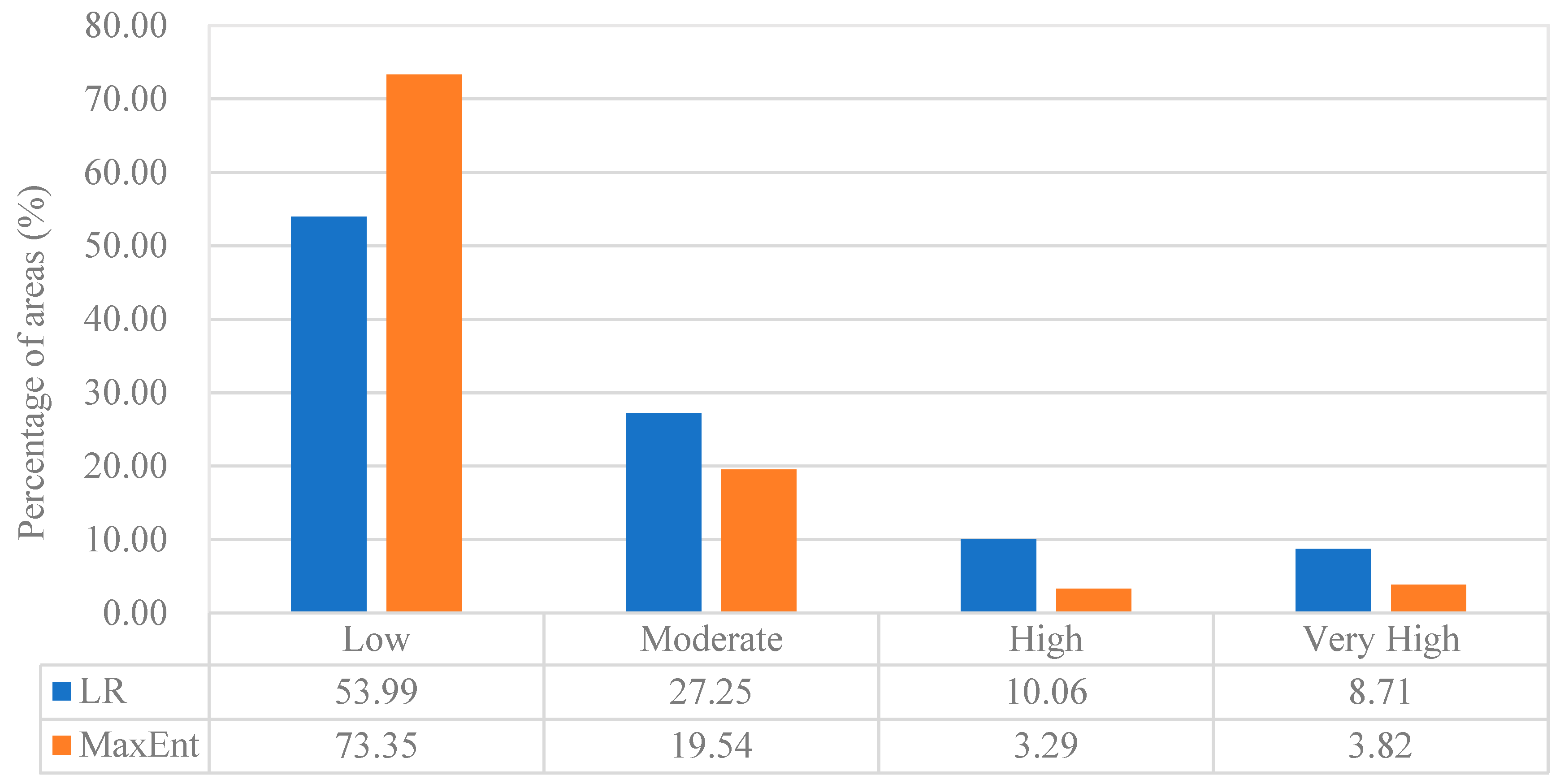
| Landslide Susceptibility Class | LR (%) | MaxEnt (%) |
|---|---|---|
| Low | 7.85 | 7.27 |
| Moderate | 19.59 | 26.24 |
| High | 15.95 | 10.37 |
| Very high | 56.62 | 56.12 |
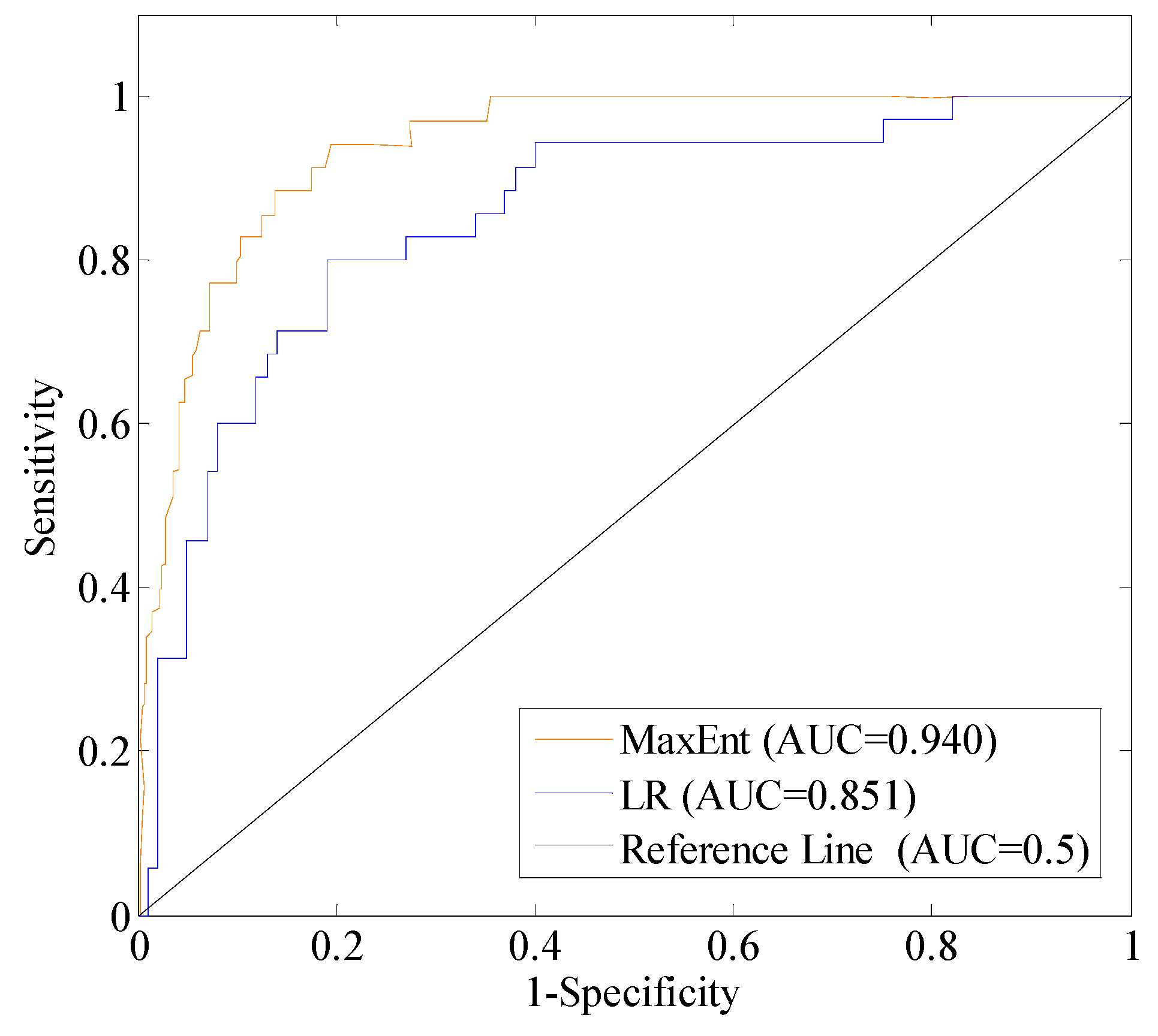
| Models | Area | Standard Error | Asymptotic Significant | Asymptotic 95% Confidence Interval | |
|---|---|---|---|---|---|
| Lower Limit | Upper Limit | ||||
| LR | 0.851 | 0.038 | 0.000 | 0.776 | 0.926 |
| MaxEnt | 0.940 | 0.031 | 0.000 | 0.844 | 0.956 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Zhao, L.; Bao, A.; Li, J.; Yan, X. Chinese High Resolution Satellite Data and GIS-Based Assessment of Landslide Susceptibility along Highway G30 in Guozigou Valley Using Logistic Regression and MaxEnt Model. Remote Sens. 2022, 14, 3620. https://doi.org/10.3390/rs14153620
Liu Y, Zhao L, Bao A, Li J, Yan X. Chinese High Resolution Satellite Data and GIS-Based Assessment of Landslide Susceptibility along Highway G30 in Guozigou Valley Using Logistic Regression and MaxEnt Model. Remote Sensing. 2022; 14(15):3620. https://doi.org/10.3390/rs14153620
Chicago/Turabian StyleLiu, Ying, Liangjun Zhao, Anming Bao, Junli Li, and Xiaobing Yan. 2022. "Chinese High Resolution Satellite Data and GIS-Based Assessment of Landslide Susceptibility along Highway G30 in Guozigou Valley Using Logistic Regression and MaxEnt Model" Remote Sensing 14, no. 15: 3620. https://doi.org/10.3390/rs14153620
APA StyleLiu, Y., Zhao, L., Bao, A., Li, J., & Yan, X. (2022). Chinese High Resolution Satellite Data and GIS-Based Assessment of Landslide Susceptibility along Highway G30 in Guozigou Valley Using Logistic Regression and MaxEnt Model. Remote Sensing, 14(15), 3620. https://doi.org/10.3390/rs14153620







