Abstract
Chlorophyll-a (Chl-a) is an important marine indicator, and the improvement in Chl-a concentration retrieval for ocean color remote sensing is always a major challenge. This study focuses on the northwest Pacific fishing ground (NPFG) to evaluate and improve the Chl-a products of three mainstream remote sensing satellites, Himawari-8, MODIS-Aqua, and VIIRS-SNPP. We analyzed in situ data and found that an in situ Chl-a concentration of 0.3 mg m−3 could be used as a threshold to distinguish the systematic deviation of remote sensing Chl-a data in the NPFG. Based on this threshold, we optimized the Chl-a algorithms of the three satellites by data grouping, and integrated multisource satellite Chl-a data by weighted averaging to acquire high-coverage merged data. The merged data were thoroughly verified by Argo Chl-a data. The Chl-a front of merged Chl-a data could be represented accurately and completely and had a good correlation with the distribution of the NPFG. The most important marine factors for Chl-a are nutrients and temperature, which are affected by mesoscale eddies and variations in the Kuroshio extension. The variation trend of merged Chl-a data is consistent with mesoscale eddies and Kuroshio extension and has more sensitive responses to the marine climatic conditions of ENSO.
1. Introduction
The northwest Pacific fishing ground (NPFG) is one of the most important fishing grounds in the world, where the catch production can reach 20 million tons, accounting for 25% of the total worldwide marine fish production, according to statistics from the Food and Agriculture Organization (FAO) of the United Nations [1]. The NPFG has unique geographical conditions and oceanographic properties and is the habitat and fishing ground for many pelagic fishery species, especially the Pacific saury (Cololabis saira), a major commercial species in this region [2]. The intersection of the Oyashio Current, Kuroshio Current, and Kuroshio extension brings abundant nutrients [3,4] to the region, while also effecting marine climate changes in the NPFG [5,6]. The Chlorophyll-a (Chl-a) concentration is an important ocean color indicator associated with phytoplankton, nutrients, and primary productivity; it also plays an important role in marine climate changes, marine current responses, marine ecosystems, and marine geochemical cycle regulation. Therefore, Chl-a concentration is a necessary factor for marine studies concerning carbon flux, marine biomes, and fisheries [7,8,9,10]. The related study of Chl-a concentration in the NPFG is essential.
Ocean color remote sensing is the most direct and effective way to observe the variation in the global distribution of Chl-a and is highly convenient for marine studies [11,12]. In 1978, the United States launched the first ocean color remote sensor, CZCS, which received considerable attention. Subsequently, SeaWIFS, MODIS, and other ocean color sensors were launched by NASA and NOAA. Japan launched its first ocean color sensor, OCTS, in 1996; European countries and ESA also launched ocean color sensors such as POLDER and MERIS [13]. China started late in the field of ocean color remote sensing but has developed rapidly. Both HY-series (Haiyang series satellites, Table 1) and FY-series (Fengyun series satellites, Table 1) satellites are equipped with ocean color sensors [14]. Countries such as India and South Korea have also launched their own ocean color sensors (Table 1) [15].

Table 1.
Representative ocean color remote sensors from various agencies in different countries.
Chl-a concentration retrieval algorithms have developed synchronously with the accumulation of ocean color data. To obtain global Chl-a concentration observations, ocean chlorophyll-a (OCx, x means the version of the algorithm) algorithms, which are widely used in remote sensing Chl-a concentration retrieval, were first proposed for SeaWIFS [16,17]. The algorithms are based on a polynomial of the spectral ratio of remote sensing reflectance (Rrs, or normalized water-leaving reflectance) and empirical coefficients obtained from regressions of spectral ratios and in situ Chl-a data [15,18]. The empirical coefficients of different sensors have also been further optimized to verify the accuracy of OCx algorithms [19]. Hu et al. found that the performance of OCx algorithms was not good at low Chl-a concentrations; hence, they proposed the color index (CI) algorithm for Chl-a concentrations < 0.15 mg m−3 and set Chl-a concentration thresholds for the application of the OCx and CI algorithms, creating the ocean color index (OCI) algorithm [20,21]. However, the OCx and OCI algorithms were both designed to achieve global ocean observations and may cause errors at regional scales due to the different optical properties caused by differences in colored dis-solved matter and phytoplankton community structure [22]. For this reason, many studies have focused on different ocean basins to assess and optimize these algorithms. The research areas include the Arctic Ocean [23], the Atlantic Ocean [24], the Mediterranean Sea [25], the Southern Ocean [26], the Indian Ocean [27], and the tropical Pacific Ocean [28]. Related studies are few regarding the NPFG.
Differences in the missions and designs of sensors lead to differences in Chl-a data quality from specific sensors [29,30], further resulting in the discontinuity and deviation of long-term Chl-a records [12,31]. Natural effects such as clouds, interorbit gaps, sun glint, and thick aerosols will prevent ocean color sensors from collecting Chl-a data, causing missing data and low data coverage [32]. To improve the consistency of Chl-a data from different sources and the coverage of final ocean color products, researchers have adopted statistical methods, such as weighted averaging, empirical orthogonal functions, machine learning, and the Bayesian maximum entropy method, to merge and improve Chl-a data from multiple sources based on existing retrieval algorithms [33,34].
Remote sensing Chl-a data have been widely used in marine studies of the NPFG. In fisheries studies of Pacific saury, Chl-a data have been utilized to study the migration routes and formation mechanisms of the fishing grounds, as these data are closely related to the food conditions of different regions and seasons [35,36,37]. Knowledge regarding the effects of environmental factors on exploited fishery stocks is key for fishery management strategies, and accurate Chl-a data could better indicate changes in Pacific saury migration routes and distribution [38]. Mesoscale eddies and Kuroshio extension are also important oceanographic phenomena in this region. The oceanographic dynamic process can cause changes in nutrients, sea surface temperature, and sea surface height, which can then lead to a change in Chl-a concentration. However, how to quantify the influence of this dynamic process on Chl-a for different scales and what kind of influence mechanism impacts different dynamic processes for marine ecosystems still need further exploration [39]. Accurate and high-coverage Chl-a data could reflect the states of mesoscale eddies and the change scales of Kuroshio extension more completely, laying a foundation for related studies. Marine climate changes, caused by typhoon weather and ENSO events, have substantial impacts on the marine ecosystem [6,40,41]. Chl-a concentration, which is sensitive to changes in the marine environment, could respond to climate changes [11,18]. However, with the exception of studies on typhoon weather and long-term climate changes, studies regarding climate change impacts on ENSO and Chl-a concentration are relatively few for the NPFG. Therefore, this paper proposes a method to acquire more accurate and higher-coverage Chl-a data in the NPFG and discusses the related oceanographic phenomena.
In this study, the main goals include the following: (a) improving the algorithms for Himawari-8, MODIS-Aqua, and VIIRS-SNPP Chl-a data in the NPFG and then proposing a method for merging them into more accurate Chl-a data; (b) exploring the role of merged Chl-a data to explain the changes in the NPFG; (c) verifying the action mechanism of merged Chl-a data to reflect the influence of mesoscale eddies, Kuroshio variations, and ENSO phenomena.
2. Materials and Methods
2.1. Data Sources
2.1.1. Satellite Chl-a Data
In this paper, the NPFG is defined as 35°N to 55°N, 140°E to 175°E, which includes the Pacific saury migration routes and habitats for different life stages (Figure 1) [35,36]. To obtain better Chl-a observation data in the NPFG, we selected three mainstream remote sensing satellites in orbit, Himawari-8, MODIS-Aqua, and VIIRS-SNPP, as data sources. MODIS-Aqua was launched in May 2002. It acquires data in 36 spectral bands and has the longest service time among the three sensors. VIIRS-SNPP, launched in October 2011, has 22 spectral bands ranging from 412 nm to 12 μm. MODIS and VIIRS are equipped on polar-orbit satellites of NASA and can make global observations (Table 1) [13,15]. Himawari-8 is not a traditional ocean color remote sensing satellite. It is a geostationary orbit satellite with 16 observed bands that was produced by the Japan Meteorological Agency (JMA) mainly for marine meteorological observations and was launched in October 2014 [14]. It can scan the whole northwest Pacific Ocean once every 10 min and shows advantages in its relatively high temporal–spatial resolution [42].
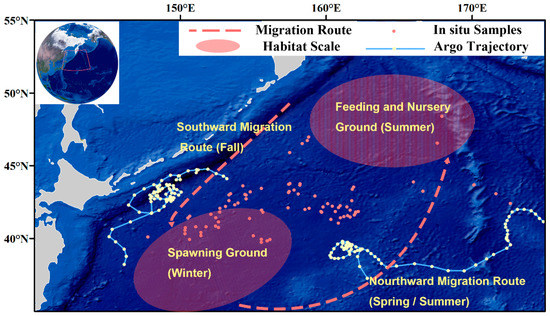
Figure 1.
Research area including the locations of observation data and Argo trajectory in NPFG. The dotted lines are the annual migration routes of Pacific saury. Feeding and nursery ground, spawning ground, and northward (southward) migration route of Pacific saury are marked in the Figure.
MODIS-Aqua and VIIRS-SNPP level 3 mapped data, including Rrs data and Chl-a concentration products, were downloaded from the NASA ocean color website (https://oceancolor.gsfc.nasa.gov/, accessed on 29 July 2020). The temporal resolution and spatial resolution of these two satellites are daily and 4 km, respectively. The level 3 Himawari-8 data are from the Japan Aerospace Exploration Agency (JAXA) P-Tree System (https://www.eorc.jaxa.jp/ptree/index.html, accessed on 30 July 2020). The daily and full-disk (5 km) data, which include the normalized water-leaving reflectance and Chl-a concentration data, were downloaded.
2.1.2. In Situ Chl-a Data
The in situ Chl-a data include fishing operation points from three years (2017~2019) of the northwest Pacific autumn survey of Zhongtai Ocean Fishery Co., Ltd. (Qingdao, China). Water samples were collected at the operation points, and the value of Chl-a was measured fluorometrically in the laboratory [43], resulting in a total of 85 surface (0 m) Chlin situ observations from the research region. A total of 164 Pacific saury fishing operation sites were also recorded in the three-year survey.
2.1.3. Chl-a Data from Argo
The Argo data are from BGC-Argo Program. We used these data as the validated data, including 60 surface (0 m) ChlArgo observations from January 2020 to January 2021. These data are collected and made freely available by the International Argo Program (https://argo.ucsd.edu, accessed on 9 July 2021) and the national programs (https://www.ocean-ops.org, accessed on 9 July 2021) that contribute to it.
2.1.4. Marine Environmental Data
Sea surface temperature (SST) data used in this paper are from the NASA ocean color website (https://oceancolor.gsfc.nasa.gov/, accessed on 30 January 2022). The resolution of SST data is 4 km. Sea level anomaly (SLA), for which the resolution is 0.25° × 0.25°, was obtained from the Copernicus Marine and Environment Monitoring Service (CMEMS, https://www.aviso.altimetry.fr/en/home.html, accessed on 15 February 2022).
2.1.5. ENSO Index
The Multivariate ENSO Index (MEI, from https://www.esrl.noaa.gov/psd/enso/mei/, accessed on 25 February 2022) was used in this paper to describe three ENSO states: El Niño (MEI ≥ 1), Neutral (−1 < MEI <1), and La Niña (MEI ≤ −1) [28,44]. The distribution of Chl-a concentration would be recorded and compared in different ENSO states based on MEI.
2.2. Chl-a Data Preprocessing
A pairwise comparison needed to be performed for the matched in situ data and satellites’ Chl-a products to validate the point-to-point accuracy. Due to cloud cover and other factors, satellite data will miss observation points and cause gaps in remote sensing products, further resulting in the failure of data matchups. In this paper, different combinations of temporal and spatial averaging were tested to find an appropriate averaging method to solve this problem. For spatial averaging, the pixel corresponding to the in situ data was regarded as the center pixel, and windows of 1 × 1, 3 × 3, and 5 × 5 pixels were extracted. Temporal averaging of 1 day, 3 (1 ± 1) days, and 5 (1 ± 2) days was performed centered around the sampling time of the in situ data. Different combinations led to different accuracies and numbers of matchups. After selecting the best combination of data, the outliers of each data set were eliminated under a 95% confidence interval.
2.3. Assessment Metrics
The in situ Chl-a data pairwise comparison results for different combinations were recorded, including the total number, percent of matches, and accuracy of matchups. Because of the small sample size of in situ Chl-a concentration data, the quantity of successful matchups was the first priority. The correlation of matchups was described by the coefficient of determination (R2) of the original algorithm fitting between the Rrs data and satellite Chl-a products.
The slope, intercept, and R2 between the in situ data and satellite data were recorded to evaluate the performance of the ocean color algorithms. For systematic estimation of the satellite Chl-a data, the log-transformed bias was used to indicate the degree of deviation from one set to another (Equation (1); bias = 1 means no deviation) [45]. The mean absolute error (MAE; Equation (2)) was calculated as the absolute value of the bias.
2.4. Remote Sensing Chl-a Algorithm Development
2.4.1. Current Chl-a Algorithms
The Chl-a products of MODIS-Aqua and VIIRS-SNPP are based on OCx algorithms (Equations (3) and (4)). For MODIS-Aqua, the maximum band ratio (MBR) is the ratio of the maximum Rrs of the blue band (λ = 443 nm or λ = 488 nm, depending on which wavelength has the larger Rrs value) to the Rrs of the green band (λ = 547 nm). For VIIRS-SNPP, the MBR is the ratio of the maximum Rrs of the blue band (λ = 443 nm or λ = 486 nm) to the Rrs of the green band (λ = 551 nm). For Himawari-8, the MBR is the ratio of the band at λ = 470 nm to the band at λ = 510 nm (Equation (3)), and the Chl-a products are created by a linear polynomial (Equation (4)) [46]. The ax terms are empirical coefficients of the algorithms (Table 2).

Table 2.
Default coefficients of the Chl-a algorithms of the sensors.
2.4.2. Coefficient Optimization
In this paper, we retained the polynomial form of the OCx algorithm and the Himawari-8 algorithm. The least-squares optimization method was used to adjust the original coefficients of the algorithms [26]. The in situ Chl-a data (Chlin situ) and log10 (MBR) were plugged into the polynomials with the original empirical coefficients as the starting coefficients to improve the original algorithms of the three sensors. Previous studies have shown that the performance of OCx algorithms is not good at low Chl-a concentrations and that systematic deviation exists [20,21,28,34]. In this study, according to the fitting results for the Chl-a data and variation of bias, the in situ data and satellite data were divided into two groups for each sensor (a low-Chl-a concentration group and a high-Chl-a concentration group). Optimization was performed for each group to generate two new algorithms for each sensor.
2.4.3. Blending Windows
The blending windows are the ranges for the application of the algorithms for each sensor. According to the distribution and systematic deviation of each data group, different thresholds were set for the three sensors. In different application ranges, the new algorithms or default algorithms of each sensor were used to generate Chl-a concentration data. Algorithms using blending windows are called blending algorithms [21,28].
2.5. Data Merging
The cross-sensor consistency of data is important for merging the data of multiple satellites [32]. The consistency is measured by the bias between two satellites’ Chl-a data. After consistency validation, the Chl-a products were merged through weighted averages. The weights of the three sensors and each pair of sensors of Chl-a products were calculated by the MAE. MAE is different from bias, and the use of MAE can avoid the impact of an uneven Chl-a data distribution on bias. As the measured criteria of MAE are the same as those for bias, the weight ratio of each satellite’s product in the data merging process depends on the difference value obtained from the subtraction between the MAE of the product and MAE = 1. Grid points with Chl-a data from only one sensor will be filled by these data. The spatial resolution of the merged products is 4 km. In the process of data merging, the products of Himawari-8 were resampled, and a 3 × 3 mean filtering process was performed for the merged data to eliminate abnormal variations in Chl-a data. Figure 2 shows the complete process of algorithm improvement.
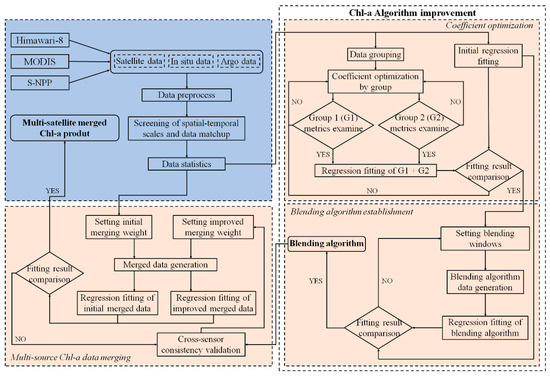
Figure 2.
The flowchart of the algorithm improvement.
3. Results
3.1. Matchups of Chl-a Data
Different matchup processes result in different numbers of pairs between in situ Chl-a data and satellite Chl-a data. The matchup information between in situ data and satellite data was evaluated to select the optimal spatial–temporal combination.
The range of the in situ Chl-a data is from 0.07 to 5.54 mg m−3. The median and mean are 0.32 and 0.48 mg m−3, respectively. For MODIS-Aqua and VIIRS-SNPP, matchup conditions of 5 × 5 pixels and 5 (1 ± 2) days of processing were selected due to their highest match percentages of 68.24% and 67.06%, respectively. The results of the regressions comparing the spectral data and satellite Chl-a data are R2 = 0.9673 and 0.9830 for MODIS-Aqua and VIIRS-SNPP, respectively, showing that this processing method is feasible. For Himawari-8, the method with conditions of 1 × 1 pixel and 1 day processing was selected due to the regression between the spectral data and Himawari-8 Chl-a data (R2 = 0.78) and a match percent of 70.59%. The numbers of matched data points are 60, 58, and 57 for Himawari-8, MODIS-Aqua, and VIIRS-SNPP, respectively (Table 3). The numbers of outliers for MODIS-Aqua, VIIRS-SNPP, and Himawari-8 are 12, 12, and 16, respectively. The distribution of the Chl-a data (without outliers) is shown in Figure 3, which shows the high productivity level in the NPFG.

Table 3.
Summary of in situ data and satellite data matchup results. The selected combinations and the basis of each selection are highlighted in red bold.
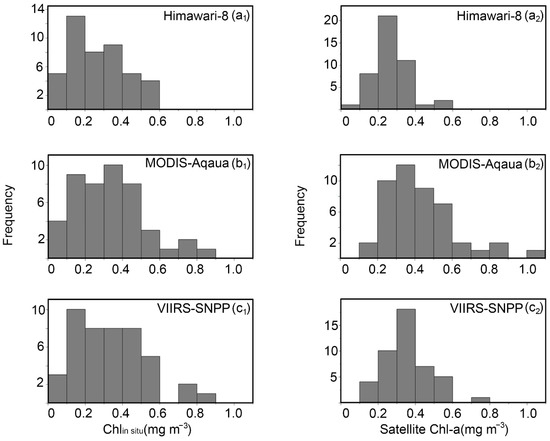
Figure 3.
Frequency distribution histogram of in situ data and satellite data. (a1–c1) show the distribution of in situ data, and (a2–c2) show the distribution of satellite Chl-a data.
The same processes were applied for the Argo Chl-a data. A total of 36, 22, and 33 pairwise data points for Himawari-8, MODIS-Aqua, and VIIRS-SNPP, respectively, were collected for later validation.
3.2. Adjustment of Chl-a Algorithm Coefficients
The linear regression of the default satellite Chl-a products and Chlin situ is shown in Figure 4. The initial fitting results show that the three satellite Chl-a products are not quite accurate in the research area. The performances of the MODIS-Aqua and VIIRS-SNPP Chl-a data are relatively good (R2 = 0.4257 and 0.3362, respectively). The performance of the Himawari-8 Chl-a data is the worst among the three satellites (R2 = 0.0622).
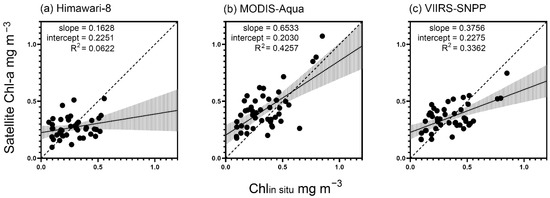
Figure 4.
Fitting results of original remote sensing Chl products and Chlin situ data. (a) Himawari-8, (b) MODIS-Aqua, (c) VIIRS-SNPP. The points are the matched data, the solid line is the slope of each sensor, and the dashed line represents 1:1. The shaded areas show the 95% confidence interval range.
From Figure 4, with an in situ Chl-a concentration = 0.3 mg m−3 as a threshold, the satellite Chl-a data are generally underestimated when the in situ Chl-a concentration > 0.3 mg m−3, and the satellite Chl-a data are generally overestimated when the in situ Chl-a concentration < 0.3 mg m−3. Figure 5 reflects the variation in bias with increasing in situ Chl-a data, including the variations in the total data set and in the data sets grouped by the threshold Chlin situ = 0.3 mg m−3. The variation lines of bias for the total data set (black lines) show a steady and continuous downward trend when the in situ Chl-a concentration > 0.3 mg m−3. Moreover, a steep drop in the red lines (variation lines of bias for grouped data) occurs at an in situ Chl-a concentration of approximately 0.3 mg m−3. Based on the results, the data are divided into two groups for each sensor (a Chlin situ > 0.3 mg m−3 group and a Chlin situ < 0.3 mg m−3 group) in the optimization process.
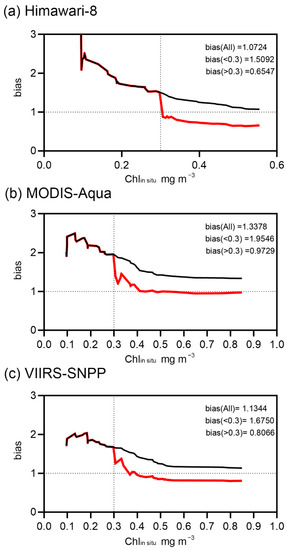
Figure 5.
Bias variation of the three satellites. The black lines are the bias variation for the total data set; the red lines are the bias variation after data grouping based on a 0.3 mg m−3 threshold in situ Chl-a concentration (the red lines of the Chlin situ < 0.3 mg m−3 group are overlapped by the black lines).
For the Chlin situ < 0.3 mg m−3 group, Himawari-8 has 26 matched data points; MODIS-Aqua has 21 matched data points; and VIIRS-SNPP has 21 matched data points. The details of the polynomial improvement are shown in Figure 6(a1–c1). The red line is the improved fitting line, and the black line is the default algorithm line. All red lines are under the black lines from Figure 6(a1–c1), which is consistent with the in situ data.
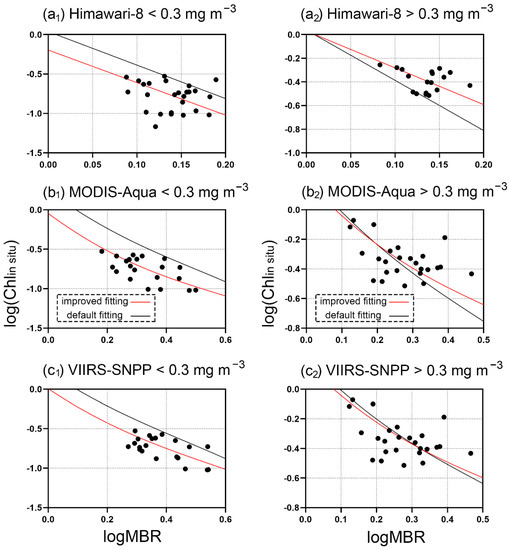
Figure 6.
The default algorithm fitting line (black line) and optimized fitting line (red line) for each sensor. (a1–c1) are the fitting lines of each sensor when the in situ Chl-a concentration > 0.3 mg m−3. The lines of the in situ Chl-a concentration > 0.3 mg m−3 group are shown in (a2–c2).
For the Chlin situ > 0.3 mg m−3 group, Himawari-8 has 18 matched data points, MODIS-Aqua has 25 matched data points, and VIIRS-SNPP has 24 matched data points. The adjusted results for the polynomials are shown in Figure 6(a2–c2). The adjustment of Himawari-8 is obvious, and the red line is above the black line. For MODIS-Aqua and VIIRS-SNPP, the trend of the line is mildly adjusted.
The new coefficients of the Chl-a algorithms are shown in Table 4. Each sensor has two algorithms for the different data groups. To avoid overfitting, the coefficients a3 and a4 of MODIS-Aqua and VIIRS-SNPP in the Chlin situ > 0.3 mg m−3 group are the default coefficients because of the small sample sizes of matchup data. The default coefficient a4 of MODIS-Aqua in the Chlin situ < 0.3 mg m−3 group is retained for the same reason.

Table 4.
New coefficients of the algorithms of the three sensors based on a 0.3 mg m−3 threshold Chl-a concentration dividing the two groups.
3.3. Performance of Improved Chl-a Algorithms
New Chl-a products of the three sensors are created by the improved algorithms. The means, biases, and MAEs of the new Chl-a products of the three sensors were calculated for comparison with the default Chl-a products (Table 5). From Table 5, the improvements in the two groups of data are obvious for each sensor: relative to the initial values, the means are all closer to the in situ means, and the biases and MAEs are closer to 1. The improvement in Himawari-8 is excellent for both data groups (the bias changes from 1.5092 to 1.0382 for the Chlin situ < 0.3 mg m−3 group and from 0.6547 to 1.0000 for Chlin situ > 0.3 mg m−3 group). The systematic deviation in the MODIS-Aqua and VIIRS-SNPP data was significantly reduced after optimization for the group of in situ Chl-a concentration < 0.3 mg m−3 (the MODIS-Aqua bias changed from 1.9545 to 1.0058; the VIIRS-SNPP bias changed from 1.6750 to 1.0589). For the in situ Chl-a concentration > 0.3 mg m−3 group, the systematic deviation of the two satellites also slightly improved (the MODIS-Aqua bias changed from 0.9729 to 0.9999; the VIIRS-SNPP bias changed from 0.8066 to 0.8668).

Table 5.
Systematic deviation metrics of satellite data before and after algorithm improvement, based on a 0.3 mg m−3 chlorophyll-a concentration as the threshold. “All” means the total matched data set.
Table 6 shows the improvement of the linear regression in terms of statistical variables. The R2, slope, and intercept of each sensor have significant improvements, especially for Himawari-8. These statistical data preliminarily prove the effectiveness of the improved grouping-based optimization method. Chl-a data samples for each sensor were generated for comparison between the default algorithms and two improved algorithms for each sensor (Figure 7). The results show clearly different distributions of Chl-a data: the Chl-a concentration values of the Chlin situ > 0.3 mg m−3 group increase significantly, while the changes in the Chlin situ < 0.3 mg m−3 group are smaller but still noticeable.

Table 6.
Metrics of the linear regression of Chlin situ data and satellite Chl-a data before and after algorithm improvement.
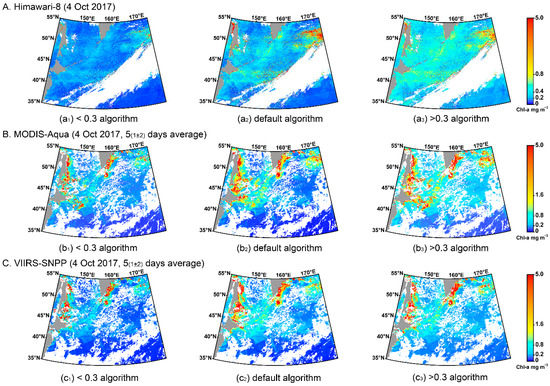
Figure 7.
Sample satellite images. (a1–a3) are Himawari-8 Chl-a data; (b1–b3) are MODIS-Aqua Chl-a data; (c1–c3) are VIIRS-SNPP Chl-a data. The images in the first column are drawn by the algorithms for the in situ Chl-a concentration < 0.3 mg m−3 group for each sensor; the images in the second column are drawn by the default algorithms; the images in the third column are drawn by the in situ Chl-a concentration > 0.3 mg m−3 group algorithms.
3.4. Establishment of Chl-a Blending Algorithm
The improved algorithms are based on optimization by data groups. Next, we integrated different algorithms to propose a blending algorithm similar to the OCI algorithm [20]. In this study, we selected the default algorithms as the transition between the two improved algorithms for each sensor and set blending windows for the transitions.
The blending windows were set according to the application scopes of the different algorithms (Table 7). Chl-a concentrations from 0.2 mg m−3 to 0.3 mg m−3 generated by the default algorithm are retained for Himawari-8 because the NPFG is a relatively productive area and the default Chl-a product of Himawari-8 is underestimated in the group of in situ Chl-a concentration > 0.3 mg m−3. For MODIS-Aqua, overestimation is obvious in the Chlin situ < 0.3 mg m−3 group, and underestimation in the Chlin situ > 0.3 mg m−3 group is not significant. Considering the mean values before improvement of the two MODIS-Aqua groups (0.3622 mg m−3 and 0.4803 mg m−3), Chl-a concentrations from 0.35 mg m−3 to 0.45 mg m−3 were selected as the application scope for the MODIS-Aqua default algorithm. For VIIRS-SNPP, overestimation also occurs in the Chlin situ < 0.3 mg m−3 group. In view of the small improvement in the Chlin situ > 0.3 mg m−3 group and the mean values of the two VIIRS-SNPP groups (0.3141 mg m−3 and 0.3958 mg m−3), the thresholds of VIIRS-SNPP were set as 0.3 mg m−3 and 0.4 mg m−3 for the default algorithm in the final products. The blending algorithms, OCNP algorithms for MODIS-Aqua and VIIRS-SNPP, and the H8-ChlNP algorithm for Himawari-8, were established after the blending windows had been determined.

Table 7.
Blending windows of different algorithms for each sensor. The interval is the Chl-a concentration in the final product.
Figure 8 shows the linear regression of the in situ data and blending algorithm data. From Figure 8, the R2, slope, and intercept of the blending algorithms are slightly worse than the results of the two new algorithms but better than the results of the default algorithms (Table 6). The result of the H8-ChlNP algorithm shows substantial improvement, and the MODIS-Aqua OCNP algorithm has the best-fitting performance among the three sensors. Table 8 shows the systematic deviation of the blending algorithms. Except for the means of Himawari-8 and VIIRS-SNPP, which deviate slightly, the biases and MAEs are significantly improved. Figure 9 presents samples of the final products of each satellite based on the blending algorithms; the original data are the same as those in Figure 7. The products are generated by the blending algorithms of each sensor, which inherit the advantages of the improved algorithms and prevent excessive variation of the data.
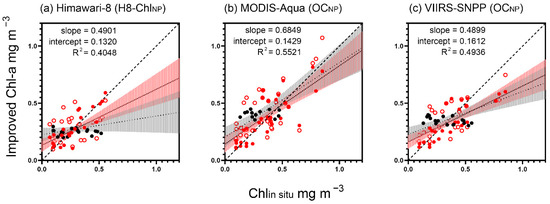
Figure 8.
Linear regression of in situ data and blending algorithm data. The black points are the data retained from the default algorithms. The red hollow points are the default match data, and the red solid points are the improved data. The black line is the optimized slope. The thick dashed line is x = y. The thin dashed line is the default algorithm line. The red shaded areas show the 95% confidence interval range of blending algorithms; the black shaded areas show the 95% confidence interval range of default algorithms.

Table 8.
Systematic deviation metrics of satellite Chl-a data before improvement and data based on blending algorithms. “M” stands for MODIS-Aqua; “V” is VIIRS-SNPP.
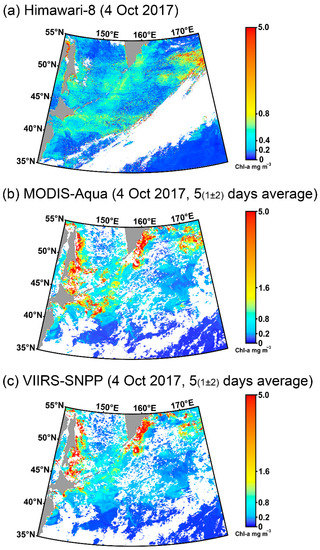
Figure 9.
Sample images of the blending algorithms. Figures (a–c) correspond to Himawari-8, MODIS-Aqua, and VIIRS-SNPP, respectively.
3.5. Merged Data of Himawari-8, MODIS-Aqua, and VIIRS-SNPP
The biases between sensor data sets were calculated to measure the consistency of the three sensors’ data (Table 9). The results show that the biases are all closer to 1 than the initial values, illustrating that the consistency of the three sensors was improved. Therefore, we sought to integrate the final products from the three sensors and chose the weighted average method.

Table 9.
Cross-consistency between sensors calculated by the bias before and after algorithm improvement.
The weights of the sensors are shown in Table 10 and are based on the MAEs in Table 8. The weights of the default algorithms were calculated for further validation. According to the MAE values of the blending algorithms, the weights changed compared to those of the default algorithms. The matched Argo data for the three sensors were used to validate the improvement in the merged data based on the blending algorithms with respect to the default algorithms. The linear regression of the Argo data and merged data is shown in Figure 10. The improvement in the merged data based on the blending algorithms is relatively significant compared with the values for the default algorithms (R2 changed from 0.2162 to 0.5186). Figure 10 also shows the variation of difference values between merged data and Argo data with the collection time. The result shows that the Chl-a data and dispersion degree have significant improvement, but for long-term variation, we still need more in situ data to study.

Table 10.
Weights of satellites in the data merging process. The weights of three satellites are used when all three satellites have data in the same location; the weights of two satellites are used when only two satellites have data in a location.
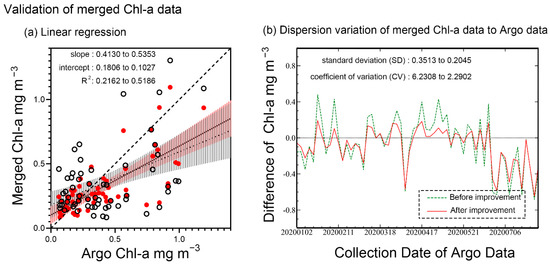
Figure 10.
Validation of merged Chl-a data. (a) Linear regression of Argo data and merged data. The black hollow points are the default matched data, and the red solid points are the data based on the blending algorithms. The thick dashed line is x = y. The thin dashed line is the default algorithm merged data line. The black line is the improved fitting line. (b) The variation of difference value between merged data and Argo data with the collection time. The green dashed line is variation of the merged data before improvement. The red line is the variation of improved merged data.
Table 11 shows the systematic deviation of the merged data. The Argo data were divided into two groups based on the threshold Argo Chl-a concentration (ChlArgo) = 0.3 mg m−3 to illustrate the improvement. Although the mean and bias of the total Argo data are slightly worse, the MAE is better than before. The two groups of data also show improvements in the merged data generated by the blending algorithms.

Table 11.
Systematic deviation of the Argo data. “All” indicates the total Argo data; “>0.3” and “<0.3” indicate the group data based on a threshold ChlArgo concentration = 0.3 mg m−3.
Figure 11 shows the monthly Chl-a data from the three satellites and the resulting merged Chl-a data. The data coverage was significantly improved. The variation trend of the data was mitigated, and the accuracy improved. The data are from the August 2019 monthly data of the three satellites.
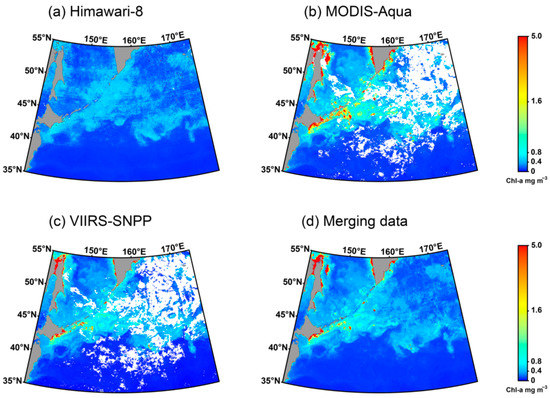
Figure 11.
Comparison of single-sensor monthly data and monthly merged data based on blending algorithms. The data are the August 2019 monthly data of the three sensors.
4. Discussion
4.1. Comparison of the Chl-a Products of Himawari-8, MODIS-Aqua, and VIIRS-SNPP
As a geostationary orbit satellite with a high temporal frequency, Himawari-8 has a large amount of data on the NPFG. From Table 3, the highest match percent of the in situ data to Chl-a products reflects the high spatial coverage and temporal resolution of Himawari-8 in the research area. MODIS-Aqua and VIIRS-SNPP are polar-orbit satellites, and their operating characteristics lead to a relatively low monitoring frequency and coverage of the NPFG. However, Himawari-8 is a meteorological satellite with only three spectral bands in the visible band and one in the near-infrared band, which cover the small spectral band range used for Chl-a retrieval [46]. Both MODIS-Aqua and VIIRS-SNPP have nine bands in the visible and near-infrared band ranges. Therefore, MODIS-Aqua and VIIRS-SNPP have better spectral band and wavelength options for Chl-a retrieval. In addition, different satellite orbits, zenith angles, azimuth angles, and other observation parameters lead to different accuracies of satellite retrieval results.
Furthermore, with differences in the spectral bands, the Chl-a retrieval algorithms are different. The Chl-a products of Himawari-8 are generated through a linear polynomial [46], while MODIS-Aqua and VIIRS-SNPP use OCx algorithms and quartic polynomials to generate Chl-a products. Different algorithm models will cause different responses of the inversion Chl-a concentration to the spectral data, which may also lead to the low accuracy of Himawari-8 Chl-a data. It is noteworthy that the NASA ocean color website provides two types of Chl-a products: one is generated by OCx algorithms, and the other is generated by OCI algorithms. The OCI algorithms are blending algorithms of OCx and CI algorithms, with Chl-a concentration = 0.15 mg m−3 as the product threshold [20]. The NPFG is a relatively productive area. From the distribution of the in situ data and corresponding remote sensing data, the Chl-a concentrations of most data points are greater than 0.15 mg m−3 (Figure 3). Therefore, Chlocx products are used as the data source in this paper instead of ChlOCI products. However, the current approach does not preclude the use of OCI algorithms in future research.
Thus, differences in the characteristics of satellites and in the Chl-a retrieval algorithms will cause differences in Chl-a products. Himawari-8 Chl-a data have a higher temporal frequency in observations and coverage of the NPFG than MODIS-Aqua and VIIRS-SNPP data. The Chl-a products of MODIS-Aqua and VIIRS-SNPP are more accurate but less spatiotemporally continuous in the NPFG.
4.2. Evaluation of Chl-a Algorithm Coefficient Optimization
In the initial process of algorithm optimization, all of the in situ data were plugged into the default algorithms to adjust the coefficients. However, the Chl-a products generated by the first improved algorithms are even worse than the default satellite Chl-a products. The results of linear regression between Chlin situ and the first improved satellite Chl-a products showed that the slope (Himawari-8 slope = 0.0984, MODIS-Aqua slope = 0.3600, VIIRS-SNPP slope = 0.3199) was smaller than those for the Chlin situ and default Chl-a products (Himawari-8 slope = 0.1628, MODIS-Aqua slope = 0.6533, VIIRS-SNPP slope = 0.3756), although R2 slightly improved.
A study has shown that OCx algorithms have 15% systematic underestimation in the Pacific Ocean [22]. Our research finds that the OCx algorithms of MODIS-Aqua and VIIRS-SNPP exhibit systematic overestimation in the NPFG, especially at low Chl-a concentrations; similarly, the OCx algorithms exhibit systematic underestimation at high Chl-a concentrations. The same results were also reflected in the Himawari-8 Chl-a data (Figure 5). Researchers have found that the performance of OCx algorithms is unsatisfactory at low Chl-a concentrations [20,21,28]. Kahru et al. found a difference in deviation in different Chl-a concentration ranges, and the first and last 25% of the data were taken to improve the algorithms in their study [34]. Considering both our results and previous studies, we decided to select an in situ Chl-a concentration of 0.3 mg m−3 as the general dividing threshold for data grouping to better distinguish the systematic deviation of satellite Chl-a data. Subsequent optimization was carried out using different data groups.
Table 5 and Table 6 show the huge improvements in the fitting results and systematic deviation for the Chl-a data from the three satellites after grouped coefficient optimization. Compared with the other two satellites, the fitting results of the improved algorithms for Himawari-8 show the greatest improvement relative to the original fitting results. The huge improvements obtained with the grouping algorithms show the effectiveness of such grouping for Himawari-8. Another reason for the improvements for Himawari-8 may be the linear polynomial algorithm, which is used to generate the Chl-a products. The linear polynomial is sensitive to changes in coefficients, and small samples of data may amplify these changes. The ChlOCx products of MODIS-Aqua have the best original fitting performance relative to the in situ Chl-a data, but the maximum deviation occurs in the group of in situ Chl-a concentration < 0.3 mg m−3 (bias = 1.9546). The same problem occurs in VIIRS-SNPP (bias = 1.6750). Possible reasons for the problem may be that OCx algorithms are more responsive to changes in Chl-specific backscatter and nonphytoplankton absorption [21], and the complex marine environment of the NPFG makes this response more intense. The systematic deviation of the in situ Chl-a concentration > 0.3 mg m−3 group is relatively insignificant for MODIS-Aqua (bias = 0.9729, MAE = 1.3175) and VIIRS-SNPP (bias = 0.8066, MAE = 1.3658). From the overall improvement results for MODIS-Aqua and VIIRS-SNPP, the improvement of VIIRS-SNPP Chl-a products is smaller than that of MODIS-Aqua products. The main reason for this may be the small sample of in situ data, which is not evenly distributed across the Chl-a concentration range in the NPFG, resulting in the improved algorithms having to retain some original coefficients to avoid large deviation of the improved algorithm in the concentration ranges where samples are deficient. The characteristics of the sensors and spectral bands used for Chl-a retrieval may also be factors [47].
Although the optimization results validate the effectiveness of grouping based on the threshold Chlin situ = 0.3 mg m−3, this threshold of data grouping is not absolute, especially for MODIS-Aqua and VIIRS-SNPP. From Figure 5, the grouping thresholds of MODIS-Aqua and VIIRS-SNPP can be even higher than 0.3 mg m−3. However, based on the small samples of in situ data, an in situ Chl-a concentration of 0.3 mg m−3 was selected as a cutoff for data grouping in this study. More in situ data are key to further verifying the grouping threshold of each satellite and improving the performance of algorithms in the NPFG. It is worth noting that large samples of data may mask the grouping trend [34]. In future research, algorithm optimization will not be limited to existing empirical algorithms, and the bio-optical models, machine learning, and artificial neural networks can also be used in the study of ocean color [33,48,49].
4.3. Influence of Chl-a Algorithm Blending Method
Grouping coefficient optimization leads to different ranges of Chl-a data for algorithm application. To integrate different algorithms for application, a suitable blending method is important. We started with the products of the two improved algorithms, integrating the two types of Chl-a data by averaging or based on a cutoff Chl-a concentration. Figure 12 is an example of Himawari-8 Chl-a retrieval algorithm blending. The Chl-a concentration data estimated by the improved algorithms of different data groups covers the whole research area, including the region where the distribution of the Chl-a concentration range is not suitable for the improved algorithm, generating error estimates of Chl-a concentration (Figure 7). Therefore, the average of two types of Chl-a concentration data generated by improved algorithms may result in greater deviation; when the two types of Chl-a products are split according to a cutoff value, the final Chl-a concentration product will show a sudden variation. Considering the distribution of Chl-a data and the method used to improve the algorithms, it is not feasible to directly blend the final products generated by the two algorithms for each sensor. In this study, the default algorithms are the basis of the two groups of improved algorithms. The polynomial form of the improved algorithms is not changed, which is different from OCI algorithms, which combine CI and OCx algorithms [20]. Therefore, the default algorithms were chosen to provide a transition between the two types of new algorithms to generate blending algorithms. The blending window can be used as a transition between algorithms to ensure a smooth variation of data and make full use of the advantages of different algorithms [20,21,28]. The size of the blending window in this paper is based on the distribution and systematic deviation of satellite Chl-a data.
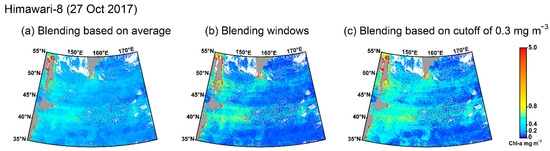
Figure 12.
Example of Himawari-8 Chl-a retrieval algorithm blending. (a) is based on the averaging of Chl-a data generated by the two improved algorithms; (b) uses blending windows; (c) uses a cutoff of Chl-a = 0.3 mg m−3 to blend the two improved algorithms.
The satellite Chl-a product accuracy goal in the open ocean is ±35%, which is generally considered acceptable by international missions [12]. Although the OCNP algorithms and the H8-ChlNP algorithm in this study satisfactorily meet this goal, the results of the OCNP algorithms and the H8-ChlNP algorithm are slightly worse than the results using the improved algorithms alone. The retention of data from the default algorithms in the blending windows are the main reason for the difference in results. Therefore, more in situ data are necessary for further blending window optimization.
4.4. Variation of NPFG and Kuroshio Extension Represented by the Merged Chl-a Data
Different ocean color sensors exhibit inconsistencies due to differences in discontinuities, calibration strategies, wavelengths, bandwidths, atmospheric correction, and data processing [28,31,32,50]. The lower the inconsistency between sensors is, the higher the complementarity between different sensors’ data. Higher cross-sensor consistency can allow data from two sensors to complement one another when a sensor ends its mission cycle, ensuring data continuity. Higher cross-sensor consistency is also the basis for sensor data merging [32]. In this paper, we tried to improve the consistency through the same in situ set. Figure 10 and Figure 11 show the advantages of merging data: more accuracy and high coverage. Additionally, the merged data integrate the advantages of each satellite data and alleviate the problem that the algorithm improvement may not be comprehensive enough due to the small in situ data sample size. Although the systematic deviation slightly fluctuates because of the small samples of Argo data, the merged data reflect the improvement obtained with the blending algorithms and the efficiency of the merging method.
As an important marine indicator of the primary productivity in the ocean, Chl-a concentration could reflect the nutrient status and feed distribution, which further affects the distribution of fishery resources [2,35]. The Pacific saury is one of the primary pelagic economic species in the NPFG, which is a highly migratory species distributed around the Kuroshio–Oyashio area with the optimal 15~18 °C water temperature [51]. They have different spawned cohorts, and mainly spawn and overwinter in the Kuroshio warmer water during winter and early spring. In the summer, the Pacific saury migrates to the Oyashio colder water for feeding and nursery [35]. The optimal temperature and food are the main driver for the north–south migration of Pacific saury, even associated with the long-term abundance variations of the population [2,52]. Therefore, the distribution of Pacific saury is not fixed, and the fishing operation sites could reflect the distribution of fish habitats and migration routes, further representing the changes in the fishing ground [53].
As the main source of influencing SST and nutrients in the NPFG, the Kuroshio and Oyashio currents and Kuroshio extension have huge impacts on marine climates and oceanographic elements of the NPFG [3,41]. The variation of Kuroshio extension itself and the influence on fish population have been widely concerned about in the NPFG. SST was used as the representation of the Kuroshio extension sphere in this paper. SST data and consistent merged Chl-a data are shown in Figure 13A with isotherms, and the threshold is set to 18 °C consistent with the max optimal temperature of Pacific saury (monthly data of August 2017). Figure 13A shows that the variation in Chl-a concentration is consistent with the SST isotherms, and the concentration of Chl-a data shows a certain stratification trend in different SST ranges, reflecting the influence intensity and range of the Kuroshio Current [3]. SST and the nutriment carried by Oyashio Current are the main factors affecting the variations of plankton, which determine Chl-a concentration [6,41]. Therefore, accurate Chl-a data could also be used to indicate the variation of Kuroshio extension.
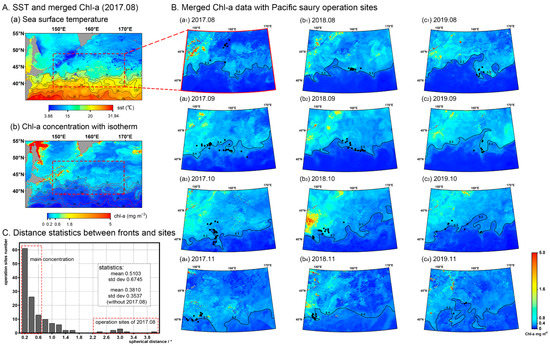
Figure 13.
(A) Comparison of Kuroshio extension (represented by SST) and merged Chl-a variation (monthly data of August 2017). (B) Monthly merged products of three satellites’ data with Pacific saury operation sites. The solid lines are the isoconcentrate lines of Chl-a. (a1–a4) are from August 2017 to November 2017; (b1–b4) are from August 2018 to November 2018; (c1–c4) are from August 2019 to November 2019. (C) Histogram of spherical distance statistics between Chl-a fronts and operation sites.
The distribution of Pacific saury fishing operation sites in 2017~2019 and the variation in Chl-a merged data by month are shown in Figure 13B. The fishing ground changed with variation in Chl-a concentration and was mainly clustered in the Chl-a concentration front, according to the merged data. From the merged Chl-a data and fishing operation sites, the Chl-a concentration fronts were 0.3~0.4 mg m−3, which were consistent with 18 °C SST front and also accord with the optimal temperature of Pacific saury in Figure 13A. Figure 13C shows that the operation sites are mainly concentrated within 0.5° spherical distance. The season habitat scales changed with the Chl-a fronts and the results could further explain the conclusions of Tseng et al. [51] that the SST front overlapped with fishing operation sites and high catch per unit effort (CPUE) during the fishing seasons from September to December. As for the part of fishing operation site that was not close to the Chl-a front in August 2017, the main reason was that the vessel was trying to escape the gale. Additionally, the variation in SST is not dramatic beyond the Kuroshio extension region where SST is suitable for phytoplankton and Pacific saury, and the Oyashio Current and related marine bio-geochemical processes predominantly influence Chl-a distribution, which further affect the distribution of Pacific saury in Oyashio water [6,8,54].
As the main indicator of plankton in the ocean, Chl-a data is a primary environmental factor for studying Pacific saury fishing grounds, migration and life history, and establishing related fishery models [2,51,55]. Additionally, Chl-a data could also be an indicator for the variation in Kuroshio extension, resulting in mutual verification when combined with oceanographic environmental factors. The integrity of merged Chl-a data with varying temporal and spatial characteristics can provide excellent support for related oceanographic research and fishery resource assessment, which can guide fishing operation and pelagic fishery in the NPFG.
4.5. Reflection of Mesoscale Eddies in Merged Chl-a Data
Mesoscale eddies are ubiquitous phenomena in the ocean which play important roles in global ocean heat budget and ecological and bio-geochemical processes through their contributions to water and vertical nutrient transport and alteration of the underwater light field [4,56]. Therefore, mesoscale eddies should exert a strong influence on Chl-a redistribution and ecosystem balance [39,57]. The convergence of Kuroshio Current and Oyashio Current makes the NPFG one of the largest eddy kinetic energy region in the world [3]. Eddy pumping should result in higher (lower) Chl-a concentration within the eddy center for a cyclone (anticyclone), which is also called warm eddy (cold eddy) in the ocean; further, wind and the features of currents would also have an impact on eddies [3,56].
The mesoscale eddies could be reflected through SLA. Figure 14a shows SLA data (monthly data of August 2017, the consistent merged Chl-a data is shown in Figure 13A). The mesoscale eddies are circled based on SLA data, for which 0.2 m and −0.1 m are defined as boundaries of warm eddies and cold eddies [56]. Figure 14b calculates the average Chl-a concentration and the percentage difference of eddy center and periphery. The results show the variation in Chl-a concentration with the eddies, demonstrating a negative correlation between SLA and Chl-a concentration in the Kuroshio extension region but a positive correlation in the Oyashio area (Figure 14b), which are consistent with the features of currents and warm eddies and cold eddies [39]. Although the variation in Chl-a concentration deviation exists in some eddy ranges for the low resolution of data and effect of other marine processes in some eddy scales, the merged Chl-a data can accurately reflect the existence and influence of eddies and abnormal sea surface height; this information can be successfully applied to the exploration of mesoscale eddies mechanisms and used to quantify their influence on the Chl-a concentration [57]. Additionally, as shown in Figure 13 and Figure 14, in the mesoscale eddies, especially warm eddies, the different characteristics (high Chl-a concentration in the eddy center or low Chl-a concentration in eddy center, and opposite distribution of Chl-a concentration in eddy periphery) exist in Kuroshio extension range. The main reason of this phenomenon is the interaction of the Oyashio and Kuroshio currents, upwelling, and different properties of water mass which affect the distribution of Chl-a concentration in the eddies [39]. Therefore, the characteristics of the distribution of Chl-a concentration in mesoscale eddies could also be used to describe the range of the Kuroshio extension.
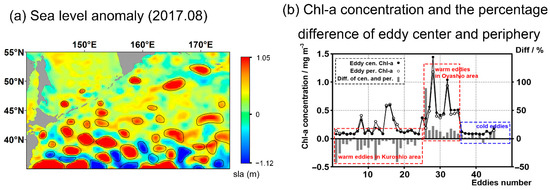
Figure 14.
The mesoscale eddies (circled based on SLA data, monthly data of August 2017) and the differences statistics of Chl-a concentration of eddy center and periphery.
4.6. Responses of Merged Chl-a Data to ENSO
ENSO is a naturally occurring anomalous state of tropical Pacific coupled ocean-atmosphere conditions, which is a primary driver of global climate modulations and can persist over several seasons and thereby produce severe regional effects [44]. ENSO would cause anomalies such as the SST, sea level pressure, and surface wind, which means abnormal changes of the SST, currents, and wind would occur during ENSO [44,58]. As an indicator of phytoplankton, Chl-a concentration is sensitive to changes of marine environment, especially SST, and marine current and wind could also affect the distribution [3,40]. Based on MEI, merged Chl-a data in different ENSO states was used to calculate the differences of Chl-a concentration after improvement, and the pixels of the Chl-a differences in different ENSO states and the improvement were recorded, the outliers of which were removed through the 95% confidence interval to reduce the error (Figure 15). For the Chl-a data before improvement, Figure 15 shows that the underestimation of Chl-a concentration mainly occurs at high latitudes, and overestimation occurs at low latitudes. The results might be related to different properties of water masses and the interaction with the Kuroshio or Oyashio intrusion, which causes the algorithms to fail to estimate Chl-a concentration accurately in areas with different optical properties. Meanwhile, the underestimation of Chl-a during El Niño is more obvious than neutral than in La Niña periods outside the Kuroshio extension region; the overestimation of Chl-a during La Niña is more obvious in the NPFG.
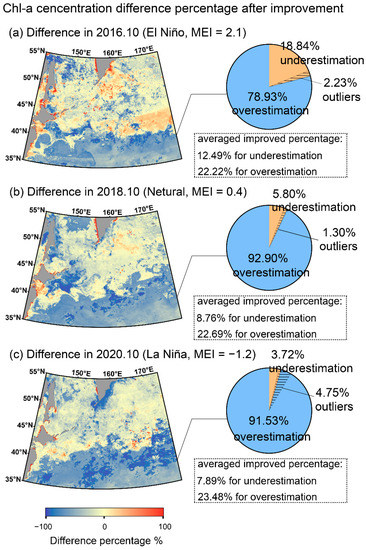
Figure 15.
The differences of merged Chl-a data in different ENSO states compared with the satellite Chl-a data before improvement. (a–c) are the differences of Chl-a data after improvement and the pie chart of pixel statistics.
The differences show that the responses of merged Chl-a data are more accurate and sensitive to marine climatic changes and correspond with the trend of 1997–1998 and 2015–2016 El Niño events [8,50]. Although the relatively short time series and large interannual variability of Chl-a data would confound long-term climate change-driven trends which rely on decadal variation trends for detection [11,59], the merged Chl-a data could aid prompt responses to short-term marine climate anomalies and better distinguish climate anomalies caused by ENSO with the assistance of SST, current, and wind data [58]. The more-accurate Chl-a data with high-coverage characteristics can also be the basis for long-term climate change and marine phenomena studies [5,6,10].
5. Conclusions
The NPFG is an important area linked with global ecology and climate change. As an important basic indicator of marine features, the accuracy of Chl-a data has a significant impact on many oceanographic studies. This paper compares and evaluates the performance of Himawari-8, MODIS-Aqua, and VIIRS-SNPP Chl-a data in the NPFG. We established the H8-ChlNP algorithm for Himawari-8 and OCNP algorithms for MODIS-Aqua and VIIRS-SNPP. The accuracy improved by 3.11%, 19.76%, and 11.86%, respectively. The weighted average method was used for data merging, and the merged data with high coverage accurately reflected the relationship between the distribution of the fishing ground and Chl-a concentration. The high-quality merged Chl-a data could provide excellent support for fisheries and has shown consistent variation with mesoscale eddies and Kuroshio extension. Furthermore, based on MEI, merged Chl-a data have different responses to ENSO states, demonstrating a maximum 16.41% difference of Chl-a data distribution. Future work will collect more in situ data for additional validation and optimization to improve the accuracy and methods for Chl-a concentration retrieval and merging, which can be combined with marine environmental data for further analysis of these marine phenomena.
Author Contributions
Data collection, C.H., Y.Z. (Yunyun Zhuang), Y.Z. (Yong Zhang), X.L. and Y.W.; data process and analysis, C.H., Y.L. (Yang Liu), Y.L. (Yanping Luo) and Y.W.; writing—original draft preparation, C.H.; writing—review and editing, Y.L. (Yang Liu) and Y.W.; supervision, Y.L. (Yang Liu) and Y.T.; funding acquisition, Y.L. (Yang Liu). All authors have read and agreed to the published version of the manuscript.
Funding
This study was supported by the Shandong Key R&D Program (No. 2019GHY112014) and the Fundamental Research Funds for the Central Universities (No. 201762015).
Data Availability Statement
The data presented in this study are available in this article.
Acknowledgments
The authors thank NASA (National Aeronautics and Space Administration) for freely providing satellite chlorophyll data for MODIS-Aqua and VIIRS-SNPP. The research product of chlorophyll data that was used in this paper was supplied by the P-Tree System, Japan Aerospace Exploration Agency (JAXA). The authors thank Zhongtai Ocean Fishery Co., Ltd. for its support with the survey. Argo data chlorophyll were collected and made freely available by the International Argo Program and the national programs that contribute to it. The Argo Program is part of the Global Ocean Observing System. The authors thank the Copernicus Marine and Environment Monitoring Service (CMEMS) for providing Sea level anomaly data. The authors are grateful to the anonymous reviewers for their constructive comments and helpful suggestions for improving the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- FAO. FAO Yearbook. Fishery and Aquaculture Statistics 2017; FAO: Rome, Italy, 2019. [Google Scholar]
- Yasuda, I.; Watanabe, T. Chlorophyll a variation in the Kuroshio Extension revealed with a mixed-layer tracking float: Implication on the long-term change of Pacific saury (Cololabis saira). Fish. Oceanogr. 2007, 16, 482–488. [Google Scholar] [CrossRef]
- Wang, Y.; Tang, R.; Yu, Y.; Ji, F. Variability in the Sea Surface Temperature Gradient and Its Impacts on Chlorophyll-a Concentration in the Kuroshio Extension. Remote Sens. 2021, 13, 888. [Google Scholar] [CrossRef]
- Zhou, J.; Zhou, G.; Liu, H.; Li, Z.; Cheng, X. Mesoscale Eddy-Induced Ocean Dynamic and Thermodynamic Anomalies in the North Pacific. Front. Mar. Sci. 2021, 8, 756918. [Google Scholar] [CrossRef]
- Messié, M.; Radenac, M.H.; Lefèvre, J.; Marchesiello, P. Chlorophyll bloom in the western Pacific at the end of the 1997–1998 El Niño: The role of the Kiribati Islands. Geophys. Res. Lett. 2006, 33, L14601. [Google Scholar] [CrossRef] [Green Version]
- Yatsu, A.; Chiba, S.; Yamanaka, Y.; Ito, S.-I.; Shimizu, Y.; Kaeriyama, M.; Watanabe, Y. Climate forcing and the Kuroshio/Oyashio ecosystem. ICES J. Mar. Sci. 2013, 70, 922–933. [Google Scholar] [CrossRef] [Green Version]
- Behrenfeld, M.J.; O’Malley, R.T.; Siegel, D.A.; McClain, C.R.; Sarmiento, J.L.; Feldman, G.C.; Milligan, A.J.; Falkowski, P.G.; Letelier, R.M.; Boss, E.S. Climate-driven trends in contemporary ocean productivity. Nature 2006, 444, 752–755. [Google Scholar] [CrossRef] [PubMed]
- Boyce, D.G.; Lewis, M.R.; Worm, B. Global phytoplankton decline over the past century. Nature 2010, 466, 591–596. [Google Scholar] [CrossRef] [PubMed]
- Chavez, F.P.; Strutton, P.G.; Friederich, G.E.; Feely, R.A.; Feldman, G.C.; Foley, D.G.; McPhaden, M.J. Biological and Chemical Response of the Equatorial Pacific Ocean to the 1997–98 El Nino. Science 1999, 286, 2126–2131. [Google Scholar] [CrossRef] [PubMed]
- Chavez, F.P.; Ryan, J.; Lluch-Cota, S.E.; Niquen, C.M. From anchovies to sardines and back: Multidecadal change in the Pacific Ocean. Science 2003, 299, 217–221. [Google Scholar] [CrossRef] [Green Version]
- Dutkiewicz, S.; Hickman, A.E.; Jahn, O.; Henson, S.; Beaulieu, C.; Monier, E. Ocean colour signature of climate change. Nat. Commun. 2019, 10, 578. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- McClain, C.R. A decade of satellite ocean color observations. Annu. Rev. Mar. Sci. 2009, 1, 19–42. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Blondeau-Patissier, D.; Gower, J.F.R.; Dekker, A.G.; Phinn, S.R.; Brando, V.E. A review of ocean color remote sensing methods and statistical techniques for the detection, mapping and analysis of phytoplankton blooms in coastal and open oceans. Prog. Oceanogr. 2014, 123, 123–144. [Google Scholar] [CrossRef] [Green Version]
- Groom, S.; Sathyendranath, S.; Ban, Y.; Bernard, S.; Brewin, R.; Brotas, V.; Brockmann, C.; Chauhan, P.; Choi, J.-K.; Chuprin, A.; et al. Satellite Ocean Colour: Current Status and Future Perspective. Front. Mar. Sci. 2019, 6, 485. [Google Scholar] [CrossRef] [Green Version]
- Werdell, P.J.; McClain, C.R. Satellite Remote Sensing: Ocean Color. In Encyclopedia of Ocean Sciences; Elsevier: Amsterdam, The Netherlands, 2019; pp. 443–455. [Google Scholar]
- O’Reilly, J.E.; Maritorena, S.; Mitchell, B.G.; Siegel, D.A.; Carder, K.L.; Garver, S.A.; Kahru, M.; McClain, C. Ocean color chlorophyll algorithms for SeaWiFS. J. Geophys. Res. Ocean. 1998, 103, 24937–24953. [Google Scholar] [CrossRef] [Green Version]
- O’Reilly, J.E.; Maritorena, S.; O’Brien, M.C.; Siegel, D.A.; Toole, D.; Menzies, D.; Smith, R.C.; Mueller, J.L.; Mitchell, B.G.; Kahru, M.; et al. SeaWiFS Postlaunch Calibration and Validation Analyses, Part 3; NASA Tech. Memo. Seawifs Postlaunch; NASA: Washington, DC, USA, 2000; Volume 11.
- Dierssen, H.M. Perspectives on empirical approaches for ocean color remote sensing of chlorophyll in a changing climate. Proc. Natl. Acad. Sci. USA 2010, 107, 17073–17078. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- O’Reilly, J.E.; Werdell, P.J. Chlorophyll Algorithms for Ocean Color Sensors-Oc4, Oc5 & Oc6. Remote Sens. Environ. 2019, 229, 32–47. [Google Scholar] [CrossRef] [PubMed]
- Hu, C.; Lee, Z.; Franz, B. Chlorophyll a algorithms for oligotrophic oceans: A novel approach based on three-band reflectance difference. J. Geophys. Res. Ocean. 2012, 117, C01011. [Google Scholar] [CrossRef] [Green Version]
- Hu, C.; Feng, L.; Lee, Z.; Franz, B.A.; Bailey, S.W.; Werdell, P.J.; Proctor, C.W. Improving Satellite Global Chlorophyll a Data Products Through Algorithm Refinement and Data Recovery. J. Geophys. Res. Ocean. 2019, 124, 1524–1543. [Google Scholar] [CrossRef]
- Szeto, M.; Werdell, P.J.; Moore, T.S.; Campbell, J.W. Are the world’s oceans optically different? J. Geophys. Res. Ocean. 2011, 116, C7. [Google Scholar] [CrossRef] [Green Version]
- Cota, G.F.; Wang, J.; Comiso, J.C. Transformation of global satellite chlorophyll retrievals with a regionally tuned algorithm. Remote Sens. Environ. 2004, 90, 373–377. [Google Scholar] [CrossRef]
- Tilstone, G.H.; Pardo, S.; Dall’Olmo, G.; Brewin, R.J.W.; Nencioli, F.; Dessailly, D.; Kwiatkowska, E.; Casal, T.; Donlon, C. Performance of Ocean Colour Chlorophyll a algorithms for Sentinel-3 OLCI, MODIS-Aqua and Suomi-VIIRS in open-ocean waters of the Atlantic. Remote Sens. Environ. 2021, 260, 112444. [Google Scholar] [CrossRef]
- Gómez Jakobsen, F.J.; Mercado, J.M.; Tovar-Salvador, M.L.; Cortés, D.; Yebra, L.; Salles, S.; Sánchez, A.; Valcárcel-Pérez, N.; Alonso, A. New algorithms for estimating chlorophyll-a in the Spanish waters of the Western Mediterranean Sea from multiplatform imagery. Int. J. Remote Sens. 2018, 39, 8837–8858. [Google Scholar] [CrossRef]
- Johnson, R.; Strutton, P.G.; Wright, S.W.; McMinn, A.; Meiners, K.M. Three improved satellite chlorophyll algorithms for the Southern Ocean. J. Geophys. Res. Ocean. 2013, 118, 3694–3703. [Google Scholar] [CrossRef]
- Wojtasiewicz, B.; Hardman-Mountford, N.J.; Antoine, D.; Dufois, F.; Slawinski, D.; Trull, T.W. Use of bio-optical profiling float data in validation of ocean colour satellite products in a remote ocean region. Remote Sens. Environ. 2018, 209, 275–290. [Google Scholar] [CrossRef]
- Pittman, N.A.; Strutton, P.G.; Johnson, R.; Matear, R.J. An Assessment and Improvement of Satellite Ocean Color Algorithms for the Tropical Pacific Ocean. J. Geophys. Res. Ocean. 2019, 124, 9020–9039. [Google Scholar] [CrossRef]
- Gregg, W.W.; Casey, N.W. Global and regional evaluation of the SeaWiFS chlorophyll data set. Remote Sens. Environ. 2004, 93, 463–479. [Google Scholar] [CrossRef]
- Wang, M.; Son, S. VIIRS-derived chlorophyll-a using the ocean color index method. Remote Sens. Environ. 2016, 182, 141–149. [Google Scholar] [CrossRef]
- Hammond, M.L.; Beaulieu, C.; Henson, S.A.; Sahu, S.K. Assessing the Presence of Discontinuities in the Ocean Color Satellite Record and Their Effects on Chlorophyll Trends and Their Uncertainties. Geophys. Res. Lett. 2018, 45, 7654–7662. [Google Scholar] [CrossRef] [Green Version]
- IOCCG. Ocean-Colour Data Merging. In Reports of the International Ocean-Colour Coordinating Group, No. 6; Gregg, W., Ed.; IOCCG: Dartmouth, NS, Canada, 2007. [Google Scholar]
- Chen, S.; Hu, C.; Barnes, B.B.; Xie, Y.; Lin, G.; Qiu, Z. Improving ocean color data coverage through machine learning. Remote Sens. Environ. 2019, 222, 286–302. [Google Scholar] [CrossRef]
- Kahru, M.; Kudela, R.M.; Manzano-Sarabia, M.; Greg Mitchell, B. Trends in the surface chlorophyll of the California Current: Merging data from multiple ocean color satellites. Deep. Sea Res. Part II Top. Stud. Oceanogr. 2012, 77–80, 89–98. [Google Scholar] [CrossRef]
- Ito, S.-i.; Sugisaki, H.; Tsuda, A.; Yamamura, O.; Okuda, K. Contributions of the VENFISH program: Meso-zooplankton, Pacific saury (Cololabis saira) and walleye pollock (Theragra chalcogramma) in the northwestern Pacific. Fish. Oceanogr. 2004, 13, 1–9. [Google Scholar] [CrossRef]
- Sugisaki, H.; Kurita, Y. Daily rhythm and seasonal variation of feeding habit of Pacific saury (Cololabis saira) in relation to their migration and oceanographic conditions off Japan. Fish. Oceanogr. 2004, 13, 63–73. [Google Scholar] [CrossRef]
- Liu, X.; Wang, M. Global daily gap-free ocean color products from multi-satellite measurements. Int. J. Appl. Earth Obs. Geoinf. 2022, 108, 102714. [Google Scholar] [CrossRef]
- Huang, W.-B. Comparisons of monthly and geographical variations in abundance and size composition of Pacific saury between the high-seas and coastal fishing grounds in the northwestern Pacific. Fish. Sci. 2009, 76, 21–31. [Google Scholar] [CrossRef]
- Kouketsu, S.; Kaneko, H.; Okunishi, T.; Sasaoka, K.; Itoh, S.; Inoue, R.; Ueno, H. Mesoscale eddy effects on temporal variability of surface chlorophyll a in the Kuroshio Extension. J. Oceanogr. 2016, 72, 439–451. [Google Scholar] [CrossRef]
- Cheung, H.-F.; Pan, J.; Gu, Y.; Wang, Z. Remote-sensing observation of ocean responses to Typhoon Lupit in the northwest Pacific. Int. J. Remote Sens. 2012, 34, 1478–1491. [Google Scholar] [CrossRef]
- Chiba, S.; Di Lorenzo, E.; Davis, A.; Keister, J.E.; Taguchi, B.; Sasai, Y.; Sugisaki, H. Large-scale climate control of zooplankton transport and biogeography in the Kuroshio-Oyashio Extension region. Geophys. Res. Lett. 2013, 40, 5182–5187. [Google Scholar] [CrossRef]
- Bessho, K.; Date, K.; Hayashi, M.; Ikeda, A.; Imai, T.; Inoue, H.; Kumagai, Y.; Miyakawa, T.; Murata, H.; Ohno, T.; et al. An Introduction to Himawari-8/9—Japan’s New-Generation Geostationary Meteorological Satellites. J. Meteorol. Soc. Jpn. Ser. II 2016, 94, 151–183. [Google Scholar] [CrossRef] [Green Version]
- Chavez, F.P.; Buck, K.R.; Bidigare, R.R.; Karl, D.M.; Hebel, D.; Latasa, M.; Campbell, L.; Newton, J. On the Chlorophyll a Retention Properties of Glass-Fiber GF/F Filters. Limnol. Oceanogr. 1995, 40, 428–433. [Google Scholar] [CrossRef]
- Zhang, T.; Hoell, A.; Perlwitz, J.; Eischeid, J.; Murray, D.; Hoerling, M.; Hamill, T.M. Towards Probabilistic Multivariate ENSO Monitoring. Geophys. Res. Lett. 2019, 46, 10532–10540. [Google Scholar] [CrossRef]
- Seegers, B.N.; Stumpf, R.P.; Schaeffer, B.A.; Loftin, K.A.; Werdell, P.J. Performance metrics for the assessment of satellite data products: An ocean color case study. Opt. Express 2018, 26, 7404–7422. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Frouin, R.J.; Shenoi, S.C.; Rao, K.H.; Murakami, H. Ocean color estimation by Himawari-8/AHI. In Remote Sensing of the Oceans and Inland Waters: Techniques, Applications, and Challenges; SPIE: Bellingham, WA, USA, 2016. [Google Scholar]
- IOCCG. Mission Requirements for Future Ocean-Colour Sensors. In Reports of the International Ocean-Colour Coordinating Group, No. 13; McClain, C.R., Meister, G., Eds.; IOCCG: Dartmouth, NS, Canada, 2012. [Google Scholar]
- El-Habashi, A.; Ahmed, S. Analyses of satellite ocean color retrievals show advantage of neural network approaches and algorithms that avoid deep blue bands. J. Appl. Remote Sens. 2019, 13, 024509. [Google Scholar] [CrossRef]
- Werdell, P.J.; Bailey, S.W. An improved in-situ bio-optical data set for ocean color algorithm development and satellite data product validation. Remote Sens. Environ. 2005, 98, 122–140. [Google Scholar] [CrossRef]
- Mélin, F.; Vantrepotte, V.; Chuprin, A.; Grant, M.; Jackson, T.; Sathyendranath, S. Assessing the fitness-for-purpose of satellite multi-mission ocean color climate data records: A protocol applied to OC-CCI chlorophyll-a data. Remote Sens. Environ. 2017, 203, 139–151. [Google Scholar] [CrossRef] [PubMed]
- Tseng, C.-T.; Sun, C.-L.; Belkin, I.M.; Yeh, S.-Z.; Kuo, C.-L.; Liu, D.-C. Sea surface temperature fronts affect distribution of Pacific saury (Cololabis saira) in the Northwestern Pacific Ocean. Deep. Sea Res. Part II Top. Stud. Oceanogr. 2014, 107, 15–21. [Google Scholar] [CrossRef]
- Tian, Y.; Akamine, T.; Suda, M. Modeling the influence of oceanic-climatic changes on the dynamics of Pacific saury in the northwestern Pacific using a life cycle model. Fish. Oceanogr. 2004, 13, 125–137. [Google Scholar] [CrossRef]
- Tian, H.; Liu, Y.; Tian, Y.; Alabia, I.D.; Qin, Y.; Sun, H.; Li, J.; Ma, S.; Saitoh, S.-I. A Comprehensive Monitoring and Assessment System for Multiple Fisheries Resources in the Northwest Pacific Based on Satellite Remote Sensing Technology. Front. Mar. Sci. 2022, 9, 808282. [Google Scholar] [CrossRef]
- Yasuda, I.; Watanabe, Y. On the relationship between the Oyashio front and saury fishing grounds in the north-western Pacific: A forecasting method for fishing ground locations. Fish. Oceanogr. 1994, 3, 172–181. [Google Scholar] [CrossRef]
- Saitoh, S.-I.; Kosaka, S.; Iisaka, J. Satellite infrared observations of Kuroshio warm-core rings and their application to study of Pacific saury migration. Deep. Sea Res. Part A Oceanogr. 1986, 33, 1601–1615. [Google Scholar] [CrossRef]
- Siegel, D.A.; Peterson, P.; McGillicuddy, D.J.; Maritorena, S.; Nelson, N.B. Bio-optical footprints created by mesoscale eddies in the Sargasso Sea. Geophys. Res. Lett. 2011, 38, L13608. [Google Scholar] [CrossRef] [Green Version]
- Zhao, D.; Xu, Y.; Zhang, X.; Huang, C. Global chlorophyll distribution induced by mesoscale eddies. Remote Sens. Environ. 2021, 254, 112245. [Google Scholar] [CrossRef]
- Jiang, W.; Huang, G.; Hu, K.; Wu, R.; Gong, H.; Chen, X.; Tao, W. Diverse Relationship between ENSO and the Northwest Pacific Summer Climate among CMIP5 Models: Dependence on the ENSO Decay Pace. J. Clim. 2017, 30, 109–127. [Google Scholar] [CrossRef]
- Henson, S.A.; Sarmiento, J.L.; Dunne, J.P.; Lima, L.; Doney, S.C.; John, J.; Beaulieu, C. Detection of anthropogenic climate change in satellite records of ocean chlorophyll and productivity. Biogeosciences 2010, 7, 621–640. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).