Inverse Synthetic Aperture Radar Imaging Using an Attention Generative Adversarial Network
Abstract
:1. Introduction
2. Strategy of Generative Adversarial Network
3. Structure of Attention Generative Adversarial Network
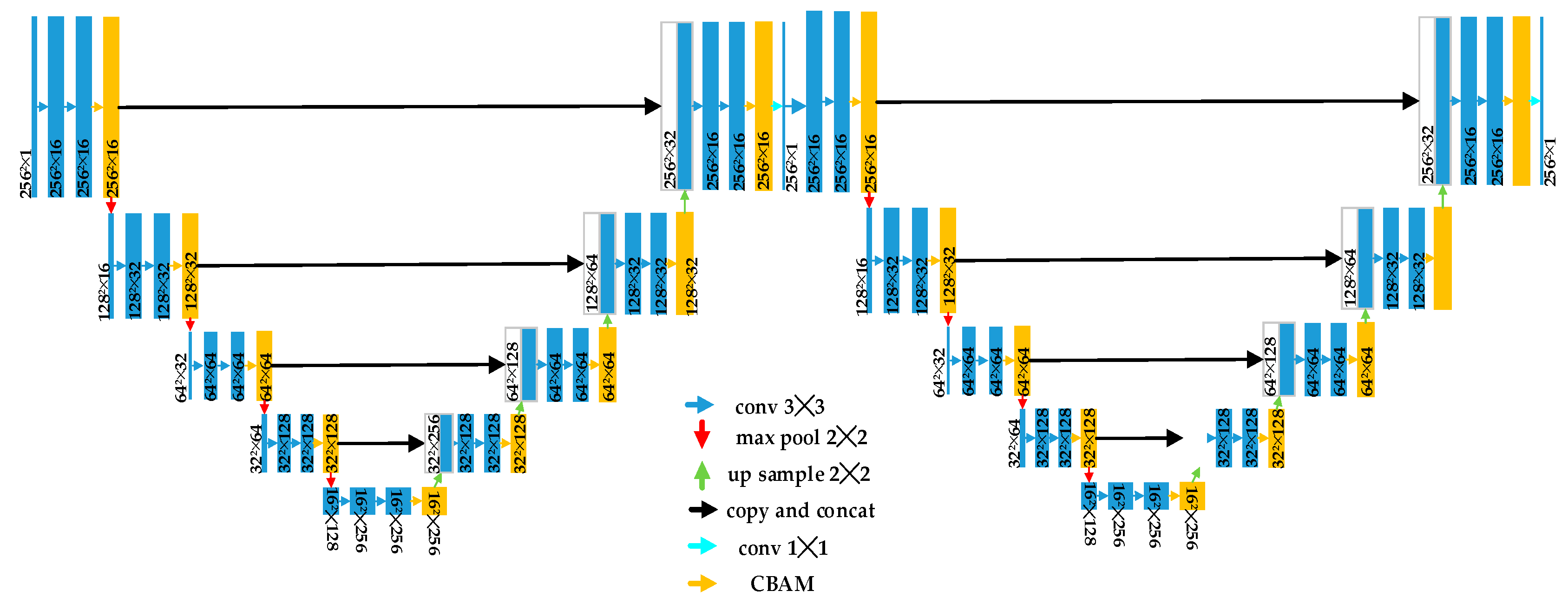
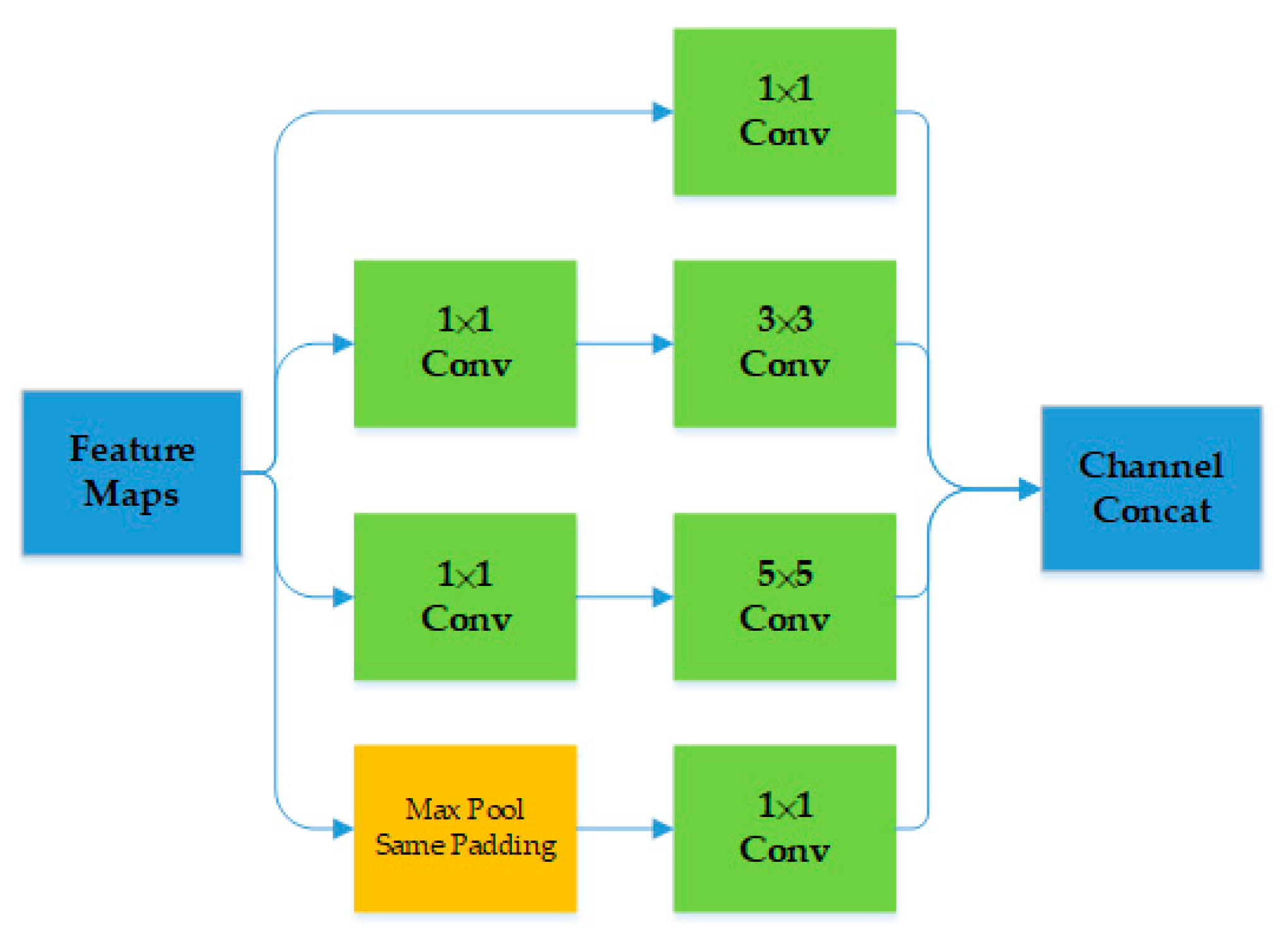
3.1. Generator Architecture
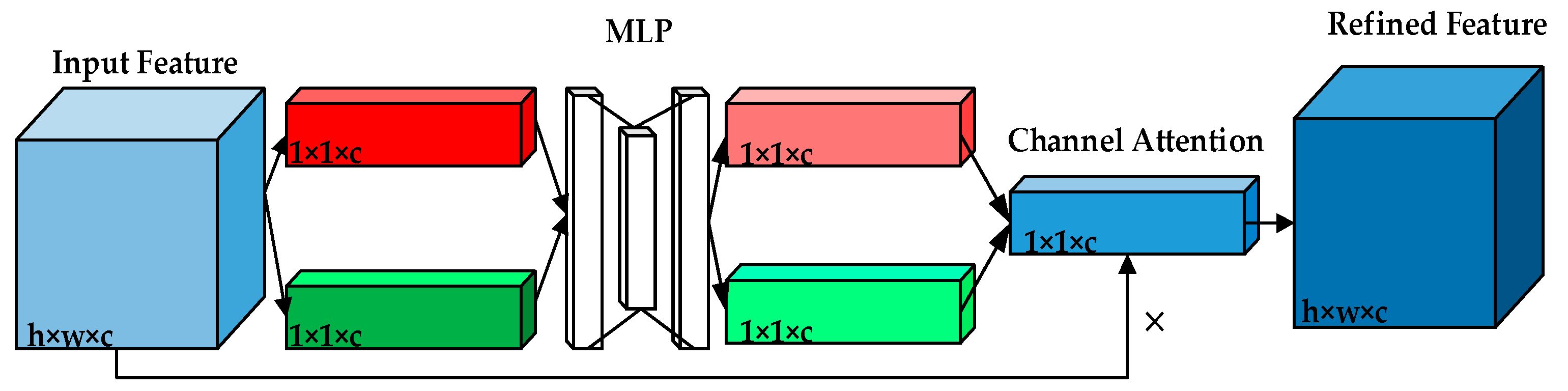
3.2. Convolutional Block Attention Module
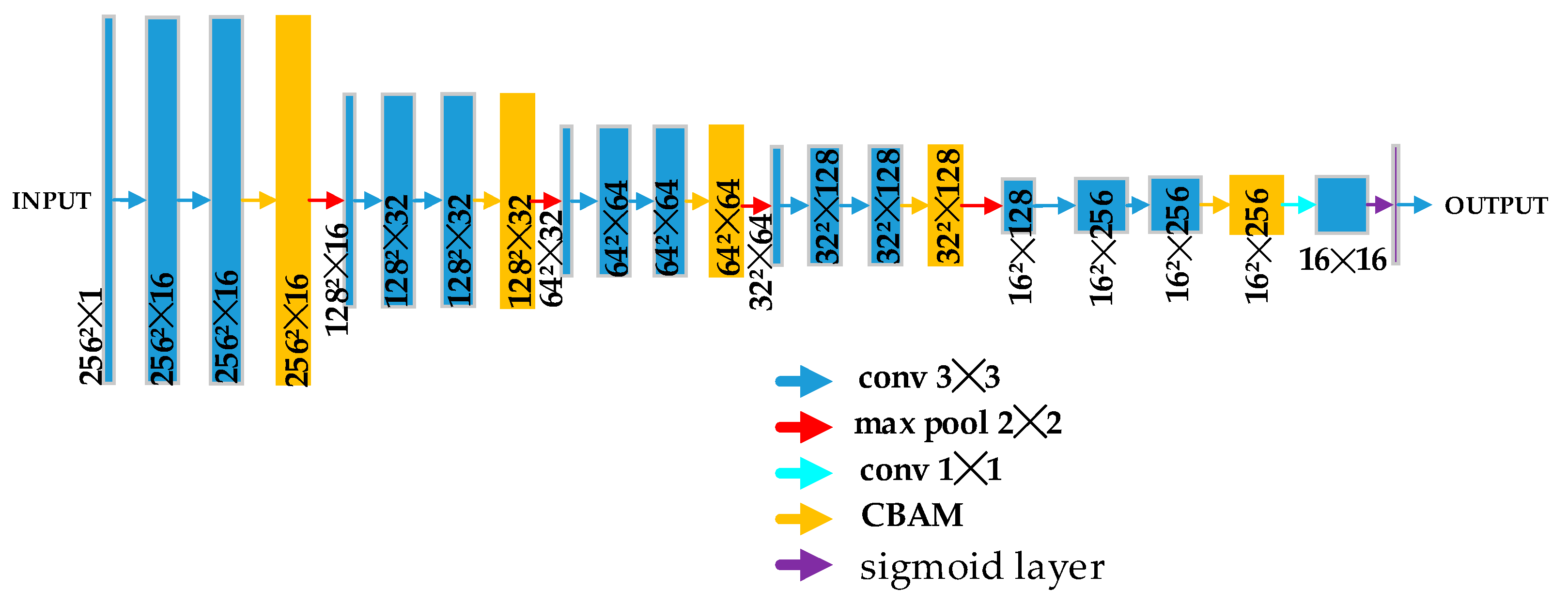
3.3. Discriminator Architecture
4. Experimental Results
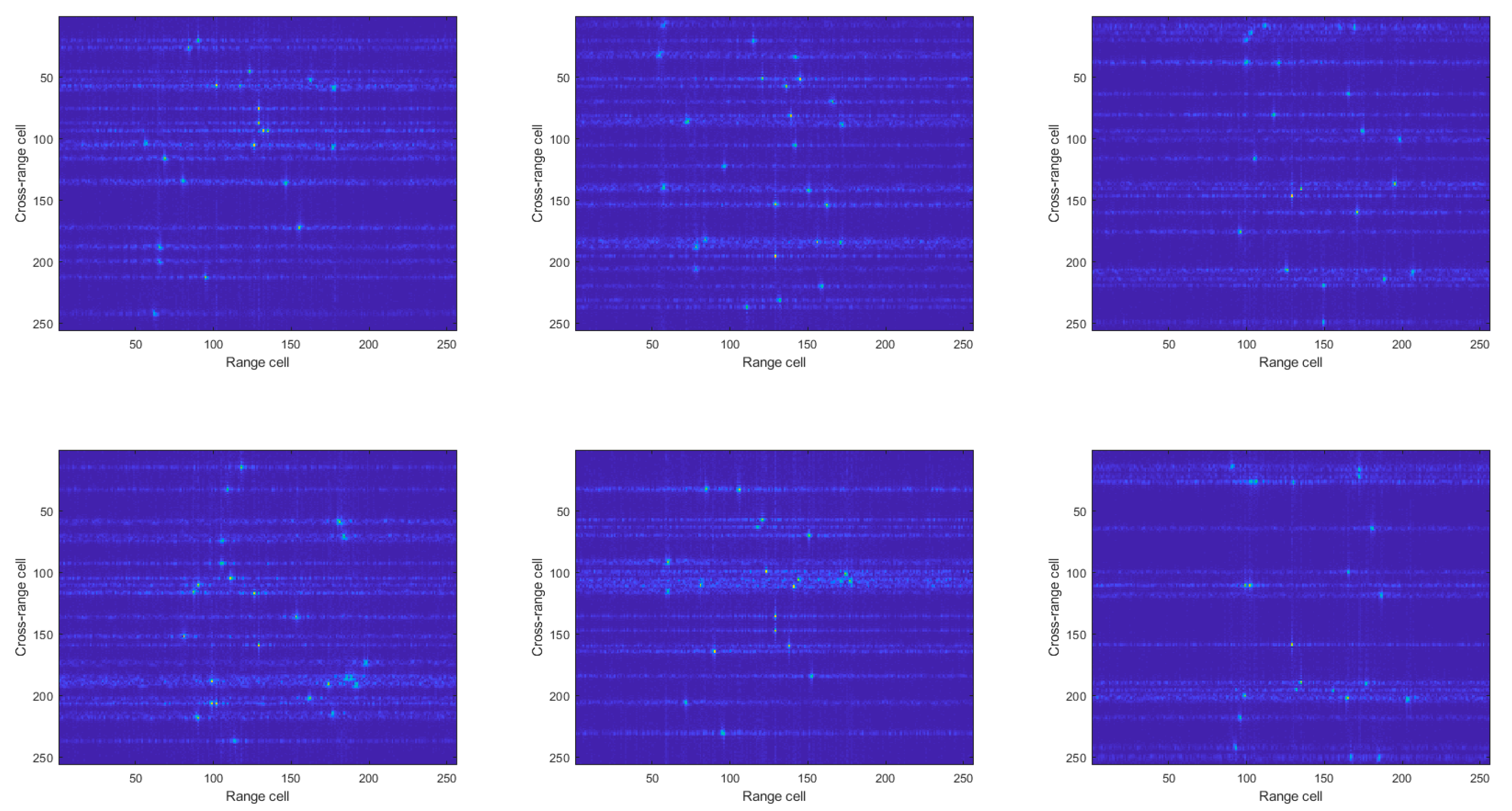
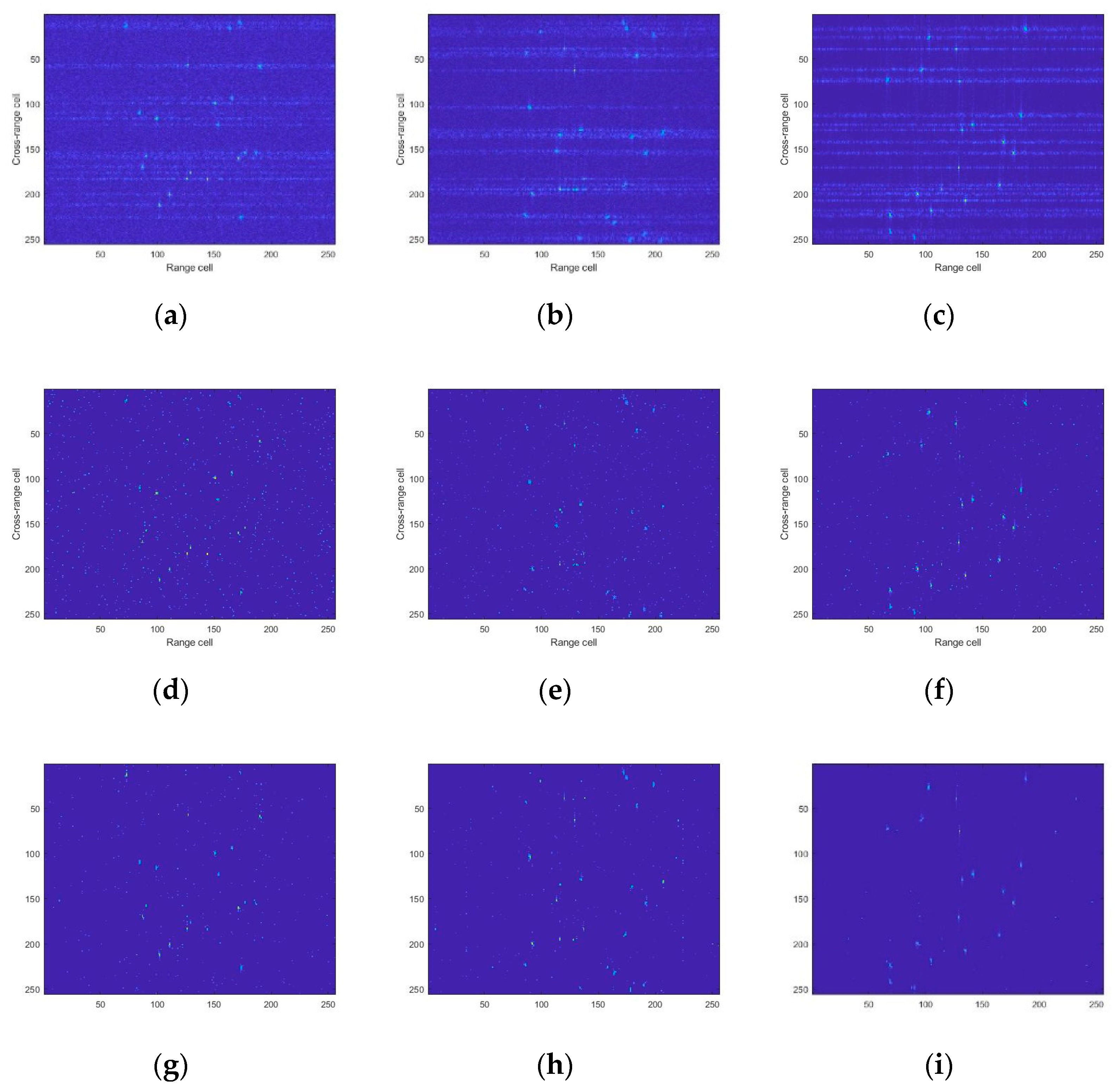
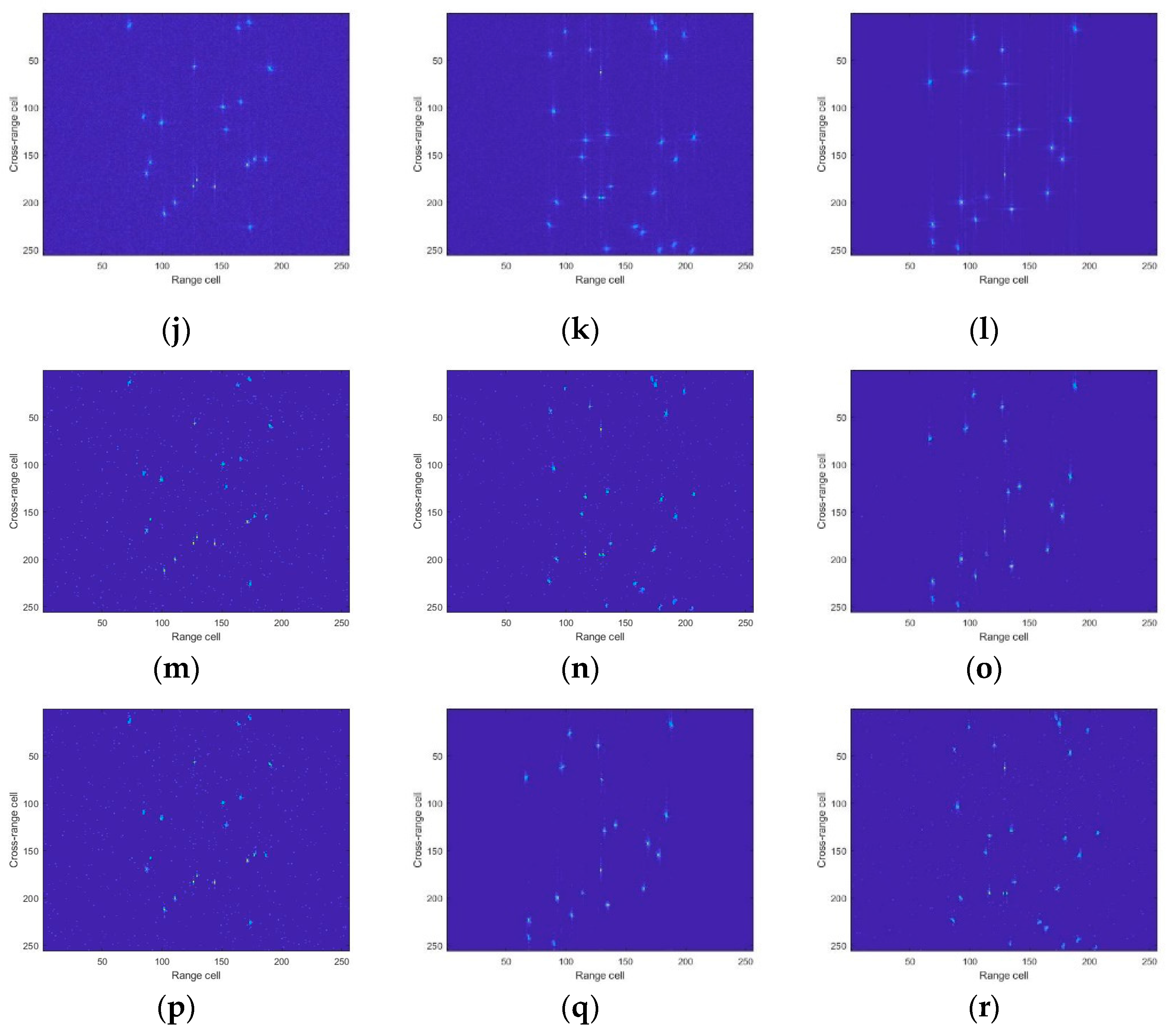
4.1. Simulated Data
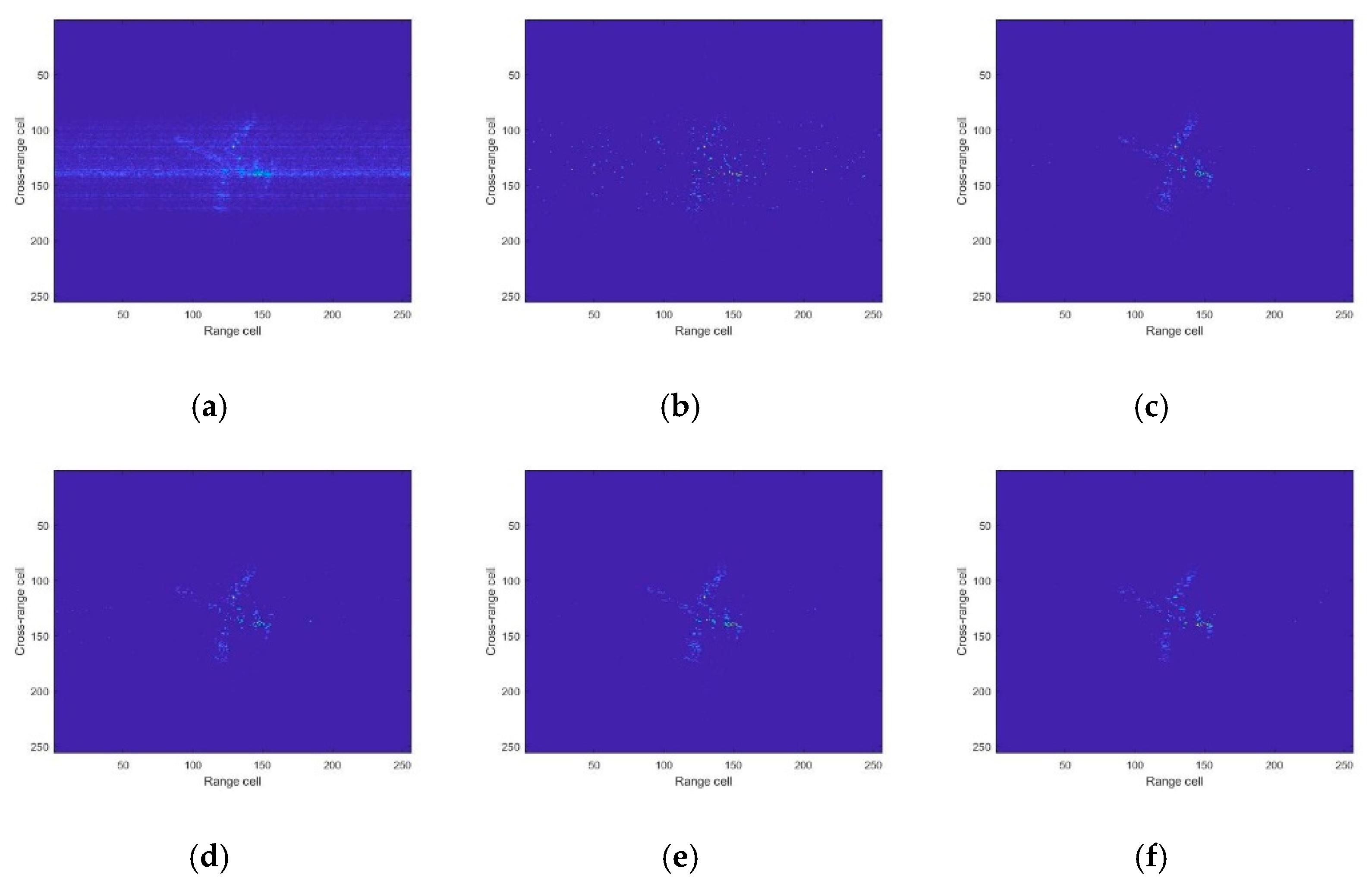
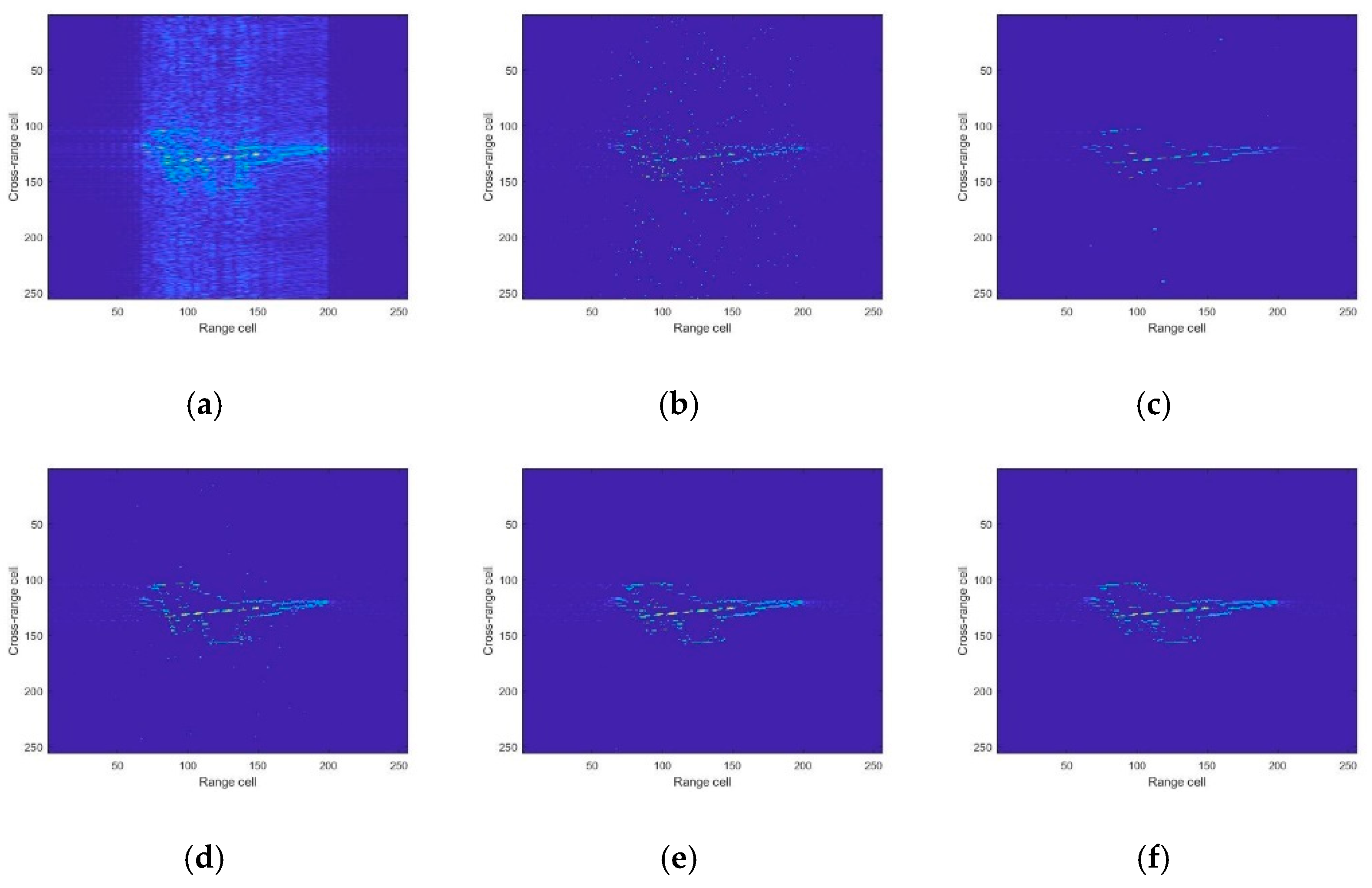
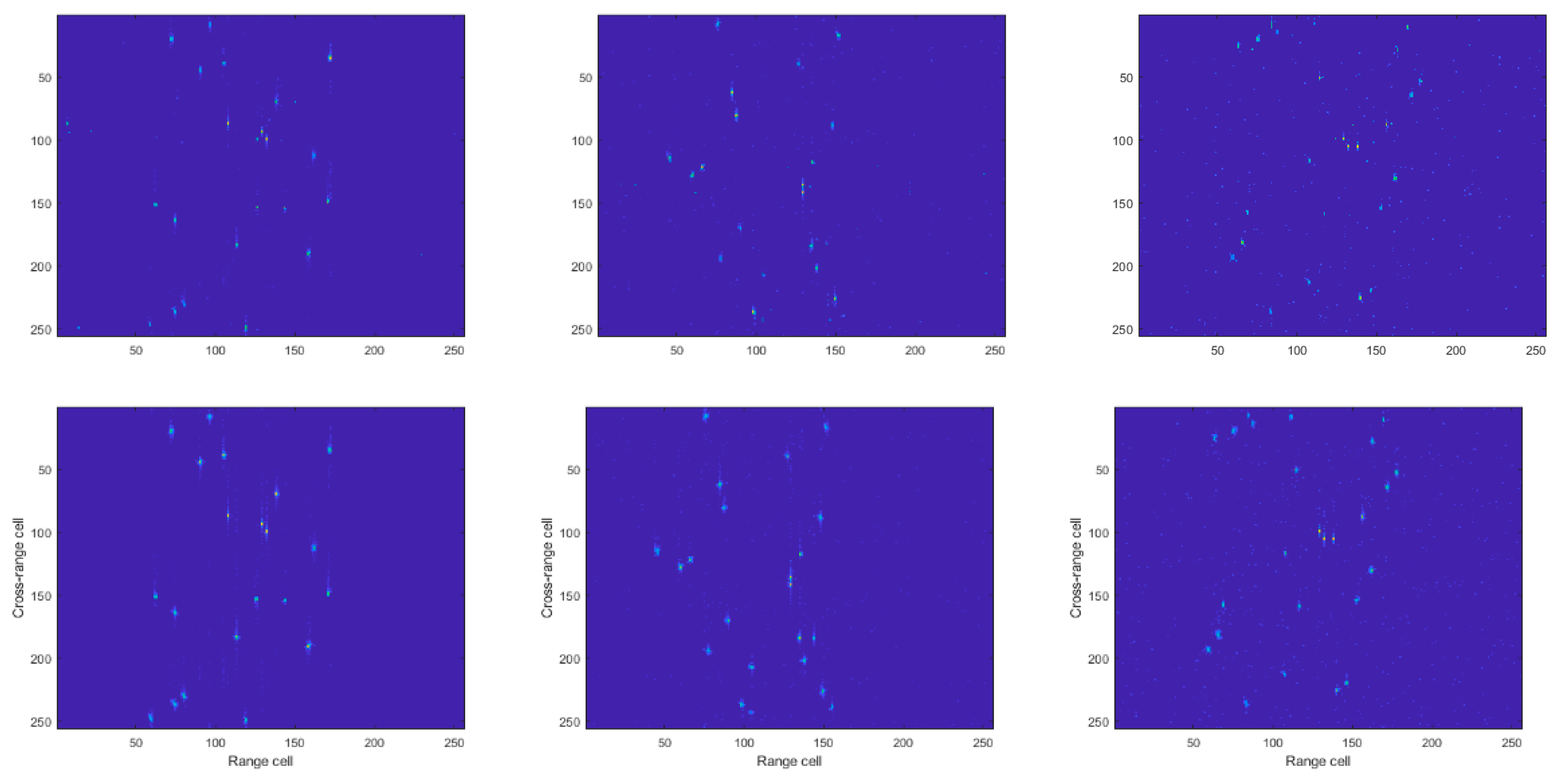
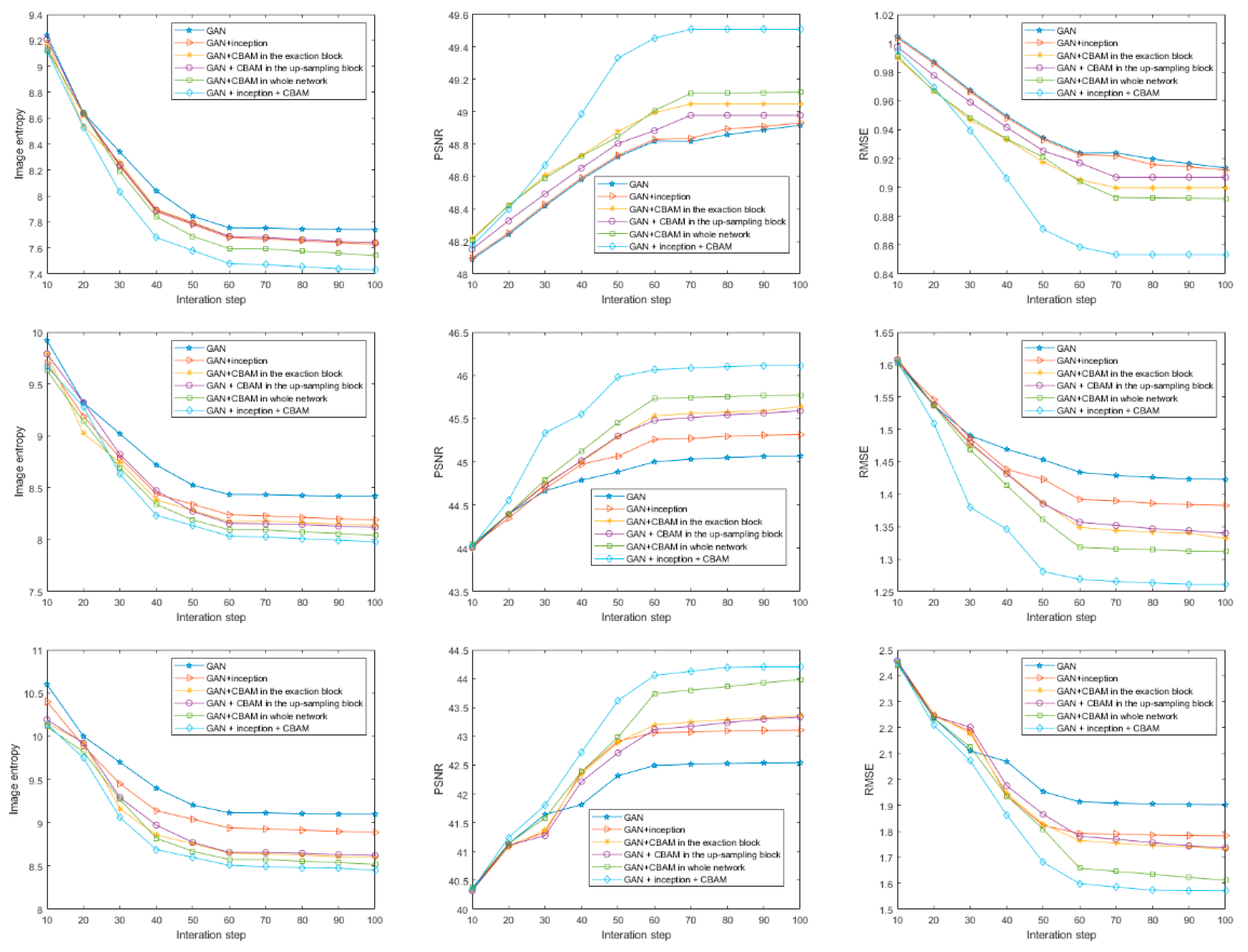
4.2. Experiment Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chen, V.; Martorella, M. Inverse Synthetic Aperture Radar; SciTech Publishing: Raleigh, NC, USA, 2014; p. 56. [Google Scholar]
- Luo, Y.; Ni, J.C.; Zhang, Q. Synthetic Aperture Radar Learning-imaging Method Based on Data-driven Technique and Artificial Intelligence. J. Radars. 2020, 9, 107–122. [Google Scholar]
- Bai, X.R.; Zhou, X.N.; Zhang, F.; Wang, L.; Zhou, F. Robust pol-ISAR target recognition based on ST-MC-DCNN. IEEE Trans. Geosci. Remote Sens. 2019, 57, 9912–9927. [Google Scholar] [CrossRef]
- Wu, M.; Xing, M.D.; Zhang, L. Two Dimensional Joint Super-resolution ISAR Imaging Algorithm Based on Compressive Sensing. J. Electron. Inf. Technol. 2014, 36, 187–193. [Google Scholar]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Hu, C.Y.; Wang, L.; Loffeld, O. Inverse synthetic aperture radar imaging exploiting dictionary learning. In Proceedings of the IEEE Radar Conference, Oklahoma City, OK, USA, 23–27 April 2018. [Google Scholar]
- Bai, X.R.; Zhou, F.; Hui, Y. Obtaining JTF-signature of space-debris from incomplete and phase-corrupted data. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 1169–1180. [Google Scholar] [CrossRef]
- Bai, X.R.; Wang, G.; Liu, S.Q.; Zhou, F. High-Resolution Radar Imaging in Low SNR Environments Based on Expectation Propagation. IEEE Trans. Geosci. Remote Sens. 2020, 59, 1275–1284. [Google Scholar] [CrossRef]
- Li, S.Y.; Zhao, G.Q.; Zhang, W.; Qiu, Q.W.; Sun, H.J. ISAR imaging by two-dimensional convex optimization-based compressive sensing. IEEE Sens. J. 2016, 16, 7088–7093. [Google Scholar] [CrossRef]
- Xu, Z.B.; Yang, Y.; Sun, J. A new approach to solve inverse problems: Combination of model-based solving and example-based learning. Sci. Sin. Math. 2017, 10, 1345–1354. [Google Scholar]
- Chang, J.H.R.; Li, C.L.; Póczos, B.; Vijaya Kumar, B.V.K.; Sankaranarayanan, A.C. One network to solve them all-solving linear inverse problems using deep projection models. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 24–27 October 2017. [Google Scholar]
- Shah, V.; Hegde, C. Solving linear inverse problems using GAN priors: An algorithm with provable guarantees. In Proceedings of the 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, AB, Canada, 15–20 April 2018. [Google Scholar]
- Zhang, K.; Zuo, W.; Chen, Y.; Meng, D.; Zhang, L. Beyond a Gaussian denoiser: Residual learning of deep CNN for image denoising. IEEE Trans. Image Process. 2017, 26, 3142–3155. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mason, E.; Yonel, B.; Yazici, Y.B. Deep learning for SAR image formation. In Proceedings of the SPIE 10201, Algorithms for Synthetic Aperture Radar Imagery XXIV, Anaheim, CA, USA, 28 April 2017. [Google Scholar]
- Li, X.; Bai, X.; Zhou, F. High-resolution ISAR imaging and autofocusing via 2D-ADMM-Net. Remote Sens. 2021, 13, 2326. [Google Scholar] [CrossRef]
- Borgerding, M.; Schniter, P.; Rangan, S. AMP-Inspired Deep Networks for Sparse Linear Inverse Problems. IEEE Trans. Signal Process. 2016, 65, 4293–4308. [Google Scholar] [CrossRef]
- Gao, J.; Deng, B.; Qin, Y.; Wang, H.; Li, X. Enhanced radar imaging using a complex-valued convolutional neural network. IEEE Geosci. Remote Sens. Lett. 2019, 1, 35–39. [Google Scholar] [CrossRef] [Green Version]
- Hu, C.; Wang, L.; Li, Z.; Zhu, D. Inverse synthetic aperture radar imaging using a fully convolutional neural network. IEEE Geosci. Remote Sens. Lett. 2020, 7, 1203–1207. [Google Scholar] [CrossRef]
- Cai, T.T.; Wang, L. Orthogonal matching pursuit for sparse signal recovery with noise. IEEE Trans. Inf. Theory 2011, 57, 4680–4688. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, Y.; Li, X.; Bi, G. Joint sparse aperture ISAR autofocusing and scaling via modified Newton method-based variational Bayesian inference. IEEE Trans. Geosci. Remote Sens. 2019, 57, 4857–4869. [Google Scholar] [CrossRef]
- Chen, C.-C.; Andrews, H. Target-motion-induced radar imaging. IEEE Trans. Aerosp. Electron. Syst. 1980, 16, 2–14. [Google Scholar] [CrossRef]
- Glorot, X.; Bordes, A.; Bengio, Y. Deep Sparse Rectifier Neural Networks. J. Mach. Learn. Res. 2011, 15, 315–323. [Google Scholar]




| Parameters | Symbol | Value |
|---|---|---|
| Carrier frequency | fc | 10 GHz |
| Bandwidth | B0 | 300 MHz |
| Pulse width | Tp | 1.58 × 10−7 s |
| Pulse repetition interval | PRI | 2.5 × 10−3 s |
| Accumulate pulse numbers | N | 256 |
| Down-sampling rate | M | 30% |
| Angular speed | w_x | 0.05 rad/s |
| SNR (dB) | Method | ENT | PSNR (dB) | RMSE | Time (s) |
|---|---|---|---|---|---|
| 0 | RD | 16.3345 | 25.2238 | 13.9749 | 0.99 |
| CS-OMP | 9.2312 | 36.5938 | 3.7744 | 25.26 | |
| AMDD-net | 8.8465 | 39.9535 | 2.5637 | 0.26 | |
| U-net | 9.0644 | 42.5274 | 1.9062 | 0.02 | |
| AGAN | 8.7498 | 44.7656 | 1.4732 | 0.03 | |
| 5 | RD | 14.3242 | 28.2860 | 9.8229 | 0.89 |
| CS-OMP | 8.3762 | 41.4228 | 2.1647 | 24.48 | |
| AMDD-net | 8.0964 | 43.4036 | 1.7233 | 0.26 | |
| U-net | 8.3343 | 45.0490 | 1.4259 | 0.02 | |
| AGAN | 8.0034 | 46.5305 | 1.2023 | 0.03 | |
| 10 | RD | 12.1105 | 29.2630 | 8.7779 | 0.86 |
| CS-OMP | 7.8545 | 45.5138 | 1.3516 | 24.11 | |
| AMDD-net | 7.6532 | 47.1892 | 1.1145 | 0.25 | |
| U-net | 7.8049 | 48.3347 | 0.9768 | 0.02 | |
| AGAN | 7.5498 | 49.2956 | 0.8745 | 0.03 |
| Methods | ENT | PSNR (dB) | RMSE |
|---|---|---|---|
| Channel + spatial | 7.6047 | 49.2976 | 0.8743 |
| Spatial + channel | 7.7754 | 48.6185 | 0.9454 |
| Spatial and channel in parallel | 7.8987 | 46.8747 | 1.1556 |
| Architecture | ENT | PSNR (dB) | RMSE |
|---|---|---|---|
| U-net | 7.8264 | 48.3347 | 0.9768 |
| GAN | 7.7439 | 48.9166 | 0.9135 |
| GAN + inception | 7.6389 | 48.9270 | 0.9124 |
| GAN + CBAM in the exaction block | 7.6486 | 48.9786 | 0.9070 |
| GAN + CBAM in the up-sampling block | 7.6455 | 49.0478 | 0.8998 |
| GAN + CBAM in whole network | 7.5463 | 49.1205 | 0.8923 |
| GAN + inception + CBAM | 7.4387 | 49.5087 | 0.8533 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, Y.; Luo, Y.; Ni, J.; Zhang, Q. Inverse Synthetic Aperture Radar Imaging Using an Attention Generative Adversarial Network. Remote Sens. 2022, 14, 3509. https://doi.org/10.3390/rs14153509
Yuan Y, Luo Y, Ni J, Zhang Q. Inverse Synthetic Aperture Radar Imaging Using an Attention Generative Adversarial Network. Remote Sensing. 2022; 14(15):3509. https://doi.org/10.3390/rs14153509
Chicago/Turabian StyleYuan, Yanxin, Ying Luo, Jiacheng Ni, and Qun Zhang. 2022. "Inverse Synthetic Aperture Radar Imaging Using an Attention Generative Adversarial Network" Remote Sensing 14, no. 15: 3509. https://doi.org/10.3390/rs14153509
APA StyleYuan, Y., Luo, Y., Ni, J., & Zhang, Q. (2022). Inverse Synthetic Aperture Radar Imaging Using an Attention Generative Adversarial Network. Remote Sensing, 14(15), 3509. https://doi.org/10.3390/rs14153509






