A Novel Frequency-Domain Focusing Method for Geosynchronous Low-Earth-Orbit Bistatic SAR in Sliding-Spotlight Mode
Abstract
:1. Introduction
- A novel equivalent bistatic range model based on circular orbit trajectory ESRM, namely BiCoT-ESRM, is proposed to accurately represent the range history of GEO-LEO BiSAR in sliding-spotlight mode. BiCoT-ESRM comprehensively considers the two major problems, i.e., curved trajectory of LEO receiver and ‘stop-and-go’ assumption error.
- Based on BiCoT-ESRM, the precise 2-D spectrum is derived, and a frequency-domain imaging method is put forward to achieve accurate focusing for sliding-spotlight GEO-LEO BiSAR.
- The modified azimuth preprocessing can remove the total Doppler aliasing caused by spatial variance of Doppler centroid and beam steering in sliding-spotlight GEO-LEO BiSAR. Moreover, the azimuth variance of motion parameters due to curved trajectory can be simultaneously eliminated by the proposed azimuth trajectory scaling (ATS).
- This experiment provides a new approach for designing the equivalent experiments to verify the theoretical studies and imaging methods related to GEO monostatic/bistatic SAR, which can be a worthwhile reference for researchers engaged in relevant studies.
2. Equivalent Range Model for GEO-LEO BiSAR
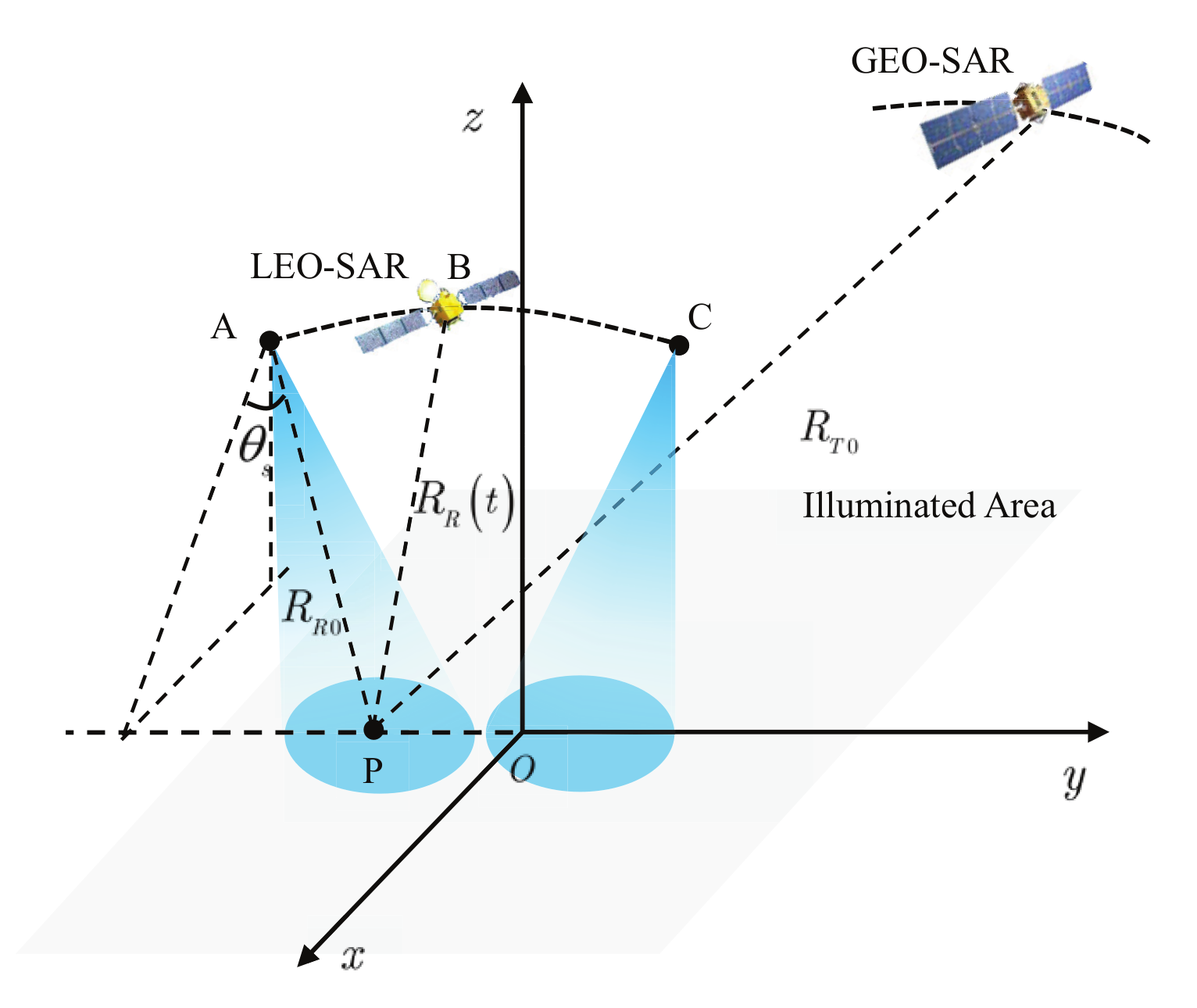
2.1. Imaging Geometry and Signal Model
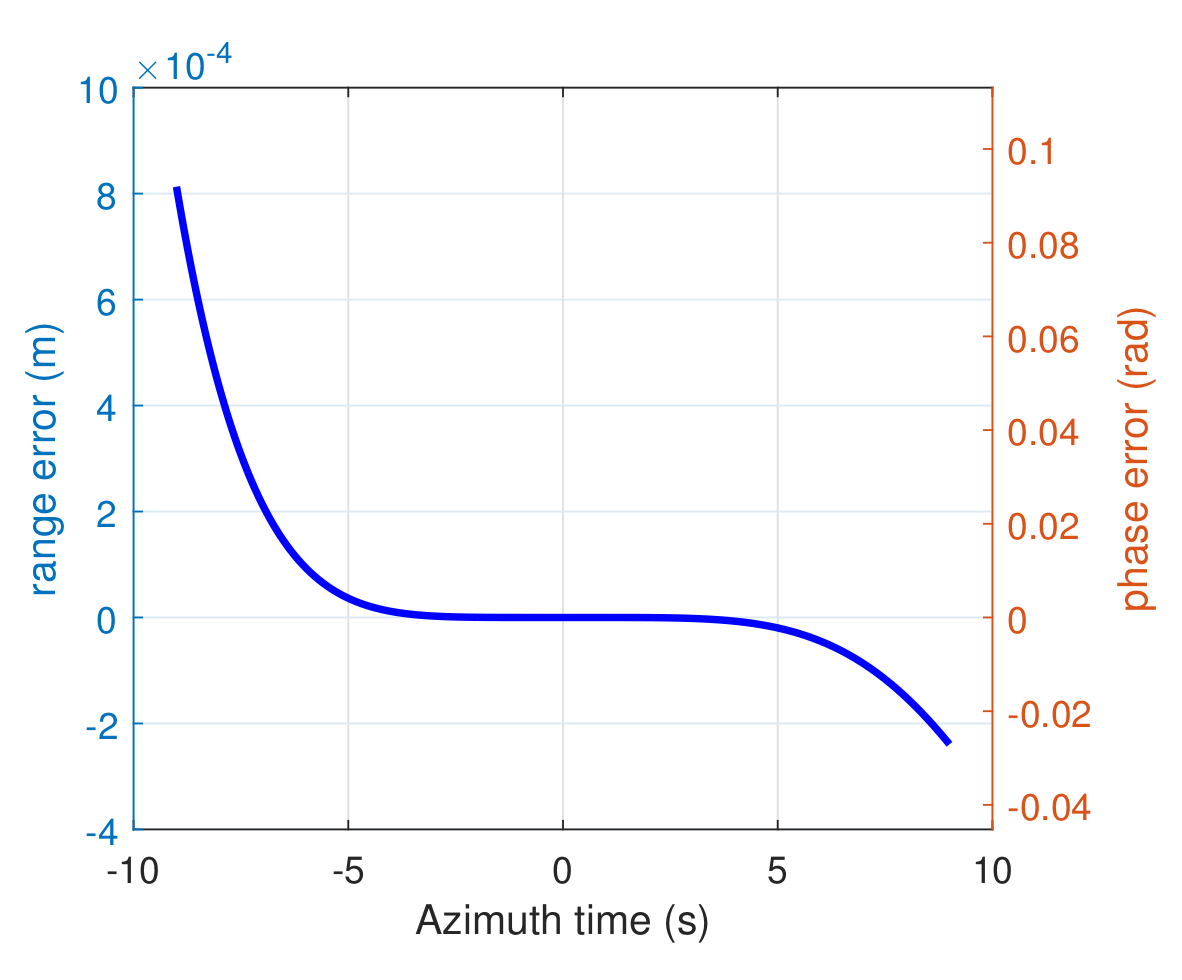
2.2. Range Model Analysis for GEO-LEO BiSAR without ‘stop-and-go’ Assumption
2.3. Equivalent Range Model for GEO-LEO BiSAR
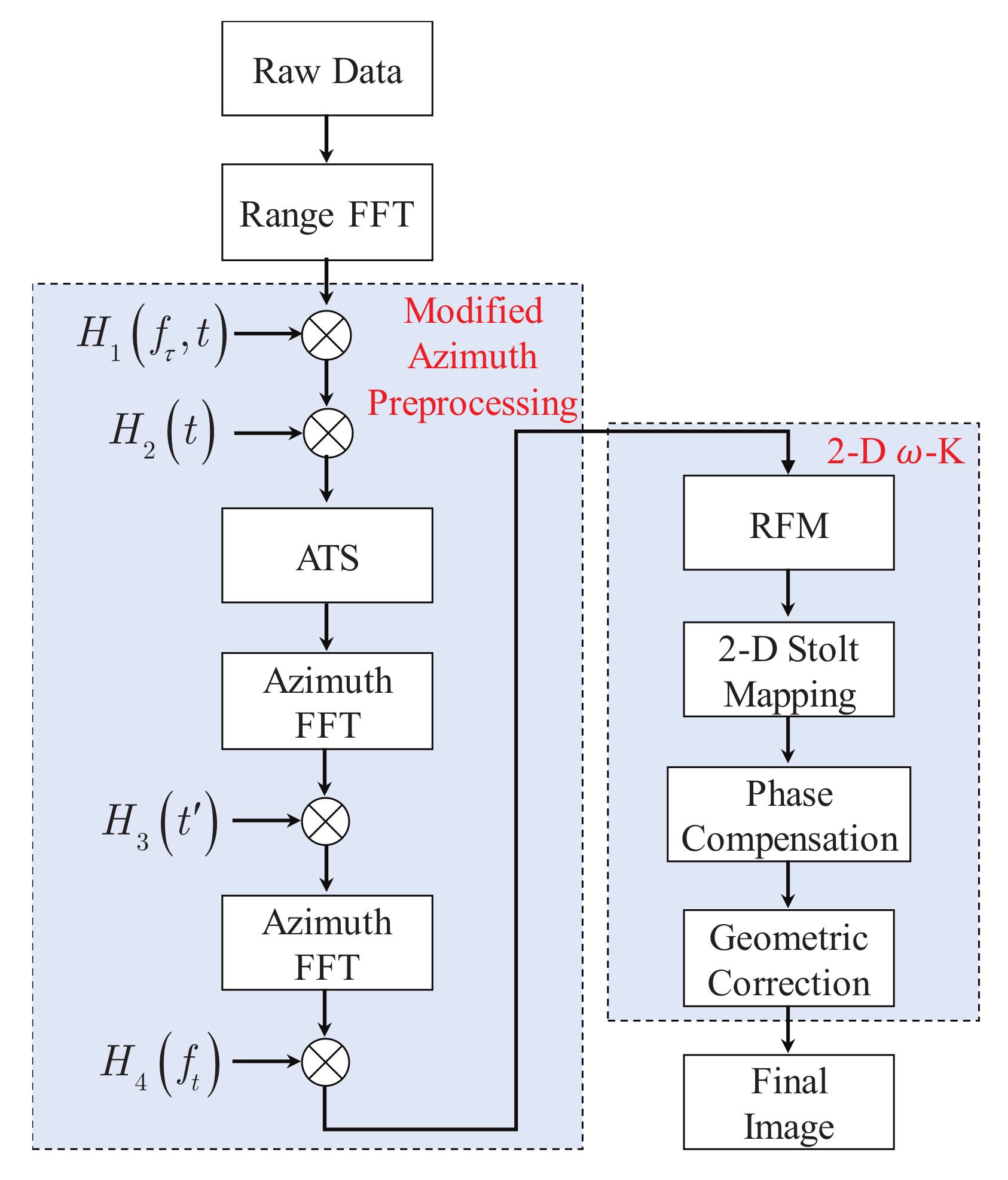
3. 2-D Frequency-Domain Focusing Based on BiCoT-ESRM
3.1. Modified Azimuth Preprocessing
3.2. 2-D Frequency-Domain Focusing Method Based on BiCoT-ESRM
4. Experimental Results
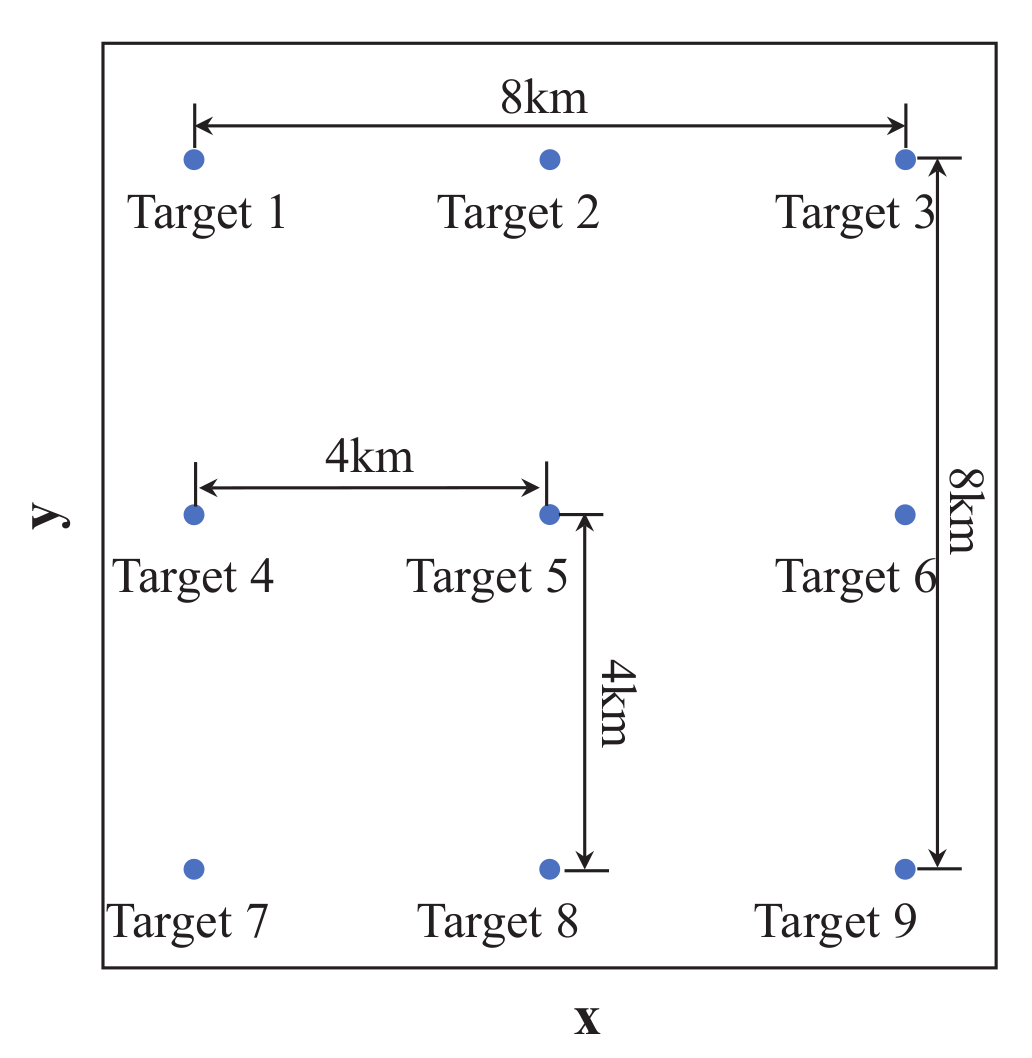
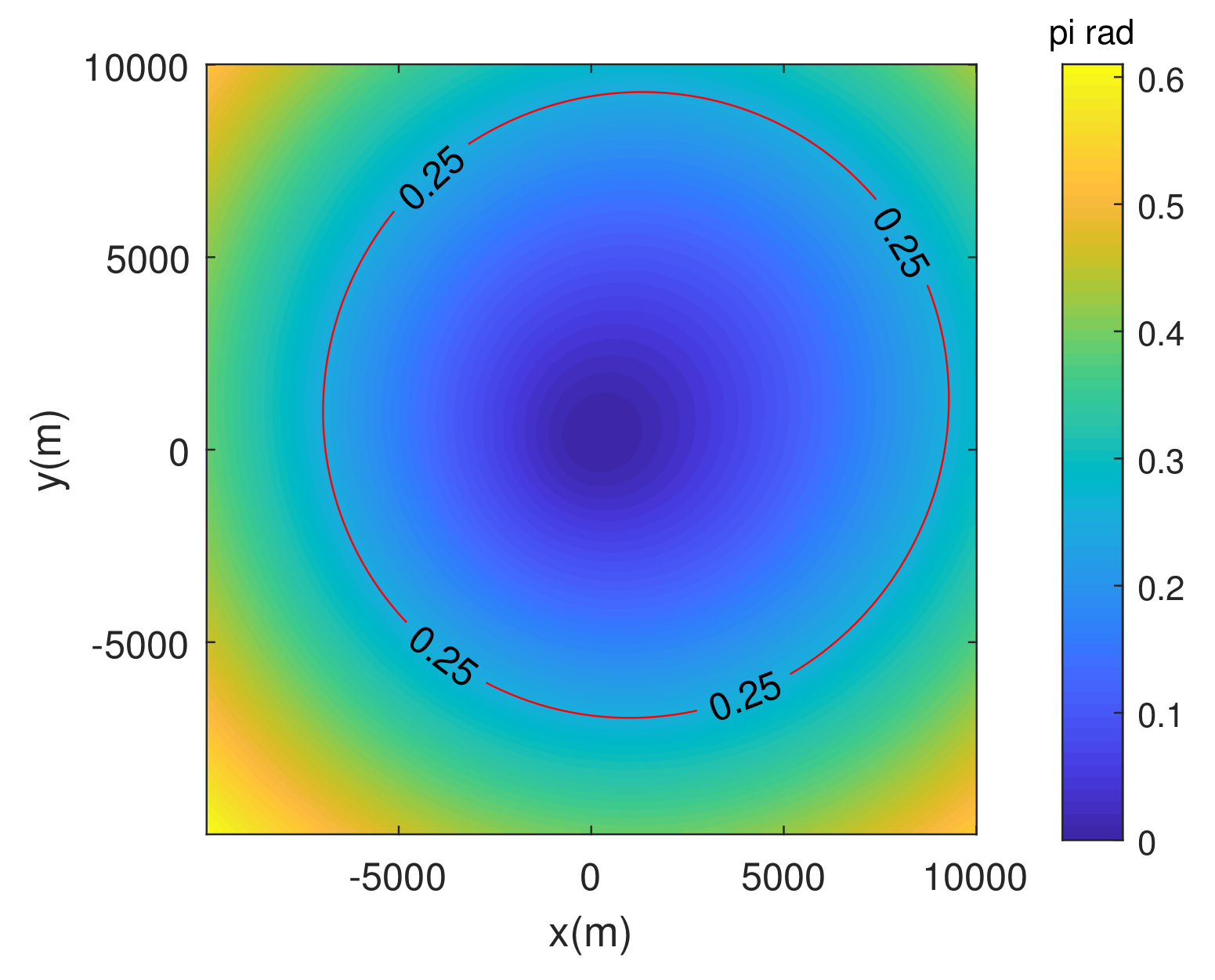
4.1. Simulation Results of Sliding-Spotlight GEO-LEO BiSAR
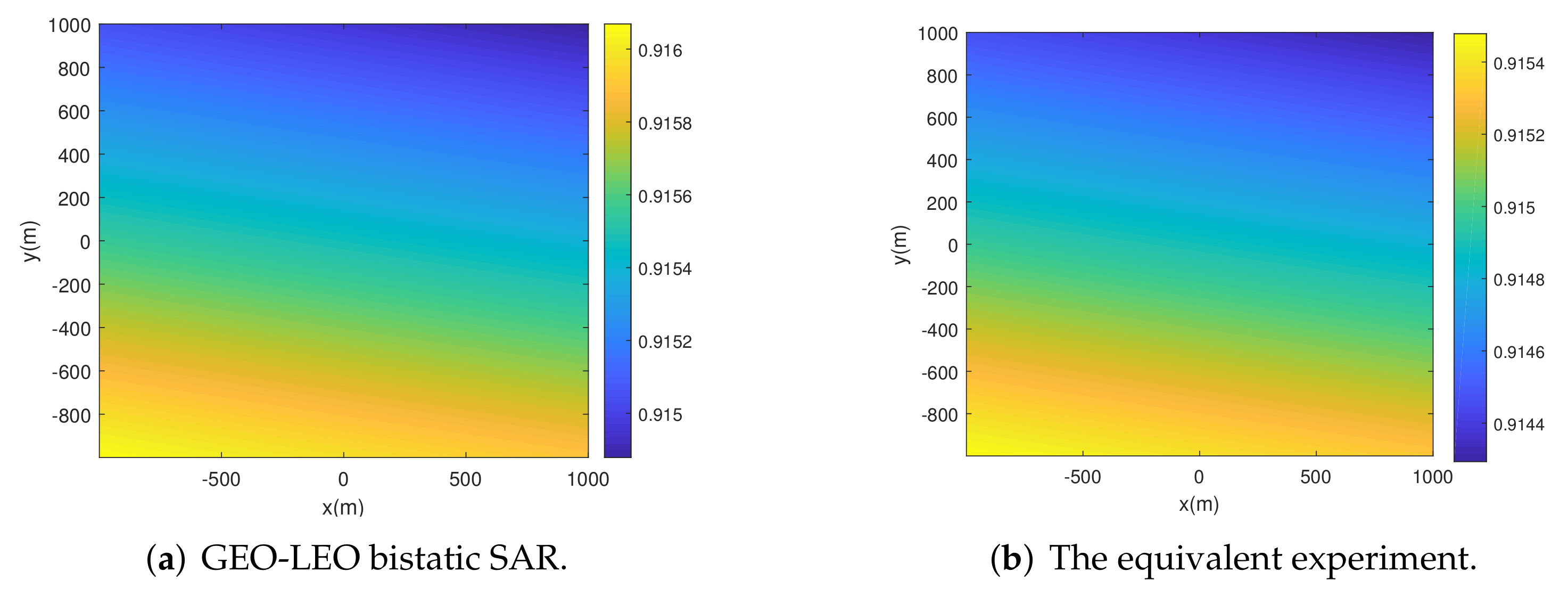
4.2. Equivalent Experiment with GF-3 Transmitter and Stationary Receiver
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. Expanding Coefficients of
Appendix A.2. Derivation of Equivalent Parameters of BiCoT-ESRM
Appendix A.3. Derivation of the Expanding Coefficients of and with Respect to y and
Appendix A.4. Derivations of p1 and q1
Appendix A.5. Derivation of p2 and q2
References
- Huang, P.; Xia, X.G.; Wang, L.; Xu, H.; Liu, X.; Liao, G.; Jiang, X. Imaging and Relocation for Extended Ground Moving Targets in Multichannel SAR-GMTI Systems. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–24. [Google Scholar] [CrossRef]
- Huang, P.; Xia, X.G.; Zhan, M.; Liu, X.; Liao, G.; Jiang, X. ISAR Imaging of a Maneuvering Target Based on Parameter Estimation of Multicomponent Cubic Phase Signals. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–18. [Google Scholar] [CrossRef]
- Huang, P.; Zou, Z.; Xia, X.G.; Liu, X.; Liao, G.; Xin, Z. Multichannel Sea Clutter Modeling for Spaceborne Early Warning Radar and Clutter Suppression Performance Analysis. IEEE Trans. Geosci. Remote Sens. 2021, 59, 8349–8366. [Google Scholar] [CrossRef]
- Li, Z.; Ye, H.; Liu, Z.; Sun, Z.; An, H.; Wu, J.; Yang, J. Bistatic SAR Clutter-Ridge Matched STAP Method for Non-stationary Clutter Suppression. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1. [Google Scholar] [CrossRef]
- Tomiyasu, K.; Pacelli, J.L. Synthetic Aperture Radar Imaging from an Inclined Geosynchronous Orbit. IEEE Trans. Geosci. Remote Sens. 1983, GE-21, 324–329. [Google Scholar] [CrossRef]
- Sun, Z.; Wu, J.; Pei, J.; Li, Z.; Huang, Y.; Yang, J. Inclined Geosynchronous Spaceborne-Airborne Bistatic SAR: Performance Analysis and Mission Design. IEEE Trans. Geosci. Remote Sens. 2016, 54, 343–357. [Google Scholar] [CrossRef]
- Ruiz-Rodon, J.; Broquetas, A.; Makhoul, E.; Monti Guarnieri, A.; Rocca, F. Nearly Zero Inclination Geosynchronous SAR Mission Analysis With Long Integration Time for Earth Observation. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6379–6391. [Google Scholar] [CrossRef]
- Long, T.; Zhang, T.; Ding, Z.; Yin, W. Effect Analysis of Antenna Vibration on GEO SAR Image. IEEE Trans. Aerosp.Electron. Syst. 2019, 56, 1. [Google Scholar] [CrossRef]
- Li, Y.; Hu, C.; Dong, X.; Zhang, B.; Li, S.; Ao, D. Influence of Orbit and System Parameters on Geosynchronous SAR Multiple-Aperture Interferometry Processing: Analysis and Validation. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2019, 12, 1798–1811. [Google Scholar] [CrossRef]
- Chen, J.; Sun, G.; Xing, M.; Yang, J.; Ni, C.; Zhu, Y.; Shu, W.; Liu, W. A Parameter Optimization Model for Geosynchronous SAR Sensor in Aspects of Signal Bandwidth and Integration Time. IEEE Geosci. Remote Sens. Letts. 2016, 13, 1374–1378. [Google Scholar] [CrossRef]
- Hobbs, S.; Mitchell, C.; Forte, B.; Holley, R.; Snapir, B.; Whittaker, P. System Design for Geosynchronous Synthetic Aperture Radar Missions. IEEE Trans. Geosci. Remote Sens. 2014, 52, 7750–7763. [Google Scholar] [CrossRef] [Green Version]
- Ding, Z.; Yin, W.; Zeng, T.; Long, T. Radar Parameter Design for Geosynchronous SAR in Squint Mode and Elliptical Orbit. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2016, 9, 2720–2732. [Google Scholar] [CrossRef]
- Hu, C.; Long, T.; Liu, Z.; Zeng, T.; Tian, Y. An Improved Frequency Domain Focusing Method in Geosynchronous SAR. IEEE Trans. Geosci. Remote Sens. 2014, 52, 5514–5528. [Google Scholar] [CrossRef]
- Sun, G.; Xing, M.; Wang, Y.; Yang, J.; Bao, Z. A 2-D Space-Variant Chirp Scaling Algorithm Based on the RCM Equalization and Subband Synthesis to Process Geosynchronous SAR Data. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4868–4880. [Google Scholar] [CrossRef]
- Zhang, T.; Ding, Z.; Tian, W.; Zeng, T.; Yin, W. A 2-D Nonlinear Chirp Scaling Algorithm for High Squint GEO SAR Imaging Based on Optimal Azimuth Polynomial Compensation. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2017, 10, 5724–5735. [Google Scholar] [CrossRef]
- Hu, B.; Jiang, Y.; Zhang, S.; Zhang, Y.; Yeo, T. Generalized Omega-K Algorithm for Geosynchronous SAR Image Formation. IEEE Geosci. Remote Sens. Letts. 2015, 12, 2286–2290. [Google Scholar] [CrossRef]
- Hu, C.; Li, Y.; Dong, X.; Wang, R.; Ao, D. Performance Analysis of L-Band Geosynchronous SAR Imaging in the Presence of Ionospheric Scintillation. IEEE Trans. Geosci. Remote Sens. 2017, 55, 159–172. [Google Scholar] [CrossRef]
- Ji, Y.; Zhang, Y.; Dong, Z.; Zhang, Q.; Li, D.; Yao, B. Impacts of Ionospheric Irregularities on L-Band Geosynchronous Synthetic Aperture Radar. IEEE Trans. Geosci. Remote Sens. 2020, 58, 1–14. [Google Scholar] [CrossRef]
- Ruiz Rodon, J.; Broquetas, A.; Monti Guarnieri, A.; Rocca, F. Geosynchronous SAR Focusing With Atmospheric Phase Screen Retrieval and Compensation. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4397–4404. [Google Scholar] [CrossRef]
- Sun, Z.; Yen, G.G.; Wu, J.; Ren, H.; An, H.; Yang, J. Mission Planning for Energy-Efficient Passive UAV Radar Imaging System Based on Substage Division Collaborative Search. IEEE Trans. Cybern. 2021, 1–14. [Google Scholar] [CrossRef]
- An, H.; Wu, J.; Teh, K.C.; Sun, Z.; Yang, J. Geosynchronous Spaceborne-Airborne Bistatic SAR Imaging Based on Fast Low-Rank and Sparse Matrices Recovery. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–14. [Google Scholar] [CrossRef]
- Wu, J.; Sun, Z.; An, H.; Qu, J.; Yang, J. Azimuth Signal Multichannel Reconstruction and Channel Configuration Design for Geosynchronous Spaceborne CAirborne Bistatic SAR. IEEE Trans. Geosci. Remote Sens. 2019, 57, 1861–1872. [Google Scholar] [CrossRef]
- An, H.; Wu, J.; Sun, Z.; Yang, J. A Two-Step Nonlinear Chirp Scaling Method for Multichannel GEO Spaceborne-Airborne Bistatic SAR Spectrum Reconstructing and Focusing. IEEE Trans. Geosci. Remote Sens. 2019, 57, 3713–3728. [Google Scholar] [CrossRef]
- Sun, Z.; Wu, J.; Li, Z.; An, H.; He, X. Geosynchronous Spaceborne-Airborne Bistatic SAR Data Focusing Using a Novel Range Model Based on One-Stationary Equivalence. IEEE Trans. Geosci. Remote Sens. 2021, 59, 1214–1230. [Google Scholar] [CrossRef]
- Zhang, Y.; Xiong, W.; Dong, X.; Hu, C. A Novel Azimuth Spectrum Reconstruction and Imaging Method for Moving Targets in Geosynchronous Spaceborne CAirborne Bistatic Multichannel SAR. IEEE Trans. Geosci. Remote Sens. 2020, 58, 5976–5991. [Google Scholar] [CrossRef]
- Dong, X.; Xiong, W.; Zhang, Y.; Hu, C.; Liu, F. A Novel Geosynchronous Spaceborne-Airborne Bistatic Multichannel Sar For Ground Moving Targets Indication. In Proceedings of the IEEE IGARSS, Yokohama, Japan, 28 July–2 August 2019; pp. 3499–3502. [Google Scholar] [CrossRef]
- Guttrich, G.; Sievers, W.; Tomljanovich, N. Wide area surveillance concepts based on geosynchronous illumination and bistatic unmanned airborne vehicles or satellite reception. In Proceedings of the IEEE National Radar Conference, Syracuse, NY, USA 13–15 May 1997; pp. 126–131. [Google Scholar] [CrossRef]
- Sarabandi, K.; Kellndorfer, J.; Pierce, L. GLORIA: Geostationary/Low-Earth Orbiting Radar Image Acquisition System: A multi-static GEO/LEO synthetic aperture radar satellite constellation for Earth observation. In Proceedings of the IEEE IGARSS, Toulouse, France, 21–25 July 2003; Volume 2, pp. 773–775. [Google Scholar] [CrossRef]
- Lu, Z.; Wang, Y.; Xu, M.; Zhu, Y.; Jian, L.; Li, Z. Spacecraft Formation Design for Bistatic SAR with GEO Illuminator and LEO Receiver. In Proceedings of the IEEE IGARSS, Valencia, Spain, 22–27 July 2018; pp. 4451–4454. [Google Scholar] [CrossRef]
- Wang, Y.; Lu, Z.; Suo, Z.; Zhu, Y.; Li, Z.; Zhang, Q. Optimal configuration of spaceborne bistatic SAR with GEO transmitter and LEO receiver. IET Radar, Sonar Navigat. 2019, 13, 229–235. [Google Scholar] [CrossRef]
- Krieger, G.; Moreira, A. Multistatic SAR satellite formations: Potentials and challenges. In Proceedings of the IEEE International Geoscience Remote Sensing Symposium (IGARSS), Seoul, Korea, 25–29 July 2005; Volume 4, pp. 2680–2684. [Google Scholar] [CrossRef] [Green Version]
- Xiao, P.; Liu, B.; Guo, W. ConGaLSAR: A Constellation of Geostationary and Low Earth Orbit Synthetic Aperture Radar. IEEE Geosci. Remote Sens. Letts. 2020, 17, 2085–2089. [Google Scholar] [CrossRef]
- Leanza, A.; Manzoni, M.; Monti-Guarnieri, A.; di Clemente, M. LEO to GEO-SAR Interferences: Modelling and Performance Evaluation. Remote Sens. 2019, 11, 1720. [Google Scholar] [CrossRef] [Green Version]
- Xiao, P.; Guo, W.; Wu, Y.; Liu, B. A Comprehensive Method of Ambiguity Suppression for Constellation of Geostationary and Low Earth Orbit SAR. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2020, 13, 3327–3335. [Google Scholar] [CrossRef]
- Zhang, S.; Li, S.; Liu, Y.; Xing, M.; Chen, J. A Novel Azimuth Doppler Signal Reconstruction Approach for the GEO-LEO Bi-Static Multi-Channel HRWS SAR System. IEEE Access 2019, 7, 39539–39546. [Google Scholar] [CrossRef]
- Zhang, S.; Gao, Y.; Xing, M.; Guo, R.; Chen, J.; Liu, Y. Ground Moving Target Indication for the Geosynchronous-Low Earth Orbit Bistatic Multichannel SAR System. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2021, 14, 5072–5090. [Google Scholar] [CrossRef]
- Yang, J.; Yi, Q.; Li, Z.; Wu, J.; Huang, Y. Efficient translational variant bistatic SAR raw data generation based on 2D inverse Stolt mapping. In Proceedings of the 2013 IEEE International Geoscience and Remote Sensing Symposium - IGARSS, Melbourne, VIC, Australia, 21–26 July 2013; pp. 2489–2492. [Google Scholar] [CrossRef]
- Xiao, P.; Guo, W.; Liu, M.; Liu, B. A Three-Step Imaging Algorithm for the Constellation of Geostationary and Low Earth Orbit SAR (ConGaLSAR). IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–14. [Google Scholar] [CrossRef]
- Zhu, Y.; Lv, Z.; Wang, W.Q.; Liao, Y.; Zhang, S.; Zheng, Z. Nufft-Based Algorithm for Bistatic SAR Imaging Via Cooperative High-Orbit and Low-Orbit Satellites. In Proceedings of the 2019 IEEE IGARSS, Yokohama, Japan, 28 July–2 August 2019; pp. 3503–3506. [Google Scholar] [CrossRef]
- Zhang, X.; Gu, H.; Su, W. Focusing Bistatic Forward-looking SAR Images use Omega-k algorithm based on Modified Hyperbolic Approximating. In Proceedings of the 2019 International Conference on Control, Automation and Information Sciences (ICCAIS), Chengdu, China, 23–26 October 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, Y.; Li, Z.; Suo, Z.; Fang, C.; Chen, J. High-Resolution Wide-Swath Imaging of Spaceborne Multichannel Bistatic SAR With Inclined Geosynchronous Illuminator. IEEE Geosci. Remote Sens. Lett. 2017, 14, 2380–2384. [Google Scholar] [CrossRef]
- An, H.; Wu, J.; Teh, K.C.; Sun, Z.; Yang, J. Nonambiguous Image Formation for Low-Earth-Orbit SAR With Geosynchronous Illumination Based on Multireceiving and CAMP. IEEE Trans. Geosci. Remote Sens. 2021, 59, 348–362. [Google Scholar] [CrossRef]
- Prats, P.; Scheiber, R.; Mittermayer, J.; Meta, A.; Moreira, A. Processing of Sliding Spotlight and TOPS SAR Data Using Baseband Azimuth Scaling. IEEE Trans. Geosci. Remote Sens. 2010, 48, 770–780. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Ding, Z.; Xu, P.; Chen, K.; Zeng, T.; Long, T. Strip Layering Diagram-Based Optimum Continuously Varying Pulse Interval Sequence Design for Extremely High-Resolution Spaceborne Sliding Spotlight SAR. IEEE Trans. Geosci. Remote Sens. 2021, 59, 6751–6770. [Google Scholar] [CrossRef]
- Liu, W.; Sun, G.C.; Xia, X.G.; You, D.; Xing, M.; Bao, Z. Highly Squinted MEO SAR Focusing Based on Extended Omega-K Algorithm and Modified Joint Time and Doppler Resampling. IEEE Trans. Geosci. Remote Sens. 2019, 57, 9188–9200. [Google Scholar] [CrossRef]
- Sun, G.C.; Wu, Y.; Yang, J.; Xing, M.; Bao, Z. Full-Aperture Focusing of Very High Resolution Spaceborne-Squinted Sliding Spotlight SAR Data. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3309–3321. [Google Scholar] [CrossRef]
- Xu, W.; Deng, Y.; Huang, P.; Wang, R. Full-Aperture SAR Data Focusing in the Spaceborne Squinted Sliding-Spotlight Mode. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4596–4607. [Google Scholar] [CrossRef]
- Yang, W.; Chen, J.; Liu, W.; Wang, P.; Li, C. A Modified Three-Step Algorithm for TOPS and Sliding Spotlight SAR Data Processing. IEEE Trans. Geosci. Remote Sens. 2017, 55, 6910–6921. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.; Liang, Y.; Xing, M.; Huai, Y.; Gao, Y.; Zeng, L.; Bao, Z. An Improved Range Model and Omega-K-Based Imaging Algorithm for High-Squint SAR With Curved Trajectory and Constant Acceleration. IEEE Geosci. Remote Sens. Lett. 2016, 13, 656–660. [Google Scholar] [CrossRef]
- Wang, P.; Liu, W.; Chen, J.; Niu, M.; Yang, W. A High-Order Imaging Algorithm for High-Resolution Spaceborne SAR Based on a Modified Equivalent Squint Range Model. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1225–1235. [Google Scholar] [CrossRef] [Green Version]
- Wu, Y.; Sun, G.C.; Yang, C.; Yang, J.; Xing, M.; Bao, Z. Processing of Very High Resolution Spaceborne Sliding Spotlight SAR Data Using Velocity Scaling. IEEE Trans. Geosci. Remote Sens. 2016, 54, 1505–1518. [Google Scholar] [CrossRef]
- He, F.; Dong, Z.; Zhang, Y.; Jin, G.; Yu, A. Processing of Spaceborne Squinted Sliding Spotlight and HRWS TOPS Mode Data Using 2-D Baseband Azimuth Scaling. IEEE Trans. Geosci. Remote Sens. 2020, 58, 938–955. [Google Scholar] [CrossRef]
- Mittermayer, J.; Moreira, A.; Loffeld, O. Spotlight SAR data processing using the frequency scaling algorithm. IEEE Trans. Geosci. Remote Sens. 1999, 37, 2198–2214. [Google Scholar] [CrossRef]
- He, F.; Chen, Q.; Dong, Z.; Sun, Z. Processing of Ultrahigh-Resolution Spaceborne Sliding Spotlight SAR Data on Curved Orbit. IEEE Trans. Aerosp.Electron. Syst. 2013, 49, 819–839. [Google Scholar] [CrossRef]
- Zhao, B.; Qi, X.; Song, H.; Wang, R.; Mo, Y.; Zheng, S. An Accurate Range Model Based on the Fourth-Order Doppler Parameters for Geosynchronous SAR. IEEE Geosci. Remote Sens. Letts. 2014, 11, 205–209. [Google Scholar] [CrossRef]
- Lanari, R.; Tesauro, M.; Sansosti, E.; Fornaro, G. Spotlight SAR data focusing based on a two-step processing approach. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1993–2004. [Google Scholar] [CrossRef]
- Ma, L.; Zhu, Y.; Zhang, F.; Liang, J.; Zheng, L.; Liu, L.; Wang, Y. Spaceborne Repeat-pass Interferometric Synthetic Aperture Radar Experimental Evaluation for the GaoFen-3 Satellite. In Proceedings of the IEEE IGARSS, Valencia, Spain, 22–27 July 2018; pp. 2168–2171. [Google Scholar] [CrossRef]


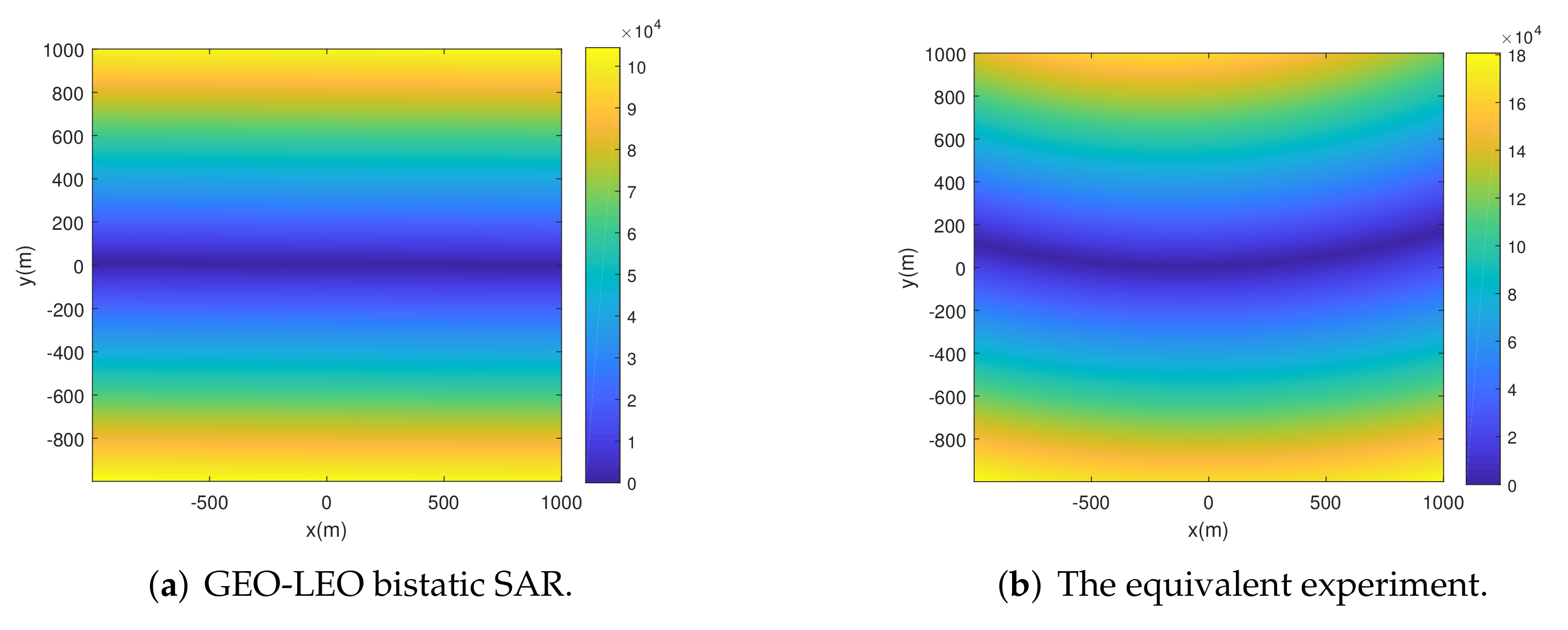


| System Parameters | |||
| Carrier fraquency | 5.4 GHz | Data take duration | 18 s |
| Signal bandwidth | 240 MHz | PRF | 5000 Hz |
| Pulse width | 45 μs | Rotation distance | 1146 km |
| Azimuth beam rotation rate | 0.37°/s | Receiver slant range | 990.4 km |
| Receiver azimuth beamwidth | 0.58° | Bistatic angle | 32.4° |
| Orbit Parameters | |||
| Platform | GEO | LEO | |
| Orbit altitude | 35,786 km | 754 km | |
| Eccentricity | 0.003 | 0.0009 | |
| Inclination | 20° | 98° | |
| Incidence angle | 43.9° | 41.2° | |
| Look angle | 6° | 36° | |
| Location | (8874, −24, 113, 26,908) km | (609, 235, 745) km | |
| Velocity | (−2661, −979, −0) km | (0, 7400, 1071) m | |
| Scene center | (0, 0, 0) m | ||
| Target Index | Azimuth | Range | ||||
|---|---|---|---|---|---|---|
| (m) | PSLR (dB) | ISLR (dB) | (m) | PSLR (dB) | ISLR (dB) | |
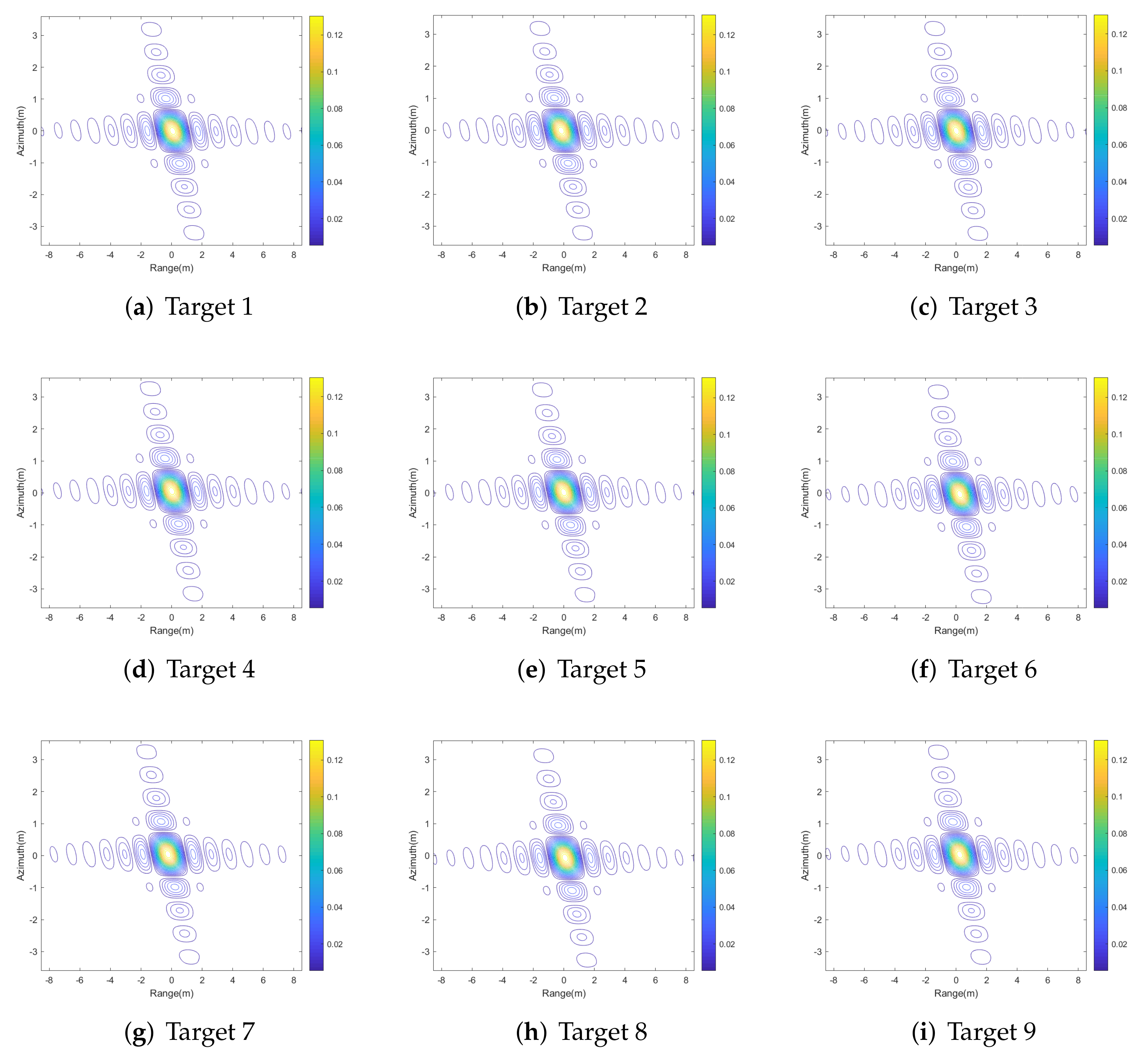
| 1 | 0.68 | −13.28 | −10.1 | 1.01 | −13.25 | −10.4 |
| 2 | 0.69 | −13.33 | −10.2 | 1.01 | −13.33 | −10.4 |
| 3 | 0.68 | −13.26 | −10.1 | 1.02 | −13.32 | −10.4 |
| 4 | 0.68 | −13.25 | −10.2 | 1.01 | −13.28 | −10.4 |
| 5 | 0.68 | −13.25 | −10.1 | 1.01 | −13.29 | −10.4 |
| 6 | 0.68 | −13.27 | −10.1 | 1.01 | −13.29 | −9.5 |
| 7 | 0.68 | −13.28 | −10.1 | 1.02 | −13.32 | −10.4 |
| 8 | 0.68 | −13.30 | −10.4 | 1.01 | −13.36 | −10.5 |
| 9 | 0.69 | −13.31 | −10.1 | 1.01 | −13.33 | −10.4 |
| Target Index | Azimuth | Range | ||||
|---|---|---|---|---|---|---|
| (m) | PSLR (dB) | ISLR (dB) | (m) | PSLR (dB) | ISLR (dB) | |
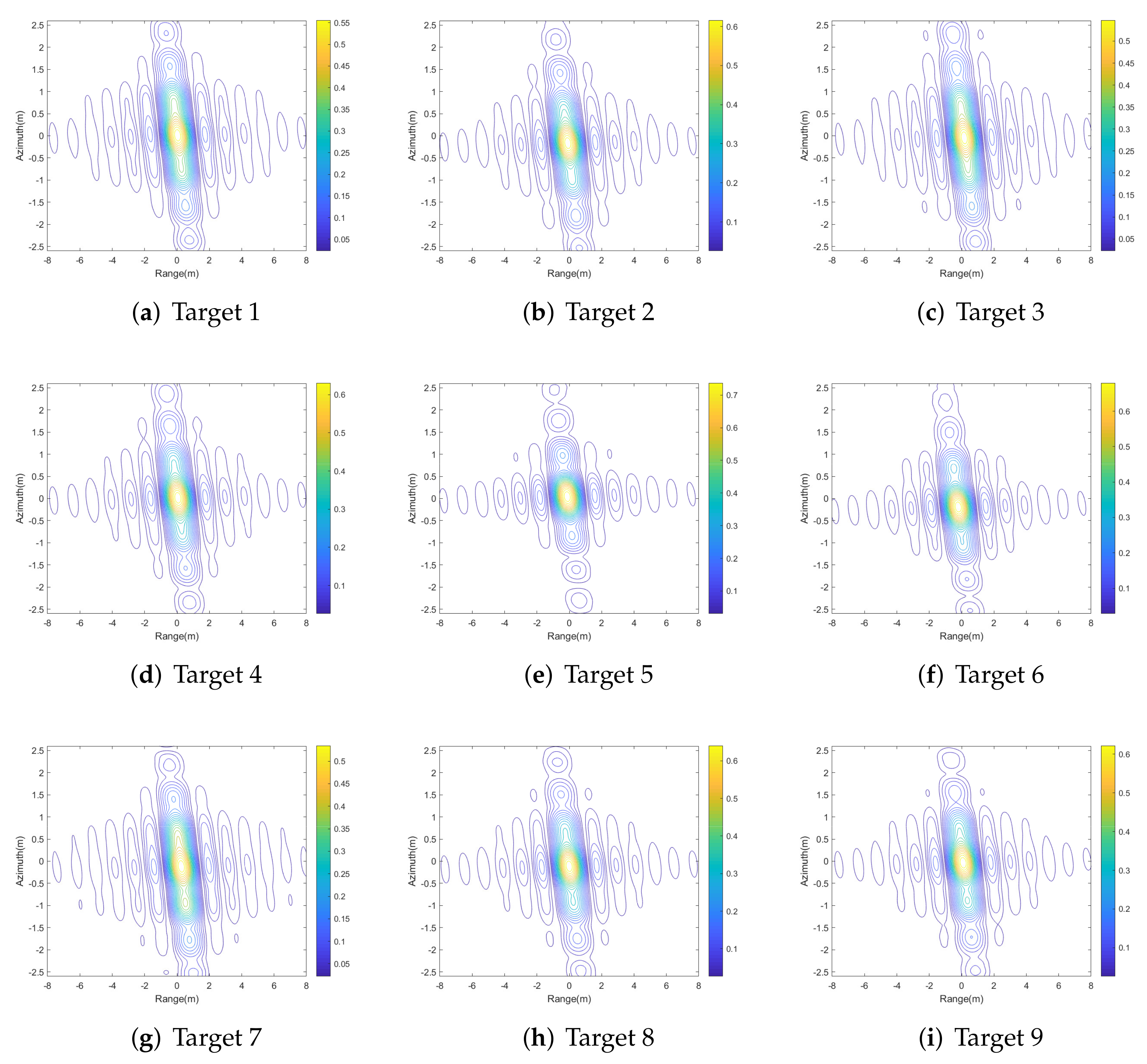
| 1 | 0.91 | −3.60 | −1.5 | 1.01 | −13.24 | −10.5 |
| 2 | 0.78 | −5.85 | −3.5 | 1.01 | −13.24 | −10.4 |
| 3 | 0.78 | −5.78 | −4.1 | 1.01 | −13.29 | −10.4 |
| 4 | 0.76 | −6.50 | −4.2 | 1.01 | −13.35 | −10.5 |
| 5 | 0.72 | −10.68 | −8.1 | 1.01 | −13.29 | −10.4 |
| 6 | 0.71 | −7.62 | −7.1 | 1.01 | −13.30 | −9.8 |
| 7 | 1.07 | −2.80 | −0.7 | 1.02 | −13.39 | −10.4 |
| 8 | 0.73 | −6.09 | −4.1 | 1.01 | −13.32 | −10.4 |
| 9 | 0.75 | −5.9 | −4.2 | 1.01 | −13.33 | −10.4 |
| System Parameters | |||
| Carrier fraquency | 5.4 GHz | Data take duration | 6 s |
| Signal bandwidth | 240 MHz | PRF | 3714 Hz |
| Pulse width | 45 μs | Rotation distance | 1091.1 km |
| Azimuth beam rotation rate | 0.387°/s | GF-3 slant range | 844.4 km |
| GF-3 azimuth beamwidth | 0.678° | Bistatic angle | 23.2° |
| Plarform Parameters | |||
| Platform | GF-3 | Stationary receiver | |
| Platform altitude | 754 km | 69 m | |
| Incidence angle | 28.3° | 86.6° | |
| Initial position | (73.8, 39.3, 74.3) km | (−155, 693, 69) m | |
| speed | (7434, −1463, −5) km | (0, 0, 0) m | |
| Isolated strong target location | |||
| location | (0, 0, 0) m | ||
| Method | Azimuth | Range | ||||
|---|---|---|---|---|---|---|
| (m) | PSLR (dB) | ISLR (dB) | (m) | PSLR (dB) | ISLR (dB) | |
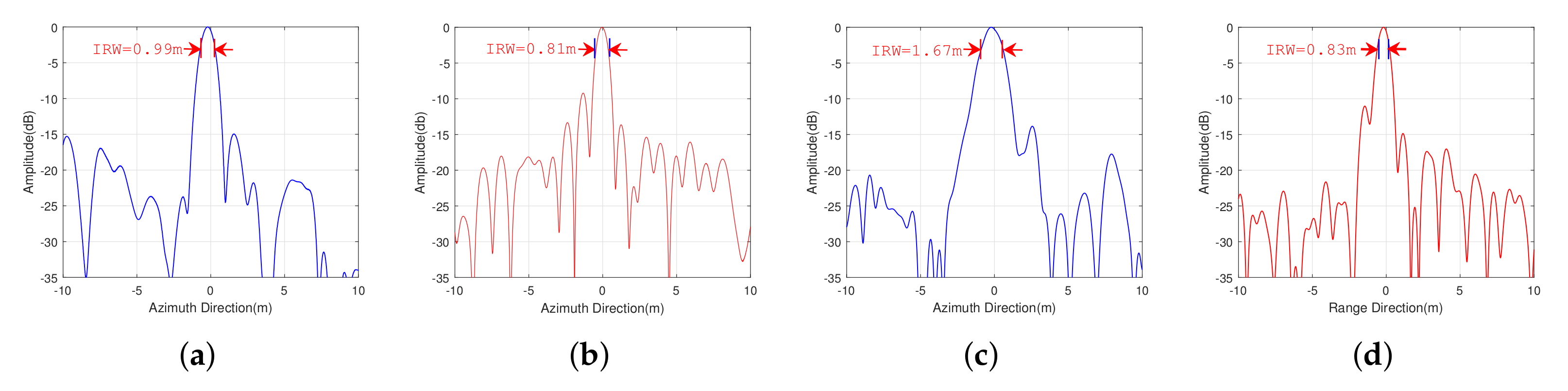
| proposed method | 0.99 | −14.97 | −9.68 | 0.81 | −9.25 | −7.28 |
| ’non-stop-and-go’ RMOSE method | 1.67 | −13.95 | −8.99 | 0.83 | −11.07 | −7.08 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Z.; Chen, T.; Sun, H.; Wu, J.; Lu, Z.; Li, Z.; An, H.; Yang, J. A Novel Frequency-Domain Focusing Method for Geosynchronous Low-Earth-Orbit Bistatic SAR in Sliding-Spotlight Mode. Remote Sens. 2022, 14, 3178. https://doi.org/10.3390/rs14133178
Sun Z, Chen T, Sun H, Wu J, Lu Z, Li Z, An H, Yang J. A Novel Frequency-Domain Focusing Method for Geosynchronous Low-Earth-Orbit Bistatic SAR in Sliding-Spotlight Mode. Remote Sensing. 2022; 14(13):3178. https://doi.org/10.3390/rs14133178
Chicago/Turabian StyleSun, Zhichao, Tianfu Chen, Huarui Sun, Junjie Wu, Zheng Lu, Zhongyu Li, Hongyang An, and Jianyu Yang. 2022. "A Novel Frequency-Domain Focusing Method for Geosynchronous Low-Earth-Orbit Bistatic SAR in Sliding-Spotlight Mode" Remote Sensing 14, no. 13: 3178. https://doi.org/10.3390/rs14133178
APA StyleSun, Z., Chen, T., Sun, H., Wu, J., Lu, Z., Li, Z., An, H., & Yang, J. (2022). A Novel Frequency-Domain Focusing Method for Geosynchronous Low-Earth-Orbit Bistatic SAR in Sliding-Spotlight Mode. Remote Sensing, 14(13), 3178. https://doi.org/10.3390/rs14133178






