Three-Dimensional Imaging with Bistatic Vortex Electromagnetic Wave Radar
Abstract
:1. Introduction
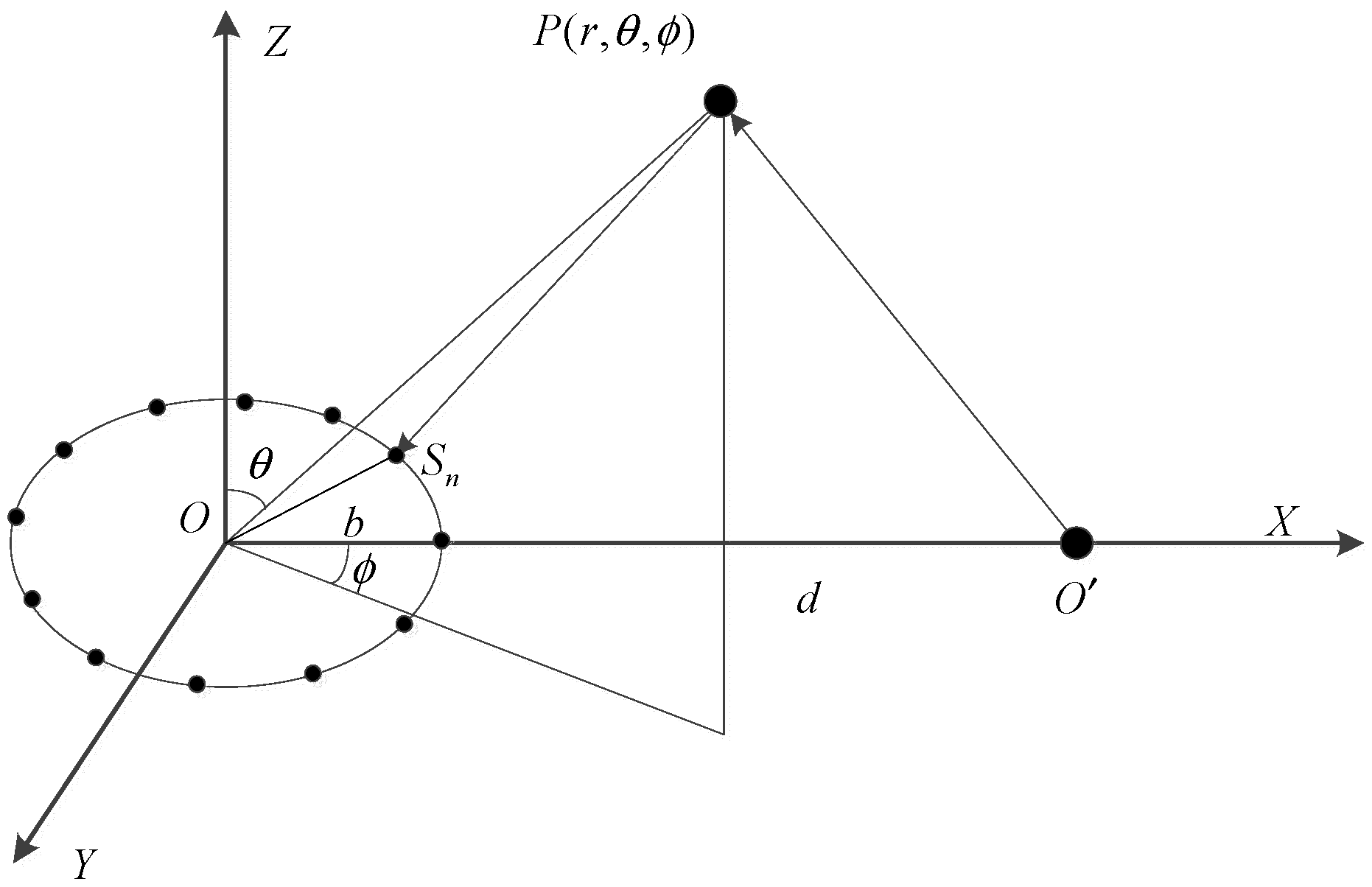
2. Echo of Bistatic Vortex EM Wave Radar
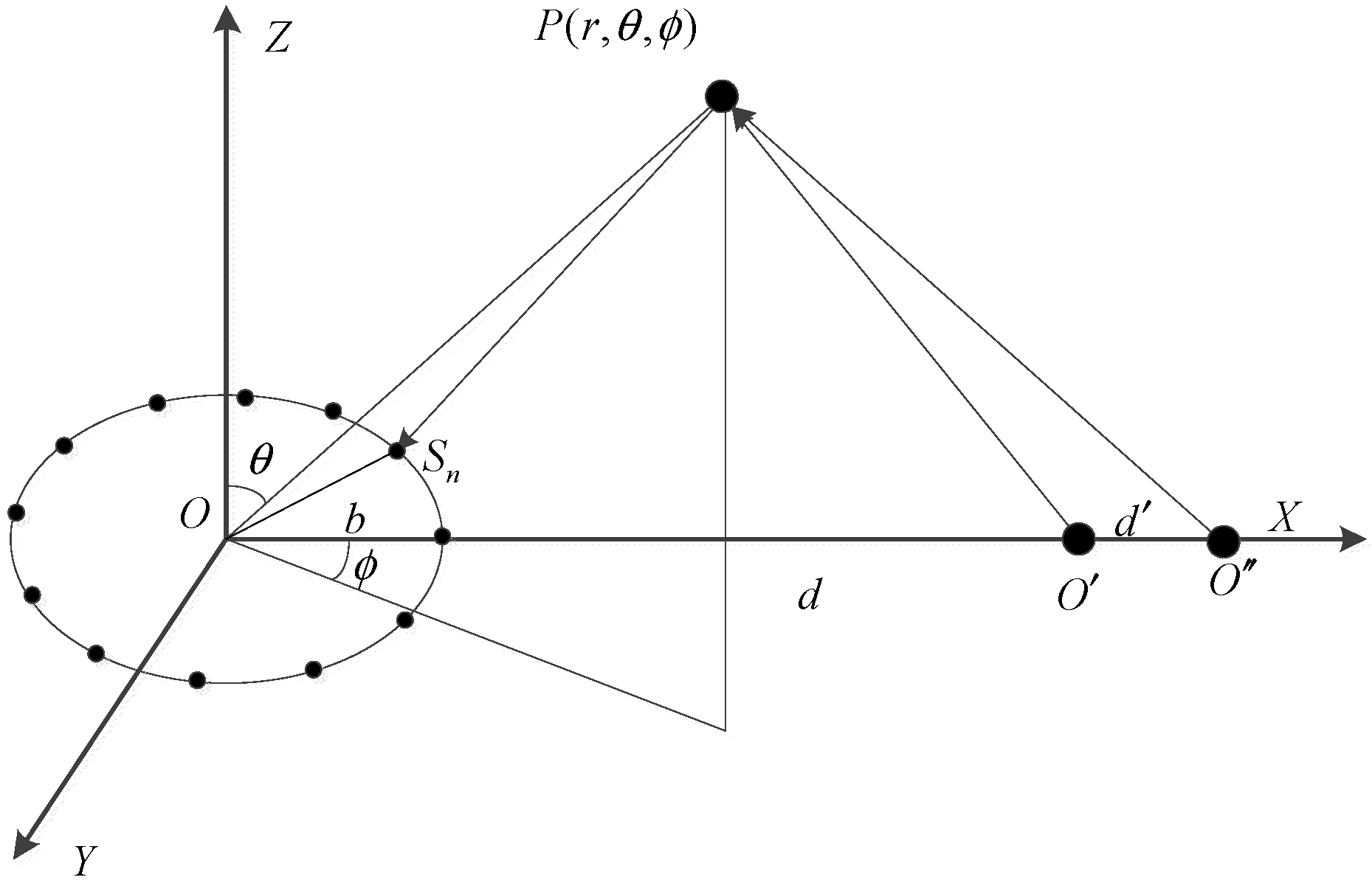
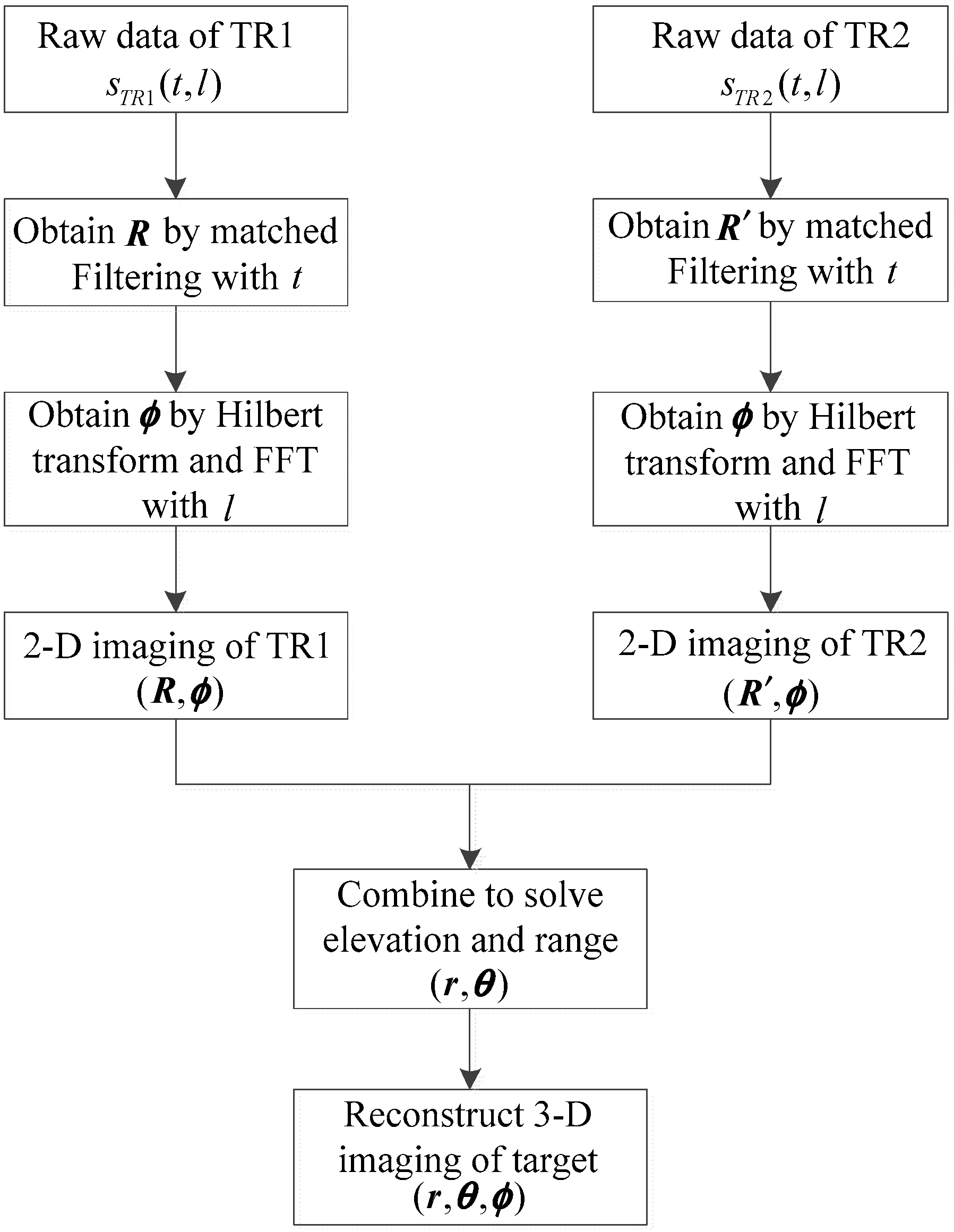
3. Three-Dimensional Imaging Method in Bistatic Geometry
4. Simulation
4.1. Range Imaging in Bistatic Geometry
4.2. 2-D Imaging in Bistatic Geometry
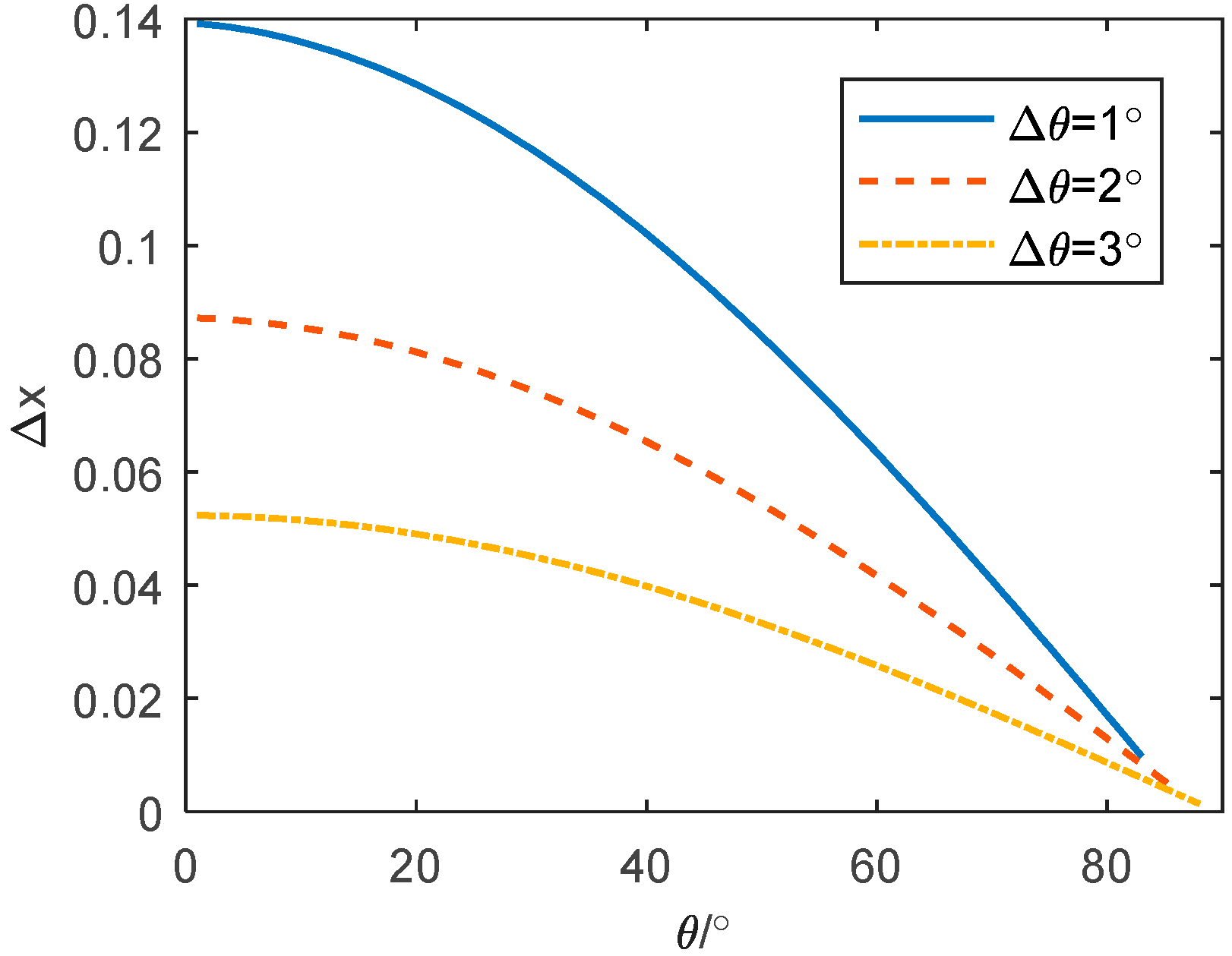
4.3. 3-D Imaging in Bistatic Geometry
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, X.-Y.; Zhu, Y.; Xie, W.; Peng, G.-H.; Wang, W. Generation of plane spiral orbital angular momentum waves by microstrip Yagi antenna array. IEEE Access 2020, 8, 175688–175696. [Google Scholar] [CrossRef]
- Liu, K.; Cheng, Y.; Yang, Z.; Wang, H.; Qin, Y.; Li, X. Orbital-Angular-Momentum-Based Electromagnetic Vortex Imaging. IEEE Antennas Wirel. Propag. Lett. 2014, 14, 711–714. [Google Scholar] [CrossRef]
- Liu, K.; Cheng, Y.; Gao, Y.; Li, X.; Qin, Y.; Wang, H. Super-resolution radar imaging based on experimental OAM beams. Appl. Phys. Lett. 2017, 110, 164102. [Google Scholar] [CrossRef]
- Liu, K.; Li, X.; Gao, Y.; Cheng, Y.; Wang, H.; Qin, Y. High-Resolution Electromagnetic Vortex Imaging Based on Sparse Bayesian Learning. IEEE Sens. J. 2017, 17, 6918–6927. [Google Scholar] [CrossRef]
- Yuan, T.; Wang, H.; Qin, Y.; Cheng, Y. Electromagnetic Vortex Imaging Using Uniform Concentric Circular Arrays. IEEE Antennas Wirel. Propag. Lett. 2015, 15, 1024–1027. [Google Scholar] [CrossRef]
- Yuan, T.; Cheng, Y.; Wang, H.; Qin, Y. Beam Steering for Electromagnetic Vortex Imaging Using Uniform Circular Arrays. IEEE Antennas Wirel. Propag. Lett. 2016, 16, 704–707. [Google Scholar] [CrossRef]
- Yuan, H.; Chen, Y.-J.; Luo, Y.; Liang, J.; Wang, Z.-H. A Resolution-Improved Imaging Algorithm Based on Uniform Circular Array. IEEE Antennas Wirel. Propag. Lett. 2021, 21, 461–465. [Google Scholar] [CrossRef]
- Chen, R.; Long, W.-X.; Gao, Y.; Li, J. Orbital Angular Momentum-Based Two-Dimensional Super-Resolution Targets Imaging. In Proceedings of the 2018 IEEE Global Conference on Signal and Information Processing (GlobalSIP), Anaheim, CA, USA, 26–29 November 2018; pp. 1243–1246. [Google Scholar] [CrossRef]
- Zeng, Y.; Wang, Y.; Chen, Z.; Zhang, J.; Zhang, J. Two-dimensional OAM radar imaging using uniform circular antenna arrays. In Proceedings of the 2020 14th European Conference on Antennas and Propagation (EuCAP), Copenhagen, Denmark, 15–20 March 2020; pp. 1–4. [Google Scholar] [CrossRef]
- Liu, Z.; Li, K.; Li, R.; Jiang, G.; Song, Z. Missile-borne Near-field Radar Coincidence Imaging Using a Uniform Circular Array. In Proceedings of the 2020 IEEE 3rd International Conference on Electronic Information and Communication Technology (ICEICT), Shenzhen, China, 13–15 November 2020; pp. 574–578. [Google Scholar] [CrossRef]
- Li, R.; Luo, Y.; Zhang, Q.; Li, B. Time-Varying Bistatic Radar Coincidence Imaging for Rotating Targets. In Proceedings of the 2019 IEEE 2nd International Conference on Electronic Information and Communication Technology (ICEICT), Harbin, China, 20–22 January 2019; pp. 495–498. [Google Scholar] [CrossRef]
- Guo, S.; He, Z.; Fan, Z.; Chen, R. CUCA Based Equivalent Fractional Order OAM Mode for Electromagnetic Vortex Imaging. IEEE Access 2020, 8, 91070–91075. [Google Scholar] [CrossRef]
- Liu, H.; Wang, Y.; Wang, J.; Liu, K.; Wang, H. Electromagnetic Vortex Enhanced Imaging Using Fractional OAM Beams. IEEE Antennas Wirel. Propag. Lett. 2021, 20, 948–952. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhou, Y.; Chen, Y.; Bu, L.; Zhao, H. A Mode Optimization Method for Vortex Electromagnetic Wave Radar Imaging. IEEE Geosci. Remote Sens. Lett. 2022, 19, 4024405. [Google Scholar] [CrossRef]
- Li, R.; Hu, H.; Lei, S.; Lin, Z.; Chen, B. Elevation imaging based on vortex electromagnetic wave. In Proceedings of the 2019 IEEE International Symposium on Antennas and Propagation and USNC-URSI Radio Science Meeting, Atlanta, GA, USA, 7–12 July 2019; pp. 827–828. [Google Scholar]
- Lin, M.; Gao, Y.; Liu, P.; Liu, J. Super-resolution orbital angular momentum based radar targets detection. Electron. Lett. 2016, 52, 1168–1170. [Google Scholar] [CrossRef]
- Zeng, Y.; Wang, Y.; Zhou, C.; Cui, J.; Yi, J.; Zhang, J. Super-resolution Electromagnetic Vortex SAR Imaging Based on Compressed Sensing. In Proceedings of the 2020 IEEE/CIC International Conference on Communications in China (ICCC), Chongqing, China, 9–11 August 2020; pp. 629–633. [Google Scholar] [CrossRef]
- Bu, X.; Zhang, Z.; Chen, L.; Liang, X.; Tang, H.; Wang, X. Implementation of Vortex Electromagnetic Waves High-Resolution Synthetic Aperture Radar Imaging. IEEE Antennas Wirel. Propag. Lett. 2018, 17, 764–767. [Google Scholar] [CrossRef]
- Fang, Y.; Wang, P.; Chen, J. A Novel Imaging Formation Method for Electromagnetic Vortex SAR Based on Orbital-Angular-Momentum. In Proceedings of the 2018 China International SAR Symposium (CISS), Shanghai, China, 10–12 October 2018; pp. 1–3. [Google Scholar] [CrossRef]
- Liu, H.; Liu, K.; Cheng, Y.; Wang, H. Microwave Vortex Imaging Based on Dual Coupled OAM Beams. IEEE Sens. J. 2019, 20, 806–815. [Google Scholar] [CrossRef]
- Jiang, Y.; Liu, K.; Wang, H.; Deng, B.; Zhuang, Z. Orbital-Angular-Momentum-Based ISAR Imaging at Terahertz Frequencies. IEEE Sens. J. 2018, 18, 9230–9235. [Google Scholar] [CrossRef]
- Xu, X.; Liu, Y. Three-dimensional Interferometric MIMO Radar Imaging for Target Scattering Diagnosis. J. Radars 2018, 7, 655–663. [Google Scholar] [CrossRef]
- Wang, J.; Liu, K.; Liu, H.; Cao, K.; Cheng, Y.; Wang, H. 3-D Object Imaging Method with Electromagnetic Vortex. IEEE Trans. Geosci. Remote Sens. 2021, 60, 2000512. [Google Scholar] [CrossRef]
- Wang, J.; Liu, K.; Cheng, Y.; Wang, H. Three-Dimensional Target Imaging Based on Vortex Stripmap SAR. IEEE Sens. J. 2018, 19, 1338–1345. [Google Scholar] [CrossRef]
- Wang, L.; Tao, L.; Li, Z.; Wu, J.; Yang, J. Three Dimensional Electromagnetic Vortex Radar Imaging Based on the Modified RD Algorithm. In Proceedings of the 2020 IEEE Radar Conference (RadarConf20), Florence, Italy, 21–25 September 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Bu, X.-X.; Zhang, Z.; Chen, L.-Y.; Zhu, K.-H.; Zhou, S.; Luo, J.-P.; Cheng, R.; Liang, X.-D. Synthetic Aperture Radar Interferometry Based on Vortex Electromagnetic Waves. IEEE Access 2019, 7, 82693–82700. [Google Scholar] [CrossRef]
- Liang, J.; Li, Y.; Zhang, P.F.; Jiang, X.W.; Cai, B. Three-Dimensional Imaging Method of Vortex Electromagnetic Wave Using MIMO Array. In Proceedings of the International Conference in Communications, Signal Processing, and Systems, Urumqi, China, 20–22 July 2019; Springer: Singapore, 2019; pp. 2350–2356. [Google Scholar]
- Yan, F.; Jin, M.; Qiao, X. Low-Complexity DOA Estimation Based on Compressed MUSIC and Its Performance Analysis. IEEE Trans. Signal Process. 2013, 61, 1915–1930. [Google Scholar] [CrossRef]


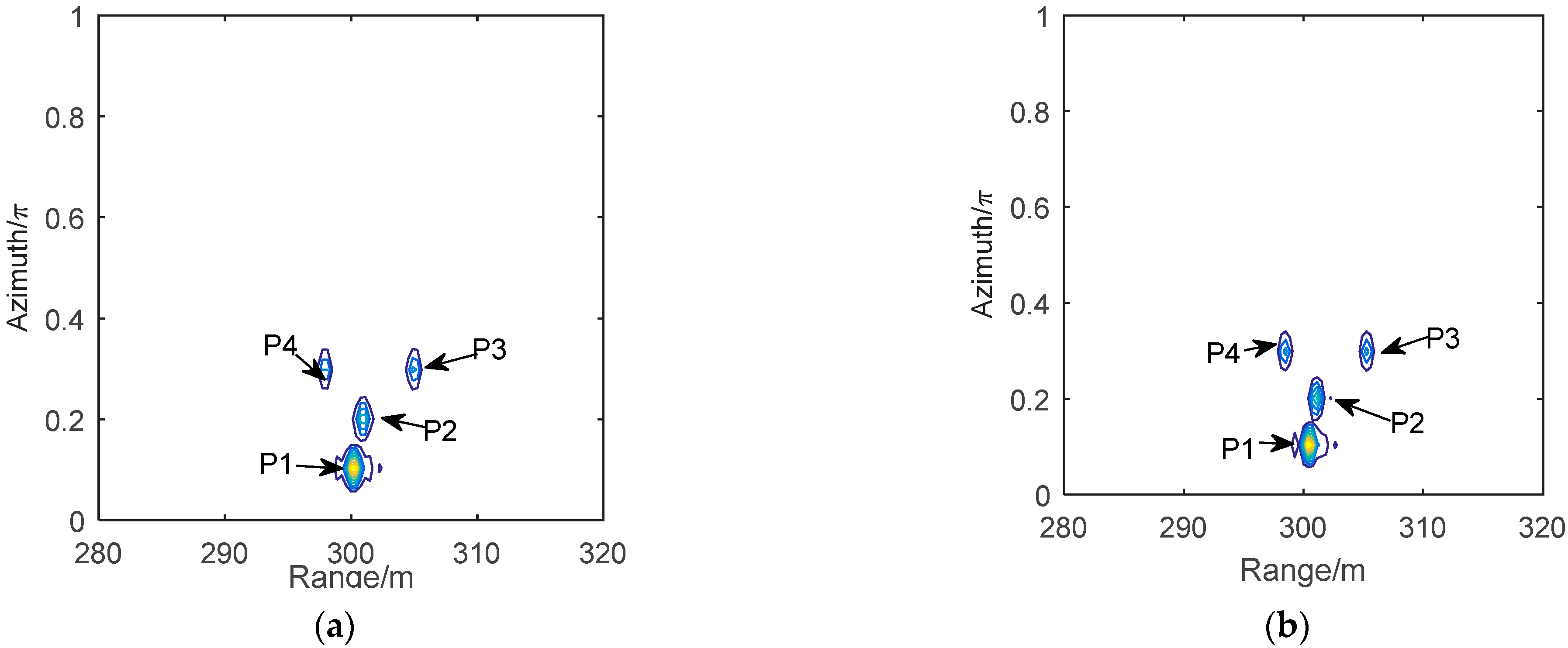
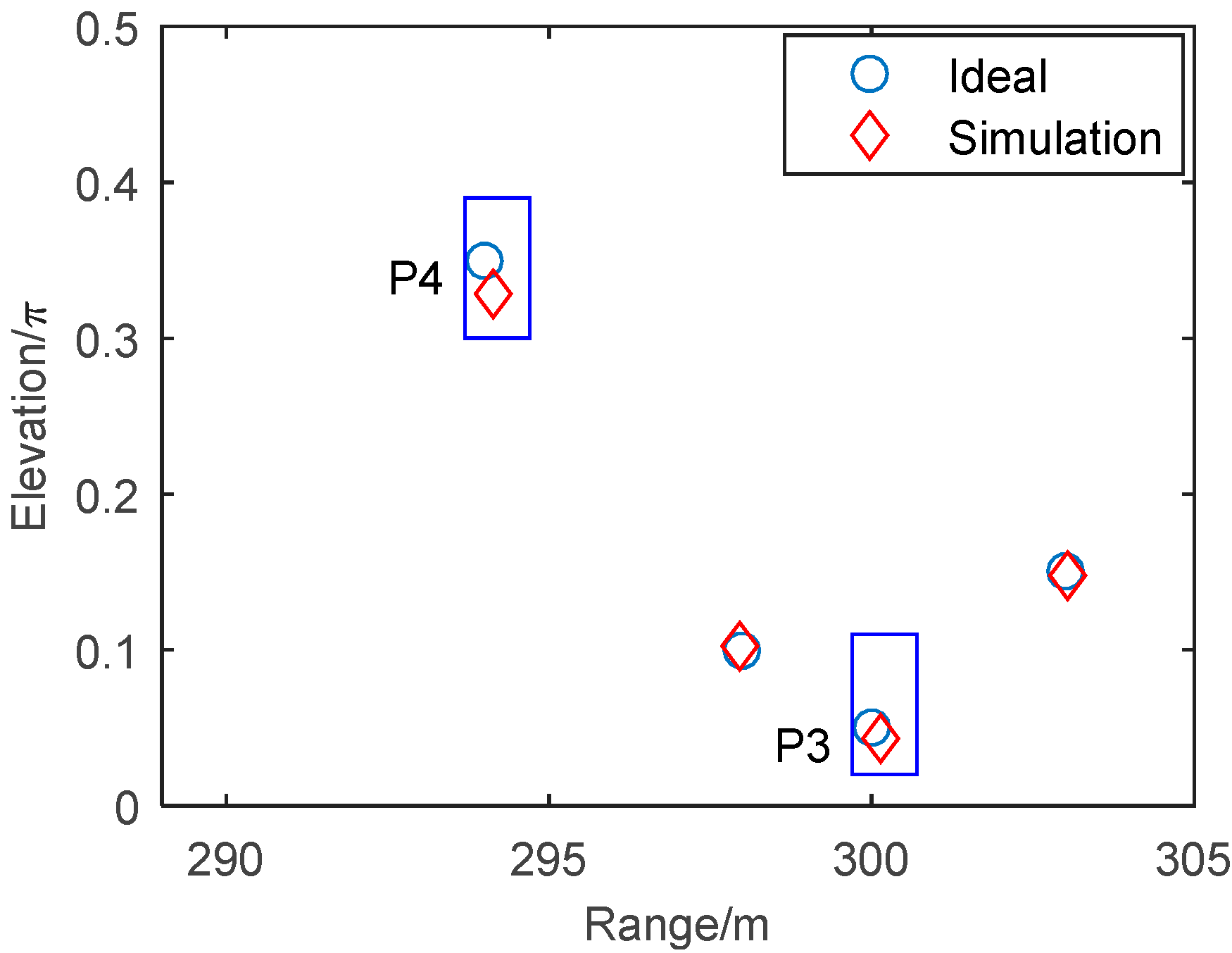

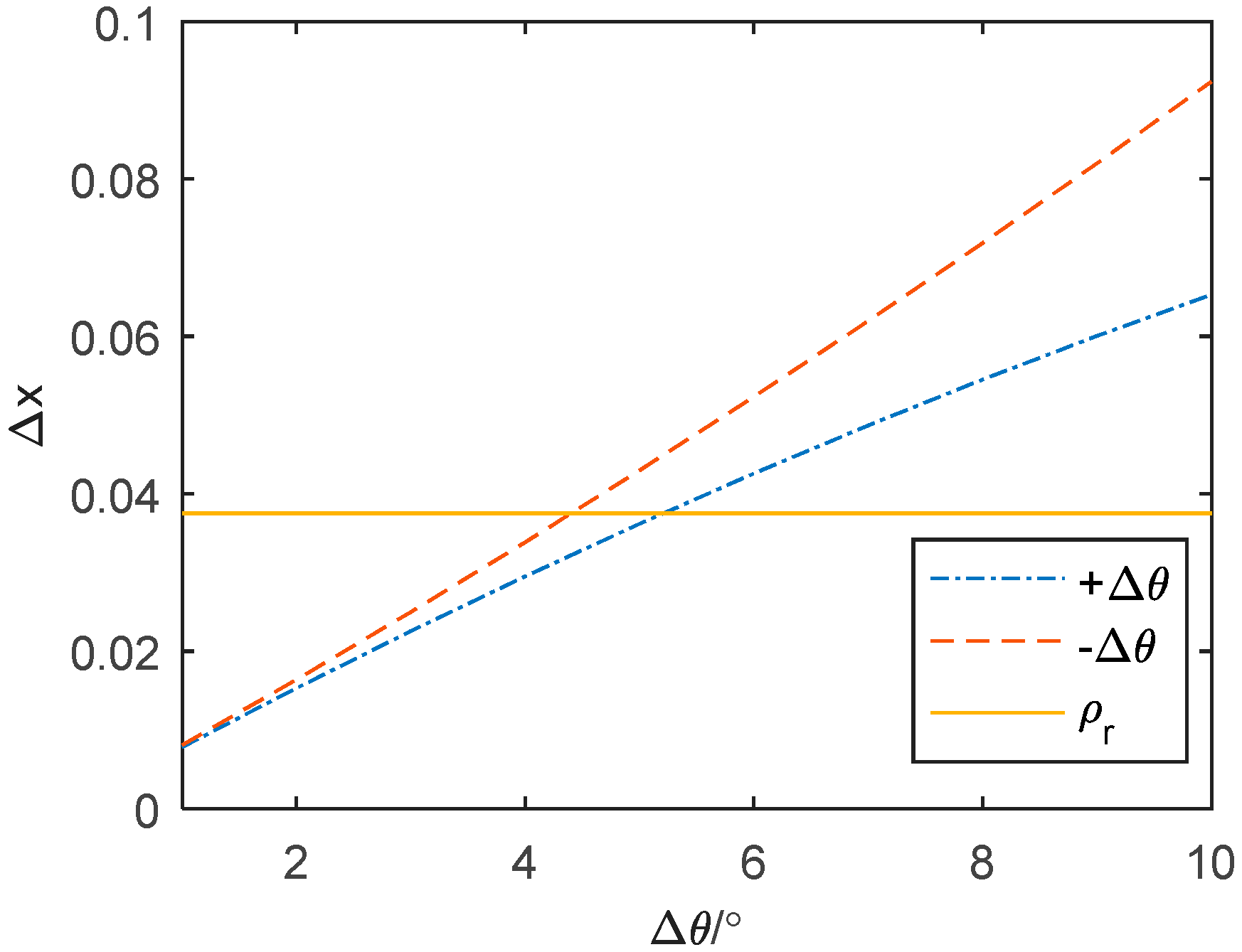
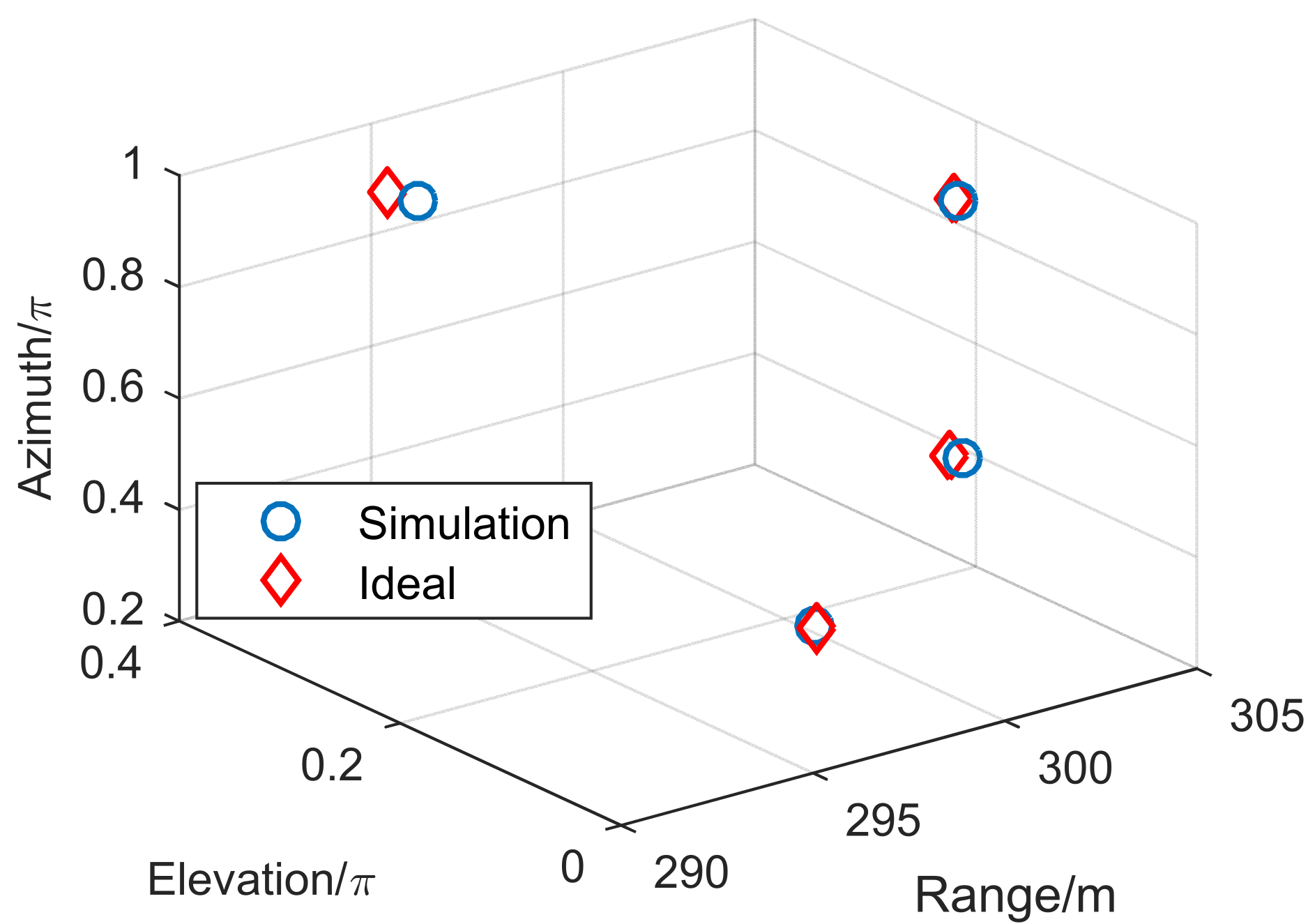
| The Number of Scatters | Range Result in Monostatic Geometry (m) | Range Result in Bistatic Geometry of TR1 (m) | Range Result in Bistatic Geometry of TR2 (m) |
|---|---|---|---|
| 298 | 300.2042 | 300.4981 | |
| 300 | 300.9492 | 301.0757 | |
| 303 | 305.0014 | 305.2682 | |
| 294 | 297.9279 | 298.4516 |
| Elevation Resolution | Method | Element Number | Calculation Amount |
|---|---|---|---|
| MUSIC | 10 | 1.98 × 103 | |
| Proposed method | 10 | 1.4 × 103 | |
| MUSIC | 20 | 8.18 × 103 | |
| Proposed method | 10 | 1.73 × 103 | |
| MUSIC | 30 | 21.87 × 103 | |
| Proposed method | 10 | 3.6 × 103 | |
| MUSIC | 40 | 38.76 × 103 | |
| Proposed method | 10 | 5.34 × 103 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, J.; Zhang, Q.; Luo, Y.; Yuan, H.; Chen, Y. Three-Dimensional Imaging with Bistatic Vortex Electromagnetic Wave Radar. Remote Sens. 2022, 14, 2972. https://doi.org/10.3390/rs14132972
Liang J, Zhang Q, Luo Y, Yuan H, Chen Y. Three-Dimensional Imaging with Bistatic Vortex Electromagnetic Wave Radar. Remote Sensing. 2022; 14(13):2972. https://doi.org/10.3390/rs14132972
Chicago/Turabian StyleLiang, Jia, Qun Zhang, Ying Luo, Hang Yuan, and Yijun Chen. 2022. "Three-Dimensional Imaging with Bistatic Vortex Electromagnetic Wave Radar" Remote Sensing 14, no. 13: 2972. https://doi.org/10.3390/rs14132972
APA StyleLiang, J., Zhang, Q., Luo, Y., Yuan, H., & Chen, Y. (2022). Three-Dimensional Imaging with Bistatic Vortex Electromagnetic Wave Radar. Remote Sensing, 14(13), 2972. https://doi.org/10.3390/rs14132972






