Abstract
The extraction of landslide deformation using terrestrial laser scanning (TLS) has many important applications. The landslide deformation can be extracted based on a digital terrain model (DTM). However, such methods usually suffer from the ill-posed problem of a multiplicative error model as illustrated in previous studies. Moreover, the edge drift of commonly used spherical targets for point cloud registration (PCR) is ignored in the existing method, which will result in the unstable precision of the PCR. In response to these problems, we propose a method for extracting landslide deformations from TLS data. To archive the PCR of different period point clouds, a new triangular pyramid target is designed to eliminate the edge drift. If a fixed target is inconvenient, we also propose a PCR method based on total station orientation. Then, the use of the Tikhonov regularization method to derive the weighted least squares regularization solution is presented. Finally, the landslide deformation is extracted by DTM deference. The experiments are conducted on two datasets with more than 1.5 billion points. The first dataset takes Lashagou NO. 3 landslide in Gansu Province, China, as the research object; the point cloud data were collected on 26 February 2021 and 3 May 2021. The registration accuracy was 0.003 m based on the permanent triangular pyramid target and 0.005 m based on the total station orientation. The landslide deforms within 3 cm due to the ablation of the frozen soil. The second dataset is TLS data from the Lihua landslide in Chongqing, China, collected on 20 April 2021 and 1 May 2021. The overall deformation of the Lihua landslide is small, with a maximum value of 0.011 m. The result shows that the proposed method achieves a better performance than previous sphere-based registration and that the weighted least square regularization iterative solution can effectively reduce the ill-condition of the model.
1. Introduction
The extraction of landslide deformation is important for many applications [1,2,3,4], such as disaster management and deformation detection. Laser scanning can be used to acquire accurate and dense 3D points from a target surface and has unique advantages when it comes to landslide monitoring, deformation extraction, and disaster management.
As the most direct manifestation of landslide stability, landslide surface deformation has received special attention from scholars [5,6,7]. Conventional landslide monitoring methods, such as using the GNSS (Global Navigation Satellite System) [8,9,10], leveling [11,12], crack gauges [13,14], etc., can only obtain sparse measurements at a few locations or within the affected slopes. Therefore, it is difficult to interpret the overall deformation characteristics of a landslide [15,16]. Terrestrial laser scanning (TLS) is a ground-based active imaging method that rapidly acquires precise and dense 3D point clouds on the surface of objects through laser ranging. Guo et al. [17] used point cloud data and the digital elevation model visualization method capable of a sky view to carry out geological disaster identification research and verified the reliability of airborne LiDAR identification results through field investigation. Abellan et al. [18] used TLS technology to monitor a dangerous rock mass in Spain, and discussed the feasibility of millimeter-level high-precision monitoring. Kayen et al. [19] used TLS to monitor nearly 400 large landslides induced by the Chuetsu earthquake in Niigata Prefecture, Japan, and greatly improved the efficiency of post-earthquake disaster assessment. Liu et al. [20] proposed a landslide displacement monitoring method based on point cloud density characteristics; the method identified the slope variation area and directly reflected the landslide surface deformation.
PCR can merge these individually scanned period point clouds. The basic idea of PCR is to seek the best transformation parameters to transform a point cloud with a local coordinate system to the same reference system [21]. PCR is divided into real-time registration and accurate registration of point clouds in different periods. Real-time registration refers to the detection of the surrounding environment while scanning and registering the real-time scanning point cloud using mobile laser scanning with the acquired point cloud. It is widely used for fast modeling, indoor navigation, and simultaneous localization and mapping (SLAM). It is a low-precision PCR method. The point cloud data of different periods is typically obtained using fixed scanners (such as TLS). The main PCR methods for different period data are marker-based registration and data-based registration.
However, there are still many problems with the application of landslide monitoring using TLS technology [22,23]. When using TLS to monitor landslide deformation, it is necessary to collect a multi-period landslide point cloud and calculate the landslide deformation by comparing the spatial position of the point cloud. Unfortunately, each period point cloud is based on an independent coordinate system, and the reference data are not unified, resulting in the low accuracy and unreliable results of landslide deformation detection [24].
The widely used marker in TLS is the standard spherical target [25,26]. Spherical targets have high precision and are easy to carry, but they are expensive, require high precision in manufacturing and maintenance, and cause edge drift because of their excessive laser reflection angle. The spherical target is shown in Figure 1, and the spherical target cloud is shown in Figure 2. Since the edge drift is concentrated away from the scanning side, it does not receive uniformly distributed random noise, which will cause non-negligible calculation errors in the spherical center coordinates. An ICP algorithm is the most used data-based PCR method due to its simple iteration and fast convergence [27]. The principle of ICP is to find the nearest correspondence in the source and the target point cloud and use the distance matrix of the nearest correspondence to estimate the rotation and translation parameters [28].

Figure 1.
Spherical target.
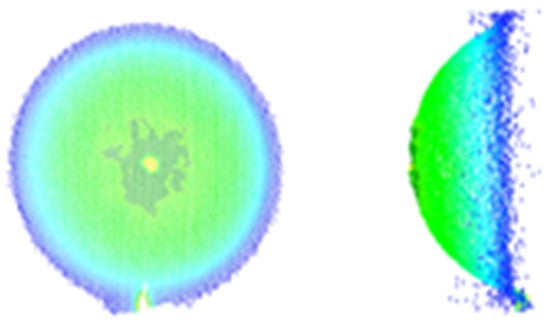
Figure 2.
Point cloud of spherical target.
The landslide deformation can be extracted based on DTM [29,30]. Unfortunately, the DTM adjustment model is a typical ill-posed multiplicative random error model [31]. The ill-posed error model widely exists in the processing of remote sensing causing the instability of the parameter solution and even serious deviations from the true value. Xu et al. [32] first proposed the least square solution for the multiplicative error model. Shi et al. [33] summarized the least square, weighted the least square, and bias-corrected the weighted least square method of the multiplicative error model, and deduced the accuracy formula for the parameter estimation. If these three methods are used to deal with the ill-posed multiplicative error model without considering the ill-posed feature of the coefficient matrix, the parameter estimation will be biased and unstable. To avoid the ill-posed coefficient matrix, Wang et al. [34] built a DTM using the points at the peaks in the simulated data. This model can only be used to process simulation data and cannot be applied to practical observational data. Due to the ill-posed coefficient matrix, the complex collinearity between the column vectors of the coefficient matrix causes the condition number of the normal equation to be too large and thus the solution is unstable. Therefore, research on ill-posed multiplicative random error model adjustment theory needs to be further studied. At present, the methods for dealing with ill-posed multiplicative error models mainly include truncated singular-value decomposition (TSVD) [35], the Tikhonov regularization method [36], the ridge estimation method [37], and the virtual observation value solution [38]. The Tikhonov regularization method is a general adjustment method that strictly adheres to the theory. It is commonly used to solve the ill-posed multiplicative random error model.
The works mentioned above have carried out detailed studies on the landslide deformation extraction from TLS. The PCR of different period point cloud and the DTM construction are the vital procedures for deformation extraction. However, the number of point clouds on a marker sphere is sparse in the scanning process of a landslide. Edge drift caused by an excessively large laser reflection angle inevitably occurs due to the characteristics of the sphere. Thus, the calculation error of the spherical center coordinates cannot be disregarded. In this research, a new triangular pyramid target was developed which can unify the data of the multi-period point cloud by three non-parallel surfaces. In addition, aiming to address the problems of poor site access conditions and inconvenient traffic, we also propose a new scheme of data acquisition and registration based on total station orientation. The DTM adjustment model is an ill-posed multiplicative error model. If an ill-posed coefficient matrix is not considered, the parameter estimation will be biased and unstable. Hence, we utilize the Tikhonov regularization method to derive the weighted least squares regularization solution.
2. Methodology
The method proposed in this paper mainly consists of three steps. First, the PCR of the multi-period point cloud data is performed. Then, considering the ill-multiplicative error model, a weighted least square regularization iterative solution is proposed for DTM construction. Finally, the landslide deformation is obtained by differential DTMs.
2.1. PCR of Multi-Period Point Cloud Data
2.1.1. PCR Based on Triangular Pyramid Target
Multi-phase point cloud is characterized by three fixed triangular pyramid vertices of concrete in the field. The source point set and the target point set are assumed in the n-dimensional space . The objective of the rigid-body registration algorithm is to find a rotation matrix and translational matrix so that the source point set and target point set can optimally correspond in space. The optimization criterion based on Euclidean distance can be written as follows [39],
ICP algorithm is widely used in rigid body registration due to its simple iteration and fast convergence. The ICP algorithm iteratively computes the rigid transformation parameters R and until the objective function converges to a local minimum. In the kth iteration, the algorithm is implemented through the following two steps,
- (1)
- Setting up the matching point correspondence of two point sets,where , , is the argument of iteration k − 1.
- (2)
- The new rotation matrices and shift vectors are computed by minimizing the square distance [40],
The condition for the end of iteration for the ICP algorithm is that the registration error is small enough or the number of iterations reaches its maximum number, then the algorithm terminates, otherwise the iteration continues [41]. We use root mean square (RMS) to evaluate the registration accuracy,
where , is the argument of iteration k.
2.1.2. PCR Based on Total Station Orientation
The point cloud coordinates are converted to the independent coordinate system using the Bursa–Wolf transformation model. The Bursa–Wolf transformations are conformal 3D Cartesian coordinate transformations commonly used in surveying, photogrammetry, and geodesy [42].
2.2. Landslide DTM Using the Weighted Least Squares Regularization Solution
Unlike common Gauss–Markov models with additive random error [43,44,45], we suppose a set of observations with multiplicative random error , and the multiplicative error model can be defined as follows [46],
where is the zero mean random error, and are the random variables, is the t-dimensional unknown parameter vector to be estimated, is the Hadamard product of matrices or vectors, and 1 is the n dimensional column vectors with all values set to 1.
Assuming that the variances of the elements in vector are equal and independent, if every is a linear function of variable , that is, , is a t-dimensional row vector, the multiplicative error model can be written as follows,
The Formula (6) can be rewritten in the following form,
where .
It is evident that the accuracy of the observation value in the multiplicative error model is proportional to the signal intensity. The stronger the signal , the greater the error. The covariance matrix is a function of the unknown parameter . The commonly used methods for solving the multiplicative error model include the least squares method and the deviation correction weight least squares method. The weighted least square regularization algorithm is applied to the ill-posed multiplicative error model in this paper.
We utilize the least square (LS) method to calculate the parameter; the parameter estimation can be expressed as follows [47],
where is the least square estimation of the multiplicative error model.
According to the law of cofactor propagation, the cofactor matrix of and is,
We also utilize an unbiased estimation of weighted least-square (bcWLS) method; the parameter estimation can be expressed as follows [48],
where is the parameter estimation using bcWLS method.
If the normal equation is ill-posed, the LS solution is unreliable. Hence, to overcome the ill-posed state of the normal equation, we use the weighted least squares regularization iterative solution (RWLS). First, a regularization factor is introduced to construct the regularization criterion of the ill-posed multiplicative error model,
According to the definition of RWLS, the parameter estimation can be expressed as follows [49],
where is the RWLS solution of ill-posed multiplicative error model, and is identity matrix. The term is added to the inversion of the normal equation, which effectively weakens the ill-posed state of the normal equation. Therefore, we can obtain a reliable and stable solution.
As evident from Equation (11), and are the function of the regularization parameter , and the L curve method is used to calculate the regularization parameters . The main procedures are as follows [50,51],
- (1)
- Taking as the x-axis coordinate and as the y-axis coordinate, we get multiple sets of coordinate points (, ),
- (2)
- These coordinate points are fitted to a curve similar to L shape, and the value corresponding to the point with the largest curvature is used as the estimation of the regularization parameter.
As evident from Equation (12), is the nonlinear function of on the left side of the Equation (12), and is the nonlinear function of on the right side of Equation (12). Hence, there is no analytical solution, only a numerical solution [52]. We can only use approximation methods to iteratively calculate the numerical solution.
The detailed procedure of RWLS solution is as follows,
- (1)
- The LS solution is used as the RWLS initial value of iteration;
- (2)
- Compute the cofactor matrix ;
- (3)
- The regularization parameter is obtained by L curve method;
- (4)
- The iterative formula is as follows:
- (5)
- Repeat steps (2)–(4) until the value of the parameter subtraction is smaller than the threshold,where is defined as 10−10 in this paper.
The unit weight variance is always an important quality index for evaluating observation results and data processing results. It is defined as follows by using the LS method,
where = unit weight variance.
The unit weight variance using bcWLS can be expressed as follows [53],
where = unit weight variance, r = freedom degree, and its value correlates with the number of observation value and parameter estimation.
The unit weight variance of the ill-posed multiplicative random error model can be expressed as follows [54],
where .
The unit weight variance using RWLS can be expressed as follows [52],
where is the unit weight variance. In Equation (19), is defined as follows,
In this paper, we use LS, bcWLS, and the RWLS method to estimate the parameters and calculate the accuracy of parameters.
In addition, the noise of point cloud data has been shown with a nature of multiplicative random error [55,56,57]. Therefore, the multiplicative error model of DTM with 6 unknown parameters is as follows [33],
where represents the x and y coordinates of the ground point, represents the corresponding elevation of the point, and represents the multiplicative error vector,
Then, we apply LS, bcWLS, and RWLS method to calculate the parameter estimation and unit weight variance. Finally, we extract the landslide deformation by the difference of DTM.
3. Experiments Data
3.1. Simulation Experiment
3.1.1. Simulation Experiment I: GNSS Elevation Point Disturbed by Multiplicative Error
GNSS is used to measure the elevation of the ground point of a road center line in a certain area. It is assumed that the ground point elevation and distance conform to the following functional model,
In this example, the value range of x is 0–300 m, and 31 points are equally spaced within the value range of x. The truth values of the parameters are 10, 4, 2, 1, 0.5, and 2.
Assuming that y is disturbed by the multiplicative random error, where the multiplicative random errors are independent of each other and follow a normal distribution with a mean value of 0 and a standard deviation of 0.1, and the corresponding observation equation of the multiplicative error model is,
where Y is the vector disturbed by multiplicative error, 1 is the 31-dimensional column vector with all elements being 1, and is the 31-dimensional multiplicative random error vector. The simulation values of the ground elevation points obtained from Equation (23) are shown in Table 1.

Table 1.
Simulation Data.
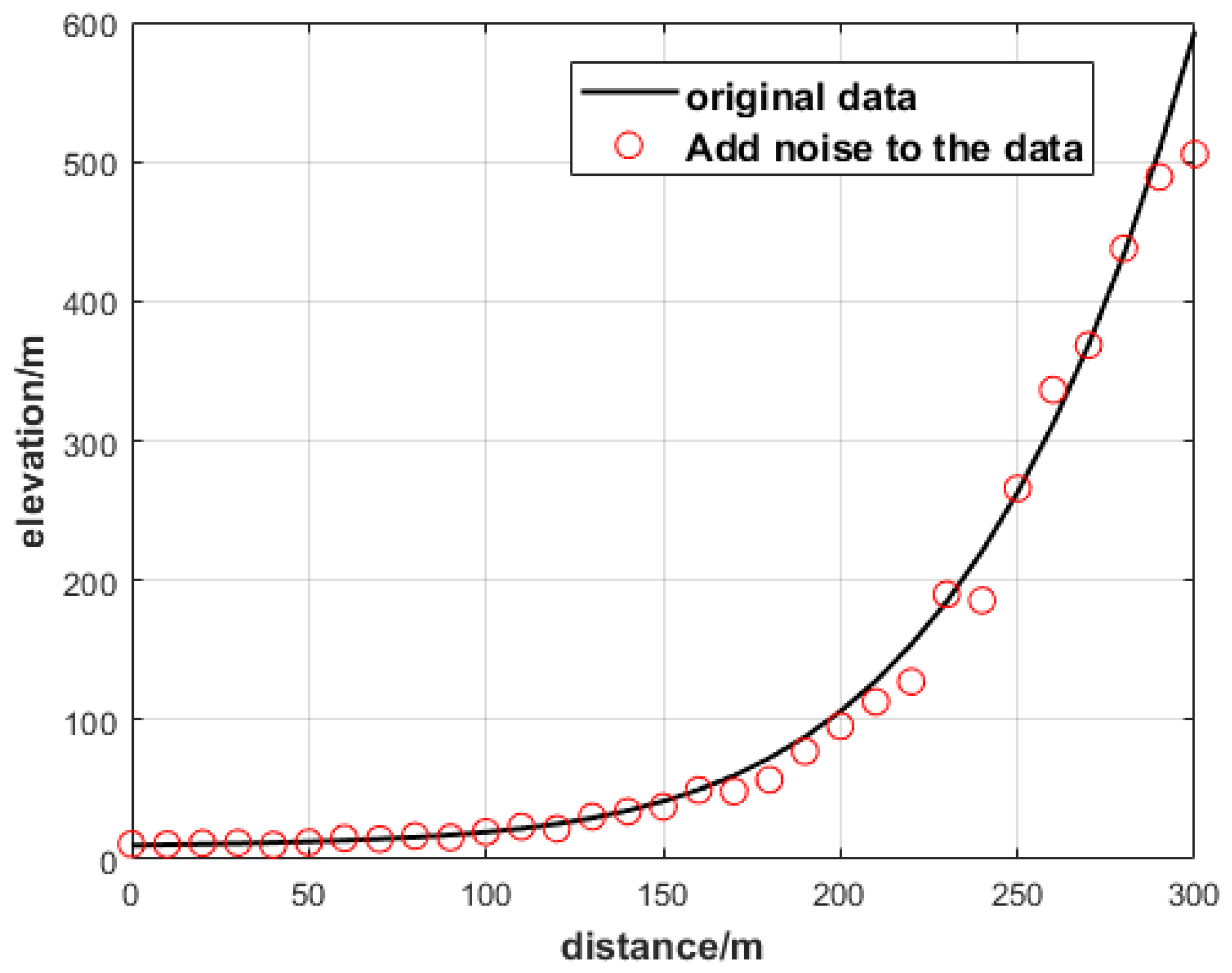
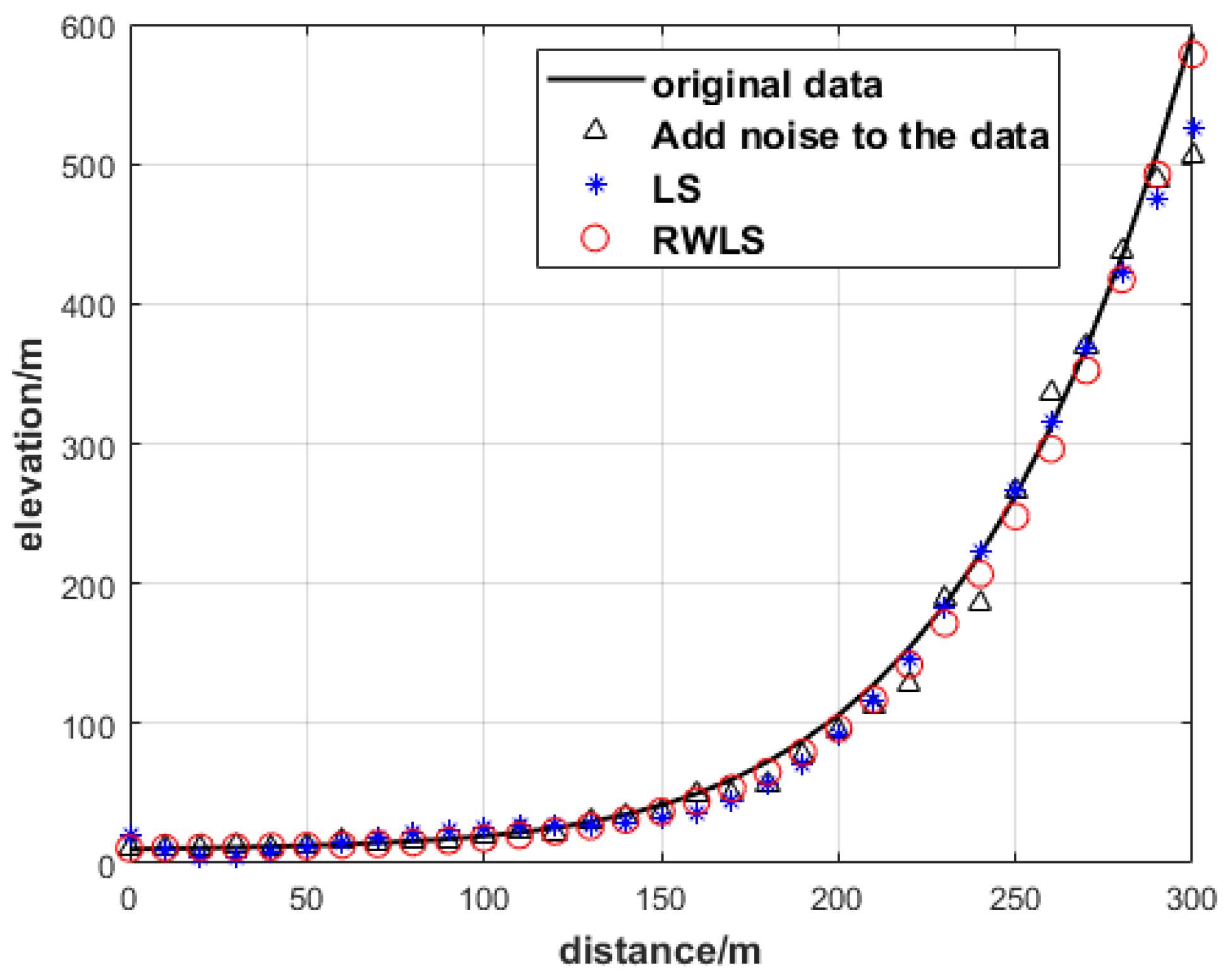
To show that the elevation points are affected by multiplicative error, the data of the ground elevation points before and after interference from multiplicative error are plotted in Figure 3.
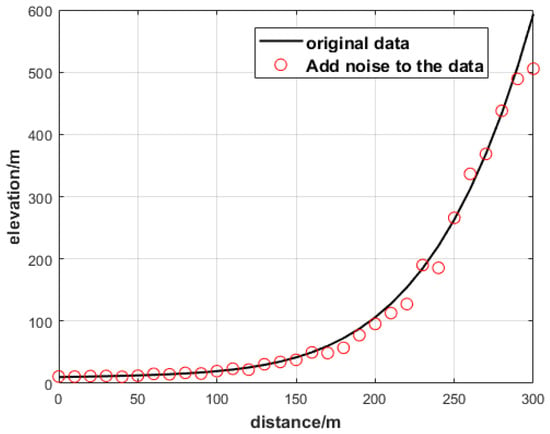
Figure 3.
GNSS elevation point before and after being disturbed by multiplicative error.
3.1.2. Simulation Experiment II
This simulation uses DTM data. This paper mainly considers that the model is ill-posed, so it simulates the ill-conditioned DTM model and generates the DTM using the interpolation function method [53]
where represents the elevation obtained by the interpolation function, x and y range from 0 m to 80 m, the interval is 2 m, and the truth values of the four parameters are −1.5, 20, 5, and −4, respectively.
The function is as follows,
The multiplicative error model is as follows,
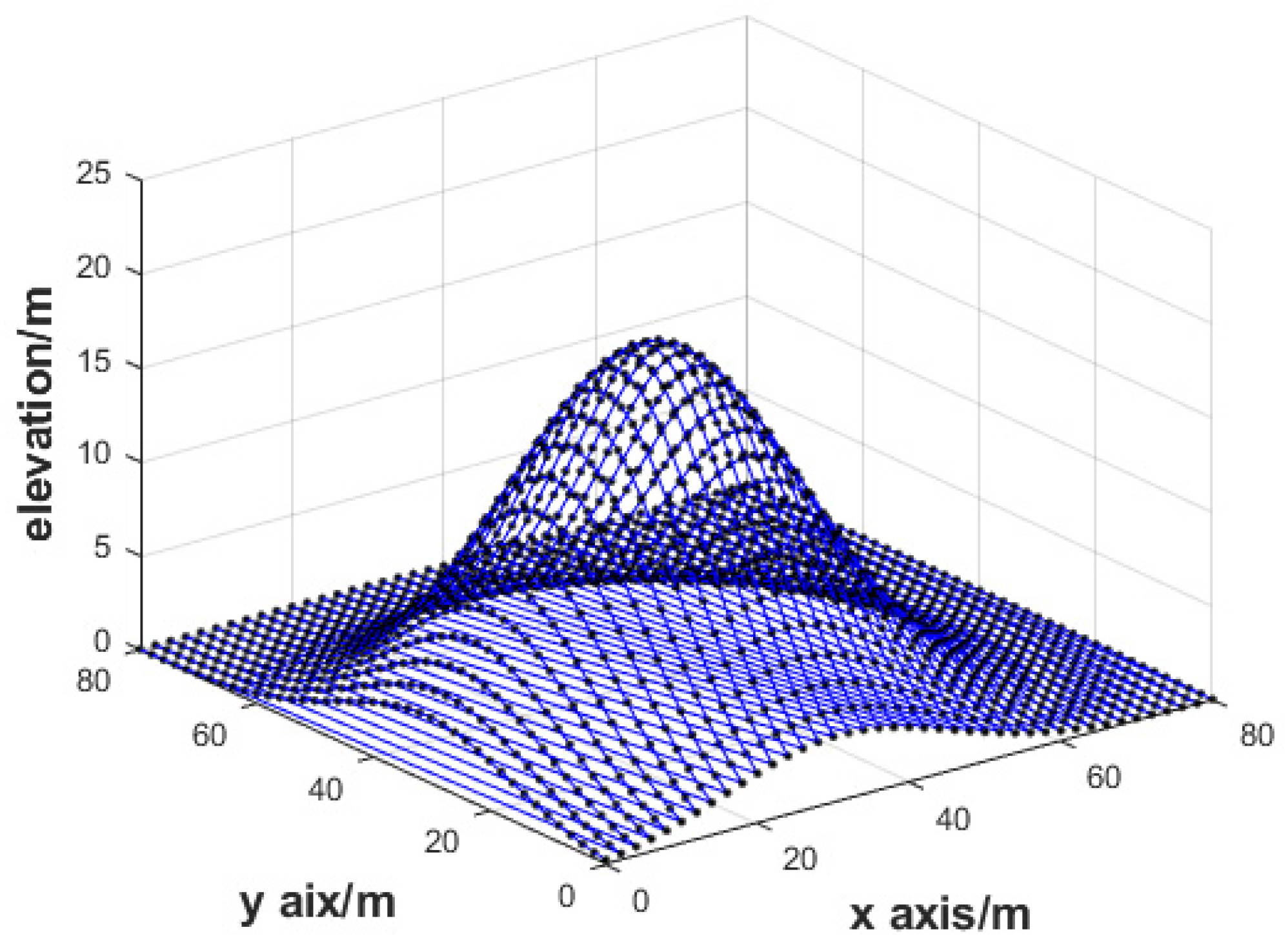
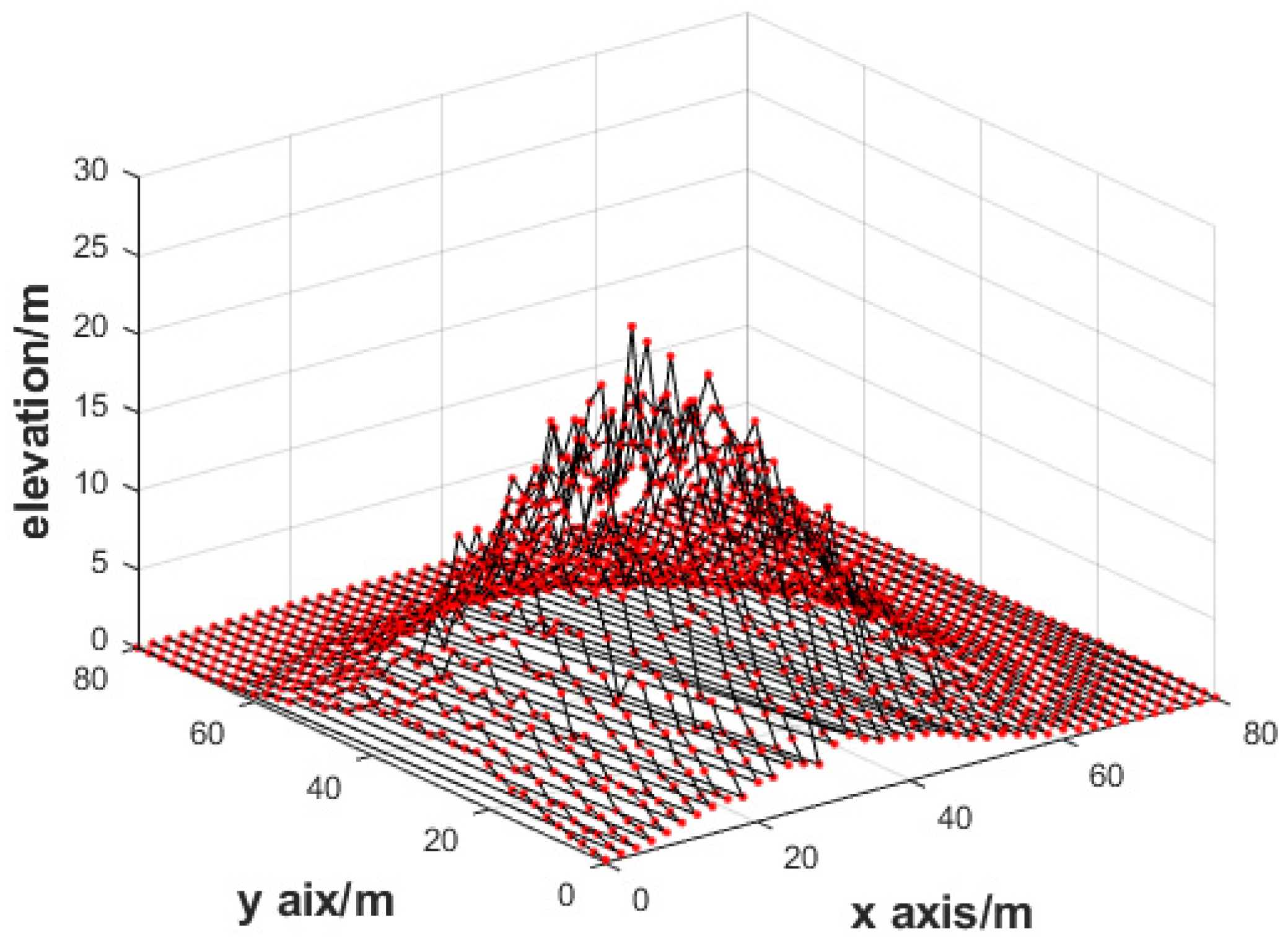
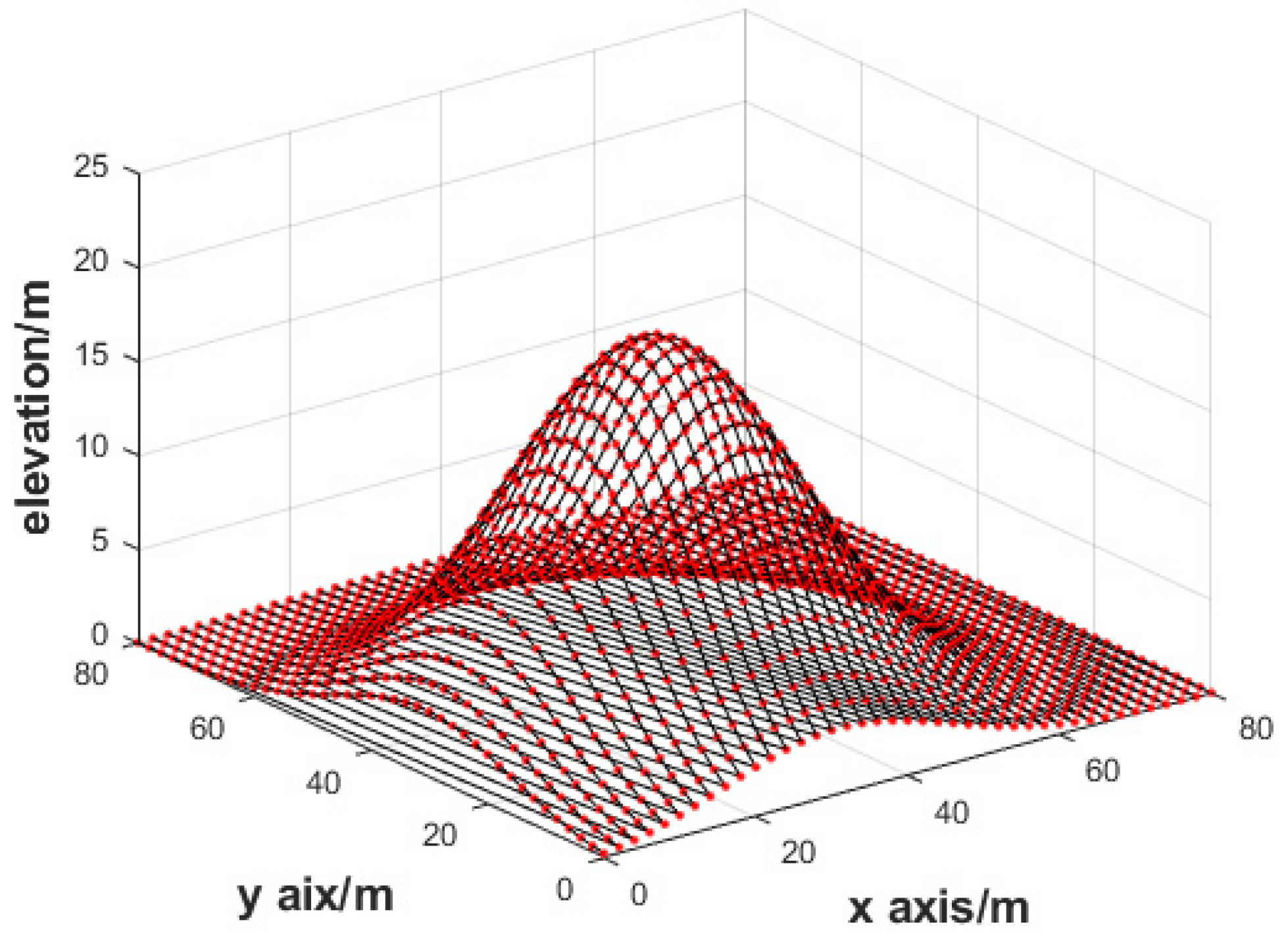
where is the vector of the observation values disturbed by multiplicative errors, 1 is the 1681-dimensional column vector whose elements are all 1, and is the 1681-dimensional multiplicative error vector values which are independent of each other. To illustrate that the DTM model is affected by multiplicative error, the DTM without the errors are plotted in Figure 4 and the DTM influenced by multiplicative random error is plotted in Figure 5. As can be seen from Figure 4 and Figure 5, although the DTM with the standard deviation has a 0.1 multiplicative error, it has a great influence on the elevation, and the condition number of the normal equation is 4.456 × 104; therefore, the equation is seriously ill.
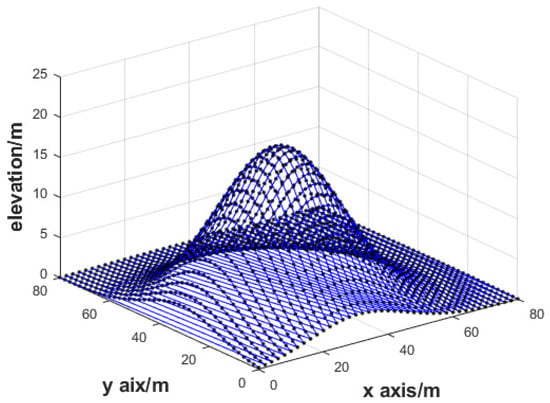
Figure 4.
DTM.
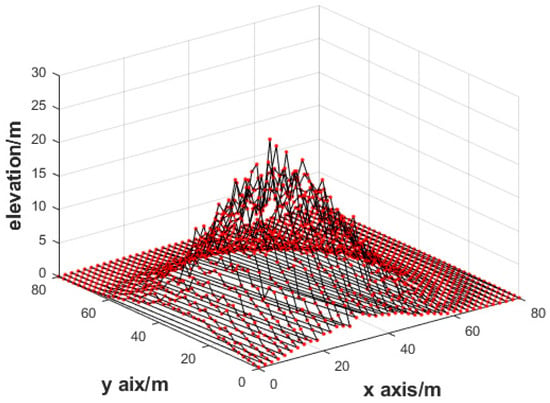
Figure 5.
DTM with multiplicative error.
3.2. Actual Experiment
3.2.1. Actual Experiment I
- (I)
- Experiment 1
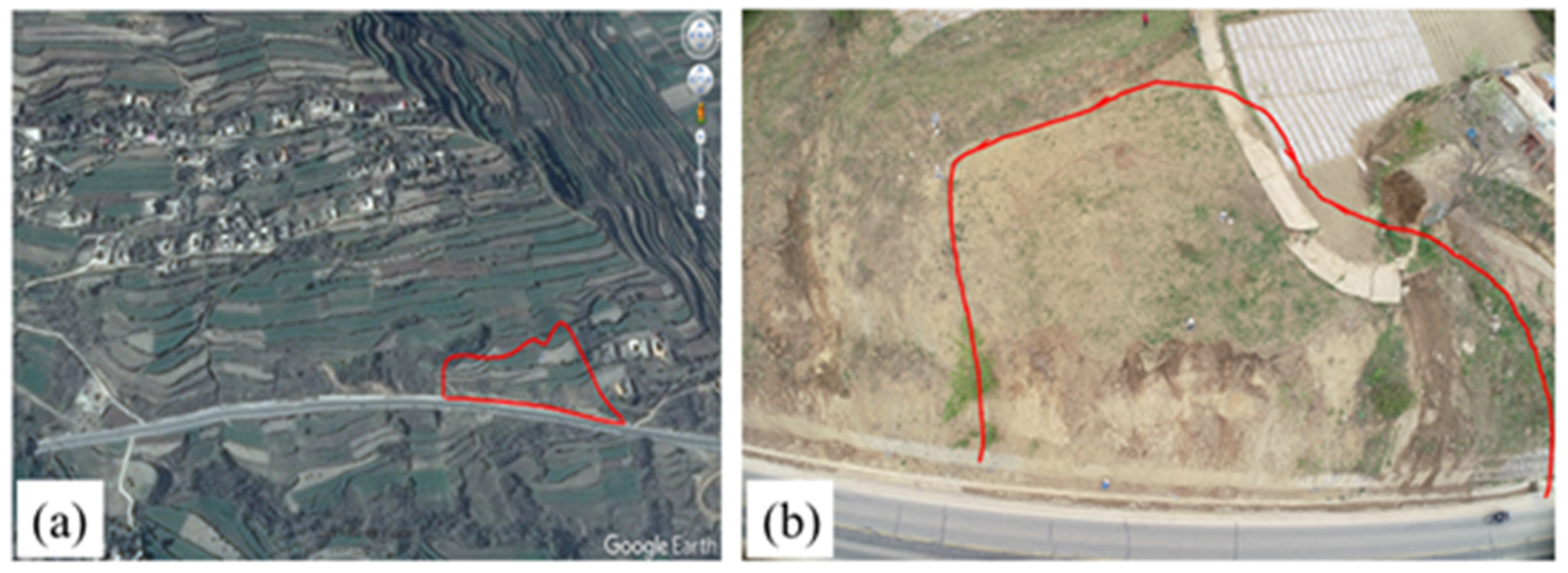
The Lashagou NO. 3 landslide was a loess landslide located at Lashagou village, Jishishan county, Gansu province, China. Its geographical coordinates are 35° 35′ 23″E, 102° 57′ 12″N. It is in the transition zone between the Tibetan Plateau and the Loess Plateau, which is typical of an excavation-related shallow loess engineering landslide [58,59]. The main stratum of the landslide is Holocene residual slope silty clay and the main stratum of the slide bed is middle and lower Pleistocene fluvial and lacustrine maroon silty clay. The central width of the slide body is 60–100 m, the axial length is 80–130 m, the area is about 25,000 m2, the thickness is 3–8 m, and the volume is about 150,000 cubic meters, belonging to the middle-shallow medium and small-sized landslide groups. The rear wall of the landslide was 0.2–0.4 m high, the natural slope was 15°, and the main slide direction was 85°. The front slope of this landslide group is mainly damaged by slime in the surface 1–3 m, but the lower soil is relatively stable, and the back edge of the landslide group is in the shape of an armchair and a gentle arc, which belongs to the traction cohesive soil landslide group. The optical remote sensing imagery of the landslide is shown in Figure 6a. As shown in Figure 6b, the toe of the Lashagou NO. 3 landslide is close to the G310 highway, which is activated or generated by the slope excavation during the construction of the G310 mountain highway. The main effects of the Lashagou NO. 3 landslide are shown in Figure 7. Figure 7b shows a local diagram of a crack 10 cm wide. Figure 7c shows the local displacement diagram of a 0.6 m staggered platform in the vertical direction of road surface formed by landslide. Figure 7d shows the local map of the road cracks formed by the landslide.
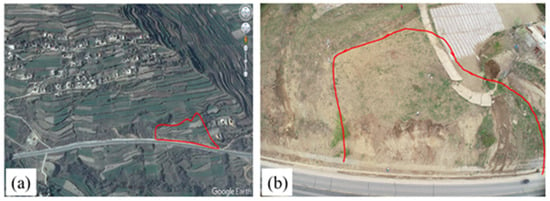
Figure 6.
(a) Optical remote sensing imagery of Lashagou NO. 3 landslide acquired from Google Earth; (b) UAV image of Lashagou NO. 3 landslide.

Figure 7.
(a) Study area and photos showing Lashagou NO. 3 landslide disease. (b) ground fracture (c) staggered platform (d) tensile crack caused by the landslide.
In this study, a Leica P50 laser scanner was used for data acquisition. The scanner is a ground-based 3D laser scanner with medium and long range, which has the advantages of obtaining high-quality point cloud data in harsh environments and a wide scanning range with minimal noise. The parameters of the Leica P50 laser scanner are shown in Table 2. In addition, A Leica Nova TS30 total station and some prism spheres are also required to collect data. The parameters of the Leica TS30 total station are shown in Table 3.

Table 2.
Parameters of Leica P50 3D laser scanner [60].

Table 3.
Parameters of Leica TS30 total station [61].
- (I)
- Triangular pyramid target point cloud acquisition
In this paper, a triangular pyramid target was developed, and three concrete triangular pyramids were poured in the study area, among which any triangular pyramid target is shown in Figure 8. The size of the triangular pyramid template is an equilateral triangle with a side length of 50 cm and a height of 15 cm. The point cloud of the triangular pyramid is shown in Figure 9.

Figure 8.
Triangular pyramid target.

Figure 9.
The point cloud of triangular pyramid.
- (II)
- Data collection based on total station orientation
In the monitoring of the landslide and other deformation forms, points in the stable zone should be taken as the monitoring benchmark. The coordinates of the four control points in the stable zone in this paper are shown in Table 4.

Table 4.
The coordinates of control points.
The point cloud of the prism sphere was collected using a Leica P50 scanner. We used the Leica Nova TS30 total station to collect the 3-D coordinates of the prism sphere simultaneously. The experiment was divided into three steps,
- (1)
- Leica TS30 total station was used to collect the coordinates of the prism balls near the landslide area.
The total station was set up at any position, and the coordinates of any two control points in the stability area were intersected to obtain the coordinates of the current measuring station. Then the central coordinates of the prism balls near the landslide area were measured. The photos of the prism balls are shown in Figure 10.

Figure 10.
Prism ball target.
- (2)
- The coordinates of the prism balls near the landslide area were obtained by fitting point cloud data collected by TLS simultaneously.
The Leica P50 scanner was set up at any position, and the point cloud data of the prism balls were obtained. Then the center coordinates of the prism balls were calculated by fitting the point cloud data of the prism balls. The transformation parameters from the point cloud coordinate system to the total station coordinate system can be obtained by using the Bursa–Wolf model.
- (3)
- The unification of the data.
The point cloud coordinates of each period were converted to the control point coordinate system of the stable area by using the transformation parameters to realize the unification of the data.
The creep deformation of a landslide is a slow dynamic process. In this paper, a one-station measurement method was adopted to avoid the error caused by multi-station data PCR, which improved the accuracy of the landslide deformation monitoring. The Leica P50 scanner was set on the highest point of the slope opposite the landslide, and the scanning accuracy was set to 3 mm@ 10 m. Considering the influence of permafrost ablation and other factors on the landslide, two period point cloud data were collected on 26 February 2021 (temperature 3 degrees Celsius, before permafrost ablation) and 3 May 2021 (temperature 28 degrees Celsius, after permafrost ablation) to analyze the landslide deformation. The data collection photo from period I (May 3, 2021) is shown in Figure 11, and the point cloud of Lashagou NO.3 landslide is shown in Figure 12.

Figure 11.
Prism ball target.

Figure 12.
Point cloud of phase 1.
3.2.2. Actual Experiment II
The Lihua landslide was on the left side of the Lihua road at Nan’an District, Chongqing, China. The relative height difference was about 10 m. It was a typical excavation-induced shallow loess engineering landslide. Once a large-scale instability occurs, it may block the Lihua road and threaten the lives and property of the nearby residents and pedestrians. We collected a two-phase point cloud of the landslide with a Leica P50 3D laser scanner on 20 April 2021 (phase 1) and 1 May 2021 (phase 2). The Lihua landslide point cloud of phase 1 is shown in Figure 13. The UAV image of the Lihua landslide acquired on 4 June 2022 is shown in Figure 14.

Figure 13.
Lihua landslide point cloud of phase 1.

Figure 14.
UAV image of Lihua landslide.
4. Analysis of Result and Discussion
4.1. The Results of Simulation Experiments
4.1.1. The Result of Simulation Experiment I
In simulation experiment 1, the square root of unit weight variance is 0.3. The parameter values obtained using the three methods are shown in Table 5.

Table 5.
Parameter estimation and accuracy.
The comparison between the RWLS method and the classical LS method is shown in Figure 15.
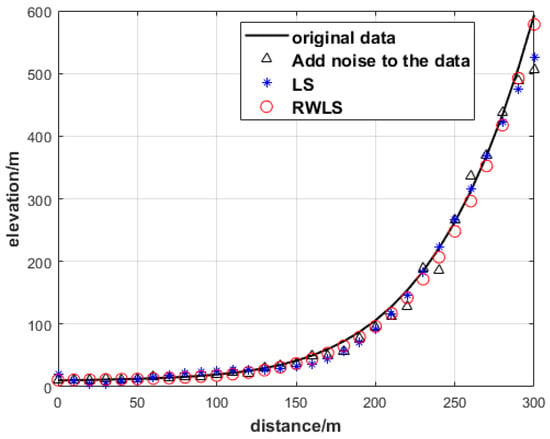
Figure 15.
GNSS elevation obtained by the RWLS method and LS.
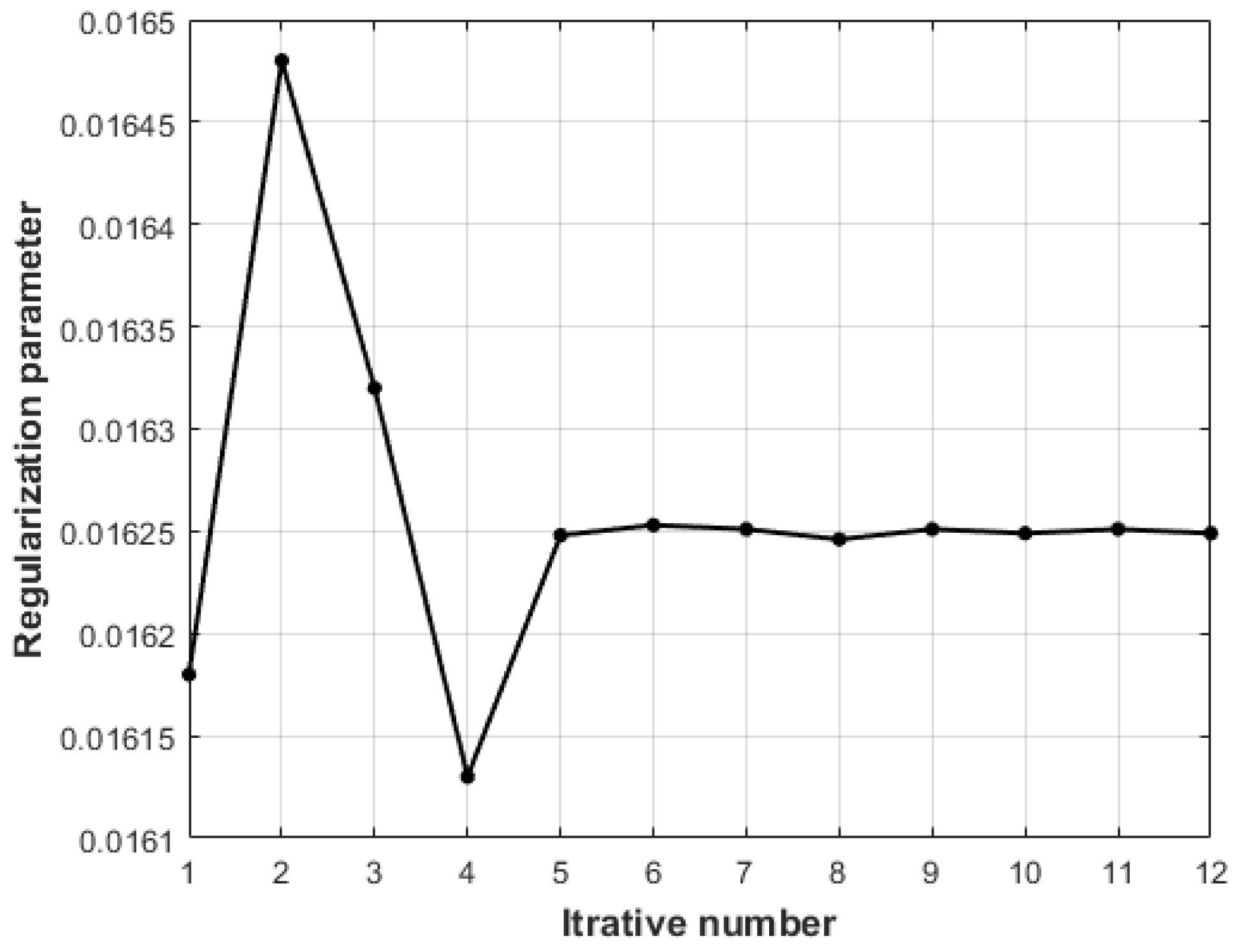
The condition number of the normal equation is 8.3098 × 105, the equation is ill-posed. The regularization parameter values in this algorithm change dynamically, and the change of the regularization parameters with the number of iterations is shown in Figure 16.
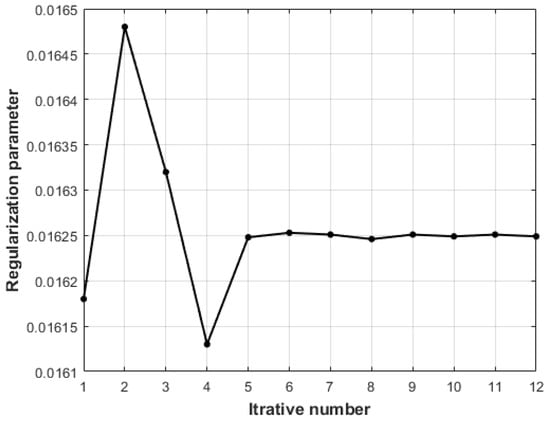
Figure 16.
The regularization parameters with the number of iterations.
It is evident from Figure 15 that ground elevation points are influenced by multiplicative error, resulting in serious deviation. It is evident from Table 5 that the obtained by LS method is the largest. The calculated by the bcWLS method is 13.61, which still deviates greatly from the truth value because the ill-posed state of the model is not considered. The calculated by the RWLS algorithm in this paper is 3.28, and the parameter estimation is closer to the true value, indicating that the RWLS algorithm has a certain effect on reducing ill-condition. It is evident from Table 5 that the bcWLS method does not consider the ill-posed nature of the model, which led to deviating from the true value. However, the RWLS algorithm takes these factors into account and the is closer to the true value, further verifying the advantages of the algorithm in this paper.
4.1.2. The Result of Simulation Experiment II
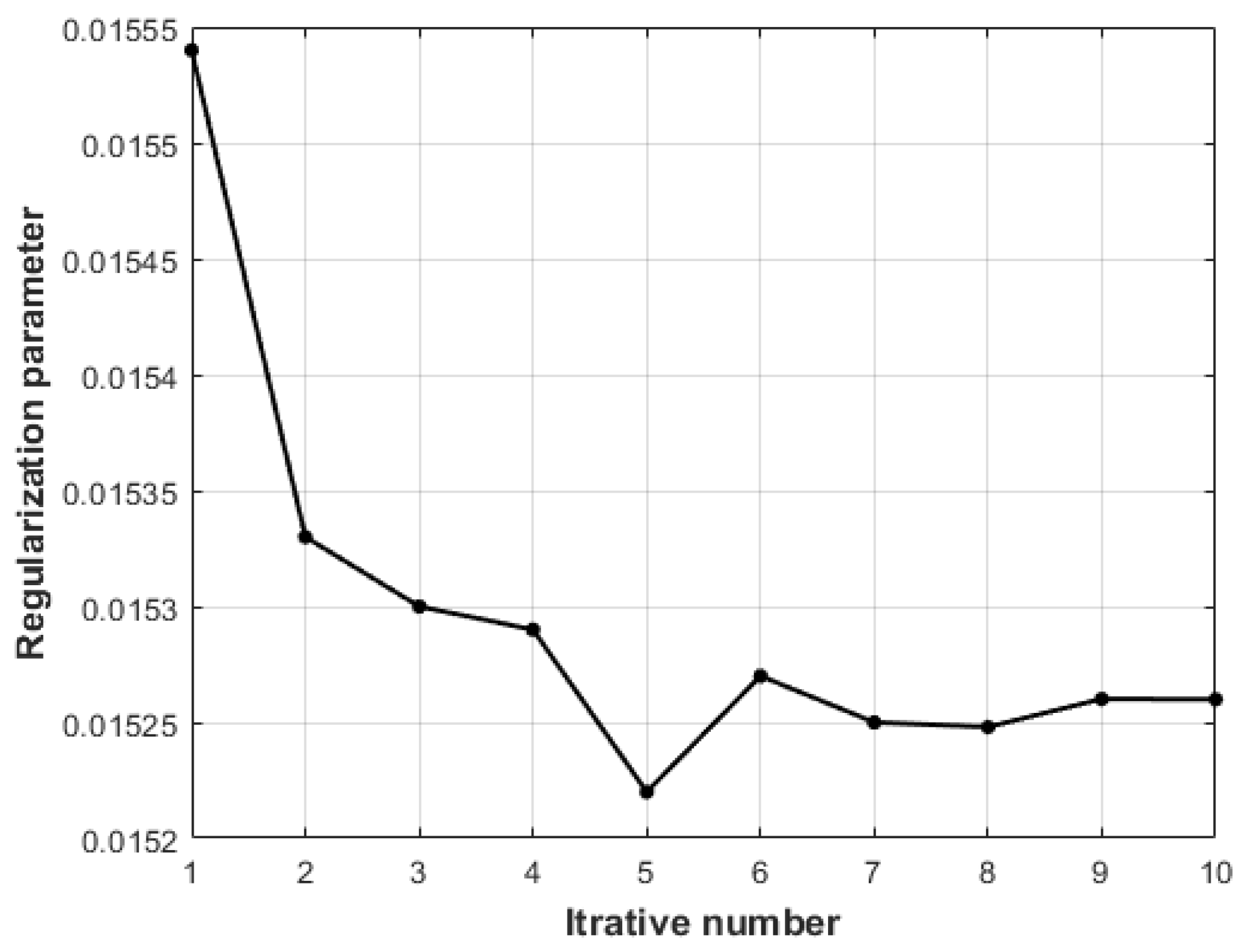
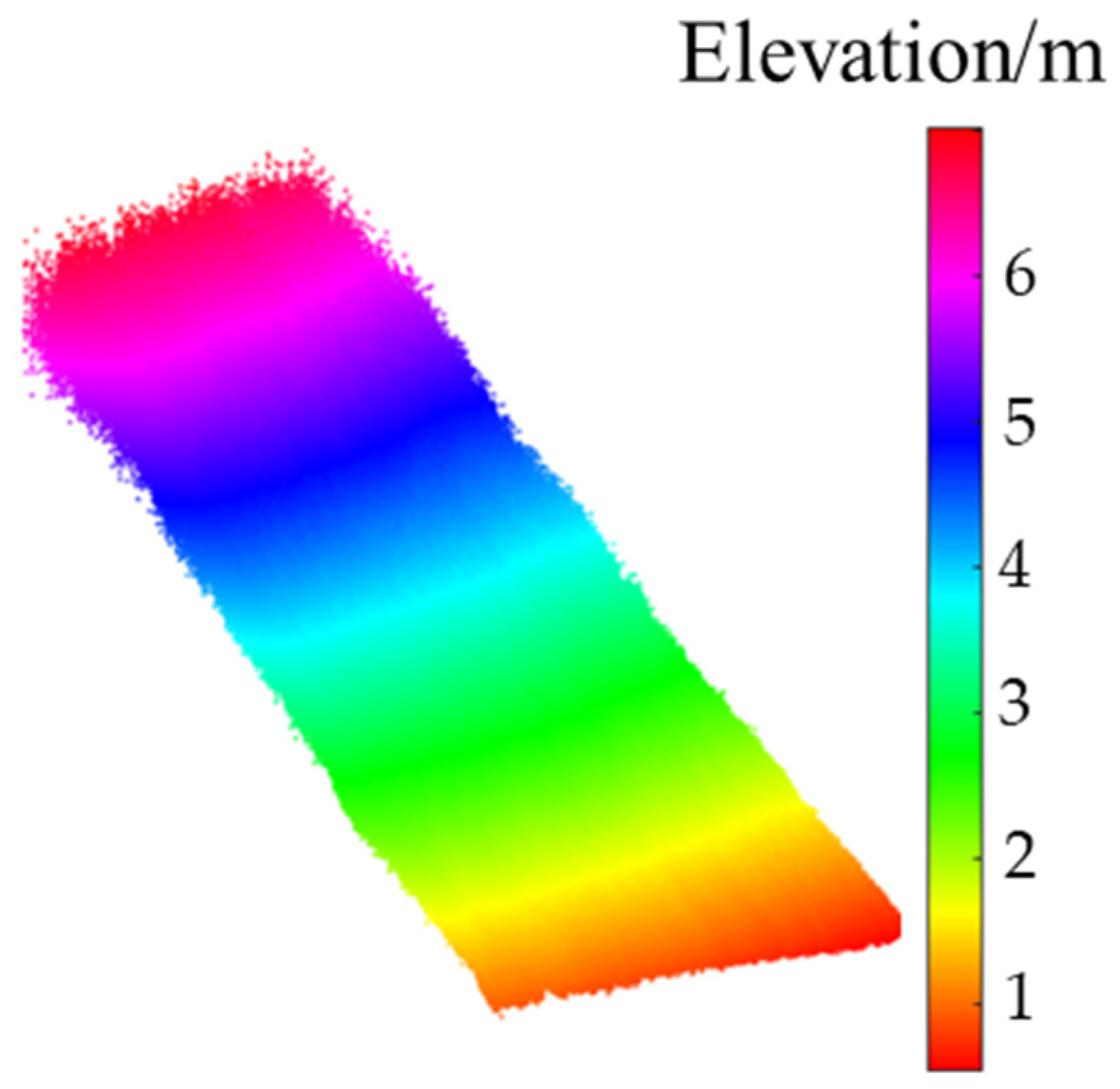
Following Xu et al. (2013), it is here assumed that is 0.3, and that the multiplicative random error vectors are independent from each other. The parameter estimation, and , calculated by LS, bcWLS, and RWLS, are listed in Table 6. The DTM made using the RWLS method is shown in Figure 17. The regularization parameters with the number of iterations are shown in Figure 18.

Table 6.
Parameter estimation and accuracy.
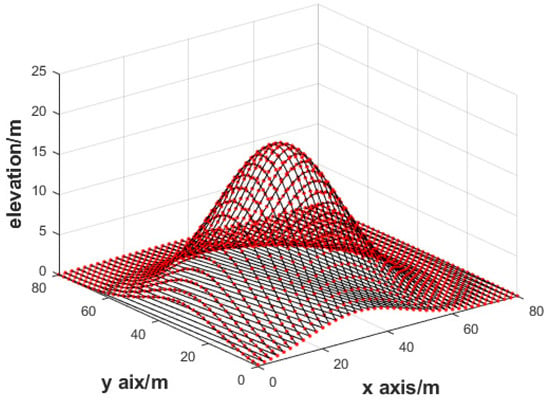
Figure 17.
DTM by the RWLS method.
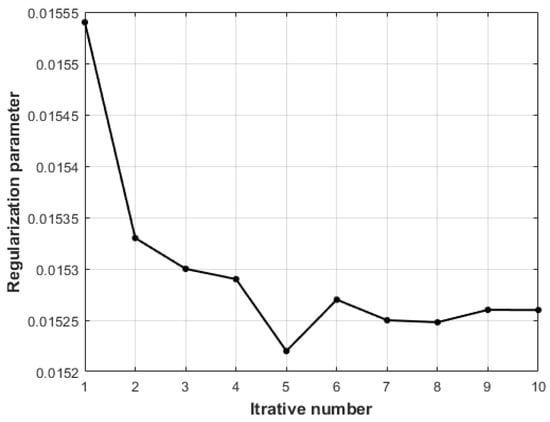
Figure 18.
The regularization parameters with the number of iterations.
As can be seen from Table 6, the parameter estimation obtained by bcWLS deviates seriously from the true value because the ill-posed state of the model is not considered, while the result obtained by the RWLS algorithm is closer to the true value. The parameter calculated by RWLS is 1.88. It is less than that of the LS method and bcWLS method, which further indicates that the algorithm in this paper has a certain effect on reducing the ill-posed state. It is evident from Table 6 that the obtained by the LS method is 4.52, and that seriously deviates from the true value. The calculated by the bcWLS method is 4.36, which is closer to the truth value, because it considers the weight of the observation value. The RWLS method considered the influence of ill-condition on the , hence the is the closest to the true value.
4.2. The Result of the Actual Experiment
- (I)
- The result of experiment I
4.2.1. The result of PCR Based on Triangular Pyramid Target
Three planes can be fitted using the point cloud of a triangular pyramid, and then triangular pyramid vertices can be intersected through the three planes. The coordinates of three triangular pyramid vertices in phase 1 and phase 2 are shown in Table 7 and Table 8, respectively.

Table 7.
Coordinates of three triangular pyramid vertices in phase 1.

Table 8.
Coordinates of three triangular pyramid vertices in phase 2.
The initial landslide point cloud of phase 1 and phase 2 is shown in Figure 19. The translation vector obtained by the fine algorithm is (0.134, 0.080, −0.038). In this paper, the rotation matrix is transformed into the rotation angle around the coordinate axis, in which the rotation angle around the X axis is 0.164°, the rotation angle around the Y axis is −0.180°, and the rotation angle around the Z axis is −46.886°.

Figure 19.
Initial point cloud of landslide in two phases.
The point cloud after unifying the data through the obtained rotation and translation parameters is shown in Figure 20. The image of the Lashagou NO.3 landslide is shown in Figure 21. It is evident that the two-phase point cloud has been accurately registered based on the triangular pyramid target. The point cloud data of the two periods are unified, which lays a foundation for landslide deformation detection.

Figure 20.
Landslide point cloud after the PCR of two period data.

Figure 21.
Photos of Lashagou NO.3 landslide.
The standard sphere target has often been used in previous studies [50,51,52,53]. Figure 1 shows that edge drift caused by an excessively large laser reflection angle will inevitably occur. Thus, the calculation error of the spherical center coordinates cannot be disregarded. Compared with previous studies [52,53], our methods handle this problem by designing a new triangular pyramid marker. As shown in Figure 9, three planes can be fitted through the triangular pyramid point cloud, and then the triangular pyramid vertices can be intersected through the three planes. The registration accuracy of the point cloud based on the triangular pyramid target is 0.003 m.
4.2.2. The result of PCR Based on Total Station Orientation
Figure 22 shows the point cloud after fine registration using the total station orientation theory. The two-phase point cloud has been accurately transformed into the control point coordinate system in the stable area, realizing the unification of the multi-phase point cloud data. The method is rigorous in theory, easy to operate in practice, free from the restriction of landslide terrain conditions, and has a wide applicability. The registration accuracy based on the total station orientation was 0.005 m.

Figure 22.
Point cloud after accurate registration.
By comparing the two PCR method with other PCR methods, it is evident that:
- (1)
- In terms of data acquisition, to ensure the accuracy of registration, the data acquisition mode which is based on a fixed triangular pyramid target is simple and is capable of fast operation. It is suitable for good visibility and convenient transportation and is easy to cast in a concrete environment. In addition, based on the total station orientation data acquisition mode, it is not limited by field conditions and has a wide applicability. Especially, in a situation where there are some control points in the stable area, the point cloud can be directly and effectively transformed into the existing coordinate system, which is of great significance to the continuous dynamic monitoring of landslide disasters based on point cloud data.
- (2)
- In terms of PCR, the PCR theory based on a fixed triangular pyramid target and total station orientation is strict. The PCR based on a fixed triangular pyramid target can overcome the problem of low precision in the sphere-based PCR method. The advantage of PCR based on total station orientation is that the point cloud coordinates can be converted to the existing control point coordinate system, which is favorable for the utilization of survey area engineering.
The proposed approach strives at addressing the unstable precision of different period TLS data. Figure 23 shows the TLS data of the 1 m wide detailed image shown in Figure 20.

Figure 23.
PCR based on triangular target (1 m wide detail in Figure 20).
As shown in Figure 23, the result after applying the target-based (triangular pyramid) PCR method suggests that the precision is stable. This may also indicate that in TLS data such methods tend to retain point cloud detail features. Compared with the spherical target [25,26], the triangular target can overcome the edge drift. After applying the PCR method based on total station backward orientation, the precision of PCR is high. Compared with a target-based PCR method [27], the station setup is flexible. In addition, it is suitable for the situations that are not easily accessible.
Our PCR method is easy to use. The center of sphere has often been used for PCR in previous studies [25]. Our conclusion about PCR based on spherical target is similar to [27], which is that it is difficult to calculate the spherical center precisely because of edge drift. Thus, a new PCR target is necessary. Compared with previous studies, our method handles this problem by designing a triangular target. The vertices can be precisely intersected by three triangular planes.
4.2.3. Landslide Based on DTM Difference
Parameter estimation values and their accuracy values are shown in Table 9. The coefficient matrix of the LS method and bcWLS method is singular and the parameter estimation does not converge due to the influence of the ill-condition. The algorithm in this paper takes ill-condition into account and has advantages for processing real data.

Table 9.
Parameters of DTM estimation and accuracy.
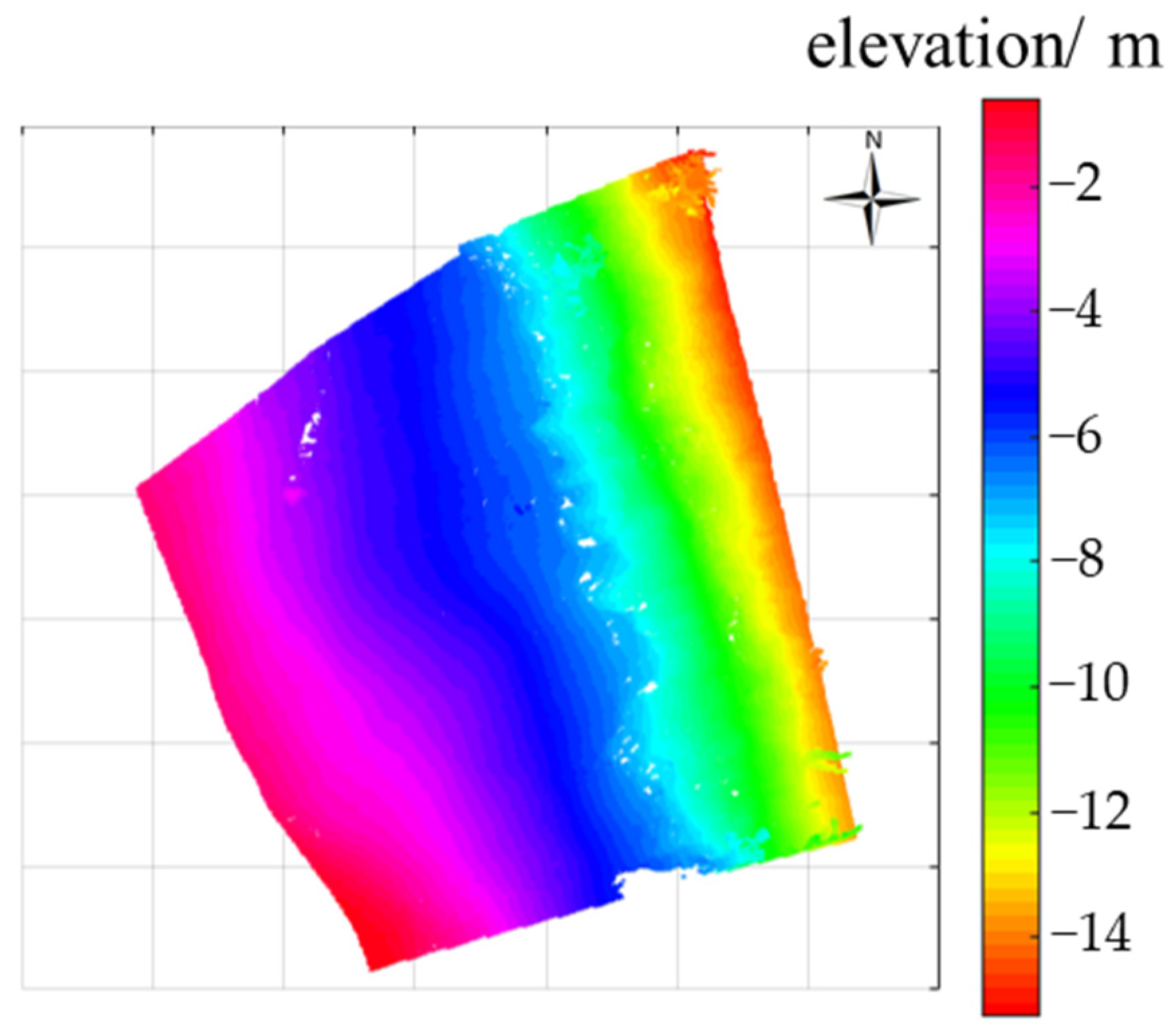
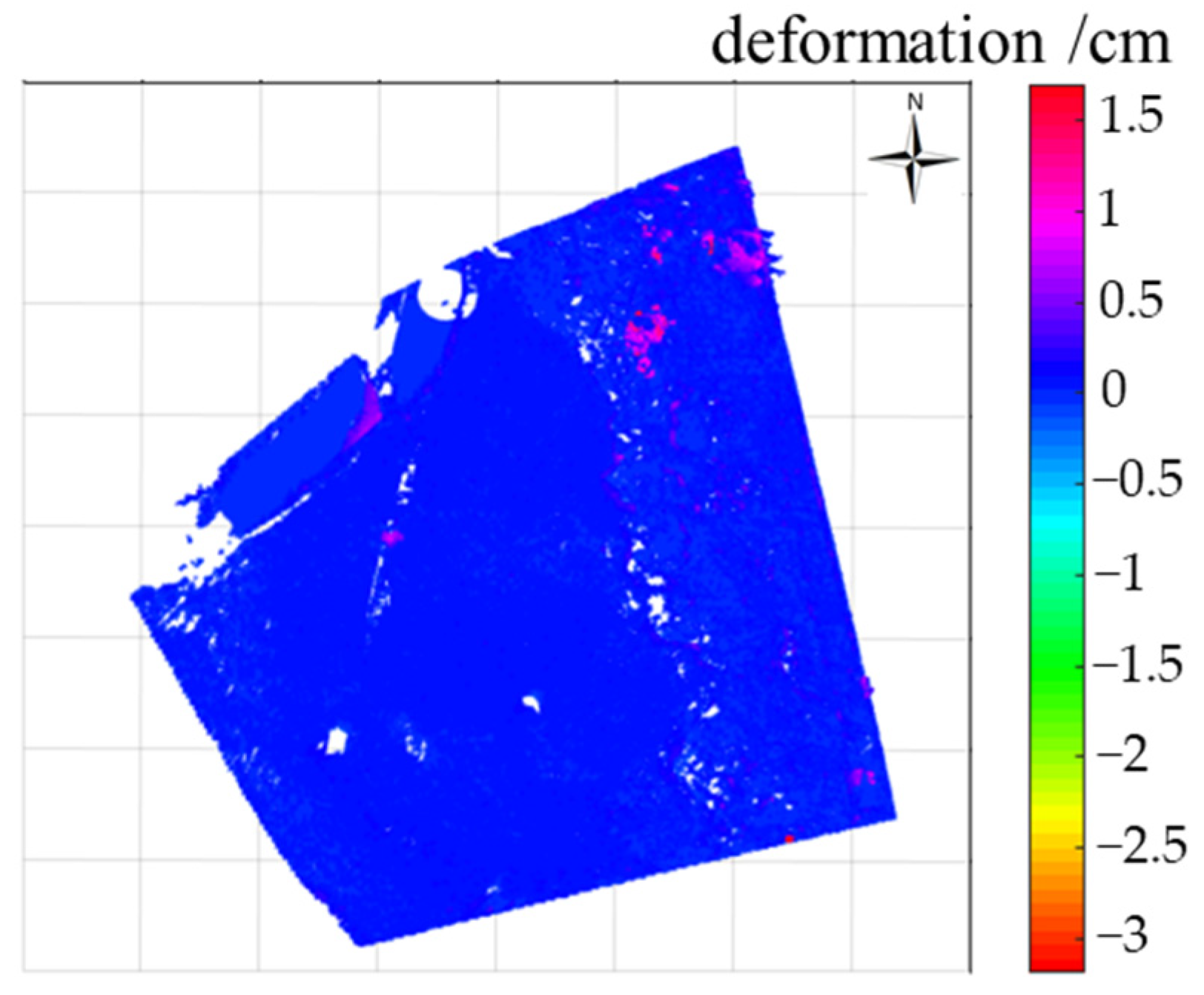
The DTM of the Lashagou NO.3 landslide is shown in Figure 24. The deformation of the Lashagou NO.3 landslide is shown in Figure 25. It is evident from Figure 25 that from 26 February 2021 to 3 May 2021, the overall deformation of the landslide was small, and its maximum value was 0.031 m. The landslide will continue to maintain a stable state without special factors, such as earthquakes, heavy rainfall, and artificial excavation.
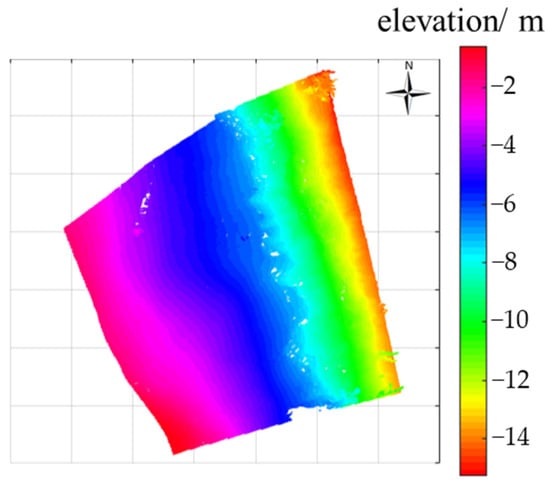
Figure 24.
Lashagou NO.3 landslide DTM.
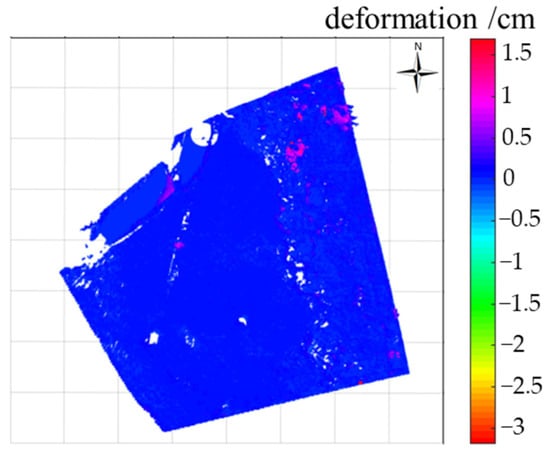
Figure 25.
Deformation of Lashagou NO.3 landslide.
- (II)
- The result of experiment II
The point cloud of the Lihua landslide (phase I) is shown in Figure 26. The DTM disturbed by multiplicative error obtained in this paper is shown in Figure 27.
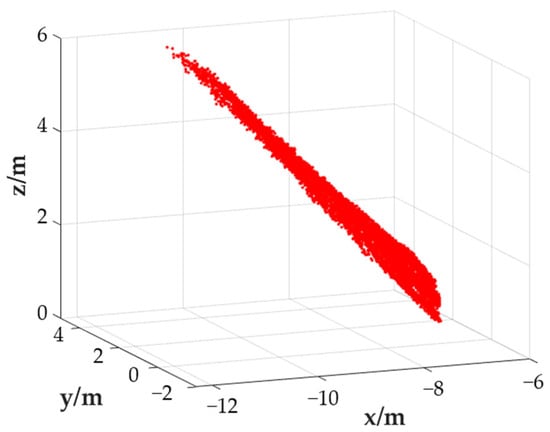
Figure 26.
Point cloud of Lihua landslide.
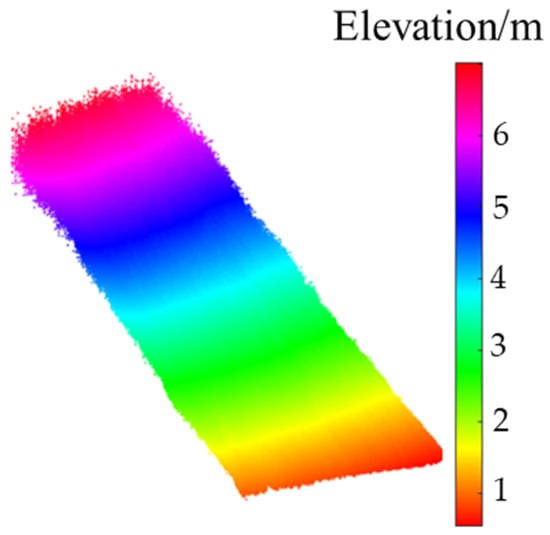
Figure 27.
DTM disturbed by multiplicative error.
The estimation and accuracy of the parameters are shown in Table 10.

Table 10.
The estimation and accuracy of DTM parameters.
The obtained by the LS method is too large, which does not conform to reality, further indicating that the LS method cannot process actual data. It can also be seen from Table 10 that the error of the parameter estimation obtained by the LS method is the largest, and that the error obtained by the RWLS method is much smaller than LS and bcWLS method.
The deformation of the Lihua landslide is shown in Figure 28. It is evident from Figure 28 that from 20 April 2021 to 1 May 2021, the overall deformation of the Lihua landslide was small, with a maximum value of 0.011 m.

Figure 28.
Deformation of Lihua landslide.
As shown in Figure 26, the DTM has a huge deviation because of the multiplicative random errors. As indicated in Table 9 and Table 10, the obtained by LS and bcWLS deviates from the true value, but RWLS can obtain a relatively reasonable result. The results show that the RWLS method is applicable to solve the ill-posed state of DTM in practical applications.
The ill-posed problem of the coefficient matrix has been ignored in previous studies, which results in an unstable or non-convergent solution [62]. We used the Tikhonov regularization method to derive the RWLS solution for an ill-posed multiplicative error model. The results of simulation I and simulation II suggest that RWLS’s solution has a better performance than other methods, such as LS [47] and bcWLS [48]. In the test on two actual landslide data sets, the LS and bcWLS methods dealt poorly with DTM construction [29,30,54], because the DTM has a huge deviation due to the random errors. Our method takes ill-condition into account. Hence, the results of actual experiment I and actual experiment II are consistent with the results of the simulation data. Thus, the RWLS method provides a new solution for the ill-posed multiplicative error model.
5. Conclusions
In this paper, TLS technology was used to extract the deformation of a landslide. We discussed the major factors affecting the landslide deformation, and attempted to reveal the relevant deformation mechanism. A new measurement and data processing strategy is proposed in this paper, aiming at extracting the deformation of a landslide. Finally, the landslide deformation was extracted by using two datasets. The first dataset is the point cloud data of the Lashagou NO.3 landslide collected on 26 February 2021 and 3 May 2021. The second dataset is the point cloud data of the Lihua landslide collected on 20 April 2021 and 1 May 2021. The main conclusions drawn from this study are as follows.
In this study, we designed a new triangular pyramid PCR marker, and a PCR experiment for different period TLS datasets based on the new marker was carried out. Compared with the commonly used spherical target, the edge drift of the sphere is overcome by the new marker-based PCR proposed in this paper. The registration accuracy based on the permanent triangular pyramid is 0.003 m. If it is not convenient to make a fixed target, we also propose a new PCR method based on total station orientation. The registration accuracy based on the unified theory of backward orientation using the total station method is 0.005 m. The results show that the new method precisely aligns the point cloud system with the engineering independent coordinate system.
The weighted least square regularization iterative method can effectively solve the ill-posed multiplicative error problem. In the tests of two simulation data set, the accuracy and reliability of the RWLS algorithm outperformed previous methods. Then, two actual landslide experiment were conducted. The results show that the RWLS solution can effectively reduce the ill-posed state of the model. The deformation of the Lashagou NO.3 landslide was small, with a maximum value of 0.031 m. The maximum deformation of the Lihua landslide was 0.011 m.
In general, the monitoring results of the DTM subtraction based on TLS data technology show that the Lashagou NO.3 landslide and Lihua landslide will continue to maintain a stable state without special factors, such as earthquakes, heavy rainfall, or artificial excavations. In cases where the point cloud system and engineering independent coordinate system are different and the DTM is disturbed by the multiplicative random error, our method is a more practical choice with stabler precision compared with previous methods.
Author Contributions
Methodology, L.Z., X.M., Z.X., S.Z., C.H. and G.C.; software, L.Z., Z.X. and G.C.; validation, Y.Z.; writing—original draft preparation, L.Z.; writing—review and editing, C.H.; visualization, C.H.; funding acquisition, S.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the National Natural Science Foundation of China under grant no. 42074041 and no. 41904171.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Yao, L.; Sun, H.; Zhu, L.; Zhou, Y. Development and application of deformation monitoring system for lanslide at Funchunjiang Dam. Surv. Rev. 2014, 46, 444–452. [Google Scholar] [CrossRef]
- Gikas, V. 3D Terrestrial laser scanning for geometry documentation and construction management of highway tunnels during excavation. Sensors 2012, 12, 11249–11270. [Google Scholar] [CrossRef]
- Vezocnik, R.; Ambrozic, T.; Sterle, O.; Bilban, G.; Pfeifer, N.; Stopar, B. Use of terrestrial laser scanning technology for long term high precision deformation monitoring. Sensors 2009, 9, 9873–9895. [Google Scholar] [CrossRef] [PubMed]
- He, M.; Zhu, Q.; Du, Z.; Hu, H.; Ding, Y.; Chen, M. A 3D shape descriptor based on contour clusters for damaged roof detection using airborne LiDAR point clouds. Remote Sens. 2016, 8, 189. [Google Scholar] [CrossRef]
- Kasperski, J.; Delacourt, C.; Allemand, P.; Potherat, P.; Jaud, M.; Varrel, E. Application of a terrestrial laser scanner (TLS) to the study of the Séchilienne Landslide (Isère, France). Remote Sens. 2010, 2, 2785–2802. [Google Scholar] [CrossRef]
- Crepaldi, S.; Zhao, Y.; Lavy, M.; Amanzio, G.; Suozzi, E.; De Maio, M. Landslide analysis by multi-temporal terrestrial laser scanning (TLS) data: The Mont de la Saxe landslide. Rend. Online Della Soc. Geol. Ital. 2015, 35, 92–95. [Google Scholar] [CrossRef]
- Wang, D.; Hollaus, M.; Schmaltz, E.; Wieser, M.; Reifeltshammer, D.; Pfeifer, N. Tree stem shapes derived from TLS data as an indicator for shallow landslides. Procedia Earth Planet. Sci. 2016, 16, 185–194. [Google Scholar] [CrossRef]
- Wang, G.; Philips, D.; Joyce, J.; Rivera, F. The integration of TLS and continuous GPS to study landslide deformation: A case study in Puerto Rico. J. Geod. Sci. 2011, 1, 25–34. [Google Scholar] [CrossRef]
- Cina, A.; Piras, M. Performance of low-cost GNSS receiver for landslides monitoring: Test and results. Geomat. Nat. Hazards Risk 2015, 6, 497–514. [Google Scholar] [CrossRef]
- Senkaya, M.; Babacan, A.E.; Karslı, H.; San, B.T. Origins of diverse present displacements in a paleo-landslide area (Isiklar, Trabzon, northeast Turkey). Environ. Earth Sci. 2022, 81, 1–24. [Google Scholar] [CrossRef]
- Stiros, S.C.; Vichas, C.; Skourtis, C. Landslide monitoring based on geodetically derived distance changes. J. Surv. Eng. 2004, 130, 156–162. [Google Scholar] [CrossRef]
- Tzenkov, T.; Gospodinov, S. Geometric analysis of geodetic data for investigation of 3D landslide deformations. Nat. Hazards Rev. 2003, 4, 78–81. [Google Scholar] [CrossRef]
- Klimeš, J.; Rowberry, M.D.; Blahůt, J.; Briestenský, M.; Hartvich, F.; Košťák, B.; Rybář, J.; Stemberk, J.; Štěpančíkováet, P. The monitoring of slow-moving landslides and assessment of stabilisation measures using an optical–mechanical crack gauge. Landslides 2012, 9, 407–415. [Google Scholar] [CrossRef]
- Baroň, I.; Supper, R. Application and reliability of techniques for landslide site investigation, monitoring and early warning–outcomes from a questionnaire study. Nat. Hazards Earth Syst. Sci. 2013, 13, 3157–3168. [Google Scholar] [CrossRef]
- Shi, X.; Hu, X.; Sitar, N.; Kayen, R.; Qi, S.; Jiang, H.; Wang, X.; Zhang, L. Hydrological control shift from river level to rainfall in the reactivated Guobu slope besides the Laxiwa hydropower station in China. Remote Sens. Environ. 2021, 265, 112664. [Google Scholar] [CrossRef]
- Guo, F.; Meng, X.; Qi, T.; Dijkstra, T.; Thorkildsen, J.K.; Yue, D.; Chen, G.; Zhang, Y.; Dou, X.; Shi, P. Rapid onset hazards, fault-controlled landslides and multi-method emergency decision-making. J. Mt. Sci. 2022, 19, 1357–1369. [Google Scholar] [CrossRef]
- Guo, C.; Xu, Q.; Dong, X.; Liu, X.; Yu, J. Geohazard Recognition by Airborne LiDAR Technology in Complex Mountain Areas. Geomat. Inf. Sci. Wuhan Univ. 2021, 46, 1538–1547. [Google Scholar]
- Abellán, A.; Vilaplana, J.; Calvet, J.; García-Sellés, D.; Asensio, E. Rockfall monitoring by terrestrial laser scanning-case study of the basaltic rock face at Castellfollit de la Roca (Catalonia, Spain). Nat. Hazards Earth Syst. Sci. 2011, 11, 829–841. [Google Scholar] [CrossRef]
- Kayen, R.; Pack, R.; Bay, J.; Collins, B. Ground-Lidar visualization of surface and structural deformatios of the Niigata Ken Chuetsu. Earthq. Spectra 2006, S1, 147–162. [Google Scholar] [CrossRef]
- Liu, W.; Xie, M. Landslide monitoring based on point cloud density characteristics. Rock Soil Mech. 2020, 41, 3748–3756. [Google Scholar]
- Zhao, J.; Du, S.; Liu, Y.; Saif, B.S.; Hou, Y.; Guo, Y.C. Evaluation of the stability of the palatal rugae using the three-dimensional superimposition technique following orthodontic treatment. J. Dent. 2022, 119, 104055. [Google Scholar] [CrossRef] [PubMed]
- Yang, M.; Gan, S.; Yuan, X.; Gao, S.; Zhu, Z.; Yu, H. Study on data acquisition and registration experiment of terretrial laser scanning point clouds under complicated banded terrain condition. Bull. Surv. Mapp. 2018, 5, 35–40. [Google Scholar]
- Zeybek, M.; Şanlıoğlu, İ. Accurate determination of the Taşkent (Konya, Turkey) landslide using a long-range terrestrial laser scanner. Bull. Eng. Geol. Environ. 2015, 74, 61–76. [Google Scholar] [CrossRef]
- Hsieh, Y.C.; Chan, Y.C.; Hu, J.C.; Chen, Y.Z.; Chen, R.F.; Chen, M.M. Direct measurements of bedrock incision rates on the surface of a large dip-slope landslide by multi-period airborne laser scanning DEMs. Remote Sens. 2016, 8, 900. [Google Scholar] [CrossRef]
- Xian, Y.; Xiao, J.; Wang, Y. A fast registration algorithm of rock point cloud based on spherical projection and feature extraction. Front. Comput. Sci. 2019, 13, 170–182. [Google Scholar] [CrossRef]
- Kümmerle, J.; Kühner, T.; Lauer, M. Automatic calibration of multiple cameras and depth sensors with a spherical target. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 1–8. [Google Scholar]
- Zhou, Y.; Han, D.; Hu, K.; Qin, G.; Xiang, Z.; Ying, C.; Zhao, L.; Hu, X. Accurate virtual trial assembly method of prefabricated steel components using terrestrial laser scanning. Adv. Civ. Eng. 2021, 2021, 9916859. [Google Scholar] [CrossRef]
- Li, J.; Hu, Q.; Ai, M. Point cloud registration based on one-point ransac and scale-annealing biweight estimation. IEEE Trans. Geosci. Remote Sens. 2021, 59, 9716–9729. [Google Scholar] [CrossRef]
- Chen, Z.; Zhang, B.; Han, Y.; Zuo, Z.; Zhang, X. Modeling accumulated volume of landslides using remote sensing and DTM data. Remote Sens. 2014, 6, 1514–1537. [Google Scholar] [CrossRef]
- Artese, S.; Perrelli, M. Monitoring a landslide with high accuracy by total station: A DTM-based model to correct for the atmospheric effects. Geosciences 2018, 8, 46. [Google Scholar] [CrossRef]
- Pawluszek, K.; Borkowski, A.; Tarolli, P. Sensitivity analysis of automatic landslide mapping: Numerical experiments towards the best solution. Landslides 2018, 15, 1851–1865. [Google Scholar] [CrossRef]
- Xu, P.; Shimada, S. Least squares parameter estimation in multiplicative noise models. Commun. Stat. Simul. Comput. 2000, 29, 83–96. [Google Scholar] [CrossRef]
- Shi, Y.; Xu, P.; Peng, J.; Shi, C.; Liu, J. Adjustment of measurements with multiplicative errors: Error analysis, estimates of the variance of unit weight, and effect on volume estimation from LiDAR-type digital elevation models. Sensors 2014, 14, 1249–1266. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Yu, D. Virtual observation method to ill-posed total least squares problem. Acta Geod. Cartogr. Sin. 2014, 43, 575–581. [Google Scholar]
- Xu, P. Truncated SVD methods for discrete linear ill-posed problems. Geophys. J. Int. 1998, 135, 505–514. [Google Scholar] [CrossRef]
- Koch, K.R.; Kusche, J. Regularization of geopotential determination from satellite data by variance components. J. Geod. 2002, 76, 259–268. [Google Scholar] [CrossRef]
- Hoerl, A.E.; Kennard, R.W. Ridge regression: Biased estimation for nonorthogonal problems. Technometrics 1970, 12, 55–67. [Google Scholar] [CrossRef]
- Wang, L.; Chen, T. Virtual Observation Iteration Solution and A-Optimal Design Method for Ill-Posed Mixed Additive and Multiplicative Random Error Model in Geodetic Measurement. J. Surv. Eng. 2021, 147, 04021016. [Google Scholar] [CrossRef]
- Du, S.; Zheng, N.; Ying, S.; Liu, J. Affine iterative closest point algorithm for point set registration. Pattern Recognit. Lett. 2010, 31, 791–799. [Google Scholar] [CrossRef]
- Li, P.; Wang, R.; Wang, Y.; Tao, W. Evaluation of the ICP algorithm in 3D point cloud registration. IEEE Access 2020, 8, 68030–68048. [Google Scholar] [CrossRef]
- Pomerleau, F.; Colas, F.; Siegwart, R.; Magnenat, S. Comparing ICP variants on real-world data sets. Auton. Robot. 2013, 34, 133–148. [Google Scholar] [CrossRef]
- Deakin, R.E. A note on the Bursa-Wolf and Molodensky-Badekas Transformations; School of Mathematical and Geospatial Sciences, RMIT University: Melbourne, VIC, Australia, 2006; pp. 1–21. [Google Scholar]
- Golub, G.H.; Van Loan, C.F. An analysis of the total least squares problem. SIAM J. Numer. Anal. 1980, 17, 883–893. [Google Scholar] [CrossRef]
- Oktaba, W. Tests of Hypotheses for the General Gauss-Markov Model. Biom. J. 1984, 26, 415–424. [Google Scholar] [CrossRef]
- Jeng, F.C.; Woods, J.W. Compound Gauss-Markov random fields for image estimation. IEEE Trans. Signal Processing 1991, 39, 683–697. [Google Scholar] [CrossRef]
- Shi, Y.; Xu, P. Adjustment of measurements with multiplicative random errors and trends. IEEE Geosci. Remote Sens. Lett. 2020, 18, 1916–1920. [Google Scholar] [CrossRef]
- Davidon, W.C. New least-square algorithms. J. Optim. Theory Appl. 1976, 18, 187–197. [Google Scholar] [CrossRef]
- Heyde, C.C. Quasi-Likelihood and Its Application: A General Approach to Optimal Parameter Estimation; Springer: New York, NY, USA, 1997; pp. 32–69. [Google Scholar]
- Gregor, J.; Fessler, J.A. Comparison of SIRT and SQS for regularized weighted least squares image reconstruction. IEEE Trans. Comput. Imaging 2015, 1, 44–55. [Google Scholar] [CrossRef]
- Hansen, P.C. Analysis of discrete ill-posed problems by means of the L-curve. SIAM Rev. 1992, 34, 561–580. [Google Scholar] [CrossRef]
- Vogel, C.R. Non-convergence of the L-curve regularization parameter selection method. Inverse Probl. 1996, 12, 535. [Google Scholar] [CrossRef]
- Wang, L.; Chen, T.; Zou, C. Weighted least squares regularization iteration solution and precision estimation for ill-posed multiplicative error mode. Acta Geod. Cartogr. Sin. 2021, 50, 589–599. [Google Scholar]
- Xu, P.; Shi, Y.; Peng, J.; Liu, J.; Shi, C. Adjustment of geodetic measurements with mixed multiplicative and additive random errors. J. Geod. 2013, 87, 629–643. [Google Scholar] [CrossRef]
- Shi, Y.; Xu, P. Comparing the estimates of the variance of unit weight in multiplicative error models. Acta Geod. Geophys. 2015, 50, 353–363. [Google Scholar] [CrossRef][Green Version]
- Hill, C.A.; Harris, M.; Ridley, K.D.; Jakeman, E.; Lutzmann, P. Lidar frequency modulation vibrometry in the presence of speckle. Appl. Opt. 2003, 42, 1091–1100. [Google Scholar] [CrossRef] [PubMed]
- Leigh, C.L.; Kidner, D.B.; Thomas, M.C. The use of LiDAR in digital surface modelling: Issues and errors. Trans. GIS. 2009, 13, 345–361. [Google Scholar] [CrossRef]
- Hladik, C.; Alber, M. Accuracy assessment and correction of a LIDAR-derived salt marsh digital elevation model. Remote Sens. Env. 2012, 121, 224–235. [Google Scholar] [CrossRef]
- Jia, C.; Jin, Z.; Yang, P.; Tang, Z. Stability analysis on landslide in section K181 + 840 ~ K182 + 040 of Lin − Da Highway. J. Lanzhou Petrochem. Polytech. 2018, 18, 26–28. [Google Scholar]
- Jia, X.; Yin, X.; Ren, Y.; Fu, Z. Climate change of Linxia of Gansu Province in recent 43 years. J. Arid Meteorol. 2012, 30, 249–254. [Google Scholar]
- Leica ScanStation P50—Long Range 3D Terrestrial Laser Scanner. Available online: https://leica-geosystems.com/products/laser-scanners/scanners/leica-scanstation-p50 (accessed on 3 June 2022).
- Leica TS30 Champion’s League. Available online: https://www.bandwork.my/product/pdf/731201461738PMTS30_Brochure_en.pdf (accessed on 3 June 2022).
- Kobler, A.; Pfeifer, N.; Ogrinc, P.; Todorovski, L.; Oštir, K.; Džeroski, S. Repetitive interpolation: A robust algorithm for DTM generation from Aerial Laser Scanner Data in forested terrain. Remote Sens. Environ. 2007, 108, 9–23. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).