An Optimal Transport Based Global Similarity Index for Remote Sensing Products Comparison
Abstract
:1. Introduction
2. Related Works
- (i)
- Category information contained in multi-source raster datasets is treated as a probability distribution of spatial information in a 2D space, and then the problem of consistency measurement between remote sensing products is converted into a measurement question of probability distribution.
- (ii)
- A max-sliced Wasserstein distance-based similarity index is designed and calculated, which could solve the product comparison problem in the case of misregistration.
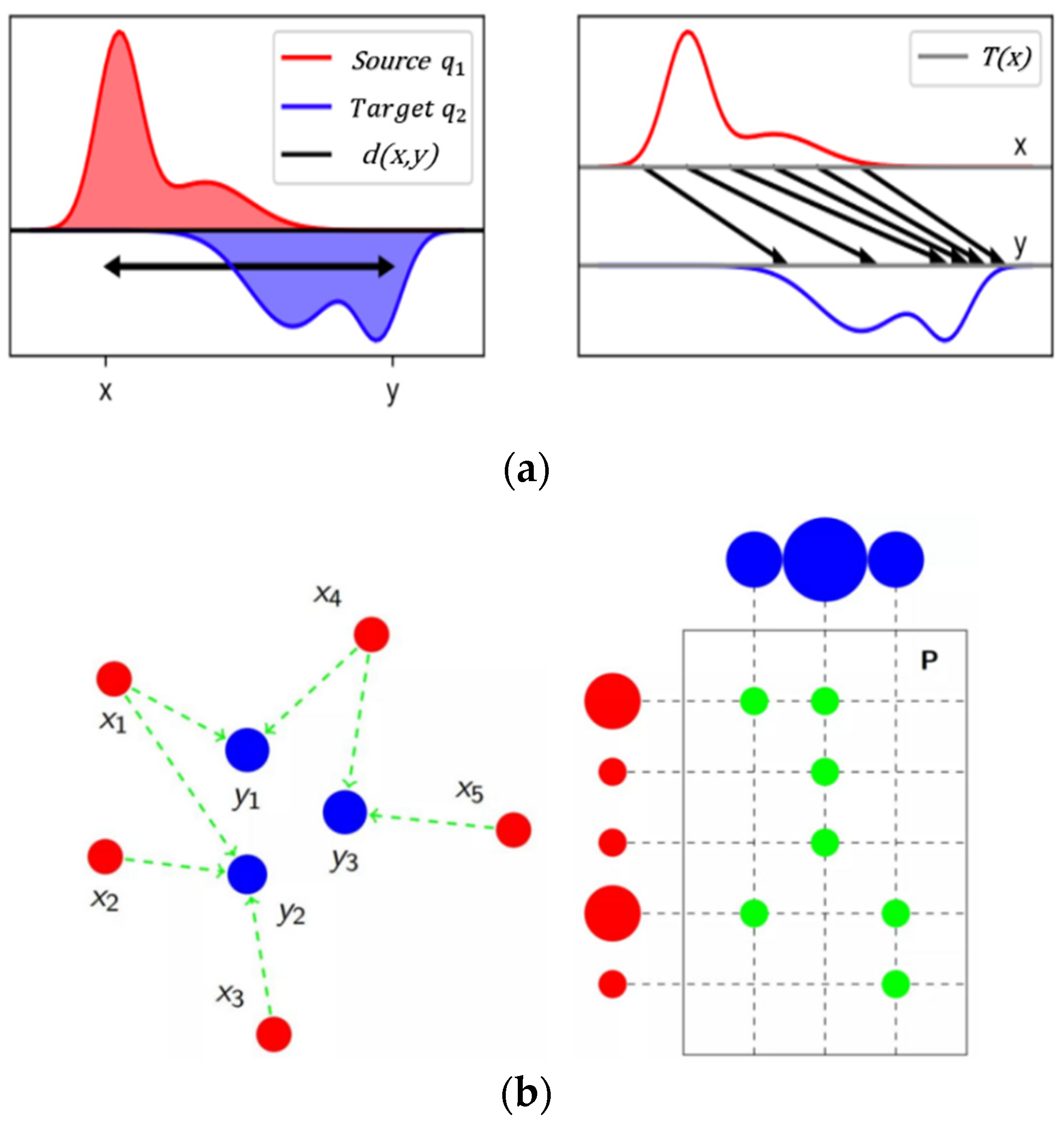
3. Methodology
4. Experiment
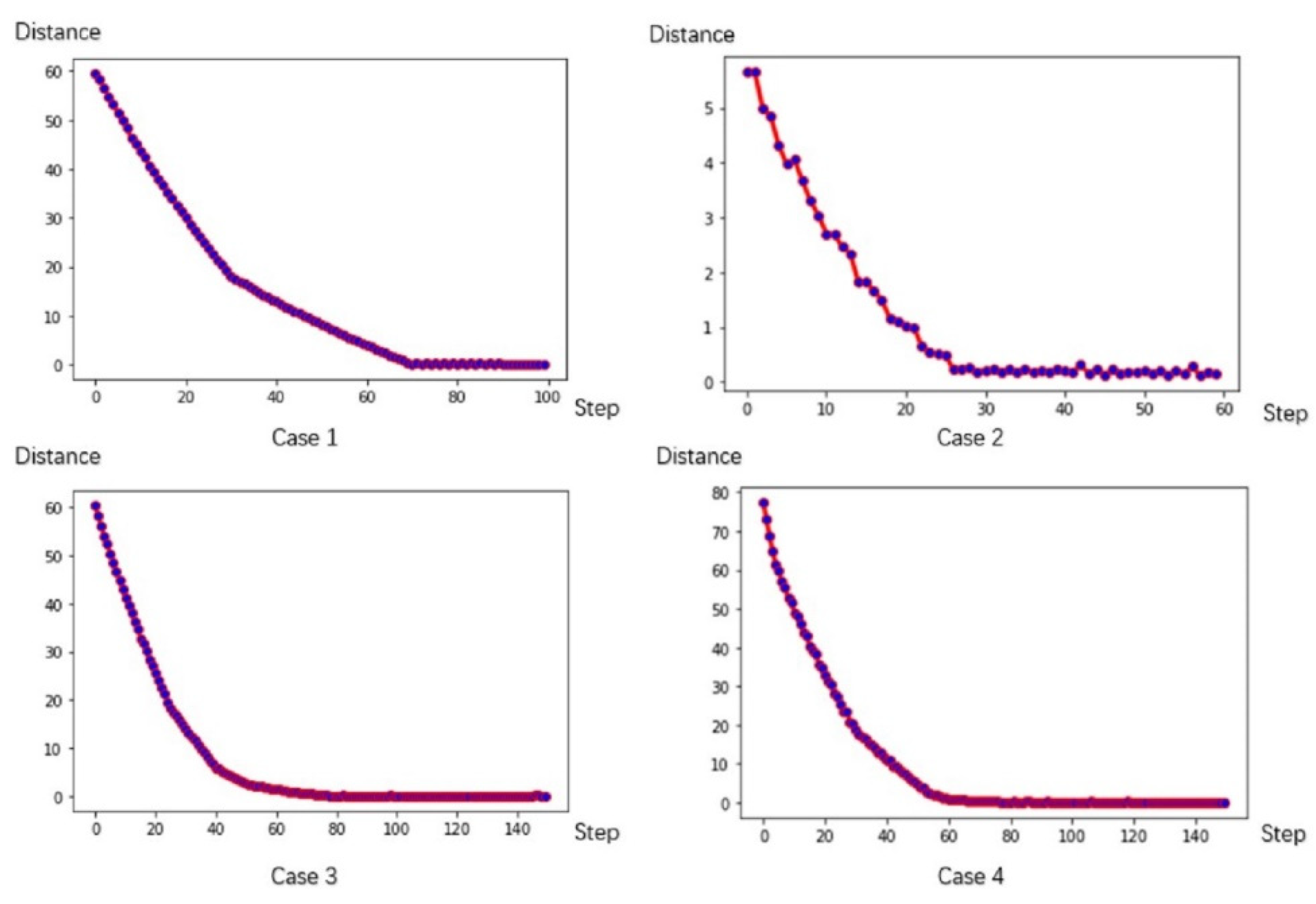
4.1. Experiments on Test Datasets
- (i)
- Max-sliced Wasserstein distance between two points
- (ii)
- Max-sliced Wasserstein distance between areas
4.2. Experiments on Real Remote Sensing Products
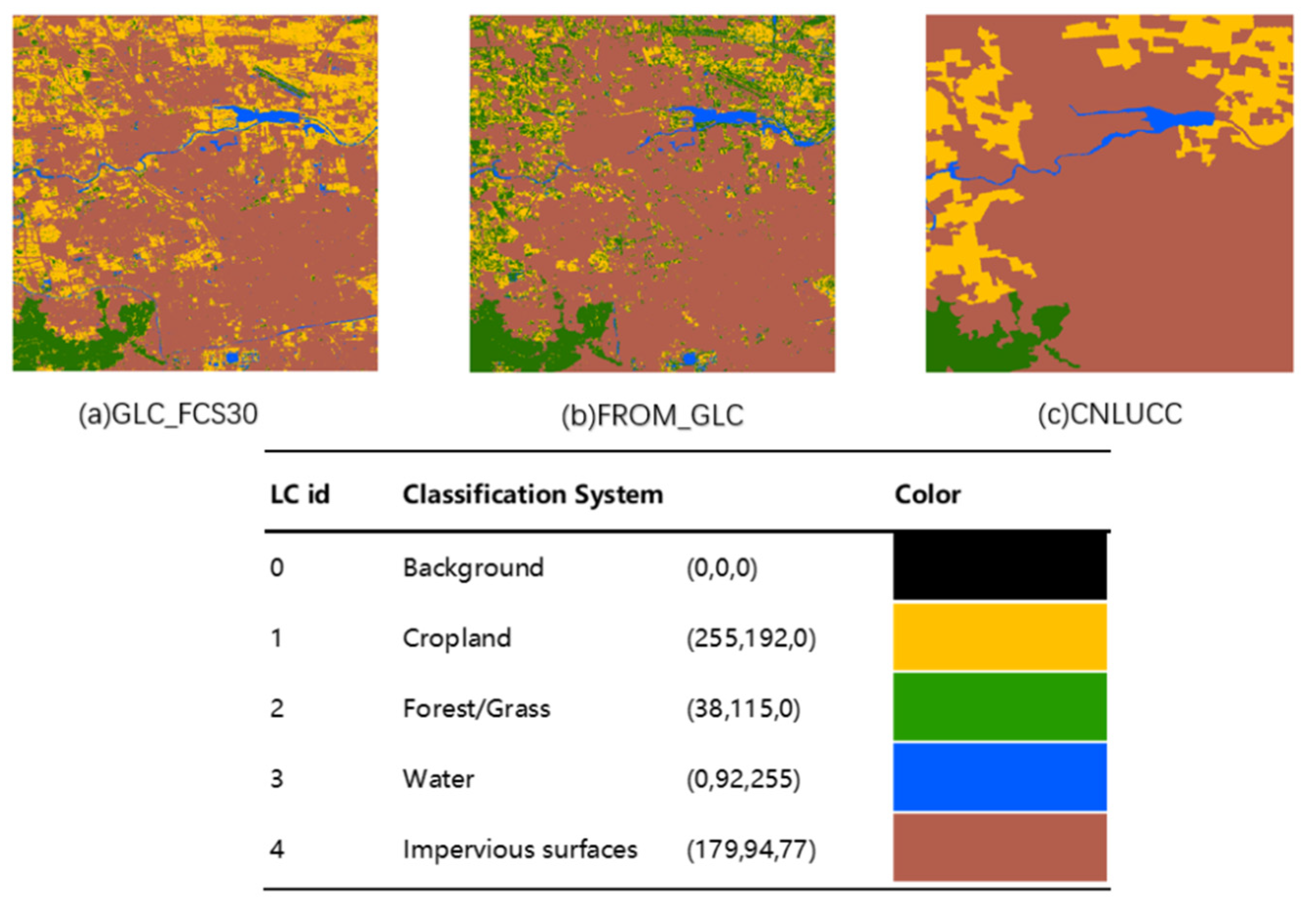
4.2.1. Dataset Preprocessing
4.2.2. Similarity Calculation
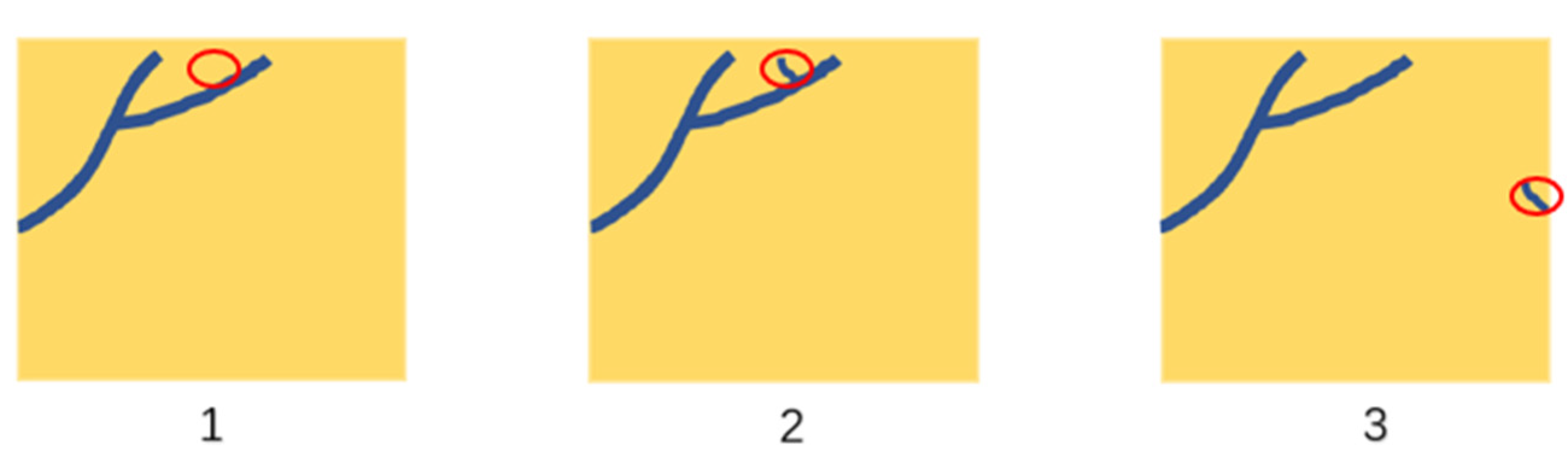
4.2.3. Comparison in Unregistered Case
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hansen, M.C.; Reed, B. A comparison of the IGBP DISCover and University of Maryland 1 km global land cover products. Int. J. Remote Sens. 2000, 21, 1365–1373. [Google Scholar] [CrossRef]
- Zhu, Z.; Waller, E. Global forest cover mapping for the United Nations Food and Agriculture Organization forest resources assessment 2000 program. For. Sci. 2003, 49, 369–380. [Google Scholar]
- Stehman, S.V. Sampling designs for accuracy assessment of land cover. Int. J. Remote Sens. 2009, 30, 5243–5272. [Google Scholar] [CrossRef]
- Visser, H.; Nijs, T.D. The Map Comparison Kit. Environ. Model. Softw. 2006, 21, 346–358. [Google Scholar] [CrossRef]
- Ma, Z.; Redmond, R.L. Tau coefficients for accuracy assessment of classification of remote sensing data. Photogramm. Eng. Remote Sens. 1995, 61, 435–439. [Google Scholar]
- Pontius, R., Jr.; Huffaker, D.; Denman, K. Useful techniques of validation for spatially explicit land-change models. Ecol. Model. 2004, 179, 445–461. [Google Scholar] [CrossRef]
- Rees, W.G. Comparing the spatial content of thematic maps. Int. J. Remote Sens. 2008, 29, 3833–3844. [Google Scholar] [CrossRef]
- Wu, B.; Zhang, L.; Zhao, Y. Feature selection via Cramer’s V-test discretization for remote-sensing image classification. IEEE Trans. Geosci. Remote Sens. 2013, 52, 2593–2606. [Google Scholar] [CrossRef]
- Ohana-Levi, N.; Gao, F.; Knipper, K.; Kustas, W.P.; Anderson, M.C.; del Mar Alsina, M.; Sanchez, L.A.; Karnieli, A. Time-series clustering of remote sensing retrievals for defining management zones in a vineyard. Irrig. Sci. 2021, 1–15. [Google Scholar] [CrossRef]
- Hagen-Zanker, A. Map comparison methods that simultaneously address overlap and structure. J. Geogr. Syst. 2006, 8, 165–185. [Google Scholar] [CrossRef]
- San-Miguel-Ayanz, G.H. Conventional and fuzzy comparisons of large scale land cover products: Application to CORINE, GLC2000, MODIS and GlobCover in Europe. ISPRS J. Photogramm. Remote Sens. 2012, 74, 185–201. [Google Scholar]
- Dou, W.; Ren, Y.; Wu, Q.; Ruan, S.; Chen, Y.; Bloyet, D.; Constans, J.M. Fuzzy kappa for the agreement measure of fuzzy classifications. Neurocomputing 2007, 70, 726–734. [Google Scholar] [CrossRef] [Green Version]
- Hargrove, W.W.; Hoffman, F.M.; Hessburg, P.F. Mapcurves: A quantitative method for comparing categorical maps. J. Geogr. Syst. 2006, 8, 187. [Google Scholar] [CrossRef]
- White, R. Pattern based map comparisons. J. Geogr. Syst. 2006, 8, 145–164. [Google Scholar] [CrossRef]
- Zhu, D.; Chen, T.; Wang, Z.; Niu, R. Detecting ecological spatial-temporal changes by remote sensing ecological index with local adaptability. J. Environ. Manag. 2021, 299, 113655. [Google Scholar] [CrossRef]
- Giri, C.; Zhu, Z.; Reed, B. A comparative analysis of the Global Land Cover 2000 and MODIS land cover data sets. Remote Sens. Environ. 2005, 94, 123–132. [Google Scholar] [CrossRef]
- Strahler, A.H.; Boschetti, L.; Foody, G.M.; Friedl, M.A.; Hansen, M.C.; Herold, M.; Mayaux, P.; Morisette, J.T.; Stehman, S.V.; Woodcock, C.E. Global Land Cover Validation: Recommendations for Evaluation and Accuracy Assessment of Global Land Cover Maps. Eur. Communities Luxemb. 2006, 51, 1–60. [Google Scholar]
- Foody, G.M. Assessing the accuracy of land cover change with imperfect ground reference data. Remote Sens. Environ. 2010, 114, 2271–2285. [Google Scholar] [CrossRef] [Green Version]
- Foody, G.M. Explaining the unsuitability of the kappa coefficient in the assessment and comparison of the accuracy of thematic maps obtained by image classification. Remote Sens. Environ. 2020, 239, 111630. [Google Scholar] [CrossRef]
- Enøe, C.; Georgiadis, M.P.; Johnson, W.O. Estimation of sensitivity and specificity of diagnostic tests and disease prevalence when the true disease state is unknown. Prev. Vet. Med. 2000, 45, 61–81. [Google Scholar] [CrossRef]
- Wu, X.; Naegeli, K.; Wunderle, S. Geometric accuracy assessment of coarse-resolution satellite datasets: A study based on AVHRR GAC data at the sub-pixel level. Earth Syst. Sci. Data 2020, 12, 539–553. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Skau, E.; Krim, H.; Cervone, G. Fusing heterogeneous data: A case for remote sensing and social media. IEEE Trans. Geosci. Remote Sens. 2018, 56, 6956–6968. [Google Scholar] [CrossRef]
- Tardy, B.; Inglada, J.; Michel, J. Assessment of optimal transport for operational land-cover mapping using high-resolution satellite images time series without reference data of the mapping period. Remote Sens. 2019, 11, 1047. [Google Scholar] [CrossRef] [Green Version]
- Deshpande, I.; Hu, Y.T.; Sun, R.; Pyrros, A.; Schwing, A. Max-Sliced Wasserstein Distance and its use for GANs. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision Workshop, Seoul, Korea, 27–28 October 2019; pp. 10648–10656. [Google Scholar]
- Gulrajani, I.; Ahmed, F.; Arjovsky, M.; Dumoulin, V.; Courville, A. Improved training of wasserstein gans. arXiv Prepr. 2017, arXiv:1704.00028. [Google Scholar]
- Kolouri, S.; Rohde, G.K.; Hoffmann, H. Sliced wasserstein distance for learning gaussian mixture models. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 3427–3436. [Google Scholar]
- Kolouri, S.; Park, S.R.; Rohde, G.K. The radon cumulative distribution transform and its application to image classification. IEEE Trans. Image Processing 2015, 25, 920–934. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, L.; Chen, X.; Gao, Y.; Xie, S.; Mi, J. GLC_FCS30: Global land-cover product with fine classification system at 30 m using time-series Landsat imagery. Earth Syst. Sci. Data 2021, 13, 2753–2776. [Google Scholar] [CrossRef]
- Gong, P.; Wang, J.; Yu, L.; Zhao, Y.; Chen, J. Finer resolution observation and monitoring of global land cover: First mapping results with Landsat TM and ETM+ data. Int. J. Remote Sens. 2013, 34, 48. [Google Scholar] [CrossRef] [Green Version]
- Xu, X.; Liu, J.; Zhang, S.; Li, R.; Yan, C.; Wu, S. China’s Multi-Period Land Use Land Cover Remote Sensing Monitoring Data Set (CNLUCC); Resource and Environment Data Cloud Platform: Beijing, China, 2018. [Google Scholar]





| Comparison Methods | Processing Unit | Qualitative/Quantitative | Evaluating Indicator | Attention Scale | |
|---|---|---|---|---|---|
| Error Matrix-based methods | Pixel-by-pixel based Statistical method [3,4,5] | pixel | qualitative | OA, UA, PA, kappa coefficient, information entropy, etc. | Local scale |
| quantitative | Mean, standard deviation, entropy, correlation coefficient, Tau coefficient, etc. | ||||
| Quantity and location-based method [6] | qualitative | Location-based kappa coefficient, quantity-based kappa coefficient, etc. | |||
| local spatial feature-based methods | Spatial distribution-based method [7,8,9] | category | qualitative | Goodman–Kruskal Cramér’s V statistics Theil’s U statistics | Global scale |
| Neighborhood-based comparison method [10] | Spatial structure and overlap index | ||||
| Other methods | Fuzzy comparison [11,12] | pixel and category | qualitative | Fuzzy Kappa coefficient fuzzy similarity index. | Specific scope |
| Curvature-fit based method [13,14] | category | Polygon matching index | Specific scope | ||
| Sliding-window based method [15] | sliding window | quantitative | Euclidean distance, correlation coefficient | ||
| Number of projections | 5 | 10 | 15 | 20 |
| Max-Wasserstein distance | 4.9700 | 4.9961 | 4.9970 | 4.9994 |
| Difference | 0.6% | 0.078% | 0.06% | 0.012% |
| Case. | Distribution | Centroid | Radius/Side Length | |||
|---|---|---|---|---|---|---|
| A | B | A | B | A | B | |
| 1 | Circle | Circle | (160,160) | (220,160) | 60 | 60 |
| 2 | Circle | Square | (160,160) | (160,160) | 60 | 60 |
| 3 | Circle | Square | (160,160) | (220,160) | 60 | 60 |
| 4 | 3 Circles | Circle | (70,70),(70,250),(250,70) | (160,160) | 50 | 60 |
| Case | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| Distance | 59.9964 | 5.6467 | 61.2305 | 77.3263 |
| Cropland | Forest/Grass | Water | Impervious Surfaces | Total | |
|---|---|---|---|---|---|
| GLC_FCS30 | 123,957 | 39,076 | 12,966 | 370,771 | 546,770 |
| FROM_GLC | 73,795 | 92,438 | 11,936 | 368,601 | 546,770 |
| CNLUCC | 95,176 | 26,149 | 8522 | 416,923 | 546,770 |
| Distance | Row × Col | Similarity | |
|---|---|---|---|
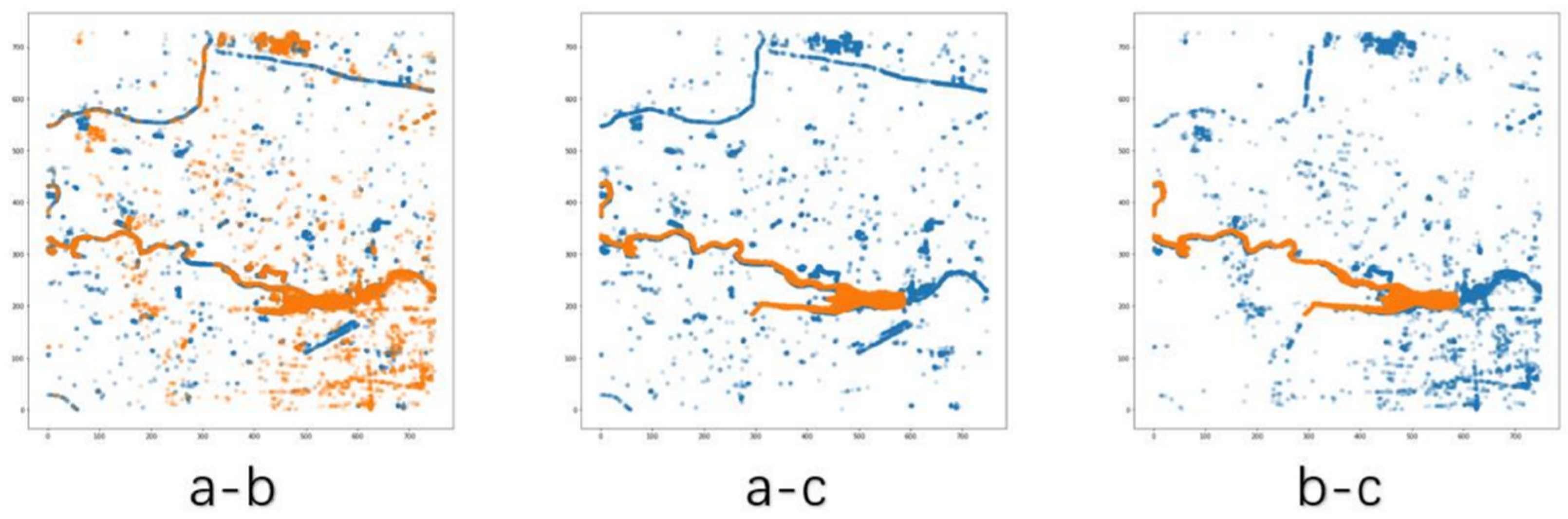
| a-b | 86.9853 | 749 × 730 | 91.49% |
| a-c | 180.1471 | 749 × 730 | 82.43% |
| b-c | 153.8637 | 749 × 730 | 85.01% |
| a-b | a-c | b-c | ||
|---|---|---|---|---|
| Cropland | Distance | 26.9367 | 93.0022 | 71.9183 |
| Similarity | 96.85% | 88.88% | 91.87% | |
| Forest/Grass | Distance | 232.7238 | 260.1100 | 423.1698 |
| Similarity | 74.71% | 72.11% | 54.62% | |
| Water | Distance | 86.9853 | 180.1471 | 153.8637 |
| Similarity | 91.49% | 82.43% | 85.01% | |
| Impervious | Distance | 13.4117 | 9.71133 | 15.3557 |
| surfaces | Similarity | 96.04% | 96.68% | 94.79% |
| Total Similarity | 93.51% | 96.89% | 89.80% |
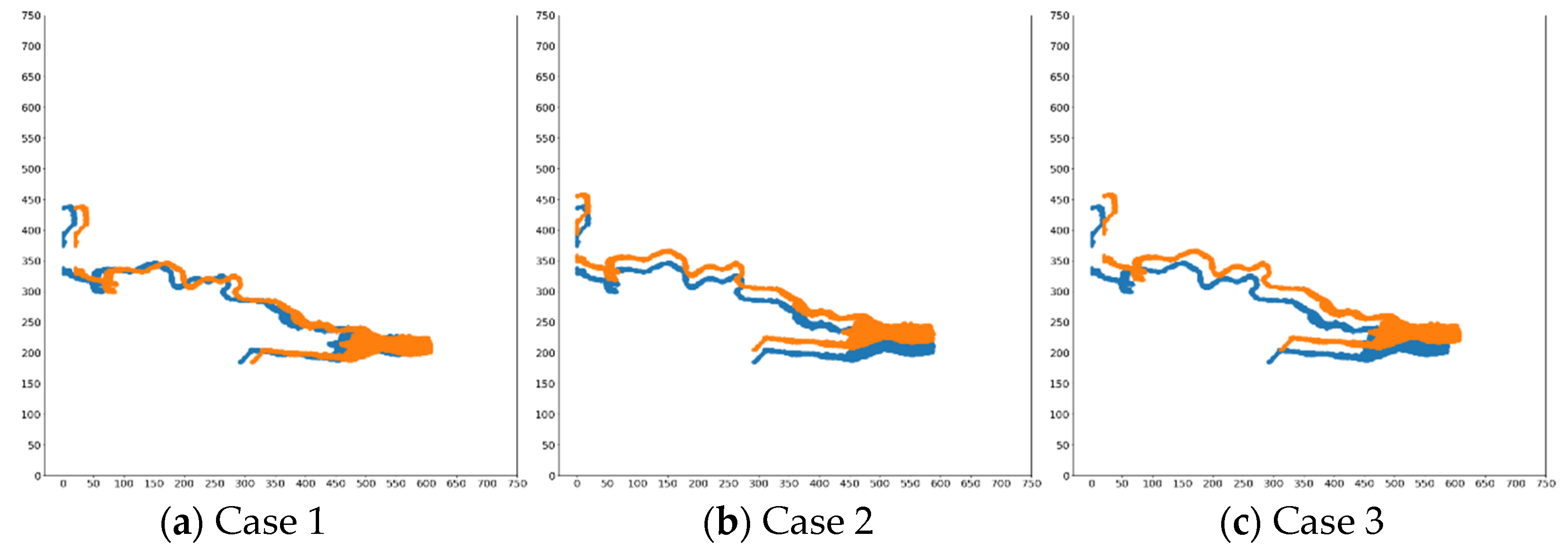
| Offset Pixel | Case 1 | Case 2 | Case 3 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Similarity | Kappa | IoU | Similarity | Kappa | IoU | Similarity | Kappa | IoU | |
| 1 | 0.9990 | 0.9460 | 0.8991 | 0.999 | 0.8961 | 0.8143 | 0.9986 | 0.8717 | 0.7756 |
| 2 | 0.9981 | 0.8963 | 0.8147 | 0.9981 | 0.7971 | 0.6669 | 0.9973 | 0.7572 | 0.6140 |
| 3 | 0.9971 | 0.8526 | 0.7465 | 0.9971 | 0.7075 | 0.5527 | 0.9959 | 0.6587 | 0.4969 |
| 4 | 0.9962 | 0.8129 | 0.6889 | 0.9961 | 0.6312 | 0.4672 | 0.9945 | 0.5796 | 0.4144 |
| 5 | 0.9952 | 0.7777 | 0.6407 | 0.9951 | 0.5715 | 0.4065 | 0.9931 | 0.5217 | 0.3596 |
| 6 | 0.9942 | 0.7470 | 0.6011 | 0.9942 | 0.5257 | 0.3632 | 0.9918 | 0.4779 | 0.3208 |
| 7 | 0.9933 | 0.7195 | 0.5671 | 0.9932 | 0.4897 | 0.3310 | 0.9904 | 0.4438 | 0.2922 |
| 8 | 0.9923 | 0.6940 | 0.5369 | 0.9922 | 0.4599 | 0.3056 | 0.989 | 0.416 | 0.2698 |
| 9 | 0.9913 | 0.6711 | 0.5107 | 0.9913 | 0.4349 | 0.2849 | 0.9877 | 0.391 | 0.2502 |
| 10 | 0.9904 | 0.6499 | 0.4873 | 0.9903 | 0.4127 | 0.2671 | 0.9863 | 0.3671 | 0.2320 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tan, Y.; Shi, Y.; Xu, L.; Zhou, K.; Jing, G.; Wang, X.; Bai, B. An Optimal Transport Based Global Similarity Index for Remote Sensing Products Comparison. Remote Sens. 2022, 14, 2546. https://doi.org/10.3390/rs14112546
Tan Y, Shi Y, Xu L, Zhou K, Jing G, Wang X, Bai B. An Optimal Transport Based Global Similarity Index for Remote Sensing Products Comparison. Remote Sensing. 2022; 14(11):2546. https://doi.org/10.3390/rs14112546
Chicago/Turabian StyleTan, Yumin, Yanzhe Shi, Le Xu, Kailei Zhou, Guifei Jing, Xiaolu Wang, and Bingxin Bai. 2022. "An Optimal Transport Based Global Similarity Index for Remote Sensing Products Comparison" Remote Sensing 14, no. 11: 2546. https://doi.org/10.3390/rs14112546
APA StyleTan, Y., Shi, Y., Xu, L., Zhou, K., Jing, G., Wang, X., & Bai, B. (2022). An Optimal Transport Based Global Similarity Index for Remote Sensing Products Comparison. Remote Sensing, 14(11), 2546. https://doi.org/10.3390/rs14112546






